Statistical methods for estimating the cumulative risk of screening mammography outcomes

Abstract

Background

This study illustrates alternative statistical methods for estimating cumulative risk of screening mammography outcomes in longitudinal studies.

Methods

Data from the U.S. Breast Cancer Surveillance Consortium (BCSC) and the Nijmegen Breast Cancer Screening Program in the Netherlands were used to compare four statistical approaches to estimating cumulative risk. We estimated cumulative risk of false-positive recall and screen-detected cancer after 10 screening rounds using data from 242,835 women aged 40-74 years screened at BCSC facilities in 1993-2012 and from 17,297 women aged 50-74 years screened in Nijmegen in 1990-2012.

Results

In the BCSC cohort a censoring bias model estimated bounds of 53.8-59.3% for false-positive recall and 2.4-7.6% for screen-detected cancer, assuming 10% increased or decreased risk among women screened for one additional round. In the Nijmegen cohort, false-positive recall appeared to be associated with subsequent discontinuation of screening leading to over estimation of risk of a false-positive recall based on adjusted discrete-time survival models. Bounds estimated by the censoring bias model were 11.0-19.9% for false-positive recall and 4.2-9.7% for screen-detected cancer.

Conclusion

Choice of statistical methodology can substantially affect cumulative risk estimates. The censoring bias model is appropriate under a variety of censoring mechanisms and provides bounds for cumulative risk estimates under varying degrees of dependent censoring.

Impact

This paper illustrates statistical methods for estimating cumulative risks of cancer screening outcomes, which will be increasingly important as screening test recommendations proliferate.

Introduction

Although the benefits of screening mammography have been established in clinical trials (1-3), uncertainty remains regarding the absolute magnitude of this benefit as well as its relative magnitude in relation to harms. Ongoing evaluation of the harms and benefits of screening mammography is needed as mammography performance and subsequent diagnostic evaluation and treatment evolve. Many of the harms and benefits of screening mammography can be estimated using observational data from routine screening. In the US where population-based national screening programs do not exist, investigators have evaluated the performance of repeat mammography according to screening guidelines using data from registries or healthcare systems (4-6). In Australia and European countries with defined cancer screening programs, outcomes of these programs have been evaluated using data from screening centers (7-13). Although most of these investigations have focused on the cumulative risks of a false-positive mammography result, cumulative risks of other screening outcomes including screen-detected cancers and interval cancers can also be estimated.

Prior research on statistical methods for estimating cumulative risk of screening mammography outcomes has focused on data from the US (14-17). Appropriate approaches for use in other settings may vary. For instance, in the US the choice of screening interval is largely an individual decision made by patients in consultation with their medical providers, while in many European nations with organized screening programs, screening interval is determined at the level of the program. These differences in the organization and delivery of screening mammography may give rise to differences in patterns of screening frequency and discontinuation of screening that affect the choice of statistical methodology.

The objective of this study is to provide guidance on appropriate statistical methodology for estimating the spectrum of cancer screening outcomes over the course of a series of repeat mammograms with a specific focus on considerations that may vary across screening settings. We review alternative censoring mechanisms and appropriate methods in the presence of each mechanism, noting where considerations may differ across outcomes or settings. Using data collected by the Breast Cancer Surveillance Consortium (BCSC) in the US and the Nijmegen Breast Cancer Screening Program in the Netherlands we compare and contrast results using alternative statistical approaches to estimating the cumulative risks of a false-positive result or a screen-detected cancer after 10 rounds of screening.

Materials and Methods

Estimating cumulative risk of screening outcomes

A common approach to assessing mammography outcomes after a specified number of screening rounds is to estimate the cumulative risk, i.e., the probability that a woman experiences the outcome of interest at least once during the course of a specified number of screens. Outcomes of interest include false-positive results, screen-detected cancers, and interval cancers. False-positive results can be further sub-divided into false-positive recalls, in which the woman is recalled for diagnostic evaluation involving imaging only, and complex or invasive false-positives in which the woman undergoes diagnostic evaluation requiring pathological evaluation of a tissue sample. The discrete-time survival model (18) provides a fundamental tool for estimating cumulative risks. This approach assumes that the risk of experiencing the outcome at a given screening round is independent of the “censoring time” defined as the number of screening rounds an individual is observed to attend.

Because this assumption was found to be violated in the case of cumulative risk of false-positive results in the US (14, 16), adjusted discrete-time survival approaches accounting for dependence between outcome risk at a given round and censoring time have been proposed. The discrete-time survival model adjusted for censoring round estimates cumulative risk assuming that, had they continued to be observed, the probability of the outcome following censoring would have remained the same as that observed prior to censoring (14). For false-positive results, this approach fails to account for differences in risk of a false-positive result across screening rounds, especially between the first and subsequent screening rounds. To overcome this limitation, the discrete-time survival model adjusted for censoring round and screening round was proposed (16). This approach estimates risk at each round using a regression model dependent on censoring time and screening round. The increase in odds associated with a given censoring time is assumed constant across screening rounds. Both of these adjusted discrete-time survival approaches rely on the assumption that risk following censoring resembles risk prior to censoring.

An alternative, the censoring bias model, assumes that risk following censoring resembles risk among uncensored individuals with some inflation or deflation factor (the censoring bias parameter) to account for systematic differences between censored and uncensored individuals (17). For outcomes such as false-positive results where it is possible to continue observing screening for an individual after an event has occurred, the censoring bias parameter can be estimated. When an event always ends the observation period, as is the case for cancer diagnosis outcomes, it is not possible to estimate the censoring bias parameter; however, the sensitivity of the results to dependent censoring can be explored by estimating cumulative risk across a range of plausible censoring bias parameter values.

Additional methods details and formulas for each of the four methods are provided in the Supplementary Methods.

Causes of censoring

There are a number of reasons that an individual may not be observed across all screening rounds of interest, giving rise to censored data. Under independent censoring, these causes are unrelated to the outcome of interest. For example, the study period may end before all participants have completed all screening rounds. Contrastingly, in the case of dependent censoring, the reason for incomplete observation is associated with the outcome. For example, women with a family history of breast cancer might be more adherent to screening and at higher risk of a false-positive result and screen-detected cancer, inducing dependence between the number of screening rounds a woman participates in and her outcome risk at each round. Statistical methods must be selected that appropriately account for the relationship between the outcome and the censoring time.

Table 1 summarizes the considerations discussed in this section for choice of statistical methodology.

Table 1.

Summary of recommended statistical methods by cause of censoring and screening outcome.

Cause of censoring	Outcome	Method
Observed covariate	False-positive, Recall, Screen- detected cancer, Interval cancer	Discrete-time survival model stratification or regression adjustment for covariates associated with censoring
Unobserved covariate	False-positive, Recall, Screen- detected cancer, Interval cancer	Censoring bias models allow exploration of sensitivity to dependent censoring attributable to unobserved covariates. Likely to be more problematic in ad hoc screening where patient characteristics play a greater role in screening frequency and duration than organized screening programs.
Competing event	False-positive, Recall, Screen- detected cancer, Interval cancer	Discrete-time survival adjusted for censoring time and cause of censoring.
Event of interest	False-positive, Recall	Censoring bias model. Adjustment for censoring time or estimation of censoring bias parameter will induce bias and should not be used.
	Screen-detected cancer, Interval cancer	Discrete-time survival model. Censoring bias model if dependent censoring is suspected.

Dependent censoring due to covariate dependence

The standard discrete-time survival model relies on the assumption of independent censoring (15). When this assumption does not hold but censoring time is only associated with outcome risk through common dependence on a set of observed covariates, conditioning on covariates through stratification or regression adjustment achieves conditional independence of censoring times and outcome risk, satisfying the independent censoring assumption. For false-positive results, where censoring time is always observed regardless of prior occurrence of a false-positive result, it is possible to test the assumption of independence of event and censoring times after adjusting for covariates using a regression approach (16). For instance, this was the case in a study of screen-detected breast cancer risk in the Spanish screening program where conditioning on age was sufficient to address dependent censoring (19). Conversely, conditioning on observed covariates was not found to sufficiently account for dependent censoring in a study of false-positive results in the US (16). Regression adjustment can be incorporated into all of the methods described in this paper.

Dependent censoring due to competing events

We next consider the case where censoring arises due to occurrence of competing events. For instance, when the outcome of interest is interval cancer, observation will be terminated if a screen-detected cancer is diagnosed. If screen-detected cancer and interval cancer share common risk factors this will induce dependence between interval cancer risk and censoring round. Similarly, false-positive results and breast cancer diagnosis share many of the same risk factors including breast density and age (5-9). This induces dependent censoring of false-positive results by cancer outcomes. In this case, risk at each round should ideally be estimated adjusting for both censoring time and cause of censoring. In practice, this may be impractical since the number of individuals censored by some causes, for instance due to interval cancer diagnosis, is likely to be very small. From a practical perspective, if certain causes of censoring are very rare it may be unnecessary to construct separate estimates simply because the number of individuals experiencing the competing event is small enough that they have no meaningful impact on risk estimates.

In addition to considering the effect of competing events on censoring time, it is also necessary to determine whether cumulative risk should be estimated in the presence or absence of competing events. Typical survival models that censor at the time of a competing event estimate the latent risk of the outcome of interest had the competing event not occurred. The alternative analysis accounting for competing events estimates the probability of experiencing the outcome of interest without positing the absence of the competing event. In effect, censoring at the time of a competing event removes individuals that experience a competing event from the denominator, computing risk only among the population that does not experience a competing event. Accounting for the presence of competing risks retains this population in the denominator, providing an estimate of the probability of the outcome of interest in the total screened population. All four of the statistical methods considered here can be used to estimate cumulative risks accounting for competing events. Methods details for estimating cumulative risk under competing events are provided in the Supplementary Methods Section S1.6.

Censoring due to event of interest

Finally, we consider the case where the event of interest causes discontinuation of screening. This will always be the case when the event of interest is a cancer diagnosis because subsequent screening in individuals with a prior cancer diagnosis is considered to be surveillance, at least for some time period after treatment. Discontinuation of screening due to the event of interest could also arise in the case of false-positive results if individuals lose confidence in the screening program and decide not to return for future screening. When the outcome itself leads to censoring, risk will be elevated in the last round attended. Graphical examination of risk as a function of screening round, stratified by censoring time, will reveal a distinctive pattern in which risk is much higher in the last observed round if the event of interest tends to lead to discontinuation of screening.

In settings where the event of interest leads to an increase in the probability of discontinuation but no dependent censoring mechanisms exist, the standard discrete-time survival model can be used. This is the standard survival analysis scenario where individuals are followed only until the first of censoring or the outcome of interest. However, if dependent censoring is believed to exist in addition to the event of interest increasing the probability of discontinuing screening then alternative methods are needed. Both of the discrete-time survival methods adjusted for censoring round overestimate the cumulative risk. Conceptually this occurs because these methods impute risk following censoring with risk prior to censoring, stratified by censoring round. When the event itself causes censoring, after stratifying by censoring round, risk will always be inflated in the last round attended making this an unsuitable estimate of what risk would have been had the woman continued to screen.

The censoring bias approach accounts for dependent censoring but does not require using estimates of risk prior to censoring to impute risk after censoring. By rescaling risk among uncensored individuals to impute risk among the censored, this approach facilitates investigation of the sensitivity of estimates to departures from independent censoring. Although it is possible to estimate the censoring bias parameter for some outcomes, doing so relies on an estimate of the association between censoring and event times, which will be inflated when occurrence of the event of interest increases the probability of censoring. Thus in this setting a range of values should be investigated, rather than estimating the censoring bias parameter based on the data.

Censoring mechanisms in different screening settings

A variety of statistical approaches have been used to investigate the cumulative risk of screening outcomes for screening mammography in the US, Europe, and Australia, most often focusing on false-positive test results. The screening context in different geographic locations varies substantially and may modify the relationships between risk of the outcomes of interest, screening round, censoring round, and covariates. The statistical approach that is most appropriate in one setting may not apply in another.

European countries offer organized population-based screening, whereas in the US, decisions about when to begin screening, how frequently to screen, and when or if to discontinue screening are more strongly influenced by decision making at the woman and provider level. Prior research investigating dependent censoring has found different results in the US compared to Europe. In the US, two studies using different data sources identified dependent censoring with respect to false-positive results (14, 16) and found that this dependence persisted after adjusting for age, screening interval, calendar year, and mammography registry (16). By contrast, two studies from Denmark found no evidence of dependent censoring (9, 20). A Spanish study found that adjusting for age was sufficient to eliminate dependent censoring (19). These results suggest that accounting for dependent censoring may be more relevant in settings without population-based screening programs.

Breast Cancer Surveillance Consortium

The Breast Cancer Surveillance Consortium (BCSC) consists of a geographically diverse collection of mammography registries from across the US that collect information from community mammography facilities. This study included data from seven BCSC registries obtained from the BCSC Research Resource (21). Radiologists’ assessments and recommendations were based on the American College of Radiology’s Breast Imaging Reporting and Data System (BI-RADS) (22). Breast cancer diagnoses were obtained through linkages with pathology databases, regional Surveillance, Epidemiology, and End Results (SEER) programs, and state tumor registries. All BCSC registries and the BCSC Statistical Coordinating Center received Institutional Review Board approval for active or passive consenting processes or a waiver of consent to enroll participants, link data, and perform analysis. All procedures were Health Insurance Portability and Accountability Act compliant, and registries and the Coordinating Center received a Federal Certificate of Confidentiality and other protections for the identities of women, physicians, and facilities.

We included women receiving their first screening examination at a BCSC facility at ages 40-74 years from 1993 to 2012. A woman’s first and all subsequent examinations were included until the earliest of death, disenrollment from the healthcare system, or a discrepancy of 6 months or more between a woman’s self-reported time since last mammography and that captured by the BCSC (to ensure that women had not received mammography outside of BCSC catchment). We defined a positive mammogram as an examination with an initial BI-RADS assessment of 0, 4, or 5 or 3 when accompanied by a recommendation for immediate evaluation. A screen-detected cancer was defined as a positive mammogram followed by a diagnosis of invasive cancer or ductal carcinoma in situ (DCIS) within 12 months and prior to the next screening mammogram. A false-positive recall was defined as a positive mammogram with no cancer diagnosis within 12 months and prior to the next screening mammogram.

Nijmegen Breast Cancer Screening Program

In Nijmegen, a city in the Eastern part of the Netherlands, a breast cancer screening program was introduced in 1975. Women in the target age range of the national screening program, 50-74 years, were invited from 1989 on (23). Data on screening invitation and attendance for each woman living in Nijmegen is collected in one registry. A separate registry collects data on women diagnosed with breast cancer and living in Nijmegen. All women consented to the use of their anonymous data for scientific research.

We included all examinations for women aged 50-74 years who received a first screening examination between 1990 and 2014. Censoring occurred due to moving out of the catchment region or death. A mammogram was classified as positive if the woman was recalled for diagnostic work-up of a suspicious finding on the screening mammogram. In the Nijmegen cohort, a screen-detected cancer was defined as a positive mammogram resulting in a diagnosis of invasive cancer or DCIS at the end of all imaging or biopsy work-up. A false-positive recall was defined as a positive mammogram where diagnostic follow-up did not confirm the presence of breast cancer during the first year after screening.

Statistical analysis

For each cohort we computed empirical estimates of risk and cumulative risk at each of the first ten screening rounds, stratified by censoring round for two outcomes: false-positive recall and screen-detected cancer. Because the same analytic considerations apply to screen-detected cancers and interval cancers, we have illustrated the alternative methods only using screen-detected cancers. We estimated cumulative risk in the absence of competing events using the four statistical methods described above. For screen-detected cancers, risk conditional on censoring time is always zero in all rounds prior to the last round attended (because the event causes censoring) which precludes estimating the discrete-time survival model adjusted for censoring round and screening round. We therefore omit this estimate for screen-detected cancer. For the censoring bias model, we obtained estimates assuming that risk increased or decreased by 10% for each additional screening round attended. The choice of 10% was motivated by prior work in the BCSC which estimated the censoring bias parameter to be 4% (17). We report point estimates of cumulative risk after 10 rounds of screening and 95% confidence intervals (CI) based on 1000 bootstrap replicates.

Results

We included 242,835 women receiving 539,330 screening mammograms in the BCSC and 17,297 women receiving 58,951 screening mammograms within the Nijmegen screening program (Table 2). Women in the BCSC cohort began screening at earlier ages and were observed over fewer rounds of screening compared to those in the Nijmegen cohort.

Table 2.

Characteristics of women in screening mammography cohorts from the BCSC and Nijmegen.

	BCSC		Nijmegen
	N	(%)	N	(%)
Age at first screening round attended
40-49	172,422	71.0	0	0
50-59	40,513	16.7	16,088	93.0
60-69	22,261	9.2	984	5.7
70-74	7,639	3.1	225	1.3
Year of first screening round attended
1990-1994	9,733	4.0	159	0.9
1995-1999	86,075	35.4	2,556	14.8
2000-2004	81,931	33.7	4,317	25.0
2005-2009	53,781	22.1	6,000	34.7
≥2010	11,315	4.7	4,265	24.7
Number of screening rounds attended
1	108,015	44.5	3,915	22.6
2	45,594	18.8	2,771	16.0
3	27,718	11.4	2,183	12.6
4	18,743	7.7	2,068	12.0
5	13,328	5.5	1,641	9.5
6	9,411	3.9	1,577	9.1
7	6,774	2.8	1,314	7.6
8	4,885	2.0	1,079	6.2
9	3,210	1.3	582	3.4
≥10	5,157	2.1	167	1.0

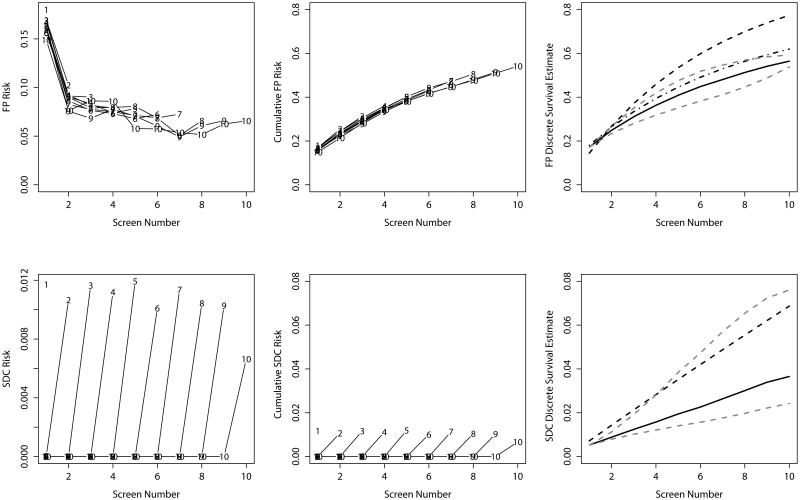
Empirical estimates of the risk of false-positive recall at each screening round in the BCSC cohort provide some suggestion of dependent censoring (Figure 1). In general, women censored earlier had higher risk of a false-positive recall while those censored later had lower risks, although this effect was minor. The BCSC cohort did not demonstrate a pattern indicative of censoring due to the event of interest for false-positive recall, with no notable increase in risk in the last round prior to censoring. At the tenth screening round, the cumulative risk of false-positive recall from the discrete-time survival model was 56.4% (95% CI [55.8, 57.2]). Estimates from both discrete time-survival models adjusted for censoring round returned higher estimates, indicative of the higher false-positive recall risk among women censored earlier. The estimate from the discrete-time survival model adjusted for censoring round and screening round was similar to the censoring bias model estimate when assuming a 10% decreased risk among individuals attending one additional round. Bounds on cumulative risk of a false-positive recall provided by the censoring bias model were 53.8-59.3%. For screen-detected cancers, the discrete-time survival model estimate after ten screening rounds was 3.7% (95% CI [3.4, 3.9]). The discrete-time survival model adjusted for censoring round returned a much higher estimate. However, this estimate is expected to overestimate risk by using the inflated risk observed in the last round prior to censoring to impute risk after censoring. The censoring bias model provides bounds of 2.4-7.6% for our risk estimate when risk is increased or decreased, respectively, by 10% for each additional round attended.

Figure 1.

Empirical risk estimates (left), empirical cumulative risk estimates (middle) and model-based risk estimates (right) for false-positive results (top) and screen-detected cancer (bottom) for the BCSC cohort. Lines in the left-hand and middle plots provide empirical risk estimates stratified by censoring time. Points on each line are labeled with the censoring time for the corresponding stratum. In the right-hand panel, the solid line gives the discrete-time survival estimate, the dashed line gives the discrete-time survival model adjusted for censoring round, the dashed and dotted line gives the discrete-time survival model adjusted for censoring round and screening round, and the dotted grey lines give the censoring bias estimates assuming 10% increased and decreased risk associated with each additional round attended.

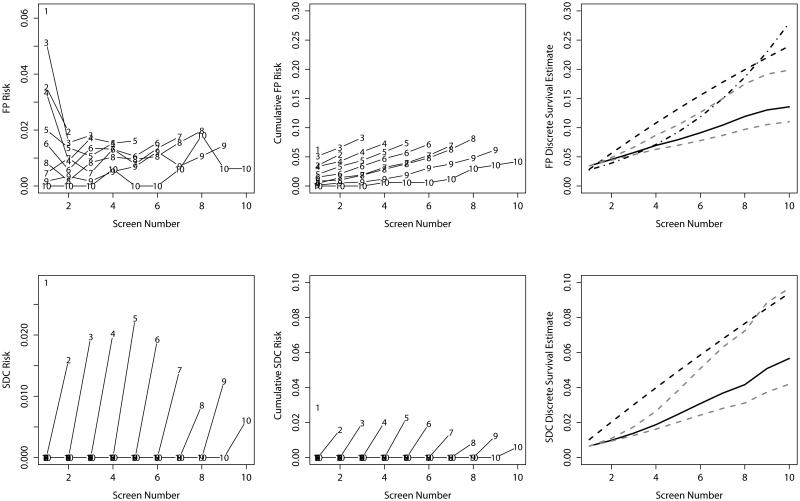
For the Nijmegen cohort, risk of a false-positive recall appears somewhat higher in the last round a woman attended (Figure 2), possibly indicative of censoring due to the event of interest. In this case, using either of the discrete-time survival models adjusted for censoring round results in over-estimating the cumulative risk. In the Nijmegen cohort, for both outcomes the discrete-time survival estimates adjusted for censoring round are notably higher than the unadjusted estimate (after 10 rounds 13.6%, 95% CI [12.2, 15.4] for false-positive recall; 5.7%, 95% CI [4.4, 7.2] for screen-detected cancer). Cumulative risk at the tenth screening round varied from 11.0-19.9% for false-positive recall and 4.2-9.7% for screen-detected cancers when we used the censoring bias model to explore 10% increased risk or decreased risk, respectively, for individuals attending one additional round of screening.

Figure 2.

Empirical risk estimates (left), empirical cumulative risk estimates (middle) and model-based risk estimates (right) for false-positive results (top) and screen-detected cancer (bottom) for the Nijmegen cohort. Lines in the left-hand and middle plots provide empirical risk estimates stratified by censoring time. Points on each line are labeled with the censoring time for the corresponding stratum. In the right-hand panel, the solid line gives the discrete-time survival estimate, the dashed line gives the discrete-time survival model adjusted for censoring round, the dashed and dotted line gives the discrete-time survival model adjusted for censoring round and screening round, and the dotted grey lines give the censoring bias estimates assuming 10% increased and decreased risk associated with each additional round attended.

Discussion

Several methods for estimating cumulative risk of screening mammography outcomes have been proposed. The foundation for these approaches is the discrete-time survival model, and a number of alternatives have been suggested to account for dependent censoring. The appropriateness of these approaches varies by screening outcome and setting. Notably, the adjusted discrete-time survival approaches will substantially overestimate risk if the event of interest is among the causes of censoring. These approaches should never be used if the outcome of interest inherently terminates observation (e.g., cancer diagnosis). An uptick in empirical risk estimates in the last screening round prior to censoring, as observed for false-positive recall in the Nijmegen cohort, is an indication that this type of censoring may be at play. In this case, the censoring bias model is recommended. Investigating a range of values for the censoring bias parameter will provide bounds for the risk estimate.

Studies of the cumulative risk of false-positive mammography results using data from the US have used a variety of methods (4, 6, 14-17). A study of censoring bias using data from the BCSC estimated that risk was 4% lower for each additional screening round a woman attended (17). Estimates of false-positive recall risk based on the discrete-time survival model adjusted for censoring round and screening round agreed well with a censoring bias estimate assuming 10% decreased odds of a false-positive recall for each additional round an individual participated in. In the setting of screening mammography in the US, it appears that dependent censoring does play a small role and that either adjusted discrete-time survival models or censoring bias models can be used to obtain risk estimates accounting for dependent censoring in this setting.

A number of prior studies have estimated the cumulative risk of a false-positive screening mammography result using data from European population-based screening programs (7-9, 12, 20). Some of these studies have used discrete-time survival estimates (7, 12, 20) while others have used simpler approximations that assume independence of risk across screening rounds (8, 9). In a recent comparison of the cumulative risk of false-positive results in Denmark using discrete-time survival methods with and without adjustment for dependent censoring, little difference in estimates was found, suggesting that dependent censoring plays little role in this setting (20). In general, dependent censoring may be less likely in European service screening programs where less patient choice is involved in the decision of starting and stopping ages and screening frequency compared to the US.

Similar to prior studies comparing screening in the US and Europe, we found substantially higher risks of false-positive recall in the BCSC compared to Nijmegen, while risks of screen-detected cancer were similar (12, 20, 24). Possible explanations for these differences include the opportunistic nature of screening in the US, as compared to organized population-based screening in Europe; differences in the medico-legal context; and differences in interpretive volumes required for radiologist accreditation. We also found that women in Nijmegen tended to discontinue screening after experiencing a false-positive recall, consistent with a prior study (25); However, this result was not found in the BCSC. Previous research in the US found that women are more likely to continue screening after a false-positive recall (26).

A few studies have used discrete-time survival models to estimate cumulative risks for outcomes other than false-positive results (19, 27, 28). These studies have not carried out adjustment for dependent censoring. As we have demonstrated here, adjusting for dependent censoring using inappropriate methods in studies with cancer as the outcome leads to substantial overestimation of risk. However, the possibility of dependent censoring does exist in this context, and we recommend exploring its potential impact through sensitivity analyses using censoring bias models.

Estimating outcomes over the course of repeat screening examinations is increasingly common and important given the large number of population-based cancer screening programs and screening recommendations currently in existence. As new screening tests become available it will be important to evaluate their long-term outcomes across multiple rounds of screening. The considerations described in this paper can be applied to repeat screening tests of many kinds and should be used to ensure that appropriate statistical methodology is selected.