Scale-Dependent Variability and Quantitative Regimes in Graph-Theoretic Representations of Human Cortical Networks

Abstract

Studying brain connectivity is important due to potential differences in brain circuitry between health and disease. One drawback of graph-theoretic approaches to this is that their results are dependent on the spatial scale at which brain circuitry is examined and explicitly on how vertices and edges are defined in network models. To investigate this, magnetic resonance and diffusion tensor images were acquired from 136 healthy adults, and each subject's cortex was parceled into as many as 50,000 regions. Regions were represented as nodes in a reconstructed network representation, and interregional connectivity was inferred via deterministic tractography. Network model behavior was explored as a function of nodal number and connectivity weighing. Three distinct regimes of quantitative behavior assumed by network models as a function of spatial scale are identified, and their existence may be modulated by the spatial folding scale of the cortex. The maximum number of network nodes used to model human brain circuitry in this study (∼50,000) is larger than in previous macroscale neuroimaging studies. Results suggest that network model properties vary appreciably as a function of vertex assignment convention and edge weighing scheme and that graph-theoretic analysis results should not be compared across spatial scales without appropriate understanding of how spatial scale and model topology modulate network model properties. These findings have implications for comparing macro- to mesoscale studies of brain network models and understanding how choosing network-theoretic parameters affects the interpretation of brain connectivity studies.

Introduction

The human connectome can be conceptualized as a network model of elements and connections, which form the human brain (Sporns et al., 2005). Brain connectivity studies using network models have identified differences between healthy control subjects' and patients' clinical conditions, which include schizophrenia, autism, and dementia (Crossley et al., 2014). The identification of such differences is important for identifying brain circuitry pathways whose existence and abnormal function are the causal factors for the development and severity of brain pathology and which can be targeted pharmacologically or electrophysiologically to ameliorate symptoms and improve patient health.

Though useful, one drawback of network-theoretic analyses of brain circuitry is that their results depend strongly on how network nodes and connectivity strengths are defined, as already found elsewhere (Zalesky et al., 2010). At the macroscopic level, nodes are typically defined by dividing the cortex into regions of variable extent based on predefined parcellation schemes, whereas the weights of connections between nodes can assume values based on parameters, such as connectivity density (CD), physical connection length (CL), and so forth. Regardless of spatial scale, however, graph properties may vary substantially depending on how nodes and edges are defined in network models, and it is important to understand how the choice of cortical parcellation and connectivity weighing can affect network-theoretic analysis. Furthermore, it is equally important to grasp the limitations of representing brain connectivity patterns using network-theoretic models as proxies of physical connectivity and delineate with precision both the advantages and disadvantages of such representations. Importantly, network models of brain circuitry are simplified representations of neural connectivity, and thus, network-theoretic analysis suffers from important drawbacks, which have been insufficiently explored by the connectomics community.

At the macroscopic scale, human brain connectivity is typically studied in vivo using magnetic resonance imaging (MRI) and diffusion tensor imaging (DTI), which can allow one to acquire high-resolution images of brain structure (in the case of MRI) and identify the direction of water diffusion along white matter (WM) tracts, which connect gray matter (GM) regions to each other (in the case of DTI) (Goh et al., 2014; Irimia and Van Horn, 2012, 2014). Such information can be used to model and investigate brain architecture using network theory, which has been widely used due to its powerful tools for the quantification, analysis, and interpretation of network model properties (Park and Friston, 2013). A variety of measures, which quantify integration, segregation, centrality, resilience, and other properties, have been proposed to describe and compare brain network models from the microscale (neuron-to-neuron connections) to the macroscale (region-to-region connections). This study examines the behavior of such measures as a function of node assignment modality and connectivity weighing scheme and thereby, implicitly, as a function of spatial scale. Explicitly, this behavior is investigated as a function of vertex definition scheme and edge weighing modality due to the importance of these factors in determining network model properties.

MRI and DTI volumes were acquired from a sample of 136 healthy adults, and both GM and WM were segmented in each subject. The cortex was parceled into a number of regions, which ranged from 2 to 50,000, and every region was represented as a node in each subject's brain network model. WM connectivity was inferred from DTI using deterministic tractography, and graph edges were assigned weights based on either anatomic or diffusion-related measures of connectivity strength. The behavior of graph genus and eight widely used graph-theoretical metrics as a function of cortical region number and connectivity weighing was then explored. Importantly, three distinct regimes of quantitative behavior assumed by the properties of brain network models as a function of spatial scale were identified.

Due to the large effect of spatial scale on the quantitative variability of graph-theoretical metrics, an important conclusion of this study is that comparing such measures across scales should not be attempted without appropriate understanding of their variability. Additionally, due to large variability in network model topology as quantified by graph genus, network metrics are challenging—if not impossible—to interpret without reference to this important property. For this reason, we conclude that understanding the topological properties of network models should be an immediate goal for researchers in the field of connectomics. The asymptotic behavior of network measures computed in this study (up to 50,000 network nodes) theoretically permits inferring the structure and properties of human brain circuitry at a spatial scale where cortical parcels are much smaller than in previous studies. For this reason, the present study has implications for bridging the gap between macro- and mesoscale investigations of brain network models and delineating the advantages as well as limitations of graph-theoretic models of brain circuitry.

Materials and Methods

Participants

The study cohort included N = 136 healthy adult subjects (42 males) with ages from 18.6 to 61.1 years (mean: 33.3 years, standard deviation: 11.6 years). Each subject provided informed written consent as required by the Declaration of Helsinki, U.S. 45 C.F.R. 46. Neuroimage volume acquisition was conducted with the approval of the local ethics committees at the respective research institutions where data were acquired. Participants were recruited by advertisements in local newspapers and campus flyers. Subjects were healthy with no self-reported history of neurological or psychiatric illnesses. None of the participants had a current or past psychiatric diagnosis (including substance abuse), and none was taking any medications for medical reasons. Exclusion criteria included left-handedness, hypertension, metal implants, neurological illness, and a history of head trauma with loss of consciousness for more than 5 min.

Neuroimage acquisition

Brain imaging data sets were fully anonymized, and no linked coding or keys to subject identity were maintained. For these reasons, in compliance with the U.S. Health Insurance Portability and Accountability Act (HIPAA; www.hhs.gov/ocr/privacy), this study does not involve human subjects' materials. Structural T₁-weighted MRI and DTI volumes were acquired from each patient using a Siemens Trio Tim 3.0 T scanner. For T₁-weighted MRI, a Turbo gradient-recalled magnetization-prepared rapid gradient echo (MP-RAGE) sequence (repetition time [T_R] = 2 sec, echo time [T_E] = 30 msec, flip angle = 25°, slice thickness = 1 mm, field of view [FOV] = 256 mm, acquisition matrix = 256 × 256, and number of slices = 256) was used. For diffusion-weighted images, a 12-channel coil and a sequence with the following parameters were used: T_R = 9.4 sec, T_E = 88 msec, flip angle = 90°, slice thickness = 2 mm, FOV = 256 mm, number of gradient directions = 68, and acquisition matrix = 128 × 128. Two nondiffusion-weighted volumes were acquired for each subject (B₀ diffusivity: 0 and 10⁻³ mm²/sec). The same scanner and sequence types were used for data acquisition from each subject.

Connectivity calculation

Before any analysis, each subject's T₁-weighted MRI volume was registered to her/his DTI volume using FSL FLIRT (Jenkinson and Smith, 2001). The cortical surface was reconstructed as a triangular tessellation (average intervertex distance of ∼1 mm, that is, ∼300,000 vertices per brain mesh) to produce a high-resolution, smooth representation of the GM–WM interface using FreeSurfer 5.3 with default settings, as detailed extensively elsewhere (Dale et al., 1999; Fischl et al., 1999). At each vertex v_i of the tessellation, cortical thickness was measured as the distance between the GM–WM boundary and the cortical surface. For each subject, DTI and MRI volumes were first coregistered using affine registration. Eddy current correction was applied to each DTI volume, followed by an appropriate rotation of the B-matrix (Leemans and Jones, 2009). Although field maps were not obtained and echo planar imaging susceptibility corrections were not implemented, a bias field correction using a fourth-order polynomial was implemented using the BrainSuite bias field corrector (Shattuck and Leahy, 2002). DTI volumes were subsequently processed using TrackVis (http://trackvis.org) to reconstruct WM streamlines using second-order Runge–Kutta deterministic tractography. A tracking mask with a thresholded fractional anisotropy (FA) value of 0.35 and a step length of 1 voxel was used. Complete (whole-brain) seeding with a turning angle of 15° was implemented. Streamline bundles shorter than 1.5 cm were discarded.

After segmenting the cortical surface and performing DTI tractography, the connectivity matrix of each subject's brain was reconstructed. Let v_i and v_j be vertices on the cortical mesh, which are linked by some WM connection c_ij. For every connection, the three-dimensional coordinates associated with the extremities of c_ij (i.e., with v_i and v_j) were identified. To associate each streamline end-point with a specific graph vertex, the shortest euclidean distance between the coordinates of the former and the cortical surface associated with the GM–WM interface was first calculated. Streamlines with end-points whose shortest distance to the cortex was greater than 1 cm were discarded. The cortical mesh vertex, which was closest to the streamline's end-point, was assumed to be the vertex to which the streamline was connected. The corresponding entry associated with that vertex and indexed by i and j in the connectivity matrix C of each subject was assigned a value, which reflected the presence of a streamline between the two vertices, and the process was repeated for each streamline.

The generation of C did not involve a predefined parcellation scheme. Because the extremity of each streamline bundle is associated with some point v_i on the cortical mesh, the dimensions of C are determined by the number of streamline bundles reconstructed via tractography rather than by a parcellation scheme, which is specified a priori. Whereas each cortical mesh contained ∼300,000 vertices (as extracted from T₁-weighted MRI using FreeSurfer), the largest number of parcels used was 50,000. Thus, at each level of spatial resolution, a different number of mesh vertices had to be combined to generate a cortical parcel. Each parcel was then equated to a node in the graph-theoretical representation of the brain network. The process of dividing the cortical mesh into parcels was implemented subject to the requirement that all parcels have approximately the same area (i.e., the total surface of the cortical mesh divided by the total number of parcels). For each pair of parcels, streamlines whose extremities ended within these parcels were modeled as forming the graph edge between the two parcels in question. The spatial location and extent of every parcel were constrained such that mapping each parcel to the FreeSurfer atlas of Destrieux and colleagues (2010) would result in the maximum atlas-space overlap across subjects.

For each connection c_ij, the mean FA over c_ij was calculated as the average of FA values over all DTI voxels traversed by c_ij from one extremity of the streamline to the other end. Similarly, at each vertex on the cortical mesh, the mean FA of streamlines linking v_i to the rest of the network was computed. The CD at each vertex was calculated as the sum of all reconstructed streamlines linking it to the rest of the brain, divided by the surface area of the vertex neighborhood and by the total number of streamlines in the brain. Here, the neighborhood of some vertex v_i denotes the portion of the mesh surface containing points that are closest to v_i. In addition to these measures, it can also be informative to compute the product between CL and CD, that is, CL × CD. This measure is somewhat analogous to the volume of a conducting cable; specifically, the CL is similar to the length of the cable, and the CD is analogous to its cross section. The product of CL and CD conveys, simultaneously, the topological distance between nodes (similar to the length of a cable) as well as the number of individual streamlines between pairs of parcels. The product of CL and CD is thus a brain network model analog of total charge, which can be accommodated along a bundle of wires within a cable: it is a surrogate measure that is proportional to the number of streamlines contained within a streamline bundle (CD) as well as to the length of the connection (CL).

Network-theoretic analysis

For all network-theoretic analyses, the graph representations of brain networks contained edges, which were weighted by their CD, FA, CL, or CL × CD. After parceling the cortex into a number of regions, which ranged from 2 (1 region per hemisphere) to 50,000, each region was then represented as a corresponding node in the reconstructed brain network model of each subject. For each parcellation, the degree distribution of the brain network model was then computed. Graph genus, defined as the smallest number g such that the graph can be drawn on a surface of genus g without any edge crossings, was also computed, as detailed elsewhere (Mohar, 1999). The behavior of eight widely used graph-theoretical metrics was then explored as a function of cortical region number and connectivity weighing. These metrics were assortativity, global clustering coefficient, modularity, mean rich-club coefficient, characteristic path length, small-world coefficient, efficiency, mean betweenness centrality, participation coefficient, and diversity coefficient. Their values were computed using the Brain Connectivity Toolbox (www.brain-connectivity-toolbox.net). The calculation of the small-world coefficient was performed using the network randomization technique, as described elsewhere (Alstott et al., 2009; Rubinov and Sporns, 2010; van Wijk et al., 2010).

Statistical analysis

To provide a quantitative description of how significantly graph-theoretical metrics vary as a function of spatial scale, a multivariate analysis of variance (MANOVA) with repeated measures was implemented following a standard approach (Rencher, 2002). The purpose of the MANOVA was to test the null hypothesis that the mean values of the p = 8 network metrics were equal across k = 3 distinct statistical treatments (levels). The three treatments consisted of parceling the cortex into 50, 500, and 50,000 regions, respectively. These specific values were selected to illustrate the variability of network model properties across spatial scales, given that dividing the cortex into 50, 500, and 50,000 regions corresponds to average parcel sizes of 50, 5, and 0.05 cm², respectively. The first case (50 cortical regions) is of interest because many recent studies have studied connectivity properties at this spatial scale [see Markov and colleagues (2013) for a thorough review]. The second case (500 regions) is informative because it translates into an average parcel size of ∼5 cm² (i.e., a circle with a diameter of ∼2.5 cm), which is at the spatial scale investigated in many functional studies (Bassett and Bullmore, 2006). Finally, the third case (50,000 regions) corresponds to the lowest spatial scale available in our study, and the lowest scale at which a study of network-theoretic properties has been attempted thus far. By conceptualizing the parcellation of the cortex into three numbers of regions as statistical treatments, we sought to explore the effects of nodal definition scheme on network model properties at different spatial scales. The statistical feature vector under consideration consisted of values associated with each of the eight graph-theoretical measures discussed in this study. Wilks' Λ test statistic was computed as Λ = |H|/|E + H|, where H and E are the hypothesis (between treatments) and error (within treatment) matrices, respectively, and | · | indicates the matrix determinant. The omnibus null hypothesis that the mean multivariate feature vectors were equal across treatments was tested after converting Wilks' Λ statistic to an F statistic via an exact transformation [cf. p. 163 in Rencher (2002)]. This F statistic has 2p and 2(v_E − p + 1) degrees of freedom (d.f.), where v_E = k(N − 1), that is, 16 and 796 d.f. in the present study. We also sought to determine which specific univariate measures contributed most to the separation between the mean feature vectors of each treatment. To do so, the eigenvalues λ_i and eigenvectors a_i of the matrix E⁻¹ H were computed via simultaneous diagonalization (Cardoso and Souloumiac, 1996). On the one hand, the eigenvalues λ_i specify the extent to which the univariate measures contribute to the variance across treatments. On the other hand, the magnitude and sign of each eigenvector coefficient a_ij (where i ranges from 1 to rank(E⁻¹ H) = k − 1 and j ranges from 1 to p) indicate which univariate measures contribute most to the separation between mean feature vectors across treatments (Rencher, 2002). To show the significance of each univariate variable's contribution to the separation between mean feature vectors across treatments, a partial F test can be implemented, where F = [(1 − Λ)(v_E − p + 1)]/(Λv_H), v_E = N − k, v_H = k − 1, and F has v_H and v_E − p + 1 d.f. In this specific instance of the partial significance test, F has 2 and 126 d.f. Wilks' Λ statistic is computed as Λ = Λ_p/Λ_p–1, where Λ_p is Wilks' Λ for all p variables, and Λ_p − 1 involves all variables except the univariate measure whose contribution above and beyond all others is being investigated [cf. p. 290 in Rencher (2002)]. A power analysis was also implemented using a standard approach involving the use of the noncentral F distribution (Butler and Wood, 2005; Van Horn et al., 1998) to investigate whether our sample size was large enough to detect an effect size η² = 0.02 at significance levels α of 0.05 and 0.01.

Results

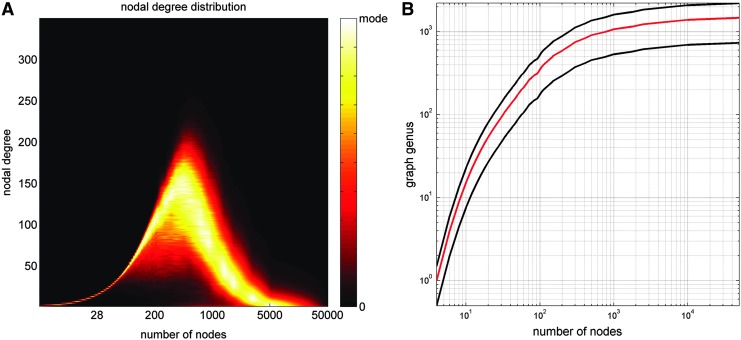
Figure 1 displays (A) the degree distribution of human brain network models and (B) the dependence of graph genus as a function of node definition scheme. Up to ∼100 nodes, the width (i.e., standard deviation) of the degree distribution is relatively low. From ∼100 to ∼500 nodes, a substantial increase in nodal degree variability is observed, peaking around ∼500 nodes. For even larger values, the standard deviation of nodal degrees decreases again, although very slowly, and reaches very small values in the limit where the number of nodes in the network is very large. Similarly, in the case of graph genus, distinct behaviors are observed for graphs with (i) under ∼100 nodes, (ii) from ∼100 to ∼500 nodes, and (iii) more than ∼500 nodes. Figure 2 illustrates how four graph-theoretical metrics, which quantify network model integration/segregation (assortativity, participation coefficient, mean rich-club coefficient, and betweenness centrality), vary as a function of node number as well as edge weighing scheme. In all figures, the quantities displayed correspond to the mean of the examined graph metrics over all subjects.

FIG. 1.

(A) The probability distribution of nodal degrees as a function of the number of nodes being used to model human brain networks. The horizontal axis indicates the number of nodes (logarithmic scale), and the vertical axis indicates the nodal degree. Color encodes the probability for a node to have a given degree and ranges from zero to the mode of the distribution. (B) Dependence of graph genus on the number of nodes used to model brain networks. The mean (red) ± the standard deviation (black) of the genus over subjects are shown. Color images available online at www.liebertpub.com/brain

FIG. 2.

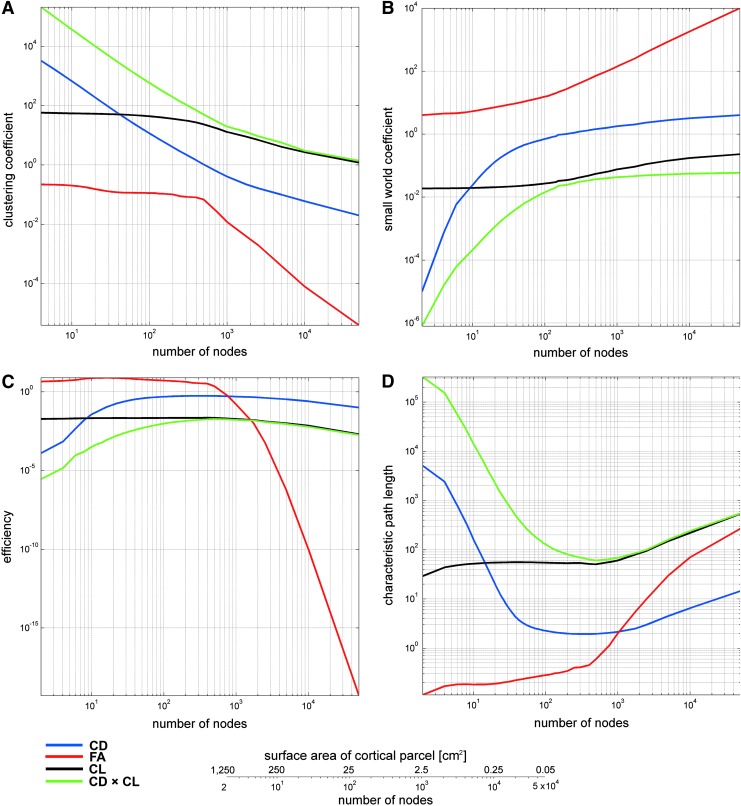
Dependence of assortativity (A), participation coefficient (B), mean rich-club coefficient (C), and mean betweenness centrality (D) on vertex definition scheme and edge weighing modality. The numerical values of each metric are shown for four weighing schemes, that is, according to whether edge weight is assigned based on the connectivity density (CD; blue), mean fractional anisotropy (FA; red), connection length (CL; black), or CD×CL product (green) of each connection. The vertical axis indicates the numerical value assumed by each measure, whereas the horizontal axis indicates the number of nodes in the cortical parcellation used to generate the connectivity matrix (please note that the vertical axis is logarithmic for some measures). The number of parcels varies from 2 (1 per hemisphere) to 50,000. The latter upper limit is imposed by the number of white matter connections, which can be identified at the spatial resolution afforded by our neuroimaging protocol (see Materials and Methods section). The conversion legend at the bottom of the figure allows one to readily translate between the number of nodes and the average surface area of every cortical parcel associated with each node. At one extreme, having two nodes in the network model corresponds to an average cortical parcel area of 1250 cm², resulting in a total cortical area of 2500 cm². At the other extreme, having 50,000 nodes in the network model results in an average parcel size of 0.05 cm². Note that, regardless of the number of nodes being used, the average total cortical area (the number of nodes multiplied by the surface area of the average cortical parcel) is constant (2500 cm²). Color images available online at www.liebertpub.com/brain

Assortativity (Fig. 2A) can be conceptualized as the preference for a network model's nodes to attach to other nodes of similar degree. For example, highly connected nodes have the tendency to be connected to other highly connected nodes, forming what is commonly known as the rich-club network. Formally, the assortativity coefficient is the Pearson product-moment correlation coefficient of degree between pairs of linked nodes (Newman, 2002). A negative assortativity value indicates a dissortative network model, whereas a large positive assortativity value indicates a highly assortative network model. For all four weighing schemes, Figure 2A indicates that human brain network models appear to be dissortative when the cortex is divided into either (i) ∼30 to 80 nodes or fewer or (ii) more than ∼4000 nodes. When the total number of nodes is between these values, the brain network model appears to be assortative and maximally so when the cortex is parceled into ∼500 nodes (this may be partially due to the fact that the degree distribution exhibits the largest standard deviation around this value). The assortativity index then exhibits an asymptotic decrease as the cortex is partitioned into more than ∼4000 nodes.

The participation coefficient (Fig. 2B) assesses the diversity of connections between a node and other modules in the network model (Guimera and Nunes Amaral, 2005). In a network model whose nodes have a relatively high average participation coefficient, the average node is more strongly linked to nodes in other modules. In contrast, low values of the average participation coefficient indicate that modules in network models have relatively fewer links between modules than in the converse scenario. Figure 2B indicates that the mean participation coefficient increases rapidly from zero to its maximum observed value as the number of cortical parcels increases from two to a few hundreds. As the number of cortical regions increases above this range, the mean participation coefficient decreases asymptotically, particularly as the number of regions increases above ∼1000. When edge weights are assigned according to the mean FA over the connections involved, the participation coefficient approaches zero very rapidly for more than ∼1000 nodes. For all other edge weighing schemes (based on CD, CL, and CD × CL), the mean participation coefficient slowly approaches a value of ∼0.3 as the number of network nodes increases up to 50,000. For two measures (CD and CD × CL), the mean participation coefficient remains relatively constant as the number of nodes increases from ∼10 to ∼1000 and then assumes an asymptotic behavior, which is similar—both qualitatively and quantitatively—to those observed in the case of FA and CD.

The rich-club coefficient conveys the extent to which network model hubs (nodes that rise to prominence in the graph-theoretical model) also tend to exchange among themselves the majority of resources flowing within the network model (Opsahl et al., 2008; van den Heuvel and Sporns, 2011). A greater average rich-club coefficient indicates that, on average, network model hubs share stronger connections with themselves (i.e., with other rich-club nodes) rather than with other nodes outside the rich club. Figure 2C indicates that the rich-club coefficient of human brain network models is the largest when the number of network model nodes is relatively low (∼10 to a few hundred nodes) and then decreases slowly as the spatial resolution at which the network model is examined increases (i.e., when the network has more than ∼500 nodes and the variability in degree distribution decreases, as seen in Fig. 1).

Betweenness centrality indicates, as its name suggests, how central a node is within a network model. For any node, it is equal to the number of shortest paths, which pass through that node from all vertices to all other vertices (Rubinov and Sporns, 2010). Nodes with high betweenness centrality have large influence on the transfer of information through the network model in the scenario where such transfers occur along the shortest paths. As in the case of the rich-club and participation coefficients, the average betweenness centrality is seen to decrease asymptotically as the number of network model nodes increases after reaching a maximum value when the brain network model has ∼10 nodes.

Collectively, the results in Figure 2 indicate that graph-theoretical measures of assortativity, participation, inclusion in the rich-club network, and centrality (i) assume their maximum values when the cortex is partitioned into ∼10 to ∼500 nodes and then (ii) decrease asymptotically as the number of network model nodes increases, thereby illustrating the ability of high-resolution graph-theoretical analyses to capture the true extent of heterogeneity in human neural circuitry.

Figure 3 continues to illustrate the behavior of important graph-theoretical metrics as a function of node definition and edge weighing schemes. The measures displayed in Figure 2 are the clustering coefficient (Fig. 3A), small-world coefficient (Fig. 3B), network efficiency (Fig. 3C), and characteristic path length (Fig. 3D).

FIG. 3.

As in Figure 2, for the clustering coefficient (A), small-world coefficient (B), characteristic path length (C), and efficiency (D). Color images available online at www.liebertpub.com/brain

The global clustering coefficient is a measure of the extent to which network model nodes tend to cluster together and is designed to provide a general indication of node aggregation in a network model (Watts and Strogatz, 1998). The nodal clustering coefficient quantifies how close the neighbors of a node are to forming a clique (i.e., complete graph). The global clustering coefficient is the average of nodal clustering coefficients over all nodes in the network model. In Figure 3A, this measure is observed to decrease asymptotically when the number of network model nodes exceeds ∼500, indicating a decreasing extent of nodal clustering as human brain circuitry is examined at higher and higher resolutions, where the variance in nodal degree decreases (see also Fig. 1).

The small-world coefficient quantifies the extent to which most nodes can be reached from every other node via a small number of steps. The small-world coefficient is calculated by comparing the clustering coefficient and characteristic path length of a given network model to those of an equivalent random network model with identical degree distribution. A small-world coefficient greater than 1 typically indicates that the network model is a small world. In Figure 3B, this is seen to be the case when either mean FA or CD is used to assign edge weights, though not when either CD×CL or CL alone is used. Nevertheless, the asymptotic behavior of the latter two measures suggests that the small-world coefficient may reach unity even for these edge weighing scenarios when the cortex is divided into (far) more than 50,000 parcels.

The global efficiency and characteristic path length of a network (Fig. 3C, D) are two related measures of network integration. The former is the average inverse shortest path length in the network model, whereas the latter is the average shortest path length, that is, the average number of steps along the shortest paths for all possible pairs of nodes. The characteristic path length is a quantifier of information transfer efficacy, which is more strongly influenced by long paths, whereas the global efficiency is more influenced by short paths (Latora and Marchiori, 2001; Watts and Strogatz, 1998). In light of these properties, the results in Figure 2C and D are complementary: as brain networks are represented using models, which consist of more and more nodes and corresponding connections, their efficiency decreases and their characteristic path length increases.

For an effect size η² = 0.02, the noncentrality parameter λ of the noncentral F distribution was found to have a value of 16.25. The power analysis indicated that, at significance levels of 0.05 and 0.01, the statistical power π of the study was found to be equal to 0.993 and 0.996, respectively. The omnibus statistical analysis indicated that the three mean feature vectors of graph-theoretical measures differed significantly across the three treatments (F_16,796 = 1143.4, p < 0.0001), that is, when the cortex was parceled into 50, 500, or 50,000 regions. The eigenvalues of the matrix E⁻¹ H were λ₁ = 92.04 and λ₂ = 2.57, indicating that 97.28% of the variance was explained by the first eigenvector a₁ with components a_1i, i = 1, …, p. As previously stated, the magnitudes of the eigenvector components a_1i indicate which univariate measures contributed most to the separation between mean feature vectors. In this study, these measures were betweenness centrality (a₁₁ = 0.7063, partial F_2,126 = 201.6, p < 0.0001) and the clustering coefficient (a₁₂ = −0.7074, partial F_2,126 = 6.3, p = 0.0025), indicating the prominence of these two measures in distinguishing the mean values of graph-theoretic metrics at representative points across each of the three spatial scales. It should be mentioned that whereas our statistical analysis focused on comparing network model behaviors when the cortex is divided into 50, 500, and 50,000 nodes, similar statistical inference results should be expected when the latter three values differ by small amounts. For example, one may reasonably expect similar conclusions when the cortex is divided, say, into 49, 490, 49,000 nodes, and so forth because the graph-theoretical metrics analyzed here vary relatively little for small deviations from each of the three selected values. In this context, the purpose of applying MANOVA using 50, 500, and 50,000 as the number of nodes into which the cortex is divided was to illustrate the variability of graph-theoretical measures across spatial scales.

Discussion

Whereas the connectome consists of all neurons in the brain and their interconnections, a graph-theoretic model of neural connectivity is a mathematical representation whose properties are dependent on the spatial scale at which the model is constructed. At this time, the compilation of a cellular-level (microscale) graph-theoretic representation of the human connectome from in vivo brain imaging is beyond reach due to methodological limitations. This implies that current investigations entail the use of simplified network-theoretic representations that are generated at spatial scales (i.e., meso- to macroscale), which are larger than the true scale of brain connectivity itself (microscale). Because network theory considers the representation of brain circuitry as a set of vertices (nodes), which are interconnected by edges, constructing graph representations of the connectome at a spatial scale above that of individual cells must thus resort to summing over neuronal assemblies and their connections when network model nodes and edges, respectively, are created. It is precisely the properties and behavior of such (simplified) network-theoretic representations of the connectome that require investigation as a function of spatial scale to assess whether it is appropriate to compare network model properties across studies, which were undertaken at distinct spatial scales.

Reliability

To address the topic of reliability, we adopt the accepted definition of this term in measurement theory, where it designates the repeatability or consistency of research measures. In this context, the reliability of our research findings can be understood to involve the ability of our adopted statistical approach (MANOVA) to test the research hypothesis of the present study with adequate statistical power and at a satisfactory confidence level. Because repeated scans of each study participant were unavailable to the authors, the reliability of our research measures (i.e., their repeatability or consistency) was investigated instead using MANOVA. This statistical approach accounts for the variance within each set of multivariate measurements across the subjects included in the study and additionally takes into account the correlation between measures both within and between treatments, as previously detailed. Errors related to modeling assumptions, measurement uncertainties, and other specific factors—such as the variability in the accuracy of reconstructed network topologies—are also accounted for in the error matrix E of MANOVA. For example, errors due to computing network measures based on potentially inaccurate network reconstructions are accounted for in the MANOVA error matrix, which is used to compute the test statistic and its confidence interval and p value. In this study, the test statistic was F_16,796 = 1143.4, and its associated p value was less than 10⁻⁴. Additionally, our power analysis found that the statistical sensitivity of the MANOVA was larger than 0.99, suggesting that statistical findings are both reliable and replicable. Consequently, despite potential modeling errors due to a variety of factors—including the inherently limited reliability of network reconstructions—the posited null hypothesis of the study that the computed graph-theoretical measures differed significantly across treatments was not accepted at a significance level of 0.05. Thus, though test–retest data sets are certainly useful for investigating the variability and accuracy of network reconstructions, the detailed investigation of these factors is outside the scope of the present study. Our current aim, instead, was to determine whether network properties differed significantly across the three statistical regimes of network behavior identified in the study, which was indeed found to be the case based on our results from MANOVA.

Interpretation

It has been estimated that there are ∼10⁶ cortical columns in the adult human brain (Krueger et al., 2008), which may imply that the largest number of nodes (∼50,000) in the network models examined in this study corresponds to an average parcel size, which is closer to the surface area of the average cortical column than in previous studies. As Figures 2 and 3 suggest, increasing the number of parcels into which the cortex is subdivided (from 2 to 50,000 in this study) allows human brain network models to be investigated using larger and larger graph-theoretical models with more and more nodes. In contrast, decreasing the number of parcels is similar to the effect of applying a spatial smoothing filter, which averages network model properties over increasingly larger portions of the cortical surface. When doing so, fine details and low-scale properties of brain network models may be lost to further analysis. In the case of assortativity (Fig. 2A), the asymptotic behavior of network models toward increasing dissortativity as brain connectivity is examined at increasingly higher resolutions (greater numbers of parcels) may capture the intrinsic heterogeneity of nodal assortativity properties. Because assortativity captures preferential attachment of nodes to nodes of similar degrees, Figure 2A suggests that, as connectivity is modeled using cortical parcel sizes whose dimensions are closer and closer to the mesoscale, the fact becomes obvious that high-degree nodes are more connected to low-degree nodes—and vice versa—than would be apparent if the number of network nodes in our connectivity models were much smaller.

Because the mean participation coefficient (Fig. 2B) assumes relatively large values when the cortex is partitioned into ∼10 up to a few hundred nodes and then asymptotes to smaller and smaller values above the latter threshold, this study indicates that modeling brain connectivity at low resolution (<∼500 nodes) may lead to an estimate of average nodal participation, which may be inappropriate in high-resolution connectomics studies. The fact that the participation coefficient decreases asymptotically as spatial resolution is increased implies that the average network node is far more weakly linked to nodes in other modules than suggested by a low-resolution analysis involving a few hundreds of nodes or fewer. This conclusion conveys, as in the case of assortativity, the heterogeneity of nodal properties and the increased ability of a high-resolution analysis—such as this one—to reveal and quantify this heterogeneity.

The results presented in Figure 3 further support the findings in Figure 2, in the sense that the heterogeneity of human brain network models is more adequately captured when these networks are represented using models, which contain more—rather than fewer—nodes. Thus, for example, clustering coefficients are seen to decrease as the network model is represented with higher spatial fidelity (Fig. 3A), and small-world coefficients increase exponentially as the number of nodes becomes greater and greater (Fig. 3B). As expected, network efficiency decreases and characteristic path length increases with the number of nodes used to represent the brain network model, despite quantitative variability in how this behavior occurs as a function of edge weighing scheme.

Network regimes

Collectively, our results suggest that brain network model properties assume three distinct regimes of quantitative behavior as a function of spatial scale. In this context, the term regime is used in analogy with statistical physics, where it denotes a class of physical conditions where a particular phenomenon is of prominent interest. In the present case, the adoption of the term illustrates the fact that graph-theoretical measures (i.e., system properties) describing brain network models assume certain behaviors (types of variability across spatial scales), which are different from those exhibited by the system in other regimes. As in statistical physics, the regimes discussed here correspond to a set of limiting conditions (i.e., transitions across spatial scales) in a measurable parameter space (i.e., the statistical space of descriptive network model properties). Specifically, when the graph is constructed using ∼50 nodes or fewer, most graph-theoretical measures can vary quite substantially depending on how many nodes are present in the network model representation (Figs. 1–3). In this regime, both mean nodal degree and graph genus vary substantially as well as a function of node number (Fig. 1). In the regime where brain networks are represented using ∼50 to ∼500 nodes, graph-theoretical metric values exhibit far less variability than in the range from 2 to ∼50 nodes, as does the average nodal degree. Finally, when the brain circuitry model is represented using (far) more than ∼500 nodes, mean nodal degree and network model metrics decrease asymptotically as the average parcel size in the brain circuitry model approaches the mesoscale. The only exceptions to this are the small-world coefficient and the characteristic path length, which increase as expected. Interestingly, dividing the cortex into ∼500 nodes results in an average parcel area of ∼5 cm² corresponding to a circle with an ∼2.5 cm diameter. This is on the spatial scale of cortical folding at gyral crowns and sulcal troughs, which suggests (unsurprisingly, perhaps) that the quantitative behavior of brain network model properties may be modulated by the spatial folding scale of the human cortex.

Comparison to previous work

Since most parcellation schemes currently available comprise at most ∼1000 brain regions (Hagmann et al., 2008), the advantage of the present approach to studying the connectivity matrix C lies in the ability of the former to construct graph-theoretic representations of connectivity, which feature substantially more graph vertices (parcels) than previously attempted, and additionally without the need for averaging connectivity measures over much larger parcels, as in the case of previous conventional parcellation approaches. For example, in the present study, C was of size ∼50,000 × ∼50,000 in each subject compared to far smaller sizes in previous studies [∼1000 × ∼1000 in Hagmann and colleagues (2008) and 4000 × 4000 in Zalesky and colleagues (2010)]. Thus, the process of generating C using the present approach carries with it the ability to study network representations whose number of graph nodes is far greater than in previous studies.

Although the effect of parcellation schemes on small-world coefficient values has been explored previously (Wang et al., 2009), few studies have undertaken analyses of graph-theoretical measure variability, which are as systematic as in the present study. Additionally, because thorough reviews and discussions of parcellation schemes in the context of network-theoretic modeling of brain connectivity are available elsewhere (de Reus and van den Heuvel, 2013; Stanley et al., 2013), we restrict ourselves to highlighting a selection of studies, which are most relevant to our own. In an excellent study by Zalesky and colleagues (2010), the behaviors of the clustering coefficient, characteristic path length, and small-world coefficient were investigated as a function of nodal number. These authors concluded, as we did, that it is crucial to account for spatial scale when interpreting the results of brain network model analyses. Whereas the conclusions of Zalesky and colleagues (2010) were based on a study of N = 3 patients, however, our sample has the advantage of being substantially larger (N = 136). The present investigation also examines the behavior of five additional graph-theoretical metrics (assortativity, participation coefficient, rich-club coefficient, betweenness centrality, and global efficiency), and the comparison is made across a wider range of cortical parcel sizes [corresponding to between 2 and 50,000 nodes in this study vs. between 82 and 4000 nodes in the study of Zalesky and colleagues (2010)]. In a recent study by Liu and Tian (2014) concerning the impact of parcel size on degree metrics in functional network models, the authors proposed that a substantial proportion of previous network-theoretic studies of brain circuitry modeling overestimated the proportion of hubs in the brain. This appears to be in agreement with our own result indicating that as the spatial scale decreases, so does the rich-club coefficient of network model graphs (Fig. 1C).

DTI limitations for network modeling

It is important to acknowledge that the analysis presented in this study is subject to limitations imposed by the MRI/DTI imaging protocol used and its parameters (e.g., scan sequence type and voxel size). High spatial resolution is desirable in a study such as ours as it may allow exploring graph-theoretical properties at a lower spatial scale. As a separate note, differences in choices of DTI tractography parameters can potentially confound direct comparison across studies. Additionally, although DTI acquisition accuracy is limited by noise, artifacts and data undersampling as a consequence of scan time constraints, DTI has been recently noted to suffer from inherent limitations in ascertaining long-range anatomical projections based on voxel-averaged estimates of WM fiber orientation (Thomas et al., 2014).

One limitation of this study is that networks with as many as 50,000 nodes are examined in it, even though the DTI volumes used for tractography have a voxel size of 2 × 2 × 2 mm. In contrast, the structural MRI volumes used to create brain surface models have a resolution of 1 mm³, and the brain meshes extracted from these volumes have an average intervertex distance of ∼1 mm. Thus, although the brain parcellations have (relatively) high resolution, the spatial resolution of DTI volumes is not as high. Because of this, it is probable that partial volume effects and other sources of error become more pronounced as the parcel size approaches the spatial resolution of DTI volumes. Though this is admittedly a limitation of our study, it is important to note that the spatial scale at which our DTI volumes were acquired is larger than that of the most detailed network models analyzed. Specifically, dividing the cortex into 50,000 parcels results in an average parcel size of ∼5 mm². For a square parcel, this corresponds to a flat surface with a side length of 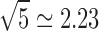 mm, implying that the smallest average size of a parcel in this study is approximately equal to the size of a DTI voxel (2 mm side length). This suggests that our most detailed cortical parcellations have approximately the same spatial scale as that of the DTI voxels from which connectivity information is extracted. Moreover, streamlines connecting vertices within a parcel to other cortical locations are averaged over the surface of the parcel when computing CD and other measures. Such an averaging plays the role of a low-pass spatial filter whose cutoff frequency is the side length of the average parcel (∼2.23 mm), and such a filter reduces the effective spatial scale where connectivity is resolved from the spatial resolution of the DTI volume to the spatial scale of the average parcel size. Thus, even if higher resolution DTI volumes had been acquired in this study, the spatial filtering effect in question would still reduce the effective spatial resolution of inferred connectivity densities, mean FA values, and so forth. Nevertheless, we acknowledge that acquiring higher resolution DTI volumes would undoubtedly be beneficial for reducing measurement error, improving the spatial resolution of DTI tractography results, and increasing the accuracy of connectivity measures.

Implications

An important topic explored in the present study is that vertex definition scheme and edge weighing modality are of substantial consequence for the network-theoretic modeling of human brain connectivity. The results of this study indicate that graph-theoretical metric values vary appreciably as a function of not only vertex number but also weighing scheme and that the results of network-theoretic modeling should be interpreted with caution because of this variability. As brain network models are represented at progressively lower spatial scales (i.e., when using more and more nodes and edges to capture connectivity information), graph-theoretical model metrics are observed to exhibit substantial variability within three spatial regimes of quantitative and qualitative behavior, which are possibly modulated by the spatial folding scale of the human cortex.

Although many researchers are interested in exploring connectomics at the scale of cortical cytoarchitecture, there is substantial interest in connectomics studies at lower scales up to and including the cellular scale (Hua et al., 2015) and particularly in bridging the gap between micro- and macroscale connectomics, efforts which are reviewed elsewhere (Helmstaedter, 2013). These efforts suggest that our study can be of potential relevance to investigators interested in this direction of research.

Significance of the topological properties of graph network models

We propose that, when reporting and quantifying graph-theoretical metrics that are descriptive of brain connectivity models, researchers should always report the parcellation scheme, graph genus, nodal number, and edge weighing modality used in their study. Because the genus is a fundamental property of graphs (Abbasi, 2000; Nguyen and Bettayeb, 2011), this property is very important, and it is substantially easier to interpret other network metrics with prior knowledge of graph genera (Harary, 1994). Similarly, when comparisons are made between different studies, such parameters should always be taken into account to preclude inappropriate conclusions. As an analogy, it is useful to consider the fact that the significance of F and t values in statistics cannot be ascertained without knowledge of the corresponding d.f. Similarly, parcellation schemes, nodal numbers, and edge weighing schemes should always be specified by investigators and taken into account when comparing network metrics across studies because such comparisons are improper without knowledge of network parameters. Whereas graph-theoretical metrics have been reported and analyzed in numerous studies of brain connectivity, the topological properties of the graphs, which are used to represent brain connections, have received hardly any attention, despite the intimate relationship between graph topology, on the one hand, and graph-theoretical metrics, on the other hand. For this reason, we propose that the latter cannot be properly interpreted without thorough understanding of the former and that an important priority of future graph modeling studies should be to understand the topological structure and properties of brain network models.

Conclusion

In this study, the behavior of graph-theoretical measures pertaining to brain network modeling was explored as a function of cortical region number and connectivity weighing and was found to exhibit three distinct regimes as a function of spatial scale. The analysis suggests that network measures exhibit appreciable quantitative variations as a function of vertex assignment convention and edge weighing scheme and that graph-theoretic analysis results should not be compared across spatial scales without appropriate understanding of how the latter modulates network model properties. Importantly, we proposed that the parcellation scheme, nodal number, edge weighing modality, graph genus, and other topological properties should always be reported by connectivity studies and taken into account when comparisons across studies are undertaken. The lowest scale at which network measure behaviors were examined in the present study is closer to that of the cortical column than previously attempted. Partly because of this, this investigation and its findings have implications for the comparison of macro- to microscale studies of brain networks and for understanding how the choice of brain network model parameters can affect the interpretation of such studies.

Acknowledgments

The authors are grateful to Carinna M. Torgerson, S.-Y. Matthew Goh, and the dedicated staff of the Institute for Neuroimaging and Informatics at the Keck School of Medicine of the University of Southern California.

Author Disclosure Statement

No competing financial interests exist.