Abstract
Brain connectivity investigations are becoming increasingly multimodal and they present challenges for quantitatively characterizing and interactively visualizing data. In this study, we present a new set of network-based software tools for combining functional and anatomical connectivity from magnetic resonance imaging (MRI) data. The computational tools are available as part of Functional and Tractographic Connectivity Analysis Toolbox (FATCAT), a toolbox that interfaces with Analysis of Functional NeuroImages (AFNI) and SUrface MApping (SUMA) for interactive queries and visualization. This includes a novel, tractographic mini-probabilistic approach to improve streamline tracking in networks. We show how one obtains more robust tracking results for determining white matter connections by utilizing the uncertainty of the estimated diffusion tensor imaging (DTI) parameters and a few Monte Carlo iterations. This allows for thresholding based on the number of connections between target pairs to reduce the presence of tracts likely due to noise. To assist users in combining data, we describe an interface for navigating and performing queries in two-dimensional and three-dimensional data defined over voxel, surface, tract, and graph domains. These varied types of information can be visualized simultaneously and the queries performed interactively using SUMA and AFNI. The methods have been designed to increase the user's ability to visualize and combine functional MRI and DTI modalities, particularly in the context of single-subject inferences (e.g., in deep brain stimulation studies). Finally, we present a multivariate framework for statistically modeling network-based features in group analysis, which can be implemented for both functional and structural studies.
Key words: : diffusion tensor imaging, functional MRI, functional connectivity, resting state FMRI, structural connectivity, tractography
Introduction
Magnetic resonance imaging (MRI) provides several techniques for investigating brain connectivity. In particular, functional MRI (FMRI) and diffusion tensor imaging (DTI) are common modalities for observing aspects of functional gray matter (GM) and structural white matter (WM) properties, respectively. Given the complementary nature of these methods, it is often desirable to combine them in studies and this has been an increasing trend in both research (Bennett and Rypma, 2013; Damoiseaux and Greicius, 2009; Greicius et al., 2009; Horn et al., 2014; Staempfli et al., 2008; Sui et al., 2014; Zhu et al., 2014) and clinical applications (Kleiser et al., 2010; Pillai, 2010; Preti et al., 2014; Zhang et al., 2013).
The Functional and Tractographic Connectivity Analysis Toolbox (FATCAT) (Taylor and Saad, 2013) was initially designed to facilitate the integration of FMRI and diffusion-based imaging modalities. It contains tools for both task-based and resting-state FMRI, as well as for both DTI and high angular resolution diffusion imaging (HARDI), data. FATCAT is publicly available as part of the open-source Analysis of Functional NeuroImages (AFNI) package (Cox, 1996) and also interfaces directly with the three-dimensional (3D) visualization tools of SUrface MApping (SUMA) (Saad and Reynolds, 2012; Saad et al., 2004). While the toolbox can be used to calculate voxel-wise quantities, such as various functional connectivity parameters, it also contains functionality to calculate and visualize nonlocal features such as functional correlation matrices, whole-brain connectivity maps, tractographic maps, and structural connectivity matrices. These network-based features quantify brain structure and function at the highest levels of organization.
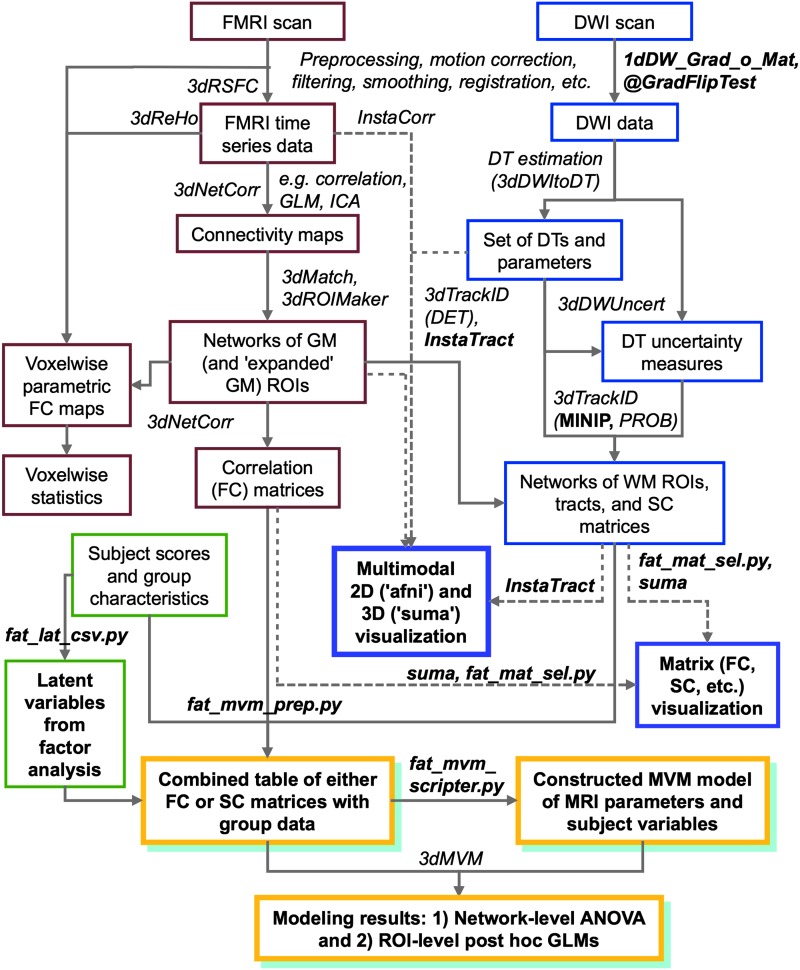
In this study, we present novel tools to facilitate multimodal network-based analyses for both individuals and groups. First, we describe a novel, mini-probabilistic (MINIP) tractography approach, which improves the robustness of streamline tract reconstructions by including DTI parameter uncertainty. Second, we discuss interactive visualization features using SUMA and AFNI, allowing the simultaneous display and investigation of DTI and FMRI data. Finally, we present a two-tiered, multivariate modeling approach for combining either functional or structural network connectivity with group characteristic data using functions in AFNI and FATCAT. Figure 1 displays a compact schematic showing the potential roles of the new features (highlighted in bold) in an analysis pipeline that includes functional, diffusion-based structural, and group characteristic data.
FIG. 1.
An example schematic for combining multimodal magnetic resonance imaging (MRI) data, that is, functional (red) and diffusion-based structural (blue), with non-MRI group characteristic information (green) using Analysis of Functional NeuroImages (AFNI), SUrface MApping (SUMA), and Functional and Tractographic Connectivity Analysis Toolbox (FATCAT). The novel tools described in this work are highlighted in bold text, and secondary colors reflect the combination of various types of data. The pipeline incorporates command line tools and interactive user visualization, which are both important features of data analysis in MRI. Color images available online at www.liebertpub.com/brain
MINIP Tracking Methods and Results
The human data shown in this work were acquired from a control subject of a larger study, which obtained participants from university campuses in Taipei. Participants were enrolled having provided written informed consent. The study was approved by the local ethics committee and conducted in accordance with the Declaration of Helsinki. Details of the scanning and acquisition parameters are provided in Taylor and Saad (2013).
MINIP tracking
Existing methods of DTI (and HARDI)-based tractography techniques fall mainly into two categories: deterministic (DET) (Basser et al., 2000; Conturo et al., 1999; Mori et al., 1999) and probabilistic (Behrens et al., 2003; Parker et al., 2003) tracking. In the first case, tracts propagate outward from seed points until some stopping criterion is reached; propagation through a given voxel may, for example, be oriented parallel to the local principal eigenvector (Mori et al., 1999; Taylor et al., 2012) or to some weighted average of neighboring eigenvectors (Lazar et al., 2003). The DET output is a set of tracts embedded within the brain volume—that is, a 1D sequence of points, each of which has three spatial coordinates and possibly attached properties such as DTI parameter values. While useful in many applications, these reconstruction methods either ignore the noise that is inherently present in the acquired data or introduce smoothing to try to reduce its impact. Noise introduces errors into DTI or HARDI model fits, and as a result, tracts that are propagated purely deterministically become susceptible to a sizeable error accumulation (both false negatives and false positives).
In contrast to DET approaches, probabilistic methods typically perform Monte Carlo simulations of repeated tracking through distributions [e.g., estimated using Bayesian (Behrens et al., 2007) or statistical resampling (Jones, 2003; Taylor and Saad, 2013; Whitcher et al., 2008) techniques] of voxel DTI parameter values. The end result of probabilistic tracking is an unordered set of voxels in 3D space through which a large fraction of generated tracts have passed, and this region is interpreted as comprising the subvolume of the brain with the highest likelihood of containing WM connections of interest. While the probabilistic methods account for noise-induced diffusion model uncertainty, they are often relatively slow and impractical for interactive investigation. Moreover, the final voxel maps that are produced lack the ordered sequential structure of the linear tract results, which are often useful for intersubject comparisons (Colby et al., 2012; Yeatman et al., 2012).
In this study, we propose a novel hybrid tractographic approach called mini-probabilistic tracking to combine benefits of both fully probabilistic (PROB) and DET techniques. The new method makes use of the voxel-wise uncertainty of DTI parameters in the tracking process, performing a small number of Monte Carlo simulations through perturbed tensor estimates. The ordered tract structure remains intact, but more robust results are obtained by including the probabilistic distribution of tensor values during tract propagation. Similar to PROB approaches, the repeated tracking reinforces the more likely locations of tract bundles,1 while noise-driven outliers tend to be isolated. However, the MINIP method is significantly faster than the full approach as it generally uses several orders of magnitude fewer tracking iterations.
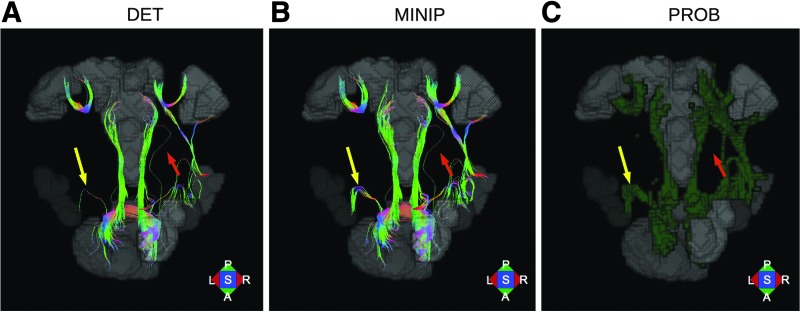
A comparative example of approaches is shown in Figure 2. Tracking was performed on a network of target regions (here, corresponding to an adult subject's default mode resting-state network, from data available in the FATCAT demo2) using AND-logic with the FATCAT 3dTrackID function in three separate modes: (A) DET, (B) MINIP, and (C) PROB. The same basic tract propagation criteria were used in each case: fractional anisotropy (FA) >0.2, turning angle <60°, and tract length >20 mm. For DET and MINIP tracking, eight seed points per voxel were used and the latter was performed using five Monte Carlo repetitions. Parameters for PROB tracking were 5 seed points per voxel, 1000 Monte Carlo iterations, and a threshold fraction of 0.05 [so that 5 × 1000 × 0.05 = 250 tracks/voxel were required to be included in the final WM regions of interest (ROIs)]. DTI parameter (FA and first eigenvector) uncertainty maps for MINIP and PROB tracking were calculated with FATCAT 3dDWUncert using 300 iterations (Taylor and Saad, 2013). While the overall locations of estimated WM ROIs are broadly similar, there are noteworthy differences across the methods.
FIG. 2.
Comparison of tractography results of FATCAT 3dTrackID in different modes: (A) deterministic (DET), (B) miniprobabilistic (MINIP), and (C) fully probabilistic (PROB). AND-logic connections are shown for a network of targets (gray) using either tracts colored by local orientation in (A, B) or probabilistic volumes shown as green surfaces in (C). The yellow and orange arrows highlight single-fiber connections between pairs of targets using the DET mode; in the MINIP results, the former appears to be reinforced by the repeated uncertainty-based tracking, while the latter remains an outlier. This is verified by comparison with the PROB results and suggests the increased robustness of the MINIP method compared with DET. Color images available online at www.liebertpub.com/brain
Arrows in Figure 2A highlight two DET tractographic bundles, each consisting of a single fiber. In Figure 2B, the MINIP results show several similar fibers for the laterofrontal connection (yellow arrow) and no additional connections for the anteroposterior fiber (orange arrow). These results suggest that the first is likely to be a bundle connection (as small perturbations produced similar tracks) and the second an artifact due to noise. A comparison with PROB volumes in Figure 2C appears to verify these interpretations. It is worth noting that several of the other fiber bundles in Figure 2B appear to be more robust than those in Figure 2A as well as in greater volumetric agreement with the PROB results. Additionally, while false positives (relative to PROB) are apparent in both the DET and MINIP results above, they are more visually apparent in the latter case. When performing DET and MINIP tracking with FATCAT 3dTrackID, bundles between targets having a small number of tracts (as highlighted in Fig. 2) can be removed to filter connections that are likely the result of noise; this editing is done by selecting a minimum threshold for the number of tracts required to be found in any bundle.
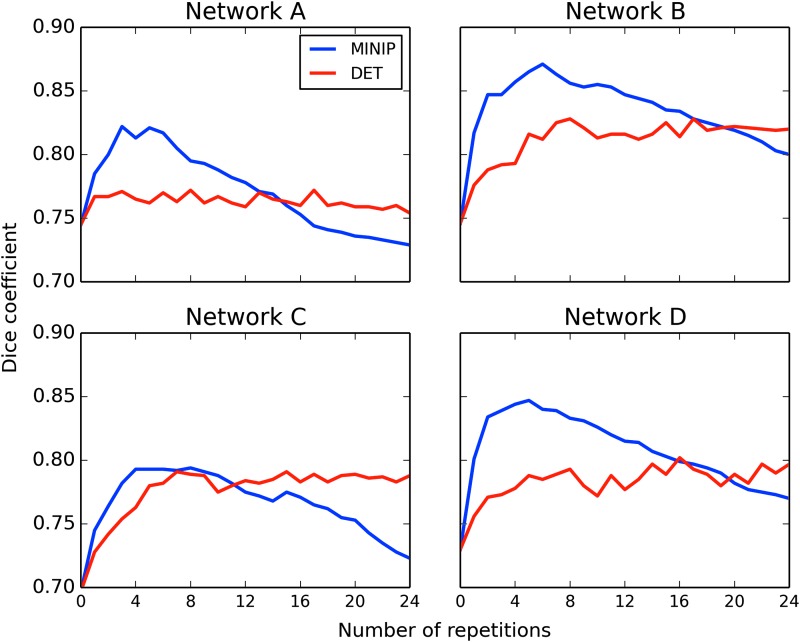
The extents of the WM regions obtained using DET and MINIP approaches were quantitatively compared with PROB results using Dice coefficients (Dice, 1945). Tracking was performed using the same basic parameters described above for the four networks available in the FATCAT Demo set (which includes the network shown in Fig. 2) using AND-logic. Volumetric masks of regions containing tracts were created for all tracking modes. In MINIP mode, the number of additional perturbed repetitions was increased from 0 to 24, and in DET mode, the number of seeds per voxel was increased to maintain an equivalent number of total initiated tracts per voxel (e.g., while MINIP had 1, 2, and 3 repetitions, there were, respectively, 16, 24, and 32 total seeds per voxel for DET). In both MINIP and DET modes, tract bundles between two targets in the ith repetition were removed if they contained fewer than 4i tracts to filter out results likely due to noise.
The Dice coefficients of overlap with the PROB masks are shown in Figure 3 for each of the four networks (Network A is the same as shown in Fig. 2). In all cases, the Dice values for MINIP results rise quickly and have a peak greater than (or in one case, approximately equal to) the DET ones. The DET results increase and reach a plateau, after which adding more seeds per voxel results in very little change in results. In the MINIP case, the addition of Monte Carlo repetitions increased the similarity to the PROB results quickly, with a peak Dice coefficient typically reached using five to seven MINIP iterations. The subsequent slow decrease of matching is due to the fact that the PROB method applies a stricter voxel-wise thresholding criterion than the bundle threshold. While artifacts are expected to be present in some degree in all tractographic reconstructions (Thomas et al., 2014), the preceding examples show that the inclusion of tensor uncertainty information greatly increases the reliability and robustness of rendered results, and in the MINIP case, with very little computational cost.
FIG. 3.
Comparison of AND-logic DET and MINIP tracking with PROB results. Dice coefficients were calculated between regions containing tracts in each of the DET and MINIP modes with those in the PROB mode. The number of Monte Carlo repetitions in the MINIP mode was increased to 24, and the number of seeds per voxel equivalently increased in the DET mode. MINIP results rise quickly and have a peak greater than (or equal to, in one case) those of DET, with a maximum occurring at approximately five to seven repetitions in each of the networks. Color images available online at www.liebertpub.com/brain
Visualization and Interaction
Visualization and user interaction when analyzing data are important for both research and clinical usage. Having multimodal data complicates these tasks as there are necessarily several different types and formats of information to combine. Moreover, in modern brain research, it is common to have several networks to analyze together even when using only a single modality, such as in resting-state FMRI. The important question arises: How can one synthesize, view, and explore the information efficiently?
FATCAT interfaces directly with the AFNI and SUMA viewers, which provide 2D and 3D representations, respectively. These viewers also communicate with each other (and with other programs), and together, AFNI and SUMA render volumes, surfaces, tracts, outlines, and matrices. SUMA and AFNI can also be controlled from the command line, making them suitable for navigating large amounts of data by scripting user interface tasks that are to be repeated for each new set of data. In this study, we highlight the more unique aspects of the software relating to network connectivity.
Tract navigation and InstaTract
Tracts are rendered as segments between the sequential control points generated by 3dTrackID, and the SUMA interface allows for the selection of individual tracts with the mouse pointer. The selected location is automatically relayed to AFNI, causing it to update its own crosshair location. When viewing whole-brain tractography results, it is often difficult to distinguish between certain tracts without pruning obstructing ones to highlight a feature of interest. In most DTI viewing software [e.g., DTI-Query (Sherbondy et al., 2005), TrackVis (Wang et al., 2007), and 3D Slicer (www.slicer.org)], the highlighting masks can be positioned on locations defined by cortical surface models or by voxel grids. Navigation of these masks within the voxel grid is usually constrained to displayed slices, which are determined by the scanner coordinate system, while navigation on surfaces is restricted to the cortical GM sheet, even though it is WM being investigated.
Similar highlighting modes exist in SUMA, termed InstaTract, in which multiple ROIs can be defined over volume or surface grids of arbitrary resolutions and orientations, but the ROIs can additionally be positioned and steered along the tracts themselves. This ability makes it possible for one to walk along a tract in 3D, instead of being confined to an arbitrary surface that is not geometrically related to the WM geometry. It also avoids a difficulty present in many software programs that are constrained to 2D slices since the fibers cross through surfaces at various angles in any given scan, posing a challenge to follow the WM trajectories and to monitor along-tract intersections. The highlighting is carried out along each tract based on the outcome of the user-defined, arbitrary Boolean function of the ROIs, which themselves can currently be spheres or parallelepipeds (boxes). Thus, users may test AND- and OR- logic of connections between simple geometric volumes in InstaTract mode, navigating the shapes along the tracts themselves by clicking or dragging. While such geometrically defined masks can be interactively repositioned and resized, arbitrary ROI surfaces/masks are stationary as they represent particular anatomical features.
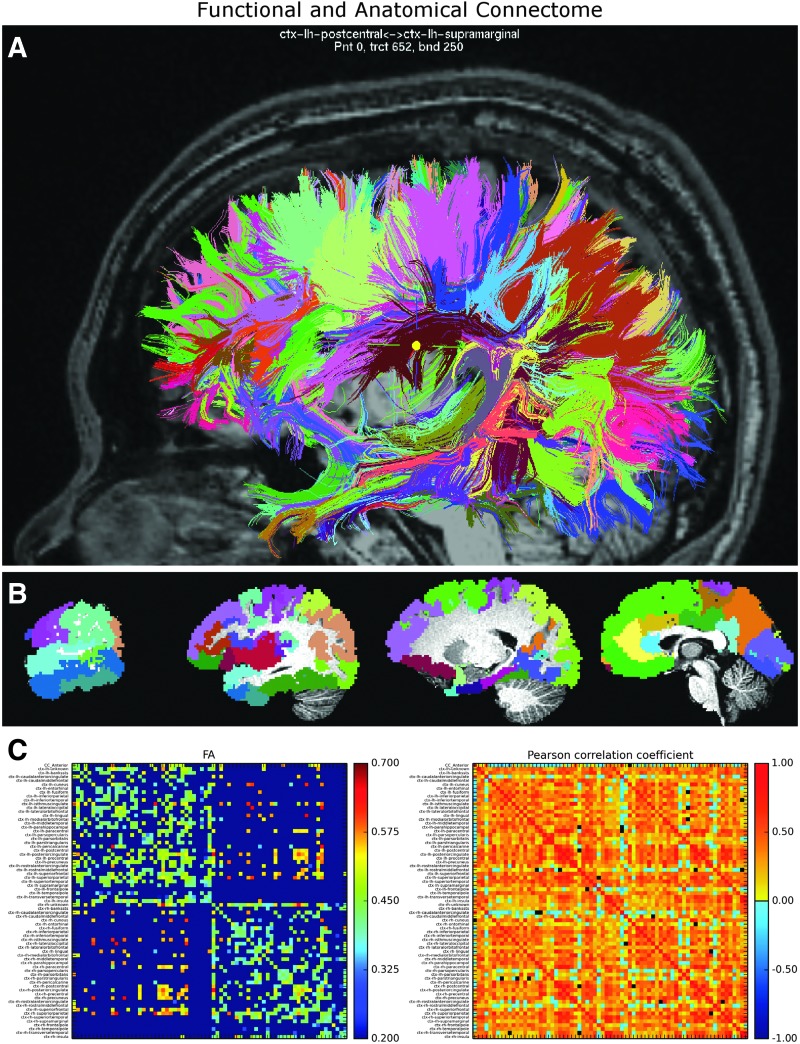
Furthermore, FATCAT groups the tracts between a given target pair into bundles that can be rendered in different colors and identified with text (i.e., the names or labels of the targets themselves) when the user selects a location on a tract. These features are useful when viewing a complicated set of tracts, for example, in the output of a connectome, which has several neighboring targets from whole-brain parcellation. The bundle viewing and selection features are shown in Figure 4A, where the names of the targets that are connected by the selected bundle (i.e., the bundle in which the crosshairs have been placed) are displayed at the top of the panel, along with the point location along the tract and the tract number designation. The tracts themselves were created using AND-logic DET tracking within a connectome whose targets are cortical regions defined by FreeSurfer (Fischl, 2012; Fischl et al., 2002) parcellation (shown in Fig. 4B).
FIG. 4.
(A) Shows tractographic connectome bundles among a set of anatomical cortical regions generated using FreeSurfer parcellation (data available in the FATCAT Demo set). Tracts are colored by bundle [i.e., the set of tracts connecting a particular pair of target regions of interest (ROIs)], and in (B), the target ROIs are shown in color as slices in a simultaneous AFNI viewer. Connectome tractography results are readily generated with a single command line; the target ROIs and tractographic results in this figure can be obtained using the guided FATCAT Demo script, Do_11_RUNdti_Connectome_Examp.tcsh, and the presented results were generated in <30 sec. An example of the labeled bundle selection is shown in (A) for the location of the yellow crosshair. (C) Shows labeled structural [fractional anisotropy (FA)] and functional (Pearson correlation) matrices for this connectome generated from a command line using fat_mat_sel.py (see the Appendix). Color images available online at www.liebertpub.com/brain
The names of the volumetric ROIs, output by FreeSurfer (and formatted using @SUMA_Make_Spec_FS) for the data in Figure 4, are stored as labels within the network data set, and label pairs are attached to each tract bundle. For ROI volumes without accompanying labels, there are AFNI tools (@MakeLabelTable or 3dROIMaker) to pair each integral ROI value with a user-defined string and to create a label table that can be attached to volumes and surface-based data sets. The labels are propagated from ROIs to their tractographic connections when using 3dTrackID, simplifying the visual interpretation and referencing of results in further AFNI and SUMA analyses. The labels are also contained in the output files of structural and functional connectivity matrices, which can be loaded into SUMA (see below in “Connectivity graphs” and in “Live computations,” and Fig. 5), as well as viewed and saved directly from the command line, as shown in Figure 4C (see also Appendix).
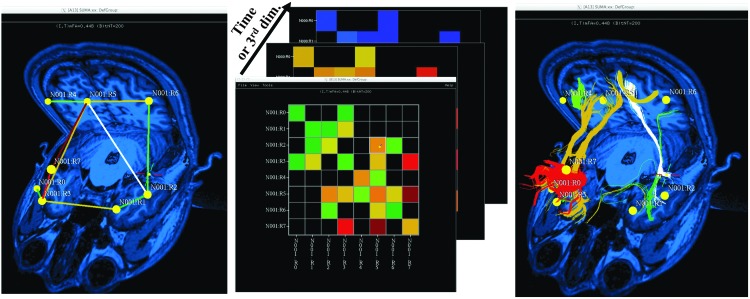
FIG. 5.
Rendering of connectivity matrices in SUMA. The first two panels show the three-dimensional (3D) graph and matrix rendering modes of the data. In this mode, off-diagonal matrix elements are rendered with straight-line edges whose colors reflect the feature's value in the matrix (middle panel), as per the user's selected settings. The panel on the right shows the same graph, but with tractography bundles used to represent the connections, as opposed to segments, and the bundle coloring remains based on the connection value in the matrix. All views support selection of either an individual connection (the equivalent of one element of the matrix) or the set of connections to and from a single node (the equivalent of one row/column of the matrix). In addition, as noted in the middle panel, one can interactively cycle through time-varying matrices or any stack of matrices with the same dimensions. The rendering of data in this figure can be obtained using the guided FATCAT Demo script, Do_09_VISdti_SUMA_visual_ex2.tcsh. Color images available online at www.liebertpub.com/brain
Connectivity graphs
Connectivity data (such as FMRI correlations from 3dNetCorr, structural WM properties from 3dTrackID, connectivity estimates from structural equation modeling, or Granger causality analysis from 1dSVAR) can be rendered as a 3D-embedded graph or as a matrix. The dual modes can be rendered simultaneously in separate linked viewers. In graph mode, the connections (i.e., off-diagonal elements of the connectivity matrix or graph edges, equivalently) can be represented by straight line segments or by tract bundles whenever available and desired, as illustrated in the left and right panels, respectively, of Figure 5. The representation is colored by the value of the connection/element, as per the settings of the data mapping interface.
A displayed connection can also be selected by clicking on it, as demonstrated by the white highlights in Figure 5. In matrix mode, a connection is represented as a colored cell element and can also be selected with a mouse click (again demonstrated in Figure 5 by the element outlined in white) to display information about the connection such as magnitudes and names of the region pair. For dense connectivity graphs, it is useful to consider connections to or from a single node at a time. This operation is done interactively by selecting the target node either by clicking on its graphical representation (e.g., a ball) or its names in both matrix and 3D graph rendering modes. We also note that the interface can handle multiple values per connection, such as a time-varying connectivity matrix or a set of matrices of different properties.
Live computations: multimodal data surfing
Navigating connectivity data is particularly challenging since it essentially squares the number of values one has to display and select. We described in the previous sections how one could highlight (or alternatively prune) tracts, bundles, and graph connectivity to digest the data for a few target regions at a single time. In this section, we present features for adding resting-state functional connectivity to results in a manner that allows one to perform interactive simultaneous anatomical and functional connectivity queries. The description also serves to illustrate other novel attributes of the software.
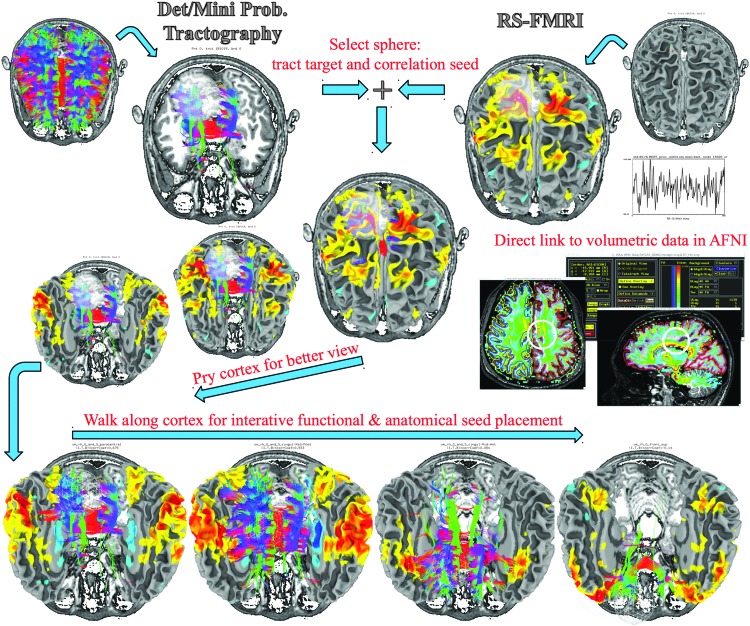
We begin by briefly describing InstaCorr, which allows one to perform interactive pattern matching (e.g., by using correlation) between a particular data source (seed) and the rest of the time series data set defined over the same domain (surface or volume). For instance, with the click (or click and drag) of the pointer, a new correlation map is computed and displayed using the seed at the pointer's location. The seed location can be set by clicking anywhere in either SUMA or AFNI: computed correlations are displayed in AFNI through InstaCorr and sent to SUMA for display on the surface models (Fig. 6). The same seed location can be used to set the location of the tract-selecting ROI mask in InstaTract. To view tracts within the surface, while still viewing the functional connectivity on the surface, one can pry apart the cortical surfaces. As illustrated in the lower part of Figure 6, the surfaces retain their coloration and a record of their coordinates in closed space during further manipulations.
FIG. 6.
An illustration of the process for interactive, single-subject functional, and anatomical connectivity queries. (Note that all displayed objects are loaded into the same AFNI and SUMA sessions, and subsets are shown at a time here for clarity.) The top row, left, illustrates whole-brain tractography results computed with 3dTrackID and displayed over a single anatomical slice for reference. The top row, right, shows the FreeSurfer-generated cortical models. Users can then select a mask (white sphere) and restrict the displayed tracts to those passing through it (via InstaTract). That same mask can be used to set the seed location for automatically generating a functional connectivity correlation map (via InstaCorr), the results of which are shown in color on the cortical surface. As described in the text, the placement of the seed can be done in the 3D views of SUMA or in the 2D views of AFNI. The results of the anatomical and functional connectivity queries are rendered together in the middle of the figure. Since seeing through the cortical surface is difficult, even when transparency is enabled (not shown here), the user can pry the cortex open with the mouse pointer, better revealing the patterns of anatomical and functional connectivity (lower middle path). The user can then navigate the seed along the pried cortex, or along any other rendered structure, to update the seed placement and to trigger an update of both the anatomical and functional connectivity results (bottom row). The illustrated tasks can be recreated with the guided FATCAT Demo script, @Do_09_VISdti_SUMA_visual_ex3.tcsh. Color images available online at www.liebertpub.com/brain
Group-Level Statistical Analyses
Multivariate modeling of networks
In this section, we describe a two-tiered analysis for investigating the associations of either functional or structural data with predictors of interest across a group. FATCAT functions are used to combine MRI results with group descriptive data and to allow the user to define a model for the AFNI multivariate modeling program, 3dMVM (Chen et al., 2014).
The first stage of analysis takes place at the network level, where multivariate modeling is performed, since it is applicable for analyzing sets of nonindependent measures. That is, a group of simultaneous, MRI-derived response variables at each spatial location (e.g., WM properties throughout a set of tracked ROIs or GM correlations within a functional network) is modeled by multiple explanatory variables (e.g., sex, age, behavioral measures, and clinical measures). This modeling can be performed independently for each separate response (data) variable, such as (depending on the types of data available) Pearson correlation, FA, mean diffusivity, T1 relaxation time, proton density, and tracked ROI volume.
Even though the conventional multivariate model precisely characterizes the above hypotheses, its power performance is lackluster in real practice. To address this, the 3dMVM function utilizes an approximation approach within the multivariate platform, which, in conjunction with a few auxiliary tests, can achieve a higher statistical power than conventional multivariate testing while still maintaining well-controlled false positives (Chen et al., 2015). This approach essentially looks for a significant effect at any single or any combination of network connections. Then, if significant effects are found at the network level, the second stage of analysis implements post hoc tests for each connection to determine, for example, which individual elements show the strongest relationships driving the network effects.
A practical example of this network analysis with 3dMVM is presented in Figure 7 for the case of a WM study (NB: the following example could equivalently be of a GM study, using functional connectivity strength as the between target quantity of interest). The researchers may pose the question: Are CASI (cognitive abilities screening assessment) score values in a particular population associated with WM properties, such as FA? This relationship can be investigated while controlling for other explanatory variables, such as age, sex, and years of education. First, the researchers generate the targets in each subject's diffusion space for tracking, perhaps by mapping sets of functional GM ROIs. Then, tractography (e.g., mini- or fully probabilistic) is performed to determine the most likely locations of WM associated with pairs of the targets, producing a set of WM ROIs throughout the network. From each region, one can calculate a representative quantity, such as the mean FA, producing a set of simultaneous measures that represent the WM connections throughout the network. The first step of 3dMVM analysis includes the full set of response variables (i.e., all mean FA values), examining whether the network's WM as a whole is related to CASI scores. If there is a relationship found at a nominal significance level (e.g., 0.05), the 3dMVM second step of analysis investigates which region(s) has(ve) the strongest associations (i.e., most statistical significance), using a general linear model for each mean FA with the same set of explanatory variables.
FIG. 7.
An example case of combining 3dTrackID tractography and 3dMVM multivariate model testing to investigate the relationships of white matter (WM) properties (here, FA) and subject test scores [here, cognitive abilities screening assessment (CASI) values] while controlling for other factors. The investigation is first made at the network level, and if significant relationships are observed, one follows up using post hoc general linear models (GLMs) for the same model for each ROI. This procedure may equivalently be performed using 3dNetCorr's functional connectivity estimates between pairs of targets in a network in place of tractography. Color images available online at www.liebertpub.com/brain
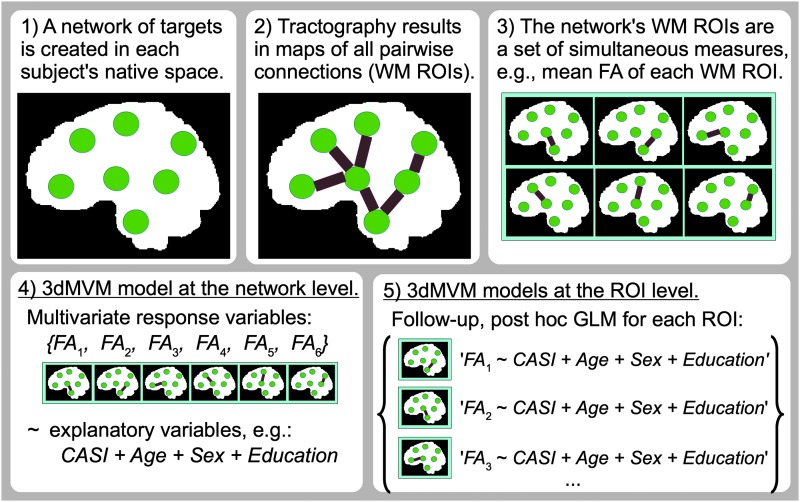
The general implementation of this process with FATCAT and AFNI 3dMVM for any functional or structural network properties is illustrated in Figure 8. Starting with (A), a network of ROIs for FMRI/DTI analysis, then 3dNetCorr/3dTrackID can be used to calculate (B) functional/structural matrices for each subject in the group. In step (C), the set of connectivity matrices is then combined with a descriptive group table that holds columns of quantitative or categorical variables such as age, sex, psychometric test scores, and genetic factors (e.g., a file exported from a spreadsheet, with one row of values per subject). The synthesis of the MRI-derived matrices and the group variables is made using fat_mvm_prep.py, which creates a single multivariate table for the group. This program also automatically selects only functional/structural matrix elements that are present for all subjects in the group as the multivariate modeling software does not currently account for missing data in individuals. This selection procedure may be necessary in FMRI studies, for example, if subjects have different numbers of ROIs in a given network, or in DTI studies, where each region is typically not directly connected to all others and the patterns of estimated connections often exhibit variation across a group.
FIG. 8.
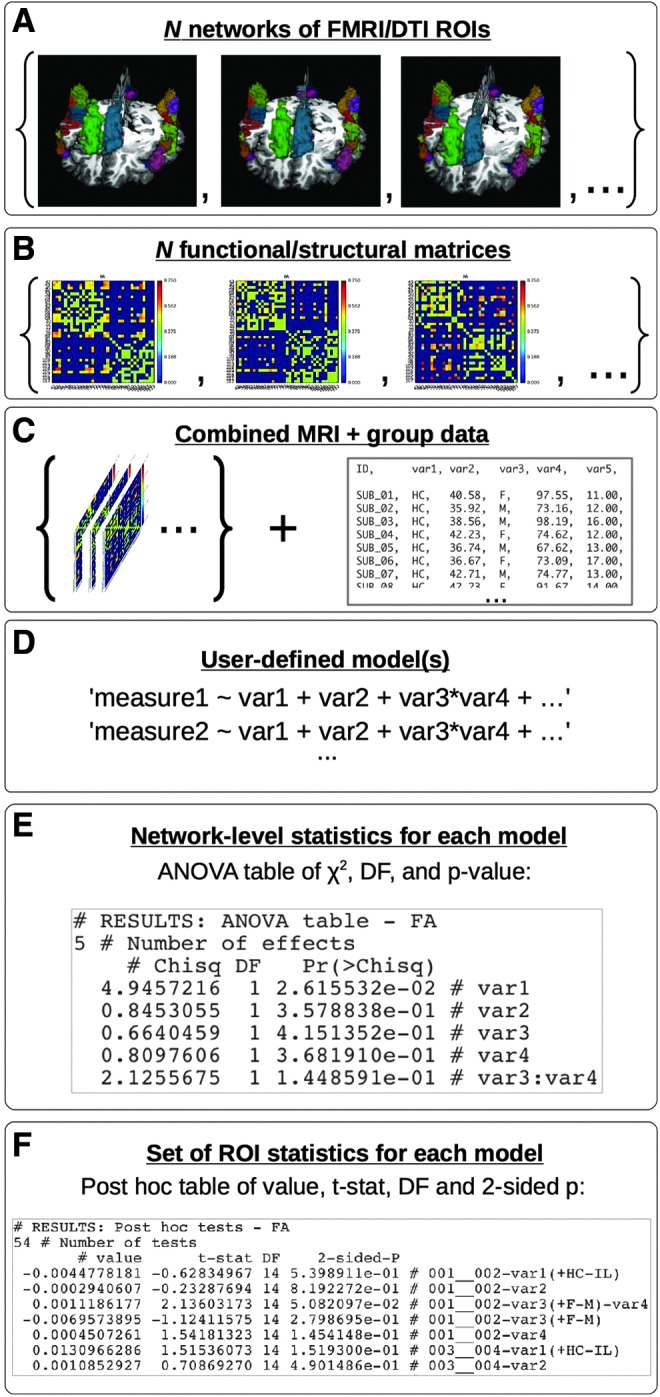
A schematic for integrating MRI-based connectivity and group characteristic data in network-based analyses using multivariate statistics with FATCAT and 3dMVM. For a detailed description of steps A-F, see the text in “Multivariate modeling of networks.” Briefly, one starts with (A) a network of ROIs, from which (B) functional or structural connectivity matrices are calculated for each subject (e.g., using 3dNetCorr or 3dTrackID, respectively). (C) The set of connectivity matrices are then combined with any group characteristic data into a single table. The user then specifies (D) a statistical model to examine relations at both (E) the network-level and (F) the individual ROI level. Color images available online at www.liebertpub.com/brain
The user then specifies symbolically (D) a model with explanatory variables from the group table variables. The model may include both quantitative and categorical variables (the latter of which are tested with omnibus F-tests), such as age and sex, as well as interactions between the variables. The model of interest is entered as a simple list to the function fat_mvm_scripter.py, which builds both the group model and the follow-up post hoc tests for each ROI in the AFNI 3dMVM command (Chen et al., 2014). The result is a script to be executed, producing both (E) network-level and (F) individual connection-based results. This methodology has been demonstrated in a DTI study of infants with prenatal alcohol exposure (Taylor et al., 2015). The two-tiered analysis was used to locate WM that showed a significant association between alcohol exposure and structural properties, as well as to determine which diffusion parameters showed the greatest sensitivity to exposure.
Creating latent variables from a group table
Often in brain imaging studies, a variety of supplementary data have been collected for subjects in the group, such as psychometric tests, neurobehavioral scores, and other descriptive characteristics. Many of these factors are often not independent, while also being attributable to a small number of underlying features of interest, such as attention, working memory, and emotional state. They may have the additional practical limitation of possessing low individual contrast. In such a scenario, factor analysis can be used to derive a set of latent variables from the original correlated group of factors, reducing the dimensionality of the data based on their covariance structure. FATCAT now includes a command line factor analysis tool to estimate such latent variables from quantitative variables in a group table.
The FATCAT program, fat_lat_csv.py, implements the function factanal() in the package FAiR (Goodrich, 2014) of the open-source language R (R Core Team, 2014). To simplify the final variable structure, the loadings table is rotated using the varimax method (Kaiser, 1958). To facilitate interpreting what features the output latent variables represent, the calculated Thompson scores (Thomson, 1951) for each factor's variables are also reported. The number of latent variables (i.e., the dimensionality reduction) can be chosen by the user or by a data-driven methodology using parallel analysis. The latter is implemented using the R function paran() in the package paran (Dinno, 2012), which utilizes Horn's method to evaluate factors (Horn, 1965). By default in fat_lat_csv.py, Horn's method is run with a large number of Monte Carlo iterations (5000) and a high centile threshold (99%) to reduce bias in the chosen number of components (Glorfeld, 1995). The estimated latent variables are then included in a new group table for use in the multivariate testing, as described above.
Discussion
We have presented several new tools3 that are available in FATCAT, highlighting their integration with novel functionality and features in AFNI and SUMA. The methods have been designed to increase the user's ability to visualize and combine FMRI and DTI modalities, as well as to easily explore statistical relationships in group studies.
MINIP tractography has been introduced as an enhancement to purely DET tracking in networks. The uncertainty-based procedure improves the detection of connections, while bundle thresholding reduces the likelihood of obtaining tracts sensitive to noise (as does the typical sparsity of target volumes in functional networks). Importantly, these benefits come at very little computational cost (unlike the full probabilistic tracking software), and this method preserves the sequential organization of fiber bundle reconstructions for individual or group analyses.
MINIP tracking has also been implemented in exploratory structural analyses, such as placing target ROIs within related WM (Taylor et al., 2015). Such investigations highlight the utility of interactive data visualization, in particular with the combination of SUMA and AFNI. These visualization methods are directly applicable in a clinical realm to investigate estimated structural maps within the brain. For example, recent studies have utilized tractography reconstructions to guide the placement of electrodes for deep brain stimulation (Rive-Posse et al., 2014). The simultaneous viewing of FMRI and DTI data allows for a more detailed representation and exploration of complicated function/structure interactions within the brain. Being able to visually navigate through multimodal data sets at the same time allows one to develop a deeper understanding of the potential, and the limitations, of the data at hand. This is a crucial exercise for enabling the discovery of otherwise un-noticeable artifacts (Jo et al., 2010) or of striking features of the data (Gotts et al., 2013). While the multimodal visualizations and explorations in this work have been focused on individual subjects, it should be noted that the InstaCorr interface in AFNI and SUMA can also be used to perform group-level, seed-based correlation contrasts interactively, which is beyond the scope of the work presented herein (Cox, 2012; Saad and Reynolds, 2012).
Finally, methods for implementing network-based statistical group analyses were described. FATCAT now contains command line programs for performing factor analysis to estimate latent variables within a group characteristic table (fat_lat_csv.py) combining functional correlation and structural matrices from MRI analyses with group tables of subject data (fat_mvm_prep.py); and building a model for multivariate analysis with AFNI 3dMVM (fat_mvm_scripter.py), calculating both the network- and ROI-based statistics. Each function is run with a simple set of options and parameter lists. There are typically several connectivity parameters calculated and output into a single file by FATCAT 3dNetCorr (e.g., Pearson correlation, Fisher Z score, and partial correlations) and 3dTrackID (e.g., WM volume, FA, MD, L1, RD, and number of tracts). For efficient examination of these parameters simultaneously, the FATCAT programs apply the user-defined multivariate models to each individual parameter matrix in parallel, and then output the results (both network and post hoc statistics) to a single file.
The presented techniques allow investigation of the network levels of brain functional and structural connectivity in an individual, which are often of interest in neuroimaging studies. In contrast to voxel-based methods, which often have tens of thousands of voxels (or more, with the increasing resolution of modern scanning techniques), this approach has the advantage of not requiring such severe corrections for multiple comparisons. As a consequence, these multivariate methods can be used to explore comparisons of properties across networks or among the parameters themselves (Taylor et al., 2015). The post hoc tests of each matrix element (i.e., target connection) then provide finer resolution for describing relative connectivity–predictor associations on a smaller local scale.
Further development of FATCAT will include approaches for utilizing along-tract statistics in characterizing individuals' WM properties. In addition, to be able to account for missing data in group tables, future versions will utilize linear mixed-effects (LME) modeling using AFNI 3dLME (Chen et al., 2013). It is also expected that (as has already happened since the initial FATCAT release) further analysis tools will be developed in response to users' requests.
Appendix
We highlight some of the additional tools and features that are newly available in Functional and Tractographic Connectivity Analysis Toolbox (FATCAT) for the processing of diffusion tensor imaging and functional magnetic resonance imaging (FMRI) data. Scripted examples of each are provided in the freely available FATCAT and FAT_MVM Demos.4 Most of these features have been developed to increase the ease of processing and investigating data, which may have the important consequence of reducing processing mistakes as well as of aiding the understanding of results.
It should first be noted that the originally separate FATCAT functions for deterministic and probabilistic tracking have been combined into a single function (3dTrackID), which can now be operated in three separate modes: DET (deterministic), MINIP (mini-probabilistic; see the introduction in the main text), and PROB (fully probabilistic). Tracking can also now be performed on data sets with multiple propagation directions per voxel, as in high angular resolution diffusion imaging (HARDI) reconstructions. HARDI model fitting is not currently available within FATCAT or Analysis of Functional NeuroImages (AFNI), but instead can easily be estimated using other packages, for example, DSI-Studio (http://dsi-studio.labsolver.org; an example processing script is included in the FATCAT Demo), Diffusion Toolkit (Wang et al., 2007), or Dipy (Garyfallidis et al., 2014). While preprocessing functions for the correction of subject motion, eddy currents, and EPI distortions are not available in FATCAT or AFNI, these may be found easily in other software, such as TORTOISE (Pierpaoli et al., 2010), which has an AFNI format output option.
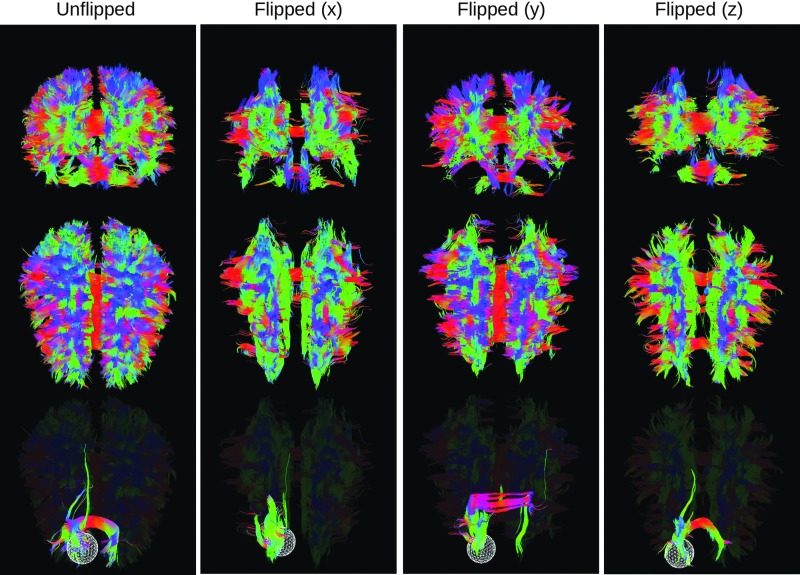
The formatting of diffusion gradient information varies across software packages and applications, requiring various conversions between rows and columns (e.g., when converting from DICOM); gradients and either row-first or diagonal-first tensors (e.g., when using TORTOISE); including b-values in a separate file or in the gradient file (e.g., if using DSI-Studio); including a row of zero gradients or not (e.g., when using AFNI 3dDWItoDT); etc. As diffusion weighted imaging (DWI) processing often requires the use of several packages and functions, it is useful to have a flexible command line tool for converting among these formats. In FATCAT, 1dDW_Grad_o_Mat is able to convert b-value and b-vector information among the above-listed format options. Additionally, the signs of gradient components can be flipped to convert a given scanner coordinate convention to that of the chosen software tool. Due to the DT symmetry properties, this sign change does not affect scalar parameters, but it will cause rotations in the eigenvectors, whose effects are highly noticeable in tractography (see comparisons with various relative gradient flips in Fig. A1). For example, often data acquired using Siemens 3T scanners (Erlangen, Germany) require a sign change in the y-component (via the switch -flip_y) before using FATCAT 3dTrackID (although each center must check their own data, particularly when preprocessing with any given software package). A FATCAT script file, @GradFlipTest, uses whole-brain tracking to estimate an appropriate gradient flip for a data set, subject to visual verification.
FIG. A1.
Effects of not correcting recorded gradient vectors by flipping the sign of an affected component. Whole-brain tractographic reconstructions are shown (from the left) for corrected gradients and gradients with alternately uncorrected x-, y-, and z-components. Views in descending order: coronal from front, axial from above, and the latter repeated with a spherical selection mask. Color images available online at www.liebertpub.com/brain
The DWI data sets may also be processed simultaneously with, and using information contained in, the gradient table. 1dDW_Grad_o_Mat utilizes the b-value or -vector information to locate b0 volumes in the DWI protocol and to average them together to create a single b0 reference with high signal-to-noise ratio (-proc_dset option). Additionally, 1dDW_Grad_o_Mat can compress acquisitions with repeated sets of gradients by averaging those volumes and adjusting the gradient table to match (-dwi_comp_fac option).
For FMRI processing, 3dNetCorr has been updated to include several features. In addition to Pearson correlation and Fisher Z-transform connectivity matrices, partial correlation matrices can be calculated (-part_corr). Moreover, when calculating connectivity matrices, one can also simultaneously generate whole-brain connectivity maps for the average time series of each region of interest (ROI), either as Pearson correlation (-ts_wb_corr) or Fisher Z scores (ts_wb_Z). The output connectivity matrices may also contain ROI labels from a user-defined table (such as from anatomical parcellations). The functional matrices (as well as those output by 3dTrackID) may be viewed as connected graphs in SUMA with the edges colored by the element values (see Fig. 5 in the main text); additionally, these matrices may be viewed and saved in two dimension using a new command line tool, fat_mat_sel.py, allowing for rapid selection and customization of the figures (Fig. 4C in the main text).
Acknowledgments
The authors would like to thank Silvina Horovitz for constructive comments on the draft and Ching-Po Lin for the use of test subject data for this work. This research was supported, in part, by the NIMH and NINDS Intramural Research Programs of the NIH (Z.S.S., G.C., and R.W.C.), NIH grant R01 HD071664 (P.A.T.), and the South African Research Chairs Initiative (P.A.T.).
Author Disclosure Statement
No competing financial interests exist.
In FATCAT, a “bundle” is defined as a collection of tracts through a single ROI (OR-logic) or those connecting a pair of ROIs (AND-logic).
Available from http://afni.nimh.nih.gov/pub/dist/tgz/FATCAT_DEMO.tgz; download and install from a Unix terminal command line using the AFNI-supplied script, @Install_FATCAT_DEMO.
More detailed help documentation for AFNI, FATCAT, SUMA, and their combination is available online, including further examples and illustrations: http://afni.nimh.nih.gov/pub/dist/doc/htmldoc/.
See main text for FATCAT Demo download. The FAT_MVM Demo is available from http://afni.nimh.nih.gov/pub/dist/tgz/FAT_MVM_DEMO.tgz; download and install from terminal command line using @Install_FAT_MVM_DEMO.
References
- Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A. 2000. In vivo fiber tractography using DT-MRI data. Magn Reson Med 44:625–632 [DOI] [PubMed] [Google Scholar]
- Behrens TEJ, Johansen-Berg H, Jbabdi S, Rushworth MFS, Woolrich MW. 2007. Probabilistic diffusion tractography with multiple fibre orientations: what can we gain? Neuroimage 34:144–155 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrens TEJ, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, Clare S, Mathews PM, Brady JM, Smith SM. 2003. Characterization and propagation of uncertainty in diffusion weighted MR imaging. Magn Reson Med 50:1077–1088 [DOI] [PubMed] [Google Scholar]
- Bennett IJ, Rypma B. 2013. Advances in functional neuroanatomy: a review of combined DTI and fMRI studies in healthy younger and older adults. Neurosci Biobehav Rev 37:1201–1210 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen G, Adleman NE, Saad ZS, Leibenluft E, Cox RW. 2014. Applications of multivariate modeling to neuroimaging group analysis: a comprehensive alternative to univariate general linear model. Neuroimage 99:571–588 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen G, Saad ZS, Adleman NE, Leibenluft E, Cox RW. 2015. Detecting the subtle shape differences in hemodynamic responses at the group level. Front. Neurosci. 9:375. doi: 10.3389/fnins.2015.00375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen G, Saad ZS, Britton JC, Pine DS, Cox RW. 2013. Linear mixed-effects modeling approach to FMRI group analysis. Neuroimage 73:176–190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colby JB, Soderberg L, Lebel C, Dinov ID, Thompson PM, Sowell ER. 2012. Along-tract statistics allow for enhanced tractography analysis. Neuroimage 59:3227–3242 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conturo TE, Lori NF, Cull TS, Akbudak E, Snyder AZ, Shimony JS, McKinstry RC, Burton H, Raichle ME. 1999. Tracking neuronal fiber pathways in the living human brain. Proc Natl Acad Sci U S A 96:10422–10447 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox RW. 1996. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res 29:162–173 [DOI] [PubMed] [Google Scholar]
- Cox RW. 2012. AFNI: what a long strange trip it's been. Neuroimage 62:743–747 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damoiseaux JS, Greicius MD. 2009. Greater than the sum of its parts: a review of studies combining structural connectivity and resting-state functional connectivity. Brain Struct Funct 213:525–533 [DOI] [PubMed] [Google Scholar]
- Dice L. 1945. Measures of the amount of ecologic association between species. Ecology 26:207–302 [Google Scholar]
- Dinno A. paran: Horn's test of principal components/factors. http://cran.r-project.org/web/packages/paran/index.html 2012. Last accessed Sep. 21, 2015
- Fischl B. 2012. FreeSurfer. Neuroimage 62:774–781 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, van der Kouwe A, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale AM. 2002. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron 33:341–355 [DOI] [PubMed] [Google Scholar]
- Garyfallidis E, Brett M, Amirbekian B, Rokem A, van der Walt S, Descoteaux M, Nimmo-Smith I; Dipy Contributors. 2014. Dipy, a library for the analysis of diffusion MRI data. Front Neuroinform 8:8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glorfeld LW. 1995. An improvement on Horn's parallel analysis methodology for selecting the correct number of factors to retain. Educ Psychol Meas 55:377–393 [Google Scholar]
- Goodrich B. FAiR: factor analysis in R. http://cran.r-project.org/web/packages/FAiR/index.html 2014. Last accessed Sep. 21, 2015
- Gotts SJ, Jo HJ, Wallace GL, Saad ZS, Cox RW, Martin A. 2013. Two distinct forms of functional lateralization in the human brain. Proc Natl Acad Sci U S A 110:3435–3444 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Supekar K, Menon V, Dougherty RF. 2009. Resting-state functional connectivity reflects structural connectivity in the default mode network. Cereb Cortex 19:72–78 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn A, Ostwald D, Reisert M, Blankenburg F. 2014. The structural-functional connectome and the default mode network of the human brain. Neuroimage 102:142–151 [DOI] [PubMed] [Google Scholar]
- Horn JL. 1965. A rationale and a test for the number of factors in factor analysis. Psychometrika 30:179–185 [DOI] [PubMed] [Google Scholar]
- Jo HJ, Saad ZS, Simmons WK, Milbury LA, Cox RW. 2010. Mapping sources of correlation in resting state FMRI, with artifact detection and removal. Neuroimage 52:571–582 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DK. 2003. Determining and visualizing uncertainty in estimates of fiber orientation from diffusion tensor MRI. Magn Reson Med 49:7–12 [DOI] [PubMed] [Google Scholar]
- Kaiser HF. 1958. The varimax criterion for analytic rotation in factor analysis. Psychometrika 23:187–200 [Google Scholar]
- Kleiser R, Staempfli P, Valavanis A, Boesiger P, Kollias S. 2010. Impact of fMRI-guided advanced DTI fiber tracking techniques on their clinical applications in patients with brain tumors. Neuroradiology 52:37–46 [DOI] [PubMed] [Google Scholar]
- Lazar M, Weinstein DM, Tsuruda JS, Hasan KM, Arfanakis K, Meyerand ME, Badie B, Rowley HA, Haughton V, Field A, Alexander AL. 2003. White matter tractography using diffusion tensor deflection. Hum Brain Mapp 18:306–321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori S, Crain BJ, Chacko VP, van Zijl PCM. 1999. Three dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol 45:265–269 [DOI] [PubMed] [Google Scholar]
- Parker GJ, Haroon HA, Wheeler-Kingshott CA. 2003. A framework for a streamline-based probabilistic index of connectivity (PICo) using a structural interpretation of MRI diffusion measurements. J Magn Reson Imaging 18:242–254 [DOI] [PubMed] [Google Scholar]
- Pierpaoli C, Walker L, Irfanoglu MO, Barnett A, Basser P, Chang L-C, Koay C, Pajevic S, Rohde G, Sarlls J, Wu M. TORTOISE: An Integrated Software Package for Processing of Diffusion MRI Data. In ISMRM 18th Annual Meeting, Stockholm, Sweden, 2010, p. 1597 [Google Scholar]
- Pillai JJ. 2010. The evolution of clinical functional imaging during the past 2 decades and its current impact on neurosurgical planning. AJNR Am J Neuroradiol 31:219–225 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preti MG, Makris N, Papadimitriou G, Laganà MM, Griffanti L, Clerici M, Nemni R, Westin C-F, Baselli G, Baglio F. 2014. A novel approach of groupwise fMRI-guided tractography allowing to characterize the clinical evolution of Alzheimer's disease. PLoS One 9:e92026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. 2014. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; www.R-project.org/ [Google Scholar]
- Riva-Posse P, Choi KS, Holtzheimer PE, McIntyre CC, Gross RE, Chaturvedi A, Crowell AL, Garlow SJ, Rajendra JK, Mayberg HS. 2014. Defining critical white matter pathways mediating successful subcallosal cingulate deep brain stimulation for treatment-resistant depression. Biol Psychiatry 76:963–969 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saad ZS, Reynolds RC. 2012. SUMA. Neuroimage 62:768–773 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saad ZS, Reynolds RC, Argall B, Japee S, Cox RW. SUMA: An Interface for Surface-Based Intra-and Inter-Subject Analysis with AFNI. In IEEE International Symposium on Biomedical Imaging: From Nano to Macro, IEEE, Arlington VA, 2004, p. 1510 [Google Scholar]
- Sherbondy A, Akers D, Mackenzie R, Dougherty R, Wandell B. 2005. Exploring connectivity of the brain's white matter with dynamic queries. IEEE Trans Vis Comput Graph 11:419–430 [DOI] [PubMed] [Google Scholar]
- Staempfli P, Reischauer C, Jaermann T, Valavanis A, Kollias S, Boesiger P. 2008. Combining fMRI and DTI: a framework for exploring the limits of fMRI-guided DTI fiber tracking and for verifying DTI-based fiber tractography results. Neuroimage 39:119–126 [DOI] [PubMed] [Google Scholar]
- Sui J, Huster R, Yu Q, Segall JM, Calhoun VD. 2014. Function–structure associations of the brain: evidence from multimodal connectivity and covariance studies. Neuroimage 102:11–23 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor PA, Cho KH, Lin CP, Biswal BB. 2012. Improving DTI tractography by including diagonal tract propagation. PLoS One 7:e43415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor PA, Jacobson SW, van der Kouwe A, Molteno CD, Chen G, Wintermark P, Alhamud A, Jacobson JL, Meintjes EM. 2015. A DTI-based tractography study of effects on brain structure associated with prenatal alcohol exposure in newborns. Hum Brain Mapp 36:170–186 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor PA, Saad ZS. 2013. FATCAT: (an efficient) functional and tractographic connectivity analysis toolbox. Brain Connect 3:523–535 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas C, Ye FQ, Irfanoglu MO, Modi P, Saleem K, Leopold DA, Pierpaoli C. 2014. The anatomical accuracy of brain connections derived from diffusion MRI tractography is inherently limited. Proc Natl Acad Sci U S A 111:16574–16579 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomson GH. 1951. The Factorial Analysis of Human Ability. London, United Kingdom, University of London Press Ltd [Google Scholar]
- Wang R, Benner T, Sorensen AG, Wedeen VJ. 2007. Diffusion toolkit: a software package for diffusion imaging data processing and tractography. Proc Intl Soc Mag Reson Med 15:3720 [Google Scholar]
- Whitcher B, Tuch DS, Wisco JJ, Sorensen AG, Wang L. 2008. Using the wild bootstrap to quantify uncertainty in diffusion tensor imaging. Hum Brain Mapp 29:346–362 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeatman JD, Dougherty RF, Myall NJ, Wandell BA, Feldman HM. 2012. Tract profiles of white matter properties: automating fiber-tract quantification. PLoS One 7:e49790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Mei S, Liu Q, Liu W, Chen H, Xia H, Zhou Z, Wang L, Li Y. 2013. fMRI and DTI assessment of patients undergoing radical epilepsy surgery. Epilepsy Res 104:253–263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu D, Zhang T, Jiang X, Hu X, Chen H, Yang N, Lv J, Han J, Guo L, Liu T. 2014. Fusing DTI and fMRI data: a survey of methods and applications. Neuroimage 102:184–191 [DOI] [PMC free article] [PubMed] [Google Scholar]