Estimation of Bone Mineral Density in Children from Diagnostic CT Images: A Comparison of Methods with and without an Internal Calibration Standard

Abstract

We investigated the feasibility and potential limitations of estimating bone mineral density (BMD) from standard diagnostic computed tomography (dCT). We analyzed three sets of BMD measurements for L1 and L2, each performed by a novice and an expert, for intra- and interobserver variance (n=43 studies from 38 patients; median age, 13.2 years) using one BMD quantification system with (conventional quantitative computed tomography (QCT)) and two without (QCT and dCT) an external calibration phantom. Using ANOVA model, means of three sets of BMD measurements analyzed by the expert differed by 2.5 mg/cm²; for the novice, by less than 1 mg/cm². Variation of measurement differences was less for the expert. Mean intra- and interobserver absolute standardized differences (ASD) were 1.77% and 1.8%, respectively. The mean ASD between phantom and phantom-less methods of QCT studies were 3.3%; mean ASD of phantom QCT versus phantom-less dCT was 14.3%. Regression modeling suggested compensation for sources of dCT BMD measurement bias can reduce the mean ASD of phantom QCT versus phantom-less dCT to 6.5%. Thus, phantom-less QCT of dCT adds clinically useful BMD information not typically attained from dCT, thereby augmenting patient care and presenting important possibilities for research without need for additional study.

Introduction

The assessment of bone mineral density (BMD) and fracture risk has become common practice amongst patients suffering from diseases which may compromise the structural integrity of bone. Dual X-ray absorptiometry (DXA) is the most widely used means of determining BMD. However, the use of quantitative computed tomography (QCT) is growing due to its ability to measure volumetric BMD in g/cm³ [1] instead of areal density as measured using DXA (g/cm²). The direct volumetric assessment of BMD circumvents measuring errors that are known to occur in growing children as a result of changing bony morphology. QCT also has the ability to differentiate between cortical and trabecular bone, which allows monitoring of the response of the more metabolically active trabecular bone compartment to interventions designed to improve BMD [2]. Anatomy located outside of a region of interest (ROI) can be eliminated using the interactive capabilities of QCT. QCT also provides greater image resolution of tissue and can display images in multiple planes. Though QCT subjects patients to greater exposure to ionizing radiation than does DXA [3], contemporary low-dose techniques directed at focused regions of interest provide diagnostic information while minimizing such exposure.

The advancement in bone densitometry has brought forth new possibilities of investigating BMD. In 3D QCT images, a mid-vertebral trabecular volume is analyzed using an elliptical ROI with results presented as two measures, Z-score and T-score. A reference phantom is typically used to standardize measurements to a mineral reference and correct for potential analytical errors arising from beam hardening and radiation scattering. While the use of a phantom is standard among CT-acquired bone densitometry studies, the phantom is not utilized during routine diagnostic CT (dCT) examinations, namely pelvic and abdominal CT studies. Thus, measurements of BMD from a dCT image slice may not be a reliable measure compared with values derived using standard QCT performed with a phantom. Furthermore, diagnostic CT’s are commonly performed after administration of an intravenous contrast agent, which has been shown to increase BMD measurements [4].

Our study is prompted by the need for a new and innovative way to measure BMD without the utilization of a phantom and minimizing patient exposure to ionizing radiation by retrospectively utilizing existing or prospective dCT data. In this study, we tested the accuracy and reliability of the Bone Investigational Toolkit^R, (BIT; Mindways Software Inc.) which enables analysis of data sets acquired without the use of a CT calibration phantom. By focusing solely on statistical measurements of BMD, we sought to evaluate values generated from these two methods (standard QCT and BIT), seek out potential sources of error and assess the utility of BIT in a clinical setting. Accurate determination of BMD using this software would obviate the need for subjecting patients (particularly children) to additional radiation exposure, without compromising the accuracy of BMD measurements. Thus, patients with unanticipated BMD deficits who might benefit from further evaluation may be assessed retrospectively. If proven successful, the implications of this research may identify previously unrecognized patient cohorts with BMD deficits. For example, if BIT can be used to accurately analyze BMD from a dCT without use of a phantom, a more detailed analysis of bone mineral density over time could be obtained. Thus, such a determination of BMD could provide clinically valuable information not typically available with dCT. Most importantly, it may reduce the need for multiple examinations, consequently decreasing cumulative radiation exposure to patients.

Methods

We analyzed CT data collected between 2003 and 2008 of pediatric and young adult patients who had undergone both a standard lumbar spine QCT and a dCT study that included vertebral bodies L1 and L2, within 24 hours of each other. This retrospective study was performed with IRB approval and data was managed according to the Health Insurance Portability and Accountability Act (HIPAA) of 1996.

We based our study on analyses performed by two categories of observers: a novice [AHH] and an expert [JKB] user of the analysis software. The novice analyzed the BMD of L1 and L2 without any previous experience in processing QCT or dCT studies. The expert observer was the developer of the software and was highly experienced in the processing of QCT and dCT studies. To determine if a learning curve was associated with the software, we analyzed both inter- and intraobserver BMD estimates of the novice and the expert.

The QCT studies evaluated L1 and L2 BMD and incorporated an external calibration phantom (Mindways Software, Austin, TX) imaged simultaneously with the subject. The dCT studies were typically performed after administration of intravenous contrast (Visipaque/Omnipaque/Isovue, 1.5 cc/kg) and opacification of the gastrointestinal tract with oral contrast; no external calibration phantom was used.

The QCT data sets were analyzed with version 4.2 of QCT-PRO™ (Mindways Software, Austin, TX) using standard methods provided by the manufacturer[5]. The QCT and dCT data sets were both analyzed using QCT-PRO™ in conjunction with version 2.0 of the Bone Investigational Toolkit™ (BIT, Mindways Software, Austin, TX). With BIT, the CT calibration information necessary for the analysis was derived from a QCT quality assurance (QA) scan involving only phantoms. The QA phantom scans were acquired on the same CT scanner, using the same kVp and reconstruction methods as was used for patient imaging. QCT BMD studies as well as dCT studies were performed on a General Electric Lightspeed Ultra 8 Detector CT scanner until late January of 2008 at which time it was replaced with a General Electric VCT XT 64 Detector unit. The dCT scans for this study were acquired at 120 kVp and the QCT scans at 80 kVp. Both types of studies were reconstructed using a standard abdomen CT reconstruction method. Note the calibration data intrinsic to the QCT data sets was ignored when analyzing the QCT data sets with the BIT software. In the case of the dCT studies, the QA studies used for calibration purposes with BIT were acquired after all of the patient data was obtained and the creatinine levels of the patients were observed within no more than 1 month prior to the dCT.

Definition of Terms

QCT

A set of CT image data including a CT calibration phantom placed under the subject during scanning.

dCT

A set of CT image data not including an external CT calibration phantom placed under the subject during scanning

PRO

A quantification system used to analyze image data with the presence of external CT calibration information in the image data. This system is used to analyze image data in the presence of a phantom.

BIT

A quantification system which may be used to analyze image data irrespective of the presence of external CT calibration information in the image data.

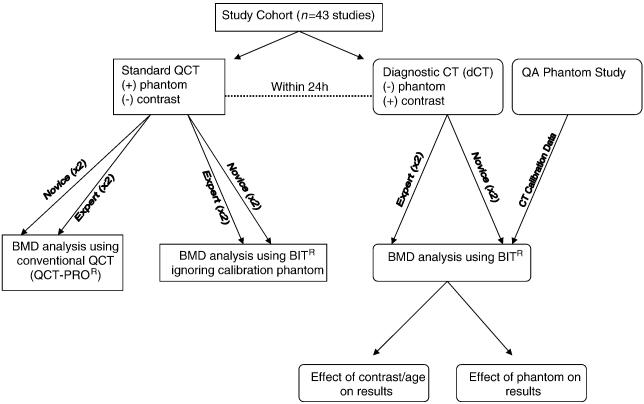
In summary, three sets of BMD measurements were derived from applying two quantification systems (PRO and BIT) to two types of imaging data sets (QCT and dCT) for each subject in this study (see Fig. 1): (1) BMD results derived using conventional QCT data sets with external phantom calibration (this set of measurement is denoted as PRO/QCT), (2) BMD results derived from dCT data sets using BIT (denoted as BIT/dCT), and (3) BMD results derived from conventional QCT data sets using BIT ignoring phantom calibration information intrinsic to and available from the QCT data sets (denoted as BIT/QCT). The above analyses were each performed twice, 4 months apart, by both readers. Inter- and intra-observer variability was characterized using ANOVA methods. The relative measurement biases for the three BMD estimates for each study were compared using ANOVA methods. The results of the QCT method were considered the gold standard for bias comparisons. For assessment, we used L1 to compare results between users and methods used, while using L2 as validation.

Figure 1.

Descriptive flowchart of methods of data analysis of 43 studies.

Statistical Analysis

For each subject, three BMD measurements were generated from two data sets: PRO quantification of QCT data, BIT quantification of QCT data, and BIT quantification of dCT data. The ultimate goal of this analysis was to obtain an estimation of BMD based on the dCT data, for which the PRO quantification of QCT data was taken as the gold standard. To reach this goal, we first compared PRO and BIT quantification of QCT data, from which the effect of phantom on the accuracy of BMD measurements could be estimated. We then compared BIT quantification of dCT data with PRO quantification of QCT data, from which other factors affecting the accuracy of BMD could be identified. Consequently, we obtained a good estimation of BMD for dCT data by removing biases caused by these factors. The BMD measurements were analyzed by two observers (novice and expert), and repeated twice for each observer. Thus, we could estimate systematic differences and variations within and between observers. We used ANOVA to assess the systematic difference (i.e., bias) between two measurements, performed by two observers, with two repetitions each, and effects of other factors such as weight, renal function,

IV contrast and age of patients. The ANOVA model includes Measurement (two levels), and/or Observer (two levels), and/or Repetition (only one repetition; two levels for this factor), and Patient (35 levels) as factors. The ANOVA model is more powerful than the simple t-test, for example, to detect the effect of Measurement by removing the effect of Patient and Repetition from the errors of model. We used the standardized absolute difference of two observations to assess the absolute difference between two types of BMD measurements. For example,

$$\text{Absolute}\text{Standardized}\text{Difference}=2\ast \mid \text{Difference}\mid ∕(\text{Observation}\text{by}\text{PRO}\text{of}\text{QCT}+\text{Observation}\text{by}\text{BIT}\text{of}\text{dCT}),$$

where Difference = Observation by PRO of QCT − Observation by BIT of dCT. A good estimator based on dCT data should have a small bias as well as a small average absolute standardized difference between PRO of QCT and BIT of dCT. Using the regression model, we identified IV Contrast and patient age to be significant factors accounting for the difference in BMD results between PRO of QCT and BIT of dCT. As IV contrast and patient age are strongly correlated, we fitted a simple regression model,

$$\text{Difference}=\text{Intercept}+\text{Slope}\ast \left(\text{IV}\text{Contrast}\right)$$

where Difference= PRO of QCT − BIT of dCT is for each patient, and IV Contrast is the volume (ml) of the intravenous contrast received by this patient. With this model, we will obtain a measure of BMD for the dCT data which improves the BIT measurement of dCT by removing a bias caused by IV Contrast.

Results

Paired measurements of a dCT and QCT within 24 hours were available for 38 patients (median age: 13.2 years; range 0.40-26.2 years). Among the 38 patients, 16 of the patients were female (42.1%) and 22 of the patients were male (57.9%). Images were collected at two longitudinal points for five of the patients. Since longitudinal observations were only available for five of the patients and most patients only had one observation, we ignored the effect of time on observations and assumed all 43 observations to be independent. We excluded four patients from the study who were younger than 2 years of age or who were afflicted with osteopetrosis. Of the 38 patients receiving a dCT, 36 were known to have received intravenous contrast (94.7%). The descriptive statistics for the three measurements of BMD for vertebrate bodies L1 and L2 by two observers (novice and expert) are given in Table 1.

Table 1.

Three BMD Measurements of Spine bones L1 and L2 by Two Observers.

Measurement (Quantification/Data)	Observer	N	Variable	Mean (SD)	Median (Min, Max)
PRO/QCT	Expert	39	BMD_L1	152.0 (39.1)	144.0 (62.7, 227.1)
		39	BMD_L2	147.6 (39.0)	142.8 (52.9, 225.5)
	Novice	39	BMD_L1	151.6 (39.5)	146.6 (64.8, 228.9)
		39	BMD_L2	146.9 (39.7)	139.1 (53.1, 228.8)
BIT/dCT	Expert	39	BMD_L1	172.4 (42.4)	170.6 (90.4, 258.1)
		39	BMD_L2	168.4 (41.6)	163.1 (80.4, 244.4)
	Novice	39	BMD_L1	174.6 (43.3)	172.8 (92.8, 269.2)
		39	BMD_L2	170.3 (41.9)	164.8 (80.6, 251.5)
BIT/QCT	Expert	39	BMD_L1	149.0 (37.7)	143.6 (60.9, 222.6)
		39	BMD_L2	144.9 (38.4)	140.38 (51.1, 222.3)
	Novice	39	BMD_L1	151.2 (38.0)	144.44 (62.0, 223.7)
		39	BMD_L2	146.6 (37.6)	141.02 (52.7, 220.9)

Differences between Measurements

Differences in BMD estimates between measurements are presented in Table 2 for the three base measurements as well as an “adjusted” measurement described later. An ANOVA model was used to test for systematic bias and systematic difference is determined by measuring the average difference between two methods.

Table 2.

Comparison of Four BMD Measurements (PRO/QCT, BIT/QCT, BIT/dCT, Adjusted BIT/dCT).

Comparison of Two BMD Measurements (Quantification/Data)	Observer	Variable	Mean Difference* (or Bias) (SD)	P-value** for testing H0: Bias=0 by ANOVA	Mean Absolute Difference	Absolute Standard Difference
PRO/QCT vs. BIT/dCT	Expert	BMD L1	−20.37 (12.73)	< 0.0001	20.37	12.8%
		BMD L2	−20.82 (11.47)	< 0.0001	20.82	13.8%
	Novice	BMD L1	−22.96 (14.27)	< 0.0001	22.96	14.4%
		BMD L2	−23.48 (12.79)	< 0.0001	23.48	15.5%
PRO/QCT vs. BIT/QCT	Expert	BMD L1	2.38 (5.80)	0.0004	5.02	3.3%
		BMD L2	2.71 (5.26)	< 0.0001	4.68	3.2%
	Novice	BMD L1	0.41 (6.68)	0.04	5.35	3.6%
		BMD L2	0.26 (7.93)	0.4	5.85	3.9%
BIT/QCT vs. BIT/dCT	Expert	BMD L1	−22.76 (11.72)	< 0.0001	22.76	14.3%
		BMD L2	−23.53 (10.62)	< 0.0001	23.53	15.7%
	Novice	BMD L1	−23.37 (12.78)	< 0.0001	23.45	14.6%
		BMD L2	−23.74 (11.62)	< 0.0001	23.96	15.6%
PRO/QCT vs. Adjusted BIT/dCT	Expert	BMD L1	1.72 (11.40)	0.46	8.96	6.5%
		BMD L2	1.17 (10.40)	0.44	7.56	5.5%
	Novice	BMD L1	−0.94 (12.85)	0.51	9.94	7.1%
		BMD L2	−1.43 (12.30)	0.47	9.44	6.9%

^*Mean Difference, Mean Absolute Difference, and Absolute Standardized Difference are calculated directly from data without modeling.

^**P-value is obtained from ANOVA model.

For the expert we found significant differences of about 2.5 mg/cm³ between the means of BMD measurements by PRO/QCT and BIT/QCT for both L1 and L2. For the novice, non-significant differences of less than 1 mg/cm³ where observed for L1 and L2. However, variance of measurement differences between two measurements by the novice is slightly larger than that by the expert. For example, in Table 2, the variance of difference between PRO/QCT and BIT/QCT is 6.68 for L1 and 7.93 for L2 by the novice, which are slightly larger than 5.80 for L1 and 5.26 for L2 by the expert. Obviously, the smaller the variance of difference in two measurements, the more consistent is the measuring by the observer. For both observers, the BMD measurements by PRO/QCT are systematically larger than the BIT/QCT measurements.

As shown in Table 2, significant differences ranging between 20 mg/cm³ and 23 mg/cm³ are observed when comparing PRO/QCT BMD measurements to BIT/dCT BMD measurements for both observers. The BIT/dCT BMD estimates are systematically larger than the corresponding PRO/QCT BMD measurements. We found similar results when comparing BIT/QCT BMD estimates with the BIT/dCT BMD estimates; the BIT/dCT is systematically larger than the BIT/QCT with a range similar to that found when comparing PRO/QCT BMD to BIT/dCT BMD (23 mg/cm³ to 24 mg/cm³).

Measurement Differences among Observers

Differences in BMD estimates between novice and expert observers are reported in Table 3. The variations of measurements within observers are given in Table 4. We used an ANOVA model to test for systematic bias; systematic difference was determined by measuring the average difference of BMD as determined between two methods.

Table 3.

Differences in BMD measurements between Two Observers (Novice minus Expert).

BMD Measurement (Quantification/Data)	Variable	Mean Difference (SD) (Novice - Expert)	P-value** for testing H0: Mean Diff=0 by ANOVA	Mean Absolute Difference	Mean Absolute Standardized Difference
PRO/QCT	BMD L1	−0.43 (3.35)	0.40	2.47	1.7%
	BMD L2	−0.73 (3.54)	0.25	2.67	1.9%
BIT/QCT	BMD L1	2.16 (4.76)	0.004	3.66	2.2%
	BMD L2	1.93 (4.48)	0.02	3.43	2.1%
BIT/dCT	BMD L1	1.55 (3.31)	0.28	2.64	1.8%
	BMD L2	1.72 (3.55)	0.01	2.63	2.1%

* Mean Difference, Mean Absolute Difference, and Absolute Standardized Difference are calculated directly from data without modeling.

^**P-value is obtained from ANOVA model.

Table 4.

Differences of BMD Measurements Repeated within Observer (First – Second).

BMD Measurement (Quantification/Data)	Observer	Variable	Mean Difference of Repetitions within Observer (SD)	P-value** for testing H0: Rep Diff=0 by ANOVA	Mean Absolute Difference	Mean Absolute Standardized Difference
PRO/QCT	Expert	BMD L1	1.51 (3.54)	0.07	2.82	1.9%
		BMD L2	1.19 (3.99)	0.29	2.98	2.1%
	Novice	BMD L1	1.03 (3.81)	0.32	2.91	2.2%
		BMD L2	0.28 (3.3)	0.75	2.40	1.8%
BIT/QCT	Expert	BMD L1	0.23 (3.78)	0.87	2.84	1.7%
		BMD L2	1.01 (5.38)	0.41	3.56	2.2%
	Novice	BMD L1	0.57 (3.48)	0.64	2.53	1.5%
		BMD L2	0.56 (3.32)	0.57	2.36	1.5%
BIT/dCT	Expert	BMD L1	0.22 (2.57)	0.93	1.87	1.3%
		BMD L2	0.84 (3.43)	0.48	2.57	1.8%
	Novice	BMD L1	0.13 (3.36)	0.86	2.46	1.7%
		BMD L2	0.45 (2.69)	0.51	2.08	1.5%

*Mean Difference, Mean Absolute Difference, and Absolute Standardized Difference are calculated directly from data without modeling.

^**P-value is obtained from ANOVA model.

In regards to PRO/QCT, no significant systematic difference was observed between the results from processing by the two users for both L1 and L2, the analysis of which is based on ANOVA with factors of observer, repetition, and patient. However, in the case of BIT/QCT, we observed significant systematic differences of about 2 mg/cm³ between the novice and expert. The measurements resulting from processing by the novice were systematically higher than those of the expert. Lastly, no significant systematic difference was observed for BIT/dCT measurements between the two observers at either L1 or L2.

Improving BIT measurement for dCT data

Recognizing the potential effect of intravenous contrast administration on the resultant BMD values, we further analyzed the effect of intravenous contrast on the results, as almost all of the patients who underwent a dCT were known to receive contrast. Using PRO of QCT as the “gold standard” of BMD measurements, we compared this result with BIT of dCT data which had been obtained after administration of an intravenous contrast agent. Using a regression model, we identified two factors: a) IV contrast and b) age that significantly affected the difference between BIT of dCT and PRO of QCT. We also found that the two variables were highly correlated. We obtained a measurement of BMD for dCT data by removing the effect of the contrast agent to improve the accuracy of BIT of dCT for BMD measurement.

To predict the difference made by IV contrast, we used the following regression model: Difference = Intercept + Slope* (IV Contrast). We used three variables to assess the effect of IV contrast agent on BMD measures: 1) intravenous volume 2) IV volume Body Mass Index (= IV volume/BMI); 3) IV volume body surface area (BSA) (= IV volume/BSA). From medical record review, we found all patients’ creatinine levels to be within the normal range at the time of dCT imaging. Thus, renal function should have had little to no effect on BMD determination relative to the impact of contrast enhancement. We found that only intravenous volume was significantly associated with the difference in BMD results through model fitting.

The parameters of fitted models were done separately for two vertebral bodies (L1 and L2) and two observers (novice and expert). The intercepts and slopes of the fitted models were found to be similar for both vertebral bodies and for both observers: −35.0 and 0.155 for L1 by Expert, −32.8 and 0.126 for L2 by Expert, −39.3 and 0.173 for L1 by Novice, −34.1 and 0.11 for L2 by Novice. The average of the intercepts was calculated as −35.3 mg/cm³ and the average of the slopes for IV contrast was calculated as 0.14 mg/cm³/ml. Using these calculations, we obtained an Adjusted BIT of dCT for measuring BMD using BIT of dCT and IV contrast by the following model:

$$\left(\text{Adjusted}\text{BIT}\text{of}\text{dCT}\right)=\left(\text{BIT}\text{of}\text{dCT}\right)-35.3\text{mg}∕{\text{cm}}^3+0.14\text{mg}∕{\text{cm}}^3∕{\text{ml}}^{\ast }\left(\text{IV}\text{contrast}\text{volume}\text{in}\text{ml}\right)$$

We examined the accuracy of the Adjusted BIT of dCT by comparing it with the standard PRO of QCT method. The difference between QCT and Corrected dCT can be illustrated with the following equation: Absolute Standardized Difference = 2*|Difference| / (PRO of QCT + Adjusted BIT of dCT), where Difference = PRO of QCT − Adjusted BIT of dCT. To illustrate the improvement of the accuracy using the Adjusted BIT of dCT data, we compared the BMD of L1 before and after implementation of the correction. When determining the difference for the expert of BMD between PRO of QCT and BIT of dCT for L1, the mean difference was −20.37 mg/cm³ (SD=12.73 mg/cm³), and the absolute standardized difference is 12.8% (SD=7.9%). However, between PRO of QCT and the Adjusted BIT of dCT for L1, the mean difference is 1.72 mg/cm³ (SD=11.4 mg/cm³) for the expert, and the absolute standardized difference was 6.5% (SD=4.5%). This example signifies an improvement in the accuracy of BMD measurements by BIT of dCT data. Measured by the absolute standardized differences to PRO of QCT data, the accuracy for the Adjusted BIT of dCT approaches that for BIT of QCT data. For the latter, between PRO of QCT and BIT of QCT for L1 determined by the expert, the mean difference was 2.38 mg/cm³ (SD=5.80 mg/cm³), and the absolute standardized difference was 3.3% (SD=2.1%).

To predict the difference between PRO of QCT and Adjusted BIT of dCT by age at examination (denoted as “Age”), we used the following regression model: Diff = Intercept + Slope*Age. Again, the parameters of fitted models were done separately for two vertebral bodies (L1 and L2) and two observers (novice and expert). The intercepts and slopes of the fitted models were similar for both vertebral bodies and for both observers: −40.8 and 1.36 for L1 by Expert, −38.0 and 1.14 for L2 by Expert, −46.9 and 1.59 for L1 by Novice, −42.8 and 1.28 for L2 by Novice. The average of intercepts was calculated to be −42.1 mg/cm³ and the average of slopes for IV contrast was 1.34 mg/cm³/ml. We then obtained a corrected dCT value by using the following model: Adjusted BIT of dCT = (BIT of dCT) − 42.1 mg/cm³ + 1.34 mg/cm³/ml* Age. We examined the accuracy of the Adjusted BIT of dCT by comparing it with the gold standard QCT using the following equation: Absolute Standardized Difference = 2*|Difference| / (PRO of QCT + Adjusted BIT of dCT). The following example illustrates how using this model can increase the accuracy of dCT measurements. Between PRO of QCT and BIT of dCT for L1, the mean difference is −22.96 mg/cm³ (SD=14.27) for the novice, and the absolute standardized difference is 14.4% (SD=8.5%). However, after using the model above, between PRO of QCT and Adjusted BIT of dCT for L1, the mean difference is −0.95 mg/cm³ (SD=10.79) for the novice, and the absolute standardized difference is 6.0% (SD=4.4%),

Both intravenous contrast and age were significantly associated with differences in BMD as determined by PRO of QCT and BIT of dCT. However, when the two variables are incorporated into a linear regression model, these differences become insignificant. As these two variables are highly correlated, it remains unclear which of the two variables is the true cause contributing to the variation in BMD results from dCT.

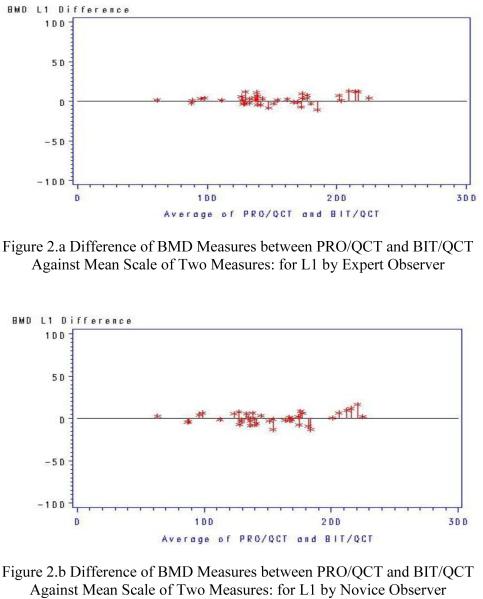
The absolute standardized difference (ASD) is a practical measurement to quantify the difference of two measurements. The difference within observer is small (mean ASD=1.77%) and it is stable for different measurements and different observers (see Table 4). The difference between observers is also small (mean ASD=1.8%) and it is stable for different measurements (see Table 3). The difference between PRO/QCT and BIT/QCT is only slightly larger (mean ASD=3.3%) than between the previous two differences, and it is stable for different bones and observers (see Table 2). The difference between PRO/QCT and BIT/dCT is substantially larger (mean ASD=14.3%) than previous three differences, and it is stable for different bones and observers (see Table 2). However, this difference can be substantially reduced by the Adjusted BIT/dCT: the difference between PRO/QCT and Adjusted BIT/dCT is substantially reduced (mean ASD=6.5%) from the previous one, and it is stable for individual vertebral bodies and observers (see Table 2). The difference between PRO/QCT and BIT/QCT sets a lower limit for difference between PRO/QCT and Adjusted BIT/dCT: 1) the difference between PRO/QCT and Adjusted BIT/dCT cannot be less than the difference between PRO/QCT and BIT/QCT; 2) the Adjusted BIT/dCT is more improved if the difference between PRO/QCT and Adjusted BIT/dCT is closer to the difference between PRO/QCT and BIT/QCT. This outcome is because PRO/QCT and Adjusted BIT/QCT are different in quantification methods, but the same in data set, whereas PRO/QCT and Adjusted BIT/dCT are different in both quantification methods and data sets. By this criterion, the Adjusted BIT/dCT is a good measurement for dCT data, because the mean percentage difference of all four measurements between Adjusted BIT/dCT and the gold standard PRO/QCT by the novice and expert listed in Table 2 (mean ASD=6.5%) is close to the mean percentage difference between the same measurements of PRO/QCT and BIT/QCT (mean ASD=3.5%). The differences of PRO/QCT and BIT/QCT observations for L1 by novice and expert observers are plotted in Figures 2a and 2b, respectively. The differences of PRO/QCT and Adjusted BIT/dCT observations (adjusted by Age; similar to that adjusted by IV Contrast) for L1 by novice and expert observers are plotted in Figures 3a and 3b, respectively.

Figure 2.

Differences in analysis results are uniformly small for both the expert and novice over the scale of 60 – 250 mg/cm³examined in the dataset.

Figure 3.

Differences in analysis results are slightly larger for both the expert and novice over the scale of 60 – 250 mg/cm³examined in the dataset when analyzing dCT but remain uniformly small.

Discussion

The PRO/QCT results reported here are conventional QCT results as used in clinical practice; derived using a CT calibration phantom imaged simultaneously with each subject. Measurement precision for this method as characterized by average absolute differences between two observations were estimated to be between 2 mg/cm³ and 3 mg/cm³ for a single lumbar vertebra when looking at both inter- and intra-observer variability (see Tables 3 and 4).

We found the observed bias between the results generated by the two methods (PRO/QCT and BIT/QCT) to be similar to or less than the observed precision of the methods. Our results showed that the QCT analysis differed from the BIT analysis by a range of 0.70 - 2.86 g/cm³, with the QCT values being higher than BIT values. This supports the feasibility of obtaining accurate QCT BMD estimates without the use of a CT calibration phantom imaged simultaneously with a patient. Thus, this analysis method allows for clinically useful retrospective determination of BMD from dCT studies obtained for reasons other than BMD determination.

Mueller et al. also studied the validity of a non-phantom based analysis tool. By comparing the BMD measurements of QCT studies with that of a phantom-less non-contrasted diagnostic CT, they found that a phantom based QCT BMD measurement reached a precision between 1.1-2.9 times better than the diagnostic CT [6]. Our results are consistent with their findings.

While consistency of BMD estimates derived using and then ignoring information from the CT calibration phantom present in the images is encouraging, conventional QCT studies differ from diagnostic CT studies in ways other than the use of a CT calibration standard. For example, dCT studies often involve the use of contrast agents, may be acquired using a higher kVp than is used for QCT and may have patients positioned differently than QCT studies. These factors, and possibly other factors, are likely contributors to our observed average bias of 20 mg/cm³ to 23 mg/cm³ between PRO/QCT and BIT/dCT measurements.

We found that the use of intravenous contrast contributes significantly to the observed bias in BMD measurements between PRO/QCT and BIT/dCT. Furthermore it appears feasible to compensate for the measurement bias as presented in the Results. While we observed no significant bias in our adjusted BIT/dCT results, the observed average absolute standard deviations of 7 mg/cm³ to 10 mg/cm³ are indicative of degradation of adjusted BIT/dCT measurement precision relative to PRO/QCT measurement precision.

Our findings support previous clinical studies on the feasibility of using a non-phantom method for BMD analysis. Bauer et al. [4] sought to determine a conversion factor between the BMD results of a QCT of the spine and hip and a contrast-enhanced standard diagnostic CT. Based on a linear regression model, they calculated following equation: BMD_QCT =0.96×BMD_MDCT − 20.9 mg/mL. This equation shows strong correlation to the differences we found between the QCT of QCT data and the dCT data.

Though many variables can contribute to disparities between the BMD measurements, we found user variability to play only a small role in these differences, while the different quantification methods and imaging modalities used accounted for the largest factor in BMD variance. While a phantom-less BMD measurement is less accurate in determining BMD compared to standard phantom-based QCT measurement, bias compensation does appear feasible with dCT images even in the presence of IV contrast agents. Some degradation of measurement precision with the adjusted BIT/dCT data is evident. However, we suggest that phantom-less QCT with dCT data potentially adds information about BMD of clinical utility that is typically not attained from a dCT. The clinical utility of software such as the Bone Investigational Toolkit™ has yet to be determined. Our study provides a framework for future study of potential uses of BIT in a clinical setting and shows promise that this software can be used to analyze the BMD of dCTs with good accuracy and precision. Our study drew its strength from the duplication of intra- and inter-observer investigation of results between extremes of user skill – novice to expert. The rigorous statistical analysis, strictly defined patient cohort and quantification of contrast volume also provide confidence in the validity of our results. In contrast, the retrospective study design, small patient sample size, limited patient age-range and single vendor CT scanner limit the strength of our results.

We have investigated the feasibility of estimating BMD from standard dCT images. Our results suggest it is possible to compensate for sources of measurement bias such as the use of IV contrast agents commonly used with dCT studies. We observed evidence of degraded BMD measurement precision when estimating BMD from contrast-enhanced dCT studies relative to conventional PRO/QCT BMD estimates. However, we suggest that even with this precision loss, phantom-less QCT of BIT/ dCT data potentially adds information about BMD of clinical utility that is typically not attained from a dCT. Thus, patient care may be augmented by this technique without need for additional study. This possibility has important ramifications for pediatric research and clinical care.

Research Highlights.

• BMD can be estimated retrospectively from diagnostic CT scan

• Method obviates additional patient exposure to ionizing radiation

• Effect of intravenous contrast can be compensated for

• •The mean inter- and intraobserver absolute standardized differences were small