Contribution of Facial Feature Dimensions and Velocity Parameters on Particle Inhalability

Abstract

To examine whether the actual dimensions of human facial features are important to the development of a low-velocity inhalable particulate mass sampling criterion, this study evaluated the effect of facial feature dimensions (nose and lips) on estimates of aspiration efficiency of inhalable particles using computational fluid dynamics modeling over a range of indoor air and breathing velocities. Fluid flow and particle transport around four humanoid forms with different facial feature dimensions were simulated. All forms were facing the wind (0.2, 0.4 m s⁻¹), and breathing was simulated with constant inhalation (1.81, 4.3, 12.11 m s⁻¹). The fluid flow field was solved using standard k-epsilon turbulence equations, and laminar particle trajectories were used to determine critical areas defining inhaled particles. The critical areas were then used to compute the aspiration efficiency of the mouth-breathing humanoid. One-tailed t-tests indicated that models with larger nose and lip features resulted in significantly lower aspiration efficiencies than geometries with smaller features, but the shape of the orifice into the mouth (rounded rectangle versus elliptical) had no effect on aspiration efficiency. While statistically significant, the magnitudes of differences were small: on average, the large nose reduced aspiration efficiency by 6.5% and the large lips reduced aspiration efficiency by 3.2%. In comparison, a change in breathing velocity from at-rest to heavy increased aspiration efficiency by an average of 21% over all particle sizes, indicating a much greater impact of aspiration efficiency on breathing rate in the facing-the-wind orientation. Linear regression models confirmed that particle diameter and breathing velocity were significant predictors to the aspiration fraction, while the facial feature dimensions were not significant contributors to a unifying model. While these effects may be less pronounced as the orientation changes from facing-the-wind, their impact confirms the importance of breathing velocity and, to a lesser extent, facial feature dimensions on exposure estimates in low freestream velocities typical of occupational environments.

INTRODUCTION

The amount of particles inhaled into a person’s respiratory system via the mouth or nose is an important component of exposure risk determination. Particle inhalability describes how efficiently the human head aspirates particles and is defined as the ratio of particles breathed in by a person relative to what exists in the surrounding environment, a concept first discussed by Ogden and Birkett (1975). The American Conference of Governmental Industrial Hygienists (ACGIH) defines the criterion for inhalable particulate mass (IPM) samplers, which was established as a sampling efficiency that matches the efficiency with which humans aspirate particles ranging up to 100 μm. This IPM fraction curve is defined by the equation:

$$\text{IPM}=0.5\left(1+{\mathrm{e}}^{-0.06d_{\text{ae}}}\right)$$ (1)

where d_ae is the aerodynamic diameter of the particle, micrometers (ACGIH, 2009). This equation indicates that small particles are inhaled with nearly 100% efficiency, but as particle size increases >50 μm, particles are inhaled at only 50% efficiency. This same performance criterion is adopted by the Comité Européen de Normalisation (CEN) and the International Standards Organisation (ISO). (CEN, 1993; ISO, 1995). Large particles exist in occupational settings where typically bulk materials are converted to aerosols via cutting, breaking, grinding, etc., and inhalable particle concentrations are of concern when health effects exist regardless of where the particles deposit in their respiratory system. Such materials, including wood dust, beryllium, scale with radioactive contamination, and many pesticides, are currently identified in the ACGIH threshold limit values (ACGIH, 2009) as having exposure limits requiring sampling using the inhalable criterion.

This criterion was generated from a series of aspiration efficiency studies in wind tunnels using continuously inhaling or cyclically breathing mannequins (Ogden and Birkett, 1975, 1978; Vincent and Armbruster, 1981; Armbruster and Breuer, 1982; Vincent and Mark, 1982; Vincent et al., 1990). These studies were typically performed at or above typical occupational indoor velocities, where 85% of measurements are reportedly <0.3 m s⁻¹ (Baldwin and Maynard, 1998). As velocity decreases and particle size increases, gravity plays a bigger role in particle transport than convective fluid forces. Hence, additional investigations into particle inhalability have been warranted to understand the aspiration efficiency of the human head at lower freestream velocities representative of indoor occupational settings. Studies in these lower velocity ranges have been conducted using wind tunnels (Kennedy and Hinds, 2002), settling chambers (Hsu and Swift, 1999), and calm air rotating mannequin/reference sampler chambers (Aitken et al., 1999). Liden and Harper (2006) summarizes these and other studies succinctly, pointing out the significant differences between the aspiration efficiency in calm air studies and those with freestream velocities exceeding 1 m s⁻¹. However, the differences in aspiration estimates among these low freestream velocity and calm air studies are also significant, likely attributable to the multiple methods used to measure the freestream reference concentrations, used as the denominator in aspiration efficiency calculations. Problems obtaining uniform suspensions of large particles in wind tunnels with large cross-sections as well as difficulties sampling large particles in nearly calm air have yet to be resolved.

To avoid these reference concentration quantification problems, computational fluid dynamics (CFDs) techniques have been used to examine particle aspiration in this flow regime. Initial numerical methods, again mostly in the outdoor air velocity regime, focused on the use of simple geometric surrogates, including cylinders (Dunnett and Ingham, 1986, 1987; Ingham and Hildyard, 1991; Chung and Dunn-Rankin, 1992), a rounded-top cylinder (Erdal and Esmen, 1995), and a sphere (Dunnett and Ingham, 1988). However, wind tunnel comparisons of a small-scale mannequin and a simplified cylinder at 0.3 m s⁻¹ freestream identified that a simple geometric cylinder over-aspirates particles when compared to an anatomical mannequin (Anthony et al., 2005).

To use CFD to investigate particle aspiration efficiency of an inhaling human, a fully three-dimensional humanoid form, with detailed facial features, was developed and used to evaluate aspiration efficiency in 0.2 and 0.4 m s⁻¹ with two inhalation rates (at-rest, 1.8 m s⁻¹ and moderate, 4.3 m s⁻¹) (Anthony and Flynn, 2006b). This work identified that the forward-facing aspiration efficiency dropped below the 50% prescribed by the IPM criterion for particles with aerodynamic diameters exceeding 68 μm. Those CFD particle simulations compared well with experimental results (Kennedy and Hinds, 2002) for particles ≤52 μm, but larger particles yielded lower aspiration efficiencies than those obtained in the wind tunnel tests. Anthony and Flynn (2006b) hypothesized that differences in facial features may have contributed to these aspiration differences; other possibilities included differences in turbulence and breathing patterns. A final hypothesis was that the isokinetic samplers, aligned with the freestream and not the predominantly downward particle trajectories, were inadequate to accurately measure large-particle reference concentrations, undersampling particles, and overestimating aspiration efficiency in the nearly calm air.

This current study focuses on the first hypothesis, namely, whether the dimensions of features associated with the human face significantly affect the IPM fraction in low-velocity environments. The practical implications associated with significant differences in aspiration due to facial features in the range of human anthropometry would indicate difficulty in determining real exposure and dose estimates for individuals using a single sampling criterion. This work explicitly evaluates changes in aspiration over a range of nose and lip dimensions, realistic ranges of occupational velocities, and steady state inhalation representing at-rest, moderate, and heavy breathing rates.

Early wind tunnel studies investigating the aspiration efficiency of the human head (Ogden and Birkett, 1975) examined the effect of smoothing the facial architecture by filling in their taylor’s mannequin’s face shape with Plasticine® between the browridge to the chin’s point and reported little effect on particle aspiration in wind tunnel studies. However, the position of the nose and lips relative to the inhalation orifice were not altered; the size of these protruding facial features may affect particle impaction and subsequently aspiration efficiency, particularly in the facing-the-wind orientation. Dunnett and Ingham (1988) identified aspiration efficiency differences in their numerical spherical head surrogate compared to that of the Ogden and Birkett (1975) experiments, particularly at the low suction-high freestream test condition. The authors postulated that in the condition of low breathing velocity, suction no longer dominates relative to the high-freestream velocities studied, so the detailed structure of the face may be important. In low-flow environments, however, even the at-rest breathing rate dominates the velocity field.

Yet, also in this low-velocity regime, gravity dominates large particle motion, and the structural features of the face may cause large particles to impact on the face, reducing the upstream area containing particles that can be aspirated into the inhaling mouth. To date, no investigations have specifically looked at how the physical geometry of facial features affects aspiration efficiency in the low-velocity indoor air conditions.

A final consideration into the sensitivity of the original CFD model’s estimates required an examination of the shape of the actual orifice inlet itself. Initial experimental work in the 1970s and 1980s used a round orifice to aspirate particles into mannequins, but later, this shape was replaced by more realistically shaped elliptical inlets. Previous humanoid CFD simulations relied on a rounded-edge rectangle, for no reason other than matching an experimental mannequin design (Anthony et al., 2005). Hence, the relative impact of this shape over the elliptical one required exploration as well.

This study examined (i) whether a larger nose ‘decreased’ particle aspiration, particularly when particle inertia prevents large particles from moving around the nose and then turning to enter the orifice, (ii) whether smaller lips ‘increased’ the aspiration efficiency of large particles, where a reduced impaction surface allows easier entry for particles into the mouth orifice, and (iii) whether the actual orifice shape had any bearing on the estimates of aspiration efficiency. Because aspiration efficiency is known to be affected by velocity and breathing rates and patterns, this work also considered two freestream and three inhalation velocities to examine their relative importance. Although this work still relied on the oversimplification of the real-world cyclical breathing pattern, the stepwise process allowed for the determination of which factors contribute more significantly to aspiration efficiency changes to help scope future cyclical breathing simulation and wind tunnel studies. While focused on CFD simulations of an abstract humanoid form, this study tests the hypothesis that persons with large facial features (nose and lips) have reduced aspiration efficiencies for inhalable particles, implying different exposures and doses compared to persons with small features in the same exposure environment. Results from these simulations also allow for a relative comparison of aspiration efficiency differences attributable to anthropometry, freestream velocity, and suction velocity as a surrogate for breathing rate. These results will provide guidance to the development of an international performance criterion for inhalable particle samplers for use in low-velocity environments, typical of many occupational settings.

METHODS

The methods for investigating the impact of facial features on particle inhalability are discussed in four parts: geometry development, fluid flow simulations, particle simulations, and resulting comparisons between aspiration estimates as a function of study variables. Details of the CFD code and verification are provided in online supplemental materials.

Geometry

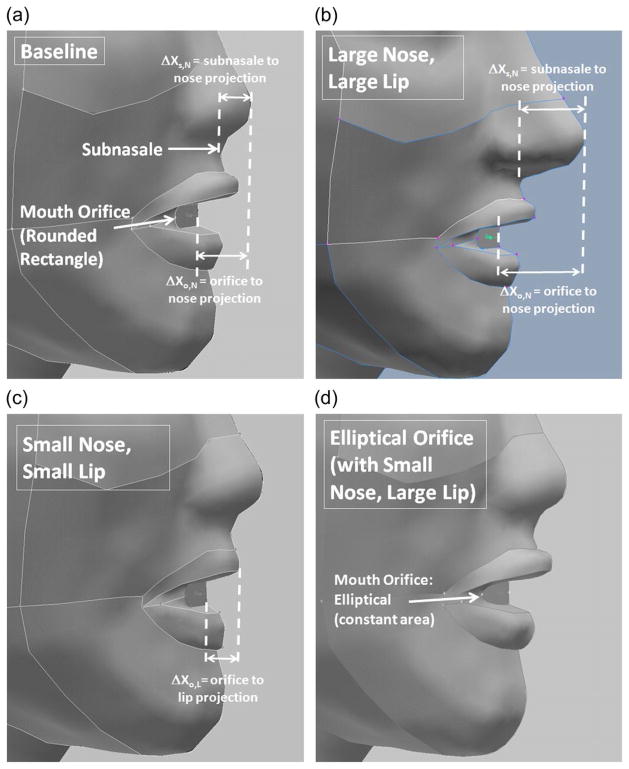
Gambit (Ansys Inc., Lebanon, NH, USA) was used to generate the geometries and mesh the computational domains. The geometry of the humanoid form used in previous work formed the baseline geometry for this work (Anthony and Flynn, 2006b). This baseline is categorized as small nose, large lips, and a round-ended rectangular orifice. The nose dimensions were small, in the range of Asian anthropometry, and the lips were larger than usual in this model to match the relative proportions of an experimental mannequin (Anthony et al., 2005). To investigate the effect of facial feature dimensions, the geometry was adjusted by increasing the nose size, decreasing the lip size, and changing the mouth orifice to an elliptical shape, one at a time. A total of four unique geometries were generated, with the details of the mouth/nose region illustrated in Fig. 1. A summary of characteristics and velocity settings is provided in Table 1. Although the geometry changes required reconstruction of the entire lip, nose, or orifice features to make a smooth and realistically human shape, only the horizontal distances between the orifice plane (X = 0) and the farthest upstream position on that feature are indicated, as a reference. For the nose, a more physiologically relevant dimension is the distance between the tip of the nose and the subnasale, the position between the lower end of the nasal septum and the skin above the upper lip, at the midline (ΔX_s,N; Fig. 1a). The small nose extended 0.009859 m anterior to the subnasale, and the large nose extended 0.022901 m or nearly 2.3 times the distance. In all models, the positions of the subnasale and the mouth orifice plane were the same. For the orifice shape variation, both areas of the round-ended rectangle and elliptical orifices remained constant (6.9496 × 10⁻⁵ m²), as did the height at centerline (0.00594 m) and width from centerline to the lateral edge of the orifice (0.012337 m).

Fig. 1.

Illustration of the four facial feature dimensions examined: (a) baseline small nose and large lips, (b) large nose and large lips, (c) small nose and small lips, and (d) baseline nose and lips but elliptical orifice.

Table 1.

Geometry and associated fluid parameters

Geometry	Nose sizea	Lip sizeb	Orifice shape	Mouth velocity, Um (m s−1)	Freestream velocity, Uo (m s−1)	Number of fluid simulations
1	Small	Large	Rounded-rectangle	1.81 (at-rest)	0.2, 0.4	6
				4.33 (moderate)	0.2, 0.4
				12.11 (heavy)	0.2, 0.4
2	Large	Large	Rounded-rectangle	1.81 (at-rest)	0.2, 0.4	6
				4.33 (moderate)	0.2, 0.4
				12.11 (heavy)	0.2, 0.4
3	Small	Small	Rounded-rectangle	1.81 (at-rest)	0.2, 0.4	4
				12.11 (heavy)	0.2, 0.4
4	Small	Large	Elliptical	1.81 (at-rest)	0.2, 0.4	4
				12.11 (heavy)	0.2, 0.4

Geometry 1 is considered the baseline. Feature in bold indicates the parameter dimension that was changed in the given geometry.

^aThe farthest position on the small nose extended 0.017061 m in front of the plane of the mouth orifice (=ΔX_o,N) and 0.009859 m anterior to the subnasale (ΔX_s,N); large extended 0.030103 m from the orifice (ΔX_o,N) and 0.022901 m from subnasale (ΔX_s,N).

^bThe farthest position on the large lips extended 0.01256 m in front of the plane of the mouth orifice (ΔX_o,M); small extended 0.009615 m (ΔX_o,M).

The remaining humanoid features were unchanged from baseline models and are explained in detail elsewhere (Anthony and Flynn, 2006b), although key dimensions are provided here for clarity. Lateral symmetry was assumed; hence, only half of the airflow surrounding the inhaling mannequin required simulation. The head height was 0.216 m and its half-width was 0.0712 m. The head and neck were constructed to mimic a humanoid form, but the torso was simplified by using an elliptical cylinder, 0.1725 m deep and 0.2325 m wide. The torso extended downward from the base of the neck only 0.2775 m, representing truncation near waist height of a 50th percentile female. Hair, ears, and arms were ignored in this model to focus on refining the details of the facial features.

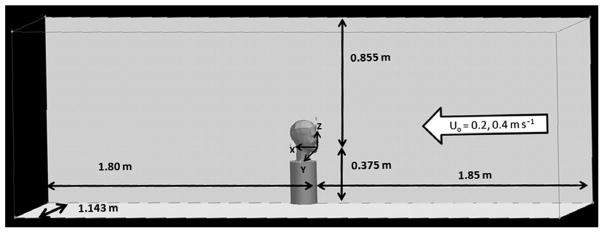
Previous simulation studies with the baseline humanoid geometry identified that the volume mesh required additional refinement to demonstrate mesh independence for all degrees of freedom. To achieve a refined mesh and to maintain the computational memory <2 GB maximum for FIDAP, the length of the computational domain required reduction. The distance between the domain inlet and bluff body was shortened to 1.85 m (inlet distance/diameter = 13.2). This still allowed the release of particles at upstream distances well over four head diameters, where the air was undisturbed by the downstream bluff body (Chung and Dunn-Rankin, 1997), and the distance between computational domain inlet and the head exceeded the 10 head diameters to ensure a stress-free boundary at the computational domain entrance. Verification of the resulting velocity profile at the upstream release locations found that the shortening of the domain continued to result in freestream velocities (0.2, 0.4 m s⁻¹) 0.75 m upstream of the humanoid form, indicating that the shortened domain should not have affected aspiration estimates. The other dimensions of the computational domain matched previous work: 1.143 m from torso center to side wall, 1.80 m from orifice to the exhaust end of the tunnel, and ceiling 0.855 m above and floor 0.375 m below the mouth opening center (Fig. 2).

Fig. 2.

Illustration of computational domain. The humanoid is facing the wind, with the positional origin located at the center of the mouth on the orifice plane. This work uses the simplified cylindrical torso. Computational domain dimensions are indicated.

Once the surface geometry was generated for each of the four conditions (baseline, large nose, small lips, and elliptical orifice), nodes were assigned along each edge, surfaces were meshed with a triangular meshing scheme, and the volume defining the computational domain’s air was meshed using a tetrahedral meshing scheme using Gambit. For each geometry, a series of three meshes were generated. Table 2 provides a summary of the mesh densities generated for this study. For all but the elliptical orifice geometry, the node spacing was reduced by a factor of 1.2 between successive meshes. However, the solutions for the elliptical orifice mesh using the same mouth refinement ratios as the round-ended rectangle simulations resulted in oscillations in the heavy breathing condition prior to converging to reasonable tolerances, so different mesh densities were required to accommodate the new mouth orifice geometry.

Table 2.

Mesh element summary for each geometry

Mesh density	Baseline		Small nose/small lip		Large nose/large lip		Elliptical orifice— at-rest breathing		Elliptical orifice— heavy breathing
	Volume	Mouth	Volume	Mouth	Volume	Mouth	Volume	Mouth	Volume	Mouth
Coarse	1,035,093	129	1,141,118	129	1,129,965	129	1,003,919	193	1,003,919	193
Middle	1,630,133	195	2,210,459	199	1,795,103	195	1,990,757	266	1,350,705	235
Fine	3,828,283	303	2,952,348	301	4,022,658	338	3,591,480	384	1,990,757	266

Values indicate the number of tetrahedral volumetric elements throughout the computational domain (volume) and number of triangular surface elements describing the mouth orifice (mouth).

Airflow simulations

Once the geometries were generated, the mesh was imported into commercially available finite element CFD software (FIDAP, Ansys, Inc.). Boundary conditions and equations of fluid flow were selected and applied. For each mesh, two freestream velocities (0.2 and 0.4 m s⁻¹) were assigned to the domain inlet and two inhalation velocities (1.81 and 12.11 m s⁻¹) were assigned to the mouth orifice, representing mean inhalation velocities for at-rest (7.5 l.p.m.) and heavy (50.3 l.p.m.) cyclical breathing rates. For the baseline and large nose model, the additional moderate inhalation velocity condition (4.33 m s⁻¹, representing mean inhalation velocity for 18 l.p.m. cyclical breathing rate) was also investigated. As with previous work, the floor and midsagittal wall were treated as planes of symmetry, allowing tangential flow in these planes but no airflow through them. For all other surfaces, no-slip conditions were applied to assign zero flow at these boundaries. Initial conditions were assigned to all other nodes comprising the computational domain: freestream velocity in the main horizontal direction (U_x to match the domain inlet velocity), zero lateral (U_y) and zero vertical (U_z) velocity, and turbulence kinetic energy (k) and dissipation (ε) associated with 8% turbulence intensity and ratio of eddy viscosity to laminar viscosity of 10, typical of wind tunnel studies.

To decouple the fluid and particle trajectory simulations, this work required the reasonable assumption that the presence of particles did not affect the surrounding airflow. As such, the airflow field was solved first. The steady state, incompressible, turbulent Navier–Stokes equations were used to model the airflow. The Boussinesq constitutive relationship was used to model the Reynolds stresses, and the standard k-epsilon equations were used to solve for turbulence. (Details of the equations are provided in supplementary data at Annals of Occupational Hygiene online).

To solve the fluid flow field, a segregated solver, pressure projection, and an element-Reynolds number relaxation scheme were used. Streamline-upwinding was used to stabilize the convective term. The iterative solvers for the linear systems were conjugate gradient-squared and conjugate residual methods. Six degrees of freedom, namely U_x, U_y, U_z, pressure (P), kinetic energy (k), and dissipation (ε), were solved on three sequentially refined meshes for each geometry and set of velocity conditions. FIDAP monitored the nonlinear convergence across all nodes in the computational domain using the traditional L₂ error norm (Supplementary data are available). Results were posted when these global solution errors (GSEs) for all degrees of freedom over all nodes reached tolerances of 10⁻³, 10⁻⁴, and 10⁻⁵. To evaluate the adequacy of the solutions provided by FIDAP at these GSE values, L₂ error norms were computed over 637 points upstream of the inhaling mannequin. Data were evaluated at upstream positions (X) from −0.011 through −0.1 m, lateral locations from Y of 0 through 0.03 m, and vertical positions from Z of −0.03 through −0.03 m. In the large feature geometries, elements of the facial features extended into some of the near-face positions (X = −0.011 m) over which these data were extracted, and values for these locations were excluded from the analysis for these geometries. The resulting L₂ error norm provided an indication of how much change occurred in the value of a degree of freedom between solutions, and a target of <5% was established a priori.

The independence of the solutions from sequential mesh densities of the same geometry and fluid conditions was examined for the three-mesh R² method described by Stern et al. (2001). Mesh convergence was indicated when local R² were less than unity for all degrees of freedom (Supplementary data are available).

The solution set where GSE tolerance was adequately low (<5% change in sequential decreases of GSE over volume of interest) and mesh independence was assured (regional R² was <1) were then used to begin particle investigations. The solution methods used in this study were validated in previous work, namely the velocity estimates at 2/3 scale at matched Reynolds numbers have been validated for the 0.4 m s⁻¹ at-rest breathing condition (Anthony and Flynn, 2006a). No wind tunnel velocity data were generated at this scale for comparison, but agreement was found between velocity solutions in the smaller scale CFD model.

Particle simulations

Aspiration efficiency calculations require the assumption of a uniform particle concentration upstream of the inhaling body. Equation 2 was used to compute aspiration efficiency (Anthony & Flynn, 2006b):

$$A=\left[A_{\mathrm{c}}{U}_{\mathrm{c}}\right]/\left[A_{\mathrm{m}}{U}_{\mathrm{m}}\right]$$ (2)

The mouth orifice area (A_m) remained constant throughout the study, even though the shape was varied in the Geometry 4 simulations. The inhalation velocity (U_m) and the critical area velocity (U_c), determined from the freestream velocity (U_o), were varied by test condition. Particle simulations using FIDAP were repeated to determine a given particle size’s critical area (A_c) for each set of test conditions. Particles were released at a series of upstream locations to identify the area in which a given size particle would travel from the freestream and terminate in the mouth orifice. To meet the requirement of a uniform particle concentration throughout the domain, all particles were assigned initial horizontal velocity (U_x) equivalent to the velocity in the freestream at that release location and initial downward vertical velocity (U_z) equivalent to the terminal settling velocity for the given particle’s aerodynamic diameter. Lateral velocity (U_y) near the midsagittal release plane was close to zero at these upstream distances, so no initial U_y was assigned to the particles.

Particle transport relied on laminar particle trajectory computations to identify upstream positions where particles traveled through the domain and terminated in the mouth. The laminar simplification provided estimates of the ‘mean’ particle path through the domain. To fully explore the ‘variability’ associated with particle aspiration, turbulent trajectory simulations would be required, which would introduce a random walk to the transport equations. This method requires multiple simulations over the same release points to determine the proportion of particles at that location that would be aspirated. This method yields a larger upstream critical area, as compared to laminar simulations, but for which each position has a probability of aspiration. Hence, both upstream critical area and probability of aspiration are needed to quantify aspiration efficiency using turbulent methods. While turbulent trajectory simulations would provide additional information on the variability of aspiration efficiency for the model and particle size of interest, preliminary simulations have indicated that the mean particle path using turbulence trajectory methods differed little from the laminar solutions in this forward-facing orientation. Hence, this work relied on laminar particle trajectory simulations. Their equations are provided in supplementary date at Annals of Occupational Hygiene online.

Calculations used generalized Stokes drag, and buoyancy was included to account for gravitational forces. The implicit backward Euler method was used, with time steps of 50 μsec with FIDAP’s default of 10 iterations within time step, which produced stable estimates of particle trajectories in replicate trials, assuring sufficiently small time steps for particle trajectory computations.

To locate positions of the upstream critical area, particles were released upstream of the head: X = −0.75 m for particles <82 μm; X = −0.4 m for ≥82 μm. These two locations were required to release particles in areas unaffected by suction and the bluff body and to accommodate gravitational settling and avoid releasing large particles at the top of the computational domain. Over a series of lateral (Y) positions, 20 particles were released across 1 cm vertical (Z) distances. The positions of the vertical releases (Z) varied by particle size and model flow conditions, but for each (X, Y) coordinate release along the Z_max to Z_min, some of the particles were required to enter the mouth and the rest to terminate on or move past the face unaspirated. Particle releases along these ΔZ lines were conducted to find the upstream particle release coordinates that defined the top of the critical aspiration area and then releases were repeated at lower ΔZ positions to identify the bottom of the critical aspiration area. Then, the process was repeated at a lateral distance (Y) 0.00025 m away, until release positions were identified as no longer resulting in particle aspiration. This lateral position defined the width of the upstream critical area. The series of (Y, Z) coordinates defined the area within which any particle was aspirated into the mouth. Releases at different upstream distances (X) would yield different (Y, Z) coordinates for the critical area, but the resulting product of critical area and freestream velocity through that area would remain the same.

In previous work, little difference in aspiration efficiency was observed over different inhalation and freestream velocities for particles <50 μm (Anthony and Flynn, 2006b). As such, this current study focused on the larger range of unit density particles (1 g cm⁻³), namely 22, 68, 82, and 116 μm. When aspiration efficiency of zero was found for 116 μm particles at a given test condition, 100 μm particles were also investigated in this study to provide additional information on the maximum inhaled particle size.

Comparative analysis

The mean, standard deviation and coefficient of variation of aspiration efficiency were computed by particle size, over all simulation conditions. This allowed the understanding of how much variability in aspiration efficiency for a given particle size can be attributed to changes in real-world parameters of facial features, indoor velocity, and breathing velocity. Data between different geometries were next paired by velocity conditions over the same particle sizes to determine whether the aspiration efficiencies were significantly different across geometry types (one-tailed t-tests, paired). Data were also paired by geometry and freestream velocity over the same particle sizes to examine the relative impact of breathing velocity on aspiration efficiencies (one-tailed t-tests, paired).

Owing to differences in the shape of the IPM criterion and low-velocity forward-facing aspiration efficiency curve, an investigation to examine the relationship between aspiration and the independent variables in this study was undertaken (linear regression; SAS 9.1.3, SAS Institute, Raleigh, NC, USA). Forms of the relationship included a linear form, such as that of Aitken et al. (1999), and transformations including those reported by Hsu and Swift (1999) with A as a function of the (log(d_ae))² and log(d_ae) and Kennedy and Hinds (2002) with A as a function of exp(d_ae). An independent variable was determined to be significant at α ≤ 0.05, using backward elimination. Additional transformations of the independent variables were also considered, including d_ae² and the velocity ratio (freestream/breathing). A separate analysis was also conducted by adding to the simulated data set values of aspiration efficiency (1.0) for a sixth particle size (1 μm) across all test conditions in attempts to force the data through the theoretical 100% aspiration efficiency for small particles. The significance of the regression terms and the magnitude of change in coefficients relative to the same model with only the actual simulation data were examined. Over all simulation conditions, the significant independent variables were then evaluated to determine the relative contribution of each factor’s influence on estimates of aspiration efficiency in attempts to find a unifying model for low-velocity aspiration at the facing-the-wind orientation.

RESULTS

Fluid dynamics

The small nose–elliptical mouth and small nose–small lip geometries were evaluated at two inhalation and two freestream velocities (eight models). The baseline and large nose–large lip geometries were evaluated at three inhalation and the same two freestream velocities (12 models). For each of these 20 test conditions, a series of at least three sequentially refined meshes were generated, netting a total of 60 fluid flow field simulations. For each of the 60 models, three sets of fluid solutions were generated (GSE of 10⁻³, 10⁻⁴, and 10⁻⁵).

Evaluation of the nonlinear convergence and mesh independence were performed for each of the 20 test conditions (Supplementary data are available). For at-rest breathing at 0.2 m s⁻¹ freestream velocity, the solutions provided at 10⁻³ GSE were insufficient for most of the mesh densities of the four geometries. For the at-rest breathing at the 0.4 m s⁻¹ freestream, this trend was seen only with the coarsest mesh. However, for all breathing and freestream conditions, very little change (<0.05%) was identified for all degrees of freedom when evaluating solutions from 10⁻⁴ and 10⁻⁵ GSE. Hence, the 10⁻⁴ or 10⁻⁵ GSE solution provided similar velocity and turbulence data in the region upstream of the inhaling mouth, and similar particle trajectories were anticipated from either solution. Solutions with the lowest GSE tolerance (10⁻⁵) were used for simulating particle aspiration.

When evaluating mesh independence for the GSE 10⁻⁴ and 10⁻⁵ solutions, all but one of the geometry and test conditions demonstrated mesh independence with all velocity terms. The single exception was the large nose geometry at 0.2 m s⁻¹ and at-rest (1.81 m s⁻¹) breathing. Here, the three-mesh error norm was computed to be 1.02 for the vertical velocity (U_z), slightly larger than the desired value of 1.0. Turbulence kinetic energy and dissipation of turbulence kinetic energy were more problematic with regards to mesh independence, particularly with at-rest breathing conditions, where the three-mesh R² exceeded unity by 20% or more for:

• 0.4 m s⁻¹ at-rest—elliptical mouth (k and ε); small lips (ε only); large nose (k and ε)

• 0.2 m s⁻¹ at-rest—elliptical mouth (ε only); large nose (k and ε).

These results indicated uncertain estimates of turbulence parameters near the head region of the humanoid form, where errors in turbulent particle trajectory computations may introduce significant errors to the estimation of critical areas needed to determine particle aspiration. However, since particle trajectory work for this study excluded turbulence in their computing particle transport, these errors were anticipated to have minimal effect on the mean estimates of aspiration efficiency as the laminar particle simulations ignored the turbulence parameters in computing mean path trajectories. Additional work, however, on the meshing regime or an alternative turbulence model is needed for at-rest breathing simulations prior to undertaking turbulent transport studies.

Fluid flow solutions for the most refined mesh and with the lowest GSE tolerance (10⁻⁵) were used for all subsequent particle aspiration studies.

Particle aspiration

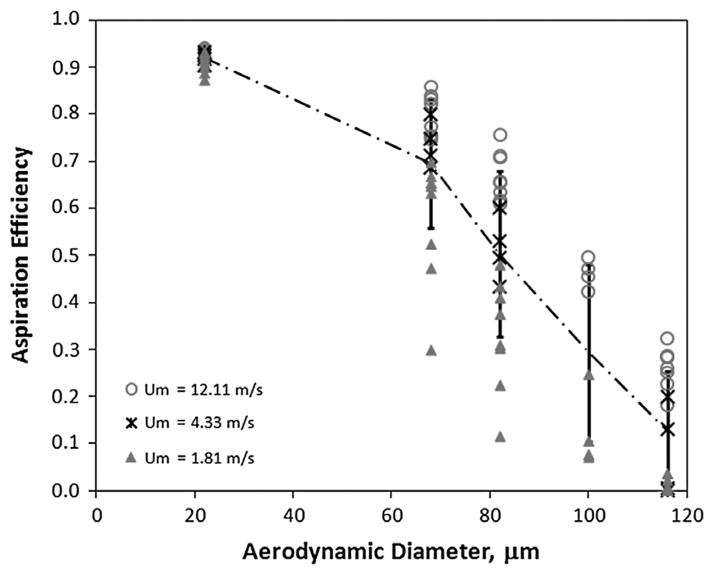
For each of the 20 combinations of geometry, freestream, and breathing condition, the computed aspiration efficiencies followed the anticipated trend of decreasing with increasing particle size. Figure 3 summarizes the resulting aspiration efficiencies by particle size, with data markers categorized by breathing velocity. Over all conditions, particles released near the centerline (Y = 0) had minimal lateral motion and impacted on the nose and lips, resulting in the decrease in critical area height near the centerline, as was seen as in previous studies (Anthony and Flynn, 2006b). The ‘width’ of this particle ‘impaction’ region did not change with increasing suction velocity, but it did increase with the larger facial feature dimension. The width of the impaction area for the large nose exceeded that of either of the small nose conditions, matching for velocity conditions: the nose was the limiting protrusion in preventing large particles from aspiration. This indicated that running simulations with large nose–small lip would likely have yielded similar results to the large nose–large lip simulations.

Fig. 3.

Aspiration efficiency over all test conditions by particle size. Data are separated by inhalation velocity (U_m, m s⁻¹). The error bars on the mean data line represent 1 SD over all data combined for each particle size, regardless of geometry or velocity conditions.

For a given geometry, the smaller suction velocity models had smaller overall width and height of the critical areas compared to larger suction, as predicted. Owing to this and the lack of change in the impaction region by geometry, the critical areas were more affected by the larger facial feature in at-rest simulations compared to moderate or heavy breathing simulations. This trend can be seen by the smaller aspiration estimates across all low-suction tests (triangular markers) when compared to moderate and heavy breathing tests in Fig. 3. Qualitative examinations grouped data by other test parameter (nose dimension, lip dimension, orifice shape, and freestream velocity) but obvious trends were not apparent, highlighting the major contribution of breathing rate on aspiration efficiency differences in this flow regime.

Table 3 provides aspiration efficiency summaries for all geometries, grouped by test velocities. The moderate breathing rate (4.33 m s⁻¹) condition was examined for only the baseline and large nose geometries (n = 2); other breathing rate conditions were evaluated for each of the four geometries. Less than 3% differences were identified over all velocity conditions at the smallest particle size (22 μm), where t-tests indicated no difference between aspiration efficiencies among test geometries (P = 0.22–0.42). Differences increased to 41% over different test conditions for 88 and for 100 μm particles and then decreased as particle size continued to increase, where the aspiration efficiency dropped toward zero. However, as particle size increased, the coefficients of variation generally increased.

Table 3.

Aspiration efficiency (fraction) and coefficient of variation (fraction) by particle size and velocity conditions (breathing rate category and freestream velocity)

Number of conditions	4	2	4	4	2	4	20
Particle size (μm)	At-rest, 0.2 m s−1	Moderate, 0.2 m s−1	Heavy, 0.2 m s−1	At-rest, 0.4 m s−1	Moderate, 0.4 m s−1	Heavy, 0.4 m s−1	All
Mean aspiration fraction
22	0.919	0.929	0.933	0.900	0.911	0.927	0.920
68	0.606	0.774	0.838	0.542	0.699	0.757	0.696
82	0.300	0.549	0.707	0.361	0.482	0.629	0.502
100	0.073	—	0.483	0.176	—	0.438	0.293
116	0.000	0.066	0.244	0.016	0.102	0.279	0.125
Coefficient of variation
22	0.023	0.005	0.006	0.021	0.012	0.002	0.018
68	0.149	0.048	0.018	0.329	0.027	0.015	0.197
82	0.438	0.137	0.059	0.323	0.141	0.034	0.351
100	0.059	—	0.036	0.570	—	0.051	0.645
116	2.000	1.414	0.181	0.965	1.346	0.143	1.022

To evaluate whether a significant decrease in aspiration efficiency was associated with the larger facial feature, one-tailed t-tests were used to compare geometry-specific aspiration efficiencies, by particle diameter, and matching by velocity conditions (Table 4). A significant decrease in aspiration efficiency was identified for the larger nose model compared to the smaller nose model (P < 0.04) for particles ≥68 μm. Over all test conditions and particle sizes, an average difference of 6.5% aspiration efficiency (range: 1–21%) was observed between large and small nose models (both large lip), with the largest differences occurring in the low suction models. For the lip comparison, the aspiration with the smaller lip geometry was significantly greater (P < 0.03) across all velocities for 88–116 μm particles: the larger lips reduced aspiration efficiency for larger particles. Over all test conditions and particle sizes, an average difference of only 3.2% aspiration efficiency (range: 0–11%) was observed between the large and small lip models (both small nose), again with the low suction condition having the largest differences owing to the overall reduced critical area containing particles capable of making it into the mouth under low suction. No significant difference was identified between the two orifice shapes, matching lip and nose dimensions.

Table 4.

One-tailed t-test P values for aspiration fractions

Particle size (mm)	Nose size	Lip size	Orifice shape	Breathing velocity
22	0.2221	0.420	0.364	0.008
68	0.0397	0.448	0.423	0.001
82	0.0369	0.026	0.496	<0.001
100	—	—	—	0.003
116	0.0250	0.032	0.794	<0.001
All	0.0007	0.015	0.276	<0.001

Comparison of aspiration estimates between at-rest and heavy breathing, by pairing matched geometry and freestream velocity, identified that larger breathing velocity yielded significantly larger aspiration estimates (Table 4, last column) over all particle sizes, including the smallest size range (P < 0.01). While the breathing velocity is directly incorporated into the computation of aspiration efficiency, these results indicate that the critical areas for heavy breathing were proportionately larger than those for at-rest breathing, even after normalizing by velocity differences. This also indicates that the human head is more efficient at aspirating large particles in heavy breathing conditions than in at-rest conditions during mouth breathing.

Aspiration determinates

As is seen in Fig. 3, the shape of the relationship between aspiration and particle size did not fit the general shape of the omnidirectional IPM criterion, where aspiration decreased to a nonzero constant as particle size increased. Linear regression models were applied to the aspiration estimates in attempts to find the optimal relationship between aspiration and study parameters. Table 5 summarizes linear models fitted to this study’s data to examine the form of model in order to relate aspiration efficiency fraction (A) to the determinants in this work, namely particle aerodynamic diameter (d_ae), freestream velocity (U_o), mouth inhalation velocity (U_m), and facial feature geometries. Both facial feature categories (0 for small and 1 for large) and actual dimensions were examined in model exploration. Only models where all independent variables were significant contributors to aspiration (α < 0.05) are reported in Table 5.

Table 5.

Linear regression equation results examining the relationship of aspiration fraction (A) and particle aerodynamic diameter (d_ae, μm)

ID	Linear regression equation	Coefficient of Determination (R2)	Comments
1	A = −5.0741 + 8.092log(dae) − 2.7016[log(dae)]2	0.8280	Form similar to Hsu and Swift (1999). Does not fit A ≅ 1 when dae is small.
2	A= 1.902 log(dae) − 0.8695 [log(dae)]2	0.9363	Form similar to Hsu and Swift (1999) without intercept. Does not fit A ≅ 1 when dae is small.
3	A= 1.168 − 0.00847dae	0.7851	Form of Aitken et al. (1999) with a fitted intercept. Decrease in A with increasing particle size. Overestimates A with small dae (A = 1.16 for dae = 1 μm).
4	A = 1.0365 − 0.0085dae + 0.02055Um	0.8806	Form similar to Aitken et al. (1999). Aspiration decreases with increasing particle size and increases with increasing mouth velocity. Shortcoming: A at dae =1 μm by as much as 28% over range of tests for high breathing velocity.
5	A = 1.2728 − 0.0085dae − 1.168(Uo/Um)	0.8603	Linear form, like ID-4, but using velocity ratio in place of Um. Coefficient of variation was reduced.
6	A= 0.8209 − 6.275 × 10−5dae2 + 0.0205Um	0.9186	Linear form using particle diameter squared. Aspiration behaves well, increasing with increased suction velocity and decreasing with increased particles size. For range tested, Um contributed 3.7–25% to aspiration estimates. A = 86% for dae = 1 μm at low and 107% for high suction.
7	A = 1.0582 − 6.251 ×10−5dae2 −1.168(Uo/Um)	0.8984	Linear form with dae2, like ID-6, but using velocity ratio in place of Um. Again, the coefficient of variation was reduced.

Other dependent variables identified as significant included mouth velocity (U_m = 1.81, 4.33, and 12.11 m s⁻¹) and freestream velocity (U_o = 0.2 and 0.4 m s⁻¹). Neither lip category (0 for small and 1 for large) nor nose category (0 for small and 1 for large) nor their actual dimensions were significant in these models. Dependent variables included were each significant at P < 0.05.

Forms fitting e^d_ae, referenced in Kennedy and Hinds (2002), were unsuccessful, likely because their form levels to constant nonzero aspiration with larger particle diameters, a trend that was not shown in the CFD modeling simulations. Models in the form of Hsu and Swift (1999), using log-transformation of particle diameter to estimate aspiration efficiency, overestimated aspiration at the smaller (<22 μm) particle sizes even though it accounted for much of the data variation (R² = 0.8280, ID-1 in Table 5). Elimination of the intercept (ID-2) identified the same significant factors, and the addition of the breathing velocity (U_m) was also found to be significant, yielding R² = 0.9234, but the parameter estimate for velocity was negative, inconsistent with trends in Fig. 3.

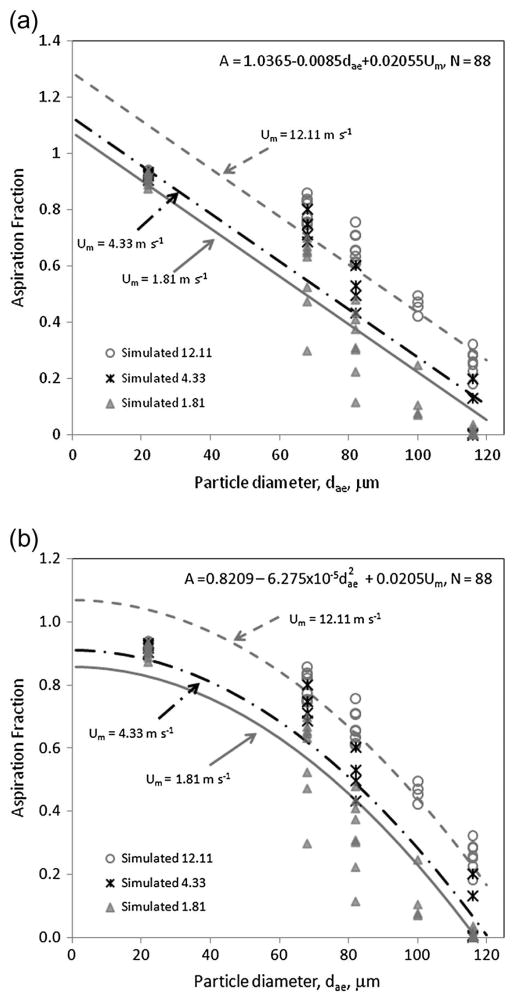
The linear relationship of Aitken et al. (1999), where aspiration decreased at a constant rate with increasing particle size (A = 1 − Kd_ae), performed moderately well using particle size alone (R² = 0.7851, ID-3 in Table 5). Improvements were again identified (R² = 0.8806, ID-4) by including the breathing velocity parameter: the resulting form of the equation included a negative relationship for particle diameter (decreased aspiration with increased particle size) and a positive relationship with breathing velocity, consistent with trends identified in Fig. 3. The resulting model is illustrated in Fig. 4a, where the lines indicate the regression model estimates and the markers indicate the simulation data used to generate the model. Inclusion of hypothetical 100% aspiration for 1 μm particles and reanalysis of the same form yielded the same significant variables as those in ID-4, with only slight improvement in the R² (0.8891), attributable to the lack of variability in these new ‘data’: A = 0.969 − 0.00754d_ae + 0.0177U_m.

Fig. 4.

Simulated (markers) and fit (solid lines) estimates of aspiration efficiency by particle size and inhalation breathing velocity using (a) linear form (ID-4) and (b) linear form with d_ae² term (ID-6).

Substituting the breathing velocity (U_m) with the velocity ratio (U_o/U_m) in the same form as ID-4 resulted in a slightly lower R² (0.8603), shown as ID-5. This yielded the same parameter estimator for d_ae as ID-4 (−0.0085), with the intercept now accommodating a wider range of velocity ratio values than the range of the breathing rate alone.

Transformation of the particle diameter into d_ae² was examined in attempts to better represent an increasing rate of aspiration decrease with increased particles size (ID-6). In this form, both the particle size and the mouth-breathing velocity were again significant contributors to a single regression form. The results from this model are illustrated in Fig. 4b, which shows the low aspiration rate underestimated aspiration at small particle sizes, but where the rate of change in aspiration efficiency decreases more with increased particle size. Inclusion of the hypothetical 100% aspiration for 1 μm particles yielded similar results, with an increase of 3% in particle size and a decrease of 15% in breathing velocity parameter estimates: A = 0.86157 − 6.482 × 10⁻⁵d_ae² + 0.01742U_m, (R² = 0.9274 comparable to ID-6). The differences in the equation above and ID-6 resulted in only 2% differences in aspiration efficiency estimates for 100 μm particles over the range of values studied for breathing velocity. Substituting the velocity ratio (U_o/U_m) for mouth-breathing velocity in this form (ID-7) again reduced the coefficient of determination (R² = 0.8984), indicating U_m is a better indicator than the velocity ratio over the small range of U_o studied.

Backward elimination methods for model fitting resulted in the elimination of nose and lip factors early in the procedure in most cases. One case yielded significant parameter estimates for lip category: the linear form (ID-4). When included, the lip category term was significant but indicated that larger lip size increased aspiration efficiency, inconsistent with the theory and simulation data, so it was excluded from consideration. This was the only case where any geometric parameter significantly contributed to a unifying model.

Neither the orifice shape nor the nose size, either as feature dimension or as categorical data, was a significant contributor to aspiration estimation for any models. Additional independent variables were combined and tested for significance as predictors. Both d_ae² U_m (a surrogate for Stokes number) and d_ae/U_m yielded some moderate significance as estimators but provided little explanation for the variability in the data.

DISCUSSION

The hypothesis of this work was to determine if larger facial features, within the range of human variability, reduce the aspiration efficiency of particles into the human mouth in environments with slow-moving air. T-tests evaluating the aspiration efficiencies of a given particle size, by matching freestream and breathing conditions over different facial feature geometries, indicated that the larger facial features of the nose and lip significantly decreased the fraction of particles that can be aspirated into the human mouth. The effect was more pronounced at low suction rates, modeled here as the mean inhalation rate of at-rest cyclical breathing. At low suction, the upstream area that contained the path tube of particles that traveled from the uniform concentration in the freestream into the inhaling mouth was smaller, resulting in a larger decrease in critical area due to particle impaction on the nose and lips compared to moderate and heavy breathing. In reality, only a small percentage of adults typically breathe orally at-rest (10–15%, Lieberman et al., 1990), so nasal investigation is more important to quantify differences between facial feature dimensions at lower breathing rates.

Unifying models and relative contribution

However, in attempting to generate a unifying model for mouth-breathing aspiration of large particles, while considering multiple velocities and incorporating either categorical or dimensional facial feature information, no facial feature term provided a statistically significant influence on the estimation of aspiration efficiency fraction. To examine the relative contribution of the independent variables on estimates of aspiration efficiency, two models from Table 5 were fitted to provide aspiration estimates in Table 6 for comparison. Increasing the breathing rate from at-rest (1.81 m s⁻¹ velocity) to heavy (12.11 m s⁻¹) increased aspiration estimates by 21%, the same as the average difference in aspiration efficiency estimate from simulation data, across all paired geometries and freestream velocities. In addition, realizing that each of the fitted models overestimated aspiration efficiency for at-rest breathing velocity compared to simulation data (Fig. 4), the difference in aspiration between heavy and at-rest breathing may be larger than what was computed in Table 6.

Table 6.

Computed aspiration efficiencies using three fitted models

ID-4						ID-6
A = 1.0365 − 0.0085dae + 0.02055Um						A = 0.8209 − 6.275 × 10−5dae2 + 0.0205Um
Um, m s−1	Particle size, μm					Um, m s−1	Particle size, μm
	25	50	75	100	125		25	50	75	100	125
1.81	0.86	0.65	0.44	0.22	0.01	1.81	0.82	0.70	0.51	0.23	−0.12
4.33	0.91	0.70	0.49	0.28	0.06	4.33	0.87	0.75	0.56	0.28	−0.07
12.11	1.07	0.86	0.65	0.44	0.22	12.11	1.03	0.91	0.72	0.44	0.09

Selection of one form of the regression equation over another is not recommended at this time because the final IPM sampling criterion for low-velocity air requires examination of other orientations relative to the freestream. The simplest linear model, using the squared particle diameter, provided best fit to the data (R²) and did the best to fit the shape of the data, particularly at the small particle sizes where aspiration approaches unity. At the facing-the-wind orientation, all fitted models overestimated aspiration efficiency for larger particles with at-rest breathing and were insufficient to adequately represent aspiration for small particles. However, the terms identified as critical in the forward-facing orientation, namely particle size and breathing velocity, should be considered at other orientations to develop an omnidirectional low-velocity IPM criterion.

Relevance

From a research perspective, this work identified that freestream velocity is not as critical as breathing rate on estimates of aspiration efficiency in low-velocity environments. Vincent et al. (1990) examined the effect of large freestream velocities (U_o) on particle aspiration and identified significant increases in aspiration with increased freestream velocity as particle size increased. Our current work, although limited in orientation relative to the wind, identified that the effect of breathing velocity was more critical than freestream velocity in the estimation of aspiration efficiency of particles into the human mouth over ranges of indoor occupational velocities. As freestream velocities decrease, aerosol transport is dominated by gravitational settling until the particles approach the region near the mouth, where inhalation velocity may or may not be sufficient to overcome the gravitational settling to move the particle into the mouth orifice.

Since the ultimate goal of this research is to develop a low-velocity inhalable sampling criterion to ensure inhalable samplers perform with the same efficiencies as an inhaling human, the dependence of human aspiration on breathing rate might pose problems. Aspiration efficiency of both the aerosol samplers and the human mouth may both be affected by realistic changes in the freestream velocity over the course of a day, hopefully similarly. For example, a sampler designed to meet a performance criterion may aspirate particles less efficiently in slower moving air, but we would expect a similar decrease in efficiency of human aspiration in that same environment. Since only 2–9% differences between aspiration estimates were identified in matched conditions between the 0.2 and 0.4 m s⁻¹ freestream velocities investigated, the contribution of these velocity changes on aspiration efficiency is anticipated to be within the range of sampling uncertainties. However, samplers typically operate at a fixed rate, not varying over the day as human activity requires respiration changes. If human aspiration efficiency of large particles is affected by ‘breathing velocity’, dose estimates from constant velocity samplers may be problematic as the sampled mass may not reflect exposure as a worker’s breathing rate changes throughout a workshift. Adjustments to computed doses may be needed to accommodate different workload and breathing rates, particularly when a significant portion of an occupational aerosol exposure contains large inhalable particles. At this point, however, time-dependent breathing simulations would be required to explore this more fully. Even so, the aspiration differences in the human head that are attributable to breathing rate changes (7–37%) may be dwarfed by bias associated with sampler placement (300% or more), recently illustrated by Lidén and Waher (2010).

Limitations and additional work required

This work focused on generating aspiration efficiency data by simulating laminar particle trajectories in a turbulent airflow field from the standard k-epsilon turbulence model. The effect of the selection of the turbulence model has not been evaluated and should be considered in future work. In addition, initial particle simulations have indicated that laminar particle trajectories trend toward the mean aspiration of turbulent particle releases, but a detailed investigation of the uncertainty and variability associated with turbulent trajectories is still required.

At this time, CFD simulations have relied on steady state simplification of breathing rather than the more complex cyclical breathing. Schmees et al. (2008) examined airflow patterns associated with cyclical breathing in low-velocity wind tunnels and identified that expiration of at-rest and moderate mouth exhalation disturbed the 0.1 m s⁻¹ air upstream of the mannequin mouth and that this continued through the next inspiration cycle. Exhalation would affect the assumption of a uniform particle concentration upstream of the inhaling mouth, particularly for the small sizes of particles that travel through a nearly horizontal streamtube projected upstream of the mouth orifice. Larger particles released with low momentum in low-velocity air travel into the breathing orifice from positions in front of and above the mouth on its path to aspiration and may be less influenced by the cyclical exhalation disturbance. This model, however, does not incorporate time-dependent breathing, and future work is needed to address these concern of cyclical breathing.

Before undertaking cyclical breathing investigations, it is important to remember that this work focused only on one orientation (facing-the-wind), which is a simplification of the complete IPM investigation for human breathing. An IPM criterion for low-velocity air requires consideration of the complete range of orientations relative to the oncoming wind. Previous higher-velocity freestream mannequin studies identified that the differences between aspiration efficiencies over velocities and breathing rates were most significant in the facing-the-wind orientation and decreased as the mannequin rotated (Vincent and Mark, 1982). Additional investigations at other orientations are required to determine whether the 7–37% differences in aspiration efficiency attributable to breathing velocity become negligible as the humanoid is rotated away from facing-the-wind.

The original motivation of this work was to determine if facial feature differences between the original humanoid CFD simulation studies and matched wind tunnel studies of Kennedy and Hinds could be attributed to differences in facial feature dimensions. Based on the work presented here, the differences attributable to facial features were minor. Even though t-tests identified significant differences between aspiration for both lip and nose size as particle diameter increased, the average differences were moderate, at 3.2 and 6.5%, respectively, when matching on velocity and other geometry dimensions. This was not enough to account for the differences in the shapes of these two aspiration efficiency curves discussed in Anthony and Flynn (2006b). The natural inclusion of turbulence in large particle aspiration studies in Kennedy and Hinds (2002) wind tunnel work was ignored in the CFD study by relying on laminar particle trajectories and still remains a source of uncertainty in the comparisons, as does the previous hypothesis associated with the alignment of the isokinetic reference probes in low-velocity wind tunnel studies.

On the other hand, this work indicates that there is no need to standardize mannequin features for low-velocity wind tunnel aspiration studies, so long as researchers realize the aspiration differences between mannequins with different facial feature dimensions (mouth and nose projections relative to the orifice inlet) may be in the range of up to 10%. The shape of the mouth orifice showed negligible effect on aspiration efficiency estimates, although a rounded orifice was specifically not included in this work owing to elliptical inlets being the most common mannequin study design for inhalability studies.

CONCLUSIONS

This study used CFD to evaluate the impact of facial features on estimates of aspiration efficiency for inhaling humans. The fluid models for moderate and heavy breathing demonstrated nonlinear convergence and mesh independence, although the at-rest breathing simulations did not show mesh independence and additional work is needed in this low-velocity regime. Although the fluid and particle trajectory studies were limited in its orientation and relied on steady inhalation and laminar particle trajectory simulations, the findings indicated that aspiration differences should be <10% between study mannequins with different facial feature dimensions. The fact that inhalation velocity accounted for an average aspiration efficiency differences of 21% over all conditions studied in low-velocity freestream represents a new complication to the exposure assessment field. Future investigation should include the influence of breathing velocity as a critical parameter to determine if the breathing velocity effects are negligible at other orientations relative to the oncoming air, as was found in higher freestream velocity studies that formed the current IPM curve or whether these differences require accommodation in the development of a low-velocity IPM criterion.

In applying this work to the development of a new low-velocity inhalable criterion, we have identified that size of facial feature dimensions has little effect on aspiration efficiency estimates compared to the breathing velocity. If this trend continues at other orientations, a new sampling criterion needs to account for breathing rate or a surrogate such as work activity, in its development to ensure the sampler provides biologically relevant exposure estimates. In the real world of exposure assessment, where workers are facing-the-wind in low-velocity environments, the CFD models indicate that aspiration efficiency of particles increases with increasing breathing rate, and not only would total mass inhaled increase but also proportionately more large particles would be inhaled.