Abstract
The objective of this research was to develop an inlet to meet the inhalable sampling criterion at 10 l min−1 flow using the standard, 37-mm cassette. We designed a porous head for this cassette and evaluated its performance using computational fluid dynamics (CFD) modeling. Particle aspiration efficiency was simulated in a wind tunnel environment at 0.4 m s−1 freestream velocity for a facing-the-wind orientation, with sampler oriented at both 0° (horizontal) and 30° down angles. The porous high-flow sampler oriented 30° downward showed reasonable agreement with published mannequin wind tunnel studies and humanoid CFD investigations for solid particle aspiration into the mouth, whereas the horizontal orientation resulted in oversampling. Liquid particles were under-aspirated in all cases, however, with 41–84% lower aspiration efficiencies relative to solid particles. A sampler with a single central 15-mm pore at 10 l min−1 was also investigated and was found to match the porous sampler’s aspiration efficiency for solid particles; the single-pore sampler is expected to be more suitable for liquid particle use.
Keywords: aerosol, computational fluid dynamics, droplet aspiration, inhalable sampler
BACKGROUND
To assess risks of occupational exposures to particles, the American Conference of Governmental Industrial Hygienists (ACGIH) specifies the use of personal sampling devices that meet size-selective sampling criterion. For particles that cause adverse health effects regardless of where they deposit in the respiratory system, ACGIH requires sampling equipment designed to meet the inhalable particulate mass (IPM) criterion, defined as where IPM (dae) is the collection efficiency and dae is the aerodynamic diameter of the particle in microns (ACGIH, 2009). This same performance criterion is advocated by the Comité Européen de Normalization (CEN) and the International Standards Organization (ISO) (CEN, 1993; ISO, 1995) This criterion was developed to match the aspiration efficiency of particles inhaled into the human head, resulting in aspiration efficiencies ranging from 100% for small particles (<1 μm) to 50% for large particles (50–100 μm).
Historically, personal exposure assessments have employed either 37-mm (USA) or 25-mm (UK) open- or closed-face sampling cassettes, which do not meet any physiologically based size-selective sampling criterion. Over the past decade, ACGIH has updated aerosol-based exposure limits to move away from traditional cassette samplers, and newer limits now require the use of size-selective sampling devices, predominantly using the inhalable criterion. In 2005, ACGIH specified inhalable exposure limits for only 38 compounds, but in 2009, 72 exposure limits were established with inhalable size fraction sampling criterion. An additional nine compounds are on the 2009 notice of intended change list to be converted from exposure limits based on old 37-mm cassette sampling techniques to samplers using the IPM criterion.
Many inhalable samplers are currently available for use, including the Institute of Medicine (IOM) inhalable sampler (SKC Inc., Eighty Four, PA, USA), the seven-hole sampler (SHS), the conical GSP inhalable sampler (Gesamtsstaubprobenhame, Deha-Haan & Wittmer GmbH, Friolzheim, Germany), the Conical Inhalable Sampler (CIS; BGI Inc., Waltham, MA, USA), and the domed, porous Button sampler (SKC Inc.). Many laboratory and field-based studies have compared the performance of different inhalable samplers; only a few are discussed here to elucidate performance differences. Vaughan et al. (1990) positioned the IOM sampler, with a single 15-mm opening, and an SHS, with seven 4-mm centrally positioned holes on the inlet face, onto a mannequin positioned in 23 work environments: on average, the IOM sampler measured 1.2 times the concentration of the SHS. Davies et al. (1999) identified that the concentration measured with a GSP sampler, with a single 8-mm conical inlet, averaged 1.7 times that of the SHS. Mark et al. (1994) concluded that the sampler that best meets the IPM criterion is the IOM but that it has greater variability than other samplers, including the SHS. Kenny et al. (1997) reported that the IOM oversampled relative to the IPM criterion and that the differences between any pair of inhalable sampler mass concentrations were at most 40%. Harper and Muller (2002) found that, in a wood-working shop, the ratio of mass concentrations between the IOM to the Button sampler, with a hemispherical meshed entry cap, ranged from 0.49 to 163 over 16 paired samples, with larger ratios associated with larger dust concentrations. These authors hypothesized that large particles were excluded by the meshed inlet of the Button sampler but were likely aspirated by the large single-pore entry of the IOM sampler. More recently, the IOM was also found to measure larger concentrations than the Button sampler in four different field applications (Linnainmaa et al., 2008). In addition to these side-by-side studies of inhalable samplers, other investigators also have compared performances of inhalable samplers to the traditional 37-mm open- or closed-face ‘total dust’ cassettes to provide factors allowing conversion of historical exposure data to newer inhalable sampling criteria.
Although most of the aerosol research community regards the IOM sampler as a reference standard, it is important to point out that inhalable dust sampling has not been widely adopted in the USA. One reason is that US regulatory agencies like the Occupational Safety and Health Administration have not integrated the concept of inhalable aerosol into occupational exposure limits and another is the perceived difficulty reported by hygienists in handling the filter or the internal cassette. Yet a third issue is the higher cost associated with inhalable sampler designs. As a result, most US industries continue to rely on the 37-mm cassette to assess particulate matter exposures.
In addition to ease-of-use requirements, an effective inhalable particulate sampler must also address the real concerns of analytical limits of detection. As exposure limits are revised to lower values, it becomes more difficult to quantify exposures using the sampling rates and analytical techniques hygienists have relied upon for decades. As the ACGIH and regulators evaluate the health effects of beryllium, for example, initial proposals recommend a 100-fold reduction in the threshold limit value (TLV) exposure limit. As summarized effectively by Ashley and Brisson (2005), current methods of inductively coupled plasma–atomic emission spectroscopy and graphite furnace atomic absorption spectroscopy cannot detect beryllium oxide at 10% of the proposed TLV, as required by the US National Institute of Occupational Safety and Health (Kennedy et al., 1998). An alternative to improving analytical instrument sensitivity would be to increase the volume of air sampled over a given exposure duration. However, current inhalable devices, such as the IOM and Button inhalable samplers, are specifically designed for operation at 2 and 4 min−1, respectively, to meet the IPM criterion. Increasing flow rates will likely affect the aspiration efficiencies of these devices, which has not been evaluated.
The objective of this research was to investigate whether the standard (and relatively inexpensive) 37-mm cassette sampler could be modified to better match the IPM criterion while operating at a high rate of flow (10 l min−1). The initial work presented here relies on computational fluid dynamics (CFD) simulations, where a three-dimensional (3-D) simulation of a 37-mm cassette with the new porous sampling head was positioned on an elliptical torso in a simulated wind tunnel. Comparisons of simulated aspiration efficiency from this new sampler were made to wind tunnel mannequin aspiration and human-form CFD simulation aspiration studies, both available at 0.4 m s−1. Investigations include the examination of particle bounce to compare the effect of the multipored sampler entry on aspiration efficiency between solid and liquid particles. Below we discuss the new inlet design for the traditional 37-mm sampler, followed by evaluation of device performance using a CFD model of both solid and liquid particle aspiration efficiency.
METHODS
Sampler design
This study provides an initial design and investigation of the personal high-flow inhalable sampler head (PHISH). To accommodate practitioner concerns and analytical limitations, this improved inhalable sampler must (i) meet the IPM sampling criteria, (ii) be operated at 10 l min−1, and (iii) be easy for practitioners to adopt. This device incorporates airflow into the central portion of the sampler face to minimize deposition at the sampler walls, a meshed entrance surface to minimize oversampling large particles, and an ability to interface with existing technology (the 37-mm sampling cassette). By operation at 10 l min−1, the PHISH device will increase the overall method detection limits by a factor of 2.5–5. This study examines how well the new sampler meets the IPM sampling criteria, specifically how well it matches the aspiration efficiency of inhaling humans in low-velocity (0.4 m s−1) indoor air.
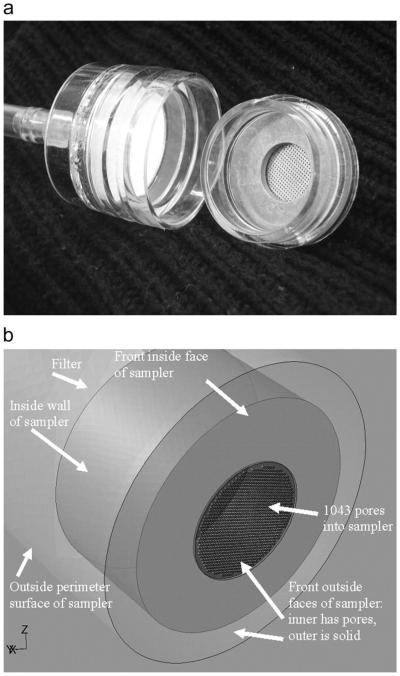
The PHISH was designed to replace the top inlet portion of the standard three-ring 37-mm cassette (Fig. 1). This design would allow users to order pre-weighed cassettes from their current laboratory, remove the top piece of the cassette without disturbing the filter, and replace the standard cap with the new inlet cap. The new cap was designed to be flat with a central 15-mm inlet containing multiple pores. The 15-mm diameter inlet was selected to provide sufficient radial distance to the wall to transport larger particles to the filter, minimizing internal wall losses due to settling. Our preliminary two-dimensional (2-D) simulations indicated that an inlet with multiple smaller pore diameters would reduce the aspiration efficiency of larger particles, preventing particles >100 μm from being sampled. Therefore, the inlet used 30 gauge (0.312 mm) stock perforated metal with 254-μm diameter pores, separated by 0.406 mm on straight centers, yielding 30% open area (No. 7/0; Harrington and King Perforated, Chicago, IL, USA). This resulted in the placement of 1043 pores in the central 15 mm of the sampler inlet.
Fig. 1.
Sampler (a) photo showing inside of prototype cap and (b) simulation geometry.
Geometry and mesh
This work was designed to simulate sampler performance when worn by a person in the workplace. Therefore, we included an elliptical torso on which we placed the multipored sampler and enclosed both in a virtual wind tunnel to simulate the airflow field around a human wearing the sampler (Fig. 2). The geometries were all created using Gambit software (Ansys Inc., Lebanon, NH, USA). A 3-D geometry most accurately represents the effects of aerosol flow and worker orientation on particle aspiration. However, the computational requirements of such a model limited our investigation to facing the wind. To investigate the importance of sampler position on the torso, two horizontal sampler configurations were investigated. The first oriented the sampler inlet with the horizon (i.e. 0° down, directly into the wind). The second positioned the sampler facing forward, but at a 30° down angle relative to the horizon (30° down). This second geometry was selected in deference to preliminary 2-D investigations, which indicated the potential for overaspiration at 0° but reduced aspiration along the centerline with downward sampler orientation. The 30° downward angle also better approximates the orientation of this sampler when placed on a worker’s lapel. The third geometry used the same 30° downward angle with the porous section replaced by an open 15-mm channel (i.e. a single pore) to examine the effects of liquid deposition at the face of the sampler’s porous inlet, anticipated to be problematic for droplet aspiration. This was similar in design to that postulated by Carlton and Flynn (1997), although the existing outer ridge on the 37-mm inlet cap was maintained by Carlton and Flynn but was replaced in this study with a flat entry to maintain similarity to the flat-entranced PHISH sampler.
Fig. 2.
Simulation geometry: wind tunnel.
The dimensions of an existing three-piece 37-mm cassette sampler, with the new porous inlet, described above, were used to generate the computer representation of the sampler. To aid in convergence, the air behind the filter and in the 4-mm diameter exit/tubing were excluded from this geometry; instead, uniform airflow was assigned to the filter face to simulate sampler suction, and the pressure drop across the filter was ignored. The effect of this filter simplification on aspiration efficiency was investigated for the horizontal sampler and compared to a model that included both a pressure drop across the filter and a uniform velocity across a 4-mm exit port behind the filter: both suction models yielded the same aspiration efficiencies into the sampler, so the simplification was used for all geometries in this study. The sampler was positioned to the right (0.042 m) of the centerline of a 0.26-m wide by 0.127-m deep elliptical torso. The top of the torso extended 0.3 m above the centroid of the sampler and extended 0.3 m below the sampler centroid to represent the sampler’s positioning at typical chest height on a worker. The elliptical cylinder height was 0.6 m, representing a truncated torso head to hip.
The surrounding domain, representing a wind tunnel that defined the volume of air to be simulated, extended 1.1 m upstream, 2 m downstream, and ±0.9 m laterally from the sampler opening, also shown in Fig. 2. The floor of this simulated wind tunnel was at the −0.3 m position at the bottom of the truncated torso, and the top of the tunnel extended 0.6 m above the finite cylinder (0.9 m above the sampler centroid). The blockage ratio of the torso in this wind tunnel was ~7%. The volume defining the wind tunnel was then split into two volumes, bisecting the torso into left and right, to better control the mesh densities in subsequent sequential meshing of the air volume within this domain.
Four fluid volume regions defined the majority of the computational domain: the two air volumes representing the large wind tunnel (+y and −y), an additional small volume just upstream of the sampler inlet (again to allow greater control of volumetric meshing), and the air inside the sampler. In addition to these four volumes, for the porous entry sampler studies, 1043 individual cylindrical volumes (254 μm in diameter and 0.3125 mm in length) were positioned as described previously to define the new pore openings in the sampler inlet.
After the geometry was created, the edges of all surfaces in the domain were subdivided into smaller segments, with nodes positioned to define these smaller lengths. From these edge nodes, surface faces bounded by these edges were paved with a triangular mesh, and a tetrahedral volumetric meshing scheme was used to generate the finite air volumes within the computational domain. For each virtual surface that was used to define adjacent volumes, the surface mesh was projected into both adjacent volumes; hence, the shared surface between two adjacent volumes required only one set of nodes where the equations of fluid flow were solved. For each of the three geometries investigated, four sequentially refined meshes were generated, and the three most refined meshes were used to study model convergence (i.e. to examine the differences between successive solutions to the equations of flow). To generate these refined meshes, the number of nodes along each edge was increased by a factor of 1.2, which achieved a volumetric mesh refinement ratio of 1.16 between the sequential refinements. For example, each of the 254-μm pores had mesh densities associated with 12, 15, and 18 nodes around its perimeter for the coarse (M1D), moderate (M2D), and fine (M3D) meshes, respectively. For the 30° down geometry, the numbers of mesh elements within each of the main volumes are given in Table 1. (Additional surface mesh details are provided in supplementary Table 1, available at Annals of Occupational Hygiene online.) Slight differences existed in the number of mesh volumes for the other geometries, but the number of nodes along each mesh edge was identical to the 30° down simulations.
Table 1.
Mesh density details: 30° down
| Name of simulation meshes | |||
|---|---|---|---|
| Volume/edge identifier | Coarse (M1D) |
Moderate (M2D) |
Fine (M3D) |
| Upstream of sampler inlet | 680 439 | 998 695 | 1 406 585 |
| Air inside sampler | 718 018 | 1 045 927 | 1 463 257 |
| Wind tunnel, +y side | 1 173 403 | 2 091 471 | 2 424 905 |
| Wind tunnel, −y side | 1 053 282 | 1 770 052 | 2 884 700 |
| Pores (average per pore) | 698 810 (670) |
1 069 075 (1025) |
1 981 700 (1900) |
| Number of nodes around each 254-μm pore perimeter |
12 | 15 | 18 |
Number indicates the number of tetrahedral mesh volumes that define the volume indicated or, for the bottom line, the number of nodes around the pore opening.
Fluid flow simulations
CFD simulations were performed using Fluent (Ansys Inc.). Except for the wind tunnel floor, all surfaces representing solid planes were set as walls, fixing zero velocity at nodes on those surfaces. The wind tunnel floor was modeled as a reflective plane, allowed to have horizontal and lateral velocities but no normal velocity (no air moving through this plane), to accommodate the truncation simplification. Where the surfaces were virtual, that is where they were used to allow control over the mesh generation rather than to represent an actual ‘wall’, these surfaces were treated as interiors and all degrees of freedom were solved in the simulation. Air through the filter in the back of the sampler was assigned as a uniform velocity, equivalent to a 10 l min−1 flow (0.1972 m s−1). Air velocity into the wind tunnel was set to 0.4 m s−1 for all simulations, the upper end of indoor occupational velocities (Baldwin and Maynard, 1998), to match existing human aspiration experimental data (Kennedy and Hinds, 2002). At the wind tunnel inlet and for initial conditions throughout the domain, an 8% turbulence intensity and a value of 10 for the ratio of turbulent to laminar viscosity (Ru) were assigned, typical of wind tunnel operation. The initial velocity condition of 0.4 m s−1 in the horizontal direction and 0 in the lateral and vertical directions were applied everywhere within the domain, except inside the sampler, where the horizontal and vertical velocity components equivalent to 10 l min−1 flow were initially applied. Fig. 2 highlights some of the boundary conditions discussed here.
To determine the airflow field, simulations used the steady-state, incompressible, turbulent Navier–Stokes equations with standard wall functions.
| (1) |
| (2) |
The standard two-equation k-epsilon model was used:
| (3) |
| (4) |
where Φ is the viscous dissipation function with the following constants:
The standard two-equation k-epsilon model was selected as it has been useful in similar low-velocity conditions, although difficulties with convergence in turbulence kinetic energy (k) and the dissipation of turbulence kinetic energy (ε) had proved difficult (Anthony and Flynn, 2006a). The mesh densities of this current study were more refined than those in previous human aspiration studies in attempts to improve convergence behaviors for this work.
An implicit pressure-based solver algorithm was applied to the 3-D turbulent flow simulation. A segregated solver, using the SIMPLE algorithm, was applied to the system of equations to obtain the pressure field by enforcing mass conservation, using second-order upwind discretization for momentum and turbulence solutions. Although Fluent literature indicated that Green–Gauss node-based gradient options were preferred, Green–Gauss cell-based methods performed better for this work. Solutions were saved as the global solution error (GSE) reached 10−3, 10−4, and 2 × 10−5 over all degrees of freedom.
Iterative tolerance was assessed using the L2 error norm [equation (5)]. Here, the subscripts refer to the level of GSE tolerance, where the smaller number (i − 1) indicates the value at the larger GSE tolerance limit. An L2 error norm value of <5% over all degrees of freedom defined an adequate mesh solution; when this was identified, the GSE tolerances were determined to be sufficiently low for the purposes of this work.
| (5) |
where f designates any degree of freedom, such as stream-wise velocity (Ux), and summation is over all nodes of the computational area of interest.
Mesh independence was assessed using equation (6), where the subscript refers to the mesh density (fine indicates the mesh with the most nodes and coarse indicates the mesh with the least number of nodes) (Roache, 1998).
| (6) |
The term εj,k is the difference between the coarser (j) and finer (k) mesh level values for a given degree of freedom. Mesh independence was indicated when local R2 are less than unity for all degrees of freedom.
Locations used to assess both of these terms for each mesh and at each GSE tolerance were selected upstream of the sampler, where subsequent particle calculations would be needed (X = −0.1, −0.2, −0.3, −0.4, −0.5, and −0.75 m), at lateral distances in 0.01-m increments through Y = ± 0.2 m and at vertical distances in 0.05-m increments extending −0.15 through +0.15 m (Z). A total of 1722 points were used to evaluate the quality of the fluid field solution.
Particle simulations
Although the fluid flow field was solved using turbulence equations, particle simulations relied on laminar trajectories to yield mean path information for particles moving through the flow field. A backward implicit Euler method was used to solve the particle momentum equation (7). Subscripts i refer to the particle position, the P designates the particle, and τ is the particle relaxation time, which is a function of particle diameter, fluid viscosity, particle Reynolds number, and coefficient of drag.
| (7) |
• = particle velocity
• ui = local fluid velocity
• ρi = particle density
• ρi = fluid density
• = forces acting on the fluid
• τ = particle relaxation time, given by
•
• μ = fluid viscosity
• dp = particle diameter
• Rep= particle Reynolds number
• sperical drag law (Morsi and Alexander, 1972)
The traditional Stokes representation of the drag coefficient would have underestimated CD for particles >50 μm, where particle Reynolds numbers exceeded unity. As such, the spherical drag law formulation, above, was used, where the constants vary over flow regime. For smaller particles in this study, this drag coefficient becomes the familiar Stokes term of CD = 24/Rep.
Particle simulations used unit density spheres with no droplet evaporation. Particle releases were simulated for 6-, 12.5-, 25-, 50-, 75-, 90-, and 100-μm diameter particles. Particle injections were conducted using 50-μm length scales and a maximum of 20 000 steps, determined from sensitivity tests to result in solutions independent of these settings. To represent a ‘uniform particle concentration’ within the wind tunnel, particle injections were made using initial velocities equivalent to the freestream velocity (Ux = 0.4 m s−1) and the terminal settling velocity of the given particle size (Uz). Particles were released from two different upstream (X) locations to ensure that releases were in areas that were not affected by the downstream presence of the bluff body. For smaller particles, X = 0.75 m upstream was sufficient. However, as particle size increased, releases at X = 0.75 m upstream required release heights (Z) near the boundary layer and above the ceiling of the computational domain. To accommodate this, the horizontal distance was shortened to 0.5 m upstream of the sampler; this still met the criteria for being out of the region affected by the presence of the bluff body, as the release height (Z) for these particles was both upstream and above the height of the torso.
For each geometry and particle size, the release position heights (Z) at a given upstream distance (X) and lateral position (Y) were obtained by trial and error to determine the general location of the critical area. Upon finding these locations, the following protocol was used to generate the coordinates of the critical area. Forty particles were released over lines extending 0.01 m vertically (Z), resulting at ΔZ = 0.25 mm between particles, at fixed distances upstream of the sampler (X = 0.75 m for particles ≤75 μm and X = 0.5 m for larger particles) and repeated at lateral (Y) locations stepped through 0.5-mm increments to determine where particles would be aspirated into the sampler. The release coordinates for the particles that were aspirated were used to compute the critical area (Ac) defined as the upstream area that encompassed all particles that were aspirated into the sampler. Equation (8) was used to compute the aspiration efficiency of the sampler at the given orientation (Anthony and Flynn, 2006b).
| (8) |
where
• Ac = critical area, defined as the upstream area where particles are aspirated into the sampler, determined with particle release simulations
• Uc = freestream velocity within this critical area
• As = total area of the sampler pores
• Us = velocity through the sampler pores
Four conditions of bounce were evaluated to examine the effect of aerosol type on the sampler’s efficiency. The first condition allowed any particle hitting any surface within the computation domain to bounce (100% reflection). For the 30° down sampler, particles hitting the top medial surface of the external sidewalls of the cassette yielded significant aspiration into the sampler. Consequently, a second bounce condition was examined where particles were not allowed to bounce after contact with the outer cassette sidewall (Fig. 1b). This allowed the evaluation of the contribution of ‘solid’ particles bouncing into the sampler from the cassette’s exterior surface. The third condition prescribed no bounce to all surfaces except the internal walls of the pores. Should a solid or liquid droplet hit the inner wall of the 254-μm pore, it was assumed that the mass of the particle would reach the filter. However, particles hitting any other surface of the sampler were considered to be removed from the flow field as liquid particles would strike and not bounce into the sampler. Finally, all surfaces in the domain were assigned no-bounce conditions, including the internal pores of the sampler inlet face, along with the outer cassette and inlet cap face. While simulations did not address modeling liquid particles specifically, namely we ignored droplet deformation, the results based on bounce behaviors were used to provide initial estimates of liquid aerosol aspiration.
For these no-bounce simulations at the sampler inlet, more refined particle simulations were required. Rather than trying to compute the critical areas associated with each of the 1043 pores defining the sampler’s inlet, the proportion of particles aspirated into the sampler from line releases were determined across sequential lateral positions (Y) between height locations (Z) associated with the critical areas identified in bounce aspiration simulations. To investigate whether the spacing between particles released was affecting the solution, 200, 300, and 400 particles were released sequentially along the same ΔZ, and the aspiration efficiencies associated with each were computed and compared. These releases were repeated at other lateral (Y) locations that defined the critical area for the bounce condition, stepping through lateral distances by ΔY = 0.5 mm. The critical areas for no-bounce conditions were determined by summing the products of lateral dimension (between particle releases, ΔY), the particle release height (ΔZ), and the fraction of particles aspirated at that Y release location:
| (9) |
where i = the step reference across the lateral (Y) positions and from 1 to n = the maximum number of steps needed to determine the critical area.
Particle releases were also explored at additional smaller lateral steps (ΔY) of 0.25 and 0.125 mm to assess whether the aspiration efficiency changed as a function of particle simulation set-ups and to generate uncertainty intervals. These uncertainties were incorporated into aspiration efficiency curves, presented later in Fig. 4a,b.
Fig. 4.
Aspiration patterns at Y = −0.02 m for (a) 6-μm particle (N = 54 at X = −0.75 m, Y = −0.02 m between Z = 0.00155 and −0.0255 m, ΔZ = 0.5 mm) and (b) 100-μm particle (N = 30 at X = −0.5 m, Y = −0.02 m between Z = 0.3365 and 0.3215 m, ΔZ = 0.5 mm). The top line indicates the trajectory for the particle released from the highest Z position and the bottom line indicates the trajectory for the particle released from the lowest Z position at the upstream (X,Y) coordinates.
RESULTS
Fluid flow evaluation
All simulations were conducted on 64-bit processor personal computers with 8 gigabytes (GB) RAM using the Windows XP operating system. For all geometries investigated, the coarse mesh simulations took <24 h of run time to complete. For the single-pore and 0° down multipore simulations, the most refined mesh took under 10 days to solve. However, the 30° down multipore geometry simulations required nearly 2 months of simulation time to solve, likely due to the complexity of the mesh both inside and below the sampler where it joined the torso. The solution time for the most refined mesh can be improved over time, however, as faster computers with additional RAM become more affordable. For each mesh geometry, the last degree of freedom to converge was the ‘continuity’ or pressure term. All other degrees of freedom had GSEs of 1 × 10−7 to 1 × 10−8, while continuity converged to ~2 × 10−5.
Before particle simulations were begun, the qualities of the air parameter solutions were assessed to ensure adequate convergence. To assess non-linear convergence, the adequacy of the GSE tolerance was assessed at three sequential levels. Table 2 provides details on the L2 error norm [equation (4)] using the 1722 points upstream of the sampler. As seen in this Table 2, the lateral (Uy) and vertical (Uz) velocities were still changing by 10% between solutions reported at GSE of 1 × 10−4 and 2 × 10−5 for the coarse mesh. However, for the more refined meshes, differences for all degrees of freedom at the most refined GSE solution were ≤2.3%. This indicated that for both the moderate and the fine meshes used to simulate the flow field into the sampler, solutions posted at GSEs of 1 × 10−4 or 2 × 10−5 may be used. For subsequent particle simulations, the solutions at 2 × 10−5 were used.
Table 2.
L2 error norm investigating non-linear convergence (30° down).
| Mesh | GSE levels | Ux (%) | Uy (%) | Uz (%) | KE (%) | E (%) | SP (%) |
|---|---|---|---|---|---|---|---|
| Coarse (M1D) | 10−3 – 10−4 | 0.05 | 0.98 | 0.56 | 0.22 | 0.54 | 0.58 |
| 10−4 – 2e10−5 | 0.69 | 9.42 | 9.31 | 2.84 | 2.19 | 6.86 | |
| Moderate (M2D) | 10−3 – 10−4 | 0.13 | 0.54 | 1.94 | 0.04 | 0.04 | 1.08 |
| 10−4 – 2e10−5 | 0.06 | 0.90 | 2.25 | 0.09 | 0.16 | 0.75 | |
| Fine (M3D) | 10−3 – 10−4 | 0.22 | 0.83 | 4.16 | 0.08 | 0.08 | 1.74 |
| 10−4 – 2e10−5 | 0.03 | 0.08 | 0.23 | 0.01 | 0.01 | 0.23 |
Bold values indicate >5% change in values. The degrees of freedom indicated are Ux is velocity in the main direction of flow (horizontal), Uy is the lateral velocity, Uz is the vertical velocity, KE is the turbulence kinetic energy, E is the dissipation of turbulence kinetic energy, and SP is the pressure.
Next, mesh independence was assessed using between-mesh data for the same 1722 locations for a given geometry. For each degree of freedom and at solutions with GSE of 1 × 10−4 and 2 × 10−5, the mesh convergence ratios were between 0 and 1, indicating monotonic convergence for solutions at both the 1 × 10−4 and the 2 × 10−5 solutions (Table 3). These three-mesh error norms indicated that the solutions posted for either the moderate mesh (M2D) and fine mesh (M3D) could be used to perform particle simulations for releases upstream of the sampler. Furthermore, these solutions at GSE of 1 × 10−4 and 2 × 10−5 yielded little difference in the upstream region tested, so either solution could be used to evaluate particle simulations. For the subsequent particle simulation work, the solutions from the moderate mesh at the smallest GSE tolerance (2 × 10−5) were used, as the fine mesh required significantly more computational memory for particle simulations, even with 8 GB RAM. Similar results were found with the 0° down and single-pore convergence studies.
Table 3.
Three-mesh L2 norms for 30° down simulations,
| GSE level | U x | U y | U z | KE | E | SP |
|---|---|---|---|---|---|---|
| 1 × 10−4 | 0.9052 | 0.9104 | 0.9258 | 0.9280 | 0.8902 | 0.8863 |
| 2 × 10−5 | 0.9013 | 0.8732 | 0.7251 | 0.3781 | 0.7279 | 0.8465 |
Particle simulations
Critical area determinations were completed for the seven particle sizes for each of the three sampler geometries and bounce conditions. Fig. 3 illustrates the shapes of the critical areas for two particle sizes, 12.5 and 100 μm, where bounce was allowed on any surface. The first item to notice is that the upstream critical areas containing the stream tube, where particles will be captured by the sampler is not centered on Y = 0. The inlet to the sampler was positioned at (Y = 0) but was positioned off center of the torso, 0.042 m to the right (+Y). Particles captured by the sampler traveled from upstream positions to the left of the sampler's center, closer to the center of the mannequin torso. For the 12.5-μm particles, the positions of the critical areas upstream of the sampler varied between geometry, but the shape and sizes of these critical areas were similar, yielding similar aspiration efficiencies (Fig. 3a). As particle size increased, the critical area decreased, more noticeably for the samplers oriented below the horizon (Fig. 3b). The critical area shape changed from oval for the 0° down sampler to much smaller oval with a peak near the center: within this peak area, particles traveled through the freestream and impacted on the top outer surface near the center of the sampler. Those that impacted close to the top center of the outside of the cassette bounced off the surface then into the aspiration area. As particle releases were positioned to the left and right (±Y) of those at the peak and at the same height (Z), they hit the sampler surface but bounced away from the inlet to the sampler and were not sampled. When particles were restricted from bouncing into the sampler (Conditions 2 through 4), these peaks disappeared, thereby reducing aspiration efficiencies due to decreased sizes of the critical areas.
Fig. 3.
Representative critical areas for (a) 12.5- and (b) 100-μm particles with bounce allowed on all surfaces (Condition 1).
From these critical area data, aspiration efficiencies were computed for the seven particle sizes, four bounce conditions and three sampler geometries and are summarized in Table 4. For the two orientations of the PHISH sampler, aspiration efficiencies are provided for each of the four bounce conditions investigated. For the 0° orientation, preventing bounce on the external sidewalls of the sampler had almost no effect on aspiration efficiency. However, this condition had a more pronounced effect for the 30° down sampler (second data column), where the proportion of particles bouncing off the external sampler perimeter and then into the sampler increased with increasing particle size. Up to 8% of the aspiration efficiency could be attributed to particle bounce off the external sampler sidewalls, primarily the medial top section, of the cassette before aspiration. Limiting the bouncing condition only to those particles hitting the inside of the pores during travel to the inside of the sampler (prohibiting particles from bouncing into the sampler after hitting either the outside surface and the front face of the cassette, Condition 3 above, third data column) reduced the aspiration for both sampler angles investigated. For the no-bounce condition, aspiration was nearly identical for the two multipore sampler orientations. The final column in Table 4 provides the aspiration data for the ‘all-bounce’ condition with the single 15-mm pore, also angled 30° below the horizon. These results compare directly to the all-bounce condition of the 30° down multipore sampler, where differences were within 3% for each particle size investigated.
Table 4.
Aspiration efficiency by sampler orientation and particle bounce condition
| 0° down (entrance perpendicular to horizon) | 30° down (entrance tilted 30 below the horizon) | Single pore, 30° down |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Aerodynamic diameter (μm) |
Bounce: all surfaces (%) |
No bounce from outside of cassette (%) |
No bounce except at pore walls (%) |
No bounce: all surfaces (%) |
Bounce: all surfaces (%) |
No bounce from outside of cassette (%) |
No bounce except at pore walls (%) |
No bounce: all surfaces (%) |
Bounce: all surfaces (%) |
| 6 | 100 | 100 | 59 | 59 | 100 | 100 | 58 | 59 | 99 |
| 12.5 | 102 | 102 | 40 | 34 | 101 | 101 | 41 | 35 | 99 |
| 25 | 102 | 102 | 38 | 23 | 98 | 97 | 34 | 20 | 96 |
| 50 | 98 | 98 | 31 | 12 | 90 | 82 | 27 | 10 | 88 |
| 75 | 92 | 92 | 25 | 8 | 62 | 55 | 16 | 5 | 65 |
| 90 | 85 | 84 | 20 | 5 | 47 | 39 | 12 | 2 | 48 |
| 100 | 76 | 75 | 18 | 3 | 32 | 27 | 8 | 1 | 33 |
Fig. 4 illustrates the behavior of 6- and 100-μm particles as they approached the entrance to the 30° down multipore inlet. Particles were released at the same lateral distance relative to the sampler inlet (Y = −0.020 m) to obtain critical areas defining an upstream region, where all particles released would be aspirated into the sampler, but at different distances upstream (X) and at different heights (Z) to accommodate differences in gravitational settling, as discussed in ‘Methods’ section. The particle trajectory lines illustrate the predominantly horizontal, but slightly upward, path associated with small particle transport, in addition to the large vertical settling component associated with large particle transport. Both images illustrate particle release within and just beyond the critical area, with bounce allowed on any surface of the sampler, and spacing of 0.5 mm between particle releases for illustration. In Fig. 4a, the upper and lower 6-μm particles released from this line of 54 particles bounced on the sampler surface and were directed away from the sampling orifice, unaspirated. Note that for these small particles, aspiration into the sampler occurred across the entire height of the porous surface. Fig. 4b illustrates 100-μm particles, again with the outermost particles (two above and one below) bouncing away from the sampler inlet, avoiding secondary aspiration. Nevertheless, most of these large particles bounced off the sampler surface multiple times prior to their eventual aspiration into one of the pores. Also illustrated in Fig. 4b, the larger particles entered into the sampler through primarily the bottom section of the inlet pores: particles released at locations above the critical area hit the top of the sampler cassette and bounced away from the sampler.
Because of these large particles’ inability to follow airflow streamlines passing into the sampler, the upstream critical area defining particle aspiration decreased with increased particle size. For the forward-facing sampler (0° down), impaction on the exterior sidewalls of the cassette prior to aspiration was less of an issue, as the sampler itself did not project into the main trajectories of particles moving toward the inlet. As such, the aspiration efficiency of the PHISH sampler oriented directly into the oncoming wind had larger aspiration efficiencies, for all particle sizes, relative to the 30° down sampler orientation.
Given the same bounce condition, the aspiration efficiencies were nearly the same for all sampler orientations up through 25 μm. However, as the particle size increased, the aspiration efficiency dropped more substantially with increased particle size for the 30° down orientation.
In addition to particle size, particle bounce played a major role in determining whether aspiration would occur. With the smallest particle size studied (6 μm), 42% of the aspiration efficiency of bouncing particles involved particles hitting the face of the sampler at least once (column 1 minus column 3 in Table 4). Over all particle sizes studied, those that hit the surface of the sampler one or more times prior to being aspirated into the sampler accounted for 24–63% of the overall aspiration efficiency: aspiration efficiencies for liquid particles would be significantly smaller than that of solid particles with the multipored sampler inlet. Over the particle size range studied, 0–19% of the ‘any bounce’ aspiration efficiency resulted from hitting the walls within the inlet pores prior to entering the sampler, as computed by subtracting the ‘no bounce-all surfaces’ data from ‘no bounce except at pore walls’ data in Table 4.
Several particle trajectory simulations were conducted to evaluate the uncertainty associated with the methods used to generate particle aspiration data. For the no-bounce conditions, <1% differences in aspiration were identified in the results between N = 200, 300, and 400 particles along the series of ΔZ heights and the stepwise lateral distances defining the critical aspiration area. Slightly larger changes (8% difference in aspiration efficiency) were identified by decreasing the ΔY spacing for particles within the critical area. Data were reported for ΔY = 0.5 mm for ≥25 μm and ΔY = 0.125 mm for 6 and 12.5 μm to maintain uncertainties <2%. These uncertainties were included as error bars in Fig. 5.
Fig. 5.
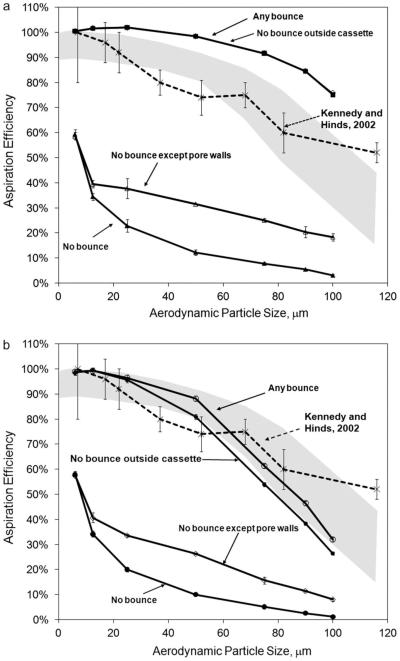
Aspiration efficiency (%) as a function of particle size and bounce condition for (a) 0° down and (b) 30° down orientations of sampler on torso. The gray band indicates the range of human aspiration efficiencies reported from humanoid CFD simulations with facing-the-wind orientation, 0.4 m s−1 freestream velocity, and moderate to at-rest breathing rates. The dashed line is from Kennedy and Hinds (2002), mannequin studies of solid aerosol aspiration. Error bars indicate the uncertainty associated with the methods used to generate critical area and aspiration efficiency; in some cases, these values are obstructed by the size of the data marker.
DISCUSSION
While the results of these simulations have not yet been validated with experimental data, they provide guidance to the design and use of multipored inhalable samplers. We note that direct comparison between the IPM criterion and the particle simulations presented here are inappropriate, as the IPM criterion is orientation averaged (360° relative to the oncoming wind) and these simulations were performed in only one direction, with the sampler-oriented facing the wind. A more reasonable approach is to compare the particle aspiration efficiency of the simulated PHISH sampler to that of a human that has matched orientation in low-velocity freestream conditions. For this, two data sets were available to compare our simulated sampler performance: mannequin studies of solid particles (Kennedy and Hinds, 2002) and CFD humanoid simulations of liquid and solid particles (Anthony and Flynn, 2006b). Both of these studies examined particle aspiration efficiencies over the same range of particle sizes, and both used a breathing human surrogate facing the wind at low indoor air velocity of 0.4 m s−1.
Fig. 5a,b illustrates the aspiration efficiencies of Table 4 along with human aspiration efficiency data for similar 0.4 m s−1 freestream studies for the 0° and 30° down PHISH orientations, respectively. The gray band provides the aspiration efficiency curve generated in previous CFD simulations of human aspiration at moderate mouth-breathing velocity and 0.4 m s−1 freestream velocity for the same forward-facing orientation (Anthony and Flynn, 2006b): the bottom of the band represents the no-bounce particle aspiration and the top of the band represents aspiration that includes particle bounce on the human face. The previous study examined aspiration of particles into a continuously inhaling mouth, where the human head had realistic facial details (nose, lips, chin, neck, etc.) but a simplified cylindrical torso. The dashed line in Fig. 5 represents the aspiration efficiency curve from mouth-breathing mannequin studies in a wind tunnel with the same forward-facing orientation and freestream velocity at a minute respirator volume of 20.8 l min−1 using solid aluminum oxide particles (Kennedy and Hinds, 2002). Therefore, these reference data are not data from geometrically identical samplers but are rather provided to represent the IPM fractions for mouth inhalation in similar low-velocity freestream environment: they represent the only data available for comparing this work’s aspiration efficiency findings for the high-volume sampler to human inhalation at the same low-velocity freestream conditions with facing-the-wind orientation. We compare our PHISH sampler aspiration efficiency to these data to evaluate whether the PHISH sampler matches the efficiency of the human head.
As is apparent from Fig. 5a, the 0° down orientation aspirated a larger fraction of solid particles relative to the human aspiration studies, both mannequin wind tunnel and humanoid CFD. Since this sampler was designed to be positioned on the torso of a worker, it would be rare to affix 37-mm sampler cassettes to an actual person in a truly horizontal orientation, as the tubing connecting the sampler to the sample pump typically interferes with such a positioning. When typically worn, the sampler has a slightly downward angle relative to the horizon.
In examining Fig. 5b, the PHISH sampler oriented 30° below the horizon demonstrated solid particle aspiration near the lower bound of the humanoid aspiration curve from the comparison humanoid CFD study. This sampler orientation illustrated a more realistic field deployment of this personal sampler on a torso. While the decrease in aspiration efficiency did not remain constant for particles 80 μm and larger, as shown in Kennedy and Hinds (2002) data, the aspiration efficiency had a similar shape and behavior as the humanoid CFD results. This decrease in aspiration efficiency, relative to the horizontal PHISH sampler orientation, was consistent with what one would expect when angling the sampler below the horizon: as the top of the sampler projected in front of the porous openings, the area through which large particles could travel and be aspirated decreased. The previous critical area figures (Fig. 3) illustrate this effect on the reduced size of these areas. One unanswered question that remains is whether this decrease in aspiration efficiency holds steady over a range of sampler orientations relative to the horizon: the actual donning of the PHISH sampler may result in a range of positions from perhaps 20 to 50° below the horizon. It would be important to quantify how much aspiration efficiencies would be affected over this range of downward orientation of the sampler’s inlet.
What may contribute more than horizontal orientation to the success of this porous sampler in meeting the 360° IPM criterion is the physical characteristic of the aerosol being sampled. As liquid particles moved toward the sampler to be aspirated, most of the particles in the critical area identified above actually hit the solid portion of the sampler face and deposited on the sampler surface (second from bottom line in Fig. 5) or within the pores of the sampler (bottom line). If the facing-the-wind aspiration orientation provides the greatest aspiration efficiency relative to the 360° positions available, these data indicate that exposures to liquid aerosols containing large droplets would be severely underestimated using this or possibly any multipored sampler. Previous developmental work (Kalatoor et al., 1995; Aizenberg et al., 2001) and field testing (Hauck et al., 1997) on the domed multipored Button sampler relied on solid particles (uranine, aluminum oxide, dust/fungal spores, respectively). Aspiration efficiencies for liquid aerosols using the multiporous Button inhalable sampler have not been reported. Although domed, the inlet surface of the Button sampler is similar in porosity and pore size to that of the sampler presented here. Practitioners should use caution when selecting a multipored inhalable sampler to assess exposures to large liquid aerosols in the workplace.
The third sampling geometry that was tested replaced the multiple pores with a single central 15-mm opening on the flat-face of the cassette inlet. Data in the right column of Table 4 provide the ‘all surface bounce condition’ of the single 15-mm pore in the new flat-topped 37-mm sampler, operated at 10 l min−1. The resulting aspiration efficiency was nearly identical to the 30° down all-bounce condition, within 3% for any particle size studied, which also resulted in reasonable agreement with the forward-facing human aspiration efficiency values. If the single 15-mm pore matched the forward-facing human aspiration curve, an obvious question is whether a high-flow sampler requires the use of a porous entry. Recall that one of the major shortcomings with the IOM sampler has been that it allows particles >100 μm to be aspirated into the cassette, which has been attributed in many studies to the oversampling of particulate mass compared to other inhalable samplers. For any aerosol sampler, a few extremely large particles can affect the total mass of aerosol sampled, which in environments with large particles, would lead to increased variability in exposure estimates. The 254-μm pore openings in the PHISH sampler restricted any particle exceeding this dimension from entering the sampler. However, this study identified concerns of under-sampling liquid aerosols using a sampler with multiple small pores on the entry surface, even at the 30% porosity studied here. If the size distribution of liquid and solid aerosols at a worksite can be confirmed to be <100 μm, a simple 15-mm hole in a flat-capped 37-mm sample cassette operated at 10 l min−1 shows promise for additional investigation as an option for meeting the IPM curve over 360° rotation relative to the oncoming wind. However, equipment and techniques to easily quantify the size distribution in work environments are not common to practitioners to test this caveat prior to selecting the sampler for fieldwork.
This work presents advancement in CFD studies of personal aerosol samplers, as the work involved 3-D simulations and bluff body to represent the torso behind the sampler. Previous CFD investigations of inhalable samplers are limited to works by Gao et al. (2002) and Bird (2005). Gao et al. (2002) used CFD methods to examine the performance of the early designs of the Button sampler. That work simplified the sampler using a 2-D axisymetric slice of the sampler, equivalent to using the top half of the centerline geometry of the sampler. This ignored the non-symmetric aspiration pattern across the entrance to the sampler as particle size increases, where large particles are incapable of moving into the sampler as efficiently from the bottom as on the top half of the horizontally oriented sampler.
Although not discussed in detail in this report, preliminary 2-D studies of this sampler design in the 0° down orientation resulted in similar aspiration efficiency estimates to the fully 3-D models for particles <90 μm (+1–5%) but began deviating with increased particle sizes. Both the 2-D and the 3-D simulations of the horizontal samplers estimated aspiration efficiencies larger than those of an inhaling human. As the samplers were rotated below the horizon, the 2-D simulations yielded larger aspiration estimates than the 3-D model for particles >50 μm. This may result from the overestimation of the effect of bounce from the exterior 2-D surface of the sampler perimeter into the sampler, as we now know that happens only over a small portion of the sampler in the downward orientation (Fig. 3b).
Since the study by Gao et al. (2002), the cost-efficient improvements in computer speed and memory have made 3-D studies more tractable. In 2005, Bird used 3-dimensional CFD simulations to examine the aspiration efficiency of a sampler with a single-pore geometry associated with conical inlet samplers, similar to the GSP and CIS, ignoring the effects of the bluff body positioned behind the sampler and focused on sampler performance out of range of typical indoor velocities of occupational conditions. While this current work is limited in orientation and velocity conditions, it provides guidance to multipored sampler design and orientation at lower velocity occupational settings.
CONCLUSIONS
This work identified modifications to the standard three-piece 37-mm cassette ‘total’ dust sampler to meet the IPM sampling criterion at a 10 l min−1 sampling rate. While CFD simulations required extremely refined meshes to represent the fluid flow field into the sampler, current 64-bit computers with 8 GB Ram desktop computers could handle these 3-D simulations within reasonable time constraints; further improvements are expected as computer speed and affordability increase. These simulations included not only the 3-D sampler but also a simplified bluff-body torso behind the sampler and a wind tunnel that provided a domain with a low 7% blockage ratio, resulting in more realistic simulations than previous 2-D and 3-D simulations without bluff bodies.
Situating the samplers onto elliptical torsos added to the complexity of the simulation, as it required a much larger computational domain; however, it forced the sampler to draw air only from upstream, which allowed us to rotate the sampler below the horizon without potentially sampling from below or behind the sampler. This better represented field deployment of the PHISH sampler as a personal sampler. It also resulted in the realistic upward component to small particle trajectories, mimicking the known upward and lateral movement of air as it moves toward and around a bluff body. This model represents a significant advance in personal aerosol sampler simulation modeling.
The standard 37-mm sampler inlet cap was replaced with a flat-fronted cap with the central 15-mm section replaced with 30% porosity surface made up of a series of on-center 254-μm pores. Simulations were performed at velocities equivalent to a 10 l min−1 sampling rate and resulting particle aspiration efficiencies resembled those reported for mannequin/humanoid aspiration studies, both laboratory and CFD simulation, with similar freestream velocities (0.4 m s−1) and mannequin/humanoid orientation (facing the wind). Given the same bounce condition, the aspiration efficiencies were nearly the same for both sampler orientations for particles ranging up through 25 μm. However, as the particle size increased, the aspiration efficiency dropped more substantially with increased particle size for the 30° down orientation.
This new sampling head, oriented 30° below the horizon, demonstrated good agreement with human-form low-velocity CFD studies for aerosols capable of bouncing off of the sampler surface and into the multipored entry. However, this CFD work did not match the aspiration efficiency of the mannequin studies, where aspiration did not begin to approach zero with increasing particle size, as shown by Kennedy and Hinds (2002). More importantly, this new sampling inlet may not be suitable for liquid aerosols: when particles cannot bounce off of the sampler surface, the aspiration efficiency of both the 0° and the 30° downward orientation undersample relative to both the CFD and the wind tunnel mannequin studies of the inhaling human. A single 15-mm entry area on a flat-faced 37-mm cassette is more desirable for sampling the inhalable fraction of liquid aerosols, but this design would not eliminate particles >100 μm from entering the sampling device. Additional laboratory investigations of this sampler at similar operating conditions will help examine the assumptions of bounce, presented here. If good agreement is found, studies at other orientations relative to the oncoming wind are needed to determine the success of this sampler to meet the orientation-averaged IPM criterion.
Supplementary Material
Acknowledgments
The content is solely the responsibility of the authors and does not necessarily represent the official views of the U.S. National Institute of Occupational Safety and Health.
FUNDING
National Institute for Occupational Safety and Health (R21OH009114).
References
- Aizenberg V, Choe K, Grinshpun SA, et al. Evaluation of personal aerosol samplers challenged with large particles. J Aerosol Sci. 2001;32:779–93. [Google Scholar]
- American Conference of Governmental Industrial Hygienists (ACGIH) Threshold limit values forchemical substances and physical agents and biological exposure indices. ACGIH; Cincinnati, OH: 2009. [Google Scholar]
- Anthony TR, Flynn MR. CFD model for a 3-D inhaling mannequin: verification and validation. Ann Occup Hyg. 2006a;50:157–73. doi: 10.1093/annhyg/mei048. [DOI] [PubMed] [Google Scholar]
- Anthony TR, Flynn MR. Computational fluid dynamics investigation of particle inhalability. J Aerosol Sci. 2006b;37:750–65. [Google Scholar]
- Ashley K, Brisson MJ. Analytical performance criteria: sampling and analysis issues relating to the ACGIH® notice of intended change for the beryllium threshold limit value. J Occup Environ Hyg. 2005;2:D97–9. doi: 10.1080/15459620500397772. [DOI] [PubMed] [Google Scholar]
- Baldwin PEJ, Maynard AD. A survey of wind speeds in indoor workplaces. Ann Occup Hyg. 1998;42:303–13. doi: 10.1016/s0003-4878(98)00031-3. [DOI] [PubMed] [Google Scholar]
- Bird AJ. Use of numerical calculations to simulate sampling efficiency performance of a personal aerosol sampler. Aerosol Sci Technol. 2005;39:596–610. [Google Scholar]
- Carlton GN, Flynn MR. Field evaluation of an empirical-conceptual exposure model. App Occup Environ Hyg. 1997;12:555–61. [Google Scholar]
- Comité Européen de Normalization (CEN) Workplace Atmospheres: Size Fraction Definitions for Measurements of Airborne Particles in the Workplace (CEN standard EN 481) CEN; Brussels, Belgium: 1993. [Google Scholar]
- Davies HW, Teschke K, Demers PA. A field comparison of inhalable and thoracic size selective sampling techniques. AnnOccup Hyg. 1999;43:381–92. [PubMed] [Google Scholar]
- Gao P, Chen BT, Baron PA, et al. A numerical study of the performance of an aerosol sampler with a curved, blunt, multi-orificed inlet. Aerosol Sci Technol. 2002;36:540–53. [Google Scholar]
- Harper M, Muller BS. An evaluation of total and inhalable samplers for the collection of wood dust in three wood products industries. J Environ Monitoring. 2002;4:648–56. doi: 10.1039/b202857n. [DOI] [PubMed] [Google Scholar]
- Hauck BC, Grinshpun SA, Reponen A, et al. Field testing of new aerosol sampling method with a porous curved surface inlet. Am Ind Hyg Assoc J. 1997;58:713–9. doi: 10.1080/15428119791012351. [DOI] [PubMed] [Google Scholar]
- International Organization for Standardization (ISO) Air Quality—Particle Size Fraction Definitions for Health-Related Sampling (ISO Standard 7708) ISO; Geneva, Switzerland: 1995. [Google Scholar]
- Kalatoor S, Grinshpun SA, Willeke K. New aerosol sampler with low wind sensitivity and good filter collection uniformity. Atmospheric Environment. 1995;29:1105–12. [Google Scholar]
- Kennedy ER, Fischbach TJ, Song R, et al. NIOSH Manual of Analytical Methods. 4th. DHHS (NIOSH); 1998. Chapter E: Development and evaluation of methods. 1994 Aug;:38. Publication 94-113. [Google Scholar]
- Kennedy NJ, Hinds WC. Inhalability of large solid particles. J Aerosol Sci. 2002;33:237–55. [Google Scholar]
- Kenny LC, Aitken R, Chalmers C, et al. A collaborative European study of personal inhalable aerosol sampler performance. Ann Occup Hyg. 1997;41:135–53. doi: 10.1016/S0003-4878(96)00034-8. [DOI] [PubMed] [Google Scholar]
- Linnainmaa M, Laitinen J, Leskinen A, et al. Laboratory and field testing of sampling methods for inhalable and respirable dust. J Occup Environ Hyg. 2008;5:28–35. doi: 10.1080/15459620701763723. [DOI] [PubMed] [Google Scholar]
- Mark D, Lyons CP, Upton SL, et al. Wind tunnel testing of the sampling efficiency of personal inhalable aerosol samplers. J Aerosol Sci. 1994;25:S339–40. [Google Scholar]
- Morsi SA, Alexander AJ. An investigation of particle trajectories in two-phase flow systems. J Fluid Mech. 1972;55:193–208. [Google Scholar]
- Roache PJ. Validation in Computational Science and Engineering. Hermosa Publishers; Albuquerque, NM: 1998. [Google Scholar]
- Vaughan NP, Chalmers CP, Botham RA. Field comparison of personal samples for inhalable dust. Ann Occup Hyg. 1990;34:553–73. doi: 10.1093/annhyg/34.6.553. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.