Isotonic estimation of survival under a misattribution of cause of death

Abstract

Several authors have indicated that incorrectly classified cause of death for prostate cancer survivors may have played a role in the observed recent peak and decline of prostate cancer mortality. Motivated by the suggestion we studied a competing risks model where other cause of death may be misattributed as a death of interest. We first consider a naïve approach using unconstrained nonparametric maximum likelihood estimation (NPMLE), and then present the constrained NPMLE where the survival function is forced to be monotonic. Surprising observations were made as we studied their small-sample and asymptotic properties in continuous and discrete situations. Contrary to the common belief that the non-monotonicity of a survival function NPMLE is a small-sample problem, the constrained NPMLE is asymptotically biased in the continuous setting. Other isotonic approaches, the supremum (SUP) method and the Pooled-Adjacent-Violators (PAV) algorithm, and the EM algorithm are also considered. We found that the EM algorithm is equivalent to the constrained NPMLE. Both SUP method and PAV algorithm deliver consistent and asymptotically unbiased estimator. All methods behave well asymptotically in the discrete time setting. Data from the Surveillance, Epidemiology and End Results (SEER) database are used to illustrate the proposed estimators.

1 Introduction

Statistics from the Surveillance, Epidemiology and End Results (SEER) program of the National Cancer Institute show that US prostate cancer mortality rates over the period of increased utilization of prostate-specific antigen (PSA) screening follow the unimodal shape of the incidence rates. However, changes in the incidence due to screening are expected to lag those of mortality as patients with prostate cancer typically have good prognosis.

One of possible explanations for the observed trend could be a misattribution of the underlying cause of death in prostate cancer patients. With the introduction of PSA testing in the late 1980s, many more men get a diagnosis of prostate cancer. Although many of these men will die from causes other than prostate cancer, a proportion of these deaths is likely to be misattributed to prostate cancer just because the men were diagnosed with it. This is often referred to as attribution bias. Feuer et al (1999) argued that this phenomenon would lead to a peak in mortality coinciding with the peak in incidence even if misattribution rate were a constant. A recent review of death certificates in New Mexico and a descriptive study by Hoffman et al (2003) indicated that misattribution may explain up to a half of mortality increase before 1995. Moreover, about 5.6% attribution bias is observed among the deaths in 1995 from the study. These studies motivated us to look at the problem of estimating a post-treatment survival function in the presence of misattribution.

Misattribution of the cause of death leads to a loss of monotonicity in naïve estimators. While there have been studies on inference under a masked cause of failure (e.g. Dinse, 1982; Goetghebeur and Ryan, 1995; Flehinger et al, 1998; Dewanji and Sengupta, 2003; Craiu and Duchesne, 2004), isotonic methods dealing with the monotonicity constraint received little attention. The reason for this is the belief that the problem is of a small-sample origin, and that non-monotonicity disappears in large samples as all methods approach the naïve NPMLE asymptotically. We found this generally not to be true in our setting.

A nonparametric maximum likelihood estimation (NPMLE) approach was used for the post-treatment survival under misattribution. Since unknown true cause of death is a missing data problem, we developed an EM algorithm in Section 3.2. Small-sample and asymptotic properties of the procedure are discussed in Section 3.3. Expecting EM to solve an unconstrained (naïve) NPMLE problem we found to our surprise that EM and constrained NPMLE are equivalent and both give biased solutions in the continuous setting. We studied other isotonic estimation techniques to remedy the problem in Section 4, and also explored their asymptotic properties. A simulation study is done to investigate the performance of the estimators in Section 5, and the methods are applied to real data from the SEER program in Section 6.

2 Assumption and notation

Suppose that we observe n independent individuals and that each individual can fail from one of two possible causes, which we term type 1 (prostate cancer) and 2 (other cause), respectively, or can be subject to an independent right censoring mechanism (type 0 failure). The observed data for individual i can be represented as (T_i, ω_i), where T is time of failure or censoring (whichever comes first), and ω = 0, 1, 2 is the observed failure type. Define the corresponding true failure type as Ω which is not observed for some individuals. The true cause-specific hazard for type j failure is given by

$${\lambda }_j(t)=\underset{h\to 0}{lim}\frac{1}{h}Pr[t\le T<t+h,\mathit{\Omega }=j\mid T\ge t]\text{for}j=0,1,2.$$

We assume the competing true causes of failure to be independent. Under this assumption, the crude hazards will be equal to their net counterparts. By the non-identifiability aspect of competing risks (Tsiatis, 1975) the dependence of risks cannot be recovered without additional assumptions. The same maximum likelihood solution is achieved for the crude cause-specific hazards regardless of whether competing risks are assumed dependent or independent (Prentice et al, 1978).

Typically, there are two types of misattribution in this setting. Assuming our interest focuses on a failure from prostate cancer (type 1 cause), define over-attribution as a death from other cause (type 2) attributed to prostate cancer (type 1). On the other hand, under-attribution is defined as a death from prostate cancer (type 1) attributed to other cause (type 2). Hoffman et al (2003) found no under-attribution in recent prostate cancer data, and we consider over-attribution as the only type operating; that is,

$$\begin{array}{l}Pr[\omega =1\mid T=t,\mathit{\Omega }=2]=r(t)\\ Pr[\omega =2\mid T=t,\mathit{\Omega }=1]=0\end{array}$$ (1)

where r is considered to be a known function of t. However, the results are easily extendable when under-attribution is also present (see Discussion).

Goetghebeur and Ryan (1995), Dewanji and Sengupta (2003) and Gao and Tsiatis (2005) proposed semi- and nonparametric inference procedures under a ’missing-at-random’ mechanism of Little and Rubin (1987). This, however, is not generally the case unless the second probability in (1) is 1 − r(t); more precisely, the chance of observing failure from type j cause does not depend on its true failure types.

Under misattribution the observed cause-specific hazard is distorted compared to the true one

$${\lambda }_j^{\mathit{obs}}(t)=\underset{h\to 0}{lim}\frac{1}{h}Pr[t\le T_i<t+h,\omega =j\mid T_i\ge t]=\{\begin{array}{ll}{\lambda }_0(t),\hfill & \omega =0,\text{censoring}\hfill \\ {\lambda }_1(t)+r(t){\lambda }_2(t),\hfill & \omega =1,\text{observed}\text{prostate}\text{cancer}\text{death}\hfill \\ {\lambda }_2(t)(1-r(t)),\hfill & \omega =2,\text{observed}\text{other}\text{cause}\text{death.}\hfill \end{array}$$ (2)

Note that

$${\lambda }_1(t)+{\lambda }_2(t)={\lambda }_1^{\mathit{obs}}(t)+{\lambda }_2^{\mathit{obs}}(t)=\lambda (t),$$ (3)

the marginal hazard of any type, as misattribution is a re-distribution of cases over the causes of failure.

3 Nonparametric maximum likelihood estimation

Let N_j(t) be the process counting failures of type j, and Y (t) be the at risk process. In the nonparametric context the model is parameterized by the jumps of the cumulative hazard function dΛ_j(t) = λ_j(t)dt. In terms of the hazard function, the loglikelihood can be written as

$$l=\int {dN}_1(t)log[d{\mathit{\Lambda }}_1(t)+r(t)d{\mathit{\Lambda }}_2(t)]+{dN}_2(t)log[\overline{r}(t)d{\mathit{\Lambda }}_2(t)]-Y(t)d\mathit{\Lambda }(t),$$ (4)

where dΛ(t) = dΛ₁(t)+ dΛ₂(t) is the jump of the marginal hazard of any type, r̄(t) = 1 − r(t), and the integral is taken over t and all the three terms. By taking derivatives of l with respect to dΛ_j(t) for all distinct observed failure times t

$$\begin{array}{l}\frac{\partial l}{\partial d{\mathit{\Lambda }}_1(t)}=-Y(t)+\frac{{dN}_1(t)}{d{\mathit{\Lambda }}_1(t)+r(t)d{\mathit{\Lambda }}_2(t)}\\ \frac{\partial l}{\partial d{\mathit{\Lambda }}_2(t)}=-Y(t)+\frac{{dN}_2(t)}{d{\mathit{\Lambda }}_2(t)}+\frac{r(t){dN}_1(t)}{d{\mathit{\Lambda }}_1(t)+r(t)d{\mathit{\Lambda }}_2(t)}\end{array}$$ (5)

and setting them to zero, we get the naïve nonparametric maximum likelihood estimates (naïve NPMLE) for type 1 and 2 failure hazard rates

$$\begin{array}{l}d{\stackrel{\sim }{\mathit{\Lambda }}}_1(t)=\frac{1}{Y(t)}\{{dN}_1(t)-\text{Odds}[r(t)]{dN}_2(t)\}\\ d{\stackrel{\sim }{\mathit{\Lambda }}}_2(t)=\frac{{dN}_2(t)}{\overline{r}(t)Y(t)},\end{array}$$ (6)

where Odds[r] = r/(1 − r). Here and in the sequel 1/Y (t) is assumed to be 0 when Y (t) = 0. Note that naïve NPMLE is a linear function of empirical estimates for the observed hazard rates

$$\begin{array}{l}d{\stackrel{\sim }{\mathit{\Lambda }}}_1(t)=d{\widehat{\mathit{\Lambda }}}_1^{\mathit{obs}}(t)-\text{Odds}[r(t)]d{\widehat{\mathit{\Lambda }}}_2^{\mathit{obs}}(t)\\ d{\stackrel{\sim }{\mathit{\Lambda }}}_2(t)={[\overline{r}(t)]}^{-1}d{\widehat{\mathit{\Lambda }}}_2^{\mathit{obs}}(t),\end{array}$$ (7)

where $d{\widehat{\mathit{\Lambda }}}_j^{\mathit{obs}}(t)={dN}_j(t)/Y(t)$ are the Nelson-Aalen estimators for the hazard of the observed failures of type j. The naïve NPMLE is unique, and the corresponding information matrix is positive-definite.

Note that we define the naïve estimator as the one derived from the equation (6) even when some of dN_j’s are zeros. When dN₁(t_α) is zero at a time t_α, the naïve estimate is negative $\text{negative}-\text{Odds}[r(t_{\alpha })]d{\widehat{\mathit{\Lambda }}}_2^{\mathit{obs}}(t_{\alpha })$. It seems reasonable to have the corresponding estimate forced to zero to respect the monotonicity restriction on the cumulative hazard (cf. constrained estimator defined below). Unfortunately, allowing for negative dΛ̃₁ is essential for the consistency of the estimator ${\int }_0^{t}d{\stackrel{\sim }{\mathit{\Lambda }}}_1(s)$, which will be discussed in Section 3.3.

Note that from (7) the monotonicity is violated when

$$d{\widehat{\mathit{\Lambda }}}_1^{\mathit{obs}}(t)<d{\widehat{\mathit{\Lambda }}}^{\mathit{obs}}(t)r(t)\text{or}\overline{r}(t){dN}_1(t)<r(t){dN}_2(t),$$ (8)

where $d{\widehat{\mathit{\Lambda }}}^{\mathit{obs}}(t)=d{\widehat{\mathit{\Lambda }}}_1^{\mathit{obs}}(t)+d{\widehat{\mathit{\Lambda }}}_2^{\mathit{obs}}(t)=({dN}_1(t)+{dN}_2(t))/Y(t)=dN(t)/Y(t)$ is the Nelson-Aalen estimate of the marginal hazard of any type.

When violation of monotonicity at a time t_α is corrected by setting dΛ₁(t_α) = 0, the model assumes all failures of type 1 at t_α are misattributed. Under this assumption, Y (t_α)r(t_α)dΛ̂^obs(t_α) = Y (t_α)r(t_α)dΛ̃(t_α) represents an estimate of the expected number of failures of type 1, by virtue of (3), while the left part of (8) is the observed counterpart of the same quantity. Hence, monotonicity is violated whenever the expected number of failures of type 1 is greater than the observed number of failures under the assumption of full misattribution. In case of untied data, according to (8), violations of monotonicity occur whenever dN₁(t) = 0 and dN₂(t) = 1, i.e. whenever type 2 failure (other cause) is observed.

3.1 Constrained estimation

Define a constrained estimator Λ̂_j, j = 1, 2 by maximizing the likelihood under the constraint of monotone Λ_js:

$$\underset{d{\mathit{\Lambda }}_j(t)\ge 0,j=1,2}{max}l({\mathit{\Lambda }}_1,{\mathit{\Lambda }}_2).$$ (9)

Note that the likelihood (4) is a sum of independently parameterized terms l = Σ_αl_α(dΛ₁(t_α), dΛ₂(t_α)) over distinct event times t_α. Therefore enforcement of the restriction proceeds separately for each such event time. The likelihood has the unique point of maximum defined by the score equations. When this point is outside of the admissible subset of parameters defined by dΛ₁(t) ≥ 0, the constrained maximum must be on the border. Therefore, constrained solution corresponds to setting any monotonicity violator in the naïve NPMLE to zero, dΛ̂₁(t_α) = 0. When dΛ₁(t_α) = 0, the optimal dΛ̂₂(t_α) = dΛ̂^obs(t_α). As noted above in this case the model presumes all observed type 1 failures are misattributed true type 2 failures in which case their incidence is the same as the observed marginal one at t_α.

As a result, the non-negative counterpart of the naïve NPMLE (7) becomes

$$\begin{array}{l}d{\widehat{\mathit{\Lambda }}}_1(t)=d{\stackrel{\sim }{\mathit{\Lambda }}}_1(t)I[\overline{r}(t){dN}_1(t)\ge r(t){dN}_2(t)]\\ d{\widehat{\mathit{\Lambda }}}_2(t)=d{\stackrel{\sim }{\mathit{\Lambda }}}_2(t)I[\overline{r}(t){dN}_1(t)\ge r(t){dN}_2(t)]+d{\widehat{\mathit{\Lambda }}}^{\mathit{obs}}(t)I[\overline{r}(t){dN}_1(t)<r(t){dN}_2(t)],\end{array}$$ (10)

where I is an indicator function I(A) = 1 if A is true and 0 otherwise. The role of indicator function in the constrained NPMLE for type 1 failure is to force the naïve estimates to zero whenever they are negative.

If data are untied, any non-empty event time point will be populated by only one failure, either type 1 or type 2, but not both types. It is clear that in this case (10) becomes

$$d{\widehat{\mathit{\Lambda }}}_j(t)=d{\widehat{\mathit{\Lambda }}}_j^{\mathit{obs}}(t),j=1,2,$$ (11)

i.e. the constrained estimators for cause-specific (net) hazards for the true failure type coincide with the (crude) estimators specific to the observed failure types. Misclassification mechanism makes the latter a distorted version of the former and leads to bias. Note that both types of estimators yield the same (asymptotically unbiased) Nelson-Aalen estimator for the marginal hazard

$$d\widehat{\mathit{\Lambda }}(t)=\sum _{j=1}^{2}d{\widehat{\mathit{\Lambda }}}_j(t)=\sum _{j=1}^{2}d{\stackrel{\sim }{\mathit{\Lambda }}}_j(t)=\sum _{j=1}^{2}d{\widehat{\mathit{\Lambda }}}_j^{\mathit{obs}}(t)=\frac{dN(t)}{Y(t)}.$$ (12)

Therefore, because of the “zero sum game” expressed by (12), Λ̂_j, will be biased in opposite directions for j = 1 vs. 2. We will study the bias later in greater detail.

3.2 EM algorithm

Several papers have developed nonparametric estimates using EM algorithm when there are some missing failure types under a non-missing at random mechanism; see, for example, Dinse (1982) and Craiu and Duchesne (2004). Pretending Ω_i is observed, define the processes counting the true failures $N_j^0(t)$, where j is the type of failure. Then the complete data loglikelihood is

$$l^c=\int {dN}_1^0(t)log[d{\mathit{\Lambda }}_1(t)]+{dN}_2^0(t)log[d{\mathit{\Lambda }}_2(t)]-Y(t)[d{\mathit{\Lambda }}_1(t)+d{\mathit{\Lambda }}_2(t)].$$ (13)

The estimates are improved by maximizing conditional expectation of the complete loglikelihood given observed data.

Suppose a failure of type ω = 1 or 2 is observed (ω = 1 corresponds to the failure type of interest while ω = 2 corresponds to other cause of failure). Given this information and the model assumptions, the distribution of the unknown true cause of failure Ω takes the form

$$P_{\mathit{\Omega }\mid \omega }(t)=Pr(\mathit{\Omega }\mid \omega ,T=t)=\frac{r{(t)}^{I(\mathit{\Omega }=2)}{\lambda }_{\mathit{\Omega }}(t)}{{\lambda }_1(t)+r(t){\lambda }_2(t)}\times I(\omega =1)+I(\mathit{\Omega }=\omega =2).$$ (14)

Consequently, imputation of the unobserved ${dN}_j^0(t)$, j = 1, 2 is given by

$$\mathrm{E}\{{dN}_j^0\mid Y,{dN}_1,{dN}_2\}=\frac{r^{I(j=2)}d{\mathit{\Lambda }}_j}{d{\mathit{\Lambda }}_1+rd{\mathit{\Lambda }}_2}{dN}_1+I(j=2){dN}_2,$$ (15)

where the dependence on t is suppressed for brevity. Assuming $d{\mathit{\Lambda }}_j^m$ in the E-step (15) is indexed by the current iteration number, m, and maximizing the complete data likelihood (13) with ${dN}_j^0$ replaced by (15) (M-Step), we obtain the EM iteration sequence

$$d{\mathit{\Lambda }}_j^{m+1}=\frac{r^{I(j=2)}d{\mathit{\Lambda }}_j^m}{d{\mathit{\Lambda }}_1^m+rd{\mathit{\Lambda }}_2^m}d{\widehat{\mathit{\Lambda }}}_1^{\mathit{obs}}+I(j=2)d{\widehat{\mathit{\Lambda }}}_2^{\mathit{obs}}.$$ (16)

A common perception is that EM solves an unrestricted MLE problem. If this were true, EM algorithm would converge to the naïve estimator (6). In our case, however, counter to this intuition, the EM solves the constrained problem (9) resulting in the estimator (10) that is biased. The key to this unexpected property is that the iterations (16) have two fixed points. The problem at hand is simple enough so we can find the fixed points explicitly. To do so assume $d{\mathit{\Lambda }}_j^{m+1}$ and $d{\mathit{\Lambda }}_j^m$ have a common limit dΛ_j, j = 1, 2, as m → ∞. Substituting the common limit into (16), written for a particular point t, and solving the resultant equations for dΛ_j(t) results in two distinct solutions. Let us write the first equation explicitly

$$d{\mathit{\Lambda }}_1(t)=\frac{d{\mathit{\Lambda }}_1(t)}{d{\mathit{\Lambda }}_1(t)+r(t)d{\mathit{\Lambda }}_2(t)}d{\widehat{\mathit{\Lambda }}}_1^{\mathit{obs}}(t).$$ (17)

First, assuming dΛ₁(t) > 0 cancels from (17), this equation enforces that the observed hazard is equal to the predicted marginal one $d{\widehat{\mathit{\Lambda }}}_1^{\mathit{obs}}(t)=d{\mathit{\Lambda }}_1(t)+r(t)d{\mathit{\Lambda }}_2(t)$. This, jointly with the second equation

$$d{\mathit{\Lambda }}_2(t)=\frac{r(t)d{\mathit{\Lambda }}_2(t)}{d{\mathit{\Lambda }}_1(t)+r(t)d{\mathit{\Lambda }}_2(t)}d{\widehat{\mathit{\Lambda }}}_1^{\mathit{obs}}(t)+d{\widehat{\mathit{\Lambda }}}_2^{\mathit{obs}}(t)$$ (18)

gives the naive estimator (6). Second, note that dΛ₁(t) = 0 also satisfies (17)! Solving the second equation (18) under dΛ₁(t) = 0 results in dΛ₂(t) = dΛ̂^obs(t) indicating that the whole marginal incidence is explained by type 2 failures. Under a violation of monotonicity when (8) is satisfied, this coincides with the constrained estimator.

Technically, when monotonicity is not violated, EM converges to the naïve estimator represented by the first fixed point. When a violation is present, the first fixed point is outside of the restricted parameter space. Trying to reach it, the EM algorithm hits the border dΛ₁(t) = 0. At this point it is stuck in the restricted subspace because (17) is satisfied, and converges to the second fixed point. The proof that (10) is actually the point of convergence is given in Appendix I.

3.3 Asymptotic properties

Let A(t) = (A₁(t), A₂(t)) denote the compensator processes for N(t)=(N₁(t), N₂(t))

$$\begin{array}{l}{A}_1(t)={\int }_0^{t}Y(s)\{d{\mathit{\Lambda }}_1(s)+r(s)d{\mathit{\Lambda }}_2(s)\}\\ A_2(t)={\int }_0^{t}Y(s)(1-r(s))d{\mathit{\Lambda }}_2(s).\end{array}$$

We have N(t) = A(t) + M(t) where M(t) = (M₁(t), M₂(t)) is a vector of 2 local square integrable martingales (Andersen and Gill, 1982). Naïve NPMLE of Λ(t) is given by ${\int }_0^{t}I(Y(s)>0)d\stackrel{\sim }{\mathbf{\Lambda }}(s)$. By Rebolledo’s theorem (Andersen et al, 1993), $\sqrt{n}(\stackrel{\sim }{\mathbf{\Lambda }}(t)-\mathbf{\Lambda }(t))$ converges weakly to a zero-mean Gaussian vector process whose covariance function can be consistently estimated by

$$n\left(\begin{array}{cc}{\int }_0^t\frac{1}{Y{(s)}^2}\{{dN}_1(s)+{\text{Odds}}^2[r(s)]{dN}_2(s)\}& -{\int }_0^t{\text{Odds}}^2[r(s)]\frac{{dN}_2(s)}{r(s)Y{(s)}^2}\\ -{\int }_0^t{\text{Odds}}^2[r(s)]\frac{{dN}_2(s)}{r(s)Y{(s)}^2}& {\int }_0^t{\text{Odds}}^2[r(s)]\frac{{dN}_2(s)}{{[r(s)Y(s)]}^2}\end{array}\right).$$ (19)

Negative covariance terms off the diagonal are a consequence of the components of Λ̃ taking simultaneous jumps in opposite directions with the occurrence of type 2 failure. Consistency of the naïve estimates follows an application of Lenglart’s inequality. Furthermore, they attain the Cramer-Rao lower bound. However, we cannot directly apply the results to constrained estimates because of the monotonicity restriction. It turns out that estimates show different behavior in the continuous and discrete case. The indicator function in constrained estimates (10) can be represented by summation over subject-i-specific processes N_ij(t), j = 1, 2

$$I\left(\sum _{i=1}^n{dN}_{i1}(t)-\text{Odds}[r(t)]{dN}_{i2}(t)>0\right).$$ (20)

Under the continuous time setting where no two events can occur at the same time, (20) behaves like a linear function in the sense that I and Σ can be interchanged. This results in the asymptotic bias of the estimator. To put it more accurately, as we show in Appendix II, E[Λ̂ (t) − Λ (t)] converges in probability to

$$\left({\int }_0^{t}r(s)d{\mathit{\Lambda }}_2(s),{\int }_0^t-r(s)d{\mathit{\Lambda }}_2(s)\right),$$

as n → ∞, which can be consistently estimated by

$$\left({\int }_0^t\text{Odds}[r(s)]\frac{{dN}_2(s)}{Y(s)},{\int }_0^t-\text{Odds}[r(s)]\frac{{dN}_2(s)}{Y(s)}\right).$$

Namely, the same amount of bias is added to both type 1 and 2 estimator but in an opposite direction.

The vector process $\sqrt{n}\left({\widehat{\mathit{\Lambda }}}_1(t)-({\int }_0^{t}d{\mathit{\Lambda }}_1(s)+r(s)d{\mathit{\Lambda }}_2(s)),{\widehat{\mathit{\Lambda }}}_2(t)-{\int }_0^t(1-r(s))d{\mathit{\Lambda }}_2(s)\right)$ is a martingale that converges weakly to a zero-mean Gaussian vector process with a consistent estimate of covariance as follows:

$$n\left(\begin{array}{cc}{\int }_0^t\frac{{dN}_1(s)}{Y^2(s)}& 0\\ 0& {\int }_0^t\frac{{dN}_2(s)}{Y^2(s)}\end{array}\right).$$ (21)

Discrete time setting, on the contrary, yields asymptotically unbiased estimators. Discrete random variable, T, in survival analysis often arises due to rounding off measurements or grouping of failure times into intervals. In case of a continuous model coarsened to a discrete one, average probabilities corresponding to grouping intervals represent the target of estimation, and bias is understood relative to this target. In discrete time setting, the summation in (20) can no longer be interchanged with the indicator function since empirical probabilities of events occurring at the same time are not negligible asymptotically. Let Δ(t_k) denote the observation time interval, t_k+1 − t_k, between two adjacent event times that may in general possess some multiplicity (ties). The asymptotic properties of Nelson-Aalen or Kaplan-Meier estimator for discrete lifetimes are based on Δ (t_k) and Pr{T ∈ [t_k, t_k+1)} becoming negligibly small uniformly in probability as the sample size increases. However, the monotonicity restriction indicator (20) converges to 1 in probability only if the number of failures in [t_k, t_k+1) is allowed to accumulate. Consider the simple case: T grouped into intervals of unit length and no censoring. Let ΔN_j(t) denote the number of failures of type j at the interval [t, t+1). Suppose the random vector (ΔN₁(t), ΔN₂(t)) conditional on Y (t) has the following distribution:

$$Pr(\mathit{\Delta }{N}_1(t)=x_1,\mathit{\Delta }{N}_2(t)=x_2\mid Y(t)=n)=\frac{n!}{x_1!x_2!(n-x_1-x_2)!}{[{\lambda }_1(t)+r(t){\lambda }_2(t)]}^{x_1}{[(1-r(t)){\lambda }_2(t)]}^{x_2}{[1-\lambda (t)]}^{n-x_1-x_2}$$

where λ_j(t) = Pr(t ≤ T < t+1, Ω = j|T ≥ t) for j = 1, 2 and λ(t)= λ₁(t)+ λ₂(t). Maximizing Π_t≥0 Pr(ΔN₁(t), ΔN₂(t)|Y(t)) under non-negative restriction on λ₁(t) and λ₂(t), we obtain an estimator for λ₁(t) as

$$\frac{1}{Y(t)}\{\mathit{\Delta }{N}_1(t)-\text{Odds}[r(t)]\mathit{\Delta }{N}_2(t)\}I[\overline{r}(t)\mathit{\Delta }{N}_1(t)\ge r(t)\mathit{\Delta }{N}_2(t)]$$

that is almost identical with the constrained NPMLE in the continuous setting except that the monotonicity constraint I converges to 1 in probability as sample size increases (see discussion below). This makes the above estimator asymptotically equivalent to the naïve (unbiased) one.

4 Isotonic estimation

In addition to the constrained NPMLE, there are other approaches to achieve monotonicity. One of them is to replace a naïve estimate at time t with the maximum value of estimates up to t: that is,

$${\widehat{\mathit{\Lambda }}}_1^S(t)=\underset{0\le s\le t}{sup}{\stackrel{\sim }{\mathit{\Lambda }}}_1(s).$$

This is motivated by Lin and Ying (1994). The sup-estimator ${\widehat{\mathit{\Lambda }}}_1^S$ (SUP) is consistent. Indeed, ${\widehat{\mathit{\Lambda }}}_1^S(t)={\stackrel{\sim }{\mathit{\Lambda }}}_1({\tau }_t)$ for some τ_t ≤ t. Then, since Λ₁ is increasing and τ_t ≤ t, we have

$${\stackrel{\sim }{\mathit{\Lambda }}}_1(t)-{\mathit{\Lambda }}_1(t)\le {\widehat{\mathit{\Lambda }}}_1^S(t)-{\mathit{\Lambda }}_1(t)\le \underset{0\le x\le t}{sup}({\stackrel{\sim }{\mathit{\Lambda }}}_1(x)-{\mathit{\Lambda }}_1(x)),$$

and consistency of the sup-estimator follows from the uniform consistency of the naïve one.

Lin and Ying (1994) argued that ${\widehat{\mathit{\Lambda }}}_1^S$ is asymptotically equivalent to Λ̃₁ in the sense that $\sqrt{n}({\widehat{\mathit{\Lambda }}}_1^S-{\mathit{\Lambda }}_1)$ converges to the same limiting distribution as $\sqrt{n}({\stackrel{\sim }{\mathit{\Lambda }}}_1-{\mathit{\Lambda }}_1)$. Finding the distribution of a supremum of a stochastic process over a finite interval is a challenge. Such properties are only known for a very restricted set of processes such as the Brownian motion possibly with a linear drift and stationary Gaussian processes with very specific correlation structures (Adler, 1990). Our $\sqrt{n}({\widehat{\mathit{\Lambda }}}_1^S-{\mathit{\Lambda }}_1)$ process is non-stationary and only becomes Gaussian in the limit. Lin and Ying (1994) argued heuristically that the sup-estimator is asymptotically equivalent to the naïve one, and their argument is applicable to our case. According to the argument ${\widehat{\mathit{\Lambda }}}_1^S-{\stackrel{\sim }{\mathit{\Lambda }}}_1$ goes to zero in probability faster than $1/\sqrt{n}$ because the natural $1/\sqrt{n}$ rate of convergence of both estimators to the common limit Λ₁ is accelerated by the convergence of τ_t to t. We have found in simulations that the variance of the sup-estimator is very close to the naïve one (19), and we have adopted the working hypothesis of equivalence implied by the heuristic argument of Lin and Ying (1994).

Another isotonic estimator, PAV, ${\widehat{\mathbf{\Lambda }}}_1^P$, can be constructed using the so-called pool-adjacent-violators algorithm; see Ayer et al (1955) and Barlow et al (1972) (pp. 13-5). Λ̂^P’s are derived as a set of Λ’s minimizing a weighted sum of squared deviations of the isotonic estimate from the naïve estimate

$${\widehat{\mathbf{\Lambda }}}^P=arg\underset{\{\mathbf{\Lambda }\in \mathit{\Psi }\}}{min}\sum _{k=1}^K{[\mathbf{\Lambda }(t_k)-\stackrel{\sim }{\mathbf{\Lambda }}(t_k)]}^{\otimes 2}\mathbf{W}(t_k),$$ (22)

where Ψ is the class of non-decreasing functions, and A^⊗2 = AA^T (T means a transposed matrix), and W is a vector of non-negative weights. This is a promising approach since the naïve estimator is consistent. Using Doob-Meyer decomposition we have the corresponding linear regression model with correlated errors

$$\stackrel{\sim }{\mathbf{\Lambda }}=\mathbf{\Lambda }+\mathit{\epsilon },$$

where ε(t) is an asymptotically Gaussian martingale (noise) with covariance obtained from a large sample limit of (19). The naïve estimator Λ̃ given by (6) is a saturated solution to the above regression problem. Therefore, absent restrictions, the solution to (22) is the naïve estimator regardless of W as long as weights are non-negative. In the above approach the naïve estimator serves as the response variable.

Alternatively, the problem can be re-formulated as a regression with the observed hazard

$$d{\widehat{\mathbf{\Lambda }}}^{\mathit{obs}}={(d{\widehat{\mathit{\Lambda }}}_1^{\mathit{obs}},d{\widehat{\mathit{\Lambda }}}_2^{\mathit{obs}})}^T={\left(\frac{{dN}_1}{Y},\frac{{dN}_2}{Y}\right)}^T$$

as a response, where T means a transposed vector. We have the model

$$\left(\begin{array}{c}\frac{{dN}_1(t)}{Y(t)}\\ \frac{{dN}_2(t)}{Y(t)}\end{array}\right)=\left(\begin{array}{cc}1& r(t)\\ 0& 1-r(t)\end{array}\right)\left(\begin{array}{c}d{\mathit{\Lambda }}_1(t)\\ d{\mathit{\Lambda }}_2(t)\end{array}\right)+d\mathit{\epsilon }(t),$$ (23)

where ε is asymptotically Gaussian with uncorrelated components and the covariance matrix given by (21)/n. Since the naïve estimate Λ̃₂ does not violate the restrictions, we will apply the corrections to Λ̃₁ only, setting ${\widehat{\mathit{\Lambda }}}_2^P(t)={\stackrel{\sim }{\mathit{\Lambda }}}_2(t)$. The contribution to the sum of squares containing Λ₁ has the form

$${\left(\int d{\mathit{\Lambda }}_1+rd{\mathit{\Lambda }}_2-\frac{{dN}_1}{Y}\right)}^{2}W,$$

where W is some weight. On substitution of the naïve estimator for Λ₂, the above expression turns into

$${\left(\int d{\mathit{\Lambda }}_1-d{\stackrel{\sim }{\mathit{\Lambda }}}_1\right)}^{2}W,$$

and the problem is equivalent to (22). We found hardly any difference between the optimal weights derived based on the error covariance matrices and constant weights, so constant weights are used for simplicity.

Asymptotic properties of ${\widehat{\mathit{\Lambda }}}_1^P$ follow from Theorem 1.6 (Barlow et al, 1972). The details are presented in Appendix III.

5 Simulation

Simulated data were generated from a population with constant cause-specific hazards, λ₁ = 0.05 and λ₂ = 0.15, and independent censoring which is uniformly distributed on (0, 15). In the continuous time setting, the observation time T is obtained by a minimum of these three event times. Five choices of misattribution were examined: (ψ₀, ψ₁) = (0.1, 0), (0.3, 0), (0.5, 0), (0.5, −0.5) and (0.5, −0.1) in logit r(t) = (logit ψ₀) + ψ₁t. First three choices represent constant misattribution 0.1, 0.3, and 0.5. In the last two models, misattribution decreases as the survival time is prolonged, which yield 0.24 and 0.43 misattribution on average, respectively. We carried out 2000 simulations with two different sample sizes, 100 and 500. The means of the naïve, constrained (EM) and isotonic estimators using the supremum (SUP) function and the Pool-Adjacent-Violator (PAV) algorithm over 2000 simulations are calculated, and values at time 4.32, Pr(T ≤ 4.32) = 0.7 in the continuous setting, are reported in Table 1 and 2. Constant versus variable weights yield very similar results, so only constant weight PAV estimates are shown. Asymptotic variances are estimated based on the asymptotic distribution (19) and (21), for the naïve and the constrained estimator, respectively. Naïve variance estimators are used with the isotonic methods for comparison and as an approximation. The empirical standard deviations and the empirical mean square errors based on 2000 simulations are also given in Table 1 and 2.

Table 1.

Simulation means for various estimators of the cumulative type 1 failure hazards at time 4.32 in the continuous setting with a sample size n = 100 under misattribution, logit r(t) = (logit ψ₀) + ψ₁t. The average of the standard error estimates (SEE), sample standard deviations (SSD) and the empirical mean square error (MSE) are also presented. The true value is 0.216.

(ψ0, ψ1)		Λ̃1	Λ̂1	${\widehat{\mathit{\Lambda }}}_1^S$	${\widehat{\mathit{\Lambda }}}_1^P$	$({\widehat{\mathit{\Lambda }}}_1^S+{\widehat{\mathit{\Lambda }}}_1^P)/2$
(0.1, 0)	Estimate	.216	.281	.223	.216	.220
	SEE	.074	.073	.074	.074	.074
	SSD	.075	.073	.073	.073	.073
	$\sqrt{\text{MSE}}$	.075	.098	.073	.073	.073
(0.3, 0)	Estimate	.217	.411	.235	.214	.225
	SEE	.097	.088	.097	.097	.097
	SSD	.099	.089	.091	.095	.092
	$\sqrt{\text{MSE}}$	.099	.215	.093	.095	.093
(0.5, 0)	Estimate	.214	.540	.249	.209	.229
	SEE	.129	.102	.129	.129	.129
	SSD	.127	.101	.110	.119	.113
	$\sqrt{\text{MSE}}$	.127	.339	.115	.119	.114
(0.5, −0.5)	Estimate	.214	.390	.224	.215	.219
	SEE	.091	.083	.091	.091	.091
	SSD	.092	.083	.088	.090	.089
	$\sqrt{\text{MSE}}$	.092	.193	.088	.090	.089
(0.5, −0.1)	Estimate	.214	.505	.241	.212	.226
	SEE	.118	.098	.118	.118	.118
	SSD	.116	.097	.104	.111	.106
	$\sqrt{\text{MSE}}$	.116	.304	.107	.111	.107

The naive Λ̃₁, the constrained Λ̂₁, the SUP ${\widehat{\mathit{\Lambda }}}_1^S$ and the PAV ${\widehat{\mathit{\Lambda }}}_1^P$ estimator

Table 2.

Simulation means for various estimators of the cumulative type 1 failure hazards at time 4.32 in the continuous setting with a sample size n = 500 under misattribution, logit r(t) = (logit ψ₀) + ψ₁t. The average of the standard error estimates (SEE), sample standard deviations (SSD) and the empirical mean square error (MSE) are also presented. The true value is 0.216.

(ψ0, ψ1)		Λ̃1	Λ̂1	${\widehat{\mathit{\Lambda }}}_1^S$	${\widehat{\mathit{\Lambda }}}_1^P$	$({\widehat{\mathit{\Lambda }}}_1^S+{\widehat{\mathit{\Lambda }}}_1^P)/2$
(0.1, 0)	Estimate	.216	.281	.218	.216	.217
	SEE	.033	.033	.033	.033	.033
	SSD	.033	.032	.033	.033	.033
	$\sqrt{\text{MSE}}$	.033	.073	.033	.033	.033
(0.3, 0)	Estimate	.216	.411	.221	.216	.218
	SEE	.044	.040	.044	.044	.044
	SSD	.043	.039	.042	.042	.042
	$\sqrt{\text{MSE}}$	.043	.199	.042	.042	.042
(0.5, 0)	Estimate	.216	.541	.226	.216	.221
	SEE	.058	.046	.058	.058	.058
	SSD	.057	.045	.054	.056	.055
	$\sqrt{\text{MSE}}$	.057	.329	.055	.056	.055
(0.5, −0.5)	Estimate	.216	.392	.217	.216	.217
	SEE	.041	.038	.041	.041	.041
	SSD	.040	.037	.040	.040	.040
	$\sqrt{\text{MSE}}$	.040	.179	.040	.040	.040
(0.5, −0.1)	Estimate	.217	.507	.224	.217	.220
	SEE	.053	.044	.053	.053	.053
	SSD	.052	.043	.050	.051	.051
	$\sqrt{\text{MSE}}$	.052	.294	.051	.051	.051

The naive Λ̃₁, the constrained Λ̂₁, the SUP ${\widehat{\mathit{\Lambda }}}_1^S$ and the PAV ${\widehat{\mathit{\Lambda }}}_1^P$ estimator

The naïve nonparametric maximum likelihood estimates are in excellent agreement with the true value. On the other hand, the constrained estimates are seriously biased, although they have uniformly less variability than the other estimators. Interestingly, the bias keeps increasing with sample size, and converges to the theoretically predicted ${\int }_0^{t}r(s)d{\mathit{\Lambda }}_2(s)$. Both of the SUP and PAV estimator seem to behave similar to the naïve estimates. However, the rate of decrease in bias with sample size for the SUP estimator becomes slower than the one for the PAV estimator as misattribution increases.

Using the same simulated data, we again compared the properties of the estimators in the discrete time case. In this setting, T is only observed as an integer value through a ceiling function; [T] = min{n ∈ Z|T ≤ n} where Z is the set of integers. The corresponding simulation-based estimates at time 7, Pr(⌊T ⌋ ≤ 7) = 0.82, are reported in Table 3 and 4.

Table 3.

Simulation means for various estimators of the cumulative type 1 failure hazards at time 7 in the discrete setting with a sample size n = 100 under misattribution, logit r(t) = (logit ψ₀)+ ψ₁t. The average of the standard error estimates (SEE), sample standard deviations (SSD) and the empirical mean square error (MSE) are also presented. The true value is 0.305.

(ψ0, ψ1)		Λ̃1	Λ̂1	${\widehat{\mathit{\Lambda }}}_1^S$	${\widehat{\mathit{\Lambda }}}_1^P$	$({\widehat{\mathit{\Lambda }}}_1^S+{\widehat{\mathit{\Lambda }}}_1^P)/2$
(0.1, 0)	Estimate	.306	.318	.312	.299	.306
	SEE	.104	.103	.104	.104	.104
	SSD	.107	.100	.102	.104	.103
	$\sqrt{\text{MSE}}$	.107	.101	.103	.104	.103
(0.3, 0)	Estimate	.300	.335	.317	.285	.301
	SEE	.137	.124	.137	.137	.137
	SSD	.134	.115	.121	.129	.123
	$\sqrt{\text{MSE}}$	.134	.119	.121	.130	.123
(0.5, 0)	Estimate	.299	.368	.333	.276	.304
	SEE	.181	.142	.181	.181	.181
	SSD	.182	.145	.157	.175	.163
	$\sqrt{\text{MSE}}$	.182	.158	.159	.178	.163
(0.5, −0.5)	Estimate	.302	.312	.304	.301	.303
	SEE	.105	.102	.105	.105	.105
	SSD	.108	.102	.106	.107	.107
	$\sqrt{\text{MSE}}$	.108	.102	.106	.107	.107
(0.5, −0.1)	Estimate	.300	.347	.320	.290	.305
	SEE	.152	.131	.152	.152	.152
	SSD	.154	.130	.139	.147	.141
	$\sqrt{\text{MSE}}$	.153	.136	.140	.148	.141

The naive Λ̃₁, the constrained Λ̂₁, the SUP ${\widehat{\mathit{\Lambda }}}_1^S$ and the PAV ${\widehat{\mathit{\Lambda }}}_1^P$ estimator

Table 4.

Simulation means for various estimators of the cumulative type 1 failure hazards at time 7 in the discrete setting with a sample size n = 500 under misattribution, logit r(t) = (logit ψ₀)+ ψ₁t. The average of the standard error estimates (SEE), sample standard deviations (SSD) and the empirical mean square error (MSE) are also presented. The true value is 0.305.

(ψ0, ψ1)		Λ̃1	Λ̂1	${\widehat{\mathit{\Lambda }}}_1^S$	${\widehat{\mathit{\Lambda }}}_1^P$	$({\widehat{\mathit{\Lambda }}}_1^S+{\widehat{\mathit{\Lambda }}}_1^P)/2$
(0.1, 0)	Estimate	.302	.302	.302	.302	.302
	SEE	.047	.046	.047	.047	.047
	SSD	.045	.045	.045	.045	.045
	$\sqrt{\text{MSE}}$	.045	.045	.045	.045	.045
(0.3, 0)	Estimate	.305	.307	.306	.303	.304
	SEE	.061	.056	.061	.061	.061
	SSD	.060	.059	.059	.060	.060
	$\sqrt{\text{MSE}}$	.060	.059	.059	.060	.059
(0.5, 0)	Estimate	.307	.316	.312	.300	.306
	SEE	.081	.064	.081	.081	.081
	SSD	.082	.076	.078	.083	.080
	$\sqrt{\text{MSE}}$	.082	.077	.078	.083	.080
(0.5, −0.5)	Estimate	.302	.302	.302	.302	.302
	SEE	.047	.046	.047	.047	.047
	SSD	.047	.046	.046	.046	.046
	$\sqrt{\text{MSE}}$	.047	.046	.046	.047	.047
(0.5, −0.1)	Estimate	.304	.308	.306	.303	.304
	SEE	.068	.059	.068	.068	.068
	SSD	.068	.065	.067	.068	.067
	$\sqrt{\text{MSE}}$	.068	.065	.067	.068	.067

The naive Λ̃₁, the constrained Λ̂₁, the SUP ${\widehat{\mathit{\Lambda }}}_1^S$ and the PAV ${\widehat{\mathit{\Lambda }}}_1^P$ estimator

Overall, the constrained estimator has uniformly the smallest variance, at the cost of the highest small sample bias representing an extreme point on the bias-variance trade-off. The SUP estimator is more small-sample efficient than the PAV estimator in both continuous and discrete case. Unlike the continuous case, consistency of the constrained estimator is guaranteed in the discrete case. However, the rate of decrease in bias is slower than the other two isotonic estimators. In fact, it has the highest small-sample bias. Among the estimators that guarantee monotonicity, the largest bias occurs at the smallest sample size of 100 and largest attribution bias of 0.5, where mean difference between the SUP and PAV estimates is also the largest. In this case, none of the estimators seems to be appropriate. It is reasonable to take an average of the SUP and PAV estimators because their biases go in opposite directions, and they have the same asymptotic properties as the naive estimator in the sense that $\sqrt{n}(({\widehat{\mathit{\Lambda }}}_1^S+{\widehat{\mathit{\Lambda }}}_1^P)/2-{\stackrel{\sim }{\mathit{\Lambda }}}_1)$ converges to zero in probability by the heuristic argument of Lin and Ying (1994). By the same argument the asymptotic variance of the averaged estimator is the same as the naïve one. The corresponding simulation results are given in the last columns in Table 1–4.

Although the estimates were presented at a single time point in each setting, we observed similar results at other time points and for other values of λ. However, results may not be the same for all models, particularly with time-dependent hazards.

6 Real Data Example

We illustrate our results using data from the Surveillance, Epidemiology, and End Results (SEER) cancer registry program. Staying close to the misattribution study of Hoffman et al (2003), we looked at 1,094 New Mexico residents diagnosed with prostate cancer in 1993. There are two causes of failure: death due to prostate cancer (type 1) and death due to causes other than prostate cancer (type 2). We tried two values for misattribution, 0.05 and 0.1, within the range deemed plausible based on Hoffman et al (2003).

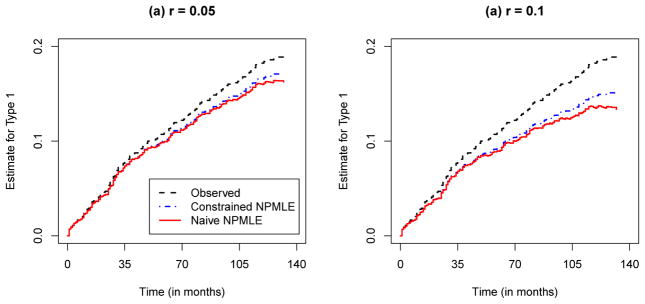
Figure 1 displays the naïve and constrained nonparametric maximum likelihood estimates for the cumulative type 1 failure hazard. In addition, the Nelson-Aalen estimates for the observed type 1 failure are also presented (dotted lines). We have omitted the isotonic estimates since they are very close to the naïve estimates. Note that monotonicity for the naïve estimates still breaks down even though the sample size is large and misattribution is low, as expected. Predictably, it gets worse as misattribution increases. In this example, the failure time is recorded by month, ranging from 0 to 132, making it close to the continuous model setting. Less discrepancy between the naïve and constrained estimates would be expected if failure time is grouped into larger bins such as year, or if more data is available. It is not surprising that the naïve estimates are nondecreasing when using the data on 9 SEER registries, 25,088 men, not just New Mexico. The corresponding estimates and 95% point-wise confidence limits are presented in Figure 2.

Fig. 1.

Naïve and constrained NPMLE of cumulative type 1 failure hazards when (a) r = 0.05 and (b) r = 0.1 with a sample size of 1,094 in the discrete setting. Data from the New Mexico SEER registry.

Fig. 2.

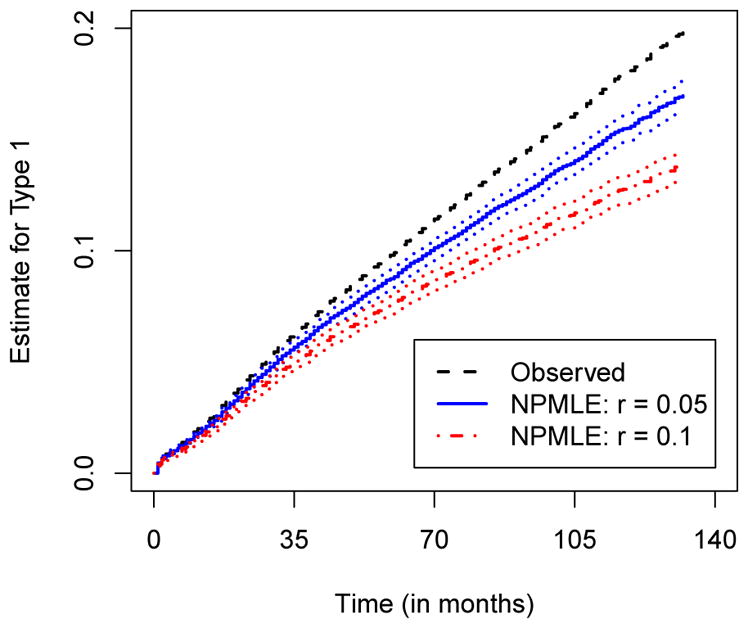
Naïve NPMLE of cumulative type 1 failure hazards when r = 0.05 and 0.1 with a sample size of 25,088 in the discrete setting. Data based on 9 SEER registries. The dotted lines represent 95% point-wise confidence limits.

7 Discussion

In this paper, we have considered the problem of fitting a hazard model to competing risks data when there is a misattribution of failure type. The nature of the misattribution mechanism makes the true failure status missing, but not at random, with the observed distorted status and time of failure providing some information.

We first presented the naïve nonparametric maximum likelihood estimator. We found that it violates the monotonicity constraint although it is consistent. Contrary to common belief, in this particular problem setting, violation of monotonicity never goes away with increasing sample size, even though the size of negative jumps of the cumulative hazard goes to zero. Following a common recipe we then derived the constrained nonparametric maximum likelihood estimator which achieved monotonicity and showed smaller variability, and surprisingly a substantial bias in the continuous setting. This led us to consider isotonic approaches using the supremum function and the pool-adjacent-violators algorithm, both providing consistent and monotonic estimates.

Another surprising finding is that the EM algorithm perceived as a local maximization method actually solves the constrained problem and converges to the biased constrained estimator. We traced the phenomenon to the specific structure of the EM iterative equations that have two fixed points, one of them associated with the unrestricted (naïve) solution, while the other fixed point corresponds to the restricted non-negative one. When the naïve solution is not admissible (non-monotonic), the iteration path of the EM is eventually locked in the restricted subspace associated with the second fixed point.

It has been generally taken for granted that constrained NPMLE and the EM algorithm have useful properties such as consistency. Consistency is perceived to be a consequence of the estimator satisfying the monotonicity constraint for large samples. However, in the present setting, we found that the constrained estimator is no longer consistent unless the failure time follows a discrete model. These methods do behave well in the discrete setting when information is allowed to accumulate at distinct time points. This is counterintuitive to the properties of standard estimators such as Nelson-Aalen or Kaplan-Meier which serve both discrete and continuous cases well.

If one is prepared to overlook a violation of monotonicity of the cumulative hazard estimates, the naive NPMLE is preferred to any other estimates. However, interpreting such estimates involves reading a monotonic curve visually into the estimate without formalizing the procedure. With this paper we are offering a tool to do this rigorously. We have found that the isotonic estimators obtained by using the supremum method and the pool-adjacent-violator algorithm behave similar to the naïve estimator yet provide monotonic cumulative hazards. From a purely function approximation standpoint, the issue is not much of a problem in large samples, since the naïve estimator is consistent.

The results can be extended to the case when both under- and over-attribution is possible with the rates r₁(t) and r₂(t), respectively. The Naïve estimator in the case of constant r₁ and r₂ takes the form

$$d{\stackrel{\sim }{\mathit{\Lambda }}}_1(t)=\frac{{\overline{r}}_{2}d{\widehat{\mathit{\Lambda }}}_1^{\mathit{obs}}(t)-r_{2}d{\widehat{\mathit{\Lambda }}}_2^{\mathit{obs}}(t)}{1-r_1-r_2}.$$

The estimator does not make sense when r₁ = r̄₂ in which case the problem is non-identifiable (only the marginal hazard can be identified). The constrained estimator’s large sample limit becomes

$$\mathrm{E}{\widehat{\mathit{\Lambda }}}_1(t)=\frac{1}{\mid r_1-{\overline{r}}_2\mid }\{\begin{array}{ll}({\mathit{\Lambda }}_1(t)r_1+{\mathit{\Lambda }}_2(t){\overline{r}}_2)r_2,\hfill & r_1>{\overline{r}}_2,\hfill \\ ({\mathit{\Lambda }}_1(t){\overline{r}}_1+{\mathit{\Lambda }}_2(t)r_2){\overline{r}}_2,\hfill & r_1<{\overline{r}}_2.\hfill \end{array}$$ (24)

Interestingly, it can be shown that (24) implies that the constrained estimator is only unbiased in two cases: (1) Either r₁ > 0, r₂ = 1, or (2) r₁ < 1, r₂ = 0. In the first case, all failures of type 2 are misclassified and ${\mathit{\Lambda }}_2^{\mathit{obs}}(t)$ is populated by a misclassified r₁-fraction of type 1 failures yielding the correct estimate dΛ̂₁(t) = dN₂(t)/(r₁Y(t)). In the second case, there is no over-attribution and ${\mathit{\Lambda }}_1^{\mathit{obs}}(t)$ is populated by non-misclassified r̄₁-fraction of type 1 failures yielding the correct estimate dΛ̂₁(t) = dN₁(t)/(r̄₁Y (t)). In all other cases there is bias. Note that the over-attribution-only setting of this paper always has a biased constrained estimate unless there is no misclassification of any kind.

We defined ’the discrete setting’ as the case where the number of failures can accumulate over a discrete mesh of the observed failure times as the sample size increases. In this setting, the constrained estimator is consistent and attains the Cramer-Rao lower bound. However, we are still faced with non-monotonicity problem in small samples. An example showed a discrepancy between the naive and constrained estimates even with a sample size more than a thousand (Figure 1), resulting in a substantial small-sample bias (Table 3). Thus, isotonic estimators are still useful in the discrete setting.

A simulation study showed that the SUP and the PAV work well even with a sample size as small as 100. Each estimator has its own advantages and disadvantages. The SUP estimator was found to be uniformly more efficient although it has relatively large small-sample bias, always over-estimated. On the other hand, the PAV technique takes the naïve estimates as a foundation and provides the amount of smoothing that is just right to fix them. Thus, the bias of the PAV estimator is less affected by small samples and high misclassification rates, and its small-sample variance is readily available through the model-based estimator (19). However, the approach will eventually break down under small-sample high misclassification challenge (see Table 3, 0.5 misattribution, sample size of 100, discrete setting). Having two potentially useful estimators with distinct small sample properties suggests a family of estimators representing a weighted average of the SUP and the PAV. Mean Squared Error could be used to resolve the tradeoff between the two. We found that the average estimator (equal weights) is quite robust against high attribution bias and often provides a better MSE value than the PAV or SUP estimators, and we recommend its use.

We argued that the naive estimator for dΛ₁(t_α) is negative if dN₁(t_α) is zero. It is generally true when misattribution is assumed to be known or estimated with a parametric model, constant or a function of t. Interestingly, this problem would not necessarily arise if r(t_α) is non-parametrically defined. Namely, if r(t_α) is estimated only with data at t_α, it becomes zero when dN₁(t_α) is zero. Thus, it makes the naive estimate for dΛ₁(t_α) equal to zero.

Knowledge of attribution bias is essential to obtain valid estimates of cause-specific hazard rates. Unfortunately, these probabilities are not identifiable given the survival data only, even if they are constant. Although there are special cases in which they are estimable with the observed data (e.g. Dinse, 1986; Craiu and Duchesne, 2004), missing-at-random assumption is in general necessary to avoid problems of nonidentifiability. The ideal solution is to obtain external data on the confirmed true underlying cause of failures such as Hoffman et al (2003). However, there is always a risk that external data would not be representative of the target population. Conducting a sensitivity analysis emerges as the only viable option in the absence of external data and any information that could lead to additional restrictions on the two hazards.

Throughout this work, we have assumed that the misattribution may depend on the time of failure and the true failure type. It is, however, possible that it is affected by other factors. Dependence on such covariates can be incorporated, for example, by assuming a logistic model for r, and a proportional hazard model for the true failure types.

Finally with the newly developed estimators, we returned to the problem of interpreting prostate cancer mortality that motivated this paper. We built a mechanistic mortality model as a convolution of latent cancer incidence, waiting time until diagnosis, the lead time measuring the amount of time by which diagnosis is advanced by screening, and survival post diagnosis. The cause-specific estimates of observed survival post-diagnosis were adjusted for misattribution using the methods of this paper. We performed a sensitivity analysis over plausible range of 14 different misattribution models with constant or decreasing (in survival time) over-attribution rate. We also allowed misattribution to vary by year of diagnosis. Our sensitivity analysis showed that constant misattribution cannot explain the observed mortality trend. However, when misattribution is allowed to change with calendar time, attribution bias can explain the increase and subsequent fall in prostate cancer mortality rates in the late 1980s and early 1990s. Details of this analysis will be reported elsewhere.

Appendix I

Convergence of EM algorithm

The likelihood is maximized only when dλ̂(t) = dλ̂^obs(t). Therefore, it is sufficient to show the convergence of estimator for dλ₁(t).

Case 1. dN₁(t) − Odds[r(t)]dN₂(t) ≥ 0

Without loss of generality, we assume that dλ⁰ ≥ 0. We prove first that $d{\mathit{\Lambda }}_1^m(t)<d{\mathit{\Lambda }}_1^{m+1}(t)\le d{\stackrel{\sim }{\mathit{\Lambda }}}_1(t)$ if $0<d{\mathit{\Lambda }}_1^m(t)<d{\stackrel{\sim }{\mathit{\Lambda }}}_1(t)$ for any $d{\mathit{\Lambda }}_2^m(t)$. First inequality can be easily proved by using the following equation: $d{\mathit{\Lambda }}_1^m(t)+d{\mathit{\Lambda }}_2^m(t)=({dN}_1(t)+{dN}_2(t))/Y(t)$. The proof of second inequality is based on the observation that $d{\mathit{\Lambda }}_1^{m+1}[.]$ is a strictly increasing function of $d{\mathit{\Lambda }}_1^m(t)$. Thus, $d{\mathit{\Lambda }}_1^{m+1}[d{\stackrel{\sim }{\mathit{\Lambda }}}_1(t)]\ge d{\mathit{\Lambda }}_1^{m+1}[x]$ for x ≤ dΛ̃₁(t) where the equality holds only if x = dΛ₁(t). Similarly $d{\mathit{\Lambda }}_1^m(t)>d{\mathit{\Lambda }}_1^{m+1}(t)\ge d{\stackrel{\sim }{\mathit{\Lambda }}}_1(t)$ if $d{\mathit{\Lambda }}_1^m(t)>d{\stackrel{\sim }{\mathit{\Lambda }}}_1(t)$ for any $d{\mathit{\Lambda }}_2^m(t)$. However, $d{\mathit{\Lambda }}_1^{m+1}(t)$ turns out to be zero whenever $d{\mathit{\Lambda }}_1^m(t)$ is.

Case 2. dN₁(t) − Odds[r(t)]dN₂(t) < 0

Similar arguments for case 1 can be used to prove that $0<d{\mathit{\Lambda }}_1^{m+1}(t)<d{\mathit{\Lambda }}_1^m(t)$ if $d{\mathit{\Lambda }}_1^m(t)>0$ where the equality holds only if $d{\mathit{\Lambda }}_1^{m+1}(t)=0(\ast )$. Similarly, if $\mathrm{d}{\stackrel{\sim }{\mathit{\Lambda }}}_1(t)<d{\mathit{\Lambda }}_1^m(t)<0$, then $d{\mathit{\Lambda }}_1^m(t)<d{\mathit{\Lambda }}_1^{m+1}(t)\le 0$. However, if $d{\mathit{\Lambda }}_1^m(t)<d{\stackrel{\sim }{\mathit{\Lambda }}}_1(t)$, then $d{\mathit{\Lambda }}_1^m(t)>d{\mathit{\Lambda }}_1^{m+1}(t)$. When $d{\mathit{\Lambda }}_1^{m+1}(t)<-\text{Odds}[r(t)]d{\widehat{\mathit{\Lambda }}}^{\mathit{obs}}(t),d{\mathit{\Lambda }}_1^{m+1}(t)$ becomes greater than zero, so it goes back to the first case (*).

Appendix II

Bias for constrained NPMLE in a continuous time case

We first fix a continuous time interval 𝒯 = [0, t] for a given terminal time 0 < τ < ∞. Let {ℱ_t; t ∈ 𝒯} be a filtration of the probability space. We have

$$\begin{array}{l}\mathrm{E}[{\widehat{\mathit{\Lambda }}}_1(t)]={\int }_0^t\mathrm{E}\left[\frac{I(Y(s)>0)}{Y(s)}\times \mathrm{E}\left[\left\{{dN}_1(s)-\frac{r(s)}{1-r(s)}{dN}_2(s)\right\}I\left(\sum _{i=1}^n{dN}_{i1}(s)-\frac{r(s)}{1-r(s)}{dN}_{i2}(s)>0\right)|{\mathcal{F}}_{s-}\right]\right]\\ =\sum _{i=1}^n{\int }_0^t\mathrm{E}\left[\frac{I(Y(s)>0)}{Y(s)}\times \mathrm{E}\left[\left\{{dN}_{i1}(s)-\frac{r(s)}{1-r(s)}{dN}_{i2}(s)\right\}I\left({dN}_{i1}(s)-\frac{r(s)}{1-r(s)}{dN}_{i2}(s)>0\right)|{\mathcal{F}}_{s-}\right]\right]\\ =\sum _{i=1}^n{\int }_0^t\mathrm{E}\left[\frac{I(Y(s)>0)}{Y(s)}\mathrm{E}[{dN}_{i1}(s)|{\mathcal{F}}_{s-}]\right]\end{array}$$

Therefore, E[Λ̂₁(t) − Λ₁(t)] turns out to be

$$\sum _{i=1}^n{\int }_0^t-Pr(Y(s)=0)d{\mathit{\Lambda }}_1(s)+Pr(Y(s)>0)r(s)d{\mathit{\Lambda }}_2(s).$$

Similarly, E[Λ̂₂(t) − Λ₂(t)] is reduced to

$$\begin{array}{l}\sum _{i=1}^n{\int }_0^t\mathrm{E}\left[\frac{I(Y(s)>0)}{Y(s)}\times \mathrm{E}\left[\{{dN}_{i1}(s)+{dN}_{i2}(s)\}I\left({dN}_{i1}(s)-\frac{r(s)}{1-r(s)}{dN}_{i2}(s)<0\right)|{\mathcal{F}}_{s-}\right]\right]-d{\mathit{\Lambda }}_2(s)\\ =\sum _{i=1}^n{\int }_0^t\mathrm{E}\left[\frac{I(Y(s)>0)}{Y(s)}\mathrm{E}[{dN}_{i2}(s)\mid {\mathcal{F}}_{s-}]\right]-d{\mathit{\Lambda }}_2(s)\\ =\sum _{i=1}^n{\int }_0^t-Pr(Y(s)=0)d{\mathit{\Lambda }}_2(s)-Pr(Y(s)>0)r(s)d{\mathit{\Lambda }}_2(s).\end{array}$$

Appendix III

Asymptotic distribution of estimator using the pool-adjacent-violators algorithm

For any a > 0, ${\widehat{\mathit{\Lambda }}}_1^S(t)-\frac{a}{\sqrt{n}}$ and ${\widehat{\mathit{\Lambda }}}_1^S(t)+\frac{a}{\sqrt{n}}$ are isotonic functions for t ∈ 𝒯, and ${\widehat{\mathit{\Lambda }}}_1^P$ is an isotonic regression of Λ₁. By Theorem 1.6 (Barlow et al (1972)),

$$\begin{array}{ll}if\hfill & {\widehat{\mathit{\Lambda }}}_1^S(t)-\frac{a}{\sqrt{n}}\le {\stackrel{\sim }{\mathit{\Lambda }}}_1(t)\le {\widehat{\mathit{\Lambda }}}_1^S(t)+\frac{a}{\sqrt{n}},\hfill \\ \hfill & \mathit{then}{\widehat{\mathit{\Lambda }}}_1^S(t)-\frac{a}{\sqrt{n}}\le {\widehat{\mathit{\Lambda }}}_1^P(t)\le {\widehat{\mathit{\Lambda }}}_1^S(t)+\frac{a}{\sqrt{n}}.\hfill \end{array}$$

Since $\sqrt{n}({\widehat{\mathit{\Lambda }}}_1^S(t)-{\stackrel{\sim }{\mathit{\Lambda }}}_1(t))$ converges to zero in probability, $\sqrt{n}({\widehat{\mathit{\Lambda }}}_1^S(t)-{\widehat{\mathit{\Lambda }}}_1^P(t))$ also converges to zero in probability. Therefore, $\sqrt{n}({\widehat{\mathit{\Lambda }}}_1^P(t)-{\mathit{\Lambda }}_1(t))$ weakly converges to the same distribution as $\sqrt{n}({\stackrel{\sim }{\mathit{\Lambda }}}_1(t)-{\mathit{\Lambda }}_1(t))$ by Slutsky’s theorem. Consistency of the estimator ${\widehat{\mathit{\Lambda }}}_1^P$ can be easily proved using similar arguments.