A unified theory for the energy cost of legged locomotion

Abstract

Small animals are remarkably efficient climbers but comparatively poor runners, a well-established phenomenon in locomotor energetics that drives size-related differences in locomotor ecology yet remains poorly understood. Here, I derive the energy cost of legged locomotion from two complementary components of muscle metabolism, Activation–Relaxation and Cross-bridge cycling. A mathematical model incorporating these costs explains observed patterns of locomotor cost both within and between species, across a broad range of animals (insects to ungulates), for a wide range of substrate slopes including level running and vertical climbing. This ARC model unifies work- and force-based models for locomotor cost and integrates whole-organism locomotor cost with cellular muscle physiology, creating a predictive framework for investigating evolutionary and ecological pressures shaping limb design and ranging behaviour.

1. Introduction

The metabolic demands of walking, running and climbing affect the costs of foraging, predator avoidance and other essential tasks, providing a potentially powerful, integrative performance variable for investigating animal evolution. Yet, despite decades of laboratory study a unified model linking proximate mechanisms of muscle physiology to the whole-body locomotor cost of legged locomotion has remained elusive [1], limiting efforts to investigate selection pressures acting on locomotor anatomy and behaviour. Work-based models perform well for vertical climbing but fail to predict the cost of walking and running on level ground or changes in cost with speed and body size [1–5]. The ground force exerted by the limbs during each step predicts observed changes in the cost of running across species and speeds, but force-based models [6,7] ignore mechanical work and do not predict climbing costs.

Here, I develop and test a mathematical model predicting the energy cost of legged locomotion from established components of muscle physiology. Locomotor cost is primarily a function of muscle metabolism [1], and can therefore be partitioned into three metabolic components of muscle contraction: activation, cross-bridge cycling and relaxation [8–11]. Cross-bridge costs, sometimes called ‘maintenance costs’ [8–11], are associated with actin–myosin cross-bridge cycling and the development of muscle tension, and have been the focus of previous locomotor cost models [1,6,12]. Activation and relaxation costs (AR costs) are not associated with cross-bridge cycling and are instead related to other processes at the initiation and end of a contraction [8–11]. AR costs are typically ignored in locomotor cost models (but see [2,7,13]). However, the limited studies examining AR costs in cyclical contractions indicate that they account for a large portion of metabolic expenditure when muscles are stimulated repeatedly in contraction–relaxation cycles with short stimulation periods, as in legged locomotion (figure 1a).

Figure 1.

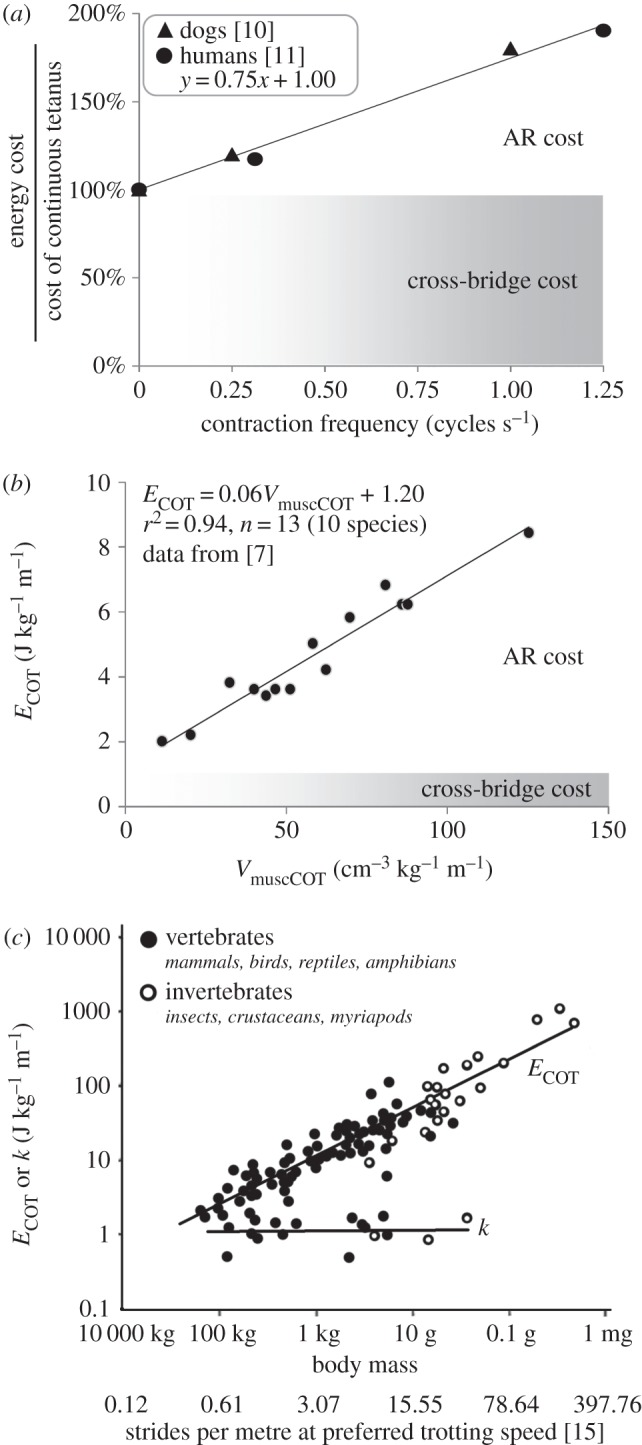
(a) AR and cross-bridge costs versus contraction cycling frequency, as a percentage of the cost of continuous contraction, from in situ studies; energy is normalized to muscle force (electronic supplementary material, text S3). (b) E_COT and V_muscCOT for running. Following equation (2.5), AR cost can be calculated from the slope of regression equation, 0.6V_muscCOT. Cross-bridge cost is given by the regression intercept, or as E_COT−AR cost. (c) Mass-specific metabolic cost, E_COT, and mechanical work, k, per metre versus body size and estimated stride cycles m⁻¹; redrawn from [3].

2. Material and methods

The ARC model developed here combines AR and Cross-bridge cycling costs. During legged locomotion each stride is a contraction–relaxation cycle for the limb muscles involved, and AR costs are a product of the volume of muscle activated per stride, V_musc, and stride frequency [10,11]. Cross-bridge costs are a product of the animal's total mechanical power, P_mech, and the metabolic cost rate per unit of mechanical power. Alexander [12] gives the metabolic cost of contracting muscle (ignoring AR costs) as F_isov_maxΦ(v/v_max), where F_iso is the isometric contraction force of the active muscle fibres, v_max is maximum muscle shortening velocity and Φ(v/v_max) is a function relating the metabolic cost of contraction as a function of v/v_max ([12]; electronic supplementary material, figure S1). Summing AR and cross-bridge costs gives the ARC model prediction for the whole-animal rate of energy expenditure Ė,

2.1

where e is the energy consumed by AR processes per unit of V_musc and F_iso/P is F_iso per unit of mechanical power.

(a). Activation–relaxation costs and force models

The AR cost term, eV̇_musc, is determined by the rate of ground force production underlying force-based cost models [6,7] as follows. For each stride cycle, the mean vertical ground force, F_ground, produced by the limbs during the period of foot–ground contact time, t_c, must equal the product of body weight, Mg and stride period, T,

2.2

where j is the ground force generated per unit volume of activated limb muscle, which is independent of body size [14]. Multiplying equation (2.2) by stride frequency, T⁻¹, gives the rate of muscle activation (i.e. the volume of muscle activated per stride multiplied by stride frequency; electronic supplementary material, text S1).

2.3

The above equation can be rewritten using the AR cost term, eV̇_musc, from equation (2.1),

2.4

where c is the metabolic energy consumed per unit F_ground and e = cj. The right side of equation (2.4) is identical to equation (1) in Kram and Taylor's seminal force-based model of locomotor cost [6]. However, as derived above, the term cMgt_c⁻¹ describes AR costs (i.e. the volume of muscle activated per second), not the rate of cross-bridge cycling initially proposed [6] as the mechanism linking t_c to locomotor cost. Force-based models of locomotor cost [6,7] are, in effect, AR cost models.

(b). Activation–relaxation and cross-bridge model cost of transport

Dividing equation (2.1) by M and travel speed, B, gives the mass-specific energy cost per distance travelled, E_COT, often called the ‘cost of transport’. Since B is equal to step length, d, divided by t_c, dividing equation (2.4) by M and B gives the AR cost of transport, eV_muscCOT = cgd⁻¹. P_mech increases nearly linearly with MB, with only slight curvilinearity with respect to B ([2]; electronic supplementary material, text S2 and figure S2). Thus, P_mech ≈ kMB, where k is the mass-specific mechanical work per distance travelled, and dividing the cross-bridge cost term in equation (2.1) by M and B gives kF_iso/Pv_maxΦ(v/v_max). Hence,

2.5

As shown in figure 1b, a model of this form fits the available data for E_COT and V_muscCOT quite well. While the ARC model is consistent with previous models and data, it makes additional predictions that can be tested against observed locomotor cost within and between species.

3. Results

One test of the ARC model is whether the ratio of AR : cross-bridge cost observed for isolated muscle contracting at a given cycling frequency matches the ratio observed in an animal running at that stride frequency (electronic supplementary material, text S3). A 100 kg animal running on level ground has a predicted stride frequency of 1.84 Hz at its preferred trotting speed [15]. The limited data from in situ studies of isolated muscle suggest a cycling frequency of 1.84 Hz produces an AR : cross-bridge ratio of approximately 1.38 (figure 1a). For comparison, the predicted AR : cross-bridge ratio for a running 100 kg animal, calculated using the observed interspecific relationship between V_muscCOT and E_COT (figure 1b; electronic supplementary material, text S3), is approximately 1.34, within 5% of the estimate from in situ studies. Whole-animal measures of locomotor cost are consistent with measures of AR cost in isolated muscle.

Human walking and running provide a second test (electronic supplementary material, text S4). Inverse dynamics yields V_muscCOT values for human walking and running of 11.4 and 32.4 cm³ kg⁻¹ m⁻¹, respectively [7], which, using the E_COT : V_muscCOT regression in figure 1b, translates to AR costs of 0.7 and 1.9 J kg⁻¹ m⁻¹ (figure 1b). Subtracting these AR costs from human E_COT values yields a cross-bridge cost of 1.3 and 1.9 J kg⁻¹ m⁻¹ for walking and running, respectively, values consistent with the magnitude of total mechanical work during both walking (approx. 0.7 J kg⁻¹ m⁻¹) and running (approx. 1.5 J kg⁻¹ m⁻¹) and the difference in mechanical work between gaits [4]. Estimated AR costs account for approximately 33% of E_COT for human walking and approximately 50% for running, which may explain the discrepancy between mechanical work and E_COT [4].

Allometric comparisons of E_COT for running and climbing provide a final set of tests for the ARC model (electronic supplementary material, text S5). Step length, d, is proportional to effective limb length, which scales with M^0.34 [16]. Since eV_muscCOT = cgd⁻¹, AR cost is predicted to increase as zM^−0.34, where z is a constant. Mass-specific mechanical work per distance, k, is independent of body mass during running ([2,3]; figure 1c), and F_iso/P and Φ(v/v_max) are expected to be independent of mass as well (electronic supplementary material, text S5). However, v_max scales with M^−0.12 [17], and cross-bridge costs, kF_iso/Pv_maxΦ(v/v_max), are therefore predicted to decrease with body size as wM^−0.12, where w is a constant. To determine z and w, we draw on the empirically determined estimates of cross-bridge cost and AR : cross-bridge cost ratio in figure 1a,b, and find these conditions are met when z = 8, w = 2 and E_COT has units J kg⁻¹ m⁻¹,

3.1

The ARC model (equation (3.1)) fits observed E_COT for mammals (figure 2a), and falls within the 95% confidence interval of the allometric relationship reported for a larger dataset including birds [18]. The ARC model remains in agreement with observed E_COT when varying z and w ± 20% and, consequently, varying the AR : cross-bridge cost ratio –33% to +50% (figure 2a; electronic supplementary material, text S6).

Figure 2.

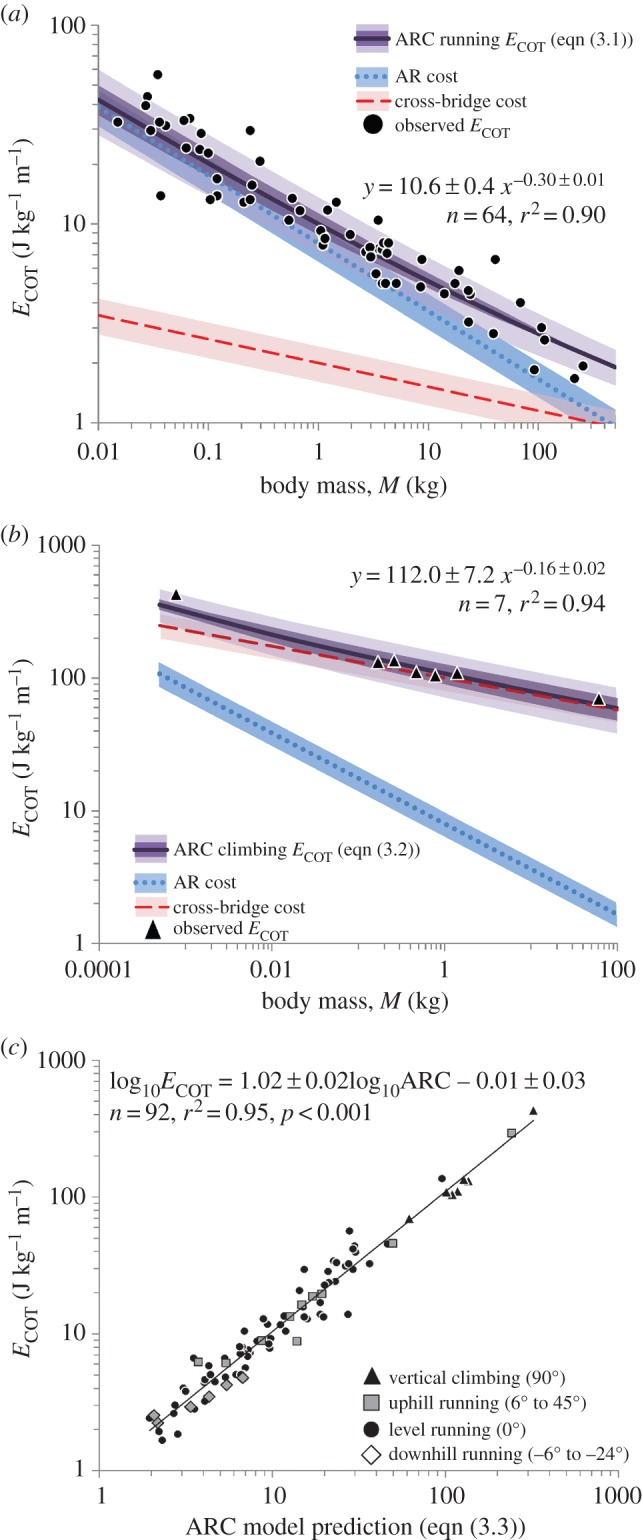
(a) Observed E_COT and ARC predictions (equation (3.1)) for level running. Shaded regions for AR and cross-bridge costs reflect varying z and w ± 20%. The darker shaded region for the ARC E_COT prediction reflects varying AR : cross-bridge ratio −33 to +50%; the light shaded region for extends ARC E_COT an additional ± 20% (electronic supplementary material, text S6). (b) Observed E_COT and ARC predictions (equation (3.2)) for vertical climbing. Shaded regions as in (a) and (c). Observed E_COT and ARC predictions (equation (3.3)) for a range of species and slopes. Data in electronic supplementary material, table S1. (Online version in colour.)

During vertical climbing, k must be at least 9.8 J kg⁻¹ m⁻¹, approximately 10-times greater than during level running. The cost function Φ(v/v_max) will also increase as higher ratios of v/v_max are used, such that w is estimated to be approximately 100 for vertical climbing (electronic supplementary material, text S5). AR costs are expected to remain largely unchanged, as d is similar on level and vertical substrates [19,20]. We can thus modify equation (3.1) for vertical climbing as

3.2

The trend line for observed climbing data (figure 2b) includes the ARC model (equation (3.2)) and is consistent with the weak allometry reported for non-human primates [5] and the relatively poor climbing efficiencies reported for cockroaches [19]. As with level running (equation (3.1)), the model remains in agreement with observed E_COT when varying z and w ± 20% and varying the AR : cross-bridge cost ratio between −33% and +50% (figure 2b; electronic supplementary material, text S6).

A generalized ARC model can be written that accounts for the change in cross-bridge cost at all inclines, essentially combining equations (3.1) and (3.2) (electronic supplementary material, text S5).

3.3

The above equation is a U-shaped function with respect to incline, and fits data from a broad range of species (cockroaches to zebu cattle) and slopes (−24° to +90°) with a regression slope of 1, an intercept of 0 and a high coefficient of determination (r² = 0.95; figure 2c; electronic supplementary material, text S5).

4. Discussion

The ARC model provides a unifying framework for several well established but poorly understood [1] phenomena in terrestrial locomotion. The greater E_COT among smaller animals during level running [18] results from their shorter limbs, faster stride cycles and greater AR costs (figure 2a). Force-based cost models [6,7] capture this allometry because AR costs predominate during level running. By contrast, mechanical work predicts E_COT during vertical climbing, in which cross-bridge costs predominate. The weak scaling of cross-bridge costs results in similar climbing E_COT for most species [5] but poor climbing efficiencies at extremely small sizes [19]. Because of their high AR costs, small animals have low apparent efficiencies during running [3] but show a small marginal increase in cost during climbing, making them appear remarkably efficient climbers [5,19]. Conversely, large animals, with long legs and low AR costs, appear to be efficient runners but inefficient climbers.

Owing to the distinct allometries of AR and cross-bridge costs (figure 2a,b), mechanical work accounts for a much larger portion of running and walking E_COT for large animals. This allometry may explain why many large species, notably humans [4], have evolved a suite of work-minimizing kinematic strategies (e.g. pendular exchange of potential and kinetic energy) that appear to be absent in smaller taxa [21]. The greater contribution of mechanical work, and the weak curvilinearity in P_mech with speed, may also account for the curvilinearity in Ė with running speed reported for some large species (e.g. horses [22]; electronic supplementary material, text S2). Minimizing summed AR and cross-bridge costs may shape kinematics and kinetics in humans and other species [13].

Tests of the ARC model here are limited by the available experimental data. Additional study of in situ or isolated muscle is needed to test whether the linear relationship between AR cost and cycling frequency in figure 1a persists at the faster cycling frequencies used by smaller species (cf. figure 1a,c) as assumed here. Simultaneous measurements of P_mech and V_musc across a range of species are also needed to test the model's allometric predictions (equation (3.1)–(3.3)). Such work may enable us to either integrate or more confidently rule out other proposed mechanisms (e.g. cross-bridge cycling frequency [6]) for explaining variation in locomotor cost.

While developed for legged terrestrial locomotion, the ARC model may prove to be a useful framework for investigating the energetics of other locomotor modes. For example, wing beat frequencies among birds and bats scale with negative allometry [23], such that smaller species have higher cycling frequencies and greater AR costs; an ARC model for flight would thus predict greater estimated efficiencies for larger flyers, consistent with empirical observation [1]. The energetics of other repetitive, muscle-driven tasks, such as tool manufacture and use or burrowing, may likewise be amenable to investigation with an ARC model. By linking whole-organism energetics to the fundamental metabolic properties of muscle, a conservative tissue [8], the ARC model may be a powerful tool for investigating the evolution of limb anatomy in a broad range of lineages, including our own.

Data accessibility

All data for figure 2 are in the electronic supplementary material, table S1.

Competing interests

The author declares no competing interests.

Funding

This work was supported by Hunter College and the City University of New York.