The risk of incomplete personal protection coverage in vector-borne disease

Abstract

Personal protection (PP) techniques, such as insecticide-treated nets, repellents and medications, include some of the most important and commonest ways used today to protect individuals from vector-borne infectious diseases. In this study, we explore the possibility that a PP intervention with partial coverage may have the counterintuitive effect of increasing disease burden at the population level, by increasing the biting intensity on the unprotected portion of the population. To this end, we have developed a dynamic model which incorporates parameters that describe the potential effects of PP on vector searching and biting behaviour and calculated its basic reproductive rate, R₀. R₀ is a well-established threshold of disease risk; the higher R₀ is above unity, the stronger the disease onset intensity. When R₀ is below unity, the disease is typically unable to persist. The model analysis revealed that partial coverage with popular PP techniques can realistically lead to a substantial increase in the reproductive number. An increase in R₀ implies an increase in disease burden and difficulties in eradication efforts within certain parameter regimes. Our findings therefore stress the importance of studying vector behavioural patterns in response to PP interventions for future mitigation of vector-borne diseases.

1. Introduction

The collective human mortality rate due to vector-borne diseases is estimated to be more than 1.5 million per annum [1]. Important examples include malaria, dengue, leishmaniasis, yellow fever, Lyme disease and the West Nile virus [2–5].

One of the most important measures of the risk of infectious disease outbreak is the basic reproductive rate, R₀. R₀ measures the average number of secondary infections caused by a single infection in a naive host population. R₀ thus establishes a threshold criteria for disease invasion; a disease has the potential to invade a population if R₀ > 1, and is unable to persist when R₀ < 1 [6–9]. In general, the higher R₀ is, the more difficult it will be to eradicate the disease [6]. In this study, we explore how personal protection (PP) interventions that protect a portion of individuals in the community affect R₀.

We use PP to refer broadly to interventions that operate at the individual or household level (rather than the community level), whether or not they kill the vectors in addition to their individualistic protection. Examples include the use of medication, personal use of insect repellent and bednets, including insecticide-treated nets (ITN) [10–14]. Residual spraying of households can also be considered as PP by our definition, if application decisions are made at the household level.

In most applied interventions, only a portion of the population receives or uses a suggested treatment. Although PP provides direct benefits to protected individuals, its population-level effects can be complex and may not always be beneficial in cases where its coverage is not complete. For example, the use of insect repellents by only a part of the population (the treated group, TG) can increase the number of bites on untreated individuals (untreated group, UTG), as repelled vectors seek alternative hosts [15]. When bites are concentrated in a fraction of the host population, the disease risk of the entire population, as represented by R₀, may increase [11,16–22]. The fact that certain treatments which benefit the TG may indirectly harm the UTG is of interest, since it raises ethical concerns that may limit their usage. An even more troubling scenario is when a PP harms the UTG to such a degree that the overall net effect is an increase in disease risk for the entire population. The possible outcomes of a partial treatment coverage given to a population are summarized in figure 1.

Figure 1.

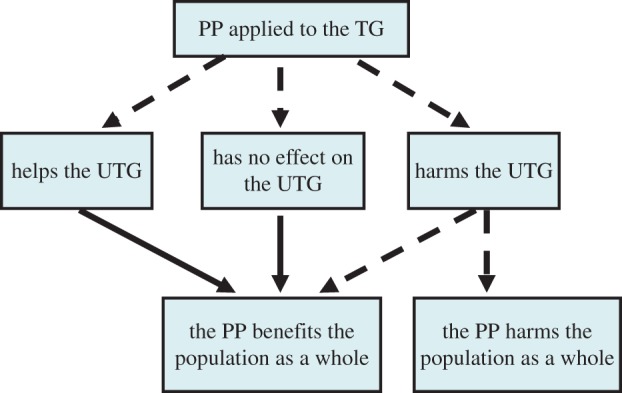
The different possible effects of PP given to the TG on the disease risk of the UTG and the entire host population. Solid and dashed arrows denote whether the outcome is obligatory or not, respectively. (Online version in colour.)

In this study, we apply a model that was originally designed to analyse a system with two host species and one vector species [20,23,24] to a single host population divided into two different groups, the TG and the UTG, and develop it to account for possible effects of PP on vector biting patterns. The goal is to analyse how partial PP coverage affects R₀ under different assumptions about the vector behavioural patterns, in particular, its response to ITN, bednets and insect repellents. The analysis of R₀ identified the conditions under which partial PP coverage will either increase or decrease it.

2. Model outlines

We explore how the basic reproductive number, R₀, depends on individual-level treatment with variable coverage rates of the host population. To calculate R₀, we modified a previously developed modelling framework [20,24] originally designed for multiple host species, to consider different host types—specifically hosts receiving (TG) and not receiving (UTG) PP treatments. We chose this model because it is a relatively simple framework that includes the details we need to explore the effects of PP on R₀. Our model considers only one host species: in particular, we do not account here for the possibility that vectors divert from biting human hosts to bite domestic animals or other non-human targets.

The model quantifies the dynamics of the susceptible, infected and removed compartments of the TG and the UTG (denoted by the subscripts T and U, respectively). By using the next-generation-operator technique, we calculate the expression of R₀ from the model equations [7] (see the electronic supplementary material for the model description and equations):

2.1

In equation (2.1), g_i = p_iq_i/δ_i is the transmission ability of host group i (i = T or U), defined as the product of probability of transmission to a vector p_i, probability of transmission from a vector q_i and the infectiousness duration (1/δ_i, see table 1 for parameters definitions) [20]. V and d are the density and the death rate of the vector, respectively, k_i is the vector biting rate (number of bites per vector per unit time) on hosts belonging to group i, and N_i is host group i density. In equation (2.1), we assumed frequency-dependent biting (i.e. the biting rate of an individual vector is independent of the host total population density, N = N_T + N_U, see the electronic supplementary material). In general, the assumption of frequency-dependent biting leads to a decrease in R₀ when host population size increases while vector density remains constant, since bites are then distributed on more host individuals, thus reducing the frequency at which individual hosts are bitten [25,26]. Similar expressions of R₀ have been obtained in the past for both, metapopulation [16] and multi-host models [20,26]. The current model builds on these by modelling the factors affecting the biting rates k_i, as elaborated below.

Table 1.

Definition of the model parameters. i = T or U.

parameter	meaning
ki	biting rate, i.e. the number of bites per unit time on hosts from group i an individual vector has
Ni	host group i population size
V	vector population size
r	vector fixed birth rate
N	the total host population size, i.e. N = Nu + NT
pi	the efficiency that an infected vector would infect a susceptible individual of host group i during one feeding event
qi	the efficiency that an infected individual of host group i would infect a susceptible vector during one feeding event
δi	recovery rate of host in group i, i.e. 1/δi is the infectiousness duration
d	vector death rate for coverage rate x (i.e. d is a function of x)
d0	basal vector death rate, i.e. death rate without treatment or without killing effect
k	the total biting rate of the vector, i.e. the number of bites per unit time of individual vector on the entire host population, i.e. k = kU + kT
gi	the transmission ability of hosts in group i. gi = piqi/δi
L	vector latent period
x	the treated population proportion, i.e. NT = xN and NU = (1 − x)N
hi1	post-biting handling time. The time the vector needs to handle a host from group i after a successful biting attempt
hi2	pre-biting handling time. The time the vector spends when occupying with host individual of group i before biting it
hi	the total handling time of host on group i. The amount of time the vector needs to spend in handling hosts of group i in order to achieve a single bite
bi	the protection time. The average time units the vector needs for a successful biting attempt on host group i individual
Ai	the general searching efficiency, the number of bites per unit time on host group i incurred by a vector that forages in host i population with unit density (Ni = 1) and zero handling times
ai	host i searching efficiency. The attractiveness of hosts belong to group i
βi	the probability that the vector would successfully bite an individual from host group i
η	a constant that determines the ability of a treatment to increase the vector death rate, or alternatively, decrease its life expectancy

We adapt a ‘classical’ saturated (Holling type II) functional response to calculate vector biting rates on each type of host [27–29]. The type II functional response is a well-known model that has been successfully applied to various consumer–resource systems [30], and which provide a natural basis to model the way vector bites are distributed as a function of searching efficiencies, host densities and handling times with respect to each group. Under these assumptions (see the electronic supplementary material), it can be shown that the vector biting rate on host group i, k_i [27,28,30] is given by:

2.2a

2.2b

2.2c

where

2.3

In equation (2.2a), h_i1 (i = T or U), the post-biting handling time, is the time the vector spends in handling host i after it has been successfully bitten. Biologically, h_i1 may include the time the vector needs for (a) resting and digesting the blood meal, (b) egg production, (c) searching for a proper incubation site and (d) laying eggs. h_i2 is the pre-biting handling time, that is, the time the vector is occupied by an individual host when flying around and trying to locate a biting site. h_i in equation (2.2a) represents the total handling time, that is, the average time the vector needs to spend in handling a single bite from hosts in group i; h_i is a weighted sum of the time the vector spends in handling a successful bite (h_i1 + h_i2 = the pre- and the post-handling times) and associated in unsuccessful attempts (h_i2 = the pre-biting handling time, equation (2.2a)). β_i (equation (2.3)) is the probability that a biting attempt on a host from group i will be successful. We assumed that the pre-biting time h_i2 is exponentially distributed with mean, b_i, the protection time, which measures the mean time it takes the vector to achieve a successful bite on group i. A_i in equation (2.2b) represents the general searching efficiency, that is the average biting rate the vector has when foraging in a population of unit density (N_i = 1) neglecting all handling times (i.e. when h_i1 = h_i2 = 0), thus, a_i can be interpreted as the attractiveness of group i to the vectors.

To model treatments that may kill the vectors, we assume that the killing acts to decrease the vector longevity, or alternatively, increase its death rate, d (provided that its life expectancy is exponentially distributed) [31]. As a simple approximation for simulation purposes, we assume that d depends bilinearly on the time the vector is exposed to the pesticide, h_T2, and the TG coverage rate x:

2.4

where, d₀ is the basal vector death rate without the killing treatment, and η is a constant representing the treatment killing efficiency; it is zero when the treatment does not kill the vector and positive when it does. From the above, N_T = xN, N_u = (1 − x)N, where N is the total host population density (N = N_T + N_U). With the aid of equations (2.1)–(2.4), R₀ can be written as:

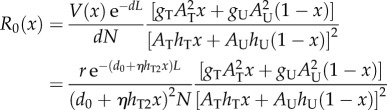2.5

where V(x) is the vector population size when a proportion x of the population is treated. In cases where the treatment does not kill the vectors, V(x) is expected to be constant (assuming that the vector population is at equilibrium), when η > 0, V(x) may decrease with x (it can be, of course, that a treatment, such as ITN, does not substantially affect the vector population size) [31]. From the model equations (electronic supplementary material, equation S1), the vector equilibrial population is r/d, where r is the vector's fixed birth rate that is assumed to be limited by other factors in the habitat (e.g. incubation sites, etc.). The expression r/d enables us to calculate the decrease in the vector population size due to the killing effect of ITN via d in equation (2.4). We add the factor exp(−dL) to equation (2.1) and obtain equation (2.5) to account for the decrease in R₀ due to a possible vector latency period, L. This factor represents the probability that an infected vector will survive the fixed latent period, L, and becomes infectious [6,31]. Definitions of all model parameters can be found in table 1.

Every PP can be characterized by different sets of the model parameters (e.g. A_T, A_U, h_T, h_U, etc.; see also table 1 and equation (2.5)). In this research, we will concentrate mainly on the effects of bednets, ITN, and insect repellents used by individuals, on R₀. The main goal of this study is to explore the conditions under which these PP techniques will reduce R₀ below its value in an otherwise untreated population, i.e. solving the inequality:

2.6

where R₀(x) is R₀ when a proportion x of the population is treated (equation (2.5)) and R₀(0) = R₀(x = 0) = rexp(−d₀L) g_u/(d₀²Nh_U²) (equation (2.5)).

3. Results

3.1. General consideration

In general, the response of R₀ to PP coverage takes two main forms depending on model parameters (figure 2): (i) the net effect of the PP always decreases R₀, or (ii) PP increases R₀ if the TG proportion is below a certain threshold x_t, and decreases R₀ thereafter (figure 2). A detailed analysis of equation (2.5), including an expression of the threshold x_t for η = 0 can be found in the electronic supplementary material. When R₀ is near 1, an increase in it will generally result in an increased population morbidity.

Figure 2.

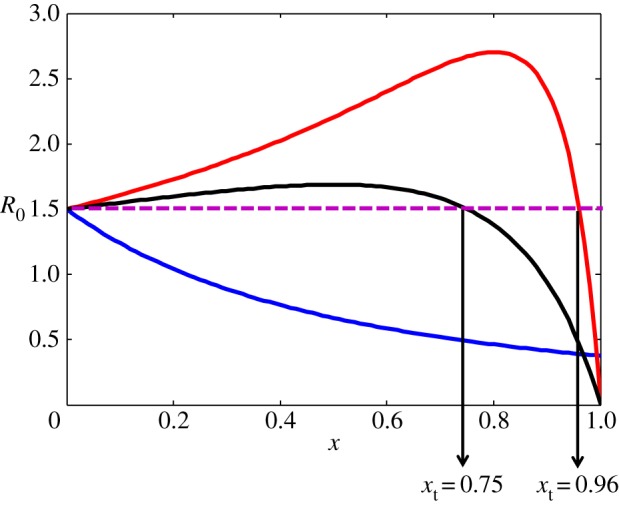
The dependence of R₀ on coverage rate. Purple horizontal line: R₀ for a naive (untreated) population (i.e. R₀(x = 0)). Blue line: h_T = 0.5, h_U = 0.25, A_T = A_U = 0.1 and x_t = −2 (see the electronic supplementary material). R₀ decreases with every TG proportion thus any PP coverage is beneficial to the population. Red and black lines: A_T = 0.1, A_U = 5, h_T = 0.5, h_U = 0.06 and x_t = 0.96 and A_T = 0.1, A_U = 5, h_T = 0.5, h_U = 0.03, and x_t = 0.75, respectively. R₀ decreases with every TG proportion x > x_t and increases with x < x_t. In all graphs g_T = g_U, η = 0 and R₀(x = 0) = rg_Uexp(−d₀L)/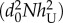 = rg_Texp(−d₀L)/ 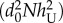= 1.5. When R₀ < 1, the disease is extinguished. (Online version in colour.)

Figure 2 demonstrates that for the chosen parameters, R₀ can reach 2.70 for coverage of 80%, exceeding the value for the untreated population by more than 80% (R₀(x = 0) = 1.5). As such an increase can lead to dramatic rise in disease burden, we will explore how common PP techniques affect the model parameters, and consequently R₀(x), thus enabling us to link between different PP and the behaviour of R₀(x) exemplified in figure 2.

3.2. The dependency of R₀ on the use of bednets, insecticide-treated nets and insect repellents

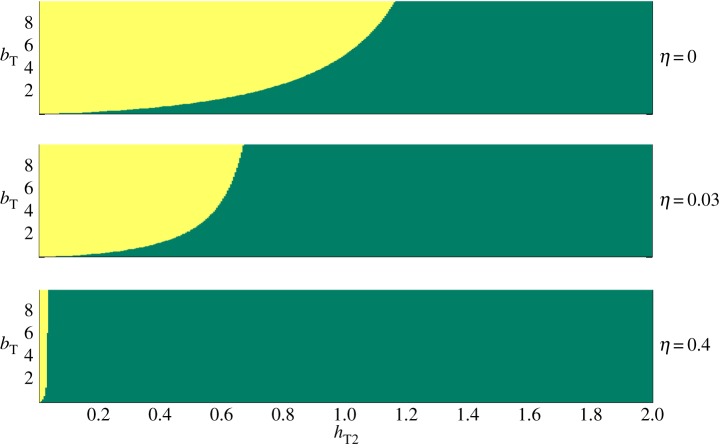
Insect repellents may affect the time the vector spends in trying to bite a host from the treated group, once located, h_T2 (the pre-biting time); the vector may spend less time in trying to bite a host with repellent, or alternatively, it may spend more time around a host with repellent in trying to locate an untreated skin area. The repellent also increases the protection time, b_T, and it may also make the host less attractive from a distance, thus decreasing a_T (equation (2.2b)). Likewise, bednets may affect h_T2; they can increase or decrease it, depending on whether nets cause the vectors to give up a protected host quickly, or alternatively, cause them to spend more time in trying to find holes or proximal body parts. Nets also increase b_T, the protection time. If bednets are also impregnated with insecticide (ITN), they also increase η, and consequently the killing rate, d (equation (2.4)). Figure 3 illustrates how the form of R₀(x) (the dependency of R₀ on coverage rate, x, as exemplified in figure 2) varies over the parameter space of h_T2, b_T and η. To the best of our knowledge, there are insufficient data available to estimate these parameters with accuracy. We therefore use upper bounds of several days for h_T2 and b_T—the life expectancy and egg production time of many vectors species [32]. We have also set d₀ = 0.088 d⁻¹ and L = 0.1 d⁻¹, the death rate and the latency period of typical Anopheles spp. (malaria vectors) [6,31]. We have chosen a range of η between 0 (bed nets without killing effect) and 0.3. When η = 0.3, the vector equilibrial population, r/d (equation (2.5)) decreases by 23%, an upper bound for a population decrease due to ITN according to a field study on Anopheles albimanus [33]. Figure 3 is thus intended to point out on general principles, not to provide quantitative information.

Figure 3.

The effect of PP with various vector pre-biting, h_T2, and protection, b_T, times, respectively, and killing ability, η (all times are in days) on the qualitative behaviour of R₀ as function of the proportion of the treated group within the population. In green: the treatment always decreases R₀. In yellow, the treatment increases R₀ below a threshold coverage rate, and decreases R₀ above it. In all simulations, g_T = g_U, h_T1 = 3, h_U = 3, a_T = a_U, L = 0.1 d⁻¹, d₀ = 0.088 d⁻¹, i.e. the treatment does not affect the host transmission ability and the attractiveness to vectors. (Online version in colour.)

Figure 3 shows parameter ranges where partial PP coverage can increase R₀ (yellow area). The border between the green and the yellow areas shows critical values of the pre-biting and protection times (h_T2 and b_T, respectively). For example, when η = 0.03 and the pre-biting time, h_T2 = 0.39 days (figure 3b), there exists a critical value of the TG protection time, b_Tc = 1.7 days, for which PP reduces R₀ at any coverage level if the protection time is less than b_Tc (green area), but increases R₀ below a threshold coverage level when the protection time is longer than b_Tc (yellow area). Thus, if it is harder for the vectors to successfully bite treated hosts (i.e. b_T increases), the disease risk for the entire population may increase when R₀ is near the threshold value of 1. This is because when b_T is long, vectors are more likely to be diverted from treated to untreated hosts, concentrating more bites per capita on the UTG.

Other parameters behave similarly. When pre-biting time h_T2 is large, R₀ decreases for every coverage rate (green zone), and if it is large enough (e.g. h_T2 > h_T2c = 1.17d, figure 3a), this decrease is independent of the value of b_T. The killing parameter, η, has a critical value as well; the higher it is, the wider the parameter range of b_T and h_T2 under which R₀ decreases for every PP coverage. If a PP intervention has very strong killing ability (i.e. η is high), then it can decrease R₀ irrespective of the coverage rate over the whole range of h_T and b_T we studied (in the simulations of figure 3, this occurs, for example, when η > 11, data not shown).

4. Discussion

In this study, we have investigated the effects of partial PP coverage and found that under some circumstances, it is plausible that partial coverage with popular PP techniques used today, such as ITN, bednets and repellents, can lead to substantial increases in the reproductive number, R₀. This result is similar to the diversity amplification effect which occurs due to vector preference towards specific host species in a two-species community [20]. In both cases, an increase in R₀ occurs when vectors divert from one host group (TG or less preferred host species) to the other (the UTG or the preferred host species).

Previous models have pointed out the potential negative effects that partial bednet coverage can have due to diversion of vectors from the TG to the UTG, when combined with low killing efficiency [11,21,34]. The effects estimated, however, were very low, particularly at the level of the entire population [11,31,32]. It has also been speculated that total population morbidity could increase with increased bednet coverage in a case where bednets were combined with vaccines that could affect the population immunity of specific vulnerable host groups [35]. Field studies, however, praise the use of ITN for their success in reducing malaria incidence, or in decreasing other important metrics of disease risk (e.g. entomological inoculation rate, human biting rate and vector population) [36–41].

This study is the first to systematically explore the effect of partial PP coverage on R₀ over a wide range of plausible parameters, and the first to find a potential for substantial increase in population-level risk; when R₀ is near its threshold (i.e. 1), any increase in it is expected to lead an increased population-level morbidity. It is important to note, however, that when morbidity and force of infection are high, an increase in R₀ caused by protecting part of the population will not always be expected to increase population-level morbidity, since the effects of increasing R₀ would be outweighed by the direct effect of protecting part of the population. Yet, the increase in R₀ in these cases may still lead to an increased risk in a portion of the population.

Our model makes the subtle yet important distinction between protection and diversion [11,21,31]. In previous studies, both diversion and protection have been related to the probability that a vector will give up a protected host and turn to look for another victim [11,21,31]. In the present framework, however, diversion is equivalent to the time duration the vector spends in trying to bite a protected host, h_T2, that is, its pre-biting time. The shorter the pre-biting time, h_T2, the stronger the diversion effect of the respective PP. The protection, b_T, in our model, is equivalent to the mean time the vector needs for a successful biting attempt of a protected host, irrespective of the time the vector actually spends in that attempt (h_T2). In our study therefore, protection and diversion are two independent properties, and hence may be affected differently by different PP interventions. Figure 3 demonstrates the counterintuitive dependency of R₀ on protection due to this differentiation; a more protective PP can increase R₀ when the vector pre-biting handling time, h_T2, is short, and the coverage rate is below a certain threshold. For longer h_T2, however, every PP coverage reduces R₀ (figure 3). Consequently, an increase in R₀ may therefore occur due to a change in the vector foraging behaviour. If vectors switch quickly on encountering nets (or on encountering ITNs), the pre-biting time, h_T2, will decrease, and consequently R₀ will increase for some levels of coverage (assuming high enough protection times, figure 3). Such a change of the vector behaviour is realistic. Avoiding landing on ITNs and spending less time in trying to bite protected individuals are traits that can increase vector longevity and fitness, and thus may spread within the population relatively fast. Changes in vector behaviour correlated with ITN usage have already been observed: mosquitoes change their activity time, host species (from human to livestock) and feeding site (indoor or outdoor) within several years in high coverage areas [39,42–45]. Unfortunately, to the best of our knowledge, there are no field or laboratory measurements regarding the time allocation used by vectors while foraging for potential hosts.

This study expands on previous work by supplementing simulation-based exploration of the various effects of PP on disease burden with analytical results on R₀, thus increasing generality and providing a better mechanistic understanding [46]. Our results are most applicable to cases where R₀ is near its threshold (i.e. 1). Under such circumstances, an increase in morbidity may occur for PP partial coverage rates if certain vector behavioural patterns exist, especially a decrease in its pre-biting handling time. This study, therefore, stresses the importance of field research on the vector's time allocation to foraging for potential hosts and its relation to the PP techniques widely used today for future elimination and mitigation of vector-borne infectious diseases.

Authors' contributions

E.M. and A.H. conceived the study. E.M. wrote the first draft of the manuscript. All authors revised the manuscript, contributed to later drafts, developed the model and analysed the results. All authors gave final approval for publication.

Competing interests

We have no competing interests.

Funding

This study was supported by the Bill and Melinda Gates Foundation Global Health Program http://www.gatesfoundation.org/ (grant no. OPPGH5336). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.