Species-dependent hydrodynamics of flagellum-tethered bacteria in early biofilm development

Abstract

Monotrichous bacteria on surfaces exhibit complex spinning movements. Such spinning motility is often a part of the surface detachment launch sequence of these cells. To understand the impact of spinning motility on bacterial surface interactions, we develop a hydrodynamic model of a surface-bound bacterium, which reproduces behaviours that we observe in Pseudomonas aeruginosa, Shewanella oneidensis and Vibrio cholerae, and provides a detailed dictionary for connecting observed spinning behaviour to bacteria–surface interactions. Our findings indicate that the fraction of the flagellar filament adhered to the surface, the rotation torque of this appendage, the flexibility of the flagellar hook and the shape of the bacterial cell dictate the likelihood that a microbe will detach and the optimum orientation that it should have during detachment. These findings are important for understanding species-specific reversible attachment, the key transition event between the planktonic and biofilm lifestyle for motile, rod-shaped organisms.

1. Introduction

Biofilms are complex, surface-adhered communities of bacteria that have increased tolerance to many different types of stress [1–6]. Stages of biofilm formation include initially approaching the surface and reversible attachment, irreversible attachment, microcolony formation, production of exopolysaccharide matrix and structured growth [7], and dispersion [1,8]. Hydrodynamics plays an important role in the early interactions between the cell and the surface, causing attraction between swimming bacteria and surfaces [9,10]. In fact, during the early development of such biofilms, bacteria can adapt their appendages for new uses, often in combination with other appendages: flagella, which are normally used for swimming, are used for swarming motility on a surface [11], and for surface attachment. It has been suggested that flagella are important for overcoming repulsive surface forces and spreading of biofilms [12]. Recent work has shown that flagella surface attachment is important on rough surfaces as flagella can reach into crevices and attach in places where the cell body cannot reach [13]. Flagella-driven near-surface swimming can work synergistically with type-IV pili to generate two distinct near-surface motility modes with drastically different trajectories. Type-IV pili are thin appendages on the cell body that are usually used for surface attachment. Interestingly, flagella can drive a diverse range of spinning movements on the surface. Such movements have been used as a powerful tool for understanding the molecular details of the flagellum motor [14]. Spinning motility on a surface is a key part of the launch sequence of Pseudomonas aeruginosa surface detachment [15,16].

Here, we report experimental observations of spinning motility in P. aeruginosa, Shewanella oneidensis and Vibrio cholerae, species with different curvature in the cell body (henceforth referred to as the ‘head’). Different angles between the cell and the surface and different rates of rotation are observed for these species. In the spirit of previous hydrodynamic models of microorganisms that successfully elucidate physical mechanisms behind a variety of complex behaviours [17–19], we develop a hydrodynamic model for spinning motility where part of the flagellum is attached to the surface. General models of free swimmers near a surface have shown how hydrodynamic interactions can trap swimmers at surfaces [9,20,21] and cause other changes in behaviour including circular swimming [22–25], suppressed tumbling [26] and self-organization [27]. Our model shows a wide range of behaviours which vary with the degree of constraint on the flagellum, the torque exerted by the flagellar motor and the flexibility of the flagellar hook. The shape of the head is different for the three bacterial species we study, thus we consider different head curvatures in our model. Importantly, our model shows that the head curvature is especially significant just before detachment, when the flagellum is only attached at its endpoint, consistent with available experimental observations. Our results suggest that observed differences in the behaviour between these species can be explained by differences in flagellum surface adhesion, flexibility of the flagellar hook and the torque exerted by the flagellum motor. Finally, our findings indicate key bacterial–surface interactions and flagellar functions that dictate the behaviours of these microbes at the critical transition between a biofilm and planktonic lifestyle, thereby providing new insight into the process of reversible attachment.

2. Overview of experimental observations

Using high-speed light microscopy, observations of bacteria at a surface include the following general features, with each species exhibiting a subset of these features: (i) the cell swims freely near the surface; (ii) the attached cell lies parallel to the surface and vibrates but does not appear to rotate or translate; (iii) the attached cell lies parallel to the surface and rotates in the surface plane, sometimes changing rotation direction; (iv) the cell transitions from a horizontal orientation (parallel to the surface) to upright, rotating faster when it stands upright; (v) the cell rotates while upright then lies down, rotating slowly when parallel to the surface (reverse of (iv)); (vi) the cell stands upright and rotates then detaches from the surface; (vii) the cell swims down to the surface and attaches in an upright position (reverse of (vi)); (viii) the cell continuously rotates in an upright position; (ix) the cell lies at the surface then detaches horizontally; (x) the cell swims parallel to the surface and then attaches in the horizontal position.

Observations of P. aeruginosa show that they often spin in a horizontal or a vertical position, but sometimes spin at an angle. They can change their orientation with respect to the surface during spinning, and generally attach in an upright position. Vibrio cholerae generally do not spin after attachment to the surface and they usually attach and detach in a horizontal position. They use two different modes of near-surface swimming motility to decide where to form microcolonies [25]. Shewanella oneidensis show intermediate behaviour between P. aeruginosa and V. cholerae behaviour: they show mostly horizontal spinning but also spin vertically before detachment. This intermediate behaviour is consistent with our observation that the head shape of S. oneidensis is slightly curved, lying between the curved V. cholerae shape and the straight P. aeruginosa shape.

3. The model

We develop a hydrodynamic model that considers the torque on the flagellum, the extent to which the flagellar filament is bound to the surface (varying between attachment of the tip of the flagellum to attachment of the entire filament), the angle of the cell body with respect to the surface and the shape of the cell.

We model the flagellum as a helical filament, and the head as a rod with helical curvature that is different for the three bacteria we consider here. Pseudomonas aeruginosa is straight, so we model the head as a cylinder; S. oneidensis is slightly curved and we model it as half a wavelength of a helix with a small helical radius; V. cholerae is more curved so we model it as half a wavelength of a helix with a larger helical radius. The Reynolds number is small so the torques are linear in the velocities and we can write the torque as a mobility matrix multiplied by the velocity vector; we use resistive force theory (RFT) to calculate each element of the mobility matrix for the head and the flagellum [25,28]. Previously, we used a similar model [25] to understand near-surface swimming of V. cholerae.

In RFT, as developed by Gray & Hancock [29], we consider the filament to be composed of many small cylindrical elements. The force on each element of length δl is decomposed into parallel and perpendicular directions with different resistance coefficients: 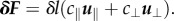The resistance coefficients for a helix near a boundary are given by Katz et al. [28]; these are 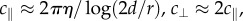where η is the bulk fluid viscosity, d is the height of the filament element above the boundary and r is the thickness of the filament. Lauga et al. successfully used RFT to explain how bacteria swim in circles close to a solid boundary and their theoretical results matched well with experiment [22].

Our model incorporates the fact that there is a flexible joint between the head and the flagellum and uses a bending potential to align the head with the flagellum with spring constant k_h. The flagellar motor exerts a torque Γ at the base of the head about the head direction which causes the flagellum to rotate with respect to the head. Part of the flagellum at the end furthest from the head is adhered to the surface and we consider the behaviour for different degrees of flagellar constraint.

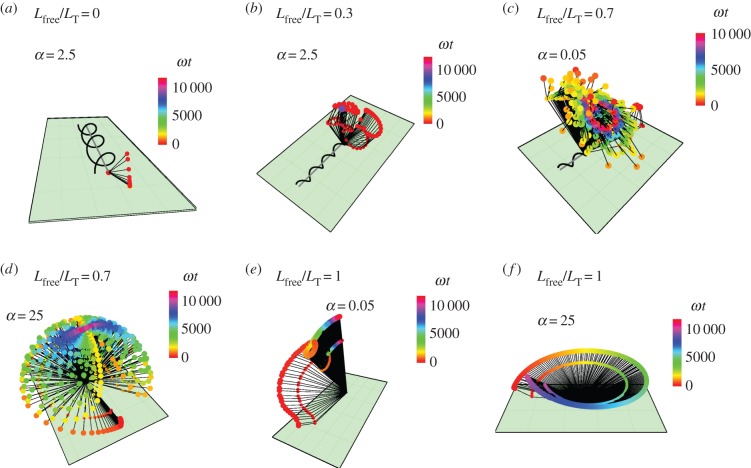
The model is shown in figure 1 where part of the helical flagellum is fixed to the surface and does not move. The remaining length of the flagellum can bend away from the fixed part and a bending potential acts to align the free part of the flagellum with the fixed part. We consider the flagellum as a bent elastic rod, so the spring constant varies with the free length of flagellum as 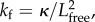where κ is constant and L_free is the free length of flagellum [30]. The geometric parameters are all defined in figure 1.

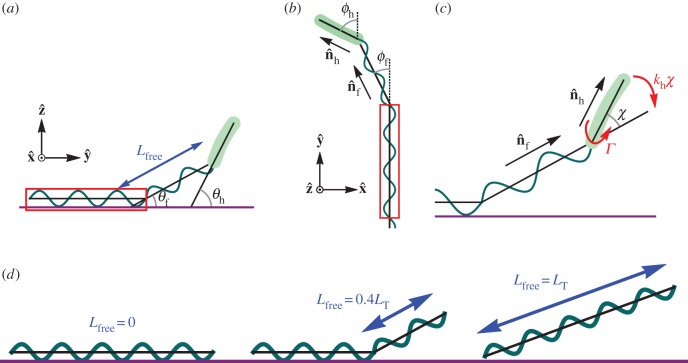
Figure 1.

Bacteria model with part of the flagellum attached to a surface. (a) Side view: the free part of the flagellum of length L_free makes an angle θ_f and the head makes an angle θ_h, with the surface. (b) Top view: the free part of the flagellum points in the direction 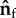and the head points in the direction 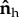. Projecting onto the surface plane, the free part of the flagellum makes an angle ϕ_f with the adhered part of the flagellum (which we define as the 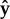-axis), and the head makes an angle ϕ_h with the 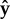-axis. (c) The flagellar motor rotates the head with respect to the flagellum and exerts a torque Γ. The head makes an angle χ with the free part of the flagellum and a bending potential acts with torque k_hχ to align the head with the flagellum. The part of the flagellum that adheres to the surface is highlighted by red boxes. The section of the flagellum inside the boxes cannot move. (d) Examples showing different values of the parameter L_free. The adhered section of the flagellum lies parallel to the surface (shown in purple) and the free part of the flagellum makes an angle with the surface. The flagellum is made up of two helices, the fixed helix and the free helix, linked by a bending potential.

The flagellar motor exerts a torque that rotates the flagellum counterclockwise (CCW) relative to the head. Since the flagellum is constrained by the surface, the motor rotates the head clockwise (CW). The total torque on the head cell head is

3.1

where M_h is the mobility matrix of the head describing the viscous resistance of the fluid, v_h is the angular velocity of the head, Γ is the torque exerted by the flagellar motor and k_h is the spring constant of the torsional spring between the head and the flagellum which mimics the flagellar hook. We calculate the mobility matrix using both RFT and results for a rotating cylinder near a wall [28,29,31].

The total torque on the free part of the flagellum is

3.2

where Λ is the constraint imposed by the fixed part of the flagellum that prevents the flagellum from spinning about its own axis. We solve for the angular velocities of the free part of the flagellum and the cell head using the torque-free condition on the head and the torque-free condition on the combined head and flagellum in the directions perpendicular to the constraining torque. We consider steric effects by including a short-range repulsive potential between the bacterium and the surface. We also consider the case where the flagellum is constrained only by a point at its end, so it can rotate about its own axis (an additional degree of freedom) but cannot translate.

We use the following geometric parameters based on observations of the different bacteria. Flagellum wavelength: 2 µm; total flagellum length: 10 µm; flagellum filament radius: 0.02 µm; flagellum helix radius: 0.4 µm; head filament radius: 0.3 µm; P. aeruginosa head length: 3 µm; S. oneidensis head wavelength: 6 µm, with total head length: 3 µm; S. oneidensis head helix radius: 0.1 µm; V. cholerae head wavelength: 4.4 µm, with total head length: 2.2 µm; V. cholerae head helix radius: 0.4 µm. We choose κ/Γ = 40 and let L_free vary between 0 and L_T, where L_T is the total flagellum length. We define α = k_h/Γ which is the ratio between the stiffness of the spring that aligns the head with the flagellum and the torque exerted by the flagellar motor and we vary α between 0.05 and 25. The inverse of α is the stall angular displacement between the head and the free part of the flagellum. The results are shown in terms of a hydrodynamic frequency 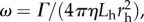where L_h is the head length and r_h is the radius of the head filament for each species; this is the angular velocity of a cylinder of radius r_h and length L_h rotated by torque Γ in bulk fluid of viscosity η. Using a flagellar motor torque of 2 × 10⁻¹⁸ Nm [14], gives the hydrodynamic frequency ω ∼ 600 rad s⁻¹ for our model. Importantly, we find that the behaviour depends on the ratios k_f/Γ and k_h/Γ.

4. Results

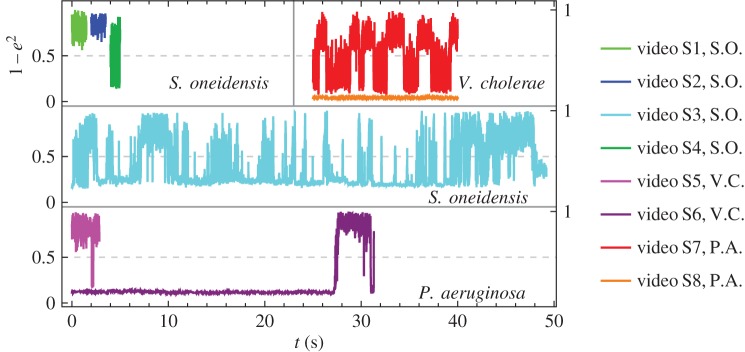
Our experimental observations are shown in electronic supplementary material, videos S1–S8. The tilt angle of the bacteria in each video is shown in figure 2. We compare our model with the experimental results for the different head curvatures that we consider.

Figure 2.

Normalized tilt angles from experimental observations versus real time, calculated as 1−e², where e is eccentricity of a fitted ellipse (see the electronic supplementary material). When the value approaches 0, the bacterium is in a horizontal orientation; when the value approaches 1, the bacterium is in a vertical position. Each colour corresponds to a different video and the species is indicated by the initials in the legend.

4.1. Shewanella oneidensis

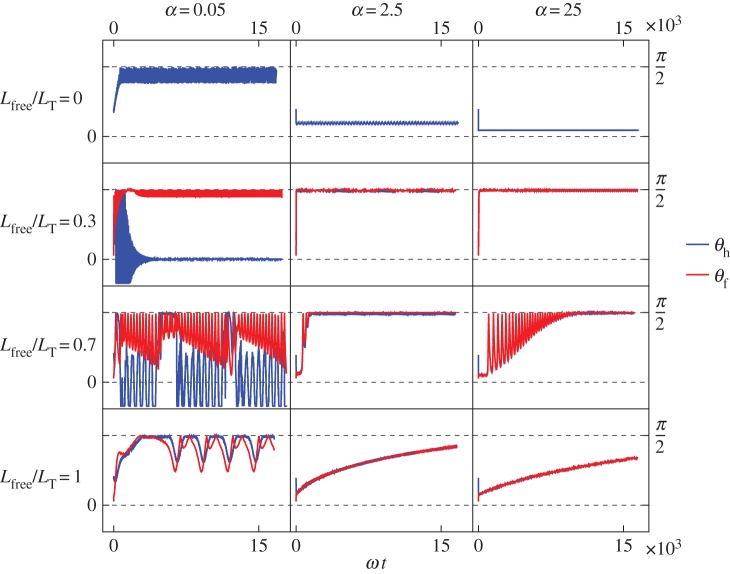
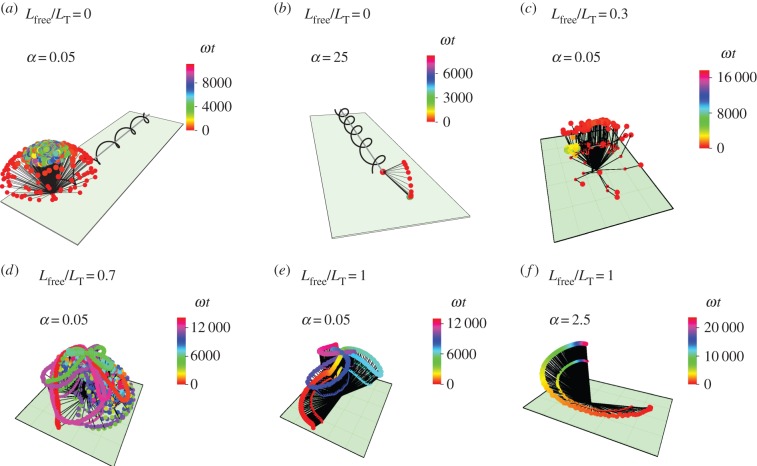
In experimental observations, S. oneidensis sometimes stays close to the surface and sometimes stands upright and rotates about the 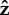-axis. In figure 3, we show the model results for orientations of the flagellum and the head, for different flagellar constraints and for different values of k_h. The three-dimensional trajectories in figure 4 show examples of the some of the different behaviours we have identified.

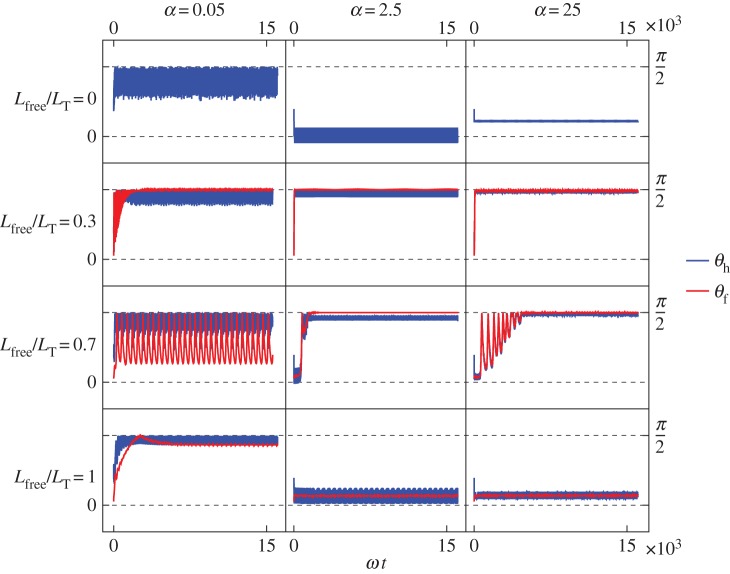
Figure 3.

Shewanella oneidensis model angles with the surface: (blue) angle between the head and the surface; (red) angle between the free part of the flagellum and the surface. From top to bottom row: L_free/L_T = 0, so the flagellum is completely adhered to surface; L_free/L_T = 0.3; L_free/L_T = 0.7; L_free/L_T = 1, so the flagellum is adhered only by the point at its end so it is completely free to rotate but cannot translate. From left column to right column: α = 0.05, α = 2.5, α = 25, where α is the ratio of the head spring constant and the flagellar motor torque.

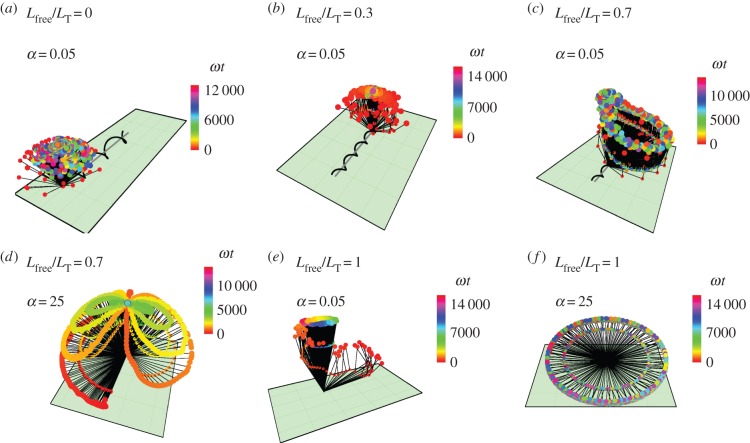
Figure 4.

Trajectories of S. oneidensis model with partially constrained flagellum. (a) L_free/L_T = 0 (flagellum completely adhered) and α = 0.05; (b) L_free/L_T = 0 and α = 25; (c) L_free/L_T = 0.3 and α = 0.05; (d) L_free/L_T = 0.7 and α = 0.05; (e) L_free/L_T = 1 (flagellum completely free) and α = 0.05; (f) L_free/L_T = 1 and α = 2.5. α is the ratio of the head spring constant and the flagellar motor torque. The black lines represent the axis of the head and the flagellum at snapshots in time. The end of the flagellum at each snapshot is shown by a small coloured spot and the end of the head is shown by a larger coloured spot. The colours correspond to the time of the snapshot, indicated by a colour scale bar for each trajectory.

In many of the cases where the flagellum is partially constrained, 0 < L_free < L_T shown in the middle rows of figure 3, the free part of the flagellum stands upright and makes an angle π/2 with the surface. When α = 2.5 or 25, the head aligns with the flagellum and also makes an angle π/2 with the surface. (Small α corresponds to a large torque or a flexible hook and large α corresponds to a small torque or a stiff hook.)

When the flagellum is completely adhered, L_free = 0 (top row of figure 3), the behaviour depends on α. The top row of figure 3 shows that when α = 0.05, the angle of the cell head has large oscillations and when α = 2.5 or 25, the head makes a small angle with the surface which we find to depend on the strength of surface repulsion. We see another important difference in behaviour when we consider rotation about the 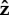-axis, which is shown in figure 4a,b). We find that for α = 0.05 (figure 4a), the cell head rotates about the 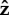-axis as well as spinning about its own axis but for α = 2.5 or 25 (figure 4b), the head does not rotate about the 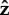-axis and just spins about its own axis while pointing in a fixed direction.

If the flagellum is completely free to rotate, L_free = L_T shown in the top row of figure 3, then for α = 2.5 or 25 the bacterium slowly stands upright at a rate that decreases with increasing α. The head and flagellum rotate slowly about the 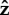-axis as they move into an upright position. When α = 0.05, the head and the flagellum align and the angle they make with the surface oscillates. There is also rotation about the 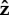-axis, resulting in the interesting trajectory shown in figure 4e.

We compare the model trajectories with experimental observations shown in electronic supplementary material, videos S1–S4, which show many of the behaviours predicted by the model. We do not observe every behaviour that is produced by the model because some of the parameters we use in the model are outside of the bacterial parameter range.

In electronic supplementary material, video S1, the cell rotates quickly about its body axis in a vertical position. We see this behaviour in the model when α = 2.5 or 25 (more rigid hook small motor torque) and the flagellum is not completely adhered nor completely free (middle rows of figure 3, middle and right columns). In electronic supplementary material, video S2, the cell orients in a vertical position and wobbles about the long axis. The motion in electronic supplementary material, video S1, without the wobbling is more common. The tilt angles from electronic supplementary material, videos S1 and S2, are shown in light green and dark blue in the top left panel of figure 2, showing the vertical orientation.

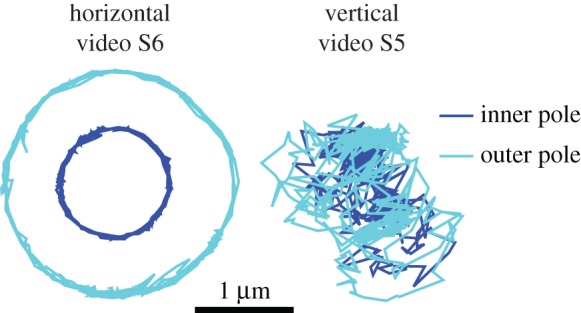
A variety of behaviours is shown in the longer electronic supplementary material, video S3. The cell rotates in vertical, horizontal and tilted positions and we see different spinning velocities. When the cell is horizontal, it can vibrate back and forth without full rotation and our model suggests that this happens when the flagellum is completely adhered. We use image analysis to look at the position of the cell poles to see if the observed behaviour is consistent with this prediction that the flagellum is completely adhered. Figure 5 shows the position of the cell poles during the various types of behaviour we see in electronic supplementary material, video S3. We see that when the cell is horizontal, there is very little movement of the inside pole, suggesting that the flagellum is not moving. Electronic supplementary material, video S3, also includes periods of nutations, a nodding motion highlighted in electronic supplementary material, video S4, where the cell oscillates between vertical and horizontal orientation while also rotating about the -axis. The model shows nutation behaviour when α = 0.05 and most or all of the flagellum is free. Figure 5 shows that there is some movement of the inside pole during nutations or vertical spinning, indicating that the flagellum is not completely adhered, as predicted by the model.

Figure 5.

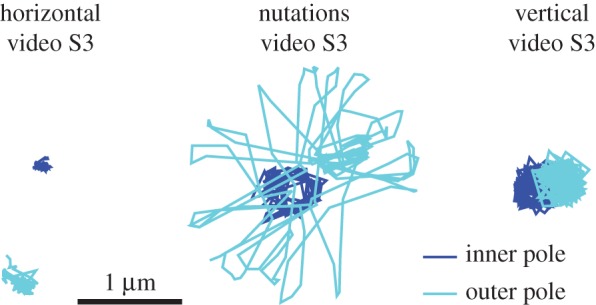
Position of poles during different behaviours observed in S. oneidensis. The poles are the foci of the fitted ellipses used in image analysis (see the electronic supplementary material).

Our model suggests that the changes in behaviours in electronic supplementary material, video S3, is produced by changes in the torque exerted by the flagellar motor and changes in how much of the flagellum is adhered to the surface.

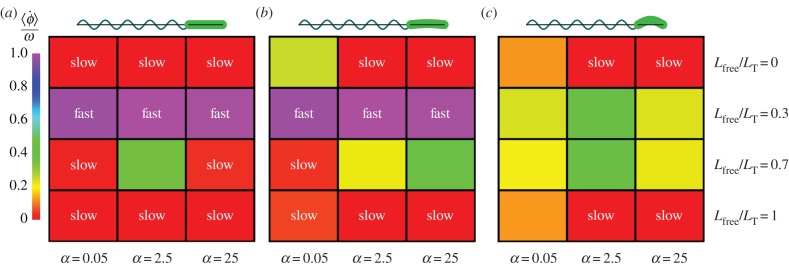
The angular velocities of the S. oneidensis model about the -axis are shown in figure 6b. The angular velocity about is faster when the cell stands upright and there is less viscous resistance from the surface and movement in the perpendicular direction to the head filament is reduced. The angular velocities for the corresponding models of P. aeruginosa and V. cholerae are also shown in figure 6a,c. The fastest angular velocity is observed for P. aeruginosa, which has a straight head, when it is in an upright configuration. Figure 7 shows the angles that the head and flagellum make with the surface.

Figure 6.

Average angular velocities about 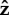-axis, 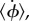in units of hydrodynamic frequency ω for hydrodynamic model of (a) P. aeruginosa, (b) S. oneidensis and (c) V. cholerae, corresponding to the trajectories shown in (a) figure 10, (b) figure 3 and (b) figure 7. The colour indicates the average angular velocity for each choice of α and L_free/L_T. α is the ratio of the head spring constant and the flagellar motor torque. A sketch of the corresponding bacterium shape is shown above each part of the figure.

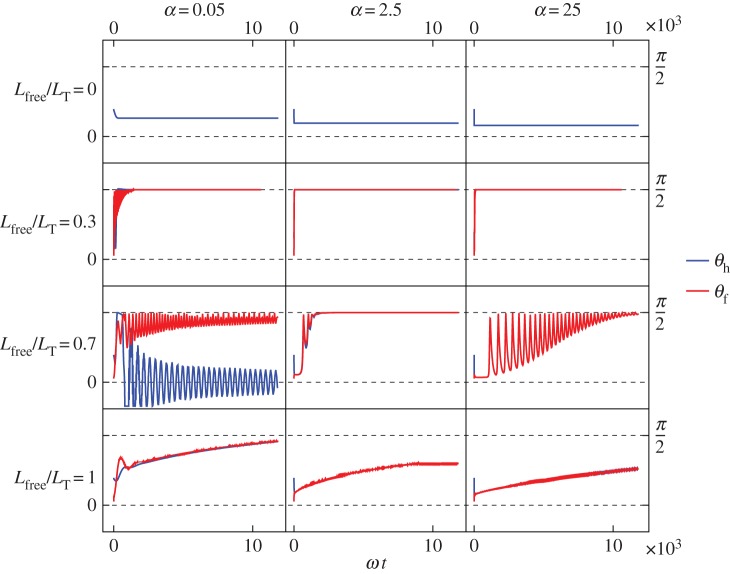
Figure 7.

Vibrio cholerae model: angles between the free part of the flagellum and the surface (red) and the cell head and the surface (blue). From top to bottom row: L_free/L_T = 0, so the flagellum is completely adhered to surface; L_free/L_T = 0.3; L_free/L_T = 0.7; L_free/L_T = 1, so the flagellum is adhered only by the point at its end and is completely free to rotate but cannot translate. From left column to right column: α = 0.05, α = 2.5, α = 25, where α is the ratio of the head spring constant and the flagellar motor torque.

4.2. Vibrio cholerae

Vibrio cholerae has a head that is more curved so we increase the helix radius of the head in the hydrodynamic model. Many general features of the model's behaviour are the same as for the S. oneidensis model. However, from the bottom row of figure 7, we see an additional behaviour for the completely free flagellum case, L_free = L_T, that the model did not show for the parameter range used with the S. oneidensis model: rotation about the 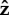-axis, while the angle between the bacterium and the surface remains small; we observe this behaviour when α = 2.5 or 25. This behaviour is shown in figure 8f alongside other examples of the behaviours we find in the model for V. cholerae. This additional horizontal behaviour is consistent with our observation that V. cholerae prefers to stay horizontal when attached to a surface. Experimental observations of V. cholerae are shown in electronic supplementary material, videos S5 and S6. The bottom panel of figure 2 shows that during observations, V. cholerae spent more time in the horizontal orientation.

Figure 8.

A selection of trajectories from the V. cholerae model with a partially adhered flagellum. (a) L_free/L_T = 0 (flagellum completely adhered) and α = 0.05; (b) L_free/L_T = 0.3 and α = 0.05; (c) L_free/L_T = 0.7 and α = 0.05; (d) L_free/L_T = 0.7 and α = 25; (e) L_free/L_T = 1 (flagellum completely free, except at endpoint) and α = 0.05; (f) L_free/L_T = 1 and α = 25. α is the ratio of the head spring constant and the flagellar motor torque. The black lines represent the axis of the head and the flagellum at snapshots in time. The end of the flagellum at each snapshot is shown by a small coloured spot and the end of the head is shown by a larger coloured spot, where the colours correspond to the time of the snapshot.

The angular velocities about the 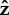-axis are shown in figure 6c. We observe that the average velocity is faster when the bacterium stands upright, which is also the case for the other bacterium shapes we consider here. However, the maximum angular velocity in the vertical orientation is slower than the maximum for S. oneidensis and P. aeruginosa with the same parameters α and L_free because of the additional friction from the large curvature of V. cholerae.

In electronic supplementary material, video S5, the V. cholerae cell spins with a vertical orientation with a large angular velocity. We find that V. cholerae does not spend much time spinning with this upright orientation. The model produces this vertical spinning when the flagellum is neither completely adhered nor completely free, shown in the middle two rows of figure 7. Electronic supplementary material, video S6, shows motion where the cell is mostly in a horizontal orientation. The cell rotates about the surface normal near one of the cell poles and there are changes in rotation direction, corresponding to changes in the flagellar motor direction. Sometimes there are pauses in the rotation and the cell vibrates without completing full rotations. Figure 9 shows the position of the poles during the vertical spinning in electronic supplementary material, video S5, and the horizontal spinning in electronic supplementary material, video S6. During vertical spinning, the inner pole moves a lot indicating that part of the flagellum is free, consistent with the model's prediction in the middle rows of figure 7.

Figure 9.

Position of poles during different behaviours observed in V. cholerae.

In the model, horizontal spinning is produced when α = 2.5 or 25 and the flagellum is completely free, and horizontal vibrations without full rotations are produced when α = 2.5 or 25 and the flagellum is completely adhered. During electronic supplementary material, video S6, the cell spends most of the time spinning horizontally. Towards the end of electronic supplementary material, video S6, the cell transitions to a vertical orientation with fast spinning about its body axis; the cell moves back to a horizontal position before detachment from the surface. This fits with our model, where a transition from partially adhered flagellum to completely free flagellum before detachment causes a transition from vertical spinning to horizontal rotations.

4.3. Pseudomonas aeruginosa

We use a cylinder to model the straight head of P. aeruginosa. Figure 10 shows the angles that the head and free part of the flagellum make with the surface in the P. aeruginosa model. The main features in behaviour in the model are also observed in the S. oneidensis (small curvature) and V. cholerae (large curvature) models. Experimental observations of P. aeruginosa are shown in electronic supplementary material, videos S7 and S8.

Figure 10.

Pseudomonas aeruginosa model: angles between the free part of the flagellum and the surface (red) and the head and the surface (blue). From top to bottom row: L_free/L_T = 0, so the flagellum is completely adhered to surface; L_free/L_T = 0.3; L_free/L_T = 0.7; L_free/L_T = 1, so the flagellum is adhered only by the point at its end and is completely free to rotate but cannot translate. From left column to right column: α = 0.05, α = 2.5, α = 25, where α is the ratio of the head spring constant and the flagellar motor torque.

When the flagellum is completely adhered in the model, the head stays close to the surface and does not rotate about the 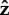-axis, as shown in figure 11a. When a small part of the flagellum is free, both the head and the flagellum stand upright, making an angle π/2 with the surface, as shown in figure 11b (the red part of the figure shows the motion from the initial condition to the preferred upright configuration).

Figure 11.

A selection of trajectories for the P. aeruginosa model with partially adhered flagellum. (a) L_free/L_T = 0 and α = 2.5; (b) L_free/L_T = 0.3 and α = 2.5; (c) L_free/L_T = 0.7 and α = 0.05; (d) L_free/L_T = 0.7 and α = 25; (e) L_free/L_T = 1 and α = 0.05; (f) L_free/L_T = 1 and α = 25. The black lines represent the axis of the head and the flagellum at snapshots in time. The end of the flagellum at each snapshot is shown by a small coloured spot and the end of the head is shown by a larger coloured spot, where the colours correspond to the time of the snapshot.

When a large proportion of the flagellum is free, for α = 2.5 or 25, there are oscillations in the surface angle before the cell stands upright (on different timescales). As shown in figure 11d, during the oscillatory stage, the bacterium also moves about the 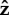-axis and follows a figure of eight trajectory, until it is in the upright position. For α = 0.05, the flagellum stands upright, with small oscillations in the angle, and the head angle oscillates about a parallel orientation to the surface and is kept sufficiently far from the surface by the upright flagellum, as shown in figure 11c.

When the flagellum is completely free to rotate, the cell stands up slowly. There is very little rotation about the 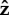-axis when α = 0.05, as shown in figure 11e. When α = 2.5 or 25, the bacterium slowly rotates about as it stands up, as shown for α = 25 in figure 11f.

Electronic supplementary material, video S7, shows horizontal, tilted and vertical spinning. We observe that the transitions between horizontal and vertical spinning occur when there is a change in rotation direction. Our model suggests that this could be because of asymmetry in the torque exerted by the flagellar motor between CW and CCW rotation, or there could be a change in how much of the flagellum is adhered to the surface when the motor reverses direction. Figure 12 shows the positions of the cell poles in different behaviours identified in electronic supplementary material, videos S7 and S8. During the vertical spinning in electronic supplementary material, video S7, there is very little movement of the inside pole, suggesting that the free part of the flagellum is also oriented vertically, as predicted by the model when a large fraction of the flagellum is adhered to the surface (see second row of figure 10).

Figure 12.

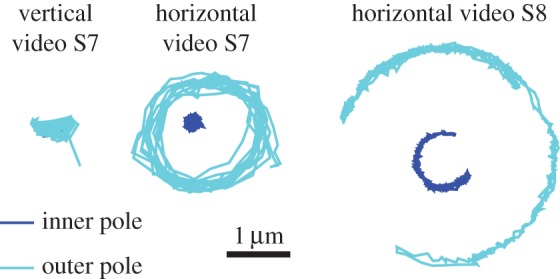
Position of poles during different behaviours observed in P. aeruginosa.

Electronic supplementary material, video S8, shows a cell in a horizontal orientation but instead of rotating fully it partially rotates and vibrates. The model produces the horizontal vibrating motion when the flagellum is completely adhered for all choices of α we have considered here. The experimental results in figure 12 show rotation of the inner pole in the opposite direction of the outer pole, suggesting that the flagellum is attached to the body slightly to the side of the inner pole. In future work, we will study the details of the flagella using fluorescence staining and compare the results with our model.

4.4. Detachment

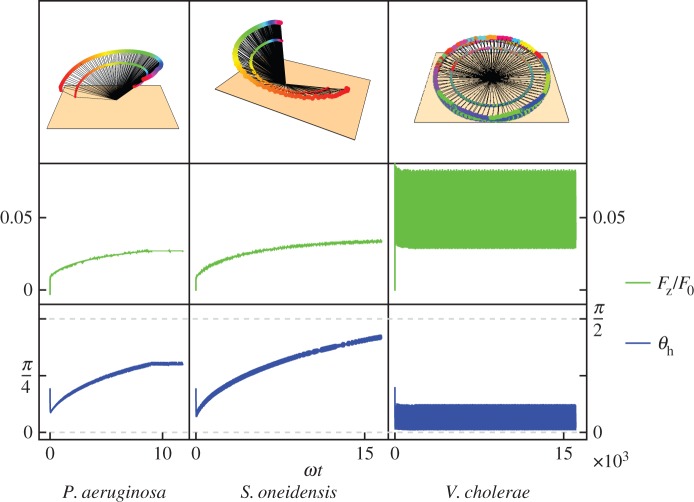
We consider the magnitude of the force acting away from the surface when the flagellum is only attached by a point at the end, the configuration immediately before detachment. Figure 13 shows the upwards force on the bacterium for the three species of different curvatures. We show the results when α = 2.5 since this value lies within the realistic range of values; the results for α = 25 are similar.

Figure 13.

Vertical force (middle row, green) on the bacterium when the flagellum is only attached by a point at its end, with corresponding orientations (bottom row, blue) and trajectories (top row). Increasing curvature goes from left to right: P. aeruginosa, S. oneidensis, V. cholerae. The vertical force increases as the head–surface angle increases for P. aeruginosa and S. oneidensis, for V. cholerae the angle oscillates at small values, so the force oscillates but at a higher value. The force is shown in units of F₀ = Γ/r_h ∼10 pN, the ratio of the torque exerted by the flagellar motor and the radius of the head.

The upwards force increases with angle and with head curvature. Pseudomonas aeruginosa and S. oneidensis have very small upwards forces when they are oriented horizontally. As the angle between the bacterium and the surface increases, the upwards force also increases. This suggests that these bacteria need to orient vertically or at a small angle from the vertical to get enough upwards force in order to detach. However, V. cholerae has higher curvature and converts more of its spinning torque into force, so even in a horizontal orientation it generates enough upwards force to detach.

5. Discussion

We have observed and described spinning motility in three different bacteria—S. oneidensis, V. cholerae and P. aeruginosa—which occurs during early biofilm development. Our hydrodynamic model considers different degrees of constraint on the flagellum: (1) the flagellum is completely attached to the surface, (2) the flagellum is partially attached with bending between free and constrained parts of the flagellum, and (3) the flagellum is completely free to rotate but attached at the end (preventing translation), consistent with the empirical observation of no movement across the surface. We have used RFT because it is fast and straightforward to compute, and although higher order methods might reveal further interesting features in the behaviour, our aim is to demonstrate that the different observed behaviour arise from hydrodynamics, and we have done this successfully at low order.

The model shows different types of behaviour when the proportion of the flagellum adhered to the surface is varied and when the ratio of hook stiffness and motor torque is varied. We do not know of evidence to suggest that the flexibility of the flagellar hook, which determines k_h, varies much between cells of a particular species. However, it has been observed that the output of the flagellum motor can be altered via addition of different stators [32]. Features in the spinning motility that we observed are produced in our model. Behaviours that arise in the model but are not observed suggest that the bacteria do not operate in the parameter ranges which give these other behaviours. The behaviour we observe in experiments corresponds to the model when α = 2.5 or 25, which we expect since the hook needs to be rigid enough to avoid buckling during forwards swimming. Buckling under compression occurs above a critical loading force 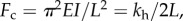where EI is the bending stiffness and L is the length of the flagellar hook [33]. The bending stiffness of the hook in Vibrio alginolyticus during forward swimming is reported to be 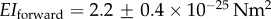in [34] and is sufficient to avoid buckling during forward swimming (although buckling is observed after reversals of the motor which unwinds the hook, reducing its stiffness by almost an order of magnitude). The length of the flagellar hook in different species of bacteria is in the range 50–100 nm [35]. Using the stiffness reported for V. alginolyticus in our model gives a value of 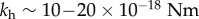, and with 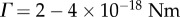[14], this gives the value α = 2.5−10, lying within the range of the two values we used in our model that give the observed behaviours.

Changes in the head curvature produce changes in behaviour for some choices of parameters, particularly when the whole flagellum is free or the hook is flexible and the torque is large, but the three curvatures show a similar range of behaviours over the other parameters we have considered. Differences in behaviour between the types of bacteria could be a result of different hook flexibilities and exerted motor torques in the different species. Our model also shows that different observed rotation speeds could be a result of different torques. However, they could also result from the angle between the bacterium and the surface, the adhered fraction of the flagellum, the shape of the head and the flexibility of the hook. We find that rotation about the vertical axis at a fixed motor torque is slower when the cell makes a small angle with the surface than when the cell stands upright. The maximum rotational velocities at a fixed motor torque are smaller for V. cholerae than for P. aeruginosa and S. oneidensis because V. cholerae is more curved.

There are two distinct timescales in our model: the fast timescale associated with the head spinning about its axis, 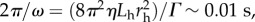and the slow relaxation timescale associated with the cell orienting from its initial condition to its preferred angle with the surface. The slower timescale has a range over three orders of magnitude, from as short as 0.04 s (only approx. four head rotations), for example when L_free/L_T = 0.3 and α = 2.5 or 25 for all bacteria to as long as 20 s (approx. 2000 head rotations), for example in P. aeruginosa when L_free/L_T = 0.7 and α = 25. If the motor reverses direction, then during the time that the torque is close to zero during the switch, we could see a change in the behaviour if the relaxation is fast. However, if the relaxation is slower than the switching of the motor, we will not see the effect of the small torque during the switch and only see the reversal of the direction of motion. The relaxation timescale is sensitive to the fraction of flagellum that is adhered to the surface.

As a test of this model, we examine whether there are situations where the model is predictive rather than descriptive. Interestingly, the model predicts that head curvature impacts the behaviour of detachment. During the detachment sequence, the flagellum will progressively decrease its adhesion on the surface and is only attached at its endpoint immediately before complete detachment. When the flagellum is completely free to rotate and only attached by its endpoint, then head curvature has an especially significant impact on the behaviour. The model predicts that V. cholerae should leave the surface in a horizontal position and that P. aeruginosa and S. oneidensis should detach at an angle closer to vertical. Indeed, we observe that V. cholerae can detach in a horizontal orientation, while P. aeruginosa and S. oneidensis generally detach in a more vertical orientation.

We have used our model to consider the upwards force on the different bacteria before complete detachment. Vibrio cholerae has a larger curvature and converts more of its spinning torque into force, so an upwards force acts even when the bacteria are horizontally oriented, allowing horizontal detachment. Pseudomonas aeruginosa and S. oneidensis are less curved and convert less torque into force. They have a smaller upwards force which increases with the angle between the bacterium and the surface. They are more likely to detach when they are at an angle close to the vertical when the upward force is larger.

Transitions between the different types of spinning behaviour in the model occur when there is a change in the fraction of the flagellum that is adhered to the surface. Changes in rotation direction are a consequence of the flagellar motor reversing its direction. If the motor changes the magnitude of the torque it exerts, then transitions in behaviour can occur: if the torque increases, then α decreases and the first two columns of figures 3, 7 and 10 show that this can cause a transition from vertical spinning to oscillations in the orientations of the head and the flagellum at the same time as rotation about the vertical axis.

6. Material and methods

Shewanella oneidensis strain MR-1 (wild-type, WT), V. cholerae strain WT O1 Serotype, El tor Biotype, A1552, and P. aeruginosa strain PA14 WT were used in this study. Vibrio cholerae were cultured in full strength Luria–Bertani (LB) broth overnight under shaking at 30°C. Prior to inoculation, the overnight culture was diluted into 2% LB (containing 171 mM sodium chloride) to an optical density at 600 nm (OD₆₀₀) in the range 0.01–0.03. Bacteria were then injected into a sterile flow cell containing the same 2% LB. Pseudomonas aeruginosa were cultured in M63 medium supplemented with 1 mM magnesium sulfate, 0.2% glucose and 0.5% casamino acids (CAA) overnight under shaking at 37°C. M63 medium contained (per litre of deionized water) 3 g potassium phosphate monobasic, 7 g potassium phosphate dibasic and 2 g ammonium sulfate. Then, a 1 : 50 dilution of cell culture was subcultured in the same medium and grown to an OD₆₀₀ of 0.4. The cell culture was then diluted to an OD₆₀₀ in the range 0.01–0.03 and injected into a sterile flow cell containing M63 supplemented with 1 mM magnesium sulfate, 0.05% glucose and 0.125% CAA. Shewanella oneidensis were cultured in LB broth overnight under shaking at 30°C. The cells from this culture were pelleted via centrifugation at 2300g for 5 min, washed twice and finally resuspended in a chemically defined medium. This medium contained (per litre of deionized water) 15.1 g PIPES buffer, 3.4 g sodium hydroxide, 1.5 g ammonium chloride, 0.1 g potassium chloride, 0.6 g sodium phosphate monobasic monohydrate, 18 mM of either sodium l-lactate or sodium dl-lactate (112.1 g mol⁻¹) as an electron donor, 10 ml of 100× amino acids stock solution, 10 ml of 100× minerals stock solution and 1 ml of 1000× vitamins stock solution. The 100× amino acids stock solution contained (per litre of deionized water) 2 g l-glutamic acid, 2 g l-arginine and 2 g dl-serine. The 100× minerals stock solution contained (per litre of deionized water) 1.5 g nitrilotriacetic acid, 3 g magnesium sulfate heptahydrate, 0.5 g manganese sulfate monohydrate, 1 g sodium chloride, 0.1 g ferrous sulfate heptahydrate, 0.1 g calcium chloride dihydrate, 0.1 g cobalt chloride hexahydrate, 0.13 g zinc chloride, 10 mg cupric sulfate pentahydrate, 10 mg aluminium potassium disulfate dodecahydrate, 10 mg boric acid, 25 mg sodium molybdate dihydrate, 24 mg nickel chloride hexahydrate and 25 mg sodium tungstate. The 1000× vitamins stock solution contained (per litre of deionized water) 20 mg biotin, 20 mg folic acid, 100 mg pyridoxine hydrochloride, 50 mg riboflavin, 50 mg thiamine hydrochloride, 50 mg nicotinic acid, 50 mg d-pantothenic acid hemicalcium salt, 1 mg vitamin B12, 50 mg P-aminobenzoic acid and 50 mg dl-α-lipoic acid. The medium was adjusted to an initial pH of 7.0. The culture in this chemically defined medium was grown again overnight under shaking at 30°C. The culture was then diluted to an OD₆₀₀ in the range 0.01–0.03 and injected into a sterile flow cell containing the same chemically defined medium.

Authors' contributions

R.R.B. and R.G. conducted the theoretical work. C.K.L., J.D.A. and G.C.L.W. performed the experiments. K.H.W., F.H.Y. and G.O.T. provided the bacterial strains. R.R.B., C.K.L., J.D.A., G.O.T., G.C.L.W. and R.G. wrote the paper.

Competing interests

We declare we have no competing interests.

Funding

We acknowledge support from HFSP (RGP0061/2013), the EPSRC, the Office of Naval Research grant N000141410051, National Institutes of Health grant R01 2 R37 AI83256-06 to G.A.O. and NIH grant AI102584 to F.H.Y.