Abstract
The shape of the non-linear relationship between temperature and mortality varies among cities with different climatic conditions. There has been little examination of how these curves change over space and time. We evaluated the short-term effects of hot and cold temperatures on daily mortality over six 7-years periods in 211 US cities, comprising over 42 million deaths. Cluster analysis was used to group the cities according to similar temperatures and relative humidity. Temperature-mortality functions were calculated using B-splines to model the heat effect (lag 0) and the cold effect on mortality (moving average lag 1-5). The functions were then combined through meta-smoothing and subsequently analyzed by meta-regression. We identified eight clusters. At lag 0, Cluster 5 (West Coast) had a RR of 1.14 (95% CI: 1.11,1.17) for temperatures of 27°C vs 15.6 °C, and Cluster 6 (Gulf Coast) has a RR of 1.04 (95% CI: 1.03,1.05), suggesting that people are acclimated to their respective climates. Controlling for cluster effect in the multivariate-meta regression we found that across the US, the excess mortality from a 24-hr temperature of 27°C decreased over time from 10.6% to 0.9%. We found that the overall risk due to the heat effect is significantly affected by summer temperature mean and air condition usage, which could be a potential predictor in building climate-change scenarios.
Keywords: climate change, health effects, temperature, meta-smoothing
Introduction
The relationship between temperature and non-accidental mortality with subsequent identification of vulnerable populations at risk is currently being investigated by public health specialists worldwide (Analitis et al 2008; Anderson and Bell 2011; Basu and Ostro 2008; Medina-Ramón and Schwartz 2007; Zanobetti et al 2012). The nature of this relationship varies depending on the geographical location and socio-economic status of affected populations (Braga et al 2001b; Hajat and Kosatky 2010; Yu et al 2010). A key issue is what dose-response curve to use for the acute effects of temperature in estimating the potential impacts of climate change.
Some studies have assumed the dose- response relationship will stay constant over time (Peng et al 2011; Voorhees et al 2011). However, cross-sectional observations contradict this in finding. In US cities that are currently warmer in the summer, higher temperatures are needed to produce the same percentage increase in mortality as occurs at less extreme temperatures in locations with milder climates. One could alternatively choose to assess the effect of e.g. a 2°C increase in mean temperature in one city by using a dose-response curve from a city that has already attained that temperature. However that assumes fairly rapid acclimatization to the new temperature régime, and the cross-sectional data provides no information on how likely that is. Clearly a more detailed assessment of how dose-response curves vary by temperature régime and how fast they change is needed to provide reasonable estimates of future risk.
A small number of studies have addressed this question. For example, in a recent paper, Deschênes and Greenstone estimated the impacts of climate change on mortality and expenditures on self-protection or adaptation using economic models. Their measure of self-protection is energy consumption, which via air conditioning (AC) is perhaps the primary form of protection against high temperatures. Their identification strategy relied on the presumed random year-to-year local variation in temperature (Deschênes and Greenstone 2011), but does not address acute episodes. Using an econometric model, Barreca et al. found that the mortality effect of an extremely hot day declined by approximately 80% between 1900-1959 and 1960-2004 in United States (Barreca et al 2013). However, that analysis was conducted at the state level, and with only monthly mortality statistics. Cunrui Huang et al. (Huang 2011) recently wrote an extensive review about projecting future heat-related mortality under climate change scenarios. In their conclusion they identified that significant differences in projected mortality can be found in different emissions scenarios, suggesting that greenhouse gas mitigation policies are important for protecting human health. They also acknowledged that further research is needed to provide a stronger theoretical framework for these types of projections, including better understanding of socioeconomic development, adaptation strategies and land-use patterns. The approaches commonly used in environmental epidemiology to study these effects are city-specific time series or case-crossover analysis (Braga et al 2001a; Curriero et al 2002). In these previously published studies, if temperature was estimated as a linear term both methods produce a parameter that expresses the logarithm of the incidence rate ratio after control for confounders, for each city included in the study. Coefficients from multiple cities can be combined into a single aggregate parameter using a univariate meta-analysis (Stieb et al 2002). However, complex associations including nonlinear J- or U-shaped relationships between temperature and mortality are usually described with functions defined by multiple parameters, and thus require more sophisticated meta-analytical approaches capable of handling the multivariate nature of the summary estimates. Moreover understanding drivers of change in response over time and adequate power for meta-regression requires more years of follow-up and more locations than have generally been reported (Gasparrini et al 2012). Astrom et al. (Astrom et al 2013) recently analyzed the relationship between extreme hot/cold temperatures and all-cause mortality, stratified by decade, sex, and age from 1901 to 2009 in Sweden. The paper focused exclusively on extreme temperatures. Specifically, the authors looked at changes in the effect above 98th percentile and below the 2nd percentile of temperature over time, and only in Stockholm. Interestingly, they found that the relative risk of total daily mortality due to heat extremes in all decades decreased linearly over time; decline in mortality with cold extremes over time was not found. Bobb and co-authors (Bobb et al 2014) recently examined heat-related mortality and found that the mortality risk decreased over time supporting the hypothesis that the population is continually adapting to heat. Also Guo and co-authors in their systematic evaluation recently reported that people have some ability to adapt to their local climate type, but both cold and hot temperatures are still associated with increased risk of mortality (Guo et al 2014).
In this study we examine the association between temperature and mortality over six 7-years periods in 211 cities in the United States, focusing particularly on changes over time, and across cities clustered by common weather patterns. Our study is not looking at extreme effects, but continuous effects of temperature, and more cities and for a longer time period than previous studies in the U.S.
We also explore the role of land use, air conditioning, etc. in predicting these changes. Several approaches to combining nonlinear curves have been proposed. Schwartz and Zanobetti proposed a method they called meta-smoothing that combined estimated effects at a series of exposures across multiple locations (Schwartz and Zanobetti 2000). Alternative methods involved combining coefficients at the knot points of splines, an approach recently updated and implemented in R through the mvmeta function (Gasparrini et al 2012). A disadvantage of this approach is that it is difficult to put the knot points at the same temperatures in cities with a wide range of climates, as in the US. To address this we initially identified clusters of cities with similar values of temperature and relative humidity and then created a large pooled exposure-response curve for each cluster. We subsequently studied how these curves changed over time and space from 1962 to 2006. Finally, using the same mvmeta function used for meta-smoothing to assess temperature risk on mortality, we performed a multivariate meta-regression analysis to assess how the risk estimates vary with potential meta-predictors, such as climatic and socio-economic variables, measured at the city level. This type of strategy could allow us to build a model to predict future fatalities, influenced by climate change in different US climate zones.
Material and Methods
Mortality data
We selected 211 US cities that had complete mortality and daily temperature (monitors that have at least 98% of the observations available) data with a nationwide geographic distribution (Figure 1). Analyses were conducted at the city level, which in most cases was restricted to a single county. However, we used multiple counties where the city's population extends beyond the boundaries of one county. Individual mortality data was obtained from the National Center for Health Statistics (NCHS) and from state public health departments. Data from 1967 to 1973 were not available because NCHS did not obtain date of death in those years. The mortality files provided information on the exact date of death and the underlying cause of death. For this study we selected all-cause daily mortality excluding any deaths from accidental causes (ICD-code 10th revision: V01-Y98, ICD-code 9th revision: 1-799). Overall, 42,471,868 deaths were included in the study.
Figure 1.
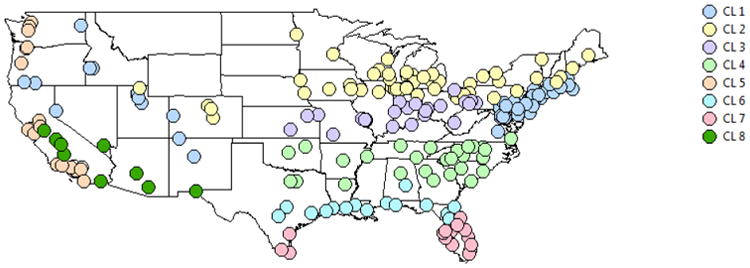
Map of the 211 cities in the U.S. corresponding to the cities included in the analysis grouped into 8 clusters.
Environmental data
Meteorological measurements were obtained from the airport weather stations nearest to each county, including daily mean temperature, wind speed, sea level pressure, visibility and dew point (National Oceanic and Atmospheric Administration [NOAA]). Relative humidity was calculated with the following formula:
where Ta represents air temperature and Td represents dew point temperature (Wanielista 1990). For days of the year where monitors had missing data, we used the values of the nearest monitor within 60 kilometers.
Socioeconomic and Land Use data
Because we are interested in factors which could potentially modify the association with temperature and particularly ones that might be modifiable, we have obtained data on socioeconomic, land use, and other factors. From the U.S. Census Summary File 3 downloaded from Social Explorer, we obtained population density, proportion of the population below poverty level, proportion of the population over 25 years of age (25+) who completed college, proportion of the population 25+ who did not complete high school, and proportion of black population for the 1960 – 2000 decennial censuses. Median family income in dollars for every ten years from 1959 to 1999 was obtained from US Census Historical Income Tables for Counties (http://www.census.gov/hhes/www/income/data/historical/county/). From the 1992 and 2001 National Land Cover datasets, available from the Multi-Resolution Land Characteristics Consortium (MRLC) and the Enhanced Historical Land Use, and Land Cover Data for 1970 – 1985 from US Geological Survey (USGS), we calculated proportion of land with green surface by county for three time periods. Green land uses include agriculture, forests, wetlands and grasslands. Census and land use data were merged to individuals based on their county of residence, we estimated percentage of households in each city with central air conditioning (AC) in 1970, 1980, 1990, and 2000 using available county level or metropolitan area level data. 1970 and 1980 county level AC data come from the US Census of Population. For later years metropolitan area data from the American Housing Survey (AHS) was used. 1990 and 2000 estimates were based on linearly interpolating data from available years which vary by city. For cities not included in the AHS, the nearest metropolitan area with available data was used. For northern New England cities, regional level data from the US Energy Information Administration, Office of Energy Consumption 2009 Residential Energy Consumption Survey were used.
Statistical analysis
Stage 1: Cluster Analysis
Cluster analysis was used to group together cities that shared common weather characteristics. The objective was to define groups of cities with similar weather patterns to increase the homogeneity within groups, while at the same time making meaningful distinctions between clusters. The variables included in the clusters analysis were the mean and standard deviation of the seasonal temperature and the relative humidity in each city. We used an agglomerative hierarchical approach: we started by defining each data point to be a cluster and then combined existing clusters at each step through the single linkage method. We used PROC CLUSTER in SAS 9.2 (Copyright © 2012 SAS Institute Inc., SAS Campus Drive, Cary, North Carolina 27513, USA).
Stage 2: City-Specific Poisson Regression
The relationship between daily mortality and temperature was estimated using an overdispersed Poisson generalized additive model (GAM). For each of the i = 1,…,c cities the model was given by the following:
| (1) |
where is the expected mortality rate for each city c on day t; β0 is the model intercept; yc is the vector of regression coefficients for day of the week for city c; DOWt is the categorical variable for day of the week; ns(timet) is a natural cubic spline of time, with 6 degrees of freedom per year. corresponds to ambient temperature on the day of death, and is the mean daily temperature over lag 1-5, computed as the moving average from day t-1 up to the previous 5 days. We have divided temperature this way because Braga (Braga 2002 et al) previously reported that the effects of cold weather persisted for about 5 days while the effects of hot temperatures were more immediate. Thus using temperature over six days, and separating out the immediate effect, seems reasonable. We used and to capture the heat and cold effect, respectively, where the θi are the coefficients of the splines. Both functions were chosen as a quadratic B-spline, defined by k-2 internal knots and 2 boundary knots, where k corresponds to the dimension of the spline basis and the number of parameters. Number and location of knots (within cluster) are chosen by Q-AIC, a modification of the Akaike information criterion for quasi-likelihood models (Peng et al 2006). In the first equation, the knot locations vary between clusters but do not vary within the same cluster. This requirement assures that the estimated coefficients θ̂i(lag0) and θ̂i(MA15) retain the same interpretation in all the studies belonging to the same cluster. We initially fit 211 GAM models, one for each city, considering the entire time series from 1962 to 2006. Secondly, we divided our analysis into specific time intervals: 1962-1966, 1973-1979, 1980-1986, 1987-1993, 1994-1999, and 2000-2006. We chose these years with enough years to produce stable results and reduce noise in the effect estimates but we also wanted enough categories to be able to detect changes over time. This modeling strategy defines the exposure on an absolute scale (°C). The two functions both labeled “s” common to all studies are coherently defined with knots placed at the same absolute exposure values so that the estimated coefficients have the same interpretation across studies. However, some have argued that it is the degree of unusualness that is central to the effect of temperature. For this reason, we conducted a sensitivity analysis where we converted the city-specific temperatures to city-specific percentiles of temperature. This method allows the comparison of studies showing even non-overlapping temperature ranges. Functions for non-linear associations are usually centered on a specific value so that the results may be interpreted as the effect of the exposure versus a reference (Cao et al 2006). To quantify effects of temperature changes, we centered the curves at 15.6°C (60 °F) following the strategy proposed by Anderson and colleagues (Anderson and Bell 2009). We report the relative risk (RR) at 26.7°C (80 °F) compared with 15.6°C (60 °F) (heat effect), and at 4.4°C (40 °F) compared with 15.6°C (60 °F) (cold effect). To quantify effects of relative temperature changes, we also calculated the RR comparing the 1st to 50th percentile (cold effect) and the 99th to 50th percentile (hot effect) of the cluster's temperature distribution. The choice of percentiles allows us to compare the effect of relative temperature changes in different clusters for the difference between a relatively typical temperature (the 50th percentile) and a relatively hot one. We have taken this value as a reference with respect to adverse environmental conditions.
Stage 3: Meta-smoothing and meta-regression
The city-specific estimates obtained from the Poisson regression model are then combined through meta-smoothing. We assume that the smooth function derived from equation 1 has been fitted to the data from each of the i = 1,…,c cities, producing k-length vectors of regression coefficients θ̂i, and associated k × k estimated co(variance) matrices Si. These regression coefficients are then used as outcomes for the third stage and are defined from here on as outcomes parameters. A model for random-effect meta-regression can be written as follows:
| (2) |
with Si + Ψ = Σi. A random effect meta-analysis assumes that the observed variation across city in the regression coefficients has two sources—stochastic variability (Si) and true differences across cities in the coefficients θi, whose variance is Ψ. These are usually referred to as the within city variability and the between city variability. In the within-city component, the estimated θ̂i is assumed to be sampled with error from Nk(θ, Si), a multivariate normal distribution of dimension k, where θi is the vector of true unknown outcome parameters for city i. In the between-city component, θi is assumed sampled from Nk(θ, Ψ), where Ψ is the unknown between-city (co)variance matrix. In this case θ can be interpreted as the pooled temperature-mortality association to plot as a single smooth function. Meta-smoothing (equation 2) was performed on each cluster and time period to obtain multiple curves for the temperature-mortality relationship. The equation was subsequently extended to a multivariate meta-regression, where the k outcomes are modeled by p meta-predictors Xi measured at the city level. The model is written as follows:
| (3) |
The kp-dimensional coefficient vector β defines the association of the k outcomes with p meta-predictors. Methods to derive tests and confidence intervals along with fit statistics (best-linear unbiased) predictions have been previously developed within the linear mixed models framework for application in this setting, together with a description of the software implementation in the r package mvmeta (Gasparrini and Armstrong 2013). For fixed meta-predictors included in the meta-regression in equation 3, we used a dummy variable that identifies the cluster and a dummy variable that identifies the time interval. In this way it is possible to estimate the overall heat and cold effects for the whole country. Other city-level factors were also included in the analysis in order to explain the heterogeneity between studies. Specifically, we used mean and standard deviation of summer and winter temperature along with socioeconomic and land use variables such as average income, education, AC, population density, % green space and race, as described previously. In our results we report statistics that provide simple summaries on the extent of heterogeneity. Specifically, the Cochran Q test for (residual) heterogeneity (Berkey et al 1996; Ritz et al 2008) and the I2 that measures the proportion of total variation attributable to heterogeneity (Rücker et al 2008). Statistical analysis was performed in R version 3.0.1 (R Development Core Team (2012), Vienna, Austria).
Results
Figure 1 shows a map of the U.S. with the 211 selected cities. The cluster analysis identified 8 clusters represented by the different colors for the cities in the map. Cluster 1 identifies cities on the east coast over large areas of land masses in the temperate regions of the mid-latitudes. The climate is humid continental with warm summers and cold, snowy winters. Cluster 2 identifies cities in the north-east of the country where winter is characterized by cold temperatures. Snow is the main form of winter precipitation, but freezing rain, sleet, and occasional rain are all possible during the winter months. Cluster 3 is characterized by a humid continental climate, with cold winters and long, hot summers. Cluster 4 is located to the center-east of the country and possesses a humid subtropical climate with most of the states having mild winters and hot summers. Cluster 5 identifies the western-most coastal cities' climates, heavily influenced by the Pacific Ocean. The climate is mild, but periods of extreme hot and cold temperatures can affect parts of the region. The influence of the ocean generally moderates temperature extremes, creating warmer winters and substantially cooler summers especially along the coastal areas. Cluster 6 identifies the cities along the Gulf of Mexico where climate is humid subtropical with hot summers. This climate is also continental, characterized by a wide annual temperature range. Periods of extreme cold that occasionally occur are short-lived so that mild weather predominates even during January. Cluster 7 identifies the cities in Florida and the southern-most cities bordering Mexico, characterized by very hot and long summers. The climate of the north and central parts of Florida is humid subtropical with south Florida having a tropical climate. Finally, Cluster 8 between California and New Mexico has a dry climate with little rainfall. In the lower elevations, the climate is primarily desert with mild winters and extremely hot summers. The higher altitude locations have an appreciably cooler climate, with cold winters and mild summers, though the climate remains semi-arid to arid. Importantly, unlike census-based regions, these clusters can be either quite relatively small but geographically split (e.g. CL7), or cut across multiple regions (e.g. CL2). Weather and mortality summary statistics are provided in Table 1. We focused descriptive results on summer and winter because they are most relevant for the aims of this paper. Cluster 5 has the highest average daily number of deaths compared to the other clusters. This is due to the high population of a select group of cities that belong to this cluster, such as Los Angeles (3,820,000 inhabitants) and San Diego (1,326,000 inhabitants). As expected, we found the highest average summer temperature in Cluster 8 with 29.17 °C and the lowest average winter temperature Cluster 2 with -3.19 °C.
Table 1. Mortality, Temperature and Relative Humidity summaries by clusters*.
| Temperature °C | |||||
|---|---|---|---|---|---|
|
|
|||||
| Season | Average daily no. of deaths | Population Range | Average | Std | |
| Cluster 1 | Summer | 17 | 47475 - 8008278 | 22.79 | 3.78 |
| Winter | 20 | 0.78 | 5.42 | ||
|
| |||||
| Cluster 2 | Summer | 11 | 42331 - 6925258 | 21.31 | 3.81 |
| Winter | 13 | -3.19 | 6.57 | ||
|
| |||||
| Cluster 3 | Summer | 12 | 92954 - 2175343 | 23.9 | 3.54 |
| Winter | 14 | 0.4 | 6.58 | ||
|
| |||||
| Cluster 4 | Summer | 10 | 68247 - 2914587 | 25.9 | 2.85 |
| Winter | 11 | 6.53 | 5.82 | ||
|
| |||||
| Cluster 5 | Summer | 27 | 128454 - 9519338 | 19.67 | 3.79 |
| Winter | 32 | 9.54 | 4.57 | ||
|
| |||||
| Cluster 6 | Summer | 10 | 51616 - 3400578 | 27.35 | 1.92 |
| Winter | 11 | 12.03 | 5.4 | ||
|
| |||||
| Cluster 7 | Summer | 14 | 16932 - 2253362 | 27.74 | 1.57 |
| Winter | 17 | 17.59 | 4.87 | ||
|
| |||||
| Cluster 8 | Summer | 12 | 74492 - 3072149 | 29.17 | 4.29 |
| Winter | 14 | 10.18 | 3.98 | ||
Mortality and average daily temperature, 1962-2006.
Mortality results across clusters
Figure 2 presents the main results applying equation 2. We report a separate pooled temperature-mortality function for each cluster, representing the population-average coefficients of the quadratic B-spline. Generally, the plot indicates an increased risk in all the clusters for non-accidental mortality on the day of the event (lag 0) for high temperatures, and an increased risk when the average temperature of the five days prior to the event was very low (MA15). There is a significant difference in the temperature-mortality function between clusters. At lag 0, Cluster 5 has a relative risk (RR) of 1.14 (95% CI: 1.11, 1.17) for temperatures of 27 °C versus 15.6 °C, and Cluster 6 has a RR of 1.04 (95% CI: 1.03, 1.05). These results suggest that people who are accustomed to living in a humid subtropical climate with hot summers like the Gulf of Mexico have a lower risk compared to people living in a mild climate like the Pacific Coast. Similarly in Cluster 2, we found a RR of 1.12 (95% CI: 1.10, 1.13) for temperatures of 26.7 °C versus 15.6 °C, and a RR of 1.05 (95% CI: 1.04, 1.06) in Cluster 4. Significant differences were also found for the cold effect. In Cluster 7 we found a RR of 1.12 (95% CI: 1.09, 1.15) for temperatures of 4.4°C versus 15.6 °C versus a RR of 1.07 (95% CI: 1.06, 1.08) in Cluster 1. These results show that in places characterized by long, cold winters as in Cluster 1, the risk is lower than in places where winters are not particularly cold as in Cluster 7. Figure 2 shows that the increase in mortality rate at -10 °C rises substantially across cluster as the frequency of colder temperatures in the cluster decreases. In general, looking across the clusters in Figure 2A indicates that heat effects become less pronounced in locations used to warm weather, and similarly for cold effects. This suggests that as climate change shifts cities across clusters, sensitivity to heat will decrease and sensitivity to cold might increase, while the prevalence of hot and cold days moves in the opposite direction.
Figure 2.
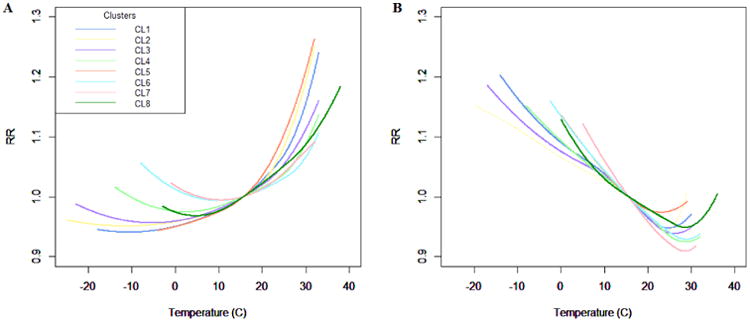
Relative risk of the pooled lag0 (A) and MA15 (B) relationship between temperature and non-accidental mortality by clusters, 1962-2006. Reference at 15.6°C (60°F).
Mortality results across time periods
We then examined how the temperature-mortality relationship within each cluster varied by years. We provide an example of this added layer of analysis with Figure 3 portraying the temperature-mortality relationship by group of years in Cluster 1, where we found a decrease in risk over the years. The RR for the heat effect changes from 1.23 (95% CI: 1.20, 1.27) during the 1962-1966 period to 1.09 (95% CI: 1.08, 1.10) during the 2000-2006 period. A similar pattern was also found for Cluster 2 with a RR of 1.25 (95% CI: 1.08, 1.10) in the 1962-1966 period and a RR of 1.08 (95% CI: 1.06, 1.09) for the 2000-2006 period. Patterns in other clusters were more complex, and are provided in the supplementary tables (S1, S2).
Figure 3.
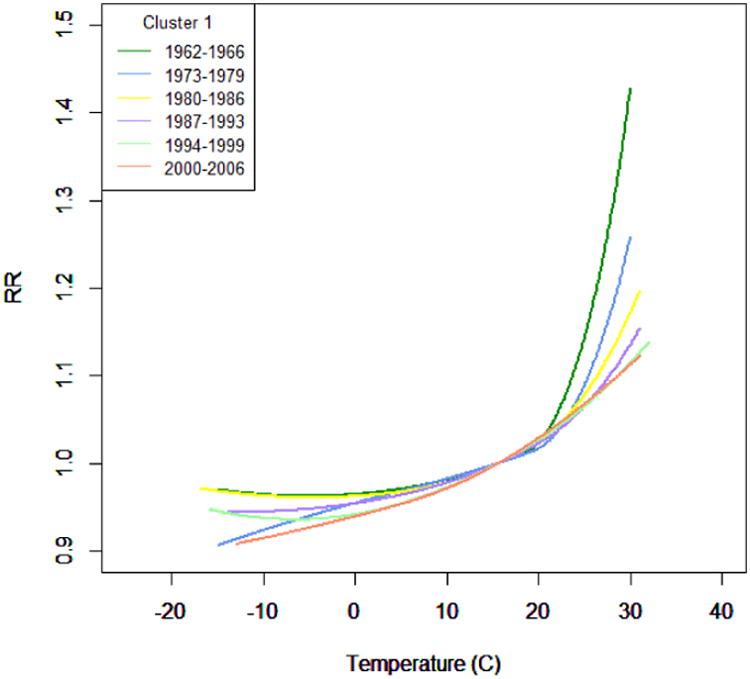
Pooled lag0 temperature-mortality functions by time period for the relative risk between temperature and non-accidental mortality by time periods in Cluster 1. Reference at 15.6°C (60°F).
Meta-regression
Meta-regressions heterogeneity tests are presented in Table 2. The Q and I2 statistics show significant heterogeneity in both the heat and cold effects across cities: 59.3% of the variability across cities in the estimated lag 0 (heat effect) and 29.1 % of the variability in the MA15 (cold effect) represented true heterogeneity in effect in the intercept only model. When cluster and time period were included in the meta-regressions, the AIC was reduced for both the heat and cold effect. The dummy variables for cluster and time period explained a substantial part of the heterogeneity between studies, with an overall I2 of 25.1% for the heat effect compared with 59.3% with no predictors, for example. We then examined the other potential explanatory variables. There was no association of the socio-economic and land-use factors with the city-specific estimates; however, mean summer temperature and AC were significant predictors of total mortality. Figure 4 shows the results of the meta-regression, where we assessed whether summer temperature, AC and groups of years in each city modify the association between heat effect and mortality. Each 5 degree increase in mean temperature was associated with a decrease in the heat effect on mortality by 1.78% (95% CI: 0.82, 2.74). Each 50% increase in air conditioning prevalence was associated with a 1.37% (95% CI: 0.48, 2.26) decrease in the heat effect on mortality. Figure 4 shows how the pooled risk of non-accidental deaths from all the clusters due to hot days decreases over time, from 10.61% (95% CI: 9.10, 12.13) during the 1962-1966 period to 0.87% (95% CI: -0.21, 1.97) in 1994-1999, taking into account the effect of summer mean and air conditioning. Hence there are other time varying factors influencing the decline in sensitivity to heat besides air conditioning or mean temperature which we were unable to identify. As a sensitivity analysis, we fit meta-regressions for each cluster separately to see whether the decrease of risk over time was consistent in each cluster. In six out of the eight clusters, there was a significant trend of decreased risk over time, and in the remaining two it was marginally significant (p-value < 0.10). The meta-regressions for the cold effect did not show any significant time trend, though the other meta-predictors in the model (clusters, winter mean temperatures) did explain variations in cold effects, reducing I2 from 29.1% to 17.0%. Sensitivity analysis using temperature percentiles did not show a major difference compared to using temperature.
Table 2.
Cochran Q test and I2 for multivariate models based on relative scale.
| Heat Effect | Cochran Q test | I2 | ||
|---|---|---|---|---|
|
|
|
|||
| Q | df | p | % | |
| Relative scale | ||||
| Intercept only | 2933.73 | 1194 | <0.001 | 59.3 |
| Clusters, Time | 1578.42 | 1182 | <0.001 | 25.1 |
| Clusters, Time, Summer Mean, AC | 1535.37 | 1179 | <0.001 | 23.2 |
|
| ||||
| Cold Effect | Cochran Q test | I2 | ||
|
|
|
|||
| Q | df | p | % | |
|
| ||||
| Relative scale | ||||
| Intercept only | 1685.12 | 1194 | <0.001 | 29.1 |
| Clusters, Time | 1436.43 | 1182 | <0.001 | 17.7 |
| Clusters, Time, Winter Mean | 1423.64 | 1181 | <0.001 | 17.0 |
Figure 4.
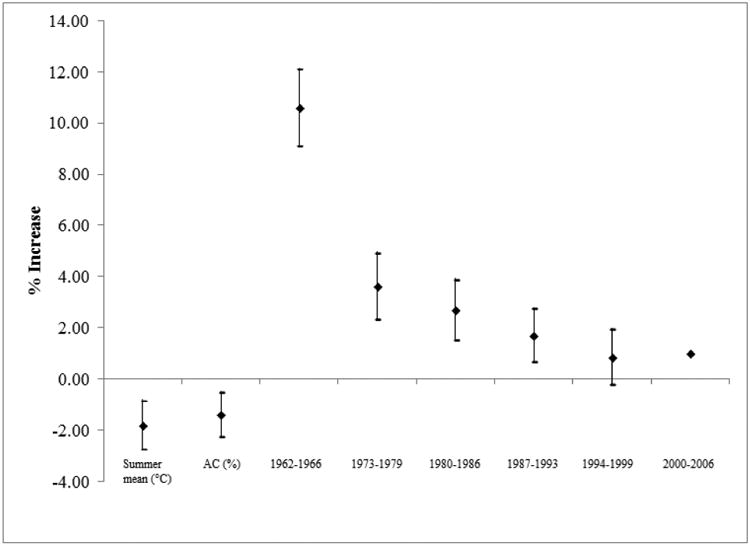
Meta-regression analysis showing decreased risk for heat effect over year, and for increases in summer mean temperature and air conditioning.
Discussion
In this paper we demonstrate a novel application of meta-regression to generate reliable estimates of the large scale, allowing us to assess temporal and geographic differences in dose-response, and to account for multiple modifiers of the temperature-mortality associations across America. By first clustering cities with common temperature and humidity patterns we were able to fit splines with knots in the same location in each cluster, making combining effects straightforward. With our large number of cities we assured that each cluster had sufficient power to stabilize results. It also enables us to better control for such diverse parameters as climate, time period, and geographic region, compared to the traditional technique of univariate meta-regression without meta-smoothing. We generated the largest known characterization to date of the heterogeneity among relative risks calculated for the heat effect. Our meta-regression explains most of this heterogeneity by the differences between clusters, between time periods, and by mean summer temperatures and air conditioning. Particularly, we demonstrate that lower summer mean temperature is associated with higher relative risk of death (β = -0.0042, p-value < 0.05) and increased use of air condition was associated with lower relative risk of death (β = -0.0003, p-value < 0.05) in association with heat. These results indicate that people living in cities with low summer temperatures have a higher risk of mortality during periods of high temperature, controlling for air conditioning. This is potentially due to these populations being less acclimated to hot temperatures, as compared to inhabitants in warmer city clusters. While it has long been known that heat related mortality is lower in warmer US cities, these results provide a quantitative estimate of that effect, and similarly for winter temperature. Importantly, these estimates are within cluster estimates of changes in dose-response as summer temperature increases, not cross-sectional estimates, and are more directly applicable to estimating future changes in dose-response. Interestingly, increases in mean summer temperature controlling for air conditioning explain more of the adaptation process (decrease in effect of hot temperature) than vice versa. This suggests there are important other adaptive mechanisms already occurring, which may be more important for the future that air conditioning, which has almost reached saturation. Physiologic adaptation is likely important, but other factors doubtless play a role. Although the effects found are modest changes in daily deaths, they apply to the entire season, and so their impact is not trivial. Moreover, our results could prove useful to understand how the risk of death due to temperature would change if there were different conditions of mean summer or winter temperature and air conditioning use in either specific areas of the United States, regions, or the country as a whole. Increases in mean winter temperature within cluster were associated with increased susceptibility to cold days. This would be quite relevant for modifying the dose-response curve used for risk assessments based on scenarios of future climate change. These results are consistent with current studies, particularly the recent publication on the temperature-mortality association in Europe (Tobias et al 2012). However, we must specify some limitations to our methods.
Though previous studies suggest that air pollution is a confounding factor on temperature and mortality, we did not have sufficient pollution data for the cities in our studies during the corresponding time frame to include in the multivariate regression analysis (Fischer et al 2008; Katsouyanni et al 1993). However, Buckley JP et al. recently argued that pollution is not really a confounder of temperature (Buckley et al). Our study presents novel findings that demonstrate a 42-year nation-wide decrease in non-accidental heat related mortality with air conditioning increases in a large number of cities while controlling for key meta-predictors (i.e. geographic cluster, mean summer temperature). In contrast, past research simply demonstrated the protective effect of air conditioning in smaller sample sizes in more brief time periods, without such control for confounders (Rogot et al 1992; Semenza et al 1996; Zanobetti and Schwartz 2005). Controlling for mean seasonal temperature and air conditioning, we still saw a substantial decrease in heat related deaths over the 42 years, with the decrease particularly rapid in the early years. Our other covariates, including socioeconomic ones were unable to explain this decline. However the decline appears to have hit its asymptote. Similarly, a recent study (Bobb et al 2014) found a decline of heat-related mortality over the years suggesting adaptation. Interestingly our study and this one found comparable results even though used a different number of cities, a different range of years, different statistical methods and different definition of regions across the US. However, they did not find an association with air conditioning. These results may be weakened by the lack of city-specific air condition usage in a few cities dictating that we assign the available state-specific usage to those cities. Another study limitation is that the American Housing Survey (AHS) only allowed us to control for air condition usage after 1973 when data was first collected. It is true that 80% of the U.S. population now makes use of air conditioning but that was not true in 1970. One of our goals was to estimate how changes in air conditioning reduced susceptibility to hot days. In addition, the remaining 20% of un-air-conditioned housing are not randomly located, but primarily in areas that have less summer heat, but where summer temperatures are likely to increase. In these locations, there is considerably greater room for air conditioning growth.
Important changes in the distribution of temperature are expected over the next 50 years, and estimating the direct effects of these changes on health has attracted national and international attention. To do so requires not just estimates of local temperature change, such as provided by downscaling models, but models of how mortality or other health endpoints will vary with temperature in 50 years. By going back 50 years in time we have shown how mortality responses to heat and to cold have changed over time and an important deviation from linearity in that relation. Our results are also comparable to Barnett and coauthors (Barnett et al 2007). They also looked at trends over time in heat- and cold-related mortality in the US and found that cold is the most consistent problem. In addition, we have identified summer mean temperature as an important explanatory factor for both changes over time, and differences between locations, allowing for an estimate of how future changes might affect the dose response relationship. We have also highlighted the effect of warmer winter temperatures on increasing the steepness of the dose response curve at cold temperatures, which will mute, and perhaps cancel any reduction in wintertime mortality from warmer winters. Both results suggest the importance of usual temperature for the season in human responses, and suggest that increased variability in temperature may be more important than increased temperature in the direct effects of temperature on mortality (Zanobetti et al 2012; Schar et al 2004). The direct effects of future climate change on health cannot be estimated using current dose-response curves, but must take into account such changes, which will likely be location specific. In conclusion, our novel application of meta-smoothing with multivariate meta-regression on a large spatial-temporal scale has allowed us to build a model that provides coefficients that could be worth considered in mortality risk assessments. The response to cold increases as winter mean temperature rises, the response to heat declines as summer mean temperature rises and as AC use increases.
Supplementary Material
Highlights.
In a study of 42 million deaths in 211 U.S. cities from the 1960's to recent years we show that the effect of hot days is diminished by increasing summer mean temperature within city, and the effect of cold days is increased by increasing winter mean temperature.
A modest protective effect of air conditioning was found controlling for the above.
Risk assessments of future temperature changes need to take these adaptive responses into account.
Acknowledgments
We thank Steve Melly from Harvard T. H. Chan School of Public Health for providing the temperature data and city-specific variables. We also thank Dominique J. Monlezun from Tulane School of Public Health for manuscript review. This work was supported by grant ES020695 and ES000002.
Footnotes
Conflict of Interest: The authors declare that they have no actual or potential conflict of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Åström DO, Forsberg B, Edvinsson S, Rocklöv J. Acute fatal effects of short-lasting extreme temperatures in Stockholm, Sweden: evidence across a century of change. Epidemiology. 2013 Nov;24(6):820–9. doi: 10.1097/01.ede.0000434530.62353.0b. [DOI] [PubMed] [Google Scholar]
- Analitis A, Katsouyanni K, Biggeri A, Baccini M, Forsberg B, Bisanti L, Kirchmayer U, Ballester F, Cadum E, Goodman P. Effects of cold weather on mortality: results from 15 European cities within the PHEWE project. American journal of epidemiology. 2008;168:1397–1408. doi: 10.1093/aje/kwn266. [DOI] [PubMed] [Google Scholar]
- Anderson BG, Bell ML. Weather-related mortality: how heat, cold, and heat waves affect mortality in the United States. Epidemiology (Cambridge, Mass) 2009;20:205. doi: 10.1097/EDE.0b013e318190ee08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson GB, Bell ML. Heat waves in the United States: mortality risk during heat waves and effect modification by heat wave characteristics in 43 US communities. Environmental health perspectives. 2011;119:210. doi: 10.1289/ehp.1002313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson JRH, Ernest E, Roach John T. A Land Use And Land Cover Classification System For Use With Remote Sensor Data. 1976 [Google Scholar]
- Barnett AG, Sans S, Salomaa V, Kuulasmaa K, Dobson AJ. WHO MONICA Project. The effect of temperature on systolic blood pressure. Blood Press Monit. 2007 Jun;12(3):195–203. doi: 10.1097/MBP.0b013e3280b083f4. [DOI] [PubMed] [Google Scholar]
- Barreca A, Clay K, Deschenes O, Greenstone M, Shapiro JS. Adapting to Climate Change: The Remarkable Decline in the US Temperature-Mortality Relationship over the 20th Century. National Bureau of Economic Research. 2013 [Google Scholar]
- Basu R, Ostro BD. A multicounty analysis identifying the populations vulnerable to mortality associated with high ambient temperature in California. American journal of epidemiology. 2008;168:632–637. doi: 10.1093/aje/kwn170. [DOI] [PubMed] [Google Scholar]
- Berkey C, Anderson J, Hoaglin D. Multiple-outcome meta-analysis of clinical trials. Statistics in medicine. 1996;15:537–557. doi: 10.1002/(SICI)1097-0258(19960315)15:5<537::AID-SIM176>3.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
- Bobb JF, Peng RD, Bell ML, Dominici F. Heat-related mortality and adaptation to heat in the United States. Environ Health Perspect. 2014 Aug;122(8):811–6. doi: 10.1289/ehp.1307392. Epub 2014 Apr 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braga AL, Zanobetti A, Schwartz J. The time course of weather-related deaths. Epidemiology. 2001a;12:662–667. doi: 10.1097/00001648-200111000-00014. [DOI] [PubMed] [Google Scholar]
- Braga AL, Zanobetti A, Schwartz J. The effect of weather on respiratory and cardiovascular deaths in 12 U.S. cities. Environ Health Perspect. 2002 Sep;110(9):859–63. doi: 10.1289/ehp.02110859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckley JP, Samet JM, Richardson DB. Commentary: Does Air Pollution Confound Studies of Temperature? Epidemiology. 2014 Mar;25(2):242–245. doi: 10.1097/EDE.0000000000000051. [DOI] [PubMed] [Google Scholar]
- Cao J, Valois MF, Goldberg MS. An S-Plus function to calculate relative risks and adjusted means for regression models using natural splines. Computer methods and programs in biomedicine. 2006;84:58–62. doi: 10.1016/j.cmpb.2006.08.004. [DOI] [PubMed] [Google Scholar]
- Curriero FC, Heiner KS, Samet JM, Zeger SL, Strug L, Patz JA. Temperature and mortality in 11 cities of the eastern United States. American journal of epidemiology. 2002;155:80–87. doi: 10.1093/aje/155.1.80. [DOI] [PubMed] [Google Scholar]
- Deschênes O, Greenstone M. Climate change, mortality, and adaptation: evidence from annual fluctuations in weather in the US. American Economic Journal: Applied Economics. 2011;3:152–185. [Google Scholar]
- Fischer P, Ameling C, Marra M. Effect of interaction between temperature and air pollution on daily mortality during heat-waves. Epidemiology. 2008;19:S379. [Google Scholar]
- Gasparrini A, Armstrong B. Reducing and meta-analyzing estimates from distributed lag nonlinear models. BMC medical research methodology. 2013;13:1. doi: 10.1186/1471-2288-13-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gasparrini A, Armstrong B, Kenward M. Multivariate meta-analysis for non-linear and other multi-parameter associations. Statistics in Medicine. 2012;31:3821–3839. doi: 10.1002/sim.5471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo Y, Gasparrini A, Armstrong B, Li S, Tawatsupa B, Tobias A, Lavigne E, de Sousa Zanotti Stagliorio Coelho M, Leone M, Pan X, Tong S, Tian L, Kim H, Hashizume M, Honda Y, Guo YL, Wu CF, Punnasiri K, Yi SM, Michelozzi P, Saldiva PH, Williams G. Global variation in the effects of ambient temperature on mortality: a systematic evaluation. Epidemiology. 2014 Nov;25(6):781–9. doi: 10.1097/EDE.0000000000000165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ha J, Kim H, Hajat S. Effect of previous-winter mortality on the association between summer temperature and mortality in South Korea. Environ Health Perspect. 2011;119(4):542–6. doi: 10.1289/ehp.1002080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hajat S, Kosatky T. Heat-related mortality: a review and exploration of heterogeneity. Journal of epidemiology and community health. 2010;64:753–760. doi: 10.1136/jech.2009.087999. [DOI] [PubMed] [Google Scholar]
- Huang C, Barnett AG, Wang X, Vaneckova P, FitzGerald G, Tong S. Projecting future heat-related mortality under climate change scenarios: a systematic review. Environmental health perspectives. 2011;119.12:1681. doi: 10.1289/ehp.1103456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katsouyanni K, Pantazopoulou A, Touloumi G, Tselepidaki I, Moustris K, Asimakopoulos D, Poulopoulou G, Trichopoulos D. Evidence for interaction between air pollution and high temperature in the causation of excess mortality. Archives of Environmental Health: An International Journal. 1993;48:235–242. doi: 10.1080/00039896.1993.9940365. [DOI] [PubMed] [Google Scholar]
- Medina-Ramón M, Schwartz J. Temperature, temperature extremes, and mortality: a study of acclimatisation and effect modification in 50 US cities. Occupational and Environmental Medicine. 2007;64:827–833. doi: 10.1136/oem.2007.033175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng RD, Bobb JF, Tebaldi C, McDaniel L, Bell ML, Dominici F. Toward a quantitative estimate of future heat wave mortality under global climate change. Environmental health perspectives. 2011;119:701. doi: 10.1289/ehp.1002430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng RD, Dominici F, Louis TA. Model choice in time series studies of air pollution and mortality. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2006;169:179–203. [Google Scholar]
- Ritz J, Demidenko E, Spiegelman D. Multivariate meta-analysis for data consortia, individual patient meta-analysis, and pooling projects. Journal of Statistical Planning and Inference. 2008;138:1919–1933. [Google Scholar]
- Rogot E, Sorlie PD, Backlund E. Air-conditioning and mortality in hot weather. American journal of epidemiology. 1992;136:106–116. doi: 10.1093/oxfordjournals.aje.a116413. [DOI] [PubMed] [Google Scholar]
- Rücker G, Schwarzer G, Carpenter JR, Schumacher M. Undue reliance on I2 in assessing heterogeneity may mislead. BMC medical research methodology. 2008;8:79. doi: 10.1186/1471-2288-8-79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schär C, Vidale PL, Lüthi D, Frei C, Häberli C, Liniger MA, Appenzeller C. The role of increasing temperature variability in European summer heatwaves. Nature. 2004 Jan 22;427(6972):332–6. doi: 10.1038/nature02300. Epub 2004 Jan 11. [DOI] [PubMed] [Google Scholar]
- Schwartz J, Zanobetti A. Using meta-smoothing to estimate dose-response trends across multiple studies, with application to air pollution and daily death. Epidemiology. 2000;11:666–672. doi: 10.1097/00001648-200011000-00009. [DOI] [PubMed] [Google Scholar]
- Semenza JC, Rubin CH, Falter KH, Selanikio JD, Flanders WD, Howe HL, Wilhelm JL. Heat-related deaths during the July 1995 heat wave in Chicago. New England Journal of Medicine. 1996;335:84–90. doi: 10.1056/NEJM199607113350203. [DOI] [PubMed] [Google Scholar]
- Stafoggia M, Forastiere F, Michelozzi P, Perucci CA. Summer temperature-related mortality: effect modification by previous winter mortality. Epidemiology. 2009;20(4):575–83. doi: 10.1097/EDE.0b013e31819ecdf0. [DOI] [PubMed] [Google Scholar]
- Stieb DM, Judek S, Burnett RT. Meta-analysis of time-series studies of air pollution and mortality: effects of gases and particles and the influence of cause of death, age, and season. Journal of the Air & Waste Management Association. 2002;52:470–484. doi: 10.1080/10473289.2002.10470794. [DOI] [PubMed] [Google Scholar]
- Survey USG. Land use and land cover digital data from 1:250,000- and 1:100,000-scale maps. 1986 [Google Scholar]
- Tobias A, Armstrong B, Zuza I, Gasparrini A, Linares C, Diaz J. Mortality on extreme heat days using official thresholds in Spain: a multi-city time series analysis. BMC Public Health. 2012;12:133. doi: 10.1186/1471-2458-12-133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voorhees AS, Fann N, Fulcher C, Dolwick P, Hubbell B, Bierwagen B, Morefield P. Climate change-related temperature impacts on warm season heat mortality: a proof-of-concept methodology using BenMAP. Environmental science & technology. 2011;45:1450–1457. doi: 10.1021/es102820y. [DOI] [PubMed] [Google Scholar]
- Wanielista MP. Hydrology and water quantity control. 1990 [Google Scholar]
- Yu W, Vaneckova P, Mengersen K, Pan X, Tong S. Is the association between temperature and mortality modified by age, gender and socio-economic status? Science of the Total Environment. 2010;408:3513–3518. doi: 10.1016/j.scitotenv.2010.04.058. [DOI] [PubMed] [Google Scholar]
- Zanobetti A, O'Neill MS, Gronlund CJ, Schwartz JD. Summer temperature variability and long-term survival among elderly people with chronic disease. Proceedings of the National Academy of Sciences. 2012;109:6608–6613. doi: 10.1073/pnas.1113070109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanobetti A, Schwartz J. Disparities by race in heat-related mortality in four US cities: the role of air conditioning prevalence. Journal of Urban Health. 2005;82:191–197. doi: 10.1093/jurban/jti043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanobetti A, O'Neill MS, Gronlund CJ, Schwartz JD. Summer temperature variability and long-term survival among elderly people with chronic disease. PNAS USA. 2012 Apr 24;109(17):6608–13. doi: 10.1073/pnas.1113070109. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


