Significance
The end-Permian mass extinction not only decimated taxonomic diversity but also disrupted the functioning of global ecosystems and the stability of biogeochemical cycles. Explaining the 5-million-year delay between the mass extinction and Earth system recovery remains a fundamental challenge in both the Earth and biological sciences. We use coupled records of uranium concentrations and isotopic compositions to constrain global marine redox conditions across the end-Permian extinction horizon and through the subsequent 17 million years of Earth system recovery. Our finding that the trajectory of biological and biogeochemical recovery corresponds to variations in an ocean characterized by extensive, shallow marine anoxia provides, to our knowledge, the first unified explanation for these observations.
Keywords: paleoredox, uranium isotopes, biogeochemical cycling, carbon isotopes, Early Triassic
Abstract
Delayed Earth system recovery following the end-Permian mass extinction is often attributed to severe ocean anoxia. However, the extent and duration of Early Triassic anoxia remains poorly constrained. Here we use paired records of uranium concentrations ([U]) and 238U/235U isotopic compositions (δ238U) of Upper Permian−Upper Triassic marine limestones from China and Turkey to quantify variations in global seafloor redox conditions. We observe abrupt decreases in [U] and δ238U across the end-Permian extinction horizon, from ∼3 ppm and −0.15‰ to ∼0.3 ppm and −0.77‰, followed by a gradual return to preextinction values over the subsequent 5 million years. These trends imply a factor of 100 increase in the extent of seafloor anoxia and suggest the presence of a shallow oxygen minimum zone (OMZ) that inhibited the recovery of benthic animal diversity and marine ecosystem function. We hypothesize that in the Early Triassic oceans—characterized by prolonged shallow anoxia that may have impinged onto continental shelves—global biogeochemical cycles and marine ecosystem structure became more sensitive to variation in the position of the OMZ. Under this hypothesis, the Middle Triassic decline in bottom water anoxia, stabilization of biogeochemical cycles, and diversification of marine animals together reflect the development of a deeper and less extensive OMZ, which regulated Earth system recovery following the end-Permian catastrophe.
The end-Permian mass extinction—the most severe biotic crisis in the history of animal life—was followed by 5 million years of reduced biodiversity (1, 2), limited ecosystem complexity (3), and large perturbations in global biogeochemical cycling (4, 5). Ocean anoxia has long been invoked both as a cause of the extinction (6–8) and as a barrier to rediversification (9). Numerous lines of evidence demonstrate widespread anoxic conditions around the time of the end-Permian mass extinction (e.g., refs. 6 and 10–12). In contrast, the prevalence of anoxia during the 5- to 10-million-year recovery interval remains poorly constrained (13, 14).
Reconstructing paleoredox conditions is challenging because some indicators of anoxia characterize only the local conditions of the overlying water column, whereas other indicators may be influenced by confounding factors, such as weathering rates on land. Here, we use paired measurements of [U] and δ238U in marine carbonate rocks to differentiate changes in weathering of U from variations in global marine redox conditions. Microbially mediated reduction of U(VI) to U(IV) under anoxic conditions at the sediment−water interface results in a substantial decrease in uranium solubility and a measureable change in 238U/235U (15–18). Because 238U is preferentially reduced and immobilized relative to 235U, the δ238U value of seawater U(VI) decreases as the areal extent of bottom water anoxia increases (Fig. S1). Consequently, a global increase in the extent of anoxic bottom waters will cause simultaneous decreases in [U] and δ238U of carbonate sediments. A previous study of δ238U variations at one stratigraphic section through the immediate extinction interval (∼40,000 y) (11) suggested a rapid onset of anoxia coincident with the loss of marine diversity. However, with only a single site, it is unclear if the signal is globally representative; moreover, the lack of data for all but the lowest biostratigraphic zone of the Triassic leaves the pattern and timing of environmental amelioration during the recovery interval unconstrained.
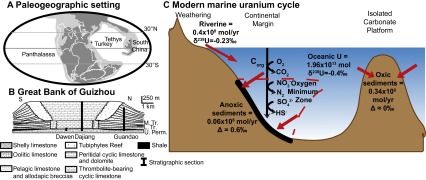
Fig. S1.
Study materials and methods. (A) Paleogeographic map showing locations of Turkey and South China, modified from ref. 19. (B) Schematic cross section and studied stratigraphic sections of the GBG, modified after ref. 20. (C) Inputs and outputs of the modern uranium cycle.
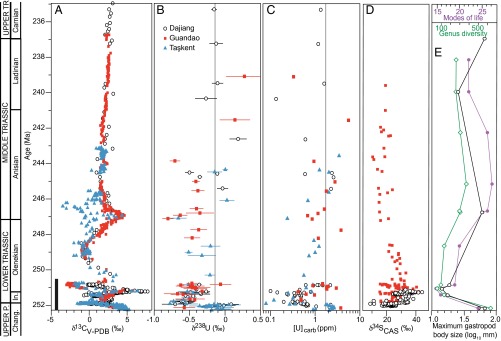
To develop a quantitative, global reconstruction of seawater redox conditions for the entire 15-million-year interval of mass extinction and subsequent Earth system recovery, we measured 58 Upper Permian (Changhsingian) through Upper Triassic (Carnian) limestone samples from three stratigraphic sections (Dajiang, Dawen, and Guandao) arrayed along a depth transect on the Great Bank of Guizhou (GBG), an isolated carbonate platform in the Nanpanjiang Basin of south China (eastern Tethys). To test the extent to which variations in [U] and δ238U within the GBG reflect global uranium cycling, we also analyzed 28 limestone samples from the Taşkent section, Aladag Nappe, Turkey, located in the western Tethys (Fig. S1). We focused our measurements on samples deposited in shallow marine environments (<100 m water depth, i.e., Dajiang, Dawen, and Taşkent) likely to have remained oxygenated. Variations in [U] and δ238U in these samples should reflect changes in global, rather than local, redox conditions.
Results
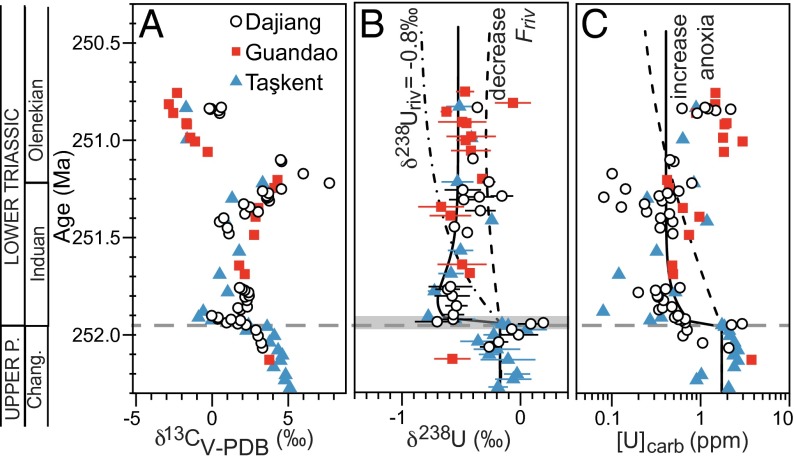
The δ238U composition of the shallow marine sections averages −0.15‰ in the Upper Permian and abruptly decreases at the extinction horizon to a minimum value of −0.77‰ (Fig. 1, Figs. S2−S4, and Dataset S1). Synchronously, [U] decreases from 3 ppm to ∼0.3 ppm. In the Induan strata, representing the first ∼0.7 My after the extinction, [U] and δ238U values remain low (0.4 ppm and −0.55‰) in both shallow marine (Dajiang and Taşkent) and slope (Guandao) environments. Lowermost Induan δ238U data from Dawen have a mean of −0.57‰ (Fig. S2). In the Olenekian strata, representing the subsequent ∼4 My, [U] and δ238U values gradually increase to 1 ppm and ∼0.35‰ (Fig. 2). In the uppermost Olenekian strata (∼247.5 Ma), [U] and δ238U decrease to 0.6 ppm and −0.65‰ at Guandao and Taşkent (Dajiang strata are dolomitized and are not considered). In limestones above the Olenekian−Anisian boundary (∼247 Ma), [U] and δ238U increase to 1.2 ppm and −0.23‰.
Fig. 1.
Late Permian (P.) to early Early Triassic (A) δ13C, (B) δ238U, and (C) [U] data and box model results. Gray dashed line indicates end-Permian extinction horizon. Shaded box in B represents the temporal extent of data reported in ref. 11. Model results are as follows: increased extent of anoxia (fanox) from modern value of 0.2% to 20% for the first ∼30,000 y and to 5% thereafter (solid line); decreased input [U] by an order of magnitude (dashed line); and decreased input δ238U value to −0.8‰ (dot-dashed line). The δ13C data are from ref. 4 (Dajiang and Guandao) and this study (Taşkent). Error bars on δ238U are 2σ of replicate analyses and are reported relative to CRM-145. Data from Dawen are shown in Fig. S2, and details of age model are shown in Figs. S2−S4. Chang., Changhsingian.
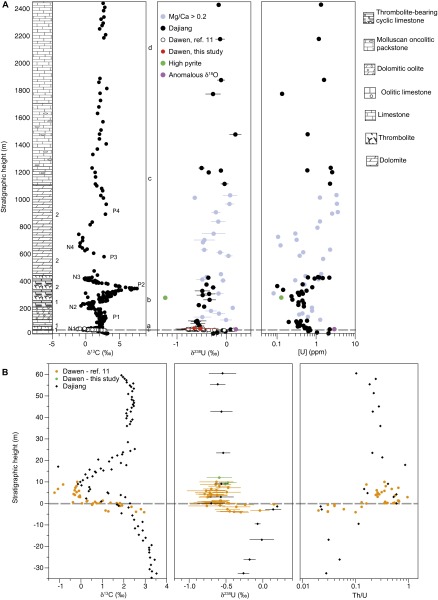
Fig. S2.
Dajiang and Dawen. (A) Stratigraphic column, δ13C (22), δ238U, and [U] data for Dajiang (black), Dawen from ref. 20 (open symbols), Dawen (this study) (red), samples with Mg/Ca > 0.2 (gray), sample with high pyrite content (green), and sample with anomalous δ18O (purple). Stratigraphy for Dajiang is comparable to Dawen at the extinction horizon (21). The δ238U error bars are 2σ. Dashed line indicates end-Permian extinction horizon. Chemostratigraphic correlations between sections are based on negative and positive local maxima in δ13C and are denoted as “N” and “P,” respectively, and numbered following refs. 5 and 22. Geochronological constraints based on δ13C are shown by “1” and “2” and refer to refs. 23 and 24, respectively. Lithologic correlation is marked by “+” and represents the start of the microbialite strata. Foraminifer (b−d) and conodont (a) first occurrences except where indicated: (a) Isarcicella isarcica, (b) last appearance datum (LAD) Postcladella kalhori, (c) Pilammina densa and Meandrospira dinarica, and (d) Aulotortus praegaschei. (B) Data from A focused on the Permian−Triassic boundary (gray line) to facilitate comparison.
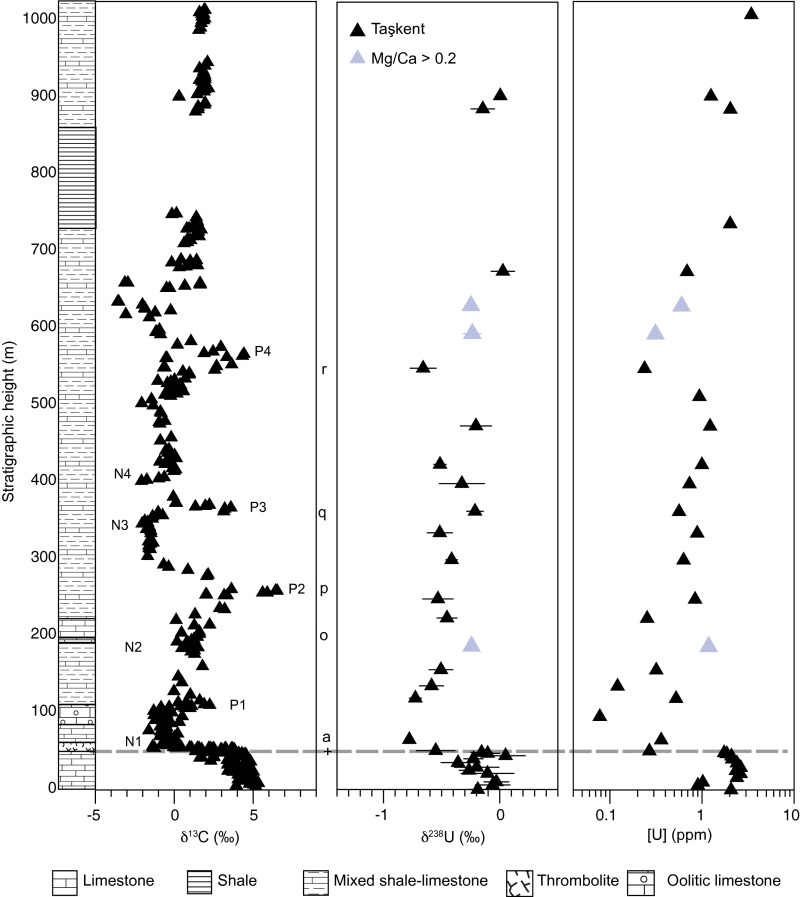
Fig. S4.
Taşkent. Stratigraphic column, δ13C (this study), δ238U, and [U] data for Taşkent (black), and samples with Mg/Ca > 0.2 (gray). The δ238U error bars are 2σ. Dashed line indicates extinction horizon. Chemostratigraphic correlations between sections are based on negative and positive local maxima in δ13C and are denoted as “N” and “P,” respectively, and are numbered following refs. 5 and 22. Refer to Fig. S2 for corresponding geochronological data. Foraminifer (c−f) and conodont (a) first occurrences except where indicated: (a) I. isarcica, (o) Postcladella grandis (last occurrence), (p) Hoyenella gr. sinensis (first appearance likely), (q) Meandrospira cheni, and (r) M. cheni (last occurrence).
Fig. 2.
Late Permian (P.) to Late Triassic (Tr.) [U] and δ238U data and global records of biogeochemical cycling and biotic recovery. (A) The δ13C data are from ref. 4 (Dajiang and Guandao) and this study (Taşkent). Vertical black bar depicts temporal extent of δ238U data from Fig. 1. (B) The δ238U data. Error bars on δ238U data are 2σ of replicate analyses and are reported relative to CRM-145. (C) [U] data. Vertical gray lines in B and C are the mean Late Permian values. (D) Carbonate-associated sulfate sulfur isotope data (δ34SCAS) (5). (E) Global trends in sampled-in-bin genus diversity (green open diamonds) (3), modes of life (purple circles) (3), and maximum gastropod body size (black open circles) (25). The age model is based on geochronology (23, 24), biostratigraphy, and chemostratigraphy (details are shown in Figs. S2−S4). Chang., Changhsingian; In., Induan.
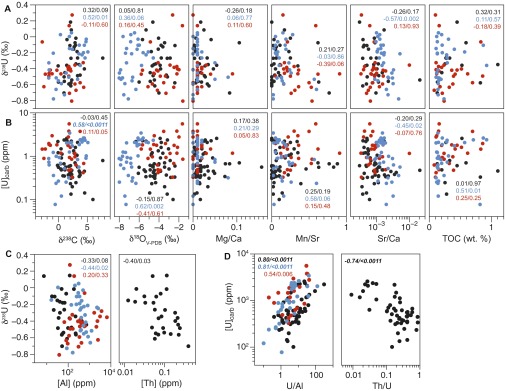
Three lines of evidence indicate that these general trends in [U] and δ238U reflect secular changes in global seawater redox conditions rather than local or diagenetic effects. First, shallow marine uranium records exhibit consistent trends and similar absolute values between China and Turkey, despite vast differences in geographic settings and burial histories. In our records, differences in [U] and δ238U across time intervals are statistically significant both within individual stratigraphic sections and across the entire dataset, whereas the values between sections are statistically indistinguishable (Table S1 and Statistical Analysis: Interpretation). Local or diagenetic controls would likely produce differences among sites rather than differences expressed across time. Second, our uranium data are not significantly correlated with indicators of diagenetic alteration such as δ18O, Mn/Sr, Mg/Ca, or organic carbon content, and do not covary with proxies for detrital contribution (normalization with Al or Th) or indictors of mineralogy (Sr/Ca) (Fig. S5 and Diagenetic Alteration and Dolomitization and Statistical Analysis: Interpretation).
Table S1.
Summary of ANOVA and Dunnett’s modified Tukey−Kramer Post-Hoc statistics
| Dunnett's modified Tukey−Kramer Post-Hoc Test | |||||||||
| ANOVA P value | δ238U | [U] | |||||||
| δ238U | [U] | Pair-wise comparison | Mean diff | Lower CI | Upper CI | Mean diff | Lower CI | Upper CI | |
| Differences between stratigraphic sections | |||||||||
| Late Permian | 0.013 | 0.045 | Dawen−Dajiang | −0.281 | −0.588 | 0.026 | – | – | – |
| Taşkent−Dajiang | −0.058 | −0.275 | 0.158 | 0.216 | −0.115 | 0.547 | |||
| Taşkent−Dawen | 0.222 | −0.069 | 0.513 | – | – | – | |||
| Induan | 0.011 | 0.081 | Dawen−Dajiang | −0.117 | −0.222 | −0.013 | – | – | – |
| Guandao−Dajiang | −0.024 | −0.205 | 0.157 | – | – | – | |||
| Taşkent−Dajiang | −0.069 | −0.229 | 0.090 | – | – | – | |||
| Guandao−Dawen | 0.093 | −0.153 | 0.339 | – | – | – | |||
| Taşkent−Dawen | 0.048 | −0.163 | 0.259 | – | – | – | |||
| Taşkent−Guandao | −0.045 | −0.276 | 0.186 | – | – | – | |||
| Olenekian | 0.753 | 0.016 | Guandao−Dajiang | – | – | – | 0.326 | −0.062 | 0.714 |
| Taşkent−Dajiang | – | – | – | −0.016 | −0.405 | 0.374 | |||
| Taşkent−Guandao | – | – | – | -0.342 | −0.653 | −0.031 | |||
| Mid−Late Triassic | 0.158 | 0.895 | – | – | – | – | – | – | – |
| Temporal trends | |||||||||
| All data | <0.001 | <0.001 | L Pm.−Ind. | −0.356 | −0.481 | −0.232 | −0.658 | −0.830 | −0.487 |
| L Pm.−Ol. | −0.161 | −0.304 | −0.017 | −0.255 | −0.476 | −0.034 | |||
| L Pm.−M/L Tr. | 0.010 | −0.200 | 0.219 | −0.140 | −0.392 | 0.111 | |||
| Ind.−Ol. | 0.196 | 0.102 | 0.290 | 0.403 | 0.210 | 0.596 | |||
| Ind.−M/L Tr. | 0.366 | 0.186 | 0.546 | 0.518 | 0.291 | 0.744 | |||
| Ol.−M/L Tr. | 0.170 | −0.025 | 0.366 | 0.114 | −0.153 | 0.382 | |||
| Dajiang | <0.001 | 0.010 | L Pm.−Ind. | −0.430 | −0.697 | −0.163 | −0.475 | −0.947 | −0.004 |
| L Pm.−Ol. | −0.253 | −0.538 | 0.032 | −0.202 | −0.854 | 0.450 | |||
| L Pm.−M/L Tr. | −0.073 | −0.420 | 0.275 | −0.042 | −0.754 | 0.669 | |||
| Ind.−Ol. | 0.177 | −0.073 | 0.427 | 0.273 | −0.159 | 0.705 | |||
| Ind.−M/L Tr. | 0.358 | 0.001 | 0.714 | 0.433 | −0.070 | 0.935 | |||
| Ol.−M/L Tr. | 0.181 | −0.097 | 0.458 | 0.160 | −0.481 | 0.801 | |||
| Taşkent | <0.001 | <0.001 | L Pm.−Ind. | −0.441 | −0.629 | −0.253 | −0.845 | −1.252 | −0.437 |
| L Pm.−Ol. | −0.257 | −0.499 | −0.016 | −0.434 | −0.726 | −0.141 | |||
| L Pm.−M/L Tr. | 0.111 | −0.103 | 0.325 | −0.067 | −0.477 | 0.343 | |||
| Ind.−Ol. | 0.184 | −0.080 | 0.447 | 0.411 | −0.043 | 0.865 | |||
| Ind.−M/L Tr. | 0.552 | 0.315 | 0.790 | 0.778 | 0.242 | 1.314 | |||
| Ol.−M/L Tr. | 0.368 | −0.120 | 0.856 | 0.367 | −0.188 | 0.922 | |||
| Dawen | <0.001 | – | L Pm.−Ind. | −0.267 | −0.447 | −0.087 | – | – | – |
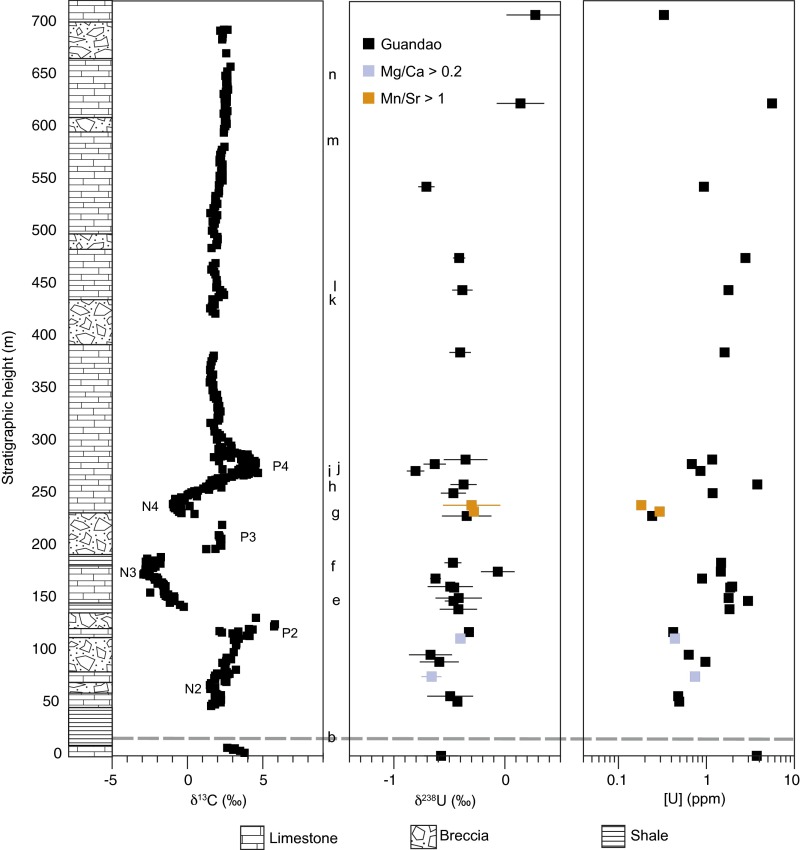
| Guandao | 0.487 | 0.078 | – | – | – | – | – | – | – |
Significant results are bolded. Dawen data are combined data from this study and ref. 11. We excluded intervals with n < 3, and, as such, we did not perform statistical comparisons for the Late Permian from Guandao. Ind., Induan; L Pm., Latest Permian; M/L Tr., Middle−Late Triassic; Ol., Olenekian.
Fig. S5.
Comparison of (A and C) δ238U and (B and D) [U] to geochemical indicators of (A and B) diagenetic alteration and (C and D) detrital influence for Dajiang (black), Taşkent (blue), and Guandao (red). (A and B) All ratios are parts per million/parts per million. The δ238U and [U] are not correlated with any of these proxies, suggesting that these records are primary. Mn/Sr ratios are low and suggest minimal diagenetic alteration. Spearman’s rank statistical results for each stratigraphic section (same color scheme as data points) are included for each indicator for diagenetic alteration. Significant P values (after Bonferroni correction, where α = 0.05/44 = 0.0011) are bolded and italicized. (C) The δ238U vs. indicators for detrital influence ([Al] and [Th]) and (D) uranium concentrations vs. normalized U/Al and Th/U ratios.
Finally, the trends in [U] from our stratigraphic sections agree with published records from shallow marine carbonates spanning the Permian−Triassic boundary interval in Saudi Arabia, Iran, Italy, and China (8, 11–13, 26, 27). Although local and diagenetic processes affect all samples of this age and undoubtedly account for some of the variation in our dataset, the most parsimonious explanation for the statistically supported trends in [U] and δ238U is that the dominant signal in the dataset is a primary signature reflecting the uranium composition of seawater.
Discussion
Statistically Significant Temporal Trends.
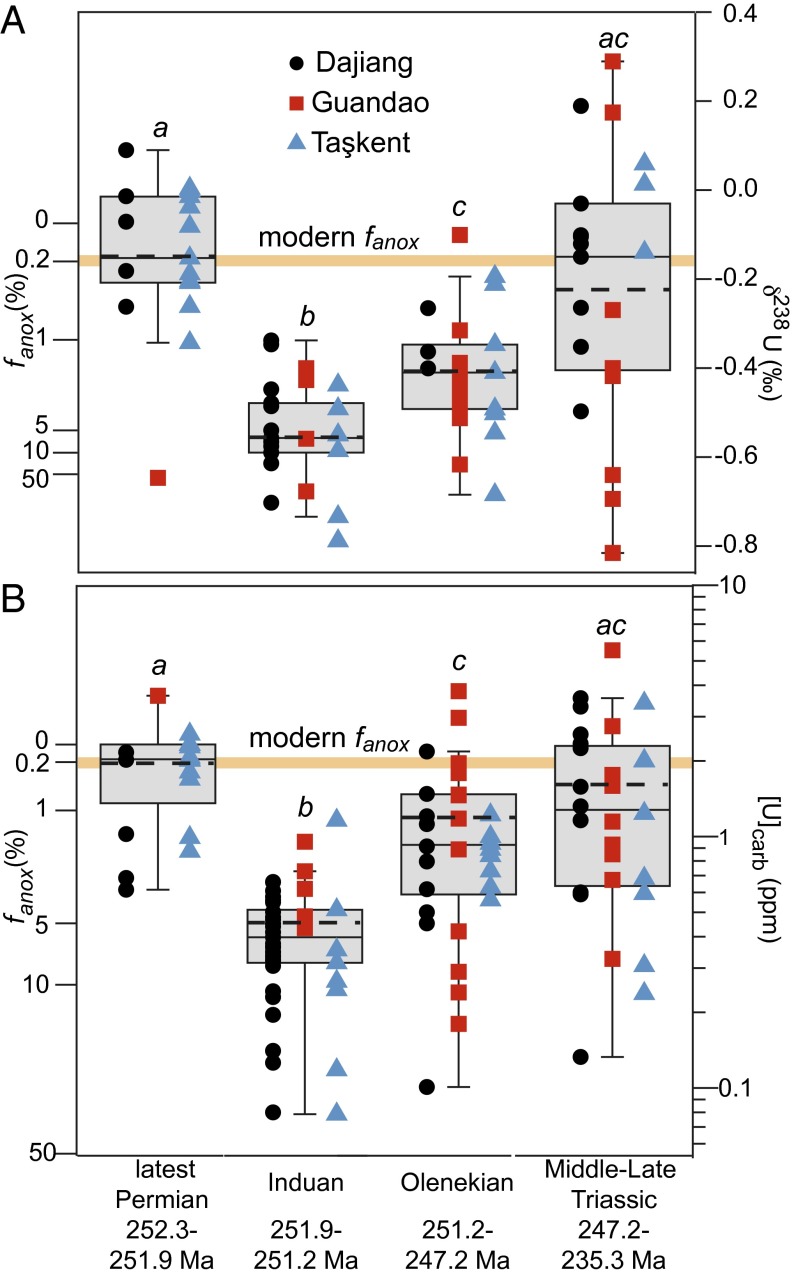
To determine whether the temporal trends we observe in δ238U and [U] are statistically significant, we used analysis of variance (ANOVA) (function aov in R) for our data categorized by general time intervals (Late Permian, Induan, Olenekian, and Middle−Late Triassic) (Table S1). Both [U] and δ238U data from shallow marine records differ significantly among time intervals (P values ≤ 0.01). We then used Dennett’s modified Tukey−Kramer Post-Hoc Test (function DTK.test in R) to run pair-wise comparisons between time intervals for all our data. The results for the combined dataset show that for both [U] and δ238U, the Induan is significantly different from the Late Permian, Olenekian, and Middle−Late Triassic compositions (Fig. 3).
Fig. 3.
(A) The δ238U and (B) [U] boxplots. Whiskers denote the minimum and maximum of data within 1.5 times the interquartile range from the median. The mean is marked by the dashed line. Steady-state model predictions for the extent of anoxia, fanox, are calculated for the best-estimate input δ238Uriv composition of −0.05‰ (Middle Trassic δ238U Composition), and suggest that, in the Late Permian and Late−Middle Triassic, the extent of anoxia was near the modern value, whereas, in the Early Triassic, the extent was larger. Statistical analyses show that latest Permian δ238U and [U] data (a) are significantly distinct from the Induan (b) but similar to the Middle−Late Triassic, whereas the Olenekian data represent a transitional period (c).
In addition, we applied one-way ANOVA and Dennett’s modified Tukey−Kramer Post-Hoc test to the [U] and δ238U records for the shallow marine stratigraphic sections (Table S1). For both Dajiang and Taşkent, the Induan δ238U values are significantly different from the Late Permian and Middle−Late Triassic, whereas [U] values are only significantly different between the Induan and the Middle−Late Triassic for Taşkent. The results from Dawen (combined with data from ref. 11) also indicate a significant difference between the Late Permian and Induan δ238U data. However, the Olenekian [U] and δ238U results are not consistent, and differ in whether or not they are significantly distinguishable from the Induan (Taşkent) or not (Dajiang).
In contrast, data from Guandao did not show significant differences between the various time intervals, suggesting that Guandao sediments on the platform slope may have been impacted by local anoxia/suboxia. These conditions could result in locally more negative δ238U if a greater proportion of 238U relative to seawater was reduced into proximally deposited sediments, which would not be captured in our measurements. Therefore, the presence of local anoxia may result in δ238U compositions that deviate from global seawater.
From these statistical results, we conclude that the Induan had significantly lower [U] and δ238U values than the uppermost Permian and the Middle−Upper Triassic at all sites, whereas the Olenekian is a transitional period. The uppermost Permian and Middle−Upper Triassic data are statistically indistinguishable, implying a recovery in [U] and δ238U to preextinction values.
Modeling Implications for Seafloor Anoxia.
A mass balance box model of seawater uranium and its isotopes (Fig. 1 and Fig. S6) demonstrates that the observed decreases in [U] and δ238U require an increase in bottom water anoxia in the global ocean. Scenarios involving a decrease in either [U] or δ238U of riverine uranium would account for a decrease in one metric but not both. Even simultaneous decreases in riverine [U] and δ238U would not reproduce the rapid observed decreases (Fig. S6). In contrast, expanding the area of seafloor impacted by anoxia efficiently removes and fractionates U, causing large, rapid, and sustained decreases in [U] and δ238U, consistent with the magnitude and rate of change of the negative shifts in [U] and δ238U at the extinction horizon.
Fig. S6.
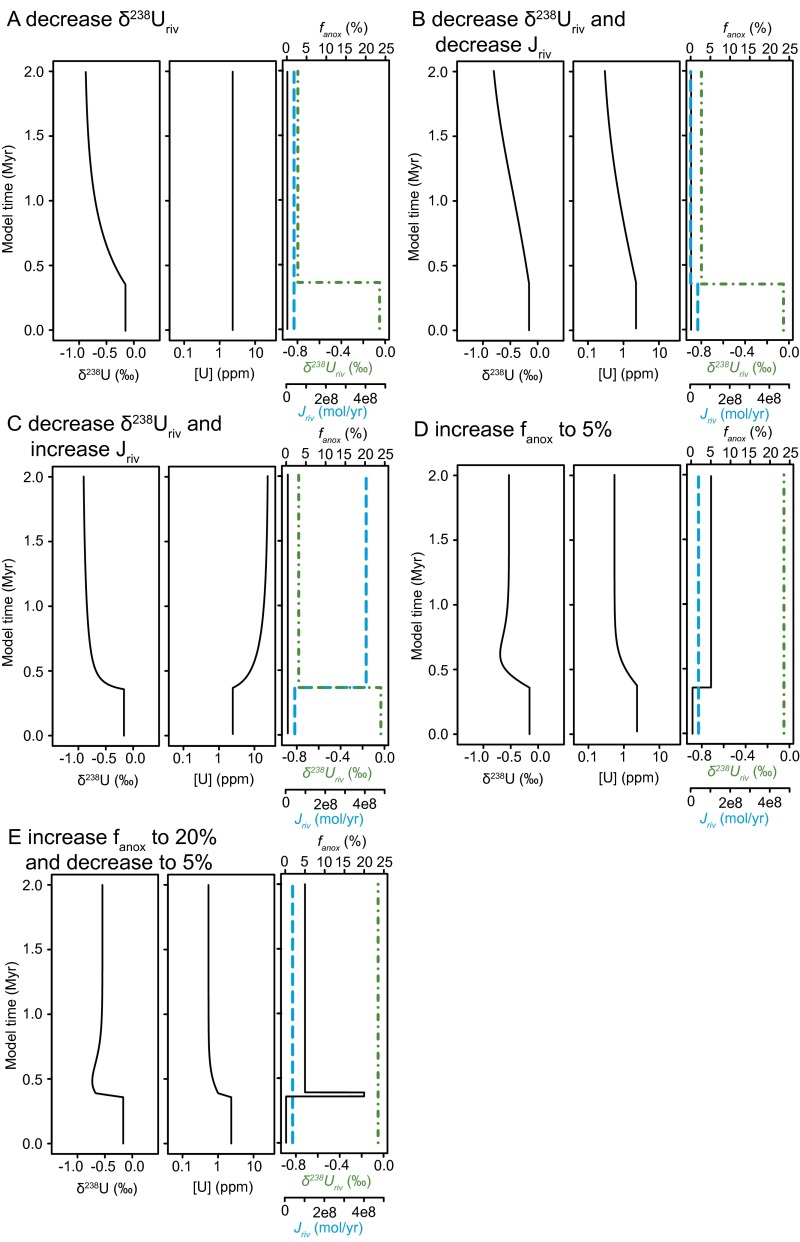
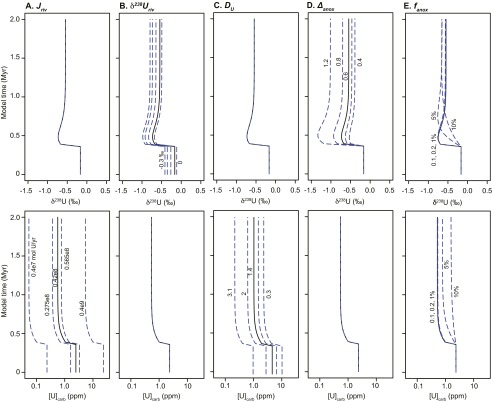
Details of box model predictions. Predicted carbonate δ238U and [U] behavior, where the third panel depicts temporal variation in forcing parameters fanox (black solid line), Jriv (cyan dashed line), and δ238Uriv (green dot-dashed line). (A) Decrease δ238Uriv to −0.8‰. (B) Decrease δ238Uriv to −0.8‰ and Jriv by an order of magnitude. (C) Decrease δ238Uriv to −0.8‰ and increase Jriv by an order of magnitude. (D) Increase fanox to 5%, comparable to steady-state estimate of increased anoxia from ref. 11. (E) Increase fanox to 20% for 3 × 105 y and maintain at 5% for 1 My.
The extent of Early Triassic anoxia implied by our box model calculations is substantial. Our model predicts an increase in the anoxic sink for uranium from 15% of the total removal flux in the latest Permian to 94% in the Induan, similar to the factor of 6 increase in the flux of U to anoxic facies calculated in ref. 11. However, the magnitude and rate of decrease in [U] and δ238U also require a factor of 100 increase in the extent of seafloor anoxia (fanox) across the extinction horizon, from 0.2% (28) to 20% of the seafloor during the extinction interval, followed by a 1.5-My interval during which 5% of the seafloor was anoxic (Figs. 1 and 3 and Fig. S6). During the rest of the Olenekian, 1% of the seafloor may have remained anoxic, still a fivefold increase over preextinction conditions (Fig. 3). Collectively, these findings indicate persistent and gradually decreasing anoxia for the 5 million years following the end-Permian mass extinction, followed by a return to preextinction conditions that are more positive than modern seawater composition (Middle Triassic δ238U Composition).
Anoxia and Earth System Recovery.
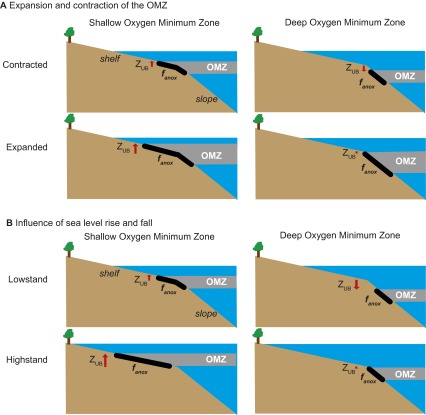
In the modern ocean, continental shelves comprise ∼7% of the seafloor area but host a disproportionate share of marine animal diversity, biomass, and the burial of biogeochemically important elements (e.g., carbon and sulfur). Our uranium data, combined with biomarker support for photic-zone euxinia (6) and petrographic, geochemical, and modeling evidence for an expanded oxygen minimum zone (OMZ) rather than deep-ocean anoxia (20, 29–31), indicate that anoxic waters may have bathed a large fraction of Early Triassic outer continental shelves and upper slopes in anoxic waters. These conditions could explain the limited diversity and ecological complexity of marine ecosystems (3), as well as the reduced maximum and mean body sizes of benthic animals (25).
Given the nonlinear hypsometry of the continental margin, fluctuations in the depth of the upper boundary of the OMZ could strongly influence the burial of reduced versus oxidized forms of carbon and sulfur, offering a potential explanation for the biogeochemical anomalies of the Early Triassic. For example, in the presence of a shallow OMZ, the area of seafloor covered by anoxic waters is sensitive to episodic expansion of the OMZ or variations in eustatic sea level (Fig. 4A and Fig. S7). Specifically, intervals of vertical expansion of the OMZ, or high sea level and extensive continental flooding, would be associated with expanding anoxic bottom waters. Consequently, the extent of seafloor anoxia (fanox) and the rate of organic carbon burial would covary with the depth of the upper boundary of the OMZ relative to the shelf−slope break (ZUB), potentially causing large δ13C excursions. Under this scenario, associated increases in pyrite burial would increase the δ34S of carbonate-associated sulfate (δ34SCAS), reduce the size of the sulfate reservoir, and promote conditions for δ34SCAS instability (5, 32).
Fig. 4.
Sensitivity of δ13C to changes in the depth of the upper boundary of the OMZ, ZUB. (A) Relationship between fanox and the depth of the upper boundary of the OMZ relative to the continental shelf−slope break, ZUB, for scenarios with a shallow OMZ (gray line) and deep OMZ (dashed blue line). (B) Temporal change in ZUB used in model. (C) Model output for δ13C. Model results are shown starting at 1 My, after the system has reached a quasi-steady state. Refer to Supporting Information for model details.
Fig. S7.
Conceptual model of the sensitivity of fanox to the depth of the upper boundary of the OMZ, ZUB. (A) The expansion of a shallow OMZ results in a greater area of continental shelf impacted by anoxic waters than an equivalent expansion of a deeper OMZ. Changes in ZUB are shown here relative to the shelf−slope break. (B) In an ocean characterized by a shallow OMZ that intersects the continental shelf, a rise in sea level results in a large increase in fanox. In an ocean with a deeper OMZ, an identical rise in sea level does not cause a large change in fanox. In both scenarios, a shallow depth of the upper boundary of the OMZ has a greater potential to affect fanox.
To test the potential for variations in ZUB to influence global carbon cycling, we constructed a box model of the geologic carbon cycle, modified from ref. 33 (Modeling the Effect of a Shallow OMZ). In the model, the magnitude of δ13C response to the same forcing can vary substantially depending upon the depth of the OMZ (Fig. 4C). Based upon our uranium data, we simulated a scenario in which the upper boundary of the OMZ deepens gradually across Early Triassic time while the frequency of oscillations in ZUB decreases (Fig. S8). By varying these two simple controls, we are able to reproduce the general behavior of the Early−Middle Triassic carbon cycle, with large, rapid excursions giving way to smaller and more prolonged variations. Importantly, we are able to produce the δ13C excursions without varying the magnitude of the forcing (variation in ZUB) or requiring any large external perturbation to the Earth system. This effect could account for the magnitude and persistence of Early Triassic δ13C and δ34S excursions after the initial negative excursion associated with Siberian Traps volcanism (4, 5, 32) (Fig. 2).
Fig. S8.
Modeling the sensitivity of δ13C to sea level change and the depth of the upper boundary of the OMZ (ZUB) and simulated Early−Middle Triassic perturbations. A, B, and E are equivalent to Fig. 4. (A) Relationship between fanox and ZUB for two scenarios: shallow and deep OMZ. (B) Temporal change in ZUB used in model. (C) Variations in fanox as determined by sensitivity to changes in ZUB. (D) Model output for Fborg. (E) Model output for δ13C. (F−H) Simulated Early to Middle Triassic δ13C perturbations. (F) Temporal fluctuations in ZUB relative to the shelf−slope break (SSB) used in model. We increase λ such that the wavelength of fluctuations in ZUB increases from ∼0.5 My to ∼3 My time scales, and with a deeper OMZ after 5 My. (G) Variations in fanox as determined by sensitivity to changes in ZUB. (H) Model output for δ13C.
In summary, uranium data confirm a central role for marine redox conditions in modulating Earth system recovery following the end-Permian extinction. The return of marine redox conditions to a preextinction state in the Middle Triassic was concurrent with stabilization of δ13C and δ34SCAS values and a return to baseline genus richness, ecological diversity, and animal body size (2, 3, 25). We propose that, as the redox gradient in the upper few hundred meters of the water column diminished due to a deepening of the OMZ and, perhaps, a reduction in total primary productivity (e.g., ref. 20), benthic communities recovered, and the sensitivity of organic carbon burial to subsequent variations decreased, stabilizing the global carbon and sulfur cycles (Fig. 4). Combined with the long-term trend of increasing seawater oxygenation during the Phanerozoic, long-term deepening of the OMZ and an associated decrease in the sensitivity of global biogeochemical cycles may also explain the trends toward greater taxonomic diversity and ecological complexity, as well as the reduced frequency of large carbon and sulfur isotope anomalies.
Materials and Methods
Uranium Box Model.
In the modern ocean, where the extent of anoxia is small (∼0.2%) (28) relative to conditions over most of Earth’s history, seawater δ238U is invariant at about −0.4‰ (15–17). If carbonates faithfully record seawater chemistry with no postdepositional effects (refs. 15–17 and 34, but see further discussion in ref. 34), then the δ238U of carbonates should decrease as regions of anoxic marine bottom waters expand. Because uranium has a residence time (3.2–5.6 × 105 y) (35) significantly longer than ocean mixing time (103 y), global seawater variations in [U] and δ238U should be reflected within local sediments.
The unique sensitivity of both δ238U and uranium concentrations to the extent of bottom water anoxia can be described by differential mass balance equations for the seawater uranium inventory and its isotopic composition, respectively,
| [1] |
| [2] |
where Nsw is the oceanic uranium inventory in moles, δ238U is the value of seawater, δ238Uriv is the value of the riverine source, Δanox = +0.6‰ is the effective fractionation factor associated with anoxic sediment deposition (17), and Δother is the effective fractionation factor associated with the remaining other sinks [+0.03‰, calculated to maintain isotopic steady state in the modern ocean (e.g., refs. 11 and 36)]. We simplify the inputs to Jriv, the riverine flux [modern value is 0.4 × 108 mol U/y (37)]. The outputs are assumed to consist of the anoxic sediment sink (Janox) and the sum of the other sinks (Jother), where Janox = 0.06 × 108 mol U/y (37) and Jother is calculated by mass balance to an initial steady-state value of 0.34 × 108 mol U/y. We further define the output flux terms Janox and Jother as
| [3] |
| [4] |
where fanox is the fraction of seafloor impacted by bottom water anoxia, and Kanox and Kother are rate constants calculated for the modern uranium system. We assume a constant Kanox, reflecting similar mechanisms of U reduction at the sediment−water interface (SWI) throughout the studied time intervals. Similarly, Kother is also assumed to be constant. The concentration of uranium in carbonates is estimated by converting the moles of U in the seawater reservoir, Nsw, and assuming constant seawater calcium concentrations and a distribution coefficient of 1.4 (38). The sensitivity of the model to varying [Ca] is evaluated in Uranium Biogeochemical Cycling and Model Sensitivity. The model was first evaluated with parameters for the modern ocean, and then the δ238Uriv term was adjusted to −0.05‰ to reflect a steady-state baseline value equal to the average Late Permian−Middle/Late Triassic seawater value as inferred from our data (Middle Trassic δ238U Composition). A detailed description of the uranium cycle is provided in Uranium Biogeochemical Cycling and Model Sensitivity, and additional box model results are presented in Fig. S6. An evaluation of model sensitivity is presented in Uranium Biogeochemical Cycling and Model Sensitivity and in Fig. S9. R code used in our analysis can be accessed at https://purl.stanford.edu/mr858ss1453.
Fig. S9.
Model sensitivity results. For each test, the U system is perturbed by increasing fanox to 20% and then sustained at 5%. Black lines represent model results for best-estimate parameter value described in Materials and Methods. (A) Jriv: values determined by uncertainty bounds on estimate from ref. 35, and extremes are order of magnitude increase and decrease. (B) The δ238Uriv: −0.3‰ [bulk earth (15, 39, 40)], −0.24‰ (16, 39–41), −0.15‰, −0.05‰, 0‰. (C) DU: 0.3 (lower bound from ref. 38), 0.6, 1.4 (38), 2, 3.1 (upper bound from ref. 38). (D) Δanox: 1.2 (maximum from ref. 17), 0.8, 0.6 (17), 0.5, 0.4. (E) Initial fanox: 0.1%, 0.2% (28), 1%, 5%, 10%.
To determine the [U] and δ238U relationships with fanox shown in Fig. 3, we assume steady-state behavior and solve Eqs. 1 and 2 for Nsw and δ238U, respectively, as a function of fanox,
| [5] |
| [6] |
Geologic Setting.
Our sample set includes three stratigraphic sections from the GBG, south China, and one stratigraphic section from the Aladag Nappe, Turkey (Fig. S1). Three of these sections were so shallow as to be oxygenated even if deeper waters (>100 m) were anoxic, and thus are less likely to have been impacted by diagenesis resulting from local redox conditions. From the GBG, we analyzed a suite of 86 samples for [U] and 55 samples for δ238U from Dajiang and 32 samples for [U] and δ238U from Guandao. We also analyzed three samples from the Dawen section, allowing us to compare our measured values across the Permian−Triassic boundary interval to those reported previously in a high-resolution δ238U and Th/U record for the 15 m spanning the extinction horizon at the same site (11). To determine whether variations in [U] and δ238U are globally reproducible, we also analyzed a suite of 36 samples for [U] and 31 samples from Taşkent, the Aladag Nappe, Turkey. We correlate the Taşkent section to the GBG using lithostratigraphy, conodont and foraminiferan biostratigraphy, and δ13C chemostratigraphy (4, 20, 42). Detailed description of the stratigraphic sections is provided in SI Materials and Methods (Figs. S2−S4).
Uranium Isotopic Analysis.
At least 4 g of sample powder was digested using 0.25 N Optima HCl, determined to be the optimal dissolution procedure (see SI Materials and Methods and Fig. S10). A 238U:236U sample to spike ratio of 10:1 was used to maximize both the internal precision and the external reproducibility of the δ238U measurements. Uranium was purified by a two-step ion exchange chromatography procedure using UTEVA resin (Eichrom), following procedures adapted from refs. 16, 43.
Fig. S10.
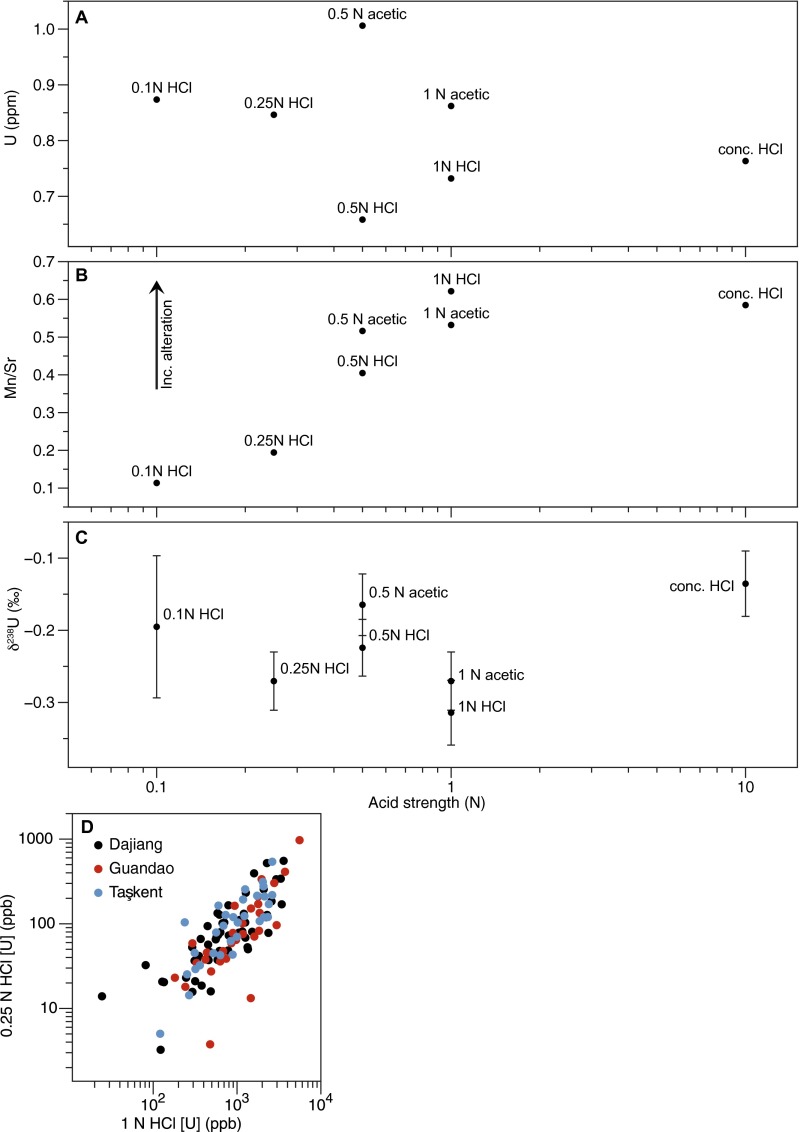
Results from carbonate leach experiments. (A) Uranium concentrations of the dissolved fraction show variation but no clear trend with acid type or strength. (B) Mn/Sr vs. [U] for different acid leaches. Higher Mn/Sr ratios are considered to be indicative of diagenetic alteration; however, all ratios here are low. (C) The δ238U for the different leaches generally fall within error of each other. Internal precision errors are 1 SE. (D) Comparison of [U] from 1 N HCl dissolution procedure (reported in Dataset S1) and [U] from 0.25 N HCl partial dissolution procedure for δ238U measurement.
Uranium isotopic compositions were measured in the ICP-MS/TIMS Facility at Stanford University on a Nu Plasma multicollector-inductively coupled plasma mass spectrometer (MC-ICP-MS). The 238U/235U ratios were corrected using an exponential law for mass bias assuming the certified spike 233U/236U ratio of 1.01906 (44), followed by correction for contribution of 238U from the spike. The 238U/235U ratios are reported relative to reference standard CRM-145 in standard delta notation. Internal precision (2 SE) of measurements of standards was typically 0.07‰. Average measurement reproducibility (2σ), assessed by replicate measurements of the same sample solution, is 0.11‰ (n = 83). Additionally, we processed four samples twice to evaluate external reproducibility, where one limestone sample had a reproducibility of <0.01‰ and three dolomitic samples had an average reproducibility of 0.4‰ (Dataset S1; discussed in Diagenetic Alteration and Dolomitization). We evaluated reference materials BCR-2 (Columbia River Basalt), HU-1 (Harwell Uraninite), CRM-129a, and an internal carbonate standard to track reproducibility and agreement with previously published values; a summary is provided in Supporting Information and Fig. S11. A full description of analytical methods is included in Supporting Information, and the data from this study are presented in Dataset S1.
Fig. S11.
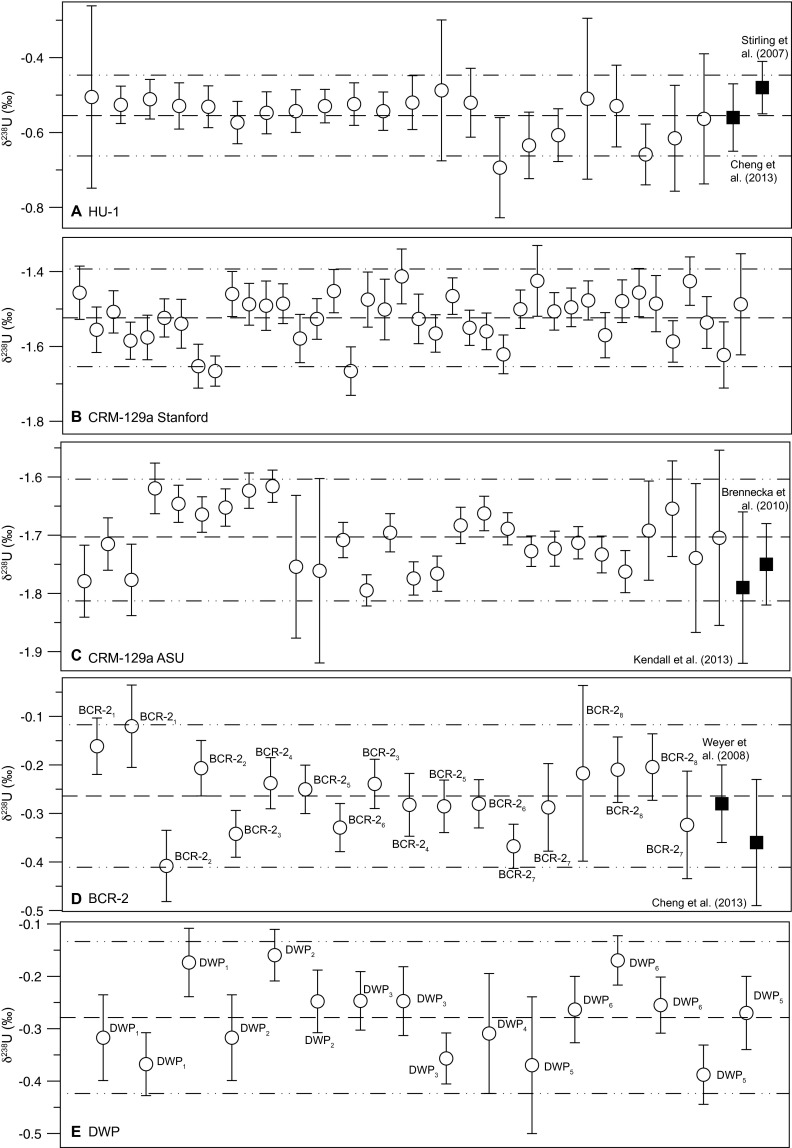
Reproducibility of standards. Our data are shown in open circles, and published values are shown as black squares. Dotted lines show the mean and 2σ of the δ238U of all analyses. (A) Measurements of HU-1 solution. (B) Measurements of Stanford CRM-129a and (C) separate aliquot of CRM-129a obtained from ASU. (D) Measurements of rock standard BCR-2. Error bars are 2 SE on the measurement (internal precision) for our data and 2 SD on total replicates for published data. Each data point represents a measurement of a total of eight replicates of BCR-2 (dissolved from powder), illustrated here by subscripts. (E) Measurements of internal carbonate standard DWP. Error bars are 2 SE on the measurement (internal precision) for our data. A total of six complete replicates of DWP (dissolved from powder) were measured, as denoted by the subscripts. Raw data are also presented in Dataset S1.
SI Summary
The uranium isotopic data presented in this study were measured from limestone samples collected from two sites located on opposite sides of the Tethys ocean: three stratigraphic sections from the GBG, an isolated carbonate platform in South China; and a stratigraphic section through a shallow mixed carbonate−clastic platform or ramp in Turkey. A summary of the geologic setting is described in SI Materials and Methods.
The uranium concentration of seawater is controlled by variations in the major inputs and output fluxes into the ocean; specifically, the concentration reflects the balance between changes in the riverine delivery of weathered U and removal via microbial reduction in marine sediments (Uranium Biogeochemical Cycling and Model Sensitivity). The uranium isotopic composition of seawater provides an additional constraint to differentiate between these controls on seawater [U], which have different consequences for seawater δ238U. To evaluate our model framework and thus the interpretations of the observed records, we analyze the sensitivity of the model to different parameter values (Uranium Biogeochemical Cycling and Model Sensitivity). In general, the analysis supports the overarching interpretations of our data: An expansion of bottom water anoxia best explains the protracted low values in [U] and δ238U during the Early Triassic.
We also evaluate indicators for diagenetic alteration in the measured limestone samples, including petrographic observations and statistical analyses of associated geochemical data. In this discussion (Diagenetic Alteration and Dolomitization and Statistical Analysis: Interpretation), we conclude that the general trends reconstructed from limestone samples, screened to exclude those with significant diagenetic alteration, represent fluctuations in global seawater uranium composition. In contrast, the dolomitized samples do not appear to be reliable recorders of seawater uranium isotopic composition.
In Middle Trassic δ238U Composition, we discuss explanations for the Late Permian and Middle−Late Triassic δ238U values that are more positive than observed in the modern ocean. Finally, we describe the framework, results, and implications of the model linking sea level and the carbon cycle in Modeling the Effect of a Shallow OMZ.
SI Materials and Methods
Geologic Setting.
Our sample set includes three stratigraphic sections from the GBG, south China, and one stratigraphic section from the Aladag Nappe, Turkey (Fig. S1A). Three of these sections are sites that were so shallow as to be oxygenated even if deeper waters (>100 m) were anoxic, and thus are less likely to have been impacted by diagenesis resulting from local redox conditions.
GBG, south China.
The GBG is an exceptionally preserved isolated carbonate platform in the Nanpanjiang Basin of the equatorial eastern Tethys (42). The platform is exposed in geologic cross section along a syncline running roughly north to south at the town of Bianyang (42). Platform architecture, sedimentology, biostratigraphy, and isotope chemostratigraphy have been well studied at the Bianyang syncline (e.g., refs. 42 and 45), and a number of geochemical studies on environmental conditions at the end-Permian mass extinction have been conducted at the GBG (e.g., refs. 11, 20, and 46).
Exposure of the platform permits measurement of stratigraphic sections and collection of high-resolution sample sets recording the full interval from platform initiation during the latest Permian to drowning and termination during the Late Triassic (Fig. S1B). At Dajiang, a 2,500-m-thick shallow marine section (intertidal to tens of meters water depth) in the platform interior, the uppermost Permian fossiliferous limestone is overlain by 8–16 m of thrombolitic microbialite at the Permian−Triassic transition (21) (Fig. S2). Lower Triassic strata continue with ∼50 m of thin-bedded lime mudstone and ∼100 m of overlying oolitic dolograinstone. The Induan−Olenekian boundary is located at the start of ∼180 m of peritidal cyclic limestone, which is overlain by ∼700 m of pervasively dolomitized peritidal facies containing the Lower−Middle Triassic boundary. Middle and Upper Triassic strata consist of fossiliferous limestone. The Dawen section is also located in the platform interior, and the stratigraphy at Dawen is similar to Dajiang across the Permian−Triassic boundary interval.
At Guandao (Fig. S3), a ∼700-m section deposited in deeper-water facies on the platform slope (hundreds of meters water depth), uppermost Permian strata consist of 5 m of lime packstone followed by ∼40 m of shale that is occasionally covered. The extinction horizon is located within this covered section. The remaining ∼700 m of strata is composed of alternating lime mudstone and breccia: Lower Triassic strata continue with ∼20 m of lime mudstone overlain by 21 m of breccia consisting of oolitic packstone clasts. The next ∼150 m consists of alternating mudstones and oolitic packstones. This is overlain by ∼460 m of alternating shale−limestone stratigraphy. We correlate within the GBG using lithostratigraphy, conodont and foraminiferan biostratigraphy, and δ13C chemostratigraphy (4, 20, 42). Details are provided in Figs. S2 and S3.
Fig. S3.
Guandao. Stratigraphic column, δ13C (22), δ238U, and [U] data for Guandao (black), samples with Mg/Ca > 0.2 (gray), and samples with Mn/Sr > 1 (orange). The δ238U error bars are 2σ. Dashed line indicates extinction horizon. Chemostratigraphic correlations between sections are based on negative and positive local maxima in δ13C and are denoted as “N” and “P”,” respectively, and are numbered following refs. 5 and 22. Refer to Fig. S2 for corresponding geochronological data. Conodont first occurrences: (b) Hindeodus parvus, (e) Neospathodus dieneri, (f) Novispathodus waageni, (g) Neospathodus bransoni, (h) Triassospathodus homeri/symmetricus, (i) Chiosella timorensis, (j) Nicoraella germanica/kockeli, (k) Paragondolella bulgarica, (l) Neogondolella constricta, (m) Budurovignathus mungoensis, and (n) Metapolygnathus polygnathiformis.
We analyzed a suite of 86 samples for [U] and 55 samples for δ238U from Dajiang and 32 samples for [U] and δ238U from Guandao. We also analyzed three samples from the Dawen section. These samples allow us to compare our measured values across the Permian−Triassic boundary interval to those reported previously in a high-resolution δ238U and Th/U record for the 15 m spanning the extinction horizon at the same site (11).
Aladag Nappe, Turkey.
To determine whether variations in [U] and δ238U are globally reproducible, we also analyzed limestone samples from the Aladag Nappe, Turkey. This region was located along the western Tethys, and is an allochthonous block that was thrust over the autochthonous series of the Tauride block during the Eocene (47–49). Taşkent contains a ∼1-km-thick shallow marine mixed carbonate and siliclastic section that spans the Upper Permian to the Middle Triassic (40) (Fig. S4). It begins with 48 m of uppermost Permian fossiliferous lime packstone. The Permian Triassic boundary is contained within a 0.5-m bed of oolitic limestone overlain by 1 m of microbialite. Lowermost Triassic strata include 20 m of lime mudstone overlain by 25 m of oolitic grainstone. The next ∼600 m, which contains the remainder of Lower Triassic stratigraphy and the Lower−Middle Triassic boundary, consists of alternating beds of 10-cm to 5-m-thick strata of fine-grained limestone, 0.5-m to 2-m-thick strata of oolitic packstone and grainstone, and <1-m to 6-m-thick strata of shale. Middle Triassic stratigraphy continues with 11 m of massive lime wackestone/packstone, overlain by 132 m of covered shale. Alternating massive lime packstone (strata of 3 m to 27 m thickness, with some oolitic beds) and covered shale (strata of 1 m to 9 m thickness) continue for the remainder of the section.
We analyzed a suite of 36 samples for [U] and 31 samples for δ238U from Taşkent. We correlate the Taşkent section to the GBG using lithostratigraphy, conodont and foraminiferan biostratigraphy, and δ13C chemostratigraphy (4, 20, 42). Details are provided in Fig. S4.
Analytical Methods.
Carbon and oxygen isotopic analyses.
Data from the GBG were previously published in refs. 4 and 20. Carbon and oxygen isotope analyses for Taşkent were performed in the Stable Isotope Biogeochemistry Laboratory at Stanford University. Three hundred and thirty-seven samples were analyzed using a Finnegan MAT252 mass spectrometer coupled to a Kiel III carbonate device. Between 50 μg and 100 μg of limestone powder were reacted in phosphoric acid (H3PO4) at 70 °C for 600 s. All δ13C and δ18O values are reported relative to Vienna Pee Dee Belemnite (V-PDB).
Concentration measurements.
Samples selected for concentration measurements were powdered using a 0.8-mm dental drill bit to target micritic areas and avoid veins possibly associated with altered carbonate. The powders were dissolved using 1 N hydrochloric acid (HCl); insoluble residues were removed via centrifugation. The liquid fraction was measured for [U] and [Th] on a Nu Attom ICP-MS at the ICP-MS/TIMS Facility at Stanford University (for Dajiang) and on a Thermo X-series 2 ICP-MS at Chemostrat, Inc. (for Taşkent and Guandao).
For U and Th analyses of Dajiang samples, gravimetric concentration standards were used to build a five-point calibration curve, and standards were run every three samples to monitor and correct for instrument drift. Concentrations between the bracketing standard and samples were matched as closely as possible, and washout between analyses was monitored until signals on the electron multiplier returned to background levels. Major and minor elemental concentrations for Dajiang samples (e.g., Ca, Mg, Al, Sr, Mn) were measured on a Thermo Scientific ICAP 6300 Duo View ICP-optical emission spectrometer (OES) in the Environmental Measurements 1 Laboratory at Stanford University. Major and minor elemental concentrations for Taşkent and Guandao samples were measured on a Thermo iCAP 6500 ICP-OES and Thermo X-series 2 ICP-MS, respectively, by Chemostrat, Inc. Because burial diagenetic fluids are typically depleted in Sr and enriched in Mn relative to seawater (50), samples for δ238U measurements were additionally screened based on measured Mn/Sr, where samples with Mn/Sr > 1 were excluded. Total organic carbon (TOC) was collected on a subset of 93 samples using a CE440 Elemental Analyzer at the Marine Science Institute Analytical Laboratory at the University of California, Santa Barbara.
Uranium isotopic analyses.
Because contamination by detrital material can substantially alter the δ238U values, we performed a series of leaching experiments on an internal carbonate standard to evaluate the influence of different acids and acid molarities, from 0.1 N HCl to concentrated HCl, and 0.5 N to 1 N acetic acid, on measured [U] and δ238U values (Fig. S10). We found that lower-molarity HCl leaches (i.e., 0.1–0.5 N HCl) appeared to selectively dissolve the primary seawater carbonate fraction based on lower Mn/Sr ratios. Whereas uranium concentrations in the digested fraction of each sample did not appear to scale with acid molarity, the concentrated HCl digestion produced the most positive δ238U value, likely indicating the dissolution of organic or detrital material. The lower-molarity HCl leaches (0.1 N, 0.25 N, and 0.5 N) all produced lower Mn/Sr ratios compared with the higher-molarity leaches, suggesting minimal incorporation of diagenetic chemical contaminants. Accordingly, we chose 0.25 N HCl for the sample dissolutions for isotopic analysis. Compared with the 1 N HCl complete dissolution used to evaluate [U], the 0.25 N HCl dissolution produced an average of 11% of the measured [U] (Fig. S10D). Nonetheless, the general trends in [U] were preserved for each stratigraphic section, and comparison of replicates suggests that the amount of U leached does not affect δ238U values.
Sample powders were produced by crushing at least 4 g of trimmed rock chips in a steel mortar and pestle. This was calculated to be the minimum amount of an average Triassic carbonate to produce enough uranium for a minimum of three replicate isotopic measurements. The homogenized bulk carbonate sample was digested using 0.25 N Optima HCl. Acid was added to the powder in aliquots of 10–20 mL, and Savillex dissolution vessels were invigorated using an ultrasonic sonicator and orbital shaker table until the digestion appeared to be complete. The soluble fraction, in addition to very fine unreactive particles remaining from the digestion, was decanted to allow fresh acid to be added to the carbonate slurry. After a total of ∼60 mL of 0.25 N HCl had been added to the digestion vessels and allowed to react, the dissolved fractions were removed via centrifugation and evaporated to dryness. These were treated with concentrated Optima nitric acid (HNO3) to remove organics, evaporated, and redissolved in 10 mL of 3 N HNO3 for column chemistry. A small fraction was removed to measure the uranium concentration via ICP-MS to determine the amount of 233U−236U double spike (IRMM-3636a) to add. A 238U:236U sample to spike ratio of 10:1 was used to maximize both the internal precision and the external reproducibility of the δ238U measurements.
Uranium was purified by a two-step ion exchange chromatography procedure using UTEVA resin (Eichrom) in 0.3-mL Teflon columns with 5-mL reservoirs, following procedures adapted from refs. 16 and 43. This procedure resulted in yields of >97% for U and appropriate separation from Th, with yields of > 87% in the Th aliquant. Procedural blanks (n = 5) yielded a mean of 73 pg U for a mean sample yield of 371 ng U obtained after column separation (∼0.02%).
After column procedures, the U fractions were evaporated to dryness and treated with concentrated HNO3 to remove organic material that may have been contributed by the column resin and then redissolved in 2% HNO3 for measurement. The isotopic composition of the resulting solutions (∼50 ng of uranium per analysis) was measured in the ICP-MS/TIMS Facility at Stanford University on a Nu Plasma MC-ICP-MS using a desolvating nebulizer (Nu Instruments DSN-100). U isotopes were analyzed statically with 238U, 236U, 235U, 233U, and 232Th measured simultaneously on Faraday collectors operating with 1011 Ω resistors. Voltages on 235U were targeted to be >50 mV to ensure optimal signal-to-noise ratios on the 235U collector. Every two to three samples were bracketed using CRM-145 [also known as NBL-112A; 238U/235U = 134.85 (51)] and corrected for drift between and within sessions. Concentrations between samples and standards were matched as closely as possible, and washout between measurements was monitored until signals on all detectors returned to background levels.
The 238U/235U ratios were corrected using an exponential law for mass bias assuming the certified spike 233U/236U ratio of 1.01906 (44), followed by correction for contribution of 238U from the spike; the contribution of 235U is negligible. The 238U/235U ratios are reported relative to a standard reference material (CRM-145) in standard delta notation. Isotope ratio errors were propagated by summation in the quadrature and reported as SDs (2σ). The abundance sensitivity of 238U on 237U was determined to be <4 ppm. Interference from 232Th hydride on 233U was minimized by ensuring adequate separation of Th during column chemistry, and 232Th was monitored during the isotopic analysis at average levels of 0.5 mV, or about 0.04% of the 233U signal. Internal precision (2 SE) of measurements of standards was typically 0.07‰. Mean measurement reproducibility (2σ), assessed by replicate measurements of the same sample solution, is 0.11‰ (n = 83). Additionally, we processed four samples twice to evaluate external reproducibility, where the limestone sample (n = 1) had a reproducibility of <0.01‰ and the dolomitic samples (n = 3) had a mean reproducibility of 0.4‰ (Dataset S1; discussed in Diagenetic Alteration and Dolomitization).
Reference materials.
Measurements of reference materials (Fig. S11) are consistent with certified or previously reported values. Aliquots of a basalt rock reference material, BCR-2 (USGS reference material from Bridal Veil Flow Quarry), were dissolved in HF−HNO3. The powders were then treated with HNO3−HCl, evaporated to dryness, redissolved in 3 N HNO3, spiked, and processed using the UTEVA column chemistry described previously. One aliquot of BCR-2 was dissolved and measured with every 25–35 unknown samples. The isotopic measurements of BCR-2 average −0.26 ± 0.15‰ (n = 18), in agreement with refs. 15 and 52. For HU-1 (Harwell Uraninite) we obtain a mean δ238U value of −0.55 ± 0.11‰ (n = 22), in agreement with refs. 16 and 52.
For the synthetic reference material, CRM-129a, we measured a mean δ238U value of −1.52 ± 0.13‰ (n = 40, Fig. S11). This value differs from previously published values of −1.79‰ (53) and −1.75‰ (54). However, an aliquot of CRM-129a obtained from Arizona State University, which was reported in ref. 53, yielded a mean δ238U value of −1.71 ± 0.10‰ (n = 28), in agreement with the previously reported values. Therefore, CRM-129a appears to be heterogeneous in 238U/235U composition.
An internal carbonate standard, DWP, was made using uppermost Permian carbonate samples from Dawen. Carbonate rock was powdered in a tungsten carbide shatterbox and prepared using the same procedure as the unknown samples. One aliquot was processed for every 25–35 unknown samples. Values of DWP average −0.28 ± 0.14‰ (n = 16); long-term averages are shown in Fig. S11.
Our results from a variety of reference materials indicate that the methods used for analytical corrections, column chemistry, and the calibrated spike concentrations result in agreement with previously reported isotopic values for samples, and reproducible results for an in-house carbonate sample.
SI Discussion
Uranium Biogeochemical Cycling and Model Sensitivity.
Marine uranium cycle.
Uranium occurs in two redox states in natural waters: U(VI) and U(IV). Under oxygenated conditions, U(VI) is abundant as the uranyl ion (UO22+) and forms a suite of aqueous calcium and carbonate complexes (55). In the absence of oxygen, U(VI) is reduced to U(IV), which is poorly soluble and precipitates as uraninite in sediments (UO2) (e.g., ref. 56). Moreover, 238U is preferentially reduced from U(VI) to U(IV) relative to 235U, leaving the residual U(VI) with a lower δ238U value compared with reduced uranium in sediments (15, 16). Therefore, if uranium reduction is increased, the residual aqueous U(VI) decreases in both [U] and δ238U.
In the modern ocean, uranium is a conservative element with a concentration of ∼13.9 ± 0.9 nM (35, 57) and a δ238U composition of approximately −0.4‰ (15–17, 39, 40, 58). The inputs into the ocean are dominated by riverine runoff (from 65% to 87% of the total input), whereas the magnitude of groundwater and aeolian fluxes are poorly constrained, but are relatively small (35, 37). Riverine δ238U values have a mean similar to the uranium isotopic composition of continental crust (i.e., basalts and granites) of −0.29‰ to −0.31‰ (15, 39, 40)), but can range from −0.72‰ to 0.06‰ (16, 39–41). Aeolian δ238U values are assumed to be near mean crustal values. The isotopic value for groundwater inputs to the ocean has not yet been determined but is likely to be similar to riverine inputs.
There are five major sinks for uranium from the ocean: anoxic/euxinic sediments, suboxic sediments, adsorption to Fe oxides and Mn oxides, hydrothermal alteration of basalt, and incorporation into carbonates (15, 16, 34, 35, 37, 53). First, removal of uranium into anoxic or euxinic (waters with free hydrogen sulfide) sediments represents 15–24% of the total sinks (35, 40), with a modern flux of ∼7–12 Mmol/y, characterized by δ238U values measured in Black Sea sediments and Phanerozoic black shales that are 0.35–0.80‰ more positive relative to seawater (15, 36). Laboratory cultures of uranium reducing bacteria demonstrate that the preferential partitioning of 283U into U(IV) is due to fractionation during biotic reduction, whereas abiotic reduction results in only a small to negligible fractionation (18, 59, 60). The observed offset between seawater and reduced marine sediments can be considered an effective fractionation factor (Δ ≈ 0.6‰), or the integrated fractionation between seawater and the sediment column where biotic reduction is occurring (17). Second, although the suboxic sediment uranium accumulation rate, normalized per unit area, is an order of magnitude less than in anoxic sediments, suboxic sediments are extensive and therefore comprise a substantial sink with a slightly more positive δ238U value relative to seawater (15, 17, 35). Third, adsorption to Fe oxides and Mn oxides represents a small removal flux of ∼1.6–6 Mmol/y (2% of total sinks) (35, 37) with a distinct negative δ238U signature that is ∼0.24‰ lighter than seawater (15, 53, 61). Fourth, hydrothermal alteration of basalt removes an estimated 5.7–27 Mmol U/y (12% of the total sinks) (35, 37), but only a small fractionation is observed (net Δ ≈ 0.2‰) (39) because uranium is assumed to be quantitatively removed by this process (15). Finally, biogenic carbonate and silica comprise about 30% of the total sinks, with minimal fractionation (35). Primary (skeletal) carbonates have δ238U compositions that reflect seawater values (15–17, 34), although a study of modern bulk carbonate sediments from the Bahamas suggests that there may be a constant, positive 0.2‰ offset from seawater in the uppermost 40 cm of the sediment column (34), possibly from small contributions of detrital material or from authigenic U precipitation with an anoxic signature.
Uranium reduction occurs primarily in sediments or at the SWI (62) where abundant mineral surfaces and microbes, such as Fe- and sulfate-reducing bacteria, overcome the inhibition imposed by the aqueous speciation of uranyl with Ca2+ and CO32− (63, 64). Because U reduction occurs in marine sediments and therefore reflects seafloor conditions, we construct a mass balance box model to directly link changes in δ238U and [U] to the area of seafloor in contact with anoxic bottom waters.
Based on our box model framework, variations in uranium input and output fluxes required to generate a rapid negative excursion in δ238U are constrained by possible variations in Jriv, δ238Uriv, and fanox (Fig. 1 and Fig. S6). Because the riverine flux is the dominant source of uranium to the ocean, changing weathering rates or source rock lithology will impact both Jriv and δ238Uriv. Decreasing Jriv produces a small, gradual, and transient decrease in δ238U (Fig. 1, dashed line). Conversely, if the riverine flux increases, then δ238U would increase by a small amount, bounded by the riverine δ238U value. An instantaneous decrease in δ238Uriv to −0.8‰ can generate a slow but large decrease in δ238U (Fig. 1 and Fig. S6A). Alternatively, simultaneously decreasing Jriv by an order of magnitude and δ238Uriv to −0.8‰ (Fig. 1 and Fig. S6B) produces a slower decrease in δ238U because the reduced input flux has less of an impact on the seawater reservoir. Finally, the observed rate of decrease in δ238U across the end-Permian extinction interval can be approximated by decreasing δ238Uriv to −0.8‰ and increasing Jriv by an order of magnitude (Fig. S6C), but this scenario results in an increase in carbonate [U], contrary to the observed decrease.
Furthermore, a change in the riverine isotopic composition of this magnitude would require the dominant weathering lithology to shift from the modern distribution, which is dominated by crustal rocks (65), to very negative sources [e.g., predominantly banded iron formations or manganese oxides, or carbonates deposited under reducing conditions (15)]. Such a complete shift is unlikely and is not supported by reconstructions of exposed lithology in the Late Permian and the Early Triassic (65). Accordingly, our quantitative analysis suggests the only way to generate rapid and large excursions in [U] and δ238U is to alter the output fluxes. The estimated steady-state value for fanox during the Induan (Fig. 3)—comparable to the modeled changes in the anoxic sink in ref. 11—would produce concurrent negative shifts in [U] and δ238U (Fig. S6D). However, these shifts do not match the rate of change demonstrated by our data (Fig. 1). If fanox is increased to 20% for 30,000 y and maintained at 5% for 1.5 My, δ238U values undergo a rapid −0.4‰ shift concurrent with a large decrease in U concentrations (Fig. 1 and Fig. S6E). This increase in the extent of anoxia best reproduces the magnitude and rate of decrease in our [U] and δ238U records.
Model sensitivity analysis.
The application of uranium isotopes to reconstruct paleoredox conditions has only recently been developed, and, as a result, the details of 238U/235U fractionation in marine settings are incompletely known. Nevertheless, the mass balance framework provides a useful approach for constraining the effects of changing inputs and outputs to the ocean. Using a uranium concentration and isotopic mass balance model, pervasive marine anoxia is the most consistent interpretation for the observed [U] and δ238U signals. Given the uncertainties in the marine uranium cycle, we address the consequences of variations in each of the key parameters by testing the sensitivity of the model to different values of these parameters (Fig. S9). As discussed in Modeling Implications for Seafloor Anoxia, changing the initial riverine U concentration or isotopic composition affects only the carbonate [U] or δ238U, but not both (Fig. 1 and Fig. S9 A and B).
The distribution coefficient of uranium into calcium carbonate (DU) has been experimentally determined to range from 0.2 to 10 at 25 °C and 1 atm (66), and, in this study, we use an average value of 1.4 observed in Ocean Drilling Program site 984 (38). The partition coefficient for uranium into aragonite has been estimated at 1.83 and is generally thought to be higher than calcite (66, 67). In addition to shifts in calcite−aragonite mineralogy, this parameter is affected by the concentration of carbonate ion and thus indirectly reflects changes in pH and temperature (68). However, the effect of mineralogy, carbonate chemistry, and temperature on 238U/235U has not been extensively characterized, although δ238U measurements of aragonite and high-magnesium calcite primary precipitates have been shown to exhibit little to no offset from seawater (34). In addition, laboratory-precipitated calcite showed only minor (<0.1‰) fractionation between the liquid medium and the solid (60). Based on these observations, changing mineralogy between aragonite and calcite polymorphs likely affects only the concentrations and not the isotopic composition, although the effect of other factors (pH, [U], etc.) remains unknown. Nonetheless, if carbonate precipitation were dominated by the aragonite polymorph at the Permian−Triassic boundary (69, 70), DU would increase. Higher seawater [Ca] from ocean acidification during the end-Permian mass extinction (46) would also result in a larger DU. However, this would predict an increase in [U] (Fig. S9C), which is counter to the observed decrease in the Induan. In fact, the decrease in Induan seawater [U] may actually have been much larger, but the ensuing decrease as recorded in the carbonate sediments was dampened by a larger DU.
Similarly, a sensitivity test of the effective fractionation factor, Δanox, also predicts a change in only the isotopic composition and not the concentrations (Fig. S9D). The fractionation factor is poorly constrained, and the effects of temperature, pH, and uranium concentrations on this parameter are still under investigation. Although unlikely based on studies to date (18, 59, 60), the effective fractionation factor could be affected by seawater [U] and the rate of microbial reduction. Furthermore, the degree of uranium drawdown influences the effective fractionation factor (17). For example, if the effective fractionation factor were expressed as its maximum potential of +1.2‰ (the full kinetic fractionation observed from microbial studies), lower values for fanox could explain the observed decrease in δ238U. Conversely, if the effective fractionation factor were <+0.6‰ because of rapid reduction and depletion of pore water U, the actual fanox would have been much larger than estimated by our model. The latter situation would occur in restricted settings or under suboxic conditions (17), and if these conditions prevailed during the Induan, the model results underestimate the extent of bottom water anoxia.
Finally, the model assumes that fanox in the latest Permian had a similar value to the modern ocean, where ∼0.2% of the seafloor experiences anoxic conditions (Fig. S9E). Previous studies do not agree on the extent of anoxic conditions during this time (e.g., refs. 8 and 71). If the oceans were more than a factor of 25 more anoxic (initial fanox ≥ 5%) before the extinction event, an instantaneous increase to 100% in our model predicts decreases in both δ238U and [U] that are much slower than observed in our record and do not reach the negative values that we observe. The slower decrease is a result of only a 20-fold (where initial fanox = 5%) or 10-fold (where initial fanox = 10%) increase in fanox at the extinction horizon, because fanox cannot exceed 100%. However, if the oceans were a factor of 5 more anoxic (initial fanox = 1%) or less, predicted [U] and δ238U values would be indistinguishable from the ones presented in Fig. 1B. This scenario is comparable to variations in Kanox, or changing the mechanism of U reduction at the SWI.
In summary, the carbonate uranium concentration and isotopic composition are uniquely sensitive to different values of the riverine flux and isotopic composition, DU, and the effective fractionation factor. Changing one of these factors may affect either [U] or δ238U but not both. Only changing the initial fanox affects both [U] and δ238U, but our modeling suggests a quantitative maximum bound on the extent of anoxia in the Late Paleozoic. Because the rapid decrease in both [U] and δ238U cannot be replicated if the initial fanox is greater than 1%, the Late Permian oceans must have been relatively well oxygenated. On the other hand, varying the effective fractionation factor, Δanox, does affect the degree to which fanox must increase to match the data. However, a large change in Δanox is not supported by studies to date. Finally, the model sensitivity tests show that altering most of the variables (Jriv, δ238Uriv, DU) affects merely the absolute values of the predicted records, but preserves the trends. Only by changing Δanox and fanox can the model generate varying magnitudes of the excursion in δ238U and rate of change in [U] and δ238U, respectively.
Diagenetic Alteration and Dolomitization.
Petrography.
Dajiang, Dawen, and Taşkent were located at shallow water depths during the Early and Middle Triassic. This is supported by thin section observations at Taşkent, where ooids and peloids are dispersed throughout the Early Triassic interval. As determined by field mapping, the depositional environment for Dajiang and Dawen is a shallow marine environment on the top of an isolated carbonate platform, and facies vary from open-marine, high-energy environments in the latest Permian to supratidal to peritidal in the Early Triassic (42). In the Middle Triassic, the platform interior is dominated by subtidal to tidal flat environments (42). At Dajiang and Dawen, field and petrographic data also support shallow water deposition, with point count data indicating a large component of sparry calcite, ooids and peloids (with abundances up to 7.2% in the Dienerian), microbial framework (maximum abundance of 4.2% in the Griesbachian), and biotic grains (abundance up to 1.7%) (72).
In contrast, the reconstructed stratigraphic architecture of the GBG suggests that the facies at Guandao evolved from deposition on the slope of low-relief bank to a highly steepened, high-relief escarpment in the Middle Triassic (42). The deeper-water environment at Guandao is also supported by mudstone−wackestone lithology throughout the section, with micrite comprising 88–98% of the abundance point count data for the uppermost Permian to the Smithian, followed by increasing amounts of sparry calcite and recrystallized clasts in the Middle and Upper Triassic (72).
Diagenetic indicators.
Neither the [U] nor δ238U data correlate with δ18O, Mn/Sr, Mg/Ca, or Sr/Ca ratios, or TOC (Fig. S5). Oxygen isotope values depleted in 18O can be indicative of postdepositional alteration; our data set includes one sample with δ18O = −8.6‰ from Dajiang, which we have eliminated as an outlier as it is 3.6‰ more negative than adjacent samples. In addition, Mn/Sr ratios, which increase with greater degrees of postdepositional alternation (50), are generally very low, with almost all of the data falling below Mn/Sr < 1. We screened any sample with Mn/Sr > 1 as diagenetically altered.
Furthermore, neither [U] nor δ238U values appear to be controlled by facies (e.g., the transition between thrombolite to limestone in the Griesbachian). Because dolomitization appears to alter the δ238U composition of the primary limestone (34), we only consider limestone samples with Mg/Ca < 0.2 [equivalent to Ca3Mg(CO3)4]. Similarly, we did not consider samples with high amounts of pyrite observed in hand sample or thin section as this is indicative of reducing conditions after deposition during early or late diagenesis. High organic carbon content in the sediments, either as organic carbon burial or as migrated secondary carbon, has been proposed to enrich authigenic uranium reduction in the sediments (34, 73, 74). This situation would result in porewater uranium concentration and isotopic signals that do not reflect primary seawater chemistry, which would then be incorporated into early diagenetic carbonate cements. For example, modern Bahamas carbonate sediments exposed to anoxic porewaters are 0.2‰ heavier than the overlying seawater (34). The TOC contents associated with the data reported in this study are generally all < 1% (Dataset S1). In addition, there is no significant correlation between TOC and [U] or δ238U values (Fig. S5), suggesting that organic carbon did not systematically alter the primary record. Therefore, we interpret the data presented in Figs. 1–3 as reflecting primary seawater composition.
In addition to redox conditions, uranium concentrations can be influenced by the amount of detrital input. Previous studies have normalized [U] to [Al] or [Th] to take into account detrital input (e.g., refs. 8, 13, and 75); our [U] record does not deviate in its pattern from U/Al or Th/U trends (Fig. S5). Moreover, our δ238U data are not positively correlated with [Al] and [Th], and therefore the detrital component is either (i) negligible in these samples or (ii) not dissolved by our 1 N HCl treatment.
Finally, uranium concentrations can vary depending on the carbonate mineralogy. Uranium uptake is higher in aragonite than in calcite (67). Thus, if local or global mineralogy shifted from aragonite to calcite at the Permian−Triassic boundary, this would result in a decrease in carbonate [U]. This is equivalent to the increase in DU described in Uranium Biogeochemical Cycling and Model Sensitivity and in Fig. S6C. However, this scenario is opposite to the aragonitic seas of the Early Triassic (76) and observations of widespread abiotic or microbially mediated carbonate cements (69, 70, 77), which, combined, would predict an increase in carbonate [U]. Therefore, the rapid decrease in [U] observed in our sections cannot be explained by a shift in mineralogy.
Dolomitization.
Dajiang was the only studied section with significant dolomitization: Extensive dolomitization occurs from 119 m to 209 m and from 435 m to 1034 m within the section. These samples likely underwent late-stage burial dolomitization and thus differ from the process described by ref. 34. Dolomitized samples have 238U/235U ratios that are much more variable relative to data collected from limestone samples (Figs. S2−S4). As another consideration of the fidelity of dolomitized samples, we measured four sample replicates (starting from powdered sample) to determine the reproducibility of the measurements: one limestone sample and three dolomite samples. Replicates of the limestone sample, PGD-75, have a 2σ reproducibility of <0.01‰, well within the average reproducibility for all samples (0.11‰). The dolomite samples, however, are more variable and could indicate significant rock heterogeneity. The replicates for PDJ-47, PDJ-244, and DJB-13 produced averaged δ238U values with 2σ reproducibility of 0.17‰, 0.63‰, and 0.15‰, respectively (Dataset S1). Although only the reproducibility of PDJ-244 was much larger than the average reproducibility for all samples, the large range highlights the potential for dolomitization to result in heterogeneous uranium isotopic compositions.
Because samples with Mg/Ca > 0.2 show poor correlation between δ238U and [U] and have poor δ238U reproducibility, burial dolomitization appears to have altered the carbonate records such that they are no longer reliable recorders of seawater uranium chemistry. This could be explained if the diagenetic fluid was reducing, leading to changes in the δ238U of the carbonate fraction and precipitation of reduced mineral forms of uranium (e.g., uraninite or mackinawite). This model would predict that a reducing dolomitizing fluid would result in extremely low [U] and negative δ238U in secondary calcite cements that are not representative of the original fluid composition. In addition, oxidation and/or remobilization of previously reduced uranium from organic-rich rocks could result in very positive δ238U precipitating in secondary calcite cements.
Statistical Analysis: Interpretation as a Global Seawater Record.
Geochemical indices.
We screened our data by considering only those where supplemental geochemical data suggest no significant alteration (Mg/Ca < 0.2, Mn/Sr < 1, and no outliers in δ18O or pyrite content). Neither our screened δ238U nor [U] data are statistically correlated with geochemical indicators of diagenetic alteration (δ18O, Mn/Sr, or TOC) or recrystallization from aragonite (Sr/Ca) or to dolomite (Mg/Ca) (Fig. S5 A and B). We calculated Spearman’s rank correlation coefficients (ρ) [function cor.test in R (78)] to evaluate our data by section. Using a Bonferroni correction to evaluate the P values (where α = 0.05/44 = 0.00011), none of the geochemical indicators are significantly correlated with either [U] or δ238U for Dajiang or Guandao. The only statistically significant correlation was between δ238U and δ13C and Sr/Ca for the Taşkent dataset (Fig. S5). This correlation is likely due to the large number of samples around the end-Permian mass extinction boundary (Fig. S4), where the uppermost Permian samples are characterized by relatively positive δ238U and δ13C values and the lowermost Triassic samples are characterized by negative δ238U and δ13C values. Statistics were not calculated for Dawen given the short temporal range of the data.
We also calculated Spearman’s rank correlation coefficients (ρ) to determine the influence of detrital components (Fig. S5 C and D). We do not observe statistically significant correlations between δ238U and [Al] or [Th] for any of the sections, suggesting that the uranium isotopic composition is not driven by either incorporation of detrital uranium during dissolution nor by significant contribution from a detrital fraction. Our analyses suggest that [U] are not statistically distinct from normalized U/Al and Th/U ratios, supporting our interpretation of the [U] record as seawater chemistry, rather than a measure of detrital input.
Differences between stratigraphic sections.
To explore the effect of sample location, we applied one-way ANOVA (function aov in R) to each time interval to compare between sections (Table S1). Although ANOVA results suggest that there are marginally significant differences, the pair-wise tests reveal insignificant differences. We used Dennett’s modified Tukey−Kramer Post-Hoc Test (function DTK.test in R) to run pair-wise comparisons between data collected from different stratigraphic sections for each time interval. This statistical test is appropriate for our dataset because the groups being compared have unequal sample sizes and unequal variances. The compared groups are statistically distinct if the confidence intervals (specified at 95% for a P value of 0.05) of the mean difference between the groups do not overlap with 0. The results from this test indicate that Induan δ238U data from Dajiang and Dawen are statistically distinct; however, a t test run between just the datasets where they overlap temporally suggests that this result is not valid, as the Induan data from Dajiang extend well past the very negative values captured in the Dawen dataset. In addition, our results demonstrate that Olenekian [U] data from Taşkent and Guandao are statistically distinct. Nonetheless, the 95% confidence interval range does not suggest a large difference during this transitional period between the most severe conditions in the Induan and the return to baseline values in the Middle−Late Triassic. These results demonstrate that neither [U] nor δ238U exhibit significant geographic variation in shallow marine settings.
We observe a general difference between the δ238U and [U] data from the slope section (Guandao) and the shallow marine sections (Dajiang and Taşkent) in Table S1 and Figs. 2 and 3: At Guandao, the sole latest Permian sample and samples from the Anisian have δ238U values that are relatively negative compared with the data from Dajiang and Taşkent. Furthermore, the negative δ238U values in the Anisian are primarily driven by Guandao data. These differences between the data from shallow marine sections and Guandao are also illustrated in Fig. 3, where the extreme data points that define the boxplots of δ238U and [U] data for each time interval are mostly from Guandao. If the deeper environment at Guandao was impacted by a higher oxygen demand, a potential explanation is that these sediments experienced a greater degree of alteration, as the uranium precipitated in the carbonate may have been affected by anoxic pore waters. Although our statistical analyses do not suggest a correlation between δ238U and [U] with any diagenetic indicator, we suggest that these sediments were more susceptible to suboxic/anoxic waters.
The scatterplots in Fig. S5 and the statistical analyses suggest that the screened uranium concentrations and isotopic composition in Dawen, Dajiang, and Taşkent have not been significantly altered due to diagenesis. These results bolster our interpretation of the combined δ238U and [U] records as a record of a primary, global seawater composition, despite different paleogeographic settings, lithologies, and diagenetic histories.
Middle Triassic δ238U Composition.
The U isotopic composition of the uppermost Permian and the Middle−Upper Triassic limestones is more positive (mean = −0.23‰, Fig. 3) than modern seawater [∼−0.4‰ (15–17, 39, 40, 58)], and this composition exists for at least 6 million years, suggesting that the steady-state seawater δ238U value in the past varied from the modern value. A higher proportion of shales and other organic-rich lithologies than the modern are estimated to have been exposed during the Permian−Triassic (65). Because organic-rich black shales and low-temperature reduced U ore deposits typically have δ238U values of −0.13 to +0.43‰ (15) and −0.21 to +0.59‰ (79), respectively, greater input of these materials into the riverine flux could have resulted in a more positive weathered U isotopic composition. We compiled the mean of published values for δ238U compositions of the range of possible exposed lithologies: carbonates [−0.4‰ (15, 16, 34)], sandstones [−0.3‰ (15)], shales [0.2‰ (15)], and volcanics [−0.3‰ (15)]. Because the U isotopic compositions of evaporites and cherts are unknown and make up a small fraction of lithologies (∼3% in the modern and ∼5% in Permian−Triassic time), we consider the influence of the weathering of these lithologies to be negligible. Using reconstructions of exposed lithologies through time (65), our calculations suggest that the modern riverine flux should have a δ238U value of −0.21‰, comparable to the measurements of modern rivers that have a mean of −0.24 ± 0.28‰ (2σ) (16, 39–41). In Permian−Triassic time, we estimate that the weathered U flux could have a significantly more positive δ238U composition, with an estimated maximum value of 0.07‰. Therefore, our mass balance estimate of δ238Uriv = −0.05‰ used to parameterize our uranium box model appears reasonable; although better constraints on the variability of modern rivers is needed, this estimate falls within the range of measurements of modern rivers, which have δ238U compositions that range from −0.72‰ to 0.06‰ (39–41) and are thought to reflect bedrock lithology.
In combination with a more positive δ238U input value, we suggest that the [U] value of the Middle−Late Triassic riverine flux was likely greater than the modern value because of enhanced continental weathering. A rapid rise in 87Sr/86Sr observed during the Early Triassic is best explained by increased erosion and weathering of the continents (80, 81). Furthermore, megamonsoons, which frequently impacted Pangaea in the later Triassic (79), may have increased the riverine flux due to a more vigorous hydrologic cycle. In addition, during regressive events, exposure of continental shelves that contain Early Triassic sediments impacted by widespread anoxia could themselves simultaneously increase the [U] and δ238U of the input flux. Thus, a change in exposed lithology may explain such a shift in input composition and, coupled with a larger flux, could explain the more positive Middle Triassic δ238U value relative to modern seawater.
Alternatively, because adsorption of U to Fe oxides and Mn oxides causes a negative fractionation (15, 16, 53, 61), a higher prevalence of these minerals could result in a more positive seawater δ238U. Low 87Sr/86Sr values (80, 81) in the Late Permian can be explained by a proportionally higher hydrothermal flux, which would have increased seawater [Fe] and [Mn] and thereby increased the prevalence of Fe oxides and Mn oxides. However, the δ238U composition of hydrothermally altered basalt is variable but has a small net positive fractionation of 0.2‰ (39), which would partially offset any effect from adsorption to Fe oxides and Mn oxides.
Modeling the Effect of a Shallow OMZ on the Carbon Cycle and δ13C Record.
Model framework.
To determine how the carbon cycle and seawater δ13C may behave in an ocean characterized by widespread shallow anoxia, we constructed a one-box carbon cycle model based on the framework presented in ref. 33. Using this model, we explored how the depth of the OMZ—specifically, the upper boundary of the OMZ—influences the carbon cycle response to expansion/contraction of the OMZ or variation in sea level. The goal of the modeling is to evaluate the processes that could have contributed to the general variability evident in the Early to Middle Triassic δ13C record, rather than to precisely match the magnitudes and durations of individual excursions.
We assume a simplified seafloor hypsometry where the slope of the seafloor changes from a low-angle slope on the continental shelf to a higher-angle slope on the continental margin (as it does today) (Fig. S10). As a result, the depth of the upper boundary of the OMZ relative to the continental shelf−slope break (ZUB) can control how much area of the seafloor the OMZ intersects (i.e., fanox) (Fig. S7A). For example, expansion of a shallow OMZ (positive ZUB) can result in larger variations in the area of shelf impacted by anoxia compared with similar expansion of a deeper OMZ (negative ZUB).
Variation in eustatic sea level can also act as a control on the depth of the upper boundary of the OMZ relative to the shelf−slope break. In our model, we assume that, as sea level changes, the position of the OMZ also shifts to maintain the same depth relative to the sea surface. In an ocean with a shallow OMZ that intersects the lower portion of the continental shelf (and thus a larger ZUB), a rise in sea level would result in a large increase in the area of seafloor impacted by anoxic bottom waters (Fig. S10B). On the other hand, if the depth of the OMZ were deeper and limited to the continental slope, an identical rise in sea level would result in a smaller increase in the area of seafloor in contact with the OMZ.
High spatial and temporal resolution data necessary to reconstruct expansion and contraction of the OMZ are sparse, and other factors can influence ZUB (and thus the area of continental shelf impacted by anoxia) in addition to sea level, including changes in productivity, nutrient delivery, temperature, and upwelling. Furthermore, expansion of the OMZ and changes in sea level could potentially be linked by mechanisms such as changes in temperature. Consequently, a combination of these effects is permissible if not likely.
The purpose of this conceptual model is to determine the extent to which fluctuations in ZUB, either via expansion of the OMZ or via changes in sea level, can cause divergent carbon cycle behavior depending on the initial depth of the OMZ. Although positive δ13C values during other time intervals have previously been linked to transgressions (82–84) and expanded anoxia, we propose that the persistence of a shallow redox gradient can increase the sensitivity of the carbon cycle, resulting in larger δ13C perturbations, such as those observed during Early Triassic time.
In the following, we note the major differences between our model and the one in ref. 33.
Linking the depth of the OMZ (ZUB) to fanox.
In contrast to the model in ref. 33, which links changes in seawater [O2] to organic carbon burial (Fborg), our model relies on varying fanox as the primary forcing. As in the uranium box model, fanox represents the extent of the seafloor impacted by anoxia. We parameterize fanox to respond to changes in ZUB (either through a sea level forcing or expansion of the OMZ) in two scenarios that represent different strengths and locations of the OMZ (Fig. 4 and Fig. S8). The first scenario represents a shallow OMZ where ZUB is above the shelf−slope break, resulting in fanox behavior that is highly sensitive to expansion of the OMZ and sea level changes (Fig. S8 A and C, solid gray line). In this scenario, increasing ZUB from 0 m to 100 m would result in fanox increasing from 0.2% to 20%. For simplicity, we assume that this relationship is linear,
| [S1] |
where ZUB is the depth of the upper boundary of the OMZ and fanox_i is the initial value of fanox, 0.2% (28).
The second scenario represents the behavior of fanox given a deep OMZ that remains below the shelf−slope break (Fig. S8 A and C, blue dashed line). Changing sea level would result in variations in fanox that range from 0% to 1% of the seafloor, which approximates an OMZ with low sensitivity to expansion of the OMZ/sea level change,
| [S2] |
To illustrate the different sensitivities of these scenarios, we vary ZUB using a cosine function with wavelength, λ, which controls the wavelength of the variations based on timesteps of 105 years,
| [S3] |
In Fig. 4 and Fig. S8 A−E, the model is run with an invariant λ = 45.
These parameterizations of fanox are hypothetical and were designed to represent the most extreme scenario. As illustrated by the steady-state fanox calculations shown in Fig. 3, [U] and δ238U values are most sensitive to fanox values between 0% and 5%; therefore, if fanox were to oscillate between 5% and 10% (for example), the associated changes in seafloor anoxia might not be detectable in the [U] and δ238U data.
Parameterization of the organic carbon burial flux, Fborg.
The flux of organic carbon burial, Fborg, is controlled by a combination of varying the burial of phosphate and changes in the C:P ratio of buried organic matter (85, 86),
| [S4] |
where Fbp is the burial flux of phosphate, kcp is the C:P ratio of buried organic matter, and Fbp_i and kcp_i are the initial values for these variables. Because anoxic conditions enhance phosphorous recycling in sediments (85, 86), we parameterize the C:P ratio of buried organic matter to be dependent on the size of the phosphate reservoir as well as the extent of anoxia, fanox,
| [S5] |
We chose a nonlinear forcing between kcp and fanox to achieve a realistic output consistent with the variability in δ13C shown in Fig. 2. Modeled variation of Fborg is shown in Fig. S8D.
In addition to these differences, the carbonate system parameters in the model for this study are calculated using the seacarb package (87) in R (function pCa). In Fig. 4, we show model results starting at 1 My, after the carbon cycle has reached a quasi-steady state. A full summary of model equations, fluxes, constants, variables, and parameterization is presented in ref. 33. R code used in our analysis can be accessed at https://purl.stanford.edu/mr858ss1453.
Model results and implications.
The goal of this model is to explore the potential for the depth of the upper boundary of the OMZ to influence the sensitivity of fanox and, accordingly, δ13C. The modeled δ13C for an ocean with a shallow OMZ exhibits a large positive excursion as ZUB increases (Fig. S8E, solid gray line), similar in magnitude to the positive excursion at the start of the Smithian (Fig. 2). Similarly, when ZUB reaches a minimum, the burial of organic carbon decreases, producing a small negative δ13C excursion of 1‰ relative to the initial value. The second modeled scenario represents a deep OMZ below the shelf−slope break. In this scenario, sea level variations can cause oscillations in fanox between 0% and 1%. Rather than the 9‰ variability exhibited in scenario 1, the range of δ13C values for the third scenario is <2‰ (Fig. S8E, blue dashed line). The larger magnitude of the initial δ13C excursion is an interesting result of our model, and is a function of the carbon cycle being perturbed by an increase in organic carbon burial. After about 0.5 My, the carbon cycle reaches a quasi-steady state: In subsequent oscillations, a memory effect from the nonsymmetric decrease in Fborg generates positive excursions that have the same magnitude.
Based on these results, our model supports a potential link between shallow anoxia and instability of biogeochemical cycles such as carbon and sulfur. Because pyrite burial is also associated with organic carbon burial, the variable and generally more positive δ34SCAS record from the Early Triassic also suggests that the sulfur cycle was unstable (Fig. 3). Whether via episodic expansion and contraction of the OMZ or via sea level fluctuations, these mechanisms do not require additional pulses of carbon cycle perturbation (through recurrent volcanism) proposed in ref. 33 to result in perturbed biogeochemical cycles. Instead, we propose that the behavior of an ocean characterized by a shallow OMZ is inherently sensitive. In addition, oscillations in the area of anoxic continental shelf would result in decreases in the area of habitable benthic seafloor, delaying Earth system recovery.
Our nonlinear parameterization of the relationship between fanox and Fborg via the positive feedback between anoxia and phosphorous recycling (Eqs. S4 and S5) means that the exponent in this relationship acts as another control on the sensitivity of kcp to changes in fanox. We use a value of 1/3, which produces results that approximate the magnitude of δ13C variability in the Early Triassic. However, if this exponent is increased, Fborg becomes much more sensitive to sea level change; conversely, decreasing this exponent results in a much more dampened response in Fborg. This exponent may represent other influences on organic carbon burial that control the efficiency of organic carbon burial in an OMZ, such as the intensity of the OMZ, reworking of sedimentary organic carbon due to biomineralization, or the proportion of labile to refractory organic matter.
Simulating the Early−Middle Triassic δ13C record.
Rather than matching every negative and positive excursion in Fig. 2, we attempt to reproduce the general patterns evident in the Early to Middle Triassic δ13C record. This is accomplished by changing only the wavelength of relative ZUB fluctuations and increasing the depth of the OMZ (i.e., decreasing ZUB) with time (Fig. S8 F−H). To allow us to control these two factors, we introduce two additional variables. First, we modulate the relationship between fanox and ZUB with a damping factor, d, which decreases with time,
| [S6] |
Decreasing d with time allows us to stimulate a deepening of the OMZ and thus a decrease in the sensitivity of fanox to ZUB with time (Fig. S8F). We parameterize d such that it decreases linearly for the first 5 million years, to approximate a gradual deepening of the OMZ through the Early Triassic, followed by an exponential decrease that represents a more rapid return to preextinction conditions.
To match the lower frequency of carbon cycle perturbations in the Olenekian, we also change the wavelength of variations in ZUB. We parameterize λ such that the frequency of ZUB fluctuations decreases linearly through the model run from <0.5-My to ∼3-My time scales (Fig. S8),
| [S7] |
By changing only these two factors (fanox and λ), we are able to approximate the key characteristic of the Early to Middle Triassic δ13C patterns, in which large δ13C, rapid excursions give way to smaller and more prolonged excursions (Fig. S8H). Our model demonstrates that the subsequent excursions may be the result of sea level variations or episodic expansion and contraction in an ocean with a shallow OMZ. Although we do not model the initial negative excursion at the end-Permian extinction boundary that is widely attributed to a release of 13C-depleted carbon associated with the Siberian Traps (e.g., ref. 1), the influx of carbon from Siberian Traps volcanism may have supplied the marine reservoir of carbon that is necessary for the substantial burial of organic carbon predicted by our model.
Supplementary Material
Acknowledgments
We thank Caroline Harris and Monique Foung for laboratory assistance and five anonymous reviewers of this and earlier versions for their constructive suggestions that improved the manuscript. This research was supported by National Science Foundation Continental Dynamics Grant EAR-0807475 (to J.L.P.) and funding from Shell International Exploration and Production and Saudi Aramco (J.L.P.), American Chemical Society Petroleum Research Fund Grants 53241-ND2 (to K.M.) and 52457-ND2 (to J.L.P.), and an Achievement Rewards for College Scientists (ARCS) Fellowship and assistance from the Stanford McGee Fund (to K.V.L.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1515080113/-/DCSupplemental.
References
- 1.Payne JL, Clapham ME. End-Permian mass extinction in the oceans: An ancient analog for the 21st century? Annu Rev Earth Planet Sci. 2012;41:89–111. [Google Scholar]
- 2.Chen Z-Q, Benton MJ. The timing and pattern of biotic recovery following the end-Permian mass extinction. Nat Geosci. 2012;5:375–383. [Google Scholar]
- 3.Foster WJ, Twitchett RJ. Functional diversity of marine ecosystems after the Late Permian mass extinction event. Nat Geosci. 2014;7:233–238. [Google Scholar]
- 4.Payne JL, et al. Large perturbations of the carbon cycle during recovery from the end-Permian extinction. Science. 2004;305(5683):506–509. doi: 10.1126/science.1097023. [DOI] [PubMed] [Google Scholar]
- 5.Song HY, et al. Early Triassic seawater sulfate drawdown. Geochim Cosmochim Acta. 2014;128:95–113. [Google Scholar]
- 6.Grice K, et al. Photic zone euxinia during the Permian-Triassic superanoxic event. Science. 2005;307(5710):706–709. doi: 10.1126/science.1104323. [DOI] [PubMed] [Google Scholar]
- 7.Wignall PB, Hallam A. Anoxia as a cause of the Permian/Triassic mass extinction: Facies evidence from northern Italy and the western United States. Palaeogeogr Palaeoclimatol Palaeoecol. 1992;93(1-2):21–46. [Google Scholar]
- 8.Wignall PB, Twitchett RJ. Oceanic anoxia and the end Permian mass extinction. Science. 1996;272(5265):1155–1158. doi: 10.1126/science.272.5265.1155. [DOI] [PubMed] [Google Scholar]
- 9.Hallam A. Why was there a delayed radiation after the end-Paleozoic extinctions? Hist Biol. 1991;5:257–262. [Google Scholar]
- 10.Loope GR, Kump LR, Arthur MA. Shallow water redox conditions from the Permian–Triassic boundary microbialite: The rare earth element and iodine geochemistry of carbonates from Turkey and South China. Chem Geol. 2013;351:195–208. [Google Scholar]
- 11.Brennecka GA, Herrmann AD, Algeo TJ, Anbar AD. Rapid expansion of oceanic anoxia immediately before the end-Permian mass extinction. Proc Natl Acad Sci USA. 2011;108(43):17631–17634. doi: 10.1073/pnas.1106039108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wignall PB, et al. An 80 million year oceanic redox history from Permian to Jurassic pelagic sediments of the Mino-Tamba terrane, SW Japan, and the origin of four mass extinctions. Global Planet Change. 2010;71(1-2):109–123. [Google Scholar]
- 13.Song HJ, et al. Geochemical evidence from bio-apatite for multiple oceanic anoxic events during Permian-Triassic transition and the link with end-Permian extinction and recovery. Earth Planet Sci Lett. 2012;353-354:12–21. [Google Scholar]
- 14.Grasby SE, Beauchamp B, Embry A, Sanei H. Recurrent Early Triassic ocean anoxia. Geology. 2012;41(2):175–178. [Google Scholar]
- 15.Weyer S, et al. Natural fractionation of 238U/235U. Geochim Cosmochim Acta. 2008;72(2):345–359. [Google Scholar]
- 16.Stirling CH, Andersen MB, Potter E-K, Halliday AN. Low-temperature isotopic fractionation of uranium. Earth Planet Sci Lett. 2007;264(1-2):208–225. [Google Scholar]
- 17.Andersen MB, et al. A modern framework for the interpretation of 238U/235U in studies of ancient ocean redox. Earth Planet Sci Lett. 2014;400:184–194. [Google Scholar]
- 18.Stylo M, et al. Uranium isotopes fingerprint biotic reduction. Proc Natl Acad Sci USA. 2015;112(18):5619–5624. doi: 10.1073/pnas.1421841112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Payne JL, et al. Erosional truncation of uppermost Permian shallow-marine carbonates and implications for Permian-Triassic boundary events. Geol Soc Am Bull. 2007;119(7-8):771–784. [Google Scholar]
- 20.Meyer KM, Yu M, Jost AB, Kelley BM, Payne JL. δ13C evidence that high primary productivity delayed recovery from end-Permian mass extinction. Earth Planet Sci Lett. 2011;302(3-4):378–384. [Google Scholar]
- 21.Lehrmann DJ, et al. Permian-Triassic boundary and a Lower-Middle Triassic boundary sequence on the Great Bank of Guzihou, Nanpanjiang basin, southern Guizhou Province. Albertiana. 2005;33:169–186. [Google Scholar]
- 22.Song HY, et al. Large vertical δ13CDIC gradients in Early Triassic seas of the South China craton: Implications for oceanographic changes related to Siberian Traps volcanism. Global Planet Change. 2013;105:7–20. [Google Scholar]
- 23.Burgess SD, Bowring S, Shen SZ. High-precision timeline for Earth’s most severe extinction. Proc Natl Acad Sci USA. 2014;111(9):3316–3321. doi: 10.1073/pnas.1317692111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ovtcharova M, et al. New Early to Middle Triassic U–Pb ages from South China: Calibration with ammonoid biochronozones and implications for the timing of the Triassic biotic recovery. Earth Planet Sci Lett. 2006;243(3-4):463–475. [Google Scholar]
- 25.Schaal EK, Clapham ME, Rego BL, Wang SC, Payne JL. Comparative size evolution of marine clades from the Late Permian through Middle Triassic. Paleobiology. 2016;42(01):127–142. [Google Scholar]
- 26.Ehrenberg SN, Svånå TA, Swart PK. Uranium depletion across the Permian–Triassic boundary in Middle East carbonates: Signature of oceanic anoxia. AAPG Bull. 2008;92(6):691–707. [Google Scholar]
- 27.Tavakoli V, Rahimpour-Bonab H. Uranium depletion across Permian–Triassic Boundary in Persian Gulf and its implications for paleooceanic conditions. Palaeogeogr Palaeoclimatol Palaeoecol. 2012;350-352:101–113. [Google Scholar]
- 28.Helly JJ, Levin LA. Global distribution of naturally occurring marine hypoxia on continental margins. Deep Sea Res Part I Oceanogr Res Pap. 2004;51(9):1159–1168. [Google Scholar]
- 29.Algeo TJ, et al. Changes in productivity and redox conditions in the Panthalassic Ocean during the latest Permian. Geology. 2010;38(2):187–190. [Google Scholar]
- 30.Algeo TJ, et al. Spatial variation in sediment fluxes, redox conditions, and productivity in the Permian–Triassic Panthalassic Ocean. Palaeogeogr Palaeoclimatol Palaeoecol. 2011;308(1-2):65–83. [Google Scholar]
- 31.Winguth C, Winguth AME. Simulating Permian-Triassic oceanic anoxia distribution: Implications for species extinction and recovery. Geology. 2012;40(2):127–130. [Google Scholar]
- 32.Luo G, et al. Isotopic evidence for an anomalously low oceanic sulfate concentration following end-Permian mass extinction. Earth Planet Sci Lett. 2010;300(1-2):101–111. [Google Scholar]
- 33.Payne JL, Kump L. Evidence for recurrent Early Triassic massive volcanism from quantitative interpretation of carbon isotope fluctuations. Earth Planet Sci Lett. 2007;256(1-2):264–277. [Google Scholar]
- 34.Romaniello SJ, Herrmann AD, Anbar AD. Uranium concentrations and 238U/235U isotope ratios in modern carbonates from the Bahamas: Assessing a novel paleoredox proxy. Chem Geol. 2013;362:305–316. [Google Scholar]
- 35.Dunk R, Mills R, Jenkins W. A reevaluation of the oceanic uranium budget for the Holocene. Chem Geol. 2002;190(1-4):45–67. [Google Scholar]
- 36.Montoya-Pino C, et al. Global enhancement of ocean anoxia during Oceanic Anoxic Event 2: A quantitative approach using U isotopes. Geology. 2010;38(4):315–318. [Google Scholar]
- 37.Morford JL, Emerson S. The geochemistry of redox sensitive trace metals in sediments. Geochim Cosmochim Acta. 1999;63(11/12):1735–1750. [Google Scholar]
- 38.Maher K, Steefel CI, DePaolo DJ, Viani BE. The mineral dissolution rate conundrum: Insights from reactive transport modeling of U isotopes and pore fluid chemistry in marine sediments. Geochim Cosmochim Acta. 2006;70(2):337–363. [Google Scholar]
- 39.Noordmann J, Weyer S, Georg RB, Jöns S, Sharma M. 238U/235U isotope ratios of crustal material, rivers and products of hydrothermal alteration: New insights on the oceanic U isotope mass balance. Isotopes Environ Health Stud. 2015;18:1–23. doi: 10.1080/10256016.2015.1047449. [DOI] [PubMed] [Google Scholar]
- 40.Tissot FLH, Dauphas N. Uranium isotopic compositions of the crust and ocean: Age corrections, U budget and global extent of modern anoxia. Geochim Cosmochim Acta. 2015;167:113–143. [Google Scholar]
- 41.Andersen MB, et al. Closing in on the marine 238U/235U budget. Chem Geol. 2016;420:11–22. [Google Scholar]
- 42.Lehrmann DJ. Controls on facies architecture of a large Triassic carbonate platform: The Great Bank of Guizhou, Nanpanjiang Basin, south China. J Sediment Res. 1998;68(2):311–326. [Google Scholar]
- 43.Potter E-K, Stirling CH, Andersen MB, Halliday AN. High precision Faraday collector MC-ICPMS thorium isotope ratio determination. Int J Mass Spectrom. 2005;247(1-3):10–17. [Google Scholar]
- 44.Richter S, et al. The isotopic composition of natural uranium samples—Measurements using the new n(233U)/n(236U) double spike IRMM-3636. Int J Mass Spectrom. 2008;269(1-2):145–148. [Google Scholar]
- 45.Lehrmann DJ, et al. An integrated biostratigraphy (conodonts and foraminifers) and chronostratigraphy (paleomagnetic reversals, magnetic susceptibility, elemental chemistry, carbon isotopes and geochronology) for the Permian–Upper Triassic strata of Guandao section, Nanpanjiang Basin, south China. J Asian Earth Sci. 2015;108:117–135. [Google Scholar]
- 46.Payne JL, et al. Calcium isotope constraints on the end-Permian mass extinction. Proc Natl Acad Sci USA. 2010;107(19):8543–8548. doi: 10.1073/pnas.0914065107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Altiner D, Özgül N. 2001. Carboniferous and Permian of the allochthonous terranes of the Central Tauride Belt, southern Turkey. PaleoForams 2001, International Conference on Paleozoic Benthic Foraminifera Guidebook, (Middle East Tech Univ, Ankara, Turkey), p 35.
- 48.Özgül N. 1997. Stratigraphy of the tectono-stratigraphic units in the region Bozkir-Hadim-Taşkent (northern central Taurides). Miner Res Explor Inst Turkey Bull 119:113–174. Turkish with English abstract.
- 49.Monod O. 1977. Recherches géologiques dans le Taurus occidental au Sud de Beysehir (Turquie) PhD thesis (Université de Paris-Sud, Orsay, France)
- 50.Brand U, Veizer J. Chemical diagenesis of a multicomponent carbonate system–1: Trace elements. J Sediment Petrol. 1980;50(4):1219–1236. [Google Scholar]
- 51.Condon DJ, McLean N, Noble SR, Bowring SA. Isotopic composition (238U/235U) of some commonly used uranium reference materials. Geochim Cosmochim Acta. 2010;74(24):7127–7143. [Google Scholar]
- 52.Cheng H, et al. Improvements in 230Th dating, 230Th and 234U half-life values, and U–Th isotopic measurements by multi-collector inductively coupled plasma mass spectrometry. Earth Planet Sci Lett. 2013;371-372:82–91. [Google Scholar]
- 53.Brennecka GA, Wasylenki LE, Bargar JR, Weyer S, Anbar AD. Uranium isotope fractionation during adsorption to Mn-oxyhydroxides. Environ Sci Technol. 2011;45(4):1370–1375. doi: 10.1021/es103061v. [DOI] [PubMed] [Google Scholar]
- 54.Kendall B, Brennecka GA, Weyer S, Anbar AD. Uranium isotope fractionation suggests oxidative uranium mobilization at 2.50Ga. Chem Geol. 2013;362:105–114. [Google Scholar]
- 55.Maher K, Bargar JR, Brown GE., Jr Environmental speciation of actinides. Inorg Chem. 2013;52(7):3510–3532. doi: 10.1021/ic301686d. [DOI] [PubMed] [Google Scholar]
- 56.Langmuir D. Uranium solution-mineral equilibria at low temperatures with applications to sedimentary ore deposits. Geochim Cosmochim Acta. 1978;42(6A):547–569. [Google Scholar]
- 57.Ku T-L, Knauss KG, Mathieu GG. Uranium in open ocean: Concentration and isotopic composition. Deep Sea Res. 1977;24(11):1005–1017. [Google Scholar]
- 58.Holmden C, Amini M, Francois R. Uranium isotope fractionation in Saanich Inlet: A modern analog study of a paleoredox tracer. Geochim Cosmochim Acta. 2015;153:202–215. [Google Scholar]
- 59.Basu A, Sanford RA, Johnson TM, Lundstrom CC, Löffler FE. Uranium isotopic fractionation factors during U(VI) reduction by bacterial isolates. Geochim Cosmochim Acta. 2014;136:100–113. [Google Scholar]
- 60.Stirling CH, Andersen MB, Warthmann R, Halliday AN. Isotope fractionation of 238U and 235U during biologically-mediated uranium reduction. Geochim Cosmochim Acta. 2015;163:200–218. [Google Scholar]
- 61.Goto KT, et al. Uranium isotope systematics of ferromanganese crusts in the Pacific Ocean: Implications for the marine 238U/235U isotope system. Geochim Cosmochim Acta. 2014;146:43–58. [Google Scholar]
- 62.Anderson RF, Fleisher MQ, LeHuray AP. Concentration, oxidation state, and particulate flux of uranium in the Black Sea. Geochim Cosmochim Acta. 1989;53(9):2215–2224. [Google Scholar]
- 63.Hua B, Xu H, Terry J, Deng B. Kinetics of uranium(VI) reduction by hydrogen sulfide in anoxic aqueous systems. Environ Sci Technol. 2006;40(15):4666–4671. doi: 10.1021/es051804n. [DOI] [PubMed] [Google Scholar]
- 64.Stewart BD, Neiss J, Fendorf S. Quantifying constraints imposed by calcium and iron on bacterial reduction of uranium(VI) J Environ Qual. 2007;36(2):363–372. doi: 10.2134/jeq2006.0058. [DOI] [PubMed] [Google Scholar]
- 65.Bluth GJS, Kump LR. Phanerozoic paleogeology. Am J Sci. 1991;291:284–308. [Google Scholar]
- 66.Meece DE, Benninger LK. The coprecipitation of Pu and other radionuclides with CaCO3. Geochim Cosmochim Acta. 1993;57(7):1447–1458. [Google Scholar]
- 67.Reeder RJ, Nugent M, Lamble GM, Drew Tait C, Morris DE. Uranyl incorporation into calcite and aragonite: XAFS and luminescence studies. Environ Sci Technol. 2000;34(4):638–644. [Google Scholar]
- 68.DeCarlo TM, Gaetani GA, Holcomb M, Cohen AL. Experimental determination of factors controlling U/Ca of aragonite precipitated from seawater: Implications for interpreting coral skeleton. Geochim Cosmochim Acta. 2015;162:151–165. [Google Scholar]
- 69.Woods AD, Bottjer DJ, Mutti M, Morrison J. Lower Triassic large sea-floor carbonate cements: Their origin and a mechanism for the prolonged biotic recovery from the end-Permian mass extinction. Geology. 1999;27(7):645−648. [Google Scholar]
- 70.Pruss SB, Bottjer DJ, Corsetti FA, Baud A. A global marine sedimentary response to the end-Permian mass extinction: Examples from southern Turkey and the western United States. Earth Sci Rev. 2006;78(3-4):193–206. [Google Scholar]
- 71.Isozaki Y. Permo-Triassic boundary superanoxia and stratified superocean: Records from lost deep sea. Science. 1997;276(5310):235–238. doi: 10.1126/science.276.5310.235. [DOI] [PubMed] [Google Scholar]
- 72.Payne JL, Lehrmann DJ, Christensen S, Wei J, Knoll AH. Environmental and biological controls on the initiation and growth of a Middle Triassic (Anisian) reef complex on the Great Bank of Guizhou, Guizhou Province, China. Palaios. 2006;21(4):325–343. [Google Scholar]
- 73.Morford JL, Martin WR, Carney CM. Uranium diagenesis in sediments underlying bottom waters with high oxygen content. Geochim Cosmochim Acta. 2009;73(10):2920–2937. [Google Scholar]
- 74.McManus J, Berelson WM, Klinkhammer GP, Hammond DE, Holm C. Authigenic uranium: Relationship to oxygen penetration depth and organic carbon rain. Geochim Cosmochim Acta. 2005;69(1):95–108. [Google Scholar]
- 75.Shen J, et al. Volcanic perturbations of the marine environment in South China preceding the latest Permian mass extinction and their biotic effects. Geobiology. 2012;10(1):82–103. doi: 10.1111/j.1472-4669.2011.00306.x. [DOI] [PubMed] [Google Scholar]
- 76.Stanley SM, Hardie LA. Secular oscillations in the carbonate mineralogy of reef-building and sediment-producing organisms driven by tectonically forced shifts in seawater chemistry. Palaeogeogr Palaeoclimatol Palaeoecol. 1998;144(1-2):3–19. [Google Scholar]
- 77.Payne JL, Lehrmann DJ, Wei J, Knoll AH. The pattern and timing of biotic recovery from the end-Permian extinction on the Great Bank of Guizhou, Guizhou Province, China. Palaios. 2006;21(1):63–85. [Google Scholar]
- 78.Team RDC. R: A Language and Environment for Statistical Computing. R Found Stat Comput; Vienna: 2008. [Google Scholar]
- 79.Brennecka GA, Borg LE, Hutcheon ID, Sharp MA, Anbar AD. Natural variations in uranium isotope ratios of uranium ore concentrates: Understanding the 238U/235U fractionation mechanism. Earth Planet Sci Lett. 2010;291(1-4):228–233. [Google Scholar]
- 80.Sedlacek ARC, et al. 87Sr/86Sr stratigraphy from the Early Triassic of Zal, Iran: Linking temperature to weathering rates and the tempo of ecosystem recovery. Geology. 2014;42(9):779–782. [Google Scholar]
- 81.Korte C, Kozur HW, Bruckschen P, Veizer J. Strontium isotope evolution of Late Permian and Triassic seawater. Geochim Cosmochim Acta. 2003;67(1):47–62. [Google Scholar]
- 82.Brasier MD, Lindsay JF. Did supercontinental amalgamation trigger the “Cambrian Explosion”? In: Zhuravlev AY, Riding R, editors. The Ecology of the Cambrian Radiation. Columbia Univ Press; New York: 2000. pp. 69–89. [Google Scholar]
- 83.Jenkyns HC, Gale AS, Corfield RM. Carbon- and oxygen-isotope stratigraphy of the English Chalk and Italian Scaglia and its palaeoclimatic significance. Geol Mag. 1994;131(1):1–34. [Google Scholar]
- 84.Saltzman MR, Edwards CT, Adrain JM, Westrop SR. Persistent oceanic anoxia and elevated extinction rates separate the Cambrian and Ordovician radiations. Geology. 2015;43(9):807–810. [Google Scholar]
- 85.Ingall ED, Bustin RM, Van Cappellen P. Influence of water column anoxia on the burial and preservation of carbon and phosphorus in marine shales. Geochim Cosmochim Acta. 1993;57(2):303–316. [Google Scholar]
- 86.Van Cappellen P, Ingall ED. Redox stabilization of the atmosphere and oceans by phosphorus-limited marine productivity. Science. 1996;271:493–496. doi: 10.1126/science.271.5248.493. [DOI] [PubMed] [Google Scholar]
- 87. Lavigne H, Epitalon J-M, & Gattuso J-P (2014) seacarb: seawater carbonate chemistry with R (R package version 3.0). Available at CRAN.R-project.org/package=seacarb.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.