Enzyme catalysis by entropy without Circe effect

Significance

One of the most influential hypotheses regarding enzyme catalysis is Jencks’s so-called Circe effect, in which the catalytic power is usually equated to proper alignment of substrates, bringing reacting groups into close proximity, and restriction of substrate motions. The entropic penalty associated with climbing the activation barrier could then be diminished because it has already been paid upon substrate binding. The enzyme cytidine deaminase appears to be the perfect example of this behavior. Here, we use extensive computer simulations to obtain thermodynamic activation parameters for this reaction. The very large activation entropy difference between the enzyme reaction and the uncatalyzed process is, however, found to be attributable to a change of reaction mechanism rather than the Circe effect.

Abstract

Entropic effects have often been invoked to explain the extraordinary catalytic power of enzymes. In particular, the hypothesis that enzymes can use part of the substrate-binding free energy to reduce the entropic penalty associated with the subsequent chemical transformation has been very influential. The enzymatic reaction of cytidine deaminase appears to be a distinct example. Here, substrate binding is associated with a significant entropy loss that closely matches the activation entropy penalty for the uncatalyzed reaction in water, whereas the activation entropy for the rate-limiting catalytic step in the enzyme is close to zero. Herein, we report extensive computer simulations of the cytidine deaminase reaction and its temperature dependence. The energetics of the catalytic reaction is first evaluated by density functional theory calculations. These results are then used to parametrize an empirical valence bond description of the reaction, which allows efficient sampling by molecular dynamics simulations and computation of Arrhenius plots. The thermodynamic activation parameters calculated by this approach are in excellent agreement with experimental data and indeed show an activation entropy close to zero for the rate-limiting transition state. However, the origin of this effect is a change of reaction mechanism compared the uncatalyzed reaction. The enzyme operates by hydroxide ion attack, which is intrinsically associated with a favorable activation entropy. Hence, this has little to do with utilization of binding free energy to pay the entropic penalty but rather reflects how a preorganized active site can stabilize a reaction path that is not operational in solution.

Many hypotheses have been put forward to explain the rate acceleration of chemical reactions by enzymes. One of the most influential of these is Jencks’ so-called “Circe effect” (1), which posits that the key catalytic effect is associated with substrate binding and that part of the favorable (negative) binding free energy is spent on destabilization of the bound substrate in its ground state. Such ground-state destabilization could, in principle, have different possible physical origins, such as reduction of translational, rotational, and conformational substrate entropies; steric and conformational strain; or electrostatic destabilization and desolvation effects (1). In particular, the entropic explanation enjoys widespread popularity and is often invoked to rationalize the catalytic power of enzymes in terms of proximity and alignment of the reacting groups (2). It is then assumed that part of the substrate-binding free energy is spent on restricting the substrate motions and correctly aligning the substrate for reaction, which implies a negative contribution to the binding entropy. This scenario, in turn, would enable the substrate to climb the activation barrier with a smaller entropy loss than in solution, because the entropic penalty for the reaction has already been paid upon binding. Accordingly, the catalytic rate constant $\left(k_{cat}\right)$ would be characterized by a more positive value of $T\mathrm{\Delta }{S}^{‡}$ than the corresponding uncatalyzed rate. Jencks estimated that the loss of translational and rotational entropy upon binding could give rise to a rate increase of as much as 10⁸ M for a bimolecular reaction $(k_{cat}/k_{non}),$ based on comparison of intramolecular and intermolecular solution reactions (1, 3). It is also interesting to note that in this context, the focus has almost exclusively been on the substrate entropy, whereas entropic contributions from the solvent or protein have usually been dismissed (1).

The hydrolytic deamination of cytidine to uracil catalyzed by cytidine deaminase appears to provide the most solid example of the Circe effect hypothesis. The slow spontaneous deamination of cytidine in aqueous solution $(k_{non}=3\times {10}^{-10}$ s⁻¹) occurs with an activation free energy of $\mathrm{\Delta }{G}^{‡}=30.4$ kcal/mol at 25 °C, and the corresponding entropic and enthalpic components are $T\mathrm{\Delta }{S}^{‡}=-8.3$ kcal/mol and $\mathrm{\Delta }{H}^{‡}=22.1$ kcal/mol (4). Cytidine deaminase from Escherichia coli catalyzes the same reaction with $k_{cat}=300$ s⁻¹ and an activation free energy of $\mathrm{\Delta }{G}^{‡}=14.0$ kcal/mol at 25 °C (4). Here, the entropic and enthalpic activation parameters are $T\mathrm{\Delta }{S}^{‡}=+0.9$ kcal/mol and $\mathrm{\Delta }{H}^{‡}=14.9$ kcal/mol (4), showing that the entropic penalty has totally vanished in the enzyme reaction. Moreover, substrate binding occurs with $\mathrm{\Delta }{G}_{bind}^0=-5.4$ kcal/mol and $T\mathrm{\Delta }{S}_{bind}^0=-7.6$ kcal/mol, that is, with a large entropic penalty that almost perfectly matches that of the solution reaction. Hence, this case would seem as a prototypic example of the Circe effect, where all of the relevant thermodynamic parameters have actually been quantified experimentally.

To examine the microscopic origin of the above effect, we have earlier characterized the uncatalyzed deamination of cytidine in water by quantum mechanical calculations and extensive computer simulations, which allowed accurate Arrhenius plots to be obtained (5). These simulations reproduced the experimentally observed activation parameters and revealed that the activation entropy is completely dominated by the solvent contribution. Neutral water attack involving an eight-membered transition state with three participating water molecules was thus found to be the favored reaction mechanism (5). To understand what causes the large negative activation entropy associated with the uncatalyzed reaction to vanish in the enzyme, it is necessary to be able to compute the thermodynamic activation parameters in the same manner also for the enzyme-catalyzed reaction.

Cytidine deaminase from E. coli is a homodimer with a zinc ion tightly bound to each subunit (6). The zinc is coordinated by two cysteines (Cys129 and Cys132) and one histidine residue (His102) from the protein in a tetrahedral geometry. The fourth ligand position of the zinc ion is occupied by the catalytic water molecule (7). The second zinc solvation shell contains a glutamate residue (Glu104) that participates in the required proton transfers (7, 8). The enzyme–substrate (ES) complex is in rapid equilibrium with free enzyme and substrate, and k_cat solely represents the chemical steps, with the reaction being pH-independent in the neutral pH region (4). The deamination of cytidine by this enzyme has been the subject of several earlier theoretical studies (9–15), but, despite similarity in the proposed chemical steps, none of these studies has provided energies compatible with the experimental values. A recent study by one of us (16) on the related E. coli cytosine deaminase enzyme yielded a detailed reaction mechanism with very reasonable energetics. However, considering the differences in active site residues between the two enzymes, these results are not immediately transferable to cytidine deaminase.

In this work, we use the same strategy as in ref. 16 to first obtain an accurate energetic description of cytidine deamination by E. coli cytidine deaminase, using density functional theory (DFT) calculations with a continuum solvent model. The DFT results for a relatively large active site model (191 atoms) are then used to construct empirical valence bond (EVB) models (17, 18) for the different reaction steps. With an EVB description of the entire cytidine deaminase reaction, it becomes possible to carry out extensive molecular dynamics (MD) sampling, which allows calculation of free-energy profiles and their temperature dependence (5). Hence, by computing Arrhenius plots in this way, we are able to extract the thermodynamic parameters for the enzyme-catalyzed reaction and directly compare these results to the experimental results of Wolfenden and coworkers (4). The computer simulations turn out to yield activation entropies in excellent agreement with the experimental data and also reveal the origin of the huge entropic contribution to catalysis.

Results

Enzyme Reaction Mechanism from DFT Calculations.

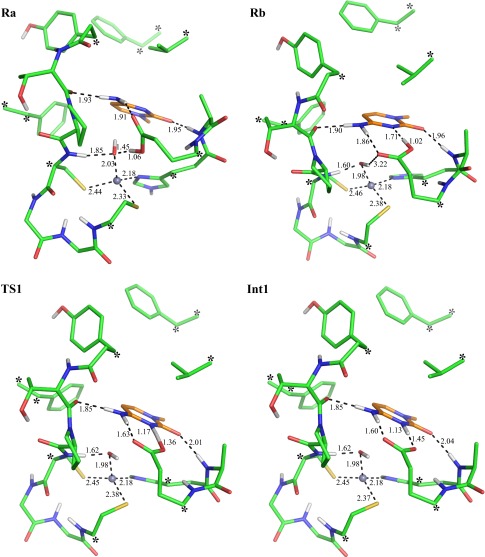
Transition state analogs with a hydroxyl group at position C4 bind strongly to the active site (19), which suggests that deamination of cytidine occurs via a tetrahedral intermediate. In studies of similar systems, tetrahedral intermediate formation was suggested to occur by nucleophilic attack of the activated water on the protonated cytidine (9, 16). In E. coli cytidine deaminase, activation of the catalytic water molecule can only be achieved by initial proton transfer from the zinc-bound water to Glu104. Moreover, our DFT calculations yielded no stationary point for the state in which the neutral water molecule is bound to the zinc ion. Instead, and regardless of the initial configuration, all geometry optimizations resulted in spontaneous proton transfer to Glu104. This observation is in agreement with a previous theoretical study at the PM3 level of theory (11) and the experimental solvent deuterium isotope effect (20). That is, k_cat was found to be insensitive to the ²H₂O solvent content, whereas an inverse isotope effect was observed for k_cat/K_M (20), and it was therefore concluded that the initial proton transfer occurs during the binding event. The zinc-bound hydroxide ion (Fig. 1, state Ra) is thus the resting state of the ES complex, and our energies are reported relative to this state (Table 1).

Fig. 1.

Schematic representation of the cytidine deamination reaction catalyzed by E. coli cytidine deaminase. The reaction mechanism is based on calculations with the DFT cluster model and MD/EVB simulations.

Table 1.

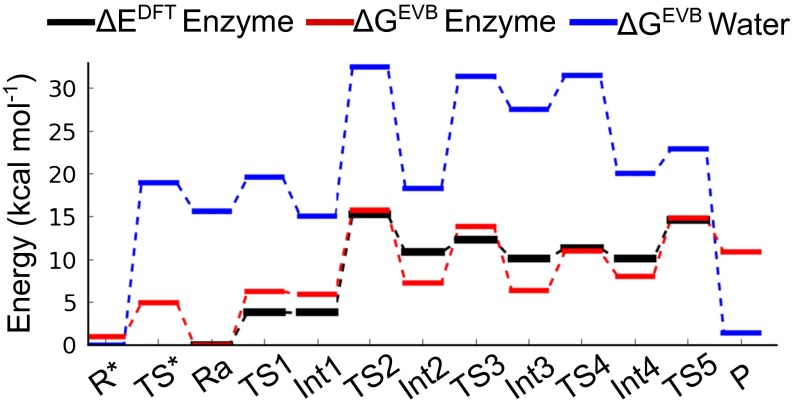
Energetics of the cytidine deaminase reaction from DFT and MD/EVB calculations

State	ΔEDFT	ΔGEVB	TΔSEVB	ΔHEVB	ΔGwat†	SEM‡
R*	—	1.0§	1.2§	2.2§	0	0.12
TS*	—	5.0§	0.4§	5.4§	19.0	0.08
Ra	0	0	0	0	15.6	—
TS1	3.9	6.3	1.6	7.9	19.6	0.03
Int1	3.8	5.9	0.5	6.4	15.1	0.03
TS2	15.3	15.7	−1.9	13.8	32.5	0.04
Int2	10.9	7.3	−2.7	4.6	18.3	0.05
TS3	12.3	13.8	−3.0	10.8	31.4	0.06
Int3	10.1	6.4	−3.0	3.4	27.5	0.06
TS4	11.4	11.0	−4.2	6.8	31.5	0.06
Int4	10.1	8.1	−2.0	6.1	20.0	0.06
TS5	14.7	14.9	0.7	15.6	22.9	0.07
P	—	10.9	2.7	13.6	1.4	0.07

All energies are in kcal/mol. —, not calculated.

^†Denotes the EVB free-energy profiles for an uncatalyzed reaction in water following the same mechanism as in the enzyme. Energies in this case are given relative to the lowest state, R*.

^‡SEM for the enzyme free energy relative to the resting state.

^§These states make no contribution to the rate-limiting step and lie before the resting state of the enzyme (Ra).

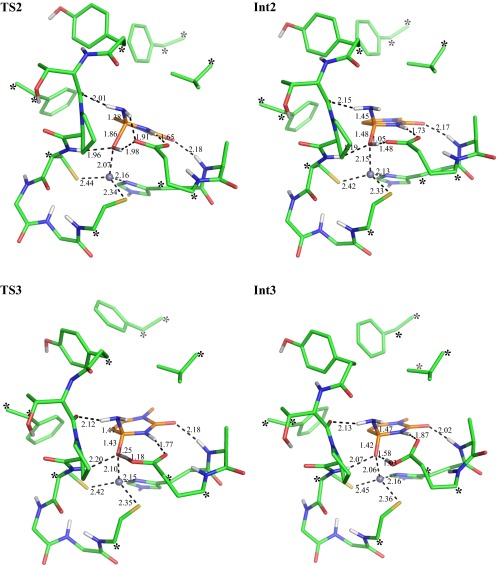
After initial proton transfer, the protonated Glu104 side chain undergoes a rotation so that the H-bond with the hydroxide ion is replaced by an H-bond with the N3 nitrogen of cytidine (Fig. 1, state Rb). The Rb intermediate lies 2.3 kcal/mol higher than Ra, and proton transfer from Glu104 to N3 costs 1.5 kcal/mol, which brings the protonated cytidine intermediate to 3.8 kcal/mol (Fig. 1, state Int1). Subsequently, the tetrahedral intermediate is formed by nucleophilic attack of the hydroxide ion on the protonated cytidine (Fig. 1, state Int2). The activation energy (Fig. 1, TS2) and reaction energy for this step are predicted to be 11.5 and 7.1 kcal/mol, respectively, so that TS2 lies 15.3 kcal/mol above Ra (Table 1).

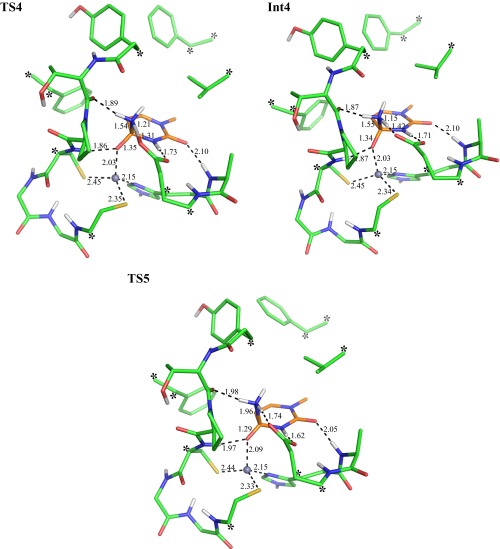
Collapse of the tetrahedral intermediate has been proposed to occur by C-N bond fission of the zwitterionic intermediate resulting from proton transfer between the hydroxyl group and the amine (9, 16). According to our calculations, this proton transfer is relayed via Glu104. First, the proton is transferred from the hydroxyl group of Int2 to Glu104, resulting in a negatively charged intermediate (Fig. 1, Int3). The negative charge on Int3 is stabilized by the zinc ion, making this step essentially isoenergetic. Formation of the zwitterionic intermediate (Fig. 1, Int4) then occurs by proton transfer from Glu104 to the amine group, which is also an isoenergetic step, with a resulting energy of 10.1 kcal/mol relative to Ra (Table 1). Following these proton transfer events, the C-N bond finally breaks to yield the products uracil and ammonia, with a predicted overall activation energy of 14.7 kcal/mol (Fig. 1, TS5). Optimization of the ternary product state (P) requires a more complete model of the enzyme active site because of the rapid diffusion of the ammonia. Because the energy of this state does not affect any of our conclusions, it was omitted from the DFT optimization and instead calculated by the EVB model, which provides a more complete representation of enzyme–solvent system. The DFT-optimized structures of the various states are given in Figs. S1–S3.

Fig. S1.

Optimized structures of the reactant state in its two conformations with respect to rotation of Glu104 (Ra and Rb), the transition state for cytidine protonation (TS1), and the protonated cytidine intermediate (Int1). Calculations were done at the B3LYP/6-31G(d,p) level of theory with the LANL2DZ pseudopotential for the zinc ion. The substrate is highlighted with orange carbons (nonpolar hydrogens omitted and distances in Å). Constrained atoms in the DFT optimizations are indicated with asterisks.

Fig. S3.

Optimized transition state structure for protonation of the tetrahedral intermediate (TS4), the zwitterionic intermediate (Int4), and the transition state for its deamination (TS5).

Fig. S2.

Optimized transition state for the nucleophilic attack (TS2), the tetrahedral intermediate (Int2), the transition state for its deprotonation (TS3), and the deprotonated tetrahedral intermediate (Int3a).

The main transition states, TS2 and TS5, identified in the DFT calculations are similar to the ones found in studies on related systems (9, 16), indicating that the key chemical steps are the same. However, the overall energy landscape differs because of the differences in the active sites and computational models. Compared with cytosine deaminase (16), the deamination of cytidine proceeds here via a different proton pathway. The necessary proton transfer steps are mediated by Glu104, and no extra water molecules (9) are implicated either in our calculations or available crystal structures (21–23). All key elements of the active site are included in our model, which represents the enzyme environment accurately, as judged by the excellent agreement between the calculated energetics and experiment. Overall, the two main transition states are of similar height, 15.3 and 14.7 kcal/mol for TS2 and TS5, respectively (Fig. 2). Both of these values are very close to the 14 kcal/mol barrier derived from the observed value of k_cat (4), and, hence, the precise rate-limiting step cannot be unambiguously identified by the DFT calculations.

Fig. 2.

Calculated energetics of cytidine deamination in the enzyme and for a reference reaction in water following the same mechanism. The DFT energy profile (black curve) includes the electronic energy calculated at the B3LYP/6-311+G(2p,2d)/LANL2TZ level of theory, ZPE, dispersion, and solvation corrections. The EVB free-energy profiles are each averaged over 20 independent MD/EVB simulations of the enzyme (red curve) and water (blue curve) reactions at 300 K.

Entropies and Enthalpies from EVB Simulations.

To be able to compute thermodynamic activation parameters for the different steps of the cytidine deaminase reaction, we calibrated an EVB model of the entire catalytic reaction path (Fig. 2). The EVB method describes chemical reactions in terms of valence bond structures represented by analytical force fields (17, 18) and therefore allows for extensive sampling of the configurational space by MD simulations. Although it is straightforward to construct EVB potential surfaces that exactly reproduce the DFT enzyme energetics, we chose here to include as an additional constraint that the EVB model simultaneously reproduces the energetics of an uncatalyzed reference reaction in water following the same reaction mechanism. That is, although we have earlier characterized the spontaneous deamination of cytidine in water (5), this process follows a different mechanism from that found for the enzyme. It is therefore useful to verify that the EVB model can describe both the enzyme energetics and the enzyme’s catalytic effect with respect to the same mechanism in solution, even if the latter is not actually operational (17, 18). Furthermore, because the enzyme reaction involves the critical role of the zinc ion, particular care has to be taken in parametrization of the zinc-ligand interactions so that both energetics and geometries are accurately reproduced. Details of the EVB parametrization are given in SI Methods and Fig. S4.

Fig. S4.

EVB parameters used in the simulations [i.e., gas-phase shifts and off-diagonal elements (1, 2)] for each of the reaction steps and the corresponding target values of $\mathrm{\Delta }{G}^{‡}$ and $\mathrm{\Delta }{G}^0$ for the uncatalyzed reference reaction in water. All energies are in kcal/mol.

The resulting EVB free-energy profiles at 300 K for both the enzyme and reference reactions are shown in Fig. 2, where it can be seen that the rate-limiting enzyme barriers obtained from DFT are well reproduced. The overall free-energy barrier for the water reference reaction following the same mechanism is 32.5 kcal/mol (Table 1), which is about 2 kcal/mol higher than the neutral water attack mechanism predicted for the uncatalyzed solution reaction (4, 5). Moreover, the EVB model closely matches the key enzyme transition states from DFT (TS2 and TS5) in terms of geometry (Fig. 3), where the tetrahedral coordination of the Zn-ligands is essential for a correct structural model of the active site. We also performed the EVB calculations for the initial proton transfer from the zinc-bound water to Glu104, which was not optimized by DFT. Although this process is over 15 kcal/mol uphill in solution (Fig. 2), because of the large pK_a difference between water and glutamate, the proton transfer is predicted by the MD/EVB simulations to be by slightly downhill in the enzyme. This effect is clearly attributable to the Zn–hydroxide interaction, and the EVB model thus provides independent support for the DFT result that the ES complex has a zinc-bound hydroxide ion. The average EVB free profile, obtained from 130 independent simulations, yields two rate-limiting barriers (TS2 and TS5) of 15.7 and 14.9 kcal/mol, respectively, in agreement with the DFT results.

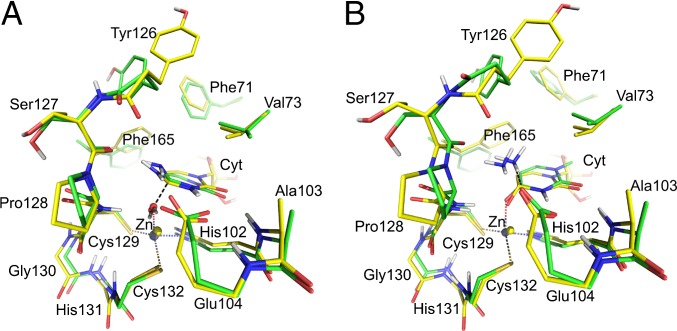
Fig. 3.

DFT-optimized transition states (green carbons) for the nucleophilic attack (A) and deamination (B) steps. The average EVB structures of the corresponding transition states are shown with yellow carbons. Nonpolar hydrogen atoms are omitted for clarity.

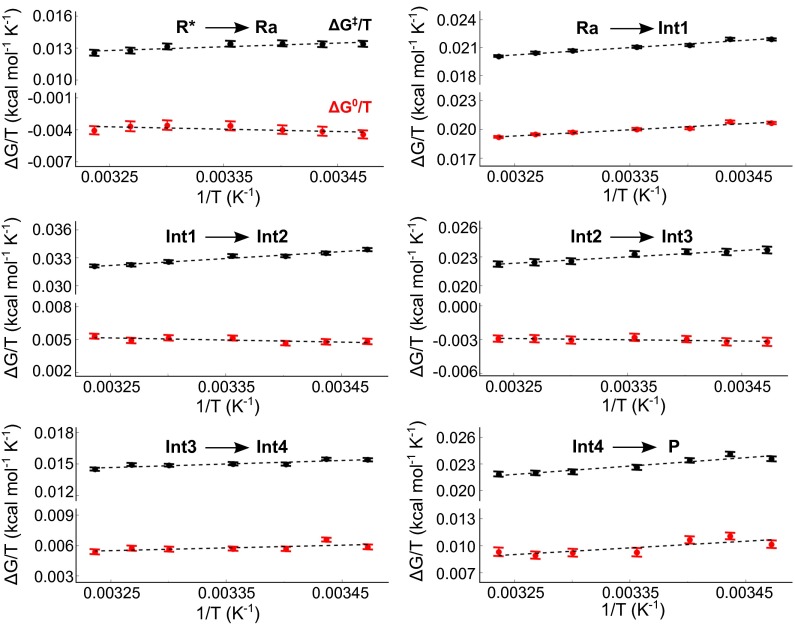
Computational Arrhenius and van’t Hoff plots of the temperature dependence of activation and reaction free energies, for each reaction step, were obtained by extensive MD/EVB simulations at seven temperatures in the range 288–309 K. These plots all give good fits to straight lines and allow activation and reaction entropies and enthalpies for the individual steps to be extracted with sufficient accuracy (Fig. 4). The overall entropies and enthalpies relative to the ES complex (Ra) along the reaction coordinate are summarized in Table 1 and data for the individual steps are given in Table S1. Of particular interest here are the activation parameters for the two highest free-energy barriers, TS2 and TS5, which are directly comparable to the experimentally derived values (4). The simulations yield $T\mathrm{\Delta }{S}^{‡}=-1.9$ and $\mathrm{\Delta }{H}^{‡}=13.8$ kcal/mol for the nucleophilic attack (TS2) and $T\mathrm{\Delta }{S}^{‡}=+0.7$ and $\mathrm{\Delta }{H}^{‡}=15.6$ kcal/mol for the zwitterion deamination (TS5), at 25 °C. It is thus noteworthy that both of the two possible rate-limiting transition states have entropy contributions close to zero, in agreement with the experimental result $T\mathrm{\Delta }{S}^{‡}=+0.9$ and $\mathrm{\Delta }{H}^{‡}=14.9$ kcal/mol (4). In fact, the measured magnitude of the ¹⁵N kinetic isotope effect suggests that C-N bond breaking is the dominant rate-limiting step in the enzyme, in contrast to the uncatalyzed reaction (20). The activation parameters for this step (TS5) are also in almost perfect agreement with the experimental values. The small energy difference between the two transition states, as predicted by the quantum mechanical calculations used to parametrize the EVB surface, is also likely within the errors of the DFT method. That is, although the DFT energetics includes the solvation free-energy contributions, thermal corrections to the gas-phase stationary points are omitted because the 191-atom cluster has some backbone atoms constrained to their crystallographic positions.

Fig. 4.

Calculated temperature dependence of the different reaction steps in the enzyme. Computed Arrhenius and van’t Hoff plots of the activation and reaction free energies $(\mathrm{\Delta }{G}^{‡}/T$ and $\mathrm{\Delta }{G}^0/T)$ versus $1/T$ are shown with black and red data points, respectively, for each reaction step. Each data point is the average of 130 independent MD/EVB simulations, with error bars denoting the SEM. The temperature interval is 288–309 K.

Hence, both experiments and calculations indicate that the second transition state is more likely to be rate-limiting than the first. The slightly unfavorable entropy of TS2 $(T\mathrm{\Delta }{S}^{‡}=-1.9\hspace{0.17em}\text{kcal}/\text{mol})$ can further be attributed to the entropy reduction associated with a bimolecular process, whereas the more positive contribution at TS5 $\left(T\mathrm{\Delta }{S}^{‡}=+0.7\hspace{0.17em}\text{kcal}/\text{mol}\right)$, in contrast, reflects the unimolecular decomposition of the zwitterionic tetrahedral intermediate. In the latter case, the decreased substrate polarization upon moving from Int4 to P (Fig. 1) also likely contributes to the positive activation entropy (5). It can further be noted that the tetrahedral intermediates between TS2 and TS5 correspond to a low-entropy region of the reaction coordinate, in agreement with the high binding affinity for transition-state analogs (19).

Comparison of Enzyme and Solution Reactions.

An immediate implication of the above results is that a direct comparison of the enzyme reaction to spontaneous cytidine deamination in water can be very misleading. That is, although the deamination reaction indeed involves a tetrahedral intermediate both in water and the enzyme, the reaction mechanism is distinctly different in the two environments. Whereas the water reaction occurs through a concerted mechanism with formation of the tetrahedral intermediate as the rate-limiting step, the enzyme proceeds via a stepwise hydroxide attack mechanism with two transition states of similar magnitude. In agreement with the small activation entropies for the enzyme reaction, our earlier calculations also gave small positive activation entropies for uncatalyzed OH⁻ attack on protonated cytidine and 5,6-dihydrocytidine in water (5). This effect could be attributed to a less polar transition state than the zwitterionic state preceding nucleophilic attack, in which strong solvation is associated with a low water entropy. However, the overall activation entropy for the stepwise mechanism in water was found to be too negative $(T\mathrm{\Delta }{S}^{‡}=-11.9\hspace{0.17em}\text{kcal}/\text{mol})$ to be consistent with experimental data (4), in contrast to the concerted mechanism $(T\mathrm{\Delta }{S}^{‡}=-9.1\hspace{0.17em}\text{kcal}/\text{mol})$. Furthermore, this overall negative activation entropy for the stepwise mechanism in water is completely dominated by the initial proton transfer from water to neutral cytidine, yielding the strongly solvated zwitterionic state (5).

In the enzyme, however, the pK_a of the zinc-bound water decreases to the extent that proton transfer to the cytidine is downhill and makes no contribution to k_cat, and this process is also associated with a small entropy change, $T\mathrm{\Delta }{S}^0=-1.2$ (Table 1). Hence, the hydroxide ion is already available in the ground state of the ES complex, and the entropy penalty for creating the ion is eliminated by the preorganized active site of the enzyme (24). This result is thus the fundamental reason for why the following transition states are not associated with large negative entropies as found for the uncatalyzed reaction (5).

SI Methods

The interaction of the zinc cation with its ligands in the cytidine deaminase active site plays a crucial role in the catalytic reaction. Electronic effects such as charge transfer and polarization has to be accounted for to capture the effect of these interactions. Although conventional force fields offer a computationally efficient method necessary for entropy calculations, the zinc cation interactions are usually not sufficiently accurately defined. To obtain a reliable description of the enzyme active site, we therefore introduced an empirical parameterization for fine-tuning of the relevant force field parameters. The partial charges on the zinc cluster were scaled down to $+1$ atomic units (au) for the zinc and $-0.5$ au for Cys129 and Cys132. This charge reduction improves the tetrahedral geometry of the zinc coordination and prohibits the artificial interaction between Glu104 and the zinc atom (Fig. 3). The partial charges of the intermediate species (Table S2) were also adjusted slightly, so that the EVB free-energy profile simultaneously reproduces the DFT results for the enzyme and the reference reaction energetics in water. The reference reaction is an extra constraint in fitting the EVB parameters, gas-phase shifts and off-diagonal elements (17, 18), for each reaction step. The final EVB parameters and reference reaction energetics are given in Fig. S4.

The energetics of the uncatalyzed reference reaction in water was estimated either from experimental data or the DFT calculations (Fig. S4). The free energy of the proton transfer steps was calculated from the relationship $\mathrm{\Delta }{G}^0=2.303RT\left[p{K}_a^{Donor}-p{K}_a^{Acceptor}\right].$ The initial proton transfer from water to Glu104 (Fig. S4, step i) yields a reaction free energy of $\mathrm{\Delta }{G}^0=15.6$ kcal/mol, with ${\mathrm{pK}}_{\text{a}}$ values of 15.7 and 4.25 for water and Glu104, respectively. The reaction free energy of the subsequent proton relay from Glu104 to the cytidine (Fig. S4, step ii) is $\mathrm{\Delta }{G}^0=-0.5$ kcal/mol, with a ${\mathrm{pK}}_{\text{a}}$ value of 4.6 for cytidine (39). The activation barriers for these steps were obtained from accurate experimental linear free-energy relationships (40, 41). The resulting activation barriers are $\mathrm{\Delta }{G}^{‡}=19.0$ and $\mathrm{\Delta }{G}^{‡}=4.0$ kcal/mol for the initial and proton transfer, respectively. The DFT results from our previous work (5) were used for the nucleophilic attack on the protonated cytidine (Fig. S4, step iii). The calculated reaction and activation free energies are $\mathrm{\Delta }{G}^0=3.2$ and $\mathrm{\Delta }{G}^{‡}=17.4$ kcal/mol, respectively. According to our DFT calculations of the enzyme reaction, the tetrahedral intermediate formation is followed by proton transfer from the hydroxyl group of this intermediate to Glu104 (Fig. S4, step iv). The ${\mathrm{pK}}_{\text{a}}$ of the tetrahedral intermediate was calculated by the method described in refs. 42 and 43. This pK_a was then estimated from two initial fragments, 2-propenol and methanol, which yielded final ${\mathrm{pK}}_{\text{a}}$ values of 11.45 and 10.46 for the intermediate, where the average value of 11 was used. The reaction free energy for deprotonation of the intermediate is thus estimated to be $\mathrm{\Delta }{G}^0=9.2$ kcal/mol from the ${\mathrm{pK}}_{\text{a}}$ difference, yielding an activation barrier of $\mathrm{\Delta }{G}^{‡}=13.1$ kcal/mol (40, 41).

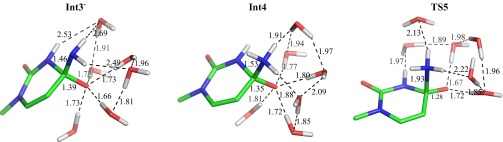
It was not possible to find experimental data for the proton transfer from Glu104 to the negatively charged intermediate (Fig. S4, step v). Therefore, the reaction free energy was calculated according to the process

$${\text{CH}}_3\text{COOH}\left(n{\text{H}}_2\text{O}\right)+\mathbf{Int}{\mathbf{3}}^{\mathrm{-}}\left(m{\text{H}}_2\text{O}\right)\to {\text{CH}}_3{\text{COO}}^{\mathrm{-}}\left(n{\text{H}}_2\text{O}\right)+\mathbf{Int4}\left(m{\text{H}}_2\text{O}\right),$$ [1]

where m and n are the number of explicit solvating waters and Int3⁻ and Int4 denote the two charged and zwitterionic cytidine intermediates (Fig. S6). The calculations were performed with the M06-2X functional (44) and the 6-311+g(2d,2p) basis set together with the SMD continuum solvent model (45). The reaction free energy from Eq. 1 is equivalent to the regular ${\mathrm{pK}}_{\text{a}}$ difference relationship. To test the accuracy of the method, the reaction free energy was calculated for proton transfer from water to acetic acid with four screening waters ($n,m=4$). The predicted reaction free energy was $\mathrm{\Delta }{G}^0=15.8$ kcal/mol, which is in good agreement with the experimental value of 14.9 kcal/mol. The reaction free energy was then calculated for proton transfer from Glu104 to the negatively charged intermediate with $n=4$ and $m=6$, which resulted in $\mathrm{\Delta }{G}^0=-7.5$ kcal/mol (Fig. S6). To test the effect of screening waters, the calculation was repeated with $n=4$ and $m=13,$ which yielded the reaction free energy of $\mathrm{\Delta }{G}^0=-7.7$ kcal/mol. Hence, it was concluded that accurate results are obtained at a reasonable computational cost with six screening waters for the intermediates, and this model was used for subsequent calculations. Based on the obtained reaction free energy, the activation barrier was again estimated by the linear free-energy relationship to be $\mathrm{\Delta }{G}^{‡}=4.0$ kcal/mol.

Fig. S6.

DFT optimized structures of the two cytidine intermediates (Int3⁻ and Int4) involved in step v and the transition state (TS5) for step vi, all in water. Geometry optimization and frequency calculations were performed at the M062X/6-311+G(2d,2p) level of theory with the SMD continuum solvent model (nonpolar hydrogens omitted and distances in Å).

The zwitterionic intermediate is deaminated in the final step (Fig. S4, step vi). To obtain the activation free energy of this step in water, the enzyme transition state was reoptimized with the M06-2X functional and the 6-311+g(2d,2p) basis set in the presence of six screening waters and the SMD continuum solvent model (Fig. S6, TS5). The activation free energy for this step was calculated to be $\mathrm{\Delta }{G}^{‡}=2.9$ kcal/mol, and the reaction free energy was taken from experimental data for the overall deamination reaction (46). The latter yields $\mathrm{\Delta }{G}^0=-1.0$ kcal/mol at a 1 M standard state and $\mathrm{\Delta }{G}^0=+1.4$ kcal/mol with correction for a 55 M standard state, corresponding to the contact complex with ammonia in water. Hence, for the last reaction step, we obtain $\mathrm{\Delta }{G}^0=-18.6$ kcal/mol as the reaction free energy relative to Int4.

Discussion

Our combined DFT and MD/EVB simulations of the cytidine deaminase reaction are found to yield energetics in excellent agreement with available experimental data (4). Remarkably, this finding is true not only for the activation free energies but also for their partitioning into entropies and enthalpies. Evaluation of this partitioning is made possible by extensive MD simulations using the fast EVB method, which enables the temperature dependence of activation free energies to be accurately evaluated via computational Arrhenius and van’t Hoff plots. The results from these calculations show that the enzyme-catalyzed reaction proceeds with a very small activation entropy contribution to k_cat, in contrast to the uncatalyzed reaction in water, where the entropy penalty is considerable and was earlier calculated to be $T\mathrm{\Delta }{S}^{‡}=-9.1$ kcal/mol (5), also in good agreement with experiment (4).

This situation would superficially appear to be the perfect example of Jenck’s Circe effect (1), in which a large entropy penalty for the uncatalyzed reaction is eliminated by the enzyme because of tight binding of the substrate. Hence, it is assumed that part of the binding free energy is spent on aligning and bringing the reacting groups into proximity (thereby paying the entropy penalty), so that the chemistry can proceed with little entropy loss. In cytidine deaminase, this picture is, however, clearly wrong. First, the large negative activation entropy for the solution reaction reflects the cost of ordering water molecules in the transition state and has little to do with motions of the cytidine reactant. Second, and most important, the near-zero activation entropy in the enzyme is primarily attributable to a change of reaction mechanism. The hydroxide attack and subsequent decomposition of the zwitterionic intermediate are intrinsically associated with only small entropy contributions, as found earlier for the water reaction (5). The major difference in the enzyme compared with water is that proton transfer from the zinc-bound water (via Glu104) to the cytidine proceeds with a positive entropy change. In water, the proton transfer reaction yielding hydroxide ion and protonated cytidine is associated with a large negative entropy change because of strong solvation of the two charged species and a major reorganization of water molecules around them. Hence, it is the preorganized enzyme active site (24) that allows the hydroxide and protonated cytidine to be formed with no entropic reorganization penalty, and here the interplay between the zinc ion and Glu104 is the most important effect.

In general, it appears that the interpretation of the enzymic entropy effects solely in terms of substrate entropies is highly oversimplified. Both in solution and in enzymes, the entropy change of the environment surrounding the reacting groups can make significant contributions to the overall entropy change and overshadow effects associated with restriction of substrate motions and alignment. In particular, when dealing with reactions involving charge separation and transfer, solvation of the charges is likely to dominate the overall entropy change, and enzyme and water environments can behave very differently in this respect. In the case of cytidine deaminase, it appears that the large negative entropy contribution to the binding free energy $(T\mathrm{\Delta }{S}_{bind}^0=-7.6\hspace{0.17em}\text{kcal}/\text{mol})$ (4) coincidentally happens to be of the same magnitude as $T\mathrm{\Delta }{S}^{‡}$ for the uncatalyzed reaction but actually has little to do with the latter quantity. It is rather often the case with protein ligands (except very hydrophobic ones) that they bind with significantly negative enthalpies and partly compensating negative entropies, which indeed reflects the reduction of configurational space accompanying bimolecular association (3). However, the evidence for such “freezing out” of substrate motions having a large impact on catalytic rates remains rather weak (25). At any rate, it is clear that to be able to computationally analyze the role of entropic effects in enzyme catalysis, it is necessary to evaluate all contributions to the activation entropies, including those from the substrates, protein, and solvent. Only then can the origin of experimentally derived thermodynamic activation parameters be meaningfully addressed on the microscopic level.

Methods

DFT Cluster Model.

The crystal structure (22) of E. coli cytidine deaminase in complex with 3-deazacytidine (Protein Data Bank ID code 1ALN) was used for constructing the DFT cluster model. The model was based on the same approach as used in a recent study of the related enzyme E. coli cytosine deaminase (16). Residues 126–132 and 102–104 make up the key interactions with the substrate and zinc ion. For these residues, both backbone and side chains were included except for His131, where the side chain was replaced with a hydrogen atom. Side chains were also included for Val73, Phe71, and Phe165, resulting in a 191-atom model with an overall charge of −1 (Figs. S1–S3). The inhibitor was converted to 1-methylcytosine as the model substrate. To mimic the effect of the enzyme backbone, certain atoms were constrained to their crystallographic positions in the DFT optimizations (Figs. S1–S3), as described earlier (16).

Structure optimizations and frequency calculations were performed with the B3LYP functional (26), the LANL2DZ pseudopotential for Zn (27) and the 6-31G(d,p) basis set for O, N, C, and H. Electronic energies were obtained by single-point calculations at the optimized geometries with the LANL2TZ pseudopotential for Zn (28, 29) and the 6-311+G(2d,2p) basis set for O, N, C, and H. Dispersion effects were calculated with Grimme’s B3LYP-D3 method with the DFT-D3 package (30, 31). To take into account the effect of the protein environment, the conductor-like polarizable continuum model (CPCM) (32) was used with a dielectric constant of 4 and UAKS atomic radii. These calculations were performed at the same level of theory as the geometry optimizations. DFT calculations were done with Gaussian 09 (33) except for the dispersion corrections (see above). Final energies are reported as electronic energies with the large basis set plus corrections for zero-point energy (ZPE), dispersion, and CPCM solvation.

EVB Simulations.

MD/EVB simulations for both reference and enzyme reactions were performed with the Q MD package (34). The EVB valence structures were described by a modified OPLS-AA force field (35) (SI Methods and Table S2). Spherical boundary conditions were used in the MD simulations, with a radius of 20 Å centered on the C4 atom of the cytidine. The TIP3P water model was used for solvation of the protein, and waters close to surface were treated with radial and polarization restraints according to the SCAAS model (34, 36). Protein residues outside the simulation sphere were excluded from nonbonded interactions and were restrained to their initial coordinates by harmonic potentials with a 200 kcal mol⁻¹ Å^-2 force constant. MD simulations were carried out with a 1-fs time step, and a 12-Å cutoff was used for direct nonbonded interactions, with electrostatic interactions beyond the cutoff treated by the local reaction field multipole expansion method (37). No cutoff was, however, applied to nonbonded interactions involving the reacting fragments.

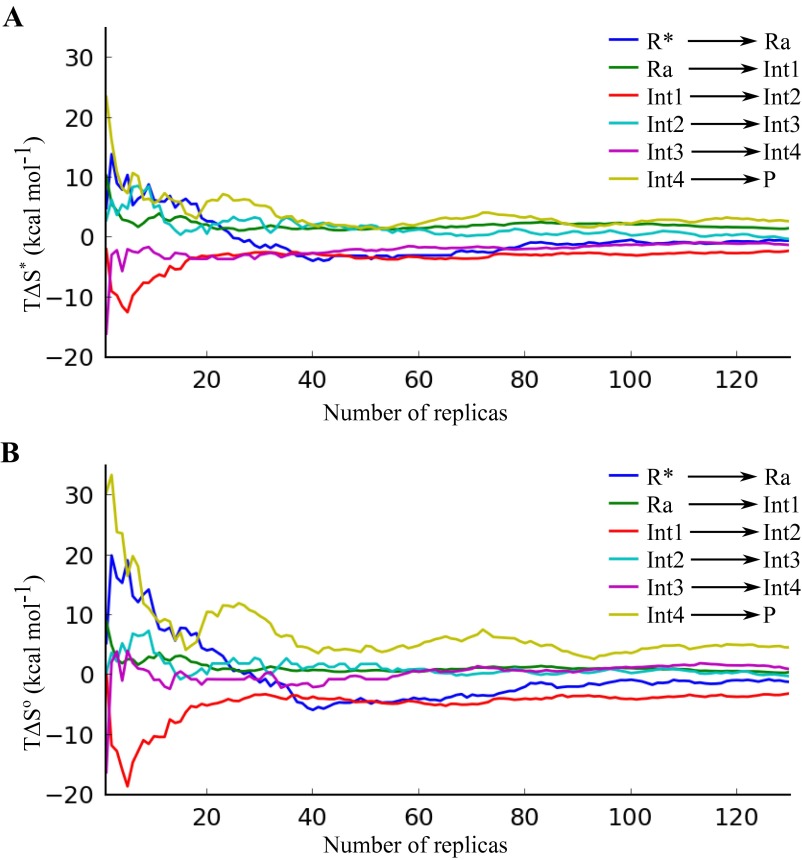
During the enzyme MD/EVB simulations, a distance restraint of 10 kcal mol⁻¹ Å^-2 was introduced between the zinc atom and its ligands His102, Cys129, and Cys132 (these restraints made a negligible contribution of ∼1 kcal/mol to the potential energy). Each reaction step was defined by a two-state EVB model, for which the initial valence bond state was transformed to the final state via 51 intermediate free-energy perturbation windows, and free-energy profiles were calculated as described elsewhere (5, 38). Entropies and enthalpies were computed by constructing Arrhenius and van’t Hoff plots from these data in the temperature interval from 288 to 309 K (Fig. 4). To achieve sufficient sampling statistics, the enzyme MD/EVB calculations were repeated 130 times with different initial velocities for each reaction step and temperature, yielding a total of about 8.35-μs simulation time for the enzyme reaction. The convergence of the calculated entropies is shown in Fig. S5. The water reference reaction simulations (Figs. S4 and S6) were repeated 20 times at 300 K, yielding a total of about 180-ns simulation time.

Fig. S5.

Convergence of the calculated activation (A) and reaction (B) entropies (kcal/mol at 25 °C) for each step of the enzyme reaction as a function of number of simulation replicas.