Comparative Ab-Initio Study of Substituted Norbornadiene-Quadricyclane Compounds for Solar Thermal Storage

Abstract

Molecular photoswitches that are capable of storing solar energy, so-called molecular solar thermal storage systems, are interesting candidates for future renewable energy applications. In this context, substituted norbornadiene-quadricyclane systems have received renewed interest due to recent advances in their synthesis. The optical, thermodynamic, and kinetic properties of these systems can vary dramatically depending on the chosen substituents. The molecular design of optimal compounds therefore requires a detailed understanding of the effect of individual substituents as well as their interplay. Here, we model absorption spectra, potential energy storage, and thermal barriers for back-conversion of several substituted systems using both single-reference (density functional theory using PBE, B3LYP, CAM-B3LYP, M06, M06-2x, and M06-L functionals as well as MP2 calculations) and multireference methods (complete active space techniques). Already the diaryl substituted compound displays a strong red-shift compared to the unsubstituted system, which is shown to result from the extension of the conjugated π-system upon substitution. Using specific donor/acceptor groups gives rise to a further albeit relatively smaller red-shift. The calculated storage energy is found to be rather insensitive to the specific substituents, although solvent effects are likely to be important and require further study. The barrier for thermal back-conversion exhibits strong multireference character and as a result is noticeably correlated with the red-shift. Two possible reaction paths for the thermal back-conversion of diaryl substituted quadricyclane are identified and it is shown that among the compounds considered the path via the acceptor side is systematically favored. Finally, the present study establishes the basis for high-throughput screening of norbornadiene-quadricyclane compounds as it provides guidelines for the level of accuracy that can be expected for key properties from several different techniques.

Introduction

The worldwide energy consumption is predicted to double within the next 40 years requiring a shift toward widespread use of renewable energy.¹ In this regard, sunlight is one of the most important energy sources, which can be harvested e.g., via photovoltaics or thermal heating for direct use. One of the challenges for the development of solar energy technologies are variations in both energy production and demand over time, which requires the use of load leveling techniques.^2,3 While electricity can be stored using batteries for on-demand power supply, this technology faces challenges with respect to cost and large-scale implementation.

An alternative is the direct conversion from solar energy to stored chemical energy. This can in principle be achieved via the conversion of water to hydrogen or the reduction of carbon dioxide to methanol,⁴ which, however, involves gaseous species. Energy storage can instead also be accomplished in closed cycle photo isomer systems. In these so-called molecular solar thermal (MOST) systems, the exposure of a low energy isomer to sunlight leads to its conversion into a high energy isomer.^5,6 The metastable high-energy isomer can be converted back to its low energy counterpart by heating or catalytic activation to release the stored energy. Several molecular and metal–organic systems have been explored in this context, notably stilbenes,^7,8 azobenzenes,⁹⁻¹¹ anthracenes,¹² ruthenium fulvalene compounds,^5,13−16 and norbornadiene-quadricyclane (N-Q) systems.¹⁷⁻¹⁹ Both experimental and theoretical aspects of this research field have been reviewed recently.^6,18,20,21

A material system that is suitable for MOST applications must fulfill a number of conditions in order to be practical:²² (i) The absorption spectrum has to be optimized with respect to the solar emission spectrum to achieve maximal efficiency (“solar spectrum match”). (ii) The energy storage density should be high, which implies a compromise between storage energy and molecular size. (iii) The barrier for the back-conversion from the high-energy to the low-energy isomer has to be sufficiently high to enable long-term storage yet be accessible via a catalytic reaction to enable timely energy release. (iv) The quantum yield for the photoconversion from the low to the high-energy isomer should be close to unity. (v) The price of the synthesized compounds must be competitive. In this study we focus on analyzing conditions i–iii with respect to substituted N-Q compounds, for which condition iv is already achieved.¹⁷

Systems based on norbornadiene (N) and its high-energy isomer quadricyclane (Q) have seen a recent resurgence, in part because of advances in synthetic chemistry that enable the systematic insertion of donor and acceptor-type substituents. We address the parent N-Q system (1) as well as five diaryl-substituted N-Q compounds (2–6), see Figure 1, which have been previously investigated experimentally.¹⁷

Figure 1.

Overview of compounds considered in this work shown in their respective norbornadiene variant. Single and double primed numbers are used to enumerate the carbon atoms in the first and second aryl ring, respectively.

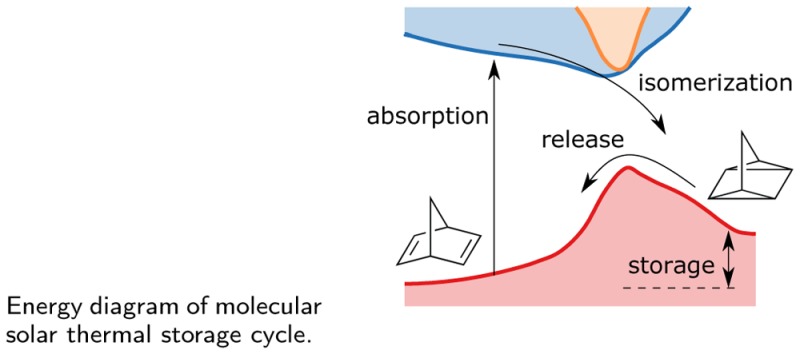
Substitution provides a powerful means for manipulating the energy landscape, which is schematically shown in Figure 2. Here, the (minimum) absorption energy hν, the storage energy ΔE, and the barrier for back-conversion ΔE^⧧, respectively, relate to conditions i–iii described above. The corresponding enthalpies are ΔH and ΔH^⧧, respectively. Here, ΔH^⧧ directly relates to the rate of the thermal back-conversion (Q → N) via the Eyring equation. While substitution provides a lot of flexibility for material optimization, it usually affects several properties simultaneously and therefore requires a detailed understanding of the effect of individual substituents as well as the interplay of donor and acceptors. Figure 2b illustrates the differences between the energy landscapes of the unsubstituted (1) and a diaryl substituted compound (2). Here, the substitution causes simultaneously a red-shift of the spectrum, a lower ΔE^⧧, and an increase of the storage energy ΔE. While the first two observations are in line with recent experimental results,¹⁷ experimental data pertaining to the storage energies is less readily available illustrating the utility of theoretical predictions.

Figure 2.

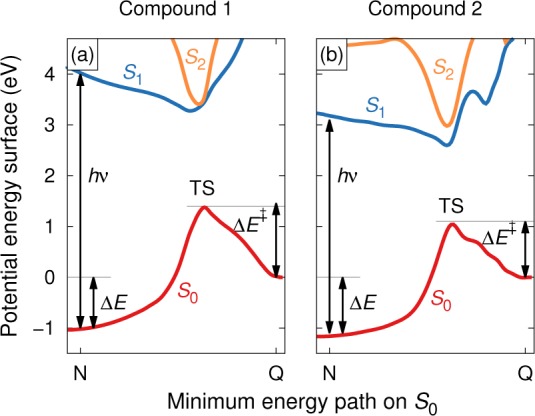
(a) Energy diagram of the parent MOST system (1). The molecule absorbs a photon with minimum energy hν and while in its electronically excited state undergoes an isomerization, forming the photoisomer. If the activation barrier (ΔE^⧧) is sufficiently high, the photoisomer is trapped over an extended period of time (i.e., typically months to years). The energy difference between the parent and the photoisomer (ΔE) is the amount of energy stored in the system and is regained as heat when the reversible isomerization is activated, either catalytically or thermally. (b) Energy diagram for a substituted compound (2). Unlike in part a, the transition state geometry was not obtained by full relaxation but constructed following the procedure described in the text. Note that the slices displayed in parts a and b are based on the minimum energy path on S₀, whence the excited state surface represents an off-center slice of the conical intersection between S₀ and S₁. The present visualization is based on (8,8) CASSCF nudged elastic band calculations of the singlet ground state (S₀) surface followed by 4-state averaged multistate CASPT2 calculations.

As the synthesis of a specific compound is still quite time-consuming, a purely experimental screening of donor–acceptor combinations is impractical. It is therefore highly desirable to complement experimental work with first-principles calculations. Because of the orbital structure of N and Q, which will be discussed in detail below, the quantum mechanical description of these systems, however, poses challenges of its own. The objective of the present study is to establish the predictive power of several computational techniques at various levels of sophistication and computational expense with respect to optical, thermodynamic, and kinetic properties of a set of prototypical substituted N-Q compounds, for which experimental data is available. In doing so we gain insight into the detailed mechanisms that govern the behavior of these compounds and address open questions pertaining in particular to the back-conversion barrier. On the basis of our data, one can formulate a strategy for the computational screening of N-Q compounds that balances computational expense and accuracy requirements, paving the way for a systematic exploration of substitution strategies.

We note that the unsubstituted N-Q system has been previously investigated using multireference methods both with regard to ground and excited state landscapes,^23,24 and several substituted N-Q systems have been explored at the level of density functional theory (DFT).^25,26 The design of MOST systems with the help of theoretical methods has also recently been considered by Olsen et al.²⁷

The paper is structured as follows: The following section provides an overview of the computational details and codes used in this study. The first three parts of the Results and Discussion section address in sequence the conditions i–iii described above following the causal logic of the storage-cycle: (i) absorption, the initialization of the photoreaction; (ii) energy storage, the harvested energy is stored in quadricyclane form; and (iii) transition state analysis, the stability of the high-energy isomer (Q) toward thermal back-conversion to the low-energy variant (N). The description of the transition states of these compounds requires multireference calculations due to their biradical character. We analyze the pitfalls of single reference methods and discuss approximative means to analyze and calculate these states from single-reference data. The fourth and final part of the Results and Discussion section provides some insight into the enhanced quantum yield of substituted systems relative to the unsubstituted compound. In the Conclusions section, the results are discussed with respect to the available experimental data and a computationally efficient screening approach is outlined.

Methods

Following the lines of recent experimental work,¹⁷ we consider substitutions on the C2–C3 double bond (see Figure 1) with an electron-donating aryl and an electron-withdrawing aryl creating a conjugated push–pull system. Where necessary, the norbornadiene and quadricyclane forms are specifically as, e.g., 1N or 1Q. The substituted compounds were created with the OpenBabel software package²⁸ using the SMILES syntax.²⁹ A preliminary conformer search was performed using OpenBabel and the Universal Force Field.³⁰ These structures were refined by subsequent B3LYP calculations (see below), from which the respective lowest energy conformation was selected. We then carried out further calculations using both single-reference methods based on DFT, which are suitable for high-throughput schemes and multireference approaches based on complete active state (CAS) techniques, which are computationally much more expensive but provide a high level of accuracy and predictive power.

Single-Reference Calculations

Density functional theory (DFT) calculations were carried out using the NWChem suite (version 6.5).³¹ Both N and Q geometries were investigated using a number of different exchange-correlation (XC) functionals including the semilocal PBE and M06-L generalized gradient approximation (GGA) functionals,³⁶ the B3LYP hybrid functional,^32,33 the range-separated CAM-B3LYP hybrid functional,³⁴ as well as three hybrid meta-GGA functionals (M06, M06-2x).³⁷ Storage energies and geometries were analyzed for all functionals; absorption spectra were calculated within the framework time dependent DFT (TD-DFT) for the PBE, B3LYP, and CAM-B3LYP functionals including the first 15 excitations. All of these calculations were carried out using a 6-311+G* basis set (split-valence triple-ζ with polarization and diffuse functions for heavy atoms).³⁸⁻⁴⁰ Storage energies were found to change by less than 2.5 kJ/mol when adding polarization and diffuse functions also for hydrogen (6-311++G**) whereas excitation energies varied by 0.01 eV or less. The effect of solvation in toluene, which is the solvent employed in a prior experimental study,¹⁷ was treated at the level of the universal solvation model introduced by Marenich et al.⁴¹

In addition, we performed single-point calculations based on B3LYP geometries at the MP2 level using an aug-cc-pvdz basis set. These calculations were complemented in the case of the unsubstituted compound by CCSD(T) single-point calculations based on relaxed MP2 geometries (CCSD(T)//MP2) to obtain a reference value for the storage energy. For the latter case, we also studied basis set convergence (see the Supporting Information).

Complementary calculations based on the PBE functional were conducted using grid based wave functions as implemented in the GPAW code⁴² with a grid spacing of 0.17 Å and a vacuum region of 6 Å as well as the Atomic Simulation Environment (ASE).⁴³ For the TD-DFT calculations, we used the real-time propagation of grid wave functions module of GPAW,⁴⁴ a grid spacing of 0.2 Å, a vacuum region of 5 Å, and a Poisson solver with multipole corrections up to l = 2.⁴⁵ In order to analyze the role of van-der-Waals (vdW) interactions between the aryl rings, we also carried out calculations using the vdW-DF method⁴⁶⁻⁴⁸ within GPAW.

Multireference Calculations

To benchmark and understand shortcomings of the single-reference calculations, several higher level methods were considered. Specifically, we performed CAS calculations both of the self-consistent field (CASSCF)⁴⁹ and second-order perturbation theory (CASPT2) kind⁵⁰ as implemented in MOLCAS 8.0.⁵¹⁻⁵³ These multireference methods provide superior accuracy compared to single-reference methods, which under multireference conditions can fail not only quantitatively but qualitatively. They are, however, computationally much more expensive and can also require considerably more guidance and knowledge. In particular, upon diaryl substitution the desired active space increases dramatically due to π-conjugation, rendering a comprehensive treatment of all compounds of interest prohibitively expensive. However, as elaborated in the Results and Discussion section, we have carefully examined the effect of reducing the active space using compound 2 as an example in order to obtain a computationally more efficient scheme. The selection of the active spaces varies with compound and context, and we describe the chosen space for each application. Unless explicitly mentioned, we use the ANO-S DZP contracted basis set⁵⁴ using the contraction (6s4p3d|3s2p1d) for second row elements and the contraction (4s3p|2s1p) for H in all multireference calculations. In single and multi state CASPT2 calculations, we use the standard ionization potential-electron affinity (IPEA shift)⁵⁵ of 0.25 hatree units and an imaginary shift⁵⁶ of 2.72 eV (0.1 hartree units).

Results and Discussion

Absorption

Single-Reference Methods

The first singlet–singlet excitation consists of a transition from a π – π (HOMO) to a π* + π* (LUMO) orbital. The absorption energy corresponds to hν in Figure 2 and thus to a vertical transition from the minimum of the S₀ surface to the S₁ surface, from which both the unsubstituted and substituted N-Q systems undergo an intrinsic [2,2]-cycloaddition reaction. Although dipole forbidden in unsubstituted norbornadiene (1N), this transition is found to be allowed with high dipole strength for all substituted norbornadienes (2N–6N). This implies that no triplet sensitizer is required and it is most likely that in the case of the substituted systems the relevant photocatalytic and thermal transitions occur exclusively on the singlet surface.

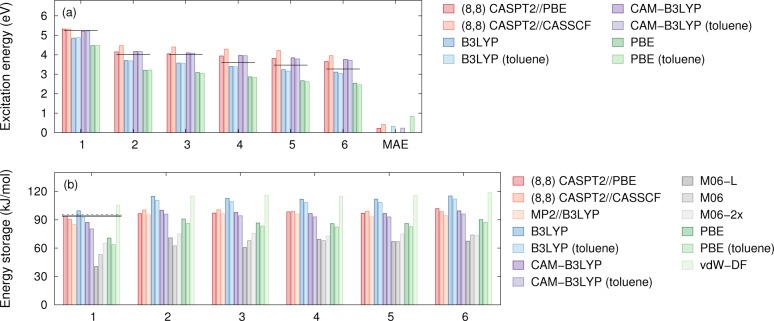
Figure 3a compares the excitation energies calculated using various approximations both excluding (vacuum) and including solvent (toluene) effects with experimental values. For compound 1, we compare the dipole forbidden transition to electron energy loss data,⁵⁷ while for 2–6 recent spectroscopic measurements are employed as reference data.¹⁷ In the latter case, the lowest optical excitation energy was identified with the first maximum of the absorption spectrum. Note that the calculations do not include vibrational effects.

Figure 3.

(a) Experimental (horizontal black lines, Gray et al.¹⁷) and computational excitation energies from (8,8) 2-SA-MS CASPT2 calculations (both DFT-PBE and CASSCF geometries) and various DFT exchange-correlation functionals. The last block reports the mean absolute error (MAE) relative to the experimental reference data. (b) Energy storage ΔE for compounds 1–6. The solid and dashed horizontal lines represent experimental and CCSD(T) values, respectively, for the storage energy ΔE of 1. More details regarding the latter can be found in the Supporting Information.

According to the calculations, the HOMO is localized on the donor while the LUMO is localized on the acceptor; the localization increases from 2 to 6 and so does the red-shift of the absorption spectrum. Solvation lowers the first optical excitation by an amount that ranges from 0.00 to 0.08 eV between 1 and 6. Both the trend and the magnitude of the effect vary only weakly between the different functionals.

As expected, DFT-PBE (similar to other nonhybrid single-reference methods) underestimates the π – π* → π* + π* excitation⁵⁸ and yields a mean average error (MAE) of 0.83 eV. (The mean average error is computed by comparing the vacuum result for 1 and the solvated data for 2–6 with the corresponding experimental data.) Relative to PBE, the fractional inclusion of the Fock-operator in the B3LYP and CAM-B3LYP hybrid functionals shifts the LUMO level upward. The resulting optical gaps are generally in much better agreement with experiment. In the case of B3LYP, the calculations systematically underestimate the reference data with a MAE of 0.32 eV whereas in the case of CAM-B3LYP a systematic overestimation by about the same magnitude is observed yielding a MAE of 0.23 eV.

Multireference Calculations

For 1, CASSCF calculations were carried out using 8 orbitals and 8 electrons (8,8) (σ + σ, σ – σ, π + π, π – π, π* – π*, π* + π*, σ* – σ*, and σ* + σ*) in the active space. The active space was chosen to comprise all single and double bonding and antibonding orbitals between the four relevant carbon atoms. The active space corresponds to the one used previously by Qin et al.,²³ and using a 6-31G* basis set, we were able to reproduce their CASSCF results for N and Q to all decimals in spite of different codes being used. The geometry of 1 was relaxed using (8,8) CASSCF, which was followed by two-state averaged (2-SA) CASPT2 calculations to obtain the lowest absorption energy. To test basis set convergence, the absorption onset energy was evaluated with various basis sets. Excitation energies of 5.32, 5.31, 5.17, and 5.12 eV were obtained with basis sets of increasing accuracy (ANO-S VDZP, ANO-L VDZP, ANO-S VTZP, ANO-L VQZP). This comparison demonstrates that a ANO-S VDZP basis set is sufficiently (<0.2 eV) converged for the present purposes, which has thus been employed in the following.

For compounds 2–6, including the full π-system in the CAS is computationally prohibitively expensive, since already in the case of compound 2 there are 4 relevant σ-electrons and 16 π-electrons. Therefore, as a first approximation, we chose to retain the same reaction center localized (8,8)-active space as in the case of 1 and performed geometry relaxations. This choice of active space allows a complete and balanced description the energetics of norbornadiene, quadricyclane, and the thermal back-conversion paths.

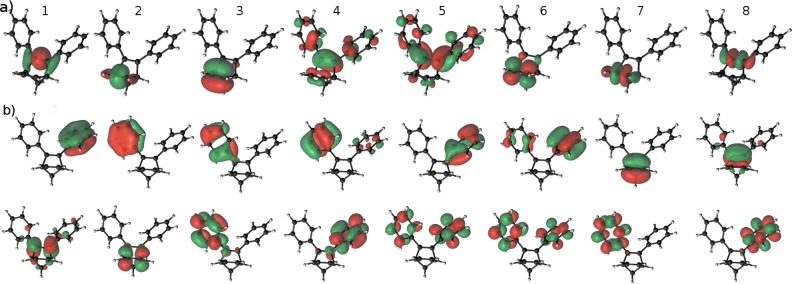
(8,8) 2-state averaged multistate (2-SA-MS) CASPT2 calculations were subsequently performed on compounds 2–6. We find that in these (8,8) CASSCF calculations, the π orbital associated with the C2–C3 bond is destabilized due to admixture of aryl π-orbitals as illustrated for compound 2 in Figure 4. Simultaneously the corresponding π* orbital is stabilized in a very similar manner as in the case of the DFT calculations. The S₀ → S₁ excitation occurs with very large weight (>95%) between these two orbitals corresponding to the transition |4²5⁰⟩→ |4¹5¹⟩, where the labels refer to the orbital enumeration in Figure 4a.

Figure 4.

(a) (8,8) active space of a 2-SA-MS-CASSCF calculation for compound 2 in DFT-PBE geometry. The corresponding orbitals in the CASSCF geometry are similar, except that the aryl π-orbitals do not hybridize as strongly with the aryl rings. (b) (16,16) active space of a 2-SA-MS-CASSCF calculation for compound 2 in CASSCF geometry.

We find that the geometry of the compounds has a significant effect on the absorption properties, especially the orientation of the aryl p-orbitals with respect to the norbornadiene p-orbitals. In the (8,8) CASSCF relaxed geometry, the reaction center localized (8,8)-active space does not conjugate as strongly with the aryl rings as in the DFT-PBE geometry. This effect is also reflected in the orientation of the aryl rings relative to the active π-orbital associated with the C2–C3 bond with a more pronounced alignment obtained in DFT-PBE calculations.

To quantify the alignment effect more systematically, we computed the angle between the vectors p and a, which specify the orientation of the active π orbital as well as either one of the aryl rings, respectively. The former vector is normal to the plane spanned by the carbon atoms 6, 2, and 3 (or alternatively 2, 3, and 5) whereas the latter is normal to the plane defined by the positions of carbon atoms 1′, 2′, and 6′ for the first and 1″, 2″, and 6″ for the second aryl ring. We find that the DFT-PBE geometries exhibit a significantly stronger alignment than the CASSCF data both on the donor and acceptor side of the compound (Table 1). Here, the DFT methods predict conjugation angles of about 24° on the acceptor and about 68° on the donor side, while CASSCF and HF yield values that are about 10° on average larger.

Table 1. Conjugation Angles Measuring the Alignment between the Orientation of the Active π-Orbital Associated with Carbon Atoms 2 and 3 and the Aryl Rings (See Figure 1)^a.

	substituents		B3LYP		CAM-B3LYP		PBE		vdW-DF		CASSCF		HF
cmpd	A	D	A	D	A	D	A	D	A	D	A	D
2	–H	–H	25.4	71.9	26.9	72.5	23.2	67.9	24.9	70.2	30.6	79.4	29.5	77.1
											(30.1)	(79.1)
3	–H	–OMe	25.5	71.0	27.1	71.9	23.1	66.6	24.5	67.1	30.9	78.7	29.8	76.2
4	–CF3	–OMe	25.0	71.2	26.7	72.6	23.6	68.8	25.5	69.2	30.6	79.3	29.3	76.9
5	–CN	–OMe	24.5	71.7	26.5	73.0	22.2	67.8	23.7	71.3	30.4	80.4	29.3	77.3
6	–CF3	–NMe2	24.9	69.8	26.4	70.8	23.0	66.4	24.0	66.1	32.1	76.7	28.9	75.0
average			25.1	71.1	26.7	72.2	23.0	67.5	24.5	68.8	30.9	78.9	29.4	76.5

^aThe CASSCF results are based on a (8,8) active space with the exception of the values in parentheses, which were obtained from (16,16)-CASSCF calculations. Columns labeled A and D report angles referring to the acceptor and donor side of the compound, respectively.

To quantify the effect of the incompleteness of the active space, for compound 2 we performed a full (16,16)-CASSCF geometry relaxation including all π-electrons in the system (but excluding the σ system). As indicated in Table 1, the geometries obtained from (8,8) and (16,16) CASSCF calculations are similar, which leads to the conclusion that the features of the CASSCF geometry alluded to above are intrinsic to the method and likely the result of the lack of dynamic correlation. Unfortunately, because of their computational expense and the need for numerical forces, geometry optimizations on the CASPT2 landscape are, however, currently impractical.

As a more practical approach, in order to approximate the effect of the geometry, we also calculated (8,8) 2-SA-MS-CASPT2 energies obtained with DFT-PBE geometries, labeled CASPT2//PBE in Figure 3a. These data exhibit a noticeable red-shift relative to the CASPT2//CASSCF and (recalling the basis set convergence and the absence of solvent effects in the CAS calculations) are overall in very good agreement with the experimental data. Specifically, for CASPT2//CASSCF and CASPT2//PBE MAEs of 0.42 and 0.22 eV are obtained, respectively. It is noteworthy that CAM-B3LYP results are in very close agreement with CASPT2//PBE as both data sets exhibit an overestimation of the data that increases along the series 2–6. This could suggest that this deviation is related to more complex vibrational effects that are not captured by the present calculations.

We note that the coupling between geometry and optical features was also reported, e.g., for the case of a 11-cis chromophore,⁵⁹ where the rotation of a β-iodine ring was found to have pronounced effects on the absorption (of order of 0.2 eV). The authors of the latter study also find that CASSCF geometries exhibited the largest conjugation angles, which limited the coupling of the π systems, while DFT yielded the smallest angle.

Dipole Strength and Attenuation Coefficient

In practical applications, the key quantity with respect to absorption (and solar spectrum match) is the molar attenuation coefficient ε, which can be obtained from a summation over the individual optical excitations weighted by their respective dipole strengths f_k. For the unsubstituted compound 1, f_k for the lowest optical excitation is zero since the transition is dipole forbidden. By contrast, for the substituted compounds 2–6 the first optical transition is allowed and the dipole strength obtained from TD-DFT calculations is at least 0.17 (PBE)/0.22 (B3LYP)/0.24 (CAM-B3LYP). To put these numbers in context, note that in order to achieve full absorption by a 1 M solution with thickness 1 cm, one requires ε ≥ 1/M cm, which with the appropriate unit conversions translates to f_k ≥ 3.5 × 10^–5.

The comparison of calculated molar attenuation coefficients with experiment (Figure 5 and Supporting Information) reveals that PBE achieves the best agreement with respect to the magnitude of ε while B3LYP and even more so CAM-B3LYP overestimate ε by up to 40%. It is furthermore evident that the experimental spectra exhibit additional features such as shoulders and double maxima that are not reproduced by the calculations. As already alluded to above in connection to the CASPT2 results, this suggests that additional vibrational and solvent effects are likely to be present in the experiment, which are included in the present calculations.

Figure 5.

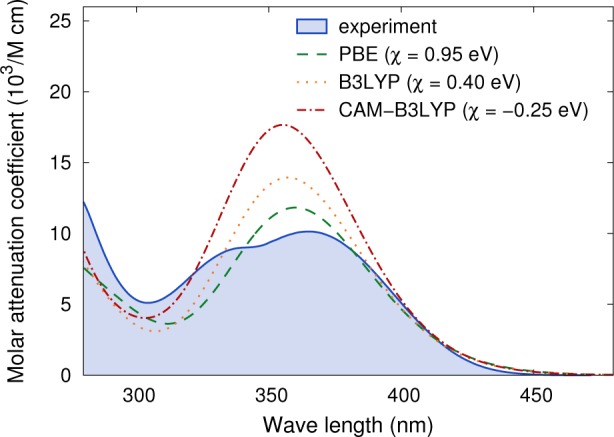
Comparison of the molar attenuation coefficient of compound 6 from experiment¹⁷ and DFT calculations. A smearing using a width of 0.25 eV was applied to the latter in order to mimic the broadening due to vibrations. The calculated spectra were rigidly shifted by a scissors correction χ for clarity. Detailed comparisons for all compounds can be found in the Supporting Information.

Energy Storage

Energy vs Enthalpy

The quantity that dictates energy storage is the enthalpy difference ΔH between N and Q. The largest contribution to ΔH is the difference in the “electronic” energies ΔE. The remaining contribution arises from differences in the vibrational spectra of N and Q (zero-point vibrations and the heat capacity term). The latter term was evaluated at the B3LYP-DFT level (vacuum), which yielded values between −2.8 and −3.3 kJ/mol for compounds 2–6 and a value of −1.9 kJ/mol for compound 1. The minor variation among the set of compounds is expected as the transition from N to Q affects the vibrations of the side groups only indirectly. Since the magnitude of this contribution to the storage enthalpy is small (≲3%) compared to the electronic energy difference and its evaluation can be very time-consuming in particular at the CAS level (and virtually impossible at the CCSD(T) level), from here on our analysis of the calculations is focused on ΔE.

Comparison to Reference Data

Compared to optical excitation energies it is relatively more difficult to obtain storage energies (or enthalpies) with good accuracy. As a result, for the substituted compounds 2–6 there are currently no reliable values available. For the unsubstituted molecule (1), a value of ΔH = 92 ± 1 kJ/mol has been determined for the storage enthalpy.⁶⁰ Assuming a vibrational correction as indicated by the calculations described in the previous paragraph, this yields a reference value for the “electronic” part of ΔE = 94 ± 1 kJ/mol. We supplemented this value with CCSD(T) calculations as described in the Supporting Information, which yield a value of ΔE = 95.5 kJ/mol.

The (8,8) CASPT2//PBE calculations reproduce these data closely [Figure 3b], whence we will consider them as reference data for compounds 2–6 below. As in the case of the optical excitation energies the (8,8) CASPT2//CASSCF calculations perform somewhat worse, presumably for the same reasons suggested above. The MP2 calculations yield even smaller storage energies.

Among the single-reference methods, the B3LYP and CAM-B3LYP values agree rather closely with the reference data. PBE-DFT exhibits a pronounced underestimation of the storage energy but still performs noticeably better than the M06-suite functionals. The latter yield values between 40 and 65 kJ/mol and thus underestimate ΔE by 30% to 57%. As will be discussed in detail in the Transition State section, a key challenge in the description of the N/Q system is related to the exchange of HOMO/LUMO character between N and Q. As a result, the description of ΔE requires an accurate description of both systems. We note that M06 and M06-2x yield, for example, smaller gaps for the Q than for the N conformations, which is in qualitatively disagreement with both experiment and higher level theory (e.g., CASPT2).

Substituted Systems

The energy storage in the substituted systems can deviate from the unsubstituted system since the C2–C3 bond couples with the aryl π-system. As a result, one can expect a lowering of the energy of the norbornadiene variants due to the delocalization of aryl π-electrons. In the quadricyclane variants, in contrast, a direct coupling is not possible since the C2–C3 bond has single bond character. This rationale explains why the substituted systems have a rather constant increase in energy storage relative to 1 regardless of the method of calculation (Figure 3b).

Comparison of the DFT data with CASPT2//PBE values, show that the CAM-B3LYP results are close to CASPT2//PBE followed by B3LYP. PBE and M06-suite functionals underestimate the storage energy, in some cases by as much as 25%. Solvation effects at the level of the implicit solvent model employed here are generally small, yielding a reduction of ΔE by about 3–4 kJ/mol.

While in the case of system 2, mirror symmetry is at least in principle possible, in practice it is prevented by steric hindrance. One of the two otherwise identical aryl rings couples more strongly to the parent π-system with a small conjugation angle between the π orbital and aryl ring. The equivalent angle is considerably larger for the second aryl ring indicating a much weaker coupling. This effect is quantified in Table 1, which shows a compilation of the conjugation angles between the aryl and norbornadiene π-systems. As in the case of the absorption spectra, the geometry can have a large effect due to its impact on the coupling of the π-systems.

The electric quadrupole as well as van-der-Waals interactions between aryls can in principle further alter the side group alignment and thereby affect the electronic coupling. Therefore, we also performed geometry relaxations with an ab initio vdW-DF functional. These calculations consistently confirm the near constant storage energy of compounds 2–6 and its increase relative to compound 1. This provides further evidence that the increase in energy storage is originating from the breaking of the conjugation in the quadricyclane variant. Finally, it should be recalled that while the storage energy is very similar for compounds 2–6, in applications it is the energy storage density that matters, which also depends on the volume of the different compounds in solution.

Transition State

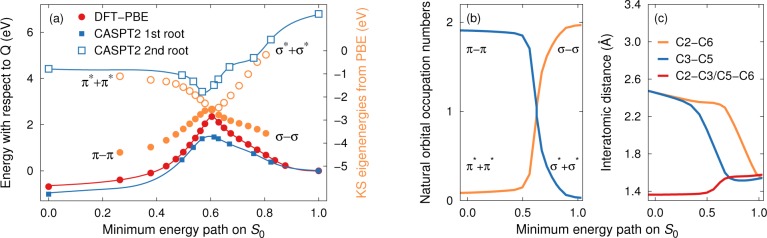
The HOMO and LUMO of the N isomers have π – π and π* + π* character, respectively, whereas they are of σ – σ and σ* + σ* type in the case of the Q variants, reflecting the transition from two double (N) to four single bonds (Q). This implies that an eigenvector exchange corresponding to the cycloaddition reaction must take place during the transition from N to Q. As shown explicitly below (Figure 6b), the system therefore exhibits multireference character near the transition state. In the fully interacting system the HOMO–LUMO gap is finite at the transition state (Figure 6a) due to an avoided crossing of the electronic states. In order to capture this effect, one requires CAS or similar techniques that can account for the mixing of these states. Single-reference methods such as DFT do not yield this effect and rather predict a crossing of the HOMO and LUMO states with a vanishing gap. (This shortcoming is related to the inability of conventional DFT methods to describe biradical systems, in a similar manner as DFT cannot describe the dissociation curve of H₂-molecule singlet ground state.) As a result, one obtains a cusp in the energy landscape rather than a proper saddle point with a finite curvature (as illustrated by the PBE data in Figure 6a). Note that DFT techniques are nonetheless useful for obtaining geometries along the path.

Figure 6.

Conversion between N and Q for compound 1. (a) Energy landscape between N and Q for the unsubstituted compound (1) from DFT-PBE and 2-SA-MS CASPT2 (8,8) calculations as well as HOMO and LUMO energies from PBE-DFT. (b) Occupation numbers of the natural orbitals of the S₀ state from CASPT2 (8,8) calculations corresponding to HOMO and LUMO levels. In substituted systems, these correspond to orbitals labeled as 4 and 5 in Figure 4a. The transition corresponds to a crossover (eigenvector exchange) of the states forming HOMO and LUMO in the N and Q variants, respectively. The deviation from integer eigenvalues near the transition point illustrates the multireference character of the thermal isomerization process of the unsubstituted N-Q system. (c) Interatomic distances between carbon atoms involved in the transformation of single and double bonds during the N → Q transition. Note that the back-conversion proceeds first by breaking the C2–C6 bond, followed by breaking of the C3–C5 bond, which occurs simultaneously with the formation of the double bonds.

Unfortunately, multireference methods such as CAS techniques are computationally too demanding to carry out a full transition path search for all substituted compounds. (As a further complication, recall that it can be argued that CASSCF geometries are actually of inferior quality compared to the molecular configurations obtained from single reference methods (PBE, B3LYP). In the case of CASPT2, at present one would have to resort to numerical differentiation to obtain forces, which renders geometry optimizations and vibrational analyses using this approach impractical, at least for the substituted compounds.) In view of these limitations, we resort to the following approach: Initial conversion paths are generated by linear interpolation of images between N and Q. The path is subsequently optimized using the nudged elastic band (NEB) method⁶¹ as implemented in ASE using DFT-PBE forces. (In practice it is difficult to converge the DFT wave function near the transition state due to the crossing of levels near the saddle point in DFT-PBE (Figure 6a). In the present calculations, a finite Fermi temperature was used in the NEB calculations to overcome this issue.) Finally, CASPT2 calculations are carried out for each image along the path using a (8,8) active space.

Unsubstituted Compound (1)

The vanishing HOMO–LUMO gap and the crossover between states of π – π/π* + π* and σ – σ/σ* + σ* character are apparent in the Kohn–Sham eigenvalues from DFT-PBE (Figure 6a).

The DFT-PBE calculations yield a value of ΔE^⧧ = 226 kJ/mol (2.35 eV) for the thermal Q → N conversion barrier for the unsubstituted compound (1) compared to the experimental value of ΔH^⧧ = 140 kJ/mol (1.45 eV).⁶² This significant overestimation is consistent with a lack of level repulsion and an avoided crossing. B3LYP-DFT calculations produce barriers that qualitatively show the same behavior with even higher barriers and were therefore not pursued further.

At the CAS level, one observes the opening of a gap due to mixing of electronic states near the saddle point (Figure 6a), which is associated with a reduction of the barrier for back-conversion. In the case of compound 1, one obtains a value of 152 kJ/mol (1.58 eV) in much better agreement with the experimental value. The multireference character of the transition state is also evident from the natural orbital occupation numbers, which strongly deviate from integer values near the saddle point (Figure 6b).

From a structural standpoint, the thermal back-conversion involves first breaking of one of the four single bonds of the four-member quadricyclane ring (C2–C6 in Figure 6c), followed by breaking of the opposing bond (C3–C5). Simultaneously with the latter event, the two remaining bonds turn into double bonds (C2–C3 and C5–C6).

We note that a vibrational analysis of the saddle point configuration, which is a prerequisite for obtaining ΔH^⧧ as opposed to only the electronic contribution ΔE^⧧, is not possible at the DFT level since the maximum along the N → Q transition path corresponds to a cusp in the energy landscape (Figure 6a). At the same time, calculating the vibrational spectrum at the CASPT2 level requires numerical differentiation, which is not only inaccurate but computationally very expensive, in particular in the case of the substituted compounds to be considered below. The rather close agreement of the value of ΔE^⧧ obtained at the CASPT2//PBE level and the experimental value for ΔH^⧧ for 1 suggests, however, that the difference between ΔE^⧧ and ΔH^⧧ is comparably small. Here, we therefore neglect the vibrational contribution to the transition barrier. (Bach et al.⁶³ report on MP2//HF calculations of the transition barrier in the case of positively charged N/Q species. The removal of one electron from the system implies a gap between two electronically similar states, which are already coupled at the single-reference level. As a result already single-reference methods yield a smooth saddle point with a well-defined vibrational spectrum.)

Substituted Compounds (2–6)

To obtain an approximative description of the transition state of the substituted systems (2–6), the geometry of carbon and hydrogen atoms in the reaction center (parent compound) were fixed to those corresponding to the minimum energy path of 1. These structures were subsequently relaxed with DFT-PBE subject to the specified constraints, followed by single point (8,8) CASPT2 calculations.

The comparison with experiment is aggravated by difficulties associated with the reliable extraction of barriers from the experimental data, see the Supporting Information. Here, we compare the calculations with the barriers extracted in the Supporting Information from the data obtained by Gray et al.¹⁷ (Table 2). As in the case of the unsubstituted compound, the DFT-PBE calculations systematically overestimate the experimental barriers by 50–60%. The CASPT2 data are in much better agreement, but the calculated barriers are still 20–30% higher than the reference data, exhibiting a larger error than in the case of 1. For the substituted compounds, there are in principle two different back-conversion paths depending on whether bond breaking occurs first on the donor or the acceptor side. Here, the calculations systematically find the acceptor side to be the preferred path.

Table 2. Barriers in kJ/mol (ΔE^⧧ in Figure 2) for the Thermal Q → N Conversion on the S₀ Surface from Calculation and Experiment^a.

	calculation ΔE⧧				experiment ΔH⧧
	DFT-PBE		CASPT2
cmpd	A	D	A	D	this work	ref (17)
1	221		152			140
2	161	177	123	131	105 ± 7	109 ± 7
3	163	171	127	129	104 ± 7	107 ± 2
4	157	172	127	133	100 ± 7	97 ± 9
5	151	174	124	138	100 ± 7	107 ± 3
6	151	165	127	132	96 ± 7	43 ± 14

^aThe reaction path with the lowest barrier is underlined and is always located on the acceptor side (A). The experimental data in the last but one column was obtained as described in the Supporting Information. The experimental data reported in the last column was taken for 1 from Frey⁶² and for 2–6 from Gray et al.¹⁷.

Tests based on fully relaxed as well as constrained geometries suggest that the effect due to the approximate transition path on the barrier amounts to less than 5 kJ/mol. The larger error in the case of the substituted systems could be associated with the limited active space. As already indicated above it should be increased even more relative to 1, which at present is, however, prevented by the associated computational expense. It is furthermore possible that solvent effects play a role in this context. This view is partially supported by the observation that the error in the barrier is more pronounced for the substituted compounds (2–6), which feature aryl rings and were measured in toluene solution,¹⁷ while the experimental value for 1 was obtained for the gas phase.⁶²

The strong coupling between the S₀ and S₁ states near the transition state alluded to above suggests a correlation between the thermal barrier ΔE^⧧ and the absorption energy hν, i.e., the offset between S₀ and S₁ for the N isomer. The decrease in the thermal stability upon red-shifting using auxochromes has been described before.^19,64 Both sets of calculations as well as the experimental data do not only show this effect (Figure 7) but also agree in the relative strength of this effect. This suggests that within the existing systems a compromise must be sought between a solar spectral match and thermal stability. More interestingly it suggests that a key to finding new and optimizing existing compounds involves the development of strategies for breaking or at least mediating the coupling between ΔE^⧧ and hν.

Figure 7.

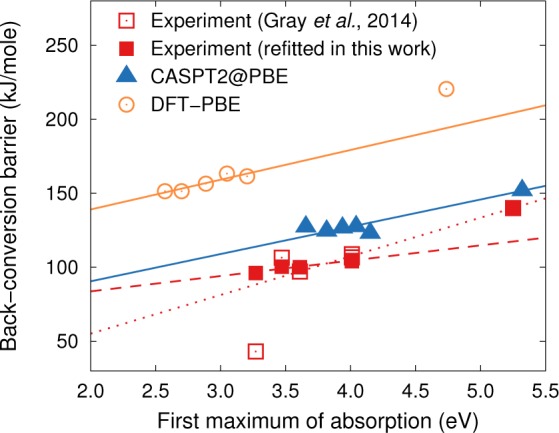
Barrier for the thermal conversion from Q to N is correlated with the first absorption maximum. While the calculations systematically overestimate the experimental data, they succeed in reproducing the correlation between the barrier and the absorption energy. Lines show the results of linear regression of the different data sets.

Quantum Yield

We do not explicitly focus on quantum yield in this work, as it would require taking into account ultra fast photodynamics along with solvent and thermal ensemble effects. Still several comments can be made based on our calculations. First, while the [2,2]-cycloaddition reaction is symmetry forbidden for the unsubstituted system, the attachment of aryls reduces the symmetry of the molecule to C₁, which also renders the two double bonds of the norbornadiene variant inequivalent.

We evaluated forces on the S₁ excited state of 1 and 2 using (8,8) CASSCF calculations. This shows that for 1 the initial forces after a vertical excitation on the S₁ Born–Oppenheimer surface are symmetric and when followed would induce simultaneous breaking of both double bonds. By contrast, in the case of 2, the forces are asymmetric and only directed toward breaking the C2–C3 bond. This can in fact already be observed from the active orbitals (Figure 4), where a S₀ → S₁ excitation turns the C2–C3 orbitals from bonding to antibonding. This mechanism is quite likely to be a deciding factor for the parent system having such a low quantum yield²² (<0.05), while the substituted compounds reach at least quantum yields of 50% and more. To truly answer this question, one should, however, locate the conical intersection seam for the photoactivated process.

Antol has established a possible explanation for the low quantum yield of the unsubstituted system using decay paths via Rydberg states and doubly excited states.²⁴ Rydberg states were not considered in this work but we point out that the S₂ as displayed in Figure 2 is a doubly excited state, and its position does not red-shift upon substitution with aryls.

Conclusions

The goal of this study was twofold: first, to gain insight into the mechanisms that govern the optical, kinetic, and thermodynamical properties of novel MOST compounds, and second to identify the level of computational methods sufficient for describing these properties.

The absorption spectrum was found to be crucially dependent on the geometry and explicitly on the π-coupling angle of the aryl rings. This is likely to also contribute to the broad line shape in the presence of a solvent and should similarly assist in lowering the onset of absorption.

The storage energy increases only slightly upon substitution, which is attributed to enhanced delocalization of π-electrons upon formation of a double bond in the norbornadiene compound. Since the increase is small and the variation of the storage energy between the substituted compounds 2–6 is even smaller, the primary optimization handle with regard to storage density is the molecular mass.

The saddle points on the S₀ surface corresponding to the barriers for the conversion between N and Q exhibit strong multireference character. Accordingly single-reference methods such as DFT yield a cusp (rather than a saddle point) along the N → Q path and overestimate the barrier by more than 50%. CAS approaches on the other hand provide values in much closer agreement with experiment; they are still somewhat too high compared to experiment, which could be due the omission of vibrational effects. The barrier calculations furthermore show the Q → N conversion via the acceptor side to be energetically preferred for all compounds considered here, which is thus likely to be solely responsible for the stability of the quadricyclane variants.

The multireference character is due to an eigenvector exchange involving HOMO and LUMO states, which implies a pronounced correlation between the first optical excitation and the barrier for back-conversion with larger red-shifts tied to a decrease in thermal stability. Here, the degree of correlation is similar between calculations and experiment. Since optimal compounds ought to combine good solar spectrum match with long-term stability, strategies ought to be developed to overcome, or at least mitigate, this coupling.

A key objective of the present study was to establish the suitability of different methods for high-throughput screening of MOST materials. It is found that PBE and even more so functionals from the M06-suite underestimate the storage energy and yield in the case of PBE a strongly red-shifted spectrum. DFT-B3LYP calculations provide both storage energies and absorption spectra in good agreement with reference data, although the latter are somewhat red-shifted while the magnitude is overestimated by up to 25%. By contrast CAM-B3LYP achieves very good excitation energies that closely match CASPT2 data but considerably overestimates the dipole strength and thus the magnitude of the attenuation coefficient. Since CAM-B3LYP calculations are computationally more expensive than B3LYP and given offsetting short-comings in either functional, the B3LYP functional appears slightly superior for screening purposes.

CASPT2 calculations provide very accurate results but are much more demanding both computationally and with regard to user interference; they are therefore (currently) not well suited for materials screening. With regard to certain properties, in particular pertaining to transition states, which require techniques such as CAS for accurate treatment, single-reference methods are quantitatively limited. They can, however, produce qualitative insight sufficient for discriminating trends and provide geometries as starting points for more refined computational techniques.

Finally, as has been remarked by other authors, in general, single-reference methods appear to yield more plausible geometries than CASSCF calculations, which is probably related to the absence of dynamical correlation in the latter.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.5b11489.

• Molecular structure of the N and Q conformations of the unsubstituted compound (1) from experiment and calculation; compilations of results from calculations of storage energy and absorption behavior; and convergence of MP2 and CCSD(T) calculations with basis set (PDF)

• Configurations relaxed at different levels of theory in CML format (ZIP)

The authors declare no competing financial interest.