Using Digital Image Correlation to Characterize Local Strains on Vascular Tissue Specimens

Abstract

Characterization of the mechanical behavior of biological and engineered soft tissues is a central component of fundamental biomedical research and product development. Stress-strain relationships are typically obtained from mechanical testing data to enable comparative assessment among samples and in some cases identification of constitutive mechanical properties. However, errors may be introduced through the use of average strain measures, as significant heterogeneity in the strain field may result from geometrical non-uniformity of the sample and stress concentrations induced by mounting/gripping of soft tissues within the test system. When strain field heterogeneity is significant, accurate assessment of the sample mechanical response requires measurement of local strains. This study demonstrates a novel biomechanical testing protocol for calculating local surface strains using a mechanical testing device coupled with a high resolution camera and a digital image correlation technique. A series of sample surface images are acquired and then analyzed to quantify the local surface strain of a vascular tissue specimen subjected to ramped uniaxial loading. This approach can improve accuracy in experimental vascular biomechanics and has potential for broader use among other native soft tissues, engineered soft tissues, and soft hydrogel/polymeric materials. In the video, we demonstrate how to set up the system components and perform a complete experiment on native vascular tissue.

Download video file ^{(25.4MB, mp4)}

Introduction

A rich history of research spanning over 50 years has been focused on quantifying the mechanical properties of vascular tissues. These studies allow us to better understand both the physiological and pathological behavior of blood vessels, provide a basis for evaluating the efficacy/compatibility of endovascular devices, and aid in the design and fabrication of engineered vascular constructs^1-6. Accurate measurement of the mechanical response of soft tissues and constitutive modeling of their mechanical properties is inherently challenging due to the mechanical heterogeneity, anisotropy, and nonlinearity exhibited by most tissue types. Moreover, experimental measurements are often confounded by local complexities introduced at sample-grip interfaces in the course of mechanical testing (i.e., bending, friction, stress concentrations, tearing) and the inevitable transition of mechanical properties once tissue is excised from the living animal.

A uniaxial tensile experiment is among the simplest mechanical tests that can be performed on a specimen made of a solid material, and is often used to assess the mechanical response of vascular tissue. Results from these experiments provide useful preliminary information for both native and engineered tissue sources, and can be used to compare the effects of certain treatments, disease states, or pharmacological compounds on the mechanical behavior of the vascular wall ^7-11.

Uniaxial mechanical testing of soft tissues is typically performed on samples with relatively uniform geometries, which are most commonly dog-bone or ring shaped ^7,8,12-14. However, significant departure from these idealized geometries can occur due to challenges associated with tissue dissection, isolation, and clamping within the testing system. Any non-uniformity in geometry will ultimately give rise to heterogeneous stress and strain fields when the sample is subjected to uniaxial extension, with the degree of heterogeneity dependent on actual sample shape, as well as sample size (relative to the grips) and the mechanical properties of the material ^9,15,16. When field heterogeneities are significant, sample strain calculations based on the relative grip positions are inaccurate and thus an insufficient basis for assessing mechanical behavior.

Video analysis systems have been widely used for strain measurements of soft tissues, often using high contrast dye markers applied to the specimen surface ^17,18. Digital image correlation, an optical metrological technique which measures full-field surface strain by comparing gray level intensity values on the specimen's surface before and after deformation, has been used in conjunction with video analyses of soft tissues ^19-21. There are several advantages of digital image correlation compared to interferometric methods that may be employed for measurements. First, as a non-contacting measurement technique, it minimizes the confounding effects of modifying material properties due to the way in which the measurement system affects the specimen. Second, it requires a much less stringent measurement environment and has a wider range of sensitivity and resolution than other methods. Third, endowed with the capability of capturing a full field of view, this technique can characterize both the average and the local mechanical responses. For detailed explanation of the method, readers are encouraged to see the book by Sutton ²².

To obtain strain fields on the specimen surface, a two-dimensional digital image correlation technique (2D-DIC) can be used. In short, images of the specimen are captured at unloaded and various loaded states. The first image is divided into small squares called subsets (M×M pixels) which form a mesh for subsequent calculation of 2D strain fields. The position of each square in the deformed specimen is obtained using an image matching algorithm. The motion of each square is then tracked, image-by-image, yielding displacement fields which can then be used to derive deformation gradients and strains via a variety of methods, including polynomial fitting or finite element interpolation. In the present manuscript, we provide a detailed methodology for assessment of the surface strain fields on native vascular tissues via integration of uniaxial tensile testing and 2D-DIC.

Protocol

NOTE: The procedures described below were performed as part of a protocol approved by the Institutional Animal Care and Use Committee at the University of South Carolina in Columbia, South Carolina.

1. Tissue Acquisition and Dissection

1. Sterilize all surgical tools prior to tissue dissection. Autoclave surgical scissors and fine standard forceps as well as surgical blades under pressure of 15 psi and temperature of 121 °C for 15 min.

2. Acquire one set of fresh porcine (7 month old Landrace males, 60-70 kg) kidneys with intact aorta from a local slaughterhouse. Transport tissue back to the laboratory in iced 1% phosphate buffered saline (PBS) solution.

3. Immediately upon arrival, isolate the abdominal aorta from surrounding tissue using surgical scissors and forceps.

4. Wash the vessel three times using a 50 ml syringe filled with PBS (pH 7.2). Using the scissors and forceps, remove as much perivascular tissue as possible without compromising the integrity of the sample.

5. Vertically position a sharp razor blade onto the middle section of the vessel and make sure it is perpendicular to the vessel longitudinal axis. Create two ring samples each with a width of approximately 20 mm by applying three sequential circumferential cuts with the razor blade.

6. Vertically position a sharp razor blade onto one ring sample such that the blade is oriented in the radial direction. Apply an acute force to yield a radial cut, which results in a strip-shaped sample for uniaxial mechanical testing. Place the sample in a 100 mm glass Petri dish and submerge in PBS until the application of surface speckling. Repeat for the second ring sample.

2. Creation of Surface Speckle Pattern

1. Connect the airbrush to the pressure valve.

2. Adjust the nozzle diameter of the airbrush to yield speckles of 60-100 µm (appropriate range for nozzle diameter should be determined from preliminary studies).

3. Pour approximately 2 ml of black tissue marking dye into the gravity feeder of the airbrush.

4. Place the airbrush approximately 0.5 m away from the sample.

5. Remove the sample from the Petri dish. Spray tissue marking dye on the intimal surface of the sample for approximately 5 sec under a spraying pressure of 100 psi. Repeat three times to ensure that the speckle pattern uniformly covers the sample surface.

3. Performance of Experiments

1. Attach each end of the sample to a plastic strip (1 cm width x 1 cm length x 0.5 cm thickness) using a tissue adhesive. Place the sample on a tissue cutting board. Position the sample such that it lies flat and measure its dimensions using a digital caliper.

2. Initiate system controls for mechanical testing. On the system controls home screen, select "Waveform" on the taskbar located on the "Setup" tab.

3. Adjust the position of the upper grip of the mechanical tester to -4 mm (4 mm extension relative to the designated initial position in the system). Gently secure one plastic strip (attached to the specimen in 3.1) into the upper grip of the mechanical tester and allow the sample to hang freely. Use the digital caliper to ensure that the distance between the sample and the upper grip is less than 2 mm.

4. Manually adjust the position of the lower grip so that the free end of the sample can be secured without extension. Gently secure the plastic strip attached to the free end of the sample into the lower grip of the mechanical tester.

   1. Use the digital caliper to ensure that the distance between the sample and the lower grip is less than 2 mm. Zero the system load cell. Measure the length of the sample and use this as the reference length for calculation of global circumferential strains.

5. Enter the mechanical testing protocol. The protocol used in this demonstration entails 4 uniaxial displacement cycles which extend the sample length by 18% at a displacement rate of 0.01 mm/sec.

6. Intermittently spray PBS on the sample throughout the remaining testing protocol to ensure that it remains hydrated.

7. Mount the camera (5 mega pixel camera, 100 mm lens, pixel size of 3.49 µm) onto a tripod which is positioned 1.5 m from the loading frame. Ensure the camera and sample surface are perpendicular by setting the camera to the lowest available field of depth and manipulating its alignment such that the entire field of view is in focus.

8. Open the image capture software.

9. Select "PGR-2" in the option "Select system".

10. Select the project path to save the images to be analyzed.

11. Click the "Time Square" icon and specify the acquisition interval as 5 sec.

12. Adjust the exposure, numerical aperture, and focus of the lens so as to get a clear view of the sample.

13. Adjust the position of LED to provide adequate lighting on the sample.

14. Click the "Start" icon in the image capture software to obtain an image of the specimen surface.

15. Open the image analysis software.

16. Import the image obtained. Zoom in on an individual speckle, and then count number of pixels within this individual speckle. Note: Identify a representative black speckle. Define the speckle size as the linear distance between pixels on both sides of the speckle that have similar high values. For an acceptable speckle size, the number of pixels across the width of a typical speckle should be greater than 3 pixels. To improve spatial resolution in the measurements, most speckles should have no more than 5-7 pixels across the width of the speckle, whenever possible. Thus, a typical speckle for this case would range between 10 μm at the smallest and 23 μm at the largest in linear dimension. To determine an appropriate subset size, a typical subset should have at least 3 white and 3 black speckles across its width. If a typical speckle is 5 pixels in linear dimension, then each 31x31 subset would be at least 105 μm in linear dimension. The spacing between subset centers should be at least 1/6 of the linear dimension. Thus, for a 31x31 subset size, the distance is 5 pixels which represents 18 μm in linear distance.

17. After verifying the quality of speckle pattern, simultaneously click the "Run" icon in the system and "Start" icon in the image capture software to start the test.

18. Capture a series of images throughout testing using the camera and image capture software.

4. Clean-up Procedures after the Experiment

1. Place the discarded sample in biohazard bag and close the bag. Call the Department of Environmental Health and Safety (EHS) at the University of South Carolina for proper disposal.

2. Prepare a phosphate-free disinfectant solution with a 1:64 dilution ratio of detergent disinfectant to distilled water. Soak the surgical tools in this solution for 20 min.

3. Thoroughly rinse the items described in 4.2 with distilled water. Dry the tools using a paper towel and then spray them with a 70% ethanol solution. Once again dry the surgical tools using a paper towel and put them back in the surgical toolbox.

5. Image Analysis to Measure the Local Strain Field

1. Open the image analysis software.

2. Click the "Speckle images" tab, select all images which need to be analyzed.

3. Click on rectangle tool and select the area of interest in the first image.

4. Enter subset size 41×41 pixels and step size 5 pixels.

5. Click start analysis tab in the software, select the interpolation as optimized 8-trap; select the criterion as zero-normalized squared differences and subset weights option as Gaussian.

6. Set the threshold options as default in the software.

7. Click on post-processing sub tab in start analysis tab. Click option strain computation and leave filter size and type of filter as default in software. Select tensor type Lagrange.

8. Select data tab and then select any analyzed image for visualization of the surface strain field.

Representative Results

The mechanical data acquired from a ramped uniaxial extension test on vascular tissue consists of load versus applied sample displacement relationships at a given displacement rate. In this study, 2D-DIC in conjunction with uniaxial mechanical testing is used to measure the surface strain fields of the specimen in orthogonal directions at various deformed states. The viscoelastic nature of vascular tissue is manifested by the notable degree of hysteresis in the load-displacement curves prior to mechanical preconditioning. To promote the reproducibility of mechanical testing and obtain an elastic mechanical response, the tissue is preconditioned via several loading-unloading cycles wherein hysteresis is gradually diminished (Figure 1). Despite the exceedingly careful sample preparation and mounting, 2D-DIC measurements demonstrate that the resultant intimal surface strain field is highly heterogeneous in both the circumferential and longitudinal directions. As expected, local circumferential strain values increase with applied sample displacement. Heterogeneity in the circumferential strain pattern generally yields values that are lower near the center of the sample as compared to near the sample-grip interface, reflecting the effects of the grip on the local strains (Figure 2). In the longitudinal direction, the resultant non-uniform compressive strains on the sample intimal surface are increased as the sample is gradually extended, and the resultant strain field exhibits a more pronounced degree of heterogeneity as compared to the circumferential direction (Figure 3). The coefficients of variation (CV) of the surface strain fields in orthogonal directions were calculated to reflect the degree of field heterogeneity at select experimental states, and were found to monotonically decrease with increased sample extension (Table 1).

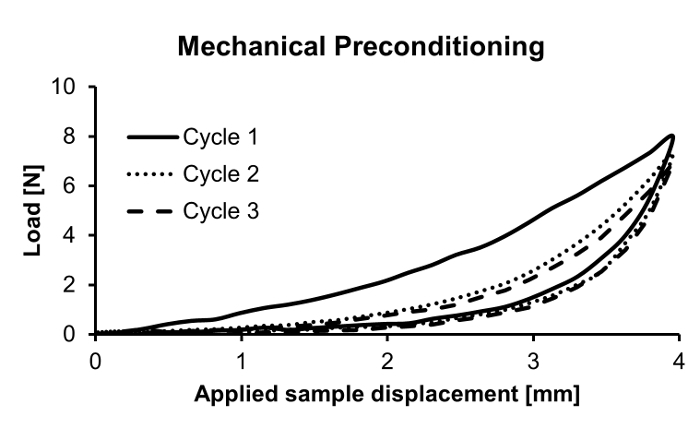Figure 1. Experimental preconditioning of vascular tissue sample for uniaxial tensile testing. A rectangular-shaped sample is preconditioned with three loading-unloading cycles to obtain a reproducible elastic response. Please click here to view a larger version of this figure.

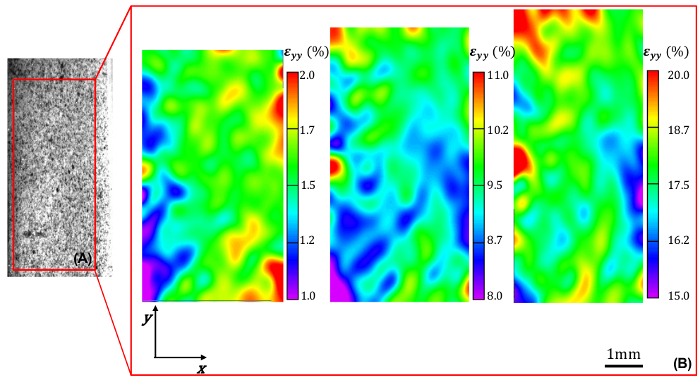Figure 2. Circumferential strain field within the sample area of interest. (A) Representative example of speckled sample intimal surface and identified area of interest. (B) Local circumferential strain ε_yy (%) within the identified area of interest at increasing levels of applied global circumferential strain (increasing from 1.6% to 9% to 18%, left-to-right). Please click here to view a larger version of this figure.

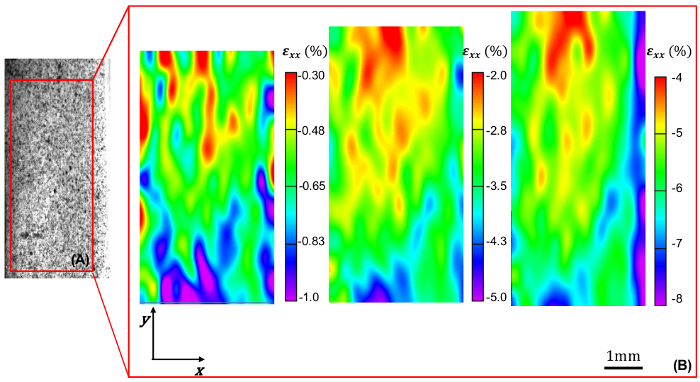Figure 3. Longitudinal strain field within the sample area of interest. (A) Representative example of speckled sample intimal surface and identified area of interest. (B) Local longitudinal strain ε_xx (%) within the identified area of interest at increasing levels of applied global circumferential strain (increasing from 1.6% to 9% to 18%, left-to-right). Please click here to view a larger version of this figure.

Global circumferential strain [%]	CV in εyy (%)	CV in εxx (%)
1.6	11.8	28.1
9.0	7.4	25.1
18.0	5.6	20.7

Table 1. Coefficients of variation of the strain fields. Coefficients of variation (CV) of sample intimal surface strain fields in both circumferential (ε_yy) and longitudinal (ε_xx) directions at select levels of applied global circumferential strain.

Discussion

Although previous studies have used a wide-range of dye-tracking video methods to assess sample strain ^{18,20,21,23,24}, our present aim is to provide a comprehensive methodology to couple uniaxial tensile testing with 2D-DIC for assessment of surface strains on vascular tissue samples. With a high resolution camera and in-house image analysis software, the strain field can be measured within a predetermined surface region as the sample undergoes uniaxial loading. Of particular relevance to mechanical testing of vascular tissue, the presented technique can be directly adapted to assess surface strains in planar bi-axial tests which in turn enable identification of constitutive material properties.

In order to facilitate digital image correlation analysis, a speckle pattern is applied to the sample surface. The paint utilized for speckling is a tissue marking dye which readily adheres to most soft tissue surfaces. To achieve a good quality of contrast and proper density of the speckle pattern, an optimal speckle size of 60-100 µm and spraying distance of 0.5 m are realized by adjusting the nozzle diameter of the airbrush and the distance between the sample and the airbrush. The speckle size used is directly related to the resolution of the resultant measurements ^23,25. Each speckle has to be sampled by at least 3-5 pixels to obtain acceptable image correlation. Given a 22 mm×18 mm field of view and the utilized speckle size, the resolution of the presented experiment is 9 µm/pixel.

A loading rate of 0.01 mm/sec is used for mechanical testing so as to obtain a series of quasi-static deformed equilibrium states for vascular tissue ^26,27. Since the camera and high-fidelity load cell are both exceedingly sensitive to vibrations, there should be minimal movement during the experiment; even if small, rigid body camera/specimen motion can occur and will confound 2D-DIC-based measurements. Similarly, sample deformation can occur due to tissue dehydration, thus it is important that PBS is applied through testing to promote the accuracy of 2D-DIC.

For 2D-DIC, required specifications include the subset size and the step size used in image matching algorithm ²². In order to obtain accurate results with negligible bias, at least 3 black and 3 white speckles should be present in each subset, with each speckle sampled by at least 3-5 pixels. Each data point in the output provides information averaged over a box that corresponds to the subset size (41x41 pixels), considered as the spatial resolution of the experiment. The distance between two data points in terms of step size is 5 pixels in this experiment. In order to maximize accuracy in the speckle displacement/surface strain measurements, an 8-tap spline interpolation method is applied to obtain accurate, sub-pixel intensity values. The 8-tap method has somewhat higher accuracy in obtaining strains when compared to results obtained using either a 4-tap or 6-tap interpolation filter. The correlation criterion "normalized squared differences" was selected for the matching since it is unaffected by a change in scale in lighting (e.g., when a deformed subset is 30% brighter than reference). This choice is the default selection in the software and usually offers the best combination of flexibility and results ²⁸. Subset weighting, which controls how the pixels within the subset are weighted in the matching process, is selected as Gaussian. With uniform weights, each pixel within the subset is considered equally; Gaussian weights provide the best combination of spatial resolution and displacement resolution.

Coefficients of variation of the surface strain field were calculated with in-house image analysis software and used to quantify the degree of strain heterogeneity. The coefficient of variation of the strain field in both the circumferential and longitudinal directions decreased with increasing global circumferential strain, which has been previously observed in analogous mechanical tests on other vascular tissue types (unpublished results). Based on this persistent trend, it is reasonable to expect that surface strain fields could sufficiently homogenize above some critical degree of extension such that global and local measurements converge. However it is likely that this critical value is tissue- and sample-specific, thereby supporting the use of local strain measurements for accurate identification of constitutive material properties.

Several limitations must be considered for proper interpretation of our presented methodology and results. We prescribed a moderate range of global circumferential strain, thus our realized local strain magnitudes in both the circumferential and longitudinal directions were significantly lower than values seen in vivo. Moreover, we assessed the uniaxial mechanical response under a single sample orientation, and therefore generate insufficient data to identify constitutive material properties for vascular tissue ^29,30. However, our aim is not to conduct a comprehensive mechanical analysis of the porcine aorta, but rather to demonstrate an experimental protocol to couple 2D-DIC to a uniaxial mechanical testing on soft tissue. The technique presented herein can be readily extended to biaxial mechanical testing and thus the quantification of the constitutive mechanical properties of vascular tissues ^31-33. The 2D-DIC method only captures a planar strain field corresponding to the sample surface. When the specimen deforms out of plane, or when the specimen is a non-planar geometry (e.g., blood vessel), stereo-vision imaging and a 3D-DIC technique can be applied for comprehensive strain measurement ^23,25.

In summary, the present manuscript provides detailed information on the methodology to integrate uniaxial tensile testing and digital image correlation to characterize the mechanical response of native vascular tissue. The method presented in this study can be readily adapted for mechanical characterization of other native and engineered soft tissues as well as soft hydrogel/polymeric materials, and is particularly useful when the sample surface strain field exhibits significant heterogeneity during mechanical testing.

Disclosures

The authors have no potential conflicts of interest.