Abstract
Quantitative measurement of localized longitudinal changes in brain abnormalities at an individual level may offer critical information for disease diagnosis and treatment. The voxel-wise permutation-based method SPREAD/iSPREAD, which combines resampling and spatial regression of neighboring voxels, provides an effective and robust method for detecting subject-specific longitudinal changes within the whole brain, especially for longitudinal studies with a limited number of scans. As an extension of SPREAD/iSPREAD, we present a general method that facilitates analysis of serial Diffusion Tensor Imaging (DTI) measurements (with more than two time points) for testing localized changes in longitudinal studies. Two types of voxel-level test statistics (model-free test statistics, which measure intra-subject variability across time, and test statistics based on general linear model that incorporate specific lesion evolution models) were estimated and tested against the null hypothesis among groups of DTI data across time. The implementation and utility of the proposed statistical method were demonstrated by both Monte Carlo simulations and applications on clinical DTI data from human brain in vivo. By a design of test statistics based on the disease progression model, it was possible to apportion the true significant voxels attributed to the disease progression and those caused by underlying anatomical differences that cannot be explained by the model, which led to improvement in false positive (FP) control in the results. Extension of the proposed method to include other diseases or drug effect models, as well as the feasibility of global statistics, was discussed. The proposed statistical method can be extended to a broad spectrum of longitudinal studies with carefully designed test statistics, which helps to detect localized changes at the individual level.
Keywords: Diffusion Tensor Imaging, Resampling, General linear model, White matter, Longitudinal study
Highlights
-
•
A nonparametric method for detecting subject-specific localized changes in longitudinal DTI
-
•
Obtain sufficient statistical power even with limited scans available
-
•
Various voxel-level test statistics for hypothesis tests among groups across time
-
•
Excellent at controlling false positive ratio with the model-based test statistics
1. Introduction
Diffusion Tensor Imaging (DTI) (Le Bihan et al., 2001, Tournier et al., 2011), which measures the random motion of water molecules, provides a non-invasive way to investigate the structural integrity of the brain. It has been widely used in investigating white matter (WM) changes caused by brain development and aging (Westlye et al., 2009), detecting abnormalities in normal-appearing WM due to disease (Weiner et al., 2000), as well as identifying pathologic severity in patients with MS (Werring et al., 1999). In recent years, there has been increasing interest in the investigation of subject-specific changes within the brain without prior information regarding the spatial distribution of the pathology. Consequently, whole brain voxel-based methods (Ashburner and Friston, 2000, Smith et al., 2006, Tustison et al., 2014) have gained much favor during recent years as an important alternative to region of interest (ROI) analysis in detecting localized changes within the brain and are most suitable when changes/effects are diffuse among individual subjects. Both parametric and nonparametric methods have been used to help identify regionally specific changes such as differences due to activation in fMRI (Nichols and Holmes, 2002), neuroanatomical differences in structure MRI data (Bullmore et al., 1999) and pathophysiology in longitudinal studies (Zhu et al., 2013, Chung et al., 2008).
Due to the non-Gaussian nature of DTI data, nonparametric voxel-based methods that do not need any parametric assumptions such as bootstrap (Heim et al., 2004, Zhu et al., 2008, Bazarian et al., 2012) and permutation-based methods (Nichols and Holmes, 2002), are more suitable. The nonparametric permutation-based method is able to devise a data-driven null distribution with only minimal assumptions, which gives the user more freedom in devising test statistics of interest. Any sensible test statistic that summarizes the local effect can be used in these hypothesis-testing procedures and the strong control of type I error is guaranteed under very mild assumptions of the null distribution. Such methods have been widely used in the area of fMRI to investigate the regionally specific effect in neuroimaging data (Nichols and Holmes, 2002). However, few of the aforementioned methods have been applied to subject-specific longitudinal studies. This is mainly because the number of available scans in a longitudinal study is often limited by practical factors such as the cost of patient recruitment, and the obtained data lacks sufficient information for a rigorous statistical inference test due to their low degrees of freedom.
The Spatial Regression Analysis of Diffusion tensor imaging (SPREAD) method previously presented (Zhu et al., 2013) combines spatial regression and resampling methods, which provides a novel and efficient whole brain analysis method for detecting localized changes in subject-specific longitudinal study without an a priori hypothesis, for DTI-derived metrics such as fractional anisotropy (FA) and mean diffusivity (MD). SPREAD requires only one scan per time point for a valid statistical inferential test, which greatly reduces the granularity of permutation. The iSPREAD method (Liu et al., in press) further improves the detection sensitivity and accuracy of SPREAD (Zhu et al., 2013) substantially by incorporating a three-dimensional (3D) nonlinear anisotropic diffusion filtering method. Both SPREAD and iSPREAD utilize a novel and effective permutation-based statistical method for whole brain analysis that relies on permuting time/scan labels and spatial kernel regression. They do not require adjustment of signal gains due to different DTI protocols at different time points and are effective for monitoring subject-specific lesion progression in longitudinal studies. However, aside from their many advantages, the following limitations exist for SPREAD/iSPREAD, which are also general to most permutation-based voxel-wise subject-specific methods applied in longitudinal studies:
-
1)
The comparison is often taken pairwise between each time point vs. baseline, which is time consuming in the presence of serial DTI studies with multiple time points.
-
2)
The potential differences caused by registration error or anatomical differences due to atrophic changes may manifest as false-positive voxels in the results. The consequences for such misalignment can either falsely identify positives or neglect true positives, both of which greatly reduce the statistical power and reliability of the results obtained.
-
3)
The apparent and useful prior information of lesion progression models is largely neglected in these existing methods.
Therefore, a general statistical framework that accommodates a serial DTI study with multiple time points while taking into consideration the specific disease progression model is desired.
The main purpose of many longitudinal studies is to identify localized temporal changes within the brain. One crucial step towards detecting localized changes is to choose test statistics that are likely to be the most sensitive and informative in depicting possible departures from the null hypothesis, which assumes that there is no difference between data obtained at different time points. The statistical properties of any given hypothesis-testing procedure depend on both the null hypothesis, which specifies the distributional properties of the measurements without true signal, and the alternative hypothesis, which specifies the possible forms of true signal (temporal changes, in this case). The non-parametric permutation-based methods, such as SPREAD/iSPREAD, permit the use of a wide range of test statistics without the need to derive closed-form distributions of these statistics under the null hypothesis with specific parametric assumptions. This flexibility enables us to focus on choosing the optimum statistics based on different alternative hypotheses.
In this study, we proposed to extend the current SPREAD/iSPREAD method to a general statistical framework that accommodates a wide range of alternative hypotheses used in longitudinal studies. Five test statistics, which were divided into two major types, were implemented in the current statistical framework to help identify several different forms of temporal changes within individual subjects. One type is based on model-free test statistics; another is based on a general linear model that incorporates a certain disease evolution model. Our statistical method is similar in spirit to two well-established methods in statistical parametric maps (SPM) for assessing the regionally specific effects within the brain, namely the subtractive method (Worsley et al., 1992, Worsley et al., 1996) and the general linear model (Friston et al., 1994), both of which have been widely used in the fMRI field for detection of brain activation. We use those theories within a nonparametric framework with carefully designed test statistics where the empirical null distribution is generated by permutation.
The aim of the present study was to describe and illustrate a statistical method that enables the investigation of longitudinal changes quantitatively. Simulation data with a predefined region of pathology and disease effects were used to evaluate the effectiveness of the proposed method. A series of DTI scans in three patients suffering from relapsing-remitting multiple sclerosis (RRMS) were used as human brain in vivo examples to demonstrate the implementation and utility of this method. Both simulations and in vivo results show that the proposed method is able to detect temporal changes in serial DTI with high sensitivity and accuracy. Extension of the proposed statistical framework to include other disease evolution/drug effect models as well as different global statistics is discussed. The method is an extension of SPREAD/iSPREAD, as well as an independent statistical framework that can be easily applied to a wide variety of longitudinal studies.
2. Material and methods
2.1. Overview of iSPREAD for serial DTI analysis
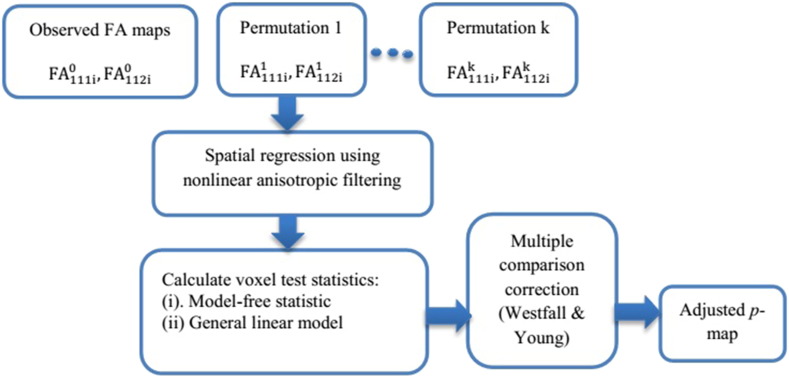
Based on the exchangeability of the time and scan labels under the null hypothesis (Zhu et al., 2013), in the first step of iSPREAD analysis, the scan/time labels for FA/MD maps from each subject are randomly permuted at each voxel for N = 1000 times to generate a permutation distribution under the null hypothesis at each voxel. The permutated images are then smoothed using the nonlinear anisotropic filtering method for edge-preserving image enhancement, as well as for preserving spatial correlation between neighboring voxels. In the third step, various voxel test statistics are chosen to depict the temporal changes in a serial DTI analysis and will be discussed in detail in the next section. The Westfall-Young procedure (Nichols and Hayasaka, 2003) is used to control the FWER in the last step. Voxels are identified as significantly changing (i.e. lesion areas) if their p-value is less than a predefined p-value (e.g. 0.05). The flowchart of the proposed framework is shown in Fig. 1.
Fig. 1.
Flow diagram of iSPREAD for serial DTI analysis.
2.1.1. The anisotropic diffusion filter
Nonlinear anisotropic diffusion filtering provides a general scale-space approach for edge-preserving piecewise smoothing of the original image. The nonlinear scale space generated by nonlinear diffusion filtering is proposed from an analogy to thermal equations that describe the diffusion process. The Perona-Malik (PM) (Perona and Malik, 1990) equation for the process is shown in Eq. (1):
| (1) |
where function is taken as the image intensity (e.g. FA or MD map in our study), and is the discrete cases. The conductance function controls the diffusion strength, which is a function of image local gradient () given by Eq. (2):
| (2) |
where |∇I | is taken as rough edge detector and κ is the diffusion contrast parameter. The ratio controls the flow strength. The maximum flow,∂tI(z, t), is obtained when gradient |∇I | = κ , which represents inhomogeneous regions, and reduces to 0 when |∇I | ≫ κ or |∇I | ≪ κ, which represents either potential edges or homogeneous regions. In general, the nonlinear anisotropic filtering method chooses intra-region smoothing over inter-region smoothing.
The proper selection of the integration constant guarantees a stable evolution of the PM equation and is given by Gerig et al. (1992) as Eq. (3):
| (3) |
where N is the number of nearest neighbors (N = 26 in a 3D case), and Δdi is the distance between the centroid and its neighboring voxels.
2.2. Statistical models for voxel-based test statistics
Two types of voxel-wise test statistics (five test statistics in total) are used to detect temporal changes due to disease evolution in longitudinal studies. The first type (Test Statistics MF1 and MF2) uses intra-subject variation, which is a natural extension of SPREAD/iSPREAD from a pairwise group comparison for two time points to a multiple group comparison for longitudinal studies that include multiple time points. The second type (Test Statistics LM, QM1, and QM2) is based on a general linear model for an across-time regression analysis. Other test statistics can also be used in longitudinal studies based upon specific needs.
The following models were used to depict the lesion evolution over time: (i) Simple linear model, which assumes that FA/MD changes by an amount equal to the regression coefficient over time; (ii) Quadratic model (second-order polynomial model), which assumes a nonlinear relationship over time.
2.2.1. Model-free voxel-wise test statistic
This model-free test statistic detects intra-subject variation across time. In the following, FA is used as an example, but similar analysis also applies to MD.
| (4) |
where can take one of the following two forms:
| (5) |
| (6) |
where FAnsti is the nth subject's sth scan at time t measured for the ith voxel (n = 1 , 2 , … , N , s = 1 , 2 , … , S , i = 1 , 2 , … , I , t = t1 , t2 , … , tT), is the scan average and is the time average for each subject respectively, and is the FA map at baseline (t = t1). There are two ways to select the baseline image: (i) with Test Statistic MF1 use the mean image of all time points as the baseline image (Eq. (5)); (ii) with Test Statistic MF2 choose the image at the first time point as the baseline image (Eq. (6)). Both test statistics represent localized temporal variation for FA/MD images at each voxel.
2.2.2. Voxel-wise statistics based on general linear model
All linear regression models for a response variable Yij (e.g. FA/MD at certain time point) at voxel j = 1 , … J can be expressed in general form (Dobson and Barnett, 2011), where a linear model with correlated errors is fitted for each individual voxel time-series Yij. The standard general linear model for an across-time regression analysis is shown as Eq. (7)
| (7) |
where i = 1 , … I indexes the observation (e.g. scans at different time points), ϵij is the error terms, and βk are kth unknown parameters for each voxel j. The response variable Y at voxel j = 1 , … , J is expressed as a linear combination of explanatory variables xik representing the conditions under which observation i was made. In a longitudinal study, xik is typically time; however, the explanatory variables might include covariates (e.g. age) or dummy variables (e.g. gender, drug type or dosage).
In our study, two special cases of the general linear model (Smith et al., 2006) were considered: a simple linear model (Eq. (8)) and a quadratic model (Eq. (9)):
| (8) |
| (9) |
In both cases, the explanatory variable ti is time (in months) and the dependent variable yij is the FA/MD value at jth voxel with which the observation i (scan at the ith time point) is made. Eq. (8) can be considered as a special case of Nichols and Holmes (2002), in which β2 = 0, namely the quadratic term vanishes. Together Eqs. (8) and (9) are useful in representing a large variety of realistic FA/MD changes over time in longitudinal studies.
The analysis of variance (ANOVA) F-test for the overall effect and t-test for individual covariates are the two main hypothesis-testing tools for multiple linear regressions. They can be used to generate the per-voxel t- or F-statistic map and check the significance of a linear association under the assumption that the measurement error is normally distributed. Both t- and F-statistic can be viewed as signal-to-noise ratios in which the denominators serve as a clever way to eliminate the unknown nuisance parameter σε2, the variance of the measurement errors. In the case of permutation-based statistical methods, the distribution of measurement errors under the null hypothesis is simulated from a resampling procedure thus it is unnecessary to resort to division to eliminate any nuisance parameter of the error distribution. The following test statistics were chosen in our study.
-
1)
Simple linear regression
The statement for the hypotheses:
| (10) |
The permutation test is carried out using the following statistic:
| (11) |
where is the estimated slope value based on the standard least-squares principle. The larger this value is, the stronger the evidence to reject H0.
-
2)
Quadratic regression
If only the coefficient for the quadratic term (nonlinearity) is of interest, the statement for the hypotheses is:
| (12) |
The permutation test is carried out using the following:
| (13) |
where is the estimated regression coefficient for the quadratic term using standard least square estimates.
If the significance of the whole regression model is of interest, the statement for the hypotheses:
| (14) |
The permutation test is carried out using the following:
| (15) |
where is the fitted value and is the variance of the fitted value .
The five test statistics mentioned above were calculated at each voxel to form the statistic images. Permutation and spatial regression were used to construct the null distribution of these statistic images. Significant voxels were identified by comparing the original (un-permuted) statistic images to their permutation counterparts. Because all five test statistics are larger under H1, the permutation p-value at a given voxel is defined as the proportion of permutation-generated test statistic that is larger than the un-permuted version. We then applied a suitable multiple testing procedure such as the Westfall-Young procedure (Westfall and Young, 1993) and the Benjamini Hochberg procedure (Benjamini and Hochberg, 1995) to these p-value maps to control for familywise error rate and false discovery rate, respectively. Technical details about the resampling procedure and multiple testing adjustments can be found in (Zhu et al., 2013).
2.3. Monte Carlo simulation
Effectiveness and statistical power of the proposed method were first validated by a Monte Carlo (MC) simulation of group comparisons of repeated measurements of the same subject with a predefined simulated disease area in serial DTIs. Simulations were performed in a similar manner as previously described in Zhu et al. (2013). Instead of performing a two-group comparison, a multiple-group comparison was simulated to mimic the disease progression in a longitudinal study. Lesions were simulated as a 5 × 5 × 3 cubic region at the center of the splenum corpus callosum with different effect sizes (es) of the largest DTI eigenvalue (λ1) added in each voxel to imitate a real brain abnormality. Values of es ranged from10 – 50%. Repeated measurements of the same subject were simulated by adding Gaussian-distributed noise to both DTIpre and DTIpost templates to achieve signal-to-noise ratio (SNR) ≈ 50 in non-diffusion weighted images. The effect of thermal noise was first generated using complex random numbers with their real and imaginary parts sampled independently from a Gaussian distribution function with a mean of zero and a standard deviation determined by the desired SNR level (Andersen, 1996, Gudbjartsson and Patz, 1995); the real parts of the complex noise signals were then added to the noise-free baseline signal S0 and DW signals Si. The magnitude of the final complex data was then used to synthesize the noisy DTI datasets that were further used for calculations of the noisy tensors. The magnitude of DTIpre and DTIpost templates were then calculated from the envelope of the complex signals. Numbers of repeated measurements were chosen from n = 2 – 5 for each group in the simulation, and a total of 100 simulations were generated for each combination of es and n.
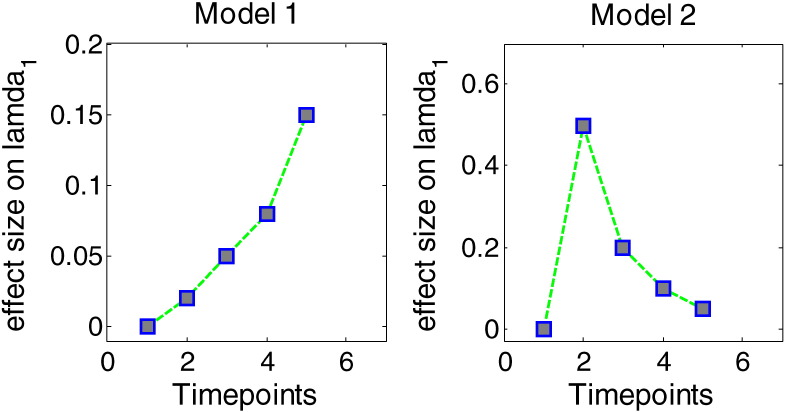
Both a linear trend and a nonlinear trend of disease progression models over time were considered, two models (Effect size on λ1 vs. Timepoints) are illustrated in Fig. 2. The linear and nonlinear trends on the largest eigenvalue λ1 also led to linear and nonlinear trends on tensor-derived parameters such as FA/MD.
-
(i)
Simple linear model: implies that white matter changes by an amount equal to the regression coefficient over time. This type of model in a longitudinal study requires at least three time points. For MC simulation, the following effect sizes were chosen at each time point to mimic a linear relationship across time: es1 = 0 , es2 = 0.02 , es3 = 0.05 , es4 = 0.08 , es5 = 0.15.
-
(ii)
Quadratic model: implies a nonlinear relationship across time. This type of model in a longitudinal study requires at least four time points. For MC simulation, following effect sizes were chosen at each time point to mimic a nonlinear relationship across time: es1 = 0 , es2 = 0.5 , es3 = 0.2 , es4 = 0.1 , es5 = 0.05, which represent different stages of the disease such as onset, peak and recovery.
Fig. 2.
Illustration of linear and quadratic simulated models (Effect size on λ1 vs. Timepoints).
Group comparisons were conducted using iSPREAD with the five proposed voxel-wise test statistics. True Positive Runs (TP_Runs) are defined as the total number of simulations within which at least one voxel was correctly detected in the disease region. False Positive Runs (FP_Runs) are defined as the total number of simulations within which at least one voxel was incorrectly detected in the non-disease region. Sensitivity and Specificity values are defined based on TP_Runs and FP_Runs as follows:
| (16) |
ROC curves were drawn by selecting the per-voxel p value from 0.01 to 0.3 with a gradual increment of 0.01. Results were compared between the five proposed test statistics.
2.4. Human in vivo brain data
2.4.1. Subjects and image acquisition
Multiple sclerosis (MS) is an inflammatory disease of the central nervous system that is thought to be a cell-mediated autoimmune disease leading to progressive neurologic dysfunction; it is classified into different categories that include relapsing remitting, progressive, and stable (Weiner et al., 2000). Relapsing-remitting MS (RRMS) is characterized by clearly defined occurrence of symptoms followed by the remission of symptoms.
In our study, three RRMS patients (2 male and 1 female, mean age 42 ± 2) from an ongoing longitudinal MS study were used as subjects. All subjects were given written informed consent and datasets were acquired using protocols approved by the local institutional review board.
Patients were scanned at baseline and every 3 to 6 months afterward for a duration of 2 years. Images were acquired using a GE HDX 3T scanner (Milwaukee, WI, USA). The Magnetic Resonance (MR) protocol consisted of: (1) a T2 FLAIR scan; (2) a T1 contrast enhanced scan; (3) a high resolution T1 SPGR scan, and (4) a DTI scan. Single-shot echo planar diffusion-weighted imaging (SS-EPI) was acquired with the following parameters:TR/TE = 10500/82 ms; FOV = 240 × 240 mm2; acquisition matrix = 128 × 128, zero-filled to matrix size = 256 × 256; slice thickness 3 mm with no gap; 24 DWIs with b = 1000 s/mm2 and 4 b0s with no diffusion weighting. Both the axial T2 FLAIR and T1 contrast enhanced scans with resolution 2 × 2 × 3 mm3 were used for anatomic definition in the examination.
2.4.2. Analysis
The data were analyzed using MATLAB (MATLAB 2013b, The Mathworks, Natick, MA, USA) and FSL (FSL5.0.4, FMRIB Analysis Group, Oxford University, Oxford, UK). The FSL package's eddy_correct tool was used to correct eddy current and motion-induced artifacts in the DTI data. The non-brain tissues were deleted using the BET tool in` FSL; FA and MD maps were generated subsequently using DTIFIT tool in FSL. To facilitate the voxel-wise comparison at each time point, FA/MD maps at later time points were first co-registered to the FA/MD images at baseline using the FNIRT tool in FSL. The co-registered FA/MD maps were then averaged, and these averaged maps were used as the subject-specific templates to avoid asymmetry-induced bias in image processing (Reuter and Fischl, 2011). The FA/MD maps at different time points were then registered to the template using the FLIRT tool of FSL. The final co-registered FA/MD maps were used for the iSPREAD analysis.
For each subject, the scan and time labels were randomly permuted at each and every voxel for N = 1000 times to generate the permutation distribution under null hypothesis. Five voxel test statistics proposed above were used to model changes in FA/MD over time. For the general linear model, both simple linear and quadratic fits were used to describe the lesion progression over time using FA/MD values as the dependent variable. The Westfall-Young method (Nichols and Hayasaka, 2003) was used to control the FWER. Both True Positive Ratio in lesions (TPRL) and False Positive Ratios in non-lesion white matter (FPRNLWM) were calculated for each test statistics to quantify the sensitivity and specificity in lesion detection, which were defined as in Eq. (17).
| (17) |
3. Results
3.1. Monte Carlo simulation
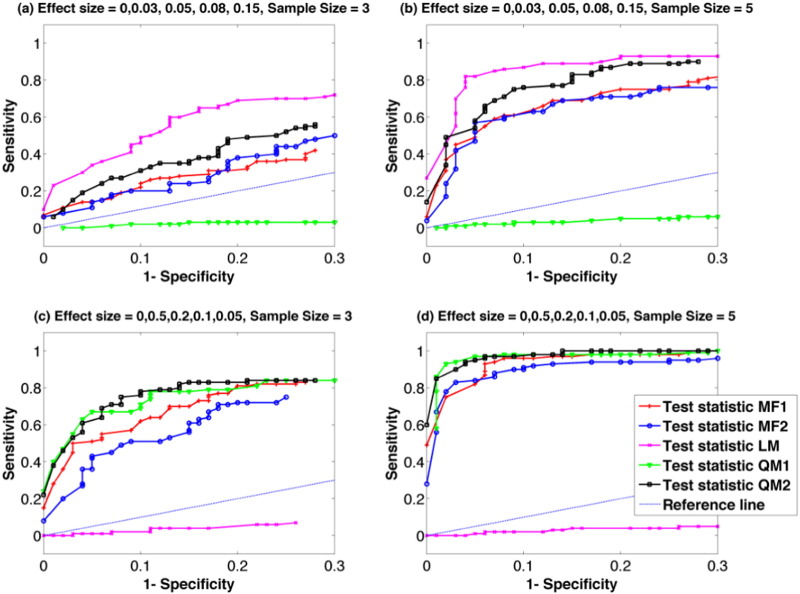
From the MC simulations, it is clear that a high sensitivity can be obtained by all test statistics for a simple linear trend (Fig. 3(a) and (b)) with the exception of Test Statistic QM1, which tested the significance of a quadratic trend. Test Statistic LM, which was the estimated slope in a simple linear regression model, yielded the highest statistical power. As a side note, while the quadratic model (Eq. (9)) includes the linear model (Eq. (8)) as a special case, Test Statistic QM2 also summarizes the variance explained by the linear component in Eq. (9). However, Test Statistic QM2 is not as “sharp” as Test Statistic LM because Eq. (9) has one more unknown parameter (the quadratic term) to estimate therefore it is not as efficient as the simple linear model.
As for the quadratic model (Fig. 3(c) and (d)), a high sensitivity can be obtained by all test statistics except for Test Statistic LM, which was the estimated slope for simple linear regression. Both Test Statistic QM1 and QM2, which were designed specifically for the quadratic model, yielded slightly superior performance than the other test statistics. The differences in results between different test statistics were reduced with the increasing sample size and effect size. For instance, a disease progressed with a fast rate (e.g. with a relatively large effect size change at each time point) will yield a higher detection sensitivity than a disease progressed with a slow rate (e.g. with a relatively small effect size change at each time point).
Fig. 3.
ROC analysis for group comparisons using iSPREAD with five proposed test statistics to identify localized changes from Monte Carlo simulated data. Disease progression models were simulated by either (a, b) a simple linear model (es1 = 0 , es2 = 0.03 , es3 = 0.05 , es4 = 0.08 , es5 = 0.15 ) or (c, d) a quadratic model (es1 = 0 , es2 = 0.5 , es3 = 0.2 , es4 = 0.1 , es5 = 0.05). Sample sizes of n = 3 and n = 5 were considered. The disease area was simulated as a 5 × 5 × 3 cubic region at the center of splenium corpus callosum. Sensitivity and Specificity were calculated using Eq. (16). Results for FA analysis are shown here as an example.
3.2. Human in vivo data
3.2.1. MS patient 1
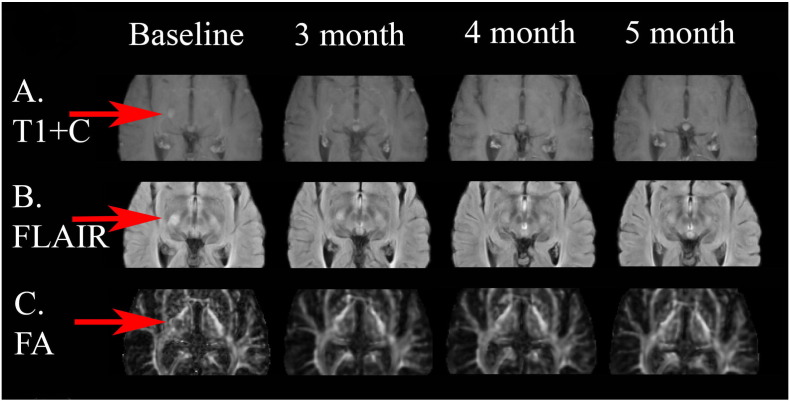
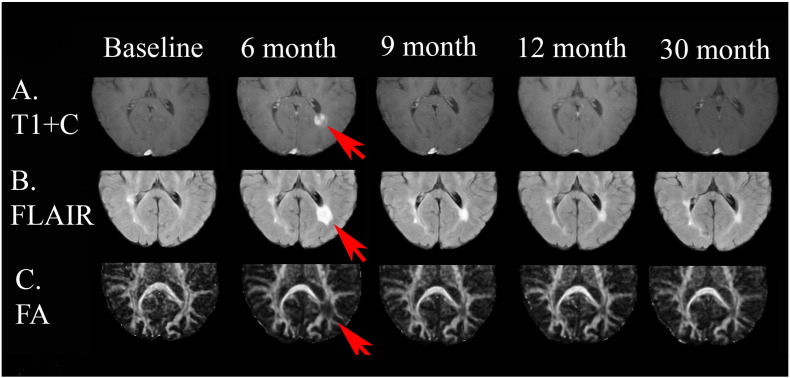
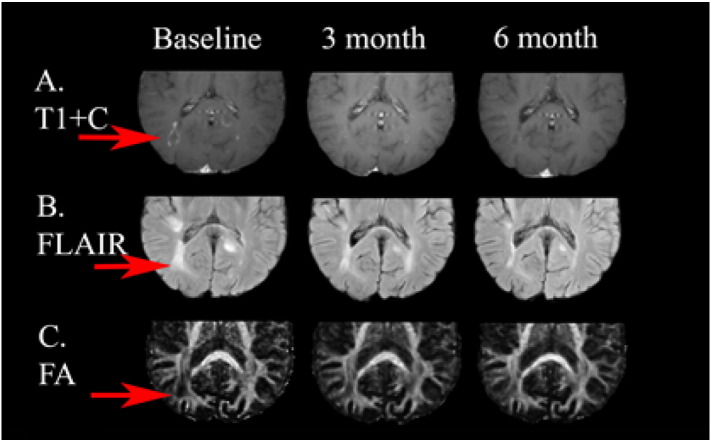
This patient had an active lesion in the posterior limb of the right internal capsule visible on the post contrast T1 images at baseline and fading over time in the follow-up scans (Fig. 4, Fig. 5).
Fig. 4.
This patient had an active lesion (red arrows) in the posterior limb of the right internal capsule visible on the post contrast T1 images at baseline and resolved in the follow-up scans. The degree of hyperintensity within the lesion lessened after 3 month and 4 month compared to the baseline scan. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
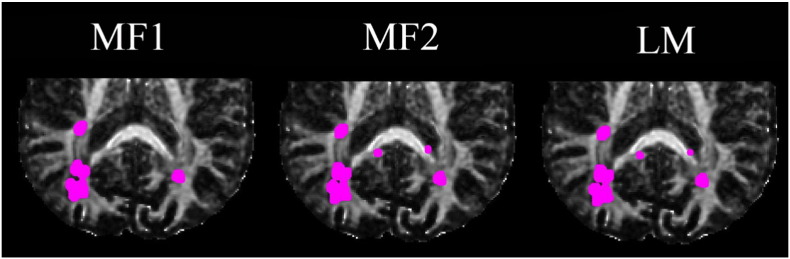
Fig. 5.
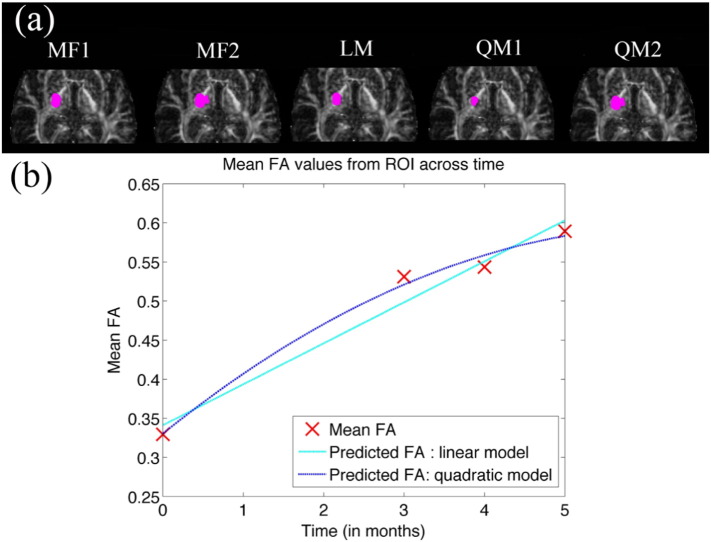
Comparison of significant voxels detected for FA (magenta dots) using iSPREAD with five proposed test statistics (a). Mean FA values calculated from gold standard ROIs at different time points were drawn in (b), together with a fitted simple linear model and a quadratic regression model for mean FAs over time. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
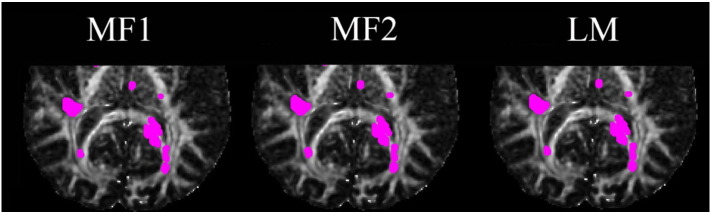
All five proposed test statistics were able to achieve an average TPRL of 88.10% and FPRNLWM of 0.07%, with a slightly decreased sensitivity achieved by Test Statistic QM1 (Table 1). While the model-free test statistics (Test Statistic MF1 and Test Statistic MF2) were able to control the FWER at a reasonable rate, with an average FPRNLWM of 0.16%, it is clear that test statistics based on a general linear model (Test Statistics LM, QM1 and QM2) were able to control the false positive even better, with an average FPRNLWM of 0.009%. FP voxels due to mis-registration and atrophy were largely suppressed. This was not obvious with simulated data because there were no such effects as mis-registration and atrophy that will potentially cause the FPs. Due to limitation of the proposed linear model, which could only accounts for majority of the variations within the disease area across time, a slight decrease in TPRL (84.92 % vs . 92.86%) were observed when using test statistics based on a general linear model compared to the model-free test statistics.
Table 1.
TPRL and FPRNLWM calculated using each test statistic for MS patient 1.
| Test statistics | MF1 | MF2 | LM | QM1 | QM2 |
|---|---|---|---|---|---|
| TPRL | 88.01% | 97.62% | 83.33% | 83.33% | 88.10% |
| FPRNLWM | 0.017% | 0.30% | 0.003% | 0.004% | 0.02% |
3.2.2. MS patient 2
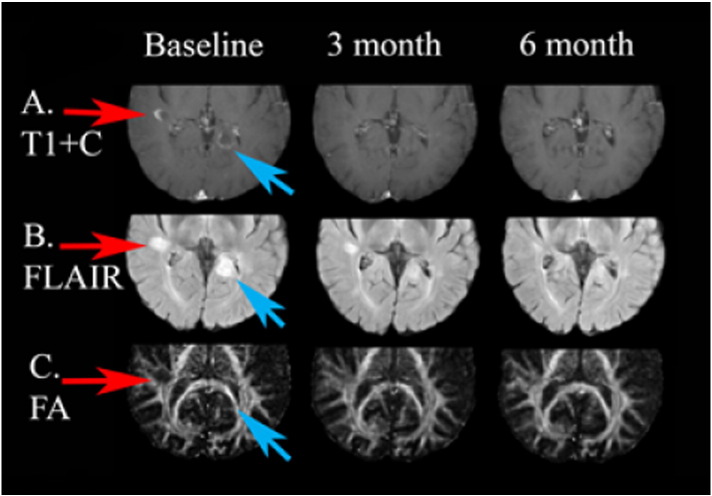
This patient had an active lesion around the atrium of the left lateral ventricle visible on the post contrast T1 images at 6 month from baseline and resolved later (Fig. 6, Fig. 7).
Fig. 6.
This patient had an active lesion around the atrium of the left lateral ventricle visible on the post contrast T1 images at 6 month (red arrows) from baseline and resolved later. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 7.
Significant voxels detected for FA (marked by magenta dots) using iSPREAD with five proposed test statistics. TPRL and FPRNLWM calculated using each test statistic by Eq. (17) are listed in Table 2. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
It can be seen from the results that while all test statistics could achieve an average TPRL of 80.78%, the test statistics based on a linear regression model yielded much lower FPs (0.07% vs. 2.32%), and had a higher ability to control the FWER (Table 2). Specifically, the average TPRL obtained by the model-free test statistics was 90.58% and the average FPRNLWM was 2.32% compared to an average TPRL of 74.24% and an average FPRNLWM of 0.07% obtained by the test statistics based on a linear regression model.
Table 2.
TPRL and FPRNLWM calculated using each test statistic for MS patient 2.
| Test statistics | MF1 | MF2 | LM | QM1 | QM2 |
|---|---|---|---|---|---|
| TPRL | 85.06% | 96.10% | 75.65% | 69.16% | 77.92% |
| FPRNLWM | 0.14% | 4.50% | 0.07% | 0.06% | 0.09% |
3.2.3. MS patient 3
This patient had three lesions located in two different slices; results from iSPREAD are shown in Fig. 8, Fig. 9 for one slice and Fig. 10, Fig. 11 for the other slice.
Fig. 8.
This patient had two new gadolinium enhancing lesions visible in this slice on the post contrast T1 images at baseline and resolved in the follow-up 3-month scan and 6-month scan. One subtle peripheral enhancing lesion (blue arrows) was within the medial aspect of the occipital horn of left lateral ventricle in the left posterior temporal area. Another one lesion (red arrows) was located in the right subcortical temporal area (near the occipital horn of right lateral ventricle). Both lesions demonstrate hyperintensity on FLAIR image at baseline, with both the size of the lesions and degree of FLAIR hyperintensity gradually lessened in the follow-up scans, which suggested a stable state. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 9.
Significant voxels detected for FA (marked by magenta dots) using iSPREAD with three proposed test statistics. TPRL and FPRNLWM calculated using each test statistic by Eq. (17) are listed in Table 3. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 10.
This patient had one new gadolinium enhancing lesions visible in this slice on the post contrast T1 images at baseline (first column, marked by red arrow) and resolved in the follow-up scans. The enhancing lesion was located in the right splenium of the corpus callosum extending to the right major forceps area and shown as hyperintensity on the FLAIR image at baseline, and gradually lessened both in size and intensity in the follow-up scans. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 11.
Significant voxels detected for FA (marked by magenta dots) using iSPREAD with three proposed test statistics. TPRL and FPRNLWM calculated using each test statistic by Eq. (17) are listed in Table 4. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
iSPREAD was able to detect all lesions with a very high sensitivity. Compared to the gold standard lesion masks, lesions were detected with an average TPRL of 88.10% and FPRNLWM of 2.15% for the two lesions on one slice in Fig. 9; an average TPRL of 93.19% and FPRNLWM of 2.15% for the lesion on the other slice in Fig. 11 (Table 3 and Table 4). Since only three scans available in this longitudinal study, only the model-free Test Statistics MF1, MF2 and Test Statistic LM (based on a simple linear model) were applied to test the localized temporal changes.
Table 3.
TPRL and FPRNLWM calculated using each test statistic on the first slice of MS Patient 3.
| Test statistics | MF1 | MF2 | LM |
|---|---|---|---|
| TPRL | 90.71% | 90.71% | 82.86% |
| FPRNLWM | 2.31% | 2.35% | 1.81% |
Table 4.
TPRL and FPRNLWM calculated using each test statistic on the second slice of MS Patient 3.
| Test statistics | MF1 | MF2 | LM |
|---|---|---|---|
| TPRL | 94.09% | 94.09% | 91.40% |
| FPRNLWM | 2.31% | 2.35% | 1.81% |
4. Discussion
In this study, a nonparametric statistical method comprised of two types of voxel-based statistics that helps in detecting subject-specific longitudinal changes in a serial DTI data is presented. Specifically, both the model-free voxel-based test statistics and the test statistics based on a general linear model were applied in the proposed statistical method to test against the null hypothesis of zero differences occurring between groups across time. While a high sensitivity and accuracy was obtained by the five proposed specific voxel-wise statistics belonging to the two types respectively, a significant improvement in specificity while including the prior information of the disease evolution. This indicates the possibility of differentiating the relative contributions of anatomical differences due to image mis-registration, atrophy (False positives) and differences in tissue compositions within a presumably homogeneous structure (True positives, e.g. lesion, tumor, normal appearing white matter). This statistical method is an extension of previously presented SPREAD/iSPREAD method, as well as an independent statistical framework that can be applied to a variety of longitudinal studies using carefully designed test statistics to help detect subject-specific local changes within the brain.
The nonparametric permutation-based methods are very suitable for analysis of data with low degrees of freedom to avoid noisy statistic images (Nichols and Holmes, 2002). However, aside from their numerous applications in the field of fMRI, their applications in longitudinal studies are sparse. Two major disadvantages of permutation-based methods prohibit their wide use; one is the computation burden they impose, the other is the need for sufficient scans in an experiment to give an enough number of possible labelings for generating the empirical null distribution (Holmes et al., 1996). While the first one is partially solved by the fast developing power computing technology, the second one can be addressed by the previously proposed SPREAD/iSPREAD method.
In most cases, the motivation that drives a longitudinal study is the alternative hypothesis that there exist temporal changes between scans at different time points; the problem then comes to which test statistic is most informative in terms of identifying localized changes. Two types of test statistics were herein proposed and tested in this study. The first type, which measures the intra-subject variability across time, is a natural extension of the test statistic used in iSPREAD for pairwise comparison. As a model-free test statistic, it requires no prior information about the disease evolution. However, such test statistics are very sensitive to registration errors or anatomical differences between the scans, therefore were not able to distinguish between significant voxels caused by pathological changes (True Positives) and anatomical differences due to atrophy or image registration error (False positives). The general linear model used in the second type of test statistics is similar in spirit to those used in parametric methods, but without the need for a parametric assumption of measurement errors. For the general linear model, it is very crucial to devise the design matrix according to the specific longitudinal study to reflect the disease evolution model. Both the simple linear model and quadratic model were chosen in this study to account for the temporal effects of the lesion progression. The models chosen in this study were simple, intuitive and easy to implement, which can depict a large number of white matter integrity changes in longitudinal studies.
The effectiveness of the proposed statistical method was validated by both simulation data and human in vivo brain data. For simulation data, while model-free test statistics (Test Statistic MF1 and MF2) were able to detect changes in lesion progressions with a high sensitivity and accuracy, Test Statistic LM, QM1 and QM2 were most useful when the lesion progression followed a specific model. Moreover, it is clear that when the disease progression model followed a specific model, the test statistics designed accordingly would have a higher statistical power than model-free test statistics. Differences between different test statistics were most significant when the effect size and sample size were small, and reduced with an increasing sample size and effect size.
For the MS patients chosen in this study, take the first two MS patient as examples, while all five test statistics could detect longitudinal changes in lesion evolution with an average TPRL of 87.31%, test statistics based on a linear model had the ability to control the FWER at a relatively low rate (with a FPRNLWM of ~ 0.04%) compared to an average FPRNLWM of ~ 1.24% obtained from model-free test statistics. FP voxels due to mis-registration, atrophy, partial volume and random scan variations were largely suppressed when the lesion progression model could be specified explicitly. Compared to the model-free test statistics, the advantage of integrating the specific lesion progression model was clear. Unlike typical independent and identically distributed (i.i.d) Gaussian noise, the effect of underlying anatomic differences caused by mis-registration, atrophy, etc., are spatially smooth thus will not be filtered out by spatial regression. These artifacts increase the total variation and drive up model-free test statistics, which in turn inflate type I error. However, these artifacts are in general specific to each scan and do not follow any specific disease progression model. By imposing a specific model of a true signal, these artifacts will be largely canceled out in the temporal direction, which reduces the type I error as a result.
It is worth pointing that for the two model-free test statistics, Test Statistic MF2 uses the image at the first time point as the baseline image while the Test Statistic MF1 uses the time average image for this purpose. Averaging images in the temporal direction reduces variability, therefore the within-group variation measured by Test statistic MF2 is larger than Test statistic MF1, which can inflate the type I error (false positives) obtained from Test statistic MF2 as compared to that from Test statistic MF1. This is the reason why there were usually more FPs in the results calculated from Test Statistic MF2 than that of Test Statistic MF1 for MS patients.
Despite its advantage of better FP control with a high accuracy with the general linear model, there are two major limitations with its use. First and foremost, in order to devise the design matrix in the general linear model for a specific study, prior information about the disease progression is desirable. This is similar to the general linear model used in fMRI; the design matrix should be devised according to the experiment design. Moreover, in order to accurately model the disease progression, an accurate model should be considered. Both the simple linear model and quadratic model are rough approximation of the temporal changes in FA/MD. The consequence of a lack of fit is usually a decrease in detection sensitivity. As showed in the results, due to limitations of the proposed linear model, which could only account for the majority of the temporal variations within the disease area across time but not all, a slightly decreased sensitivity were obtained by test statistics using a general linear model compared to the model-free test statistics, with a TPRL of 92.17% for the model-free test statistics versus a TPRL of 83.35% for the test statistics based on a general linear model. A more precise and robust time series regression model is therefore needed to accurately examine the localized temporal changes in a longitudinal study and the test statistics could be designed accordingly. However, this is not easy for a voxel-based method as the temporal change trends may vary within disease area. Fortunately, there are many previous fMRI studies we can refer to (Friston et al., 1994, Bullmore et al., 1996). Moreover, when a specific drug effect/disease evolution is of interest; such effect can be easily detected with corresponding design matrix, avoiding the disruption of other “unwanted” signals. The second limitation lies in situations when dealing with data of low degrees of freedom. Although the iSPREAD method greatly reduces the granularity of permutation and makes the permutation-based method feasible with data of low degrees of freedom, the multiple regression still needs the number of data points N > k + 1, where k is the number of variables. Since the degrees of freedom for a multiple regression is N − k − 1, as the number of data points decreases, the ability to test the model erodes accordingly. Therefore, the simple linear model requires at least three scans, one at each time point and even more scans are needed for a quadratic model. However, neither of these limitations mentioned above are specific to this approach, but rather are caused by the inherent characteristic of the methodology.
The current statistical framework can be improved in at least two aspects. In iSPREAD, a nonlinear diffusion filtering method was used to preserve the correlation of the heterogeneous spatial structure and greatly improve the statistical power. For a longitudinal study, the data can be seen as 4D, with the fourth dimension being the time series. In that sense, a 4D filtering method can be applied to preserve the correlation between neighboring voxels in the temporal direction, which is expected to further promote the statistical power of the method. However, in the case of longitudinal study with low degrees of freedom (with few time points available), this needs more careful consideration.
The proposed statistical method provides a novel and simple way of depicting subject-specific localized temporal changes, and is especially suitable for datasets with low degrees of freedom. However, the application for this study is not restricted to investigating lesion evolution, but also for detecting longitudinal changes due to aging, drug effects or other neurodegenerative diseases. The proposed statistical method can be easily generalized to include a broad spectrum of longitudinal studies as well as readily applied to other imaging applications such as fMRI when the degrees of freedom of data are small. It is also a natural extension of this study to include more test statistics according to the different lesion evolution models. Although the voxel-wise test statistics tend to be more sensitive and appropriate to identify focal differences (e.g. lesion, tumor) between groups, global summary statistics are usually used to identify diffuse changes between groups (Nichols and Holmes, 2002). Therefore, different choices of global test statistics such as different norms can be used in the presence of diffuse changes within the brain (e.g. mild traumatic brain injury) to give the researchers information regarding the severity of the brain injury, which merits further investigation.
5. Conclusion
We have presented a permutation-based voxel-wise whole brain analysis method as an extension of SPREAD/iSPREAD that facilitates detecting longitudinal changes in serial DTI studies. This method can obtain a high statistical power even with limited scans available, and thus is very suitable for longitudinal studies with low degrees of freedom. The method described is shown to be accurate and able to achieve a high sensitivity while controlling FWER at a relatively low rate when the test statistic was designed according to the disease progression model being investigated. The proposed framework can be easily generalized to accommodate a variety of longitudinal studies using carefully designed test statistics, which will greatly increase the scope of analysis methods available for longitudinal studies at an individual level.
Footnotes
This work is supported in part by the University of Rochester Center for AIDS Research grant P30AI078498.
References
- Andersen A.H. On the Rician distribution of noisy MRI data. Magn. Reson. Med. 1996;36(2):331–332. doi: 10.1002/mrm.1910360222. [DOI] [PubMed] [Google Scholar]
- Ashburner J., Friston K.J. Voxel-based morphometry—the methods. NeuroImage. 2000;11(6):805–821. doi: 10.1006/nimg.2000.0582. [DOI] [PubMed] [Google Scholar]
- Bazarian J.J., Zhu T., Blyth B., Borrino A., Zhong J. Subject-specific changes in brain white matter on diffusion tensor imaging after sports-related concussion. Magn. Reson. Imaging. 2012;30(2):171–180. doi: 10.1016/j.mri.2011.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y., Hochberg Y. Controlling the false discovery rate — a practical and powerful approach to multiple testing. J. R. Stat. Soc. B Met. 1995;57(1):289–300. [Google Scholar]
- Bullmore E., Brammer M., Williams S.C., Rabe-Hesketh S., Janot N., David A., Mellers J., Howard R., Sham P. Statistical methods of estimation and inference for functional MR image analysis. Magn. Reson. Med. 1996;35(2):261–277. doi: 10.1002/mrm.1910350219. [DOI] [PubMed] [Google Scholar]
- Bullmore E.T., Suckling J., Overmeyer S., Rabe-Hesketh S., Taylor E., Brammer M.J. Global, voxel, and cluster tests, by theory and permutation, for a difference between two groups of structural MR images of the brain. IEEE Trans. Med. Imaging. 1999;18(1):32–42. doi: 10.1109/42.750253. [DOI] [PubMed] [Google Scholar]
- Chung S., Pelletier D., Sdika M., Lu Y., Berman J.I., Henry R.G. Whole brain voxel-wise analysis of single-subject serial DTI by permutation testing. NeuroImage. 2008;39(4):1693–1705. doi: 10.1016/j.neuroimage.2007.10.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobson A.J., Barnett A. 2011. An Introduction to Generalized Linear Models: CRC Press. [Google Scholar]
- Friston K.J., Holmes A.P., Worsley K.J., Poline J.P., Frith C.D., Frackowiak R.S. Statistical parametric maps in functional imaging: a general linear approach. Hum. Brain Mapp. 1994;2(4):189–210. [Google Scholar]
- Gerig G., Kubler O., Kikinis R., Jolesz F.A. Nonlinear anisotropic filtering of MRI data. IEEE Trans. Med. Imaging. 1992;11(2):221–232. doi: 10.1109/42.141646. [DOI] [PubMed] [Google Scholar]
- Gudbjartsson H., Patz S. The Rician distribution of noisy MRI data. Magn. Reson. Med. 1995;34(6):910–914. doi: 10.1002/mrm.1910340618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heim S., Hahn K., Sämann P., Fahrmeir L., Auer D. Assessing DTI data quality using bootstrap analysis. Magn. Reson. Med. 2004;52(3):582–589. doi: 10.1002/mrm.20169. [DOI] [PubMed] [Google Scholar]
- Holmes A.P., Blair R., Watson G., Ford I. Nonparametric analysis of statistic images from functional mapping experiments. J. Cereb. Blood Flow Metab. 1996;16(1):7–22. doi: 10.1097/00004647-199601000-00002. [DOI] [PubMed] [Google Scholar]
- Le Bihan D., Mangin J.F., Poupon C., Clark C.A., Pappata S., Molko N., Chabriat H. Diffusion tensor imaging: concepts and applications. J. Magn. Reson. Imaging. 2001;13(4):534–546. doi: 10.1002/jmri.1076. [DOI] [PubMed] [Google Scholar]
- Liu B., Qiu X., Zhu T., Tian W., Hu R., Ekholm S., Schifitto G., Zhong J. Improved Spatial Regression Analysis of Diffusion tensor Imaging for Lesion Detection during Longitudinal Progression of Neurodegenerative Disease in Individual Subjects. Phys. Med. Biol. 2016;00:1–17. doi: 10.1088/0031-9155/61/6/2497. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols T., Hayasaka S. Controlling the familywise error rate in functional neuroimaging: a comparative review. Stat. Methods Med. Res. 2003;12(5):419–446. doi: 10.1191/0962280203sm341ra. [DOI] [PubMed] [Google Scholar]
- Nichols T.E., Holmes A.P. Nonparametric permutation tests for functional neuroimaging: a primer with examples. Hum. Brain Mapp. 2002;15(1):1–25. doi: 10.1002/hbm.1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perona P., Malik J. Scale-space and edge-detection using anisotropic diffusion. IEEE Trans. Pattern Anal. 1990;12(7):629–639. [Google Scholar]
- Reuter M., Fischl B. Avoiding asymmetry-induced bias in longitudinal image processing. NeuroImage. 2011;57(1):19–21. doi: 10.1016/j.neuroimage.2011.02.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith S.M., Jenkinson M., Johansen-Berg H., Rueckert D., Nichols T.E., Mackay C.E., Watkins K.E., Ciccarelli O., Cader M.Z., Matthews P.M. Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. NeuroImage. 2006;31(4):1487–1505. doi: 10.1016/j.neuroimage.2006.02.024. [DOI] [PubMed] [Google Scholar]
- Tournier J.D., Mori S., Leemans A. Diffusion tensor imaging and beyond. Magn. Reson. Med. 2011;65(6):1532–1556. doi: 10.1002/mrm.22924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tustison N.J., Avants B.B., Cook P.A., Kim J., Whyte J., Gee J.C., Stone J.R. Logical circularity in voxel-based analysis: normalization strategy may induce statistical bias. Hum. Brain Mapp. 2014;35(3):745–759. doi: 10.1002/hbm.22211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiner H.L., Guttmann C.R., Khoury S.J., Orav E.J., Hohol M.J., Kikinis R., Jolesz F.A. Serial magnetic resonance imaging in multiple sclerosis: correlation with attacks, disability, and disease stage. J. Neuroimmunol. 2000;104(2):164–173. doi: 10.1016/s0165-5728(99)00273-8. [DOI] [PubMed] [Google Scholar]
- Werring D., Clark C., Barker G., Thompson A., Miller D. Diffusion tensor imaging of lesions and normal-appearing white matter in multiple sclerosis. Neurology. 1999;52(8):1626. doi: 10.1212/wnl.52.8.1626. [DOI] [PubMed] [Google Scholar]
- Westfall P.H., Young S.S. Wiley; New York: 1993. Resampling-based Multiple Testing: Examples and Methods for P-value Adjustment; p. xvii. (340 pp.) [Google Scholar]
- Westlye L.T., Walhovd K.B., Dale A.M., Bjørnerud A., Due-Tønnessen P., Engvig A., Grydeland H., Tamnes C.K., Ostby Y., Fjell A.M. Life-span changes of the human brain white matter: diffusion tensor imaging (DTI) and volumetry. Cereb. Cortex. 2009:bhp280. doi: 10.1093/cercor/bhp280. [DOI] [PubMed] [Google Scholar]
- Worsley K.J., Evans A.C., Marrett S., Neelin P. A three-dimensional statistical analysis for CBF activation studies in human brain. J. Cereb. Blood Flow Metab. 1992;12:900. doi: 10.1038/jcbfm.1992.127. [DOI] [PubMed] [Google Scholar]
- Worsley K.J., Marrett S., Neelin P., Vandal A.C., Friston K.J., Evans A.C. A unified statistical approach for determining significant signals in images of cerebral activation. Hum. Brain Mapp. 1996;4(1):58–73. doi: 10.1002/(SICI)1097-0193(1996)4:1<58::AID-HBM4>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- Zhu T., Hu R., Tian W., Ekholm S., Schifitto G., Qiu X., Zhong J. Spatial regression analysis of diffusion tensor imaging (SPREAD) for longitudinal progression of neurodegenerative disease in individual subjects. Magn. Reson. Imaging. 2013;31(10):1657–1667. doi: 10.1016/j.mri.2013.07.016. [DOI] [PubMed] [Google Scholar]
- Zhu T., Liu X., Connelly P.R., Zhong J. An optimized wild bootstrap method for evaluation of measurement uncertainties of DTI-derived parameters in human brain. NeuroImage. 2008;40(3):1144–1156. doi: 10.1016/j.neuroimage.2008.01.016. [DOI] [PubMed] [Google Scholar]