Network analysis of functional brain connectivity in borderline personality disorder using resting-state fMRI

Abstract

Borderline personality disorder (BPD) is associated with symptoms such as affect dysregulation, impaired sense of self, and self-harm behaviors. Neuroimaging research on BPD has revealed structural and functional abnormalities in specific brain regions and connections. However, little is known about the topological organizations of brain networks in BPD. We collected resting-state functional magnetic resonance imaging (fMRI) data from 20 patients with BPD and 10 healthy controls, and constructed frequency-specific functional brain networks by correlating wavelet-filtered fMRI signals from 82 cortical and subcortical regions. We employed graph-theory based complex network analysis to investigate the topological properties of the brain networks, and employed network-based statistic to identify functional dysconnections in patients. In the 0.03–0.06 Hz frequency band, compared to controls, patients with BPD showed significantly larger measures of global network topology, including the size of largest connected graph component, clustering coefficient, small-worldness, and local efficiency, indicating increased local cliquishness of the functional brain network. Compared to controls, patients showed lower nodal centrality at several hub nodes but greater centrality at several non-hub nodes in the network. Furthermore, an interconnected subnetwork in 0.03–0.06 Hz frequency band was identified that showed significantly lower connectivity in patients. The links in the subnetwork were mainly long-distance connections between regions located at different lobes; and the mean connectivity of this subnetwork was negatively correlated with the increased global topology measures. Lastly, the key network measures showed high correlations with several clinical symptom scores, and classified BPD patients against healthy controls with high accuracy based on linear discriminant analysis. The abnormal topological properties and connectivity found in this study may add new knowledge to the current understanding of functional brain networks in BPD. However, due to limitation of small sample sizes, the results of the current study should be viewed as exploratory and need to be validated on large samples in future works.

Highlights

• •We analyzed the topology and connectivity of functional brain networks in BPD.
• •Patients with BPD showed altered small-world properties and network efficiency.
• •Patients with BPD showed altered nodal centrality at specific brain regions.
• •An interconnected subnetwork showed significantly lower connectivity in BPD.
• •Key network measures were correlated with clinical symptom scores.

1. Introduction

Borderline Personality Disorder (BPD) is a serious and complex mental illness characterized by a pervasive pattern of instability in affect regulation, interpersonal relationships, impulse control, and self-image. It affects about 1.6% of adults in the United States (“NIMH · Borderline Personality Disorder”). Currently, BPD is diagnosed by a mental health professional based on a thorough interview and a discussion about symptoms. No single test can diagnose the disease, and unfortunately, it is often underdiagnosed or misdiagnosed (“NIMH · Borderline Personality Disorder”). Furthermore, the neurobiology of BPD is poorly understood, and this limited knowledge hinders progress in developing novel, neuroscience-based treatments that target specific biological abnormalities. There is now increasing interest in identifying the structural and functional brain abnormalities associated with BPD, which could help in gaining knowledge about the underlying neurophysiological basis of the disease.

Neuroimaging techniques have recently become one of the most influential tools to detect structural and functional brain abnormalities in patients with BPD (See Krause-Utz et al., 2014b, New et al., 2012 for recent neuroimaging findings in BPD). At the structural level, structural magnetic resonance imaging (sMRI) studies have reported consistent findings of volume reduction in limbic and paralimbic areas (Goodman et al., 2011, Nunes et al., 2009), prefrontal cortex (Sala et al., 2011, Soloff et al., 2012), and various regions of the temporal and parietal lobes (Soloff et al., 2008), in patients with BPD compared with healthy subjects. At the functional level, a number of functional MRI (fMRI) studies have revealed hyperreactivity of limbic areas and hypoactivation of frontal brain areas in response to emotional stimuli, in patients with BPD (Mauchnik and Schmahl, 2010). Furthermore, in addition to examination of regional activation, recent fMRI studies have begun to focus on quantifying functional coupling between brain regions, primarily using seed-based correlation (Biswal et al., 1995, Fox et al., 2005) or independent component analysis (ICA) (Calhoun et al., 2001, Van De Ven et al., 2004). Aberrant functional coupling between limbic and frontal areas during emotional challenge (Cullen et al., 2011, Kamphausen et al., 2012), as well as altered resting-state functional connectivity in the default mode network and the executive network were observed in patients with BPD (Doll et al., 2013, Wolf et al., 2011). Together these findings suggest disruptions of functional connectivity between brain regions in BPD.

Although brain dysfunctions have been previously shown in patients with BPD, prior studies have largely been based on specific regions of interest, i.e., regional functional activations and between-area functional connections. However, whether BPD affects the topological organizations in the whole-brain functional networks has not yet been investigated. For example, how different brain areas are integrated and segregated for communication and specialized processing remains unknown. Given the complexity of BPD psychopathology, knowledge about possible disruptions of topological properties in functional brain networks could potentially advance current understanding of brain dysfunctions associated with the disease, and suggest new avenues for developing neuroscience-based treatment. However, to the best of our knowledge, no study has reported results on the global and local topological properties of functional brain networks in patients with BPD.

Recent research has shown that graph-theory based complex network analysis provides a powerful framework for examining the topological properties of brain networks, where nodes represent brain regions, and edges represent the anatomical or functional connections between brain regions (Bassett and Bullmore, 2009, Bullmore et al., 2009, Rubinov and Sporns, 2010, Stam, 2010). Network analysis of structural and functional connectivity data for healthy people have revealed important “small-world” properties in the healthy brain, characterized by high clustering coefficient and low mean path length (Achard et al., 2006, He et al., 2007, Salvador et al., 2005, Stam, 2004, Strogatz, 2001). High clustering is associated with high local efficiency of information transfer for specialized processing (functional segregation); while short mean path length indicates high global efficiency of parallel information transfer for distributed processing (functional integration) (Bassett and Bullmore, 2009). Knowledge about these informative topological properties could advance a comprehensive understanding of how brain networks are organized and how they generate complex dynamics. Furthermore, comparisons of network topology between healthy subjects and psychiatric patients have reported significant abnormalities of brain connectivity networks in patients with schizophrenia (Bassett et al., 2012, Liu et al., 2008, Lynall et al., 2010, van den Heuvel et al., 2010), Alzheimer's disease (He et al., 2008, Sanz-Arigita et al., 2010, Stam et al., 2009, Supekar et al., 2008), and depression (Leistedt et al., 2009, Zhang et al., 2011). These promising results motivate us to explore BPD-related patterns of topological properties in the functional brain networks, which have not been investigated in previous studies.

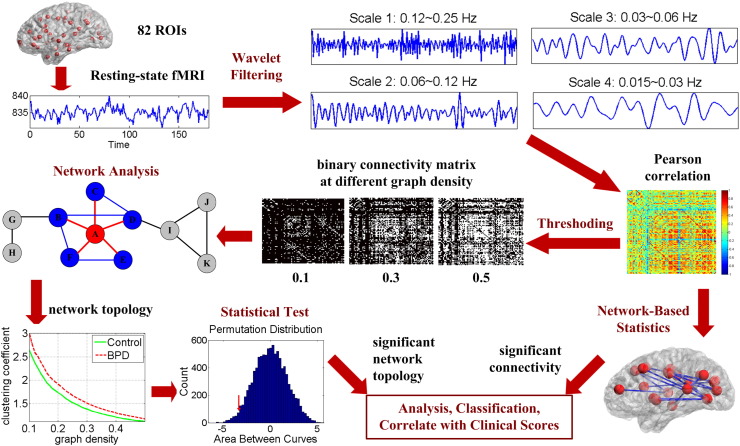
In this study, we performed graph-theory based network analysis on resting-state fMRI data to explore the topology and connectivity in whole-brain functional networks in 20 adults with BPD versus 10 matched healthy controls. The central hypothesis was that BPD disrupts the global and regional topological organizations in functional brain networks, as well as specific connections between regions. To test this hypothesis, we first constructed frequency-specific connectivity graphs by correlating wavelet filtered fMRI signals from different brain regions. Next, we quantified network topological properties (small-world properties, network efficiency, and nodal centrality) and compared these properties between groups. We computed a variety of global and nodal network measures, including the clustering coefficient, characteristic path length, small-worldness, local efficiency, global efficiency and degree (Rubinov and Sporns, 2010). Non-parametric permutation tests were used for group comparisons. In tandem with the characterization of topological properties, we also investigated the functional connectivity in resting-state brain networks. A recently-developed network-based statistic (NBS) approach (Zalesky et al., 2010) was employed to identify altered functional connections in patients with BPD. NBS is a family-wise error rate (FWER) control approach specifically designed under the framework of a network model. It offers high sensitivity in detecting dysconnections in a network by exploiting the extent to which the abnormal connections are interconnected (Zalesky et al., 2010). After identifying BPD-related abnormalities in functional brain network topology and connectivity, we examined correlations between the significant network measures and clinical symptom scores, and used the network features to distinguish BPD patients from healthy controls with a machine learning classifier. The framework of the study design is shown in Fig. 1. Details of the data analysis procedures are described in Section 2.

Fig. 1.

Framework of the study design.

2. Materials and methods

2.1. Subjects

The participants in the current study were a sub-group of a larger, multi-site clinical trial study for adults with BPD (Black et al., 2014) (overall PI: Black, site PI: Schulz). A subset of participants in the University of Minnesota site of the larger study were invited to participate in a supplemental neuroimaging study, in which they would undergo neuroimaging before and after the study treatment. A sample of 10 healthy controls was recruited to undergo diagnostic and neuroimaging procedures as a comparison group. The study was approved by the University of Minnesota Institutional Review Board. Interested and eligible participants completed a separate consent form for the neuroimaging portion of the study.

The participants of the present study included 20 patients with BPD aged 20 to 45, and 10 healthy controls aged 19 to 45. The two groups of subjects did not differ significantly in gender (p-value = 0.802) and age (p-value = 0.56). The subjects could not be entered if taking medication within last six weeks, so no subjects were taking any medication at the time of these scans. None of the control subjects met criteria for a psychiatric or neurological disease or had any major medical illnesses, either currently or historically. All the patients met the DSM-IV-TR criteria (American Psychiatric Association, 2000) for BPD diagnosis, and met the criteria for BPD using the Revised Diagnostic Interview for Borderlines (Zanarini et al., 1989). A minimum score of 9 for total score on the Zanarini Rating Scale for Borderline Personality Disorder (ZAN-BPD) was used as a criterion (Zanarini et al., 2003). In order to reduce confounds associated with diagnostic comorbidity, the patients included in this study did not have a history of any psychotic disorder, bipolar disorder, major depressive disorder with psychotic features, obsessive–compulsive disorder, generalized anxiety disorder, social phobia, or post-traumatic stress disorder. The Structured Clinical Interview for DSM-IV (SCID) (Spitzer et al., 1994) was used to screen for the presence of co-morbid Axis I psychiatric disorders. Among the selected patients, five had history of non-psychotic major depressive disorder and four had history of substance abuse. However, these diagnoses were in remission at the time of the current study. Table 1 lists the demographic information of the subjects, including three commonly used clinical measures for BPD diagnosis: the ZAN-BPD (Zanarini et al., 2003) interview (ZAN-BPD—I) and self-rating (ZAN-BPD—SR), and the symptom checklist 90 (SCL90) (Derogatis and Unger, 2010).

Table 1.

Demographic information.

	Control	BPD
Gender (male/female)	4/6	7/13
Age (mean years ± SD)	27 ± 7.5	29 ± 7.3
ZAN-BPD—I total score (mean ± SD)	N/A	18.65 ± 4.32
ZAN-BPD—SR total score (mean ± SD)	N/A	16 ± 6.4
SCL90 total score (mean ± SD)	N/A	113.55 ± 59

SD: standard deviation; SCL90: symptom checklist 90.

ZAN-BPD—I: Zanarini Rating Scale for Borderline Personality Disorder, interview score.

ZAN-BPD—SR: Zanarini Rating Scale for Borderline Personality Disorder, self-rating score.

2.2. fMRI data acquisition and pre-processing

Structural and functional MRI data were acquired at the University of Minnesota's Center for Magnetic Resonance Research, using a Siemens 3T TIM Trio scanner. Whole-brain anatomical images were acquired using a T1-weighted high-resolution magnetization prepared gradient echo (MPRAGE) sequence: TR = 2530 ms; TE = 3.65 ms; TI = 1100 ms; flip angle = 7°; FOV = 256; voxel size 1 × 1 × 1 mm; GRAPPA = 2. The 6-minute resting-state fMRI scans were obtained using 180 contiguous echo planar imaging (EPI) whole brain volumes with TR = 2000 ms; FOV = 220; voxel size = 3.43 × 3.43 × 4 mm; 34 slices. Subjects were instructed to relax, try not to think about anything in particular, and remain awake with their eyes closed. Physiological data, including heart rate and respiration, were acquired during the fMRI scan. A field map was collected with compatible acquisition parameters as the resting state fMRI data. The scanning protocol also included diffusion imaging and magnetic resonance spectroscopy (which was collected between the T1 scan and the resting-state fMRI scan) and two task fMRI experiments, which were collected after the resting-state fMRI scan. The current paper focuses only on the baseline resting-state fMRI and T1 data.

FreeSurfer (surfer.nmr.mgh.harvard.edu) was used to process the T1 data including brain extraction and parcellation of data into a standard set of anatomically-based regions of white and grey matter. FreeSurfer output was visually inspected on a slice-by-slice basis and manually corrected when deemed necessary. The fMRI data was registered to the T1 data using bbregister. For the resting fMRI data, a de-noising procedure was applied incorporating RETROICOR (Glover et al., 2000) to remove the physiological noises caused by cardiac and respiratory cycles as well as any linear trends. The fMRI processing was mainly conducted using tools from the FMRIB software library (FSL; http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/). Initial processing included brain extraction and motion correction. Correction for magnetic field inhomogeneity-induced geometric distortion was conducted using the field map. FreeSurfer-generated regions of interest (ROIs) for lateral ventricles (cerebrospinal fluid; CSF) and white matter (WM) were aligned to the fMRI data. We performed a regression of each other voxel's time series on eight nuisance variables: WM time series, CSF time series, and the six motion parameters. Data scrubbing was performed following guidelines proposed by previous research (Power et al., 2012), excluding any volume with a DVARS value exceeding 8 and/or a framewise dependent value exceeding 0.5, along with the previous volume and the two following volumes. The deleted volumes were then linearly interpolated by averaging previous and following undeleted volumes to make sure all time series have the same number of time points. Finally, mean fMRI time series from 82 cortical and subcortical areas (41 for each hemisphere) were obtained for network analysis. Table 2 lists the selected ROIs.

Table 2.

List of FreeSurfer-based regions-of-interest (ROIs).

No.	Region of interest (ROI)	Abbr.	No.	Region of interest (ROI)	Abbr.
1	Banks superior temporal sulcus	BANK	22	Posterior-cingulate cortex	PCC
2	Caudal anterior-cingulate cortex	CauACC	23	Precentral gyrus	PreCG
3	Caudal middle frontal gyrus	CauMFG	24	Precuneus cortex	PCUN
4	Cuneus cortex	CUN	25	Rostral anterior cingulate cortex	RosACC
5	Entorhinal cortex	EC	26	Rostral middle frontal gyrus	RosMFG
6	Fusiform gyrus	FFG	27	Superior frontal gyrus	SFG
7	Inferior parietal cortex	IPC	28	Superior parietal cortex	SPC
8	Inferior temporal gyrus	ITG	29	Superior temporal gyrus	STG
9	Isthmus—cingulate cortex	ICC	30	Supramarginal gyrus	SMG
10	Lateral occipital cortex	LatOC	31	Frontal pole	FPO
11	Lateral orbital frontal cortex	LatOFC	32	Temporal pole	TPO
12	Lingual gyrus	LING	33	Transverse temporal cortex	TTC
13	Medial orbital frontal cortex	MedOFC	34	Insula	INS
14	Middle temporal gyrus	MTG	35	Thalamus	THA
15	Parahippocampal gyrus	PHG	36	Caudate	CAU
16	Paracentral lobule	PCL	37	Putamen	PUT
17	Pars opercularis	ParsOPE	38	Pallidum	PAL
18	Pars orbitalis	ParsORB	39	Hippocampus	HIP
19	Pars triangularis	ParsTRI	40	Amygdala	AMYG
20	Pericalcarine cortex	PCAL	41	Accumbens	ACCU
21	Postcentral gyrus	PoCG

2.3. Construction of frequency-specific functional brain networks

Observations from previous studies have shown that the strength of functional connectivity between brain regions is not equal at all frequencies (Achard et al., 2006), and the sensitivity of different frequencies to disease-related alternations of brain connectivity is different (Skidmore et al., 2011, Supekar et al., 2008). In this study, we applied a 4-level stationary discrete wavelet transform (SDWT) (Nason and Silverman, 1995, Shensa, 1992) with ‘db4’ wavelet, to filter the fMRI signal into different frequency bands. The SDWT overcomes the lack of translation-invariance of traditional decimated wavelet transform by removing the downsamplers and upsamplers, and upsampling the filter coefficients. The filtered signal at each wavelet scale approximately corresponded to frequency ranges of 0.12–0.25 Hz (scale 1), 0.06–0.12 Hz (scale 2), 0.03–0.06 Hz (scale 3), and 0.015–0.03 Hz (scale 4), respectively. We next estimate the functional connectivity by computing the Pearson linear correlation coefficients between all possible pairs of fMRI time series at each wavelet scale separately for each subject. At each wavelet scale, a frequency-specific 82-by-82 undirected connectivity graph was constructed based on the 3321 correlation coefficients.

2.4. Graph analysis of network topological organizations

2.4.1. Thresholding

To analyze the topological properties of brain networks using graph measures, the original weighted connectivity matrices were first converted to binary matrices by applying a set of thresholds to the correlation coefficients, such that if the correlation coefficient between two ROIs exceeded a threshold, a connection was defined between the two ROIs. To ensure that the graph measures were mathematically comparable across subjects, subject-specific thresholds were used so that the connectivity graphs from different subjects had the same graph density, i.e., the ratio of the number of existing links over the number of all possible links in the graph. Instead of studying network properties at a single graph density, we thresholded the connectivity matrices repeatedly over a wide range of graph densities between 0.1 and 0.5, with an increment of 0.01. A graph density of 0.1, for example, means keeping the top 10% of the highest correlation coefficients. This specific graph density range is chosen to ensure that the graph is sparse and the small-world properties are estimable (Watts and Strogatz, 1998).

2.4.2. Network topology measures

The thresholding procedure reduced the weighted connectivity matrix to a set of binary graphs, each of which we characterized using a variety of graph-based measures. See (Rubinov and Sporns, 2010) for review of complex network measures of brain connectivity. In this study, we specifically investigated the: small-world properties (Watts and Strogatz, 1998), network efficiency (Latora and Marchiori, 2001), and nodal centrality.

2.4.2.1. Small-world properties

Prior functional neuroimaging studies have shown that functional connectivity networks in a healthy brain can be modeled as a “small-world” system (Achard et al., 2006, Salvador et al., 2005, Stam, 2004). A small-world system has the ability for specialized processing to occur within densely interconnected groups of brain regions (highly segregated), and also has the ability to combine specialized information from distributed brain regions (highly integrated) (Rubinov and Sporns, 2010). The small-world properties of a network are mainly quantified by the clustering coefficient and the characteristic path length of the network. The clustering coefficient c_i of a node i is defined as the ratio of the number of existing links and the number of all possible links between the direct neighbors of the node. High value of c_i implies that most of the neighbors of the node are also neighbors of each other. The clustering coefficient C_net of the entire network is the mean c_i of all nodes in the network. This global measure quantifies the cliquishness of a network. The characteristic path length L_net quantifies the integration ability of a network. The original definition of L_net is the average distance between any two nodes in the network. To avoid the disconnection problem, i.e., the distance between some nodes is infinity, the harmonic mean version of the original definition is used in this study: $L_{\mathit{net}}=\frac{N\left(N-1\right)}{{\displaystyle \sum _{i\ne j\in G}{d}_{\mathit{ij}}^{-1}}}$, where G is the set of all nodes in the network, N is the total number of nodes in the network, and d_ij is the shortest path length between node i and node j (Newman, 2003).

To diagnose the small-world properties, C_net and L_net are normalized by the same metrics estimated from random networks with same number of nodes, edges and degree distribution. The normalized network clustering coefficient is defined as C_norm = C_net/C_rand, while the normalized characteristic path length is defined as L_norm = L_net/L_rand. A small-world network is expected to have high local clustering and low path length, i.e., C_norm > 1 and L_norm ≈ 1. Finally, a scalar summary of the small-worldness of the network is defined as: S = C_norm/L_norm (Humphries and Gurney, 2008). A small-world network has S > 1.

2.4.2.2. Network efficiency

Network efficiency measures how efficiently information is exchanged over the network. Small-world networks are seen as systems that are both globally and locally efficient (Latora and Marchiori, 2001). The global efficiency of the network is defined as the mean inverse shortest path length between all node pairs in the network: $E_{\mathit{glob}}=\frac{{\displaystyle \sum _{i\ne j\in G}{d}_{\mathit{ij}}^{-1}}}{N\left(N-1\right)}$. The local efficiency of node i is defined in the subgraph of the direct neighbors of i: $e_{\mathit{loc},i}=\frac{{\displaystyle {\sum }_{j,h\in G_i}[d_{\mathit{jh}}\left(G_i\right)}]{}^{-1}}{k_i\left(k_i-1\right)}$, where G_i is the set of nodes that are directly connected to node i, d_jh(G_i) is the shortest path length between node j and node h that contains only direct neighbors of node i, and k_i is the number of direct neighbors of node i. The local efficiency of the whole network is the mean e_loc , i of all nodes in the network: $E_{\mathit{loc}}=\frac{1}{N}{\displaystyle \sum _{i\in G}{e}_{\mathit{loc},i}}$. This metric plays a similar role to the clustering coefficient, and it shows how efficient the communication is between the direct neighbors of node i when i is removed (Latora and Marchiori, 2001).

2.4.2.3. Nodal centrality

Degree k_i was used to measure the centrality of a node. It is defined as the number of links connected to the node. Hub regions often interact with many other regions in the network and thus have high centrality.

2.4.3. Statistical test

The set of graph metric values computed at each single graph density form a functional curve, where the x-axis represents the graph density and the y-axis represents the graph metric value. To determine whether there exists significant between-group difference in the graph measures, we performed non-parametric permutation tests on the area under the graph-metric-versus-graph-density curve of each graph metric. The area under curve (AUC) is computed by integrating the curve over specified density range, which serves as a scalar feature for the topological property of the network. We first calculated the difference D between the mean AUC of control group and patient group. To test the null hypothesis that the observed group difference (BPD > control or BPD < control, directed hypothesis) could occur by chance, we then randomly reassigned the group identity (healthy control or BPD patient) for each subject without replacement. Difference D' between the mean AUC of the two pseudo groups were recorded for each permutation. This procedure was repeated 10,000 times, and the p-value of the group difference was defined as the number of times that D' is greater or less than D, divided by 10,000, depending on the sign of D.

In addition to the p-value, the effect size and the power for each significant graph measure (p-value < 0.05) were also analyzed. The effect size of the group mean difference is measured using Cohen's d with pooled standard deviation (Cohen, 1988). The statistical power of the test with significance level 0.05 is calculated based on the group means, standard deviations and sample sizes, using online power calculator (“Power and Sample Size | Free Online Calculators,” n.d.). To note, before group comparison of each graph measure using permutation tests, the confounding factors of gender and age were removed by multiple linear regression (independent variables: gender and age; dependent variables: the AUC of each graph measure).

2.5. Analysis of altered functional connectivity

The functional brain networks consisted of 3321 edges resulting from the pair-wise correlation of the 82 brain regions. To identify altered functional connectivity between nodes in the network, we employed the NBS approach (Zalesky et al., 2010), which is based on the idea of cluster-based thresholding of statistical maps. It is a method of controlling the FWER in the context of a large number of univariate tests are computed at each connection of the network. Specifically, we first computed the t-score for each pairwise connection separately. Then, we applied a primary threshold to the t-scores to select a set of suprathreshold links with t-score exceeding the threshold. The thresholding procedure was performed for links with positive and negative t-scores separately to identify connected components where subjects with BPD had either significantly higher or significantly lower connectivity strength compared to controls (directed hypothesis). Connections comprising this set represented potential candidates for which the null hypothesis could be rejected.

Note that the primary threshold is a user-determined parameter in NBS framework, and there is no definite rules guiding how to choose it. Conservative thresholds, e.g., p-value < 0.001, characterize strong, topologically focal differences, while liberal thresholds, e.g., p-value < 0.05, characterize subtle yet topologically extended differences (Zalesky et al., 2010). Therefore, we tested different primary thresholds in this study. Fortunately, although the choice of primary threshold affects the sensitivity of the method, the control of FWER is guaranteed irrespective of the threshold choice (Zalesky et al., 2010). Next, we identified any connected components in the set of suprathreshold links and stored the size of each component. To determine the significance of each component, we performed non-parametric permutation test. For each permutation, all subjects were randomly reallocated into control group and patient group. The t-score was computed independently for each link, and the size of the largest connected component (LCC) within the suprathreshold links was recorded. This procedure was repeated 10,000 times to obtain the null distribution of the pseudo size of the connected component. Finally, the corrected p-value for a true component of size M was determined by the proportion of permutations with size of LCC larger than M.

2.6. Correlation of network and connectivity measures with clinical symptom scores

We examined clinical correlates of the AUC of significant network topology measures and of the mean connectivity in the significant connected component identified by NBS approach. The clinical scores include: 1) ZAN-BPD (interview and self-rating) total score and 13 sub-scores (anger, moodiness, chronic emptiness, identity problems, suspiciousness, fear of abandonment, suicidal thoughts and self-injurious behaviors (STSIB), impulsivity, relationship problems, sum affect, sum cognitive, sum impulsivity, and sum relationships) (Zanarini et al., 2003); 2) SCL90 total score and 13 sub-scores: somatization, obsessive–compulsive symptoms (OCS), interpersonal sensitivity, depression, anxiety, hostility, phobic anxiety, paranoid ideation, psychoticism, additional items, general severity index (GSI), positive symptom distress index (PSDI), positive symptom total (PST) (Derogatis and Unger, 2010). Linear partial correlation coefficient was used to examine the relationships between network properties and the symptoms of the disease, while controlling the gender and age effects. In addition to age and gender, depressive symptoms measured by the Montgomery–Åsberg Depression Rating Scale (MADRS) (Montgomery and Asberg, 1979) were also partialed out, considering the high comorbidity with depression in major depressive disorder.

2.7. Classification of BPD patients vs. healthy controls

The AUC of significant topology measures and the mean connectivity in the significant connected component identified by NBS approach were used as features, based on which a linear discriminant analysis (LDA) classifier (Mika et al., 1999) was trained to distinguish BPD patients from healthy controls. A leave-one-out cross-validation (LOO-CV) procedure was followed during classification. Each time, 29 subjects were used for classifier training, while the other one subject was used for testing the classification accuracy. The procedure as repeated 30 times until each subject has been used as a testing sample. The machine learning based classification scheme provides a framework for evaluating the discriminating power of network measures in BPD identification.

3. Results

3.1. Altered small-world properties and efficiency of functional brain networks in BPD

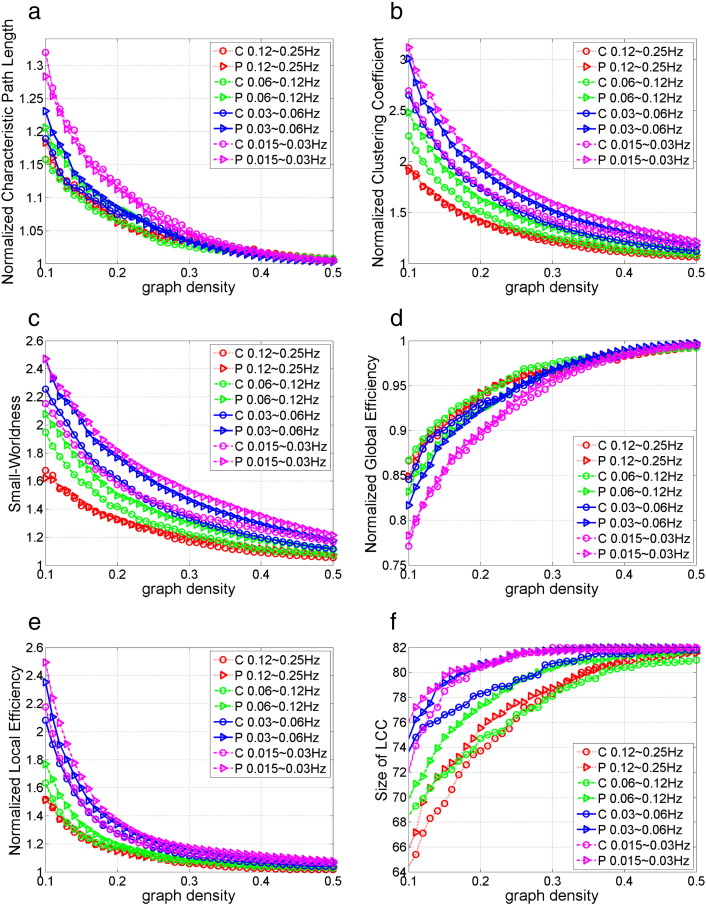
Fig. 2 shows the group mean curve of six global network measures versus graph densities in 4 frequency bands. Fig. 2a–c shows the three small-world measures, including the normalized characteristic path, normalized clustering coefficient, and small-worldness. The functional brain networks of both healthy controls and BPD patients showed small-world properties within density range 0.1 to 0.5: C_norm > 1, L_norm ≈ 1, and S > 1. Furthermore, the small-worldness and the clustered structure were more salient in low frequency bands compared to in high frequency bands: scale 4 (0.015–0.3 Hz) ≈ scale 3 (0.03–0.6 Hz) > scale 2 (0.06–0.12 Hz) > scale 1 (0.12–0.25 Hz), for S and C_norm. This finding is consistent with previous fMRI study that examined the small-world properties in multiple wavelet scales in healthy brain (Achard et al., 2006).

Fig. 2.

Mean global network measures across graph densities in 4 frequency bands for control group (C) and BPD group (P): (a) normalized characteristic path length, (b) normalized clustering coefficient, (c) small-worldness, (d) normalized global efficiency, (e) normalized local efficiency, (f) size of largest connected component.

Fig. 2d–e shows the normalized global and local network efficiency across graph densities. From Fig. 2d, we can observe that the E_glob is slightly lower than one, and it approaches one as graph density increases. This is consistent with the findings that the L_norm is slightly greater than one but approaches one as graph density increases, since both the characteristic path length and the global efficiency are based on the average distance between nodes in the network. The shorter the characteristic path length is, the higher the global efficiency. The values of L_norm and E_glob together show that resting-state functional brain networks have slightly longer but almost equal path length as degree-preserved random networks with same number of nodes and edges. From Fig. 2e, we can observe that the values of E_loc in scale 4 ≈ E_loc in scale 3 > E_loc in scale 2 > E_loc in scale 1 > 1 across graph densities. This is consistent with the C_norm measure, since both C_norm and E_loc measure the local cliquishness, i.e., clustered structure, in a network.

Besides the small-world properties and network efficiency, another simple but important graph measure, the size of largest connected component (LCC) is shown in Fig. 2f. We can observe that as the graph density decreases, a few nodes become disconnected, and that the number of disconnected nodes is larger in high frequency bands compared with in low frequency bands.

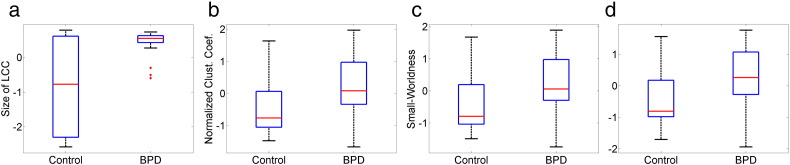
We next analyzed the between-group difference of the graph measures by non-parametric permutation test of the AUC, as described in Section 2.4.3. Although all graph measures defined in this study can deal with disconnected nodes, the AUC for group comparison was computed within density range 0.2 to 0.5, instead of the whole small-world regime 0.1 to 0.5. This density range was chosen so that the network was connected with just a few disconnected nodes. Permutation test results showed that the between-group difference of network topology is the most significant in the 0.03–0.06 Hz frequency range. At this frequency band, BPD patients showed significantly (p-value < 0.05) increased size of LCC, C_norm, S, and L_norm, compared with healthy controls. The boxplots of these significant features are shown in Fig. 3, and the corresponding p-value, effect size and power are listed in Table 3. BPD patients also showed increased C_norm in 0.015–0.03 Hz network, and greater size of LCC and C_norm in the 0.06–0.12 Hz frequency bands. No between-group differences were found in the 0.12–0.25 Hz frequency range.

Fig. 3.

Boxplots of global network measures in 0.03–0.06 Hz that show significant between-group difference (p-value < 0.05): (a) size of the largest connected component (LCC), (b) normalized clustering coefficient, (c) small-worldness, (d) normalized local efficiency.

Table 3.

p-Value, effect size, and power of global network measures in 0.03–0.06 Hz frequency band that show significant between-group difference (p-value < 0.05).

Graph measures	p-Value	Effect size	Power
Size of LCC	0.0008	1.2049	0.8295
Normalized clustering coefficient	0.0285	0.7550	0.3918
Small-worldness	0.0308	0.7263	0.3789
Normalized local efficiency	0.0193	0.8155	0.4415

The increased size of LCC, C_norm, S, and L_norm together suggests increased local cliquishness (clustering) in the intrinsic functional brain networks in patients with BPD versus controls. Table 4 lists the brain regions that showed both increased nodal clustering coefficient and nodal local efficiency in patients. These regions are mainly located within the limbic system, which is associated with various structural and functional abnormalities in BPD, as reported by previous neuroimaging studies.

Table 4.

Brain regions that show significantly (permutation p-value < 0.05, uncorrected) increased clustering coefficient and local efficiency in 0.03–0.06 Hz band network.

Brain regions	Clustering coefficient			Local efficiency
p-Value	Effect size	Power	p-Value	Effect size	Power
Right temporal pole	0.0004	1.3596	0.8711	0.0004	1.3161	0.8753
Left temporal pole	0.0029	1.1129	0.7154	0.0022	1.0724	0.7329
Right pallidum	0.0053	1.0349	0.6681	0.0087	0.9511	0.6102
Left entorhinal	0.0197	0.7489	0.4612	0.0161	0.7832	0.5106
Right amygdala	0.0257	0.7588	0.4356	0.0137	0.8187	0.5351
Left amygdala	0.0432	0.6246	0.3525	0.0251	0.7237	0.4515

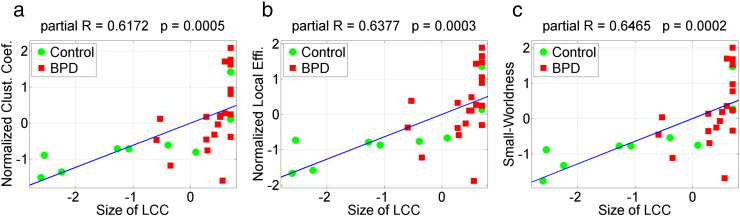
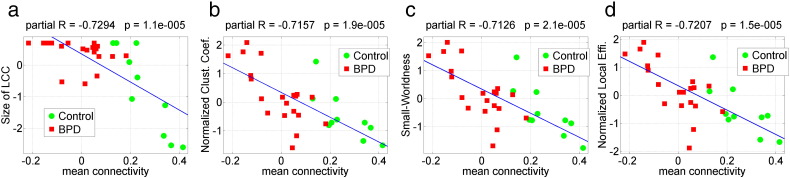
It is noteworthy that a simple measure, the size of LCC, showed the most significant between-group difference compared with other discriminating global network measures (Fig. 3). Previous fMRI study of resting-state functional brain connectivity has suggested that the size of LCC is a non-trivial predictor of a wide variety of other graph metrics, and is sensitive to disease state (Bassett et al., 2012). In Fig. 4, we show the scatter plot of the size of LCC against other discriminating graph measures in the 0.03–0.06 Hz band network, including the normalized clustering coefficient, normalized local efficiency, and small-worldness. Correlation analysis (age and gender partialed out) shows that the size of LCC is positively correlated with all these three significant graph measures.

Fig. 4.

Scatter plot of the size of largest connected component (LCC) in 0.03–0.06 Hz band network against other significant graph measures. The size of LCC is positive correlated with (a) the normalized clustering coefficient, r = 0.6172, p = 5–4, (b) normalized local efficiency, r = 0.6377, p = 3e–4, and (c) small-worldness, r = 0.6465, p = 2e–4.

3.2. Alterations of nodal centrality in functional brain networks in BPD

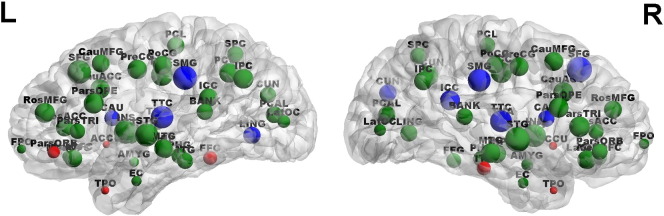
Fig. 5 shows the degree distribution of brain regions in the 0.03–0.06 Hz functional brain network, and marks the brain regions with significantly increased or decreased degree (permutation p-value < 0.05, uncorrected) in BPD patients. The permutation p-values of the discriminating regions are listed in Table 5. BPD patients showed increased degree at several brain regions with low degree, and decreased degree at several brain regions with high degree, indicating reduced number of connections to hub nodes and increased number of connections to non-hub nodes in the resting-state functional brain network. Furthermore, we observed that brain areas that show increased clustering coefficient and local efficiency (Table 4), including the bilateral temporal poles, bilateral amygdala, pallidum, and entorhinal cortex, are nodes with low degree. This finding suggests that the increased local cliquishness in BPD is located at non-hub nodes in the functional brain networks.

Fig. 5.

Degree distribution in the 0.03–0.06 Hz functional brain network. The size of a node reflects the value of degree associated with the node. Nodes with large size represent hub regions with high degree. The red and blue nodes are regions that show significantly increased and decreased degree in patients, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table 5.

p-Value, effect size and power of brain regions that showed significant (permutation p-value < 0.05, uncorrected) between-group difference in degree. Full name of the brain regions are listed in Table 2.

BPD > control				BPD < control
Region	p-Value	Effect size	Power	Region	p-Value	Effect size	Power
ParsORB.L	0.001	1.176	0.676	ICC.R	0.008	− 0.995	0.5533
TPO.L	0.007	1.02	0.5996	SMG.R	0.008	− 1.024	0.5539
TPO.R	0.008	0.97	0.5567	TTC.R	0.023	− 0.84	0.4205
ACCU.L	0.014	0.917	0.5143	TTC.L	0.027	− 0.77	0.4015
ACCU.R	0.014	0.939	0.5048	LING.L	0.031	− 0.722	0.4055
ITG.R	0.026	0.778	0.4187	CAU.L	0.033	− 0.736	0.381
FFG.L	0.042	0.691	0.3488	SFG.R	0.033	− 0.734	0.3707
				CAU.R	0.034	− 0.759	0.3867
				CUN.R	0.038	− 0.704	0.3695
				SMG.L	0.043	− 0.664	0.3471

3.3. Alterations of functional brain connectivity in BPD

The NBS approach identified an interconnected subnetwork in 0.03–0.06 Hz frequency band, which showed significantly (corrected p-value < 0.05) lower connectivity strength in BPD patients. No connected components showed significantly increased connectivity in patients in this frequency range, and no significant between-group difference were found in other three frequency bands.

The size of the connected subnetwork in 0.03–0.06 Hz that showed lower connectivity in BPD is related to the choice of primary threshold in NBS test, as discussed in Section 2.5. Table 6 lists the number of nodes and links in the subnetwork with different primary thresholds. Generally speaking, the size of the subnetwork increases when the primary threshold is lower, since more candidate links are admitted to the suprathreshold link set. However, significant results cannot always be found with arbitrary choice of primary threshold. If the threshold is chosen too low, e.g., p = 0.05, large components can arise in the permuted data as a matter of chance and thereby reduce the sensitivity. In contrast, if the threshold is set too high, e.g., p = 0.001, connections comprising the effect of interest may not be admitted to the set of suprathreshold links (Zalesky et al., 2010).

Table 6.

Number of nodes and links, and the corrected p-value of the connected subnetwork in 0.03–0.06 Hz that show lower connectivity in BPD patients, under different primary threshold in NBS test.

Primary threshold	No. of nodes	No. of links	Corrected p-value
t = 1.75, p ≈ 0.05	No significant result
t = 2.05, p ≈ 0.025	68	205	0.048
t = 2.5, p ≈ 0.01	49	87	0.0408
t = 2.75, p ≈ 0.005	40	57	0.0298
t = 3.05, p ≈ 0.0025	26	26	0.0304
t = 3.4, p ≈ 0.001	No significant result

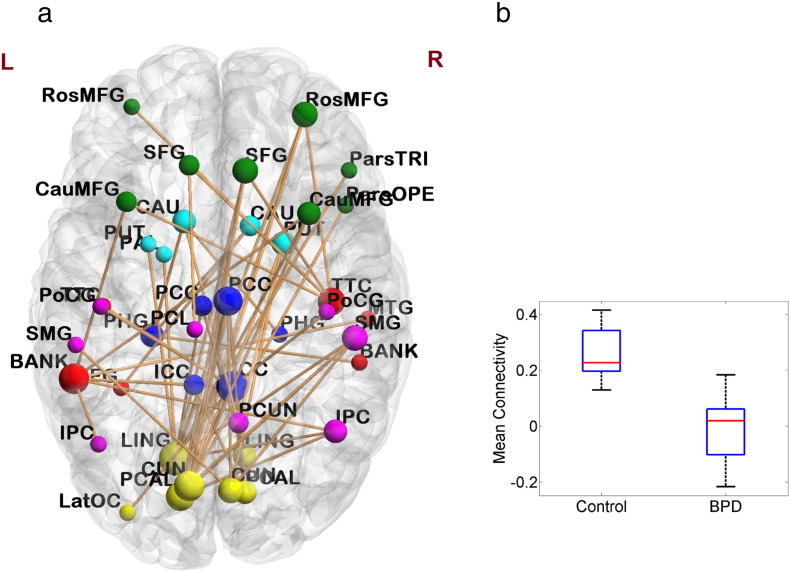
Fig. 6 shows the subnetwork obtained with primary threshold t-score = 2.75, and the boxplot of the mean connectivity in this subnetwork. The 40 nodes covered frontal, temporal, parietal, occipital and limbic lobes; and included all brain areas with decreased nodal centrality in patients, such as the lingual gyrus, cuneus cortex, isthmus—cingulate cortex, superior frontal gyrus, supramarginal gyrus, transvers temporal cortex and caudate (Table 4). The 57 links in the subnetwork were mainly long-distance connections that connected brain regions located at different lobes, e.g., between medial occipital lobe and cingulate cortex, between medial occipital lobe and frontal lobe, and between medial occipital lobe and inferior parietal lobe. All the connections within the subnetwork showed lower values of correlation coefficient in patients as compared with in controls.

Fig. 6.

(a) The connected subnetwork in 0.03–0.06 Hz frequency band that showed significantly lower connectivity in BPD patients identified by NBS approach with primary threshold t-score = 2.75. Size of the nodes corresponds to the number of dysconnections to the nodes, and the color of the nodes represents different lobes: yellow: occipital, red: temporal, purple: parietal, green: frontal, blue: limbic, light blue: basal ganglia. (b) Boxplot of the mean connectivity in the subnetwork. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

After identifying the subnetwork that differentiated patients versus controls, we further investigated the relationship between the reduced connectivity in the subnetwork, and the significant network topology measures that are increased in BPD. Fig. 7 shows the scatter plot of the mean connectivity in the subnetwork with primary threshold t-score = 2.75, against the size of LCC, normalized clustering coefficient, normalized local efficiency and small-worldness. Mean connectivity of the subnetwork was negatively correlated with all these four graph topology measures (age, gender partialed out).

Fig. 7.

Scatter plot of the mean connectivity of the subnetwork that showed lower connectivity in BPD identified by NBS method (primary threshold t-score = 2.75), against the four significant graph measures. The mean connectivity of the subnetwork shows significant negative correlations with: (a) size of largest connected component, r = − 0.7294, p = 1.1e–6, (b) the normalized clustering coefficient, r = − 0.7157, p = 1.9e–5, (c) small-worldness, r = − 0.7126, p = 2.1e–5, and (d) normalized local efficiency, r = − 0.7207, p = 1.5e–5.

3.4. Correlation of network measures with clinical symptom scores

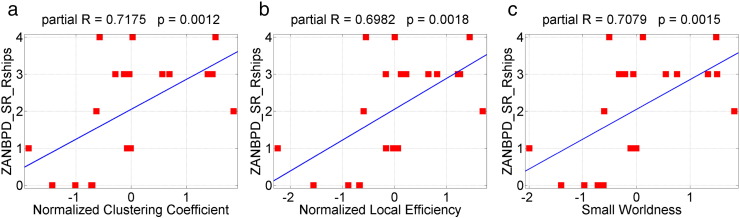
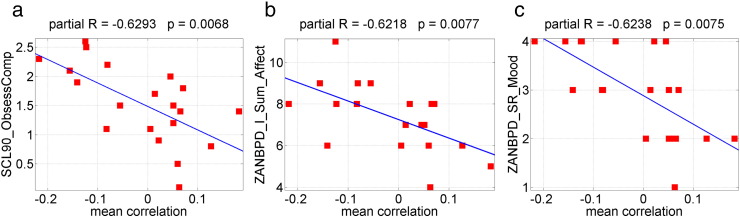
The normalized clustering coefficient, the small-worldness and the local efficiency are positively (p-value < 0.05, uncorrected) correlated with ZANBPD relationship, anger and affect scores (Table 7, Fig. 8). The higher the values of the topological measures are, the higher these correlated clinical scores. The mean connectivity in the subnetwork identified by NBS method with primary threshold t-score = 2.75 is negatively (p < 0.05, uncorrected) correlated with a variety of SCL90 and ZANBPD symptom scores (Table 8, Fig. 9). As shown in Section 3.3, the mean connectivity in the NBS network is significantly reduced in patients. The lower the mean connectivity is, the higher these correlated clinical scores. These results together suggest that altered functional brain network topology and connectivity may contribute to specific symptoms of the disease.

Table 7.

Correlations between clinical scores and global network topology measures (age, gender and MADRS partialed out).

	Normalized clust. coef.		Normalized local efficiency		Small-worldness
	r	p-Value	r	p-Value	r	p-Value
ZANBPD—SR relationship	0.7175	0.0012	0.6982	0.0018	0.7079	0.0015
ZANBPD—I relationship	0.6683	0.0034	0.6942	0.002	0.6619	0.0038
ZANBPD—I anger	0.5317	0.0281	0.5663	0.0178	0.543	0.0243
ZANBPD—I sum affect	0.519	0.0328	0.4977	0.0421	0.516	0.034

ZAN-BPD—I: Zanarini Rating Scale for Borderline Personality Disorder interview score.

ZAN-BPD—SR: Zanarini Rating Scale for Borderline Personality Disorder self-rating score.

Fig. 8.

Scatter plots of ZANBPD—SR relationship problem scores against three global network topology measures: (a) normalized clustering coefficient, r = 0.7175, p = 0.0012, (b) normalized local efficiency, r = 0.6982, p = 0.0018, (c) small-worldness, r = 0.7079, p = 0.0015.

Table 8.

Correlations between clinical scores and mean connectivity in the subnetwork that show significantly reduced connectivity in BPD identified by NBS method (primary threshold t-score > 2.75). Age, gender and MADRS score were partialed out.

SCL90	r	p	ZANBPD—I	r	p	ZANBPD—SR	r	p
OCS	− 0.6293	0.0068	Sum affect	− 0.6218	0.0077	Mood	− 0.6238	0.0075
Depress	− 0.6235	0.0075	Sum total	− 0.5961	0.0116	Sum affect	− 0.5064	0.0381
Hostility	− 0.5164	0.0338	Sum impulsivity	− 0.5369	0.0263	Relationships	− 0.4951	0.0433
GSI	− 0.5064	0.0389	Sum relationships	− 0.4865	0.0477
Total	− 0.5024	0.0391

OCS: obsessive–compulsive symptoms; GSI: general severity index; ZAN-BPD—I: Zanarini Rating Scale for Borderline Personality Disorder interview score; ZAN-BPD—SR: Zanarini Rating Scale for Borderline Personality Disorder self-rating score; SCL90: symptom checklist 90.

Fig. 9.

Scatter plot of the mean connectivity of the connected subnetwork that showed lower connectivity in BPD identified by NBS method with primary threshold t-score = 2.75, against several clinical scores. The mean connectivity of NBS network is negatively correlated with: (a) SCL90 obsessive–compulsive symptoms, (b) ZANBPD—I sum affect, and (c) ZANBPD—SR mood scores. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.5. Classification of BPD patients and healthy controls with network features

Given the significant between-group difference of functional brain connectivity and network topology, we tested whether these measures could be used as features to distinguish BPD patients from healthy controls using LDA classifier. Table 9 lists the leave-one-out classification results using single global network measures that showed significant between-group difference, including the mean connectivity in the subnetwork identified by NBS approach with primary threshold t-score = 2.75, size of largest connected component, normalized clustering coefficient, normalized local efficiency, and small-worldness of the whole network. The best classification result was achieved using the mean connectivity of NBS subnetwork (90% sensitivity and 90% specificity). Besides the discriminating global network features, the left and right temporal poles showed the most significant between-group differences in nodal topological measures compared with other brain areas (Table 4, Table 5). Table 10 lists the classification results using nodal network measures of these two regions, including nodal clustering coefficient, local efficiency and degree. The best classification result was achieved using the clustering coefficients of these two regions (90% sensitivity and 70% specificity).

Table 9.

Classification results using single global network measure: mean connectivity in the NBS network ($\bar{r}$), size of largest connected component (size), normalized clustering coefficient (C_norm), normalized local efficiency (E_loc) and small-worldness (S).

	Accuracy	Specificity	Sensitivity
$\bar{r}$	0.9	0.9	0.9
size	0.7667	0.6	0.85
Cnorm	0.6667	0.7	0.65
Eloc	0.6667	0.7	0.65
S	0.6667	0.7	0.65

Table 10.

Classification results using pairs of regional network measures of the left and right temporal poles, including clustering coefficient (c), local efficiency (e_loc), and degree (k).

	Accuracy	Specificity	Sensitivity
c	0.8333	0.7	0.9
eloc	0.8	0.6	0.9
k	0.7	0.7	0.7

4. Discussions

4.1. BPD-related alterations of functional brain network topology and connectivity

Using graph-theory based complex network analysis and network-based statistic approach, we examined the topology and connectivity in resting-state functional brain networks of adults with BPD versus healthy controls. As hypothesized, patients with BPD showed evidence for abnormalities both in topological structure and in connectivity in the intrinsic functional brain networks. These abnormalities appear to be related to specific symptoms of BPD, and can be used as features to distinguish patients with BPD from healthy controls using a machine learning classifier. These findings add to prior neuroimaging studies that have reported abnormal connections between specific brain regions in BPD, and may provide new, clinically-relevant knowledge about the neurophysiology of the disease.

The emergence of graph-theory based complex network analysis provides an important mathematical framework to characterize the global and regional topology in brain connectivity networks. Our graph analysis identified significant alterations of small-world properties and network efficiency in patients with BPD versus healthy controls at the 0.03–0.06 Hz frequency band, including increased size of largest connected network component (LCC), small-worldness, clustering coefficient and local efficiency. The increased size of LCC indicates a lower number of disconnected nodes in the network. Previous fMRI study of resting-state functional brain networks has reported increased size of LCC in schizophrenia patients, and suggested that the size of LCC is a predictor of other graph measures in graph analysis (Bassett et al., 2012). This is consistent with our finding that the size of LCC is positively correlated with other discriminating network topology measures, including the small-worldness, clustering coefficient and local efficiency.

The higher values of clustering coefficient and local efficiency together suggest greater network cliquishness, i.e., clustered structure, within the resting-state functional brain networks in BPD patients. Brain regions that showed increased local cliquishness in patients include the bilateral temporal poles, bilateral amygdala, right pallidum, and left entorhinal cortex. These regions are mainly located within the limbic and paralimbic systems. Abnormalities of limbic regions in BPD have been consistently reported by both structural and functional neuroimaging studies (Krause-Utz et al., 2014a, Krause-Utz et al., 2014b, New et al., 2012). For example, the amygdala, which plays a crucial role in emotion processing and in the initiation of fear and stress responses (Ochsner and Gross, 2007), has been considered to be highly relevant to BPD psychopathology (Leichsenring et al., 2011). Neural imaging studies reported volume reduction (Nunes et al., 2009), hyperreactivity in response to emotional stimuli (Krause-Utz et al., 2014b), and increased functional connectivity in resting-state (Krause-Utz et al., 2014a), at this area in BPD patients. Note that hyperconnectivity of brain regions implicated in emotion processing may reflect clinically well-observed BPD features such as affective hyperarousal and intense emotional reactions (Krause-Utz et al., 2014b). The bilateral temporal poles, i.e., the anterior-most portion of the temporal lobes, are also associated with significantly increased local cliquishness in patients. Temporal pole is often considered part of an extended limbic system, which is lateral to the amygdala and has tight connectivity to limbic and paralimbic regions. Research has suggested that this area binds complex, highly processed perceptual inputs to visceral emotional responses (Olson et al., 2007). Structural and functional deficits of this area in patients with BPD have also been reported by previous neuroimaging studies (Buchheim et al., 2013). The finding in this study that in resting-state functional brain networks, patients with BPD show higher levels of local cliquishness at the amygdala and temporal poles, which are responsible for processing negative emotion and visceral responses to negative emotion, could potentially explain the vulnerability in this patient group for a rapid rise to negative affect that is difficult for them to regulate.

In addition to the small-world properties and network efficiency, we also investigated the centrality of brain regions, which characterizes the importance of a node in the whole brain network. On the one hand, BPD patients show higher nodal centrality than controls at several brain regions with low degree, such as temporal poles and the nucleus accumbens. On the other hand, patients with BPD showed lower nodal centrality than controls at several hub nodes in the network, such as the supramarginal gyrus and the transverse temporal cortex. These findings suggest that BPD might cause an increased number of connections to non-hub nodes and a decreased number of connections to hub nodes in functional brain networks. Furthermore, we also noticed that brain regions where patients with BPD showed increased local cliquishness are associated with low degree, suggesting that the increased local cliquishness in the whole brain network discussed above occurs in non-hub nodes. These alterations in the topological organizations of functional brain networks may add new knowledge to the current understanding of neural dysfunction in BPD.

Functional brain networks are constructed by pair-wise connections between all nodes in the network. In addition to exploring the topological properties, we also explored functional connectivity between brain regions in the resting-state networks. By applying the NBS approach, we identified an interconnected subnetwork in the 0.03–0.06 Hz frequency band that showed significantly lower connectivity strength in patients with BPD compared to controls. The nodes in the subnetwork were mainly located at the medial occipital lobe (lingual gyrus, cuneus cortex and pericalcarine cortex), cingulate cortex (posterior and isthmus divisions), temporal lobe (banks of superior temporal sulcus, transverse temporal cortex), prefrontal lobe (middle frontal gyrus, superior frontal gyrus), inferior parietal lobe (inferior parietal cortex, supramarginal gyrus), and basal ganglia areas (caudate, putamen). The links in the subnetwork were mainly long-distance connections between regions located at different lobes. The most number of dysconnections existed between the medial occipital lobe and cingulate cortex, medial occipital lobe and prefrontal cortices, medial occipital lobe and inferior parietal lobe, temporal lobe and prefrontal cortices, as well as between temporal lobe and inferior parietal lobe. Note that the posterior cingulate cortex, medial prefrontal cortex, inferior parietal lobe, superior temporal gyrus and cuneus are considered as core regions in the default mode network (DMN) (Buckner et al., 2008, Sreenivas et al., 2012, Wolf et al., 2011). A recent fMRI study using ICA-based correlation analysis also reported altered resting-state functional connectivity in DMN regions, including decreased connectivity in the cuneus, inferior parietal lobule and middle temporal cortex, in patients with BPD compared with healthy controls (Wolf et al., 2011). Together these findings suggest alterations in long-distance functional connections between regions associated with self-referential processes in patients with BPD. Previous fMRI study using ICA approach also reported increased resting-state functional connectivity in the left frontal–parietal cortices and left insula in DMN (Wolf et al., 2011), which was not identified in this study. A possible reason is that the NBS approach focuses on dysconnections that form an interconnected structure, rather than isolated links. Therefore, some suprathresholded links with increased connectivity in patients may not be considered significant if they could not form a connected component with enough size. Nevertheless, the finding of impaired long-distance connectivity in this study may add new insight into previous connectivity analysis for BPD that used ICA or seed-based correlation analysis (Doll et al., 2013, Krause-Utz et al., 2014a, Wolf et al., 2011).

In our study, we found several important relationships among the network measures and between network and clinical measures, which add strength and validity to the overall findings. First, mean connectivity within the subnetwork differentiating patients with BPD from controls at the 0.03–0.06 Hz frequency band was associated with significant alterations of network topology. Interestingly, the mean connectivity of this subnetwork was negatively correlated with all four global network topology measures that had shown significant group differences (higher in patients), including the size of largest graph component, normalized clustering coefficient, small-worldness, and normalized local efficiency. In these relationships, participants with lower mean connectivity showed higher values of the global measures. This finding suggests a possible relationship between the functional connectivity between brain areas and the topological organizations of whole-brain functional networks. Second, the properties of small-worldness, clustering coefficient and local efficiency all showed positive correlations with key BPD symptoms, including problems in relationships, anger and affect problems. The decreased functional connectivity in the NBS subnetwork showed negative correlations with a variety of key BPD symptoms, such as depression, obsessive–compulsive symptoms, hostility, affect, impulsivity, and relationship problems. Although these correlation analyses were exploratory and the results were not corrected for multiple comparisons, the preliminary findings suggest that the aberrant topological and connectivity features may have important clinical relevance. BPD is very heterogeneous, and so treatments will optimally be tailored to each individual's aberrant pattern of neurobiology. By better characterizing the neural underpinnings of specific facets of illness, this type of research will pave the way for conceptualizing and testing more targeted, neuroscientifically-informed treatments. Last but not least, the significant network topology and connectivity features showed promising classification accuracy in distinguishing BPD patients from healthy controls with LDA classifier, which further demonstrated the between-group differences of these network properties showed in statistical tests. Together these findings suggest that the network measures derived from graph theory in this study are clinically meaningful, and may shed light on the neurobiological underpinnings of BPD, and could eventually have potential in clinical applications such as diagnosis and treatment selection.

Finally, we wish to highlight that we consider this exploratory study is a first and important step. The preliminary findings of group differences and relationships with clinical measures reported here require replication with larger samples. Once confirmed, these findings could form the basis for longitudinal studies testing important questions such as: (1) how topological network structure and functional connectivity change in patients with BPD across stages of illness; (2) whether these abnormalities present early in development, even before onset of the disorder; (3) which factors contribute to development of network organization abnormalities; and (4) whether and how interventions for BPD impact these aspects of neural network organization and connectivity.

4.2. Methodological considerations

To compute various network topology measures, after obtaining the correlation coefficients between all brain regions, we used thresholding to remove weak and non-significant links, since they may represent spurious connections and may obscure the topology of strong and significant connections in functional brain networks (Rubinov and Sporns, 2010). Negative connections, i.e., functional anti-correlations, and self-connections were ignored in the present study, as suggested in (Rubinov and Sporns, 2010). We applied a set of subject-specific correlation thresholds to ensure that all networks have the same number of nodes and links at each graph density. To determine the statistical significance of each graph measure, an efficient test is needed to compare the graph-metric-versus-graph-density curves between groups. Instead of performing massive comparisons at each single density, we performed non-parametric permutation test on the AUC of each graph measure, which serves as a scalar summary of the curve values across densities. This approach offers a comprehensive examination of the entire topological structure of the original weighted connectivity graph over specific density range of interest. In addition, a machine learning classifier was applied to classify BPD patients from healthy controls based on the discriminating network measures. The significant network features and the machine learning based classification scheme may have potential to be used in a computer-aided objective test to assist in clinical diagnosis of BPD.

To identify functional dysconnections in BPD from more than 3000 links in the whole brain network, it is necessary to control the FWER due to multiple comparisons. In this study, we employed the recently-developed NBS approach, instead of traditional false-discovery rate (FDR) controlling procedure that calculates the test statistic and corresponding p-value independently for each link (Genovese et al., 2002). The main considerations here are two-fold. On the one hand, NBS approach aims at detecting altered functional connectivity that exists in a connected component, rather than disconnected abnormal links. In our functional brain network analysis, brain regions are defined to be interconnected. Therefore, focal dysconnections can propagate along interconnected pathways, which is suitable for NBS method to detect (Zalesky et al., 2010). Such interconnected structure of dysconnected links was not explored in previous seed-based or ICA-based correlation analysis with traditional FDR controls (Doll et al., 2013, Krause-Utz et al., 2014a, Wolf et al., 2011). On the other hand, compared with traditional FDR control procedure, the NBS approach offers greater sensitivity in graph analysis. Under traditional FDR control, to survive from thousands of multiple comparisons, the link-based p-values need to be very small, less than 1e–5 in this study, which leads to high false negative rates. However, under the NBS framework, the link-based p-value only needs to be significant enough to pass a primary threshold to be admitted into the suprathreshold link set. Connections can be declared significant if they form an interconnected component. Despite these advantages of NBS in identifying significant connections, there are limitations of this approach. First, when using NBS, a rather arbitrary choice must be made to select the primary threshold used to define the set of suprathreshold links. Second, the localizing power of NBS is coarser than traditional link-based approach. Third, only a connected component can be declared significant, but the individual connections comprising the component cannot (Zalesky et al., 2010).

4.3. Limitations

The limitation of the study is the small sample size (20 patients vs. 10 controls), which leads to low statistical power: 0.38–0.83 (mean 0.51, SD 0.214) for global measures and 0.35–0.875 (mean 0.518, SD 0.15) for nodal measures. Low statistical power not only reduces the probability of detecting a true effect, but also reduces the probability that a statistically significant results reflects a true effect (Button et al., 2013). The effect sizes (Cohen's d) for the four global topology measures are 0.726–1.205 (mean 0.875, SD 0.222), indicating medium to large effects (Cohen, 1988). The absolute values of effect size for nodal topology measures are 0.625–1.36 (mean 0.888, SD 0.193), also indicating medium to large effects (Cohen, 1988). These effect sizes are comparable with previous effect sizes reported in neuroimaging studies that have compared BPD subjects and healthy volunteers (Bøen et al., 2014, Buchheim et al., 2008, Nunes et al., 2009, Reitz et al., 2015). However, they might be overestimated due to low statistical power (Button et al., 2013). Besides the power issue, small number of subjects does not allow us to assess the relative differences between subtypes of the disease, or design more complex classification models which might cause data overfitting. Therefore, the findings of this study should be viewed as exploratory, and need to be validated and extended on large samples with high statistical power.

Some other limitations of the current work need to be further addressed. First, 82 cortical and subcortical regions were chosen as nodes in the functional brain networks. Brain networks derived using different parcellation schemes may show different topological structures. In addition, linear correlation coefficients were used to measure the functional connectivity in the network, which could only measure the linear relationship between two time series. There are other types of connectivity measures like coherence, and mutual information, which could account for time lags and measure non-linear correlations between two time series. Further studies are needed to compare the topology and connectivity of functional brain networks constructed with different node sets and connectivity measures. Lastly, it is important to note that the current study considers a single static network structure as an average representation of the overall resting-state functional connectivity over 6 minute time duration. This method is consistent with other similar studies on topological organization of functional brain networks (Bassett et al., 2012, Supekar et al., 2008, Zhang et al., 2011). However, recent fMRI research has shown that resting-state functional brain connectivity is not static (Chang and Glover, 2010). Therefore, future work is needed to explore the dynamic network topology changes across longer time durations.

5. Conclusions

The present study applied graph-theory based complex network analysis and network-based statistic to investigate BPD-related alterations of topological organizations and connectivity in resting-state functional brain networks. In the 0.03–0.06 Hz functional brain networks, BPD patients showed increased local cliquishness characterized by increased size of largest connected component, clustering coefficient, local efficiency, and small-worldness, particularly at the limbic areas. Patients also showed decreased nodal centrality at several hub nodes, but increased nodal centrality at several non-hub nodes in the network. Furthermore, an interconnected subnetwork in the 0.03–0.06 Hz frequency band showed significantly lower connectivity strength in BPD patients, the mean connectivity of which was negatively correlated with the increased topology measures. In addition, the significant network measures were correlated with several clinical symptom scores for BPD diagnosis, and showed high predictive power in patient vs. control classification using a machine learning classifier. The findings of this work may help in gaining new knowledge into the neural underpinnings of BPD. However, due to limitation of small sample sizes, the reported results should be viewed as exploratory and need to be validated on large samples in future works. Future efforts will be directed towards studying functional brain networks constructed with different node sets and connectivity measures, exploring the dynamic network structure across time, and testing the results on a larger sample size. Future work will also be directed towards comparing the topological properties of functional brain networks in different psychiatric disorders, including BPD, obsessive compulsive disorder, and major depressive disorder.