Modular Brain Networks

Abstract

The development of new technologies for mapping structural and functional brain connectivity has led to the creation of comprehensive network maps of neuronal circuits and systems. The architecture of these brain networks can be examined and analyzed with a large variety of graph theory tools. Methods for detecting modules, or network communities, are of particular interest because they uncover major building blocks or subnetworks that are particularly densely connected, often corresponding to specialized functional components. A large number of methods for community detection have become available and are now widely applied in network neuroscience. This article first surveys a number of these methods, with an emphasis on their advantages and shortcomings; then it summarizes major findings on the existence of modules in both structural and functional brain networks and briefly considers their potential functional roles in brain evolution, wiring minimization, and the emergence of functional specialization and complex dynamics.

INTRODUCTION

Behavior and cognition are associated with neuronal activity in distributed networks of neuronal populations and brain regions. These brain networks are linked by anatomical connections and engage in complex patterns of neuronal communication and signaling. In recent years, the convergence of two major scientific developments has prompted a new network-based perspective on brain function (Bressler & Menon 2010, Bullmore & Sporns 2009, Park & Friston 2013, Sporns 2014, Sporns et al. 2004). On the one side, improved capabilities in brain imaging and recording have provided new ways to measure the brain's anatomical (structural) as well as dynamic (functional) connections. These developments have given rise to the emerging field of brain connectivity (Jirsa & McIntosh 2007, Sporns 2011). On the other side, the availability of increasingly complex data in the social, technological, and biological sciences has led to the development of new tools and methods for representing and analyzing networks, giving rise to the new discipline of network science (Börner et al. 2007). The network science of the brain, or network neuroscience, is still a very recent endeavor, and new observational techniques and analytic methods (Rubinov & Sporns 2010) are continually emerging. Here we provide a survey of the state of the art in both methods and principal findings in a particularly active area of network neuroscience: modular brain networks.

Structural and Functional Brain Networks

Data about relations between elements, for example, connections among brain regions, can be summarized and represented as a set of nodes and edges forming a network (Figure 1a). The construction of brain networks begins with the collection of observational data on how brain regions, neuronal populations, or neurons are connected. A major distinction is that between structural and functional networks. Structural networks correspond to a pattern of anatomical connections, summarizing synaptic links between neurons or projections among brain regions. Most relevant for studies of the human brain are large-scale networks of interregional pathways that link cortical and subcortical gray matter regions, which taken together form the human connectome (Sporns 2013, Sporns et al. 2005). In contrast, functional networks are assembled from estimates of statistical dependencies between neuronal or regional time series data (Friston 2011). Although many different measures of functional connectivity exist (Smith et al. 2011), most human neuroimaging studies currently employ Pearson cross-correlations of hemodynamic or electrophysiological time courses. Unlike large-scale structural networks (which are thought to be stable on shorter timescales of seconds to minutes), functional networks are highly variable, exhibiting spontaneous dynamic changes during rest (Hutchison et al. 2013) as well as characteristic modulations in different task conditions (Cole et al. 2014).

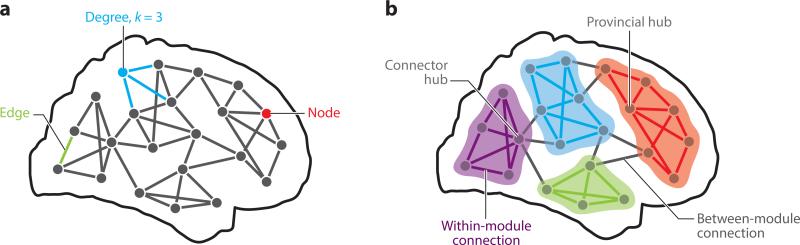
Figure 1.

Schematic diagram of a brain network introducing basic terminology. (a) Networks consist of nodes and edges. The node degree corresponds to the number of edges that are attached to each node. (b) Networks can be decomposed into communities or modules. Connections (edges) are either linking nodes within modules or between modules. Highly connected nodes are hubs, and they either connect primarily with other nodes in the same community (provincial hub) or with nodes that belong to different communities (connector hub).

Network Analysis and Modularity

Modules are encountered across a broad range of networks. They may correspond to groups of individuals in social networks, ensembles of interacting proteins, or coregulated genes in cellular networks. In this article, the term module refers exclusively to building blocks in the organization of brain networks; this usage of the term is distinct from concepts like modularity of mind in cognitive theory (Fodor 1983). Modules in networks, generally speaking, correspond to clusters of nodes that are densely connected, also called network communities (Figure 1b). Modules derive from a decomposition of the network into subcomponents that are internally strongly coupled, but externally only weakly coupled. This near-decomposability has long been regarded as a hallmark of complex systems (Simon 1962). Importantly, modules can be detected in a purely data-driven way, based only on the topology of the network, and understanding which nodes belong to which modules can yield important insights into how networks function. Although network modules seem to be easy to define, their detection presents significant obstacles and is subject to several misinterpretations and biases.

Outline of Article

First, we survey various methods for detecting modules in brain networks, evaluate their advantages and shortcomings, and discuss some practical issues. We then review the evidence for the existence of modules in both structural and functional brain connectivity data sets. Finally, we briefly consider the potential functional roles of modules from a variety of perspectives, including brain evolution, wiring minimization, and the emergence of functional specialization and complex dynamics.

METHODS FOR MODULE DETECTION

The notion of module detection refers to a collection of methods used to uncover a network's latent community structure. Most of the methods covered in this section use only the information encoded in a network's connectivity matrix to assess whether or not a network has modules/communities, and, if so, to which module each node should be assigned (for an encyclopedic review of many different approaches to module detection in networks, see Fortunato 2010). The terms community and module both refer to subnetworks that are embedded within a larger network and will be used interchangeably. A related term is partition, which refers to any division of network elements into communities. Although most module detection methods yield nonoverlapping communities, in which each network node belongs to one and only one module, it is possible in principle to partition a network into communities that overlap.

Modularity Maximization

A method for community detection that is widely applied in the detection of brain modules is known as modularity maximization. This method aims to partition a network's nodes into K nonoverlapping communities, C₁, . . . C_K, so as to maximize the modularity quality function, Q (Newman & Girvan 2004). Conceptually, a partition is considered high quality (and hence achieves a greater Q score) if the communities it defines are more internally dense than would be expected by chance. The partition that achieves the greatest value of Q, then, is taken to be a good estimate of a network's community structure. This intuition can be formalized as

$$Q=\frac{1}{2m}\sum _{ij}[a_{ij}-p_{ij}]\delta ({\sigma }_i,{\sigma }_j).$$

In this expression, a_ij represents the number of links between nodes i and j. The term p_ij stands in for the expected number of links according to a null model, whose precise form is left up to the user. The de facto null model is one that preserves each node's degree but otherwise allows connections to be formed at random. For an undirected network, this model gives an expected weight of $p_{ij}=\frac{k_i{k}_j}{2m}$, where $k_i={\sum }_j{a}_{ij}$ is a node's degree and $2m={\sum }_{ij}{a}_{ij}$ is the total number of connections in the network. The Kronecker delta function, δ(σ_i, σ_j), which is equal to unity when nodes’ community assignments, denoted by σ_i ∈ {1, . . . , K}, are the same and is zero otherwise, ensures that contributions to Q come only from the {i, j} where σ_i = σ_j, i.e., from pairs of nodes assigned to the same community. Whereas this description of Q is suitable for undirected networks, the form of the quality function Q can be easily adapted to work for weighted and directed networks (Leicht & Newman 2008).

The process of optimizing Q is known as modularity maximization and presents a challenge, because it is computationally intractable to exhaustively search the space of all possible partitions, even for small networks. To this end, many heuristics have been proposed to uncover partitions with large Q scores, with the hope of approximating the partition corresponding to the global maximum Q. These methods include divisive algorithms (Girvan & Newman 2002), spectral decomposition (Newman 2004), extremal optimization (Duch & Arenas 2005), greedy algorithms (Blondel et al. 2008, Clauset et al. 2004), and simulated annealing (Guimera & Amaral 2005), among others.

Modularity Maximization in Signed Networks

In human neuroimaging, functional brain networks are commonly estimated from the signed correlation matrix, r_ij, of hemodynamic time series. This matrix is often converted to a sparse positive-only matrix (amenable to standard graph analysis) by applying a threshold to retain coefficients r_ij ≥ τ. However, weak and negative correlations may reflect neurobiologically relevant patterns, in which case the thresholding step can offer only a partial view of the topology. In order to retain negative correlations and still use modularity maximization to define communities, the definition of a community must be slightly reformulated. In the context of signed networks, communities can be thought of as groups of nodes that are internally positively correlated but externally anticorrelated. The standard modularity function can be adapted and made consistent with this intuition by separately modeling the contributions of positive and negative correlations. To calculate such a modularity, it is useful to first define the matrices $r_{ij}^{+}$ and $r_{ij}^{-}$, which contain only positive and negative correlation coefficients, respectively, and satisfy the expression $r_{ij}=r_{ij}^{+}-r_{ij}^{-}$. The positive (+) and negative (−) modularities are then given by

$$Q^{\pm }=\frac{1}{2m^{\pm }}\sum _{ij}[r_{ij}^{\pm }-p_{ij}^{\pm }]\delta ({\sigma }_i,{\sigma }_j).$$

These signed modularities can be scaled and combined to represent the total modularity of the system (Gómez et al. 2009, Rubinov & Sporns 2011, Traag & Bruggeman 2009). The simplest formulation is

$$Q=\frac{2m^{+}}{2m^{+}+2m^{-}}{Q}^{+}-\frac{2m^{-}}{2m^{+}+2m^{-}}{Q}^{-}.$$

Here the positive modularity, Q⁺, which represents the excess of positive correlation coefficients within modules, serves to increase the total modularity. The negative modularity, Q⁻, which represents the excess of negative coefficients within modules, acts to decrease total modularity.

It is useful to note that, again, the precise form of the null model, $p_{ij}^{\pm }$, was left unspecified. Typically its value is given by the familiar expression $p_{ij}^{\pm }=\frac{k_i^{\pm }{k}_j^{\pm }}{2m^{\pm }}$, though some authors have proposed alternative models that may be more compatible with the Pearson correlation measure (Bazzi et al. 2014, MacMahon & Garlaschelli 2015).

Methodological Issues and Extensions of Modularity Maximization

Despite its widespread use, modularity maximization (and in some cases the enterprise of community detection, more generally) encounters a number of shortcomings that limit its practical applicability. Some of these shortcomings are mainly conceptual and relate to how one interprets the estimated community structure obtained by modularity maximization. In other cases, they represent fundamental limits of the measure itself.

Degenerate partitions

As a network's size and its number of communities increase, the number of partitions that achieve a near-maximal Q grows exponentially, leading to a degeneracy of high-quality partitions (Good et al. 2010). This degeneracy becomes especially problematic if the partitions are dissimilar to one another. In that case it becomes difficult to choose a single (“best”) representative partition. In fact, this is an issue shared by quality functions other than Q, some of which will be discussed in later sections. The issue may be addressed by expressing the optimal partition not as a single “best” partition but as a meaningful average across multiple near-optimal partitions, and by treating nodes’ community affiliations as fuzzy variables (Bellec et al. 2010, Rubinov & Sporns 2011) or characterizing them by probabilistic clustering (Hinne et al. 2014), rather than as hard assignments. Some practical guidelines for obtaining a consensus partition are discussed below.

Resolution limit and multiresolution modularity

Another methodological issue facing modularity maximization is that, under certain conditions, it may be impossible to detect communities below a certain scale (size), even if those communities are otherwise well defined (e.g., internally maximally dense). This problem is called the resolution limit of modularity (Fortunato & Barthelemy 2007) and arises from a trade-off between the number of communities into which a network is partitioned and the Q value associated with those partitions. At some optimal number of communities, this trade-off achieves a peak corresponding to the partition with the maximum value of Q. The location of this peak, however, is a consequence of how Q is formally defined and may not reflect the network's true community structure. In practical terms, the resolution limit implies that the communities obtained by simply maximizing modularity may contain several smaller and better-defined communities.

To circumvent the resolution limit issue, a number of multiresolution techniques have been proposed (Arenas et al. 2008, Reichardt & Bornholdt 2006). These techniques incorporate resolution parameters into the Q measure that can be tuned to uncover communities of different sizes. In the formulation of Reichardt & Bornholdt (2006), for example, the resolution parameter, γ, scales the importance of the null model:

$$Q\left(\gamma \right)=\frac{1}{2m}\sum _{ij}[a_{ij}-\gamma p_{ij}]\delta ({\sigma }_i,{\sigma }_j).$$

When γ < 1, larger communities are resolved, whereas γ > 1 yields more communities containing fewer nodes. It is important to note, however, that varying γ only makes it possible to detect communities of different sizes; it does not solve the issue of the resolution limit (Lancichinetti & Fortunato 2011). That is, for any value of γ, the resolution limit still exists, and at that level it remains impossible to detect communities of certain sizes.

A number of methods to choose the resolution parameter have been proposed. Many modularity maximization techniques contain a stochastic element, so that their output varies from run to run, as is the case for the method of Blondel et al. (2008) or simulated annealing. This means that in practice these algorithms should be run multiple times, thereby generating an ensemble of high-quality partitions. One suggested method for choosing γ takes advantage of the variability within a partition ensemble, reporting community structure at the value of γ at which partitions are most similar to one another (Bassett et al. 2013). The similarity of two partitions can be computed, for example, as the normalized mutual information, the Jaccard index, or the Rand index. However, because the precise values of these similarity measures are often difficult to interpret, it is good practice to use the z-scores, rather than the raw scores, of these measures (Traud et al. 2011). Alternative approaches for choosing γ include cross-validation using metadata or domain-specific knowledge. For example, Betzel et al. (2013) identified multiscale modules from brain structural networks, reporting the resolution at which the structural modules were most similar to brain functional connectivity. Alternatively, detailed comparison to an appropriately constructed null model can be used to select the γ at which community structure deviates most from what would be expected under the null model (Traag et al. 2014). In general, although many older studies of brain networks have not explicitly considered the resolution limit inherent in Q, it is now increasingly clear that exploring a range of γ values yields a more comprehensive view of a network's modular organization.

Multiresolution, multislice modularity

Brain networks are most often analyzed as single-slice networks, or snapshots, providing a picture of how one single instance of a network is configured. Although this approach may be appropriate in cases in which brain networks reflect static arrangements of nodes and edges (as in many anatomical networks or longtime averages of resting-state functional networks), it fails to capture situations in which the research objective is to compare modularity in networks collected across multiple time points, many individual participants, or different experimental conditions. A number of studies have begun to investigate multislice representations of brain networks (Bassett et al. 2011, 2013, 2015; Cole et al. 2014) in which multiple instances of a single network (a slice) form a multislice stack. If the connectivity in a single-slice network is encoded in the matrix, a_ij, the connectivity of a multislice network is given by a_ijs, where the additional subscript, s, indexes slices.

Given a series of network slices, it might be interesting to characterize community structure across slices. A naïve way to accomplish this is to maximize the modularity of each slice independently. This comparison, however, requires matching communities across slices, a process that often leads to ambiguities. An alternative approach for finding communities in multislice networks (Mucha et al. 2010) consists of introducing a coupling parameter that links corresponding nodes across slices and then using a quality function that extends Q(γ) multislice networks. The new quality function reads

$$Q(\gamma ,\omega )=\frac{1}{2\mu }\sum _{ijsr}[(a_{ijs}-{\gamma }_s{p}_{ijs})\delta ({\sigma }_{is},{\sigma }_{js})+\delta (i,j)\cdot {\omega }_{jrs}]\delta ({\sigma }_{is},{\sigma }_{jr}).$$

The expression (a_ijs – γ_s p_ijs)δ(σ_is, σ_js), with the exception of the slice subscript, s, corresponds to the summand in the single-slice version of multiscale modularity. The additional term, δ(i, j)·ω_jrs, defines the strength of coupling of nodes between slices. The other delta function, δ(σ_is, σ_jr), ensures that the {i, j, r, s} that fall outside of communities are not counted in the total summation.

One of the advantages of this method is that community labels are consistent across slices. In other words, nodes assigned to some community C, irrespective of the slice in which they appear, all reference the same community, which makes matching communities across slices unnecessary. As with multiscale modularity, there is the issue of how one should choose the parameters {γ, ω}. The choice is nontrivial and as yet there is no clear method for doing so. Bassett et al. (2013) advocated making detailed comparisons to null models (e.g., coupling node i to j ≠ i across slices) and focusing on the {γ, ω} pair corresponding to the maximum difference between some measure—e.g., the quality of the partition Q(γ, ω)—taken on the real community structure and the same measure taken on the communities obtained from the null model.

Participation coefficient

Once a network has been partitioned into modules, individual network nodes can be classified based on how they are embedded within and between communities. Two measures that have proven fruitful in this endeavor are a node's participation coefficient and the z-score of its within-community degree (Guimera & Amaral 2005). The participation coefficient, p_i, expresses the degree to which a node's connections are distributed across communities. If its value is close to unity, the node's connections fall uniformly across all communities; if its value is close to zero, most of its connections fall within a single community. The z-score of a node's within-community degree, z_i, expresses the number of connections a node makes to other nodes in the same community in terms of standard deviations above or below the mean. Positive z-scores indicate that a node is highly connected to other members of the same community; negative z-scores indicate the opposite.

Guimera & Amaral (2005) suggested that nodes’ functional roles could be gleaned from the combination of p_i and z_i. The first distinction is between nodes that serve as hubs and those that are considered part of the network's periphery (nonhubs). Intuitively, hub nodes make disproportionately more connections to nodes within their own module compared to peripheral nodes, and therefore correspond to nodes with the highest z_i. Hub nodes can be further classified according to the magnitude of their participation coefficient. As the value of p_i increases from zero to unity, a node's connections are distributed more uniformly across modules. The smallest participation coefficients identify provincial hubs whose connections are largely restricted to their own module. At the opposite extreme are kinless hubs, with connections in virtually all modules. Intermediate participation coefficients highlight connector hubs, whose links fall between a few different modules.

An appealing aspect of assigning roles to nodes based on module partitions is that this approach can be applied to both structural and functional networks, and it can reveal which nodes are especially important for maintaining intermodule communication. Alternative ways to express the relations of nodes across multiple modules include the measurement of regional connection diversity (analogous to the entropy of the node's module-by-module connection strengths), which can also be adapted for use with signed networks (Rubinov & Sporns 2011).

Alternatives to Modularity Maximization

Though modularity maximization is the most common method for identifying a network's communities, there are a multitude of alternative techniques. These alternatives present attractive opportunities for network neuroscience; however, only a subset has so far been applied to brain data. Here we review some of them.

Distance-based modules

One of the simplest methods for detecting modules in complex networks is to extend distance-based clustering techniques to be compatible with network data (Hastie et al. 2009). This method assumes that network nodes can be embedded in a high-dimensional space and that modules correspond to clusters near one another in that space. How distance in that space is measured is flexible, though one common choice is to set the distance of node i to j equal to d_ij = 1 – J_ij, where $J_{ij}=\frac{\mid {\mathbf{a}}_i\cap {\mathbf{a}}_j\mid }{\mid {\mathbf{a}}_i\cup {\mathbf{a}}_j\mid }$ is the Jaccard index and a_i is the connectivity profile of node i (i.e., the set of all other nodes it is connected to). In this case, the greater the overlap in nodes’ connectivity profiles, the closer they will be to one another. Given the complete set of pairwise distance relationships, modules can then be recovered using standard distance-based algorithms such as k-means or hierarchical agglomerative clustering. Although this process is simple, and deterministic in the case of hierarchical clustering, its definition of a community as a spatial cluster diverges from the intuition (inherent in modularity maximization) of communities as defined by internally dense connectivity.

Infomap

Another interesting class of community detection methods is grounded in information theory (Aldecoa & Marin 2011, Ronhovde & Nussinov 2009). The most commonly used is the Infomap algorithm (Rosvall & Bergstrom 2008), which casts community detection in terms of the path that a random walker traces as it hops from node to node, using connections as pathways to traverse the network. A random walk on a network defines a Markov chain whose states correspond to the network's nodes, where the transition probability from node i to j is given by ${\pi }_{i\to j}=\frac{a_{ij}}{k_i}$. If a random walker makes L steps, the sequence of nodes it visits is given as X = {x₁, . . . , x_L}, where x_t ∈ {1, . . . , N} is the node the walker visits at step t of the walk.

The aim of Infomap is to describe an infinite-length walk as succinctly as possible. A naïve approach would be to assign each node a name, with the shortest names reserved for the nodes that are visited most frequently. This strategy is usually suboptimal: Because each node needs a unique name to unambiguously describe the walk, the description tends to be long. The random walk can be described more succinctly by taking into account regularities in the process that generated X. Networks with communities, for example, introduce biases in random walks. If a walker starts in a community, it will likely dwell inside that community for many steps due to the preponderance of within-community connections. A more efficient description of the random walk takes this bias into account by using two separate lists of names: One list assigns communities unique names, whereas the other list is a reusable set of names reserved for nodes within communities. Using these lists along with an indicator that tells when the walker is entering a new community, one can describe the random walk much more efficiently (Rosvall et al. 2009). This intuition forms the basis of the Infomap algorithm. The same way modularity maximization uses Q to score the quality of a partition, Infomap scores partitions by their description length; the optimal partition is the one that can compress the description of a random walk by the greatest amount.

Block models

Community detection can also be recast as a statistical inference problem by fitting what are known as block models to network data (Carrington et al. 2005, Hastings 2006). A block model is an example of a network generative model, which makes assumptions about the process underlying a network's formation and estimates the likelihood that this process generated the network. In the simplest case, block models assume that all connections are made independent of one another, and that the probability of a connection forming between nodes i and j depends only on the communities σ_i and σ_j to which those nodes are assigned. Usually these community assignments and the intercommunity connection probabilities θ_rs, where r and s are different communities, are unknown and treated as free parameters. The aim of block modeling, then, is to reverse engineer the generative model by estimating those parameters for which the likelihood that the resulting block model generated a given network is maximized.

It may seem that the added complication of having to estimate θ in addition to nodes’ community assignments (not to mention the fact that the number of communities usually has to be specified ahead of time) makes block modeling unattractive. However, block modeling actually offers more flexibility than other community detection methods, because it can identify more diverse architectures than the standard community definition of internally dense and externally sparse groupings of nodes. These architectures include core-periphery and bipartite organizations. As an example, consider the following intercommunity connection probability matrix:

$$\theta =\left[\begin{array}{cc}\hfill 0.8\hfill & \hfill 0.2\hfill \\ \hfill 0.2\hfill & \hfill 0.8\hfill \end{array}\right].$$

If we generated synthetic networks using this matrix as a template, we would expect that virtually any community detection method would be able to resolve the two communities, given that the two communities are clearly defined through their internally dense connections.

Contrast this with another example of a network with a dense core and sparse periphery:

$$\theta =\left[\begin{array}{cc}\hfill 0.8\hfill & \hfill 0.2\hfill \\ \hfill 0.2\hfill & \hfill 0.1\hfill \end{array}\right].$$

In this case, the first group is still community-like, but nodes in the second group are more likely to make connections to nodes in the first group than to nodes in their own group. Approaches such as modularity maximization or Infomap, if applied to synthetic networks generated using this set of parameters, would fail to deliver anything resembling the matrix θ. A block model, instead, easily detects this type of organization. In general, block models can be used to detect more varied types of communities than most other methods because the definition of communities is not prespecified, but rather inferred from the network data and encoded in the elements of θ.

Overlapping communities

All the community detection methods that have been reviewed to this point partition networks into nonoverlapping communities. An alternative set of methods returns overlapping communities, so that nodes can be affiliated with more than one subnetwork simultaneously. Clique percolation is one of the earliest methods for identifying overlapping communities (Palla et al. 2005). This method is based on the intuition that communities tend to be comprised of cliques, that is, fully connected subgraphs. To identify communities, all cliques of a fixed size k must first be enumerated, and a clique adjacency matrix is constructed. Two cliques are considered adjacent if they share k – 1 nodes. Communities correspond to the connected components of the clique adjacency matrix. Because nodes can participate in multiple cliques, mapping the communities from the clique level back to the node level may result in nodes being assigned to multiple communities.

Another set of methods for detecting overlapping communities involves transforming a network into its corresponding line graph. Nodes in a line graph represent connections in the original network. Line graph nodes are connected to one another if the corresponding connections share a node in the original network. For example, if {h, i} and {i, j} are edges in some network, they would be linked in that network's line graph because they are both incident on node i, whereas {h, i} and {j, k} would not. There exist several similar approaches for using a network's line graph to obtain overlapping communities. The simplest approach is the one advocated by Evans & Lambiotte (2009), which assigns weights to the connections via a normalization step and then applies nonoverlapping community detection methods (e.g., modularity maximization) to the resulting line graph's connectivity matrix. When the resulting edge communities are mapped back to nodes, nodes may have multiple community affiliations.

A second approach for clustering a network's line graph, proposed by Ahn et al. (2010), weights line graph connections according to their similarity (Jaccard index). Line graph nodes are aggregated into communities using agglomerative hierarchical clustering, and the hierarchical tree is cut at a level that maximizes the partition density quality function, which is the average density of connections within communities, weighted by the size of each community. Interestingly, partition density does not suffer from a resolution limit.

Independent component analysis

In the neuroimaging literature, an important technique for uncovering communities from functional data is independent component analysis (ICA) (Beckmann & Smith 2005, McIntosh & Mišić 2013). ICA assumes that voxels’ time series are linear combinations of a smaller set of archetypical time series. Unlike the similar technique of principal component analysis, in which the archetypes are both spatially and temporally independent, ICA yields archetypes that are maximally independent in one or the other domain. If one specifies spatial independence, the result is a loading of voxels onto minimally overlapping spatial archetypical patterns, which can be interpreted as communities. Interestingly, the patterns obtained from clustering or performing community detection on functional magnetic resonance imaging (fMRI) functional connectivity networks are often quite similar to those obtained with ICA (Bellec et al. 2010, Power et al. 2011, Yeo et al. 2011). In contrast to network-based approaches to modularity, ICA requires the user to select a desired number of components (i.e., a model order) and provides no information about how these components are related (e.g., through between-module connections).

Practical Issues in Module Detection

To this point we have discussed a number of popular community detection methods, emphasizing those that have been applied to brain data. In doing so, we necessarily omitted many methods that may yet prove useful in network neuroscience, including several based on random walks (Delvenne et al. 2010, Pons & Latapy 2005), belief propagation (Zhang & Moore 2014), and phase synchronization (Boccaletti et al. 2007). This section is concerned with practical issues related to community detection (see example in Figure 2), specifically the choice of method for module detection, and with the significance and robustness of module partitions.

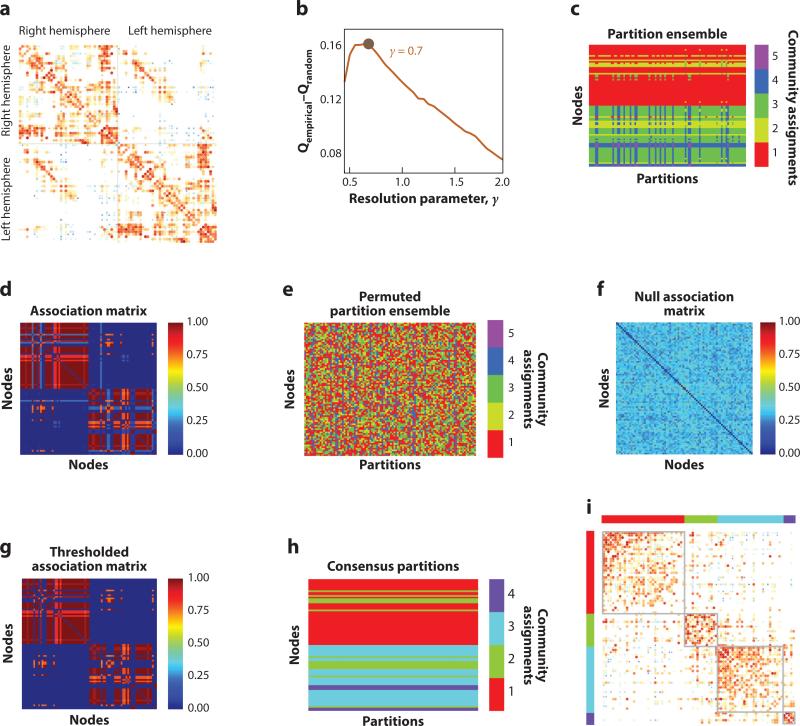
Figure 2.

Illustration of multiscale modularity maximization for a structural (diffusion spectrum imaging) brain network (a). The size and brightness of connections indicate the number of subjects for which a connection is present and the log-transformed weight of that connection, respectively. For this network and for 20 random networks (rewired to preserve degree sequence), we maximized modularity using the Louvain algorithm (Blondel et al. 2008) and varied the resolution parameter from γ ∈ [0.5, 2.0] in increments of 0.05. As a function of γ, we obtained the mean modularity for the empirical and randomized networks, Q_empirical and Q_random. To report community structure, we chose the scale of γ at which the quality of empirical partitions exceeded that of random partitions by the greatest amount (b). At this scale (γ = 0.7) we further examined 100 partitions of the empirical network (c), which revealed that nodes’ community assignments were inconsistent. To resolve this variability, we performed consensus clustering, following Bassett et al. (2013) and Lancichinetti & Fortunato (2012). We constructed the association matrix (d) counting the number of times that node pairs were assigned to the same community. We generated many realizations of null partition ensembles by randomly permuting the columns of the partition ensemble matrix (e) and constructed null association matrices (f). We thresholded the empirical association matrix (g), retaining only elements greater than the maximum value of any null association matrix. We then reclustered the thresholded matrix to obtain consensus communities (h). Finally, we visualized community structure by reordering the connectivity matrix so that nodes in the same community would be next to one another (i).

Choice of method

The choice of method for detecting communities first depends on how network communities are conceptualized. Are communities taken to be groups of tightly connected nodes? Do they represent groups with similar connectivity profiles? Can nodes belong to more than one community? Another factor influencing the choice of method is the nature of the neurobiological data and the empirical question that is being explored. For example, signed correlation matrices derived from functional connectivity may require approaches that can deal with signed connections (unless only positive connections are deemed of interest). Similarly, a research question dealing with the time evolution of networks strongly suggests multislice approaches. These conceptual data- and research-driven considerations motivate the use of certain methods while excluding others and should be carefully examined before beginning community detection.

An important factor for choosing a method is how well community detection algorithms perform in identifying planted communities in synthetic benchmark networks. A benchmark network usually contains multiple clusters of nodes that can be made more or less community-like by tuning a parameter that controls the ratio of within-cluster to between-cluster connections. The best benchmark networks also incorporate as many properties of real-world networks as possible, for example, heterogeneous degree distributions and communities of different sizes (Lancichinetti et al. 2008). Several recent studies have undertaken the task of benchmarking community detection methods, including many of those surveyed here (Danon et al. 2005, Lancichinetti et al. 2009). Interestingly, these studies report a stratification of community detection methods, with some clearly outperforming others in terms of both computational complexity and the ability to successfully identify communities in benchmark networks. The more recent study (Lancichinetti et al. 2009) found that Infomap, a modularity maximization algorithm (Blondel et al. 2008) and a multiresolution algorithm that maximizes a quality function similar to Q (Rondhove & Nussinov 2009), performed the best across all test cases. (The algorithm by Blondel et al. returns a hierarchy of communities; the lowest level of hierarchy—i.e., the smallest communities—was used to benchmark the algorithm.) It should be noted that the benchmark networks used in these tests lacked some important features typically found in real-world networks (e.g., hierarchical communities).

Consensus communities

Given that different methods have sometimes complementary strengths or weaknesses, it may be advantageous to combine the outputs of multiple methods (or multiple runs of a single method to address degeneracy of module partitions) to obtain average or consensus communities. One approach for doing so is to generate and iteratively cluster a network's association matrix through a process called consensus clustering. Given an ensemble of partitions acquired from several community detection methods (or multiple runs), the association matrix is an n × n matrix whose element t_ij counts the number of times that nodes i and j are assigned to the same community across the full ensemble. To obtain consensus communities, one can simply recluster the consensus matrix using the same community detection algorithms that generated the original ensemble of partitions. To amplify the contribution of node pairs that are consistently assigned to the same community while silencing those that are not, researchers often impose a threshold on the consensus matrix prior to reclustering, setting any elements t_ij < τ equal to zero. Lancichinetti & Fortunato (2012) advocated exploring a range of thresholds, because smaller or larger values of τ may produce correspondingly larger or smaller consensus communities. Alternatively, one can choose τ in a data-driven way by comparison with a postoptimization null model. Bassett et al. (2013) suggested setting the threshold equal to the maximum value of a randomized association matrix, $t_{ij}^r$, constructed by permuting the node order of each partition in the ensemble and generating an association matrix from the randomized partitions. In any case, the partitions obtained after reclustering the thresholded consensus matrix are usually more similar to one another than are the partitions used as input, and they often converge into a single consensus partition. Another approach that does not require thresholding involves finding the partition that maximizes the modularity $Q={\sum }_{ij}[t_{ij}-t_{ij}^r]\delta ({\sigma }_i,{\sigma }_j)$, where $t_{ij}^r$ is the mean association weight across an ensemble of randomized association matrices. As an alternative to consensus clustering, one can also calculate, for every partition in an ensemble, its mean similarity with respect to all other partitions and choose as the consensus partition the one with greatest average similarity (Doron et al. 2012).

Statistical significance and robustness

Once a network's community structure has been estimated, there remain some challenging technical and theoretical questions. For instance, how “good” do the communities have to be before we can confidently say that a system is modular? It is important to remember that most module detection methods will converge on module partitions even for random networks.

There are multiple ways of addressing this question. One approach consists of comparing the quality of the community structure estimated from the empirical network with the same measure made on an ensemble of totally random networks (e.g., preserving the degree sequence of the original network, but otherwise randomizing the placement of connections). For example, comparison of the estimate Q for the empirical network to 〈Q_random〉 and $\langle Q_{\text{random}}^2\rangle -Q_{\text{random}}^2$ obtained from an ensemble of random networks can yield a z-score, $Q_z=\frac{Q-\langle Q_{\text{random}}\rangle }{\sqrt{\langle Q_{\text{random}}^2\rangle -Q_{\text{random}}^2}}$. There are some issues with this approach, as certain classes of networks can be more modular than chance without possessing any true community structure (e.g., lattice networks), whereas there are networks with a clear community structure but whose overall Q is not statistically different than chance (Karrer et al. 2008). Nonetheless, Q_z can provide some general indication as to whether a system is, indeed, modular.

Another approach, known as robustness testing, entails adding a small amount of noise to the community detection process to induce change in a network's community structure (Gfeller et al. 2005, Karrer et al. 2008, Wu & Huberman 2004). Intuitively, the estimates of community structure for networks with well-defined communities will be similar both pre- and postperturbation, whereas networks with ill-defined or brittle communities are more likely to experience larger changes in their estimated community structure or in the quality of communities following the perturbation. The perturbations can be subtle—e.g., rewiring a small fraction of connections, adding noise to the network's edge weights, shuffling edge weights, changing by a small amount the scale of a resolution parameter, or using an altogether different quality function. This approach has a number of downsides. For instance, it requires that the community detection process be repeated multiple times for each perturbation tested, which may be time consuming. It also introduces several free parameters, such as the number of edges to be rewired, the nature of the noise added to the edge weights, or the amount of variation in the resolution parameter. Despite these issues, robustness testing represents a powerful method for teasing apart the aspects of a network's community structure that are fragile in the presence of noise.

The approaches described above entail comparing estimates of a network's community structure to estimates made on a null (or noisy) model in an effort to determine whether those communities are statistically significant or robust to perturbations. Another set of methods attempts to detect ab initio only the most statistically significant communities. One such method is OSLOM (Order Statistics Local Optimization Method) (Lancichinetti et al. 2011), which scores communities based on how likely it is to find a community with similar properties in a random network with no community structure (Lancichinetti et al. 2010). OSLOM identifies significant communities using a growing-pruning model in which a community's statistical significance is assessed after both adding new nodes and pruning existing ones. Because communities are detected using only local information, this method does not suffer from a resolution limit, and it also allows for communities to overlap. OSLOM is also unique in that it can detect no communities in the event that no possible grouping results in a statistically significant community. This is the outcome one would expect if OSLOM were given a totally random network as its input. OSLOM also makes another unique contribution, in that it detects communities using only the local properties of a network. Other approaches, like modularity maximization, pursue global optimization strategies; this entails that, if new nodes were added to a given network, the overall community structure would likely change, whereas with OSLOM this is typically not the case.

EVIDENCE FOR MODULES IN BRAIN NETWORKS

The focus of the previous section was on the methods and technical challenges associated with detecting communities in complex networks. We now turn to a brief review of the empirical evidence for modularity in brain networks.

Brain Networks in Model Organisms

Significant evidence for modularity in neural systems comes from the anatomical neural networks of model organisms such as the nematode Caenorhabditis elegans and various mammalian species. Brain networks of model organisms are generally mapped using various techniques, including reconstruction from serially sectioned electron micrographs (White et al. 1986) or the aggregation of data from anatomical tract-tracing experiments (Kötter et al. 2004, Markov et al. 2014, Oh et al. 2014, Scannell et al. 1995, Stephan et al. 2001).

The neuronal network of C. elegans contains more than 300 neurons and several thousand electrical and chemical synapses. Since its reconstruction in the early 1980s (White et al. 1986), this network has been the subject of many graph-theoretical analyses (Varshney et al. 2011), including several that have attempted to elucidate its division into communities. These studies have employed a wide range of methods for uncovering C. elegans’ community structure, including modularity maximization (Bassett et al. 2010, Sohn et al. 2011, Towlson et al. 2013), simulated annealing (Sohn et al. 2011), divisive algorithms (Towlson et al. 2013), and spectral decomposition (Jarrell et al. 2012, Pan et al. 2010, Sohn et al. 2011) as well as stochastic block models (Pavlovic et al. 2014), Infomap, and link-clustering (Jarrell et al. 2012). Despite the varied approaches to community detection, the results of these analyses largely converge in that the resulting communities resemble, at some level, the functional organization of the C. elegans’ nervous system. For example, Jarrell et al. (2012) analyzed the subnetwork of neural circuitry and musculature involved in mating. Among the communities uncovered in this analysis were groups of sensory neurons and interneurons for detecting the mate's vulva and initiating a motor response, along with another group of mostly motor neurons associated with locomotion. Analyses of the complete C. elegans network have reported similar results, with communities revealing known functional groups (Pan et al. 2010, Sohn et al. 2011) or novel network properties, such as cores (Pavlovic et al. 2014), the roles of hub nodes (Towlson et al. 2013), and the hierarchical organization of communities nested within communities (Bassett et al. 2010, Sohn et al. 2011).

Similarly, meta-analytic cortical networks for both the cat and the macaque (Felleman & van Essen 1991, Scannell et al. 1995) have been described as modular by Hilgetag et al. (2000). These early analyses predated the Q quality function, so the authors developed their own module detection approach called optimal set analysis (OSA). When applied to the cat cortical network, OSA returned four prominent clusters corresponding to visual, auditory, frontolimbic, and somatosensory areas. Corresponding clusters were detected in the macaque cortex, with the visual cluster subdivided into dorsal and ventral streams. Using the cat data set, Zamora-Lopez et al. (2010) discovered that a small number of hub regions extend connections across community boundaries to other hub regions, forming a higher-level community situated on top of the four communities detected by Hilgetag et al. (2000). Confirming these earlier findings, de Reus & van den Heuvel (2013) have described specific patterns of directed connections that interlink hubs and network communities in cat cortex.

More recently, using a different macaque data set, researchers have detected a slightly different set of communities using modularity maximization and taking the partition with the highest Q (Harriger et al. 2012, Modha & Singh, 2010). These communities were largely the same as in Hilgetag et al. (2000), though the frontolimbic community was now fractured into two communities. Using yet another (incomplete) macaque data set, Goulas et al. (2015) maximized Q (again treating the partition with the highest Q as the optimal partition), which returned five communities, corresponding roughly to parieto-motor, occipito-temporal, temporal, frontal, and somato-motor communities. Anatomical modules that map onto functionally related network nodes have also been identified in the Drosophila (Shi et al. 2015), mouse (Wang et al. 2012), and rat (Bota et al. 2015) brain. In general these studies, together with community analyses of the cellular network of C. elegans, support the notion that brain networks are organized into communities whose boundaries largely agree with known functional subdivisions.

Despite their generally converging results, these efforts also have shortcomings. Nearly all of these references optimized single-scale modularity to uncover communities, reporting only the partition corresponding to the observed maximum Q. Given the resolution limit associated with Q and the near-degeneracy of solutions, future studies would benefit from performing detailed comparisons against null models, expressing communities not as hard assignments but as fuzzy assignments over an ensemble of partitions, or testing the robustness of the observed communities to network perturbations.

It is interesting to note that most of the studies discussed here report communities whose members (neurons or brain regions) are spatially contiguous. In other words, nodes assigned to communities are not only densely connected, but also spatially proximal to one another. On the one hand, spatial contiguity is consistent with the hypothesis that neural systems attempt to reduce total metabolic and material cost by preferentially forming short-range connections, a well-documented aspect of the C. elegans nervous system (Chen et al. 2006, Cherniak et al. 2004, Nicosia et al. 2013). Indeed, the spatial compactness of anatomical communities may reflect an evolutionary drive to place functionally related neural elements near one another, thereby reducing the total cost of wiring. On the other hand, a system that strictly minimizes wiring cost will tend to form a geometric lattice, which can give the impression of comprising communities because it possesses a greater Q score than chance, although in fact it has no true community structure (Henderson & Robinson 2013, Samu et al. 2014). If this is the case, then observed communities may be a reflection of spatial clustering and not functional relatedness of neurons.

Thus, a network's spatial embedding can confound the interpretation of its communities. In effect, it introduces ambiguity about the process under which the communities were generated: Does the density of internal connections reflect spatial or functional relationships? If one is using modularity maximization for community detection, this issue can in part be addressed by modifying the connectivity null mode, p_ij, so that the expected density of connections depends on distance (Expert et al. 2011). Maximizing such a quality function returns communities whose internal density of connections exceeds what is expected given not only the nodes’ degrees but also the internode distances within those communities.

So far, the majority of network studies in animal models have focused on anatomical connectivity. The availability of large-scale cellular-resolution recording methods will soon provide data sets that are amenable to the detection of functional modules in dynamic brain activity. For example, clusters of highly correlated brain regions can be derived from optical recordings of neural activity (Ahrens et al. 2013) or from spike time series on multielectrode arrays (Shimono & Beggs 2015). In general, network-based module detection methods are important tools for dimension reduction and compact descriptions of functional neuronal assemblies in animal recordings.

Human Brain Networks

Unlike the anatomical networks discussed in the previous section, networks of the human brain are estimated noninvasively, usually using MRI technology. The indirect manner in which these data are acquired raises questions about the sensitivity and reliability with which human brain networks can be mapped, issues that are extensively covered in the extant neuroimaging literature. Nonetheless, the fact that neuroimaging can be performed in vivo on cognitively engaged individuals makes these methods indispensable for investigating how human brain networks relate to brain function and behavior. Here we briefly review what has been learned to date about the modular organization of the human brain. We will leave aside an extremely active research area focusing on disturbances of modular organization in the context of clinical disorders (Alexander-Bloch et al. 2012, Fornito et al. 2015), because even a cursory overview of this topic is far beyond the scope of the present article.

Anatomical networks

Despite considerable methodological differences, human brain networks share many of the same properties with those of model organisms, including community structure. The study by Hagmann et al. (2008), one of the first to note this, used spectral decomposition to maximize Q, which yielded six spatially contiguous communities: two positioned medially over the posterior cingulate cortex and precuneus and two pairs of bilaterally symmetric communities centered on the frontal and temporoparietal cortex. Highly connected brain regions situated along the midline formed links to multiple communities and served as connector hubs, whereas regions within the more lateral communities maintained most of their connections within their own community, thus forming provincial hubs. These results were expanded upon in recent work showing that hub regions, in particular those that are densely interconnected as part of the human brain's anatomical rich club, are located at the interface of many functional resting state networks and may play an important role in regulating information flow (van den Heuvel & Sporns 2011, 2013). As in analyses of modules in model organisms, findings from human studies again indicate a close correspondence of membership in structural modules with functional relations expressed across different domains of behavior and cognition.

As noted above, Q suffers from a resolution limit, the effects of which can be partially mitigated by exploring the range of communities encountered upon varying a resolution parameter. Two recent papers examined the multiscale organization of human anatomical networks by varying the resolution parameter in the multiscale modularity generalization (Lohse et al. 2014) and by recasting community detection in terms of a random walker moving over the network at different timescales (Betzel et al. 2013). Both studies reveal interesting community-level organization at multiple scales. Lohse et al. (2014) found that community radius, a measure of the spatial compactness of communities, increased the community size, a relationship that would be absent in a network with inefficient spatial embedding. Furthermore, they demonstrated that the way specific variables fluctuated as a function of the resolution parameter was useful for identifying whether a subject was diagnosed with schizophrenia or was part of a control population. Betzel et al. (2013) detected communities by maximizing the partition stability quality function (Delvenne et al. 2010) and looked for the resolution parameter for which the relationship between the structural communities was most predictive of brain functional connectivity. Interestingly, the scale at which this relationship peaked was far from the default scale, further motivating the exploration of multiscale community structure.

Functional networks

Community detection can be readily applied to brain functional networks, though some care must be taken in matching the community detection method to the method used for estimating functional connections. For example, if a functional network is estimated using full (Pearson) or partial correlation as the measure of connectivity, then there may be many connections with negative weights. Very few community detection methods, other than the signed variant of Q, are capable of dealing with negative edge weights. Although most studies remove negative correlations (by thresholding) from the analysis, it should be noted that this step may inadvertently discard neurobiologically relevant information. Alternative non-negative measures of functional connectivity like coherence or mutual information allow the use of any community detection method that can handle weighted connections.

Numerous studies have shown that the brain is organized into clusters or modules of functionally interconnected regions (Meunier et al. 2009b) with reproducible boundaries and that resolve subject-specific aspects of the brain's intrinsic functional organization (Laumann et al. 2015). One of the best examples of community structure in brain functional networks (Power et al. 2011) extracted communities from resting-state fMRI data and, using a map of task-based activations, mapped these communities to cognitive/behavioral function. An outstanding feature of this study is its use of multiple methods for detecting communities (Infomap and modularity maximization). Comparison of these methods showed significant agreement but also small differences in partitions obtained using Infomap versus those obtained using modularity maximization. Analysis of the relation between network communities and cognitive/behavioral function revealed some interesting features of communities obtained from functional brain networks that were not usually present in structural brain networks. In functional networks, connections correspond to statistical relationships between brain regions rather than physical linkages, and therefore carry no direct metabolic or material cost. Thus, there is no obvious penalty to forming strong long-distance functional connections. Accordingly, many of the communities observed in brain functional networks are spatially distributed. For example, Power et al. (2011) identify large communities corresponding to the default mode network and to the frontoparietal control, dorsal attention, and ventral attention networks, each of which are made up of multiple spatially remote components.

Another study, rather than directly measuring functional connectivity, relied on a meta-analytic approach for building brain coactivation maps (Crossley et al. 2013). In this case, the authors used the thousands of images detailing the foci of task-based brain activations available in the database BrainMap (Laird et al. 2005), along with the conditions under which those activations were reported. Regions that became active under similar task conditions across a range of tasks were considered adjacent to one another in a coactivation network. This network is different from most functional networks in that the connections represent coactivation rather than correlations among time courses, and in that the data are derived from task-evoked rather than resting brain activity. Modularity maximization yielded four communities corresponding to four behavioral domains: emotion, perception, action, and mixed. A parallel analysis carried out on a resting-state functional connectivity network revealed similar communities, confirming earlier work on the similarity of task-evoked and resting brain networks (Smith et al. 2009).

These studies demonstrate that module detection is important for mapping the basic functional organization of resting and task-evoked connectivity. Going beyond these relatively static descriptions of functional brain modules, modularity can also reveal characteristic changes in functional networks in the course of changes in an individual's cognitive state (Andric & Hasson 2015, Godwin et al. 2015) or with aging (see sidebar Functional Modules Across the Human Lifespan). Such changes in network architecture have also been documented over the course of a motor learning paradigm (Bassett et al. 2011, 2013). In the first of these studies (Bassett et al. 2011), subjects were asked to respond to particular visual stimuli with a specific motor action. The researchers repeated this analysis three times over the course of three days. Subjects were also scanned during the task, which allowed the authors to extract hemodynamic time courses from different brain regions and to construct functional brain networks. Each scan session was divided into a series of nonoverlapping blocks, and for each block a functional brain network was constructed. Rather than estimating community structure for each block independently, the authors made use of the multiscale, multislice variant of Q, which allowed them to track the affiliation of brain regions to specific modules over the course of time. Using a novel measure called flexibility, which counts the number of times that a node changes its module affiliation from one slice to the next, the authors discovered that with practice, flexibility varied. From the first experimental session to the second, flexibility increased on average, whereas the opposite was true moving from the second to the third session. Interestingly, flexibility was also predictive of the overall learning rate. In general, subjects whose community structures were more flexible over time (brain regions moved between modules) learned at a greater rate than those whose flexibility was low (brain region community assignments were relatively static across time).

In a second study (Bassett et al. 2013) using a similar learning paradigm, the authors investigated which brain regions were flexible and which were not. What they found was a relatively inflexible set of core regions, comprised mostly of visual and sensorimotor areas, which formed cohesive modules that were relatively fixed over time. Higher-order association areas tended to be more promiscuous, in the sense that they changed their module allegiance more often. These observations support the notion that the brain exhibits a kind of core-periphery organization. Importantly, static estimates of community structure are incapable of revealing this type of organization, which can only be revealed by examining the time evolution of communities.

FUNCTIONAL ROLES OF MODULES

Modularity is a general hallmark of complex biological systems. Potential functional roles of modules have been considered across multiple different biological domains, from evolution and development to metabolism and information processing. Here we outline potential roles for modular brain networks in promoting evolvability, conserving wiring cost, and in creating specialized information and complex dynamics.

Evolution and Development

An important idea in evolutionary theory is that modularity in the organization of biological systems confers significant advantages in an evolutionary setting, by supporting adaptability and robustness and thus increasing the system's evolvability (Kirschner & Gerhart 1998). From an evolutionary perspective, uniformly strong interdependence of biological processes may be undesirable, because changes to single components would tend to have widespread (and generally maladaptive) consequences. Keeping the system largely compartmentalized would limit the interdependence of processes that are part of different modules and thus promote greater resilience in the context of continuous genetic and developmental changes. Modularity has also been demonstrated to promote adaptation and increase flexibility in response to a changing environment (Kashtan & Alon 2005, Kashtan et al. 2007). In the face of unpredictable endogenous or exogenous changes, swapping or rearranging maladaptive modules is less costly than redesigning the entire system. In a similar vein, Ellefsen et al. (2015) demonstrated that modular brain networks can help prevent catastrophic forgetting, that is, the loss of a previously learned skill upon learning a new one.

A second benefit of modular organization is increased robustness in response to sudden perturbations. In modular system architectures, the effects of local perturbations remain largely confined to the module within which they originate (and this is used for detecting modules with methods like Infomap). In a sense, modules allow a system to buffer the effects of randomly introduced fluctuations. These fluctuations may be internally generated (e.g., stochastic noise in neural activity) or externally triggered (e.g., as a result of environmental stimulation). In genetics, such external fluctuations could relate to the effects of cryptic genetic variation, which uncovers novel phenotypes under conditions of environmental change (Gibson & Dworkin 2004), thus potentially promoting increased robustness. Taken together, there are many reasons to view modularity as essential for the generation of stable heritable variation and for the emergence of new solutions to unanticipated changes in the environment.

Conservation of Wiring Cost

The evolutionary and developmental benefits of modular organization beg the question of how or why modularity itself evolved. Clune et al. (2013) have argued that the adaptive advantages of modularity, for example, in yielding a more flexible system design, may not be sufficiently strong or direct to explain the modularity currently observed in biological organisms. Instead, they argue that modularity has evolved as a by-product of strong selection pressure on reducing the cost of connections in networks. Indeed, the notion that wiring cost is a major constraint on the layout of (structural) brain networks has a long history in neuroscience. Wiring cost has many dimensions, from the physical volume occupied by the wiring, to the processing cost imposed by conduction delays, to the metabolic cost of supporting neuronal processes and synapses (Bullmore & Sporns 2012). Modular architectures can help conserve wiring cost if modules are spatially compact, as indeed appears to be the case for modules in most, if not all, structural brain networks. The role of cost conservation in generating modular brain architectures has also been demonstrated in an analysis of the anatomical networks of C. elegans and the macaque cerebral cortex (Chen et al. 2013). In addition to the spatial layout of nodes, specific functional constraints, for example, on the network's processing efficiency, were found to be important as well, supporting the idea that brain network topology is shaped by a trade-off between spatial and functional factors (Bullmore & Sporns 2012).

Information and Complex Dynamics

Another driving force for the emergence of modular organization in brain networks may be related to neural processing that is specialized and unfolds on multiple timescales. In molecular regulatory pathways, modularity has been shown to promote specialization (Espinosa-Soto & Wagner 2010), and it has been suggested that the persistence of modular organization cross-linked by long-distance weak ties is crucial for preserving functional specialization in brain networks (Gallos et al. 2012). Modular organization of brain networks shapes how information is distributed and processed: Regions that are functionally close and tend to share information are members of the same cluster or module. Modular networks allow for richer patterns of distribution of information than systems that are nonmodular. In a computational modeling study, Yamaguti & Tsuda (2015) have shown that evolutionary algorithms that aim to maximize bidirectional information transmission between neuronal populations favor the emergence of modular structures.

Modularity has a major role in constraining the dynamics of neural activity as well. For example, modular networks give rise to more complex dynamics than random networks (Sporns et al. 2000), and they promote metastability (Wildie & Shanahan 2012) and synchronizability (Arenas et al. 2006) as well as the separation of timescales (Pan & Sinha 2009). These effects are particularly evident in networks that exhibit hierarchical modularity, i.e., are characterized by the existence of modules-within-modules across multiple spatial scales (Kaiser et al. 2010). Network models suggest that hierarchical modularity is an important structural ingredient for enabling the dynamic regime of criticality (Rubinov et al. 2011), which is characterized by spontaneous and persistent fluctuations, long transients following perturbations, and high information transfer. The importance of modular brain networks for shaping brain dynamics is a strong motivation for ongoing empirical work examining changes in modularity associated with disturbances of brain function in clinical disorders (Fornito et al. 2015).

CONCLUSION

In this article, we provided an overview of methods for detecting modules in brain network data as well as a brief survey of studies that have examined modules in the structural and functional connectivity of animal and human brains and have illuminated their many potential functional roles. Module detection requires appropriate use of network and statistical tools and should avoid known confusions and biases, while including an assessment of the statistical significance and robustness of network partitions. Despite great heterogeneity in methods and statistical practices, virtually all studies across all species support the existence of modules in both structural and functional brain networks. Theoretical work points to the importance of modules for promoting stability and flexibility, conserving wiring cost, and enabling complex neuronal dynamics. As analytic methods mature and richer brain network data become available, the topic of modular brain networks will likely continue to evolve for many years to come.

FUNCTIONAL MODULES ACROSS THE HUMAN LIFESPAN.

Modules in functional brain networks are thought to represent groups of brain regions that are collectively involved in one or more cognitive domains. A number of recent studies have presented evidence suggesting that the brain becomes increasingly less modular (i.e., less segregated) with age. Meunier et al. (2009a) compared groups of younger and older adults, using single-scale modularity maximization to discover modules for both groups. The older group formed fewer modules containing groups of brain regions that, in the younger group, had formed distinct modules. Corroborating these results, Geerligs et al. (2015) compared populations of young and old participants, reporting a decrease in modularity, Q, driven by decreased internal connectivity within control, default mode, and somatomotor modules along with increased intermodule connections. Two recent studies have tracked the modularity of functional brain networks continuously with age. Chan et al. (2014) used communities defined in an earlier study (Power et al. 2011) and reported an overall decrease in segregation with age, an effect driven by both association and sensorimotor systems. Concurrently, and using a different definition of communities (Yeo et al. 2011), Betzel et al. (2014) reported decreased modularity with age in modules associated with cognitive control and attention.

SUMMARY POINTS.

1. Modularity is a key characteristic of structural and functional brain networks across species and scales.

2. The most widely applied method for module detection, modularity maximization, is subject to several biases and limitations that can and should be addressed through modifications in optimization and statistical techniques.

3. Important extensions to modularity maximization include the application of multislice approaches that can detect variations of modular organization across subjects or time points.

4. Alternative approaches like clique percolation, block modeling, and detection of overlapping communities offer attractive opportunities for more detailed analyses of brain networks.

5. Anatomical modules generally reflect functional associations among neurons and brain regions.

6. Structural modules are often spatially compact, whereas functional modules can be more widely distributed and fluctuate in relation to cognitive states.

7. Modular organization may confer increased robustness and more flexible learning, help to conserve wiring cost, and promote functional specialization and complex brain dynamics.

FUTURE ISSUES.

1. Sophisticated applications of community detection methods to brain data sets will uncover network modules with increasing emphasis on their significance and robustness.

2. Overcoming the resolution limit will allow mapping network modules across several scales and spatial resolutions.

3. Significant attention will be devoted to untangling the contributions of spatial embedding and functional specialization to the definition of network communities.

4. Multislice functional network approaches will reveal characteristic changes in modular architecture across time, for example, in the course of task performance and learning.

5. Module detection methods applied to cellular-resolution data from high-density functional recordings and/or microscale reconstructions of neuronal circuits will be instrumental for defining anatomical and functional microcircuits.

Network: a set of elements (nodes) and the pairwise interactions (edges) among those elements

Module: a subnetwork of densely interconnected nodes that is connected sparsely to the rest of the network

Modularity: the scoring of a partition according to whether the internal densities of its modules are greater or less than the expected density

Community structure: a partition that induces the division of a network into modules, usually such that no modules overlap

Community detection: a set of tools used for identifying a network's community structure based on its topology

Modularity maximization: a set of community detection methods aimed at uncovering partitions that maximize the modularity quality function

Partition degeneracy: the tendency for community detection algorithms to uncover partitions of nearly identical quality that nonetheless induce very different modules

Resolution limit: a shortcoming of the modularity function that under certain conditions prevents it from detecting small modules

Resolution parameter: a parameter that tunes the size and number of communities obtained from modularity maximization

Multislice network: a representation of a network as a series of slices, in which each slice represents a separate observation of the network

Participation coefficient: a measure that quantifies how evenly or unevenly a node's connections are distributed across a set of modules

Random walk: a traversal over a network where each step from one node to another is randomly chosen

Block model: model-based community detection method whose parameters are selected to maximize the likelihood that the model generated an observed network

Clique: a group of fully connected nodes

Line graph: network transformation in which edges in the original network are linked to one another if they share a node

Independent component analysis: a multivariate method usually applied to fMRI time series for identifying maximally independent spatial maps (modules)

Wiring cost: the material and metabolic expenditure associated with supporting an organism's neural wiring

Evolvability: the capacity of a system to generate useful variation that promotes adaptive evolution through natural selection

Hierarchical modularity: organization of a module into submodules, of submodules into sub-submodules, and so on

Criticality: state situated between complete randomness and order, a hallmark of which is the absence of a characteristic scale of description