Estimation of causal effects of binary treatments in unconfounded studies

Abstract

Estimation of causal effects in non-randomized studies comprises two distinct phases: design, without outcome data, and analysis of the outcome data according to a specified protocol. Recently, Gutman and Rubin (2013) proposed a new analysis-phase method for estimating treatment effects when the outcome is binary and there is only one covariate, which viewed causal effect estimation explicitly as a missing data problem. Here, we extend this method to situations with continuous outcomes and multiple covariates and compare it with other commonly used methods (such as matching, subclassification, weighting, and covariance adjustment). We show, using an extensive simulation, that of all methods considered, and in many of the experimental conditions examined, our new ‘multiple-imputation using two subclassification splines’ method appears to be the most efficient and has coverage levels that are closest to nominal. In addition, it can estimate finite population average causal effects as well as non-linear causal estimands. This type of analysis also allows the identification of subgroups of units for which the effect appears to be especially beneficial or harmful.

1. Introduction

1.1. Overview

The goal of many studies in biomedical and social science is to estimate the causal effects of a binary treatment W on an outcome Y. Although randomized trials are the gold standard for inferring causal effects, in many settings, they may be impractical because of financial, logistical, or ethical considerations, and researchers are forced to use non-randomized observational studies, where it is difficult to attribute differences in outcomes to differences in treatments received because baseline characteristics that influence treatment decisions also influence the outcomes.

To overcome this issue, observational studies first should be designed to approximate randomized experiments as closely as possible and second should be analyzed using a predefined estimation procedure [1]. These two phases are commonly referred to as the design phase and the analysis phase. The design phase includes contemplating, collecting, organizing, and analyzing data without seeing any outcome data [1,2]. In observational studies, methods such as subclassification [3], matching on covariates or functions of them [4–7], and calculation of weights [8, 9] have been proposed to help approximate hypothetical randomized experiments and thus are part of the design phase. These methods do not rely on any outcome data, and Rubin [1] advocated that they should be conducted without any access to outcome data to assure the objectivity of the design. A critical additional activity in the design phase is the specification of a protocol for the estimation procedure to be used once outcome data are revealed.

The statistical literature includes many procedures for estimating treatment effects in observational studies. Gutman and Rubin [10] showed that when Y and X are scalar and continuous, and treatment assignment only depends on X, only a few of the common procedures are generally statistically valid, with the most promising ones being matching with replacement for effect estimation, with or without covariance adjustment, combined with within-treatment group matching for sampling variance estimation, suggested by Abadie and Imbens [11], and called in Gutman and Rubin [10] M–N–m and M–C–m (M, cross-group matching for point estimate; C/N, with/without covariance adjustment; m, matching within treatment group for sampling variance estimate).

Recently, Gutman and Rubin [12] described a new procedure called multiple imputation (MI) with two subclassification splines (MITSS) that explicitly views causal effect estimation as a missing data problem [13, 14] but only considered binary outcomes and a scalar covariate. Here, we extend this procedure to settings with multiple covariates and multiple continuous outcomes. The proposed extended procedure shares conceptual similarities with a procedure proposed by Little and An [15] for missing data imputation and relies on an initial propensity score estimation.

We compare the validity and performance of MITSS to the most promising methods identified by Gutman and Rubin [10] using Neyman’s framework of frequentist operating characteristics, in which an α-level interval estimate is ‘valid’ if, under repeated sampling from the population (finite or super), it covers the estimand in at least α percent of the samples. In addition to validity, we compare the accuracy, biases, and mean square errors (MSEs) of point estimates. Of all the methods considered, and across most of the conditions examined, when the distributions of the covariates in the control and treatment groups have adequate overlap, as defined in Sections 3 and 4, the new procedure, MITSS, is superior. When there is limited overlap, no method can be trusted because they all rely on unassailable extrapolation assumptions.

1.2. Framework

For a group of N units in the population indexed by i = 1, …, n ≤ N, n₀ units receive the control treatment (W_i = 0) and n₁ = n − n₀ units receive the active treatment (W_i = 1). Let Y_i(0) and Y_i(1) be the ‘potential’ outcomes corresponding to the appropriate treatment level at a specific point time; the use of potential outcomes to define causal effects is due to Neyman [16] in the context of randomization-based inference in randomized experiments and generalized to other settings in Rubin [17]. Assuming the stable unit treatment value assumption [18, 19], we can write the observable outcome for unit i as

$$Y_i^{\mathit{obs}}=W_i{Y}_i(1)+(1-W_i)Y_i(0).$$ (1)

For each unit i, there is also a vector of covariates with dimension L that are unaffected by W, X_i = (X_i1, …, X_iL) (X_i could also include higher order interactions and non-linear terms in basic covariates). For causal inference, we need the probability that each unit received the active rather than the control treatment, that is, the assignment mechanism. Assuming unconfoundedness [19] and that units can be modeled independently given the parameters, then the assignment mechanism for unit i can be written as

$$P(W_i=1\mid {\mathbf{X}}_i,Y_i(0),Y_i(1),\varphi )=P(W_i=1\mid {\mathbf{X}}_i,\varphi )\equiv e({\mathbf{X}}_i),$$ (2)

where e(X_i) is the propensity score for unit i [6], and the dependence on ϕ is notationally suppressed in (2). Throughout, we assume, as is typical in practice in observational studies, that e(X_i) is unknown and only an estimate of it, ê(X_i), is available. Estimating e(X_i) is part of the design phase of observational studies [1], and many procedures have been proposed to perform it (see [20] for a review). In this manuscript, we assume that the propensity scores have been estimated to the satisfaction of the researcher without observing any outcome variables. Thus, the observed data for person i comprise the vector { $Y_i^{\mathit{obs}}$, X_i, W_i, ê(X_i)}.

1.3. Estimands

Causal effects are summarized by estimands, which are functions of the unit-level potential outcomes on a common set of units [13, 17]. There are two main types of estimands in statistics: finite population (N < ∞) and super-population (N = ∞). A commonly used estimand is the super-population average treatment effect (ATE), γ₁ ≡ E(Y(1) − Y(0)), where the expectation is taken over the entire population. The finite population ATE is ${\gamma }_1^{FP}\equiv \frac{1}{N}{\sum }_{i=1}^N(Y_i(1)-Y_i(0))$. A generalization of the ATE can be obtained by summarizing the effects for a subpopulation of units based on X. Letting E(Y(w)|X) = h_w(X) for w = 0, 1, one generalization of the ATE is the average difference between the two response surfaces at X = x, h₁(x) − h₀(x), and in the finite population, $\frac{1}{N(x)}{\sum }_{i:\mathbf{X}=x}(Y_i(1)-Y_i(0))$, where N(x) is the number of units in the population for which X = x.

Another generalization of the ATE uses non-linear functions of the potential outcomes. For example, when Y_i(w), w ∈ {0, 1} are continuous, an estimand of interest is the proportion of units for whom the treatment is not useful or even harmful. More specifically, γ₂ = E(δ(Y(1) − Y(0))), where δ(a) is one if a ≤ 0 and zero otherwise, and its finite population counterpart is ${\gamma }_2^{FP}=\frac{1}{N}{\sum }_{i=1}^N(\delta (Y(1)-Y(0)))$.

Most of the commonly used causal inference procedures are implicitly intended for super-population linear estimands. We propose new procedures that rely on MI [21, 22], which allow the estimation of both finite and super-population estimands as well as non-linear estimands, but focus here on the more common super-population estimands.

1.4. Current methods

When X_i and Y_i are scalar and continuous, and the distributions of X in the control and active treatment groups differ, Gutman and Rubin [10] identified the two most promising procedures for inference for the ATE: matching for effect estimation combined with within group matching for sampling variance estimation (M–N–m) [11], and matching for effect estimation with covariance adjustments combined with within group matching for sampling variance estimation (M–C–m) [11, 23]. This sampling variance estimation allows for heteroskedasticity across treatment groups and levels of the propensity score as described in Section 4 of Abadie and Imbens [11]. Because procedures that perform marginally worse with scalar X may perform better than the most promising scalar procedures when dealing with multiple X, three additional mostly valid procedures were included here. The three procedures include full matching (FM) [24, 25], weighting (IPW₁) [9], and a so-called doubly robust method (DR) [8, 9]. For concise description of these procedures, see Gutman and Rubin [10]. These five procedures are compared here with the newly proposed procedure for both scalar X and multivariate X. Other procedures such as regression adjusted subclassification were not included, because they were generally invalid even with scalar X [10].

2. MI with two splines in subclasses (MITSS)

We propose a new procedure that addresses causal effect inference from a missing data perspective [14] by multiply imputing the missing potential outcomes.

The response surfaces, h₀(X) and h₁(X), are considered unknown and are approximated by h̃₀(X, θ₀) and h̃₁(X, θ₁), respectively, where h̃_w has a known parametric form, and θ_w (w ∈ {0, 1}) are unknown vector parameters.

MITSS shares some similarities with the penalized spline propensity prediction model [15, 26] proposed for missing–data imputation. Relying on the missing at random assumption [14], penalized spline propensity prediction imputes missing values using an additive model that combines a penalized spline on the probability of being missing and linear model adjustments on all other orthogonalized covariates. Formally, MITSS assumes that

$${\stackrel{\sim }{h}}_w({\mathbf{X}}_i,{\mathit{\theta }}_w)=g^{-1}(f_w(u(\widehat{e}({\mathbf{X}}_i)),{\mathbf{B}}_w)+{\mathbf{X}}_i^{\mathit{ort}}{\mathit{\beta }}_w^{or{t}^{\prime }}),$$ (3)

where g is commonly referred to as the link function [27], f_w is a spline with K knots, u(x) = log(x/(1 − x)), ${\theta }_w=\{{\mathbf{B}}_w,{\mathit{\beta }}_w^{\mathit{ort}}\}$ is a vector parameter defining the splines and linear adjustments orthogonal to them, and ${\mathbf{X}}_i^{\mathit{ort}}=(X_{i2}^{\mathit{ort}},\dots ,X_{iL-1}^{\mathit{ort}})$, with $X_{il}^{\mathit{ort}}$ being X_il orthogonal to u(ê(X_i)) [28]. Operationally, regress X_il on u(ê(X_i)), and set $X_{il}^{\mathit{ort}}$ to the residuals of this regression. Throughout, we assume that g is the identity link function.

The intuition behind functional form (3) is first to subclassify on the estimated propensity score, so that within each subclass, X^ort is well balanced across treatment groups; second, to fit a spline across propensity subclasses, because Bayesian models for missing data that include e(X_i) are likely to be well calibrated [29]. Causal effects estimation can be viewed as a missing data problem [13], and Bayesian modeling has been used to make inferences when missing data occur [30]. Here, we use Bayesian modeling to make causal inferences; and third, to use simple linear model adjustments for X^ort to gain efficiency and control for minor residual imbalances. A more complex function of X^ort, such as a spline function for each dimension of X^ort or an interaction term between each subclass indicator and each dimension of X^ort, can be used to replace the linear adjustments; however, because the differences in covariates’ distributions are mostly captured by the spline along the propensity score, and X^ort is well balanced within each subclass, the gain in efficiency might not justify the added model complexity and were not examined here.

Formally, let γ= τ(Y(0), Y(1))), where τ is a known function, and Y(w) = {Y₁(w), …, Y_n(w)}^T. A Bayesian approach to estimating γ will condition on the observed values, Y^obs, X, W, and approximate the distribution p(γ | Y^obs, X, W). Assuming (2), this distribution is

$$\begin{array}{l}p(\gamma \mid {\mathbf{Y}}^{\mathit{obs}},\mathbf{X},W)=\int p(\gamma \mid {\mathbf{Y}}^{\mathit{obs}},{\mathbf{Y}}^{\mathit{mis}},\mathbf{X},W)p({\mathbf{Y}}^{\mathit{mis}}\mid {\mathbf{Y}}^{\mathit{obs}},\mathbf{X},W)d{\mathbf{Y}}^{\mathit{mis}}\\ =\int p(\gamma \mid {\mathbf{Y}}^{\mathit{obs}},{\mathbf{Y}}^{\mathit{mis}},\mathbf{X},W)p({\mathbf{Y}}^{\mathit{mis}}\mid {\mathbf{Y}}^{\mathit{obs}},\mathbf{X})d{\mathbf{Y}}^{\mathit{mis}},\end{array}$$ (4)

where ${\mathbf{Y}}^{\mathit{mis}}=\{Y_1^{\mathit{mis}},\dots ,Y_n^{\mathit{mis}}\}$ and $Y_i^{\mathit{mis}}=W_i{Y}_i(0)+(1-W_i)Y_i(1)$. Equation (4) shows that in order to estimate γ, we only need to estimate the probability of p(Y^mis | Y^obs, X), because p(γ | Y^obs, Y^mis, X, W) is a degenerate distribution for finite population estimands and a known function for super-population estimands.

Let ψ_w(θ_w | Y^obs, X) be the posterior density of θ_w (i.e., θ_w’s conditional distribution given Y^obs and X). Assuming that Y_i(1) and Y_i(0) are conditionally independent given X and θ_w, and that the prior distributions of θ₁ and θ₀ are independent, then ψ₀ and ψ₁ are independent given Y^obs and X. This assumption is also known as no contamination of imputation across treatments [31], and it is sometimes implicitly made (e.g., with DR methods), and sometimes explicitly not made [31]. Based on this assumption, we have the following:

$$\begin{array}{l}p({\mathbf{Y}}^{\mathit{mis}}\mid {\mathbf{Y}}^{\mathit{obs}},\mathbf{X})={\int }_{{\theta }_1}{\int }_{{\theta }_0}p({\mathbf{Y}}^{\mathit{mis}}\mid {\mathit{\theta }}_0,{\mathit{\theta }}_1,\mathbf{X},{\mathbf{Y}}^{\mathit{obs}})p({\mathit{\theta }}_0,{\mathit{\theta }}_1\mid \mathbf{X},{\mathbf{Y}}^{\mathit{obs}})d{\mathit{\theta }}_{0}d{\mathit{\theta }}_1\\ ={\int }_{{\theta }_1}{\int }_{{\theta }_0}p({\mathbf{Y}}^{\mathit{mis}}\mid {\mathit{\theta }}_0,{\mathit{\theta }}_1,\mathbf{X},{\mathbf{Y}}^{\mathit{obs}}){\psi }_0({\mathit{\theta }}_0\mid {\mathbf{Y}}^{\mathit{obs}},\mathbf{X}){\psi }_1({\mathit{\theta }}_1\mid {\mathbf{Y}}^{\mathit{obs}},\mathbf{X})d{\mathit{\theta }}_{0}d{\mathit{\theta }}_1\\ ={\int }_{{\theta }_1}{\int }_{{\theta }_0}p(\mathbf{Y}{(0)}^{\mathit{mis}}\mid {\mathit{\theta }}_0,\mathbf{X},{\mathbf{Y}}^{\mathit{obs}})p(\mathbf{Y}{(1)}^{\mathit{mis}}\mid {\mathit{\theta }}_1,\mathbf{X},{\mathbf{Y}}^{\mathit{obs}})\times {\psi }_0({\mathit{\theta }}_0\mid {\mathbf{Y}}^{\mathit{obs}},\mathbf{X}){\psi }_1({\mathit{\theta }}_1\mid {\mathbf{Y}}^{\mathit{obs}},\mathbf{X})d{\mathit{\theta }}_{0}d{\mathit{\theta }}_1\\ ={\int }_{{\theta }_0}p(\mathbf{Y}{(0)}^{\mathit{mis}}\mid {\mathit{\theta }}_0,\mathbf{X},{\mathbf{Y}}^{\mathit{obs}}){\psi }_0({\mathit{\theta }}_0\mid {\mathbf{Y}}^{\mathit{obs}},\mathbf{X})d{\mathit{\theta }}_0\times {\int }_{{\theta }_1}p(\mathbf{Y}{(1)}^{\mathit{mis}}\mid {\mathit{\theta }}_1,\mathbf{X},{\mathbf{Y}}^{\mathit{obs}}){\psi }_1({\mathit{\theta }}_1\mid {\mathbf{Y}}^{\mathit{obs}},\mathbf{X})d{\mathit{\theta }}_1\\ ={\int }_{{\theta }_0}\prod _{W_i=1}p(Y_i(0)\mid {\mathit{\theta }}_0,\mathbf{X},{\mathbf{Y}}^{\mathit{obs}}){\psi }_0({\mathit{\theta }}_0\mid {\mathbf{Y}}^{\mathit{obs}},\mathbf{X})d{\mathit{\theta }}_0\times {\int }_{{\theta }_1}\prod _{W_i=0}p(Y_i(1)\mid {\mathit{\theta }}_1,\mathbf{X},{\mathbf{Y}}^{\mathit{obs}}){\psi }_1({\mathit{\theta }}_1\mid {\mathbf{Y}}^{\mathit{obs}},\mathbf{X})d{\mathit{\theta }}_1,\end{array}$$ (5)

where Y(0)^mis comprise the potential outcomes under control for all the units with W_i = 1 and Y(1)^mis comprise the potential outcomes under the active treatment for all the units with W_i = 0.

Using Equation (5), an estimate for ${\gamma }_1^{FP}$ is obtained by $E\left({\gamma }_1^{FP}\mid {\mathbf{Y}}^{\mathit{obs}},\mathbf{X}\right)$, which reduces to

$${\widehat{\gamma }}_1^{FP}=\frac{1}{N}\sum _{i=1}^N\left({\widehat{Y}}_i(1)-{\widehat{Y}}_i(0))\right),$$

where

$${\widehat{Y}}_i(w)=\{\begin{array}{ll}{Y}_i^{\mathit{obs}}\hfill & \text{if}{W}_i=w\hfill \\ E_{{\mathit{\theta }}_w}({\stackrel{\sim }{h}}_w({\mathbf{X}}_i,{\mathit{\theta }}_w))\hfill & \text{if}{W}_i\ne w\hfill \end{array}.$$ (6)

Analogously, letting Δ(X) be the density of X_i in the super-population, estimate γ₁ by

$${\widehat{\gamma }}_1={\int }_{\mathbf{X}}\left({\widehat{Y}}_i(1)-{\widehat{Y}}_i(0))\right)\mathbf{\Delta }(\mathbf{X})d\mathbf{X}.$$

Estimating Δ(X) is part of the design phase of observational studies, because it does not involve any outcomes. The standard error of ${\widehat{\gamma }}_1^{FP}$ and γ̂₁ is obtained using MI. This point estimate may have some vague resemblance to the DR estimate, but it differs by at least three important aspects. First, it does not rely on weights, which may result in large biases and sampling variance in certain situations [32, 33]. Second, it introduces flexible spline models and adjustments for orthogonalized covariates. Third, it integrates over the posterior distribution of the parameters and explicitly imputes the missing potential outcomes. Thus, the proposed procedure is not restricted to specific parameter estimation and can provide point and interval estimates for estimands that do not have a closed form (e.g., ${\gamma }_2^{FP}$ and γ₂).

We now explicate and summarize this procedure:

1. Partition the n units into at most six subclasses, such that there are at least three units from each treatment group in each of the subclasses: the partitioning is performed using X_i when it is scalar, or ê(X_i) when X_i comprises multiple covariates, for example, using the method described in Imbens and Rubin [34]. The number 3 was chosen so that all of the parameters of the spline model can be estimated even when using an improper prior distribution.

2. From observed data { $Y_i^{\mathit{obs}}$, X_i, i ∈ 1, …, N}, independently estimate E(Y_i(0) | X_i, θ₀) = h̃₀(X_i, θ₀) and E(Y_i(1) | X_i, θ₁) = h̃₁(X_i, θ₁), using regression splines with knots located at the borders of the subclasses and a linear combination of X^ort, as in (3); the location of the knots is guided by step 1, so that the distribution of ${\mathbf{X}}_i^{\mathit{ort}}$ in each subclass is similar in the control and treatment groups.

3. Draw the vector parameters θ₁ and θ₀ from their independent posterior distributions.

4. Using the drawn values of θ₁ and θ₀, independently impute the missing control potential outcomes in the active treatment group, the Y_i(0) with W_i = 1, and the missing active treatment potential outcomes in the control group, the Y_i(1) with W_i = 0.

5. Repeat steps 4 and 5 M times (in our simulations, M = 25).

6. Estimate the treatment effect γ and its sampling variance in each of the imputed datasets; from imputed dataset m, let γ̂^(m) be the estimated treatment effect, and let V̂^(m) be its estimated sampling variance, m = 1, …, M. When γ is a finite-sample estimand, V̂^(m) = 0.

7. Estimate γ by $\widehat{\gamma }=\frac{1}{M}{\displaystyle \sum _{m=1}^M}{\widehat{\gamma }}^{(m)}$ and its standard error by

   $$\sqrt{\frac{1}{M-1}\sum _{m=1}^M{({\widehat{\gamma }}^{(m)}-\widehat{\gamma })}^2+\frac{1}{M}\sum _{m=1}^M{\widehat{V}}^{(m)}}.$$

8. Calculate the interval estimate for γ, using the t approximation for the posterior variance of γ given by Barnard and Rubin [35].

When M is large (e.g., > 100), the last two steps may be replaced by using percentiles of γ̂^(m), to obtain posterior interval for γ.

3. Scalar X_i

To investigate the performance of MITSS in comparison with current statistically approximately valid procedures, we used simulation analysis with scalar X_i, because methods that perform poorly with a single covariate will generally perform poorly with multiple covariates. The simulation configurations are identical to these in Gutman and Rubin [10] and comprise two types of situational factors. The first type is either known to the investigator, such as sample sizes, or can be easily estimated without examining any outcome data, such as the covariate (X_i) distributions. The second type of factor is not known to the investigator and cannot be estimated for the data at the design phase; these define the response surfaces generating the outcome data from the covariates. See Table II from Gutman and Rubin [10] for more details. The changes in the current scalar X_i simulations are that MITSS is now included, and of the procedures listed in Table I in Gutman and Rubin [10], only M–N–m, M–C–m, FM, IPW₁, and DR are included, because they were the most promising.

Table II.

Median log difference across configurations of bias, interval width, and RMSE between valid statistical procedures and MITSS, by interval estimates coverage for scalar X (monotone response surfaces).

Method	Type	Percent	Absolute bias	Interval width	RMSE
IPW1	A	59	1.06	0.22	0.28
	B	10	0.32	0.78	0.65
	C	20	1.70	−0.68	0.11
	D	11	0.85	−0.15	0.56
DR	A	51	0.50	−0.03	−0.02
	B	4	0.90	0.84	0.77
	C	28	1.07	−0.60	−0.06
	D	17	0.42	−0.27	0.29
M–N–m	A	73	0.43	0.17	0.18
	B	11	−0.02	0.31	0.22
	C	6	0.76	−0.57	−0.14
	D	9	0.40	0.15	0.31
M–C–m	A	73	0.26	0.17	0.18
	B	12	0.19	0.32	0.24
	C	7	0.38	−0.66	−0.40
	D	9	0.25	0.12	0.19
Full match	A	55	0.47	0.03	0.05
	B	9	−0.32	0.02	−0.05
	C	24	0.61	−0.41	−0.24
	D	12	0.42	−0.35	0.22

Differences are displayed as alternative methods to MITSS.

The types are configurations for which 95% interval estimates has the following coverages characteristics: A, MITSS ≥ 0.9 Method ≥ 0.9; B, MITSS < 0.9 Method ≥ 0.9; C, MITSS ≥ 0.9 Method < 0.9; D, MITSS < 0.9 Method < 0.9.

Overall, there are 3⁵ × 2 different configurations of known factors, and 3⁶ (3⁵) monotone (non-monotone) response surface configurations, resulting in a 3¹¹ × 2 (3¹⁰ × 2) factorial design for monotone (non-monotone) response surfaces. For each configuration, N_rep = 100 replications were produced. As in Gutman and Rubin [10], throughout this simulation, we restrict the analysis of results to configurations for which the Jensen–Shannon divergence (JSD) [36] was less than 0.3, so there is reasonable overlap in the X distributions between the two treatment groups. JSD is a measure that quantifies differences between distributions and is defined by

$$\lambda Q_{KL}(G_1\mid \lambda G_1+(1-\lambda )G_0)+(1-\lambda )Q_{KL}(G_0\mid \lambda G_1+(1-\lambda )G_0),$$ (7)

where G₀ and G₁ are the distributions of X in the control and active treatment, respectively, Q_KL is the Kullback–Leibler divergence [37], and λ is the proportion of treated units in the population (see [10] for additional details).

3.1. Results for interval coverages

We compare the coverages of the five promising methods identified by Gutman and Rubin [10] to MITSS. Estimation of the propensity score for the weighting methods was accomplished using the algorithm described by Imai and Ratkovic [38]. For MITSS, we assumed that Y_i(W)|X, θ_W, σ_W ~ 𝒩(h̃_W(θ_W, X), σ_W), where 𝒩 is the is the Normal distribution, and, for analysis, we also assumed the commonly used independent improper prior distribution for θ_W and σ_W:

$$p({\mathit{\theta }}_{\mathbf{0}},{\mathit{\theta }}_{\mathbf{1}},log({\sigma }_0),log({\sigma }_1))=p({\mathit{\theta }}_{\mathbf{0}},log({\sigma }_0))p({\mathit{\theta }}_{\mathbf{1}},log({\sigma }_1))\propto 1.$$ (8)

For simplicity, the estimand of interest was the super-population ATE. For each of the five procedures and MITSS, at each configuration, and at each of the 100 replications, we calculated the estimated treatment effect, the estimated sampling variance, and the corresponding interval width and determined whether the 95% interval covered the true treatment effect. Using these values, we calculated for each configuration the estimated coverage rate, the bias, the mean sampling variance, and the mean interval width. Throughout, coverage rates are summarized by the proportions of configurations with over 90% coverage for a 95% interval estimate that are expressed as percentages, as well as by the medians, the inter-quartile ranges, and the 25% percentiles across configurations that are expressed as decimals.

Table I displays the proportion of configurations in which the different methods lead to over 90% coverage, as well as the median and inter-quartile range of the coverage rate of the intervals, for the six methods when response surfaces were monotone. MITSS has 79% of the configurations with at least 90% coverage, which is second only to M–N–m and M–C–m. The rest of the methods had less than 75% of the configurations with over 90% coverage.

Table I.

95% Coverage for the average treatment effect across simulated configurations for monotone response surfaces (scalar X).

Method	Overall	Null			Non-Null
	% of Configurations with over 90% coverage	Median	25%	75%	Median	25%	75%
IPW1	70	0.98	0.86	1	0.97	0.82	1
DR	55	0.92	0.70	0.96	0.91	0.65	0.96
FM	64	0.96	0.93	0.99	0.93	0.83	0.98
M–N–m	84	0.94	0.90	0.97	0.98	0.94	1
M–C–m	84	0.93	0.89	0.96	0.98	0.94	1
MITSS	79	0.94	0.91	0.96	0.94	0.91	0.96

Null configurations are simulation conditions in which h₁(x) = h₀(x) ∀x ∈ ℝ, and non-null configurations are all other configurations. For both null and non-null configurations, MITSS has median interval coverages that are close to and also most concentrated around 95%. Similar results with slightly different numbers occur for non-monotone response surfaces (Supporting Information).

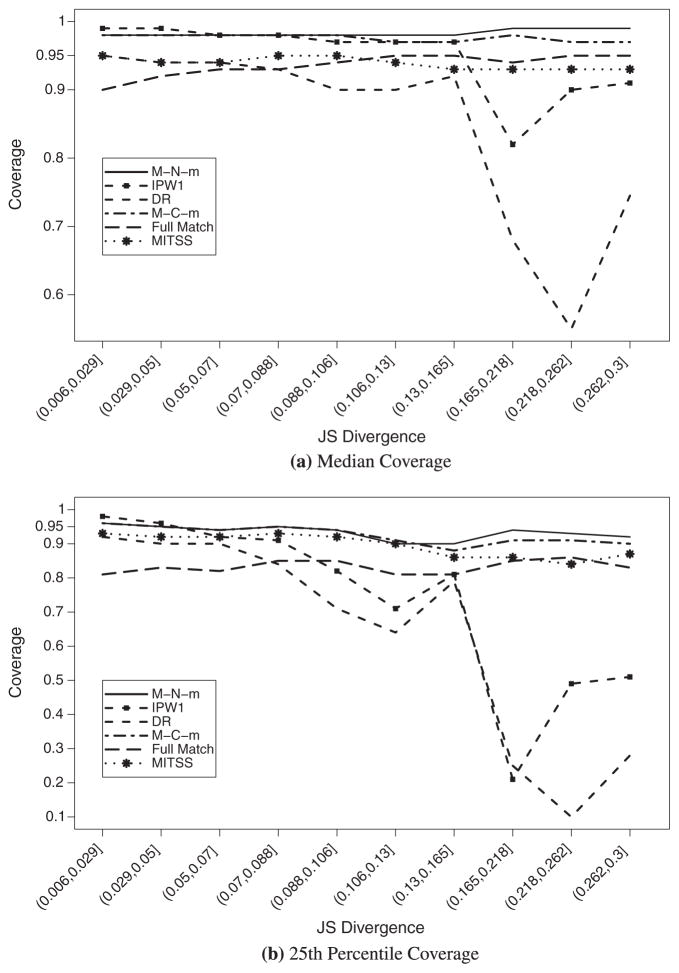
Figure 1 summarizes the median and the 25th percentile of the coverages as functions of the JSD for monotone response surfaces. The median coverages of M–N–m and M–C–m are above 95% for every value of the JSD, which suggests over-coverage. MITSS and FM generally result in median coverages that are close to nominal. However, the 25th percentile plot shows that all methods have decreased coverage as the JSD increases, with MITSS, M–N–m, and M–C–m having 25th percentiles still close to 95%, even for large JSD values. IPW₁ and DR have median coverage that is higher than 95% for lower JSD values, but they have substantial under-coverage for larger JSD values. Similar trends are observed for non-monotone response surfaces (Supporting Information).

Figure 1.

Median and 25th percentile of 95% interval estimates coverage for the average treatment effect across simulated configurations by JSD for statistically valid procedures (monotone response surface with scalar X).

3.2. Results for biases, RMSEs, and intervals widths

Table II compares the median log differences in absolute bias, interval widths, and root MSEs (RMSEs) across configurations with monotone response surfaces for the six procedures. We compared MITSS with each of the five procedures separately, by classifying the configurations into four types (A, B, C, D). Type A comprises configurations where both MITSS and the compared procedure have 95% interval estimates with coverages that are higher than 0.9. For all of the methods, the majority of the configurations are classified as type A (IPW₁ = 59%, DR = 51%, M–N–m = 73%, M–C–m = 73%, Full Match = 55%). In these configurations, MITSS had smaller median bias, and except for DR, it also had smaller median RMSE and median interval width. In configurations where MITSS had lower than 0.9 coverage and the other methods had higher than 0.9 coverage (labeled type B), MITSS had larger bias than M–N–m and FM, but smaller bias than M–C–m and the weighting methods; MITSS’s interval widths in these configurations were generally too short. In configurations where MITSS had intervals with coverages that were higher than 0.9, and the other methods had coverages that were lower than 0.9 (labeled type C), MITSS had smaller median bias and wider median interval width; similar trends are observed for non-monotone response surfaces (Supporting Information). Other than M–N–m and M–C–m, MITSS had significantly more type C configurations than type B (Table II).

This analysis shows that, in comparison with the other methods, MITSS is generally valid and it has point estimates with smaller biases and generates shorter 95% intervals. It is also interesting to note that IPW₁ and DR had the largest biases, and IPW₁ also had the largest interval widths. Similar results appear for non-monotone response surfaces. These results support the analyses performed by Kang and Schafer [32] and Waernbaum [33], that IPW₁ and DR methods are often statistically inferior methods.

When the distributions of X in the treatment and control groups differ substantially, none of the methods are statistically valid (labeled type D). To avoid these situations, it is important, at the design stage, to examine the overlap of the distributions of X in the control and treated groups. Units in one group that have no close match in the other group should be discarded, and causal inferences restricted to the region of X where there is overlap. The new estimand differs from the original estimand, which is generally impossible to estimate without making empirically unassailable assumptions. Our summary of the simulations with scalar X is that, of the methods considered, MITSS has the best statistical properties.

4. Multivariate X

When investigating multiple covariates, we consider the methods described in Section 3 modified so that they are matched/subclassified based on the estimated propensity score, instead of scalar X. Covariance adjustment for M–C–m was performed using linear regression that included X^ort. We also considered three versions of MITSS with cubic splines along the propensity score: (i) the original MITSS; (ii) MITSS with 15 instead of six subclasses (MITSS-15); and (iii) MITSS with six subclasses but without linear adjustment for covariates orthogonal to the propensity score (MITSS-PS). All three versions of MITSS assumed that Y_i(W) ~ 𝒩(h̃_W(θ_W, X), σ_W) with corresponding h̃_W and prior distributions (8).

Based on the results of the scalar covariate simulation, we also supplemented all of the methods with a preliminary step that discarded all units without ‘close’ X_i matches in the other treatment group. This step was introduced because the chance that units in the treatment and control groups will have close X_i matches in the other group decreases with the number of covariates.

The general advice for discarding units is that it should be performed with scientific knowledge and is usually study specific. However, in a simulation, a context-free discarding rule needs to be specified explicitly. One possible rule is to keep all units with estimated propensity scores between [ê_min(X), ê_max(X)], where ê_min(X) = max{min{ê(X_i) | W_i = 0}, min{ê(X_i | W_i = 1)} and ê_max(X) = min{max{ê(X_i) | W_i = 0}, max{ê(X_i | W_i = 1)}. Crump et al. [39] proposed a different rule that enjoys an optimal precision criterion and keeps all units with propensity scores between (0.1, 0.9). The results using either of these rules are quite similar, with a slight bias advantage to the rule that discards more observations. Thus, we only display the results for the [ê_min(X), ê_max(X)] discarding rule. Overall, we compare eight procedures each of them with and without discarding.

4.1. Covariate distributions

Let ${\mathbf{X}}_i=\{{\mathbf{X}}_i^{\prime },{\mathbf{X}}_i^{″}\}$, J is the dimension of ${\mathbf{X}}_i^{\prime }$; X′ is a matrix with n rows and J columns; ${\mathbf{X}}_i^{″}$ includes all the second-order interactions of ${\mathbf{X}}_i^{\prime }$. Formally, ${\mathbf{X}}_i^{″}=\{{\mathbf{X}}_{i{j}_1}^{\prime }\times {\mathbf{X}}_{i{j}_2}^{\prime },\forall j_1\ne j_2{j}_1,j_2=1,\dots ,J\}$; X″ is a n × (J(J − 1)/2) matrix, and X is an n × L matrix, where L = J + J(J −1)/2. The values of ${\mathbf{X}}_i^{\prime }$ were generated from two different multivariate skew-t distributions [40].

$$\begin{array}{ll}\hfill \text{For}{W}_i& =1,i=1,\dots ,n_1,\text{and}{W}_i=0,i=n_1+1,\dots ,n_1+r\times n_1,\hfill \\ \hfill X_i\mid W_i& =0\stackrel{\text{i.i.d.}}{\sim }\mathit{Skew}-t_{df,J}\left(\mathbf{0},I,{\mathbf{\eta }}_{\mathbf{0}}\right),i=n_1+1,\dots ,n_1+r\times n_1,\hfill \\ \hfill X_i\mid W_i& =1\stackrel{\text{i.i.d.}}{\sim }\mathit{Skew}-t_{df,J}\left(\stackrel{\sim }{\mathbf{\mu }},\mathbf{\Omega },{\mathit{\eta }}_{\mathbf{1}}\right),i=1,\dots ,n_1,\hfill \end{array}$$

where I is the identity matrix, μ̃ = (μ̃, 0, …, 0), Ω is a diagonal matrix with entries (ν₁, ν₂, …, ν₂), η₀ = (η₀, 0, …, 0), η₁ = (η₁, 0, …, 0), and df are the degrees of freedom. We indexed the distance between the treated and the control groups’ means in terms of the standardized bias, $SB=\frac{\stackrel{\sim }{\mu }}{\sqrt{J\frac{1+{{\nu }_1}^2}{2}}}$. It should be noted that the initial bias is only in the first component, but it is a function of the dimension of ${\mathbf{X}}_i^{\prime }$. This idea also appeared in Rubin [41] and Rubin and Thomas [42] and, in the case of ellipsoidally symmetric distributions, corresponds to adding a constant bias to each component.

For each configuration defined by the factors SB, ${\nu }_1^2,{\nu }_2^2$, η₀ and η₁, N_rep = 100 replications were generated. Table III describes the three levels of each of these factors. The factors J, df, r and n₁ also vary in each of the settings, yielding a factorial design with 3⁵ × 2³ × 3 levels.

Table III.

Factors and corresponding levels used in the simulation analysis.

Factor	Levels multivariate X	Description
r	{1, 2}	Ratio of sample sizes
n	{300, 600, 1200}	Treatment group population size
η0	{−3.5, 0, 3.5}	Skewness of the first covariate in the treatment group
η1	{−3.5, 0, 3.5}	Skewness of the first covariate in the control group
B	$\left\{\frac{1}{4},\frac{1}{2},1\right\}$	Standardized bias for first covariate
${\nu }_1^2$	$\left\{\frac{1}{2},1,2\right\}$	Ratio of variances for first covariate
βX	{0.5, 1, 2}	Correlation between X1iand Yi(W)
${\nu }_2^2$	$\left\{\frac{1}{2},1,2\right\}$	Ratio of variances of all covariates except the first covariate
df	{7, ∞}	Degrees of freedom of skewed t-distribution
J	{2, 5, 10}	Number of covariates
CX	{2, 3, 5}	Complexity of multivariate function
G0(x) and G1(x)		Described in the Supporting Information and response surfaces

For all of the methods and all of the configurations, ê(X_i) was estimated using logistic regression model that included X, $X_1^2,\dots ,X_J^2$, and X_p1 × X_p2, ∀p₁, p₂ ∈{1, …, J}, p₁ ≠ p₂. In cases where the logistic regression did not converge within 25 iterations, linear discriminant analysis was used instead to estimate ê(X_i).

When the dimension of the covariate increases, estimating the JSD for two distributions can become computationally intensive owing to the need for estimating multivariate integrals. To save computation time, we estimated the JSD for the distributions of the estimated propensity scores in the treatment and control group using kernel-density estimation [43]. We considered only configurations that had JSD < 0.3 on the estimated propensity scores without any discarding, and in a separate analysis, we considered these configurations after discarding non-overlapping units.

4.2. Response surfaces for potential outcomes given covariates

In each simulation replication, we randomly generate the continuous outcome data from

$$Y_i^{\mathit{obs}}=W_i{F}_1\left(X_i,{\mathbf{B}}_1,{\sigma }^Y\right)+(1-W_i)F_0\left(X_i,{\mathbf{B}}_0,{\sigma }^Y\right),$$ (9)

where F₁ and F₀ are normal distributions with conditional means f₀(X, B₀) and f₁(X, B₁), respectively, and conditional variances σ^Y; σ^Y, B₁ and B₀ are parameters unknown to the investigator. The functions f₀ and f₁ covered a wide range of possibilities. They were generated by an algorithm that was controlled by four factors responsible for different characteristics of the multivariate functions: β_X ∈ B_W governed the correlation between ${\mathbf{X}}_{i1}^{\prime }$ and Y_i(W); C_X ∈ B_W governed the ‘complexity’, and $I_{\mathit{inc}}^W$, W ∈ {0, 1} controlled whether Y_i(W) was influenced by second-order interactions. Detailed implementation of the procedure is described in the Supporting Information.

For each configuration of the factors that are known to the investigator, as well as β_X, C_X, and $I_{\mathit{inc}}^W$, the generating procedure was replicated 100 times, thereby investigating monotone and non-monotone response surfaces and the effect of different functional factors on the success of the estimation procedures.

4.3. Results

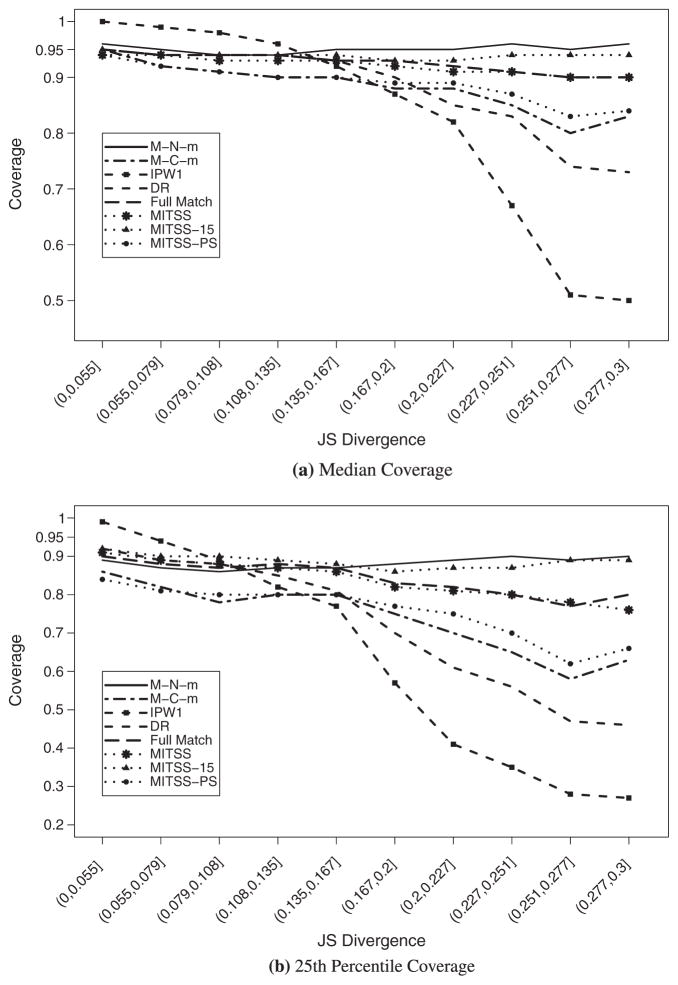
Using the same methodology as in Section 3.1, we examined the coverage of the methods described in Section 3 for 95% nominal intervals for configurations with JSD < 0.3 on the estimated propensity score (Table IV). MITSS, MITSS-15, FM, and M–N–m are the only methods with coverage that is higher than 90% in at least 60% of all configurations. The rest of the methods have less than 56% of the configurations with coverage over 90%. Figure 2 displays the median and 25% coverage across configurations for different JSD values. M–N–m, FM, MITSS-15, and MITSS all have median coverage that is close to nominal even for large JSD values. Each of IPW₁ and DR have median coverage that decreases sharply with increasing JSD, and M–C–m and MITSS-PS have a more moderate median coverage decline. The 25% coverage figure shows similar trends, with more pronounced decreases in coverage for MITSS and FM as JSD increases.

Table IV.

Coverages of 95% intervals for the average treatment effect across simulated configurations for JSD < 0.3 (multivariate X).

Method	Overall	Null			Non-null
	% of configurations with over 90% coverage	Median	25%	75%	Median	25%	75%
MITSS-PS	49	0.9	0.76	0.96	0.89	0.75	0.95
MITSS	63	0.92	0.83	0.96	0.92	0.85	0.95
MITSS-15	73	0.94	0.88	0.97	0.94	0.89	0.96
M–N–m	72	0.96	0.90	0.98	0.95	0.87	0.98
M–C–m	48	0.89	0.74	0.95	0.89	0.74	0.95
DR	56	0.92	0.69	0.97	0.92	0.71	0.96
IPW1	52	0.93	0.58	1	0.90	0.54	0.99
FM	64	0.94	0.86	0.97	0.92	0.84	0.96

Figure 2.

Median and 25th percentile of 95% interval estimates coverage for the average treatment effect across simulated configurations by JSD for statistically valid procedures (multivariate X).

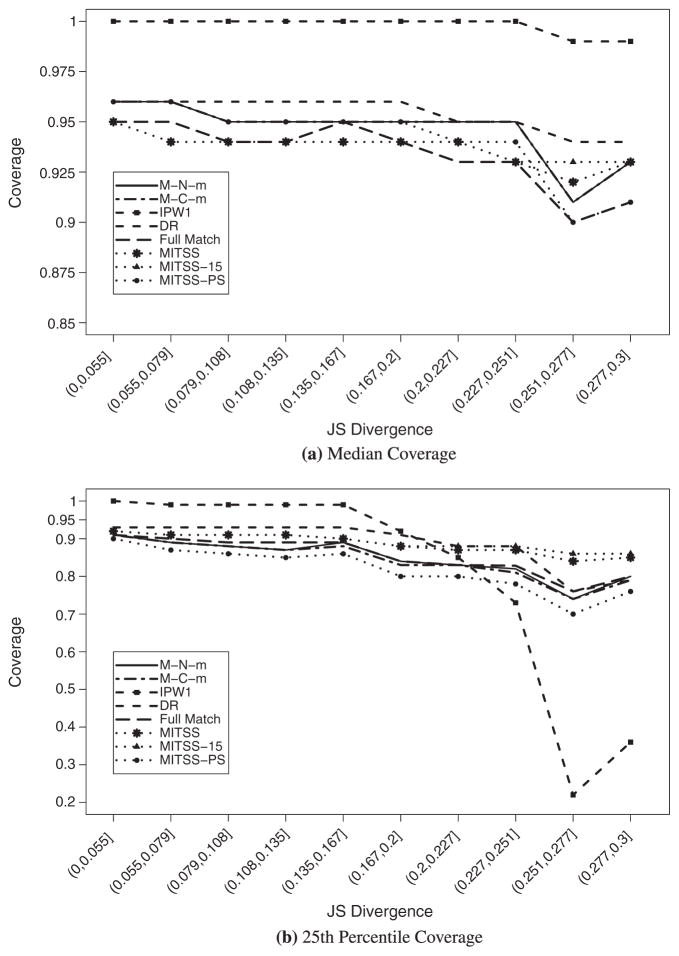
Of the configurations with JSD < 0.3, 94.8% had at least 15 units in each treatment group that satisfied the [ê_min(X), ê_max(X)] rule in all of the 100 replications. Less than 2% of the configurations had fewer than 15 units in at least one of the treatment groups that satisfied this rule for all 100 replications and were removed from the analysis. Table V displays the 95% coverage for configurations with JSD < 0.3 after discarding observations that did not overlap. All of the methods, except for M–N–m, improved in terms of coverage. MITSS, MITSS-15, DR, and IPW₁ are the only methods with over 70% of the configuration having at least 90% coverage. However, the IPW₁ 25th percentile is higher than nominal, indicating that its interval estimates may be inefficient. Except for IPW₁, all of the methods have median coverages that are close to nominal after discarding non-overlapping units (Figure 3(a)). Figure 3(b) shows that the coverages at the 25th percentile drop sharply for IPW₁ when JSD increases, and only moderate decreases are observed for the other methods.

Table V.

Coverages of 95% intervals for the average treatment effect across simulated configurations for JSD < 0.3 with removal of non-overlapping units (multivariate X).

Method	Overall	Null			Non-Null
	% of configurations with over 90% coverage	Median	25%	75%	Median	25%	75%
MITSS-PS	65	0.96	0.84	0.99	0.94	0.82	0.97
MITSS	74	0.94	0.89	0.97	0.94	0.9	0.96
MITSS-15	75	0.94	0.89	0.97	0.94	0.9	0.96
M–N–m	68	0.96	0.85	0.98	0.94	0.85	0.97
M–C–m	68	0.96	0.85	0.98	0.94	0.85	0.97
DR	78	0.96	0.91	0.98	0.95	0.91	0.98
IPW1	80	1	0.98	1	1	0.96	1
FM	68	0.96	0.87	0.98	0.93	0.86	0.96

Figure 3.

Median and 25th percentile of 95% interval estimates coverage for the average treatment effect across simulated configurations by JSD for statistically valid procedures with removal of non-overlapping units (multivariate X).

Table VI compares the median log differences in absolute bias, interval widths, and RMSEs. For all of the methods, most of the configurations are classified as type A (both MITSS and the compared method have over 90% coverage). In configurations of type A, MITSS generally has smaller bias and RMSE, and except for M–N–m and FM, MITSS also has shorter interval width. In configurations of type B (MITSS has less than 90% coverage and the other method more than 90%), MITSS has lower median bias and median RMSE in comparison with all three methods but wider interval widths in comparison with FM and M–N–m. It is important to note that in these configurations, MITSS has coverage that is smaller than nominal in comparison with the other methods and is thus generally invalid. With configurations of type C (MITTS has coverage over 90% and the other method less than 90%), MITSS has smaller bias, interval width, and RMSE compared with MITSS-15, MITSS-PS, IPW₁, and M-n-m, but larger bias and RMSE compared with FM, DR, and M–C–m. However, in these configurations, MITSS is generally statistically valid, and the other methods are not. In summary, without any discarding, M–N–m, FM, MITSS-15, and MITSS are generally valid for smaller JSD values, and MITSS generally has smaller bias and RMSE in comparison with these methods.

Table VI.

Median log difference across configurations of bias, interval width, and RMSE of methods described in Section 1.4 versus MITSS, by interval estimates coverage for multivariate X (for all configurations with JSD < 0.3).

Method	Type	Percent	Absolute bias	Interval width	RMSE
MITSS-PS	A	41	0.27	0.15	0.27
	B	8	0.42	0.09	0.42
	C	22	0.19	0.38	0.19
	D	29	0.34	0.19	0.34
MITSS-15	A	61	0.41	0.52	0.41
	B	12	1.43	1.68	1.43
	C	2	0.21	0.35	0.21
	D	25	0.36	0.31	0.35
M–N–m	A	51	0.13	−0.13	0.13
	B	22	0.21	−0.37	0.21
	C	12	0.08	0.19	0.08
	D	15	0.18	−0.27	0.18
M–C–m	A	37	0.22	0.1	0.22
	B	10	0.36	0.02	0.36
	C	26	−0.12	0.09	−0.12
	D	27	0.1	−0.06	0.1
DR	A	46	0.28	1.05	0.28
	B	9	1.95	2.38	1.95
	C	17	−0.97	−0.39	−0.97
	D	28	−0.51	−0.09	−0.51
IPW1	A	39	2.85	3.68	2.85
	B	13	1.94	2.28	1.94
	C	24	1.73	3.13	1.77
	D	24	0.86	1.61	0.88
FM	A	48	0.21	0.03	0.21
	B	16	0.33	−0.15	0.33
	C	15	−0.08	0.00	−0.08
	D	21	−0.10	−0.44	−0.11

Differences are displayed as alternative methods to MITSS.

The types are configurations for which 95% interval estimates has the following coverages characteristics: A, MITSS ≥ 0.9 and Method ≥ 0.9; B, MITSS < 0.9 and Method ≥ 0.9; C, MITSS ≥ 0.9 and Method < 0.9; D, MITSS < 0.9 and Method < 0.9.

Table VII compares the median log differences in absolute bias, interval widths, and RMSEs between the methods examined in Section 3 and MITSS. After discarding, the majority of the configurations are classified as type A. In configurations of type A, MITSS has smaller bias, shortest interval width, and smaller RMSE in comparison with all of the methods, except for MITSS-15, for which it has approximately equal bias, interval width, and RMSE. In fact, except for DR and MITSS-15, MITSS has smaller bias, shortest interval width, and smaller RMSE even in configurations of type C. Furthermore, the adjustments for the components of the covariates orthogonal to the estimated propensity score are beneficial as revealed by the comparison of MITSS with MITSS-PS. In summary, after discarding, almost all of the methods improved their coverage, and MITSS generally has smallest bias and RMSE, and shortest interval width.

Table VII.

Median log difference across configurations of bias, interval width, and RMSE of methods described in Section 1.4 versus MITSS, by interval estimates coverage for multivariate X (for all configurations with JSD < 0.3 with only overlapping units).

Method	Type	Percent	Absolute bias	Interval width	RMSE
MITSS-PS	A	58	0.27	0.11	0.27
	B	7	0.38	−0.01	0.37
	C	17	0.16	0.39	0.16
	D	19	0.22	0.02	0.22
MITSS-15	A	72	0.0	0.0	0.0
	B	3	0.01	0.11	0.01
	C	2	−0.01	0.02	−0.01
	D	23	0.0	0.03	0.0
M–N–m	A	60	0.4	0.27	0.4
	B	8	0.54	0.14	0.54
	C	15	0.3	0.5	0.3
	D	17	0.36	0.06	0.36
M–C–m	A	59	0.4	0.27	0.4
	B	8	0.54	0.14	0.54
	C	15	0.3	0.5	0.3
	D	17	0.36	0.06	0.36
DR	A	68	0.54	1.36	0.54
	B	10	1.54	2.11	1.55
	C	6	−0.26	0.31	−0.26
	D	16	0.01	0.23	−0.01
IPW1	A	68	4.83	3.92	4.83
	B	12	3.86	2.89	3.86
	C	7	1.97	4.70	2.21
	D	13	1.63	3.09	1.71
FM	A	60	0.49	0.43	0.49
	B	8	0.76	0.32	0.76
	C	15	0.41	0.55	0.41
	D	17	0.30	0.05	0.30

Differences are displayed as alternative methods to MITSS.

The types are configurations for which 95% interval estimates has the following coverages characteristics: A, MITSS ≥ 0.9 and Method ≥ 0.9; B, MITSS < 0.9 and Method ≥ 0.9; C, MITSS ≥ 0.9 and Method < 0.9; D, MITSS < 0.9 and Method < 0.9.

5. Simulations Using Real Data

In Sections 3 and 4, the covariate distributions and the response surfaces were simulated from analytic distribution. We now apply MITSS and M–N–m to real X and Y^obs data, where we simulate only the unobserved potential outcomes. The dataset for this analysis is from Shadish et al. [44], which was designed to estimate the effects of a specific training program on mathematics and vocabulary scores of undergraduates; thus, the potential outcomes were two-dimensional vectors of the two scores. The study also includes a rich set of covariates. In our analysis, we treat all of the students as part of one observational study with an unconfounded assignment mechanism.

5.1. Partially simulated data

We conducted two sets of simulations. The first set assumed that the intervention had a constant (additive) effect, and the unconfounded assignment mechanism involved ten randomly selected covariates, five randomly selected squared covariates, and five randomly selected second-order interactions. In the second set of simulations, we imputed unobserved potential outcomes by searching for the ‘most similar’ student, in terms of the 28 basic covariates, among those who received the other training. The most similar student to student i was chosen by first finding a donor pool of K_i students (1 ≤ K_i ≤ n) with the smallest Hamming distance [45] from student i, based on sex, marital status, preference for literature, ethnicity, and whether the student was a math major. Among the K_i students, the student with the smallest Mahalanobis distance [46] to student i on the continuous covariates (such as pre–training scores, ACT and SAT scores, and GPA) was declared as the most similar student to student i. The observed values of the two potential outcomes for the most similar student were imputed for the missing potential outcomes for student i. Once all of the missing potential outcomes were imputed, treatment assignments were obtained in a way similar to the constant effects simulation setting. Each student’s potential outcome vector included the treatment (mathematics) and the control (vocabulary) scores. In our simulations, we generated 50 different treatment assignment probability models, and for each of these, we generated 40 realizations of potential outcomes.

MITSS used the following bivariate regression model for multiply imputing the missing outcomes:

$$\left(\begin{array}{c}{Y}_i^M(W)\\ Y_i^V(W)\end{array}\right)=\left(\begin{array}{c}{\stackrel{\sim }{h}}_W^M({\mathbf{X}}_i,{\beta }_W^M)\\ {\stackrel{\sim }{h}}_W^V({\mathbf{X}}_i,{\beta }_W^V)\end{array}\right)+{\mathrm{\Phi }}_2(0,{\mathrm{\sum }}_W),$$

where $Y_i^M(W),Y_i^V(W)$ are the potential outcomes for the mathematics and vocabulary scores, respectively; for unit i receiving treatment W, ${\stackrel{\sim }{h}}_W^M({\mathbf{X}}_i,{\beta }_t^M)$ and ${\stackrel{\sim }{h}}_W^V({\mathbf{X}}_i,{\beta }_t^V)$ were defined by (3), and Φ₂ is a bivariate Normal random variable, with mean vector zero and covariance matrix Σ_W. The prior distributions were $p({\mathrm{\sum }}_0,{\beta }_0^M,{\beta }_0^V)\propto {\mid {\mathrm{\sum }}_0\mid }^{-1}$ and $p({\mathrm{\sum }}_1,{\beta }_1^M,{\beta }_1^V)\propto {\mid {\mathrm{\sum }}_1\mid }^{-1}$.

5.2. Results

The estimated propensity score was obtained using the algorithm described in Imbens and Rubin [34, Chapter 13]. Following Shadish et al. [44], we defined the estimand of interest to be γ₁. Because γ₁ is now a two-component vector, there are several ways to construct interval estimates for it. For example, one can use either an ellipsoidal 95% region or a rectangular region obtained from a combination of single coordinate 95% interval estimates. The latter region analytically has less than 95% family-wise coverage. Table VIII displays the median bias, coverage, interval width, and RMSE across assignment probability models for both interval estimate constructions, as well as for configurations with constant and heterogeneous treatment effects. Both methods covered the true treatment effect at a rate that is higher than or equal to nominal for both configurations when using rectangular confidence intervals. In addition, MITSS produced valid ellipsoidal confidence regions. In principal, one could implement a multivariate normal analysis using M–N–m and obtain an ellipsoidal confidence region. However, here we illustrate the scalar analysis that is generally performed in practice. In both sets of simulations, MITSS has generally smaller bias than M–N–m, and it always enjoys shortest interval widths and smaller RMSEs.

Table VIII.

Median bias, reduction in bias, coverage, and RMSE of the mathematics and vocabulary treatment effect estimates for RAS and MITSS in simulations based on Shadish et al. [44] data.

	Constant effect		Heterogeneous effect
	M–N–m	MITSS	M–N–m	MITSS
Bias math	0.04	0.04	0.04	0.03
Bias vocabulary	0.07	0.04	0.05	0.04
% Reduction in bias math	0.81	0.76	0.72	0.79
% Reduction in bias vocabulary	0.67	0.69	0.59	0.65
Coverage super-population math	0.95	0.98	0.98	1.00
Coverage super-population vocabulary	0.95	0.98	0.98	0.98
Coverage super-population joint	—	0.98	—	1.00
Super-population interval width math	0.77	0.68	0.85	0.76
Super-population interval width vocabulary	0.82	0.73	0.83	0.74
RMSE math	0.40	0.37	0.44	0.38
RMSE vocabulary	0.42	0.38	0.43	0.38

Finally, we are also interested in an estimand that describes the proportion of people for whom the mathematics training is not useful or even harmful. This estimand cannot be obtained using simple weighting or subclassification methods, and its sampling variance is not readily available from M–N–m or M–C–m. However, both the estimand and its sampling variance are readily available from MITSS. MITSS’s coverage of this estimand was higher than nominal (97.7%) with bias that was less than 0.02. This type of analysis allows the identification of subgroups for which the active treatment could be harmful relative to the control.

6. Discussion

The simulation demonstrates that, in the configurations examined, for both scalar and multivariate X with overlapping distributions in the treatment and control groups, MITSS is a generally valid procedure that is more accurate and precise than the other valid procedures. However, when there are non-overlapping units, the splines in MITSS are implicitly used to extrapolate to units with covariate values that are not observed for that treatment, which is known to be ‘dangerous’ [47], leading to increased bias. Attempting to address this issue using more complex splines (e.g., MITSS-15) results in better coverage, but generally larger biases, interval widths, and RMSEs. This conclusion agrees with the previous literature, which suggests that there are only small gains in terms of bias reduction when more than six subclasses/knots are used [3,48]. Of course, the results here are confined to the sample sizes, and simulation configurations examined.

Although the general statistical validity of interval estimates obtained using MITSS arises from smaller biases and smaller RMSEs, it is not the most efficient procedure in all configurations. For example, in some cases, scientific knowledge may support the claim that Y(0) and Y(1) are nearly parallel linear combinations of X, which can be estimated accurately and efficiently using multiple linear regression. Other scientific knowledge may be that Y(0) and Y(1) are monotone in X, and more efficient estimators can be obtained by better approximating the response surfaces in step 2 of MITSS (e.g., [49]). This type of knowledge is likely to be more recondite when the dimension of X is larger. Another option is to assume that the values of the missing potential outcomes are all represented in the empirical distribution of the observed potential outcomes and employ predictive mean matching [50,51] for approximating the response surfaces. Nevertheless, any scientific knowledge used in situations where the distributions of X in the control and treatment groups do not overlap should be treated with extreme scrutiny, because model-based extrapolation is inevitably involved.

When it is impossible to obtain full overlap of the covariate distributions between the treatment group and the control group, no method can provide generally valid statistical inferences. In such cases, the investigator should consider discarding some of the units that do not overlap, so that a valid inference on a restricted population can be obtained [1]. The general advice is that such restrictions should be made with scientific knowledge, which is usually study specific. Here, we examined a rule that discards observations for which the propensity scores are in the intersection of the range of the two treatment groups and showed that MITSS was generally valid.

The results presented here for scalar X and continuous outcome parallel the results obtained for scalar X and dichotomous outcomes [12]. Because the same trends were also observed here for multivariate X, we conjecture that MITSS can be generally applied to both dichotomous and continuous outcomes with scalar or multivariate X.

Another advantage of MITSS over the previously proposed procedures is the freedom to define relevant estimands, such as finite population ones, non-linear ones, and estimands that are based on multivariate potential outcomes. Finite population estimands are sometimes of interest when a possible intervention is to be applied to all of the units in the population (e.g., the 50 states in the United States and all of the nursing homes in the United States). Because MITTS assumes that Y_i(0) and Y_i(1) are independent given X, the finite sample interval estimates may be too short when this assumption is not approximately correct. One possible solution is to include more covariates, including the second-order interaction terms. The selection of these terms should be performed before any examination of the observed outcomes, so that the design and analysis phases are performed separately. A different approach in situations where there is a priori knowledge that the treatment effect is constant is to change step 2 of MITSS and use a single spline with constant treatment effect instead of the two independent models. However, constant treatment effects are not always realistic, because it is hard to believe that units with different initial characteristics will respond to the active treatment versus control treatment in the same way. This situation is more prevalent in studies with heterogeneous units. A more reasonable solution is to use the sampling variance of the super-population estimate. The super-population sampling variance is equal to the largest finite sample variance in completely randomized experiments [52]. This approach was used throughout this manuscript and had good frequentist properties. Further discussion of this point with Shadish’s data simulation is discussed in the Supporting Information.

In conclusion, multiply imputing the potential outcomes and discarding observations that do not overlap in terms of covariates result in efficient inferences for the treatment effect.