A Bayesian Perspective on Tinnitus Pitch Matching

Abstract

Objectives

New tinnitus therapies are being developed and marketed that target the patient’s tinnitus frequency. This frequency is estimated clinically by pitch matching, which has the patient identify the pure tone that is closest to the perceived tinnitus frequency. Though widely used, pitch matching is heavily criticized as unreliable, and the degree of reliability varies among patients. At the very least, it is recommended that multiple pitch matches be used to identify the patient’s tinnitus frequency. Even so, it is not clear how many pitch matches to collect, how they should be combined, or how doing so will enhance the audiologist’s certainty about the true tinnitus frequency. In this article, we describe a simple Bayesian method of sequentially combining pitch matches until acceptable precision is achieved and illustrate the method in 10 patients with chronic tinnitus.

Design

Subjects were recruited from previous study participants and support group attendees at the National Center for Rehabilitative Auditory Research. Thirty tinnitus pitch matches were elicited from 10 patients with chronic, monotonal tinnitus.

Results

A Bayesian sequential analysis yielded estimated tinnitus frequencies for 7 patients that were within one-quarter octave of their true value with 90% certainty. Between four and twenty pitch matches were required to achieve acceptable results in these seven patients.

Conclusions

Despite criticism, pitch matching is widely used to estimate tinnitus frequency. We address reliability concerns with a Bayesian sequential analysis to jointly estimate tinnitus frequency and reliability. The method is easily applied.

INTRODUCTION

Tinnitus is an auditory disorder that is experienced by 10 to 15% of adults (Hoffman & Reed 2004). A great deal of research is underway to develop effective therapies for tinnitus (Hobson et al. 2010; Martinez-Devesa et al. 2010; Hoare et al. 2013; Pichora-Fuller et al. 2013). Therapies can be classified into two general types: treatments for the reactions to tinnitus and treatments for the perception of tinnitus (Dauman & Tyler 1992; Dobie 2004). Treatments for the reactions to tinnitus focus on developing psychological tools that assist the tinnitus patient in disregarding the tinnitus sound. Treatments for the perception of tinnitus attempt to reduce the perceived loudness of the tinnitus.

There is a growing literature assessing sound therapies for tinnitus (e.g., Henry et al. 2008; Hobson et al. 2010; McNeill et al. 2012; Shekhawat et al. 2013). Some studies that applied background sound to the hearing loss (tinnitus frequency) region have reported positive effects (Davis et al. 2008) and others negative ones (Vanneste et al. 2013), while sound therapies using notched music or off-frequency listening (these sounds purportedly distributing lateral inhibition into the tinnitus region) have reported benefits for tinnitus patients (Herraiz et al. 2010; Okamoto et al. 2010). These approaches to reducing the perception of tinnitus involve stimulating either the frequency region containing the predominant tinnitus frequency or regions surrounding the tinnitus frequency region. Numerous investigators are exploring this treatment modality for relief of chronic tinnitus.

The obvious dilemma with approaches that target the frequency region of perceived tinnitus is that tinnitus pitch is not directly observable despite being an absolutely necessary parameter for the correct application of these therapies. The standard approach is to use pitch matching to estimate a patient’s tinnitus frequency (Henry et al. 2000). A pitch match is a protocol whereby a patient listens to a variety of pure tones and is asked to identify the tone that most closely matches the perceived tinnitus. Given a tinnitus pitch match, the clinician can infer the underlying tinnitus frequency so that a suitable therapy can be applied. Tinnitus pitch matching is a fundamental measure of the perception of tinnitus.

The pitch match approach to tinnitus frequency estimation can be accomplished using standard audiometric technology and is widely used. Even so, tinnitus pitch matching has been heavily criticized. It is deemed “unreliable” in the sense that repeated pitch matches typically vary over 2 to 3 octaves (Penner 1983; Tyler & Conrad-Armes 1983; Burns 1984; Henry et al. 2004). Sources of variability can include test–retest variability, normal tinnitus fluctuations, and tinnitus changes caused by the test stimulus itself (Tyler 2000). The degree of reliability also varies among patients, with some patients consistently providing the same pitch match and others varying wildly across the pitch spectrum. This has led to outright skepticism of the utility of pitch matching, though tinnitus frequency-targeted acoustic therapies require an estimate of the patient’s tinnitus frequency.

Given this need and recognizing the difficulties with pitch matching, two remedial approaches can be suggested: (1) retain standard pitch matching protocols and combine several pitch matches to more accurately estimate tinnitus frequency (Tyler & Conrad-Armes 1983; Tyler & Babin 1993; Henry et al. 2013) and (2) develop more reliable (and unbiased) tinnitus frequency estimation technology. Our current focus is on the former, while recognizing the undeniable value of enhanced measurement technology.

The motivation for combining several pitch matches for estimating tinnitus frequency is straightforward. Additional pitch matches increase the amount of information about the underlying tinnitus frequency. More pitch matches enhances the precision with which tinnitus frequency is estimated and, assuming that the pitch matches are unbiased, improves the accuracy of the estimate. The natural follow-up question is how many pitch matches should one collect on a patient? The answer depends on the desired level of precision of the estimated tinnitus frequency. Many more pitch matches are required if the clinician or the therapeutic protocol requires an estimate that is within 1/48th octave of the true tinnitus frequency than if one requires an estimate that is only within one octave of the true tinnitus frequency. Furthermore, the achieved level of precision of the tinnitus frequency estimate depends not only on the number of pitch matches but also on the patient’s reliability in accomplishing the task. Clearly, there is no all-purpose sample size recommendation suitable for all patients, because the achieved precision of the tinnitus frequency estimate in a particular patient depends on that patient’s a priori unknown reliability.

The clinical problem of tinnitus frequency estimation is therefore far from trivial. The general dissatisfaction with pitch matching, despite its widespread use, motivates a discussion about pitch matching protocols. In this article, we consider a Bayesian approach to this problem whereby clinicians iteratively collect pitch matches and update the precision of the estimate until the desired level of precision is achieved. Technical details of the Bayesian framework are mostly omitted. The reader is instead directed to several references that cover various levels of detail (Box & Tiao 1992; Lee 1997; Spiegelhalter et al. 2004). The proposed method does not affect the methodological aspects of pitch matching in any way and is easy to implement with an automated testing device (e.g., Henry et al. 2013), a computerized spreadsheet, a smart phone application, or can even be computed by hand. A simple spreadsheet application that completes all of the necessary calculations is included with this article as Supplemental Digital Content 2 (http://links.lww.com/EANDH/A162).

METHODS

In this section, we describe an automated testing device and a sample of 10 individuals with chronic tinnitus recruited to illustrate the clinical application of our methodology. We conclude this section with statistical details of Bayesian sequential analysis and outline relevant inferences available with this methodology.

Study Participants

Potential study participants were identified from a database of individuals who had previously participated in research at the National Center for Rehabilitative Auditory Research (NCRAR). Additional participants were recruited from attendees of a tinnitus support group held at the NCRAR. Individuals were considered potential candidates for the study if they had tinnitus and a previous audiogram showing normal or near normal hearing (if available). These individuals were contacted, and screening was conducted over the phone by a member of the study team. Candidates were asked “If you listen for tinnitus in a quiet room, how often do you hear it—always, almost always, sometimes, almost never, or never?” Only those who responded “almost always” or “always” were considered eligible. Candidates were also asked whether their tinnitus was tonal and whether they felt their tinnitus was constant and could be “measured.” These questions served to identify candidates who would have the best chance of finding a pitch match, that is, not those who hear multiple tones or whose tinnitus is sporadic or inconsistent.

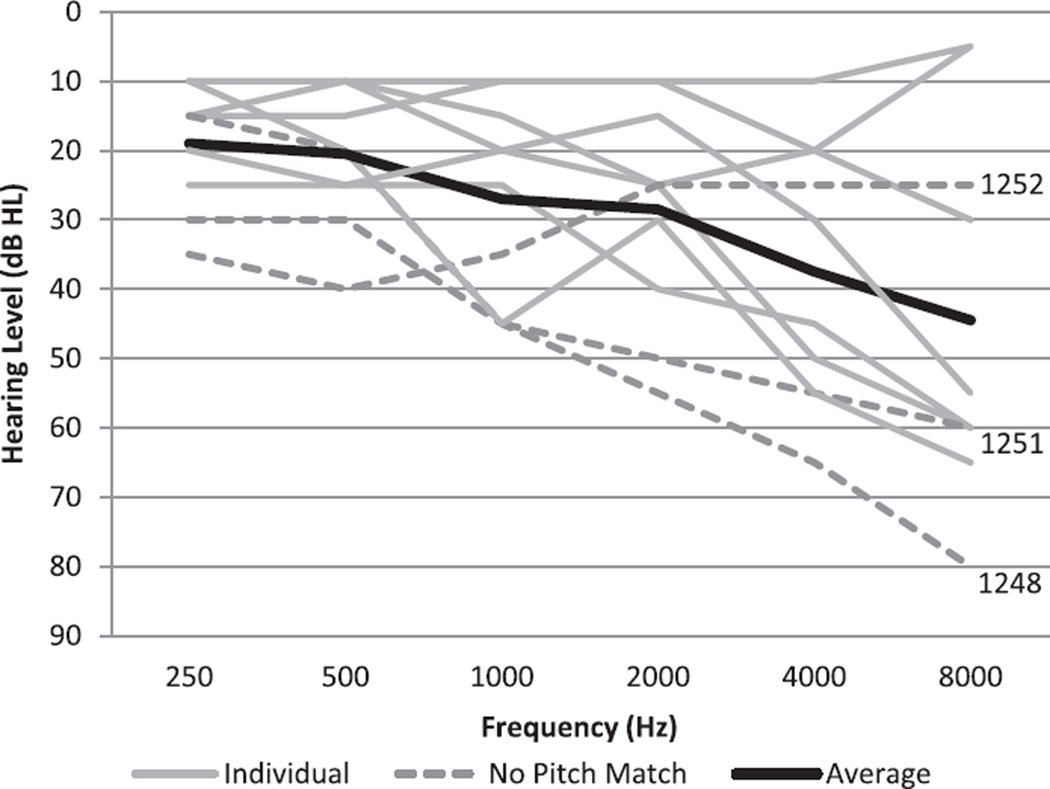
Candidates who passed the telephone screening were scheduled for a study visit. At their appointment, they signed a consent form and then had their hearing evaluated by an audiologist (conventional hearing threshold evaluation with results in dB HL). Exclusion criteria included visible signs of middle or outer ear problems; air-bone gaps of 15 dB at two or more frequencies in one ear; or an air-bone gap of 20 dB or greater at any one frequency. A maximum hearing loss criterion was also used— participants were excluded if they had more than one threshold of 70 to 75 dB HL or any one threshold greater than 80 dB HL in the test ear that would be used to deliver test stimuli from the Tinnitus Evaluation System (TES). This maximum hearing loss criterion was imposed to ensure that participants could hear the test stimuli delivered from the TES. As potential candidates were selected on the basis of having normal or near normal hearing, no one was excluded for this reason. See Figure 1 for individual and mean threshold data. In previous studies, it has been observed that participants may often confuse the concepts of loudness and pitch (Vernon & Fenwick 1984). Thus, following the hearing evaluation, a loudness versus pitch differentiation protocol was completed to optimize performance on the pitch matching task (Henry et al. 2001). This protocol was completed with the last five of the 10 study participants (for the first five, the difference between loudness and pitch was explained more informally). Participants then completed questionnaires providing demographic data and characteristics of tinnitus (duration, tonality, location, etc.). Participants received $10 for their involvement in the study.

Fig. 1.

Individual hearing thresholds for all 10 participants (gray lines) and overall mean (thick black line). Subjects never achieving an acceptable tinnitus frequency estimate are shown as dashed lines.

Testing Equipment

Audiometric and TES testing were conducted in an Acoustic Systems Model RE-245S double-walled sound-attenuated suite. The TES runs a series of completely automated testing sequences and has been described in detail (Henry et al. 2013). For testing with the TES, participants sat facing a laptop computer. Instruction screens on the computer screen guided them through the tests. The TES was configured to test at any or all of 19 available test frequencies: 1/3-octave steps from 250 to 16,000 Hz. For all tests, a sound was presented and participants turned a dial on the “Pod” (peripheral patient–control device) to control output level or frequency of the sound. Pushbuttons on the Pod were depressed to make response choices. ER-4B insert earphones (Etymotic Research, Inc.) are permanently attached to the Pod, which connects to a computer via a USB port. The Pod was calibrated in the laboratory (using a Bruel and Kjaer Type 2231A sound level meter and Type 4157 Ear Simulator) and then delivered to the test booth. Calibration was checked in the booth using an Extech Model 407768 sound level meter. Participants turned a knob/dial on the Pod to control output level or frequency of test stimuli. Four pushbuttons on the Pod facilitated responses.

Procedures

A “tinnitus ear” and contralateral “stimulus ear” were assigned to each participant (Vernon & Meikle 1981; Vernon & Fenwick 1984). If one ear (or side of the head) had more predominant tinnitus, that ear was designated the “tinnitus ear” and the contralateral ear was the “stimulus ear.” If tinnitus was symmetrical, the ear with better hearing was chosen to be the “stimulus ear.” Participants with symmetrical tinnitus and hearing were given the choice as to which ear received the stimulus. Before testing, the audiologist placed the appropriate insert earphone in the stimulus ear.

A test battery was programed with the TES including loudness matching and pitch matching procedures. These testing procedures have been described previously (Henry et al. 2013). However, the pitch matching procedure was modified for the current study. Instead of 10 repeated pitch matches as previously described, all participants did 30 repeated pitch matches. The current version of the TES is not yet capable of stopping when the desired level of precision in the pitch match estimate is reached (see Statistical Methods); thus, all participants provided a large number of pitch matches (30) and the analysis was performed after testing was completed. It was thought that 30 was a tolerable number of matches to complete in one sitting and anyone who did not achieve the desired level of precision by that point was likely never going to. Participants were warned before starting the test that it would be quite repetitive and asked to do their best to provide accurate responses from beginning to end. Participants could perform all 30 pitch matches within 5 to 10 minutes.

Statistical Methods

We conceive of a patient’s tinnitus frequency and reliability as unknown quantities that adhere to a well-specified probability distribution. Within this framework we can state, for example, that we are 90% certain that the underlying tinnitus frequency is between 2 and 12 kHz. In this example, the interval 2 to 12 kHz is called a “90% Bayesian Credible Interval.” Pitch matches elicited during the clinical appointment successively modify the probability distribution, with the anticipated effect that the credible interval is narrowed. Thus, after several pitch matches, we may be 90% certain that the true tinnitus frequency is now between 6 and 9 kHz, which is considerably more precise than where we started. When the desired level of precision is achieved, then the pitch match procedure is completed and the tinnitus frequency is determined, usually as the mean or median of the probability distribution. This is a Bayesian statistical analysis and is ideally suited to the clinical problem of tinnitus frequency estimation.

At this point, it is natural to wonder about the “desired level of precision.” This is not a statistical or methodological problem, but depends on the needs of the clinical application or a manufacturer’s requirements for an acoustic therapy device. Obviously, more precise estimates (i.e., smaller credible intervals) require more pitch matches than less precise estimates. We used one-quarter octave as our target precision, meaning that pitch matches were elicited until we were 90% certain that the true, underlying tinnitus frequency was within one-quarter octave of the estimated tinnitus frequency. This is solely for illustration, and the clinical context should guide the target precision.

An outline of the Bayesian approach is as follows:

1. Propose a probability model, called the “likelihood,” that ties the observed pitch match to the underlying tinnitus frequency and pitch match reliability. We assume the log₂ of the pitch matches (Hz) are Gaussian random variables with mean equal to the true log₂ tinnitus frequency denoted θ. The Gaussian variance is denoted φ and is related to the patient’s reliability such that the reliability is equal to $2\sqrt{\frac{\phi }{\pi }}$. The reliability is the theoretical mean octave difference between pairs of pitch matches.

2. Propose a “prior” probability distribution for the true log₂ tinnitus frequency θ and variance φ corresponding to the clinician’s initial beliefs about these unknown parameters. This can be based on published data or on the expert opinion of the audiologist under the particular clinical circumstance. Our approach is to characterize the prior distribution via a hierarchical analysis of 40 subjects who were recruited in a previously published study (Henry et al. 2013). This approach is described in supplemental Appendix A (http://links.lww.com/EANDH/A161).

3. Elicit a pitch match from the patient and apply Bayes theorem to revise the prior beliefs about θ and φ. This revision is expressed as a probability distribution called the “posterior,” and is proportional to the product of the likelihood in step (a) and the prior in step (b). The posterior is used to estimate the tinnitus frequency, the precision of that estimate, and the patient’s reliability (see below).

4. Repeat step (c) until the desired level of precision is achieved, substituting the prior from the previous iteration with the “revised” prior, given all pitch matches elicited so far from that patient.

This is called Bayesian sequential analysis and is a remarkably easy and intuitive process. In fact, the relevant computations involve nothing more than basic arithmetic and standard statistical tables, all of which are easily programmed into a spreadsheet or accomplished by hand. A worked example will be shown below.

The technical details of this approach can be found in Lee (1997, p. 69) or in Box and Tiao (1992, p. 92). We use a Normal-Inverse Gamma prior for step (b), which is conjugate to the Gaussian likelihood in step (a). Consequentially, all of the calculations are particularly simple and do not require simulation-based approaches (e.g., Markov Chain Monte Carlo) for evaluating the posterior distributions of a particular patient.

On the log₂ scale, the posterior mean of θ is the tinnitus frequency in octaves from 1 Hz. Computing 2 raised to the power of the posterior mean of θ gives the posterior median tinnitus frequency in hertz. One might prefer working with the posterior mean tinnitus frequency (Hz), which is given by 2 raised to the power of the posterior mean of θ plus half the posterior mean of φ times ln(2). We are averse to this estimator primarily because the posterior mean in hertz is sensitive to the reliability. In any event, the reliability and the precision are calculated on the more intuitive, octave scale.

Let y_i denote the ith log₂ pitch match (Hz) elicited from a tinnitus patient, where i = 1 is the first pitch match taken, i = 2 is the second pitch match and so forth. The posterior distributions of θ and φ are derived from the following recursive equations:

$$n_i=n_{i-1}+1$$

$$v_i=v_{i-1}+1$$

$${\theta }_i=\frac{n_0·{\theta }_0+i·ȳ}{n_i}$$

$$S_i=S_0+\sum {(y-ȳ)}^2+{(\frac{1}{n_0}+\frac{1}{i})}^{-1}{({\theta }_0-ȳ)}^2$$

The summations and the averages in the equations for ȳ and S_i are over all the log₂ pitch matches up to and including the ith elicitation. We set n₀ = 1, v₀ = 1.73, θ₀ = 12.77, and S₀ = 0.22, which generate the prior distributions on the variance and mean log₂ tinnitus frequency in a new patient (see supplemental Appendix A, http://links.lww.com/EANDH/A161). Setting n₀ to 1 corresponds to the belief that the previous study results are “informationally equivalent” to one pitch match observed on a new subject. Other values of n₀ may be chosen, depending on the degree to which the clinician thinks the new patient is similar to subjects described in Henry et al. (2013). This point is discussed further below. The recursive equations provide the following inferences about a patient’s tinnitus:

• –The estimated tinnitus frequency (in Hz) is equal to 2^θi.
• –A 90% credible interval (in Hz) for the estimated tinnitus frequency is $2^{{\theta }_i\pm t_{{\upsilon }_i}\sqrt{\frac{S_i}{{\upsilon }_i•n_i}}}$, where t_vi is the 90th percentile from a t-distribution with v_i degrees of freedom.
• –The precision (in octaves) of the estimated tinnitus frequency is $t_{{\upsilon }_i}\sqrt{\frac{S_i}{{\upsilon }_i·n_i}}$. After the ith elicitation, one is 90% certain that the estimate is within $t_{{\upsilon }_i}\sqrt{\frac{S_i}{{\upsilon }_i·n_i}}$ octaves of the true tinnitus frequency.
• –The reliability, operationally defined as the expected octave difference between any pair of pitch matches, is equal to $2\sqrt{\frac{S_i}{\pi ·{\upsilon }_i}}$.

RESULTS

Ten subjects were recruited into this study. All were male, ranging in age from 37 to 71 years (mean age = 55.2 years). Audiograms are shown in Figure 1. Three subjects with comparatively unusual audiometric configurations are indicated by dashed lines and are discussed further below.

Tinnitus frequency estimates follow the algorithm described in the statistical methods section. A worked example for test subject 1246 is shown in Table 2. Table 2 was generated using an MS Excel spreadsheet that is available as Supplemental Digital Content 2 (http://links.lww.com/EANDH/A162) to this article. Computations follow the recursions shown above. The first pitch match is 4000 Hz, n₁ is n₀ + 1 = 2, v₁ = 1.7269 + 1 = 2.7269, θ₁ is simply the average of θ₀ and log₂ (4000) = 12.37, and S₁ is equal to S₀ plus one-half the squared difference between θ₀ and log₂(4000). Based on these calculations after the first pitch match,

1. The estimated tinnitus frequency is 2^12.37 ≈ 5280 Hz.

2. A 90% Bayesian interval of the tinnitus frequency is 2,784 to 10,012 Hz.

3. The precision of the tinnitus frequency (in octaves) is equal to $t_{2.73}\sqrt{\frac{0.55}{2.73•2}}=0.92$, meaning that we are 90% certain that the true tinnitus frequency is estimated to within slightly less than an octave.^*

4. The reliability (in octaves) is given by $2\sqrt{\frac{0.55}{\pi ·2.73}}=0.5$, meaning that this subject’s pitch matches are expected to differ by about half an octave on retest.

Additional pitch matches generate posterior inferences in the same way, as dictated in the equations above. We continue eliciting pitch matches until the estimated precision goes below 0.25 or one-quarter octave, which occurs after the sixth pitch match. At this point, we have achieved a level of precision for which we are 90% certain that the estimate of 6020 Hz is within one-quarter octave of the true tinnitus frequency.

TABLE 2.

Final results of all 10 test subjects

Subject	Final Sample Size	Tinnitus Frequency (Hz)	Precision (Octaves)	Reliability
1244	4	8536	0.24	0.31
1245	4	9363	0.25	0.32
1246	6	6020	0.24	0.38
1248	30*	1992	0.37	1.38
1249	5	5526	0.25	0.36
1250	3	6492	0.23	0.25
1251	30*	1928	0.34	1.26
1252	30*	4164	0.35	1.31
1253	20	887	0.25	0.75
1254	4	7429	0.21	0.27

Subjects labeled with an “*” did not achieve acceptable precision by the 30th pitch match.

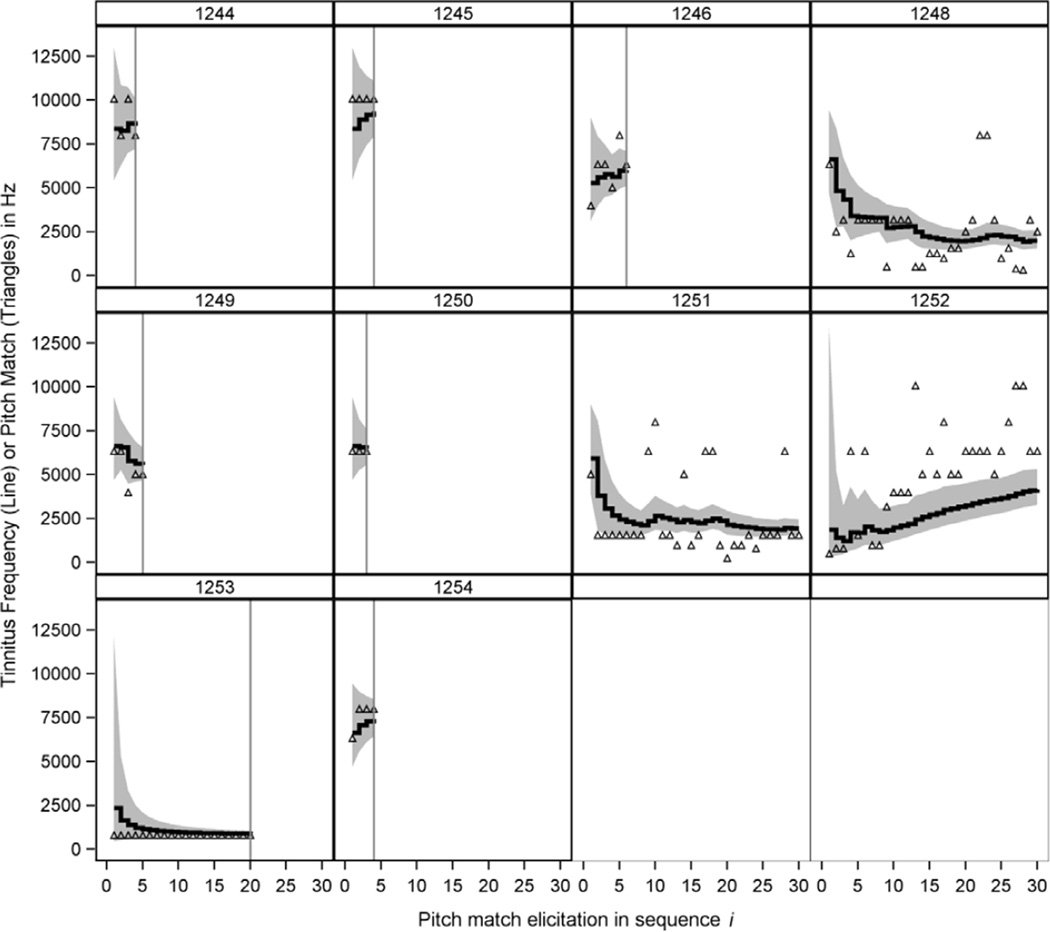
Sequential analysis of all 10 subjects is shown in Figure 2, and the final results for each are shown in Table 2. Each panel represents each subject’s data, which is ordered on the x-axis in sequence of the pitch match elicitation. The vertical axis is in hertz, with the open triangles showing the pitch matches and the solid step function showing the estimate of the underlying tinnitus frequency. Note that the solid line is not a running average or locally weighted curve fit to observed pitch matches, but is a Bayesian sequential estimate of the true tinnitus frequency. The shaded region is the 90% Bayesian credible interval. For each subject, pitch matches are elicited until we achieve our quarter-octave precision criteria. The speed at which the subjects achieve that criterion depends on their reliability and on their tinnitus frequency, as well as the prior. Subject 1250 consistently provided a pitch match of 6340 Hz, very close to the prior median of about 6968 Hz and completed testing after only three pitch matches. Five other subjects (1244, 1245, 1246, 1249, and 1254) completed testing by the sixth pitch match.

Fig. 2.

Posterior estimates of tinnitus frequency (solid lines) and 90% Bayesian credible intervals (shaded region) for 10 subjects. Open triangles show the pitch match results at each test ordered on the x-axis. Vertical reference lines are stopping points when the subject’s tinnitus frequency was estimated to within one-quarter octave with 90% certainty. Panel headers correspond to subject numbers in Table 2.

Three subjects, 1248, 1251, and 1252, never achieved the desired level of precision by the 30th pitch match, at which time the experiment automatically stopped. Their responses were clearly unreliable. It also appears as if subject 1251 generated pitch matches centered around two frequencies: a lower frequency of about 1600 Hz and a higher frequency closer to about 6340 Hz. It is entirely possible that this subject has a bitonal tinnitus and really is not suitable for this type of testing. If this is true, the Bayesian algorithm correctly ‘refused’ to stop the subject’s testing because the minimum level of precision was never reached. Subject 1252 had a distinctive pattern of continuously increasing pitch matches. Typically, this indicates a dependency between the response and the temporal position in the task, which is not technically amenable to the analysis that we describe. These three subjects for whom tinnitus frequency could not be estimated had somewhat worse hearing than the remaining subjects (Fig. 1). This is discussed further below.

Subject 1253 is an interesting case study. The subject, a musician, consistently presented a pitch match at 800 Hz. The algorithm continued to elicit pitch matches until the 20th response, at which time the precision criteria was achieved. The tinnitus frequency was estimated at 887 Hz with an estimated test–retest reliability of 3/4th octave. It seems counter-intuitive that the subject required 20 measurements to achieve precision criterion and had comparatively poor estimated reliability despite 20 identical pitch matches. However, these are not at all unusual given the framework of the model. The subject’s tinnitus frequency appears to be unusually low compared to the prior, which was centered at about 7000 Hz. The result was that quite a bit of data was needed to convincingly produce an estimate as low as the pitch matches provided. Any small deviation from 800 Hz will result in a large octave-scaled difference between test and retest. The comparatively large 3/4th octave reliability is also a consequence of the prior selection in conjunction with this patient’s unusual tinnitus frequency.

To illustrate the prior effects, we reanalyzed subject 1253’s data with the n₀ parameter set to 0.1. This leads to a more diffuse prior that accepts more varied tinnitus configurations. The result was that only eight pitch matches were needed to achieve precision criterion and the estimated reliability was about 1/3rd octave between test and retest, which seems more sensible. Unfortunately, reducing the n₀ parameter also results in more pitch match elicitations needed for the other subjects and comparatively poorer reliability estimates. It is a simple fact of Bayesian analysis that more diffuse priors admit a wider range of plausible tinnitus frequencies and reliabilities, but also increase sampling requirements for subjects that are close to the center of the prior distribution.

DISCUSSION

The tonal frequency of a patient’s tinnitus is unobservable and is almost always estimated by pitch matching. However, pitch matching is deemed unreliable so that several pitch matches are needed to estimate tinnitus frequency. Unfortunately, it is impossible to recommend a fixed minimum number of pitch matches because patients can vary widely in their reliability. A dynamic algorithm for estimating tinnitus frequency on a case-by-case basis was needed. Our approach applied Bayesian sequential analysis of successively elicited pitch matches to update the tinnitus frequency estimate until an acceptable level of precision was achieved. This approach yielded tinnitus frequency estimates that were within one-quarter octave of their true value with 90% certainty for 7 of 10 subjects. Six of the seven subjects achieved acceptably precise tinnitus estimates within six pitch matches.

It is noteworthy that, of the three subjects who provided the least reliable results (subjects No. 1248, 1251, and 1252), two had the poorest high-frequency thresholds (1248 and 1251) and one had the poorest low-frequency thresholds (1252). Subjects with poor hearing sensitivity pose a unique problem for psychoacoustic testing of tinnitus. Hearing sensitivity ranges up to about 20 kHz for normal-hearing people. Testing in the extended frequency range has been validated for ototoxicity monitoring (Fausti et al. 1993), and our TES has been validated for testing up to 16 kHz (Henry et al. 2000). It is well-known that about 90% of patients with tinnitus have some degree of hearing loss; thus, many of these patients would not be capable of providing responses to 16 kHz. The TES is programmed to test up to the highest frequency that is responded to by a patient. For example, if a patient does not respond to threshold testing above 8 kHz, then the system will only conduct loudness matching and pitch matching through 8 kHz.

An obvious question is what if a patient’s perceived tinnitus frequency is above the frequency for which thresholds are obtained? This concern could be resolved somewhat if the maximum output levels were increased to above what is currently possible. Otherwise, patients who cannot respond to the highest available frequencies could have a perceived frequency that cannot be matched. Fundamentally, this is a problem of potential bias in the pitch match protocol. Bias is a systematic departure of the pitch match from the true tinnitus frequency, and many causes of bias can be imagined. The most obvious is outright deception by the patient. This limitation must be acknowledged, although any form of tinnitus psychoacoustic testing would have the same limitation.

There are Bayesian approaches to handling bias (e.g., Spiegelhalter et al. 2004), though these require strong prior judgments about the magnitude and direction of bias, and implementing these methods involve sophisticated computational approaches. These approaches may not be ready for clinical application any time soon, though are well within the scope of laboratory research.

Previous research suggests that tinnitus frequency can depend on pathological conditions and hearing loss configuration. The largest available surveys of tinnitus pitch matches show that, in the majority of patients, the pitch is at or above 3000 Hz (Meikle & Taylor-Walsh 1984; Meikle 1995; Reed 1960). Even so, there appears to be a striking and very orderly inverse relationship between the pitch of tinnitus and the severity of hearing loss (Meikle 1995). In that study, patients with the lowest tinnitus pitch matches tended to have the greatest hearing loss, both in terms of the extent of loss and the frequency range affected. Conversely, those with the highest-pitch tinnitus tended to have the least hearing loss. Nodar and Graham (1965) compared pitch matches for subjects with Meniere’s disease, conductive hearing loss, and sensorineural hearing loss. All Meniere’s subjects had pitch matches below 1000 Hz (median 320 Hz), which agreed with findings of Walsh (1956), Caparosa (1963), and Day (1963). The conductive hearing loss group had a median pitch match of 490 Hz (range 90–1450 Hz), which differed significantly from the sensorineural group (median 3900 Hz, range 545–7500 Hz) in agreement with the findings of Graham and Newby (1962).

The fact that tinnitus frequency varies among clinical subpopulations does not indict or even change our approach to tinnitus frequency estimation. However, a more careful selection of priors is advisable. If sufficient resources are available to the clinician, a reasonably large number of patients in the subpopulation of interest can be recruited and tested, and the hierarchical model described in the Supplemental Appendix A (http://links.lww.com/EANDH/A161) applied. A simpler approach is to use our prior with a smaller value of n₀. Different values of n₀ indicate different weighting of the prior on the posterior estimate of the tinnitus frequency. In the analyses shown in Figure 2 and Tables 1 and 2, we set n₀ = 1, meaning that the prior is equivalent to one pitch match on a patient. We might consider reducing n₀ to 0.5 or 0.1, meaning that we place less emphasis on the prior. For our sample, we tested the results with n₀ set to 0.1 and achieved our precision-based stopping criteria at six or fewer tests for all subjects except 1248, 1251, and 1252, who, as before, never meet satisfactory performance. As noted in the results section, subject 1253 achieved the stopping criteria after only eight pitch matches, since the new prior weighting admits a much wider range of tinnitus frequencies with higher probability. In the absence of a clinically relevant sample for establishing a new prior model, we recommend setting n₀ to 0.1 in a clinically distinct subpopulation, such as patients with Meniere’s disease or conductive hearing loss.

TABLE 1.

Worked example of the pitch match calculations given by the recursive equations listed in the text

i	Pitch Match (kHz)	log2 Pitch Match	ni	vi	θi	Si	Tinnitus Frequency (Hz)	Bayesian Lower 90% Limit(Hz)	Bayesian Upper 90% Limit (Hz)	Precision (Octaves)	Reliability (Octaves)
1	4000	11.97	2	2.73	12.37	0.55	5280	2784	10012	0.92	0.50
2	6340	12.63	3	3.73	12.45	0.59	5612	3856	8167	0.54	0.45
3	6340	12.63	4	4.73	12.50	0.61	5786	4432	7552	0.38	0.41
4	5040	12.30	5	5.73	12.46	0.65	5628	4563	6942	0.30	0.38
5	8000	12.97	6	6.73	12.54	0.86	5968	4902	7265	0.28	0.40
6	6340	12.63	7	7.73	12.56	0.87	6020	5097	7109	0.24	0.38

The index i denotes the sequentially ordered pitch matches.

Ultimately, clinicians will likely adopt an entirely different paradigm for tinnitus frequency estimation. For example, Penner (1992) used the forced-choice double staircase (FCDS) method to measure tinnitus pitch repeatedly and obtained standard deviations that were much smaller than those obtained in pitch-match studies. The FCDS procedure as described in their study would be too time-consuming for clinical use. The procedure can be modified, however, to be conducted rapidly, which we accomplished for our previous study. Combined with a full tinnitus psychoacoustic battery, however, adding the shortened FCDS was too difficult for the majority of subjects in that study, resulting in unreliable data. For that reason, we do not plan to continue using the FCDS to identify the tinnitus frequency. However, investigators are encouraged to continue looking for novel approaches to tinnitus frequency estimation.

Clinical audiologists often obtain measures of tinnitus perception (Henry & Meikle 2000; Henry 2004; Hiller & Goebel 2007). Although the clinical value of these measures is questioned, they currently are used most commonly to enhance counseling. Additionally, pitch matches are obtained with different sound therapy techniques to spectrally shape the auditory stimulus (e.g., Vernon & Meikle 2000; Davis et al. 2007; Stracke et al. 2010). When pitch matching is repeated, however (even within a session), the responses typically vary over 2 to 3 octaves (Penner 1983; Tyler & Conrad-Armes 1983; Burns 1984; Henry et al. 2004). With the known variability of pitch matches, the validity of any approach that is based on the pitch match must be questioned. It is therefore essential to establish a pitch matching method that provides a more accurate estimate of the perceived tinnitus frequency.

Conclusions

We have developed an approach that combines prior experience and expertise with sequentially observed pitch matches to estimate the frequency of a patient’s tinnitus. The approach is flexible enough to allow different clinicians to modify the protocol for their own prior beliefs by downplaying the prior weight. Though relatively simple, we are sensitive to discomfort that clinicians may have with the level of computation. Modern, portable computing power should greatly facilitate the application of this methodology.