Quantum Plasmonics: Optical Monitoring of DNA-Mediated Charge Transfer in Plasmon Rulers

Gold and silver nanoparticles (NP) exhibit unique optical properties in the visible range of the electromagnetic spectrum where the incident light excites coherent collective electron oscillations (plasmons) of conduction band electrons in these nanoscale structures.^[1] If two particles approach each other to approximately one NP diameter (D), the plasmons of the individual NPs couple, which confines and enhances the electromagnetic field in the gap between the NPs by orders of magnitude.^[2] The distance dependent near-field coupling between the NPs leads to spectral shifts in the far-field,^[3] and an accurate characterization of distance dependent plasmon coupling between NPs has been subject of intense experimental and theoretical research.^[4] In general, two distinct coupling regimes can be differentiated. The classical electromagnetic coupling regime is dominated by capacitive coupling in which the dominating longitudinal bonding dipolar plasmon mode (BDP) continuously red-shifts with decreasing interparticle separation, S. An intuitive physical model to approximate the distance dependent plasmon resonance wavelength, λ_res, in this regime is the so-called universal scaling relationship.^{[5, 6]} This model fails at very short interparticle separations where the classical electromagnetic coupling breaks down as quantum mechanical tunneling between the NPs reduces the charge pileup on both sides of the gap.^{[7, 8]} As a consequence, the BDP resonance wavelength does not continue to red-shift with decreasing S but instead stagnates or even blue-shifts. Provided sufficient current density, a tunneling charge transfer plasmon (tCTP) can then also be detected at a significantly longer wavelength than the BDP.^{[7, 9, 10]} The plasmon driven charge transfer between NPs in the quantum plasmonic regime is currently of high interest for developing new non-linear spectroscopies,^[11] sensors,^[12] and potentially catalysts.^[13]

The probability for electrons to tunnel between two individual NPs decays exponentially with interparticle separation and typical threshold separations, S_thresh, for the detection of quantum mechanical tunneling are on the order of S_thresh ≤ 0.5 nm.^[14] If molecules in the gap connect the gap defining NPs, this separation can be increased by through bond tunneling.^[15] Nijihuis and coworkers have shown that in the case of silver nanocubes functionalized with a self-assembled monolayer of the small molecule 1,4-benzenedithiolates (BDT), through bond tunneling results in sufficient charge transfer to generate a detectable charge transfer plasmon up to S = 1.3 nm. This separation represents the maximum spacing accessible with BDT.^[10] If BDT is replaced as linker between individual NPs by DNA, one obtains the so-called plasmon ruler (PR), which allow much longer interparticle separations and whose properties in the classical electromagnetic coupling regime have been investigated in detail.^{[16, 17]} Due to its specific four base code, DNA is a uniquely programmable and widely used scaffold for NP assemblies. DNA is, however, more than a simple non-conducting structural building block. Charge transport in DNA has been investigated in detail and though research continues to uncover new insights into the conductive behavior, it is thought that charge transfer occurs via coherent tunneling for separations up to 3 nm after which incoherent charge hopping dominates.^[18] A non-zero DNA conductivity raises the question how the presence of the DNA impacts the coupling between DNA connected NPs in PRs and other DNA-NP hybrid structures. Although one early study indicated the existence of a distinct quantum plasmonic and a classical electromagnetic coupling regime in silver PRs,^[17] the properties of PRs in the quantum plasmonic regime and the effect of a potentially increased DNA-mediated tunneling on plasmon coupling remain insufficiently characterized. In this Communication, we combine spectroscopy and quantum corrected electromagnetic simulations^{[14, 19]} to explore the role of DNA mediated charge transfer in PRs and present experimental evidence of DNA mediated optical tunneling in PRs for separations as long as 2.8 nm.

One requirement for probing the potential role of DNA in promoting direct charge exchange between the NPs in the quantum plasmonic regime is the ability to consistently assemble PRs with very short gaps. To that end, we used assembly strategy A1 outlined in Figure 1A. Two flavors of NPs (D = 38.5 ± 4.6 nm) functionalized with self-assembled monolayers of complementary 40 nucleotides (nts) long single-stranded DNAs were annealed in 60 mM NaCl in 10 mM Tris buffer for 5 minutes after which non-thiolated complementary DNAs were added to “quench” the reaction and to prevent the formation of larger clusters. For more details regarding the assembly and characterization of the PRs used in this work, please refer to the Supporting Information. The PRs were immobilized on a polylysine coated carbon film to measure S values on the single dimer level by high-resolution transmission electron microscopy (TEM). The dimers showed a narrow S distribution (Figure 1B) with an average S of 1.5 ± 0.5 nm. To generate PRs with longer S, we applied assembly strategy A2 (Figure 1A). Here, we reduced the number of DNA tethers in the PRs by replacing the number of complementary tether DNAs on one of the NPs by a shorter 20 nts spacer DNA. After 48 hours of incubation in 60 mM NaCl in 10 mM Tris buffer, complementary DNA was again added to stop the formation of larger agglomerates and to convert all single-stranded DNA into double-stranded DNA. The S value distribution of these PRs as determined by TEM is significantly broadened and shifted to longer gap width (Figure 1B). The average S was determined as 10.8 ± 7.7 nm. For both classes of PRs, A1 and A2, we assembled PRs with adenine-thymine (AT) or cytosine-guanine (CG) rich DNAs (see m) to evaluate potentially sequence specific differences in the conductivity.^{[20, 21]} The AT/CG composition of the 20 nts long surface passivating DNA in A2 mimicked that of the long DNA tethers.

Figure 1.

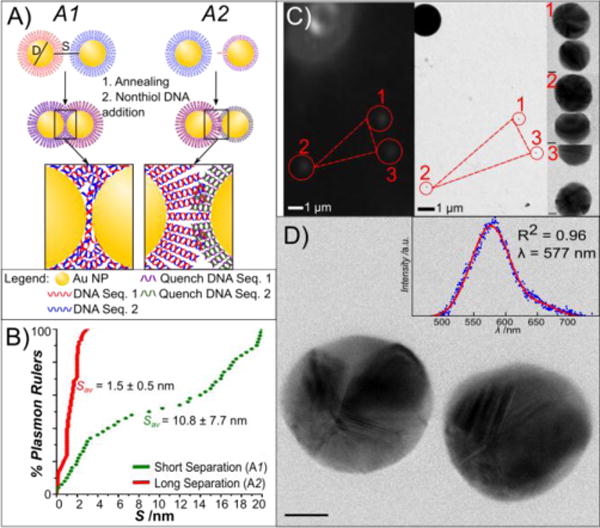
DNA-programmed self-assembly of PRs and correlated spectral/structural characterization. A) Scheme of PR assembly strategies. Approach A1 uses a high density of hybridizing DNA, whereas synthesis approach A2 uses a 1:1 ratio of handle DNA to NP. B) Cumulative probability distribution plots of the interparticle separation, S, for assembly strategies A1 and A2. Gap separations over 20 nm were not considered as PRs. C) Correlation of darkfield microscopy/spectroscopy (left) and transmission electron microscopy (right). NP patterns (here marked 1–3) in the vicinity of PS marker beads are used to localize PRs characterized by optical spectroscopy in the TEM at low magnification (210x). Images are then recorded at higher resolution (180kx) to obtain structural details of the PRs, shown to the left of the image. D) Correlated TEM image and darkfield spectra (inset) of a PR. Scale bar is 10 nm.

To obtain BDP resonance wavelengths of individual dimers with known S, we combined darkfield spectroscopy with high-resolution TEM (Figure 1C) of the same field of view to correlate elastic scattering spectra and structures on the single PR level.^[22] The PRs were immobilized on a polylysine treated TEM grid, immersed in index-matching glycerol and then first characterized by optical spectroscopy to avoid any changes induced by the electron beam.^[22] After the spectral analysis, the glycerol was removed by rinsing with methanol and the samples were transferred into the TEM for optical inspection. We validated in control experiments that the glycerol treatment did not affect the interparticle separation of the surface immobilized NPs (Figure S1, Supporting Information). The alignment of the darkfield and TEM images was alleviated by polystyrene beads (2 μm) bound to the TEM grids. The beads formed easily detectable patterns in both optical and electron microscopy (Figure 1C), which allowed the identification of PRs previously characterized by optical spectroscopy in the TEM. The structure of the individual PRs was characterized with a spatial resolution of down to ~1 Å. Figure 1D shows an example of a paired TEM image and scattering spectrum for an arbitrarily chosen PR obtained with assembly strategy A2.

The NPs used in this study show a natural distribution in size and shape, which influences the PR spectral response. As this work focuses on the distance dependent aspect of plasmon coupling in dimers with very short interparticle separations, we included only PRs containing NPs with a maximum diameter of D = 38.5 ± 4.6 nm and with an aspect ratio < 1.2. Asymmetrical dimers, whose NP diameters deviated more than 15%, were also removed from the analysis. The peak BPD resonance wavelength (λ_res) for the individual PRs was determined from Gaussian fits to the scattering spectra (Figure 1D) after background subtraction and normalization by the profile of the excitation light profile. The monomer resonance wavelength of λ₀ = 562 ± 4 nm was obtained as average of 30 spherical monomeric NPs. Figure 2A summarizes the resulting normalized spectral shift Δλ/λ₀, where Δλ = λ_res − λ₀, as function of the ratio S/D, for PRs containing AT or CG rich DNAs. Figure 2B compares the Δλ/λ₀ distributions for PRs with short separations (yellow shaded area in Figure 2A) and AT or CG rich DNA tethers, indicating that there is no observable difference in the Δλ/λ₀ distributions between the sequences used. We will discuss this point in more detail below. Overall, we characterized 165 PRs with separations between S = 0.5 nm and S = 40.9 nm. Those PRs with S values significantly longer than the DNA contour length (15.9 nm) reflect a small fraction of PRs whose DNA tether rips during the immobilization on the TEM grid. As the NP plasmons still couple at this separation, we included these dimers in Figure 2A in order to map plasmon coupling over the largest possible distance range. Figure 2C provides tentative structural models for DNA tethered NPs in different distance ranges as marked in Figure 2A. Depending on the gap separation, the DNA structure changes from extended to bent to melted at very short separations.

Figure 2.

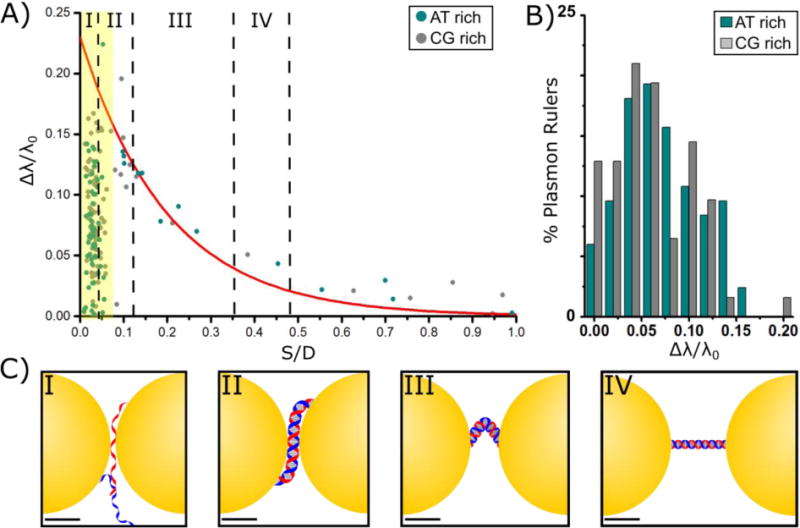
Distance dependent plasmon coupling in PRs. A) Normalized spectral shift, Δλ/λ₀, as function of the ratio of interparticle separation to NP diameter, S/D. Blue circles belong to PRs containing CG enriched DNA, black black circles correspond to PRs with AT enriched DNA. The continuous red line represents the universal scaling law prediction. The yellow area highlights S/D ≤ 0.07 (S ≤ 2.8 nm) where the experimental spectra deviate from the classical electromagnetic prediction. B) Histogram of Δλ/λ₀ for PRs containing CG enriched (blue) or AT enriched (gray) DNA. C) Possible DNA configurations at varying lengths. At longer separations than IV the DNA is ruptured and does no longer span the gap between the NPs. Scale bars are 10 nm.

The predicted distance dependence for Δλ/λ₀ according to the universal scaling law for plasmon coupling between two gold NPs is included in Figure 2A as red continuous line.^[6] For S/D > 0.07 (S > 2.8 nm) the measured Δλ/λ₀ for both the AT- and CG-rich sequences are in good agreement with the prediction, confirming that this separation range is dominated by classical electromagnetic coupling. However, for S/D ≤ 0.07 (S ≤ 2.8 nm) we observe a dramatic asymmetric broadening of the λ_res distribution. The measured wavelength shifts lie broadly scattered below the predicted Δλ/λ₀ values. The systematic blue-shift relative to the classical prediction indicates a weakening of the interparticle coupling.

The experimentally observed departure from classical electromagnetic coupling for S ≤ 2.8 nm is a first indication of an efficient charge transfer between the NPs reducing the charge density on both side of the gap. The sudden onset of the spectral broadening and decreased Δλ/λ₀ in Figure 2A is consistent with a coherent charge transport phenomenon, as incoherent charge hopping processes would result in a gradual (linear) decrease of conductivity as function of S.^[23] Importantly, the observed threshold separation S_thresh = 2.8 nm is close to the reported onset of coherent charge transport in DNA at 3 nm,^[24] which further supports the hypothesis of a direct tunneling through the DNA as cause for the spectral changes. However, nonlocal effects of the metal dielectric function also impact charge screening and spill out of electron density out of NPs in PRs with short interparticle separations.^[25] These effects are known to induce a relative blue-shift of the BDP in metal NPs, as well.

To verify the role of the DNA tether in determining the relative BDP blue-shift in PRs with S ≤ 2.8 nm we, therefore, compared the scattering spectra of identical PRs with and without DNA tether. To that end, we acquired the scattering spectra of at least 300 PRs obtained through assembly strategy A1 (average interparticle separation, S = 1.5 ± 0.5 nm) by hyperspectral imaging with a tunable filter before and after removal of DNA through mild plasma cleaning. In these experiments we used a series of monochromatic images recorded in 20 nm intervals between 500 nm and 700 nm to acquire the scattering spectra of all PRs in the field of view (143 × 143 μm²) simultaneously and determined the peak wavelength, λ_res, from the fitted spectra. The plot of the fitted λ_res before and after removal of the DNA for a representative field of view in Figure 3A–C illustrate a drastic red-shift of the PR spectra upon DNA removal. For the PR marked with a white + in Figure 3B and C we included the complete spectra before and after removal of DNA as obtained through hyperspectral imaging. The presence of a systematic spectral shift upon DNA removal is corroborated by a statistical analysis of the fitted λ_res values for all > 300 investigated PRs (Figure 3E).

Figure 3.

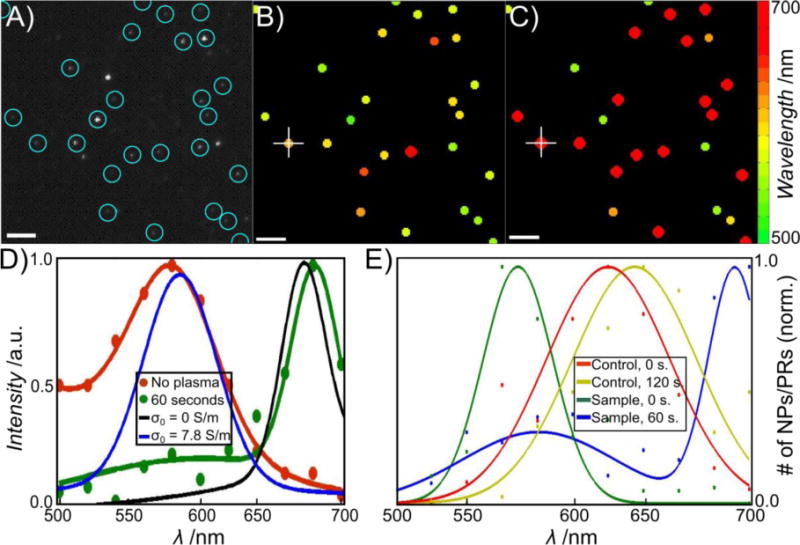
DNA removal through plasma cleaning red-shifts the plasmon resonance of PRs with short interparticle separation (average interparticle separation: S = 1.5 ± 0.5 nm). A) Monochromatic darkfield image of arbitrarily chosen field of view. PRs present before and after plasma cleaning are encircled. B) Peak wavelengths of the individual PRs before plasma cleaning as determined by hyperspectral imaging (see text). The peak wavelength is encoded in the color as given by the color map. C) Peak wavelengths of the same PRs after 60 seconds of plasma cleaning. D) Sample spectra obtained from hyperspectral imaging before (red) and after (green) plasma cleaning for the PR marked with white + in B and C. Simulated spectra of PRs before (σ₀ = 7.8 S/m) and after (σ₀ = 0) plasma cleaning are included in blue and black, respectively. E) Distribution of the fitted resonance wavelength of > 300 PRs with short interparticle separation before (green) and after (blue) plasma cleaning. The spectra after plasma cleaning are significantly red-shifted. Distributions for PRs with 80 bps spacer before (red) and after (yellow) plasma cleaning are included as larger interparticle separation control.

We performed two systematic controls to elucidate the nature of the large spectral shift observed upon removal of the DNA in PRs with very short interparticle separations. First, we systematically increased the average interparticle separation by assembling PRs with a 80 bps long DNA tether using strategy A2. The distribution of the resulting λ_res values is red-shifted and broadened when compared with that obtained for PRs with the average interparticle separation of S = 1.5 ± 0.5 nm before plasma cleaning (Figure 3E). Importantly, the λ_res distribution of the PRs with the longer DNA tether shows a much smaller red-shift upon plasma cleaning than the PRs with the very short interparticle separation. Furthermore, a closer analysis of the spectra of individual PRs before and after plasma cleaning reveals that the spectral shift of the 80 bps DNA containing PR distribution after plasma cleaning is primarily caused by a sub-population at the low energy side of the distribution (Figure S2, Supporting Information) whose initial λ_res values overlap with the spectral range of PRs with S = 1.5 ± 0.5 nm. In contrast, PRs with initial λ_res values consistent with classical electromagnetic coupling show only negligible red-shifts. In a second set of control experiments we compared the scattering spectra of individual DNA functionalized 80 nm gold NP before and after plasma cleaning. The two conditions resulted in nearly identical λ_res distributions (Figure S3, Supporting Information). Based on these controls, we rule out structural changes as cause for the plasma-cleaning induced spectral changes. Instead, we attribute the observed red-shift after plasma cleaning of PRs with short interparticle separations, S ≤ 2.8 nm, to the termination of a DNA-mediated charge transfer between the NPs upon removal of the DNA. The decrease in charge transfer between the NPs results in an increase of the charge polarization across the NP gap, which strengthens the capacitive plasmon coupling and accounts for the observed red-shift of the BDP.

To further validate the observed relative blue-shift of λ_res and to account for the observed spectral spread for S ≤ 2.8 nm, we applied the quantum corrected model introduced by Aizpurua, Nordlander and colleagues^{[7, 14, 19]} to simulate the effect of DNA-mediated coherent charge transfer on the distance-dependent optical tunneling between the NPs. In this model the tunneling current density in the gap is mimicked by a classical current density provided by an effective material placed in the gap (Figure 4A). We assumed that the current I in the gap experiencing a local E-field is determined by the conductivity of the DNA. For the sake of simplicity we assume a homogenous field and express I(ω) in the adiabatic limit as: I(ω)= G₀×E(ω)×S where G₀ is the static conductance of the gap. For a justification of the adiabatic assumption, please refer to ref^[14]. G₀ depends on the morphology of the gap and its conductivity as: G₀ = σ₀×A/S. Here, σ₀ is the static conductivity of DNA in the coherent tunneling regime and A is the cross-section of the conducting gap region, defined by the radius, R. We assumed a DNA conductivity of σ₀ = 7.8 S/m in our simulations. This value represents the average of the DC conductivities of AT enriched DNA and CG enriched DNA in the coherent tunneling regime.^[26] We validated in test-calculations that the difference in longitudinal conductivity between AT and CG DNAs did not result in a notable shift of the plasmon resonance (Figure S4, Supporting Information).^[21] This result is consistent with our experimental observations shown in Figure 2B. With σ₀ in hand, we calculated the effective permittivity for selected PR geometries (S, R, D were determined from the high resolution TEM images as shown in Figure 4B – D) as ɛ(S,A) = 1 + i4π σ₀(S,A)/ω and simulated the PR spectra using the finite difference time domain (FDTD) method for numerically solving Maxwell’s equations (see Supporting Information). Figure 4B – D compares the experimental and simulated spectra for selected PR geometries. Our results show that, provided the morphology of the gap region is correctly accounted for, simulation and experiment are in excellent agreement. In the next step, we assumed an average R = 10 nm and simulated λ_res as function of S. In the coherent tunneling regime (S < 3 nm) we assumed σ₀ = 7.8 S/m and we set σ₀ = 0.6 S/m for S > 3 nm consistent with a much lower conductivity of DNA over longer length scales.^[21] The resulting plot in Figure 4E successfully reproduces the main features of the experimental data. It shows an abrupt blue shift in Δλ/λ₀ relative to the classical electromagnetic coupling model at S/D ≅ 0.07 (S ≅ 2.8 nm) and for S > 2.8 nm the curve shows a continuous red-shift with decreasing interparticle separation. A plot of Δλ/λ₀ for σ₀ = 7.8 S/m and σ₀ = 0 S/m over the entire S/D range and the scattering spectra for a fixed S value (2 nm) but different σ₀ values are shown in Figures S5 and S6 of the Supporting Information for completeness. The reproduction of the main features in the Δλ/λ₀ vs. S/D relationship through the quantum corrected model with constant R in Figure 4E confirms that a correct prediction of the PR response at short interparticle separations with high local E-fields requires an explicit consideration of the DNA conductivity through coherent charge transfer. Furthermore, the almost perfect reproduction of the experimental PR spectra in the nonclassical regime through a quantum corrected model that explicitly considers the actual PR structure (Figure 4B–D) reveals that the observed broad spread of the measured resonance wavelength for S ≤ 2.8 arises from the strongly gap morphology dependent conductance.

Figure 4.

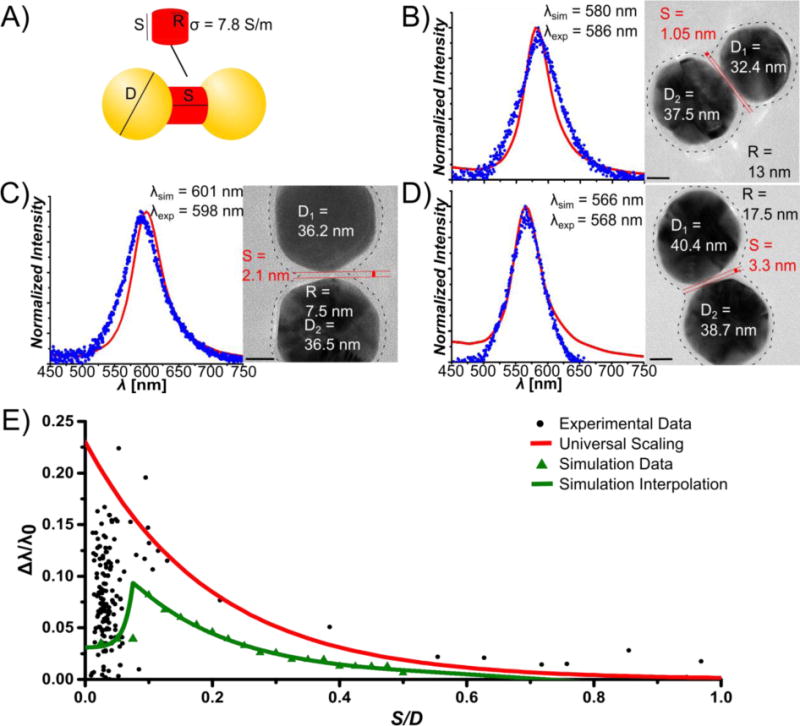
FDTD Simulations of Plasmon Rulers. A) Structural parameters for quantum corrected model containing a conductive junction to mimic tunneling through a DNA linker. B–D) Comparison of the simulated and experimental spectra for three selected PRs with minimum interpartice separations of S = 1.05 nm (B), S = 2.1 nm (C), S = 3.3 nm (D). The fitted experimental and simulated peak resonance wavelengths λ_exp and λ_sim are noted. TEM images for the individual PRs, together with the geometric parameters S, R, D are included. The circumference of the DNA corona around the NPs is indicated as dashed line. R was determined from the separation of the dotted lines in the center of the interparticle gap. E) Simulated Δλ/λ₀ vs. S/D plot (green triangles) assuming a quantum corrected model with a gap conductivity of σ₀ = 7.8 S/m for S < 3 nm and σ₀ = 0 for S > 3 nm (R = 10 nm). The universal scaling prediction (red line) and experimental data (black circles) are included for completeness.

In conclusion, chemical assembly strategies can create plasmonic gap structures with truly molecular dimensions, but the properties of the molecules in these electromagnetic hot-spots and their influence on the resonant properties of the coupled plasmonic system still pose many questions. We have demonstrated in this Communication that the conductivity of the DNA linker at short separations profoundly affects the spectral response of PRs in the quantum plasmonic regime and extends the range of coherent charge transfer between gold NPs to S_thresh ≈ 2.8 nm. Besides improving the fundamental understanding of the PRs, the characterization of PRs in the non-classical plasmon coupling regime has important tangible applications. For instance, in combination with the PR mediated ability to optically monitor the conductivity in the DNA containing gap region, DNA mediated tunneling up to S_thresh ≈ 2.8 nm paves the path towards utilizing changes in the tunneling current due to ion or protein binding to DNA as a new biosensor concept.