Automated segmentation of chronic stroke lesions using LINDA: Lesion identification with neighborhood data analysis

Abstract

The gold standard for identifying stroke lesions is manual tracing, a method that is known to be observer dependent and time consuming, thus impractical for big data studies. We propose LINDA (Lesion Identification with Neighborhood Data Analysis), an automated segmentation algorithm capable of learning the relationship between existing manual segmentations and a single T1‐weighted MRI. A dataset of 60 left hemispheric chronic stroke patients is used to build the method and test it with k‐fold and leave‐one‐out procedures. With respect to manual tracings, predicted lesion maps showed a mean dice overlap of 0.696 ± 0.16, Hausdorff distance of 17.9 ± 9.8 mm, and average displacement of 2.54 ± 1.38 mm. The manual and predicted lesion volumes correlated at r = 0.961. An additional dataset of 45 patients was utilized to test LINDA with independent data, achieving high accuracy rates and confirming its cross‐institutional applicability. To investigate the cost of moving from manual tracings to automated segmentation, we performed comparative lesion‐to‐symptom mapping (LSM) on five behavioral scores. Predicted and manual lesions produced similar neuro‐cognitive maps, albeit with some discussed discrepancies. Of note, region‐wise LSM was more robust to the prediction error than voxel‐wise LSM. Our results show that, while several limitations exist, our current results compete with or exceed the state‐of‐the‐art, producing consistent predictions, very low failure rates, and transferable knowledge between labs. This work also establishes a new viewpoint on evaluating automated methods not only with segmentation accuracy but also with brain–behavior relationships. LINDA is made available online with trained models from over 100 patients. Hum Brain Mapp 37:1405‐1421, 2016. © 2016 Wiley Periodicals, Inc.

INTRODUCTION

Studies of brain and behavior in clinical populations provide insight into functional organization and potential for recovery after brain damage. Stroke is one of the most frequent causes of brain lesion, with ∼610,000 new cases each year in the US alone [Mozaffarian et al., 2015]. Nearly 80% of stroke cases are ischemic, while the remaining 20% are hemorrhagic [Mozaffarian et al., 2015]. In either case, the lesion is usually abrupt and focal, allowing for damage to be demarcated on in vivo magnetic resonance or computed tomography neuroimages. This may not be true for other types of naturally occurring lesions, such as tumors, where the tissue might be displaced and the true extent of the damage might go beyond the signal abnormality observed in in vivo images [Anderson et al., 1990; Karnath and Steinbach, 2011].

The current procedures for lesion‐based analyses have two conflicting requirements. On one hand, lesions follow the pattern of the vasculature, creating highly correlated patterns of brain damage (that is, if a voxel is lesioned, the neighboring voxel is likely to be lesioned as well). Consequently, a large number of subjects is needed in order to differentiate functional specialization in neighboring brain areas [Kimberg et al., 2007]. On the other hand, the current gold standard for lesion segmentation is manual tracing, a procedure that requires time, knowledge, and effort, and is inconsistent from rater to rater [Ashton et al., 2003; Fiez et al., 2000]. To eliminate inter‐rater variability, studies often rely on the work of a single expert, who must personally trace or closely overlook the tracing process. While this solution works for studies with small sample size, it becomes increasingly impractical for studies with large sample size. The bottleneck created by performing manual tracings in studies that require large sample sizes is further highlighted by the wide availability of MRI scanners and the advent of big data science.

Computational algorithms propose to overcome this problem. Because these methods only approximate manual tracings, they must be tested for their reliability with respect to expert labelers. Conceptually, automatic algorithms fall primarily into two broad categories: (i) supervised methods that use machine learning to train the algorithm with manually traced lesion examples, and (ii) unsupervised methods that use mathematical models to achieve the best accuracy with tunable parameters. The number of images (or channels) required by the algorithm is another factor to consider. Monochannel algorithms use a single volume (i.e., T1, or T2, or FLAIR) to achieve the segmentation, while multichannel algorithms use parallel information from multiple volumes of the same subject (T1, and T2, and FLAIR). Algorithms that use multiple channels have access to more information, and typically offer higher predictive accuracy [Maier et al., 2015]. Multiple modalities, however, are not always available, and they increase acquisition times, patient burden, acquisition costs, and chances of motion related artifacts.

Independently of the category on which it falls, each automatic algorithm is typically created and tested to predict a specific lesion type; i.e., stroke [Mitra et al., 2014; Seghier et al., 2008; Shen et al., 2010; Stamatakis and Tyler, 2005], multiple sclerosis [Geremia et al., 2011; Jain et al., 2015; Roura et al., 2015; Schmidt et al., 2012], white matter hypointensities [Caligiuri et al., 2015], micro bleeds [Kuijf et al., 2012], etc. The accuracy of the method outside of the domain it was created for is typically scarce.

In stroke, lesion masks are often used to perform voxel‐based lesion‐to‐symptom mapping (VLSM), which reveals topologic and functional organization of cognitive systems [Bates et al., 2003; Committeri et al., 2007; Dronkers et al., 2004; Schwartz et al., 2009]. VLSM allows researchers to achieve greater statistical rigor by using population data to evaluate and expand models of functional organization beyond single‐case studies. Lesions masks are also used in predictive models that attempt to estimate the clinical recovery of patients who suffer stroke [for a review on prediction studies, see Gabrieli et al., 2015; Hope et al., 2013; Seghier et al., 2016; Wang et al., 2013]. To obtain lesion masks automatically from stroke patients, several groups have proposed specific workflows [Mitra et al., 2014; Seghier et al., 2008; Shen et al., 2010; Stamatakis and Tyler, 2005]. While overlap and displacement measures are used to investigate the accuracy of these methods, the impact of automated lesion segmentation on neurobehavioral analyses, such as VLSM, is unknown. For example, predicted lesion maps may contain systematic error in certain areas of the brain, or may not follow the complex spatial shape of lesions. Such errors may accumulate in a population and lead to unreliable or misleading VLSM results. If automated methods are to be of real practical use, it is critical to investigate not only segmentation overlap measurements but also the impact on inferences such as neurocognitive organization or prediction of clinical course. Another pitfall of many proposed methods is that they are tested on limited samples of real cases. This increases the risk of the method to be less accurate when applied to independent datasets with more variability (i.e., see Wilke et al., 2011 for an example). These effects highlight the need to test automated predictions on larger sample sizes.

In this study, we propose a supervised lesion segmentation algorithm named Lesion Identification with Neighborhood Data Analysis (LINDA). This method performs hierarchical improvements of lesion estimation from low to high resolution, considering both the signal in the voxel itself and the signal of neighboring voxels. The consideration of neighborhood voxels enables the algorithm to learn rules based on the surrounding context, an ability that is required to perform conditional segmentation. For example, recent guidelines for expert manual tracing suggest that white matter hyperintensities should be labeled as lesion only if they extend from the core ischemic zone [Crinion et al., 2013]. Voxel‐based classification methods cannot learn this rule. Also, recent evidence has demonstrated that the inclusion of regional neighborhood information significantly improves the accuracy of automated predictions [Ozenne et al., 2015]. LINDA uses a new computational platform proven successful in the implementation of segmentation algorithms [i.e., tumor segmentation, Tustison et al., 2015, winner of the BRATS 2013 challenge]. For a proper testing, LINDA was applied on a consistent sample of 60 left hemispheric stroke brains and validated with k‐fold and leave‐one‐out procedures. To investigate error accumulation with automated predictions and impact on cognitive neuroscience hypothesis testing, we also compared VLSM maps obtained from manual tracings with those obtained with LINDA. Finally, we verified the algorithm's performance on data collected at another institution. Thus, a series of advantages are introduced compared to previous work, such as, a large number of patients (∼100), investigation of prediction stability, investigation of cross‐institutional applicability, and comparative LSM analyses on manual vs. predicted lesion maps.

METHODS

Patients

The method was developed and tested on a set of 60 patients with chronic left hemispheric stroke (age: 57.2 ± 11.5 yrs, post‐stroke interval: 2.6 ± 2 yrs, 26 female). Patients were part of an ongoing project aimed at investigating the mechanisms of language disruption following brain lesions caused by stroke [Kimberg et al., 2007; Mirman et al., 2015a; Schwartz et al., 2009, 2011, 2012; Thothathiri et al., 2012; Walker et al., 2011; Zhang et al., 2014]. All patients were medically stable, without major psychiatric or neurological disorders, premorbidly right‐handed, native English speakers, and preliminary tests showed adequate vision and hearing abilities.

Lesion size was 68 mL ± 64 mL (range 5–288 mL) in native space and 69 mL ± 61 mL (range 5–256 mL) in template space. The average post‐stroke interval at which the scans were obtained was 32 ± 32 months (range 3–154 months).

Controls

Neuroimaging data from 80 healthy controls was used as reference for some of the features. The control group was matched for age and gender with the stroke patients (mean age: 59.2 ± 13.5 years, 34 female), and their neuroimaging data were collected from the same scanner used for patients.

Image Acquisition

Neuroimaging data were collected at the University of Pennsylvania using a Siemens Trio 3T scanner. Both patients and controls were scanned during a similar 10‐year period (range 2004–2014, group comparison for date of acquisition W = 2144.5, P = 0.28). The T1‐weighted volume was acquired with a 3D inversion recovery sequence, consisting of 160 axial slices acquired with a TR = 1,,620 ms, inversion time = 950 ms, TE = 3.87 ms, FOV = 192 × 256 mm², voxel size = 0.98 × 0.98 × 1 mm. T1 volumes were visually inspected for each subject, and no volume with artifacts or motion was included in the study.

Manual Lesion Tracing

A single expert (HBC) either drew the lesions (approximately two‐thirds) or reviewed the tracings completed by individuals he had trained. MRIcron software (http://www.mricro.com/mricron/) was used to trace each lesion in axial orientation, on the same T1 volume later used for automated segmentation. The multi‐view mode was on at all times, such that the shape of the lesion could be understood from multiple orientations.

Complementary Stroke Dataset

A second dataset of 45 patients (age: 59.6 ± 9.5 years, post‐stroke interval: 3.6 ± 3.1 years, 17 female) was included at later stages of the study to validate the method with independent data. Patients were recruited for a clinical trial of transcranial direct current stimulation for aphasia (http://ClinicalTrials.gov #NCT01709383) and cross sectional multimodal MRI studies on post‐stroke plasticity [Xing et al., 2015]. Data were acquired on a Siemens TIM Trio 3T scanner at Georgetown University with the following parameters: TR = 1900 ms; TE = 2.56 ms; flip angle = 9°; 160 contiguous 1 mm sagittal slices; field of view = 246 × 256 mm²; matrix size = 250 × 250, slice thickness = 1 mm, voxel size = 0.98 × 1.02 × 1.0 mm³. Lesions were delineated manually on the T1‐weighted images in native space using MRIcron, and by a neurologist (P.E.T.). The lesion size for this dataset was 90 mL ± 68 mL (range 2–287 mL) in native space and 92 mL ± 71 mL (range 3–319 mL) in template space. All 45 patients were left hemispheric stroke cases, medically stable, and without major psychiatric/neurological disorders.

Software and Computational Platform

Computations were performed on a server cluster operated under CentOS 6.6 with multiple Xeon E4‐2450, 2.1GHz processors. The LINDA prediction toolkit was built on Advanced Normalization Tools [ANTs ver. 2.1.0; Avants et al., 2011] and its R implementation [ANTsR ver. 0.3.1; Avants, 2015]. Additional packages used in R were: randomForest [Liaw and Wiener, 2002], cocor [Diedenhofen and Musch, 2015], ggplot [Wickham, 2009], RcppArmadillo [Eddelbuettel and Sanderson, 2014], and caret [Kuhn, 2008]. The final prediction pipeline is available at http://dorianps.github.io/LINDA/. All statistical comparisons within and between groups were performed using Wilcoxon tests in R.

Accuracy and Comparison Metrics

The measures utilized to assess the accuracy of segmentations are:

Dice similarity coefficient

This is a spatial overlap index between two areas, ranging between 0 and 1. For example, a perfect overlap between predicted and manual lesions would be equal to 1, while no overlap at all would be equal to 0. The formula for its calculation divides the overlapping area by the sum area occupied by both masks, multiplied by two: “[(A ∩ B)*2/(A ∪ B)]”.

Hausdorff distance

This is a metric measure of the maximal displacement between two areas. It is calculated by computing all the possible distances from each contour point in map A to the nearest point in map B, and selecting the highest value [Hausdorff, 1962]; thus, it is the maximum value in the list of minimum distances between the estimated and the target segmentation.

Average displacement

This is a metric measure similar to Hausdorff, but rather than measuring the maximal displacement, it computes the average distance of the contours of manual and predicted lesion maps. Because displacement is measured as nearest point from one contour to the other, the measure is asymmetric with respect to which image is considered reference. To obtain a measure that considers displacement in both directions, we computed the displacement from both sides and averaged the values.

Sensitivity (or true positive rate)

It measures the proportion of lesioned voxels that are correctly identified as such.

Precision (or positive predictive value)

It measures the ratio between the number of correctly identified lesioned voxels and the total number of voxels predicted as lesioned.

Lesion volume

This is one of the most important predictors of cognitive dysfunction [Hope et al., 2013]. It is obtained by counting the lesioned voxels after bringing the lesion mask in template space. The correlation between predicted and manual lesion volumes was investigated, as well as any tendency of the automated prediction to underestimate or overestimate the lesion volume.

Other measures of accuracy measurement are available in separate files as Supplementary Material.

Image Preprocessing

Because of changes in scanner hardware/software, older scans showed more noise in the image than newer scans. To achieve a comparable noise level in all scans, noise‐reduction was applied to our dataset of 60 patients using an edge‐preserving anisotropic algorithm (Perona–Malik implemented in the “ImageMath“ function in ANTs). The conductance (or strength) of the noise reduction algorithm was linearly proportional to the year of the scan, from 0.8 for 2004 scans to 0.2 for 2009 and later scans. The number of iterations was kept fixed at 10. After noise reduction, all images were corrected for signal inhomogeneity with the N4 algorithm [Tustison et al., 2010, 2014], and the skull was removed with an automated algorithm (‘antsBrainExtraction.sh’ in ANTs).

Extraction of Features from T1‐weighted MRI

A series of 12 features was created from the T1‐weighted images available for each subject. Supplementary Material: Table 1 shows the 12 features and the basic scripting commands used in ANTsR to obtain them. Features were selected based on ease of computation, interpretability and complementarity. LINDA features capture aspects of: geometry, subject specific anomalies (e.g., asymmetry), deviation from an atlas, and deviation from controls. Geometric features include mathematical processing variants of the patient's T1 volume, such as, the gradient magnitude, laplacian and k‐mean segmentations. The subject specific anomaly was computed as an asymmetry measure by flipping the T1 in the Y‐axis and subtracting it from the unflipped image. Two features were created to measure the deviation from the atlas: the subtraction of the patient's T1 from the template, and the map of correlation values between the neighborhood of respective voxels in the template and the patient's T1. Deviation from controls was computed by subtracting geometry and anomaly features from the respective averages obtained in the 80 controls. Once created, all features were downsampled at 2 × 2 × 2 mm³ to reduce computation times during testing.

Table 1.

Regional lesion‐to‐symptom mapping

VLSM test	Regional correlations	Common top 3 t‐scores
Comprehension	0.59	1. Inf. frontal, triangular 2. Precentral gyrus
Repetition	0.93	1. Supramarginal gyrus 2. Superior temp. gyrus
Naming	0.75	1. Supramarginal gyrus 2. Rolandic operculum 3. Superior temp. gyrus
Auditory Discrim.	0.84	1. Superior temp. gyrus 2. Supramarginal gyrus
Rhyme Discrim.	0.72	1. Inf. frontal, triangular 2. Superior temp. pole

Values indicate Pearson correlation of the 37 regional t scores obtained with manual and predicted lesions. Common top 3 t scores show regions that are listed both in manual and in predicted RLSM analyses.

Selection of Best Features Using an Empirical Method

The 12 features described above might contain redundant information that is not useful for lesion segmentation. To improve computational efficiency for future applications, we selected the necessary features with a forward inclusion procedure as follows. The 60‐patient sample was split into a training group of 48 patients and a test group of 12 patients, both with similar lesion sizes (created with “createDataPartition” function in R). The two groups were kept fixed, and training‐test loops were run while incrementally adding features. The first time, a single feature was used for predictions (see next paragraph for detail), and the feature with the best dice overlap with manual segmentation was selected. The second time, models were built with the first winning feature and each of the remaining ones. Dice overlaps were obtained again with manual segmentation, and compared with the model with only one feature. The feature with the highest t‐score in paired t tests was added to the model. The procedure was repeated with a third feature, fourth feature, etc., until no further improvement was possible and the significance of paired t tests were all P > 0.1. This procedure is similar to a forward stepwise regression, where variables are added if they provide a significant gain in prediction.

Building the Trained Model in a Multi‐resolution Framework

The multi‐resolution voxel‐neighborhood random forest algorithm was utilized for lesion segmentation (“mrvnrf” command in ANTsR). Figure 1 displays the full algorithm with the “mrvnrf” workflow in the lower part. The algorithm works in the following manner. During training, a series of random forest (RF) models are trained at different image resolutions, starting at low resolution and ending at high resolution. At each level, a matrix containing data from all subjects is used to train the RF model. Each row of the matrix contains information about a single voxel of a single subject, and includes values from neighboring voxels on all features as columns. Thus the model is trained to classify voxels based not only on the value of the voxel itself but also on its neighbors. The status of the voxel (e.g., 1 = healthy, 2 = lesion) is used as ground truth outcome to train the RFs. Once training is performed at the coarsest resolution level, it is immediately applied to the same subjects in order to obtain a set of additional features consisting of posterior probability maps (i.e., posterior probability of healthy tissue, posterior probability of lesion). These new features are passed to the next (usually finer scale) resolution step together with the existing features, and a new RF model is trained at this resolution. Then, a new set of posterior probabilities are obtained and passed at the successive resolution step. This procedure is repeated hierarchically up to the highest resolution, and RF models are produced at all resolutions (i.e., three RF models for three resolution steps). Once the training is finished, the hierarchical prediction model can be applied to segment new cases. To predict the lesion map in new patients, the algorithm follows the same hierarchical steps, but uses the trained RF models to create the posterior probabilities at each resolution step and predict the unknown outcome/label. At the highest resolution, posterior probabilities are converted into a discrete segmentation map; i.e., each voxel is classified with the highest posterior probability at that voxel (i.e., 60% healthy and 40% lesioned is classified as healthy).

Figure 1.

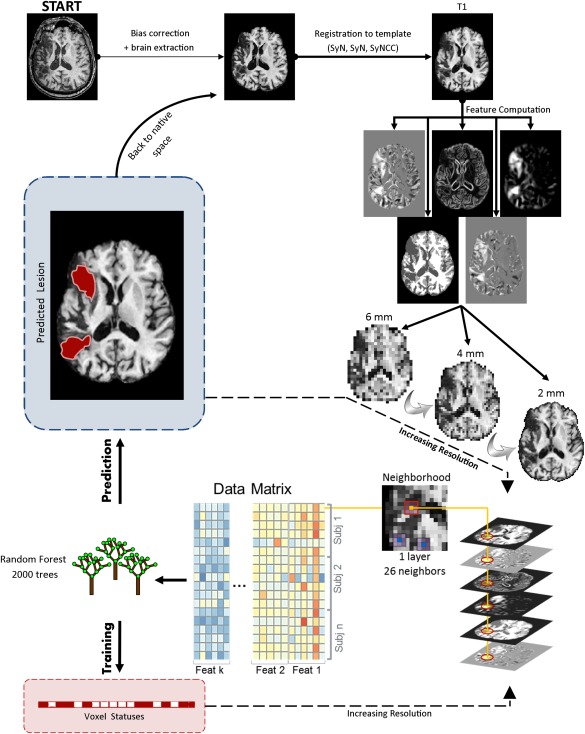
Depiction of the LINDA workflow. The multi‐resolution voxel neighborhood random forest algorithm is displayed on the lower part. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

In this study, we utilized three hierarchical steps with downsampling factors of 3, 2, and 1. Given our 2mm data, these steps correspond to image resolutions of 6, 4, and 2 mm (or volumes of 31 × 42 × 28, 47 × 63 × 43, and 94 × 125 × 85 voxels, respectively). The neighborhood radius was ‘1’ for all hierarchical steps, consisting in a single layer of 26 neighboring voxels surrounding the voxel of interest. Note that low resolution steps have larger voxels, and, consequently, the neighborhood information is wider (forming a 1.8 cm patch at the coarsest level). The number of trees in the random forest models was set to 2000, although the results are not heavily dependent on this value (assuming a reasonable minimum number of trees, e.g., 500).

If we combined all voxels and their neighborhoods from all features and all subjects, the memory and CPU requirements would be impossible to satisfy. Fortunately, RF training does not need information from every single voxel to learn the relationship between features and tissue classification. Therefore, we trained RFs with a subset of 200 randomly selected voxels from each tissue class (i.e., 200 lesioned voxels + 200 healthy voxels). We chose 200 from each label class in order to help balance the training paradigm. The mask from which voxels were selected was taken from the template segmentation, after setting to “lesioned” voxels in which at least 50% of the training subjects had a lesion.

Feature Extraction and Prediction of a New Test Image Using Register‐Predict‐Register Loop

All computations, feature creation, feature selection, and lesion predictions were performed in template space. Because both patients and controls were registered on the same template, we used a mixed template built from 208 elderly subjects (115 elderly controls and 93 patients with various diseases, such as, Parkinson's, fronto‐temporal dementia, mild cognitive impairment, and Alzheimer; template available online with the LINDA toolkit). The template was built with the ‘buildtemplateparallel.sh’ script in ANTs. The registration of lesioned brains to template is a delicate step that requires the elimination of the lesion from computations to avoid unrealistic deformations [Andersen et al., 2010; Ripolles et al., 2012]. Good template registration is also necessary because some features are computed as deviations from the template or from the control population. Thus, a good registration is a precondition for good automated segmentation. However, the lesion mask necessary to perform registration is not known for new cases. To resolve this dependency, we developed LINDA in two stages, a partially automated stage and a fully automated stage. During the partial stage, we investigated the prediction routine with registrations that used manual lesion masks during template registration. At this stage, we performed feature selection (see section “Selection of best features using an empirical method” above) and evaluated the stability of predictions when the training group changed randomly. To investigate prediction stability, we ran a six‐fold validation for ten times. The six‐fold procedure consists in randomly splitting the patients in six groups (N = 60/6 = 10) and predicting each group (N = 10) with a model trained on the remaining subjects (N = 50). This process was repeated 10 times with random grouping, and, consequently, each subject received 10 lesion predictions. The variance between the 10 predictions was investigated as an indicator of performance stability.

After investigating the prediction routine at the partially automated stage, we finalized the automatic pipeline by running “register‐predict‐register” loops. This process is designed to gradually improve both the registration and the prediction accuracy. The loops started by computing an approximate lesion mask from the subtraction of the T1 image to its own reflection on the Y axis (flipped, affine registered to itself, and subtracted). This mask roughly exposed the lesion and allowed to initiate the cycles with a first registration to template. Following the first registration, a lesion prediction was obtained in template space and backprojected in subject space. The predicted lesion mask constituted the cost function mask necessary to obtain a second registration to template. After the second registration, another lesion prediction was obtained in template space and backprojected in subject space, and so on. In total, three iterations were performed, the first two with a fast nonlinear registration to template (5 min on a single CPU core, option “SyN” for antsRegistration function in R), and the last with a robust cross‐correlational registration (∼70 min computation, option “SyNCC” for antsRegistration function in R). Following the third registration, one last lesion prediction was obtained in template space, and was considered final.

The Number of Tissues to Segment

LINDA learns the difference between lesion and nonlesion through manual segmentation examples that have a discrete value (i.e., 1 = healthy brain, 2 = lesion). However, the number of tissues on which the model is trained may impact the quality of segmentation. For example, a model that is trained on more tissues (WM, GM, CSF, and lesion) can explain more variance in the image, and might distinguish better the lesion. To investigate the validity of this hypothesis, we compared results obtained two‐class (healthy and lesion) and four‐class (CSF, GM, WM, lesion) models. For two tissue classes, the algorithm was trained with a composite image where the manual lesion (label 2, damaged) was added to the brain mask (label 1, healthy). For four tissue classes, the algorithm was trained with a composite image where the manual lesion (label 4, damaged) was added to the k‐mean segmentation image, which originally contained three tissue classes (CSF, GM, WM). The accuracy of the prediction of the two variants was measured with respect to manual tracing, and the best achieving option was selected for future use.

Computational Considerations

All individual predictions were performed with a leave‐one‐out procedure. The training of the model on 59 examples required ∼4 h on a single CPU core at 2.1 GHz, and ∼25 Gb of memory. While we performed this step many times for the purpose of this study, training is normally a one‐time process that produces the model for future use. When applying LINDA to new cases, the amount of memory needed is ∼7 Gb, and the total time required is ∼3 h. Within this arc, time is spent on skull stripping (∼25 min), three registrations (two of 5 min each, one of ∼70 min), three predictions (∼2 min each), and other steps such as feature generation, image reflection, etc.

Lesion‐to‐Symptom Mapping Validation

Comparative analyses of lesion–behavior relationships were performed between predicted and manual lesions. All LSM analyses were performed in R. Five language measures were tested: (i) “Comprehension” subscore from WAB [Kertesz, 1982], (ii) “Repetition” subscore from the WAB, (iii) accuracy of “Naming” of pictures in the Philadelphia Naming Test [PNT; Roach et al., 1996], (iv) “Auditory Discrimination” of phonemes [Martin et al., 2006], and (v) “Rhyme Discrimination” for words played from tape [Freedman and Martin, 2001]. Recent work has shown that post‐stroke interval is a major contributor in the variance of cognitive scores [Hope et al., 2013]. For such, we regressed out the variance explained by this variable and utilized residualized scores. LSM analyses were performed both voxel‐wise (VLSM) and region‐wise (RLSM). For VLSM, a standard procedure was followed consisting in massive t‐tests on voxels lesioned in more than 10% of the subjects [Bates et al., 2003; Dell et al., 2013; Schwartz et al., 2012]. Approximately 30,000 voxels satisfied this criterion for manual or predicted lesions. Single tailed P values of t tests were corrected for multiple comparisons with the false discovery rate method [FDR, Benjamini and Hochberg, 1995; Genovese et al., 2002; Rorden and Karnath, 2004], and results were thresholded at α = 0.05. Finally, thresholded t‐maps were smoothed with a 3.5‐mm kernel. Continuous dice was used to compare manual vs. predicted t‐maps. Continuous dice is similar to standard dice, but it considers also discrepancies in continuous data; it is calculated as sum(2×min(A|B))/sum(A+B) where A and B are the t‐maps. To understand the potential displacement of the most relevant voxel in VLSM analyses, we computed the peak‐to‐peak distance between manual and predicted VLSM maps. Finally, the Pearson correlation between t values of voxels included both in manual and in predicted LSM was obtained (∼26,000 voxels in common).

For RLSM analyses, the parcellation from the AAL atlas [Tzourio‐Mazoyer, et al., 2002] was overlaid on each subject's lesion map, and the number of lesioned voxels was counted for each AAL region. Regions in which fewer than 10% of the subjects had lesions were eliminated from the analyses. After applying this criterion, 37 left hemispheric regions were included in the analysis. RLSM analyses were performed by running linear regressions between the cognitive score and the regional lesion values. Results were thresholded at α = 0.05 after correcting with the FDR method. To compare RLSM obtained with manual and predicted lesions, the array of 37 t scores obtained from manual lesions was correlated with the array of 37 t scores obtained from predicted lesions. Moreover, we investigated whether the top significant regions obtained with predicted lesions corresponded to those obtained with manual lesions. This matching was performed by listing the top three most significant regions from both manual and predicted lesions, and marking those regions that were listed on both sides.

RESULTS

Stepwise feature selection identified six features that gradually improved the dice overlap of prediction with manual segmentation (in order of selection): (1) deviance of k‐mean segmentation from control average, (2) gradient magnitude, (3) deviance of T1 from controls, (4) k‐mean segmentation, (5) deviance of T1 asymmetry from controls, and (6) raw T1 volume. No other feature improved the prediction any further.

Partially Automated Stage

During this stage, lesion predictions were performed with a two‐tissue‐class model (1 = healthy, 2 = lesion) and stability measures were obtained from six‐fold validation. The comparison of the ten predictions obtained for each subject showed an average dice between predictions of 0.94 ± 0.01 and average Hausdorff distance of 5.4 mm ± 2.8 mm. The average overlap of each individual's predictions with manual tracing was 0.72 ± 0.30. The average standard deviation of the ten prediction dice overlaps was ±0.026 in average. These results show that models created from different groups lead to similar predictions on new subjects, producing stable and robust results independently of the examples used for training.

After establishing prediction stability, a leave‐one‐out procedure was used at all times (i.e., train on 59 patients, predict one). At the partially automated stage, the average dice overlap of leave‐one‐out prediction with manual tracing was 0.718 ± 0.15 and Hausdorf distance was 19 ± 11 mm.

Fully Automated Stage

At this stage, the pipeline was extended to include fully automated registration and prediction. First, the number of tissue classes used to train the model was investigated. The overlap with manual segmentations was slightly higher for four‐tissue‐class predictions (0.696 ± 0.16) compared to 2‐tissue‐class predictions (0.679 ± 0.19), a difference that was statistically significant (gain 0.018, W = 406, P = 0.007, paired test). A similar improvement was observed with decreased Hausdorff distance (19 mm vs. 20 mm, gain −1.15 mm, W = 406, P < 0.001) and decreased average displacement (2.54 mm vs. 2.72 mm, gain −0.18mm, W = 526, P = 0.004). The correlation of manual lesion volume with predicted lesion volume was excellent with both options, but the four‐tissue‐class showed a significant improvement (Pearson r: 0.961 and 0.952, respectively; Hotelling's t[57] = −2.89, P = 0.005; comparison between correlations performed with package “cocor” in R). Given the overall advantage of the four‐tissue‐class predictions, this option was selected for future use.

To investigate the cost of shifting from partially automated to fully automated predictions, we compared respective measures obtained with four‐tissue‐class predictions. A small but significant drop in accuracy was observed when predictions shifted to fully automated. Dice overlap decreased by 0.022 (from 0.718 to 0.696, W = 1424, P < 0.001) and average displacement increased by 0.22 mm (from 2.32 mm to 2.54 mm, W = 1357, P = 0.001). No change was observed in Hausdorff distance (both 19 mm, W = 813, P = 0.92). The predicted lesion volumes correlated similarly with manual lesion volumes whether obtained with fully automated or partially automated procedures (0.961 and 0.954, respectively; Hotelling's t[57] = 1.5, P = 0.12). However, lesion volumes obtained from partially automated predictions slightly underestimated the lesion volume (W = 1231, P = 0.02), while lesion volumes obtained from fully automated predictions showed no difference with manually traced lesion volume (W = 976, P = 0.66).

Figure 2 shows a spaghetti plot of the final results obtained with four‐tissue‐class predictions. Lesion size positively correlated with dice overlap (r = 0.55, P < 0.001) but not with Hausdorff distance or average displacement (r = −0.17 and r = −0.19, respectively, P > 0.1). As mentioned, dice overlap with manual tracing was 0.696 ± 0.16 for these predictions, while sensitivity (true positive rate) and precision (positive predictive value) were 0.721 ± 0.19 and 0.732 ± 0.16, respectively. An array of other segmentation measures can be found in Supplementary Material, including Jaccard Coefficient, Area Under ROC curve, Cohen Kappa, Rand index, Adjusted Rand Index, Interclass Correlation, Mahanabolis Distance, Global Consistency Error, Sensitivity, Specificity, Precision, Accuracy, and Fallout (false positive rate).

Figure 2.

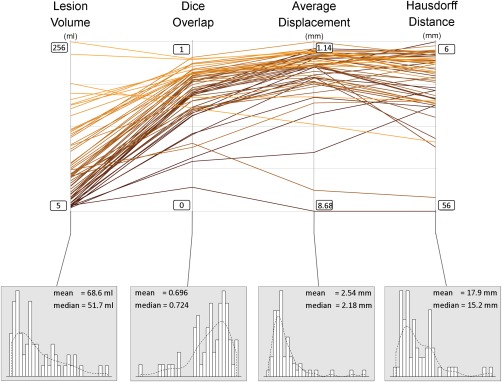
Spaghetti plot showing the lesion size, dice overlap, Hausdorff distance, and average displacement, for all 60 subjects. Lower panels show the distribution of the data for each of these variables. Scales for Hausdorf and average displacement are inverted such that the upper part of the graph is consistently showing better values for all measures. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Given that 12 of the 60 patients were utilized as reference during feature selection, we report here also the results from the restricted group of 48 patients that were not used as reference. They showed a dice overlap of 0.683 ± 0.17, Hausdorf distance of 19 ± 11 mm, and sensitivity of 0.711 ± 0.20. Wilcoxon t tests between the 48 patients and the 12 patients showed no significant difference in any of the above measures (all P > 0.1).

Investigating the Least Successful Predictions

In general, all cases received a successful automated segmentation (i.e., a lesion mask was predicted which partially overlapped with the manual mask). However, the distribution of dice overlaps was left skewed, with a handful of cases in the low end of the scale (Fig. 2). The four worst predictions were cases 43, 53, 23, 55 (see Supporting Information: Individual Predictions). Interestingly three of these cases showed a pattern that indicated an inconsistent application of rules in manual tracings. For example, unlike manual tracings, the prediction for cases 53 and 23 extended beyond the stroke core zone in adjacent areas with low T1 signal. The reversed pattern was observed for case 55, whose prediction did not extend in areas with low T1 signal while manual tracing extended in these areas. This indicates that some part of the prediction error might be related to the variability in manual tracings [Ashton et al., 2003; Crinion et al., 2013; Fiez et al., 2000].

Application of Alternative Method on the Same Dataset

To further evaluate the accuracy of LINDA with respect to existing methods we obtained lesion predictions from our dataset of 60 patients with the “Automatic Lesion Identification” method [ALI; Seghier et al., 2008]. This method uses an outlier detection approach to identify “abnormal” voxels with respect to a set of healthy controls. We used the most recent version of this toolbox (ALI v.3.0 for SPM12), which has the same default parameters of earlier versions. Our set of 80 controls was segmented with the same toolbox and constituted the reference for outlier detection. Within our patient population, ALI produced 56 successful predictions—that is, with some degree of overlap with manual tracings—and four failed predictions (7%). Among the successful predictions, dice overlap was 0.44 ± 0.21, sensitivity was 0.38 ± 0.22, precision was 0.69 ± 0.27, and Hausdorf distance was 44 ± 27 mm.

Lesion to Symptom Mapping: VLSM and RLSM Analyses

Figure 3 displays the comparison between predicted and manual VLSMs. In general, the correspondence was good and continuous dice overlap was above 0.6. Substantial difference was observed for “Comprehension,” where the peak values were 64‐mm apart. The closest peak‐to‐peak distance was observed for “Auditory Discrimination” (5 mm).

Figure 3.

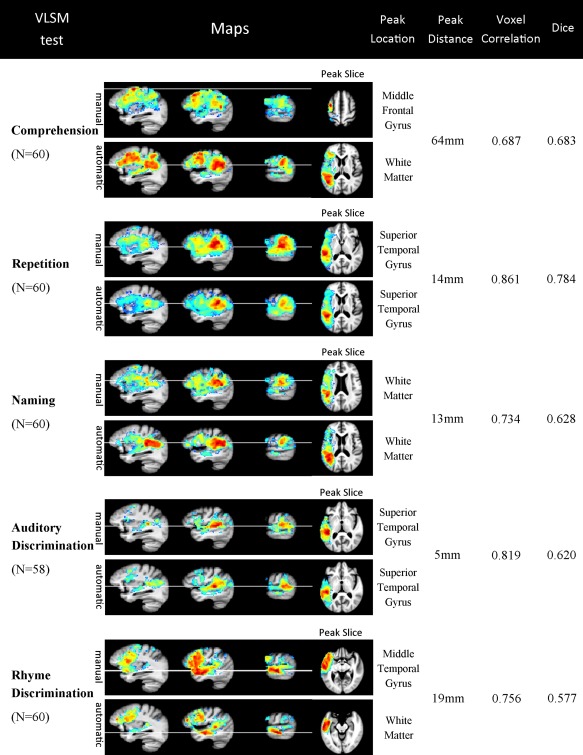
VLSM maps for the five behavioral scores, obtained with manual (top rows) and predicted (bottom rows) lesion masks. “Peak location” indicates the label of the voxel with highest t score obtained from the AAL atlas. “Peak distance” indicates the distance of peak voxels between the two VLSM analyses, manual and predicted. Voxel correlation shows the correlation of t‐scores (Pearson's r) of the 26,320 voxels that were included both in manual and in predicted lesion analyses (no threshold was applied). Dice indicates the continuous dice overlap between the two maps, after thresholding at α = 0.05 (FDR corrected, see text for continuous dice calculation). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 1 shows the results of RLSM analysis for the five cognitive variables. The average correlation of the 37 regional t‐scores was 0.77 (±0.11, range: 0.70–0.92). Concordant top t‐scores were found for all five analyses between predicted and manual RLSM, with at least two regions matching in every RLSM test. For “Naming,” all three regions matched between manual and predicted lesions.

Validation of LINDA on the Complementary Dataset

To investigate whether the method can be used on other datasets obtained at a different scanner and manually traced by other experts, we applied LINDA on the complementary dataset from Georgetown University. The processing pipeline was the same as above, utilizing a leave‐one‐out procedure to obtain predictions. Note, the same 80 controls scanned at our institution were utilized for reference for control deviation features, and, thus, patients and controls were scanned on different scanners. Results showed that the accuracy rates were relatively similar to those obtained from our dataset. However, one of the 45 cases failed to receive a prediction (case 5 in Supporting Information: Individual Predictions from Complementary Dataset). The 44 cases with an available prediction had dice overlap with manual segmentation of 0.696 ± 0.16, Hausdorff distance of 24 ± 10 mm, average displacement of 3.25 ± 3.00 mm, sensitivity of 0.656 ± 0.16, and precision of 0.770 ± 0.19. The correlation between predicted lesion volume and manual lesion volume was r = 0.957. These values are similar but slightly worse than those obtained with our main dataset, a drop that might be related to the reduced training sample and the utilization of data from different scanners, as well as the fact that the reference template is biased towards PENN data.

Cross Institutional Prediction

A fundamental quality of LINDA is that a segmentation model can be trained with data from a certain lab and the model can be transferred for use in other labs. To investigate how well a “foreign” model can match manual tracings in a new institution, we trained a model with the 60 patients in our main dataset and applied it to the 44 patients of the complementary dataset (the failed case was excluded). This is a complete cross‐institutional transfer, where a model trained on rules followed by a certain expert is tested on manual tracings provided by other experts, on data that are acquired on different scanners. Thus, a drop in accuracy is expected particularly because of differences in the procedures for drawing lesion tracings between experts at different institutions. To our surprise, the dice overlap with manual tracings decreased only by 0.028 ± 0.048, reaching an average overlap of 0.668 ± 0.15. The two predictions obtained from two different models (i.e., same institution vs. different institution) showed an average dice overlap of 0.857 ± 0.092. These results indicate that LINDA captures some universal rules of segmentation that experts use at different institutions, and that trained models can be safely transferred between labs without risking substantial failures related to the heterogeneity between training and predicting data.

DISCUSSION

In this study we introduce LINDA, a lesion segmentation algorithm capable of identifying chronic stroke lesions from a single T1‐weighted MRI image. The method is trained on existing manual tracings and tested on two separate datasets of 60 and 45 subjects with left hemispheric chronic stroke. In addition, within the 60‐subject cohort, we compared lesion‐to‐symptom mapping results of manual vs. predicted lesions to investigate whether automated predictions are feasible for neurobehavioral analyses.

LINDA relies on a set of virtual features derived from the T1‐weighted volume that fall into four categories: geometric, atlas‐based deviation, control‐based deviation, and subject specific anomalies (including self‐asymmetry). Our feature selection procedure showed that nearly all categories were important for accurate lesion segmentation. Interestingly, deviances of processed images (i.e., deviance of k‐mean segmentation from controls) were more relevant than the T1 image itself, as the latter entered the algorithm at a later stage during feature selection. Of note, atlas‐based features did not enter the winning algorithm. One of the main reasons for this could be that the template used to derive atlas‐based deviation was created using a mixed population of healthy and diseased brains. It is possible that other templates could be more useful for feature calculation and could help improve performance. In general, the strategy of obtaining additional features from a single T1 image demonstrated to be successful when considering the high accuracy and the low degree of failure obtained with LINDA.

Beside the virtual features, LINDA integrates concepts that are shown to be successful in other contexts. First, the inclusion of neighborhood information can significantly improve accuracy, more so when the information is not strictly local but incorporates regional longer range data [Ozenne et al., 2015]. LINDA uses both long range information at low resolutions and short range information at high resolutions. The presence of contextual information is important when considering the conditional rules outlined for expert manual tracing [i.e., white matter hyperintensity should be considered lesion if it's proximal to the ischemic core; Crinion et al., 2013], and the low spatial variability of stroke lesions [i.e., if a voxel is lesioned, chances are the next voxel is lesioned as well, Kimberg et al., 2007]. Second, LINDA uses random forests, a mathematical approach that can find non‐linear relationships between signals, and is robust to noise and outliers [Breiman 2001]. Algorithms that use RFs have been among the top performers in recent segmentation challenges (see http://mrbrains13.isi.uu.nl/results.php). Third, LINDA uses one of the top performing non‐linear registration algorithms [i.e., SyN; Klein et al., 2009; Ripolles et al., 2012]. To further improve registration accuracy, registrations are performed with cost‐masking function, a choice that is overlooked in some automated algorithms, but which is important for avoiding significant shrinking of the lesion [Andersen et al., 2010; Ripolles et al., 2012]. The importance of accurate registrations is appreciated if one considers that enlarged ventricles can easily be mistaken as lesion by automated algorithms [Seghier et al., 2008; Stamatakis and Tyler, 2005; Wilke et al., 2011]. Our pilot data showed that periventricular errors decrease if enlarged ventricles are correctly registered to the template. Finally, LINDA introduces the concept of cyclic register‐predict‐register, which resolved the registration dilemma for lesioned brains; i.e., to predict a lesion mask a registration is needed which requires a lesion mask.

LINDA relies on the same computational platform used by a recent tumor segmentation algorithm [Tustison et al., 2015]. It also uses a similar machine learning process based on random forests. However, LINDA uses different strategies to regularize the predicted segmentation, such as, a multi‐resolution pyramid and voxel neighborhood, while Tustison et al. [2015] use Markov Random Field segmentation cycles. In addition, LINDA uses a single MRI modality while Tustison et al. [2015] use several MRI modalities. Also, LINDA uses a new iterative register‐predict‐register algorithm designed to resolve the dependency between steps; i.e., to predict a lesion mask a registration is needed which requires a lesion mask.

In considering the comparison of LINDA with other methods of lesion segmentation, it should be noted that not all studies report the same measures utilized here. Also, some measures are sample‐dependent, and, therefore, may lead to erroneous conclusions. Overlap measures, for example, such as Dice or Jaccard overlap, are notably dependent on lesion size (e.g., correlation of r = 0.55 in our study). While overlap depends on lesion size, lesion sizes are not always reported [Seghier et al., 2008; Shen et al., 2010]. Whenever reported, lesion sizes show large variability from study to study (i.e., 20 mL in Mitra et al. [2014], 42 mL in Ozenne et al. [2015], and 68 mL in our study). Metric displacement measures are independent of lesion size, but these are rarely reported and might be occasionally misleading. For example, Hausdorff distance is susceptible to occasional outlier departures from the target (the pan handle effect), while average displacement is rarely reported.

Despite this, we consider here similarities and discrepancies of LINDA with other methods of lesion segmentation in stroke. A method which relies on a similar machine learning process has been proposed by Mitra et al. [2014]. This method utilizes random forest training using voxel neighborhood information from multiple MRI sequences (T1, T2, FLAIR, etc.). While similar in some aspects to LINDA, this method achieved smaller dice overlap accuracy (i.e., 0.60 vs. 0.70), less accurate estimation of lesion volume (correlation with manual tracing: 0.76 vs. 0.96), and slightly larger average displacement (3.06 mm vs. 2.54 mm). Thus, LINDA shows an advantage on several dimensions. This result is counterintuitive in that one would expect multiple MRI sequences to outperform a single MRI sequence for lesion segmentation. Differences in technical choices of each method might explain this effect. For example, the neighborhood information used in LINDA consists in a layer of adjacent voxels, whereas Mitra et al. use random blocks around the voxel (see Geremia et al. [2011] for details); LINDA is not constrained on which features to use while Mitra et al.'s method relies on FLAIR for first lesion screening; LINDA uses multi‐resolution images while Mitra et al. uses only high resolution images; LINDA uses deformable registration while Mitra et al. uses a rigid registration which, as noted above, may increase the error.

Another approach for finding lesions is the one proposed by Seghier et al. [2008; ALI]. ALI aims at identifying “unusual” voxels within segmented tissues (GM, WM, and CSF). A substantial difference with LINDA is that ALI uses single voxel properties without neighborhood information. While the overlap accuracy of ALI has been reported to be 0.64 [Seghier et al., 2008; or 0.49 in Wilke et al., 2011], the application of ALI on our data yielded a dice overlap of 0.44 and 7% failed predictions. Thus, with respect to ALI, LINDA produced lower failure rates (<1%) and more accurate results (dice 0.70). It is possible that ALI may perform much better if its application was guided directly by the algorithm author and if a full parameter search were performed to optimize ALI on this data. We did not seek to provide a deep understanding of the performance differences between LINDA and ALI as that would involve much greater involvement from the author of ALI and is beyond the scope of the current work.

Another algorithm has been proposed by Shen et al. [2008, 2010], which uses a concept of voxel‐wise deviance from normality. Simulations showed that the accuracy of this method depends on the degree of signal abnormality; i.e., dark lesions with clear contours on T1 are segmented more accurately (sensitivity: ∼0.79) than gray lesions with fuzzy contours (sensitivity: ∼0.35). In contrast, LINDA achieves high sensitivity rates from all real brain lesions (i.e., 0.72) and can learn easily to extend the lesion prediction in areas of subtle intensity change (see examples in Supporting Information).

Beside the segmentation methods for chronic stroke, some groups have focused on lesion segmentation at the subacute level [1 week to 3 months post‐stroke; Maier et al., 2015; Ozenne et al., 2015]. A direct comparison of these methods with LINDA is not possible given the differences in lesion appearance at this phase [Rekik et al., 2012] and the frequent use other low resolution MRI sequences (i.e., FLAIR, DWI).

Several authors have proposed semi‐automated methods for lesion segmentation, which facilitates the manual work rather than replacing it. The semi‐automated method proposed by Wilke, et al. [2011] achieved a similar accuracy as ALI, albeit the semi‐automated method was able to avoid failures. More recently, de Haan et al. [2015] showed that a semi‐automated algorithm can be used to segment stroke lesions in any of the available modalities (T1, T2, DWI, CT), achieving excellent accuracy rates (i.e., dice of 0.87 on T1 images with 32 min human interaction per segmentation). Such high segmentation accuracy shows that human intervention can greatly improve computerized segmentation. On the downside, the expertise of human raters is still required and observer bias cannot be avoided.

In this study, for the first time, we report comparative lesion‐to‐symptom mapping based on manual and predicted lesions. One previous study reported LSM from predicted lesions, but not a comparison with manual lesions [Gilleber et al., 2014]. Overall, VLSM and RLSM showed converging results between automated predictions and manual tracings. The peak voxel showed <2‐cm displacement in 4/5 VLSM maps. The peak voxel for “comprehension” measure showed a large displacement of 64 mm between predicted and manual VLSM. The interpretation of this discrepancy requires multiple theoretical considerations, which go beyond the scope of this article. However, the result found with predicted lesions are is not atypical. In fact, the peak was located in posterior perisylvian areas (near the Wernicke's area), a region known to support comprehension [Dronkers et al., 2004; Hickok and Poeppel, 2004; Mirman et al., 2015a, 2015b; Silbert et al., 2014]. On the contrary, the frontal region has been less frequently associated with comprehension. When a frontal involvement in comprehension is reported, the area of relevance is more inferior [i.e., inferior frontal gyrus; Friederici et al., 2003] or more anterior [i.e., dorsolateral prefrontal cortex, BA 46; Barbey et al., 2014; Dronkers et al., 2004] than our finding with with manual tracings (see Fig. 3).

Differently from VLSM maps, RLSM comparison showed more consistent results. For “Repetition,” “Naming,” and “Auditory Discrimination”—the three tests that visibly showed more consistent VLSM maps—a higher correlation was observed between the 37 regional t scores than was seen with the ∼26.000 voxel t scores. Additionally, top RLSM regions for all five behavioral scores matched between manual and predicted lesion masks (see Table 1). These results indicate that RLSM might be more robust to the accumulation of errors derived from automated segmentations compared to VLSM. Two reasons that might explain why RLSM is more robust to errors than VLSM are: (i) it sums the voxels into broader areas, less susceptible to local error, and (ii) it uses a continuous measure of damage instead of a binary voxel‐wise measure. While RLSM analyses have been gradually abandoned in the lesion‐mapping research field, our results suggest that RLSM analyses can be useful when faced with inherently erroneous segmentations. Future studies can combine VLSM and RLSM to take advantage of each method's strength, namely, spatial resolution and reliability.

Feature Selection and Overfitting

In this study, we selected a subset of six features out of twelve features available. For this purpose, 12 patients were used as reference, raising concerns whether the features selected represent an overfitting of these specific subjects. However, the procedure we followed and the subsequent results do not support the presence of overfitting. First, the procedure did not rely solely on the features and ground truths of 12 subjects, but on a cross‐over prediction which used the model built on the other 48 patients as substrate for building the predictions of 12 patients. In this scenario, there is little reason for one to expect that some features would be useful only for these 12 subjects, and not for the other 48, given that the random forest weights that lead to the prediction were derived from the 48 patients. Second, the random forest procedure is well‐known to avoid overfitting by testing its predictions via the “out‐of‐bag” error (although, admittedly, this approach is not perfect). Third, if overfitting occurred during feature selection, we would expect a dramatic accuracy drop in the remaining patients. To investigate this hypothesis, we compared the 12 and 48 groups on dice overlap, Hausdorf distance, and sensitivity, and found no statistical difference (Wilcoxon tests, all P > 0.1). Further supporting this evidence, the accuracy with the Penn nd Georgetown datasets was similar; if the initial feature selection identified only the “preferential” features of 12 Penn patients, we would have seen major discrepancies when using the method on another dataset. Ultimately, even when the model was built on Penn data and applied on Georgetown data—a scenario with high risk for overfitting due to the scanner, the expert labeler, the features, etc.—the drop in accuracy was minimal (dice decreased from 0.69 to 0.67). While the possibility that some overfitting might have occurred cannot be completely excluded, these results suggest that this effect, if present, is small.

Strengths and Limitations of LINDA

One of the advantages of LINDA is that it offers not only automated segmentation, but also registration to template. In fact, the largest part of the time necessary to obtain a new prediction is template registration.

What might be considered both strength and limitation is the reliance on existing manual segmentations. On one side, this allows labs to switch to automated segmentations and grossly retain the rules applied by the expert (i.e., if the expert drew only the lesion core, so will do LINDA). On the other side, many labs do not own numerous examples to train the model. This limitation may be resolved if trained models are made publicly available. To encourage this practice, we have included our trained models in the prediction toolkit (http://dorianps.github.io/LINDA/). Note, we also showed that models trained with data from a certain institution can be safely applied to data obtained at another institution with minimal loss in predictive power. The preserved accuracy of predictions emerged because experts follow substantially similar rules of tracing, and because LINDA was able to capture those fundamental rules.

Another advantage of LINDA is that it produces graded posterior probability maps. These maps currently reflect the uncertainty of the model instead of the uncertainty of the expert (i.e., values are still high in adjacent areas with partially damaged tissue because the model is trained to consider those areas as pure lesion). However, LINDA can be trained with graded lesion maps to produce graded segmentations that reflect the uncertainty of an expert or a group of experts. Although no study to date have used graded lesion maps, this is a natural development for future studies given recent evidence that shows graded blood perfusion or BOLD signal near the lesion contours [de Haan et al., 2013; Ftizmorris et al., 2015].

One of the limitations of LINDA is the influence received from inconsistent manual tracings. This effect was observed when investigating the cases with low dice overlap. This is a common limitation of all supervised methods, while unsupervised methods [Seghier et al., 2008; Shen et al., 2010] are not affected by manual tracings at all. However, this vulnerability also suggests that the accuracy of LINDA might further improve with more consistent manual examples.

A limitation that LINDA shares with other methods is the need for a healthy control dataset. Moreover, the control dataset should match patients for age and gender, and the number healthy subjects must be large to avoid instabilities derived by small control numbers [Wilke et al., 2014]. To partially solve this limitation we have included in the prediction toolkit the control averages necessary to produce deviation features from new stroke subjects.

In this study, we used a set of 12 features and selected the best set for the segmentation. Other features may exist that we did not explore here (i.e., wavelets, Fourier features, patch‐based features, HOGG or SIFT features, etc.). Future implementations can take in consideration these features as potential candidates for automated prediction. Moreover, we used a linear model to select the features to include in the final algorithm instead of using the Gini impurity measures derived from random forests. This choice was made because LINDA uses several random forest models at different resolutions, and introduces new features during the learning process, limiting the interpretability of Gini impurity measures.

A limitation of LINDA is that lesion maps have smoother contours than manual predictions (see examples in Supplementary Material). This effect arises because the cascade predictions start at low resolution (i.e., produce a coarse map) and use always voxel neighborhood information to classify the voxel. Because each voxel is considered in a context, lesioned voxels surrounded mostly by healthy voxels are more likely to be considered healthy. Thus, sharp deviances from the lesion maps are disfavored. One way to mitigate this effect in future implementations is to train the model at higher resolution steps (i.e., 1 mm) allowing for more refined spatial distinctions.

Another limitation of LINDA is that it uses high resolution T1 images obtained for research purposes. The applicability of the method to other types of images, including low resolution clinical images has not been tested yet. Extending LINDA to these images could facilitate studies aiming to estimate long‐term prognosis based on clinical scans obtained at the time of an acute stroke.

Finally, despite the overall accurate lesion segmentation, there is still a chance that small lesions in the periphery might be mistaken as normal variation in gyri and sulci, offering less accuracy in some scenarios.

CONCLUSIONS

In this study, we built and tested LINDA, a tool for automatically segmenting chronic stroke lesions from a single T1‐weighted MRI. The method showed accurate lesion identification and low failure rates in a large number of patients. For the first time, we also tested the method with cross‐institutional data, achieving similarly accurate results. In addition, we tested the effects of automated lesion segmentations on lesion‐to‐symptom mapping analyses and found quite similar results for four of five cognitive measures. The next frontier of machine learning in medical imaging will necessarily include not only structural data but also patient cognitive measurements, if this field is to bridge the (still substantial) gap between research and practical applicability. In the spirit of open source science, we have packed all the tools and data necessary to apply LINDA in a single toolkit available online (http://dorianps.github.io/LINDA/).

Supporting information

Supporting Information

Supporting Information

Supporting Information