Structural Properties, Order–Disorder Phenomena, and Phase Stability of Orotic Acid Crystal Forms

Abstract

Orotic acid (OTA) is reported to exist in the anhydrous (AH), monohydrate (Hy1), and dimethyl sulfoxide monosolvate (S_DMSO) forms. In this study we investigate the (de)hydration/desolvation behavior, aiming at an understanding of the elusive structural features of anhydrous OTA by a combination of experimental and computational techniques, namely, thermal analytical methods, gravimetric moisture (de)sorption studies, water activity measurements, X-ray powder diffraction, spectroscopy (vibrational, solid-state NMR), crystal energy landscape, and chemical shift calculations. The Hy1 is a highly stable hydrate, which dissociates above 135 °C and loses only a small part of the water when stored over desiccants (25 °C) for more than one year. In Hy1, orotic acid and water molecules are linked by strong hydrogen bonds in nearly perfectly planar arranged stacked layers. The layers are spaced by 3.1 Å and not linked via hydrogen bonds. Upon dehydration the X-ray powder diffraction and solid-state NMR peaks become broader, indicating some disorder in the anhydrous form. The Hy1 stacking reflection (122) is maintained, suggesting that the OTA molecules are still arranged in stacked layers in the dehydration product. Desolvation of S_DMSO, a nonlayer structure, results in the same AH phase as observed upon dehydrating Hy1. Depending on the desolvation conditions, different levels of order–disorder of layers present in anhydrous OTA are observed, which is also suggested by the computed low energy crystal structures. These structures provide models for stacking faults as intergrowth of different layers is possible. The variability in anhydrate crystals is of practical concern as it affects the moisture dependent stability of AH with respect to hydration.

1. Introduction

Hydrates are the most common solvates encountered in pharmaceutical compounds,¹⁻⁵ since water is ever present in the manufacturing environment of fine chemicals (atmospheric moisture or water in solvents, reactants, or excipients). The properties, e.g., mechanical properties and physical and chemical stability, are often different between a hydrate and its corresponding anhydrate^6,7 and may affect drug processability and the performance of a final drug product. A hydrate form may be advanced through drug development, therefore studying and understanding dehydration mechanisms is crucial from practical and theoretical aspects.

One of the main factors affecting the stability of a hydrate is the role played by water molecules in the crystal structures.⁸ Thus, it is important to correlate phase stability and transitions with structural features. When changes in temperature, pressure, or humidity occur, a hydrate can transform into an anhydrate polymorph or may collapse into an (intermediate) amorphous solid which can recrystallize to a (metastable) anhydrate. Furthermore, the water-free phase may become thermodynamically unstable and revert to the hydrate at ambient conditions.⁹ When regarding structural aspects, (de)hydration classifications proposed by Petit and Coquerel (“Rouen 96 model”)¹⁰ and Galwey¹¹ are frequently applied. The “Rouen 96 model” is based on mechanical and structural changes upon dehydration, and they divide the dehydrated products into two classes: class I, where no transmission of structural information occurs during dehydration, and class II, where there is (some) transmission of the structural information. Galwey classified the dehydration process according to water evolution type (WET) based on structural, observational, and kinetic criteria. This model specifies six classes (i.e., crystal structure maintained, diffusion across an adherent barrier layer, interface advance/nucleation and growth or contracting envelope, homogeneous reactions in crystals, melting and formation of impervious outer layer, and comprehensive melting) and also takes kinetic and rate controlling phenomena into consideration.¹¹ The latter two classifications and other frequently cited ones are based on either structural aspects of the hydrate,¹²⁻¹⁵ sorption/desorption behavior,¹⁶ thermal dehydration behavior,^17,18 or relative stability estimations (thermodynamics) of two crystal forms (e.g., anhydrate and hydrate) at a given temperature and relative humidity.¹⁹ Therefore, none of the existing classifications can on its own reflect the complex interplay of structure, kinetics, and thermodynamics observed in (de)hydration processes, which are often difficult to control.^6,20−31

To obtain a better understanding of hydrate formation, (de)hydration processes, and stability of hydrates, we are systematically investigating organic (pharmaceutical) model hydrate systems.³²⁻³⁸ This will provide the basis for making the phenomenon of hydrate formation and understanding a hydrate’s stability range more predictable. Orotic acid (OTA, uracil-4-carboxylic acid, Figure 1) was chosen as a model for a slightly water-soluble compound (room temperature monohydrate solubility in water: ∼1.7 mg/mL³⁹), forming a very stable hydrate phase and upon dehydration resulting in an anhydrate phase showing diffuse scattering in X-ray powder diffraction experiments. The substance occurs naturally (e.g., in milk products) and plays a key role in the biosynthesis of pyrimidine derivatives. Historically, OTA was incorrectly thought to be a vitamin and therefore often referred to as “vitamin B13”.⁴⁰ The substance is used as a food supplement and shows therapeutic effects such as increase in cognitive performance and learning potential, cardioprotection, and the reduction of serum lipids.⁴¹ A monohydrate (Hy1),^42,43 dimethyl sulfoxide monosolvate (S_DMSO),⁴⁴ and anhydrous form are known, and both the anhydrate and monohydrate are commercially available.⁴⁵

Figure 1.

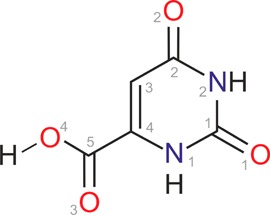
Molecular diagram of orotic acid (uracil-4-carboxylic acid, OTA).

Our aim in this study is to link the observed hydration/dehydration behavior to the hydrated and water-free structures, including determining the elusive anhydrate structure. Therefore, we developed a consistent picture of the structural, kinetic, and thermodynamic features of the OTA solid forms. Hy1, AH, and S_DMSO were characterized by thermal analytical methods (hot-stage microscopy, differential scanning calorimetry, thermogravimetic analysis), powder X-ray diffraction, spectroscopy (solid-state NMR, infrared and Raman), moisture sorption/desorption studies, and slurry and water activity measurements. The complementarity of the applied techniques provides moisture and temperature dependent stability data, key information for anhydrate/hydrate systems. Crystal structure prediction (CSP) studies and chemical shift calculations were performed in order to derive structural information on anhydrous OTA. The computational approaches allowed us to obtain a deeper understanding of the order–disorder phenomena in the anhydrate structure by proposing a variety of ordered structure models. By contrasting the thermodynamically feasible anhydrate and monohydrate crystal structures with structure and stability information derived for the experimental forms, we unravel also factors that control crystallization of OTA.

2. Experimental Section

2.1. Materials

OTA monohydrate (O-2625, Lot 37H2529) and the anhydrous compound (O-2750, Lot 77H2616) were purchased from Sigma. The “anhydrous” compound contained ca. 1% water. The used solvents and reagents were purchased from Sigma and were of analytical grade.

The anhydrate sample 1 (AH_s1) was prepared by either stepwise drying the monohydrate at 120, 130, and 140 °C, holding the temperature for 3 h at each step, or by dissolving 0.5 g of anhydrous OTA under gentle heating in 15 mL of DMF and adding chloroform as an antisolvent. AH_s2 (sample 2) was obtained by dehydration of the monohydrate in a sealed glass ampule at 142 °C. The third anhydrate sample (AH_s3) was prepared by stirring a suspension of AH_s1/AH_s2 in a methanol/water mixture (water activity ∼ 0.26) between 15 and 25 °C for 40 days.

The OTA monohydrate (Hy1) was obtained by stirring the anhydrate in a water/EtOH (3:1 vol %) mixture at room temperature. The dimethyl sulfoxide solvate (S_DMSO) was prepared by dissolving 3.66 g of anhydrous OTA in 21.5 mL of DMSO at 110 °C. The hot solution was filtered, and 19 mL of chloroform was added. Immediate precipitation of S_DMSO occurred. The dimethylammonium orotate–orotic acid (1/1) salt cocrystal was obtained after heating 25 mg of OTA and 0.05 mL of DMF in a high-pressure DSC capsule to 180 °C.

2.2. Thermal Analysis

2.2.1. Hot-Stage Microscopy (HSM)

For HSM investigations a Reichert Thermovar polarization microscope, equipped with a Kofler hot stage (Reichert, Austria), was used. Photographs were taken with an Olympus DP71 digital camera (Olympus, Germany).

2.2.2. Differential Scanning Calorimetry (DSC)

DSC thermograms were recorded on a DSC 7 or Diamond DSC (PerkinElmer Norwalk, CT, USA) controlled by the Pyris 7.0 software. Using a UM3 ultramicrobalance (Mettler, Greifensee, Switzerland), samples of approximately 2–25 mg were weighed into open/closed aluminum pans or hermetically sealed (high-pressure) pans. For the construction of the temperature/composition phase diagram, Hy1/AH_s1 mixtures were prepared by gently mixing the two phases. The Hy1/water mixtures were prepared by placing precisely weighed amounts of Hy1 and pure water (with the aid of a Hamiltion syringe) into high-pressure DSC pans followed by a second accurate weight measurement. The sealed sample pans were stored for 24 h before the DSC runs were started to equilibrate the mixtures. For low temperature measurements the samples were frozen (liquid N₂) before the DSC runs. The samples were heated using rates ranging from 2 to 20 °C min^–1, with dry nitrogen as the purge gas (purge: 20 mL min^–1). The two instruments were calibrated for temperature with pure benzophenone (mp 48.0 °C) and caffeine (236.2 °C), and the energy calibration was performed with indium (mp 156.6 °C, heat of fusion 28.45 J g^–1). The errors on the stated desolvation temperatures (extrapolated onset temperatures) and enthalpy values were calculated at the 95% confidence intervals (CI) and are based on at least five measurements.

2.2.3. Thermogravimetric Analysis (TGA)

TGA was carried out with a TGA7 system (PerkinElmer, Norwalk, CT, USA) using the Pyris 2.0 software. Approximately 4–7 mg of sample was weighed into a platinum pan. Two-point calibration of the temperature was performed with ferromagnetic materials (Alumel and Ni, Curie-point standards, PerkinElmer). Heating rates ranging from 2 to 10 °C min^–1 were applied, and dry nitrogen was used as purge gas (sample purge, 20 mL min^–1; balance purge, 40 mL min^–1).

2.3. Powder X-ray Diffractometry (PXRD)

The PXRD patterns were obtained using an X’Pert PRO diffractometer (PANalytical, Almelo, The Netherlands) equipped with a θ/θ coupled goniometer in transmission geometry, programmable XYZ stage with well plate holder, Cu Kα_1,2 radiation source, and a solid-state PIXcel detector. The patterns were recorded at a tube voltage of 40 kV, tube current of 40 mA, applying a step size of 2θ = 0.007° with 80 or 400 s per step in the 2θ range between 2° and 40°.

The room temperature diffraction patterns were indexed using the first 20 peaks with DICVOL04 and the space groups determined based on a statistical assessment of systematic absences,⁴⁶ as implemented in the DASH structure solution package.⁴⁷ Pawley fits⁴⁸ were performed with Topas Academic V5.⁴⁹

2.4. Determination of Water Content and Gravimetric Moisture Sorption/Desorption Studies

Titrimetric water determinations were performed using a Karl Fischer Titrator E 551 (Metrohm AG, Herisau, Switzerland) and commercially available pyridine-free reagents (Merck, Darmstadt, Germany).

Manual water sorption/desorption studies were performed at 25 °C over a desiccant (P₂O₅) or various saturated salt solutions providing relative humidities (RH) of 9, 24, 36, 43, 53, 62, 75, 84, 92, and 97%. The uptake or loss of water as a function of time at different RHs was determined gravimetrically⁵⁰ with a below-weighing balance (AT 250 semimicro balance, Mettler Instrumente AG, Greifensee, Switzerland). The sample mass used in these studies was about 200 mg.

Automatic moisture sorption and desorption studies were performed with the multisample gravimetric moisture sorption analyzer SPS23-10μ (ProUmid, Ulm, Germany). Approximately 150–400 mg of the solid forms was used for the investigations. The measurement cycles were started at 0% with a sorption cycle (increasing humidity) up to 95%, followed by a desorption cycle to 0% RH. The RH changes were set to 5% for all cycles, and the equilibrium condition for each step was set to a mass constancy of ±0.001% over 60 min.

2.5. Determination of the Critical Water Activity (Slurry Method)

Excess of OTA AH_s1/AH_s2 was stirred (500 rpm) in 2 mL of methanol/water mixtures, each containing a different mole fraction of water corresponding to a defined water activity^51,52 (section 12 of the Supporting Information) at 25.0 ± 0.1 °C for 40 days. Samples were withdrawn and filtered, and the resulting phase was determined using PXRD and TGA.

2.6. Spectroscopy

2.6.1. Infrared Spectroscopy

FT-IR spectra were recorded with a Bruker Vertex 70 spectrometer (Bruker Analytische Messtechnik GmbH, Germany). Potassium bromide (KBr) disks (13 mm) were prepared by gently grinding and mixing 0.5 mg of OTA with 200 mg of KBr in a mortar with pestle, evacuating of the mixture in the pressing tool for 20 s at ∼10 mbar, and applying a pressure of about 800 MPa for about 60 s using a hydraulic press. The spectra were recorded in the range of 4000 to 400 cm^–1 at an instrument resolution of 2 cm^–1 (64 scans per spectrum).

2.6.2. Raman Spectroscopy

FT-Raman spectra were recorded with a Bruker RFS 100 Raman spectrometer (Bruker Analytische Messtechnik GmbH, Germany), equipped with a Nd:YAG laser (1064 nm) as the excitation source and a liquid-nitrogen-cooled, high sensitivity Ge detector. The spectra (256 scans per spectrum) were recorded in aluminum sample holders with a laser power of 400 mW and a resolution of 2 cm^–1.

2.6.3. Solid-State NMR

All NMR measuremants were performed using a Bruker 400 MHz Avance III solid-state NMR spectrometer equipped with a triple resonance probe at frequencies 400.23 MHz (¹H), 100.64 MHz (¹³C), and 40.56 MHz (¹⁵N). Materials were packed in the 4 mm zirconia rotors and rotated at an MAS rate of 10 kHz. All materials were characterized using ¹H single pulse, ¹H–¹³C and ¹H–¹⁵N cross-polarization magic angle spinning (CP/MAS) techniques (¹H π/2 pulse length 3.5 μs, ¹³C π/2 pulse length 3.5 μs, ¹⁵N π/2 pulse length 4.5 μs, ¹H–¹³C and ¹H–¹⁵N CP contact time 2 ms, SPINAL64 decoupling was used during signal acquisition). Recycle delay for Hy1 and S_DMSO was 20 s. Due to significant differences in signal intensities, recycle delay was optimized for each anhydrous material with different order–disorder level in series of CP/MAS NMR experiments (see section 8 of the Supporting Information). The Hartmann–Hahn conditions for ¹H–¹³C CP/MAS NMR experiment were set with hexamethylbenzene (HMB). Typically, 64 scans were acquired for anhydrous materials and 256 scans for Hy1 and S_DMSO. The ¹³C chemical shifts were recorded with respect to TMS and ¹⁵N chemical shifts are given with respect to liquid NH₃ at 0 ppm setting reference peak of glycine to 33.4 ppm.⁵³

¹H–¹³C heteronuclear correlation (HETCOR)⁵⁴ MAS NMR spectra were acquired using frequency-switched Lee–Goldburg (FSLG) homonuclear decoupling with ¹H rf field of ca. 92.6 kHz and SPINAL64 heteronuclear decoupling during acquisition. ¹H–¹³C CP contact times of 0.3 and 2 ms and recycle delay of 2 s were used. Sample was placed in 4 mm zirconia rotor, and MAS rate of 10 kHz was applied. A total of 128 increments were acquired in indirect dimension with 128 scans per increment.

High resolution ¹H spectra were recorded using the FSLG homonuclear decoupling pulse sequence at an MAS spinning rate of 6.8 kHz.⁵⁵ In ¹H 1D and ¹H(SQ)–¹H(SQ) 2D CRAMPS (combined rotation and multiple pulse spectroscopy experiments) 32 μs wplmg1 cycle was applied with effective rf decoupling power of 100 kHz.⁵⁶ A short acquisition window (10–15 ms) was applied in order to acquire a complete data set and to avoid probe overheating. In 2D CRAMPS experiment acquisition time of 15 ms, dwell time of 25 μs and 0.5 ms mixing time were used. A total of 128 increments were acquired in indirect dimension with recycle delay of 4 s leading to experimental time of 2 h 17 min.

¹H spin–lattice relaxation times (T₁) were measured using the inversion–recovery method at 25 °C. Sixteen increments were acquired with a maximum time delay of 300 s and recycle delay of 210 s. Obtained data were fitted using Bruker Topspin 3.1 software (for more details see section 8 of the Supporting Information).

2.7. Computational Generation of the Anhydrate and Monohydrate Crystal Energy Landscapes and Chemical Shift Calculations

Hypothetical crystal structures of OTA anhydrates (Z′ = 1) and monohydrates (Z′ = 1), for each of the two planar diketo conformations (Figure S1), obtained from potential energy surface calculations with Gaussian09,⁵⁷ were generated with the program CrystalPredictor.⁵⁸⁻⁶⁰ 300,000 anhydrate and 330,000 monohydrate structures were generated randomly in 48 space groups, keeping the molecular geometry rigid. The structures were relaxed to a local minimum in the intermolecular lattice energy, calculated from the FIT⁶¹ exp-6 repulsion–dispersion potential and atomic charges which had been fitted to electrostatic potential around the PBE0/6-31G(d,p) charge density using the CHELPG scheme.⁶² The energies of all structures within 30 kJ mol^–1 of the global anhydrate or monohydrate lattice energy minima were refined (5,000 anhydrate and 16,500 monohydrate structures), using DMACRYS⁶³ with a more realistic, distributed multipole model⁶⁴ for the electrostatic forces which had been derived using GDMA2⁶⁵ to analyze the PBE0/6-31G(d,p) charge density. The orientation of the C3–C4–C5–O5 torsion (Figure 1) in the 1,000 most stable anhydrate and 1,500 monohydrate structures (20 and 15 kJ mol^–1 range with respect to the global minimum structures) was minimized with the program Crystal Optimizer.⁶⁶ Conformational energy penalties and isolated molecule charge densities were computed at the PBE0/6-31G(d,p) level.

More computationally demanding calculations based on different models for the lattice energy were also performed on the low energy structures to further investigate the sensitivity of the crystal energies to theoretical methods. CASTEP plane wave code⁶⁷ calculations used the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) exchange-correlation density functional⁶⁸ and ultrasoft pseudopotentials,⁶⁹ with the addition of either the Tkatchenko and Scheffler (TS)⁷⁰ or Grimme06 (G06)⁷¹ model. PIXEL calculations⁷²⁻⁷⁴ were performed on the low energy PBE-TS structures to estimate the repulsive (E_R), dispersion (E_D), electrostatic (Coulombic, E_C), and polarization (also called induction, E_P) contributions from individual pairs of molecules within a crystal. For more details on the DFT-D and PIXEL calculations see sections 1 and 3 of the Supporting Information.

The relationships between crystal structures were examined using the XPac program.^75,76 The results described were obtained using all non-hydrogen atoms and routine medium cutoff parameters (δ_ang = 10°, δ_tor and δ_dhd = 18°).

NMR shielding calculations were performed on PBE-TS optimized structural models of OTA using the CASTEP NMR code and on the fly pseudopotentials.⁷⁷ The CASTEP computed shielding constants, σ_calc, were converted to chemical shifts, δ_calc, according to δ_calc = σ_ref – σ_calc using a reference value, σ_ref, taken from the zero intercepts of the fits of the calculated shielding vs experimental chemical shift plot (σ_Castep = −x·δ_exptl + σ_ref). For more details see section 4 of the Supporting Information.

3. Results and Discussion

3.1. Crystallographic Information on OTA Solid Forms

The Cambridge Structural Database (CSD)⁷⁸ contains entries for two solid forms of OTA, the Hy1 (Ref-Code family: OROTAC^42,43) and S_DMSO (XARBEZ⁴⁴). In Hy1 (P1̅) the OTA molecule forms four strong hydrogen bonds, N–H···O or O–H···O, to adjacent OTA molecules and three hydrogen bonds to water molecules, leading to perfectly planar arranged layers (Figure 2a). The layer stacks are not linked by hydrogen bonds. The conformation observed in Hy1 can be related to the global conformational energy minimum (section 1.1 of the Supporting Information, Figure S1). This is in contrast to the OTA molecule in S_DMSO (P2₁/c). The OTA COOH function is rotated by 180° in S_DMSO, leading to the local conformational energy minimum, which was calculated in the gas phase to be ca. 10 kJ mol^–1 less stable than the global energy minimum conformation. The OTA molecules form centrosymmetric dimers in S_DMSO, N–H···O hydrogen bonds, which are connected via DMSO molecules, N–H···O and O–H···O hydrogen bonds, to form chains (Figure 2b).

Figure 2.

Hydrogen bonding motifs observed in (a) Hy1^42,43 and (b) S_DMSO.⁴⁴

Moreover, three structures containing the OTA molecule as a component can be found in the CSD: a monohydrate cocrystal with melamine (LIDCAE⁷⁹), a layer structure, and two dimethylammonium orotate–orotic acid complexes showing different stoichiometries (XARBID and XARBOJ⁴⁴). Both dimethylammonium structures form rippled planes interlinked via the dimethylammonium cation. All five of the structures containing OTA exhibit an essentially planar diketo tautomer as opposed to possible enol tautomers.⁸⁰ No structural information for anhydrous OTA has been found in literature.

3.2. Thermal Analysis and AH/Hy1 Temperature–Composition “Phase Diagram”

3.2.1. Monohydrate

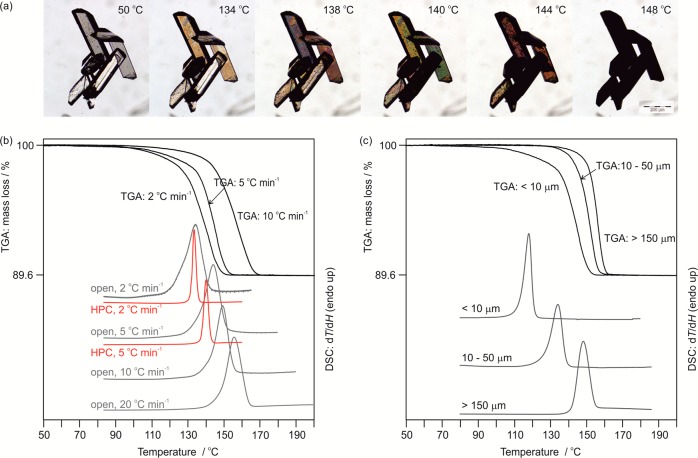
The dehydration process of OTA Hy1 starts at temperatures above 125 °C (heating rate < 5 °C min^–1) and is indicated by the appearance of dark spots on the surface of the crystals (Figure 3a). The spots are the nucleation centers of the AH, and the number increases with increasing temperature, resulting in very small crystals (size of a few μm). From HSM investigations it could be concluded that the dehydration mechanism involves a high nucleation but low growth rate with the reaction propagating slowly from the surface to the interior of the crystals. Dehydration results in aggregates with the original shape of the Hy1 crystals consisting of small crystals of AH (called “pseudomorphosis”⁸¹), which is characteristic of the desolvation of stoichiometric hydrates.³³ At 148 °C the process is completed. The high dehydration temperature indicates a high thermal stability of Hy1. A homogeneous melting process of the hydrate was never observed, not even by heating Hy1 at higher rates (>10 °C min^–1, DSC) or in an oil embedding (high viscosity silicon oil, HSM).

Figure 3.

HSM, DSC, and TGA thermograms of OTA Hy1. (a) Photomicrographs showing the dehydration (pseudomorphosis) of OTA Hy1 to AH in the temperature range 50–148 °C. (b) DSC and TGA thermograms recorded at different heating rates (2–10 °C min^–1) and at different atmospheric conditions (open pan or hermetically sealed high-pressure capsule (HPC)). (c) Influence of particle size on dehydration temperature, heating rate 5 °C min^–1, sealed DSC pans.

The impact of atmospheric conditions, heating rate, and particle size on the Hy1 to AH dehydration reaction was investigated using DSC and TGA. The dehydration is observed at higher temperatures (ΔT ∼ 30 °C) if the heating rate or particle size is increased (Figure 3b,c). The heat of dehydration of Hy1 to AH_s1 (sample 1), Δ_dehyH, was measured to be 52.7 ± 0.6 kJ mol^–1 using open DSC pans. According to eq 1 the heat of hydrate to anhydrate transformation, Δ_trsH_Hy1-AHs1, could be estimated by subtracting the heat of vaporization, Δ_vapH, of 1 mol of water at the dehydration temperature⁸² from Δ_dehyH.

1

This resulted in a Δ_trsH_Hy1-AHs1 value of 14.3 ± 0.7 kJ mol^–1. Repeating the experiments using closed, but not hermetically sealed, DSC pans resulted in a Δ_trsH_Hy1-AHs2 value of 9.6 ± 1.1 kJ mol^–1. In hermetically sealed DSC pans a heat of dissociation, Δ_dissH_Hy1-AHs2, of 10.4 ± 0.7 kJ mol^–1 was measured. The atmospheric conditions did not influence the dehydration/dissociation temperature, but influenced the measured ΔH values and the rate of the dehydration process, as exemplarily shown in Figure 3b for open and hermetically sealed DSC thermograms. Moreover, the desolvation product obtained by dehydration experiments in open DSC (AH_s1) differs in its PXRD, IR, and Raman fingerprints from samples (AH_s2) which were obtained in hermetically sealed/closed DSC pans. The observed differences may be associated with order/disorder phenomena and will be discussed in section 3.5.

The mass loss of 10.33 ± 0.12% determined in the TGA experiments corresponds to exactly 1 mol of water per mol of OTA, confirming the presence of a monohydrate. All TGA dehydration experiments, in agreement with the open DSC pan dehydration experiments, resulted in AH_s1.

3.2.2. Dimethyl Sulfoxide Monosolvate

The S_DMSO shows a similar desolvation behavior as Hy1. Desolvation is indicated by the appearance of dark regions (nucleation and growth of AH) that expand from the surface to the interior of S_DMSO crystals on heating (Figure 4a). The process, starting at the surface and macroscopic defects, is dominated by the nucleation and growth of AH, and results in the formation of aggregates of homogeneously sized AH_s1 crystals. The outer shape of the original solvate crystals is maintained (pseudomorphosis). The desolvation process occurs between 105 and 145 °C.

Figure 4.

HSM, DSC, and TGA thermograms of OTA S_DMSO. (a) Photomicrographs showing the desolvation (pseudomorphosis) of OTA S_DMSO to AH in the temperature range 75–130 °C. (b) DSC and TGA thermograms recorded at different heating rates (2–10 °C min^–1) and at different atmospheric conditions (open pan or hermetically sealed high-pressure capsule (HPC)).

The observed mass loss of 33.27 ± 0.22% (TGA, Figure 4b) confirms the presence of a monosolvate (calculated value for a monosolvate is 33.36%), and the TGA desolvation product shows the AH_s1 characteristics. The heating rate and particle size dependent impact on the desolvation temperatures was found to be less pronounced for S_DMSO than Hy1. Analogous to the Hy1 dehydration, the atmospheric conditions influenced the AH crystallization product, i.e., order–disorder phenomena, with AH_s1 obtained in open pan DSC experiments and AH_s2 in hermetically sealed/closed DSC runs. Δ_trsH_DMSO-AHs1 was measured to be 62.2 ± 2.1 kJ mol^–1 and Δ_dissH_DMSO-AHs2 to be 19.1 ± 1.0 kJ mol^–1. Due to the higher solubility of OTA in DMSO compared to water, OTA partly dissolved in the solvent released from S_DMSO.

3.2.3. Anhydrate

Anhydrate samples were subjected to DSC and TG analyses. Upon heating, OTA AH shows strong sublimation at temperatures above 280 °C. The sublimed OTA crystals show the characteristic PXRD features of AH_s1 (see section 3.5.1). Variation of the sublimation temperature or the temperature of the surface to which the sublimation occurred had no influence on the order−disorder characteristics of anhydrous OTA. On fast heating (≥20 °C min^–1), the AH melting process, overlapping with decomposition, can be observed above 355 °C (Figures S7–S9).

3.2.4. Dimethylammonium Orotate–Orotic Acid (1/1) Salt Cocrystal

Upon heating the mixed dimethylammonium orotate–orotic acid (1/1) salt cocrystal to 280 °C, a transformation/reaction to anhydrous OTA occurs. The product corresponded to AH_s2.

3.2.5. Temperature/Composition “Phase Diagram”

The phase diagram (Figure 5) was constructed using Hy1 and AH materials with similar particle size distribution (20 to 50 μm) and heating rates of 5 °C min^–1. Thus, temperature and size dependent influences on the dehydration of OTA were avoided. Within the hydrate/water region (>0 to 50 mol % OTA), no interaction between free (unbound) water and Hy1 is observed. The DSC curves showed the melting of pure ice, the Hy1 to AH dehydration endotherm at 140 °C, and at higher temperatures further nonreproducible thermal events. The nonreproducible events could be assigned to chemical decomposition (discoloration of OTA) and/or the release of water vapor from the DSC pan after the dehydration event. The melting temperature of ice and the (onset) Hy1 dehydration temperature were found to be independent of the Hy1/water composition. Since we never observed a melting process for Hy1, the dehydration reaction limits the upper presentable phase border in the experimental phase diagram (Figure 5). This border in the OTA Hy1/water region resembles the situation of a miscibility gap, with minor interactions between water and OTA, which is also illustrated by the very low water solubility of the compound. The dominating phase boundary of the right part of the diagram (AH/Hy1 region, 50 to <100 mol % OTA) is again the dehydration process of Hy1 at 140 °C. Due to the very weak interaction between OTA and water and because of the thermal decomposition of the substance, it was not possible to measure a solid–liquid phase transition (defining the liquidus line) above this dehydration temperature (Figure 5). The decomposition of anhydrous OTA occurs at temperatures above 290 °C.

Figure 5.

Temperature/composition “phase diagram”. Hy1, monohydrate; AH, anhydrate; W, water; s, solid; l, liquid.

3.3. Gravimetric Moisture Sorption/Desorption Experiments

Moisture sorption/desorption data of OTA solid forms (Figure 6) were derived at 25 °C. Anhydrate samples AH_s1 and AH_s2, despite showing a comparable particle size distribution, differ substantially in their water sorption characteristics (Figure 6a,b). The sorption process of AH_s1 to Hy1 was completed within two to four days at RHs ≥ 84%. At an RH of 75% the conversion took three weeks; at 61% and ≤53% RH only 0.5 molar equiv of water (50% Hy1 and 50% AH_s1) and no water absorption was seen after one year, respectively. The sorption measurements were repeated at RH values of 61, 75, 84% using AH_s2 (Figure 6b). No water uptake was recorded during storage of AH_s2 for two months at 61% RH, and only 0.03 mol of water per mol of OTA was adsorbed to the surface at 75% RH. At the highest investigated RH level, 84% RH, 40% of the AH_s2 had transformed to Hy1 (Figure 6b) within two months. Structural differences of the two samples will be addressed in section 3.5.

Figure 6.

(a,b) Moisture sorption kinetics of OTA AH_s1 (a) and AH_s2 (b) stored at different RHs. (c) Sorption isotherm of AH_s1 OTA and desorption of Hy1 at 0% RH (stored for one year). (d) Sorption isotherm of S_DMSO. The circles present data points that fulfill the present equilibrium condition (mass change), whereas crosses mark measurement values that did not reach the equilibrium within the allowed time limit of the automated measurements in panel (d). All measurements were performed at 25 °C.

AH_s1 water sorption values, measured after one year, are given in Figure 6c. It has to be noted that the maximum water content did not exceed 0.9 mol of water per mol of OTA, as additionally confirmed with Karl Fischer titration (addressed in section 3.7). A Hy1 sample stored for one year over P₂O₅ (0% RH) lost less than half of its crystal water, resulting in a mixture of AH_s1 and Hy1.

The S_DMSO started to transform to Hy1 at RH values > 30% (Figure 6d). Even after storing the solvate for half a year at the driest conditions (P₂O₅), no transformation to anhydrous OTA was observed.

3.4. Determination of the Critical Water Activity at 25 °C (Slurry Method)

OTA AH_s1/AH_s2 mixtures were added to methanol/water mixtures of various compositions (section 12 of the Supporting Information) and equilibrated under stirring for 40 days. Samples were withdrawn periodically and analyzed with PXRD. In contact with methanol/water, at a water activity (a_w) ≤ 0.66, the AH_s3 was the only solid phase at equilibrium. At a_w ≥ 0.67 the Hy1 was obtained as the most stable form, suggesting that the system, OTA AH_s3 ↔ Hy1, is in equilibrium at a_w ∼ 0.67 at 25 °C. These results agree with the kinetic studies of AH_s2, but not AH_s1. Therefore, a “transformation” (ordering) of AH_s1 to AH_s2 and AH_s3 may occur during stirring, and it was not possible to measure the transition point for AH_s1 (AH_s2) and Hy1 using slurry experiments. Indeed, the anhydrate samples produced in a slurry at a_w ≤ 0.66 showed the characteristics of AH_s2 within days, and upon prolonging the experiments (stirring), the PXRD reflections and IR/Raman bands sharpened further. After approximately three weeks a sample with characteristics corresponding to AH_s3 was obtained (see section 3.5.1). Hardly any changes in the X-ray powder pattern and spectra were observed upon further slurrying the sample. Thus, the measured critical a_w of ∼0.67 is only valid for the pair AH_s3 and Hy1, and the order–disorder of anhydrous OTA influences its hydration stability and will be further addressed in section 3.7.

The results of this a_w study also illustrate that the thermodynamic equilibrium between a hydrate and an anhydrate may be situated on one side of the hysteresis range observed in the moisture sorption/desorption experiments and not in the center (Figure 6c). This suggests that the kinetic mechanisms and activation barriers of these two reversible processes (hydration ↔ dehydration) may vary considerably. The rate of Hy1 to AH transformation (dehydration) is slower than the reversible process (hydration), as indicated by the fact that the dehydration occurs only very slowly at 0% RH and thus far below the true equilibrium a_w value of ∼0.67. In contrast, hydration occurs at an atmospheric moisture condition which is very close to the equilibrium state and indicates that there is a significantly lower driving force for hydration. Defects in the crystal lattice (see section 3.6.4) allow the AH_s1 to Hy1 transformation to occur even at lower RH values (at 61% RH, see Figure 6a), i.e., below the critical AH_s3/Hy1 a_w. Thus, it should be emphasized that only at high RH values (≥67% RH) is Hy1 the thermodynamically most stable OTA phase. However, the hydrate exhibits a very high kinetic stability, which is illustrated by the fact that no transformation to the AH was observed during storage of Hy1 at ambient conditions (RH between 20 and 40% RH, 25 °C) for 20 years.

3.5. Structural Characterization of OTA Solid Forms

3.5.1. Powder X-ray Diffraction

The produced anhydrous OTA samples could be classified into three groups, AH_s1–AH_s3, according to their PXRD patterns, with AH_s1 showing a lower degree of long-range order in contrast to AH_s2 and AH_s3 samples. The broadened Bragg reflections in the anhydrate PXRD patterns (Figure 7), in particular AH_s1, may be indicative of short-range order/diffuse scattering. AH_s2 and especially AH_s3 exhibit, compared to AH_s1, sharper reflections.

Figure 7.

Experimental powder X-ray diffraction patterns (AH_s1–AH_s3) recorded at room temperature compared with a simulated pattern (λ = 1.5418 Å) for a computationally generated anhydrate structure (calc_A1, −273 °C, see section 3.6.2). For computed structure A1 the optimization was repeated keeping the experimentally derived AH_s3 lattice parameters fixed (calc_A1, 25 °C). Asterisks “*” indicate the (200), (011̅) and (012̅) reflections which are shifted/broadened.

It was possible to correlate OTA anhydrate preparation methods to PXRD characteristics. AH_s1 samples were obtained in desolvation/dehydration reactions in which the entrapped solvent molecule could escape the system. Desolvation under isochoric conditions (composition of the binary system remains unchanged) or the chemical reaction from salt cocrystal to neutral OTA (occurring at distinctively higher temperatures) resulted in AH_s2. The presence of solvent molecules as well as the higher temperature may act as mediator leading to a more ordered phase. Slurry experiments, often applied in solid form screenings to find and identify the thermodynamically most stable phase, allowed the phase to slowly relax to an even more ordered phase, AH_s3. It has to be noted that the three different anhydrate samples represent different degrees of ordering, with AH_s1 being the least ordered and AH_s3 the one with the highest degree of order.

3.5.2. Vibrational Spectroscopy

The S_DMSO Raman and IR spectra differ substantially from the vibrational spectra of the other OTA solid forms (Figures S10–S13), in particular in the region of the antisymmetric and symmetric C–S–C stretching (720 and 687 cm^–1) and ν(C–H₃) vibrations of the DMSO molecule.

The two solvate forms differ from the AH samples in the region of ν(C=O), indicating differences in intermolecular interactions due to the loss of COOH···solvent molecule interactions upon desolvation of Hy1 and D_DMSO.

The anhydrate samples AH_s1–AH_s3 show essentially the same Raman and IR characteristics, differ by a maximum of 3 wavenumbers in band positions (Tables S15 and S16), in addition to differences in intensities and in particular sharpness of the bands. Thus, the Raman and IR spectra suggest that hydrogen bonding interactions are essentially the same in the three anhydrate samples, but the samples differ in degree of order–disorder (long-range order). These observations were furthermore complemented and confirmed with solid-state NMR experiments.

3.5.3. Solid-State NMR

The desolvation of Hy1 or S_DMSO to the anhydrous form of OTA leads to stacking faults, which may result in local disorder or a domain structure. Analysis of this process through PXRD is difficult as a domain structure also manifests itself as a lack of long-range ordering and the broadening of the PXRD peaks is observed (Figure 7). In this case the application of methods which are sensitive to the local environment of atoms, namely, solid-state NMR, can give further insight.

¹H–¹³C CP/MAS solid-state NMR spectra of different forms of OTA show similar peak positions. Each spectrum contains five distinct peaks which can be assigned to five different carbon atoms in the OTA structure. Only S_DMSO shows two additional peaks at 39.0 and 38.4 ppm which can be assigned to DMSO (Figure 8b). The number of magnetically nonequivalent carbon sites indicates that all OTA solid forms contain one molecule in the asymmetric unit, which is in agreement with the previously reported crystal structures (section 3.1). This is further corroborated by ¹H–¹⁵N CP/MAS NMR spectra of different OTA forms, which show one peak for each structurally nonequivalent nitrogen atom (Figure 8a). The assignment of different carbon and nitrogen sites was made based on CASTEP calculations, ¹H–¹³C CP/MAS NQS (nonquaternary suppression) and ¹H–¹³C HETCOR experiments (see section 8 of the Supporting Information). It is known that CASTEP accurately predicts the chemical shift order of even slightly inequivalent sites,^83,84 and hence can be used here to predict the order of three carbonyls (C1, C2, C5) in the ¹³C spectrum and both nitrogen sites. These are difficult to distinguish using any other method.

Figure 8.

¹H–¹⁵N CP/MAS (A) and ¹H–¹³C CP/MAS NMR (B) spectra of different crystalline forms of OTA (spinning sidebands are labeled with asterisks).

The ¹³C and ¹⁵N spectra before and after desolvation show significant changes in positions of the peaks of the carbons C3 and C5 and nitrogen N1 atoms (Figure 1). Both C5 and C3 carbons undergo significant downfield shifts of ca. 3 ppm after desolvation. This may be related to a shielding effect of structural water and/or changes in hydrogen bonding pattern upon desolvation. Nitrogen N1 close to the carboxylic acid motif undergoes a dramatic upfield shift of ca. 6 ppm, while the effect of these structural changes on the other nitrogen site is only minor (ca. 1.5 ppm downfield).

Comparison of both AH and Hy1 with S_DMSO reveals very different patterns of interactions. While the C3 carbon peak is in the same position as in the spectrum of anhydrous material, both C2 and C5 carbons show significant upfield shift of ca. 3 and 4 ppm when DMSO is present in the structure. Similarly, changes in the chemical shifts of nitrogen (N1) can be seen, which again confirms the importance of the interactions of this site with the solvent molecules and hydrogen patterns in the crystal structure. In S_DMSO the solvent molecule hydrogen bonds to N1 (N1–H···O_DMSO, Figure 2b), and in Hy1 the N1–H group is in close proximity to the water molecule (N1···O_water distance: 3.7 Å). The N2, showing hardly any up-/downfield shifts, is involved in a dimeric hydrogen bonding interaction (N2–H···O) in S_DMSO and Hy1. Furthermore, the differences in the hydrogen bonding patterns in both S_DMSO and Hy1 are well indicated in the 1D ¹H CRAMPS spectra (see section 8 of the Supporting Information). The two distinct protons H_N1 and H_N2 can be distinguished in the spectrum of the S_DMSO structure, indicating very different environments of the hydrogen atoms which take part in the bonding motif. In comparison, the ¹H 1D CRAMPS spectrum of the structure Hy1 shows overlapping peaks of both hydrogen sites (H_N1 and H_N2) indicating a similar local environment of protons.

Anhydrous OTA materials with different levels of order–disorder show significant differences in both ¹³C and ¹⁵N solid-state NMR spectra. When low-ordered material (AH_s1) is compared with the AH_s2 and AH_s3 samples, a substantial increase of fwhm (full width at half-maximum) of the peaks together with no or little changes in the peak areas, determined by integration, can be observed (Figure 9, Table 1). This indicates an increased distribution of possible orientations of both nuclei. The broadening of the peaks varies between different carbon and nitrogen sites. Carbon peaks which broaden the most are C3 (66%), C5 and C4 (ca. 40%) which agrees with the carbon sites mostly affected by the chemical shift changes between anhydrous and Hy1 structure (C3, C5 downfield shift of ca. 3 ppm; C4 downfield shift of ca. 1.5 ppm) and corresponds well to the transformation mechanism proposed in section 3.7. ¹⁵N spectra of anhydrous OTA with different degree of order–disorder show not only broadening of the peaks but also additional shifts in peak positions for both nitrogen sites. With a decreasing degree of order the N1 site shifts 0.6 ppm upfield while the N2 site is shifted 0.4 ppm toward lower frequencies. As ¹⁵N NMR has much larger chemical shift scale (1000 ppm) as compared to ¹³C NMR (200 ppm), even small differences in the local environment of atoms can be observed.

Figure 9.

¹H–¹⁵N CP/MAS (A) and ¹H–¹³C CP/MAS (B) NMR spectra of anhydrous orotic acid with different level of order–disorder (AH_s1, AH_S2, AH_s3).

Table 1. Comparison of Peak Heights, Integrals, and FWHM for Different Carbon and Nitrogen Sites of Anhydrous OTA with Different Level of Order–Disorder.

	height		integration		fwhm
peak (ppm)	AHs1/AHs2	AHs1/AHs3	AHs1/AHs2	AHs1/AHs3	AHs1/AHs2	AHs1/AHs3
C2 (170.8)	0.81	0.70	0.96	0.92	1.14	1.33
C5 (165.4)	0.80	0.68	0.92	0.98	1.13	1.42
C1 (152.6)	0.88	0.80	0.95	0.94	1.03	1.13
C4 (143.3)	0.79	0.69	0.95	0.98	1.19	1.39
C3 (105.5)	0.71	0.55	1.00	0.96	1.32	1.66
N1 (161.6–161.0)	0.79	0.78	1.13	1.17	1.41	1.76
N2 (130.2–130.6)	0.89	0.83	0.98	1.10	1.15	1.44

3.6. Computational Modeling

The experimental characterization of the known OTA solid forms was complemented with the computational generation of the anhydrate and monohydrate crystal energy landscapes. The anhydrate crystal energy landscape was used to propose³³ possible anhydrate structure(s).

3.6.1. Comparison of Calculated and Experimental Monohydrate Structures

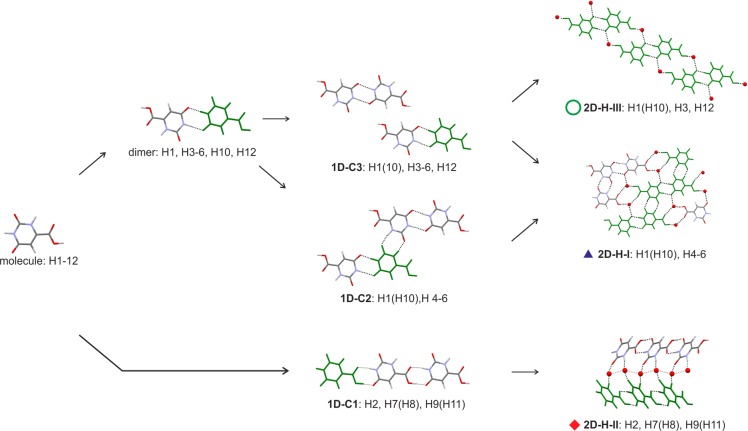
The lattice energy landscape of OTA monohydrates (Figure 10) has the experimental Hy1 structure as global minimum. Other structures were calculated within the energy range found for experimentally observed polymorphs.⁸⁵ Overall, the most stable computationally generated structures are clustered in two groups based on their packing efficiency, with the less densely packed structures being more stable than the dense packing arrangements. The 12 most stable hydrate structures, labeled in Figure 10, were analyzed in more detail, with respect to conformation, hydrogen bonding,⁸⁶ and packing similarity.⁷⁶

Figure 10.

Lowest energy OTA monohydrate crystal structures generated in CSP searches (PBE-G06), with the experimental structure corresponding to the global minimum. Each symbol corresponds to a computationally generated crystal structure. The lowest energy hydrate (H) structures are labeled according to their rank and are classified according to packing similarity (Figure 11). Isostructural packings are labeled with dashed ellipses or connected with an arrow.

All 12 low energy structures adopt a planar conformation closely related to “Conf A” (Figure S1), and the O=C2–N2 group forms either the 1-dimensional C1 chain (1D-C1, Figure 11), involving COOH and CONH functionalities, or a by an inversion symmetry related dimer (dimer, Figure 11). Based on the dimer motif two recurring 1D packing arrangements were identified, 1D-C2 and 1D-C3. Each of the most stable structures forms at least one of the three recurring 2-dimensional (2D) packing arrangements depicted in Figure 11, i.e., stacks of 1D-C3 chains (2D-H-III), double stacks of 1D-C1 chains (2D-H-II), or 2D-H-I layers involving the 1D-C2 and 1D-C3 chains. Structures H9 and H11, as well as structures H7 and H8, are isostructural, closely related in energy and differing only in the position of one of the water protons. Furthermore, structures H1 (experimental) and H10 differ mainly in the orientation of the water molecule, with the H10 structure being less densely packed and able to transform to the experimental one if one O_water–H···O hydrogen bond is rearranged. The 2D-H-III packing arrangement can be found in the experimental structure and in high density structures. The 2D-H-II arrangement is only seen in less densely packed monohydrate structures, and 2D-H-I is spanning the entire range from low to high packing indices.

Figure 11.

Illustration of the packing similarities of common building blocks in labeled structures on the OTA monohydrate crystal energy landscape (Figure 10).

The different stages of lattice energy estimation (section 2.7) had either H10 or H1 as the lowest energy structure, making the isostructural packing arrangement 2D-H-III (if water is ignored) the most stable one. This outcome is independent of the lattice energy calculation method used and supports that the most stable Z′ = 1 packing has been found experimentally.

3.6.2. Computationally Generated Anhydrate Structures

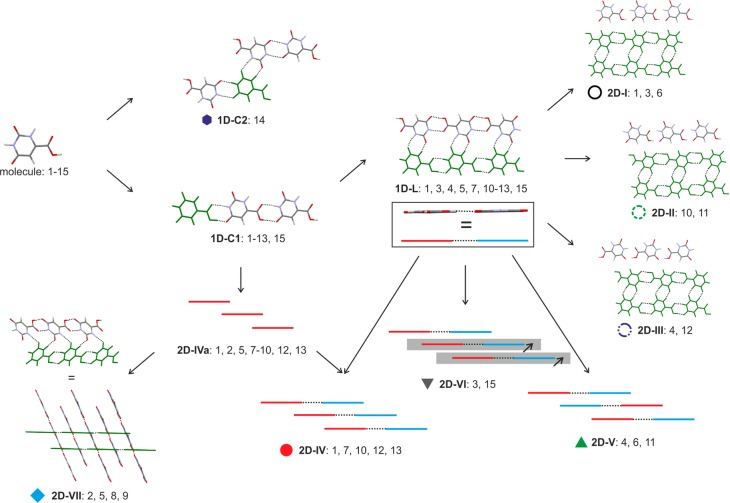
No structural information for anhydrous OTA can be found in the literature. With the computational method having been successful in predicting the Hy1 structure as the most stable (Figure 10), as well as for other small (drug) molecules,³⁶ we used CSP to elucidate the structural information.

All computationally generated lowest energy structures, labeled on Figure 12, have approximately the same conformation, as found in Hy1. The anhydrate lattice energy landscape differs from Figure 10 in that the lowest energy structures show a distinctively smaller variability in packing indices. A consistent feature in all computed structures, anhydrates, and monohydrates is π···π stacks of OTA molecules, with a stacking distance of approximately 3.1 Å. The different stages of lattice energy estimation (section 2.7) always had A1 as the lowest energy structure.

Figure 12.

Lowest OTA anhydrate crystal structures generated in CSP searches (PBE-G06). Each symbol corresponds to a computationally generated anhydrate structure. The lowest energy structures are labeled according to their rank and classified according to packing similarity (Figure 13).

Analyses of the packing and hydrogen bonding motifs present in the lowest energy structures identified a chain arrangement, 1D-C1, as the most common and most favorable among anhydrous OTA structures (Figure 13), an arrangement also seen in hypothetical low-energy hydrate structures (Figure 11). All of the most stable structures, with the exception of structure A14, show the 1D-C1 building block. Structure A14, a layer based structure, exhibits the 1D-C2 hydrogen bonded chain of Hy1 (Figure 11). Overall, hydrate and anhydrate structures share 1D packing modes.

Figure 13.

Illustration of the packing similarities of common building blocks in labeled structures on the OTA AH crystal energy landscape (Figure 12).

A double 1D-C1 chain, 1D-L, is present in 10 out of the 14 most stable structures. This arrangement is also a common extended structure motif in barbiturates,⁸⁷ a chemically related class of drug compounds. The strongest intermolecular interactions, N–H···O hydrogen bonds (for PIXEL energy calculations see section 3 of the Supporting Information), are present exclusively within the 1D-L motif, making this packing motif the most favorable arrangement. Seven out of the ten 1D-L based structures (1, 3, 4, 6, 10–12) are layer based and differ solely in their packing of the 1D-L building blocks. Three distinct layers, 2D-I to 2D-III (Figure 13), can be identified differing in the connectivity of close C–H···O contacts. The latter intermolecular interactions contribute substantially to the lattice energy as derived from the PIXEL pairwise energy estimations (section 3 of the Supporting Information). Furthermore, the seven structures can be classified into three groups based on the π···π stacked 1D-L chains, i.e., 2D-IV to 2D-VI (Figure 13). Like the C–H···O contacts also the π···π close contacts were identified as integral to the overall stability of the structures.

Transformations between selected theoretical 1D-L layer based structures could be possible without breaking the strong 1D-L building blocks, i.e., between selected structures of groups 2D-I to 2D-III or 2D-IV and 2D-VI. However, this would require energy for breaking C–H···O and/or π···π close contacts. Thus, the computed OTA crystal energy landscape, complemented with PIXEL pairwise energy calculations, supports the assumption that OTA may show stacking faults/intergrowths, as observed and predicted for other small organic molecules (eniluracil,⁸⁸ aspirin,^89,90 and phloroglucinol dihydrate^33,91). The small variability in packing indices, as opposed to the broader range of densities found for the computed lowest energy monohydrate structures, further supports this assumption.

3.6.3. Ordered Anhydrate

By comparing the experimental AH PXRD patterns to the simulated powder patterns of the computationally generated low-energy anhydrate structures it should be possible to derive structural information. Simulated PXRDs of computed structures A1 (P1̅), A3 (P1̅), A4 (P2₁/c), A6 (C2/c), A10 (P1̅), A11 (P2₁/c), and A12 (C2/c) show resemblance to AH_s2, AH_s3 (and AH_s1) patterns (Figure S23). The seven structures have in common that they can be classified as layer structures and show an intense reflection in the range between 28.8 and 29.5 2θ, corresponding to the spacing of OTA layers. The closest matching powder pattern is the pattern simulated from the global minimum structure A1 (Figure 7), although the comparison ignores temperature effects. In addition, the experimental AH patterns were successfully indexed (Table 2) and the obtained lattice parameters and volume contrasted to the Figure 12 structures. The best solution closely matches the parameters calculated for structure A1. Repeating the CASTEP geometry optimization of structure A1, and keeping the experimental RT lattice parameters fixed, results in an AH_s3 structure model whose simulated PXRD pattern gave an excellent match with the experimental phase, apart from peak broadening in the observed patterns (Figure 7). Thus, the global energy minimum in Figure 12 can be described as the ordered OTA AH structure.

Table 2. Comparison of Calculated and Experimental OTA AH Lattice Parameters.

phase	T/K	a/Å	b/Å	c/Å	α/deg	β/deg	γ/deg	V/Å3
A1a	0	5.456	5.964	9.043	95.41	94.28	97.18	289.5
AHs1b	RT	5.643(2)	5.906(3)	9.069(6)	97.89(2)	97.32(4)	97.00(2)	294.0(3)
AHs2b	RT	5.595(1)	5.899(1)	9.136(2)	98.17(<1)	96.91(<1)	96.91(<1)	293.5(1)
AHs3b	RT	5.557(1)	5.887(1)	9.198(2)	97.01(<1)	96.63(<1)	96.43(<1)	293.5(1)

^aComputationally generated structure.

^bDerived from indexing PXRD patterns.

The A1 structure forms two kinds of strong H-bonded inversion related R₂²(8) ring motifs, which are formed between N–H···O and O–H···O hydrogen bonds (Figure 14). A third R₂(8) ring motif involves C–H···O close contacts. All three ring motifs are located within layers parallel to (11̅2̅). Stacked layers are spaced by 3.1 Å, stabilized by π···π close contacts only.

Figure 14.

Hydrogen bonding motifs (a) and stacking (b) observed in the A1 structure (Figure 12).

3.6.4. Stacking Faults Derived from PXRD and Computationally Generated Crystal Energy Landscape

To identify alternate structures which may lead to possible stacking faults/local disorder, the computed layer-based OTA anhydrates were examined in more detail. Figure 15 schematically summarizes the distinct possible stacking and layer arrangements of the seven OTA layer–structure variations. The hydrogen bonded 1D-L motif is the common building block, i.e., the structures vary in differently π···π stacked 1D-L motifs and/or C–H··O close contacts of adjacent ladder units, i.e., within layers.

Figure 15.

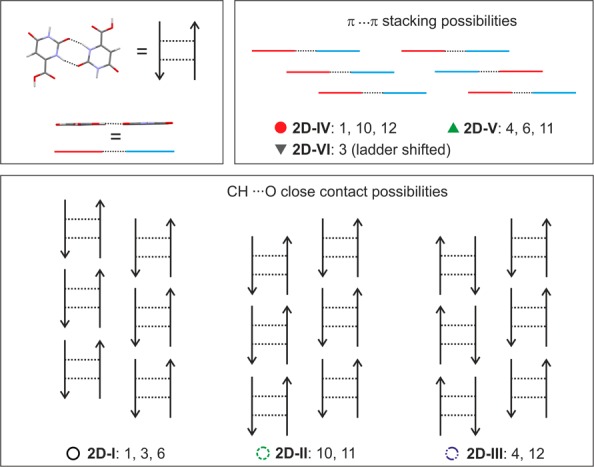
Packing comparison between lowest energy computationally generated OTA anhydrate structures based on 2D packing motifs 2D-I to 2D-VI (Figure 13).

Assuming that A1 is the dominant structural OTA arrangement and the 1D-L motif is present, as inferred from Figure 13 and PIXEL energy calculations (see section 3 of the Supporting Information), two distinct possibilities for stacking faults could be identified: (a) Different stacks of 2D-I layers. This would imply that all strong hydrogen bonding interactions, in addition to the C–H···O close contacts, are maintained and the stacking interactions differ in π···π close contacts, possibly involving structures A1, A3, and A6. (b) The 1D-L motif and π···π stacks between the latter motif are maintained throughout the crystal (2D-IV building block), but C–H··O close contact interactions vary, leading to a different arrangement of adjacent 2D-IV building blocks. This could involve a combination of structures A1, A10, and A12. Structures A4 and A11 are less likely to be observed as domains in A1, as the latter structures exhibit only 1D similarity with A1 and are less likely to be observed on the route of desolvation (see section 3.7).

The interpretation of the possible stacking faults, discussed below, was complemented with DFT shielding calculations on low energy structures presented in Figure 12 (Table 3 and Table S14). Structures A3, A4, A6, A7, and A12 were calculated to differ by less than 1.0 ppm in ¹³C band positions, structures A2, A5, A8, A9, A11, and A15 by less than 2.0 ppm, and structures A10, A13, and A14 by more than 2.8 ppm. Only broadening but no distinct peak shifts were experimentally observed for anhydrate samples AH_s1–AH_s3 (Figure 9). Difference (Δppm) of the experimental N1 and N2 band positions agrees well with the difference of the computed ¹⁵N chemical shifts.

Table 3. Experimental and Computed ¹³C Chemical Shifts Derived from AH and A1–A15 Structure Models^a.

structure	C2b	Δ(A1–x)c	C5b	Δ(A1–x)c	C1b	Δ(A1–x)c	C4b	Δ(A1–x)c	C3b	Δ(A1–x)c
exptl	170.8		165.4		152.6		143.2		105.6
A1	169.4		169.0		151.0		144.6		106.0
A2	169.1	0.3	169.0	0.0	149.4	1.5	145.0	–0.3	106.0	0.0
A3	169.8	–0.4	168.1	0.9	150.6	0.3	144.2	0.5	106.8	–0.8
A4	169.2	–0.2	169.2	0.2	151.1	0.1	144.3	–0.4	105.6	–0.4
A5	168.1	1.3	168.9	0.1	149.6	1.4	143.9	0.8	107.3	–1.2
A6	168.8	0.6	169.3	–0.3	151.0	0.0	143.9	0.7	105.5	0.5
A7	169.0	0.4	169.3	–0.3	150.5	0.4	145.1	–0.5	105.8	0.2
A8	168.7	0.7	168.8	0.2	149.9	1.1	144.6	0.0	105.6	0.4
A9	168.0	1.4	168.4	0.7	149.8	1.1	145.1	–0.5	104.3	1.7
A10	167.8	1.6	168.4	0.7	150.3	0.6	145.3	–0.7	102.5	3.6
A11	168.2	1.2	168.4	0.6	150.7	0.2	145.0	–0.3	104.1	1.9
A12	168.3	1.1	168.9	0.2	150.1	0.8	143.9	0.7	105.1	0.9
A13	167.6	1.8	168.1	1.0	150.5	0.5	144.9	–0.3	103.1	2.9
A14	170.5	–1.1	165.4	3.6	150.2	0.7	142.9	1.7	105.1	0.9
A15	168.7	0.7	167.3	1.8	149.9	1.1	144.8	–0.1	105.4	0.6

^aLayer structures are highlighted in gray.

^bCarbon atoms according to Figure 1. Values correspond to δ_exptl (experimental chemical shifts) or δ_calc (calculated chemical shifts).

^cDifference between calculated chemical shifts using A1 as reference.

3.6.4.1. Possibility A: 2D-I Common Fragment (A1, A3, A6)

Structures A1 and A3 are both triclinic (P1̅), whereas structure A6 is monoclinic (C2/c). The three structures differ in the stacking of the 1D-I layers as schematically illustrated in Figure 16. Based on the ¹³C chemical shift calculations, the three structures show very similar ¹³C solid-state NMR spectra, which is consistent with the experimental ¹H–¹³C CP/MAS NMR spectra of the three anhydrate batches. A transformation from A3 to A1, “ordering” process, would be possible but require appreciable activation energy, as can be derived from the PIXEL pairwise energy calculations, i.e., π···π close contacts contribute significantly to the stability of the structures (Tables S4 and S6). This would explain the experimental ordering process, AH_s1 to AH_s3, found to be possible but only in slurry experiments (stress conditions). Storage of an AH_s1 sample for 20 years at ambient conditions did not result in a change of its PXRD pattern, indicating that the observed ordering effect has an energy barrier and that the AH_s1 domains show a high kinetic stability.

Figure 16.

Illustration of the computationally generated lowest energy structures showing the 2D-I layer motif.

A transformation of A6 domains to A1 or A3 is unlikely to occur in the solid state, as this would require a 180° flip of 2D-I OTA layers. The potential presence of A6 domains in A1 and/or A3 would explain why it was not possible to produce an ordered anhydrate sample.

3.6.4.2. Possibility B: 2D-IV Common Fragment (A1, A10, A12)

The low-energy structures form essentially the same strong intermolecular N–H···O and O–H···O hydrogen bonds but differ in selected π···π and the C–H··O close contacts. Structure A10 adopts the A1 space group P1̅, whereas A12 is monoclinic (C2/c). Like A4, structure A12 is unlikely to be observed upon desolvation, making this packing arrangement unlikely to be observed as domains. In structure A10 the C3 atom has a similar environment as in Hy1, also seen from the chemical shift predictions (Hy1: 102.2 ppm (102.9 ppm at RT), A10: 102.0 ppm, A1: 105.5 ppm), which disagrees with the experimental observation in Figure 9. Thus, stacking faults arising from A10 or A12 domains are unlikely.

3.7. Proposed Mechanism of Hy1 ↔ AH Transformation

The OTA Hy1 and AH phases have the inversion related N1–H···O R₂²(8) dimer in common, in agreement with Figure 8, which indicates that C1 is in a very similar environment (Δppm = 0.1) in the two phases. The N1–H···O R₂(8) dimer accounts in Hy1 for the strongest and in the AH structures for the second most stable pairwise intermolecular interaction (section 3 of the Supporting Information). Furthermore, the OTA molecules are arranged in layer stacks in the two phases. A possible dehydration mechanism is given in Figure 17. Loss of water results in non-H-bonded COOH groups. Since the water molecules are located at isolated sites, their removal requires the breaking of strong intermolecular interactions and a certain degree of structural rearrangement. Water egress could occur along the crystallographic c axis (Figure 17a), under widening/breaking the N2–H···O R₂²(8) dimers, to which water molecules hydrogen bond. The COOH function can then build strong heteromeric R₂(8) dimers with the N2–H and C5=O functions, leading to the strongest pairwise intermolecular interaction present in the layer AH structures, and together with the N1–H···O R₂²(8) dimer resulting in 1D-L motifs (Figure 17b). Adjacent ladder motifs (in layer plane) will rearrange as evidenced from Figure 8 (C3 band position differs in Hy1 and AH) to 2D-I layers, which are according to Figure 12 the most stable OTA crystal layer motif. Stacking of 2D-I layers will optimize upon dehydration, with three competing packings being thermodynamically feasible (ΔE_latt < 6 kJ mol^–1), i.e., A, A3, and A6. The computed energy difference between the domains is in good agreement with the measured Δ_dehyH energy differences (section 3.2.1).

Figure 17.

A model for the rearrangement of OTA Hy1 to AH layer 2D-I. (a) OTA Hy1 2D-H-I layer, with background colors indicating OTA and water regions, viewed along crystallographic c axis. (b) A hypothetical intermediate showing the possible rearrangement of OTA molecules to form the 1D-L motif. (c) 2D-I layer.

The degree of ordering of anhydrous OTA has been shown to influence the transformation of AH to Hy1. A lower degree of ordering not only shows a distinctly faster AH to Hy1 transformation (Figure 6) but also a slightly lower RH dependent stability. Hydration of AH_s1 samples was observed at a lower RH value (∼61% RH) compared to AH_s2 and AH_s3. Hydration of AH_s1 was observed even below the critical a_w value of AH_s3/Hy1 measured at ∼0.67 (corresponding to ∼67% RH). Thus, distinct domains being present in the AH are likely to show different critical a_w values. Only the slurry experiments of anhydrous OTA in water/methanol mixtures at a_w ≥ 0.67 resulted in a 100% transformation of AH to Hy1. In contrast, storage experiments of anhydrous OTA over saturated salt solutions resulted in a conversion rate of about 90% only (Figure 6a). This indicates again the structural reorganization problem in OTA, which may be attributed to stacking faults/domains, e.g., A6 domains. A solid-state transformation appears to be difficult as hydrogen bonded layers have to be flipped by 180° (Figure 16). Storage at higher RH (>90%) results in slightly higher AH to Hy1 conversion rate, suggesting that surface dissolution may occur.

4. Conclusions

Orotic acid solid forms (anhydrate, monohydrate, and DMSO monosolvate) and their transformation pathways were rationalized using a multidisciplinary approach, comprising a broad range of experimental and computational techniques.

The computationally generated anhydrate and monohydrate crystal energy landscapes, which have the experimental monohydrate and ordered anhydrate phase as global energy minima, confirmed that the stable Z′ = 1 neat and hydrated forms have been found. The anhydrate crystal energy landscape shows that closely related structures, exhibiting 2D packing similarity and similar packing indices and lattice energies, can account for stacking faults. Hence, the modeling indicates that experimental anhydrous OTA can be expected to lack long-range ordering, similar to predicted and observed eniluracil⁸⁸ and phloroglucinol dihydrate.^33,91 Detailed analysis of powder X-ray diffraction and solid-state NMR data showed that the degree of disorder varies between anhydrate samples prepared under different conditions, i.e., dehydration conditions (open and isochoric conditions) and treatment of anhydrate samples (slurry experiments below the critical water activity). The production of a fully ordered anhydrate structure, based on exhaustive experiments, seems to be unlikely.

Solid-state NMR spectroscopy in combination with computational modeling (CSP, lattice energy, and chemical shift calculations) allowed us to elucidate the characteristics of the disorder, stacking faults of perfectly planar layers. In addition to the strong intermolecular hydrogen bonding interactions within the layers also C–H···O close contacts and π···π stacking are essential for the stability of the structures. The π···π interactions are likely responsible for the kinetic stability of the domains in anhydrous OTA. The fact that no increase in crystallinity was observed in a disordered OTA anhydrate sample, after 20 years of storage at ambient conditions, confirms that the structural reorganization is kinetically hindered.

The temperature/composition phase diagram, thermal desolvation behavior, moisture sorption/desorption studies, water activity measurements, and structural information derived from CSP studies provide the essential kinetic and thermodynamic data needed to avoid phase transformations during handling, processing, and storing of OTA. Anhydrous OTA absorbs water, depending on stacking faults, at relative humidities starting from ca. 60%. Sample treatment, inducing an “ordering” transformation, increases the moisture dependent stability of the anhydrate, shifting the thermodynamic transition point above 66% RH at 25 °C. The monohydrate shows a very high thermal stability and is very persistent even in dry air. The dissociation to the anhydrate occurs above 135 °C, and the release of water at room temperature occurs only at 0% RH (over P₂O₅), whereas the process takes years. The exceptionally high stability of OTA hydrate can be related to the optimal number of strong hydrogen bonding interactions. The phase transformation enthalpy of the monohydrate to disordered and higher ordered anhydrate was measured as 14.3 ± 0.7 kJ mol^–1 and 9.6 ± 1.1 kJ mol^–1, respectively. Monitoring the loss of water by thermal analytical methods revealed that OTA shows only minor interactions with water apart from the incorporation of crystal water in the hydrate.

The DMSO solvate differs from the anhydrate and monohydrate in that it does not form a layer structure. Compared to the monohydrate the solvate shows a slightly lower thermal stability. At RH > 30% a transformation to the monohydrate occurs, at significantly lower RH values than the anhydrate to monohydrate phase transformation.

In summary OTA can be seen a special case of hydrate/anhydrate system, maintaining perfectly planar layers as a key structural feature upon dehydration but variations in the stacking arrangement resulting consistently in disordered anhydrate(s). This behavior is unique for small organic molecules and illustrates that desolvation processes in organic solvates are complex reactions, which may result in partially disordered phases with an extraordinarily high kinetic stability. Though we did not use the term “polytypism” in the structure discussion, it should be mentioned that most of the computationally generated anhydrate structures could be classified as “polytypes”. Only the complementarity of a broad range of experimental and computational techniques allowed us to provide an understanding of the complex structural, thermodynamic, and kinetic features of OTA, which are needed to safely handle, process, and store the pharmaceutically and biologically relevant molecule.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.molpharmaceut.5b00856.

• Computational and experimental details (PDF).

The authors declare no competing financial interest.