Controlling the hydration rate of a hydrophilic matrix in the core of an intravaginal ring determines antiretroviral release

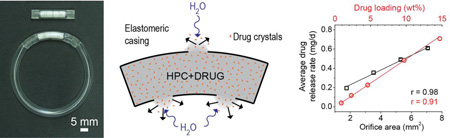
Abstract

Intravaginal ring technology is generally limited to releasing low molecular weight species that can diffuse through the ring elastomer. To increase the diversity of drugs that can be delivered from intravaginal rings, we designed an IVR that contains a drug matrix encapsulated in the core of the IVR whereby the mechanism of drug release is uncoupled from the interaction of the drug with the ring elastomer. We call the device a flux controlled pump, and is comprised of compressed pellets of a mixture of drug and hydroxypropyl cellulose within the hollow core of the ring. The pump orifice size and chemistry of the polymer pellets control the rate of hydration and diffusion of the drug-containing hydroxypropyl cellulose gel from the device. A mechanistic model describing the hydration and diffusion of the hydroxypropyl cellulose matrix is presented. Good agreement between the quantitative model predictions and the experimental studies of drug release was obtained. We achieved controlled release rates of multiple antiretrovirals ranging from µg/day to mg/day by altering the orifice design, drug loading, and mass of pellets loaded in the device. This device could provide an adaptable platform for the vaginal drug delivery of many molecules.

Graphical abstract

Introduction

Over 2 million new HIV infections occur annually, predominately through sexual transmission [1], urging the development of new technologies to control the pandemic. Recently, several clinical trials have provided evidence that prophylactic oral and vaginal administration of antiretrovirals can prevent the sexual transmission of HIV [2, 3]. However, clinical studies evaluating a 1% tenofovir vaginal gel resulted in modest to no reduction in HIV incidence [4, 5]. The clinical failures of the tenofovir gel likely stemmed from low user adherence and application dependent drug pharmacokinetics of the gel formulation [5, 6] leading to an insufficient drug concentration in the local tissue where the initial transmission events occur [7, 8]. This has driven the developmental efforts towards longer duration delivery systems like intravaginal rings (IVRs) that may provide higher adherence than gels [9–11] and improved drug pharmacokinetics as a result of the sustained drug delivery [8, 12]. Despite more than four decades of research into IVR technology, the chemical properties and delivery requirements of the drug typically governs the elastomer selection, previously limiting this product for delivery of hydrophobic molecules [8, 13, 14]. However, the need for new HIV prevention technologies resulted in a resurgence of IVR development in the last decade. This has led to new ring designs and utilizing new polymers to enable the delivery of hydrophilic and macro-molecules at mg/d delivery rates that were previously unachievable [12, 15–19]. Of particular interest to this work are pod/insert vaginal rings where small drug delivery systems are held within the ring body, separating the drug delivery requirements from the mechanical properties [15, 18, 20, 21]. Nevertheless, even with these new materials and designs, to achieve extended duration release the drug molecule must still diffuse through either the ring elastomer or the polymer of a drug delivery device embedded in the ring body leading to the requirement to match the polymer to the drug. New IVR designs where drug release does not depend on the drug solubility and diffusivity in the polymers of the IVR are needed and would enable the delivery of drugs irrespective of the chemical properties of the drug.

Osmotic pumps can achieve controlled and sustained release of drugs with a range of chemical properties and molecular weights, with the drug potentially acting as the osmotic agent or simply releasing as a suspension of particles in a solution or semisolid gel [22, 23]. However, osmotic pump technology has been under-utilized for topical drug delivery. We designed the first intravaginal osmotic pump tablet for multiday antiretroviral delivery and achieved controlled release over 10 days in sheep [17]. We then modified the osmotic pump design by substituting the function of the semipermeable membrane with orifices in a rigid non-water permeable casing. The orifices and hydration properties of the polymer pellet control both water entry into and release of a drug containing semisolid gel from the orifices of this flux controlled pump (FCP) [24]. The design and function of the FCP is fundamentally different from an osmotic pump. Fluid entry occurs through the semipermeable membrane of an osmotic pump, whereas fluid entry only occurs through the orifices of a FCP, reducing the hydration kinetics and thereby resulting in longer duration controlled release. However, in both osmotic pump tablet and FCP designs, we exploited the expansion of a high molecular weight polymer caused by hydration to deliver a drug-loaded gel through an orifice [17, 24].

Herein we present the design and evaluation of a FCP integrated into an IVR with pseudo zero-order release kinetics of many leading HIV prevention antiretrovirals. We demonstrated a linear relationship between the release rate of the hydrophobic drug IQP-0528 from the device to drug loading and orifice area in vitro. Depending on the molecule delivered, we observed that the hydration kinetics and dissolution properties of the polymer pellet control drug release. This suggests that for hydrophobic and macro-molecules, the drug solubility and diffusivity in the swollen polymer matrix has a negligible influence to the overall drug release, whereas for more hydrophilic molecules, the drug diffusion through the polymer matrix contributes to drug release. This differentiates the FCP from other IVR platforms where drug release depends entirely on drug diffusion and solubility in the ring elastomer [8, 13, 14]. In addition, to aid in the design of this system, we developed a finite element model that reproduces the drug release behavior for different orifice geometries, and drug type and loading. This model is a fast and accurate tool to design this FCP device and supports the hypothesis that polymer hydration controls drug release from these systems.

MATERIALS AND METHODS

Fabrication of flux controlled pumps

IQP-0528 (ImQuest Biosciences, Frederick, MD), dapivirine and maraviroc (DPV and MVC respectively; International Partnership for Microbicides, Silver Spring, MA), tenofovir and tenofovir disoproxil fumarate (TFV and TDF respectively; Gilead Sciences, Foster City, CA), and 10 kDa rhodamine B dextran (Sigma Aldrich, St. Louis, MO) were each geometrically mixed with hydroxypropyl cellulose (HPC; GF, MW = 370 kDa; Klucel Pharm, Hercules, Wilmington, DE) to achieve a range of loadings from 0.9–15 wt% IQP-0528 in HPC, 10 wt% DPV, MVC, TFV and TDF in HPC, and 0.9 wt% rhodamine B dextran in HPC. Pellets, 4 mm in diameter and 51 ± 1 mg, were formed by compression as previously described [24]. Tecoflex aliphatic polyether thermoplastic polyurethane (EG-65D; Lubrizol Advanced Materials, Wickliffe, OH) tubing was fabricated by hot-melt extrusion to create final tubing dimensions of 0.7 mm wall thickness and 5.5 mm diameter [12]. The tubing was cut to a length of 36, 40, and 44 ± 0.5 mm for FCP with 2, 3 and 4 pellets respectively. Tubing lengths were chosen so that 2, 3 and 4, 50 mg pellets fit snugly inside the device. One end was sealed by inductive tip-forming welding (PlasticWeld Systems, Inc., Newfane, NY). The orifices were manually drilled and the diameter was measured using a stereomicroscope and compared to a scale. The standard deviation of the orifice diameter was 3–4% of the diameter (at least 3 orifice with 3–4 measurements each). Next 2, 3 or 4 compressed pellets were inserted into the open end of the device followed by sealing the second end by inductive tip-forming welding similarly to the first weld.

In vitro drug release testing

In vitro drug release was measured from individual FCPs in 20 mL of 25 mM acetate buffer pH 4.2 at 37°C and 80 rpm shaking (N = 3). Sink conditions for the polymer were maintained. The release media was replaced daily. To measure the release rates of IQP-0528 and DPV, the complete release media was collected on days 1, 2, 3, 5, 7, 10, 15, 20, 25 and 30 and diluted with methanol to dissolve the released drug. To measure the release rates of TFV, TDF, MVC and rhodamine B dextran an aliquot of the release media was collected for analysis on the same schedule and the remainder discarded. Cumulative release was estimated by integration of the release rate profile using a trapezoidal approximation. Average release rates were calculated as the cumulative release divided by the elapsed time. For FCPs with four to one, 1.5 mm orifices the mass of the device was measured on the same days the media was collected.

To measure the decay of the pseudo zero-order portion of the release rate profile dimensional analysis was performed. The IQP-0528 release was plotted with both variables normalized to the maxima of the experiment. Then a linear fit from the maximum release rate to the end of the release curve was performed and the dimensionless slopes were compared. The day 30 point was excluded for the FCPs containing two, 50 mg pellets with two, 1.5 mm orifices, and four, 50 mg pellets with four, 1.5 mm orifices since the release on that day was drastically different from the preceding days. All linear and power law curve fitting were performed using OriginPro8 (OriginLab Corporation, Northampton, MA).

Drug extraction from pellets and FCPs

For determination of drug loading in the pellets, pellets were placed in a volumetric flask and dissolved overnight in methanol or 1:1 water:methanol mixture for TFV. Upon completion of in vitro release studies, FCPs were cut into multiple pieces and placed in a 50 mL centrifuge tube with methanol or 1:1 water:methanol mixture for TFV and shaken overnight. The solution was transferred to a volumetric flask and the FCP casing was rinsed at least 5 times. Drug content was determined by UV-HPLC. To determine the amount of pellet, i.e. the sum of drug and HPC, remaining, a portion of the extraction solution was dried to constant mass. To confirm drug recovery, known amounts of drug and HPC were dissolved in parallel with a similar amount of Tecoflex EG-65D present in the case of FCP extractions.

Measuring drug diffusivity in HPC solutions

The diffusivity of TFV, TDF and MVC were measured as a function of HPC concentration using Franz cells (Permegear, Hellertown, PA). The solutions were made with 0.1 wt% drug and 1.2, 2, 3, 5 and 10 wt% HPC in 25 mM acetate buffer pH 4.2. The concentration of each drug in the HPC solutions was determined by dissolving 0.1 mL of gel in a 10 mL volumetric flask with methanol for TDF and MVC or 1:1 methanol:water for TFV. Durapore membrane filters (hydrophilic PVDF, 25 mm diameter, 0.45 µm pore size; Millipore, Billerica, MA) were fitted to a Franz cells with a 20 mm orifice diameter and receptor compartment with 15 mL of 25 mM acetate buffer pH 4.2. Then 1.5 mL of each drug-HPC solution at 37°C was placed on the donor compartment and covered with parafilm to minimize evaporation. Samples of 0.5 mL were taken from the receiver compartment with an analytical syringe at predetermined time points: 10, 20, 30, 45, 60, 75 and 90 mins; and then replaced with fresh buffer. The drug concentration at each time point was measured by UV-HPLC. The cumulative amount of drug that diffused from the donor compartment to the receptor (M_t) with respect to the square root of time was plotted and the slope of the line was used to calculate the diffusion coefficient, D, according to the diffusion equation (Eq. 1) solved for semi-infinite geometry and a completely dissolved solute [25] where C_o is the initial drug concentration in the HPC solution, and A is the exposed area. All data are presented as the mean ± SD.

$$M_t=2C_{0}A\sqrt{Dt/\pi }$$ Eq. 1

Drug content analysis

IQP-0528 [26], TDF [27], and TFV [12] concentration for extraction and in vitro release studies was measured by UV-HPLC methods described previously. The same method was used for TDF and MVC as described previously with the addition of monitoring 197 ± 4 nm to quantify MVC [27]. DPV was quantified by UV-HPLC using an Agilent 1260 Infinity series system with an Eclipse XDB-C18 column (4.6×150 mm, 5 µm; Agilent, Santa Clara, CA) at 25°C at a flow rate of 1.5 mL/min. Data was collected at 280 ± 8 nm. A gradient of 0.1% TFA in acetonitrile (ACN) - 0.1% TFA in water (0–1 min: 30% 0.1% TFA in ACN, 1–9 min: 30–95% 0.1% TFA in ACN, 9–10 min: 95–30% 0.1% TFA in ACN) was used for elution. Rhodamine B dextran concentration was determined by reading the fluorescence using a Synergy2 plate reader (BioTek, Winooski, VT) at 540 ± 20 nm excitation and 620 ± 40 nm emission wavelengths.

Model of drug release

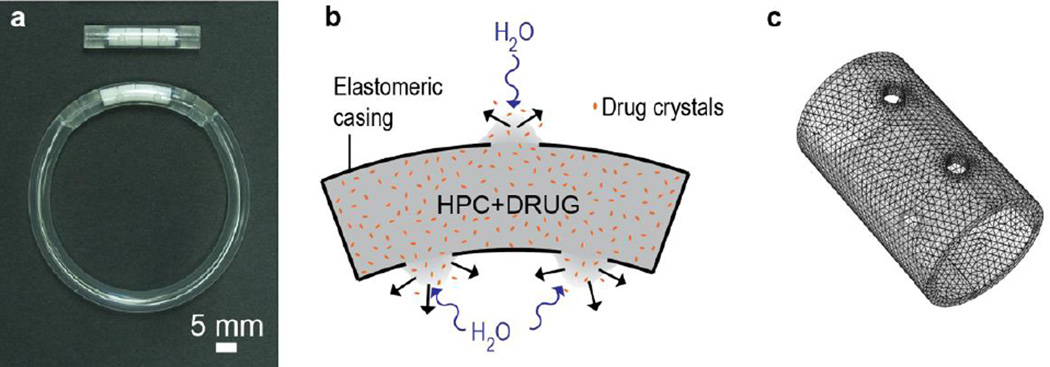
The release kinetics of FCPs under in vitro conditions was modeled using a transport model based on a generalized diffusion equation. For the model calculations we implemented a finite element analysis in a cylindrical geometry following the dimensions described above (Fig. 1c). The mass transport is modeled with a diffusion equation of the form (Eq. 2) [25]:

$$\frac{\partial C_k}{\partial t}=\frac{\partial }{\partial x}\left(D_k\frac{\partial C_k}{\partial x}\right)+\frac{\partial }{\partial y}\left(D_k\frac{\partial C_k}{\partial y}\right)+\frac{\partial }{\partial z}\left(D_k\frac{\partial C_k}{\partial z}\right)$$ Eq. 2

Where k represents each of the diffusing components of the system, and C_k and D_k are their concentration and diffusion coefficients respectively.

Figure 1.

Photograph and schematics of the flux controlled pump-IVR. (a) The photograph depicts an FCP (top), and an FCP integrated into an IVR (bottom). The FCP contains compressed pellets of drug and hydrophilic polymer within a sealed polymer tube with orifices. (b) Schematic of drug (orange dots) release from an FCP with water entry through the orifices causing polymer hydration and diffusion of a drug-loaded gel from the device. (c) Scheme of the geometry implemented in the finite element calculation (three orifices of 1.5 mm diameter).

The model assumes that the release kinetics of the FCP system is mainly governed by the hydration and diffusion of the polymeric matrix (HPC). Thus, the two components that we consider are (1) water and (2) HPC. As drug transport is not directly considered in this model, drug release profiles were obtained by applying the weight fraction of drug in the HPC released.

We assumed that the release dynamics of the HPC depend on the extent of hydration, thus, more hydrated regions diffuse faster than less hydrated ones. To describe the water concentration dependence of the diffusion coefficients we used a Fujita dependence [28], which is based on a free volume approach. This type of model has been successfully used to model drug diffusion in hydroxypropyl methylcellulose (HPMC) [29, 30], polymer diffusion in polyethylene oxide (PEO) [31] and other similar systems [32–34]. In this approach, diffusion coefficients are dependent on the water concentration according to Eq. 3:

$$D_k=D_{k,eq}\mathit{\text{exp}}(-{\beta }_k(1-\frac{C_{\mathit{\text{water}}}}{C_{\mathit{\text{water}}},eq}\left)\right)$$ Eq. 3

where C_k are the concentrations of each species (k), D_k are diffusion coefficients and β_k is a constant that characterizes the water concentration dependence of the diffusion coefficient. D_{k, eq} represent the diffusion coefficients of each species at the maximum water concentration C_{water, eq} (in equilibrium with the swollen matrix).

The solution of the diffusion equation in the geometry of the device was obtained using the COMSOL Multiphysics package (COMSOL Inc., Burlington, MA). We used the following assumptions and boundary conditions:

1. Diffusion is isotropic and there is no convective flow.

2. There is no water in the device at time equal to zero (dry matrix condition).

3. The concentration of water outside the device is constant and equal to C_{water eq}.

4. The concentration of HPC and drug outside the device is equal to zero (perfect sink conditions).

5. The water and drug transport through the casing is negligible

Comparison between model and experiments

For the model to help in the design of FCPs we fitted the parameters of Eq. 3 to experimental data for a device with three orifices of 1.5 mm in diameter and four, 50 mg pellets containing 10 wt% IQP-0528 in HPC. This allowed us to test the flexibility of the model under new experimental conditions. The fitted parameters are: D_{HPC, eq} = 1.02 × 10⁻¹⁰ m²/s, β_HPC = 2.1 and β_water = 0.5 and D_{water, eq} = 5.6 × 10⁻¹⁰ m²/s. All other device configurations are predicted using these parameters.

To test the performance of the model we compared the values of cumulative release at different experimental conditions. The comparison was made by the coefficient of determination (R²) and by the root mean square deviation (RMSD) between the model and the experimental data. Additionally, we consider that the experimental average release rate and the model release rate are not a good quantity to be compared. This is due to the fact that the experimental release rate is a measure of amount released per day while the model release rate is the derivative of the cumulative release with a higher time resolution. Therefore, we included the values of release rate for the model but the comparison of the performance of the model was done on the cumulative release only.

RESULTS

Effect of orifice size and number on the IQP-0528 release rate

We measured the in vitro drug release kinetics as a function of orifice size of FCPs with four, 50 mg pellets of 10 wt% IQP-0528 in HPC with different orifice configurations, one, two, three, and four orifices of 1.5 mm in diameter (Fig. 2a and b) and three orifices of 2.3 and 2.7 mm in diameter (Fig. 2d and e). A larger orifice area generally resulted in a higher release rate due to the higher rate of water entry (Fig. 2c). However, after ~75% cumulative release was attained, the drug release rate dropped dramatically. In the first 10 days the average release rates for FCPs with four, three, two, and one, 1.5 mm orifices were 700 ± 60, 570 ± 14, 410 ± 33, and 170 ± 32 µg/d respectively. This corresponded to peak drug release rates of 900 ± 38, 670 ± 29, 480 ± 110, and 224 ± 40 µg/d for the devices containing four to one orifices respectively (Fig. 2a). However, the drug release rates from the FCPs with four and three orifices reduced to the level of the two orifice FCPs by day 25. This resulted in 30-day average drug release rates of 610 ± 12, 490 ±12, 350 ± 15, and 190 ± 19 µg/d, and calculated cumulative drug releases of 93 ± 1.8, 75 ± 1.8, 54 ± 2.3, and 30 ± 2.9% for four, three, two, and one, 1.5 mm orifice FCPs respectively (Fig. 2b, p < 0.001, single factor ANOVA). The 30-day average release rates and orifice areas presented a linear dependence for FCPs with one to four, 1.5 mm orifices (Fig. 2f, Spearman correlation of r = 0.97 and p = 0.0002). The 30-day IQP-0528 cumulative release calculated from the release rate was comparable to values measured by residual drug extraction for FCPs with one to four, 1.5 mm orifices (p = 0.33, 0.65, 0.042 and 0.12 for one to four, 1.5 mm orifice FCPs respectively; paired t-test for means). This confirms the discrete integration method utilized for calculating cumulative release profiles.

Figure 2. In vitro release of IQP-0528 comparing different orifice configurations.

(a and d) IQP-0528 release rate and (b and e) cumulative release from FCPs with four, three, two, and one, 1.5 mm diameter orifices and three, 2.7, 2.3, and 1.5 mm diameter orifices containing four, 50 mg pellets of 10 wt% IQP-0528 in HPC. Panels a, b, d and e compare the experimental (symbols) and model (solid lines) results. (c) Cumulative water uptake as measured by device mass increase and calculated cumulative pellet release. (f) 30-day average release rates and the hydration-scaling factor correlated linearly with orifice area for FCPs with four, three, two, and one, 1.5 mm orifices (Spearman correlation of r = 0.97 and p = 0.0002, for the 30-day average release rate, and r = 0.91 and p < 0.0001 for the hydration-scaling factor). The hydration-scaling factor was from fitting the cumulative water uptake of each device to a power law equation.

Comparing the IQP-0528 release rate from FCPs containing three orifices of 2.7, 2.3, and 1.5 mm in diameter (Fig. 2d and e), we found the peak release rates were 1.9 ± 0.055, 1.3 ± 0.075 and 0.70 ± 0.014 mg/d respectively. This corresponded to 10-day average release rates of 1.4 ± 0.16, 1.1 ± 0.027 and 0.57 ± 0.014 mg/d for three, 2.7, 2.3, and 1.5 mm orifice FCPs respectively. The drug release rate for FCPs with three, 2.7 and three, 2.3 mm orifices dropped to nearly 0 on day 20 and day 25 respectively and remained low for the study duration. The drastic reduction of the release rate on days 20 and 25 corresponded to calculated cumulative release of 90 ± 8.0% on day 20 for the three, 2.7 mm orifice FCPs and 99 ± 6.8% on day 25 for the three, 2.3 mm orifice FCPs. (Fig. 2e) This confirms that the severe decrease of the release rate resulted from an insufficient amount of drug remaining within the device.

The release rate displayed a biphasic behavior with a few day lag time to reach a maximum release followed by a pseudo-steady state that decayed for the remainder of the 30 days (Fig. 2a). For FCPs with four to one, 1.5 mm orifices, the 10-day average release rate was higher than the 30-day average release rate for each design except the one, 1.5 mm orifice devices. This difference resulted from a more extreme maximum release rate for the four, three, and two, 1.5 mm orifice FCPs and the differences in the decay of the release rate after the maximum release rate was achieved. To enable comparisons of the release rate decay in the later portion of the curve between devices with different release rates, we performed dimensional analysis by normalizing the IQP-0528 release rate and time to the maximum values. Then we performed a linear fit of the portion of the plot after the initial lag from the peak release rate and beyond. A steeper slope i.e. a slope with a reduced negative value represents increased release rate decay. The slopes of such fits were −1.0, −0.93, −0.57 and −0.36 for the four, three, two, and one, 1.5 mm orifice FCPs respectively (R² = 0.961, 0.992, 0.998, and 0.549). For FCPs with three, 2.3 and 2.7 mm orifices, the decay slopes were −1.4 and −1.9 respectively (R² = 0.992, and 0.875). The lower R² value for the one, 1.5 mm orifice FCPs (R² = 0.549) suggests that orifice configuration did not exhibit a linear decay. The 30-day time point was excluded from the fitting for the four, 1.5 mm orifice FCPs due to the anomalous behavior. Similarly, days 25 and 30 for three, 2.3 mm, and days 15–30 for three, 2.7 mm FCPs were excluded since the release dropped to negligible levels. Generally, a larger orifice area corresponded to a greater decay of the release rate during the later portion of the release profile.

To understand hydration kinetics, we measured the mass of the FCPs with one to four, 1.5 mm orifices on the same days media was collected for drug concentration analysis. We estimated the cumulative media uptake in the FCPs (Fig. 2c) by adding the cumulative pellet release, assuming the HPC and IQP-0528 were released concurrently, to the increase in FCP mass. An increased orifice area, changed here by increasing the number of 1.5 mm orifices, correlated to increased hydration kinetics. The only exception was on day 30 for the four, 1.5 mm orifice devices where we hypothesize that the HPC polymer remaining in the FCP was sufficiently small to lead to a dilute solution inside the FCP that readily diffused out of the device. Next the cumulative media uptake curves were fitted to a power law equation (y = a*t^b where y is the cumulative media uptake and t is time). The exponent b, which determines the shape of the curve, was similar for the different devices containing one to four, 1.5 mm orifices (p = 0.11, single factor ANOVA). The hydration-scaling factor, a, that determines the magnitude of the curve, exhibited a linear relationship to the total orifice area (Fig. 2f, Spearman correlation of r = 0.91 and p < 0.0001). This provides evidence that the dependence on the release with respect to the orifice area correlates with the hydration kinetics.

Effect of orifice size and number in the model

The model parameters were optimized for the FCP with three orifices of 1.5 mm in diameter and four, 50 mg pellets of 10 wt% of IQP-0528, as mentioned above. Using these parameters, we calculated the effect of the orifice number shown in Fig. 2a and b (solid lines). The model predictions are in good agreement with the experimental data. The comparison of the cumulative release between the model and the experiments (Fig. 2b) exhibited an R² of 0.983, 0.998, 0.990, and 0.975 for four, three, two, and one orifice respectively. The RMSD of the model with respect to experiments was ±5.2, ±1.3, ±2.0 and ±1.7% for four, three, two, and one orifice respectively. When we investigated the effect of the orifice size on the behavior of the model (Fig. 2d and e, solid lines) we observed that the model was again in good agreement with the experimental data. The comparison of the cumulative release between the model and the experiments (Fig. 2e) had an R² of 0.998, 0.992 and 0.957 for the devices with three orifices of 1.5, 2.3 and 2.7 mm respectively. The RMSD of the model was ±1.3, ±4.5 and ±6.9% for 1.5, 2.3 and 2.7 mm respectively. Slightly higher deviations are observed when we modify the orifice diameter compared to altering the orifice number (Fig. 2a and d). Nevertheless, the R² shows that the deviations are still comparable with the deviations from the experimental data.

Effect of the drug loading on the drug release rate

We observed a linear increase in drug release with the increase of IQP-0528 loading in the pellets (Fig. 3a, b and c). This was readily apparent when the cumulative drug release was normalized to the IQP-0528 loading and presented as a percent (Fig. 3b), and from the linear correlation of the 30-day average IQP-0528 release rate and IQP-0528 loading (Fig. 3c, Spearman correlation of r = 0.98 and p < 0.0001). The 30-day average release rates for FCPs with 0.9 and 15 wt% IQP-0528 were 40 and 700 µg/d respectively. The 30-day cumulative release was 68 ± 2.0, 77 ± 3.3, 74 ± 3.6, 81 ± 0.93 and 72 ± 1.9% for FCPs containing 0.9–15 wt% IQP-0528 in HPC pellets (Fig 3b). Additionally, upon dimensional analysis, comparable release rate decay beyond day 5 was observed for all IQP-0528 loadings tested. For FCPs with 10 wt% IQP-0528 in HPC and three, 1.5 mm orifices, the cumulative percent release of IQP-0528 correlated linearly to the cumulative percent release of the pellet i.e. the sum of IQP-0528 and HPC measured from residual content on days 10, 20 and 30 (Fig. 3c, Spearman correlation of r = 0.95 and p = 0.004). Taken together the data suggests that the release rate of insoluble IQP-0528 was controlled by the polymer hydration and diffusion with negligible contributions from drug diffusion through the hydrated HPC semisolid.

Figure 3. Loading dependent in vitro release of IQP-0528 and other antiretrovirals.

(a) IQP-0528 release rate and (b) cumulative release from FCPs with three, 1.5 mm orifices with pellets of 0.9–15 wt% IQP-0528 in HPC represented in µg/d (a), and as a percent of loaded IQP-0528 (b). (c) 30-day average IQP-0528 release rate linearly correlated to the IQP-0528 loading with devices containing pellets with 0.9–15 wt% IQP-0528 in HPC (Spearman correlation of r = 098 and p < 0.001). The cumulative pellet release linearly correlated to the cumulative IQP-0528 release after 10, 20 and 30 days of release for FCPs with three, 1.5 mm orifices and 10 wt% (Spearman correlation of r = 0.95 and p = 0.004). (d) Diffusivity of TDF, MVC and TFV as function of HPC concentration. (e) Cumulative percent release of multiple different drugs loaded into FCPs. Panels a, b and e compare the experimental (symbols) and model (solid lines) results.

We then evaluated the release kinetics of other antiretrovirals, DPV, TDF, TFV and MVC in addition to the model macromolecule rhodamine B dextran loaded into the pump with three, 1.5 mm orifices (Fig. 3e). To compare the release of the different compounds the release was normalized to the total drug load. The average release calculated over 30 days was 2.5 ± 0.06, 2.7 ± 0.08, 2.6 ± 0.04, 3.0 ± 0.20, 3.1 ± 0.37, and 3.5 ± 0.01%/d for IQP-0528, DPV, rhodamine B dextran, TDF, TFV, and MVC respectively. The average release rate and cumulative release of TFV (p = 0.06), TDF (p = 0.01), and MVC (p = 0.001) were all higher than that of IQP-0528, however only MVC and TDF were significantly higher than IQP-0528 (paired t-test for means). MVC, TFV and TDF are ~100,000× more water soluble than IQP-0528 with solubilities in 25 mM acetate buffer pH 4.2 of 11 mg/mL for MVC and 7 mg/mL for TDF and TFV compared to 0.14 µg/mL for IQP-0528. The antiretrovirals with a higher aqueous solubility were observed to solubilize within the device during in vitro release testing with dissolution initial observed near the orifice and then spread along the length of the device. We measured the diffusivity of the three more hydrophilic antiretrovirals as a function of the HPC concentration. We observed a comparable trend of an exponential decrease of the diffusivity of MVC, TDF and TFV in HPC solutions as the HPC content was increased (Fig. 3d) suggesting differences in diffusivity do not explain the different drug release rates observed.

Effect of the drug loading in the model

We show in Fig. 3a and 3b the comparison between experimental observations (symbols) and the model predictions (solid lines) for different initial loadings of IQP-0528 in the HPC pellets. The model was in good agreement with the experimental data for different loadings of IQP-0528 (Fig. 3a and b). The R² of the model for the cumulative release was 0.998, 0.996, 0.995, 0.998, and 0.997 for 0.9, 2, 4, 10 and 15 wt% IQP-0528 in HPC respectively. The RMSD of the model for the cumulative release was ±3.5, ±2.2, ±3.7, ±1.3, and ±2.0% for 0.9–15 wt% respectively. Fig. 3e shows that the drug release profile displays an almost identical behavior for DPV as with IQP-0528, despite the difference in the chemistry between the two drugs. The R² between model and DPV was 0.998 with an RMSD of ±3.7% for the cumulative release. In the case of rhodamine B dextran the hydrophilic character of the molecule probably does not play a role since the high molecular weight of the molecule limits the diffusivity in the HPC matrix. The R² between model and rhodamine B dextran was 0.997 with an RMSD of ±1.3 % for the cumulative release. However, we see deviations between the model predictions and the experimental results for TDF, TFV and MVC. The R² between model and TDF, TFV and MVC was 0.984, 0.964, and 0.992 respectively with an RMSD of ±12.0, ±7.9, and ±21.3% for the cumulative release.

Effect of number of pellets on the drug release rate

We measured the release kinetics of IQP-0528 from FCPs with two, 1.5 mm orifices and two, three, and four, 50 mg pellets of 10 wt% IQP-0528 in HPC and observed an increased rate of decay of the release rate for devices loaded with a smaller number of polymer-drug pellets (Fig. 4). We reduced the FCP length to correspond to the reduced length of less pellets. The 30-day cumulative release from the FCPs with two, 1.5 mm orifices and two, three, and four, 50 mg pellets were 9.8 ± 0.35, 9.9 ± 0.07, and 11 ± 0.35 mg corresponding to 110 ± 4.0, 73 ± 0.49 and 60 ± 1.9% respectively (Fig. 4b). By performing dimensional analysis of the IQP-0528 release rate, the FCPs with two pellets exhibited an increased decay in the release rate compared to the three pellet FCPs that in turn decayed more readily than four pellet FCPs. This can be seen particularly on days 15, 20 and 25 as the differences in the drug release rates between the three configurations increased. The slopes of the normalized drug release and time plots for FCPs containing two, three, and four pellets were −0.90, −0.76, and −0.50 respectively (R² ≥ 0.98). On day 30, the FCPs with two pellets and two, 1.5 mm orifices demonstrated a burst similar to FCPs with four pellets and four, 1.5 mm orifices (Fig. 2a and 4a). This was likely caused by the low concentration and viscosity of the polymer solution remaining within the device and easily diffusing out of the FCP from shaking during in vitro release testing. Therefore, we did not include day 30 for this device configuration for the calculation of the release rate decay.

Figure 4. In vitro release of IQP-0528 comparing four, three, and two pellets per FCP.

(a) IQP-0528 release rate and (b) cumulative release from FCPs with two, 1.5 mm orifices and four, three, and two, 50 mg pellets of 10 wt% IQP-0528 in HPC comparing results from experiments (symbols) and the model (solid lines).

Effect of number of pellets in the model

Reducing the number of pellets within the device was modeled by reducing the length of the cylindrical geometry that represents our system. The results are presented in Fig. 4 (solid lines). Since the experimental data was measured in a FCP with an orifice configuration (two, 1.5 mm orifices) that differed from the design used to fit the model parameters (three, 1.5 mm orifices), some differences appear between the model predictions and the experimental results. Nevertheless, the model predictions are in good agreement with the experimental data. The R² of the model for the cumulative release was 0.990, 0.995, and 0.988 for four, three, and two pellets respectively. The RMSD of the model for the cumulative release of four, three, and two pellets was ±2.0, ±3.4 and ±4.5% respectively for the cumulative release.

DISCUSSION

We designed a device for the sustained and controlled drug delivery to the vaginal mucosa. This design presents a number of advantages compared to previous IVR delivery technologies, particularly for the delivery of hydrophobic drugs. First the mechanism of release from this IVR can decouple drug release from the drug solubility and diffusivity in the ring elastomer and the polymer of the insert, which can lead to high and controlled drug release rates irrespective of the solubility of drug molecule in the elastomer. The release rate can easily be modulated over a significant range of low µg/d to mg/d quantities by altering the orifice size and number (Fig. 2), and drug loading in the water-soluble polymer pellets (Fig. 3). The polymer chemistry and molecular weight of the hydrophilic polymer within the device can be altered to achieve vastly different release rates and durations [24]. As a potential approach to improve user demand and adherence, there is a compelling interest to develop multipurpose technologies for the prevention of HIV, unwanted pregnancy and/or other sexually transmitted infections [35]. Such multipurpose technologies will likely require segmented IVR incorporating segments of dissimilar materials and designs to tailor the drug release rate for drugs with disparate physical properties and delivery requirements [12, 15, 16, 36, 37]. We designed the FCP to be incorporated into a ring as a segment occupying less than a quarter of the total ring with the remainder of the ring containing another drug delivery segment (Fig. 1a). Additionally, since polymer hydration rate is the predominate factor controlling drug release, one can deliver one or multiple drugs at differing fluxes by changing the drug loading in the hydrophilic polymer pellet. This could be utilized to delivery multiple antiretrovirals for improved potency and a higher barrier to the development of drug-resistant virus strains [38, 39].

We present a model based on a finite element calculation of the diffusion of the water into and drug containing semisolid gel from the device that supports the idea that the hydration and dissolution properties of the polymer and the orifice area are the controlling factors for drug release in this FCP design. When the FCP contacts in vitro release media, a steep water concentration gradient exists at the interface of the polymer pellet at the orifice resulting in water entry into the polymer contained in the device (Fig. 1b). As the polymer hydrates, polymer chain relaxation occurs and the semisolid gel containing the drug diffuses from the device. Following this idea our model uses a Fujita free-volume theory [28]; as the water concentration increases and the polymer concentration decreases inside the device, the free volume available for diffusion increases, resulting in an increase in the diffusivity of the water and polymer. The water diffusion mechanism in polymer is still a matter of debate [40], but by fitting the model parameters to the experimental drug release data, we determined the effective concentration dependent water and polymer diffusivities. In addition to polymer release driven by polymer diffusion, release could be driven by swelling and extrusion of the polymer from the device. However, the model does not differentiate between these possible mechanisms of release, or include the details of these contributions. The model performed remarkably well for different configurations suggesting that the parameterization captured the main mechanism of release. The model offers a fast and efficient tool to aid in the design of new FCP geometries and configurations.

We determined that the total orifice area (varied herein by changing both orifice diameter and number) (Fig. 2) as well as the drug loading in the HPC pellets (Fig. 3) are important design parameters controlling the IQP-0528 release rate and duration. We observed a linear dependence between orifice area and average drug release rate (Fig. 2f), and IQP-0528 loading and average drug release rate (Fig. 3c). The good agreement of the model with the experimental data when we varied IQP-0528 loading in the HPC from 0.9 to 15 wt% (Fig. 3a and b) and the number of 1.5 mm orifices from one to four (Fig. 2a and b) implies that the model mechanistically captures the hydration and diffusion of the polymer with these configurations. However, we observed increased deviations (RMSD) between the model and experimental results for the largest orifice areas tested compared to altering the IQP-0528 loading in the HPC or the number of 1.5 mm orifices (Fig. 2 and 3). This can be interpreted as a missing term due to the transport resistance imposed by the orifice that is implicitly taken in account into the parameters D_HPC and β_HPC. Re-fitting of these parameters to a new geometry can minimize the error in the predictions from geometry to geometry. Nevertheless, providing the design critical parameters of the device (type of drug, orifice size and number), the model represents a robust, fast and accurate way to predict the drug release performance of these FCPs, with a deviation in the prediction lower than 7% and R² higher than 0.9 for all of the configurations tested with IQP-0528.

The daily release rate of IQP-0528 appeared biphasic, with a lag time in the first few days to reach a maximum followed by near constant drug release that decayed with time (Fig. 2a and 3a). We quantified the release rate decay by performing a linear fit of the decay portion of the normalized release profile. Generally, larger orifice areas that corresponded to higher release rates were also associated with increased release rate decay (Fig. 2a and d). From monitoring the cumulative uptake of release media into the FCP, we found that the increased drug release rate associated with a larger orifice area corresponded to an increased hydration rate (Fig. 2c). Interestingly, we observed a linear dependence between the hydration-scaling factor and orifice area (Fig. 2f). These observations together with the correlation of the cumulative release of IQP-0528 and the pellet i.e. IQP-0528 and HPC (Fig. 3c) support the hypotheses that the release of IQP-0528 was controlled by the hydration and dissolution of the polymer and the orifice area, and not the drug diffusivity in the swollen polymer pellet.

Additionally, we tested a number of more water-soluble antiretrovirals in this system to further understand the mechanism of drug release, specifically to increase the drug solubility and diffusivity in the hydrated HPC matrix and contribute to drug release from the FCP (Fig. 3e). The experimental release data of MVC, TDF and TFV were higher than both the measured and model predicted IQP-0528 release. This likely occurred due to an additional mechanism of drug release from the drug diffusing through the HPC matrix. This can be explained by the much higher aqueous solubility of MVC, TDF, and TFV compared to IQP-0528. Additionally, the inclusion of a hydrophilic drug in the HPC matrix could increase the hydration kinetics of the pellet contributing to the observed increased drug release rates. To accurately predict the drug release for MVC, TDF, and TFV using the model we need to add an additional component of the drug dissolution and diffusion in the hydrated polymer matrix and determine if MVC, TDF, or TFV alter the device hydration kinetics. The model was in good agreement with the release of the high molecular weight compound rhodamine B dextran suggesting that despite the hydrophilic nature of the molecule, the diffusivity in the swollen HPC matrix was sufficiently hindered to not contribute to the overall release. The model only takes into account the hydration and diffusion of the HPC polymer and therefore accurately predicts the drug release when the drug diffusion through the swollen polymer network does not contribute to the overall release and the hydrophilic character of the drug does not alter the hydration kinetics (Fig. 3e).

We observed a relationship between the IQP-0528 release rate and the total polymer and drug loading (Fig. 4). Devices with a smaller drug and polymer load exhibited a slight increase in the decay rate of the release rate from day 10 and beyond, and the model accurately reproduced this change in the drug release rate due to the change in the number of pellets (Fig. 4). Specifically this signifies that FCPs with two pellets did not contain sufficient water-soluble polymer inside the device to sustain the same release rate as the FCPs with four pellets. A similar behavior existed with FCPs with the two largest orifice areas tested: three, 2.3 or 2.7 mm orifices. After ~75% of the drug was released, the drug release rate drastically reduced (Fig. 2b). Together these observations support our initial hypothesis that release was controlled by the polymer hydration and diffusion from the device. After a certain cumulative release was achieved, the polymer concentration within the device was insufficient to drive the diffusive release of the drug-containing semisolid gel out of the FCP orifice.

CONCLUSIONS

We describe the design of an extended duration, vaginal drug delivery system where the drug release is predominately controlled by the hydration and dissolution of a hydrophilic matrix contained within the IVR. This is in contrast to other IVR designs where drug release occurs by drug diffusing through the IVR elastomer. Because of the unique mechanism of drug release, this type of system is capable of high, mg/d drug release rates of both hydrophobic small molecules and macromolecules, something previous IVRs were incapable of achieving. Finally we also describe a model to aid in the design of future FCP configurations, providing accurate information of the release dynamics with an easy implementation.