Water spin dynamics during apoptotic cell death in glioma gene therapy probed by T_1ρ and T_2ρ

Abstract

Longitudinal and transverse relaxations in the rotating frame, with characteristic time constants T_1ρ and T_2ρ, respectively, have potential to provide unique MRI contrast in vivo. On-resonance spin-lock T_1ρ with different spin-lock field strengths and adiabatic T_2ρ with different radiofrequency-modulation functions were measured in BT4C gliomas treated with Herpes Simplex Virus thymidine kinase (HVS-tk) gene therapy causing apoptotic cell death. These NMR tools were able to discriminate different treatment responses in tumor tissue from day 4 onwards. An equilibrium two-site exchange model was used to calculate intrinsic parameters describing changes in water dynamics. These results are consistent with destructive intracellular processes associated with cell death and the increase of extracellular space during the treatment. Furthermore association between longer exchange correlation time and decreased pH during apoptosis is discussed. In this study we demonstrated that T_1ρ and T_2ρ MR imaging are useful tools to quantify early changes in water dynamics reflecting treatment response during gene therapy.

INTRODUCTION

Malignant gliomas are the most common primary tumors of the central nervous system. These tumors are often resistant to treatment and carry poor prognosis. Recent studies show that gene therapy may be an effective treatment (1–4). One of the most commonly tested approaches exploit the thymidine kinase enzyme (tk) from the Herpes Simplex Virus (HSV). This enzyme can metabolize intravenously administered ganciclovir (GCV) to produce a nucleotide analog that is selectively toxic for dividing cells (1, 3) which is very important in the brain with healthy neurons existing around the tumor (3, 5). It has been demonstrated that HSV-tk-ganciclovir has a therapeutic potential both in experimental and in clinical settings (2, 6, 7).

Magnetic resonance imaging (MRI) and spectroscopy (MRS) have been proven to be sensitive to cell death related processes in several different experimental disease models (8–14). MRI and MRS methods can detect treatment response in brain tumors at very early stages during cytotoxic treatment with anticancer drugs or irradiation (15), and provide information about tumor size, perfusion, molecular tumbling, chemical exchange, diffusion, and metabolite levels (16).

MRI permits proton relaxation studies which can be used to obtain information about water interactions and dynamics. The longitudinal relaxation time constant (T₁) depends on the external magnetic field (B₀), and it detects magnetic field fluctuations caused by molecular dynamics on the order of MHz, near of the Larmor precession frequency (ω₀ = γB₀ in which γ is the gyromagnetic ratio). The longitudinal relaxation time in the rotating frame (T_1ρ) offers a valuable tool to study dipolar fluctuations in the tissue, arising from slow atomic motions in viscous liquids and proteins (17–20). The value of T_1ρ is sensitive to molecular dynamics taking place on the order of kHz (ω₁ = γB₁, where B₁ is the radiofrequency magnetic field), which is nearer to the frequencies at which much of the dipolar fluctuations occur in tissue (18, 21). It has been suggested that T_1ρ predominantly reflects water-protein interactions in tissue and therefore, it can be used to generate a novel MRI contrast (8, 9). Furthermore, it has been shown that T_1ρ is one of the earliest markers of the positive treatment response in gene therapy and chemotherapy (22–24), and it provides an indication of neural loss during neurodegenerative disorders (25).

Transverse relaxation in the rotating frame (T_2ρ) can occur during a frequency-modulated pulse such as an adiabatic full-passage (AFP) pulse (26–28). The magnetization vector that initially lies in the x′y′-plane of the rotating frame will undergo rotation in the plane perpendicular to the sweeping effective magnetic field (B_eff). The theoretical analysis of the T_2ρ behavior shows that the range of spin dynamics to which T_2ρ is sensitive extends to slow motion with correlation times (τ_c) up to ~ 10⁻⁴ s (29). Recently, this inherent property of the adiabatic Carr-Purcell (CP) pulse sequence was used to probe exchanging systems (27, 28) and was applied to the human brain to generate novel tissue contrast in MRI (25). Despite much progress in the understanding of T_1ρ relaxation in NMR, theoretical descriptions and applications of transverse relaxation in the rotating frame T_2ρ have been limited (29–32). It has been demonstrated that during AFP pulses, exchange-induced and dipolar relaxation contributions to T_2ρ (T_2ρ,ex and T_2ρ,dd, respectively) depend on the choice of amplitude- and frequency-modulated functions used in the AFP pulses (26, 27, 33). Theory of the T_2ρ,ex relaxation due to exchange between spins with a non-zero chemical-shift difference (δω ≠ 0, the anisochronous exchange) has been presented for the spin-lock (34) and time-dependent relaxation during adiabatic rotation (26, 28, 35). The dependence of the relaxation rate during AFP pulses on the modulation functions was recently used to generate tissue contrast in the human brain and to determine fundamental relaxation parameters in tissue (27).

The aim of this study was, for the first time, to investigate the sensitivity of adiabatic T_2ρ measured with different pulse modulation functions to treatment response during glioma gene therapy. Furthermore, on-resonance spin-lock T_1ρ with different spin-lock field strengths combined with T_2ρ measurements were used to assess alterations in intrinsic relaxation parameters in tumor tissue during gene therapy. These alterations include: dipolar and exchange correlation times as well as relative populations of the exchanging sites, such as water associated with macromolecules and free water.

MATERIALS AND METHODS

Tumor model

BT4C gliomas were induced by implanting 10⁴ HSV-tk positive cells into the corpus callosum of female BDIX rats (n = 14) as described previously (23, 24, 36). Rats in the treatment group (n = 9) were injected with Ganciclovir (GCV, 25 mg/kg, i.p., twice a day) for 8 days. Untreated tumor-bearing animals served as controls (n = 5) and they were injected with a saline solution. All animal experiments were approved by the ethical committee of the National Laboratory Animal Centre at the University of Kuopio.

Magnetic resonance imaging

MRI experiments were carried out in a 4.7 T horizontal magnet (Magnex Scientific Ltd., Yarnton, Oxfordshire, UK) equipped with actively shielded gradients (Magnex) interfaced to a ^UnityInova (Varian Inc, Palo Alto, CA, USA) console. A quadrature half-volume coil (Highfield Imaging, Minneapolis, MN, USA, loop diameter 28 mm) was used in transmit/receive mode. MR data were collected on alternate days. During MRI the animals were anesthetized with halothane (maintenance level of 1%) in N₂O/O₂ (75%:25%) and fixed into a custom-built head holder using teeth bar and ear pins.

To measure the tumor volume, T₂-weighted spin echo multislice images were acquired with the following parameters: repetition time (TR) 2.5 s, echo time (TE) 65 ms, field of view 35 × 35 mm², matrix size 128 × 256, slice thickness 1 mm.

T_1ρ and T_2ρ data were acquired from a single transversal slice positioned in the centre of the tumor based on volumetric T₂-weighted images. On-resonance T_1ρ was measured using a spin-lock pulse having variable length (SLT), following excitation by an adiabatic half passage (AHP) pulse having a constant length (T_p) equal to 4 ms (37). Four different spin-locking times (SLT = 12, 24, 48 and 96 ms) were used. Following the spin-lock pulse, a reverse AHP pulse (T_p = 4 ms) was used to return magnetization back to the +z′-axis. Then, after applying a crusher gradient, the prepared magnetization was readout using a fast spin echo imaging sequence (38). The acquisition parameters were: TR = 2.5 s, field-of-view = 25.6 × 25.6 mm², matrix size = 64 × 128, slice thickness = 1.5 mm, 16 echoes with echo-spacing of 10 ms (38). In these experiments, the peak value of the B₁(t) function (B_1max) used in the AHP pulses was fixed at 0.4 G, while the amplitude of the spin-lock pulse was varied according to B₁ = 0.02, 0.04, 0.06, 0.08, 0.1, 0.15, 0.2, 0.3, 0.4, 0.6, 0.8, 1.0, 1.2 and 1.4 G.

AFP pulses are especially well-suited for π rotations because they can provide broad bandwidth and accurate flip angles with high tolerance to spatial variations in radiofrequency (RF) field intensity. The present experiments were conducted with, adiabatic full-passage (AFP) pulses of the hyperbolic secant (HS) type which have modified amplitude and frequency modulation functions (HSn pulses) (39–41). HSn pulses are stretched versions of the original hyperbolic secant pulse (39), where n denotes the stretching factor (40, 41). As n becomes larger, the HSn pulse amplitude-modulation (AM) function becomes flatter, and progressively resembles that of the chirp pulse (e.g., the AM function flattens and the frequency sweep approaches linearity) (Figure 1). Thus, the time evolution of magnetization during a HSn pulse can change significantly with a change of n. For T_2ρ experiments, a train of HSn pulses was placed after coherent excitation by an AHP pulse. To obtain data for estimating T_2ρ values, the experiment was repeated with a variable number (m) of HSn pulses in the AFP pulse train (m = 4, 8, 16 and 32). Three separate T_2ρ measurements were performed, each using HSn pulses with n = 1 (no stretching), 4, or 8. All HSn pulses were transmitted using B_1max = 0.8 G and T_p = 3 ms. The MLEV-4 phase cycle was used (42). Because no time intervals occurred between the AFP pulses in the train, the signal decay was governed solely by T_2ρ relaxation. The same fast spin echo imaging readout was used for the T_2ρ and T_1ρ measurements.

Fig. 1.

Amplitude (a) and frequency (b) modulation functions for three different AFP pulses, HS1, HS4 and HS8.

MR parameter maps were calculated using standard 2-parameter monoexponential relaxation formulae on a pixel-by-pixel basis. Regions of interests (ROI) covering the whole tumor were selected in control and in treated animals using T₂-weighted images. ROIs from contralateral brain were selected to analyze the results of normal tissue.

Histology

After MRI scans, animals were sacrificed with CO₂ and transcardially perfused with 0.9% NaCl for 10 min (30 ml/min), followed by 4% paraformaldehyde in 0.1 M phosphate buffer, pH 7.4, for 10 min (30 ml/min). Fixed brains were removed from the skull, rinsed in phosphate-buffered saline, and cryoprotected (24 h in 20% glycerol in 0.02 M potassium phosphate-buffered saline) for cryosectioning. Histological sections (20 μm) were stained with the Nissl method, staining the ribonucleic acids within the cell body, rough endoplasmic reticulum and the nucleus, allowing for assessment of cytoarchitecture and cell counts. Cell counting was performed using Stereo Investigator software in a NeuroLucidia morphometry system (MicroBrightField, Colchester, VT). Only cells with intact, well-defined margins were included.

Theory

All MR signal intensities measured with the T_1ρ and T_2ρ techniques clearly exhibited monoexponential decay, within the spin-lock time range used in this study. Thus, for the interpretation of NMR data the dynamic processes were modeled with an equilibrium two-site exchange (2SX) approximation, comprising two water populations coupled by an equilibrium exchange: the water population associated with macromolecules (A), and the free water population (B).

The dipolar fluctuation contribution to the rotating frame longitudinal relaxation rate constant at one specific site (A or B) is given by (30, 33)

$$R_{1\mathrm{\rho },\text{dd}}=\frac{1}{10k_{\text{dd}}}\left(\frac{3}{1+4{{\mathrm{\omega }}_1}^2{{\mathrm{\tau }}_{\mathrm{c}}}^2}+\frac{5}{1+{{\mathrm{\omega }}_0}^2{{\mathrm{\tau }}_{\mathrm{c}}}^2}+\frac{2}{1+4{{\mathrm{\omega }}_0}^2{{\mathrm{\tau }}_{\mathrm{c}}}^2}\right),$$ [1]

where

$$\frac{1}{k_{\text{dd}}}=2\mathrm{I}\left(\mathrm{I}+1\right){\hslash }^2{\mathrm{\gamma }}^4{r}^{-6}{\mathrm{\tau }}_{\mathrm{c}},$$ [2]

where r is the internuclear distance (1.58 Å), τ_c is the correlation time for populations A and B (τ_A and τ_B, respectively), ħ is Planck’s constant and I is the spin quantum number. In fitting, the free water correlation time τ_B was assumed to be 10⁻¹² s.

For the case of fast chemical exchange (FXR) between identical spins having a chemical-shift difference δω, under continuous wave (cw) on-resonance spin-lock irradiation, the exchange rate constant R_1ρ,ex is given by

$$R_{1\mathrm{\rho },\text{ex}}=\frac{P_A{P}_B\mathrm{\delta }{\mathrm{\omega }}^2{\mathrm{\tau }}_{\text{ex}}}{{{\mathrm{\omega }}_1}^2{{\mathrm{\tau }}_{\text{ex}}}^2+1}.$$ [3]

Here, P_A and P_B are the fractional populations of the two sites A and B, which are related by P_A + P_B = 1, τ_ex is the mean lifetime of the exchanging species at the two sites, and δω is the difference between chemical shifts of the two sites. To reduce the number of fitted parameters and keep fitting unambiguous, δω was assumed to be a constant value of 125 Hz. This was found to give the best fitting of the complete data set in initial test fittings with several different δω values between 0 and 2 kHz. The contributions of dipolar relaxation pathways and the anisochronous exchange to observed R_1ρ (R_1ρ,obs) are given by

$$R_{1\mathrm{\rho },\text{obs}}=P_A{R}_{1\mathrm{\rho }A,\text{dd}}+P_B{R}_{1\mathrm{\rho }B,\text{dd}}+R_{1\mathrm{\rho },\text{ex}}.$$ [4]

The parameters, P_A, τ_A, and τ_ex, were estimated from the R_1ρ,obs measurements using the Levenberg-Marquardt non-linear least-squares regression algorithm implemented in Matlab.

During the radiofrequency-modulated HSn pulses, the relaxation rate constant will be time dependent, i.e., R_2ρ(t) (= 1/T_2ρ(t)), due to the continuously varying magnitude and orientation of the effective field (B_eff(t)) in the frequency-modulated rotating frame (28, 41). The time-dependent angle between the vector B_eff and the +z′-axis is given by

$$\mathrm{\alpha }\left(t\right)={tan}^{-1}\left(\frac{{\mathrm{\omega }}_1(t)}{\mathrm{\Delta }\mathrm{\omega }(t)}\right),$$ [5]

where Δω(t) = (ω₀ − ω_RF(t)) and ω_RF(t) is the time-dependent pulse frequency. The effective frequency ω_eff(t) is

$${\mathrm{\omega }}_{\text{eff}}\left(t\right)=\mathrm{\gamma }{\mathrm{B}}_{\text{eff}}\left(t\right)=\sqrt{{{\mathrm{\omega }}_1}^2\left(t\right)+\mathrm{\Delta }{\mathrm{\omega }}^2\left(t\right)}.$$ [6]

The contribution of dipolar interactions between identical spins to the rotating frame transverse relaxation rate constant is given by (27, 30, 33)

$$R_{2\rho ,\text{dd}}\left(t\right)=\frac{1}{40k_{\text{dd}}}\left(\begin{array}{l}3{\left(3{\text{cos}}^2\mathrm{\alpha }\left(t\right)-1\right)}^2+\frac{30{\text{sin}}^2\mathrm{\alpha }\left(t\right){\text{cos}}^2\mathrm{\alpha }\left(t\right)}{1+{{\mathrm{\omega }}_{\text{eff}}}^2\left(t\right){{\mathrm{\tau }}_{\mathrm{c}}}^2}+\frac{3{\text{sin}}^4\mathrm{\alpha }\left(t\right)}{1+4{{\mathrm{\omega }}_{\text{eff}}}^2\left(\mathrm{t}\right){{\mathrm{\tau }}_{\mathrm{c}}}^2}\\ +\frac{\left(20-6{\text{sin}}^2\mathrm{\alpha }\left(t\right)\right)}{1+{{\mathrm{\omega }}_0}^2{{\mathrm{\tau }}_{\mathrm{c}}}^2}+\frac{8+12{\text{sin}}^2\mathrm{\alpha }\left(t\right)}{1+4{{\mathrm{\omega }}_0}^2{{\mathrm{\tau }}_{\mathrm{c}}}^2}\end{array}\right),$$ [7]

where k_dd is given by Eq. [2].

Theory predicts R_2ρ,ex to be dependent on the choice of amplitude- and frequency-modulation functions used in the AFP pulses via their α(t)- and ω_eff(t)-dependencies for spin populations with different chemical shifts (δω ≠ 0, the anisochronous mechanism) (26, 28). Within the instantaneous approximation (34), the exchange-induced R_2ρ relaxation in the FXR (τ_ex⁻¹ ≫ δω) is

$$R_{2\mathrm{\rho },\text{ex}}=P_A{P}_B\mathrm{\delta }{\mathrm{\omega }}^2{\mathrm{\tau }}_{\text{ex}}{\text{cos}}^2\mathrm{\alpha },$$ [8]

and the observed R_2ρ,obs is given by (43)

$${\overline{R}}_{2\mathrm{\rho },\text{obs}}=\frac{P_A}{T_{\mathrm{P}}}{\int }_0^{T_{\mathrm{P}}}{R}_{2\mathrm{\rho }A,\text{dd}}\left(t\right)\mathrm{d}t+\frac{P_B}{T_{\mathrm{P}}}{\int }_0^{T_{\mathrm{P}}}{R}_{2\mathrm{\rho }B,\text{dd}}\left(t\right)\mathrm{d}t+\frac{1}{T_{\mathrm{P}}}{\int }_0^{T_{\mathrm{P}}}{R}_{2\mathrm{\rho },\text{ex}}\left(t\right)\mathrm{d}t.$$ [9]

Statistical analysis

Results are shown as mean ± SEM. Statistically significant differences were estimated using Student’s t test. Results obtained using theoretical calculations are presented with 95% confidence intervals for the non-linear least-squares parameter estimates.

RESULTS

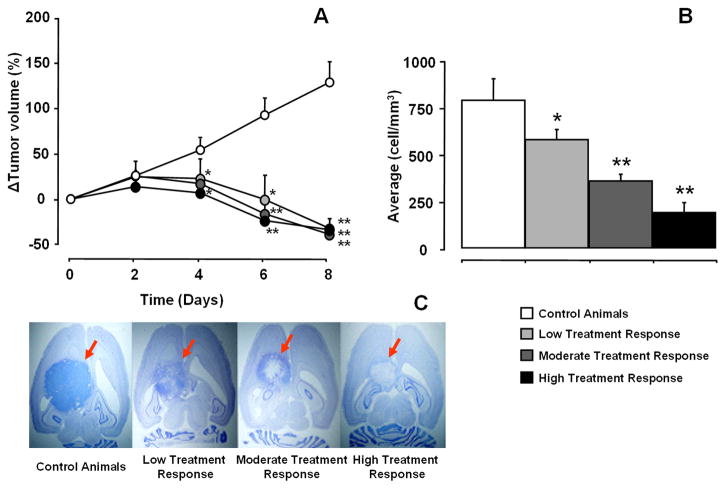
Animals showed variable response to treatment and were divided into three groups based on histology: low treatment response (< 30% of cell death, n = 2), moderate treatment response (cell death 30–75%, n = 5) and high treatment response group (> 75% of cell death, n = 2) (Fig. 2).

Fig. 2.

Relative tumor volumes (a) and average cell densities (cell/mm³) (b) counted from Nissl stained histological sections (c) on day 8. Tumors are indicated by red arrows. All values are given as mean ± SEM. Statistically significant difference for treated animals from the control animals were analyzed using Student’s paired t-test (* p < 0.05; ** p < 0.01).

Tumor volumes were measured from T₂-weighted images on alternate days. Changes in tumor volume revealed a continuous growth in control group for 8 days (Fig. 2a). In treated animals, during first two days of the treatment, tumor volumes increased by 15–26% relative to their volumes on day 0. On the following days, tumor volumes decreased by 59–65%. From day 4, tumor volumes in all treatment groups were significantly different as compared to the control group. It should be noted that there was no statistically significant difference in reduction of tumor volume between low, moderate and high treatment response groups, in spite of clearly different cell densities assessed from histology (Fig. 2b and c). This result indicates that tumor volume alone was not a good marker of magnitude of the treatment response.

T_1ρ and T_2ρ maps from a high treatment response animal are shown in Figure 3. Relaxation times increased with increasing B₁ and n in T_1ρ and T_2ρ measurements respectively, both in glioma and in normal brain tissue as also shown in previous studies (23, 27, 44). Before treatment, there was very little contrast between tumor and normal tissue in T_1ρ and T_2ρ maps, and also there was no difference between control group and treated groups. Treatment response was evident from day 4 onwards (Fig. 4). The initial increase of T_1ρ on day 4 was practically independent of B₁, but on treatment days 6 and 8 higher B₁ values resulted in higher contrast. Similar behavior of sensitivity differences could be also seen in T_2ρ maps with the increase of n of the HSn pulses. No changes in the relaxation time constants were detected in non-treated animals.

Fig. 3.

T_1ρ maps (a) from a high treatment response animal with spin-lock field of 0.02, 0.8 and 1.4 G. T_2ρ maps (b) from the same animal with HS1, HS4 and HS8 pulses on day 0 and day 8. Tumors are indicated by white arrows.

Fig. 4.

T_1ρ values (ms) from treated and control animals with different B₁ values (a: 0.02 G, b: 0.8 G and c: 1.4 G), and T_2ρ values (ms) from treated and control animals calculated with different adiabatic full passage pulses during 8 days (d: HS1, e: HS4 and f: HS8) (● high, moderate and low treatment response groups; ○ control animals). All values are given as mean ± SEM. Statistically significant differences for treated animals from the control animals were analyzed using Student’s paired t-test (* p < 0.05; ** p < 0.01).

Figure 5 shows measured R_1ρ (= 1/T_1ρ) values and the corresponding fitting obtained using the two-pool fast exchange model presented in Methods section (Eq. [4]). The model resulted in excellent fitting to our experimental data. On day 8 (Fig. 5b), R_1ρ showed clearly different treatment response as compared to controls.

Fig. 5.

Calculated longitudinal relaxation rate constants R_1ρ on day 0 (a) and day 8 (b) (● high, moderate and low treatment response groups; ○ control animals; △ normal tissue). The points represent the experimental data and all values are given as mean ± SEM. The lines represent the fitting.

Estimated parameters P_A, τ_A, and τ_ex, and the corresponding 95% confidence intervals are summarized in Fig. 6. There were no differences observed between groups in any of the fitting parameters before treatment or in the control group during the treatment. During the treatment with ganciclovir, the fractional population of the water pool associated with macromolecules (P_A) decreased reflecting treatment response (Fig. 6b). Because P_A + P_B = 1, the fractional population associated with free water showed the opposite response, as free water increased during the treatment. On day 0, τ_A was ~ 4 × 10⁻⁹ s for control and treatment response groups, which is consistent with a previous study of human brain (33). For treated animals, τ_A increased to 1.0 × 10⁻⁸ ± 0.4 × 10⁻⁸ s in the high treatment response group (Fig. 6a). The exchange correlation time between pools A and B was ~ 8 × 10⁻⁵ s on day 0 and increased due to treatment effects (Fig. 6c).

Fig. 6.

Calculated parameters estimated from the R_1ρ,obs measurements using the Levenberg-Marquardt non-linear least-squares regression algorithm ( high, moderate and low treatment response groups; control animals; normal tissue). Results are presented with 95% confidence intervals.

R_2ρ values were calculated using parameters obtained from the R_1ρ fitting (Fig. 7a–c). Calculated R_2ρ values were slightly lower than experimental values and the difference increased with increasing n of the HSn pulses. To further investigate how treatment effects could be explained by our model we normalized R_2ρ values by dividing them with pretreatment values. From Figure 7d–f it was evident that our modeling described well the changes caused by treatment despite a small discrepancy in absolute relaxation rate constants.

Fig. 7.

Calculated transverse relaxation rate constants R_2ρ with HS1 (a), HS4 (b) and HS8 (c) AFP pulses and normalized R_2ρ with HS1 (d), HS4 (e) and HS8 (f) AFP pulses (● high, moderate and low treatment response groups; ○ control animals; △ normal tissue).

Discussion

Our T_1ρ and T_2ρ data showed excellent sensitivity to cell death in glioma during gene therapy. These NMR tools were able to detect a significant decrease of the tumor mass as observed from day 4 onwards and discriminate between different treatment responses as indicated by histological cell density calculations in tumor tissue. It should be noted that the measurements of tumor volumes were unable to differentiate between different treatment response groups on day 8.

In tumor tissue, both translational and rotational water mobility increases over time after treatment, and the magnitude of the change is related to the effectiveness of the therapy. This is caused by a subsequent reduction in cell density and an increase of the extracellular space. Changes in translational motion are most often probed non-invasively by water diffusion that is inversely correlated to the cell density (10, 45). Our results show that changes in rotational mobility and exchange can be measured by T_1ρ and T_2ρ from day 4 onwards with different B₁ values and HSn pulses respectively, which is earlier than conventional T₁ and T₂ changes are detected in this model (24, 44). The sensitivity to the earliest apoptotic response to treatment was very similar for all HSn pulse shapes and over the B₁ range used in this study. On the other hand, at days 6 and 8 when necrotic centres started to form in these tumors, higher B₁ values and higher n of HSn pulses provided more contrast between normal and tumor tissue. These findings point to the different sensitivity of these techniques to various cellular and structural changes occurring during apoptotic and necrotic cell death.

The proposed simple two pool fast exchange model provided excellent fits for estimating R_1ρ values, and thus, appears to reasonably describe alterations in water dynamics during gene therapy-induced treatment response. Of course any model which is used for such an analysis is a simplification of the complex interactions that water molecules experience in living tissue. The model parameters are therefore considered as apparent values that describe the weighted average of the multiple molecular processes. Nevertheless, some degree of clear correspondence with known features in responding tumors in this model can be found. An increase of free water and a decrease of water associated with macromolecule populations are consistent with shrinkage of the cells during apoptosis and cell death, both leading to increased extracellular volume (15, 46). Furthermore, the correlation time of water associated with macromolecules substantially increases, as intracellular space becomes more crowded. A part of the increase in exchange correlation time on day 8 could be associated with decreased pH known to take place during apoptosis (47). However, when considering the changes in exchange time, it should be noted that in our simplified model the exchange term includes all dynamic dephasing contributions, including not only chemical exchange but also diffusion in local field gradients. Furthermore, a fixed value for Δω was used in the fitting. It cannot be ruled out that possible change in Δω during disease progression could have contributed to the fitting results.

Unequivocal fitting of the 2SX model using the R_2ρ data was not possible due to a limited amount of data points measured. For comparison, T_2ρ values were simulated using parameters obtained from T_1ρ fitting. The calculated values were slightly different from experimental R_2ρ values and the difference slightly increased with the increase of n of the HSn pulses. Importantly, the normalized data showed that in spite of this discrepancy the model almost completely explained the changes due to treatment. Our data indicate that a treatment independent factor was not included in the present simple model. The most likely explanation for this discrepancy is the contribution of intermediate exchange, or possible magnetization transfer effects due to saturation of the macromolecular pool by the preparation pulses (48).

Relatively long preparation pulses or pulse trains with high B₁ values have high specific absorption rate (SAR) of RF energy and could potentially lead to tissue heating. The SAR value was calculated using the conservative assumption that all RF energy was deposited into 10 g of tissue. The calculated SAR values for the longest spin-lock time of 96 ms were 3.0 W/kg and 34 W/kg for B₁ of 0.4 G and 1.4 G, respectively, in cw-T_1ρ measurements. In spite of high SAR values, similar and higher B₁ fields in T_1ρ measurements under identical conditions did not cause measurable heating effect in the brain tissue even when perfusion was reduced (49). In a previous study, the accuracy of measured T_1ρ in detecting treatment response was high and comparable when using low and high B₁ values at the same stages of treatment (44). This is consistent with the findings of this work, showing B₁ independent T_1ρ response in the earliest time points. T_2ρ measurement with HSn pulses provides an alternative way of reducing delivery of RF energy to tissue, as the SAR of an HSn pulse train is always lower than that of a cw-type T_1ρ experiment with equal maximum B₁. An interesting option for future studies is the recently introduced adiabatic T_1ρ measurement, which can also be performed with HSn pulse trains (33). It should be noted that both T_1ρ and T_2ρ MR imaging have already been applied to human studies (27, 33, 38). Therefore, our present findings support the idea that these novel MRI techniques may provide useful clinical MR imaging contrast for patients with glioma.

In summary, we were able to show that T_1ρ and T_2ρ can provide early evidence of glioma treatment efficacy in one of the most commonly used gene therapy models. Furthermore, intrinsic parameters describing changes in water dynamics were obtained from a simple 2SX model and were associated with known cellular and structural changes taking place during treatment. The use of T_1ρ and T_2ρ MR imaging has tremendous potential for monitoring early changes in tumors that undergo a treatment response.