Abstract
A new method to measure rotating frame relaxation and to create contrast for MRI is introduced. The technique exploits relaxation along a fictitious field (RAFF) generated by amplitude- and frequency-modulated irradiation in a sub-adiabatic condition. Here, RAFF is demonstrated using a radiofrequency pulse based on sine and cosine amplitude and frequency modulations of equal amplitudes, which gives rise to a stationary fictitious magnetic field in a doubly rotating frame. According to dipolar relaxation theory, the RAFF relaxation time constant (TRAFF) was found to differ from laboratory frame relaxation times (T1 and T2) and rotating frame relaxation times (T1ρ and T2ρ). This prediction was supported by experimental results obtained from human brain in vivo and three different solutions. Results from relaxation mapping in human brain demonstrated the ability to create MRI contrast based on RAFF. The value of TRAFF was found to be insensitive to the initial orientation of the magnetization vector. Finally, as compared with adiabatic pulse trains of equal durations, RAFF required less radiofrequency power and therefore can be more readily used for rotating frame relaxation studies in humans.
Introduction
As magnet technology continues to advance, the field strength (B0) used for NMR has steadily increased. This trend has been fueled mainly by the quest for increased signal-to-noise ratio. On the other hand, as B0 increases, the laboratory frame T1 becomes less sensitive to slow molecular motions because T1 is dominated by dipolar fluctuations occurring mainly near the Larmor frequency, ω0 = γB0 (1), where γ is the magnetogyric ratio. Reduced sensitivity to slow molecular motions is particularly relevant to the field of biomedical MRI, since tissue-specific differences in T1 are relied upon for one of the most important forms of image contrast (i.e., T1-weighting) (2). Alternatively, it has been known for many years that relaxation in the presence of radiofrequency (RF) irradiation, i.e., the rotating frame longitudinal and transverse relaxation times (T1ρ and T2ρ, respectively), can provide information about slow molecular motions at any field strength (3–8). Although T1ρ is also known to depend on B0, the relaxation rate increases when the spins experience dipolar fluctuations with relatively long correlation times (τc ≫ ω0−1), and it is in this manner that T1ρ probes slow molecular dynamics. Although T1ρ and T2ρ measurements have classically been performed with time-invariant RF pulses, these experiments can also be performed with pulses utilizing amplitude- (AM) and frequency-modulated (FM) functions which have been designed to execute adiabatic full-passage (AFP) (9–11). Some studies have shown that rotating frame relaxation times can be more informative than T1 and T2 in assessing specific tissue properties and in detecting certain pathologic changes (12–16). For example, in a recent pilot study of patients with Parkinson’s disease, adiabatic T2ρ (T2ρ,adiab) was more sensitive than T2 to pathological changes occurring in the brain, which is likely due to iron accumulation in substantia nigra. In addition, adiabatic T1ρ (T1ρ,adiab) reflected likely nigra neuronal degeneration (17).
A potential limitation to making rotating frame relaxation measurements in living systems is the required RF power (i.e., specific absorption rate (SAR)) and concern about tissue heating. In certain cases, only low RF power is required to measure T1ρ with the classical spin-lock experiment. For example, T1ρ measured with low spin-lock power (B1=2.0·10−6 T) provided an excellent imaging biomarker to detect gene therapy response in a rodent glioma model (16). On the other hand, the RF power needed for spin-locking often limits the application of classical T1ρ experiments to studies of humans at high magnetic fields. To avoid off-resonance artifacts, the magnetization vector should be “locked” along a specified orientation in the rotating frame. To satisfy this requirement, the effective field should be larger than the local field gradients reflected by the linewidth of the resonance. To overcome the power limitation, the off-resonance T1ρ experiment is frequently used (18), although this method is sometimes limited by B1 and B0 inhomogeneities which are difficult to eliminate in MRI (19). Likewise, in some cases, the RF power required to fulfill the adiabatic condition for adiabatic T1ρ and T2ρ measurements may not be permissible within SAR guidelines.
In the case of frequency-modulated pulses (adiabatic and sub-adiabatic pulses alike), the analysis is performed in a tilting rotating frame in which the effective field also remains larger than the local frequency variations and is close to stationary despite these frequency variations. With this approach, we describe here a novel method to create and exploit a “fictitious” magnetic field for rotating frame relaxation studies. The fictitious field is created by a rapid, sub-adiabatic modulation of the RF amplitude and frequency, whereby the effective field consists of B1 and B0 components, as well as a fictitious field component. The method is called RAFF (relaxation along a fictitious field). Employing second order perturbation theory, we demonstrate the sensitivity of RAFF to long rotational correlation times, τc. Experimental measurements performed on solutions and human brain demonstrate the potential of RAFF to assess molecular dynamics and to generate contrast for MRI, while requiring less RF power than that typically used for T1ρ and T2ρ measurements.
Theoretical Description and Bloch Simulations of RAFF
An understanding of T1ρ and T2ρ methods utilizing AM and FM pulses can be facilitated by analyzing the magnetic field components and motion of the magnetization vector M in two different rotating coordinate frames. The first frame rotates in synchrony with the time-dependent pulse frequency (ωRF(t)), and is thus known as the ωRF-frame with axis labels x′, y′, and z′ (20). In the ωRF-frame, during an AFP pulse the orientation of B1 is fixed (by convention, B1 is along the x′-axis). The effective field (Beff(t)), which sweeps from +z′ to −z′ (or vice versa), is given by
| [1] |
where Δω(t) is the time-dependent offset frequency
| [2] |
The AM and FM functions of an AFP pulse produce a sweep of Beff(t), with a tilt angle relative to the z′ axis given by
| [3] |
where
| [4] |
Because Beff is time-dependent during an AFP pulse, the adiabatic rotating frame relaxation time constants (T1ρ,adiab and T2ρ,adiab) are also time-dependent. At any given time point during the pulse, the relaxation rate will depend on the orientation and amplitude of Beff(t), as well as the orientation of M relative to Beff(t) at that moment in time. When the adiabatic condition is well satisfied throughout an AFP pulse, the component of M that is initially aligned with Beff will remain approximately aligned (or “locked”) with Beff(t) during the pulse; accordingly, this magnetization experiences time-dependent T1ρ relaxation. In this manner, T1ρ contrast can be produced in MRI by transmitting a windowless train of AFP pulses prior to the excitation pulse (11). Likewise, if M is placed perpendicular to Beff at t = 0, M will evolve with the effective frequency ωeff(t) = γBeff(t) and will lie close to the plane perpendicular to Beff(t) at all times during the AFP pulse. Hence, by first creating transverse magnetization (Mxy) and subsequently transmitting a windowless train of AFP pulses, T2ρ,adiab contrast can be generated (10).
The description above applies to the situation in which the adiabatic condition, Beff(t) ≫ |γ−1dα/dt|, is fulfilled throughout the pulse. Conversely, in the RAFF method the adiabatic condition is purposefully violated by choosing the modulation functions to satisfy the condition Beff(t) = |γ−1dα/dt|. To facilitate an understanding of RAFF, the vector analysis must move to a second frame of reference (Fig. 1) which is a doubly rotating frame known as the ωeff-frame, with axis labels x″, y″, and z″ (20). In the ωeff-frame, by definition the orientation of Beff remains fixed along the z″ axis. Initially (t = 0), the ωRF-frame and ωeff-frame are superimposed (i.e., z″ = z′), and at later times, the two frames are related by the Beff rotation which takes place around y′ (= y″) of the ωRF-frame. The time derivative of this rotation in the ωRF-frame (i.e., dα/dt) gives rise to a fictitious field in the ωeff-frame directed along y″ and has a magnitude equal to |γ−1dα/dt|. The effective field vector E(t) in the ωeff-frame is thus the vector sum of Beff(t) ẑ″ and the fictitious field, [γ−1dα/dt] ŷ″. As such, the magnitude of E is given by
Fig. 1.
The coordinate system used for describing the fictitious ωE-frame of reference (x‴, y‴, z‴). The effective field Beff (grey arrow) undergoes rotation with frequency ωRF(t) relative to the laboratory frame. The rotation of Beff in the y′z′ plane of the first rotating frame (not shown) leads to the fictitious field component γ−1dα/dt along the y″-axis in the ωeff-frame (x″, y″, z″). The Beff is aligned along ±z″-axis in the ωeff-frame and the fictitious field E is the vector sum of Beff and γ−1dα/dt ŷ″. The angle ε between Beff and E depends on the magnitudes of ωeff and γ−1dα/dt, and it is equal to π/4 with condition Beff(t) = |γ−1dα/dt|. In the ωE-frame, E field is collinear with the z‴ axis.
| [5] |
The angle between E and Beff is defined as (20,21),
| [6] |
The E field is utilized for spin-locking in the RAFF method. When Beff(t) = |γ−1dα/dt|, a stationary E exists in the ωeff-frame at an angle ε = π/4 relative to the z″ axis. To facilitate the theoretical analysis of the relaxation occurring with RAFF, a third frame of reference can be defined (the ωE-frame with axes x‴, y‴, z‴), in which E remains stationary and collinear with z‴ during the pulse (Fig. 1). Although E has been previously described (22) and used to excite magnetization (20), its usefulness in rotating frame relaxation experiments has apparently not been explored prior to this study.
Satisfaction of the condition Beff(t) = |γ−1dα/dt| with sine and cosine functions (SC) leads to the condition
| [7] |
where ωE = γE and is the maximum value of the AM and FM functions, which are
| [8] |
| [9] |
Here, φ0 =0 when t ∈ [0,Tp/4]. Tp is the pulse length in seconds defined by
| [10] |
With this pulse, the frequency function (Eq. [9]) sweeps from its initial value ( ) toward the resonance condition (Δω = 0) and beyond (Δω < 0), while the pulse amplitude (Eq. [8]) varies in a sinusoidal manner. The argument of both modulation functions must be the same (2−1/2ωEt+φ0) to create the condition ε = π/4. It should be noted that, with a given setting of , the effective field is larger with RAFF as compared with the on-resonance T1ρ spin-lock field (i.e. ωE > ω1).
Magnetization response to RAFF can be visualized by considering the motion of M in the ωeff-frame, with M initially along the z″ axis (Fig. 2b). In this case, M evolves around the axis of a cone, which is defined by E and the angle ε = π/4 (20). When satisfying the conditions defined above, M undergoes a π rotation on the cone and thus attains a final orientation along y″. This rotation is equivalent to a net rotation of π/2 in both rotating frames, since y″ = y′. Hereafter, the RF modulation functions producing this rotation will be denoted by the operator P, in accordance with nomenclature used previously (23).
Fig. 2.
a) Amplitude- and phase- modulated functions of the SC pulse used for RAFF. The π shift in the phase modulated function between P and P−1 (and between Pπ and ) is required for rotation of M from y″ back to z″. b) The evolution of M during the P and P−1 portions of the pulse. The phase modulation during P is obtained by integrating the frequency modulation function given by Eq. [9] over the first quarter of the pulse duration (Eq. [10]) using Eq. [12]. With these definitions, the condition Beff(t) = |γ−1dα/dt| is fulfilled.
After accomplishing the first P segment in the time interval [0,Tp/4], the magnetization is returned to the z″ axis using the inverse pulse P−1 during the interval [Tp/4, Tp/2] (Fig. 2). The inverse is created by performing a π phase shift and setting
| [11] |
in Eqs. [8] and, [9]. In Bloch simulations of the SC pulse, the P−1 segment was necessary to compensate B1 inhomogeneity.
To simplify the pulse and for ease of implementation, the FM function can be converted to the equivalent phase modulation function given by
| [12] |
In the AM and phase modulated format, P−1 is created by adding π to the phases of P and reversing the time dependencies of the AM and phase functions (Fig. 2a).
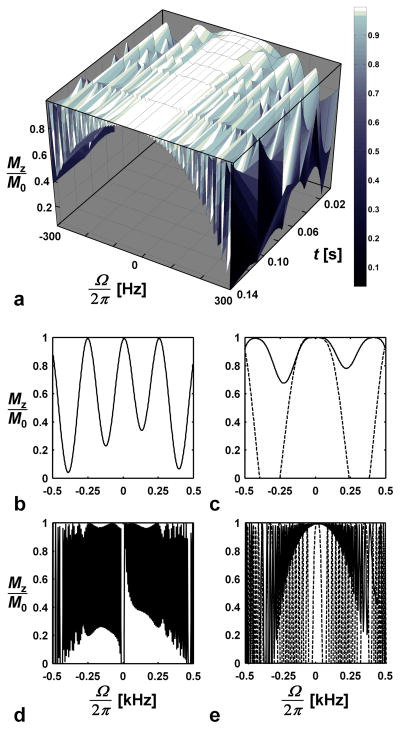
To compensate other types of frequency shifts (Ω) that can arise from imperfections such as B0 inhomogeneity and magnetic susceptibility differences in the sample, the P P−1 segment is followed by the segment , which is formed by adding π to all phases in P P−1. The resulting composite pulse, , with length Tp given by Eq. [10], defines the fundamental element from which RAFF trains are composed. In Bloch simulations of RAFF, satisfactory performance was obtained when using pulse trains composed of increasing numbers of the basic element, , despite the existence of B1 inhomogeneity and frequency shifts (Ω) larger than typical water linewidths (Fig. 3a). For comparison, simulations were performed using only the P P−1 segment as the basic element of the RAFF train. As compared with (Figs. 3c,e, solid line), the P P−1 segment by itself exhibited poor off-resonance performance (Figs. 3b,d). In addition, when the frequency response profile of was compared to the profile of a simple (square) π pulse train, a wider profile was achieved with the SC pulse (Figs. 3c,e, dashed line).
Fig. 3.
a) The longitudinal magnetization profile (Mz/M0) after several SC pulse durations as a function of pulse train length. The basic RAFF pulse packet , with the pulse train length of 4.53 ms (c) and 144.82 ms (e) are compared to the packet P P−1 P P−1, with the same durations (b and d), respectively. The dashed lines in (c) and (e) are pulse train profiles for 8 and 256 hard π pulses ( ) evenly spaced between 0 and 4.53 ms in (c) and 0 and 144.82 ms in (e). The simulations were carried out with 8 pulse train durations (a) and 500 off-resonance steps (a–e) using Bloch equations.
It can be shown that the fictitious field E acts as a locking field. This was demonstrated by performing Bloch simulations when placing M initially along the direction of E (M0=[0, 2−1/2, 2−1/2]) and applying continuously the SC pulse according to Eqs. [8], and [9]. It can be seen (Fig. 4) that the magnetization vector remains locked along E during the application of the SC pulse. This demonstrates that E effectively acts as a locking field.
Fig. 4.
Trajectories of M (solid line), E (o), and Beff (dotted line) during the execution of the SC pulse in the ωRF-frame. The evolution of initial M along E (thick arrow) was calculated using Bloch simulation during one sine/cosine period with the parameters: , 500 points during the length of one cycle of duration 1.6 ms. Relaxations during the SC pulses were ignored. E (=γ−1[ω1, dα/dt, Δω]) was plotted in every 6th point of the pulse. For comparison, Beff (=γ−1 [ω1, 0, Δω]) is shown.
Relaxation Calculations
Here we consider dipolar relaxation between two identical isolated spins. It has been shown that a complete description of the relaxation in the presence of AM and FM irradiation requires consideration of the time-dependence of the relaxation functions (24). The Wigner rotation matrices were used to transform between the various frames of interest with the following substitutions (24)
| [13] |
These transformations have been used to describe relaxation that occurs during the execution of adiabatic π pulses belonging to the hyperbolic secant (HS) family (10,24). In the current work, for the calculation of the relaxation functions during RAFF an additional transformation to the third frame of reference (the ωE-frame) is needed, which is performed by rotating the ωeff-frame by the angle ε which for generality is allowed to be time-dependent.
Following the procedure of Abragam (3), the relaxation rate constants in the ωE-frame were obtained using spectral density functions written in the laboratory frame and transformed first to the ωeff-frame, and then to the ωE-frame using Wigner rotation matrixes (24,25). The time-dependent spectral densities in this case are written in the frame rotating doubly at ω0 and ωE(t). The expansion for the dipolar Hamiltonian in the ωE-frame is written as (24)
| [14] |
Here F2m(t) is a time-dependent stochastic function that models the interaction of the spin system with its environment and is a second rank irreducible spherical tensor transformed to the ωE-frame. Following standard methods from angular momentum theory (25),
| [15] |
where are the second rank Wigner rotation matrices that are used to transform the second rank tensors from the laboratory frame to the ωE-frame and ψ is the angle evolved around ωE:
| [16] |
The second rank Wigner rotation matrix elements are (24,25)
| [17] |
The second rank reduced Wigner matrix elements are
| [18] |
where the sum is over the values of the integer l for which the factorial arguments are greater or equal to zero and the elements are calculated following Refs. (24,25). Therefore, the final expressions for the longitudinal and transverse relaxation rate constants in the ωE-frame are
| [19] |
| [20] |
where b = −μ0ħγ2/(4πr3), μ0 is the permeability of vacuum, ħ is Planck’s constant, and r is the radius of dipolar interaction, with all measures given in SI units. When the SC pulse with ε = π/4 acts on magnetization that is initially along the z axis, RRAFF (≡TRAFF−1) will be the average of T1ρ,E−1(t) and T2ρ,E−1(t) over the duration of the pulse as given by
| [21] |
To allow a comparison with the theoretical formalism above, Bloch equations were also used to simulate signal decay during the pulse train using SC pulses with the refocusing scheme . To obtain the τc dependence for dipolar interaction, T1 and T2 values corresponding to given values of τc were calculated based on existing theory (26) and then used as inputs to the Bloch equations. From the simulations, the time-dependence of the magnetization was obtained separately for M initially along ±z′.
Experimental Methods
Phantom experiments
All phantom experiments were carried out using a 40-cm-bore 4.7 T magnet (OMT, Inc., Oxon, UK) with a Varian UNITYINOVA console (Varian Inc., Palo Alto, CA). RF power was transmitted and received using a home-built linearly-polarized surface coil.
Confounding effects from B1 inhomogeneity were minimized using localized spectroscopy. Immediately after executing a given preparation sequence (composed of either SC pulses for TRAFF or AFP pulses for T1ρ,adiab measurements), the magnetization was rotated onto the transverse plane using a π/2 excitation pulse and then detected using single-voxel localization based on LASER (localization by adiabatic selective refocusing) (20). For T2ρ,adiab experiments, the π/2 excitation was applied prior to the AFP preparation pulses. Excitation was performed with an adiabatic half-passage (AHP) using and pulse length = 3 ms. The six HS pulses used for localization in LASER were transmitted with and pulse length = 3 ms, with a 1 ms delay between HS pulses giving an echo time 37 ms. The repetition time was 5 s. Voxel dimensions ranged from 4 x 4 x 4 mm3 to 4 x 6 x 6 mm3.
To assess dipolar relaxation, measurements were performed on 100 mM acetate in glycerol/water (ratio = 0.9/0.1 by weight). Sodium acetate (Sigma-Aldrich Inc., USA) and glycerol (99.9% grade, Fischer Scientific Inc., USA) were used as received. The signal intensity produced by the methyl protons of acetate (chemical shift = 1.9 ppm) was measured as a function of SC pulse train length (i.e., by increasing the number of packets) using ) and Tp ≈ 2.263 ms. The total number of SC packets was 2, 4, 8, 16, 24, 32, 40, 64, or 2, 16, 32, 48, 64, leading to pulse train lengths from 4.53 to 144.82 ms. With RAFF, the signal intensity evolves to a steady state. Therefore, a simple mono-exponential decay model cannot be used for the analysis. The contribution from the steady-state magnetization to the estimated RRAFF value was examined by inverting M prior to applying the SC pulse train.
To investigate the possible existence of steady-state magnetization during the RAFF preparation sequence, experiments were performed on an aqueous solution of 5 mM gadolinium diethylenetriamine penta-acetic acid (Magnevist, Berlex Laboratories, Wayne, NJ). In separate experiments, the SC pulse train was applied immediately after an initial tip of the magnetization to the angle (α) = 0, π/3, π/2, and π. The initial tips of α = π/3 and π/2 were performed with BIR-4 pulses (23) (length = 6 ms and ), whereas the initial tip of α = π rad was performed using a HS pulse (length = 6 ms, bandwidth = 1667 Hz, and ).
Measurements of T1ρ,adiab and T2ρ,adiab were performed with a preparation sequence composed of AFP pulses (27), as described previously (9,11). In all T1ρ,adiab and T2ρ,adiab experiments, the AFP pulses were HS pulses. In T1ρ,adiab measurements, the train of AFP pulses was placed prior to the AHP pulse in LASER, whereas in the T2ρ,adiab measurements, the train of AFP pulses was placed between the AHP pulse and the HS pulses of LASER. Measurements of T1ρ,adiab and T2ρ,adiab were performed with number of AFP pulses = 4, 8, 16, 20, 24, 28 and 32, with each pulse having a length = 3.2 ms and . Inversion of M prior to the AFP pulse train in T1ρ,adiab and prior to the AHP pulse in T2ρ,adiab experiments was performed, as in the RAFF experiment, to investigate steady-state formation.
For comparison with RAFF, conventional continuous wave (cw) on- and off-resonance T1ρ,off measurements were also conducted, using an adiabatic spin-lock pulse (13). The adiabatic spin-lock pulse was composed of an AHP pulse followed by a cw spin-lock pulse. Magnetization was excited to α = π/2 and α = π/4 in the on- and off-resonance experiments, respectively, and locked at these angles by the cw portion of the adiabatic spin-lock pulse. After the spin-lock pulse, the magnetization was returned back to the z axis using a reverse AHP pulse and LASER was then used for signal localization. For the relaxation measurements, the spin-lock duration was incremented while the RF power was fixed at .
The sensitivity of RRAFF to changes in RF amplitude ( ) and offset frequency (Ω) was investigated and compared with off-resonance T1ρ (T1ρ,off≡ R1ρ,off−1) using a 1:1 mixture of water and ethanol (>99.5%, Sigma-Aldrich Inc., USA). The value of RRAFF and R1ρ,off were measured starting with M along +z and −z in separate experiments. The offset frequency was varied in 13 increments between ±120 Hz, with 10 different settings of in the range of 300 to 800 Hz.
Human experiments
All human experiments were performed according to procedures approved by the Institutional Review Board of the University of Minnesota Medical School. Healthy volunteers, (4 males and 1 female, ages 31 ± 15 years (mean ± std.)) were scanned after obtaining informed consent. The total scan time was approximately 60 minutes per subject.
The MRI system consisted of a Varian UNITYINOVA console (Varian Inc., Palo Alto, CA, USA) interfaced to a 90 cm bore 4 T magnet (OMT, Inc., Oxon, UK). A volume coil based on the transverse electromagnetic design (28) was used for RF transmission and reception. After global shimming, 11 transverse slices were acquired using a T2-weighted fast spin-echo sequence with repetition time = 4.5 s, matrix size = 256 x 128, field-of-view = 20 x 20 cm2, echo train length = 8, with echo spacing = 15 ms, and slice thickness = 3 mm. Following a preparation sequence to create TRAFF, T1ρ,adiab, or T2ρ,adiab weighting, the signal was measured in a single slice containing striatum using a TurboFLASH readout (29) with TR = 10 ms and echo time = 5 ms. Other parameters were: delay time between k-space segments = 5 s, number of segments = 4, number of excitations = 4, matrix size = 256 x 256, field-of-view = 20 x 20 cm2, and slice thickness = 3 mm. In obtaining relaxation maps with RAFF, the parameters of the SC pulses were chosen to be similar to those used in the solution experiments ( and Tp ≈ 2.263 ms), and the number of packets = 2, 16, 32, 48, and 64. Measurements of, T1ρ,adiab and T2ρ,adiab were performed with HS pulses using pulse length = 6 ms, bandwidth = 1667 Hz, , and number of HS pulses = 4, 8, 12, and 16. The RF amplitude was calibrated in each human experiment using a square excitation pulse in LASER, with voxel coordinates matched to the position and size of the midbrain area. For T1 mapping, images were collected with TurboFLASH following adiabatic HS inversion and a recovery period. This experiment was repeated using 6 different recovery delays evenly spaced between 0.3 and 1.4 s. To investigate whether a steady state contributed to any of the rotating frame signal decay curves (S(t)), the experiments were repeated with the inversion pulse placed prior to the SC and AFP pulse trains. Free-precession T2 values were measured using an adiabatic double-spin echo pulse sequence and by varying the echo delays around the two AFP pulses (9). For the T2 measurements, echo time was varied between 12 and 128 ms. B1 maps were measured from two volunteers to ascertain B1 homogeneity within the area of the deep brain structures. The B1 maps were generated from 20 images that were acquired following the application of a square pulse of variable duration (30). The length of the square pulse was evenly incremented between 0.1 and 0.8 ms.
The RF power delivered to the coil was limited to a safe operating range using the hardware monitoring module of the Varian console. In addition, the RF power output over the full range of settings used in these experiments was measured with an oscilloscope connected to the coil port. From these measured values, the average RF power delivered to the coil was computed by integration of all RF pulses in the sequence, and SAR was estimated assuming a tissue load of 3 kg in the coil. When using the longest pulse train, the estimated SAR in RAFF and T2ρ,adiab experiments was 2.1 W/kg, and in the T1ρ,adiab experiment it was 1.7 W/kg. These SAR values are below the FDA limit of 3 W/kg averaged over the head for 10 min (http://www.fda.gov/cdrh/ode/mri340.pdf).
Data analysis
Analyses were performed on data obtained from Bloch simulations and experimentation, using initial magnetization along −z′ and +z′ separately. A non-linear least-squares fitting was performed simultaneously on data obtained with initial −z′ and +z′ magnetization orientations. An empirical equation was used to model the observed exponential decay and approach to steady state,
| [22] |
Here S0 is the initial intensity (t = 0), R is the relaxation rate constant describing the decay, and SSS is the steady-state intensity at t → ∞. The steady-state quantity (SS) is defined here by SS=SSS/S0. Note, the same formalism is usually applied in the estimation of T1 from data acquired with rapid pulsing (31). Relaxation maps were generated by non-linear regression fits of pixel intensities using the model of Eq. [22]. A comparison was performed with RAFF maps generated using a single mono-exponential function for decay of M from +z. Regions of interests were outlined for globus pallidus, putamen and caudate nuclei. Relaxation time constants were determined from these regions of interest and average values over the subjects were calculated. All values are presented as mean ± standard deviation. Because there is no formation of the steady state during on-resonance T1ρ measurements, a simple two parameter mono-exponential function was used for fitting the on-resonance T1ρ data.
Estimation of τc in the glycerol water mixture was carried out using models given in Refs. (24,32,33), and by fitting modeled relaxation rates to experimentally obtained T1ρ,on, T1ρ,off, T1ρ,adiab, and T2ρ,adiab values. Least square fitting with the trust-region-reflective Newton algorithm was used. Two strategies were used for τc estimation: i) separate estimates using each method, and ii) one estimate using all methods.
Results
Relaxation calculations
Relaxation rates expected from theory were calculated to investigate the relative sensitivities of the different relaxation methods (TRAFF, T1, T2, T1ρ,on, T1ρ,off, and T1ρ,adiab and T2ρ,adiab) to changes in τc. The calculations were performed for two isolated spins ½ nuclei undergoing dipolar interactions. In figures 5a,b, respectively, the longitudinal and transverse rate constants are plotted as a function of τc. It can be seen that R2 (≡1/T2) and R1ρ,on (≡1/T1ρ,on) exhibit the greatest sensitivity to changes in correlation time. As expected for this dipolar system (32), the plots show R1ρ,on = R2. With RAFF, the sensitivity to τc is similar to that of R1ρ,on when calculating longitudinal and transverse RAFF rate constants from Eqs. [19] and [20]. On the other hand, Bloch simulations yield slower RAFF relaxation rates than those predicted from Eqs. [19] and [20]. The value of RRAFF calculated from Eqs. [19] and [20] is ≈70% larger than the value obtained from Bloch simulations. Possible explanations for this difference are discussed further below.
Fig. 5.
Calculated relaxation rate constants a) for T1ρ,on, T1ρ,E, T1ρ,off, TRAFF, T1ρ,adiab, TRAFF, T1ρ,off, and T1 methods; and b) for T2, T2ρ,adiab, T2ρ,off, T2ρ,E, T2ρ,on, and TRAFF methods. Inserts show expanded views for short τc range. The value of RRAFF was estimated using Bloch simulation, whereas R1ρ,E and R2ρ,E were obtained using Eqs. [19] and [20], respectively. The other curves in the figure were calculated using the dipolar relaxation model based on reference (32). On- and off-resonance cw spin-lock were calculated with and additionally Δω/(2π) = 625 Hz (α = π/4) for off-resonance spin lock. The pulse modulation functions given in reference (20) were used for calculating R1ρ,adiab and R2ρ,adiab curves with pulse length = 3.0 ms and in a similar manner to that in Refs. (10,11). In all calculations, μ0 = 4π·10−7, ħ =1.0546·10−34 Js, γ =2π·42.58·106 rad/(sT), r = 158 pm and B0 = 4.7 T were used.
Phantom experiments
Relaxation measurements of acetate (−CH3 resonance) dissolved in glycerol/water mixtures were performed to probe a system undergoing dipolar relaxation. Comparisons were made between data measured with RAFF, T1ρ, and T2ρ techniques. In Figure 6a, the results are shown for acetate dissolved in a 0.9:01 mixture of glycerol and water (a viscous solution, η ≈ 220 cp (34)). The signal recovery after the inversion pulse demonstrates the formation of a steady state with RAFF. The results of the analysis using Eq. [22] reveal comparable rate constants for RAFF and adiabatic T1ρ methods (RRAFF = 6.6 s−1, R1ρ,adiab = 6.5 s−1). On the other hand, T2ρ,adiab and cw T1ρ,on and T1ρ,off methods yield similar rate constants (R2ρ,adiab = 10.5 s−1, R1ρ,on = 9.9 s−1, and R1ρ,off = 10.0 s−1). The difference in relaxation rates between these two groups is ≈4 s−1; thus, a more complex relaxation model may be needed.
Fig. 6.
a) Signal intensity decay curves of acetate (100 mM) dissolved in glycerol/water (0.9/0.1) mixture measured with RAFF pulse (○) with , T1ρ,adiab (□), T2ρ,adiab (△), T1ρ,on (×) with , and T1ρ,off (+) with . Two independent acquisitions are presented for RAFF and adiabatic relaxation techniques. Top: M was not perturbed prior to the SC pulses; bottom: M was inverted prior to the SC pulses. Relaxation curves (solid lines) were fitted using Eq. [22]. b) Normalized decay curves S(t)/S0 obtained with RAFF in 5 mM gadolinium diethylenetriamine penta-acetic acid in deionized aqueous solution. Magnetization (M) was rotated to the different angles (0, π/3, π/2, and π) relative to the z′ axis prior to the application of the SC pulse trains. Solid lines represent fittings to the experimental data using Eq. [22]. The relaxation rate constants and the SS values were independent of the initial angle between M and z′. The results are normalized to the fitted S0 obtained from the 0 rad experiment. In the present sample, RRAFF = 30.7 ± 1.4 s (mean ± sd) and SS = 0.684 ± 0.001. The BIR-4 pulse (20) (pulse length = 6 ms, ) was used to excitation of angles π/3 and π/2, and the HS pulse (pulse length = 6 ms, ) for angle π. Note that the additional SC pulse train of duration 289.64 ms was added to better observe steady-state formation.
From simulations (Fig. 5), the experimentally observed R1ρ,on and R1ρ,off values are consistent with τc values equal to 1.9·10−10 s and 2.2·10−10 s, respectively. The slight difference between τc estimated based on T1ρ,on and T1ρ,off might be attributed to the experimental inaccuracies in the initial flip angle and phase during the T1ρ,off experiment, since this experiment is prone to errors in the initial preparation of M. With T1ρ,adiab and T2ρ,adiab methods, the τc values estimated from the simulations are 1.3·10−10 s and 2.1·10−10 s, respectively. The combination of all reference methods (T1ρ,on T1ρ,off, T1ρ,adiab, and T2ρ,adiab) yield τc = 1.9·10−10 s. With RAFF, τc is 1.9·10−10 s based on the Bloch simulations, whereas Eqs. [19], and [20] predict τc to be 1.4·10−10 s. Potential reasons for this difference will be discussed later.
The steady-state fraction is similar for RAFF and off-resonance cw T1ρ methods (SS = 0.4 and 0.42, respectively). In experiments with adiabatic T1ρ and T2ρ methods, negligible steady state formation is present (SS = −0.03 – 0.04).
The existence of a steady state contribution was also examined in experiments using gadolinium diethylenetriamine penta-acetic acid solution. This system was chosen because the water signal decays rapidly, and thus, the steady state could be attained with the pulse train lengths used in this work. As shown in Figure 6b, the experiment demonstrates how the signal always reaches the same steady-state level, despite using several different initial tip angles.
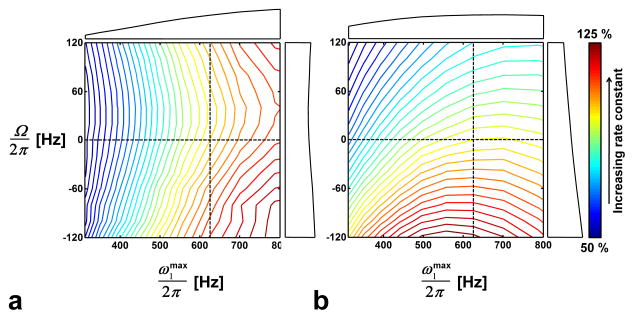
Measurements were also performed to investigate the robustness of the RAFF method to experimental imperfections. These measurements were performed on a 1:1 mixture of ethanol and water (a proton exchanging spin system) in order to have high dynamic range to define the signal decay over the pulse lengths used in this study and to have high signal-to-noise ratio to achieve accurate mapping of the relaxation dependencies on RF amplitude ( ) and offset frequency (Ω). With the same SC pulse pattern, the RAFF relaxation rate constant (RRAFF) was measured in separate experiments using different settings of and Ω. Immediately following the SC preparation sequence, LASER was used to measure the intensity of the water/ethanol hydroxyl resonance (a singlet due to fast proton exchange; e.g. in the absence of exchange, the chemical-shift between the proton resonances of water and the ethanol hydroxyl group is 0.85 ppm). For comparison, the experiment was repeated using off-resonance T1ρ preparation. Contour plots reveal the dependencies of the relaxation rate constant (percent change) as a function of and Ω, when measured with RAFF (Fig. 7a) and T1ρ,off (Fig. 7b) methods. From Figure 7a, it is apparent that off-resonance variations larger than ± 50 Hz, due either to chemical shift or B0 variation, will significantly affect the RAFF rate constant. It can also be seen that, as compared to the off-resonance T1ρ experiment (Fig. 7b), the RAFF method is less sensitive to chemical shift or B0 variation in the range −50 Hz < Ω < 50 Hz. On the other hand, RAFF is more sensitive to variations. Thus, a relatively homogeneous B1 is desirable in RAFF relaxation measurements. Despite these potential sources of experimental imperfections, RRAFF values were highly reproducible between experiments, particularly when care was taken to minimize B1 inhomogeneity (e.g., by limiting the volume) and by using a calibration procedure to attain the same setting each time.
Fig. 7.
Contour plots of the relaxation rate constants of a) RAFF and b) off-resonance cw spin-lock T1ρ,off in ethanol/water mixture. Every contour line designates a 2.5% change in the rate constant from the nominal values measured with ω1max/(2π) = 625 Hz and Ω = 0. The nominal rate constants were RRAFF = 5.3 s−1 and R1ρ,off = 3.9 s−1. The horizontal and vertical profiles from the dashed lines are presented on the top and left side of the contour plots, respectively. Fittings for both methods were performed using the model given in Eq. [22].
Human experiments
Although relaxation parameters are typically estimated by fitting data to a single mono-exponential function, this approach did not produce satisfactory estimates of TRAFF. Specifically, when using Eq. [22] and simultaneous fitting of z and −z data (i.e., magnetization initially unperturbed and inverted, respectively), the RAFF relaxation time constants (TRAFF) in human brain tissue were ≈20% smaller than the TRAFF values obtained when fitting the +z′ data to a single mono-exponential function (Fig. 8). This difference is due to neglect of the steady state contribution in the single mono-exponential analysis. Thus, Eq. [22] should be used in RAFF relaxation analyses even when a steady state is not reached with the longest pulse train length. The SS map (Fig. 8c) shows the spatial variation of the steady-state signal in the mid brain areas.
Fig. 8.
The RAFF relaxation time maps calculated a) with a single mono-exponential fitting and b) using Eq. [22] with c) a map of the fractional steady state (SS = SSS/S0) obtained from the fitting in (b).
The feasibility to create MRI contrast based on RAFF was assessed in studies of healthy human brain at 4T, using the RAFF pulse train as a preparation sequence preceding image readout. For comparison, maps of T1, T2, T1ρ,adiab, and T2ρ,adiab were generated from the same imaging slice as RAFF (Fig. 9). The values of TRAFF were larger than T2 and T2ρ,adiab and smaller than T1ρ,adiab and T1 (Table 1), and these differences were significant (p<0.001, paired student’s t-test without correction for multiple comparisons).
Fig. 9.
Representative relaxation time maps from human brain obtained using a) T1, b) T1ρ,adiab, c) RAFF, d) T2ρ,adiab, and e) T2 relaxation mapping techniques.
Table 1.
Comparison of the RAFF Relaxation Time (TRAFF) with T1, T2, T1ρ,adiab, and T2ρ,adiab in Representative Midbrain Areas of Normal Human Brain at 4 T (n = 5)*
| T1 (ms) | T1ρ,adiab (ms) | TRAFF (ms) | T2ρ,adiab (ms) | T2 (ms) | |
|---|---|---|---|---|---|
| GP | 1045.4 ± 42.2 | 161.3 ± 2.8 | 105.4 ± 2.2 | 55.4 ± 3.1 | 46.5 ± 1.8 |
| P | 1324.9 ± 37.5 | 189.2 ± 3.4 | 126.8 ± 3.1 | 65.7 ± 1.9 | 51.4 ± 3.2 |
| CN | 1420.5 ± 48.2 | 221.0 ± 8.1 | 134.8 ± 3.1 | 76.6 ± 3.0 | 64.8 ± 2.1 |
GP = globulus pallidus; P = putamen; CN = caudate nuclei.
Discussion
With an adiabatic pulse, a fictitious field component (γ−1dα/dt ŷ ″) arises due to the rotation of Beff in the x′z′ plane. When executing the pulse in an adiabatic manner, this additional field component can usually be neglected since Beff ≫ γ−1dα/dt (the adiabatic condition). However, strict adherence to the adiabatic condition is not a requirement to rotate magnetization with FM pulses (20). For example, adiabatic full-passage can be performed under conditions which do not seem to be highly adiabatic (e.g., Beff ≈ 5·γ−1dα/dt) (35,36). During an adiabatic rotation, M experiences an effective field comprised of multiple field components including Beff, γ−1dα/dt ŷ ″, and in some cases, additional higher order fictitious fields (also called higher order inertial fields (35)).
The objective of the current study was to consider the case in which a strong γ−1dα/dt ŷ″ field component exists (i.e., a FM pulse in a sub-adiabatic condition). To facilitate the study of relaxation in the presence of this strong fictitious field, the simplest case was chosen (the SC pulse) which produces equal and constant field amplitudes, γ−1dα/dt = Beff, with no added complications from higher order inertial fields (i.e., γ−1dε/dt = 0, because ε = constant). In the current work, the effective field E is the resultant of the RF field (B1) and the fictitious components, γ−1Δωẑ′ and γ−1dα/dt ŷ″. Thus, rotating frame relaxation occurs along the net field E, which includes both fictitious and non-fictitious components.
When using the SC pulse described by Eqs. [8] and [9], the component of M initially along the direction of E will remain locked during the whole RF pulse. Likewise, rotation about E occurs for any components of M which are initially perpendicular to E. Because frequency shifts and B1-inhomogeneities are difficult to avoid in practice, the RAFF pulse train must offer the ability to periodically refocus components of M. In this regard, as demonstrated by Bloch simulations, the four segment SC pulse ( ) is needed to make the RAFF method usable in vivo. It is interesting to note that the composite structure is the same as that used in the composite adiabatic pulse, BIR-4 (23), which also tolerates a reasonable amount of frequency shift and B1 inhomogeneity.
In this work, a theoretical description of the effects of dipolar relaxation on RAFF has been introduced (Eqs. [19] and [20]). Bloch simulations and experimental data reveal some limitations of the proposed theory and point to the need for further work and understanding. Although the three spin system (−CH3) was investigated, the application of two spin formalism is justified for the spin dynamics of this methyl group in liquid due to degeneracy of energy states (37). When using the experimentally determined relaxation rate constants obtained from acetate in a glycerol/water mixture as inputs to the Bloch simulations, good agreement between τc values was obtained despite using several different methods (RAFF, T1ρ,adiab, T2ρ,adiab, cw T1ρ,on, and cw T1ρ,off). However, the τc value of acetate calculated from Eqs. [19] and [20] is ≈27% smaller than that predicted from Bloch simulations, when using the measured relaxation parameters as inputs. Most likely, the discrepancy between estimates made using Eqs. [19] and [20] versus Bloch simulation for RAFF originates from the assumption of initially averaged T2ρ,E in the plane perpendicular to E in Eq. [20]. With each packet, the magnetization experiences two inversions (or flips) of E. For the perpendicular components of M, these E flips produce refocusing (a rotory echo) along the z′ axis. Eq. [20] cannot account for the constrained evolution and periodic refocusing of the perpendicular components of M. Hence, a more complete theoretical formalism, which includes the E flips, is still needed to allow accurate assessments of dipolar as well as other potentially important mechanisms such as exchange.
With RAFF, the RF irradiation has a periodical pattern which leads to the formation of steady-state magnetization. In this study, it was shown that in a viscous dipolar system where T1 ≠ T2, the steady state has a significant influence on the signal decay and therefore has to be accounted for in the data analysis. All data measured in this study were readily fit with the empirical model which includes a steady-state term (Eq. [22]). Further investigation is needed to fully understand and utilize the steady state formation during SC pulse train. In the future, it may be possible to exploit the distribution of SS to enhance the contrast between different tissues.
The experiment performed using gadolinium diethylenetriamine penta-acetic acid water solution demonstrated that the relaxation rate constants of RAFF are not dependent on the initial tip angle. Hence, the RAFF experiment does not necessarily require an initial tip of the magnetization, unlike the classical cw T1ρ experiment in which a relatively uniform tip angle to the desired α value is needed prior to the application of the spin-lock pulse. For accurate estimation of steady state with short SC pulses, a measurement with the inversion prior to the SC pulses is expected to be beneficial.
Using the ethanol/water solution, the sensitivity of RAFF to common experimental imperfections (frequency offsets and B1-inhomogeneity) was studied and compared with the T1ρ,off experiment. The relaxation rate constants obtained using RAFF were more uniform as a function of frequency offset, whereas RAFF required a more homogenous B1 field than T1ρ,off. Hence, RAFF experiments may need to be performed with a relatively homogeneous RF coil or with volume selection.
The results from human brain show that TRAFF maps can be obtained in vivo at 4 T and that the measured value of TRAFF is between the values of T1ρ,adiab and T2ρ,adiab, in agreement with theoretical predictions (Fig. 5). However, the exchange relaxation pathway may be a significant contributor to the in vivo brain contrast observed with RAFF, because in the viscous acetate solution (a dipolar system) the values of TRAFF and T1ρ,adiab were comparable (see Fig. 5a). Therefore, as mentioned above, the theoretical model of Eqs. [19] and [20] should be considered to represent a simplified treatment, rather than the complete relaxation model which will be needed to describe in vivo RAFF contrast.
The lower RF power required by RAFF is a significant advantage of this technique as compared to adiabatic T1ρ and T2ρ methods. Due to its amplitude modulation, the SC pulse deposits only 61% of the RF power (SAR) of a cw pulse, when transmitting for the same duration and with the same setting. In this study, the average power delivered to the brain tissue during adiabatic T1ρ, T2ρ, and RAFF acquisitions were 1.07 W/kg, 1.48 W/kg, and 1.10 W/kg, respectively. Because the longest pulse train duration of RAFF was 1.5 times longer than that used in the adiabatic T1ρ experiment, the average power depositions were similar. The delivered RF energy during the pulse train unit time for RAFF irradiation was 83% and 63% of the energies of adiabatic T1ρ and T2ρ irradiations, respectively. In the future, an alternative to using the preparation sequence might be to use the SC pulse as an excitation pulse for an imaging readout, in which case it would be possible to obtain RAFF contrast with substantially improved acquisition efficiency.
Conclusions
In this work, a novel method based on the relaxation along fictitious field (RAFF) was developed. It was shown how MRI contrast based on rotating frame relaxation could be generated in vivo using frequency-swept pulses under a sub-adiabatic condition. The method eliminates the need for an initial tip of the magnetization vector to an angle α (as needed in conventional T1ρ experiments) and demands less RF power for implementation than other rotating frame relaxation methods. RAFF contrast was shown to be different as compared to T1, T2, adiabatic T1ρ, and adiabatic T2ρ, and therefore, may have use in detecting certain pathologies in vivo. It can be concluded that the RAFF method holds promise as a tool to access different time scales of molecular dynamics and to generate MRI contrast with sensitivity to long correlation times. In addition, the principles described herein are expected to have relevance to many types of experiments using adiabatic and sub-adiabatic rotations.
Acknowledgments
The authors thank Dr. Silvia Mangia for constructive discussions during this work and the following agencies for financial support: Instrumentarium Science Foundation (TL), Orion Corporation Research Foundation (TL), Finnish Cultural Foundation Northern Savo (TL), and NIH grants P30 NS057091, P41 RR008079, R01NS061866 and R21NS059813.
References
- 1.Andrew E, Bydder G, Griffiths J, Iles R, Styles P. Clinical magnetic resonance: imaging and spectroscopy. Chichester: John Wiley & Sons; 1980. [Google Scholar]
- 2.Rooney WD, Johnson G, Li X, Cohen ER, Kim SG, Ugurbil K, Springer CS., Jr Magnetic field and tissue dependencies of human brain longitudinal 1H2O relaxation in vivo. Magn Reson Med. 2007;57(2):308–318. doi: 10.1002/mrm.21122. [DOI] [PubMed] [Google Scholar]
- 3.Abragam A. In: Principles of nuclear magnetism. Adair R, Elliott R, Marshall W, Wilkinson D, editors. Oxford: Oxford University Press Inc; 1963. [Google Scholar]
- 4.Solomon I. Rotary spin echoes. Phys Rev Lett. 1959;2:301–305. [Google Scholar]
- 5.Abergel D, Palmer A., III On the use of the stochastic Liouville equation in nuclear magnetic resonance: application to R1ρ relaxation in the presence of exchange. Concepts Magn Reson A. 2003;19(2):134–148. [Google Scholar]
- 6.Palmer A, Kroenke C, Loria J. Nuclear magnetic resonance methods for quantifying microsecond-to-millisecond motions in biological macromolecules. Meth Enzymol. 2001;339:204–238. doi: 10.1016/s0076-6879(01)39315-1. [DOI] [PubMed] [Google Scholar]
- 7.Fischer M, Majumdar A, Zuiderweg E. Protein NMR relaxation: theory, applications and outlook. Prog NMR Spectrosc. 1998;33:207–272. [Google Scholar]
- 8.Korzhnev D, Billeter M, Arseniev A, Orekhov V. NMR studies of Brownian tumbling and internal motions in proteins. Prog NMR Spectrosc. 2001;38:197–266. [Google Scholar]
- 9.Michaeli S, Gröhn H, Gröhn O, Sorce D, Kauppinen R, Springer C, Ugurbil K, Garwood M. Exchange-influenced T2ρ contrast in human brain images measured with adiabatic radio frequency pulses. Magn Reson Med. 2005;53:823–829. doi: 10.1002/mrm.20428. [DOI] [PubMed] [Google Scholar]
- 10.Michaeli S, Sorce D, Idiyatullin D, Ugurbil K, Garwood M. Transverse relaxation in the rotating frame induced by chemical exchange. J Magn Reson. 2004;169:293–299. doi: 10.1016/j.jmr.2004.05.010. [DOI] [PubMed] [Google Scholar]
- 11.Michaeli S, Sorce D, Springer C, Ugurbil K, Garwood M. T1ρ MRI contrast in the human brain: modulation of the longitudinal rotating frame relaxation shutter-speed during an adiabatic RF pulse. J Magn Reson. 2006;181:138–150. doi: 10.1016/j.jmr.2006.04.002. [DOI] [PubMed] [Google Scholar]
- 12.Borthakur A, Mellon E, Niyogi S, Witschey W, Kneeland JB, Reddy R. Sodium and T1ρ MRI for molecular and diagnostic imaging of articular cartilage. NMR Biomed. 2006;19(7):781–821. doi: 10.1002/nbm.1102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gröhn HI, Michaeli S, Garwood M, Kauppinen RA, Gröhn OH. Quantitative T1ρ and adiabatic Carr-Purcell T2 magnetic resonance imaging of human occipital lobe at 4 T. Magn Reson Med. 2005;54:14–19. doi: 10.1002/mrm.20536. [DOI] [PubMed] [Google Scholar]
- 14.Gröhn OH, Kettunen MI, Mäkelä HI, Penttonen M, Pitkänen A, Lukkarinen JA, Kauppinen RA. Early detection of irreversible cerebral ischemia in the rat using dispersion of the MRI relaxation time, T1ρ. J Cereb Blood Flow Metab. 2000;20:1457–1466. doi: 10.1097/00004647-200010000-00007. [DOI] [PubMed] [Google Scholar]
- 15.Hakumäki JM, Gröhn OH, Tyynelä K, Valonen P, Ylä-Herttuala S, Kauppinen RA. Early gene therapy-induced apoptotic response in BT4C gliomas by magnetic resonance relaxation contrast T1 in the rotating frame. Cancer Gene Ther. 2002;9(4):338–345. doi: 10.1038/sj.cgt.7700450. [DOI] [PubMed] [Google Scholar]
- 16.Kettunen MI, Sierra A, Närväinen MJ, Valonen PK, Ylä-Herttuala S, Kauppinen RA, Gröhn OH. Low spin-lock field T1 relaxation in the rotating frame as a sensitive MR imaging marker for gene therapy treatment response in rat glioma. Radiology. 2007;243(3):796–803. doi: 10.1148/radiol.2433052077. [DOI] [PubMed] [Google Scholar]
- 17.Michaeli S, Oz G, Sorce DJ, Garwood M, Ugurbil K, Majestic S, Tuite P. Assessment of brain iron and neuronal integrity in patients with Parkinson’s disease using novel MRI contrasts. Mov Disord. 2007;22(3):334–340. doi: 10.1002/mds.21227. [DOI] [PubMed] [Google Scholar]
- 18.Witschey WR, Borthakur A, Elliott MA, Mellon E, Niyogi S, Wang C, Reddy R. Compensation for spin-lock artifacts using an off-resonance rotary echo in T1ρ,off-weighted imaging. Magn Reson Med. 2007;57(1):2–7. doi: 10.1002/mrm.21134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Witschey WR, Borthakur A, Elliott MA, Mellon E, Niyogi S, Wallman DJ, Wang C, Reddy R. Artifacts in T1ρ-weighted imaging: compensation for B1 and B0 field imperfections. J Magn Reson. 2007;186(1):75–85. doi: 10.1016/j.jmr.2007.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Garwood M, DelaBarre L. The return of the frequency sweep: designing adiabatic pulses for contemporary NMR. J Magn Reson. 2001;153:155–177. doi: 10.1006/jmre.2001.2340. [DOI] [PubMed] [Google Scholar]
- 21.Bendall MR, Garwood M, Ugurbil K, Pegg DT. Adiabatic refocusing pulse which compensates for variable RF power and off-resonance effects. Magn Reson Med. 1987;4(5):493–499. doi: 10.1002/mrm.1910040510. [DOI] [PubMed] [Google Scholar]
- 22.Bendall MR, Pegg DT. Uniform sample excitation with surface coils for in vivo spectroscopy by adiabatic rapid half passage. J Magn Reson. 1986;67(2):376–381. [Google Scholar]
- 23.Garwood M, Nease B, Ke Y, deGraaf R, Merkle H. Simultaneous compensation for B1 inhomogeneity and resonance offsets by a multiple-quantum NMR sequence using adiabatic pulses. J Magn Reson A. 1995;112:272–274. [Google Scholar]
- 24.Sorce D, Michaeli S, Garwood M. Relaxation during adiabatic radiofrequency pulses. Curr Anal Chem. 2007;3:239–251. [Google Scholar]
- 25.Rose ME. Elementary theory of angular momentum. New York: John Wiley & Sons; 1957. [Google Scholar]
- 26.Levitt M. Spin dynamics. Chichester: John Wiley & Sons Ltd; 2008. [Google Scholar]
- 27.Silver MS, Joseph RI, Chen CN, Sank VJ, Hoult DI. Selective population inversion in NMR. Nature. 1984;310(5979):681–683. doi: 10.1038/310681a0. [DOI] [PubMed] [Google Scholar]
- 28.Vaughan JT, Adriany G, Garwood M, Yacoub E, Duong T, DelaBarre L, Andersen P, Ugurbil K. Detunable transverse electromagnetic (TEM) volume coil for high-field NMR. Magn Reson Med. 2002;47(5):990–1000. doi: 10.1002/mrm.10141. [DOI] [PubMed] [Google Scholar]
- 29.Haase A. Snapshot FLASH MRI: application to T1-, T2-, and chemical shift imaging. Magn Reson Med. 1990;13:77–89. doi: 10.1002/mrm.1910130109. [DOI] [PubMed] [Google Scholar]
- 30.Vaughan JT, Garwood M, Collins CM, Liu W, DelaBarre L, Adriany G, Andersen P, Merkle H, Goebel R, Smith MB, Ugurbil K. 7 T vs. 4 T: rf power, homogeneity, and signal-to-noise comparison in head images. Magn Reson Med. 2001;46(1):24–30. doi: 10.1002/mrm.1156. [DOI] [PubMed] [Google Scholar]
- 31.Hsu J, Glover G. Rapid MRI method for mapping the longitudinal relaxation time. J Magn Reson. 2006;181:98–106. doi: 10.1016/j.jmr.2006.03.014. [DOI] [PubMed] [Google Scholar]
- 32.Blicharski J. Nuclear magnetic relaxation in rotating frame. Acta Physica Polonica. 1972;A41(2):223–236. [Google Scholar]
- 33.Michaeli S, Sorce D, Springer C, Ugurbil K, Garwood M. T1ρ contrast generated by adiabatic HSn pulses in human brain at 4 T. Dipolar cross-relaxation mechanism in tissue. Proc Int Soc Magn Reson Med. 2005 [Google Scholar]
- 34.Weast RC, editor. CRC handbook of chemistry and physics. CRC Press; 1977–1978. [Google Scholar]
- 35.Deschamps M, Kervern G, Massiot D, Pintacuda G, Emsley L, Grandinetti PJ. Superadiabaticity in magnetic resonance. J Chem Phys. 2008;129(20):204110. doi: 10.1063/1.3012356. [DOI] [PubMed] [Google Scholar]
- 36.Rosenfeld D, Zur Y. Is the sech/tanh adiabatic pulse really adiabatic. J Magn Reson. 1998;132:102–108. [Google Scholar]
- 37.Fagerness P, Grant D, Kuhlmann K, Mayne C, Parry R. Spin-lattice relaxation in coupled three spin systems of the AIS type. J Chem Phys. 1975;63(6):2524–2532. [Google Scholar]