In silico prediction of drug therapy in catecholaminergic polymorphic ventricular tachycardia

Abstract

Key points

• The mechanism of therapeutic efficacy of flecainide for catecholaminergic polymorphic ventricular tachycardia (CPVT) is unclear.

• Model predictions suggest that Na⁺ channel effects are insufficient to explain flecainide efficacy in CPVT.

• This study represents a first step toward predicting therapeutic mechanisms of drug efficacy in the setting of CPVT and then using these mechanisms to guide modelling and simulation to predict alternative drug therapies.

Abstract

Catecholaminergic polymorphic ventricular tachycardia (CPVT) is an inherited arrhythmia syndrome characterized by fatal ventricular arrhythmias in structurally normal hearts during β‐adrenergic stimulation. Current treatment strategies include β‐blockade, flecainide and ICD implementation – none of which is fully effective and each comes with associated risk. Recently, flecainide has gained considerable interest in CPVT treatment, but its mechanism of action for therapeutic efficacy is unclear. In this study, we performed in silico mutagenesis to construct a CPVT model and then used a computational modelling and simulation approach to make predictions of drug mechanisms and efficacy in the setting of CPVT. Experiments were carried out to validate model results. Our simulations revealed that Na⁺ channel effects are insufficient to explain flecainide efficacy in CPVT. The pure Na⁺ channel blocker lidocaine and the antianginal ranolazine were additionally tested and also found to be ineffective. When we tested lower dose combination therapy with flecainide, β‐blockade and CaMKII inhibition, our model predicted superior therapeutic efficacy than with flecainide monotherapy. Simulations indicate a polytherapeutic approach may mitigate side‐effects and proarrhythmic potential plaguing CPVT pharmacological management today. Importantly, our prediction of a novel polytherapy for CPVT was confirmed experimentally. Our simulations suggest that flecainide therapeutic efficacy in CPVT is unlikely to derive from primary interactions with the Na⁺ channel, and benefit may be gained from an alternative multi‐drug regimen.

Key points

• The mechanism of therapeutic efficacy of flecainide for catecholaminergic polymorphic ventricular tachycardia (CPVT) is unclear.

• Model predictions suggest that Na⁺ channel effects are insufficient to explain flecainide efficacy in CPVT.

• This study represents a first step toward predicting therapeutic mechanisms of drug efficacy in the setting of CPVT and then using these mechanisms to guide modelling and simulation to predict alternative drug therapies.

Abbreviations

APD

action potential duration

BCL

Basic Cycle Length

CaMKII

Ca²⁺/calmodulin‐dependent protein kinase

CASQ2

calsequestrin

CPVT

catecholaminergic polymorphic ventricular tachycardia

DAD

delayed afterdepolarizations

EAD

early afterdepolarizations

ICD

implantable cardioverter defibrillator

ISO

isoproterenol

KO

knockout

PKA

cAMP‐dependent protein kinase

PMF

potential of mean force

P_o

open probability

RyR2

ryanodine receptor

SCaR

spontaneous Ca²⁺ release event

T_c

mean closed time

T_o

mean open time

TB

tonic block

VT

ventricular tachycardia

WT

wild‐type

Introduction

First‐line pharmacotherapy for treating catecholaminergic polymorphic ventricular tachycardia (CPVT) patients utilizes β‐blockade at maximally tolerated doses; however, 30% of patients continue to experience arrhythmic episodes and often require mechanical implantable cardioverter defibrillator (ICD) implantation (Liu et al. 2008). β‐Blockade is associated with fatigue, diminished physical activity level and reduced quality of life, while ICD discharge is associated with significant pain and anxiety, which can induce additional episodes of electrical storm (Sears et al. 1999; Nakamura et al. 2007).

CPVT is an inherited arrhythmia syndrome arising from mutations in the ryanodine receptor (RyR2) as well as the calcium buffer and regulator of RyR2, calsequestrin (CASQ2). As its name suggests, CPVT sets up a pathological substrate for arrhythmogenesis under the influence of a catecholamine surge, which leads to bidirectional and polymorphic ventricular tachycardia. Sudden cardiac arrest and death are not uncommon for individuals harbouring CPVT mutations, and a lethal episode may present as the first manifestation of disease (Priori et al. 2002).

Flecainide, a class IC antiarrhythmic suppresses the emergence of CPVT in both mice harbouring the CASQ2(−/−) mutation and humans with either a CASQ2 or RYR2 (S412G) mutation (Watanabe et al. 2009; van der Werf et al. 2011). However, the mechanism and efficacy of flecainide remain disputed. For example, Katz et al. (2010) found little efficacy for CASQ2 subtypes, while Liu et al. suggested virtually no effect on Ca²⁺ handling properties, rather proposing that flecainide is effective due to its Na⁺ channel blocking properties (Watanabe et al. 2011; Liu et al. 2011 a). Still other studies demonstrated flecainide interaction and blockade of RyR2 (Hilliard et al. 2010; Galimberti & Knollmann, 2011; Mehra et al. 2014).

Studies of other class I antiarrhythmics showed that only those that modulated RyR2 activity demonstrated efficacy in models of CPVT, including propafenone (Hwang et al. 2011). Moreover, the type of interaction with the RyR2 was found to be significant as well; tetracaine, an RyR2 closed state blocker, failed to regulate Ca²⁺ properties in a CASQ2(−/−) model of CPVT (Galimberti & Knollmann, 2011). The late Na⁺ channel blocker ranolazine has also been studied for treatment of CPVT; however, two studies reveal conflicting results: Parikh et al. (2012) demonstrated strong interaction between ranolazine and RyR2, whereas Galimberti & Knollmann (2011) failed to demonstrate such an interaction.

Discrepant experimental observations, likely to be due to different experimental set‐ups and models of CPVT, make reconciling the aforementioned studies difficult. Thus, the focus of the present study is to use a computational modelling approach to understand the dominant mechanism(s) underlying antiarrhythmic drug success and failure. In particular, is the effect of flecainide to normalize aberrant Na⁺ channel activation sufficient to explain observed clinical efficacy? The latter would be particularly important, given the wealth of clinical (The Cardiac Arrhythmia Suppression Trial (CAST) Investigators, 1989; Nakamura et al. 2007) and experimental data (Moreno et al. 2011) that reveal flecainide‐induced proarrhythmia. Finally, can we use the model as a therapeutic prediction tool to optimize a multidrug regimen in CPVT?

Methods

Ethics approval

Animal use was approved by the Institutional Animal Care and Use Committee, Baylor College of Medicine, and conformed to the Guide for the Care and Use of Laboratory Animals (National Research Council, 2011).

Experimental methods

Eight animals (six R176Q/+ and two wild‐type (WT)) were studied with ECG telemetry as previously described (van Oort et al. 2010). Telemeters (Data Sciences International, St Paul, MN, USA) were implanted in the abdominal cavity with subcutaneous lead placement in a lead II configuration. Following telemetry implantation, mice were injected with subcutaneous 0.3 mg kg⁻¹ buprenorphine. The isoflurane was discontinued and mice were placed on a warming pad with blow‐by oxygen. They were observed continuously until awake with normal breathing pattern and spontaneous movement. The mice were observed continuously for the first 2 h then daily for 7 days. Buprenophine, 0.2–0.3 mg kg⁻¹ subcutaneous injection, was provided every 6–12 h for the first 24 h. Ambulatory telemetry recordings were obtained after all animals had at least 7 days’ recovery from surgery and a 24 h baseline recording. Repeat baseline recordings were obtained 15 min prior to all injections. Mice were injected with a single intraperitoneal (i.p.) dose of adrenaline (120 mg kg⁻¹, Sigma‐Aldrich, St Louise, MO, USA) and caffeine (120 mg kg⁻¹, Avantor Performance Materials, Center Valley, PA, USA) in sterile saline followed by continuous 24 h telemetry recordings. After a 7 day wash‐out period, all mice underwent repeated injections with pretreatment. Baseline ECG telemetry was recorded for 15 min. Separate i.p. injections were given of flecainide (12 mg kg⁻¹, Sigma‐Aldrich), metoprolol (10 mg kg⁻¹, Sigma‐Aldrich) and KN‐93 (30 μmol kg⁻¹, Calbiochem). All drugs were mixed in sterile water. After 30 min, mice were injected with a single i.p. dose of adrenaline (2 mg kg⁻¹) and caffeine (120 mg kg⁻¹). Following injection of adrenaline and caffeine, the mice were monitored by telemetry for a total of 8 h. Data collection was performed using Dataquest A.R.T. version 4.31 (Data Sciences International, St Paul, MN, USA). Off‐line analysis was performed by ECG Auto analysis version 3.1 (EMKA technologies, Falls Church, VA, USA).

Molecular dynamics and free energy simulations

Force‐field parameters for flecainide were developed using the general automated atomic model parameterization (GAAMP) server developed by Huang & Roux (2013). Briefly, all geometry optimization, charge fitting and torsional parameter fitting were done using B3LYP functional at the 6–31G*(2d,2p) level of theory. Umbrella sampling simulations for partitioning of the neutral and cationic forms of flecainide into model POPE bilayer (128 lipids) were performed using a protocol described previously by Li et al. (2008). Harmonic constraints of 5 kcal (mol Å²)⁻¹ were applied to the drug's centre of mass along the reaction coordinate spanning 62 Å from −31 Å to 31 Å normal to the membrane plane. We used five starting conformations for the drug and 124 windows spaced every 0.5 Å to describe drug partitioning into the bilayer. A flat‐bottomed cylindrical restraint with R = 15 Å was used to confine drug in the xy plane along the reaction coordinate. It allows for good sampling in a lateral plane. Each potential of mean force (PMF) window was equilibrated for 2.5 ns in the presence of restraining potential and then subjected to a 5 ns production run. The resulting 1D PMF was reconstructed with the weighted histogram analysis method (WHAM) (Roux, 1995). The WHAM convergence tolerance was set at 0.0001 kcal mol⁻¹. We used symmetrized density to compute resulting PMFs. The statistical uncertainties were estimated by separating the data into seven blocks and were found to be within ±1.5 kcal mol⁻¹ for neutral and charged forms of flecainide, respectively.

Computational ventricular myocyte models

Briefly, we developed mouse and rabbit in silico models of catecholaminergic polymorphic ventricular tachycardia (CPVT) by ‘knocking out’ the SR Ca²⁺ buffer calsequestrin (Kornyeyev et al. 2012) in the Morotti–Grandi mouse cardiac cell model (Morotti et al. 2014) and in the Soltis–Saucerman rabbit cardiac cell model (Soltis & Saucerman, 2010), respectively. Flecainide interactions with the ryanodine receptor were modelled assuming open state associations (Hilliard et al. 2010). We also incorporated the model of the cardiac Na⁺ channel and I _Kr and their interaction with flecainide as previously (Moreno et al. 2011, 2013). We utilized the Morotti–Grandi computational model for mouse (Morotti et al. 2014) and the Soltis–Saucerman computational model for rabbit (Soltis & Saucerman, 2010), which included all the relevant components required for a detailed analysis, including accurate cellular electrophysiology, Ca²⁺ handling (Shannon et al. 2004) and the cAMP‐dependent protein kinase (PKA) (Saucerman et al. 2003) and Ca²⁺/calmodulin‐dependent protein kinase (CaMKII) (Soltis & Saucerman, 2010) phosphorylation pathways. The computational model for flecainide interaction with the cardiac Na⁺ channel is from (Moreno et al. 2011), with adaptations designed to recreate the CPVT phenotype and flecainide's interaction with the RyR2, informed and validated by experimental data (Hilliard et al. 2010; Hwang et al. 2011).

Wild‐type Na⁺ channel models and inclusion of drug binding

The wild‐type drug‐free Na⁺ channel model was used as previously described (Moreno et al. 2013). The Na⁺ drug‐channel model parameters for the on‐ and off‐rates of flecainide, ranolazine and lidocaine are taken from experiments where available. These include diffusion rates that indicate drug on‐rates ‘k _on’ = [drug] × D (diffusion rate) and affinities (K _d) to discrete conformations that determine drug off‐rates ‘k _off’ = K _d × D (diffusion rate). Rates were also constrained by experimental data (described in detail below) and microscopic reversibility as in Colquhoun et al. (2004). The transition rates are given in Table 1.

Table 1.

Markov model transition rates (ms⁻¹) for Drug free WT Na⁺ channel

States of Markov model	Rate constants
IC3 →IC2, C3→C2, BC3→BC2	α11 = 8.5539/(7.4392e‐2*exp(‐V/17.0)+2.0373e‐1*exp(‐V/150))
IC2→IF, C2→C1, BC2→BC1	α12 = 8.5539/(7.4392e‐2*exp(‐V/15.0)+2.0373e‐1*exp(‐V/150))
C1→O, BC1→BO	α13 = 8.5539/(7.4392e‐2*exp(‐V/12.0)+2.0373e‐1*exp(‐V/150))
IC2→IC3, C2→C3, BC2→BC3	β11 = 7.5215e‐2*exp(‐V/20.3)
IF→IC2, C1→C2, BC1→BC2	β12 = 2.7574*exp(‐(V‐5)/20.3)
O→C1, BO→BC1	β13 = 4.7755e‐1*exp(‐(V‐10)/20.3)
IC3→C3, IC2→C2, IF→C1	α3 = 5.1458e‐6*exp(‐V/8.2471)
C3→IC3, C2→IC2, C1→IF	β3 = 6.1205*exp(V/13.542)
O→IF	α2 = 13.370*exp(V/43.749)
IF→O	β2 = (α13* α2* α3)/(β13* β3)
O→IS	αx = 3.4229e‐2*α2
IS→O	βx = 1.7898e‐2*α3
C3, C2, C1, O → BC3, BC2, BC1, BO	μ1 = 2.0462e‐7
BC3, BC2, BC1, BO → C3, C2, C1,O	μ2 = 8.9731e‐4

Flecainide

The flecainide model was used as previously described (Moreno et al. 2011), but now includes a drug‐bound bursting regime (drug binding to red states as indicated in Scheme 1; Tope 8 states are ‘normal’ gating mode, while red states indicate burst mode). Rate constants in the upper (normal mode) states are from

Scheme 1

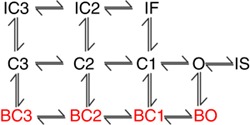
Moreno et al. (2011). Bursting state affinity for the charged form of flecainide was initially set at the value found by assuming the affinity of tonic block of late I _Na was equal to K _d at −100 mV. The value for K _d,0 was then calculated and used as an initial value in the optimization. For example, the affinity of tonic block (TB) I _Na,L for WT is ∼44 μM (Nagatomo et al. 2000); if that value is assumed to equal K _d,−100mV, K _d,0,bursting was initially set at 3.202 μM (e.g. the K _d,0,bursting that would give K _{d,−100mV,bursting} = 44 μM). The optimized K _d,0,bursting was 95.2165 μM. Full parameters are given in Table 2.

Table 2.

Markov model transition rates (ms⁻¹) for Flecainide

Parameter Name	Value
kon = kclosed, on	[D+]*Diffusion
koff = kclosed, off	kd, open *Diffusion; (kdopen = 11.2e‐6*exp(‐0.7*V*F/R*T))
kbursting, on = kclosed bursting, on	[D+]*Diffusion
kbursting, off = kclosed bursting, off	kdBursting,Open *Diffusion; (kdBursting,Open = 95.2165e‐6*exp(‐0.7*V*F/R*T))
kneutral, on	[D]*Diffusion
kneutral, off	400e‐6*Diffusion
kneutral, inactivated, on	kneutral, on/2
kneutral, inactivated, off	5.4e‐6*Diffusion
kneutral, closed, on	kneutral, on/2
kneutral, closed, off	800e‐6*Diffusion
Diffusion	5500 M−1ms−1
States of Markov model	Rate constants
D+IC3 →D+IC2, D+C3→D+C2,	α11
DIC3 →DIC2, DC3→DC2
D+IC2→D+IF, D+C2→D+C1,	α12
DIC2→DIF, DC2→DC1
D+IC2→D+IC3, D+C2→D+C3,	β11
DIC2→DIC3, DC2→DC3
D+IF→D+IC2, D+C1→D+C2,	β12
DIF→DIC2, DC1→DC2
D+O→D+IS	αx1 = 5.7839e‐5*αx
D+IS→D+O	βx1 = 1.6689e‐8 *βx
DO→DIS	αx2 = 2.6126e‐1 *αx
D+C1→D+O	α13c = 3.6324e‐3*α13
DC1→DO	α13n = 2.6452e+0*α13
D+O→D+C1	β13c = (β13*kcon*koff*α13c)/(kon*kcoff*α13)
DO→DC1	β13n = (β13*kc_on*α13n*k_off)/(kc_off*α13*k_on)
DIS→DO	βx2 = (βx*k_on* αx2*ki_off)/(αx*ki_on*k_off)
D+O→D+IF	α22 = 1.4847e+3 *α2
DO→DIF	α_22 = 4.2385e+1 *α2
D+IF→D+O	β22 = (α13c* α22* α33)/(β13c* β33)
DIF→DO	β_22 = (α_33*α13n*α_22)/(β_33*β13n)
D+C3→D+IC3, D+C2→D+IC2, D+C1→D+IF	β33 = 1.7352e‐6 *β3
DC3→DIC3, DC2→DIC2, DC1→DIF	β_33 = 2.1181e+0*β3
D+IC3→D+C3, D+IC2→D+C2, D+IF→D+C1	α33 = 6.7505e‐5 *α3
DIC3→DC3, DIC2→DC2, DIF→DC1	α_33 = (ki_off* α3*kc_on* β_33)/(ki_on*kc_off* β3)
D+IF→D+IT	α44 = 2.4135* α2
D+IT→D+IF	β44 = 4.9001e‐2 *α3
DIF→DIT	α_44 = 1.0326e‐3 *α2
DIT→DIF	β_44 = 2.1378e‐2 *α3

Ranolazine

The ranolazine–Na⁺ channel drug interaction model was as previously described (Moreno et al. 2013) and the transition rates are given in Table 3.

Table 3.

Markov model transition rates (ms⁻¹) for Ranolazine

Parameter Name	Value
kon = kclosed, on	[D+]*Diffusion
koff = kclosed, off	kd, open *Diffusion; (kdopen = 100.5e‐6*exp(‐0.7*V*F/R*T))
kbursting, on = kclosed bursting, on	[D+]*Diffusion
kbursting, off = kclosed bursting, off	kdBursting,Open *Diffusion; (kdBursting,Open = 1.5012e‐6*exp(‐0.7*V*F/R*T))
kneutral, on	[D]*Diffusion
kneutral, off	400e‐6*Diffusion
kneutral, inactivated, on	kneutral, on
kneutral, inactivated, off	5.4e‐6*Diffusion
kneutral, closed, on	kneutral, on
kneutral, closed, off	800e‐6*Diffusion
Diffusion	5500 M−1ms−1
States of Markov model	Rate constants
D+IC3 →D+IC2, D+C3→D+C2,	α11
DIC3 →DIC2, DC3→DC2
D+IC2→D+IF, D+C2→D+C1,	α12
DIC2→DIF, DC2→DC1
D+IC2→D+IC3, D+C2→D+C3,	β11
DIC2→DIC3, DC2→DC3
D+IF→D+IC2, D+C1→D+C2,	β12
DIF→DIC2, DC1→DC2
D+O→D+IS	αx1 = 4.4923e+3 *αx
D+IS→D+O	βx1 = 2.7031e‐1 *βx
DO→DIS	αx2 = 1.4947e+1 *αx
D+C1→D+O	α13c = 3.6811*α13
DC1→DO	α13n = 2.3570e+2*α13
D+O→D+C1	β13c = (β13*kcon*koff*α13c)/(kon*kcoff*α13)
DO→DC1	β13n = (β13*kc_on*α13n*k_off)/(kc_off*α13*k_on)
DIS→DO	βx2 = (βx*k_on* αx2*ki_off)/(αx*ki_on*k_off)
D+O→D+IF	α22 = 6.8705e+4 *α2
DO→DIF	α_22 = 2.1182e+2 *α2
D+IF→D+O	β22 = (α13c* α22* α33)/(β13c* β33)
DIF→DO	β_22 = (α_33*α13n*α_22)/(β_33*β13n)
D+C3→D+IC3, D+C2→D+IC2, D+C1→D+IF	β33 = 1.7561e‐1 *β3
DC3→DIC3, DC2→DIC2, DC1→DIF	β_33 = 1.2197e‐3*β3
D+IC3→D+C3, D+IC2→D+C2, D+IF→D+C1	α33 = 4.0832e‐2 *α3
DIC3→DC3, DIC2→DC2, DIF→DC1	α_33 = (ki_off* α3*kc_on* β_33)/(ki_on*kc_off* β3)

Lidocaine

The wild‐type lidocaine model was as previously described (Moreno et al. 2011), but now includes a drug‐bound bursting (lower 4 states) regime. Non‐bursting rates were from (Moreno et al. 2011). Bursting state affinity for the charged form of lidocaine was initially set at the value found by assuming the affinity of tonic block of late I _Na was equal to K _d at −100 mV. K _d,0 was then calculated and used as an initial value in the optimization. For example, the affinity of TB I _Na,L for WT is ∼12 μM (Fedida et al. 2006); if that value is assumed to equal K _d,−100mV, K _d,0,bursting was initially set at 0.80 μM (e.g. the K _d,0,bursting that would give K _{d,−100mV,bursting} = 12 μM). The optimized K _d,0,bursting was 0.9810 μM. The transition rates are given in Table 4.

Table 4.

Markov model transition rates (ms⁻¹) for Lidocaine

Parameter Name	Value
kon = kclosed, on	[D+]*Diffusion
koff = kclosed, off	kd, open *Diffusion; (kdopen = 318e‐6*exp(‐0.7*V*F/R*T))
kbursting, on = kclosed bursting, on	[D+]*Diffusion
kbursting, off = kclosed bursting, off	kdBursting,Open *Diffusion; (kdBursting,Open = 0.981e‐6*exp(‐0.7*V*F/R*T))
kneutral, on	[D]*Diffusion
kneutral, off	400e‐6*Diffusion
kneutral, inactivated, on	kneutral, on/2
kneutral, inactivated, off	3.4e‐6*Diffusion
kneutral, closed, on	kneutral, on/2
kneutral, closed, off	900e‐6*Diffusion
Diffusion	500 M−1ms−1
States of Markov model	Parameters
D+IC3 →D+IC2, D+C3→D+C2,	α11
DIC3 →DIC2, DC3→DC2
D+IC2→D+IF, D+C2→D+C1,	α12
DIC2→DIF, DC2→DC1
D+IC2→D+IC3, D+C2→D+C3,	β11
DIC2→DIC3, DC2→DC3
D+IF→D+IC2, D+C1→D+C2,	β12
DIF→DIC2, DC1→DC2
D+O→D+IS	αx1 = 6.3992e‐7*αx
D+IS→D+O	βx1 = 1.3511e+0 *βx
DO→DIS	αx2 = 1.3110e‐1 *αx
D+C1→D+O	α13c = 5.6974e‐3* α13
DC1→DO	α13n = 8.4559e+1*α13
D+O→D+C1	β13c = (β13*kcon*koff*α13c)/(kon*kcoff*α13)
DO→DC1	β13n = (β13*kc_on*α13n*k_off)/(kc_off*α13*k_on)
DIS→DO	βx2 = (βx*k_on* αx2*ki_off)/(αx*ki_on*k_off)
D+O→D+IF	α22 = 6.7067e‐6 *α2
DO→DIF	α_22 = 1.7084e‐5 *α2
D+IF→D+O	β22 = (α13c* α22* α33)/(β13c* β33)
DIF→DO	β_22 = (α_33*α13n*α_22)/(β_33*β13n)
D+C3→D+IC3, D+C2→D+IC2, D+C1→D+IF	β33 = 1.9698e‐5 *β3
DC3→DIC3, DC2→DIC2, DC1→DIF	β_33 = 4.8477e+0*β3
D+IC3→D+C3, D+IC2→D+C2, D+IF→D+C1	α33 = 3.2976e+0 *α3
DIC3→DC3, DIC2→DC2, DIF→DC1	α_33 = (ki_off* α3*kc_on* β_33)/(ki_on*kc_off* β3)

RyR2–flecainide drug‐channel interaction model development

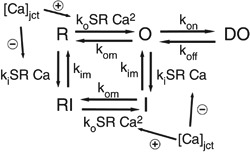
The Shannon–Bers Markov model formulation of the RyR2 (Shannon et al. 2004) was modified to include a drug bound state DO with transitions k _on = D × [drug] and k _off = D × IC_50,drug to and from the open state O, which represent the drug diffusing to the receptor and binding or dissociating from the channel, respectively, as done previously (Moreno et al. 2011). The diffusion rate of flecainide (Scheme 2) was estimated at 5500 M⁻¹ ms⁻¹ (Zhu et al. 2006).

Scheme 2

Isoproterenol‐stimulated Ca²⁺ waves in CASQ2 knockout (KO) CASQ2(−/−) mice were inhibited by flecainide with an IC₅₀ of 2.0 ± 0.2 μM (Hwang et al. 2011), while other experimental preparations measured an IC₅₀ range from 2 to 17 μM (Brunton et al. 2010; Hilliard et al. 2010; Hwang et al. 2011; Mehra et al. 2014). Drug binding was modelled as open‐state block, using experimental data for drug affinity to the open state to determine off and on rates, respectively. We also predicted cases for variable flecainide IC₅₀ = 3, 4, and 5 μM shown in Fig. 1. We examined the cases of 3, 4 and 5 μM of IC₅₀ acting on each of the targets under the influence of 1 μM isoproterenol, over a range of clinically relevant pacing frequencies, from 0.5 to 3.0 Hz (30–180 beat min⁻¹; Leenhardt et al. 1995), at 0.01 Hz increments.

Figure 1. Testing IC₅₀ of flecainide in the cell model for I_Na, RyR2 and both targets in combination .

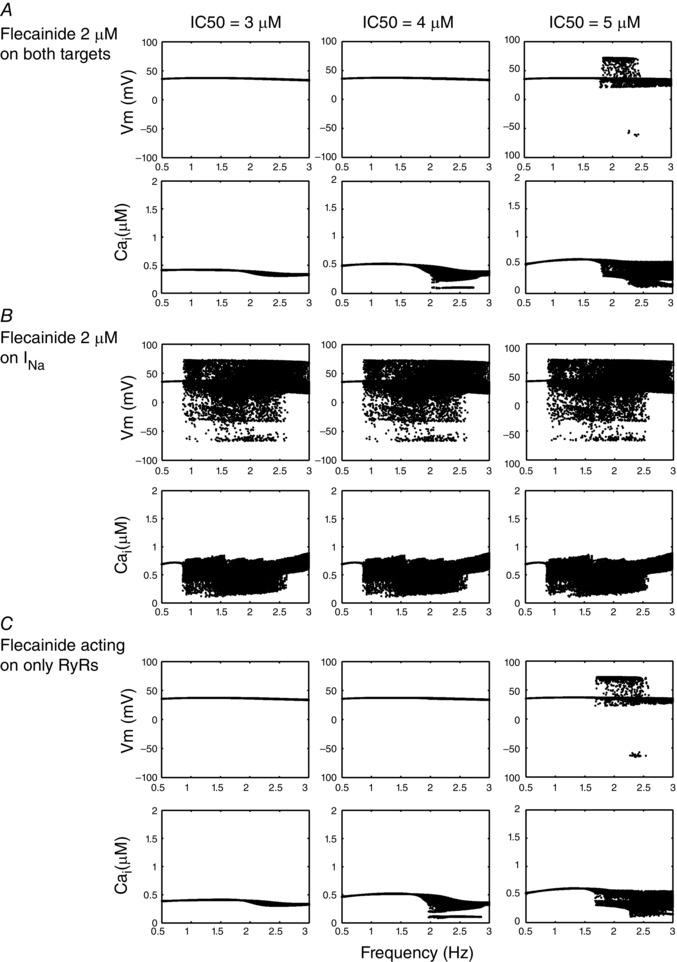
Voltage dynamics is shown for each IC₅₀ case, and the voltage and Ca²⁺ transient maxima are binned for each pacing frequency between 0.5 and 3 Hz during the second half of a 2 min simulation time course. A, CASQ2(−/−) myocytes with 3, 4 and 5 μM IC₅₀ effects on both Na⁺ channels and RyRs. B, flecainide interaction with just Na⁺ channels. C, flecainide concentrations acting on only RyRs.

We assumed rapid partitioning of flecainide into its charged (98% at pH 7.4, pK _a = 9.3) and neutral (2%) fractions (Liu et al. 2003), diffusion of the neutral component across the membrane, and equilibration on the cytosolic side, resulting in equimolar concentrations of flecainide inside and outside of the cell, consistent with experimental observations and the mechanism of flecainide's interaction with the Na⁺ channel (Liu et al. 2003). The kinetics of the state transitions for the channel are adjusted for temperature by a Q ₁₀ factor of 1.5 (Sitsapesan et al. 1991). The presence of a 20% RyR subconductance state in response to flecainide binding of the channel (Hilliard et al. 2010) is modelled at the whole cell level as a reduction to 20% maximal conductance of the channel.

In single channel simulations mimicking the experimental conditions tested, the IC₅₀ of 16 μM was used to validate the model. It is important, however, to justify the use of the 2 μM IC₅₀ value used in cellular and tissue level simulations. The 16 μM IC₅₀ value corresponds to single channel conditions (Hilliard et al. 2010), which does not account for the influence of coupling between adjacent ryanodine receptors on the kinetics of the channel (Marx et al. 2001). Similarly, the IC₅₀ value of 16 μM for spark inhibition in permeabilized myocytes cannot be used, due to the constant maintenance of [Ca²⁺] in those experiments – the high concentration of Ca²⁺ used to elicit consistent Ca²⁺ sparks in experiments is static and is an unrealistic representation of paced myocytes (Galimberti & Knollmann, 2011). The high external Ca²⁺ concentration used would cause a higher IC₅₀ than that seen using a lower Ca²⁺ concentration in the intact myocyte used to generate Ca²⁺ waves during diastole, due to a persistently overactive ryanodine receptor by constitutive cytosolic activation.

Thus the measured IC₅₀ for wave inhibition in the isoproterenol‐stimulated Ca²⁺ waves in CASQ2(−/−) mice (IC₅₀ = 2.0 ± 0.2 μM; Hwang et al. 2011), was used, since it reflects realistic conditions for our model system. Its weakness is that the IC₅₀ does not separate out external contributions to the IC₅₀, such as lowered junctional Ca²⁺ by I _NCX activity via lowered [Na⁺]. Experiments in paced rat myocytes indicate that this contribution may significantly influence flecainide's ability to inhibit spontaneous Ca²⁺ wave formation, and thus future work will need to evaluate whether the contribution of I _NCX regulation of Na⁺ is indeed significant in influencing flecainide's efficacy (Sikkel et al. 2013).

$$\begin{array}{ccc}\hfill k_{\mathrm{CaSR}}& =& \mathrm{Ma}{\mathrm{x}}_{\mathrm{SR}}-\frac{\mathrm{Ma}{\mathrm{x}}_{\mathrm{SR}}-\mathrm{Mi}{\mathrm{n}}_{\mathrm{SR}}}{1+{\left(\frac{\mathrm{E}{\mathrm{C}}_{50,\mathrm{SR}}}{{\left[\mathrm{Ca}\right]}_{\mathrm{SR}}}\right)}_{\mathrm{SR}}^H}\hfill \\ \hfill k_{\mathrm{oSRCa}}& =& \frac{k_{\mathrm{oCa}}}{k_{\mathrm{CaSR}}}\hfill \\ \hfill k_{\mathrm{iSRCa}}& =& k_{\mathrm{iCa}}{k}_{\mathrm{CaSR}}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \frac{\mathrm{dR}}{\mathrm{d}t}& =& \left(k_{\mathrm{im}}\mathrm{RI}-k_{\mathrm{iSRCa}}{\left[\mathrm{Ca}\right]}_{\mathrm{jct}}\mathrm{R}\right)-\left(k_{\mathrm{oSRCa}}{\left[\mathrm{Ca}\right]}_{\mathrm{jct}}^2\mathrm{R}-k_{\mathrm{om}}\mathrm{O}\right)\hfill \\ \hfill \frac{\mathrm{dO}}{\mathrm{d}t}& =& \left(k_{\mathrm{oSRCa}}{\left[\mathrm{Ca}\right]}_{\mathrm{jct}}^2\mathrm{R}-k_{\mathrm{om}}\mathrm{O}\right)-\left(k_{\mathrm{iSRCa}}{\left[\mathrm{Ca}\right]}_{\mathrm{jct}}\mathrm{O}-k_{\mathrm{im}}\mathrm{I}\right)\hfill \\ & & -(k_{\mathrm{on}}\mathrm{O}-k_{\mathrm{off}}\mathrm{DO})\hfill \\ \hfill \frac{\mathrm{dI}}{\mathrm{d}t}& =& \left(k_{\mathrm{iSRCa}}{\left[\mathrm{Ca}\right]}_{\mathrm{jct}}\mathrm{O}-k_{\mathrm{im}}\mathrm{I}\right)-\left(k_{\mathrm{om}}\mathrm{I}-k_{\mathrm{oSRCa}}{\left[\mathrm{Ca}\right]}_{\mathrm{jct}}^2\mathrm{RI}\right)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \frac{\mathrm{dDO}}{\mathrm{d}t}& =& k_{\mathrm{on}}\mathrm{O}-k_{\mathrm{off}}\mathrm{DO}\hfill \\ \hfill \mathrm{RI}& =& \left(k_{\mathrm{om}}\mathrm{I}-k_{\mathrm{oSRCa}}{\left[\mathrm{Ca}\right]}_{\mathrm{jct}}^2\mathrm{RI}\right)\hfill \\ & & -\left(k_{\mathrm{im}}\mathrm{RI}-k_{\mathrm{iSRCa}}{\left[\mathrm{Ca}\right]}_{\mathrm{jct}}\mathrm{R}\right)\hfill \\ \hfill J_{\mathrm{SRCaRel}}& =& k_{\mathrm{s}}\left(\mathrm{O}+0.2\times \mathrm{DO}\right)\times \left({\left[\mathrm{Ca}\right]}_{\mathrm{SR}}-{\left[\mathrm{Ca}\right]}_{\mathrm{jct}}\right)\hfill \\ \hfill J_{\mathrm{SRLeak}}& =& K_{\mathrm{SRleak}}\left({\left[\mathrm{Ca}\right]}_{\mathrm{SR}}-{\left[\mathrm{Ca}\right]}_{\mathrm{jct}}\right)\hfill \end{array}$$

The parameters are presented in Table 5.

Table 5.

Parameters for SR Ca²⁺ release

Parameter Name	Value / Units
kon	[D+]*Diffusion
koff	0.011
Diffusion	5500 M−1ms−1
ks	25 ms−1
koCa	10 mM−2ms−1
kom	0.06 ms−1
kiCa	0.5 mM−1ms−1
kim	0.005 ms−1
EC50‐SR	0.45 mM
MaxSR	15
MinSR	1
HSR	2.5
KSRleak	5.348e‐6 ms−1

Simulation of I _Kr blockade

To simulate the effects of flecainide or ranolazine on I _Kr current, we decreased the peak conductance, G _IKr in a concentration dependent fashion using a concentration–response relationship with a Hill coefficient of 1 (n = 1) as follows:

$$G_{\mathrm{IKr}}=G_{\mathrm{IKr},\max }\times \left(\frac{1}{1+{\left(\left[\mathrm{Drug}\right]/\mathrm{I}{\mathrm{C}}_{50}\right)}^n}\right)$$

where G _IKr,max is the nominal conductance value from the given rabbit ventricular myocyte model (Soltis & Saucerman, 2010) and IC₅₀ is the concentration of drug that produces a 50% inhibition of I _Kr current. The IC₅₀ values for the drug to inhibit I _Kr current are for flecainide 1.5 μM (Belardinelli et al. 2013) and for ranolazine 12 μM (Rajamani et al. 2008).

Simulation of effect of metoprolol on β‐adrenergic activity and CaMKII blocking effects of KN‐62

We modelled the β₁ and CaMKII blocking effects of metoprolol (IC₅₀ = 105 nM) and KN‐62 (IC₅₀ = 468 nM) as a competitive inhibitor of β‐agonist and limiter of free endogenous total CaMKII, respectively. Dose–response curves (Fig. 2) for the effect of metoprolol on β‐adrenergic activity were extracted from an E _max experimental model (Abrahamsson et al. 1990), where the percentage inhibition of E _max represents the fraction of ISO inhibition. In preliminary tests of the computational model involving myocyte pacing, 50 nM ISO achieved 98% of the maximal response to agonist; ISO inhibition was therefore modelled as a percentage of 50 nM applied ISO. Thus, in Fig. 2 A, percentage β₁‐receptor blockade refers to the percentage of β₁‐receptors that are competitively blocked by metoprolol. KN‐62 was modelled as an inhibitor of endogenously available CaMKII (Tokumitsu et al. 1990). Dose–response data were obtained from Davies et al. (2000) and fitted to a percentage block of CaMKII for given doses of KN‐62; similarly, percentage CaMKII inhibition in Fig. 2 B refers to the percentage of endogenous CaMKII that is inhibited by KN‐62. Data are from Abrahamsson et al. (1990) (metoprolol) and Tokumitsu et al. (1990) (KN‐62). We applied the E _max model from Abrahamsson et al. (1990) to determine our dose–response relation as follows:

$$\%\beta -\mathrm{Blockade}\mathrm{or}\%\mathrm{CaMKII}\mathrm{inhibition}=\frac{E_{\max }\times C}{\mathrm{I}{\mathrm{C}}_{50}+C}$$

where E _max = 100%, and C is the metoprolol or KN‐62 concentration.

Figure 2. Dose–response curves for metoprolol on β₁‐receptor blockade and KN‐62 on CaMKII inhibition .

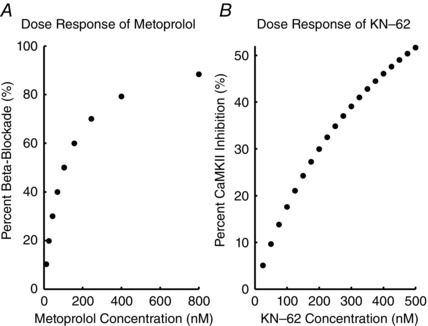
A, dose–response curves for the effect of metoprolol on β‐adrenergic activity were extracted from an experimental model (Abrahamsson et al. 1990). B, dose–response data were obtained from (Davies et al. 2000) and fitted to a percentage block of CaMKII for given doses of KN‐62.

CPVT CASQ2(−/−) model development

The CPVT phenotype was modelled via a computational CASQ2(−/−) (Knollmann et al. 2006) by modifying the Soltis–Saucerman model (Soltis & Saucerman, 2010). We set the calsequestrin buffer concentration and the time derivative of the calsequestrin buffer concentration to 0. While this has no direct effect on regulating RyR2 function, it was expected to still demonstrate a functional effect on RyR2 activity because of alterations to intracellular SR Ca²⁺. Equations for the regulation of Na⁺/K⁺‐ATPase activity by PKA as mediated by phospholemman were incorporated from the Yang–Saucerman model (Yang & Saucerman, 2012). Our previously validated Na⁺ channel (Moreno et al. 2011) and modified RyR2 channel were inserted into the cellular model (Soltis & Saucerman, 2010).

Stochastic single channel RyR2 simulations

Individual RyR2 channels were modelled stochastically in Monte Carlo simulations using Gillespie's algorithm (Gillespie, 1977). Parameters were constrained by fixed concentrations of flecainide (0 and 50 μM), luminal Ca²⁺ (1 mM), and junctional Ca²⁺ (0.1 μM), mimicking experimental conditions (Hwang et al. 2011). Stochastic error diminishes over a large number of simulations, approaching the expected mean open time (T _o), mean closed time (T _c), and open probability (P _o) as derived by the methods of Colquhoun & Hawkes (1981).

Cellular and tissue simulations

Mouse ventricular myocyte model

The I _Na channel was replaced in the Morotti–Grandi mouse cardiac cell model (Morotti et al. 2014) with our published Markov model (Moreno et al. 2013). We then adjusted three transition rates for the mouse model to simulate the mouse I _Na kinetics as follows: O→C1, β₁₃ × 0.45; O→IF, α₂ × 0.45; O→IS, α_x × 0.45. Virtual myocytes were paced using a −9.5 pA pF⁻¹ current stimulus for 5 ms in single cells for 150 s at 2 Hz pacing frequency in the presence and absence of drug and 0.5 μM isoproterenol (ISO).

Rabbit ventricular myocyte model

Virtual whole cells and tissues (both WT and KO) were allowed to ‘rest’ without external stimuli for 10 min to establish initial conditions. Cells were then virtually paced (using a −80 pA pF⁻¹ current stimulus for 0.5 ms in single cells and −500 pA pF⁻¹ stimulus for 2.0 ms in tissues) for 5 min at specific pacing frequencies in the absence of drug or agonist. Cells were finally paced for an additional 2 min in the presence and absence of drug and 1 μM ISO. Parameters including upstroke velocity, action potential duration (APD) and the number of early and delayed afterdepolarizations (EADs and DADs) were tracked over the course of each simulation.

One‐dimensional (1D) tissue was simulated as a fibre of 165 cells (1.65 cm) (Glukhov et al. 2010) with reflective boundary conditions. Transmural heterogeneity was incorporated into the tissue by a linear decrease to 25% maximal I _to conductance (Myles et al. 2010), corresponding to a linear transition from epicardial to endocardial tissue (Fedida & Giles, 1991) and an APD gradient of 205–224 ms. The diffusion coefficient D_x was set to 0.002 cm² ms⁻¹ to establish a conduction velocity of 61–73 cm s⁻¹ (epicardium–endocardium in WT conditions) (Brugada et al. 1990).

Code for simulations and analysis was written in C++ and MATLAB 2014a (The Math Works, Inc., Natick, MA, USA). Code was run on an Apple Mac Pro machine with two 2.93 GHz 6‐Core Intel Xeon processors, and an HP ProLiant DL585 G7 server with a 2.3 GHz 48‐core AMD Opteron processor. Code was compiled with the Intel ICC compiler 2013. Numerical results were visualized using MATLAB R2014b. All source code used in this paper is available online or can be obtained by emailing ceclancy@ucdavis.edu.

Results

We modelled the interaction between flecainide and RyR2 by modifying the Shannon–Bers model of the cardiac RyR2 channel (Shannon et al. 2004) (see Methods) that reproduces gain and fractional SR Ca²⁺ release, and includes regulation by both luminal and junctional Ca²⁺ fractions. Based on experimental data, drug binding was modelled as voltage‐independent open‐state block that results in a ∼20% subconductance state (Hilliard et al. 2010; Hwang et al. 2011; Mehra et al. 2014). A different recent study suggested that flecainide does not block the RyR (Bannister et al. 2015). These effects are also included in the cellular level simulations as no RyR block by flecainide.

This assumption resulted in predictions of drug effects that were consistent with experiments in single channel lipid bilayer studies (Hilliard et al. 2010). Stochastic Monte Carlo simulations reveal intermittent closures that interrupt channel openings, corresponding to flecainide binding and unbinding the open‐state (Fig. 3 A) (Hwang et al. 2011). Figure 3 B shows model predictions (lines) closely match experimental measurements (symbols) of drug concentration‐dependent effects on channel open probability (left) and channel mean open time (middle) (Hwang et al. 2011). Mean closed time displays no dose dependence in this binding scheme, as in experimental findings (Fig. 3 B, right). We modelled flecainide interactions with the Na⁺ and hERG K⁺ channel as described previously (Moreno et al. 2011) (Moreno et al. 2013).

Figure 3. Simulated interaction of flecainide with single ryanodine receptors .

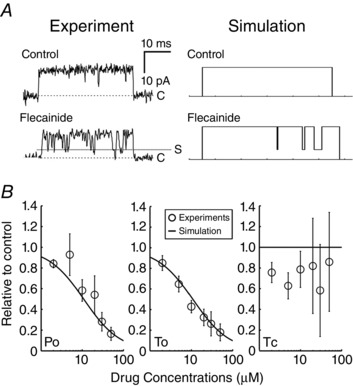
A, experimental single RyR channels in bilayers (left) compared with stochastic model simulations (right), in the absence (top) and presence (bottom) of 50 μM flecainide. B, measured and simulated dose dependence of flecainide on channel open probability (P _o, left), mean open time (middle, T _o), and mean closed time (T _c). Experimental data points (circles) and simulated results from ∼1,000,000 stochastic openings and closures at concentrations as indicated (lines). Experimental data are from Hilliard et al. (2010 and Hwang et al. (2011).

We generated a virtual calsequestrin knockout mouse cardiac myocte (CASQ2(−/−)) by setting the concentration of CASQ to zero in the Morotti–Grandi model of the mouse ventricular myocyte, which includes the β‐adrenergic signalling and CaMKII pathways (Morotti et al. 2014). We then predicted the effects of the virtual CASQ2(−/−) on electrical and Ca²⁺ dynamics. Figure 4 A–D shows action potentials (APs) (top) and Ca²⁺ transients (bottom) of cells paced at a frequency of 2 Hz. As expected, the Ca²⁺ transient amplitude increases upon application of 0.5 μM isoproterenol (ISO) (Fig. 4 B). In the absence of ISO, CASQ2(−/−) myocytes demonstrate reduced but intact Ca²⁺ transients and APs compared with control (compare Fig. 4 C to Fig. 4 A) consistent with experimental observations in CSQN mutant and CSQN underexpression mouse myocytes (Viatchenko‐Karpinski et al. 2004; Terentyev et al. 2008; Gyorke & Terentyev, 2008). Consistent with multiple experimental observations, application of 0.5 μM ISO induces spontaneous Ca²⁺ release events (red arrows Fig. 4 D, bottom), which drive afterdepolarizations (Knollmann et al. 2006; Gyorke & Terentyev, 2008; Hilliard et al. 2010; Liu et al. 2013). Following development of the virtual mouse model of CPVT, which is validated by many published experimental data, we generated a virtual calsequestrin rabbit knockout (CASQ2(−/−)). This approach allows for cross species testing, e.g. to predict how larger animals (more ‘human‐like’) would respond, and to also look for model independence of our findings.

Figure 4. An in silico calsequestrin (CASQ2(−/−)) knockout model recapitulates the CPVT phenotype .

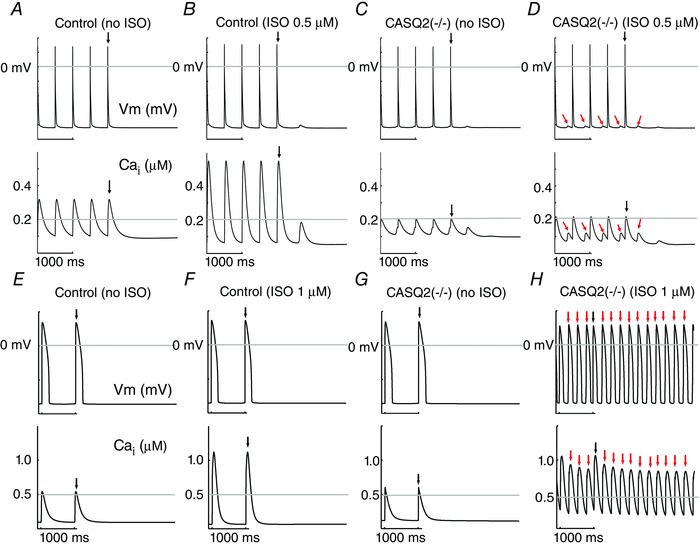
In each panel, simulated membrane voltage (top) and intracellular Ca²⁺ transients (bottom) are shown during 2 Hz pacing in the mouse virtual myocyte (A–D) and 1 Hz in the rabbit virtual myocyte (E–H). A, simulated control mouse ventricular myocytes. B, control mouse cell with 0.5 μM simulated isoproterenol (ISO). C, simulated CASQ2 knockout mouse. D, 0.5 μM ISO applied to the simulated CASQ2 knockout mouse. E, simulated control rabbit ventricular myocytes. F, control rabbit cell with 1 μM simulated isoproterenol (ISO). G, simulated CASQ2 knockout rabbit. H, 1 μM ISO applied to the simulated CASQ2 knockout rabbit. Red arrows indicate spontaneous triggers. Black arrow is the final stimulus.

The rabbit model was constructed by setting the concentration of CASQ to zero in the Soltis–Saucerman model of the rabbit ventricular myocyte, which contains the β‐adrenergic signalling and CaMKII pathways. Figure 4 E–H shows simulated rabbit APs (top) and Ca²⁺ transients (bottom) of control cells paced at a frequency of 1 Hz. As observed in the mouse model, the Ca²⁺ transient amplitude increases upon application of 1 μM ISO (Fig. 4 F). In the absence of ISO, CASQ2(−/−) myocytes demonstrate morphologically similar Ca²⁺ transients and APs to control (compare Fig. 4 G to Fig. 4 E). No differences were found with other pacing frequencies. Consistent with experimental observations (Kornyeyev et al. 2012), application of 1 μM ISO induces spontaneous Ca²⁺ release events (red arrows Fig. 4 H, bottom), which drive depolarizations that trigger APs (red arrows in Fig. 4 H, top).

Recent publications have suggested that flecainide may be insufficiently concentrated inside the cell to affect the RyR directly (Liu et al. 2011 a, 2012). Thus, we employed a novel atomic scale modelling approach to compute free energy profiles for flecainide transport in the extracellular, membrane and intracellular compartments (Fig. 5 A).

Figure 5. Atomic scale prediction of flecainide transport across the membrane .

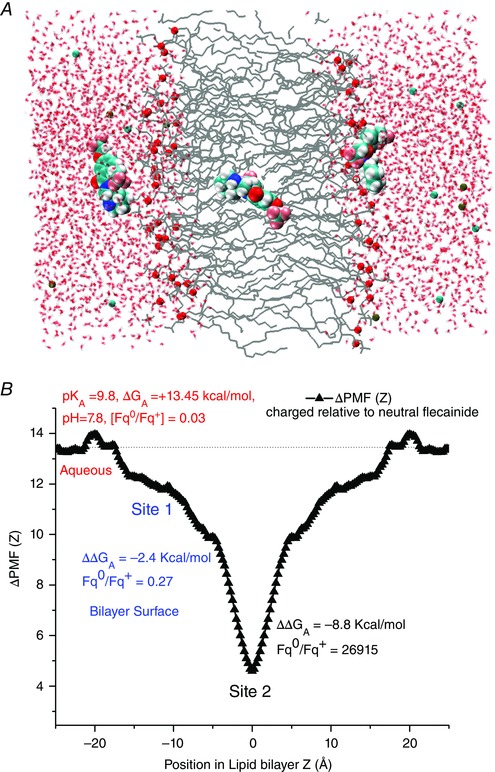
A, visualization of flecainide transport. B, the difference between the potentials of mean force (ΔPMF (Z)) across the bilayer, and position‐dependent free energies for charged and neutral flecainide (ΔΔG _A) at the membrane interface (site 1) and hydrophobic core of the bilayer (site 2). Relative fractions of neutral to charged drug (Fq^o/Fq⁺) in the aqueous solution (red), site 1 (blue) and site 2 (black) are shown.

With a pK _a value of 9.8, 97% of flecainide will exist in the protonated form at physiological pH. However, recent studies suggest that the hydrophobic environment of the lipid bilayers promotes stabilization of the neutral form, allowing for flecainide entry upon deprotonation. To assess feasibility of this mechanism, we determined the underlying thermodynamics governing flecainide movement on the surface and in the hydrophobic core of the membrane and the barriers associated with transport of cationic or neutral forms.

Force (PMF) (or Potential mean force free energies (ΔG _A)) for partitioning of charged and neutral flecainide

Both forms of flecainide display preference for interfacial partitioning with stabilization of about 8 and 11 k _B T for charged and neutral flecainide, respectively. The simulations show that concentration of neutral flecainide will increase substantially on the surface as compared to the bulk phase and will be predominant in the hydrophobic core of the bilayer (site 2). There is a substantial penalty for protonated drug to cross a hydrophobic core, although it will act as a sink for a neutral flecainide with a very small crossing barrier for the drug (∼2k _B T not shown).

The difference between the potentials of mean force (ΔPMF (Z)) across the bilayer, and position‐dependent free energies for charged and neutral flecainide (ΔΔG _A) at the membrane interface (site 1) and hydrophobic core of the bilayer (site 2) are shown in Fig. 5 B. We calculated the pK _a shift due to drug deprotonation upon partitioning into lipid bilayers from the difference between the position‐dependent free energies for charged and neutral flecainide (ΔΔG _A).

$$\Delta \Delta G_{\mathrm{deprot}}=W_{\mathrm{Fle}{\mathrm{c}}^0}\left(z\right)-W_{\mathrm{Fle}{\mathrm{c}}^{+}}\left(z\right)$$

$$\Delta \mathrm{p}{K}_{\mathrm{A}}=\frac{\Delta \Delta G_{\mathrm{deprot}}}{2.3k_{\mathrm{B}}T}$$

ΔpK _a values are also indicated as relative fractions of neutral to charged drug (Fq^o/Fq⁺) in the aqueous solution (red), site 1 (blue) and site 2 (black) in Fig. 5 B. The pK _a shift is close to zero in the bulk (as expected) and then sharply drops at site 1. This indicates that flecainide will readily lose its proton in the membrane environment.

Is diffusion of neutral flecainide sufficient for effective accumulation? We estimated diffusion coefficients from local friction factors along the reaction coordinate in free energy simulations (from fluctuations in the constraining force) (Boggara & Krishnamoorti, 2010). The diffusion coefficient for flecainide was calculated as ∼4.9 × 10⁻⁷ cm² s⁻¹ in the bilayer, about an order of magnitude lower than bulk water similar to previously reported values for various drugs (Boggara & Krishnamoorti, 2010). Flecainide is predicted to undergo extremely rapid equilibration.

We next predicted the effects of flecainide on control and CASQ2(−/−) rabbit ventricular myocyte models for clinically relevant frequencies at a high therapeutic dose of flecainide (2 μM). In order to map the action potential (AP) dynamics–frequency relationship for the CPVT CASQ2(−/−) with flecainide, the maximum values of the voltage following the upstroke of the AP were collected during the second half of a 2 min simulation and binned vertically for each constant pacing frequency; for clarity, only steady state behaviour is shown (t = 60–120 s). In the control simulation there was a stimulus to AP ratio of 1:1 (Fig. 6 A). The time course of AP at 2 Hz (grey line) is shown on the left (Fig. 6 A, C, E, G and I). The peak of the calcium transient was similarly monitored (control – Fig. 6 B), with the time course of the calcium transient at 2 Hz (grey line) in the left of each of the right panels (Fig. 6 B, D, F, H and J).

Figure 6. Model prediction of flecainide mechanism .

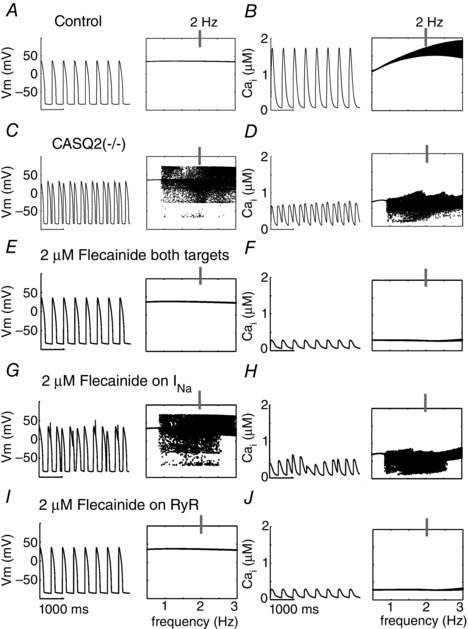
The time course of action potentials is in left columns and calcium transients (CaTs) in right columns at 2 Hz. Voltage and Ca²⁺ transient dynamics over a range of physiological frequencies is shown to the right of each simulated time course at 2 Hz: the voltage maxima are binned for each pacing frequency between 0.5 and 3 Hz during the second half of a 2 min simulation time course. A and B, control APs, CaTs. C and D, CASQ2(−/−) APs, CaTs. E and F, CASQ2(−/−) myocyte APs and CaTs with high clinical dose (2 μM) flecainide effects on both Na⁺ channels and RyRs. G and H, high dose flecainide acting only on Na⁺ channels. I and J, high dose flecainide (2 μM) on only RyRs.

In the absence of drug, CASQ2(−/−) myocytes displayed triggered APs at frequencies greater than 0.95 Hz (notice the horizontal line in the plot at frequencies slower than 0.95 Hz, corresponding to a stimulus to AP ratio of 1:1), when challenged by 1 μM ISO (Fig. 6 C). Pathological electrical activity was preceded by spontaneous Ca²⁺ release events from the RyR2 (Fig. 6 D), which, when resulting in a sufficient release of Ca²⁺, can integrate in time to induce electrogenic forward‐mode sodium–calcium exchange current (3 inward Na⁺/1 outward Ca²⁺) and depolarize the cell, ultimately activating I _Na.

Application of a high therapeutic dose flecainide (2 μM), acting on the rabbit RyR2, I _Kr and I _Na rectified the electrical activity at all frequencies tested (Fig. 6 E). The electrical stability coincided with suppression of diastolic Ca²⁺ release, but was also accompanied by a markedly reduced Ca²⁺ transient (Fig. 6 F). The therapeutic range of plasma concentrations for flecainide is 0.5–2.0 μM (Brunton et al. 2010). We examined the cases of 0.5, 1.0 and 1.5 μM flecainide acting on each of the targets under the influence of 1 μM isoproterenol, over a range of clinically relevant pacing frequencies, from 0.5 to 3.0 Hz (30–180 beats min⁻¹; Leenhardt et al. 1995), at 0.01 Hz increments (Fig. 7). Low dose flecainide (0.5 μM) failed to suppress Ca²⁺ alternans, a marker of proarrhythmia (Chudin et al. 1999), which emerged at frequencies greater than 1.6 Hz and suggests incomplete efficacy in the lower range of therapeutic dosing (Fig. 7 A).

Figure 7. Full parameter space of flecainide efficacy for I_Na, RyR2 and both targets in combination .

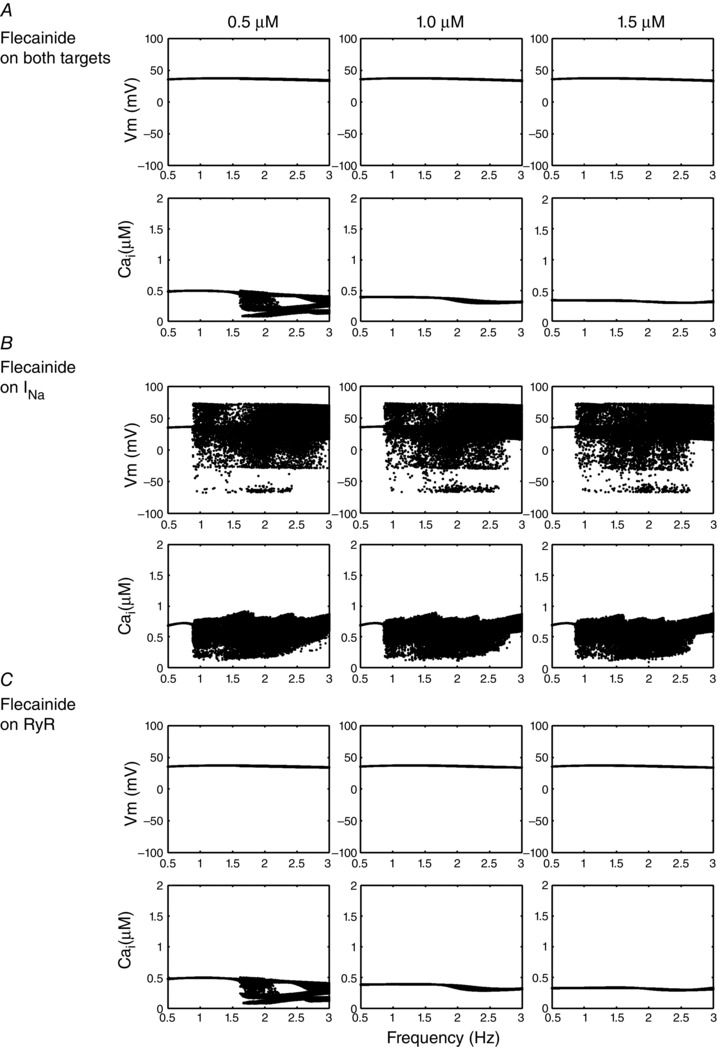
Voltage dynamics is shown for each flecainide case, and the voltage and Ca²⁺ transient maxima are binned for each pacing frequency between 0.5 and 3 Hz during the second half of a 2 min simulation time course. A, CASQ2(−/−) myocytes with 0.5, 1.0 and 1.5 μM flecainide effects on both Na⁺ channels and RyRs. B, flecainide concentrations acting on only Na⁺ channels. C, flecainide interaction with just RyRs.

We next simulated drug action on the Na⁺ current or RyR alone to determine the contributions of each target to drug efficacy. The rabbit model predicted that neither the high dose of flecainide (2 μM in Fig. 6 G and H), nor any lower concentrations, when tested on Na⁺ current alone, eliminated pathological activity at all pacing frequencies (Fig. 7 B). As expected from flecainide's use‐dependent blocking behaviour of I _Na, higher concentrations and faster pacing frequencies eliminated some arrhythmogenic behaviour, but DADs and triggered action potentials persisted. Derangement of Ca²⁺ activity also persisted, and was largely unaffected by drug effects on the Na⁺ current (Fig. 6 H).

Selective application of flecainide on RyR2 yielded results comparable to the case flecainide acting on both targets (compare Fig. 6 I and J (selective RyR2) with Fig. 6 E and F (both targets)). Mid‐ and high‐dose flecainide acting on the RyR2 alone resolved pathological behaviour at the cellular level, though Ca²⁺ alternans and DADs still emerged at lower doses (Fig. 7 C).

We next modelled the physiological effects of acute application of isoproterenol on heart rate, mimicking acute sympathetic stimulation. In Fig. 8, rabbit cells were paced to steady‐state (for 500 s) at 1 Hz and then subjected to isoproterenol and an increase in pacing frequency (cycle length = 600 ms). Compared with control virtual cells that responded uneventfully to sympathetic challenge (Fig. 8 A), the virtual CASQ2(−/−) CPVT mutation generated multiple spontaneous APs, observed in the histogram of peak voltages in time (left side of left panels) and in the time course of the membrane potential (right of left panels during the time indicated by the boxed region in the left panels). As observed for steady‐state pacing, simulated 2 μM flecainide application on both the Na⁺ current and RyR (Fig. 8 C) normalized aberrant behaviour, while flecainide effects on the Na⁺ channel alone were insufficient (Fig. 8 D). A dose of 2 μM flecainide acting on the RyR alone normalized the membrane potential and prevented spontaneous Ca²⁺ release (Fig. 8 E). We also tested different pacing cycle lengths from 300 ms to 500 ms, and found similar results (data not shown).

Figure 8. Simulation of the physiological effects of isoproterenol on heart rate .

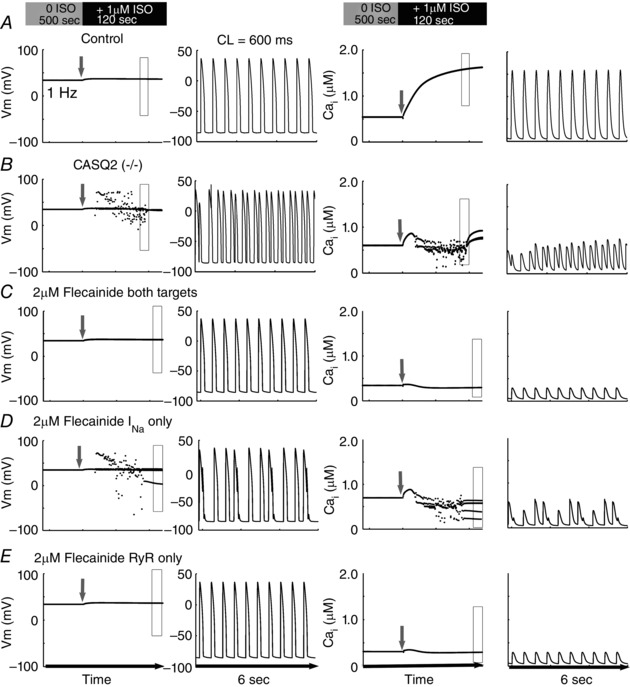
Five hundred beats were paced in control cells at Basic Cycle Length (BCL) 1000 ms (1 Hz) without ISO; cycle length was abruptly decreased to 600 ms with concomitant application of ISO (1 μM). Peak voltages in time are shown in the left columns, and a representative time course (expanded rectangle of left panels) of the membrane potential action potentials is in the 2nd column. Corresponding peak Ca²⁺ transients are in column 3, with a representative time course shown in the far right columns. The grey arrow in each panel denotes onset of pacing acceleration and application of ISO.

We next predicted the effects of flecainide in a rabbit one‐dimensional (1D) transmural heterogeneous tissue. Stimulation was applied to the endocardial site of the CASQ2(−/−) rabbit tissue at 2 Hz (120 beats min⁻¹) with 1 μM ISO, in the presence or absence of flecainide. Spontaneous Ca²⁺ releases from the RyR2 often resulted in sufficient calcium loading to drive inward I _NCX, causing DADs that were occasionally sufficient in amplitude to activate Na⁺ channels for a triggered AP (red arrows – Fig. 9 A).

Figure 9. Space–time representations of one‐dimensional simulations of flecainide effects on CPVT at BCL 500ms .

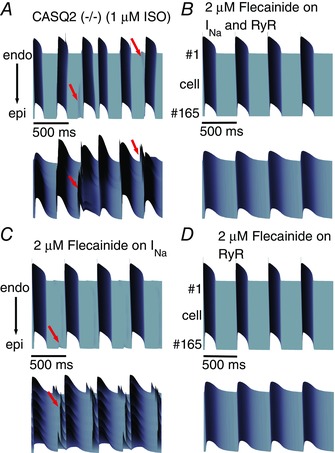
For each set of panels, voltage time course is on the top, calcium transient is on the bottom. A, simulated one‐dimensional coupled tissue harbouring the CASQ2(−/−) CPVT mutation in the absence of drug. B, effect of flecainide (2 μM) on I _Na and RyR. C, flecainide (2 μM) effects on I _Na alone. D, simulated effects of 2 μM flecainide on the RyR alone. Red arrows indicate spontaneous DADs, triggered action potentials and Ca²⁺ transients.

Flecainide at 2 μM acting on both the Na⁺ channels and the RyRs suppressed propagated arrhythmogenic activity by regulating underlying SR Ca²⁺ release (Fig. 9 B). Also consistent, 2 μM flecainide acting on I _Na alone did not prevent spontaneous Ca²⁺ release and DADs (Fig. 9 C). However, 2 μM flecainide acting on the RyR2 alone was sufficient for therapeutic suppression of DADs and triggered APs (Fig. 9 D). Notably, 2 μM flecainide acting on I _Na (e.g. Fig. 9 B and C) slowed tissue conduction velocity from 66 to 44 cm s⁻¹ as compared with 2 μM flecainide acting on RyR2 alone, consistent with well‐documented detrimental conduction velocity in coupled tissue (Starmer et al. 1991; Moreno et al. 2011).

We further probed concentration dependence of our RyR2‐specific effects of flecainide, and found strong dose dependence. Subthreshold DADs arising from spatially discordant Ca²⁺ alternans emerged in the presence of 0.5 μM and 0.65 μM flecainide acting on RyR2 (Fig. 10), alone and in combination with I _Na block (not shown). Figure 10 B and D show the time course of the Ca²⁺ mediated alternans development for 0.5 μM and 0.65 μM flecainide, respectively, acting on RyR2 alone.

Figure 10. Simulated effects of low clinical dose flecainide effect on RyR only in CPVT one‐dimensional tissue .

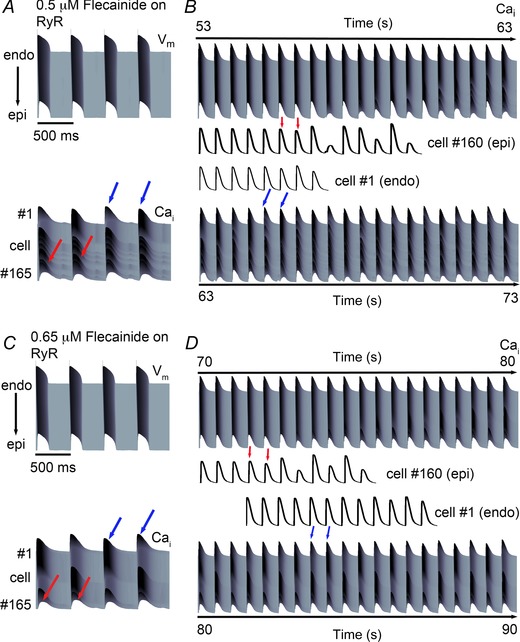
Ca²⁺ alternans developed slowly over time, originating from the epicardial end (red arrows) and continued to the endocardium (blue arrows). A, simulated effects of low clinically relevant dose of 0.5 μM flecainide acting on the RyR alone on action potentials (top) and Ca²⁺ transients (bottom). B, spatially discordant Ca²⁺ alternans emerge over time. Red arrows correspond to epicardial (Epi) Ca²⁺ alternans, while blue arrows correspond to endocardial (Endo) Ca²⁺ alternans. Cell no. 160 (Epi) is shown from the time 53 s (bottom), and Cell no. 1 (Endo) is shown from the time 63 s (top). C, a modest increase in flecainide (0.65 μM) decreased the transient amplitude difference between beats and prolonged the onset of alternans. D, extended time course of Ca²⁺ alternans development for 0.65 μM flecainide on the RyR alone. Cell no. 160 (Epi) is shown from the time 70 s (bottom), and Cell no. 1 (Endo) is shown from the time 80 s (top). In panels B and D, arrows mark the first instance of alternans, which persist for the duration of the simulation.

Given the therapeutic potential of flecainide to normalize Ca²⁺ anomalies in the CPVT‐linked CASQ2(−/−), we set out to predict whether other Na⁺ channel blockers might suppress emergent‐triggered activity in rabbit ventricular myocyte models. We simulated the pure Na⁺ channel blocker lidocaine (20 μM) and the late Na⁺ current/hERG channel blocker ranolazine (5 μM) (Moreno et al. 2013). Lidocaine and ranolazine have both failed to demonstrate efficacy in the suppression of Ca²⁺ wave formation (Galimberti & Knollmann, 2011). For both lidocaine and ranolazine devoid of RyR2 interaction, our results mimicked selective I _Na inhibition by flecainide. Lidocaine (Fig. 11 A) and ranolazine (Fig. 11 B) did not prevent spontaneous depolarizations at all frequencies. Protocol is as in Fig. 6.

Figure 11. Simulated high clinically relevant doses of lidocaine and ranolazine in CPVT myocytes .

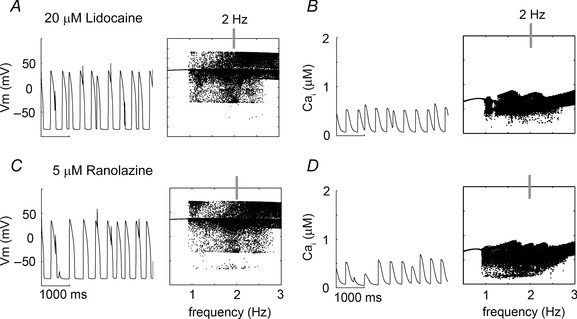
Single cell time course is shown at 2 Hz (left) and voltage and calcium transient maxima over a range of frequencies (0.5–3 Hz, right). A and B, high clinically relevant dose (20 μM) of the pure Na⁺ channel blocker lidocaine on voltage and Ca²⁺ transient, respectively. C and D, clinically relevant dose (5 μM) of the antianginal and late Na⁺ current blocker ranolazine on voltage and Ca²⁺ transient, respectively.

Low dose flecainide is predicted to be insufficient for normalizing the CASQ2(−/−) CPVT mutation‐induced proarrhythmia in simulated cells and tissues. The extension of these results is that high doses may be required for clinical therapy, which may paradoxically promote arrhythmia. β‐Blockade is associated with suboptimal management and pronounced side effects. Thus, we set out to utilize modelling and simulation to guide a novel form of virtual pharmacopoeia in an attempt to identify alternative CPVT therapy. We considered combinations of on‐market or preclinical drugs that would cumulatively regulate the RyR2 at lower concentrations, and minimize risk associated with off‐target interactions of each drug.

We used the computational model to test the hypothesis that a multidrug combination of flecainide, β‐blockade, and CaMKII inhibition would demonstrate efficacy in CPVT. Although little is known about CaMKII inhibition in humans, the signalling molecule regulates many targets and is highly distributed in the brain; thus it is expected that high doses of CaMKII inhibition should be avoided (Ledoux et al. 1999; Kaurstad et al. 2012). However, both β‐blockers and CaMKII inhibitors are classes of drugs that functionally modulate RyR2 activity (Fig. 12 A), and are suggested to provide efficacy in the management of CPVT (Pott et al. 2011; Liu et al. 2011 b; Di Pasquale et al. 2013).

Figure 12. Predicted low‐dose polytherapy for CPVT .

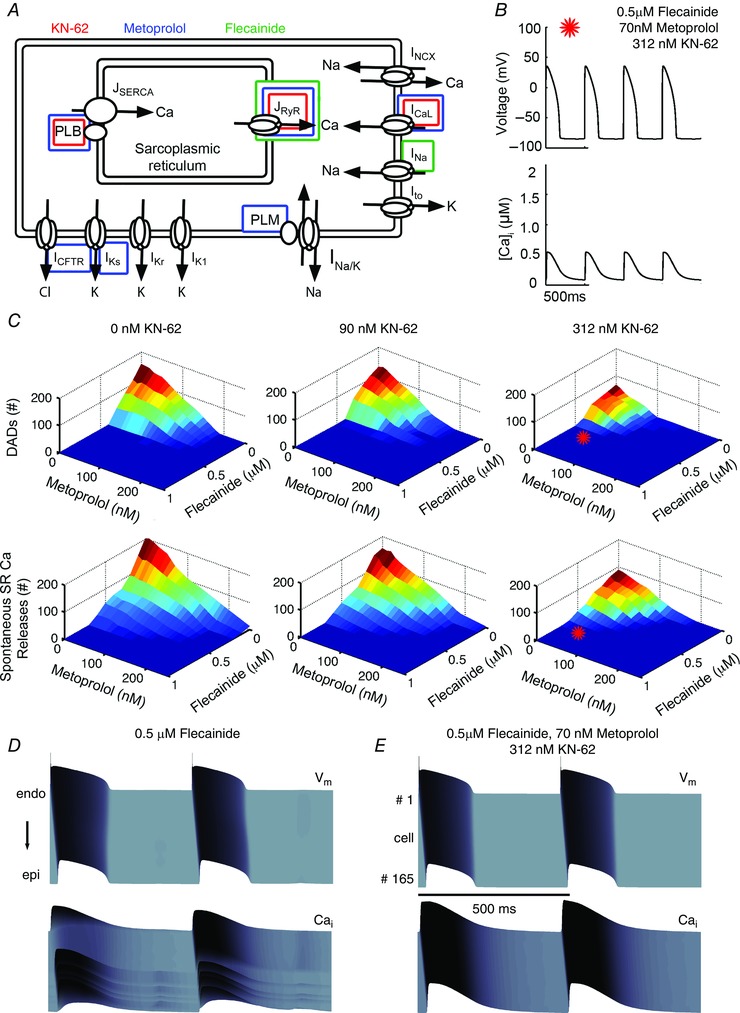
A, schematic diagram showing the primary targets of flecainide, metoprolol, and KN‐62. B, prediction of low‐dose combined therapy on action potentials (top) and calcium transients (bottom) at 2 Hz C, 3 drug combination parameter space simulated in single cells tracking the number of DADs (top) and spontaneous Ca²⁺ releases (bottom). Red stars denote the location of the case in B of 0.5 μM flecainide, 70 nM metoprolol and 312 nM KN‐62. D, simulated tissue effects of low dose flecainide. E, predicted tissue effects of combined simulated therapy.

We modelled the β₁‐blocking effects of metoprolol (IC₅₀ = 105 nM) as a competitive inhibitor of β‐agonist, and CaMKII inhibition by KN‐62 (IC₅₀ = 468 nM) as a limiter of free endogenous total CaMKII (see Fig. 2; individual drug efficacy of β‐blockade and CaMKII).

We tested in a full factorial combination: the range of relevant concentration combinations in single cells at 2 Hz 0–1 μM flecainide (0.1 μM increments), 0–420 nM metoprolol (corresponding to 0–80% block of β‐receptors, at 8% increments), and 0–468 nM KN‐62 (corresponding to 0–50% CaMKII inhibition at 5% increments). Among the combinations tested, a combined dose of 0.5 μM flecainide, 70 nM metoprolol and 312 nM KN‐62 resulted in controlled Ca²⁺ and voltage activity over the duration of single cell pacing at 2 Hz (Fig. 12 B). Parameter space maps were generated for the three‐drug combination indicating ranges of dose to prevent DAD formation and spontaneous Ca²⁺ release events. Among the 1331 combinations tested, the surfaces shown in Fig. 12 C represent the efficacy of these combinations on voltage (top row) and spontaneous Ca²⁺ releases (bottom row). When the surface is dark blue, no DADs occurred (voltage), while the dark blue surface in the bottom panels of Fig. 12 C indicates that no spontaneous Ca²⁺ release events occurred. Even for some drug combinations that remediated DADs, spontaneous Ca²⁺ releases still occurred (indicated by larger blue area in the DAD row than the spontaneous Ca²⁺ release row). The effect of flecainide alone is contained within these graphs where the concentration of the other drugs is zero. The red stars in Fig. 12 C, right, show one predicted optimal therapeutic combination, a combined dose of 0.5 μM flecainide, 70 nM metoprolol and 312 nM KN‐62, resulted in just one effective combination that remediated Ca²⁺ and voltage activity (indicated by a star). This is within a parameter space of local minima, indicating eradication of single cell proarrhythmia event markers (e.g. DADs and spontaneous Ca²⁺ release (SCaR) events).

Finally, we simulated our drug combination of 0.5 μM flecainide, 70 nM metoprolol and 312 nM KN‐62 in CASQ2(−/−) in 1D tissue, and compared the results with a simulated tissue pretreated with 0.5 μM flecainide (Fig. 12 D). Compared with flecainide alone, combination therapy was superior by (i) requiring a lower dose of flecainide (and thus maintaining conduction velocity 41 cm s⁻¹ for flecainide vs. 59 cm s⁻¹ for combination therapy); (ii) fully suppressing all DADs and triggered APs; (iii) reducing APD₉₀; (iv) normalizing [Ca]_i; and (v) preventing the occurrence of spatially discordant Ca²⁺ alternans (see Table 6).

Table 6.

CASQ2(−/−) with ISO 1 μM at 2 Hz (rabbit)

Drug concentration	CV (cm s−1)	APD90 (ms)	[Ca]i (μM)
Drug free	60	Triggered APs	0.6
Flecainide 2 μM	41	192.5	0.285
Flecainide 0.5 μM + 70 nM Metoprolol + 312 nM KN‐62	59	177.8	0.55

We next tested if the rabbit model prediction for flecainide, β‐blockade and CaMKII polytherapy would hold true in the computational mouse model, as a test of the model independence of our findings. Just as we observed for the rabbit model predictions, high dose (2 μM) flecainide effects on both I _Na and the RyR normalized the CASQ2(−/−) CPVT phenotype as shown in Fig. 13 A. Application of flecainide in the mouse model did not affect the amplitude of the Ca²⁺ transients, consistent with experimental observations in the mouse genetic models (Hilliard et al. 2010). Also consistent, the effects of high dose (2 μM) flecainide on I _Na alone was predicted to be insufficient for normalizing the CASQ2(−/−) CPVT mutation‐induced afterdepolarizations and spontaneous Ca²⁺ release events as shown in Fig. 13 B. However, 2 μM flecainide acting on the RyR2 alone was sufficient for therapeutic suppression of DADs (Fig. 13 C). Low dose 0.5 μM flecainide acting on I _Na and the RyR2 did not ablate spontaneous Ca²⁺ release events as shown in Fig. 13 D. We also tested if one of the predicted polytherapy combinations that was found to be effective in the rabbit model simulations was also effective in the mouse. The result, shown in Fig. 13 E, shows that the drug combination of 0.5 μM flecainide, 70 nM metoprolol and 312 nM KN‐62 in the mouse CASQ2(−/−) virtual myocyte completely normalized the cellular phenotype.

Figure 13. Simulated drug effects in mouse ventricular myocytes .

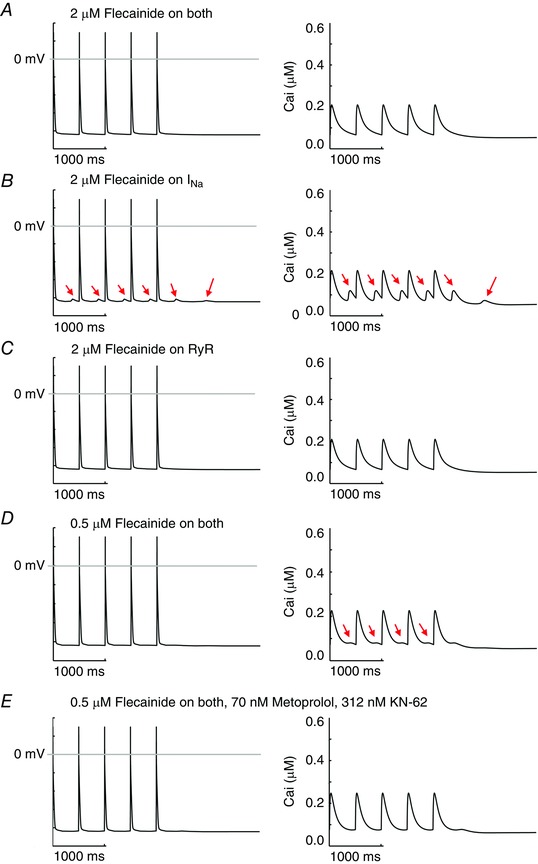
In each panel simulated membrane voltage (left) and intracellular Ca²⁺ transients (right) are shown during 2 Hz pacing. A, CASQ2(−/−) myocyte APs and CaTs with high clinical dose (2 μM) flecainide effects on both Na⁺ channels and RyRs. B, high dose flecainide acting only on Na⁺ channels. C, high dose flecainide (2 μM) on only RyRs. D, low dose flecainide 0.5 μM on both Na⁺ channels and RyRs. E, simulated test of predicted polytherapy in mouse ventricular myocytes.

We next set out to experimentally test if the model prediction for flecainide, β‐blockade and CaMKII polytherapy would be effective in the R176Q/+ CPVT experimental mouse model, an alternate CPVT genotype. The results are shown in Fig. 14. A knock‐in R176Q/+ CPVT mouse model was used (six R176Q/+, two WT). R176/+ mice develop bidirectional ventricular tachycardia (VT) with catecholamine provocation. At baseline, neither the WT nor the R176Q/+ mice demonstrated ventricular arrhythmias and average heart rate was 462 beats min⁻¹ (R176Q/+) and 574 beats min⁻¹ (WT) (Table 7). After injection of adrenaline (2 mg kg⁻¹ i.p.) and caffeine (120 mg kg⁻¹ i.p.), six of six R176Q/+ mice developed bidirectional VT as shown in Fig. 14 A and C. Ventricular tachycardia initiated within 30 s to 6 min and lasted between 1 and 51 min in length (average 21 min) with an average ventricular rate of 807 beats min⁻¹. Both WT and R176Q/+ mice demonstrated T‐wave alternans lasting several hours after injection of adrenaline and caffeine. After a 7 day wash‐out, the mice were injected with adrenaline and caffeine (2 mg kg⁻¹ and 120 mg kg⁻¹ i.p., respectively); however, 30 min prior, all mice were given pre‐treatment with i.p. injections of flecainide (12 mg kg⁻¹, Sigma‐Aldrich), metoprolol (10 mg kg⁻¹, Sigma‐Aldrich) and KN‐93 (30 μmol kg⁻¹, Calbiochem). All mice demonstrated statistically significant PR, QRS and QTc prolongation 30 min after administration of flecainide, metoprolol and KN‐93 (Table 8). Some mice exhibited ST segment changes (data not shown). Heart rates were lower after drug administration but not significantly (Table 8). Adrenaline and caffeine following pre‐treatment with flecainide, metoprolol and KN‐93 failed to induce ventricular tachycardia in all R176Q/+ mice. Mice demonstrated T‐wave alternans (one WT and five R176Q/+) and single premature ventricular contractions (four R176Q/+); however, higher‐grade ectopy and the typical bidirectional VT were not seen as shown in Fig. 14 B and C.

Figure 14. Experimental test of predicted polytherapy .

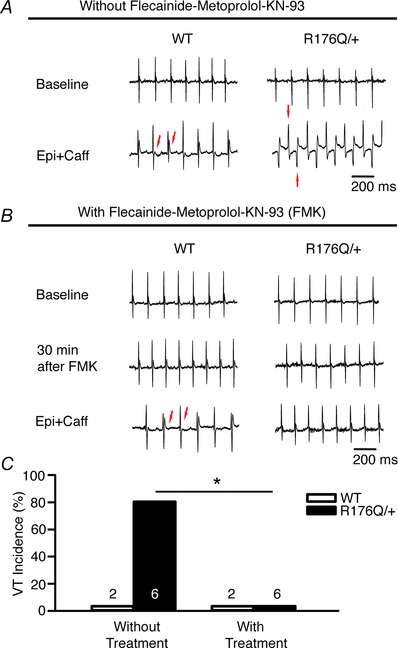
A and B, representative tracings from WT and R176Q/+ mice are shown at baseline and after sympathetic challenge with no drug (A) and following administration of flecainide, metoprolol and KN‐93 (B). C, summary of data without (left) and following (right) pre‐treatment with flecainide, metoprolol and KN‐93, which suppressed VT in all R176Q/+ mice (*P = 0.015).

Table 7.

ECG measurement comparing wild type and R176Q/+ mice before and after treatments

	Without treatment						With treatment
	Baseline			Epi + Caffeine			Baseline			Flec + Metop + KN‐93			Epi + Caffeine
	WT	R176Q/+	P	WT	R176Q/+	P	WT	R176/+	P	WT	R176Q/+	P	WT	R176Q/+	P
Heart rate (beats min−1)	574	462	0.18	588	466	0.09	442	467	0.73	385	375	0.93	424	328	0.25
PR (ms)	35	38	0.34	36	40	0.26	36	38	0.40	45	50	0.60	43	55	0.23
QRS (ms)	12	11	0.72	13	15	0.08	12	12	0.78	16	16	0.76	18	21	0.63
QTc (ms)	45	46	0.69	46	49	0.28	49	49	0.99	45	48	0.26	45	43	0.37

Adrenaline (2 mg kg⁻¹) and caffeine (120 mg kg⁻¹) were initially injected intraperitoneal (i.p.) without pre‐treatment (Without treatment). Mice were then given a pre‐treatment dose of flecainide (12 mg kg⁻¹, i.p.), metoprolol (10 mg kg⁻¹, i.p.), and KN‐93 (30 μmol kg⁻¹, i.p.) followed 30 min later by an injection of the same i.p. dose of adrenaline and caffeine (With treatment). Flec, flecainide (12 mg kg⁻¹); Metop, metoprolol (10 mg kg⁻¹); KN‐93 (30 μmol kg⁻¹).

Table 8.

Comparison of ECG measurements before and after treatment with flecainide, metoprolol and KN‐93

		Flecainide,
	Baseline	Metoprolol, KN‐93	P
Heart rate (beats min−1)	461	378	0.14
PR (ms)	37	48	0.01
QRS (ms)	12	16	< 0.001
QTc (ms)	49	47	0.12

Discussion

The optimal pharmacological management of CPVT remains a clinical challenge. The current mainstay of pharmacotherapy often involves maximally tolerated β‐blockade despite high (∼30–50%) failure rates (Priori et al. 2002; Liu et al. 2008). In conjunction with pharmacotherapy, mechanical ICD implantation (Miyake et al. 2013) and left cardiac sympathetic denervation (Wilde et al. 2008) have been used clinically, but carry inherent morbidity and fail to target the mechanistic underpinnings of the CPVT arrhythmia triggers.

While alternative class I antiarrhythmics have been suggested (Galimberti & Knollmann, 2011; Hwang et al. 2011), only flecainide has shown moderate clinical success. Its well‐studied mechanism of action is inhibition of the inward sodium current (I _Na), but data suggest that flecainide interacts with I _Kr and RyR2 (Hilliard et al. 2010; Galimberti & Knollmann, 2011). Flecainide has demonstrated lethal proarrhythmic effects in other patient populations (Echt et al. 1991), and previous clinical failures were largely the result of an incomplete understanding of the emergent proarrhythmic risk.

Recent studies have suggested that because flecainide is 97–99% ionized at physiological pH, it is insufficiently concentrated inside the cell to act on the RyR (Liu et al. 2011 a, 2012), though the study cited as evidence showed the opposite result (Liu et al. 2003). The authors made permanently charged flecainide, which when applied intracellularly (via a pipette) led to the same effect as when the same concentration of unadulterated flecainide was applied externally (in the bath). Permanently charged flecainide had no effect when applied externally, showing that the drug action cannot be via an extracellular path.

Here, we utilized a physics‐based molecular dynamics approach to simulate the partitioning of flecainide by computing free energy profiles for flecainide transport in the extracellular, membrane and intracellular compartments (Fig. 5). The simulations suggest that flecainide accumulates on the membrane surface in cationic and neutral forms after which deprotonation occurs at the surface binding site and promotes membrane crossing down the concentration gradient. The drug then reacquires a proton once it is in the intracellular milieu. This process is extremely rapid, occurring with a diffusion coefficient of ∼10⁻⁷ cm s⁻¹, only an order of magnitude lower than in the bulk water.

Our predictions support the existing experimental data suggesting the following cell entry model for flecainide transport: (i) drug accumulates on the membrane surface in cationic and neutral forms; (ii) deprotonation occurs at the surface binding site (site 1) and promotes membrane crossing down the concentration gradient; and (c) drug acquires a proton once it is in the intracellular milieu.

As demonstrated in Fig. 4, virtual mouse and rabbit CASQ2(−/−) cells with β‐agonist display increased Ca²⁺ transients and spontaneous Ca²⁺ release events, which are sufficient to drive triggered cellular electrical activity, and reproduce clinical behaviour of the CVPT phenotype (Liu et al. 2011 a). The absence of calsequestrin as a buffer speeds up the dynamics of SR refilling, providing more interaction time for SR Ca²⁺ to activate the RyR2, and results in functionally upregulated RyR2 activity. The resulting spontaneous Ca²⁺ release events and depolarizations of the membrane persist after cessation of pacing, owing to cyclic refilling of the SR, spontaneous release of Ca²⁺ into the cytoplasm via the RyR2, activation of I _Na by inward I _NCX, influx of Ca²⁺ via activation of I _CaL and reuptake of Ca²⁺ into the SR via SERCA. It is important to note that diastolic intervals in the rabbit are longer than in the mouse, and the model predicted that they could allow sufficient time to promote spontaneous diastolic release and triggered activity. Our model predicted that high dose flecainide prevents aberrant spontaneous Ca²⁺ releases with resultant resolution of triggered AP activity in single virtual myocytes of mouse and rabbit and in rabbit transmural 1D virtual cardiac tissue (see Figs 6, 8 and 9), consistent with experimental data (Hilliard et al. 2010; Galimberti & Knollmann, 2011).

There is considerable disagreement in the literature as to whether the antiarrhythmic effects seen with flecainide are predominately the result of Na⁺ channel blockade, RyR2 blockade, or both. Studies by Watanabe et al. (2009) and others (Hilliard et al. 2010; Galimberti & Knollmann, 2011; van der Werf et al. 2011) have documented a substantial interaction between flecainide and RyR2. They proposed that flecainide acts as a RyR2 open state blocker, with resultant increase in Ca²⁺ spark rate, a decrease in Ca²⁺ spark mass and disruption of Ca²⁺ wave propagation.

Other studies have failed to document any effects of flecainide on RyR or Ca²⁺ handling, and suggested flecainide's efficacy is almost entirely due to its Na⁺ channel blocking effects (Liu et al. 2011 a; Bannister et al. 2015). There are a few potential explanations for these disparate findings, including a lower than expected flecainide concentration within the cell in Liu's study, given rapid diffusion of neutral flecainide through the membrane and repartitioning within the bath solution, and potential mutation‐induced lowered affinity of flecainide for RyR2.

When we decoupled flecainide's presumed RyR2 activity from its well‐known Na⁺ channel blockade, we were surprised to find that the model predicted that Na⁺ channel blockade – even at the high clinical doses – was not sufficient to explain the antiarrhythmic effects seen clinically with flecainide. As seen in Fig. 6 and 8 (single cells) and Fig. 9 (1D tissue), pure Na⁺ channel blockade failed to inhibit spontaneous Ca²⁺ release, and subsequent triggered activity, whereas the RyR2‐specific flecainide interaction was predicted to yield results similar to flecainide acting on both targets.

Interestingly, our simulations with lidocaine (Moreno et al. 2011) as an additional control of pure Na⁺ channel blockade resulted in good concordance with experimental results (Katz et al. 2010; Galimberti & Knollmann, 2011; Hwang et al. 2011), namely that as a monotherapeutic approach, Na⁺ channel blockade is insufficient to resolve CPVT arrhythmia triggers. Consistent with experimental evidence in support of this mechanism of action, flecainide's interaction with the Na⁺ channel did resolve arrhythmia triggers in higher dimensions, but proarrhythmic DADs persisted.

Lastly, because the drugs used to treat CPVT act on different targets, we hypothesized that their actions might prove synergistic when used as a combination therapy. We tested the full parameter space of clinically relevant combination therapy with β‐blockade, flecainide and CaMKII inhibition (Fig. 12), and found that all three drugs achieved better efficacy when used in combination with either or both of the other drugs tested. The potential to achieve therapeutic efficacy at lower drug concentrations potentially limits the danger of off‐target and drug‐related side‐effects and are consistent with clinical reports of improved therapy with combined β‐blockade and flecainide (Pott et al. 2011; Pflaumer & Davis, 2012).

Importantly, our polypharmacy simulations go beyond confirmation that a multidrug regimen is superior; for the first time (to our knowledge), our simulations are a proof‐of‐concept for prediction of a dosing strategy, and simulate a virtual phase 1–2 clinical trial of dose escalations with several thousand combinations of clinically relevant dosages.

We then utilized an experimental protocol to validate the virtual trial in R176Q/+ CPVT mice (Fig. 14). The CPVT R176/+ mice developed bidirectional ventricular tachycardia (VT) with catecholamine provocation. But, as predicted by the computer model in both rabbit (Fig. 12) and mouse (Fig. 13) virtual myocytes, pre‐treatment with flecainide, metoprolol and KN‐93 prevented catecholaminergically induced ventricular tachycardia in all R176Q/+ mice.

Our study is not without limitations. Most importantly, different CPVT mutations demonstrate differences in ultrastructure (Liu et al. 2013), protein expression (Song et al. 2007), RyR2 structural conformation and functionality (Cerrone et al. 2005; Goddard et al. 2008), and Ca²⁺ dynamics (Viatchenko‐Karpinski et al. 2004; Terentyev et al. 2006). As flecainide and β‐blockade have been used clinically, we know that the adverse effect profiles are concentration dependent. Little is known about the clinical consequences of CaMKII inhibition, and our predictions will obviously require careful testing and validation prior to clinical use.

Another important limitation of our study is that the models that we have utilized do not explicitly represent subcellular Ca²⁺ dynamics. For this reason, we are not able to simulate subcellular Ca²⁺ waves and the effects of the drugs on them. This will be an important subject of a future study. In addition, a full experimental follow‐up study to further test and hone the therapeutic efficacy of alternate polytherapy approaches needs to be conducted.

In conclusion, we utilized a computational modelling approach, informed by, and validated with experimental and clinical data, to make therapeutic predictions of drug mechanism and efficacy in the setting of CPVT. Our study sought to answer three fundamental questions of current pharmacotherapy for CPVT. (i) Is flecainide interaction with the Na⁺ channel sufficient for therapy? (ii) Can we predict if other Na⁺ channel blockers will be equally efficacious? (iii) Can a multi‐targeted pharmacologic approach synergize to yield greater success than with individual therapeutics?

Additional information

Competing interests

C.E.C. has a research grant from Gilead Sciences, not involved in this study.

Author contributions

P.‐C.Y. and J.D.M. designed and performed simulations, analysed data, and prepared the manuscript; S.B.V.‐B., M.‐T.J. and S.N. designed and performed simulations; C.Y.M. and X.H.T. designed and performed experiments, and drafted the manuscript; E.G. analysed data, and revised the manuscript; C.E.C. designed simulations and experiments, analysed data, coordinated and oversaw the project, and prepared the manuscript. All authors have approved the final version of the manuscript and agree to be accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

American Heart Association (GIAs (10GRNT3880050, 13GRNT14370019), Western States Affiliate), the National Institutes of Health NHLBI RO1‐HL‐085592, NHLBI R01‐HL‐085592‐S1, R01 HL105242‐05, 1U01HL126273‐01A1 and Gilead Sciences (to C.E.C.). Canadian Institutes for Health Research (MOP‐186232) and Heart and Stroke Foundation, Alberta (GIA) (to S.N.). NIH‐NHLBI (HL089598, HL091947, HL117641, HL129570), the American Heart Association (13EIA14560061) to XHT.