Abstract
A tumour control probability computational model for fractionated radiotherapy was developed, with the goal of incorporating the fundamental interplay between hypoxia and proliferation, including reoxygenation over a course of radiotherapy. The fundamental idea is that the local delivery of oxygen and glucose limits the amount of proliferation and metabolically-supported cell survival a tumour sub-volume can support. The model has three compartments: a proliferating compartment of cells receiving oxygen and glucose; an intermediate, metabolically-active compartment receiving glucose; and a highly hypoxic compartment of starving cells. Following the post-mitotic cell death of proliferating cells, intermediate cells move into the proliferative compartment and hypoxic cells move into the intermediate compartment. A key advantage of the proposed model is that the initial compartmental cell distribution is uniquely determined from the assumed local growth fraction (GF) and volume doubling time (TD) values. Varying initial cell state distributions, based on the local (voxel) GF and TD, were simulated. Tumour response was simulated for head and neck squamous cell carcinoma using relevant parameter values based on published sources. The tumour dose required to achieve a 50% local control rate (TCD50) was found for various GFs and TD’s, and the effect of fraction size on TCD50 was also evaluated. Due to the advantage of reoxygenation over a course of radiotherapy, conventional fraction sizes (2–2.4 Gy fx−1) were predicted to result in smaller TCD50’s than larger fraction sizes (4–5 Gy fx−1) for a 10 cc tumour with GFs of around 0.15. The time to eliminate hypoxic cells (the reoxygenation time) was estimated for a given GF and decreased as GF increased. The extra dose required to overcome accelerated stem cell accumulation in longer treatment schedules was estimated to be 0.68 Gy/day (in EQD26.6), similar to published values derived from clinical data. The model predicts, for a 2 Gy/weekday fractionation, that increased initial proliferation (high GF) should, surprisingly, lead to moderately higher local control values. Tumour hypoxia is predicted to increase the required dose for local control by approximately 30%. Predicted tumour regression patterns are consistent with clinical observations. This simple yet flexible model shows how the local competition for chemical resources might impact local control rates under varying fractionation conditions.
1. Introduction
It has long been a central goal to understand radiotherapy (RT) response as a function of the fractionation schedule. Usually, the linear-quadratic (L-Q) model has been combined with a simplified kick-off to accelerated clonogen accumulation (Travis and Tucker 1987, Fowler 1989). For a more detailed representation of the effect of proliferation/repopulation, some authors incorporated tumour growth kinetics into the L-Q model (O’Donoghue 1997, Dawson and Hillen 2006, McAneney and O’Rourke 2007). Others have investigated the effect of hypoxia on the tumour response model, based on the oxygen enhancement ratio (OER) of radiosensitivity in hypoxic subpopulations (Buffa et al 2001, Nahum et al 2003, Wang et al 2006). However, the relationship between hypoxia and proliferation during RT, and the presumed ‘kickoff’ to accelerated clonogen proliferation has usually been modelled in an ad hoc manner.
In order to rationalize future fractionation and non-uniform dose approaches to RT, a tumour control probability (TCP) model is needed that includes the interplay between oxygen and glucose availability, on proliferation, hypoxia, and treatment response. Several models used in selective dose painting or dose redistribution incorporate potential effects of local hypoxia (Popple et al 2002, Søvik et al 2007). Recently, several researchers have developed stochastic computer simulation models, in which various biological processes are implemented in three dimensions, for the evaluation of tumour response (Borkenstein et al 2004, Dionysiou et al 2004, Titz and Jeraj 2008).
In this paper, a compartmental ‘tumourlet’-response model is developed, along the lines of ecological matrix models (Caswell 2001) or other matrix/state models developed in RT (Roti Roti and Dethlefsen 1975a, 1975b). Overall TCP is then computed as the product of tumourlet responses. In this way, heterogeneity could be easily incorporated. The objective of this work was to build a model that: (i) is conceptually and mathematically simple, (ii) uses available data as inputs, and (iii) is powerful enough to incorporate radiobiological phenomena of known importance, such as the anti-correlation between proliferation and hypoxia. The model includes three compartments with different levels of proliferation, hypoxia, and cell loss. A ‘doomed’ sub-compartment was incorporated into each compartment to track cell-kill phenomena and cell removal lysis during tumour reoxygenation and regression. Initial proliferation and hypoxia compartment apportionments are determined by the growth fraction (GF) and the volume doubling time (TD) for a PET-voxel-comparable size of tumourlet. The response for a larger, homogeneous tumour is then easily computed. In this paper, we do not address the important issue of intra-tumour heterogeneity, which is a straightforward extension of the model. The treatment response for a range of schedules was simulated.
We will add cell cycle effects to our model for a separate paper, in preparation, that focuses on hypofractionated response (1–3 fxs), where cycle-dependent changes in radiosensitivity might be important. In this paper, we focus on response from five fractions up to standard 2 Gy/weekday treatments.
2. Methods
2.1. The ‘tumourlet’ concept and the assumption of blood supply invariance
The model assumes that a tumour is comprised of many small subsets (‘tumourlets’) that mathematically are considered homogeneous. That is, the variance inside a tumourlet was not considered.
The tumourlet might be identified with a given voxel at the treatment planning phase, based on pre-RT PET images. Here, each tumourlet was considered to be independent from each other and have a variable size over the course of therapy, with a constant number of tumourlets in a tumour. The initial number of cells in a tumourlet generally decreases during RT with volume shrinkage, although the volume might even increase if the treatment is not sufficient to counteract tumour growth. This is therefore not, strictly speaking, a ‘voxel’ simulation, except in the sense that a tumourlet could be identified with a given voxel at the treatment planning phase.
For purposes of modelling, we assume that each tumourlet has a constant blood (oxygen and nutrient) supply over a course of RT. This simplifies the model, and allows us to introduce the fundamental idea of the model, which is that every tumourlet has an inherent blood supply available and therefore, an inherent proliferative cell capacity. It seems likely there is some variation in blood flow during RT, the impact of variations in blood flow in our simulations (reported below) showed that this has only a modest impact. Given that the tumour vasculature (especially larger vessels) is relatively radioresistant and the damage to vascular endothelial cells in conventional RT is manifested in a relatively late phase of RT, the change of blood supply during RT might not be extensive (Park et al 2012). However, this would not be true for acute (or transient) hypoxia, in which the blood supply changes over a short period of time. It would not be difficult to include temporal changes in blood supply in the model. However, initially we focus on effects from non-transient (diffusion limited) hypoxia in this work.
2.2. The three basic model compartments: proliferative, intermediate, and hypoxic
We attempt to introduce the smallest number of compartments/states needed to model the interplay between hypoxia and proliferation, and to account for variations in GF and tumour doubling time. As shown, these can all be naturally accounted for in a parsimonious model.
The model explicitly accounts for proliferation and hypoxia, which are thought to be the most important factors in tumour growth and response to RT (Hoogsteen et al 2007, Wijffels et al 2008). In particular, we consider tumour ‘zones’ that are oxygen rich versus oxygen poor, and glucose rich versus glucose poor. We assume that cells with access to oxygen also have access to adequate glucose. This classification is consistent with the study performed by Kiran et al (2009), in which avascular tumour growth was measured and also simulated with three different zones. Based on the diffusion and consumption of two principal nutrients—glucose and oxygen—and cell death processes, the model could predict the size of each zone and showed excellent agreement with experimental data. Some growth pattern similarities were also reported between the avascular tumour and a tumourlet supported by a single blood vessel inside a vascular tumour (Roose et al 2007).
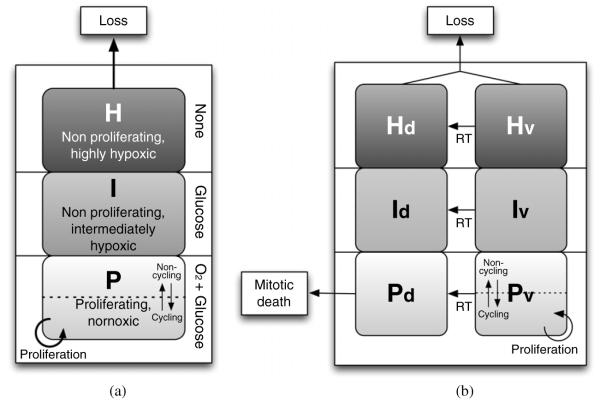
The three model compartments are proliferative (P), intermediate (I), and hypoxic (H). The P-compartment is comprised of cells that have a sufficient oxygen and glucose supply to proliferate. Considering the variable nature of the blood supply (Nilsson et al 2002, Cárdenas-Navia et al 2008), only a fraction of cells in P are assumed to be in cell cycle at any time. For simplicity, this fraction was set to be 50% for a fully occupied P-compartment (variation of this fraction does not have a strong effect, as shown below). As the total number of cells decreases over the course of RT and becomes less than the capacity of the P-compartment (determined by the local blood supply), the fraction of cells in P that are in the cell cycle is assumed in the model to linearly increase to unity, due to a decreased competition for oxygen and nutrients (Ljungkvist et al 2006). This assumption agrees with the observation that the proliferation and GF in a tumour increase during radiation therapy (Petersen et al 2003, Oka et al 1993, Peters et al 1988). The I-compartment is a mildly hypoxic compartment that is assumed to have an adequate glucose supply for tumour cell survival. Without enough oxygen, cells in the I-compartment presumably do not proliferate but can still survive as metabolically-active cells outside the cell cycle (Hlatky et al 1988). No cell loss is assumed to take place in the I-compartment in the absence of radiation. The H-compartment, in contrast, is filled with ‘starving’ cells that are extremely hypoxic, with inadequate glucose and thus has a non-zero death rate even in the absence of radiation. Nevertheless, the ‘viable’ (non-doomed) cells in the I- and H-compartments are assumed to have a latent capability to proliferate if they eventually reach the P-compartment where a sufficient oxygen and glucose supply exists (Hoogsteen et al 2005). Cells that lose proliferative potential due to RT, but potentially remain metabolically active, are referred to as ‘doomed’ cells. A schematic diagram of the resulting model is shown in figure 1.
Figure 1.
Schematic diagram of the model: (a) just prior to the initiation of radiation therapy, and (b) after radiation therapy begins, with doomed sub-compartments in each compartment. The dotted lines and arrows in both directions in the P and PV compartments indicate that, on average, only a fraction of the cells in the compartment are in cell cycle and proliferating, due to the variable nature of the local tumour blood supply.
In this model, the transition of cells from one compartment to another is not determined by ‘transfer rates,’ which is commonly used in other kinetic models. Rather, the cells in the tumourlet are thought to behave like water in a water reservoir that has three divisions along its height, as shown in figure 1(a). When the number of cells in a compartment reaches maximum, the extra cells are pushed up into the next compartment (i.e., P to I or I to H), because P and I have limited capacities. Conversely, if there is room available in a better-oxygenated compartment, cells fill in without any assumed delay. In other words, the transition of cells between compartments is governed by the inherent nutrient capacity of each compartment in that tumourlet.
2.3. Proliferation and cell loss
Since each proliferating cell produces two cells after a cell division, in the absence of other effects, the number of proliferating cells would double in the time it takes to complete one cell cycle (TC). Therefore, the proliferation of a given tumourlet depends on both the size of the P-compartment and the fraction of cells in cell cycle () at any given time. The change in number of cells in a small time step, in the P-compartment due to proliferation can be calculated as follows:
| (1) |
where is the number of viable cells in the P-compartment, is the fraction of cells in active proliferation in the P-compartment, TC is the cell cycle time, and Δt is the time step of the calculation. The resulting number of cells might exceed the capacity of the P-compartment, and if so these extra cells would be pushed up into the I-compartment (for example on weekend breaks).
Extremely hypoxic cells in the H-compartment undergo cell loss, which might be caused by various processes, such as tissue or cellular necrosis, apoptosis, metastasis, cell migration and any other type of cell shedding. Among these, necrotic cell death is thought to be a major factor in cell loss, due to the insufficient oxygen and nutrient supply in the H-compartment (Wouters 2009). Similar to Chvetsov et al (2008), cell loss is assumed to follow exponential decay with a cell loss half-time (T1/2,loss), as shown in equation (2):
| (2) |
where NH is the total number of cells in the H-compartment (viable or doomed), and T1/2,loss is the cell loss half-time in the H-compartment. Equations (1) and (2) are discrete functions, and the number of cells in each compartment is updated with a small time step of Δt (taken to be a quarter of an hour).
2.4. GF and TD for microenvironmental conditions
We build the model input around the established basic concepts of GF and TD, which have often been measured experimentally (e.g., Steel 1977). A key advantage of the proposed model is that the initial compartmental cell distribution is uniquely determined from the assumed local GF and TD values. GF is defined as the fraction of cells in an active cell division at a given time and TD is defined as the time it takes for the tumour volume to double (if it were homogeneous).
GF directly determines the relative number of cells in the P-compartment. Since the fraction of actively dividing cells in the P-compartment is determined by (initially with a full P-compartment), the fraction of the cells in the P-compartment is equal to of the GF. When the GF is 0.2, and is set to 50%, the fraction of cells in the P-compartment becomes 40%. The TD, together with GF, determines the size of the remaining compartments (I and H) (see appendix).
The GF and TD parameters are used only to find the relevant initial distribution of cells in the tumourlet. After RT begins, the GF and TD change with the updated cell distribution in each compartment; the GF increases and TD decreases as the number of cells in the I- and H-compartments decreases.
2.5. Cell-kill model and oxygen enhancement ratio
Sterilization from radiation is calculated based on the L-Q model. However, cell kill in this model does not imply a prompt death of the affected cells. Lethally damaged cells were assumed to become ‘doomed’ but able to survive metabolically, eventually dying during failed mitosis. Equations (3) and (4) represent the damage of viable cells and build up of doomed cells in a compartment for a given fraction of RT:
| (3) |
| (4) |
where NX (t) and NX (t+Δt) are the number of viable or doomed cells in a certain compartment X (P, I, or H) before and after the fraction of RT, respectively, αX and βX are the L-Q parameters for the X compartment, and d is the fractional dose. After several cell cycles, the doomed cells die through mitotic cell death and then are physically removed from the tumourlet through a lysis process that is discussed in section 2.8.
Hypoxic cells are known to be more difficult to sterilize than normoxic cells, as expressed by the OER. The OER represents the ratio of dose required to achieve the same level of cell kill compared with that required for normoxic cells in the P-compartment. The alpha and beta values of the L-Q cell-kill model were modified for different compartments based on the OER of the compartment and radiosensitivity values of the P-compartment, as follows (Carlson et al 2006):
| (5) |
where αX and βX are the alpha and beta values for a given hypoxic compartment X (either I or H), and αP and βP are the alpha and beta values for the normoxic cells in the P-compartment.
2.6. Recompartmentalization and reoxygenation
After each fraction of RT, some viable cells become doomed. The doomed cells are metabolically fit but die probabilistically following mitosis (one or a small number of divisions). The main mechanism of doomed cell death is thought to occur through mitotic catastrophe or mitotic failure (Okada and Mak 2004, Brown and Attardi 2005). Therefore, as the proliferation rate increases for a compartment, so does the death rate of doomed cells.
Mitotic death does not always occur in the first attempt and may occur after several subsequent attempts (Forrester et al 1999). Therefore, the survival probability of each progeny (km) after mitosis was applied to the calculation of mitotic cell death of doomed cells, as shown in equation (6). The zero survival probability of each progeny (km = 0) represents mitotic death in the first attempt of mitosis, with the half-life equivalent to the doubling time of viable cells. Since the number of doomed cells increases after mitosis for km values larger than half, the probable range of km is thought to be 0.1 to 0.4.
| (6) |
As doomed cells die in the P-compartment, oxygen becomes available to other cells and a recompartmentalization takes place, as shown in figure 2. In this process, reoxygenation of the hypoxic cells also occurs.
Figure 2.
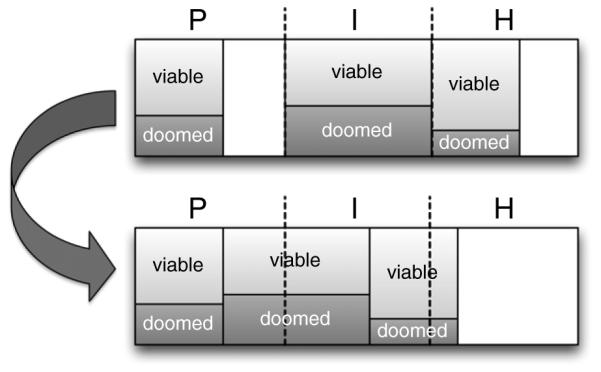
Schematic of recompartmentalization and reoxygenation pattern after the post-mitotic death of doomed cells in the P-compartment. As long as cells are available, the P-compartment ‘tops up’ at each time step.
2.7. Programming implementation
Simulations were performed using the Matlab (TM) software system (Mathworks, Inc., Natick, MA). A simplified flow chart of the simulation procedure is shown in figure 3. The main simulation algorithm is comprised of two main parts. In the first part, the initial distribution of cells in the compartments was determined based on GF and TD. In the second part, RT begins and RT fractions are delivered until the treatment goal is achieved. During RT, radiation-induced cell death, proliferation, cell loss, and recompartmentalization are executed for each compartment. After the simulation is completed, the response of the tumour is evaluated. As a discrete-time simulation algorithm, the code execution time is only a few seconds. The matrix formulation is flexible, and states and transition probabilities can easily be added or modified.
Figure 3.
Simplified flow chart of the simulation procedure.
2.8. Parameter values for head and neck cancer response
To investigate the predictions of the model, we selected parameter values for head and neck squamous cell carcinoma (HNSCC) as shown in table 1.
Table 1.
The parameters used to demonstrate the model for HNSCC.
| Parameters | Values |
|---|---|
| Tumour parameters | |
| Tumour cell density (ρt) | 106 mm−3 (Zips 2009) |
| Volume of a tumourlet (vt) | 64 mm3 (typical PET voxel size) |
| Total number of cells in a tumourlet (nt) | 6.4 × 107 (ρt · vt) |
| Stem cell fraction (fs) | 0.01 (Hemmings 2010) |
| Cell cycle time (TC) | 2 days (Malaise et al 1973) |
|
| |
| Compartment parameters | |
| Initial proliferation fraction in P () | 0.5a |
| Cell loss half-time in H (T1/2, loss) | 2 days (Ljungkvist et al 2005) |
| Survival rate of progeny after mitosis (km) | 0.3a |
| Lysis half-time (T1/2, lysis) | 3 daysa |
|
| |
| Radiosensitivity parameters | |
| Linear radiosensitivity coefficient (αP) | 0.382 Gy−1 (Pekkola-Heino et al 1995) |
| Quadratic radiosensitivity coefficient (βP) | 0.0576 Gy−2 (Chapman 2003) |
| OER of the I-compartment (OERI) | 2.0a |
| OER of the H-compartment (OERH) | 1.37 (Chan et al 2008) |
|
| |
| System parameters | |
| Time step of the calculation (Δt) | 15 min |
Assumed parameters.
Tumour growth is thought to depend on a small subset of tumour cells that have stem-cell-like properties with the ability for self-renewal (Baumann et al 2008). This cancer stem cell hypothesis was applied to the model, and the fraction of cells that are stem cells (i.e., they have the clonogenic ability to repopulate a tumour) was set to be 0.01 of the total number of viable cells in the tumourlet (Hemmings 2010). However, this number is poorly known and might vary widely. With the model’s tumour cell density of 109 cm−3, the clonogenic (stem) cell density becomes 107 cm−3, which corresponds to published values in the range of 106–108 cm−3.
Chapman (2003) reported that the quadratic term of radiosensitivity (β) is relatively fixed, compared to the linear term (α) that varies significantly among different tumours. From the average value of the 11 tumour cell lines reported in the paper, the quadratic radiosensitivity of the normoxic P-compartment (βP) was determined to be 0.0576 Gy−2. With the βP value, the linear term (αP) was then determined based on the survival fraction at 2 Gy (SF2) measured for 37 head and neck tumour cell lines in the normoxic condition (Pekkola-Heino et al 1995), which turned out to be 0.382 Gy−1, with the alpha-beta ratio (α/β) of 6.63 Gy (denoted 6.6 in subscripts).
The OER of the extremely hypoxic H-compartment (OERH) was assumed to be 1.37, based on the work of Chan et al (2008), in which a reduced OER was observed for extremely hypoxic cells due to the decreasing availability of homologous recombination. This observation is in agreement with several other reports (Berry et al 1970, Pettersen 1996, Zölzer and Streffer 2002). Chan et al also showed that the time of cells in hypoxic condition affected the OER: cells exposed to hypoxia for less time had a higher OER. Hence, the cells in the I-compartment might have a higher OER than cells in the H-compartment. Because there is no clear guidance regarding the OER of the I-compartment cells (OERI), three different values (1.2, 1.37, and 2.0) were evaluated (data not shown). The resulting TCD50’s were judged to be much more realistic with an OERI of 2.0, which still is consistent with the clinical observation that hypoxia worsens the response, as shown in the review by Overgaard (2007).
Cell lysis half-time (T1/2, lysis) was assumed to be three days and was applied to all dead cells, either from cell loss in the H-compartment or from mitotic cell death in the P-compartment.
A time step (Δt) of 15 min was used, which is sufficiently small, compared with the cell cycle time. The parameter sensitivity test was carried out in section 3.6. The impact of parameter variations was investigated, and results are discussed below.
2.9. Initial cell distribution based on GF and TD
The number of cells in each compartment before RT was determined based on GF and TD, which represents the microenvironment of a tumourlet. As shown in the appendix, GF and TD, along with model assumptions, perhaps surprisingly, imply a unique distribution among the compartments. Put simply, a higher GF always implies a higher fraction of cells in the P-compartment. Once this is fixed, variations in TD determine the fractions of cells in the I- and H-compartments.
In figure 4, the initial distributions are shown for various GF’s and TD’s. The distribution significantly differs for different GFs, since the number of cells in the P-compartment is directly determined by the GF. The size of the H-compartment becomes smaller as the TD decreases, resulting in reduced cell loss and faster overall growth. Compared to the effect of GF, the initial distribution is less sensitive to TD.
Figure 4.
The initial number of cells in each compartment before RT begins, based on various GFs and four different tumour doubling times (TD’s) for a 4×4×4 mm3 tumourlet voxel. Note that the GF of 0.05 was not high enough to yield a TD of 30 days even with no hypoxic cells.
3. Results
Tumour response was evaluated based on the calculated initial clonogen distribution. The results presented in this section focus on the variation of GF and fraction size with a fixed TD of 60 days. For a more direct comparison with clinical results, the response of an idealized, homogeneous tumour was evaluated. The tumour dose for 50% control (TCD50) can be estimated by assuming the total TCP of a tumour is the product of the TCPs of each tumourlet (or TLCP), as shown in equation (7) (Sanchez-Nieto and Nahum 1999, Buffa and Nahum 2000).
| (7) |
Table 2 shows the variation in the tumour dose required for 50% of control depending on the tumour size. Note that this is not intended to reproduce an entire clinical dose response curve; heterogeneity between tumours and within tumours (Suit et al 1992) has been neglected.
Table 2.
Model-predicted tumour dose required to achieve at least 50% of control (TCD50) depending on tumour size for a GF of 0.2, TD of 60 days, and fraction size of 2 Gy fx−1.
| Tumour diameter (cm) |
Tumour volumea (cc) |
No. of tumourlets in a tumour |
Required TLCPb |
TCD50 (Gy) |
|---|---|---|---|---|
| 1 | 0.52 | 8 | 0.918 766 | 54 |
| 2 | 4.19 | 65 | 0.989 465 | 60 |
| 3 | 14.14 | 221 | 0.996 867 | 66 |
| 4 | 33.51 | 524 | 0.998 677 | 68 |
| 5 | 65.45 | 1023 | 0.999 322 | 70 |
| 6 | 113.10 | 1767 | 0.999 608 | 74 |
| 7 | 179.59 | 2806 | 0.999 753 | 76 |
Tumour volume was calculated assuming the tumour is spherical.
Required TLCP was calculated from equation (7).
3.1. Tumour response over the course of RT
Tumour responses of a 10 cc tumour over the course of RT were compared for two different fraction sizes (2 versus 5 Gy fx−1). Beginning with the initial distribution calculated for a GF of 0.2 and a TD of 60 days, the change in the number of cells in each compartment was simulated during the course of radiation therapy.
For the conventional fraction size of 2 Gy fx−1, the change in number of viable cells during RT is shown in figure 5. In model results, it takes less than five days for the H-compartment to empty, and the overall reoxygenation time—the amount of time it took for all the hypoxic cells in the I- and H-compartments to be completely removed from the tumourlet—was found to be about 20 days from the inception of RT. After this time, all the cells are in the P-compartment, and both the cell-kill effect of a RT fraction and repopulation effect during weekend break become larger. From the number of remaining viable cells, the tumour dose for 50% control (TCD50) was estimated to be 64 Gy at 43 days, which is thought to be a clinically relevant value for a 10 cc tumour.
Figure 5.

The expected number of viable stem cells in a 10 cc tumour during the course of RT with a GF of 0.2 and a volume doubling time (TD) of 60 days for the conventional fraction size of 2 Gy fx−1 (from which TCP can be estimated).
For the hypofractionation case shown in figure 6, a faster cell-kill effect was observed with the larger fraction size of 5 Gy fx−1. Nonetheless, the estimated TCD50 was slightly higher than that for the conventional fraction size of 2 Gy fx−1 (65 versus 64 Gy). When the dose is expressed in terms of the equieffective dose in 2 Gy fractions (EQD26.6 = 87.6, following the equieffective dose concept proposed by Bentzen et al (2012)), it can be seen that the effectiveness of this larger fraction size is unexpectedly low. This is because the tumour is not reoxygenated until it achieves a 50% TCP without enough time for the doomed cells to die and leave the tumour. At the end of RT, the majority of viable cells are in the radioresistant I-compartment without reoxygenation, as shown in figure 6.
Figure 6.
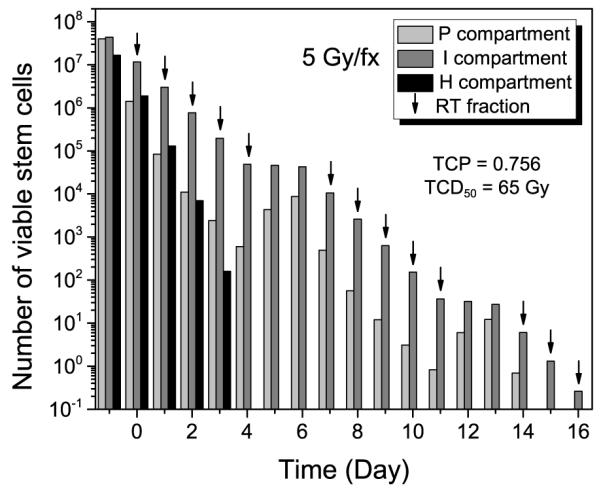
The expected number of viable stem cells in a 10 cc tumour during the course of RT with a GF of 0.2 and a volume doubling time (TD) of 60 days for hypofractionation using 5 Gy fx−1 (from which TCP can be estimated).
3.2. TCD50 versus GF for several fraction sizes
To compare the effect of various GFs and fraction sizes on tumour response, TCD50 was found for each initial distribution with different fraction sizes. Note that TCP cannot be exactly 50% in the calculation due to the discrete nature of the fractionation. Typical cases are shown in figure 7 for a 10 cc tumour. We can observe the interplay between hypoxia and proliferation from the result. In general, a tumour with a higher GF requires a smaller dose, mainly because the ratio of radioresistant hypoxic cells in the tumour decreases as the GF increases. Also, reoxygenation occurs faster with a higher GF since the size of the P-compartment, where the mitotic cell death of doomed cells takes place, is proportional to the GF.
Figure 7.
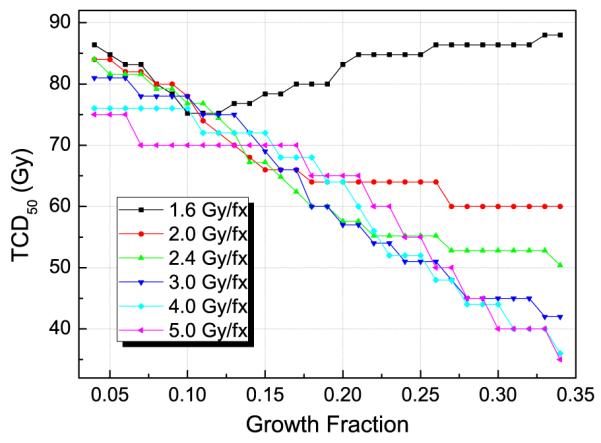
Model-predicted tumour dose required to achieve at least 50% of control (TCD50) for a 10 cc tumour versus the GF for several different fraction sizes with a volume doubling time (TD) of 60 days. Note that the TCD50 values are shown in physical dose, not in equieffective dose.
For smaller fraction sizes, however, the TCD50 did not keep decreasing as GF increased, because the proliferation capacity also increases with GF and the smaller daily fraction sizes were not enough to deal with the higher proliferation. For a fraction size of 1.6 Gy fx−1, the required TCD50 increased with increasing GF.
Interestingly, larger fraction sizes were not always more effective; for GF values of around 0.15, conventional, smaller fraction sizes (2–2.4 Gy fx−1) resulted in lower TCD50 values than those for larger fraction sizes (4–5 Gy fx−1), due to the advantage from reoxygenation.
3.3. Reoxygenation time
The reoxygenation time was calculated in two different ways, depending on the GF for the fraction size of 2 Gy fx−1 and volume doubling time of 60 days. First, the time was found when the change of the total number of hypoxic cells has a maximum curvature on a semi-log plot. Second, the full-reoxygenation time was found when all the hypoxic cells are removed from the tumour. These two values were not significantly different; they differed by less than one day. The full-reoxygenation time was shown in table 3. The reoxygenation time decreased as the GF of a tumour increased, due to higher cell death and clearance capacity with the larger P-compartment. For a GF of 0.2, the reoxygenation time was estimated to be about three weeks, which is consistent with proposed ‘kickoff’ times for accelerated clonogen accumulation (Fowler 1989). For GF of 0.05, the reoxygenation time exceeded 100 days, due to the very small size of the P-compartment.
Table 3.
Model-predicted reoxygenation times for a fraction size of 2 Gy fx−1 (TD = 60 days).
| GF | Full-reoxygenation timea (Day) |
|---|---|
| 0.05 | 131.5 |
| 0.1 | 57.6 |
| 0.15 | 33.0 |
| 0.2 | 20.6 |
| 0.25 | 13.2 |
| 0.3 | 8.1 |
When all the hypoxic cells are removed from the tumour.
3.4. Extra dose for longer treatment duration
TCD50 was also evaluated for various overall treatment durations, simulated by manipulating the fraction size for a given GF. For all cases, one fraction per weekday (5 days/week) was simulated. The results were affected by both reoxygenation and repopulation patterns, as shown in figure 8. Compared with the reoxygenation time for a given GF in table 3, it can be seen that the optimal schedule with lowest TCD50 appears shortly after reoxygenation. For a GF of 0.2, the TCD50 was lowest at about 25 days (reoxygenation time is about 21 days). Before this optimal point, there was not enough time for the doomed cells to be cleared out, resulting in poor reoxygenation. After that optimal time, repopulation increases the required TCD50.
Figure 8.
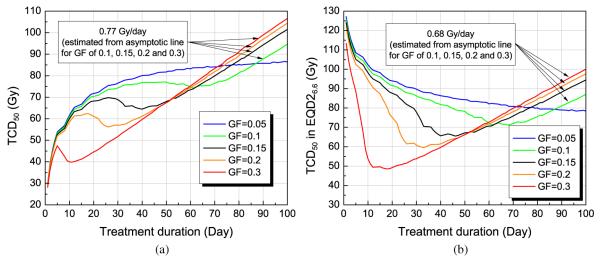
Tumour dose required to achieve at least 50% of control (TCD50) versus treatment duration for a 10 cc tumour, assuming one fraction per day (five days/week) for several different GFs with a volume doubling time (TD) of 60 days. The TCD50 values are shown in (a) physical dose or (b) equieffective dose (EQD26.6).
An asymptotic line was found for GFs of 0.1 to 0.3, and the slope of the line was found to be approximately 0.77 Gy/day, which implies the extra dose is required to overcome the loss of local control due to the prolongation of treatment time. When expressed in EQD26.6 (figure 8(b)), the estimated extra dose per day was found to be about 0.68 Gy/day.
3.5. Tumour regression patterns
Tumour regression patterns were simulated depending on the GF for a fraction size of 2 Gy fx−1. The basic assumption is that the volume of a tumour is proportional to the total number of cells in the tumour. In addition to the doomed cells, cells in lysis after mitotic death or cell loss from the H-compartment were also included.
In figure 9, the tumour regression pattern is shown for several different GF values for a fraction size of 2 Gy fx−1 and a TD of 60 days. It is shown that the regression of a tumour becomes faster with a higher GF. The black straight line is the median regression rate of HNSCC, which was clinically measured during fractionated RT (Barker et al 2004). The regression pattern for a GF of 0.1 to 0.2 seems to agree with clinically observed rate. However, the clinically measured tumour size is determined not only by the number of tumour cells, and we might also need to consider a fraction of other cells that are non-tumour cells, such as stroma.
Figure 9.
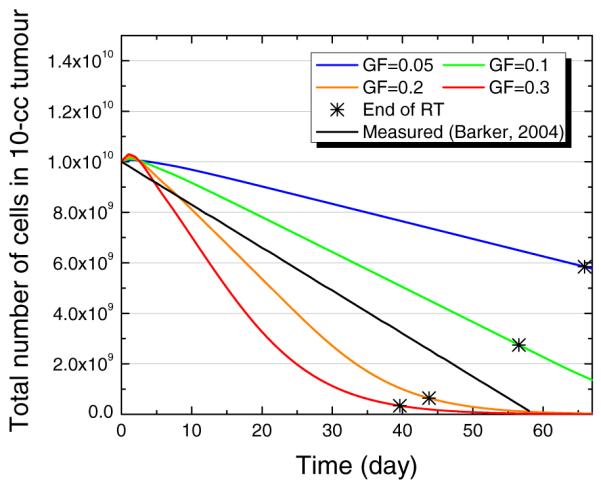
Model-predicted tumour regression pattern of 10 cc tumour depending on the GF. The star signs (*) indicate the time when RT has been finished, with TCD50 for each GF. For all cases, the TD was set to be 60 days and the fractional dose was 2 Gy fx−1.
3.6. Parameter variability effects
The model was tested for variation of model parameter values. Based on the default model values, ± 20% of variations were applied for each parameter value. For the stem cell fraction (fs), ± 20% of variations in log scale were tested. The results are summarized in table 4.
Table 4.
Model sensitivity test on the variations of model parameter values (±20% of variations, except for fs and kb) for 10 cc tumour with a GF of 0.2, TD of 60 days, and fraction size of 2 Gy fx−1 (significant change when larger than 5% was shaded).
| Parameter values | TCD50 (Gy) | Full- reoxygenation time (day) |
Extra dose for longer schedule (Gy/day) |
|
|---|---|---|---|---|
| Defaulta | 64 | 20.6 | 0.772 | |
|
| ||||
| Tumour parameters | ||||
| ρ t | 8×105 mm−3 | 64 | 20.6 | 0.773 |
| 1.2×106 mm−3 | 64 | 20.6 | 0.769 | |
| vt | 51.2 mm3 | 64 | 20.6 | 0.773 |
| 76.8 mm3 | 64 | 20.6 | 0.769 | |
| fs | 0.004b | 60(−6%) | 20.6 | 0.773 |
| 0.025b | 68 (6%) | 20.6 | 0.767 | |
| TC | 1.6 days | 76(+19%) | 16.3 (−21%) | 0.935 (+21%) |
| 2.4 days | 60 (−6%) | 25.0 (+21%) | 0.650 (−16%) | |
|
| ||||
| Compartment parameters | ||||
| 0.4 | 64 | 14.3(−31%) | 0.775 | |
| 0.6 | 66 (+3%) | 26.9 (+31%) | 0.770 | |
| T 1/2, loss | 1.6 days | 64 | 21.3 (+3%) | 0.780 (+1%) |
| 2.4 days | 64 | 20.0 (−3%) | 0.775 | |
| km | 0.24 | 66 (+3%) | 16.5(−20%) | 0.773 |
| 0.36 | 64 | 28.0 (+36%) | 0.752 (−3%) | |
|
| ||||
| Radiosensitivity parameters | ||||
| α P | 0.33 Gy−1 | 84(+31%) | 21.5 (+4%) | 0.905(+17%) |
| 0.49 Gy−1 | 54 (−16%) | 20.1 (−2%) | 0.668 (−13%) | |
| β P | 0.0461 Gy−2 | 68 (6%) | 20.8 (+1%) | 0.787 (+2%) |
| 0.0691 Gy−2 | 60 (−6%) | 20.4 (−1%) | 0.758 (−2%) | |
| OERI | 1.6 | 58 (−9%) | 20.4 (−1%) | 0.772 |
| 2.4 | 68 (+6%) | 20.8 (+1%) | 0.769 | |
| OERH | 1.10 | 64 | 20.6 | 0.772 |
| 1.64 | 64 | 20.6 | 0.772 | |
|
| ||||
| Change of blood supply | ||||
| kb c | −10%/wk | 64 | 35.6(+73%) | n/ad |
| +10%/wk | 64 | 16.3 (−21%) | 0.770 | |
Default parameter values: ρt = 106 mm−3, vt = 64 mm3, fs = 0.01, TC = 2 days, = 0.5, T1/2, loss = 2 days, km = 0.3, αP = 0.382 Gy−1, βP = 0.0576 Gy−2, OERI = 2.0, and OERH = 1.37.
±20% variations in log scale were tested.
Either linear increase or decrease of 10% per week was tested (±10%/wk).
Due to the assumption, simulation for more than 10 weeks (70 days) was not possible.
Generally, radiosensitivity-related parameters (αP, βP and OERI) had the most impact on TCD50, while compartment-related parameters ( and km) mainly affected reoxygenation time. The cell cycle time (TC) significantly affected all three evaluated aspects (TCD50, reoxygenation time, and extra dose for longer schedule). The stem cell fraction (fs) moderately affected the TCD50. The extra dose required to compensate for longer schedule was sensitive to cell cycle time (TC) and linear radiosensitivity (αP).
The effect of a change of nutrient supply (kb) was also tested by assuming a 10% linear increase or decrease per week (±10%/wk). This significantly affected the full-reoxygenation time, but did not affect the estimated TCD50 values.
4. Discussions
A mechanistically-motivated compartmental TCP model that encapsulates the cellular competition for resources, and the resulting interplay between proliferation and hypoxia, was developed. Three theoretical compartments were modelled based on access to oxygen and glucose.
It is a strength of the model that the initial (relative) clonogen distributions are completely fixed by knowing the GF and TD. A simpler model with any fewer compartments would not be able to naturally integrate GF and TD values. A more complicated model would be under-determined. The size of the P-compartment is proportional to the GF, and the size of the H-compartment is proportional to the product of GF and TD. The I-compartment, of course, is the remainder (see appendix).
The estimated TCD50 for a 10 cc homogeneous tumour with a GF of 0.2 and a TD of 60 days was 64 Gy, with the conventional fraction size of 2 Gy fx−1, which is consistent with clinical experience. Except for the fraction size of 1.6 Gy fx−1, or very high GFs with 2.0 Gy fx−1, the TCD50 value predicted by the model decreases as GF increases, implying that a more proliferative tumour might have a more favourable prognosis, compared with hypoxic tumours. The prognostic value of proliferation for HNSCC measured by Ki-67 labelling index is still controversial (Pich et al 2004). Several authors have reported that high proliferation correlates with a favourable response, when treated with radiation therapy (Kropveld et al 1998, Raybaud et al 2000). Although higher proliferation results in faster repopulation of tumour cells, it also implies less intermediately hypoxic cells and more rapid reoxygenation.
Since the extremely hypoxic H-compartment is assumed to have a modest OER value of 1.37, and the cells in the H-compartment vanish relatively rapidly (less than five days for a GF of 0.2; figures 5 and 6), the metabolically-active I-compartment is more important to RT response. The effect of different OER values of the I-compartment (1.2, 1.37, and 2.0) was significant (data not shown). For OERI values of 1.2 and 1.37, the hypoxic effect was smaller than the proliferation effect in magnitude, and the dose required for a hypoxic tumour (lower GF) was evaluated to be smaller than for a normoxic tumour (high GF). From clinical observations, it is known that hypoxic tumours require higher doses for control (Overgaard 2007), and an OERI of 2.0 seems to be more clinically relevant, although clearly there is significant uncertainty associated with this value. For a 10 cc tumour with an OERI of 2.0 (figure 7), the dose difference (Δ) between a tumour with significant hypoxia and one with little hypoxia, for 2 Gy fx−1, was about 20 Gy.
For acutely (intermittently) hypoxic cells, the OER value might be as high as 3. Although acute hypoxia was not considered in this work, a maximum OER of 3 was tested to examine the extent of the effect. When the OER of the H-compartment (OERH) was assumed to be 3, the resulting TCD50 was not significantly affected, except for very high GFs, in which an increase of about 7% was observed (data not shown). This could be expected, considering the lower contribution of the H-compartment that vanishes relatively quickly. When the OER of the I-compartment (OERI) was assumed to be 3, however, the evaluated TCD50 values were significantly affected depending on the GF (figure 10). Although a modest effect was observed for higher GFs (GF = 0.2–0.3), the required TCD50 increased as GF decreased. For a GF of 0.05, which represents a very hypoxic tumour with a small fraction of proliferating cells, the TCD50 was found to be almost double that of a normoxic tumour with a higher GF (GF = 0.2–0.3). This seems to overestimate the effect of hypoxia, and the OER value for the I-compartment used in this work (OERI = 2) seems to adequately represent the clinical reality.
Figure 10.

Comparison of TCD50 values found for different assumptions of I-compartment conditions, based on OER value and proliferation status. The results are shown for four different GFs.
There is some evidence that some cells in intermediately hypoxic conditions can also proliferate (Wijffels et al 2008). The current model assumed no proliferation in the hypoxic compartments (both I- and H-compartments). To estimate the effect of proliferation under hypoxic conditions, a 10% proliferation rate was assumed in the I-compartment, and the tumour responses were reevaluated. Proliferation in the I-compartment had two different effects: first, the higher proliferation capacity of the population resulted in a higher required dose; second, with larger mitotic cell death capacity, reoxygenation time decreased which reduces the required dose. These two effects were against each other depending on the GF: for a higher GF, the required TCD50 increased with higher proliferation capacity; for a lower GF, increased mitotic cell death capacity reduced the required TCD50. In general, however, the effect was not that significant, with changes of less than 10%, as shown in figure 10.
The effect of fraction size was evaluated for various GFs. TCD50 is predicted to be relatively insensitive to fractionation, except when reoxygenation occurs before the end of therapy. For a small (10 cc) tumour, this only happens with high GF values and 2.0 Gy fx−1 or lower GF values and 1.6 Gy fx−1. For larger tumours, reoxygenation is likely to occur well before a tumouricidal dose is obtained, and hypofractionation may be an advantage as proposed by Fowler et al (2004).
The effect of overall treatment time on TCD50 was evaluated. The pattern was again closely related to reoxygenation, as dose was lost due to clonogen proliferation. For tumours with a high GF, the dependence of overall time on total dose forms a shape that might be identified as the ‘Withers dog-leg effect’ (Withers et al 1988). Accelerated clonogen proliferation after a certain ‘kick-off time’ (often modelled by assuming a kick-off time of—three to four weeks) arises naturally from this simple model and thus explains the kick-off time in terms of the competition for resources. The result suggests that there might exist an optimal fractionation schedule if the GF were known. The extra dose required to compensate for the loss of local control due to longer treatment time was estimated to be 0.77 Gy/day and is driven by kinetic and radiosensitivity parameters. When the total dose is normalized to 2 Gy fractionation (EQD26.6), the extra dose per day was estimated to be 0.68 Gy/day (figure 8(b)), which agrees well with Hendry et al’s estimate from clinical data (0.64 Gy/day, 95% Cl [0.42; 0.86]) for HNSCC (Hendry et al 1996).
Except for cell cycle time (TC) and the linear radiosensitivity coefficient (αP), all the other parameters showed almost no effect on the estimated extra dose required to overcome a longer schedule of treatment. At the end of RT, when the success or failure of the treatment is determined, all the viable cells are in the P-compartment for the longer schedule. Therefore, the extra dose per day depends on the cell proliferation capacity of the P-compartment, which is unaffected by those parameters. Failure of local control occurs in the P-compartment for the conventional fractionation schedule. This could be a possible explanation for the accelerated repopulation and rapid relapse of the tumour that is observed after completing a course of radiation therapy (Withers et al 1988).
By incorporating a doomed sub-compartment in the model, clinically realistic tumour reoxygenation patterns emerge. Reoxygenation takes place as doomed cells are removed from the tumourlet and the cells in the hypoxic compartments return to the (intermittently) normoxic P-compartment. Since the rate of doomed cell death increases as the GF increases, resulting in a larger P-compartment, reoxygenation becomes faster. In this model, the reoxygenation phenomenon is explicitly described based on a constant oxygenation capacity of a tumourlet, which corresponds to the classical view of reoxygenation based on the limited oxygen diffusion from a capillary (Hall and Giaccia 2006). This seems to be a more realistic representation, compared with other models in which reoxygenation is modelled by assuming either a constant hypoxic fraction (Popple et al 2002) or a constant reoxygenation rate (Søvik et al 2007).
It is important to note that the model does not account for all types of hypoxia. For example, the natural growth of a tumour, and the extraction of oxygen and glucose ‘upstream’ in the vasculature system, might permanently starve other tumour regions causing non-uniform growth or regression. Moreover, potentially important transient changes during RT, such as vascular remodelling (Johansson and Ganss 2012), or reductions in interstitial fluid pressure due to tumour regression, are not included in the model. It therefore cannot be view as a definitive model, but rather as an elaboration beyond previous models.
The regression pattern also depends on the removal of doomed cells and was evaluated by incorporating mitotic cell death of doomed cells and the subsequent lysis mechanism into the model. A tumour having a GF of 0.1 to 0.2, which is thought to be the most clinically relevant range, showed good agreement with clinical observations, as shown in figure 9. The regression pattern was not significantly different for different fraction sizes (data not shown). As in reoxygenation, the delayed clearance of doomed cells seems to determine the rate of regression, which is mainly governed by the size of the P-compartment or the GF. Some researchers have developed tumour regression models based on the half-life of doomed cell disintegration (Chvetsov et al 2008, 2009, Huang et al 2010). Chvetsov et al (2009) evaluated clinical data for HNSCC and estimated that the half-life of normoxic doomed cells is about 18 days. In our model, the disintegration of doomed cells consists of two steps: mitotic cell death and lysis. The effective half-life was found to be about 15 days, which is similar to Chvetsov’s result. Also, this pattern provides valuable information for RT that is adaptive between fractions (Chvetsov et al 2008).
With a GF of 0.2 and a TD of 60 days for a 10 cc tumour, the model results are consistent with clinical experience, including a TCD50 of 64 Gy, a reoxygenation time of about three weeks, an extra dose per day of 0.68 Gy/day, and a kick-off time of about—three to four weeks. Although the tumour regression pattern suggests a GF of about 0.15 to be most clinically relevant, this discrepancy might be explained by considering non-tumour cells, such as stroma, that exist in the tumour volume.
In the current study, the initial distribution of cells in each compartment was derived from the GF and TD, and the feasibility of the model was investigated. The method to produce the initial distribution from a PET image should be developed, so that this model can be used for adaptive radiation therapy, in which a boost dose is given in voxel dimension.
Potentially, a model such as this could be helpful in the optimization of non-uniform dose distribution for voxel-based adaptive radiation therapy.
5. Conclusions
A model has been introduced to describe the competition for chemical resources, resulting in hypoxia and limited proliferation, and the resulting impact on RT. An effort was made to make the model as simple as possible, but not too simple. Several features consistent with clinical RT experience emerged from simulation results, including: reasonable doses required for local control, tumour regression rates, and the dose required to compensate for accelerated clonogen accumulation.
Interestingly, simulations for an assumed growth fraction of 0.15, consistent with typical tumour regression patters, support an optimal fractionation schedule of about 2 Gy/day, at least when critical normal tissue endpoints would have a similar alpha/beta ratio (6.6 Gy). Potentially, more optimal overall treatment times could be customized if patient-specific growth fractions and tumour doubling times could be measured. At very low growth fractions, hypofractionation might be preferable, depending on normal tissue tolerance, because reoxygenation will not occur during a standard regimen.
It should be pointed out, however, that the model is a crude approximation of a complicated bio-physical reality, and should be extensively tested and potentially refined using clinical and pre-clinical data.
Acknowledgments
The authors thank Dr Alan E Nahum and Dr Jack F Fowler for reading and commenting on this paper. This research was supported by Enid A Haupt Medical Physics Endowed Chair fund at Memorial Sloan-Kettering Cancer Center, as well as the Nuclear Science and Engineering Institute of the University of Missouri, and the Department of Radiation Oncology of the Washington University School of Medicine.
Appendix. Analytic solution for the initial cellular distribution
Given the model assumptions, the initial distributions of cells in each compartment can be analytically derived based on the growth fraction (GF) and cell loss factor (CLF). The CLF is defined as the rate of cell loss from a tumour, as a proportion of the rate at which cells are being added to the tumour by mitosis:
| (A.1) |
Proliferation only takes place in the P-compartment, for a fraction of cells in active proliferation. Cell loss only occurs in the H-compartment following exponential decay with cell loss half-time. The rates of proliferation and cell loss can be expressed as follows:
| (A.2) |
From the definition of CLF (equation A.1) and rates of proliferation and cell loss (equation A.2), the number of cells in the H-compartment (NH) can be expressed in terms of the number of cells in the P-compartment (NP) in terms of CLF as follows:
| (A.3) |
It can be seen that the number of cells in the H-compartment (NH) is proportional to the number of cells in the P-compartment (NP) and the proportional constant can be directly determined from the CLF, the fraction of cells in active proliferation in the P-compartment, and the ratio of cell loss half-time and cell cycle time.
The number of cells in the P-compartment (NP) is defined based on the GF, as a fraction of the total number of cells (Ntotal). From the relation between NHand NP (equation A.3), the number of cells in the H- and I-compartments (NHand NI) can be calculated. The number of cells in each compartment satisfying a given GF and CLF are therefore as follows:
| (A.4) |
When the CLF is less than 1, the total number of cells () increases and the rate of increase can be determined from the following rate equation:
| (A.5) |
By solving the differential equation with initial total number (), we get the following equation:
| (A.6) |
From the above equation (A.6), the volume doubling time (TD) can be found in terms of CLF, GF and TC, assuming the tumour volume is proportional to the number of cells. The exponential term of equation (A.6) can be expressed as 2(1–CLF)·GF·t/Tc and the volume doubling time can be found as the following equation:
| (A.7) |
Therefore, the initial number of cells in each compartment (equation A.4) can also be expressed in terms of GF and TD as follows:
| (15) |
References
- Barker JL, Jr, et al. Quantification of volumetric and geometric changes occurring during fractionated radiotherapy for head-and-neck cancer using an integrated CT/linear accelerator system. Int. J. Radiat. Oncol. Biol. Phys. 2004;59:960–70. doi: 10.1016/j.ijrobp.2003.12.024. [DOI] [PubMed] [Google Scholar]
- Baumann M, Krause M, Hill R. Exploring the role of cancer stem cells in radioresistance. Nature Rev. Cancer. 2008;8:545–54. doi: 10.1038/nrc2419. [DOI] [PubMed] [Google Scholar]
- Bentzen SM, Dörr W, Gahbauer R, Howell Howell R W, Joiner MC, Jones B, Jones DTL, van der Kogel A J, Wambersie A, Whitmore G. Bioeffect modeling and equieffective dose concepts in radiation oncology-terminology, quantities and units. Radiother. Oncol. 2012;105:266–8. doi: 10.1016/j.radonc.2012.10.006. [DOI] [PubMed] [Google Scholar]
- Berry RJ, Hall EJ, Cavanagh J. Radiosensitivity and the oxygen effect for mammalian cells cultured in vitro in stationary phase. Br. J. Radiol. 1970;43:81–90. doi: 10.1259/0007-1285-43-506-81. [DOI] [PubMed] [Google Scholar]
- Borkenstein K, Levegrün S, Peschke P. Modeling and computer simulations of tumor growth and tumor response to radiotherapy. Radiat. Res. 2004;162:71–83. doi: 10.1667/rr3193. [DOI] [PubMed] [Google Scholar]
- Brown JM, Attardi LD. The role of apoptosis in cancer development and treatment response. Nature Rev. Cancer. 2005;5:231–7. doi: 10.1038/nrc1560. [DOI] [PubMed] [Google Scholar]
- Buffa FM, Nahum AE. Monte Carlo dose calculations and radiobiological modelling: analysis of the effect of the statistical noise of the dose distribution on the probability of tumour control. Phys. Med. Biol. 2000;45:3009–23. doi: 10.1088/0031-9155/45/10/318. [DOI] [PubMed] [Google Scholar]
- Buffa FM, West C, Byrne K, Moore JV, Nahum AE. Radiation response and cure rate of human colon adenocarcinoma spheroids of different size: the significance of hypoxia on tumor control modelling system. Int. J. Radiat. Oncol. Biol. Phys. 2001;49:1109–18. doi: 10.1016/s0360-3016(00)01533-9. [DOI] [PubMed] [Google Scholar]
- Cárdenas-Navia LI, Mace D, Richardson RA, Wilson DF, Shan S, Dewhirst MW. The pervasive presence of fluctuating oxygenation in tumors. Cancer Res. 2008;68:5812–9. doi: 10.1158/0008-5472.CAN-07-6387. [DOI] [PubMed] [Google Scholar]
- Carlson DJ, Stewart RD, Semenenko VA. Effects of oxygen on intrinsic radiation sensitivity: a test of the relationship between aerobic and hypoxic linear-quadratic (LQ) model parameters. Med. Phys. 2006;33:3105–15. doi: 10.1118/1.2229427. [DOI] [PubMed] [Google Scholar]
- Caswell H. Matrix Population Models: Construction, Analysis, and Interpretation. Sinauer; Sunderland, MA: 2001. [Google Scholar]
- Chan N, Koritzinsky M, Zhao H, Bindra R, Glazer PM, Powell S, Belmaaza A, Wouters B, Bristow RG. Chronic hypoxia decreases synthesis of homologous recombination proteins to offset chemoresistance and radioresistance. Cancer Res. 2008;68:605–14. doi: 10.1158/0008-5472.CAN-07-5472. [DOI] [PubMed] [Google Scholar]
- Chapman JD. Single-hit mechanism of tumour cell killing by radiation system. Int. J. Radiat. Biol. 2003;79:71–81. [PubMed] [Google Scholar]
- Chvetsov AV, Dong L, Palta JR, Amdur RJ. Tumor-volume simulation during radiotherapy for head-and-neck cancer using a four-level cell population model. Int. J. Radiat. Oncol. Biol. Phys. 2009;75:595–602. doi: 10.1016/j.ijrobp.2009.04.007. [DOI] [PubMed] [Google Scholar]
- Chvetsov AV, Palta JJ, Nagata Y. Time-dependent cell disintegration kinetics in lung tumors after irradiation. Phys. Med. Biol. 2008;53:2413–23. doi: 10.1088/0031-9155/53/9/013. [DOI] [PubMed] [Google Scholar]
- Dawson A, Hillen T. Derivation of the tumour control probability (TCP) from a cell cycle model. Comput. Math. Methods Med. 2006;7:121–41. [Google Scholar]
- Dionysiou DD, Stamatakos GS, Uzunoglu NK, Nikita KS, Marioli A. A four-dimensional simulation model of tumour response to radiotherapy in vivo: parametric validation considering radiosensitivity, genetic profile and fractionation. J. Theor. Biol. 2004;230:1–20. doi: 10.1016/j.jtbi.2004.03.024. [DOI] [PubMed] [Google Scholar]
- Forrester HB, Vidair CA, Albright N, Ling CC, Dewey WC. Using computerized video time lapse for quantifying cell deathof X-irradiated rat embryo cells transfected with c-myc or c-Ha-ras. Cancer Res. 1999;59:931–9. [PubMed] [Google Scholar]
- Fowler JF. The linear-quadratic formula and progress in fractionated radiotherapy. Br. J. Radiol. 1989;62:679–94. doi: 10.1259/0007-1285-62-740-679. [DOI] [PubMed] [Google Scholar]
- Fowler JF, Tomé WA, Fenwick JD, Mehta MP. A challenge to traditional radiation oncology. Int. J. Radiat. Oncol. Biol. Phys. 2004;60:1241–56. doi: 10.1016/j.ijrobp.2004.07.691. [DOI] [PubMed] [Google Scholar]
- Hall EJ, Giaccia AJ. Radiobiology for the Radiologist. Lippincott Williams & Wilkins; Philadelphia, PA: 2006. [Google Scholar]
- Hemmings C. The elaboration of a critical framework for understanding cancer: the cancer stem cell hypothesis. Pathology. 2010;42:105–12. doi: 10.3109/00313020903488773. [DOI] [PubMed] [Google Scholar]
- Hendry JH, Bentzen SM, Dale RG, Fowler JF, Wheldon TE, Jones B, Munro AJ, Slevin NJ, Robertson AG, Cowles A. A modelled comparison of the effects of using different ways to compensate for missed treatment days in radiotherapy. Clin. Oncol. 1996;8:297–307. doi: 10.1016/s0936-6555(05)80715-0. [DOI] [PubMed] [Google Scholar]
- Hlatky L, Sachs RK, Alpen EL. Joint oxygen-glucose deprivation as the cause of necrosis in a tumor analog. J. Cell. Physiol. 1988;134:167–78. doi: 10.1002/jcp.1041340202. [DOI] [PubMed] [Google Scholar]
- Hoogsteen IJ, Marres HA, Bussink J, van der Kogel A J, Kaanders JH. Tumor microenvironment in head and neck squamous cell carcinomas: predictive value and clinical relevance of hypoxic markers a review. Head Neck. 2007;29:591–604. doi: 10.1002/hed.20543. [DOI] [PubMed] [Google Scholar]
- Hoogsteen IJ, Marres HA, Wijffels KI, Rijken PF, Peters JP, van den Hoogen F J, Oosterwijk E, van der Kogel A J, Kaanders JH. Colocalization of carbonic anhydrase 9 expression and cell proliferation in human head and neck squamous cell carcinoma. Clin. Cancer Res. 2005;11:97–106. [PubMed] [Google Scholar]
- Huang Z, et al. Predicting outcomes in cervical cancer: a kinetic model of tumor regression during radiation therapy. Cancer Res. 2010;70:463–70. doi: 10.1158/0008-5472.CAN-09-2501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johansson A, Ganss R. Remodeling of tumor stroma and response to therapy. Cancers. 2012;4:340–53. doi: 10.3390/cancers4020340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiran KL, Jayachandran D, Lakshminarayanan S. Mathematical modelling of avascular tumour growth based on diffusion of nutrients and its validation. Can. J. Chem. Eng. 2009;87:732–40. [Google Scholar]
- Kropveld A, Slootweg PJ, Blankenstein MA, Terhaard CHJ, Hordijk GJ. Ki-67 and p53 in T2 laryngeal cancer. Laryngoscope. 1998;108:1548–52. doi: 10.1097/00005537-199810000-00023. [DOI] [PubMed] [Google Scholar]
- Ljungkvist ASE, Bussink J, Kaanders JHAM, Rijken PFJW, Begg AC, Raleigh JA, van der Kogel A J. Hypoxic cell turnover in different solid tumor lines. Int. J. Radiat. Oncol. Biol. Phys. 2005;62:1157–68. doi: 10.1016/j.ijrobp.2005.03.049. [DOI] [PubMed] [Google Scholar]
- Ljungkvist ASE, Bussink J, Kaanders JHAM, Wiedenmann NE, Vlasman R, van der Kogel A J. Dynamics of hypoxia, proliferation and apoptosis after irradiation in a murine tumor model. Radiat. Res. 2006;165:326–36. doi: 10.1667/rr3515.1. [DOI] [PubMed] [Google Scholar]
- Malaise EP, Chavaudra N, Tubiana M. The relationship between growth rate, labelling index and histological type of human solid tumours. Eur. J. Cancer. 1973;9:305–12. doi: 10.1016/0014-2964(73)90099-6. [DOI] [PubMed] [Google Scholar]
- McAneney H, O’Rourke SFC. Investigation of various growth mechanisms of solid tumour growth within the linear-quadratic model for radiotherapy. Phys. Med. Biol. 2007;52:1039–54. doi: 10.1088/0031-9155/52/4/012. [DOI] [PubMed] [Google Scholar]
- Nahum AE, Movsas B, Horwitz EM, Stobbe CC, Chapman JD. Incorporating clinical measurements of hypoxia into tumor local control modeling of prostate cancer: implications for the α/β ratio. Int. J. Radiat. Oncol. Biol. Phys. 2003;57:391–401. doi: 10.1016/s0360-3016(03)00534-0. [DOI] [PubMed] [Google Scholar]
- Nilsson J, Lind BK, Brahme A. Radiation response of hypoxic and generally heterogeneous tissues. Int. J. Radiat. Biol. 2002;78:389–405. doi: 10.1080/09553000110113038. [DOI] [PubMed] [Google Scholar]
- O’Donoghue JA. The response of tumours with Gompertzian growth characteristics to fractionated radiotherapy. Int. J. Radiat. Biol. 1997;72:325–39. doi: 10.1080/095530097143329. [DOI] [PubMed] [Google Scholar]
- Oka K, Nakano T, Hoshi T. Transient increases of growth fraction during fractionated radiation therapy for cervical carcinoma ki-67 and pc10 immunostaining. Cancer. 1993;72:2621–7. doi: 10.1002/1097-0142(19931101)72:9<2621::aid-cncr2820720917>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- Okada H, Mak TW. Pathways of apoptotic and non-apoptotic death in tumour cells. Nature Rev. Cancer. 2004;4:592–603. doi: 10.1038/nrc1412. [DOI] [PubMed] [Google Scholar]
- Overgaard J. Hypoxic radiosensitization: adored and ignored. J. Clin. Oncol. 2007;25:4066–74. doi: 10.1200/JCO.2007.12.7878. [DOI] [PubMed] [Google Scholar]
- Park HJ, Griffin RJ, Hui S, Levitt SH, Song CW. Radiation-induced vascular damage in tumors: implications of vascular damage in ablative hypofractionated radiotherapy (SBRT and SRS) Radiat. Res. 2012;177:311–27. doi: 10.1667/rr2773.1. [DOI] [PubMed] [Google Scholar]
- Pekkola-Heino K, Jaakkola M, Kulmala J, Grenman R. Comparison of cellular radiosensitivity between different localizations of head and neck squamous cell carcinoma. J. Cancer Res. Clin. Oncol. 1995;121:452–6. doi: 10.1007/BF01218360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters LJ, Ang KK, Thames HD. Accelerated fractionation in the radiation treatment of head and neck cancer A critical comparison of different strategies. Acta Oncol. 1988;27:185–94. doi: 10.3109/02841868809090339. [DOI] [PubMed] [Google Scholar]
- Petersen C, Eicheler W, Frömmel A, Krause M, Balschukat S, Zips D, Baumann M. Proliferation and micromilieu during fractionated irradiation of human FaDu squamous cell carcinoma in nude mice. Int. J. Radiat. Biol. 2003;79:469–77. doi: 10.1080/09553000310001609224. [DOI] [PubMed] [Google Scholar]
- Pettersen EO. Radiation-modifying effect of oxygen in synchronized cells pre-treated with acute or prolonged hypoxia. Int. J. Radiat. Biol. 1996;70:319–26. doi: 10.1080/095530096145058. [DOI] [PubMed] [Google Scholar]
- Pich A, Chiusa L, Navone R. Prognostic relevance of cell proliferation in head and neck tumors. Ann. Oncol. 2004;15:1319–29. doi: 10.1093/annonc/mdh299. [DOI] [PubMed] [Google Scholar]
- Popple RA, Ove R, Shen S. Tumor control probability for selective boosting of hypoxic subvolumes, including the effect of reoxygenation. Int. J. Radiat. Oncol. Biol. Phys. 2002;54:921–7. doi: 10.1016/s0360-3016(02)03007-9. [DOI] [PubMed] [Google Scholar]
- Raybaud H, Fortin A, Bairati I, Morency R, Monteil RA, Têtu B. Nuclear DNA content, an adjunct to p53 and Ki-67 as a marker of resistance to radiation therapy in oral cavity and pharyngeal squamous cell carcinoma. Int. J. Oral Maxillofac. Surg. 2000;29:36–41. [PubMed] [Google Scholar]
- Roose T, Chapman SJ, Maini PK. Mathematical models of avascular tumor growth. SIAM Rev. 2007;49:179–208. [Google Scholar]
- Roti Roti J L, Dethlefsen LA. Matrix simulation of duodenal crypt cell kinetics: I. The steady state. Cell Tissue Kinet. 1975a;8:321–33. doi: 10.1111/j.1365-2184.1975.tb01497.x. [DOI] [PubMed] [Google Scholar]
- Roti Roti J L, Dethlefsen LA. Matrix simulation of duodenal crypt cell kinetics: II. Cell kinetics following hydroxyurea. Cell Tissue Kinet. 1975b;8:335–53. doi: 10.1111/j.1365-2184.1975.tb01498.x. [DOI] [PubMed] [Google Scholar]
- Sanchez-Nieto B, Nahum AE. The delta-TCP concept: a clinically useful measure of tumor control probability. Int. J. Radiat. Oncol. Biol. Phys. 1999;44:369–80. doi: 10.1016/s0360-3016(99)00029-2. [DOI] [PubMed] [Google Scholar]
- Søvik Å , Malinen E, Bruland S, Bentzen SM, Olsen DR. Optimization of tumour control probability in hypoxic tumours by radiation dose redistribution: a modelling study. Phys. Med. Biol. 2007;52:499–513. doi: 10.1088/0031-9155/52/2/013. [DOI] [PubMed] [Google Scholar]
- Steel GG. Growth Kinetics of Tumours : Cell Population Kinetics in Relation to the Growth and Treatment of Cancer. Clarendon; Oxford: 1977. [Google Scholar]
- Suit H, Skates S, Taghian A, Okunieff P, Efird JT. Clinical implications of heterogeneity of tumor response to radiation therapy. Radiother. Oncol. 1992;25:251–60. doi: 10.1016/0167-8140(92)90244-o. [DOI] [PubMed] [Google Scholar]
- Titz B, Jeraj R. An imaging-based tumour growth and treatment response model: Investigating the effect of tumour oxygenation on radiation therapy response. Phys. Med. Biol. 2008;53:4471–88. doi: 10.1088/0031-9155/53/17/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Travis EL, Tucker SL. Isoeffect models and fractionated radiation. Int. J. Radiat. Oncol. Biol. Phys. 1987;13:283–7. doi: 10.1016/0360-3016(87)90141-6. [DOI] [PubMed] [Google Scholar]
- Wang JZ, Li XA, Mayr NA. Dose escalation to combat hypoxia in prostate cancer: a radiobiological study on clinical data. Br. J. Radiol. 2006;79:905–11. doi: 10.1259/bjr/18700614. [DOI] [PubMed] [Google Scholar]
- Wijffels KI, Marres HA, Peters JP, Rijken PF, van der Kogel A J, Kaanders JH. Tumour cell proliferation under hypoxic conditions in human head and neck squamous cell carcinomas. Oral Oncol. 2008;44:335–44. doi: 10.1016/j.oraloncology.2007.04.004. [DOI] [PubMed] [Google Scholar]
- Withers HR, Taylor JMG, Maciejewski B. The hazard of accelerated tumor clonogen repopulation during radiotherapy. Acta Oncol. 1988;27:131–46. doi: 10.3109/02841868809090333. [DOI] [PubMed] [Google Scholar]
- Wouters BG. Cell death after irradiation: how, when and why cells die. In: Joiner M, van der Kogel A, editors. Basic Clinical Radiobiology. Hodder Arnold; London: 2009. pp. 27–40. [Google Scholar]
- Zips D. Tumor growth and response to radiation. In: Joiner M, van der Kogel A, editors. Basic Clinical Radiobiology. Hodder Arnold; London: 2009. pp. 78–101. [Google Scholar]
- Zölzer F, Streffer C. Increased radiosensitivity with chronic hypoxia in four human tumor cell lines. Int. J. Radiat. Oncol. Biol. Phys. 2002;54:910–20. doi: 10.1016/s0360-3016(02)02963-2. [DOI] [PubMed] [Google Scholar]