An Introduction and Integration of Cross-Classified, Multiple Membership, and Dynamic Group Random-Effects Models

Abstract

In longitudinal studies, time-varying group membership and group effects are important issues that need to be addressed. In this article we describe use of cross-classified and multiple membership random-effect models to address time varying group membership, and dynamic group random-effect models to address time-varying group effects. We propose new models that integrate features of existing models, evaluate these models through simulation, provide guidance on how to fit these models, and apply the models in two real data examples. The discussion focuses on challenges in the application of these models.

The design of many studies in the social sciences involves individuals who are measured over time and are members of groups (e.g., schools, families, therapy groups). In order to address the dependency or correlation among individuals within the same group it is now common practice to fit a multilevel model, otherwise known as a hierarchical linear model or mixed-effects model (Hedeker & Gibbons, 2006; Hox, 2002; Raudenbush & Bryk 2002; Snijders, & Bosker, 1999). In some studies however there is additional complexity introduced when individuals change groups over time. For instance, in a study comparing two types of treatments for an anxiety disorder some individuals may receive treatment from one therapist and then switch to another therapist during the course of the study. Given that a multilevel model that assumes individuals remain in the same groups over time would be inappropriate, cross-classified random-effect models were developed that allowed for group membership to be a time-varying random effect (Goldstein, 1987; Raudenbush, 1993). That is, these models allow for the dependency in observations within a group to be modeled based on the group an individual belongs to at a particular point in time. Further extensions were developed to address people being members of more than one group simultaneously, which we refer to as multiple membership (e.g., Hill & Goldstein, 1998; Goldstein, 2003; Raudenbush & Bryk, 2002). Several simulations have shown that misspecification of a model with a population cross-classified or multiple membership structure can lead to inaccurate estimates of random effects and fixed effect standard errors (Chung & Beretvas, 2012; Luo & Kwok, 2009, 2012; Myers & Beretvas, 2006; Roberts & Walwyn, 2012). How might this impact tests of the treatment effect in our hypothetical study comparing anxiety disorder treatments? If the standard error of the time by treatment interaction is systematically overestimated due to inappropriately modeling time-varying group effects (Luo & Kwok, 2012), then we risk having standard errors that are artificially high, decreased power to detect effects, and confidence intervals that are too wide. Moreover, it might be of interest to know how much of the variability in the outcome is attributable to the therapist or which therapists perform particularly good or bad. If the therapist variance is underestimated because we have misspecified the model with respect to group membership (Luo & Kwok, 2012), then we risk understating the therapist effect and incorrectly identifying particular therapists with good or bad performance. Therefore, it becomes important that the model is specified as accurately as possible with respect to group membership.

A conceptually distinct issue from the one above is the effect of the groups over time. In a conventional multilevel model if an individual remains in the same group over time then that model assumes that the group exerts a constant force on that individual’s response (and all other individuals who belong to that group). It is important to distinguish the concept presented here from the one presented in the preceding paragraph. If an individual changed groups over time, then cross-classified and multiple membership random-effect models would allow for the different groups to affect the person’s response differently, but the effect of each group would still be assumed to be constant over time. A constant group effect is a tenuous assumption, given that characteristics of groups change over time, leading to an effect that depends on time. It might be reasonable, for example, to expect that the group effect for measurements taken closer together in time would be more similar than those taken farther apart. For instance, in a psychological treatment study, the effect of the therapist on the person’s outcome would likely be more similar if we compared their effect in the first and second months of therapy than if we compared the effect in the second and tenth month. Given the possibility of non-constant group effects, a distinct line of statistical research has developed models that allow for greater flexibility in how the effects of groups on individual responses are quantified, referred to as dynamic group models (Bauer, Gottfredson, Dean, & Zucker, 2013; Leckie & Goldstein, 2009, 2011; Paddock, Hunter, Watkins, & McCaffrey, 2011). Use of dynamic groups could be motivated by concerns related to misspecfication and its impact on model estimates, similar to those described above. Moreover, dynamic group models may offer additional insight into the impact of therapists, in particular the ability to evaluate the correlation of the therapist effect over time. For instance, a higher correlation for the therapist effect observed for measurements taken closer together in time than for measurements taken farther apart would suggest that good therapists stay good and bad therapists stay bad over short periods of time, but that the pattern attenuates over longer periods of time (Bauer et al., 2013). Collectively, dynamic group models offer greater flexibility than conventional approaches, which may translate to more accurate parameter estimates and novel insights into the effect of groups over time.

In light of the methodological developments related to modeling group membership and group effects over time, the objective of this paper is to provide the reader with an introduction to these statistical models, but going beyond existing didactic resources (e.g., Goldstein, Browne & Rasbash, 2002; Raudenbush & Bryk, 2002; Rasbash & Browne, 2008) in several respects. In addition to a thorough presentation of the models, we show how aspects of these models can be integrated together, evaluate the models through simulation, illustrate how to use general purpose software to fit these models, and illustrate their application in two data sets.

Two Real Data Examples

In this paper we analyze data from two studies. The first is a longitudinal study designed to examine predictors (e.g., student gender, school-type) of growth in mathematics achievement of students during elementary and middle school, with some students changing schools during the study period. Therefore, we have students measured over time on their math achievement, with their school or “group” membership possibly changing from one time to the next. In order to maximize the chances that our model produces trustworthy results, perhaps most importantly for the fixed effects (e.g., gender by time interaction), it is important to incorporate the student’s changing school membership in the analysis. It might be especially important in this example to also consider the possibility that past group affiliations affect a student’s current achievement. This corresponds to the idea that at a particular point in time a student’s mathematics achievement is impacted by both their past and current school memberships, and this historical multiple membership shapes their achievement. In this study we also want to be cognizant of how the group effects are treated in any modeling approach, ascertaining whether these effects are constant or have some form of dynamic structure. If a dynamic structure is more appropriate we would seek to specify the structure as accurately as possible in order to minimize model specification errors, as well as to identify a structure that might tell us something about the schools themselves.

The second study examines clinician’s attitudes towards evidence-based practice over time, as part of an implementation study (i.e., studies focused on examination of factors that support broader adoption, use, and scale-up of evidence-based interventions in usual care settings; Aarons, Hurlburt, & Horwitz, 2011). The main question of interest is whether there is a change of these attitudes over time as a function of whether they are in one of four conditions, they administer the evidence-based practice (Yes/No) × they are monitored to ensure adequate administration (Yes/No). Clinicians are supervised and during the course of the study they may change from one supervision group to another. As with the first study, accurate accounting of supervision group membership over time, as well as possible dynamic group effects, is important to increase the likelihood that the model yields accurate results. Here we are primarily concerned with the condition by time interaction, but learning about the manner in which the groups change over time would be also be of interest.

Time-Varying Group Membership

Nested vs. Crossed Effects

A nested factor is one in which any level of one factor can only be measured within a single level of another factor, whereas if any level of a factor can be measured across multiple levels of another factor, the two factors are crossed (West, Welch, & Galecki, 2007). Correspondingly, if we consider one factor to be group membership and the other factor time within person, then if group membership remains the same for each person over time, then such a factor is referred to as nested. In contrast, if changes to group membership occur for some individuals over time then such an effect is referred to as crossed. In Table 1 we display the data for the first five people from a simulated dataset of 50 individuals, each measured on four occasions, who may be a member of one of 10 groups at any point in time. If each individual remained in the same group over time we would say that measurements of individuals over time (factor 1) are nested within group (factor 2). Clearly, this is not the case, since some individuals switch groups over time (persons 2, 3, & 4), and therefore we say that these two factors are crossed. The nested vs. crossed distinction applies equally well to either fixed or random effects, but we focus on how they pertain to modeling group random effects in this paper. The running example we will use to describe some of the statistical concepts in this article is based on the second empirical example of this paper, where clinicians are measured over time on their attitudes toward evidence-based practice, with some clinicians changing membership in supervision groups over time.

Table 1.

Illustration of Crossed Factors

Person	Time	Group	x	y
1	0	1	1	0.53
1	1	1	1	2.86
1	2	1	1	4.40
1	3	1	1	6.06
2	0	1	0	0.28
2	1	5	0	0.62
2	2	5	0	2.19
2	3	5	0	2.80
3	0	1	1	1.38
3	1	1	1	2.10
3	2	1	1	2.96
3	3	4	1	4.63
4	0	1	1	0.79
4	1	7	1	1.95
4	2	7	1	3.57
4	3	7	1	3.81
5	0	1	1	0.34
5	1	1	1	2.24
5	2	1	1	3.03
5	3	1	1	4.47

Note: Bold values indicate changes in group membership for a particular individual from a previous time point.

Nested Linear Mixed Models

Often when a crossed factor is present in one’s data and it is conceived as a random effect, a restrictive form of a linear mixed model is applied that treats the effect as if it were nested. One such model is a three-level model in which time is nested within person and people are nested in groups (Hedeker & Gibbons, 2006; Hox, 2002; Raudenbush & Bryk 2002; Snijders, & Bosker, 1999). For ease of presentation all models are presented as linear mixed models but use of generalized linear models with alternative distributions for outcomes will be addressed in the discussion. This model is displayed below:

• Level1 Model

  $$Y_{ijk}={\pi }_{0jk}+{\pi }_{1jk}{t}_{ijk}+e_{ijk}$$ (1)
• Level2 Model

  $${\pi }_{0jk}={\theta }_{00k}+b_{0jk}$$

  $${\pi }_{1jk}={\theta }_{10k}+b_{1jk}$$
• Level3 Model

  $${\theta }_{00k}={\gamma }_{000}+c_{00k}$$

  $${\theta }_{10k}={\gamma }_{100}$$

where Y_ijk is the outcome for person j in group k at time i, π_0jk is the expected score on the outcome for person j in group k at t =0, π_1jk is the expected growth rate in the outcome for person j in group k, and e_ijk ~ N(0, σ²) is a random within–person residual assumed normally distributed with 0 mean and constant variance. Further, the θ s and γ s correspond to fixed-effects in the model and the b s and c to random effects. We might also assume bivariate normality for the person-level random effects, $\left(\right[\begin{array}{c}\hfill b_{0jk}\hfill \\ \hfill b_{1jk}\hfill \end{array}]~N[\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),\begin{array}{cc}\hfill {\sigma }_{b00}^2\hfill & \hfill {\sigma }_{b01}^2\hfill \\ \hfill {\sigma }_{b10}^2\hfill & \hfill {\sigma }_{b11}^2\hfill \end{array}\left]\right)$, and normality for the random group intercept, $c_{00k}~N(0,{\sigma }_{c00}^2)$. This model allows individuals to have randomly varying intercepts and slopes (and for them to covary) at the person level, and intercepts to vary randomly as a result of group membership. The model can also be augmented to include a random group effect for the slope, c_10k, as well as other fixed and random effects. Generally, this type of model frequently serves as the default for analysis of crossed random effects because assuming a nested structure is conventional and easy to implement using existing software, but as we show these models can easily be adapted to allow for crossed random effects of people/time by groups.

Cross-Classified Random-Effects Models (CCREM)

Cross-Classified Random-Effects Models (CCREM) are models that were developed to allow for crossed random effects (Goldstein, 1987; Raudenbush, 1993). Raudenbush and colleagues (Raudenbush, 1993; Raudenbush & Bryk, 2002) describe CCREM for the analysis of longitudinal data with crossed random effects. These authors distinguish between two types of models in this context: acute-effects and cumulative-effects. In the acute-effects model the random group effects are modeled in such a way that the only the effect of being in a particular group at a particular time can influence the response at a fixed point in time, whereas in a cumulative-effects model both past and current group memberships can act on the response at a fixed point in time. From the running example the acute-effects model would translate to a supervision group only influencing the attitudes of a clinician at the time the clinician is a member of that group. In contrast, in a cumulative-effect model the attitudes of the service provider could be influenced by both current and past supervision group memberships.

Early formulations of the acute-effects CCREM (Raudenbush, 1993) displayed the group membership effect in the Level 1 portion of the model, corresponding to this effect varying with time (notation is based on the original article):

• Level1 Model

  $$Y_{ij}={\pi }_{0j}+{\pi }_{1j}{t}_{ij}+\sum _{k=1}^K{c}_k{D}_{kij}+e_{ij}$$ (2)
• Level2 Model

  $${\pi }_{0j}={\theta }_{00}+b_{00j}$$

  $${\pi }_{1j}={\theta }_{10}+b_{10j}$$

where Y_ij is the outcome for person j at time i, π_0j is the expected score on the outcome for person j at t = 0, π_1j is the expected growth rate in the outcome for person j, and e_ij ~ N(0, σ²) is a random within–person residual assumed normally distributed with 0 mean and constant variance. The θ s represent the fixed-effects and the b s and c are random-effects. The b s in this model correspond to the person-level random intercept and slope effects, and as in (1) we assume $\left(\right[\begin{array}{c}\hfill b_{00j}\hfill \\ \hfill b_{10j}\hfill \end{array}]~N[\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),\begin{array}{cc}\hfill {\sigma }_{b00}^2\hfill & \hfill {\sigma }_{b01}^2\hfill \\ \hfill {\sigma }_{b10}^2\hfill & \hfill {\sigma }_{b11}^2\hfill \end{array}\left]\right)$. Further, we assume that $c_k~N(0,{\sigma }_{c00}^2)$ is a random-effect due to a person encountering a group at a particular time. The D_kij term is a dummy indicator with a value of 1 if person j encounters group k at time i, 0 otherwise. The representation of the acute-effects model in (2) has more recently been abandoned in favor of displaying the group effects as part of the Level 2 portion of the model (the notation is based on Raudenbush & Bryk, 2002), possibly to highlight the impact that these random effects can have on the person (see below), although both formulations are equivalent:

• Level1 Model

  $$Y_{ijk}={\pi }_{0jk}+{\pi }_{1jk}{t}_{ij}+e_{ijk}$$ (3)
• Level2 Model

  $${\pi }_{0jk}={\theta }_{00}+b_{00j}+c_{00k}$$

  $${\pi }_{1jk}={\theta }_{10}+b_{10j}$$

One way to understand the acute effects model is to compare it to a model with group membership that does not change over time (nested). Specifically, we compare predictions from these two models for a single person who switches groups at each time, initially belonging to group 1 (Time 0), then group 2 (Time 1), and group 3 (Time 2), but could have belonged to any one of k such groups at a given point in time. The predictions would consist of:

• Nested

  $${Ŷ}_{0j1}={\theta }_{00}+b_{00j}+c_{001}$$

  $${Ŷ}_{1j2}={\theta }_{00}+b_{00j}+{\theta }_{10}+b_{10j}+c_{001}$$

  $${Ŷ}_{2j3}={\theta }_{00}+b_{00j}+2({\theta }_{10}+b_{10j})+c_{001}$$
• Acute-Effects CCREM

  $${Ŷ}_{0j1}={\theta }_{00}+b_{00j}+c_{001}$$

  $${Ŷ}_{1j2}={\theta }_{00}+b_{00j}+{\theta }_{10}+b_{10j}+c_{002}$$

  $${Ŷ}_{2j3}={\theta }_{00}+b_{00j}+2({\theta }_{10}+b_{10j})+c_{003}$$

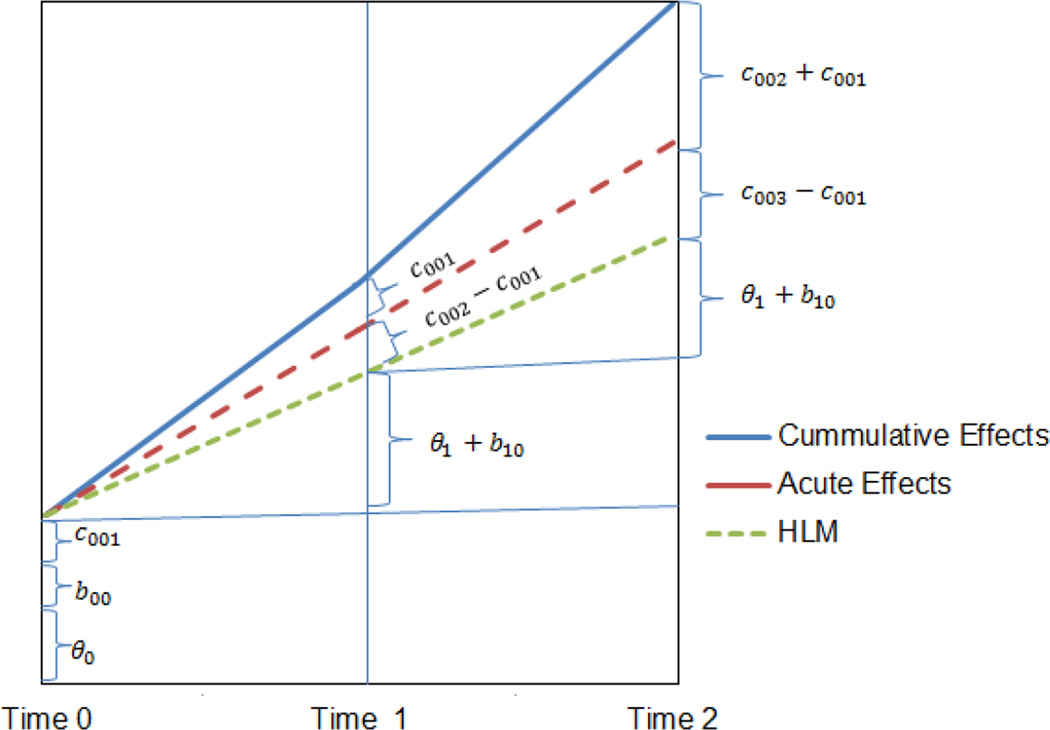
Notice that there is no difference in prediction between the two models at time 1, but at time 2 the difference is c₀₀₂ − c₀₀₁, and at time 3 this difference is c₀₀₃ − c₀₀₁. Luo and Kwok (2012) provide a nice graphical display of this comparison, which we have adapted and present in Figure 1. What the equations and Figure 1 illustrate is that changes to group membership can impact or alter a person’s growth curve relative to a nested specification. Therefore these different model parameterizations can have different effects on the slope through how they treat group membership. This may not be apparent given that the random effect is written as part of the intercept portion of Level 2 in equation (3), but is nonetheless true. Lastly, it is important to note that the acute-effects model could be adapted to include a group random-effect for the slope as well, but this would imply that the group effects vary linearly with time, which may be too restrictive (Bauer et al., 2013) and why we consider alternatives in the section on time-varying group effects.

Figure 1.

A Pictoral Comparison of HLM, Acute-Effect and Cummulative-Effect CCREM

Note: This figure assumes that c₀₀₁ < c₀₀₂ < c₀₀₃

Further insight about the acute-effects model can be gained by comparing it to a nested model with respect to the random-effect design matrix and vector of random effects for group membership. Consider a matrix representation of (3) for the j^th person:

$${\mathit{Y}}_{\mathit{j}}={\mathit{X}}_{\mathit{j}}\mathit{\theta }+{\mathit{A}}_{\mathit{j}}{\mathit{b}}_{\mathit{j}}+{\mathit{Z}}_{\mathit{j}}{\mathit{c}}_{\mathit{j}}+{\mathit{\epsilon }}_{\mathit{j}}$$ (4)

with X_j representing the fixed-effects design matrix, θ the vector of fixed effects, A_j the random-effects design matrix for person effects (slope and intercept) and b_j the corresponding vector of random effects, Z_j the random-effects design matrix for group membership with c_j the corresponding vector of random effects, and ε_j the vector of within-person residuals. Consider a hypothetical person that changes groups three times over three time periods. The random-effect design matrix and vector of random effects for group membership are then:

• Nested

  $${\mathit{Z}}_{\mathit{j}}=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\dots \hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\dots \hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\dots \hfill & \hfill 0\hfill \end{array}\right]{\mathit{c}}_{\mathit{j}}=\left[\begin{array}{c}\hfill c_{001}\hfill \\ \hfill c_{002}\hfill \\ \hfill c_{003}\hfill \\ \hfill ⋮\hfill \\ \hfill c_{00k}\hfill \end{array}\right]$$
• Acute-Effects CCREM

  $${\mathit{Z}}_{\mathit{j}}=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\dots \hfill & \hfill 0\hfill \end{array}\right]{\mathit{c}}_{\mathit{j}}=\left[\begin{array}{c}\hfill c_{001}\hfill \\ \hfill c_{002}\hfill \\ \hfill c_{003}\hfill \\ \hfill ⋮\hfill \\ \hfill c_{00k}\hfill \end{array}\right]$$

For the nested model, we assume that the person is retained in the first group over time. More importantly, what can be seen here is how the 1s in Z_j activate the group effects, with the nested model activating the same effect at each time and the acute-effects CCREM allowing for the activation of different effects at each time.

In a cumulative-effects CCREM model both past and current group memberships can affect a person’s response at a particular point in time. To see this consider the cumulative-effects model (Raundebush & Bryk, 2002):

• Level1 Model

  $$Y_{jt}={\pi }_{0jt}+{\pi }_{1jt}t+e_{jt}$$ (5)
• Level2 Model

  $${\pi }_{0jt}={\theta }_{00}+b_{00j}+\sum _{k=1}^K\sum _{h=0}^t{D}_{hjk}{c}_{00k}$$

  $${\pi }_{1jt}={\theta }_{10}+b_{10j}$$

Here again, we have adopted the notation of Raudenbush and Bryk (2002), who change notation from the acute-effects model to accommodate the carryover of random effects over time. In this context time is represented by t, person by j, and group by k. D_hjk is a dummy indicator, 1 if person j is in group k at time h, 0 otherwise. The double summation allows the group effects to carry over time. This model is similar to the acute-effects models, except at each time point group-specific deviations from previous time points are carried forward. We can see this by examining the predictions from this model for the same set of circumstances described above:

• Cummulative-Effects CCREM

  $${Ŷ}_{0j1}={\theta }_{00}+b_{00j}+c_{001}$$

  $${Ŷ}_{1j2}={\theta }_{00}+b_{00j}+{\theta }_{10}+b_{10j}+c_{001}+c_{002}$$

  $${Ŷ}_{2j3}={\theta }_{00}+b_{00j}+2({\theta }_{10}+b_{10j})+c_{001}+c_{002}+c_{003}$$

If we compare the predictions from this model to the acute-effects model, we see that there is no difference in prediction between the two models at time 1, but at time 2 the difference is c₀₀₁, and at time 3 this difference is c₀₀₂ + c₀₀₁. This is illustrated in Figure 1. What the equations and figure are conveying is that relative to the acute-effects parameterization, the cumulative-effects model can have a different effect on the person’s growth curve by carrying forward the effect of previous group memberships. The random effect design matrix and the vector of random effects for group membership for the cummulative-effects CCREM based on (4) would consist of:

• Cummulative-Effects CCREM

  $${\mathit{Z}}_{\mathit{j}}=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\dots \hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 0\dots \hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\dots \hfill & \hfill 0\hfill \end{array}\right]{\mathit{c}}_{\mathit{j}}=\left[\begin{array}{c}\hfill c_{001}\hfill \\ \hfill c_{002}\hfill \\ \hfill c_{003}\hfill \\ \hfill ⋮\hfill \\ \hfill c_{00k}\hfill \end{array}\right]$$

Note that the random effects design matrix is for the same hypothetical person as illustrated for the nested and acute effects model, but in this case the design matrix is activating multiple group effects at the second and third time points, such that group effects from previous time points are being carried forward. This is characteristically different than the nested and acute-effects model which only activate a single group effect at each time point.

Multiple Membership Models

An often cited alternative to CCREM are multiple membership models. We introduce these models for two reasons. First, given that multiple membership models might be used instead of CCREM, it is important to understand their differences so that an informed decision can be made about which to use. Second, understanding the features of multiple membership models can be important when encountering a situation that requires a model with such features. At a conceptual level multiple membership models are defined as lower-level units being members of more than one higher-level unit at the same time (Hill & Goldstein, 1998; Goldstein, 2003). From this point of view these models can be viewed as generalizations of acute-effects CCREM, because the latter only allow for a lower-level unit (person) to be a member of a single higher-level unit (group) at a time. This would not apply to cummulative-effects CCREM however because such models do allow for multiple memberships (i.e., both current and historical memberships), therefore they may be regarded as a kind of multiple membership model. From the perspective of model parameterization, CCREM and the conventional multiple membership model applied to longitudinal studies (Goldstein, Rasbash, Browne, Woodhouse, & Poulain, 2001; Goldstein 2003; Goldstein, Burgess, & McConnell, 2007; Roberts & Walwyn, 2012) are quite disparate because in the latter time is not explicitly part of the model, there are no fixed or random effects to represent a time effect. This is fundamentally different from the CCREM we have considered thus far, where the effect of time is explicitly modeled with fixed and random effects. Rather, the role of time in multiple membership models is implicit, playing a role in the selection of weights used to weigh the random effects (and fixed group effects).

To better understand how weights are used in longitudinal multiple membership models, consider the following simplified multiple membership model:

• Level1

  $$Y_{jk}={\pi }_{0k}+e_{jk}$$ (6)
• Level2

  $${\pi }_{0k}={\theta }_{00}+\sum _{k=1}^K{W}_{jk}{c}_{0k}$$

  $$\text{with }\sum _{k=1}^K{W}_{jk}=1\text{for each}j$$

At level 1, Y_jk is outcome for individual j in group k, π_0k is the expected score on the outcome for individual j in group k, and e_jk ~ N(0, σ²) is a random within–subject residual. At level 2, θ₀₀ represents the average score on the outcome, with c_0k a level 2 residual, $c_{0k}~N(0,{\sigma }_{c00}^2)$, and W_jk representing a weight. In a longitudinal study, such as we have in our running example, one possibility for the selection of weights is the proportion of time clinician j spends in supervision group k, with the restriction that the weights for each clinician sum to 1 (Goldstein et al., 2001; Goldstein 2003; Goldstein et al. 2007; Roberts & Walwyn, 2012). For example, consider person 1 from Table 1, who only belongs to group 1 (k=1) during the course of the study, the random level-2 portion for this person would consist of : $\sum _{k=1}^K{W}_{jk}{c}_{0k}=W_{j1}{c}_{01}=1c_{01}=c_{01}$. Contrast this with person 2, who spends one-fourth of their time in group one (k=1) and three-fourths in group five (k=5), the random part of level 2 would look like: $\sum _{k=1}^K{W}_{jk}{c}_{0k}=W_{j1}{c}_{01}+W_{j5}{c}_{05}=\frac{1}{4}{c}_{01}+\frac{3}{4}{c}_{05}$. Collectively, we can see that multiple membership models and CCREM are quite different with respect to the how they are specified.

Although different, by combining an acute-effects CCREM with weights similar to those found in multiple membership models, it is possible to obtain a model akin to a cumulative-effects CCREM. Notably, combinations of CCREM with multiple membership have been undertaken in the past (Goldstein et al., 2007; Grady & Beretvas 2010), although our model parameterization here is different in order to draw a closer connection with the cumulative-effects CCREM presented thus far. Specifically, we substitute W_hjk into (5) to obtain:

• Level1 Model

  $$Y_{jt}={\pi }_{0jt}+{\pi }_{1jt}t+e_{jt}$$ (7)
• Level2 Model

  $${\pi }_{0jt}={\theta }_{00}+b_{00j}+\sum _{k=1}^K\sum _{h=0}^t{W}_{hjk}{c}_{00k}$$

  $${\pi }_{1jt}={\theta }_{10}+b_{10j}$$

  $$\text{with }\sum _{k=1}^K{W}_{tjk}=1\text{for fixed }t\text{ and}j$$

The restriction in the weights above indicates that at a particular point in time t the weights for the j^th person sum to one. This restriction on the weights isn’t a necessary modeling constraint, but as indicated above is consistent with respect to how multiple membership models are often parameterized. If we seek a model comparable to the cummulative-effects CCREM we might select weights that lead to the following random-effects design matrix (for the same individual previously considered) :

• Multiple Membership CCREM

  $${\mathit{Z}}_{\mathit{j}}=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\dots \hfill & \hfill 0\hfill \\ \hfill .5\hfill & \hfill .5\hfill & \hfill 0\dots \hfill & \hfill 0\hfill \\ \hfill \overline{.3}\hfill & \hfill \overline{.3}\hfill & \hfill \overline{.3}\dots \hfill & \hfill 0\hfill \end{array}\right]{\mathit{c}}_{\mathit{j}}=\left[\begin{array}{c}\hfill c_{001}\hfill \\ \hfill c_{002}\hfill \\ \hfill c_{003}\hfill \\ \hfill ⋮\hfill \\ \hfill c_{00k}\hfill \end{array}\right]$$

As mentioned earlier, one general option for the weights is to take on values to represent the proportion of time an individual has spent in a group in the past up through the time they are assessed (Goldstein et al., 2001; Goldstein 2003; Goldstein et al. 2007; Roberts & Walwyn, 2012). A variation on this theme is to use the square root of the weight, since the weight will be squared when used to calculate the variance of the random effect. Alternatively, weights may take on values that weigh more heavily group memberships that are closer to the present time or equally weigh group membership in the past and present (Goldstein et al., 2007). The extent to which these parameterizations yield model estimates that are different from one another or a cumulative-effects CCREM is unclear, however simulations with a model comparable to that presented in (7) do not suggest substantial differences in model fixed and random effects when the weights are correctly vs incorrectly specified (Wolff Smith & Beretvas, 2014). Nevertheless, as pointed out by an anonymous reviewer, this specification is much more flexible than the simple active/inactive or cumulating random effect structures implied in the acute- and cummulative-effects models, which may have utility in other applications.

Features of multiple membership models might also be usefully combined with CCREM for situations when a person is actively a member of two or more groups at one time. Such a context can arise when evaluating efficacy/effectiveness of a treatment provided to a person simultaneously by several groups (i.e., clinicians or doctors) over time. For instance, in one trial that compared treatments for chronic fatigue syndrome, patients were randomized to either medical care (from a doctor) alone or in combination with one of the following administered by a clinician: cognitive behavioral therapy, graded exercise therapy, or adaptive pacing therapy (White et al., 2011). Patients were evaluated at baseline, 12, 24, and 52 weeks on several questionnaires, including a measure of fatigue. The analysis consisted of assigning each person to only one doctor or therapist (whoever saw the patient most frequently) when considering the effect of group membership on the person’s response. At the very least patients in the combined treatment arms will belong to two groups during the course of the study (possibly more if the same doctor/clinician doesn’t administer the treatment to the person over time), one based on the doctor administering medical care and the other based on the clinician administering the other treatment received. A model that includes weights could be used to account for these multiple group memberships by allowing each person to have multiple weighted group residuals at each time they are assessed.

Time-Varying Group Effects

An important recent advancement in the analysis of repeated measures data for individuals nested within groups is dynamic group modeling (Bauer et al., 2013). With few exceptions (Leckie & Goldstein, 2009, 2011; Paddock et al., 2011) a frequent assumption made when modeling such data is that groups are static over time, when in fact there are several factors that should lead us to regard groups as dynamic entities. Among these are changes to the structure of the group (e.g., individuals leaving or being added to the group), events impacting one or more individuals in the group, natural changes in group dynamics that occur over time (e.g., evolution of interpersonal interactions), or some combination of these (Bauer et al., 2013). In the running example, if the supervision group exerted the same effect on the clinician over time then this would correspond to a group effect that is static, but otherwise the presence of any non-constant effect would be regarded as a group effect that is dynamic. It should be clear that the issue of static vs. dynamic group effects applies equally to nested mixed models as it does to CCREM. Bauer et al. (2013) apply dynamic group models to nested data, and we show here how they might also be incorporated into CCREM.

Consider either the nested or time-varying group membership models described thus far in which there is only a random group effect for the intercept, with the assumption that $c_{00k}~N(0,{\sigma }_{c00}^2)$. Bauer et al. (2013) consider what such a model would imply about the group effect over time by changing the subscripting of c_00k in these models to c_00ik to reflect that the value of the group residual now depends on time (recall i indexes time in these models). By extension assume that these residual are distributed as multivariate normal, c_00k ~ N(0, Σ_c00), so that for I time points, there are I distinct values that c_00k can take on, such that c_00k = (c_001k, c_002k,…c_00Ik)'. This implies that the covariance matrix of the group residuals over time can be expressed as (with I =4):

$${\mathbf{\Sigma }}_{{\mathit{c}}_{00}}={\mathrm{\sigma }}_{{\mathit{c}}_{00}}^2\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right]$$ (8)

By separating the group variance, ${\mathrm{\sigma }}_{{\mathit{c}}_{00}}^2$, from the correlation matrix, we can see that such a model implies perfect correlations over time. In the running example this would translate to a supervision group effect at any one point in time being exactly the same as the effect at any other point in time, a tenuous assumption at best. It is important to note the addition of a random group effect for the slope would imply that the group effects vary linearly with time, c_00ik = c_00k + c_10k t_i, but the deterministic nature of this relationship combined with an inability to examine the viability of different correlation structures makes it less appealing than other dynamic group models (Bauer et al., 2013). While Bauer et al. (2013) only considered nested dynamic group models, we see that such models can just as easily be applied in situations with time-varying group membership.

Many covariance structures for Σ are possible, including but not limited to: unstructured, toeplitz, stabilized banded, compound symmetric, first-order autoregressive, and first-order autoregressive with heterogeneous variances. Here we review only a few structures that are most pertinent to the simulations and empirical examples considered later on. The most general structure is an unstructured covariance matrix, which allows for the variances and covariances or correlations to be distinct at each time point/lag. This structure with four time points is:

$$\left[\begin{array}{cccc}\hfill {\sigma }_1^2\hfill & \hfill {\sigma }_1{\sigma }_2{\rho }_{12}\hfill & \hfill {\sigma }_1{\sigma }_3{\rho }_{13}\hfill & \hfill {\sigma }_1{\sigma }_4{\rho }_{14}\hfill \\ \hfill {\sigma }_2{\sigma }_1{\rho }_{21}\hfill & \hfill {\sigma }_2^2\hfill & \hfill {\sigma }_2{\sigma }_3{\rho }_{23}\hfill & \hfill {\sigma }_2{\sigma }_4{\rho }_{24}\hfill \\ \hfill {\sigma }_3{\sigma }_1{\rho }_{31}\hfill & \hfill {\sigma }_3{\sigma }_2{\rho }_{32}\hfill & \hfill {\sigma }_3^2\hfill & \hfill {\sigma }_3{\sigma }_4{\rho }_{34}\hfill \\ \hfill {\sigma }_4{\sigma }_1{\rho }_{41}\hfill & \hfill {\sigma }_4{\sigma }_2{\rho }_{42}\hfill & \hfill {\sigma }_4{\sigma }_3{\rho }_{43}\hfill & \hfill {\sigma }_4^2\hfill \end{array}\right]$$ (9)

In their review of covariance structures, Bauer et al (2013) do not favor this structure because it is not parsimonious, may not be computationally feasible (i.e., may not converge), and is not as informative about how the group effects change over time, relative to other covariance structures. One important advantage of this model however is that it makes no assumption about the temporal structure of the group effect and therefore is not prone to model misspecification. Furthermore, in the case of only a few time points, such a model may be more computationally feasible and interpretable. Therefore, such a model should not be disregarded a priori. Lastly, a model with an unstructured covariance matrix is particularly useful for unequally spaced time measurements because it does not assume equal correlations within the same lag. For instance, Time 1–4 may represent measurements taken at 0,1,3,5 years, respectively (see Example 1). An unstructured matrix does not assume that measurements Lag 1 apart have equal correlations (ρ₁₂ ≠ ρ₂₃ ≠ ρ₃₄) or Lag 2 (ρ₁₃ ≠ ρ₂₄).

At the other extreme is a compound symmetry covariance structure:

$${\sigma }^2\left[\begin{array}{cccc}\hfill 1\hfill & \hfill \rho \hfill & \hfill \rho \hfill & \hfill \rho \hfill \\ \hfill \rho \hfill & \hfill 1\hfill & \hfill \rho \hfill & \hfill \rho \hfill \\ \hfill \rho \hfill & \hfill \rho \hfill & \hfill 1\hfill & \hfill \rho \hfill \\ \hfill \rho \hfill & \hfill \rho \hfill & \hfill \rho \hfill & \hfill 1\hfill \end{array}\right]$$ (10)

Despite its lack of flexibility it can be used with unequally spaced measurements because it assumes the same correlation irrespective of the lag. Nevertheless, this covariance structure seems implausible in most applications. A more plausible covariance structure is first-order autoregressive, which allows for decreasing association with increasing lag:

$${\sigma }^2\left[\begin{array}{cccc}\hfill 1\hfill & \hfill \rho \hfill & \hfill {\rho }^2\hfill & \hfill {\rho }^3\hfill \\ \hfill \rho \hfill & \hfill 1\hfill & \hfill \rho \hfill & \hfill {\rho }^2\hfill \\ \hfill {\rho }^2\hfill & \hfill \rho \hfill & \hfill 1\hfill & \hfill \rho \hfill \\ \hfill {\rho }^3\hfill & \hfill {\rho }^2\hfill & \hfill \rho \hfill & \hfill 1\hfill \end{array}\right]$$ (11)

An even more flexible version of this matrix is one that allows the variances to change over time as well, known as a heterogeneous first-order autoregressive structure:

$$\left[\begin{array}{cccc}\hfill {\sigma }_1^2\hfill & \hfill {\sigma }_1{\sigma }_2\rho \hfill & \hfill {\sigma }_1{\sigma }_3{\rho }^2\hfill & \hfill {\sigma }_1{\sigma }_4{\rho }^3\hfill \\ \hfill {\sigma }_2{\sigma }_1\rho \hfill & \hfill {\sigma }_2^2\hfill & \hfill {\sigma }_2{\sigma }_3\rho \hfill & \hfill {\sigma }_2{\sigma }_4{\rho }^2\hfill \\ \hfill {\sigma }_3{\sigma }_1{\rho }^2\hfill & \hfill {\sigma }_3{\sigma }_2\rho \hfill & \hfill {\sigma }_3^2\hfill & \hfill {\sigma }_3{\sigma }_4\rho \hfill \\ \hfill {\sigma }_4{\sigma }_1{\rho }^3\hfill & \hfill {\sigma }_4{\sigma }_2\rho \hfill & \hfill {\sigma }_4{\sigma }_3\rho \hfill & \hfill {\sigma }_4^2\hfill \end{array}\right]$$ (12)

The first-order autoregressive structures are appealing for use with equally-spaced time measurement data because they are plausible and parsimonious in how they model the correlation among repeated measurements. These structures assume equal correlations for measurements within the same lag, therefore they are inappropriate for unequally-spaced measurements. A more general version of a first-order autoregressive structure called spatial power, can be used with unequally spaced time measurements. The idea with spatial power is to allow for the correlation to attenuate with increasing distance in time between measurements. The correlation between any two time points is based on ρ^d_ij, where d_ij is the distance in time between the i^th and j^th time points, with i ≠ j:

$${\sigma }^2\left[\begin{array}{cccc}\hfill 1\hfill & \hfill {\rho }^{d_{ij}}\hfill & \hfill {\rho }^{d_{ij}}\hfill & \hfill {\rho }^{d_{ij}}\hfill \\ \hfill {\rho }^{d_{ij}}\hfill & \hfill 1\hfill & \hfill {\rho }^{d_{ij}}\hfill & \hfill {\rho }^{d_{ij}}\hfill \\ \hfill {\rho }^{d_{ij}}\hfill & \hfill {\rho }^{d_{ij}}\hfill & \hfill 1\hfill & \hfill {\rho }^{d_{ij}}\hfill \\ \hfill {\rho }^{d_{ij}}\hfill & \hfill {\rho }^{d_{ij}}\hfill & \hfill {\rho }^{d_{ij}}\hfill & \hfill 1\hfill \end{array}\right]$$ (13)

For instance, if measurements are taken at 4 time points corresponding to years 0,1,3,5 (Example 1) the result is the following covariance structure:

$${\sigma }^2\left[\begin{array}{cccc}\hfill 1\hfill & \hfill \rho \hfill & \hfill {\rho }^3\hfill & \hfill {\rho }^5\hfill \\ \hfill \rho \hfill & \hfill 1\hfill & \hfill {\rho }^2\hfill & \hfill {\rho }^4\hfill \\ \hfill {\rho }^3\hfill & \hfill {\rho }^2\hfill & \hfill 1\hfill & \hfill {\rho }^2\hfill \\ \hfill {\rho }^5\hfill & \hfill {\rho }^4\hfill & \hfill {\rho }^2\hfill & \hfill 1\hfill \end{array}\right]$$ (14)

Model Application: Data Formatting & Analysis, Model Selection, and Software Functionality

One impediment to the application of CCREM and multiple membership models is an absence of guidance on how to fit these models using general purpose software. While such examples are available for cross-sectional models (e.g., Myers & Beretvas, 2006), the same is not true of longitudinal models. In Web Appendix A on the journal website we describe estimation of longitudinal acute-effect CCREMs using SAS, SPSS, and R. We also illustrate how to fit cumulative-effect CCREMs/multiple membership models with SAS. Fitting dynamic group effect models for nested mixed models is relatively straightforward (see Appendix of Bauer et al., 2013), but we show in our Appendix how to combine an acute-effects CCREM with the dynamic group effects. Therefore, we first describe the general formatting of data required to fit these models, the general logic of the syntax needed, a strategy for selecting among several competing models, and describe the strengths and weakness of several of the software programs and the specific procedures/functions contained therein.

We begin by describing generically the approach required to fitting these models with general purpose computer software. The layout of the dataset can generally be described as “long” or “person-period”. Table 1 provides an illustration of the layout using the first five observations from a simulated dataset (the full dataset is obtainable as part of the online material, see appendix for details about how these data were generated and syntax that can be used to analyze the data). Most importantly, the data are organized in such a way that each row represents an observation at a point in time on a particular person. The data in Table 1 are sorted first by person and then by time to highlight the layout that is required. In addition to variables identifying the person and time period, we require three other variables, the group the person belongs to at a particular point in time, a predictor with a fixed effect of interest (here a binary variable ‘x’), and an outcome ‘y’. The group variable is particularly important, notice how it can change for a particular person over time. This is in contrast to the values the group variable would take on if a nested model were being fit, in that case a person would be restricted to belonging to a single group over time. Therefore, the general layout of the data is the same for a nested and CCREM, but the values of the group variable will be different.

In terms of analysis, the software programs are sufficiently similar with respect to syntax that a general description can be provided, at least for the acute-effects CCREM. All programs require for random effects that two parts be specified, an effect and a subject. In a growth model with random intercepts and slopes for the person, the effects are intercept and slope, and the subject is the person. In a nested model with a random intercept for the group, the intercept is the effect and the subject is the group. Exactly the same is true in the acute-effects CCREM, the intercept is the effect and the subject is the group. The only differences of course are the values that the group variable takes on in the nested vs. acute-effects CCREM.

Incorporating dynamic group effects into an acute-effects CCREM is straightforward. The way to do this is to change the effect from ‘intercept’ to ‘time’ while keeping group as the subject. Time refers to a variable that captures the time at which the person or group is measured, but importantly, this variable should be interpreted by the program being used as a multi-valued nominal variable. Lastly, a covariance structure needs to be specified for this time effect (e.g., first-order auto regressive).

Some complexity is introduced when attempting to fit a cummulative-effects CCREM. In general what is required is that past group memberships are carried forward in time. The approach we take (see Web Appendix A on the journal website) is to construct this random-effects design matrix for group membership from scratch and to feed that into the software program to make it fit the cummulative-effects CCREM. Specifically, for each person we construct the random-effects design matrix for group membership in such a way that if the person switches groups, the matrix would have values of 1 in multiple columns and in at least one row there would be more than one value of 1. This design matrix is captured by the addition of columns/variables to the existing dataset (the number of columns/variables equals the number of groups), and collectively these variables are used to define a random effect. The random effect will generally be for the intercept with group being the subject. This approach is appealing because it can easily be applied in other contexts. For instance, in the study by White et al. (2011) described in the multiple membership model section, where individuals are members of multiple groups at the same time, the random effects design matrix for group membership would have 1s whenever a patient was a member of a group and 0 otherwise, allowing for a person to be a member of more than one group at a point in time. We note that while it would be desirable to combine dynamic group effects with a cummulative-effects CCREM, we were unable a way to implement such a model in any of the general statistical packages we considered.

In light of the large number of models considered in this paper, it is worthwhile to consider how to decide among them. If group membership is time-varying, then to address this aspect of the data there is a choice that needs to be made between acute-effects and cummulative-effects CCREM, and possibly variations on the cummulative-effects model (e.g., using weights that sum to 1 within person, using weights that weigh later memberships more heavily, see model (6)). Irrespective of whether group membership is time varying, time-varying group effects should be evaluated. If time measurements are unequally spaced then only a select number of covariance structures are applicable, whereas if they are equally spaced then there are a large number of covariance structures that can be fit. We suggest considering the most flexible and restrictive dynamic group models, and some structures that are in between. Specifically, the most flexible dynamic group model is the unstructured matrix, the most restrictive is compound symmetry (the stable group model is more restrictive), and a first-order auto regressive structure would be an example of being in the middle on the flexibility spectrum. One way to guide selection of models with intermediate covariance structures is to examine the estimated variance-covariance/correlation matrices of these group-time effects and select a covariance structure that most closely (and parsimoniously) resembles the observed structure. When group membership is time-varying and group effects are considered time-varying, this leads to a larger number of models that can be evaluated, but as we show in Examples 1 & 2, the number can be manageable. There are several useful tools in selecting among models. For nested models, a likelihood ratio test is possible. For non-nested models, fit statistics can be compared. Importantly, there are two ways to calculate the number of parameters with fit statistics (e.g., Akaike’s Information Criterion (AIC), AIC finite sample correction (AICC), Bayesian Information Criterion (BIC)) when restricted maximum likelihood is used, one uses only the number of random parameters and another uses both the number of fixed and random parameters (West et al., 2007). Also, the manner in which sample size enters into calculation of these indices can vary, either using the number of total observations (i.e., observations at Level 1), the number of clusters, or the value of 1 (Beretvas & Murphy, 2013). The choices about how to calculate these fit statistics can affect model selection, but a reasonable approach is to use the number of random parameters and the total number of observations in calculation of these fit statistics (Beretvas & Murphy, 2013).

Given the wide variety of software programs available for the analysis of data with time-varying group membership and time-varying group effects, including such specialized mixed model software programs like HLM and MLwiN, it may be difficult to choose among them. A general and recent review of software for mixed models is very informative for choosing among software programs to fit the models described in this paper (see Table 1, West & Galecki, 2011). Here we briefly discuss our own experience with fitting the models described in this paper using three general purpose software programs: SAS, SPSS, and R. SAS has four procedures for fitting mixed models: Mixed, Glimmix, Hpmixed, Nlmixed, but we only describe the first three. For linear mixed models all procedures can fit the acute-effects CCREM, but only Glimmix can fit the cummulative-effects CCREM and longitudinal multiple membership models. Among the three procedures Hpmixed is the fastest for linear mixed models because it implements a sparse matrix algorithm. Only Glimmix can be used for generalized linear mixed models. All procedures can fit dynamic group models, but among these procedures Hpmixed has a somewhat more limited selection of covariance matrices that can be used. SPSS has much the same functionality as the procedures available in SAS through its two procedures, Mixed and Genlinmixed. The Mixed procedure is for linear mixed models and is comparable to the Mixed procedure in SAS in terms of its functionality. Genlinmixed is comparable to a hybrid of the Glimmix and Hpmixed procedures of SAS insofar as it is fast (i.e., utilizes a sparse matrix algorithm), can be used with non-linear models, but has fewer covariance structures to select from relative to the Mixed procedure. We have not been able to determine if SPSS has the capability to fit the cummulative-effects CCREM and other longitudinal multiple membership models. Lastly, we consider lme (nlme package), lmer and glmer (lme4 package) functions of R. The lme and lmer functions are for linear mixed models. While lme does offer flexibility in specifying a covariance structure for the group random effects, there is no off-the-shelf way to estimate a CCREM, but through some manipulation it appears that it can be used for this purpose (Lockwood, Doran, McCaffrey, 2003). Both lmer and glmer are fast and can be used to easily estimate an acute-effects CCREM (but not a cummulative-effects CCREM or other longitudinal multiple membership models), with glmer designed for generalized linear mixed models. One of the biggest drawbacks of lmer/glmer is an inability to model a covariance structure for the time-varying group effects, apart from possibly the most basic structures (e.g., unstructured). For models with both time-varying group membership and group effects we generally recommend SAS, but if only either time-varying group membership or group effects are of interest, any of the three software programs will suffice.

Simulation

In this section we consider three studies related to the models described in this paper, study one is related to time-varying group membership, study two is related to time-varying group effects, and study three combines features of studies one and two. Study one is motivated by an absence of information related to the performance of longitudinal CCREM in the context of studies with smaller sample sizes, such as those often found in psychology. Luo and Kwok (2012) present the results of simulations evaluating time-varying group membership (acute-effects CCREM) with a relatively large number of clusters and cluster sizes. The primary aim of study one is to explore the performance of the acute-effects CCREM with a smaller numbers of clusters and cluster sizes. The aim of study two is to evaluate the performance of models with time-varying group effects. Lastly, in study three we evaluate the performance of models with both time-varying group membership and group effects.

Simulation 1 Data Generation Process

SAS 9.4 was used to generate and analyze the data. The data were generated according to the following model:

• Level1 Model

  $$Y_{ijk}={\pi }_{0jk}+{\pi }_{1jk}{t}_{ijk}+e_{ijk}$$ (15)
• Level2 Model

  $${\pi }_{0jk}={\theta }_{00}+b_{00j}+{\theta }_{01}{\mathit{\text{Treat}}}_j+c_{00k}$$

  $${\pi }_{1jk}={\theta }_{10}+b_{10j}+{\theta }_{11}{\mathit{\text{Treat}}}_j$$

The model is the same as presented in (3) with the same definition of parameters, except with the addition of two fixed effects, θ₀₁ and θ₁₁. The effects are person-level covariates intended to represent the effect of receiving treatment on the intercept and slope. Treat_j was generated as Bernoulli(.5), with θ₀₁ = θ₁₁ = θ₁₀ = .5 and θ₀₀ = .1. In terms of the random parameters, e_ijk ~ N(0,.40), $\left(\right[\begin{array}{c}\hfill b_{00j}\hfill \\ \hfill b_{10j}\hfill \end{array}]~N[\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),\begin{array}{cc}\hfill .10\hfill & \hfill .025\hfill \\ \hfill .025\hfill & \hfill .05\hfill \end{array}\left]\right)$, and $c_{00k}~N(0,{\sigma }_{c00}^2)$ with ${\sigma }_{c00}^2$ being a design factor that was manipulated (see below).

Our study consisted of manipulating several factors including: the amount of mobility in and out of groups over time, magnitude of the group variance, number of clusters, and the cluster size. Mobility was based on allowing a person to have some probability of changing groups at each point in time, based on Bernoulli(p) with p = .05, .20, or .35. The group variance was set to ${\sigma }_{c00}^2=.10\mathit{\text{or }}.20$. This corresponds to ICCs for the smaller and larger group variance conditions of .17 and .29, respectively. The number of clusters was set to 10 or 30, and the cluster size was set to either 5 or 15. Therefore our design was a 3×2×2×2 design, resulting in a total of 24 conditions. With the exception of the number of clusters and cluster size, the parameters held fixed and manipulated were based on those used in simulation two of Luo and Kwok (2012). The justification they provide for the values used are also reasonable for many psychological studies. For instance, in our experience ICCs in these types of studies are often in the range of .17 to .29, although in some applications may be smaller. In example one the conditional ICC after fitting a simple acute-effects CCREM was estimated to be .19 and in example two .09. The number of clusters and cluster sizes also correspond to the range observed in our research experience, 10 clusters with 5 observations per cluster on the low end and 30 clusters with 15 observations on the higher end.

For each condition we evaluated performance of an acute-effects model (correct model) and a nested model (incorrect model). We also evaluated a nested model for data with no person mobility over time, which may provide a reference point for the performance of the acute-effects model. For each condition and model we evaluated the percent relative bias and root mean square error (RMS) for the random parameters of the model, as well as the standard error percent relative bias for the time by treatment interaction (the standard error for this parameter is of greatest interest in this type of study). Percent relative bias is defined as: (θ̂ − θ)/θ, averaged over the simulations and multiplied by 100. RMS is the (θ̂ − θ)² averaged over the simulations and square-rooted. Standard error (SE) percent relative bias was calculated as $(\widehat{SE}-{\widehat{SE}}_{\mathit{\text{Empirical}}})/{\widehat{SE}}_{\mathit{\text{Empirical}}}$, averaged over the simulations and multiplied by 100, where ${\widehat{SE}}_{\mathit{\text{Empirical}}}$ is the standard deviation of the standard error estimates from the correct model. For each condition we evaluated 1000 simulated cases.

Simulation 2 Data Generation Process

The data generation process was based on the nested model described in (1), but with the addition of two person-level fixed effects to represent treatment, as in study 1:

• Level1 Model

  $$Y_{ijk}={\pi }_{0jk}+{\pi }_{1jk}{t}_{ijk}+e_{ijk}$$
• Level2 Model

  $${\pi }_{0jk}={\theta }_{00k}+b_{0jk}+{\theta }_{01}{\mathit{\text{Treat}}}_k$$ (16)

  $${\pi }_{1jk}={\theta }_{10k}+b_{1jk}+{\theta }_{11}{\mathit{\text{Treat}}}_k$$
• Level3 Model

  $${\theta }_{00k}={\gamma }_{000}+c_{00k}$$

Treat_j was generated as Bernoulli(.5), with θ₀₁ = θ₁₁ = θ₁₀ = .5 and θ₀₀ = .1. In terms of the random parameters, e_ijk ~ N(0,.40), $\left(\right[\begin{array}{c}\hfill b_{00j}\hfill \\ \hfill b_{10j}\hfill \end{array}]~N[\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),\begin{array}{cc}\hfill .10\hfill & \hfill .025\hfill \\ \hfill .025\hfill & \hfill .05\hfill \end{array}\left]\right)$, and c_00k ~ N(0,Σ_c00).

Our study manipulated magnitude of the group variance, number of clusters, cluster size, and the covariance matrix of group effects over time (Σ_c00). We considered two covariance matrices, first-order autoregressive (AR) as in (11) and first-order autoregressive with heterogeneous variances (ARH) as in (12). In both cases, ρ = .8. Note that this value of rho was chosen based on the result of Example 2 of this paper and Example 2 in Bauer et al. (2013). For the AR structure we considered two group variances, ${\sigma }_{c00}^2=.10\mathit{\text{or }}.20$. For ARH the variances at times 1–4 were fixed at: .1, .12, .14, .16. Small to moderate combinations of cluster and cluster sizes were based on crossing the number of clusters (10 or 30) with the cluster size (5 or 15), with a larger combination based on 50 clusters and a cluster size of 50. For each condition we evaluated performance of the correctly specified dynamic group model and the incorrectly specified stable group model. For each condition and model we evaluated the percent relative bias and root mean square error (RMSE) for the random parameters of the model, as well as the standard error percent relative bias for the time by treatment interaction. For each condition we evaluated 1000 simulated cases.

Simulation 3 Data Generation Process

The data were generated according to the following model:

• Level1 Model

  $$Y_{ijk}={\pi }_{0jk}+{\pi }_{1jk}{t}_{ijk}+e_{ijk}$$ (17)
• Level2 Model

  $${\pi }_{0jk}={\theta }_{00}+b_{00j}+{\theta }_{01}{\mathit{\text{Treat}}}_j+c_{00k}$$

  $${\pi }_{1jk}={\theta }_{10}+b_{10j}+{\theta }_{11}{\mathit{\text{Treat}}}_j$$

Treat_j was generated as Bernoulli(.5), with θ₀₁ = θ₁₁ = θ₁₀ = .5 and θ₀₀ = .1. In terms of the random parameters, e_ijk ~ N(0, .40), $\left(\right[\begin{array}{c}\hfill b_{00j}\hfill \\ \hfill b_{10j}\hfill \end{array}]~N[\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),\begin{array}{cc}\hfill .10\hfill & \hfill .025\hfill \\ \hfill .025\hfill & \hfill .05\hfill \end{array}\left]\right)$, and c_00k ~ N(0,Σ_c00). We fixed Σ_c00 to an AR structure with ρ = .8 and mobility was based on a 20% chance of changing groups at each point in time, Bernoulli(.2). We manipulated magnitude of the group variance, number of clusters, and cluster size. The group variance was set to either .1 or .2. Small to moderate combinations of cluster and cluster sizes were based on crossing the number of clusters (10 or 30) with the cluster size (5 or 15), with a larger combination based on 50 clusters and a cluster size of 50.

For each condition we evaluated performance of the correctly specified acute-effects dynamic group model and the incorrectly specified nested stable group model. For each condition we evaluated 1000 simulated cases.

Summary of Simulation Results

Detailed results of the simulation are presented in Web Appendix B on the journal website. Simulation one identified underestimation of the group variance and overestimation of the slope and residual variances in the misspecified nested model, resulting in the standard error of the time by condition interaction being overestimated. In contrast the acute-effects CCREM has much less bias and greater overall accuracy in estimating the random parameters. These findings are consistent with those of Luo and Kwok (2012), suggesting that the acute-effects CCREM performs well and superior to a nested model even with smaller numbers of clusters and cluster sizes. In simulation two we observed that the incorrectly specified stable group model has more bias and greater inaccuracy in estimating the random parameters of the model relative to the correctly specified dynamic group AR model, specifically underestimation of the group variance and covariance and overestimation of the slope and residual variances. However, these biases did not translate to bias in the standard error of the time by condition interaction, as they did in study one. In simulation three, which combined features of simulations two and three with respect to time-varying group membership and dynamic group effects, we found increased inaccuracy and bias in the variance estimates in the incorrectly specified nested model relative to the correctly specified CCREM with dynamic group effects. The one exception is with respect to accuracy in estimating the group variance, which was superior in the correctly specified model only with more modest number of clusters (30 clusters) and cluster sizes (15 observations per cluster).

Real Data Examples

Example 1: Modeling Childhood Mathematics Achievement

The first example uses data from the Early Childhood Longitudinal Study–Kindergarten Cohort (ECLS-K). This is a longitudinal study designed in part to examine predictors of growth in mathematics achievement during elementary and middle school years. Some students change schools during the study period, therefore this dataset has been used in the past to illustrate fitting of CCREM (Grady & Beretvas 2010; Luo & Kwok, 2012). Luo and Kwok (2012) identified a sample of 4,301 children with complete information on the response, predictors, and school membership, and use three waves of data (kindergarten, 1^st grade, and 3^rd grade). We use a subset of 500 children for our analysis and include a fourth wave of data (5^th grade). The use of a smaller subset of children is intended to decrease the time required to fit some models, and a larger number of time points is used to fit a wider range of dynamic group covariance structures. In our restricted dataset, between kindergarten and 1^st grade 4.8% of the children changed schools, between 1^st and 3^rd grade 8.6% changed schools, and between 3^rd and 5^th grade 8.0% changed schools. Math achievement is the outcome with student gender and school type (public vs. private) the predictors.

The stable group acute-effects model is:

• Level1 Model

  $$Y_{ijk}={\pi }_{0jk}+{\pi }_{1jk}{t}_{ijk}+e_{ijk}$$ (18)
• Level2 Model

  $${\pi }_{0jk}={\theta }_{00}+{\theta }_{01}{(\mathit{\text{Female}})}_j+b_{00j}+{\gamma }_{01}{(\mathit{\text{Public}})}_k+c_{00k}$$

  $${\pi }_{1jk}={\theta }_{10}+{\theta }_{11}{(\mathit{\text{Female}})}_j+b_{10j}$$

  $$\text{with }\left(\begin{array}{c}\hfill b_{00j}\hfill \\ \hfill b_{10j}\hfill \end{array}\right)~N\left[\right(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}),(\begin{array}{cc}\hfill {\sigma }_{b_{00}}^2\hfill & \hfill {\sigma }_{b_{00},b_{10}}\hfill \\ \hfill {\sigma }_{b_{10},b_{00}}\hfill & \hfill {\sigma }_{b_{10}}^2\hfill \end{array}\left)\right]\text{ and }{c}_{00k}~N(0,{\sigma }_{c00}^2)$$

We fit three dynamic group alternatives, such that c_00k ~ N(0,Σ_c00), with the following covariance structures for Σ_c00: Unstructured (UN), Compound Symmetric (CS), and Spatial Power (SP). We also consider stable group cummulative-effects CCREMs. We do not consider dynamic group alternatives to the cumulative-effects CCREM, because unlike the acute-effects CCREM, it was not possible to fit such models. One cumulative-effects CCREM is:

• Level1 Model

  $$Y_{jt}={\pi }_{0jt}+{\pi }_{1jt}t+e_{jt}$$ (19)
• Level2 Model

  $${\pi }_{0jt}={\theta }_{00}+{\theta }_{01}{(\mathit{\text{Female}})}_j+b_{00j}+{\gamma }_{01}{(\mathit{\text{Public}})}_k+\sum _{k=1}^K\sum _{h=0}^t{D}_{hjk}{c}_{00k}$$

  $${\pi }_{1jt}={\theta }_{10}+{\theta }_{11}{(\mathit{\text{Female}})}_j+b_{10j}$$

  $$\text{with }\left(\begin{array}{c}\hfill b_{00j}\hfill \\ \hfill b_{10j}\hfill \end{array}\right)~N\left[\right(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}),(\begin{array}{cc}\hfill {\sigma }_{b_{00}}^2\hfill & \hfill {\sigma }_{b_{00},b_{10}}\hfill \\ \hfill {\sigma }_{b_{10},b_{00}}\hfill & \hfill {\sigma }_{b_{10}}^2\hfill \end{array}\left)\right]\text{ and }{c}_{00k}~N(0,{\sigma }_{c00}^2)$$

An alternative specification of the cumulative-effects CCREM is one that uses weights in formulation of the random effects, as described in (7). Here we use weights that equally weigh past and present group membership:

• Level1 Model

  $$Y_{jt}={\pi }_{0jt}+{\pi }_{1jt}t+e_{jt}$$ (20)
• Level2 Model

  $${\pi }_{0jt}={\theta }_{00}+{\theta }_{01}{(\mathit{\text{Female}})}_j+b_{00j}+{\gamma }_{01}{(\mathit{\text{Public}})}_k+\sum _{k=1}^K\sum _{h=0}^t{W}_{hjk}{c}_{00k}$$

  $${\pi }_{1jt}={\theta }_{10}+{\theta }_{11}{(\mathit{\text{Female}})}_j+b_{10j}$$

  $$\text{with }\left(\begin{array}{c}\hfill b_{00j}\hfill \\ \hfill b_{10j}\hfill \end{array}\right)~N\left[\right(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}),(\begin{array}{cc}\hfill {\sigma }_{b_{00}}^2\hfill & \hfill {\sigma }_{b_{00},b_{10}}\hfill \\ \hfill {\sigma }_{b_{10},b_{00}}\hfill & \hfill {\sigma }_{b_{10}}^2\hfill \end{array}\left)\right]\text{ and }{c}_{00k}~N(0,{\sigma }_{c00}^2)\text{ and }\sum _{k=1}^K{W}_{tjk}=1\text{for fixed }t\text{ and}j$$

The notation indicates that weights are only applied to the random effects in this model. We could fit a model that incorporates weights into the fixed school type effect, an approach undertaken elsewhere (Grady & Beretvas 2010), but we do not pursue such a model here because our focus is exclusively on comparison of models with different specifications of random effects. Sample codes for fitting Models 18–20 are included in Web Appendix A on the journal website.

We can see in Table 2 that among the stable group models, the acute- vs. cumulative-effects specification does not substantially change the fit according to the information criteria (AIC, AICC, BIC). The dynamic group acute-effects models resulted in substantially improved fit relative to the stable group acute-effects models according to likelihood ratio tests, for example stable group acute-effects vs. unstructured dynamic group, χ² (9) = 176.41, p < .05. Among the dynamic group models, the unstructured model provided the best fit according to the likelihood ratio tests, unstructured vs. compound symmetric, χ² (8) = 56.65, p < .05, unstructured vs. spatial power, χ² (8) = 57.18, p < .05, and therefore we rely on this model for interpretation. The covariance and correlation matrices are presented in Table 3. Based on this Table we see the school variance is largest in 1^st grade, 3^rd grade, 5^th grade, and Kindergarten, respectively. Furthermore, we can see a decline in the correlations over time, although the pattern is not a function of distance in terms of the spacing of measurements over time, as specified by the spatial power model. Generally, higher correlation for the school effect are observed for measurements taken closer together in time than for measurements taken further apart, suggesting good schools stay good and bad schools stay bad over short periods of time, but that the pattern attenuates over longer periods of time. In terms of the magnitude of the cross-classified random effect, a comparison of its time-specific variance to the variance of the growth rate (Raudenbush & Bryk, 2002) yields ratios of 2.6, 12.09, 8.4, 6.8 for Kindergarten through 5^th grade, respectively, suggesting that at a given point in time the effect of school contributes more to the variability in math achievement scores than the variability in individual growth rates among students. Finally, with respect to the fixed effects we see that public schools were associated with lower math achievement scores than private schools (Table 4).

Table 2.

Comparison of Fit for Models in Example 1

	Stable Group Acute- Effects Model (6)	Stable Group Cummulative- Effects Model (7)	Stable Group Cummulative- Effects Model (8)	Dynamic Group Acute-Effects Model (6) with a covariance structure for Σc00
				UN	CS	SP
Total # of parameters	10	10	10	19	11	11
# of random parameters	5	5	5	14	6	6
Model Fit
−2 RES LL	15305.83	15304.28	15307.59	15129.42	15186.07	15186.60
AIC	15315.83	15314.28	15317.59	15157.42	15198.07	15198.60
AICC	15315.86	15314.31	15317.62	15157.63	15198.11	15198.60
BIC	15343.83	15342.28	15345.59	15235.83	15231.68	15232.21

Note: RES LL= Residual Log Likelihood, AIC=Akaike’s Information Criterion, AICC= Akaike’s Information Criterion Finite Sample Correction, BIC= Bayesian Information Criterion, UN=unstructured, CS=compound symmetry, SP=spatial power

Table 3.

Covariance and Correlation Matrices for Groups Over Time

	Covariance Matrix				Correlation Matrix
	T1	T2	T3	T4	T1	T2	T3	T4
T1	17.31 (5.27)	23.73 (8.37)	12.09 (7.37)	8.94 (7.23)	1.00	0.63	0.39	0.32
T2	23.73 (8.37)	81.49 (16.33)	53.32 (14.24)	26.38 (14.39)	0.63	1.00	0.78	0.43
T3	12.09 (7.37)	53.32 (14.24)	56.74 (15.51)	40.87 (15.19)	0.39	0.78	1.00	0.80
T4	8.94 (7.23)	26.38 (14.39)	40.87 (15.19)	45.79 (17.13)	0.32	0.43	0.80	1.00

Note: Values in parentheses are standard errors

Table 4.

Results for Acute-Effects CCREM with Unstructured Covariance Matrix from Example 1

Fixed Effects	Estimate	SE	P
Intercept, θ0	35.83	1.82	<.001
Time, θ1	16.12	0.47	<.001
Female, β01	−0.89	0.91	.327
Public, β02	−6.09	1.35	<.001
Female*Time, β11	−0.37	0.29	.210
Random Effects
Initial Status, ${\sigma }_{b_{00}}^2$.	67.22	6.82	-
Growth Rate, ${\sigma }_{b_{10}}^2$	6.74	1.59	-
Covariance, initial status & growth rate σb10, b00	12.69	0.74	-
Residual Error, σ2	37.67		-
Group Effect, Σc00	See Table 3

Example 2: Modeling Clinician Attitudes Towards Evidence-Based Practice

This example involves a study of the implementation of an evidenced-based practice (EBP) designed to reduce child neglect in the state of Oklahoma. There are four levels of data: time, clinician, supervision group, and region. The study is a 2×2 design in which regions in Oklahoma were experimentally assigned to either SafeCare (i.e, the EBP or hereafter “EB”) or services as usual (SAU), and within each region, supervision groups were randomized to fidelity monitoring or no monitoring. Therefore, both region and supervision groups were randomized. The design of the trial remained intact for the first four waves of data collection, thereafter regions originally assigned to the SAU condition began to adopt SafeCare. Thus, we utilized only the first four waves of data. The current study involves data collected from 208 clinicians over four bi-annual waves, with membership in a supervision group changing for some clinicians over time. Of interest is how clinician attitudes towards evidenced-based practice change over time as a function of the condition they are in. The outcome being evaluated in the present study is provider attitudes toward evidenced-based practices (Aarons et al., 2010).

A couple of points are noteworthy. First, for the purposes of this example what defines a supervision group as a distinct entity that can be tracked over time is the supervisor. Second, because a clinician may change supervision groups over time, they may also change study conditions, therefore our models described below allow these fixed effects to vary over time (i.e., are part of Level 1 portion of the model), but only 8 of the 208 switch conditions. Third, although supervision groups are nested in regions, our models do not include random region effects because the variance is near zero. Lastly, because the design of the study involves rolling admission of clinicians into supervision groups, with respect to modeling clinician effects, time is the number of years the clinician has been enrolled in the study (0, .5, 1, and 1.5, years). In contrast, for the group random effects time is the number of years the group has existed since the study began. Between 0 years and .5 years 13.6% of the clinicians changed supervision groups, between .5 years and 1 year 20.7% of the clinicians changed groups, between 1 year and 1.5 years 11.2% changed groups.

The acute-effects CCREM with stable group effects is:

• Level1 Model

  $$Y_{ijk}={\pi }_{0jk}+{\pi }_{1jk}{t}_{ijk}+{\pi }_{2jk}E{B}_{ijk}+{\pi }_{3jk}{\mathit{\text{Monitoring}}}_{ijk}+{\pi }_{4jk}(E{B}_{ijk}*{\mathit{\text{Monitoring}}}_{ijk})+{\pi }_{5jk}(E{B}_{ijk}*t_{ijk})+{\pi }_{6jk}({\mathit{\text{Monitoring}}}_{ijk}*t_{ijk})+{\pi }_{7jk}(E{B}_{ijk}*{\mathit{\text{Monitoring}}}_{ijk}*t_{ijk})+e_{ijk}$$ (21)
• Level2 Model

  $${\pi }_{0jk}={\theta }_0+b_{00j}+c_{00k}$$

  $${\pi }_{1jk}={\theta }_1+b_{10j}$$

  $$\text{with }\left(\begin{array}{c}\hfill b_{00j}\hfill \\ \hfill b_{10j}\hfill \end{array}\right)~N\left[\right(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}),(\begin{array}{cc}\hfill {\sigma }_{b_{00}}^2\hfill & \hfill {\sigma }_{b_{00},b_{10}}\hfill \\ \hfill {\sigma }_{b_{10},b_{00}}\hfill & \hfill {\sigma }_{b_{10}}^2\hfill \end{array}\left)\right]\text{ and }{c}_{00k}~N(0,{\sigma }_{c00}^2)$$

We fit six dynamic group alternatives to this model, such that c_00k ~ N(0,Σ_c00), with the following covariance structures for Σ_c00: Unstructured (UN), Toeplitz (TOEP), Stabilized Banded-Lag 2 (SB-2), Compound Symmetric (CS), First-Order Autoregressive (AR), and First-order Autoregressive Moving Average (ARMA).

As in Example 1, we also consider two stable group cumulative-effects CCREM.

• Level1 Model

  $$Y_{jt}={\pi }_{0jt}+{\pi }_{1jt}t+{\pi }_{2jt}E{B}_{jt}+{\pi }_{3jt}{\mathit{\text{Monitoring}}}_{jt}+{\pi }_{4jt}(E{B}_{jt}*{\mathit{\text{Monitoring}}}_{jt})+{\pi }_{5jt}(E{B}_{jt}*t)+{\pi }_{6jt}({\mathit{\text{Monitoring}}}_{jt}*t)+{\pi }_{7jt}(E{B}_{jt}*{\mathit{\text{Monitoring}}}_{jt}*t)+e_{jt}$$ (22)
• Level2 Model

  $${\pi }_{0jt}={\theta }_{00}+b_{00j}+\sum _{k=1}^K\sum _{h=0}^t{D}_{hjk}{c}_{00k}$$

  $${\pi }_{1jt}={\theta }_{10}+b_{10j}$$

  $$\text{with }\left(\begin{array}{c}\hfill b_{00j}\hfill \\ \hfill b_{10j}\hfill \end{array}\right)~N\left[\right(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}),(\begin{array}{cc}\hfill {\sigma }_{b_{00}}^2\hfill & \hfill {\sigma }_{b_{00},b_{10}}\hfill \\ \hfill {\sigma }_{b_{10},b_{00}}\hfill & \hfill {\sigma }_{b_{10}}^2\hfill \end{array}\left)\right]\text{ and }{c}_{00k}~N(0,{\sigma }_{c00}^2)$$

An alternative specification of the cumulative-effects CCREM is one that uses weights in formulation of the random effects. Here we use weights that equally weigh past and present group membership:

• Level1 Model

  $$Y_{jt}={\pi }_{0jt}+{\pi }_{1jt}t+{\pi }_{2jt}E{B}_{jt}+{\pi }_{3jt}{\mathit{\text{Monitoring}}}_{jt}+{\pi }_{4jt}(E{B}_{jt}*{\mathit{\text{Monitoring}}}_{jt})+{\pi }_{5jt}(E{B}_{jt}*t)+{\pi }_{6jt}({\mathit{\text{Monitoring}}}_{jt}*t)+{\pi }_{7jt}(E{B}_{jt}*{\mathit{\text{Monitoring}}}_{jt}*t)+e_{jt}$$ (23)
• Level2 Model

  $${\pi }_{0jt}={\theta }_{00}+b_{00j}+\sum _{k=1}^K\sum _{h=0}^t{W}_{hjk}{c}_{00k}$$

  $${\pi }_{1jt}={\theta }_{10}+b_{10j}$$

  $$\text{with }\left(\begin{array}{c}\hfill b_{00j}\hfill \\ \hfill b_{10j}\hfill \end{array}\right)~N\left[\right(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}),(\begin{array}{cc}\hfill {\sigma }_{b_{00}}^2\hfill & \hfill {\sigma }_{b_{00},b_{10}}\hfill \\ \hfill {\sigma }_{b_{10},b_{00}}\hfill & \hfill {\sigma }_{b_{10}}^2\hfill \end{array}\left)\right]\text{ and }{c}_{00k}~N(0,{\sigma }_{c00}^2)\text{ and }\sum _{k=1}^K{W}_{tjk}=1\text{for fixed }t\text{ and}j$$

Sample codes for fitting Models 21–23 are included in Web Appendix A on the journal website.

We can see in Table 5 that among the stable group models, the acute-effects specification provides slightly better fit according to the information criteria (AIC, AICC, BIC). Among the dynamic group acute-effects models the autoregressive structure appears to provide the overall best fit according to the information criteria. A comparison of the stable group acute-effects model to the first-order autoregressive acute-effects model is not quite significant by a likelihood ratio test, χ² (1) = 3.82, p = .051, but we chose to interpret the latter model nevertheless. We observe that the correlation among supervision groups on the response decays over time: .761 (Lag 1), .579 (Lag 2), .441 (Lag 3), suggesting that supervision groups that have higher ratings of evidence-based practice and those with lower ratings stay that way over short periods of time, but that the pattern attenuates over longer periods of time. In terms of the magnitude of the cross-classified random effect, comparing its variance to the variance to the growth rate (ratio of 2.17) suggests that supervision group membership at a given point in time contributes more to the variability in responses than the variability in individual growth rates among clinicians.

Table 5.

Comparison of Fit for Models in Example 2

	Stable Group Acute- Effects Model (9)	Stable Group Cummulative- Effects Model (10)	Stable Group Cummulative- Effects Model (11)	Dynamic Group Acute-Effects Model (9) with a covariance structure for Σc00
				CS	AR	SB-2
Total # of parameters	13	13	13	14	14	15
# of Random parameters	5	5	5	6	6	7
Model Fit
−2 RES LL	568.81	569.18	569.47	566.78	564.99	564.94
AIC	578.81	579.18	579.47	578.78	576.99	578.94
AICC	578.95	579.32	579.61	578.98	577.19	579.20
BIC	599.15	599.52	599.81	603.19	601.40	607.42

Note: The model with unstructured covariance matrix did not converge and the model with a toeplitz structure yielded a non-positive definite G matrix, therefore the model fit for these models are not reported.

RES LL= Residual Log Likelihood, AIC=Akaike’s Information Criterion, AICC= Akaike’s Information Criterion Finite Sample Correction, BIC= Bayesian Information Criterion, CS=compound symmetry, AR=First-Order Autoregressive, SB-2= Stabilized Banded-Lag 2.

Next we turn to the primary research question of interest, are there differences among the treatment groups. Based on the significant EB by Monitoring by Time interaction (Table 6), we sought to determine if the condition receiving monitoring only was significantly different from each of the other three conditions in terms of their growth rates. To test these hypotheses, we re-specified the model in such a way that the no monitoring/ no EB was the reference group for each of three dummy coded variables representing the four conditions. The results of this model indicate a significant difference between no monitoring/ no EB with each of the following groups in terms of their growth rates: monitoring/EB, b = .158, se =.068, p = .024, no monitoring/ EB, b = .144, se =.064, p = .027, and monitoring/no EB, b = .226, se =.080, p = .006. As might be expected, individuals in either of the two EB conditions have more favorable rates of growth in EBPAS scores relative to no monitoring combined with no EB condition. Unexpectedly, monitoring combined with no EB also had more favorable rates of growth in EBPAS scores relative to no monitoring combined with no EB condition.

Table 6.

Results for Acute-Effects CCREM with First-Order Autoregressive Covariance Matrix from Example 2

Fixed Effects	Estimate	SE	P
Intercept, θ0	2.880	.082	<.001
Time, θ1	−.117	.051	.023
EB, π2jk	−.172	.110	.125
Monitoring, π3jk	−.037	.120	.760
EB*Monitoring, π4jk	.096	.167	.568
EB*Time, π5jk	.144	.064	.027
Monitoring*Time, π6jk	.226	.080	.006
EB*Monitoring*Time, π7jk	−.212	.099	.036
Random Effects
Initial Status, ${\sigma }_{b_{00}}^2$	.121	.023	<.001
Growth Rate, ${\sigma }_{b_{10}}^2$	.012	.007	.051
Covariance, initial status & growth rate σb10, b00	−.003	.011	.801
Residual Error, σ2	.095	.016	<.001
Group Variance, ${\sigma }_{c00}^2$	.026	.013	.020
Group Correlation (Lag 1), ρ	.761	.181	<.001

Discussion

Changes in group membership and group effects over time are important issues to address in longitudinal studies. In the presence of time-varying group membership we encourage researchers to use either CCREMs or multiple membership models. There is little justification for using nested random-effect models given that the implementation of the acute-effects CCREM is just as simple as a nested model with general purpose software programs, and our simulations and others (Luo & Kwok, 2012) suggest greater accuracy of the acute-effects CCREM in estimating the random model parameters and standard errors of the fixed effects. We also encourage researchers to fit models with time-varying group effects. Models with stable group effects are on face value implausible and our simulations indicate they lead to errors in estimation of the random parameters similar to those resulting from fitting a nested model in the presence of time-varying group membership. Models with time-varying group effects are also simple to implement, therefore this should not impede their use. Lastly, we propose, evaluate through simulation, and apply models that allow for both time-varying group membership and group effects. These models generally perform better than nested stable group alternatives and are also quite easy to put into practice. It should be noted however that we did not exhaust in our simulation designs all situations that might be encountered in applied settings (e.g., very small degrees of group variance) and therefore our simulations are limited in this regard.

The models advocated in this paper raise some interesting challenges and areas for future development. First, the choice among an extensive selection of dynamic group models can seem daunting. For this reason we recommend testing models at the extremes of the spectrum of restrictiveness, and a few models that are more intermediate. Second, the models presented assume linear growth over time. A more flexible alternative is to fit models with a piecewise constant specification of time (Pallardy, 2010). Incorporating features of such a model to those already proposed would be an important area of future development. Third, we were unable to identify a way to estimate a model with both cummulative cross-classified random effects and dynamic group effects, but this would be an important area to pursue. Lastly, there may be situations where there is more than one group that individuals are crossed with and we think of these crossings as random variables. This would be a relatively straightforward extension of the models and programming logic provided, which would only involve adding separate random effects that correspond to any additional crossing of individuals with groups. While extensions to other response distributions would generally be straightforward, this may not be the case with modeling time to event data with crossed random effects. One possible solution involves a grouped-time survival analysis approach, in which survival time is treated as an ordinal outcome or a binary response with a set of dichotomous indicators (Hedeker, Siddiqui, & Hu, 2000). If the survival times are continuous these models can still be applied if survival times are separated into event time deciles (Liu & Huang, 2008).

The implementation of the models described in this paper was with general purpose software, in particular SAS because it offers the greatest amount of flexibility in fitting models with both time-varying group membership and group effects. There are several other specialized software packages that researchers might want to consider using, such as HLM and MLwiN. There can be a variety of reasons for using these software packages. For instance HLM makes it especially easy to fit both acute- and cummulative- effects CCREM and MLwiN allows for easy use of multiple membership models and Bayesian estimation using Markov Chain Monte Carlo. In general, the choice of software package will be motivated by a variety of factors, but as long as the software can effectively address the issues described in this paper, the choice of which program to use becomes less important.

There is increasing emphasis on appropriately modeling longitudinal data in psychological studies. The models advocated in this paper can be viewed as taking researchers one step closer to more accurately modeling their data, and in turn to providing better answers to research questions.