Abstract
How are spatial and object attention coordinated to achieve rapid object learning and recognition during eye movement search? How do prefrontal priming and parietal spatial mechanisms interact to determine the reaction time costs of intra-object attention shifts, inter-object attention shifts, and shifts between visible objects and covertly cued locations? What factors underlie individual differences in the timing and frequency of such attentional shifts? How do transient and sustained spatial attentional mechanisms work and interact? How can volition, mediated via the basal ganglia, influence the span of spatial attention? A neural model is developed of how spatial attention in the where cortical stream coordinates view-invariant object category learning in the what cortical stream under free viewing conditions. The model simulates psychological data about the dynamics of covert attention priming and switching requiring multifocal attention without eye movements. The model predicts how “attentional shrouds” are formed when surface representations in cortical area V4 resonate with spatial attention in posterior parietal cortex (PPC) and prefrontal cortex (PFC), while shrouds compete among themselves for dominance. Winning shrouds support invariant object category learning, and active surface-shroud resonances support conscious surface perception and recognition. Attentive competition between multiple objects and cues simulates reaction-time data from the two-object cueing paradigm. The relative strength of sustained surface-driven and fast-transient motion-driven spatial attention controls individual differences in reaction time for invalid cues. Competition between surface-driven attentional shrouds controls individual differences in detection rate of peripheral targets in useful-field-of-view tasks. The model proposes how the strength of competition can be mediated, though learning or momentary changes in volition, by the basal ganglia. A new explanation of crowding shows how the cortical magnification factor, among other variables, can cause multiple object surfaces to share a single surface-shroud resonance, thereby preventing recognition of the individual objects.
Keywords: Surface perception, Spatial attention, Transient attention, Sustained attention, Object attention, Object recognition, Parietal cortex, Prefrontal cortex, Attentional shroud, Crowding
1. Introduction
Typical environments contain many visual stimuli that are processed to varying degrees for perception, recognition, and control of action (Broadbent, 1958). Attention allocates visual processing resources to pursue these purposes while preserving reactivity to rapid changes in the environment (Kastner & Ungerleider, 2000; Posner & Petersen, 1990). If, for example, a car is coming towards us at high speed, the immediate imperative is to get out of the way. Once it has passed, we may want to determine its make and model to file a police report. However, to succeed at either task, the visual system must first learn what an object is. Under unsupervised learning experiences, nothing tells the brain that there are objects in the world, and any single view of an object is distorted by cortical magnification (Daniel & Whitteridge, 1961; Drasdo, 1977; Fischer, 1973; Polimeni, Balasubramanian, & Schwartz, 2006; Schwartz, 1977; Tootell, Silverman, Switkes, & De Valois, 1982; Van Essen, Newsome, & Maunsell, 1984). Yet the brain somehow learns what objects are. This article develops the hypothesis that information about an object may be accumulated as the eyes foveate several views of an object. Similar views learn to activate the same view category, and several view categories may learn to activate a view-invariant object category. The article proposes how at least two mechanistically distinct types of attention may modulate the learning of both view categories and view-invariant object categories.
While we can easily describe the subjective experience of attention (James, 1890), a rigorous description of the underlying units or mechanisms has proved elusive (Scholl, 2001). This may in part be due to the emphasis on describing attention as acting on the visual system rather than acting in the visual system. Early models, such as the `spotlight of attention' (Duncan, 1984; Posner, 1980; Scholl, 2001) and biased competition types of models (Grossberg, 1976, 1980b; Grossberg, Mingolla, & Ross, 1994; Itti & Koch, 2001; Treisman & Gelade, 1980; Wolfe, Cave, & Franzel, 1989), suggested that attention could enhance and suppress aspects of a visual scene, but most of these early models did not consider what attention must accomplish to lead to behavior, notably the learning and recognition of the objects that are situated in a scene. A notable exception is Adaptive Resonance Theory, or ART, which predicted how learned top-down expectations can focus attention upon critical feature patterns that can be quickly learned, without causing catastrophic forgetting, when the involved cells undergo a synchronous resonance (Carpenter & Grossberg, 1987, 1991, 1993; Grossberg, 1976, 1980b). Since that time, the modeling of Grossberg and his colleagues have distinguished at least three distinct types of “object” attention, and described different functional and computational roles for them:
-
(1)
Surface attention (Cao, Grossberg, & Markowitz, 2011; Fazl, Grossberg, & Mingolla, 2009; Grossberg, 2007, 2009): Spatial attention can fit itself to an object's surface shape to form an “attentional shroud” (Cavanagh, Labianca, & Thornton, 2001; Moore & Fulton, 2005; Tyler & Kontsevich, 1995). Such a shroud is formed and maintained through feedback interactions between the surface and spatial attention to form a surface-shroud resonance.
-
(2)
Boundary attention (Grossberg & Raizada, 2000; Raizada & Grossberg, 2001): Boundary attention can flow along and enhance an object's perceptual grouping, or boundary (Roelfsema, Lamme, & Spekreijse, 1998; Scholte, Spekreijse, & Roelfsema, 2001), even across illusory contours (Moore, Yantis, & Vaughan, 1998; Wannig, Stanisor, & Roelfsema, 2011). Both boundary and surface attention can facilitate figure-ground separation of an object (Grossberg & Swaminathan, 2004; Grossberg & Yazdanbakhsh, 2005).
-
(3)
Prototype attention (Carpenter & Grossberg, 1987, 1991, 1993; Grossberg, 1976, 1980b): Prototype attention can selectively enhance the pattern of critical features, or prototype, that is used to select a learned object category (Blaser, Pylyshyn, & Holcombe, 2000; Carpenter & Grossberg, 1987; Cavanagh et al., 2001; Duncan, 1984; Grossberg, 1976, 1980b; Kahneman, Treisman, & Gibbs, 1992; O'Craven, Downing & Kanwisher, 1999).
Early ART models focused on prototype attention and its role in the learning of recognition categories. In particular, ART predicted how prototype attention can help to dynamically stabilize the memory of learned recognition categories, notably view categories. Surface attention, represented as an “attentional shroud”, has more recently been proposed to play a critical role in regulating view-invariant object category learning. In particular, the ARTSCAN model (Cao et al., 2011; Fazl et al., 2009; Grossberg, 2007, 2009) predicted how the brain knows which view categories, whose learning is regulated by prototype attention, should be bound together through learning into a view-invariant object category, so that view categories of different objects are not erroneously linked together. The ARTSCAN model hereby proposed how spatial attention in the where cortical processing stream could regulate prototype attention within the what cortical processing stream.
The current article builds on this foundation by developing the distributed ARTSCAN, or dARTSCAN, model. ARTSCAN modeled how parietal cortex within the where cortical processing stream can regulate the learning of invariant object categories within the inferior temporal and prefrontal cortices of the what cortical processing stream. In ARTSCAN, a spatial attentional shroud focused only on one object surface at a time. Such a shroud forms when a surface-shroud resonance is sustained between cortical areas such as V4 in the what cortical stream and parietal cortex in the where cortical stream. The dARTSCAN model extends ARTSCAN capabilities in three ways.
First, dARTSCAN proposes how spatial attention may be hierarchically organized in the parietal and prefrontal cortices in the where cortical processing stream, with spatial attention in parietal cortex existing in either unifocal or multifocal states. In particular, dARTSCAN suggests how the span of spatial attention may be varied in a task-sensitive manner via learning or volitional signals that are mediated by the basal ganglia. In particular, spatial attention may be focused on one object (unifocal) to control view-invariant object category learning; spread across multiple objects (multifocal) to regulate useful-field-of view, and may vary between video game players and non-video game players; or spread across an entire visual scene, as during the computation of scenic gist (Grossberg & Huang, 2009). This enhanced analysis begins to clarify how, even when spatial attention seems to be focused on one object, the rest of the scene does totally vanish from consciousness.
Second, dARTSCAN does not rely only on the sustained spatial attention of a surface-shroud resonance. It also proposes how both sustained and transient components of spatial attention (Corbetta, Patel, & Shulman, 2008; Corbetta & Shulman, 2002; Egeth & Yantis, 1997) may interact within parietal and prefrontal cortex in the where cortical processing stream. Surface inputs to spatial attention are derived from what stream sources, such as cortical area V4, that operate relatively slowly. Transient inputs to spatial attention are derived from where stream sources, such as cortical areas MT and MST, that operate more quickly.
This analysis distinguishes two mechanistically different types of transient attentional components. ARTSCAN already predicted how a shift of spatial attention to a different object, that can occur when a surface-shroud resonance collapses, triggers a transient parietal signal that resets the currently active view-invariant object category in inferotemporal cortex (IT), and thereby enables the newly attended object to be categorized without interference from the previously attended object. In this way, a shift of spatial attention in the where cortical stream can cause a correlated shift of object attention in the what cortical stream. Chiu and Yantis (2009) have described fMRI evidence in humans for such a transient reset signal. This transient parietal signal is a marker against which further experimental tests of model mechanisms can be based; e.g., a test of the predicted sequence of V4-parietal surface-shroud collapse (shift of spatial attention), transient parietal burst (reset signal), and collapse of currently active view-invariant category in cortical area IT (shift of categorization rules).
The transient parietal reset signal that coordinates a shift of spatial and object attention across the where and what cortical processing streams, respectively, is mechanistically different from transient attention shifts that are directly due to where stream inputs via MT and MST, which are predicted below to play an important role in quickly updating prefrontal priming mechanisms and explaining two-object cueing data of Brown and Denney (2007).
Third, dARTSCAN models how prefrontal cortex and parietal cortex may cooperate to control efficient object priming, learning, and search.
This dARTSCAN analysis provides a neurobiological explanation of how attention may engage, move, and disengage, and how inhibition of return (IOR) may occur, as objects are freely explored with eye movements (Posner, 1980; Posner, Cohen, & Rafal, 1982; Posner & Petersen, 1990).
These three innovations are described in greater detail in Section 3 and beyond. Given these enhanced capabilities, the dARTSCAN model is able to explain, quantitatively simulate, and predict data from three experimental paradigms: two-object priming, useful-field-of-view and crowding. The two object priming task, first used by Egly, Driver, and Rafal (1994), investigates object-based attention by measuring differences in reaction time (RT) between a validly cued target, an invalidly-cued target that requires a shift of attention within the cued object, and an invalidly-cued target which requires a shift of attention between two objects. Two adaptations of the original task are examined, an extension of the original that includes location cues and targets (Brown & Denney, 2007) and a version of the task that examines individual differences between subjects (Roggeveen, Pilz, Bennett, & Sekuler, 2009). The useful-field-of-view (UFOV) task, first used by Sekuler and Ball (1986) measures the ability of a subject to detect the location of an oddball among many distracters over a wide field of view in a display, which is masked after a brief exposure. Crowding is a phenomenon in which a letter which is clearly visible when peripherally presented alone, is unrecognizable when surrounded by two nearby flanking letters (Bouma, 1970, 1973; Green & Bavelier, 2007; Levi, 2008). These data and concepts about the coordination of spatial and object attention are more fully explained in the subsequent sections.
2. Spatial attention in the regulation of invariant object category learning
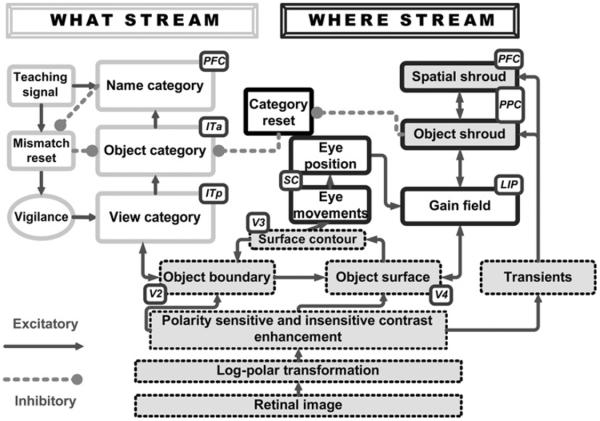
How does the brain learn to recognize an object from multiple viewpoints while scanning a scene with eye movements? How does the brain avoid the problem of erroneously classifying parts of different objects together? How are attention and eye movements coordinated to facilitate object learning? The dARTSCAN model builds upon the ARTSCAN model (Fig. 1; Cao et al., 2011; Fazl et al., 2009; Grossberg, 2007, 2009), which showed how the brain can learn view-invariant object representations under free viewing conditions. The ARTSCAN model proposes how an object's pre-attentively formed surface representation in cortical area V4 generates a form-fitting distribution of spatial attention, or “attentional shroud” (Tyler & Kontsevich, 1995), in the parietal cortex of the where cortical stream. All surface representations dynamically compete for spatial attention to form a shroud. The winning shroud remains active due to a surface-shroud resonance that is supported by positive feedback between a surface and its shroud, and that persists during active scanning of the object with eye movements.
Fig. 1.
Circuit diagram of the ARTSCAN model. A FACADE model (Grossberg, 1994, 1997; Grossberg & Todorović, 1988) simplified front end is in dashed boxes. What cortical stream elements are in gray outlined boxes, while where cortical stream elements are in black outlined boxes.
A full understanding of the structure of surface-shroud resonances will require an analysis of how an object's distributed, multiple-scale, 3D boundary and surface representations in prestriate cortical areas such as V4 (e.g., Fang & Grossberg, 2009; Grossberg, Kuhlmann, & Mingolla, 2007; Grossberg, Markowitz, & Cao, 2011; Grossberg & Yazdanbakhsh, 2005) activate parietal cortex in such a way that different aspects of the boundary and surface representations can be selectively attended. The simple visual stimuli used in the psychophysical experiments that are explained in this article can be simulated with correspondingly simple surface-shroud resonances. Once such a shroud is activated, it regulates eye movements and category learning about the attended object in the following way.
The first view-specific category to be learned for the attended object also activates a cell population at a higher processing stage. This cell population will become a view-invariant object category. Both types of categories are assumed to form in the inferotemporal (IT) cortex of the what cortical processing stream. For definiteness, suppose that view categories get activated in posterior IT (ITp) and view-invariant categories get activated in anterior IT (ITa) (Baker, Behrmann, & Olson, 2002; Booth & Rolls, 1998; Logothetis, Pauls, & Poggio, 1995).
As the eyes explore different views of the object, previously active view-specific categories are reset to enable new view-specific categories to be learned. What prevents the emerging view-invariant object category from also being reset? The shroud maintains the activity of the emerging view-invariant category representation by inhibiting a reset mechanism, also in parietal cortex, that would otherwise inhibit the view-invariant category. As a result, all the view-specific categories can be linked through associative learning to the emerging view-invariant object category. Indeed, these associative linkages create the view invariance property.
These mechanisms can bind together different views that are derived from eye movements across a fixed object, as well as different views that are exposed when an object moves with respect to a fixed observer. Indeed, in both cases, the surface-shroud resonance corresponding to the object does not collapse. Further development of ARTSCAN, to the pARTSCAN model (Cao et al., 2011) shows, in addition, how attentional shrouds can be used to learn view-, position-, and size-invariant object categories, and how views from different objects can, indeed, be merged during learning, and used to explain challenging neurophysiological data recorded in monkey inferotemporal cortex, if the shroud reset mechanism is prevented from acting (e.g., Li & DiCarlo, 2008, 2010). Although the objects that are learned in psychophysical displays are often two-dimensional images that are viewed at a fixed position in depth, ART models are capable of learning recognition categories of very complex objects–e.g., see the list of industrial applications at http://techlab.bu.edu/resources/articles/C5–so the current analysis also generalizes to three-dimensional objects.
Shroud collapse disinhibits the reset signal, which in turn inhibits the active view-invariant category. Then a new shroud, corresponding to a different object, forms in the where cortical stream as new view-specific and view-invariant categories of the new object are learned in the what cortical stream. The ARTSCAN model thereby begins to mechanistically clarify basic properties of spatial attention shifts (engage, move, disengage) and IOR.
The ARTSCAN model has been used to explain and predict a variety of data. A key ARTSCAN prediction is that a spatial attention shift (shroud collapse) causes a transient reset burst in parietal cortex that, in turn, causes a shift in categorization rules (new object category activation). This prediction has been supported by experiments using rapid event-related functional magnetic resonance imaging (fMRI; Chiu & Yantis, 2009). Positive feedback from a shroud to its surface is predicted to increase the contrast gain of the attended surface, as has been reported in both psychophysical experiments (Carrasco, Penpeci-Talgar, & Eckstein, 2000) and neurophysiological recordings from cortical areas V4 (Reynolds, Chelazzi, & Desimone, 1999; Reynolds & Desimone, 2003; Reynolds, Pasternak, & Desimone, 2000). In addition, the surface-shroud resonance strengthens feedback signals between the attended surface and its generative boundaries, thereby facilitating figure-ground separation of distinct objects in a scene (Grossberg, 1994; Grossberg & Swaminathan, 2004; Grossberg & Yazdanbakhsh, 2005; Kelly & Grossberg, 2000).
In particular, surface contour signals from a surface back to its generative boundaries strengthen consistent boundaries, inhibit irrelevant boundaries, and trigger figure-ground separation. When the surface contrast is enhanced by top-down spatial attention as part of a surface-shroud resonance, its surface contour signals (which are contrast-sensitive) become stronger, and thus its consistent boundaries become stronger as well, thereby facilitating figure-ground separation. This feedback interaction between surfaces and boundaries via surface contour signals is predicted to occur from V2 thin stripes to V2 pale stripes.
Corollary discharges of these surface contour signals are predicted to be mediated via cortical area V3A (Caplovitz & Tse, 2007; Nakamura & Colby, 2000) and to generate saccadic commands that are restricted to the attended surface (Theeuwes, Mathot, & Kingstone, 2010) until the shroud collapses and spatial attention shifts to enshroud another object.
Why is it plausible, mechanistically speaking, for surface contour signals to be a source of eye movement target locations, and for these commands to be chosen in cortical area V3A and beyond? It is not possible to generate eye movements that are restricted to a single object until that object is separated from other objects in a scene by figure-ground separation. If figure-ground separation begins in cortical area V2, then these eye movement commands need to be generated no earlier than cortical area V2. Surface contour signals are plausible candidates from which to derive eye movement target commands because they are stronger at contour discontinuities and other distinctive contour features that are typical end points of saccadic movements. ARTSCAN proposed how surface contour signals are contrast-enhanced at a subsequent processing stage to select the largest signal as the next saccadic eye movement command. Cortical area V3A is known to be a region where vision and motor properties are both represented, indeed that “neurons within V3A…process continuously moving contour curvature as a trackable feature…not to solve the “ventral problem” of determining object shape but in order to solve the “dorsal problem” of what is going where” (Caplovitz & Tse, 2007, p. 1179).
Last but not least, ARTSCAN quantitatively simulates key data about reaction time costs for attention shifts between objects relative to those within an object (Brown & Denney, 2007; Egly et al., 1994). However, ARTSCAN cannot simulate all cases in the Brown and Denney (2007) experiments. Nor was ARTSCAN used to simulate the UFOV task or crowding.
3. Sustained and transient attention, spatial priming, and useful-field-of-view
The dARTSCAN model incorporates three key additional processes to explain a much wider range of data about spatial attention:
-
(1)
The breadth of spatial attention (“multifocal attention”) can vary in a task-selective and learning-responsive way (Alvarez, Horowitz, Arsenio, Dimase, & Wolfe, 2005; Cavanagh & Alvarez, 2005; Cave, Bush, & Taylor, 2010; Franconeri, Alvarez, & Enns, 2007; Green & Bavelier, 2003; Jans, Peters, & De Weerd, 2010; McMains & Somers, 2004, 2005; Muller, Malinowski, Gruber, & Hillyard, 2003; Pylyshyn & Storm, 1988; Pylyshyn et al., 1994; Scholl, Pylyshyn, & Feldman, 2001; Tomasi, Ernst, Caparelli, & Chang, 2004; Yantis & Serences, 2003). The current model proposes how spatial attention can be distributed across multiple objects simultaneously, while still being compatible with the strictly unifocal attention in ARTSCAN.
Below we illustrate how flexibly altering the maximal distribution of spatial attention can be volitionally regulated by the basal ganglia using an inhibitory mechanism that is predicted to be homologous to the one that regulates visual imagery (Grossberg, 2000b) and the storage of sequences of items in working memory (Grossberg & Pearson, 2008).
-
(2)
Both sustained surface-driven spatial attention and transient motion-driven spatial attention interact to control maintenance and shifts of spatial attention (Fig. 2). A large experimental literature attempts to anatomically and functionally differentiate components of sustained and transient attention (Dosenbach, Fair, Cohen, Schlaggar, & Petersen, 2008; Dosenbach et al., 2007; Gee, Ipata, Gottlieb, Bisley, & Goldberg, 2008; Gottlieb, Kusunoki, & Goldberg, 2005; Hillyard, Vogel, & Luck, 1998; Ploran et al., 2007; Reynolds, Alborzian, & Stoner, 2003; Yantis & Jonides, 1990; Yantis et al., 2002). The ARTSCAN model only incorporates sustained, surface-driven attention necessary for view-invariant category learning. On the other hand, as noted in Section 1, ART-SCAN also posits a transient reset signal that coordinates shifts of spatial attention with shifts of categorization rules.
-
(3)
In addition to parietal cortex, prefrontal cortex plays a role in priming spatial attention (Fig. 2). Many experiments document such a role for prefrontal cortex (Boch & Goldberg, 1989; Goldman & Rakic, 1979; Kastner & Ungerleider, 2000; Ungerleider & Haxby, 1994; Zikopoulos & Barbas, 2006). The ARTSCAN model is agnostic about the role of PFC in deploying spatial attention.
The above three sets of processes, working together, enable our model to explain a much larger range of data about how attention and recognition interact, notably to better characterize how multifocal attention can help to track and recognize multiple objects in familiar scenes, and focal attention can support view-invariant object category learning for unfamiliar objects.
Fig. 2.
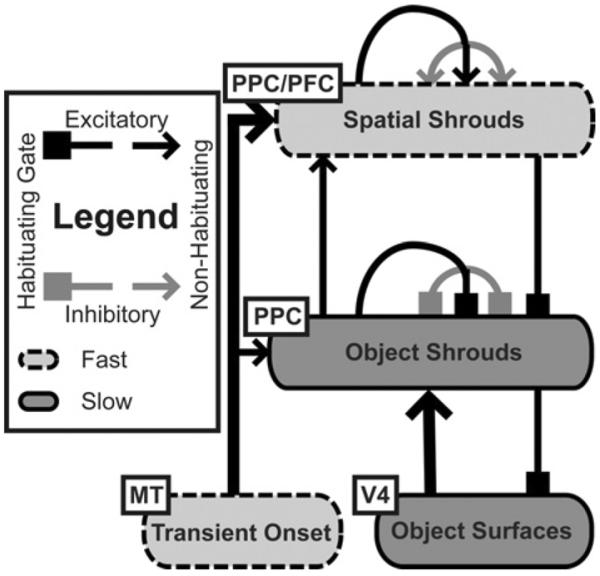
The recurrent, feedforward and feedback connections of object and spatial shrouds. Hemifield separation is not shown.
The large cognitive literature about multifocal attention (Cavanagh & Alvarez, 2005; Pylyshyn et al., 1994) produced concepts such as Fingers of Instantiation (FINST; Pylyshyn, 1989, 2001), Sprites (Cavanagh et al., 2001), and situated vision (Pylyshyn, 2000; Scholl, 2001) which have in common an idea that objects which are not being focally attended are nonetheless spatially represented in the attentional system (Scholl, 2001). This is necessary to allow rapid shifts of attention between objects, to track several identical objects simultaneously, and to underpin visual orientation by marking the allocentric coordinates of several objects in a scene (Mathot & Theeuwes, 2010a; Pylyshyn, 2001). Such concepts are consistent with the daily experience that scenic features outside our focal attention do not disappear.
One challenge to extending the ARTSCAN shroud architecture is how these ideas might be integrated into a system that continues to allow the learning of view-invariant object categories over several saccades, which requires that attention be object-based and unifocal. Multiple shrouds cannot exist during multi-saccade exploration because saccades from one attended object to another would fail to reset the active view-invariant object category, causing distinct objects to be falsely conflated as parts of a single object. Moreover, since multiple surfaces would be recipients of contrast gain from shroud-to-surface feedback, peripheral parts of the object being learned and other objects nearby could similarly be conflated. This suggests that there are at least two model states in which stable shrouds can form. In one, unifocal attention can be maintained on a single surface over multiple saccades, allowing the learning of view-invariant object categories. In the other, multiple shrouds can simultaneously coexist, at a lower intensity not sufficient to gate multi-saccade learning, but allowing rapid recognition of familiar objects and attention to be deployed on multiple objects, regardless of familiarity, between saccades. As noted in item (1) above, volitional control of inhibition in the attention circuit, likely mediated by the basal ganglia (Brown, Bullock, & Grossberg, 2004), allows unfamiliar objects that have weak shrouds to be foveated, followed by an increase in competition to create a single strong shroud that can support learning of a view-invariant object category.
As noted in item (3) above, another challenge, for both the ARTSCAN model, as well as other biased competition models (Itti & Koch, 2001; Lee & Maunsell, 2009; Reynolds & Heeger, 2009; Treisman & Gelade, 1980; Wolfe et al., 1989), is to understand the mechanism of attention priming. Brief transient cues orient attention to an area of a visual scene, which leads to improved behavioral performance if a task-relevant stimulus is presented at the same position within several hundred milliseconds (Desimone & Duncan, 1995; Posner & Petersen, 1990). If the experiment continues and a second task-relevant stimulus appears at the same position after the first has disappeared or is no longer task-relevant, it takes longer for that area to be attended again, due to inhibition-of-return (Grossberg, 1978a, 1978b; Koch & Ullman, 1985; Posner et al., 1982; see Itti and Koch (2001) for a review). ARTSCAN and biased competition models can account for IOR, but they do not incorporate a mechanism that can explain how a brief bottom-up input onset can prime visual attention in the absence of intervening visual stimuli for several hundred milliseconds. But such priming seems to be necessary to explain an extension by Brown and Denney (2007) of the two-object cueing task first used by Egly et al. (1994); see Fig. 3. Priming by prefrontal cortex is incorporated into the model as a natural complement to allowing multifocal attention within the model parietal cortex (Fig. 2).
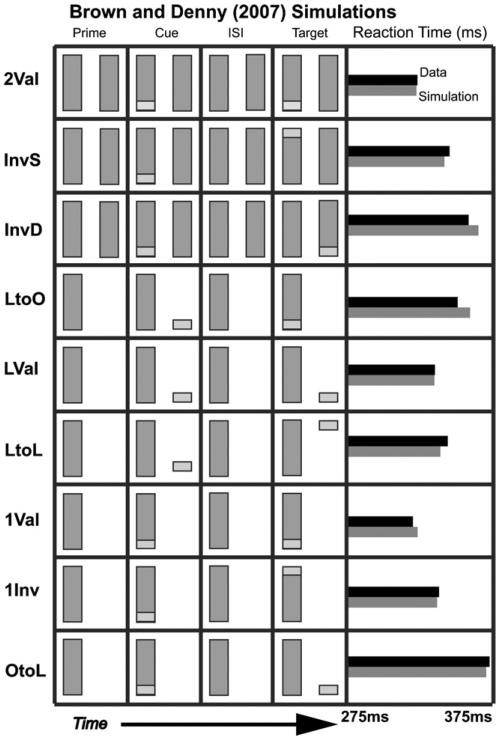
Fig. 3.
Brown and Denney (2007) data and reaction time (RT) simulations. Each experimental case is shown, with the four columns corresponding to what is seen in each display segment. Experimental RTs (black) and simulated RTs (gray) are shown at the far right. [Data reprinted with permission from Brown and Denney (2007).]
We hereby propose that a hierarchy of attentional shrouds in parietal and prefrontal cortex (Figs. 1 and 2) can smoothly switch between behavioral modes, while being sensitive to both transient event onsets and offsets, as well as to sustained shroud-mediated spatial attention, and which we will employ in order to explain key properties of cognitive models of multifocal attention, such as FINST (Pylyshyn, 1989, 2001).
The idea of a hierarchy of attention is consistent with accumulating anatomical and physiological evidence that magnocellular pathways play a role in priming object recognition in inferotemporal cortex through orbitofrontal cortex (Bar et al., 2006; Zikopoulos & Barbas, 2006). Evidence for multiple attention representations has also been found by mapping retinotopy in the visual system using fMRI, which has shown multiple, attention-sensitive maps in connecting areas of the intra-parietal sulcus (Silver, Ress, & Heeger, 2005; Swisher, Halko, Merabet, McMains, & Somers, 2007), as well as in retinotopic and head-centric representations in other areas of parietal cortex and areas of prefrontal cortex such as the frontal eye fields and dorsolateral prefrontal cortex (Saygin & Sereno, 2008).
The lower shroud level in the hierarchy, the object shroud layer, behaves similarly to the shrouds found in the ARTSCAN model (Fazl et al., 2009; PPC in Figs. 1 and 2). Neurons in this layer can resonate strongly with a single surface to gate learning in the what stream to allow the formation of view-invariant object categories. Multiple ensembles of neurons in the object shroud layer can also weakly resonate with several surfaces, allowing multifocal attention and rapid recognition of familiar scenes. Object shroud neurons can thus exist in two different regimes, which alternate reactively in response to changing visual stimuli, or can be volitionally controlled by modifying the inhibitory gain through the basal ganglia (Brown et al., 2004; Matsuzaki, Kyuhou, Matsuura-Nakao, & Gemba, 2004; Xiao, Zikopoulos, & Barbas, 2009). The first regime was studied in the original ARTSCAN model, where a single high-intensity shroud covers an object surface and gates learning during a multi-saccadic exploration of an unfamiliar object. The second regime allows multiple low-intensity object shrouds to exist simultaneously, supporting rapid recognition of a familiar scene's “gist”. Gist was modeled in the ARTSCENE model (Grossberg & Huang, 2009; Huang & Grossberg, 2010) as a large-scale texture category. Since object shroud neurons gate learning regimes lasting several seconds, they provide sustained attention and are slow to respond to changes in a scene.
In contrast to this property, reaction times in response to scenes that contain several objects are reduced if a task-relevant stimulus appears at one of the object positions within a few hundred milliseconds (Desimone & Duncan, 1995; Posner & Petersen, 1990). The attentional shrouds of the ARTSCAN model require a surface to be present to sustain a shroud-surface resonance. If that surface disappears, its corresponding shroud will collapse and another shroud will form over the next most salient object in a scene, which will start a new learning regime. This means that if a location is briefly cued, attention will shift once the cue disappears and the cued location will immediately be subject to IOR, which is inconsistent with attentional priming. Also in the ARTSCAN model, spatial attention is not preferentially sensitive to the appearance of a new object of equal contrast to the existing objects in a scene, unless the other objects in a scene had already been attended. Thus both attentional priming and fast reactions to cue changes are not adequately represented in the ARTSCAN model.
These ARTSCAN properties derive from that model's exclusive consideration of focal sustained attention and how it shifts through time. The dARTSCAN model also incorporates, and elaborates functional roles for, inputs that are sensitive to stimulus transients (Fig. 2, MT; also see Section 5.6 and Appendix A.6), consistent with models of motion perception (Berzhanskaya, Grossberg, & Mingolla, 2007) and models that combine transient and sustained contributions to spatial attention (e.g., Grossberg, 1997). Moreover, the model proposes how such transient inputs can contribute both to the formation of shrouds in the parietal cortex, and to the development of top-down priming from the prefrontal cortex.
Accordingly, in the higher level of the hierarchy, the spatial shroud level is formed by ensembles of neurons primarily driven by transient signals from the where cortical processing stream (see Sections 5.8 and Appendix A.8), notably signals due to object appearances, disappearances, and motion (PFC, Fig. 2). Unlike object shrouds, several shrouds in the spatial shroud layer can coexist at all times. This allows objects unattended in the object shroud layer to maintain spatial representations, allowing rapid (between saccades) shifts of attention, transient interruption of multiple-view learning, and attentional priming of locations at which an object recently disappeared or was occluded. Recurrent feedback allows a spatial shroud to stay active at a cued location for several hundred milliseconds, regardless of whether a surface is present at the location. Spatial shroud neurons also improve reaction times to transient or otherwise highly salient stimuli through top-down feedback onto object shroud neurons.
Top-down priming feedback enables quantitative simulation of reaction time differences in several cases presented in Brown and Denney (2007), particularly the LVal case (Fig. 3, row 5) where there is a valid location cue. As described in greater detail in Section 6.1.1, without priming, there would be no attentional representation of the cue through the interstimulus interval (ISI). In particular, as noted above, the original ARTSCAN model requires a surface to be present to sustain a shroud-surface resonance. This means that if a location is briefly cued, attention will shift once the cue disappears, and the cued location will immediately be subject to IOR. Prefrontal attentional priming overcomes this deficiency by sustaining an attentional prime throughout the ISI.
4. Individual differences and the basal ganglia: useful-field-of-view and RT
There are systematic individual differences in how attention is deployed and maintained (Green & Bavelier, 2003, 2006a, 2006b, 2007; Richards, Bennett, & Sekuler, 2006; Scalf et al., 2007; Sekuler & Ball, 1986; Tomasi et al., 2004). Green and Bavelier have, in particular, compared how video game players (VGPs) and non-video game players (NVGPs) perform in spatial attention tasks. Another line of research examined the differences in performance in the same individual under different conditions, such as before and after a training session (Green & Bavelier, 2003, 2006a, 2006b, 2007; Richards et al., 2006; Scalf et al., 2007; Tomasi et al., 2004). Finally, on psychophysics tasks such as the two object-cueing task first used by Egly et al. (1994), bootstrapping methods have been used to study between-subject differences on the same task, rather than the average population response to differing stimuli (Roggeveen et al., 2009). The dARTSCAN model proposes how these multiple modes of behavior and performance differences between individuals may arise from differences in inhibitory gain, mediated by the basal ganglia. We suggest how volitional or learning-dependent variations in the strength of inhibition that governs attentional processing may explain individual differences. As noted above, variations of this mechanism may be used in multiple brain systems to control other processes, such as visual imagery (Grossberg, 2000b) and working memory storage and span (Grossberg & Pearson, 2008).
VGPs have been found to have superior performance in several tasks involving visual attention, including flanker recognition, multiple object tracking (MOT), useful-field-of-view (UFOV), attentional blink, subitizing, and crowding (Green & Bavelier, 2003, 2006a, 2006b; Sekuler & Ball, 1986). Additionally, VPG's have better visual acuity than NVGPs (Green & Bavelier, 2007). Most of these performance improvements have also been found when a group of NVGPs trains on action video games for various periods of time typically 30–60 h; e.g., Green and Bavelier (2003). This indicates that playing action video games causes substantial changes in the basic capacity and performance of the visual attention system that is not specific to any individual or subpopulation. In some tasks, such as UFOV, similar changes have been found as the result of aging (Richards et al., 2006; Scalf et al., 2007; Sekuler & Ball, 1986).
As described above, the object shroud layer can switch between unifocal and multifocal attention through volitional control of inhibitory gain mediated by the basal ganglia. The model predicts that training through action video games increases the range of volitional control available in both shroud layers. Similarly, aging reduces the range of inhibitory control in both shroud layers. This allows VGPs (and the young) to spread their attention more broadly in the spatial shroud player, and increases the capacity of the object shroud attention layer so that the same object causes less inhibition than it would in a NVGP. We test this prediction using the UFOV task. The results are shown in Section 6.2 and Fig. 6 below. Roggeveen et al. (2009) revisited the two-object cueing task of Egly et al. (1994), who found that people respond faster when an invalid cue is presented on the same object as the target, than when the cue is presented on a different object. Roggeveen et al. (2009) reported that, while part of their subject pool showed the same effect, another part showed the opposite effect and responded faster when the invalid cue was on the other object. They also found that a valid cue improves reaction time in nearly all subjects. These data are challenging to explain in an object-based attention paradigm because, if the object is attended, how can a target on an unattended object lead to a faster response? The current model is able to produce both effects by varying the relative strength of the slower, surface-(object shroud) resonance, and the faster, transient-driven response of spatial shrouds. The model predicts that the rate with which attention spreads on a surface varies for each individual, which is attributed to different relative gains between the surface-(object shroud) resonance and the (object shroud)-(spatial shroud) resonance. For those individuals who respond faster when the invalid cue is on the other object, attention in the object shroud layer has not yet completely covered the cued object. Since inhibition in the object shroud attention layer is distance-dependent, the area of a surface immediately beyond the leading edge of the spread of attention is actively suppressed relative to the un-cued object (see Figs. 6 and 7, Section 6.1). This parametric modification leads to the model prediction that varying the cue and ISI duration will shift the proportion of subjects who exhibit same-object preference. The model also predicts that altering the visual geometry of the display or the strength of the cue will alter the width and slope of the distribution of individual differences.
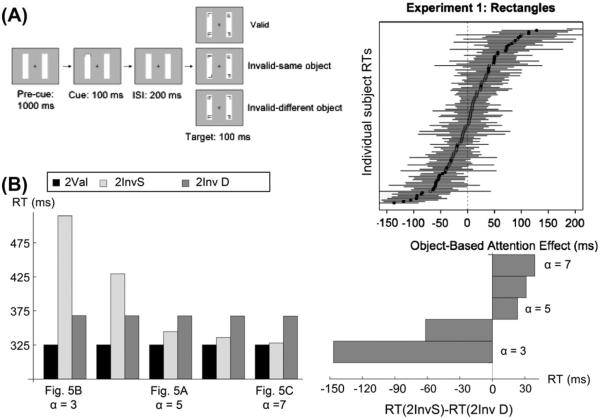
Fig. 6.
Roggeveen et al. (2009) individual difference data and modeled behavior. (A) The experimental paradigm and individual preferences for InvS, and InvD targets. (B) Simulated reaction times for two-object conditions (left plot), and reaction time differences (right plot) between InvS and InvD conditions, as the (spatial shroud)-(object shroud) resonance changes from weakest (left, α = 3, Eq. (33)) to strongest (right, α = 7, Eq. (33)) by increasing the response gain to changing inputs in the object shroud layer. This shifts preference from InvD (bottom) to InvS (top). [Data reprinted with permission from Roggeveen et al. (2009).]
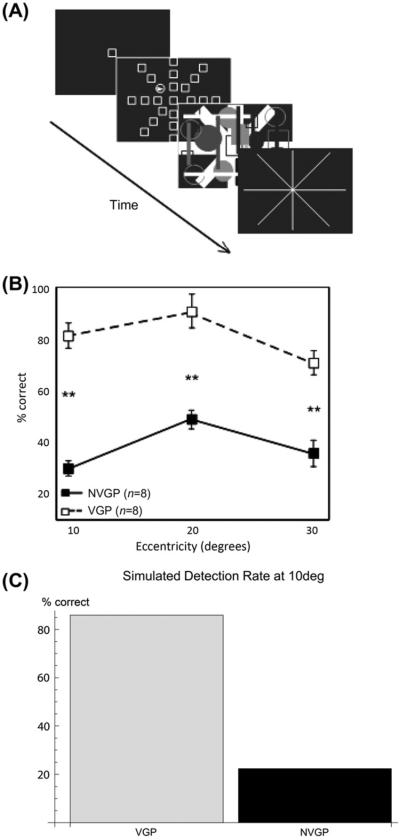
Fig. 7.
Green and Bavelier (2007) useful-field-of-view data and simulations. (A) Experimental paradigm used by Green and Bavelier (2003): After fixation, a brief (10 ms) display with an oddball is shown, followed by a mask. The task is to pick the direction of the oddball. (B) Experimental data for video game players (VPGs) and non-video game players (NVGPs) from Green and Bavelier (2003). [(A) and (B) reprinted with permission from Green and Bavelier (2007).] (C) VGPs are simulated by having 20% lower inhibitory gain in the object and spatial shroud layers (see T = .04 and TC = .032 in Eq. (36) as well as W = .04 and WC = .00016 in Eq. (42)), which facilitates detection through the mask period.
5. Model description
The dARTSCAN extension of the ARTSCAN model focuses on the where stream side of the original model (Fig. 1). Both models share similar boundary and surface processing. The current model uses a simpler approximation of cortical magnification to reduce the computational burden in simulation due to adding transient cells, prefrontal priming, and variable field-of-view. As briefly summarized above, both parietal and prefrontal shrouds are now posited: object shrouds, which are similar to the original ARTSCAN shroud representation and are primarily driven by surface signals, and spatial shrouds, which are primarily driven by transient signals (Fig. 2).
5.1. Cortical magnification
Visual representations in the early visual system are subject to cortical magnification, which has often been simulated using a log-polar approximation (Fazl et al., 2009; Polimeni et al., 2006). Working with models that include cortical magnification creates several complications. Because cortically magnified images are spatially variant, depending on the center of gaze, fixed convolutions or center-surround processing create effects that vary with eccentricity (Bonmassar & Schwartz, 1997). In addition, log-polar transformations do not fit neatly into the neighborhood relations of a matrix, which is the most convenient data structure for representing images and layers of neurons computationally.
It is possible, however, to maintain cortical magnification as a function of eccentricity while also keeping the neighborhoods of the matrix form, by approximating the central portion of the visual field using radial symmetric compression instead of a log-polar mapping. This has the advantage of simplifying computation of the model without ignoring the basic geometry reflected in the anatomy of the visual system (see Appendix A.1).
Given that model preprocessing before cortical activation is highly simplified, it is assumed that the model retina, rather than cortical area V1, already samples input images in a spatially-variant manner, using symmetric log compression to approximate cortical magnification, so that objects near the fovea have magnified representations and objects near the periphery have compressed representations. This is important in the model to bias attention towards foveated stimuli, which have correspondingly larger representations. Model retinal cell activities are normalized by receptive field size, and serve as input to the model lateral geniculate nucleus (LGN).
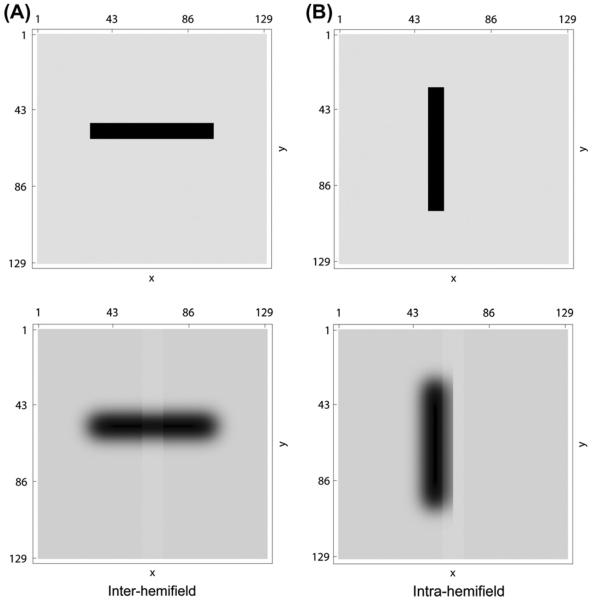
5.2. Hemifield independence
Model interactions also exhibit hemifield independence, which is consistent both with the anatomical separation of processing as well as behavioral observations (Alvarez & Cavanagh, 2005; Luck, Hillyard, Mangun, & Gazzaniga, 1989; Mathot, Hickey, & Theeuwes, 2010; Swisher et al., 2007; Youakim, Bender, & Baizer, 2001). Hemifield independence is implemented by using different sets of connection weights to control the strength of connections between neurons in the same hemifield, and neurons of opposite hemifields (see Appendix A.2, Eqs. (10)–(13)). Left and right hemifield representations use one set of distance-dependent connection weights between neurons that are in the same hemifield of the respective layer, or projecting layers. They use a different set of distance-dependent connection weights for neurons that are in the opposite hemifield of the same layer, or projecting layers. The connection strength between neighboring neurons is weighted near network boundaries to normalize the total input for each neuron (Grossberg & Hong, 2006; Hong & Grossberg, 2004). Thus, there are no boundary artifacts, either near the vertical meridian or the edges of the visual field.
5.3. LGN polarity-sensitive ON and OFF cells
The model LGN normalizes contrast of the input pattern using polarity-sensitive ON cells that respond to input increments and OFF cells that respond to image decrements. ON and OFF cells obey cell membrane, or shunting (Eqs. (1)–(3)), equations that receive retinal outputs within on-center off-surround networks that join other ON and OFF cells, respectively (Eqs. (14) and (15)). These single-opponent cells output to a layer of double-opponent ON and OFF cells in the what cortical processing stream (Eqs. (18) and (19)), as well as to transient cells in the where cortical processing stream (Eqs. (30)–(32)).
5.4. Boundaries
The model omits oriented simple cell receptive fields and various properties of ocularity, disparity-sensitivity, and motion processing that are found in primary sensory cortex, since no inputs used for the current model simulations require it. Instead, polarity-insensitive complex cells are directly computed at each position as a sum of rectified signals from pairs of polarity-sensitive double-opponent ON and OFF cells (Eq. (20)).
Object boundaries (Eq. (21)) are computed using bottom-up inputs from complex cells (Eq. (20)) that are amplified through a modulatory input from top-down inputs from surface contour cells (see Appendix A.4 and Eq. (23)). Surface contour signals are generated by surfaces that fill-in within closed boundaries. They select and enhance the boundaries that succeed in generating the surfaces that may enter conscious perception, thereby assuring that a consistent set of boundaries and surfaces are formed, while also, as an automatic consequence, initiating the figure-ground separation of objects from one another (Grossberg, 1994, 1997).
Surface contours are generated by contrast-sensitive networks at the boundaries of successfully filled-in surfaces; that is, surfaces which are surrounded by a connected boundary and thus do not allow their lightness or color signals to spill out into the scenic background. During 3-D vision and figure-ground separation, not all boundaries are connected (Grossberg, 1994). However, in response to the simplified input images that are simulated in this article, all object boundaries are connected and cause successful filling-in. As a result, surface contours are computed at all object boundaries, and can strengthen these boundaries via their positive feedback. Moreover, when the contrast of a surface is increased by feedback from an attentional shroud, the surface contour signals increase, so the strength of the boundaries around the attended surface increase also.
More complex boundary computations, such as those in 3D laminar visual cortical models (e.g., Cao & Grossberg, 2005; Fang & Grossberg, 2009) can be added as the model is further developed to process more complex visual stimuli, without undermining the current results.
5.5. Surfaces
Bottom-up inputs from double-opponent ON cells (Eq. (18)) trigger surface filling-in via a diffusion process (Eq. (26)) which is gated by object boundaries (Eq. (28)) that play the role of filling-in barriers (Grossberg, 1994; Grossberg & Todorović, 1988). The ON cell inputs are modulated by top-down feedback from object shrouds (Eq. (33)) that increase contrast gain during a surface-(object shroud) resonance. Such a resonance habituates through time in an activity-dependent way (Eq. (29)), thereby weakening the contrast gain caused by (object shroud)-mediated attention. Winning shrouds will thus eventually collapse, allowing new surfaces to be attended and causing IOR.
Filled-in surfaces generate surface contour output signals through contrast-sensitive shunting on-center off-surround networks (Eq. (23)). As noted above, surface contour signals provide feedback to boundary contours, which increases the strength of the closed boundary representations that induced the corresponding surfaces, while decreasing the strength of boundaries that do not form surfaces.
Although surface filling-in has often been modeled by a diffusion process since computational models of filling-in were introduced by Cohen and Grossberg (1984) and Grossberg and Todorović (1988), Grossberg and Hong (2006) have modeled key properties of filling-in using long-range horizontal connections that operate a thousand times faster than diffusion.
5.6. Transient inputs
Where stream transient cells in cortical area MT are modeled using a leaky integrator (Eq. (30)). Transient cells receive bottom-up input from double-opponent ON cells (Eq. (18)) proportional to the ratio of the contrast increment between previous and current stimuli at their position (Eq. (31)) for a brief period (Eq. (32)) after any change. Such ratio contrast sensitivity is a basic property of responses to input increments in suitably defined membrane, or shunting, equations (Grossberg, 1973, 1980a, 1980b). Any increment in contrast will trigger a transient cell response. After the period of sensitivity ends, transient activity quickly decays. OFF channel transient cells were omitted since only stimuli brighter than the background were simulated.
5.7. Object shrouds
The model where cortical stream enables one or several attentional shrouds to form in the object shroud layer, thereby supporting two different modes of behavior. The first, in which only a single shroud forms, allows an object shroud to perform the same role as in the original ARTSCAN model, gating learning when a sequence of several saccades explores a single object's surface to learn a view-invariant object category. The second, where multiple, weaker, shrouds can simultaneously coexist, supports conscious perception and concurrent recognition of several familiar object surfaces.
Object shroud neurons (Eq. (33)) receive strong bottom-up input from surface neurons (Eq.(26)) and modulatory input from transient cells to help salient onsets capture attention during sustained learning (Eq. (30); see Fig. 2). Object shroud neurons also receive top-down habituating (Eq. (38)) feedback from spatial shroud neurons (Eq. (39)), as well as recurrent on-center off-surround (Eqs. (35) and (36)) habituating (Eq. (37)) feedback from other object shroud neurons. Recurrent feedback among object shroud neurons habituates faster than spatial shroud feedback, which in turn habituates faster than feedback onto the surface layer. This combination of feedback produces several important effects. The first loop, surface-(object shroud)-surface (Fig. 2), enables a local cue on a surface that has successfully bid for object shroud attention to trigger the filling-in of attention along the entire surface (Eqs. (26)–(28)). Fully enshrouding an object which attracts attention through a local cue is slow compared to transient capture of highly salient objects, since it depends on slower surface dynamics. The second loop, recurrent on-center off-surround feedback in the object shroud layer, allows object shrouds to compete weakly in the multifocal case, to provide contrast enhancement, and strongly in the unifocal case, so that view-invariant object categories may be learned. Once a shroud has won in the unifocal case, surface-(object shroud) resonance dominates until habituation occurs. The level of competition between object shrouds depends on the inhibitory gain (Eq. (36)), which can be volitionally controlled through the basal ganglia. The third loop, (object shroud)-(spatial shroud)-(object shroud) enhances responses to salient transient signals, facilitates the spread of object shroud attention along surfaces, and helps maintain an (object shroud)-surface resonance over the whole surface, as parts of the object shroud start to habituate, by up-modulating the bottom-up surface signal. Once an object shroud that has habituated is out-competed and collapses, it is difficult for a new object shroud to form in the same position until the habituating gates recover, leading to IOR.
5.8. Spatial shrouds
When object shrouds are supporting view-invariant category learning, they must be stable on the order of seconds, to allow multiple saccades to explore an object (Fazl et al., 2009). The visual system however, is also capable of considerably faster responses, in particular to transient events (Desimone & Duncan, 1995). Spatial shrouds allow the model to respond quickly to transient stimuli when they are present, without compromising the stability required to support view-invariant object category learning in more stable environments (see Fig. 2). This basic fast-slow dynamic also underpins the model's explanation of individual difference data in the two-object cueing task, and allows the model to successfully simulate cases in the Brown and Denney (2007) data which require rapid responses to transient cues and targets, as is explained in Section 3.1.
Spatial shrouds (Eq. (39)) receive bottom-up input from transient neurons (Eq. (30)), and weaker bottom-up input from object shroud neurons (Eq. (40)). Spatial shroud neurons interact via a recurrent on-center off-surround network (Eqs. (41) and (42)) that does not habituate. As a result, multiple spatial shrouds can survive for hundreds of milliseconds in relatively stable environments unless they are out-competed by new transients. Spatial shroud cells are always sensitive to salient environmental stimuli and can mark multiple objects simultaneously, even if these objects are not being actively learned or recognized, allowing maintenance of allocentric visual orientation consistent with situated vision (Pylyshyn, 2001). The spatial shroud layer has non-habituating recurrent feedback capable of maintaining spatial shroud activity through time, so that an active spatial shroud can persistently prime object shroud formation over a surface presented at the corresponding location, unless the object shroud neurons are deeply habituated, causing IOR. There is no volitional attention from planning areas in the model, although we hypothesize that feedback to the spatial shroud layer might come from planning and executive control areas.
5.9. Computing model behavioral data
The data sets that are simulated use reaction time and detection thresholds to assess behavioral performance. We simulate these behavioral outputs by measuring activity levels at regions of interest (ROIs) important for the experimental display. To measure reaction time, we integrate activity in the object shroud layer over time until it reaches a threshold (chosen for best fit in the 2Val condition), then assume a constant delay between detection and motor output. To measure detection performance in the UFOV, we use the size of a Weber fraction comparing the level of response in the object shroud layer for the target and distracters at the end of the masking period as a direct proxy for performance.
6. Results
6.1. Two-object cueing
The two-object cueing task (Egly et al., 1994) is a sensitive probe to examine the object-based effects of attention. Two versions of the experiment extend the basic two-object task. One version includes one object and non-object positions with the same geometry (Brown & Denney, 2007). The second version shows that the general population effect found in Brown and Denney (2007) for same-object vs. inter-object attention switches is not uniform among all subjects. In both experiments, presentation occurs in four states (see Fig. 3). The first stage, called “prime,” displays two rectangles, equidistant from the fixation point, equal in size and such that the distance between the two ends of a rectangle is the same as the distance between the rectangles (Fig. 3, column 1, rows 1–3). In the cases of one object with possible position cues and targets, only one of the two rectangles is shown (see Fig. 3, column 1, rows 4–9). The rectangles can either cross the vertical meridian, or be presented in separate hemifields. In the second stage of the experiment (Fig. 3, column 2), one end of a rectangle (or the equivalent location, if there is only one rectangle) is cued, which is followed by the ISI (Fig. 3, column 3). Finally, a target is presented at one of the four possible cue positions (Fig. 3, column 4). This cue can be valid to the target or invalid.
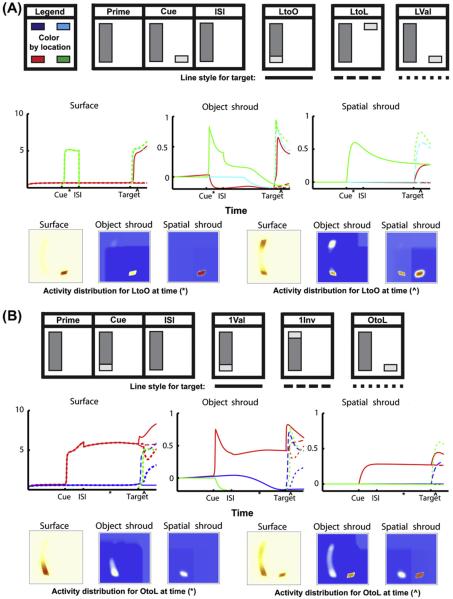
The original ARTSCAN model could simulate the order of reaction times in four of the main cases presented in Brown and Denney (2007); namely, the primary cases that illustrate the object cueing advantage (cases 2Val, InvS, InvD and OtoL in Fig. 3). The hierarchy of attentional interactions between PPC and PFC in the dARTSCAN model can simulate all nine cases successfully. This can be done due to the addition of transient cells, which shorten reaction times for targets, and by replacing the single shroud layer with the PPC-PFC hierarchy, which allows attention priming and balancing between the dynamics of the fast spatial shroud layer and the slower object shroud layer.
The following cases explain how the model fits the entire data set.
6.1.1. Valid cues
There are three display conditions in which the cue is valid. From fastest to slowest reaction times, these are:
-
(1)
One rectangle is presented throughout the experiment, with the cue and the target at the same position on the rectangle (1Val; Figs. 3 and 4).
-
(2)
Two rectangles are presented throughout the experiment, with the cue and target at the same position (2Val; Figs. 3 and 5).
-
(3)
One rectangle is presented throughout the experiment, with the cue and the target presented outside the object (LVal; Figs. 3 and 4).
Fig. 4.
Simulations of Brown and Denney (2007) one-object cueing data showing the dynamics of the surface, object shroud, and spatial shroud layers. The top row in each panel shows a schematic of input presentations for the one-object cases used to fit the Brown and Denney (2007) data, with colors corresponding to each region of interest (ROI) indicated at the upper left corner (not all positions are shown in each plot). In all simulations, the temporal dynamics of surface (S, Eq. (26)), object shroud (AO, Eq. (33)), and spatial shroud (AS, Eq. (39)), variables are shown in the first, second and third columns respectively, for each ROI. Solid, dashed and dotted lines show the target conditions that are defined in the top row. The bottom row of each panel shows the distribution of activity in the same layers at the times (*) and (^). (A) The three cases where a position is cued. Note that while the object shroud over the cued location falls to zero, the spatial shroud is maintained, thereby priming object shroud formation when the target is valid. (B) The three cases where there is one object, which is cued.
Fig. 5.
Simulations from Brown and Denney (2007) two-object cueing data, and individual difference data from Roggeveen et al. (2009) showing surface, object shroud, and spatial shroud dynamics. The top row shows a schematic of input presentations for the three two-object cases used to fit the Brown and Denney (2007) data, with colors corresponding to each ROI indicated at the upper left corner (not all positions are shown in each plot). In all simulations, the temporal dynamics of surface (S, Eq. (26)), object shroud (AO, Eq. (33)), and spatial shroud (AS, Eq. (39)), variables are shown in the first, second and third columns respectively, for each ROI. (A) The surface activity for the 2InvS case (dark blue) starts to increase slightly before target presentation, as does the activity of the object shroud. This indicates that the surface is about to be completely enshrouded, and that active inhibition has been released from the end of the rectangle opposite the cue because it has passed the edge separating the inhibitory surround from the excitatory center of the resonating shroud. This set of simulations corresponds to the behavioral results shown in middle simulation of Fig. 6B (α = 5, Eq. (33)). (B) The surface activity of the case in which 2InvD response is faster than 2InvS (green vs. dark blue), corresponding to the far left simulations in Fig. 6B (α = 3, Eq. (33)). Note that the bubble of inhibition (blue curve, object shroud layer is less than 0 and decreasing) corresponding to the 2InvS target is forming when the target is presented. (C) The surface activity of the case in which 2InvS response is faster than 2InvD (dark blue vs. green), corresponding to the far right simulations in Fig. 6B (α = 7, Eq. (33)). Note that surface-(object shroud) resonance has enshrouded the entire object prior to the InvS target being presented. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
The 1Val condition has a faster reaction time than the 2Val condition, because the presence of the second rectangle bidding for attention adds to the inhibition that the cued object must overcome to resonate with an object shroud. In both the object-valid conditions, there is a surface visible at the location of the cue throughout the experiment, and a resonant object shroud is maintained from cue presentation through target detection. In the LVal case, on the other hand, this does not occur: only a spatial shroud corresponding to the cued location endures through the ISI. While the spatial shroud primes the object shroud when the target appears, the object shroud cannot resonate until a new surface representation is formed. This in turn cannot take place until new boundaries have formed, something unnecessary when changing the contrast of an existing visible surface. If there were no spatial shroud present to prime the object shroud, the process would take longer, since after the surface representation formed, it would then have to bid for attention against a weak shroud representation on the rectangle visible throughout the experiment, substantially delaying the formation of a resonant shroud.
6.1.2. Invalid cues: one object
There are four display conditions in which one rectangle is visible throughout the experiment, but the cue is invalid. From fastest to slowest in human and model reaction times, these are:
-
(1)
The cue is presented at one end of the (only) rectangle, and the target appears at the far end of the rectangle (1Inv; Figs. 3 and 4).
-
(2)
The cue is presented at a position outside the rectangle, and the target is presented at another location outside the rectangle consistent with the spacing of 1Inv (LtoL; Figs. 3 and 4).
-
(3)
The cue is presented at a position outside of the rectangle, and the target within it (LtoO; Figs. 3 and 4).
-
(4)
The cue is presented in the rectangle, and the target is presented at a position outside of it (OtoL; Figs. 3 and 4).
Condition 1Inv has the quickest reaction time because a strong object shroud has spread over the cued object, facilitating detection. It is slower than the valid case because un-cued portions of the attended object lack a strong spatial shroud in addition to the strong object shroud. The more interesting cases are the middle two: why should a target at an invalid position be detected faster than an invalidly-cued target on an un-cued, but visible, object that has a weak object shroud formed over it? It is because the model is sensitive to transient events. An existing (object shroud)-surface resonance, especially one supporting view-invariant object category learning, is difficult to break. It can be broken through inhibition created by a competing shroud, or by exhausting its habituating gates. The model responds locally to transient effects as a function of the contrast ratio in the surround. This contrast-sensitive response is larger when a target appears against the background of the display, than on a rectangle of the display. This implies that a relatively intense spatial shroud forms on the target in the LtoL case, which allows a rapid where stream transient input to create a strong (object shroud)-(spatial shroud) resonance. This process can occur faster than more modest contrast increment on the weakly attended surface in the LtoO, which will continue to be supported by a slower surface-(object shroud) resonance. This transient-activated shroud hierarchy does not provide the same level of benefit in the OtoL case, however, since in the OtoL case a strong object shroud (rather than a weak one) has formed over the object because it was cued, thereby creating a much higher hurdle to overcome.
6.1.3. Invalid cues: two-objects and individual differences
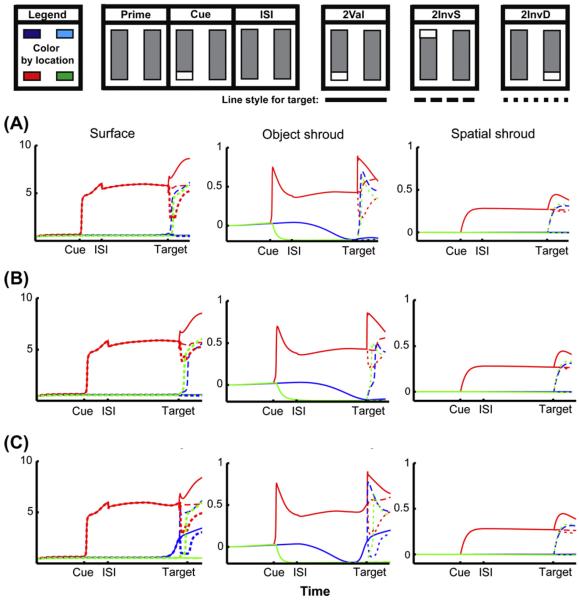
The classic finding of Egly et al. (1994) supporting object-based attention is that, when there are two identical rectangles presented at a distance equal to their length throughout the experiment, and one end of one rectangle is cued, reaction times occur in the following order:
- (1)
-
(2)
A target appearing on the other end of the same rectangle (InvS; Figs. 3 and 5).
-
(3)
A target appearing at the same end on the other rectangle (InvD; Figs. 3 and 5).
Brown and Denney (2007) replicated this finding by measuring mean reaction times for 30 subjects (Fig. 3). Roggeveen et al. (2009) re-examined the paradigm using a variant of this task (Moore et al., 1998) and focused on the object-based attention for each individual, rather than over the population as a whole. They found that about 18% of individuals had significantly better reaction times for InvS than InvD, while another 18% of individuals had a significant reverse effect, preferring InvD to InvS. The rest of the subjects showed smaller differences in both directions, creating a fairly smooth distribution. Nearly all (96%) of subjects reacted more quickly to a valid cue.
This variant of the task requires discrimination between a target and distracters, rather than simple detection (Moore et al., 1998), which means that in all invalid trials, there is a distracter at the cued location. This is the likely cause of the comparatively large size of reaction time differences, about 200 ms faster for a valid cue, compared to the detection paradigm used in Brown and Denney (2007), which showed 40 ms differences for the same comparison. However, this does not explain why some subjects reacted more quickly to an invalidly-cued target on the same rectangle, and some reacted faster to an equidistant invalidly-cued target on the other rectangle.
As noted in Section 4, our model predicts that the difference between individuals who react faster for an invalidly-cued target on the same object, and those that do the opposite, is the relative gain between the faster dynamics of (spatial shroud)-(object shroud) resonance, and the slower dynamics of surface-(object shroud) resonance. As can be seen in Fig. 6, as the relative strength of the spatial shroud resonance is increased (from left to right on the bottom row), reaction time decreases slightly across the board, but massively for InvS. This is because a strong object shroud can spread over the rectangle before the target and distracters appear (see Fig. 5C vs. B), which diminishes the effect of the distracter at the cued location, where there is also a strong spatial shroud. If the shroud has not had time to spread over the entire bar (as in the left hand case) then there is a bubble of inhibition at the far end of the cued bar, suppressing attention to the target, while enhancing the distracter. This predicted difference between the slower parietal-V4 vs. faster prefrontal–parietal resonances may be testable using rapid, event-related fMRI or EEG/MEG.
Goldsmith and Yeari (2003) employ a variation of the Egly et al. (1994) task with two cue conditions: in the `exogenous' condition, the cues appear at one of four locations at the ends of the two rectangles, while in the `endogenous' task a third rectangle, smaller and oriented towards one of the four target locations appears near the fixation point. Since the model does not explicitly consider the effects of orientation, or learning that an oriented bar may cue a distant location, it is beyond the purview of the model to account for the endogenous-target-valid case. However, given the interference of a highly transient third object (the `endogenous' cue), and the model's clarification of how spatial attention may learn to be focused or spread, depending on task conditions, it is consistent with the findings of the current model that there is little reaction time difference between the invalid-same object and invalid-different object cases, since attention has been drawn away from both of them.
6.2. Useful-field-of-view
The UFOV paradigm measures how widely subjects can spread their attention to detect a brief stimulus that is then masked (Fig. 7A; Green & Bavelier, 2003; Sekuler & Ball, 1986). The task starts with a fixation point, which is followed by a brief (10–30 ms presentation) appearance of 24 additional elements, all but one of which is identical to the fixation point. The elements are arranged in eight spokes, at equally spaced angles and at three eccentricities. A mask then appears, followed by an eight-spoke display of lines. The subject then indicates the direction along which the oddball appeared. VGPs perform better at this task than non-VGPs (Fig. 7B).
We simulated a simplified version of this display with a contrast increment oddball, with video game players having a 20% lower inhibitory gain in the object shroud and spatial shroud layers (see Eqs. (36) and (42)). The results show that just this small change in inhibitory gain in both the PPC and PFC attentional networks has a large effect on the detection performance.
This occurs because the inhibitory gain in the attention layers of the model serves as a resource constraint, which helps VGPs detect the location of the oddball in two distinct ways. The spatial shroud layer receives strong transient input, which is excited by the appearance of the target and distracters. Initially, all the targets and distracters are represented in the spatial shroud layer before recurrent feedback causes competition. The initial signal that each element can project to the spatial shroud layer through transient response is determined by the inhibitory gain in that layer. Therefore, VGPs have an early spatial shroud response to the target which is less likely to be washed out by competition from distracters and the mask. Inhibitory gain also serves as a resource constraint in the object shroud layer. However, since shrouds in the object shroud layer require surface resonance, and object shrouds will expand over any surface that begins resonating with its corresponding shroud, the resource constraint is how many objects can be represented in the object shroud layer. Decreasing the inhibitory gain the object shroud layer increases the chance that an object shroud can begin resonating with the target before the mask, rendering its location detectable.
6.3. Crowding
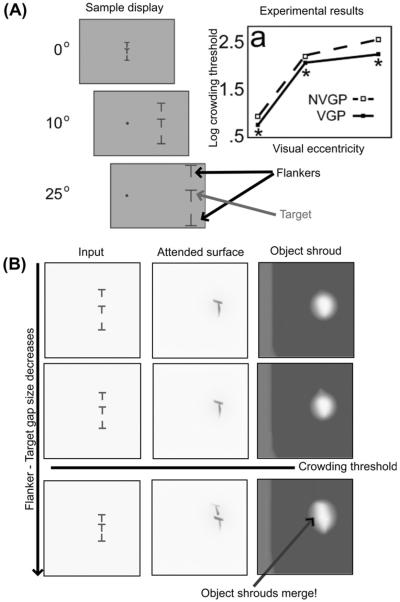
In the crowding paradigm, an object, such as a letter, is visible and recognizable when presented by itself, but it is not recognizable when the letter is presented concurrently with similar flanking letters (Green & Bavelier, 2006a; Levi, 2008; Toet & Levi, 1992). The distance between the target letter and the flanking letters at which the target letter becomes unrecognizable is called the crowding threshold, and is a function of the eccentricity of the target and the flankers, and their relative position (Bouma, 1970, 1973; Levi, 2008). A related concept is the spatial resolution of attention (Intriligator & Cavanagh, 2001), which is the minimum distance between several simple identical objects, like filled circles, that allow an observer to covertly move attention from one circle to another based on a set of instructions, without losing track of which circle they should attend. The spatial resolution of attention is also proportional to eccentricity, and falls off faster than acuity loss due to cortical magnification (He, Cavanagh, & Intriligator, 1996; Intriligator & Cavanagh, 2001).
Crowding has been attributed both to pre-attentive visual processing in early visual areas, as well as to attentional mechanisms (see Levi (2008) for a review). It is likely that it is a combination of the two. Some models of early vision, such as LAMINART, predict how flankers can cause either facilitation or suppression of stimuli between them, depending on distance and contrast (Grossberg & Raizada, 2000) using interacting pre-attentive grouping and competitive mechanisms. A second proposal is that larger receptive fields in the what stream capture features from multiple objects and conflate them. A third proposal is that observers confuse the location of the target and the flankers due to positional uncertainty, but that object-feature binding remains intact. Yet another proposal is that crowding is the result of failed contour completion (Levi, 2008). However, because of the similarities between crowding and the spatial resolution of attention, measured without the use of flanking objects (He et al., 1996; Intriligator & Cavanagh, 2001; Moore, Elsinger, & Lleras, 2001), it is unlikely that crowding is solely due to pre-attentive factors in early visual processing.
Our model has a natural explanation for crowding due to its linkage of where stream spatial attentional processes to what stream object learning and recognition processes. In particular, the model predicts that when at least three peripherally presented similar objects are nearby, and subject to the cortical magnification factor, an object shroud forming over one object can spread to another object, confounding recognition when several objects are covered by a single shroud (see Fig. 8). Said in another way, when a single shroud covers multiple objects, it defeats figure-ground separation and forces the objects to be processed like one larger unit. This means that there is both featural and positional confusion, but this is the result of how the shroud forces the failure of object recognition, rather than being due to large receptive fields or simple positional uncertainty. This does not occur with just two peripheral objects, since the highest intensity part of each object shroud can shift to the most distant extrema of the two objects, and can thereby inhibit the gap between the objects.
Fig. 8.
Green and Bavelier (2007) crowding data and qualitative behavioral simulations. (A) Top panels show a crowding display and data from Green and Bavelier (2007), which show lower thresholds for VGPs. [Data reprinted with permission from Green and Bavelier (2007).] (B) Bottom panels show simulations of the object shrouds that form in response to three displays. The three inputs are all at the same eccentricity, but the gap between the target and flankers shrinks from top to bottom. At the smallest gap, a single object shroud forms over multiple objects, so that individual object recognition is compromised.
In summary, our proposed explanation of crowding exploits the dARTSCAN predictions of how where stream processing of attentional shrouds influences what stream learning and selection of object recognition categories, and how cortical magnification influences attention within and between object surfaces.
7. Discussion
The current article introduces three innovations to further develop the original ARTSCAN model concept of how where stream spatial attention can modulate what stream recognition learning and attention (Cao et al., 2011; Fazl et al., 2009; Grossberg, 2007, 2009): First, we show how both where stream transient inputs from object onsets, offsets, and motion can interact with what stream sustained inputs from object surfaces to control spatial attention. Second, we show how both parietal object shrouds and prefrontal spatial shrouds can help to regulate the priming, onset, persistence, and reset of spatial attention in different ways and at different speeds. Third, we show how basal ganglia control of inhibition across spatial attentional regions can control focal vs. multifocal attention, either through fast volitional control or slower task-selective learning. The interactions among these processes can explain a seemingly contradictory set of data, notably how both same-object and different-object biases are both compatible with a model founded on object-based attention.
7.1. Comparison with other models
Recent models of attention can be split into several groups. Successors to Feature Integration theory (Treisman & Gelade, 1980), such as Guided Search (Wolfe, 2007; Wolfe et al., 1989) and Itti and Koch (2001), rely on biased competition between parallel visual representations, whereby each presentation highlights a specific feature of the visual input. The ARTSCENE model, which uses attentional shrouds in addition to saliency maps, can explain similar data using object-based, rather than pixel-based attention, and regional, rather than local, competition (Grossberg & Huang, 2009; Grossberg et al., 1994; Huang & Grossberg, 2010), as well as data that cannot be explained by saliency maps alone. Using objects and regions as the key substrate of competition allows the model to learn gists as large-scale texture categories (Grossberg & Huang, 2009) and to explore their importance in processing natural scenes.
All of these models incorporated attentional circuits defined by top-down, modulatory on-center, off-surround networks whose cells obey shunting dynamics with activity-dependent gain control that divisively self-normalizes cell responses (Bhatt, Carpenter, & Grossberg, 2007; Carpenter & Grossberg, 1987, 1991, 1993). Related models of how attention interacts with neurons in the visual system, especially V4, used similar properties of gain control, contrast enhancement, and divisive normalization to the response characteristic of neurons under varying attention conditions (Ghose, 2009; Lee & Maunsell, 2009; Reynolds & Heeger, 2009). Finally, cognitive theories of attention and object recognition have introduced seminal concepts such as FINSTs and Sprites, but are not computational models (Cavanagh et al., 2001; Pylyshyn, 1989, 2001; Scholl, 2001), with the notable exception of Logan (1996). The ARTSCAN model and its extension in the current article offer computational rigor and new explanations of challenging data as manifestations of emergent properties of multiple brain mechanisms as they interact on multiple time scales in a hierarchy of attentionally-modulated cortical processing stages.
7.2. Transients, sustained resonance, and priming
In the current model, transient inputs can activate sustained priming activity in the spatial shroud layer. On the other hand, surface inputs slowly create object shroud attention, but sustaining that attention requires a surface-shroud resonance until eye-movement-contingent inhibition-of-return and habituative gates cause it to collapse. When such an object shroud collapses, spatial shrouds can continue to prime lower levels, thereby maintaining sensitivity to future salient events.
7.3. Gain control, normalization, and capacity
As noted above, several recent models have focused on describing the effect of attention on neuronal responses in visual cortex, particularly V4. In particular, the models of Reynolds and Heeger (2009), Ghose (2009), and Lee and Maunsell (2009) explore the mechanism through which attention enhances the processing of selected areas of the visual field. They conclude that divisive normalization using center-surround processing is the most reasonable model for the effects of attention on V4 neurons. The recurrent shunting on-center off-surround networks that form the basis of the object and spatial shroud layers produce divisive normalization. Indeed, the exact form factor for doing this that was proposed by Reynolds and Heeger (2009) was earlier used by Bhatt et al. (2007), and variants of it have often been used to explain attentional dynamics in models by Grossberg and his colleagues (e.g., Berzhanskaya et al., 2007; Carpenter & Grossberg, 1987, 1991; Gove, Grossberg, & Mingolla, 1995; Raudies & Neumann, 2010) since the original proposal of how shunting dynamics can normalize the activities of neurons in center-surround networks of neurons was demonstrated in Grossberg (1973). Furthermore, the current model can explain individual differences in attentional capacity and performance, as in individual differences in useful-field-of-view, by varying inhibitory gain of attention via the basal ganglia.
As with the general theme of normalization, volitional control of inhibitory gain, and thus the strength of normalization, seems to use a similar mechanism across many parts of the brain. Indeed, such volitional control is predicted to determine whether top-down attention is modulatory or can elicit visual imagery in visual cortex (Grossberg, 2000b), and whether bottom-up inputs are stored or not in prefrontal working memory (Grossberg & Pearson, 2008). This latter property may help to explain individual differences in working memory capacity (Vogel & Machizawa, 2004). Thus, the capacity of spatial attention and that of visual working memory may share an underlying neural mechanism, albeit one that is expressed in different brain regions. In all these cases, the simplest hypothesis (Grossberg, 2000b) is that inhibitory interneurons in cortical layer 4 of the target area are inhibited by the basal ganglia. This disinhibitory effect can convert a modulatory on-center response, due to balanced excitation and inhibition, into a driving suprathreshold response. The anatomy and control dynamics of this predicted volitionally-sensitive gain control mechanism require more experimental study.
7.4. Normalization controls attentional capacity
Cognitive theories of attention and short-term memory fall into two groups, the first, invoked by the phrase “the magical number 7,” (Miller, 1956) posits a certain number of `slots' which objects or some other fundamental unit fill (Fukuda, Awh, & Vogel, 2010). The second posits that resource constraints variably filled by different traits, details, and features limit capacities (Alvarez & Cavanagh, 2005; Alvarez & Franconeri, 2007; Alvarez et al., 2005; Verghese & Pelli, 1992). In the latter, objects are not the fundamental unit, because individuals can track or remember several simple objects, but only a few complex ones.
Objects are an important basis of attention (Fallah, Stoner, & Reynolds, 2007; Kahneman et al., 1992; Lamy & Egeth, 2002; Martinez et al., 2006; Mitchell, Stoner, & Reynolds, 2004; O'Craven, Downing, & Kanwisher, 1999; Pylyshyn et al., 1994; Roelfsema et al., 1998; Scholl, 2001; Scholl et al., 2001; Serences, Schwarzbach, Courtney, Golay, & Yantis, 2004; Shomstein & Yantis, 2004). It is difficult to track one end of a tumbling symmetrical object, attention spreads over surfaces slanted or curved in depth (He & Nakayama, 1995; Moore & Fulton, 2005; Moore et al., 1998; Scholl et al., 2001), and one of two co-localized objects can be distinguished and tracked solely through different features (Blaser et al., 2000). Neural correlates of object-based attention have also been found in fMRI and EEG/MEG work by a number of labs (Egeth & Yantis, 1997; Martinez et al., 2006; O'Craven et al., 1999; Serences et al., 2004; Theeuwes et al., 2010).
However, objects are not the whole story. Limited information is retrievable about any given object when attention is split during unique object tracking (Horowitz et al., 2007). It is also possible to track objects while also performing a visual search task (Alvarez et al., 2005), suggesting that attention can also be spatially deployed without destroying object-based attention representations. Behavioral and imaging studies have shown sensitivity to the number of objects (Culham, Cavanagh, & Kanwisher, 2001; Culham et al., 1998; Franconeri et al., 2007; Tomasi et al., 2004), speed, size, proximity, and object mutation (Alvarez & Franconeri, 2007; Alvarez & Scholl, 2005; McMains & Somers, 2004, 2005; Scalf & Beck, 2010).
The dARTSCAN model uses normalization in the two shroud layers to produce a dual resource constraint that makes objects the dominant, but not exclusive, unit of attention. The primary constraint on the number of objects that can be attended at any given time is the inhibitory load in the object shroud layer, which varies based on the size, complexity and salience of objects in a scene, as well as the center of gaze, due to divisive normalization and variations in basal ganglia inhibitory modulation. The number of spatial positions that can simultaneously be primed is dependent on the resultant inhibitory load in the spatial shroud layer, where attended objects enjoy considerable competitive advantage but are not preeminent. An excellent example of non-object attentional factors occurs during scene understanding, including the perception of a scene's gist, which has been modeled as a large-scale texture category (Grossberg & Huang, 2009). Object categories in the what cortical stream, and position categories in the where cortical stream can define distinct, but often cooperating, contexts for driving search, learning, and recognition, as is well-studied in the contextual cueing literature (e.g., Chun & Jiang, 1998; Grossberg, 1972, 1980a, 1980b; Olson & Chun, 2001), and modeled by neural mechanisms that are compatible with the current analysis (Huang & Grossberg, 2010).
7.5. Prefrontal priming of what and where
The ARTSCAN model showed how complementary object and spatial properties (Grossberg, 2000a) of the what and where streams (Haxby et al., 1991; Ungerleider & Haxby, 1994) produce view-invariant object category learning, while the ARTSCENE model (Grossberg & Huang, 2009; Huang & Grossberg, 2010) showed how the same type of architecture, extended to include working memory and categorizing roles for perirhinal, parahippocampal, and prefrontal cortices, can support object and spatial context priming and learning, including gist learning, that is capable of driving efficient visual search, learning, and recognition of objects in complex scenes; see Section 7.7.
An emerging body of anatomical and imaging experiments suggests rapid magnocellular pathways to prefrontal cortex can prime object categories or contexts that aid in rapid object and scene recognition (Bar et al., 2006; Gronau, Neta, & Bar, 2008; Kveraga, Boshyan, & Bar, 2007). Recent electrophysiology studies in V4 have found that, in addition to contrast gain due to spatial attention, there is also independent feature-based attention that modifies spectral tuning of preferred spatial frequencies (David, Hayden, Mazer, & Gallant, 2008; Hayden & Gallant, 2005, 2009). The dARTSCAN model shows how multifocal spatial attention that allows view-invariant object category learning leads to prefrontal priming. This suggests how broadly distributed, multifocal attention in the where stream may contextually prime the what stream for rapid recognition in familiar scenes, facilitating the later volitional deployment of unifocal attention to novel or behaviorally salient objects.
7.6. Gain fields and predictive remapping
Stable visual orientation and object constancy require that the visual system keep track of the relative positions of objects in a scene during saccades (Mathot & Theeuwes, 2010a, 2010b). The cortically magnified, retinotopic map of the visual field found in early visual areas creates highly dissimilar representations of the same scene for different centers of gaze. This suggests that the visual system needs either a visual area with a coordinate system that is insensitive to gaze location, or that some of the retinotopic areas in the visual system have their activity remapped by saccades (Duhamel, Colby, & Goldberg, 1992; Gottlieb, Kusunoki, & Goldberg, 1998; Mathot & Theeuwes, 2010a; Melcher, 2007, 2008, 2009; Saygin & Sereno, 2008; Tolias et al., 2001). Attentionotopic maps of the visual system produced using fMRI suggest that many dorsal stream areas sensitive to visual attention have retinotopic coordinates (Saygin & Sereno, 2008; Silver et al., 2005; Swisher et al., 2007). However, there is at least one area in anterior parietal cortex has been found to show head-centered coordinates (Sereno & Huang, 2006). Electrophysiological studies have shown perisaccadic (around the time of the saccade) remapping of receptive fields in frontal eye fields (Goldberg & Bruce, 1990) and parietal areas, including LIP (Andersen, Bracewell, Barash, Gnadt, & Fogassi, 1990; Duhamel et al., 1992), as well as more modest remapping in V4 (Tolias et al., 2001). In particular, attended targets do not cause new transient activity in these regions after saccades (see Mathot and Theeuwes (2010a) for a review).
Behavioral results are consistent in finding a brief retinotopic facilitation (priming) effect and a sustained spatiotopic IOR effect (Posner & Petersen, 1990). More recent evidence also finds a longer lived spatiotopic facilitation along with the short term retinotopic facilitation in certain task conditions (Golomb, Chun, & Mazer, 2008; Golomb, Nguyen-Phuc, Mazer, McCarthy, & Chun, 2010; Golomb, Pulido, Albrecht, Chun, & Mazer, 2010). The original ARTSCAN model used a head-centric attention layer that interacts with retinotopic surface and eye-movement related areas of the model through an LIP gain field (Fig. 1). The current dARTSCAN model uses a retinotopic representation of attention in both the object and spatial shroud layers, so that stimulus eccentricity biases competition. Since the present study focuses on data which were collected while subjects were fixating, remapping was not implemented.
7.7. Where's Waldo? From where to what and from what to where
The current article focuses on brain mechanisms whereby spatial attention in the where stream can influence prototype attention in the what stream. It is also the case that prototype attention in the what stream can influence spatial attention in the where stream, as when a human or animal tries to solve the Where's Waldo problem; that is, to efficiently search for a desired target object in a cluttered scene. For this to work well, a desired target category in the what stream needs to be primed and used to discovery the location in space to which spatial attention in the where stream should be directed. Towards this goal, Huang and Grossberg (2010) have modeled how a human can learn to more efficiently search for a target in a scene by learning to accumulate both object and spatial contextual evidence from scenic targets and distractors with which to direct the search. This analysis proposes how the perirhinal and parahippocampal cortices, interacting with ventrolateral and dorsolateral prefrontal cortices, among other brain regions, help to accumulate object and spatial evidence for target location as the eyes scan a scene. This ARTSCENE model quantitatively simulates a large body of psychophysical data about contextually cued visual search, notably data of Marvin Chun and his colleagues; e.g., Chun (2000), Chun and Jiang (1998), Jiang and Chun (2001), and Olson and Chun (2002).
7.8. Other model extensions
There are many databases that an extension of the current model could naturally explain in a unified way. Extending towards cognitive and planning areas, including explicit basal ganglia gating circuits, and prefrontal working memory, planning, and performance circuits, as developed in other recent models (Brown, Bullock, & Grossberg, 1999; Grossberg & Pearson, 2008; Huang & Grossberg, 2010; Srihasam, Bullock, & Grossberg, 2009), such an enhanced model could use view-invariant object representations to choose novel objects while exploring complex scenes. Extension in these directions would further probe the limits and consequences of volitional gain control and the effects of training, such as are found in VGPs or the aging.
The model can also naturally be extended back into the early visual areas, to explore the interaction between attentional shrouds, figure-ground separation, and laminar cortical processing (Cao & Grossberg, 2005; Grossberg & Swaminathan, 2004). Similarly, there is an extended literature on multiple-object tracking that would be available if early motion perceptual mechanisms, including the object-sensitive dynamics of transient cell responses, were integrated into the model (Berzhanskaya et al., 2007; Grossberg, Mingolla, & Viswanathan, 2001). This would allow motion-sensitive spatial shroud cells to help drag object shroud-surface resonances along with tracked objects in multiple-object tracking, providing an implementation of the FINST concept (Pylyshyn, 1989, 2001).
Acknowledgments
Supported in part by CELEST, an NSF Science of Learning Center (SBE-0354378), the SyNAPSE program of DARPA (HR0011-09-03-0001, HR001-09-C-0001), the National Science Foundation (BCS-0235398), and the Office of Naval Research (N00014-01-1-0624).
Appendix A. Model equations
The model is a network of point neurons with single compartment membrane voltage, V(t), that obeys the shunting equation:
| (1) |
(Grossberg, 1973; Grossberg, 1980a, 1980b). There are two constants: Cm controls the membrane capacitance and the constant conductance γleak controls membrane leakage. The time varying conductances γexcite and γinhib, respectively, represent the total excitatory and inhibitory inputs to the neuron as specified by the model architecture. The three E terms represent reversal potentials. Solved at equilibrium, the above equation can be rewritten as:
| (2) |
Thus, increases in excitatory conductance depolarize the membrane while increases in inhibitory conductance hyperpolarize it. All conductances contribute to divisive normalization of the membrane, as shown in the denominator. This divisive effect includes a special case of pure “shunting” inhibition, when the reversal potential of the inhibitory channel is close to the neuron's resting potential (Borg-Graham, Monier, & Fregnac, 1998). Equation (1) can be re-written as:
| (3) |
by setting X = V, Ax = γleak, Eleak = 0, Bx = Eexcite, and Cx = −Einhib. Sometimes there are signal functions used in γexcite or γinhib, which are denoted by f(a) or h(a). Often signals are half waved rectified, such that:
| (4) |
A.1. Log polar processing
Cortical magnification is approximated using radial symmetric compression proportional to a log transform in the following algorithm:
Let IInt be the cubic interpolation (Press, 1992) of the input I (Fig. 9A).
Set n to be the smallest distance between our fovea, (x0, y0) = (1024, 1024), and an edge of the image.
Let M = Iint[x0 + r * Cos(θ), y0 + r * Sin(θ)] for r = [ − n, n], η = [0, 2π] in 2m steps.
Since this creates mirror representations of I, discard the lower half of M so that it is n × m (Fig. 9B).
- Create a k × n logarithmic compression matrix, C, with non-zero elements using the following recurrent formula:
and
such that for the jth row of C,
with k × n to compress the data in the r dimension. This causes smaller weights as j increases and, for each row j, there exists a proportionally longer section of non-zero elements so that C compresses M ∞ eαj to approximate a log-polar map (Fig. 9C). Let MC = C.M, and use the map inverse to step 3 to create the symmetric log compressed image Ic (Fig. 9D)
Fig. 9.
Schematic showing the primary stages of log-polar processing (see Section 5.1 and Appendix A.1). (A) Original input image. (B) Original input image projected into polar coordinates. (C) Transformed image from (B) compressed logarithmically along the r-dimension. (D) Compressed image from (C) projected back into Cartesian coordinates.
A.2. Hemifield independence
Except for diffusive surface filling-in in V4 (Appendix A.5), neurons interact with neighbors in their own hemifield using a center-surround architecture with Gaussian kernels, as described in Section 5.2. Neurons near the vertical meridian interact with neurons in the opposite hemifield (and hence, hemisphere of the brain) using a different, narrower, Gaussian kernel to reflect the relative paucity of connections between hemispheres (Fig. 10). Neurons near boundaries, either of the hemifield or the visual field, obey the normalized weighting method of Grossberg and Hong (2006); see also Hong and Grossberg (2004). Following this method, suppose that:
| (5) |
defines boundary-normalized connection strengths. In (5), W is a gain coefficient and ψpq denotes the cell activity at position (p, q) within a layer of neurons. This activity is filtered by the normalized Gaussian kernel:
| (6) |
with standard deviation σ and boundary-normalizing coefficients:
| (7) |
The Gaussian kernel operates within the following neighborhoods:
| (8) |
wherein cells are found. In particular, p ∈ (0, 63) is used for the left hemifield, p ∈ (64, 127) is used for the right hemifield and p ∈ (MV ± 3σ) is used for the area near the vertical meridian MV that defines inter-hemifield connectivity. Finally,
| (9) |
defines the maximum distance at which any two cells directly interact through the Gaussian kernel in Eq. (7). The only difference between and NΓ is that is constrained by the boundary of the image at the hemifield edges, while NΓ, which defines the whole kernel, is not. This ensures that kernels do not extend beyond the borders of the image or the vertical meridian and are appropriately weighted to eliminate boundary-based artifacts.
Fig. 10.
Identical bars oriented to cross the vertical meridian (A) or stay within one hemifield (B). Top row: Input, I. Bottom Row: On-center processing with hemifield independence, χ(2, 1, 5, 2, I) (see Eq. (13)).
Neurons near the vertical meridian interact with neurons in both their own hemifield, and in the opposite hemifield. The degree of hemifield independence at each layer of the model is controlled by W and σ, as specified for Gpqij in Eqs. (6) and (7). The area of overlap between the hemifields, (MV ± 3σ), ψC, and the left and right hemifields, ψL and ψR, respectively, are normalized so that no neuron is gain privileged, such that:
| (10) |
| (11) |
and
| (12) |
These functions allow us to define a general function, χ, that describes the complete set of connection weights to any neuron in layer Ψ:
| (13) |
where tr(a) is the trace of a, WLR is the intra-hemifield gain, WC is the inter-hemifield gain, σLR controls maximal extent of intra-hemifield connectivity, and σC controls the maximal extend of inter-hemifield connectivity. Figs. 10A and B illustrate input horizontal and vertical bars and the corresponding function χ(2, 1, 5, 2, I). The bar in 10A crosses the hemifield, whereas the bar in 10B does not.
A.3. LGN polarity sensitive cells: On and Off Channels
There are four types of cells in the model LGN: single opponent ON-cells (, Eq. (14)), single opponent OFF-cells (, Eq. (15)), double opponent ON-cells (, Eq. (18)) and double opponent OFF-cells (, Eq. (19)).
Single opponent cells are computed using feed-forward shunting networks solved at equilibrium (Eq. (3)). At position (i, j), the output signal from the single opponent ON-cell is:
| (14) |
and the output signal from the single opponent OFF-cell is:
| (15) |
where Q+ = 5 and Q− = 1 represent tonic bias factors, while
| (16) |
and
| (17) |
compute the center-surround sampling of the compressed input image. The parameters were chosen to satisfy the property of featural noise suppression; that is, the LGN ON cells have 0 response to constant luminance of any intensity; they only respond in the vicinity of luminance gradients. Due to the fact that Q− > Q+ in Eqs. (14) and (15), OFF cells are tonically active in the presence of uniform inputs, including in the dark. However, they do not project to the surface layer in the model, and thus do not affect filling-in.
The output signal from the double-opponent ON-cell at position (i, j) is:
| (18) |
and from the double-opponent OFF-cell is:
| (19) |
Note that the output signals from all four types of LGN cells are half-wave rectified, see Eq. (4).
A.4. Boundaries
Because the model inputs are simple, the double opponent LGN outputs require little additional processing to create effective boundaries. Simplified complex cell outputs such as those found in primary visual cortex are modeled by polarity-insensitive cells, Zij, at position (i, j) that add ON (, Eq. (18)) and OFF (, Eq. (19)) channel inputs from double-opponent cells:
| (20) |
The ON-channel is scaled to be stronger than the OFF-channel so that the model responds robustly over a wide range of local contrasts. Object boundary contours, Bij, at position (i, j) are defined by the equation:
| (21) |
Eq. (21) says that an object boundary Bij is activated by complex cell outputs Zij that are modulated by feedback signals (, Eq. (22)) from the contours of successfully filled-in surfaces that are fed back to their inducing boundaries. These feedback signals are accordingly derived from surface contours (Cij, Eq. (23)). In (21), the feedback signal to position (i, j) of the boundary is:
| (22) |
where function χ is defined by Eq. (13). The surface contour output signal, Cij, at position (i, j) is computed by ON and OFF shunting on-center off-surround networks that are sensitive to the contrast of filled-in surface activity (Sij, Eq. (26)). They are therefore positive at the positions of successfully filled-in object boundaries:
| (23) |
where
| (24) |
and
| (25) |
compute the ON and OFF representations of the filled-in surfaces, respectively, at position (i, j).
Surface contours are computed at the boundaries of successfully filled-in surfaces; that is, surfaces which are surrounded by a connected boundary and thus do not allow their lightness or color signals to spill out into the scenic background. Grossberg (1994, 1997) analyzed how connected boundaries play a special role in 3-D vision and figure-ground separation. In this more general situation, not all boundaries are connected. However, in response to the simplified input images that are simulated in this article, all object boundaries are connected and cause successful filling-in. As a result, surface contours are computed at all object boundaries, and can strengthen these boundaries via their positive feedback in Eq. (21). When the contrast of a surface is increased by feedback from an attentional shroud (see term Lij in Eqs. (26) and (27), the surface contour signals increase, so the strength of the boundaries around the attended surface increase also.
A.5. Surfaces
Object surface activity, Sij, at position (i, j) obeys the boundary-gated diffusion equation:
| (26) |
solved at equilibrium, where (Eq. (18)) provides bottom-up double-opponent ON-cell input and
| (27) |
modulates this bottom-up input with attentional feedback from object shroud neurons (Eq. (33)) mediated by the sigmoid signal function . Diffusive surface filling-in between the cell at (i, j) and its nearest neighbors (m, n) ∈ [{i − 1, j}, {i − 1, j}, {i, j − 1}, {i, j + 1}] is gated by the intervening boundaries via the boundary-sensitive permeability:
| (28) |
where Bij and Bmn are the boundary contours (Eq. (21)) at positions (i, j) and (m, n) respectively (Grossberg & Todorović, 1988). Eqs. (26) and (27) show how boundaries form filling-in barriers that divisively gate, or inhibit, the spread of surface lightness and color. Eqs. (26) and (27) show how top-down feedback from object shrouds can increase the filled-in contrast of a surface and, due to the distributed on-center in Lij, also spill out over the defining boundary of a surface. This latter property is important in our explanation of crowding.
The attentional feedback from active object shrouds (see Sections 5.7 and Appendix A.7) habituates slowly over time in an activity-dependent way, thereby weakening the corresponding surface-(object shroud) resonance. The rate of habituation between object shroud neurons and surface neurons at position (i, j) in Eq. (27) is controlled by the habituative gate equation (Grossberg, 1972, 1980a, 1980b):
| (29) |
where the habituative gate recovers to the value 2 and habituates at a rate that depends on the object shroud activity Habituation occurs at slower rate than either of the shroud habituative gates (Eqs. (37) and (38)) and should be thought of as a mechanism underlying adaptation.
A.6. Transient inputs
Several model simulations use sequential, static displays as stimuli but no simulation uses stimuli in motion. Thus, a simplified model of MT cells in the where cortical stream is employed to produce transient inputs to model attentional processes. The activity, Rij, of the transient cell at position (i, j) accordingly responds briefly to contrast increments between successive displays:
| (30) |
where
| (31) |
is activated by contrast increments between the input to the model at time t0, which is the last time step for which a prior input was being presented, and time t1, which is the first time step for which a new input is presented, as modified by the sigmoid signal function unbounded transient responses. A switch function,
| (32) |
controls the duration of transient cell sensitivity to changes in input, where n = 30 time steps.
A.7. Object shrouds
Object shroud neurons are similar to the shrouds in the ARTSCAN model. If an object shroud neuron corresponding to a visible surface reaches a threshold level of activity, then attention will spread over the entire surface. The shroud intensity is a function of surface activity, previous attention activity in the object shroud and spatial shroud layers, and inhibitory gain, which is volitionally controlled in some simulations. There are two stable dynamical modes for the object shroud layer: focal, or winner-take-all, to support view-invariant object category learning; and multifocal to support multiple shrouds and surface perception. The activity of the object shroud neuron, , at position (i, j) obeys:
| (33) |
where α ∈ [3, 7] is a rate parameter, usually set at α = 5 but was varied in the simulation shown in Fig. 6 from 3 to 7 in increments of 1. Object shroud neurons receive Gaussian-filtered bottom-up input from surface activity (Sij, Eq. (26)):
| (34) |
where the sigmoid signal function . The Gaussian spread of bottom-up input from a surface can activate spatial attention at positions adjacent to, but outside, the surface. This kind of Gaussian filtering in both the bottom-up pathway from surface to attention, and the top-down pathway from attention to surface, is important in our explanation of crowding.
The bottom-up surface input is modulated by three types of signals: bottom-up input from transient cell activity (Rij, Eq. (30)) at corresponding positions and, via the interaction term:
| (35) |
which includes habituating (, Eq. (37)) recurrent excitation from half-wave rectified neighboring cells, as part of a recurrent shunting on-center (Oij, Eq. (35)) off-surround (Tij, Eq. (36)) network that helps to choose active shrouds; and Gaussian-filtered excitatory habituating feedback (, Eq. (38)) from half-wave rectified spatial shroud neurons (, Eq. (39)) to sustain surface-(object shroud) resonances. Both habituative terms are modified by the sigmoid signal function to provide contrast enhancement that facilitates competition between surfaces bidding for spatial attention. Object shroud neurons also compete for attention via recurrent inhibitory signals in the on-center off-surround network. This inhibition habituates at the same rate as the recurrent on-center excitation, and is filtered by the same sigmoid signal function:
| (36) |
The strength of recurrent inhibition in Eq. (36) is controlled by two gain parameters, one for within-hemifield inhibition, which is usually set at T = .05, except for videogame players (VGPs) in the useful-field-of-view (UFOV) task, where T = .04, and the other for inter-hemifield inhibition, which is usually set at TC = .04, except for VGPs in the UFOV simulation where TC = .032.
The rate of habituation and recovery of recurrent excitation (Eq. (35)) and inhibition (Eq. (36)) in the object shroud layer at position (i, j) is controlled by:
| (37) |
where the habituative gate recovers to the value 2 and habituates at a rate that depends on the object shroud activity at a timescale mediating IOR. The habituation of spatial shroud feedback to the object shroud layer at position (i, j) in Eq. (35) obeys a similar equation in which object shroud activity is replaced by spatial shroud activity :
| (38) |
Feedback from spatial shroud neurons habituates faster than feedback from object shroud (and much faster than the feedback to surface neurons (Eq. (29))) neurons to increase sensitivity to transient inputs.
A.8. Spatial shrouds
Spatial shroud neuron activity at position (i, j) obeys the equation:
| (39) |
In (39), there is strong bottom-up input from corresponding transient cell positions as well as a half-wave rectified Gaussian input from the object shroud layer:
| (40) |
Recurrent feedback is received from a shunting on-center (Uij, Eq. (41)) off-surround (Wij, Eq. (42)) network with on-center excitation:
| (41) |
and off-surround inhibition:
| (42) |
Both on-center and off-surround recurrent signals are modified by the sigmoid signal function . The inhibitory gain in (42) is controlled within hemifields by W = .005, except for the VGP UFOV simulation, where W = .004; and between hemifields by WC = .002, except for the VGP UFOV simulation, where WC = .00016.
In all, spatial shroud neurons receive bottom-up input from transient cells and object shroud neurons while exciting their nearby neighbors and inhibiting their distant neighbors. Small spatial shrouds can hereby survive for several hundred milliseconds in the absence of bottom-up input before decaying if there is little new transient input or activity causing competition. Recurrent competition can attract or repel spatial shrouds without bottom-up support, causing them to move slightly from their initial positions over time. Spatial shrouds cover the extent of a surface only if that surface resonates with an object shroud. When this occurs, however, the coverage is often not uniform in intensity, and hotspots of activity will form at salient areas of objects such as corners.
A.9. Parametric sensitivity
The behavior of recurrent neural network models, especially those with several interacting recurrent loops, can exhibit different modes of behavior depending on how parameters of the model are chosen. Some of these parameters can incrementally change model behavior, such as with the UFOV simulations (see Sections 6.2, Appendices A.7 and A.8). Further changes in those same parameters can cause a state change in model behavior, where attention goes from being multifocal to unifocal (see Section 3). Other parameters are set to obey specific properties, such as suppression of uniform input patterns (see Appendix A.3) and otherwise support a wide range of possible parameters without modifying the model behavior. Finally, some parameters depend on the simulation environment (such as the number of neurons in each layer, the array size of the inputs), notably the spatial extents of the Gaussian kernels controlling feed-forward, feedback and lateral communication between different model neurons, have to be rescaled for larger or smaller simulation environments. All of the parameters in the front end of the model, in Appendices A.2–A.4 and A.6, fall into the latter two categories.
More interesting are the parameters that control the recurrent circuits between the surface, object shroud and spatial shroud layers of the model. These equations fall into three general categories: the first is the lateral inhibition between model neurons, as well as the kernels controlling the strength of inter-layer connections ((Eqs. (27), (34)–(36), and (40)–(42)). The second is the various sigmoid signal functions (f(a)) that control three important qualities: size, range of sub-linear, linear and super-linear response, and the steepness of the linear response. Finally, there are habituating gates (Eqs. (29), (37), and (38)) that control the rate of habituation for different types of feedback within the model.
The primary loop in the model, is the surface-(object shroud)-surface loop, controlled by Eqs. (27), (29), and (34)–(37) and related signal functions. There are several important parts of this loop: the bottom-up connections from the surface to the object shroud layer (Eq. (34)) controls how objects of different luminance and size bid for object-based attention. Increasing the gain of the kernels in Eq. (34) increases response of objects across the board (while also increasing the competition in the object-shroud layer, since it increases the denominator of the divisive inhibition), while decreasing it has the converse effect. Increasing the half-max point (1.55) or exponent (6) of the corresponding signal function means that perceptually brighter (or attended) objects are accorded a better bid than dimmer objects, while decreasing it closes the gap. While these parameters are all important, and the model behavior (though not the ability to form shrouds) is sensitive to relatively small changes (10%) in any of them, in practice, these provided a baseline for detailed fitting in the feedback and competition related parameters of the model. Competition between shrouds in the model is controlled through the balance of lateral excitation and inhibition (Section 6.2 and Eqs. (35)–(37)), and feedback to the surface layer (Eqs. (27) and (29)) which makes attended objects brighter, thereby increasing their bids through the bottom-up connections previously described. The strength of the effects of increasing lateral inhibition relative to excitation are determined by the corresponding signal function, and is important in every simulated fit (shrouds will still form after a 10% perturbation of any of these parameters, but simulated RTs will change).
The secondary loop in the model is the (object shroud)-(spatial shroud)-(object shroud) loop. The time constant in the habituating gate between spatial and object shrouds (Eq. (38)) controls the duration of priming, while the strength of feedback between spatial and object shrouds (Eq. (35)) directly controls the strength of priming. Changes in parameters for either equation will change the RTs in the location cued fits. Another important aspect of the spatial shroud layer is how closely the contrast ratio between transient stimuli is preserved, in the balance of lateral excitation and inhibition (Eqs. (41) and (42)) which helps successful detection in the UFOV simulations. Other parameters in the spatial shroud layer can be perturbed by 10% without significantly affecting current results. The dynamics in this layer would become more sensitive if the model was extended to simulate multiple-object tracking, or experiments with endogenously cued attention.
References
- Alvarez GA, Cavanagh P. Independent resources for attentional tracking in the left and right visual hemifields. Psychological Science. 2005;16(8):637–643. doi: 10.1111/j.1467-9280.2005.01587.x. doi: PSCI1587 [pii] 10.1111/j.1467-9280.2005.01587.x. [DOI] [PubMed] [Google Scholar]
- Alvarez GA, Franconeri SL. How many objects can you track? Evidence for a resource-limited attentive tracking mechanism. Journal of Vision. 2007;7(13):10–11. doi: 10.1167/7.13.14. doi: 14 10.1167/7.13.14/7/13/14/ [pii] [DOI] [PubMed] [Google Scholar]
- Alvarez GA, Horowitz TS, Arsenio HC, Dimase JS, Wolfe JM. Do multielement visual tracking and visual search draw continuously on the same visual attention resources? Journal of Experimental Psychology: Human Perception and Performance. 2005;31(4):643–667. doi: 10.1037/0096-1523.31.4.643a. doi: 2005-09705-001 [pii] 10.1037/0096-1523.31.4.643a. [DOI] [PubMed] [Google Scholar]
- Alvarez GA, Scholl BJ. How does attention select and track spatially extended objects? New effects of attentional concentration and amplification. Journal of Experimental Psychology: General. 2005;134(4):461–476. doi: 10.1037/0096-3445.134.4.46. doi: 2005-14939-002 [pii] 10.1037/0096-3445.134.4.46. [DOI] [PubMed] [Google Scholar]
- Andersen RA, Bracewell RM, Barash S, Gnadt JW, Fogassi L. Eye position effects on visual, memory, and saccade-related activity in areas LIP and 7a of macaque. Journal of Neuroscience. 1990;10(4):1176–1196. doi: 10.1523/JNEUROSCI.10-04-01176.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker CI, Behrmann M, Olson CF. Impact of learning on representation of parts and wholes in monkey inferotemporal cortex. Nature Neuroscience. 2002;5:1210–1216. doi: 10.1038/nn960. doi: 10.1038/nn960. [DOI] [PubMed] [Google Scholar]
- Bar M, Kassam KS, Ghuman AS, Boshyan J, Schmid AM, Dale AM, et al. Top-down facilitation of visual recognition. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(2):449–454. doi: 10.1073/pnas.0507062103. doi: 0507062103 [pii] 10.1073/pnas.0507062103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berzhanskaya J, Grossberg S, Mingolla E. Laminar cortical dynamics of visual form and motion interactions during coherent object motion perception. Spatial Vision. 2007;20(4):337–395. doi: 10.1163/156856807780919000. doi: 10.1163/156856807780919000. [DOI] [PubMed] [Google Scholar]
- Bhatt R, Carpenter GA, Grossberg S. Texture segregation by visual cortex: Perceptual grouping, attention, and learning. Vision Research. 2007;47(25):3173–3211. doi: 10.1016/j.visres.2007.07.013. doi: S0042-6989(07)00309-4 [pii] 10.1016/j.visres.2007.07.013. [DOI] [PubMed] [Google Scholar]
- Blaser E, Pylyshyn ZW, Holcombe AO. Tracking an object through feature space. Nature. 2000;408(6809):196–199. doi: 10.1038/35041567. doi: 10.1038/35041567. [DOI] [PubMed] [Google Scholar]
- Boch RA, Goldberg ME. Participation of prefrontal neurons in the preparation of visually guided eye movements in the rhesus monkey. Journal of Neurophysiology. 1989;61(5):1064–1084. doi: 10.1152/jn.1989.61.5.1064. [DOI] [PubMed] [Google Scholar]
- Bonmassar G, Schwartz EL. Space-variant Fourier analysis: The exponential chirp transform. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1997;19(10):1080–1089. [Google Scholar]
- Booth MC, Rolls ET. View-invariant representations of familiar objects by neurons in the inferior temporal visual cortex. Cerebral Cortex. 1998;8:510–523. doi: 10.1093/cercor/8.6.510. [DOI] [PubMed] [Google Scholar]
- Borg-Graham LJ, Monier C, Fregnac Y. Visual input evokes transient and strong shunting inhibition in visual cortical neurons. Nature. 1998;393(6683):369–373. doi: 10.1038/30735. doi: 10.1038/30735. [DOI] [PubMed] [Google Scholar]
- Bouma H. Interaction effects in parafoveal letter recognition. Nature. 1970;226(5241):177–178. doi: 10.1038/226177a0. [DOI] [PubMed] [Google Scholar]
- Bouma H. Visual interference in the parafoveal recognition of initial and final letters of words. Vision Research. 1973;13(4):767–782. doi: 10.1016/0042-6989(73)90041-2. [DOI] [PubMed] [Google Scholar]
- Broadbent DE. Perception and communication. Pergamon Press; New York: 1958. [Google Scholar]
- Brown J, Bullock D, Grossberg S. How the basal ganglia use parallel excitatory and inhibitory learning pathways to selectively respond to unexpected rewarding cues. Journal of Neuroscience. 1999;19(23):10502–10511. doi: 10.1523/JNEUROSCI.19-23-10502.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown JM, Denney HI. Shifting attention into and out of objects: Evaluating the processes underlying the object advantage. Perception and Psychophysics. 2007;69(4):606–618. doi: 10.3758/bf03193918. [DOI] [PubMed] [Google Scholar]
- Brown JW, Bullock D, Grossberg S. How laminar frontal cortex and basal ganglia circuits interact to control planned and reactive saccades. Neural Networks. 2004;17(4):471–510. doi: 10.1016/j.neunet.2003.08.006. doi: 10.1016/j.neunet.2003.08.006S0893-6080(03)00252-1 [pii] [DOI] [PubMed] [Google Scholar]
- Cao Y, Grossberg S. A laminar cortical model of stereopsis and 3D surface perception: Closure and da Vinci stereopsis. Spatial Vision. 2005;18(5):515–578. doi: 10.1163/156856805774406756. [DOI] [PubMed] [Google Scholar]
- Cao Y, Grossberg S, Markowitz J. How does the brain rapidly learn and reorganize view- and positionally-invariant object representations in inferior temporal cortex? Neural Networks. 2011;24:1050–1061. doi: 10.1016/j.neunet.2011.04.004. [DOI] [PubMed] [Google Scholar]
- Caplovitz GP, Tse PU. V3A processes contour curvature as a trackable feature for the perception of rotational motion. Cerebral Cortex. 2007;17(5):1179–1189. doi: 10.1093/cercor/bhl029. [DOI] [PubMed] [Google Scholar]
- Carpenter GA, Grossberg S. A massively parallel architecture for a self-organizing neural pattern recognition machine. Computer Vision, Graphics, and Image Processing. 1987;37(1):54–115. [Google Scholar]
- Carpenter GA, Grossberg S. Pattern recognition by self-organizing neural networks. MIT Press; Cambridge, Mass.: 1991. [Google Scholar]
- Carpenter GA, Grossberg S. Normal and amnesic learning, recognition and memory by a neural model of corticohippocampal interactions. Trends in Neurosciences. 1993;16(4):131–137. doi: 10.1016/0166-2236(93)90118-6. doi: 0166-2236(93)90118-6 [pii] [DOI] [PubMed] [Google Scholar]
- Carrasco M, Penpeci-Talgar C, Eckstein M. Spatial covert attention increases contrast sensitivity across the CSF: Support for signal enhancement. Vision Research. 2000;40(10–12):1203–1215. doi: 10.1016/s0042-6989(00)00024-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavanagh P, Alvarez GA. Tracking multiple targets with multifocal attention. Trends in Cognitive Sciences. 2005;9(7):349–354. doi: 10.1016/j.tics.2005.05.009. doi: S1364-6613(05)00149-X [pii] 10.1016/j.tics.2005.05.009. [DOI] [PubMed] [Google Scholar]
- Cavanagh P, Labianca AT, Thornton IM. Attention-based visual routines: Sprites. Cognition. 2001;80(1–2):47–60. doi: 10.1016/s0010-0277(00)00153-0. [DOI] [PubMed] [Google Scholar]
- Cave KR, Bush WS, Taylor TG. Split attention as part of a flexible attentional system for complex scenes: Comment on Jans, Peters, and De Weerd (2010) Psychological Review. 2010;117(2):685–696. doi: 10.1037/a0019083. doi: 2010-06891-014 [pii] 10.1037/a0019083. [DOI] [PubMed] [Google Scholar]
- Chiu YC, Yantis S. A domain-independent source of cognitive control for task sets: Shifting spatial attention and switching categorization rules. Journal of Neuroscience. 2009;29(12):3930–3938. doi: 10.1523/JNEUROSCI.5737-08.2009. doi: 29/12/3930 [pii] 10.1523/JNEUROSCI.5737-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chun MM. Contextual cueing of visual attention. Trends in Cognitive Sciences. 2000;4:170–178. doi: 10.1016/s1364-6613(00)01476-5. [DOI] [PubMed] [Google Scholar]
- Chun MM, Jiang Y. Contextual cueing: Implicit learning and memory of visual context guides spatial attention. Cognitive Psychology. 1998;36(1):28–71. doi: 10.1006/cogp.1998.0681. doi: S0010-0285(98)90681-8 [pii] 10.1006/cogp.1998.0681. [DOI] [PubMed] [Google Scholar]
- Cohen MA, Grossberg S. Neural dynamics of brightness perception: Features, boundaries, diffusion, and resonance. Perception and Psychophysics. 1984;36:428–456. doi: 10.3758/bf03207497. [DOI] [PubMed] [Google Scholar]
- Culham JC, Brandt SA, Cavanagh P, Kanwisher NG, Dale AM, Tootell RB. Cortical fMRI activation produced by attentive tracking of moving targets. Journal of Neurophysiology. 1998;80(5):2657–2670. doi: 10.1152/jn.1998.80.5.2657. [DOI] [PubMed] [Google Scholar]
- Culham JC, Cavanagh P, Kanwisher NG. Attention response functions: Characterizing brain areas using fMRI activation during parametric variations of attentional load. Neuron. 2001;32(4):737–745. doi: 10.1016/s0896-6273(01)00499-8. doi: S0896-6273(01)00499-8 [pii] [DOI] [PubMed] [Google Scholar]
- Corbetta M, Patel G, Shulman GG. The reorienting system of the human brain: From environment to theory of mind. Neuron. 2008;58:306–324. doi: 10.1016/j.neuron.2008.04.017. doi: 10.1016/j.neuron.2008.04.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbetta M, Shulman GL. Control of goal-directed and stimulus-driven attention in the brain. Nature Reviews Neuroscience. 2002;3:201–215. doi: 10.1038/nrn755. [DOI] [PubMed] [Google Scholar]
- Daniel P, Whitteridge D. The representation of the visual field on the cerebral cortex in monkeys. Journal of Physiology. 1961;159:203–221. doi: 10.1113/jphysiol.1961.sp006803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- David SV, Hayden BY, Mazer JA, Gallant JL. Attention to stimulus features shifts spectral tuning of V4 neurons during natural vision. Neuron. 2008;59(3):509–521. doi: 10.1016/j.neuron.2008.07.001. doi: S0896-6273(08)00570-9 [pii] 10.1016/j.neuron.2008.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desimone R, Duncan J. Neural mechanisms of selective visual attention. Annual Review of Neuroscience. 1995;18:193–222. doi: 10.1146/annurev.ne.18.030195.001205. doi: 10.1146/annurev.ne.18.030195.001205. [DOI] [PubMed] [Google Scholar]
- Dosenbach NU, Fair DA, Cohen AL, Schlaggar BL, Petersen SE. A dual-networks architecture of top-down control. Trends in Cognitive Sciences. 2008;12(3):99–105. doi: 10.1016/j.tics.2008.01.001. doi: S1364-6613(08)00027-2 [pii] 10.1016/j.tics.2008.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosenbach NU, Fair DA, Miezin FM, Cohen AL, Wenger KK, Dosenbach RA, et al. Distinct brain networks for adaptive and stable task control in humans. Proceedings of the National Academy of Sciences of the United States of America. 2007;104(26):11073–11078. doi: 10.1073/pnas.0704320104. doi: 0704320104 [pii] 10.1073/pnas.0704320104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drasdo N. The neural representation of visual space. Nature. 1977;266(5602):554–556. doi: 10.1038/266554a0. [DOI] [PubMed] [Google Scholar]
- Duhamel JR, Colby CL, Goldberg ME. The updating of the representation of visual space in parietal cortex by intended eye movements. Science. 1992;255(5040):90–92. doi: 10.1126/science.1553535. [DOI] [PubMed] [Google Scholar]
- Duncan J. Selective attention and the organization of visual information. Journal of Experimental Psychology: General. 1984;113(4):501–517. doi: 10.1037//0096-3445.113.4.501. [DOI] [PubMed] [Google Scholar]
- Egeth HE, Yantis S. Visual attention: Control, representation, and time course. Annual Review of Psychology. 1997;48:269–297. doi: 10.1146/annurev.psych.48.1.269. doi: 10.1146/annurev.psych.48.1.269. [DOI] [PubMed] [Google Scholar]
- Egly R, Driver J, Rafal RD. Shifting visual attention between objects and locations: Evidence from normal and parietal lesion subjects. Journal of Experimental Psychology: General. 1994;123(2):161–177. doi: 10.1037//0096-3445.123.2.161. [DOI] [PubMed] [Google Scholar]
- Fallah M, Stoner GR, Reynolds JH. Stimulus-specific competitive selection in macaque extrastriate visual area V4. Proceedings of the National Academy of Sciences of the United States of America. 2007;104(10):4165–4169. doi: 10.1073/pnas.0611722104. doi: 0611722104 [pii] 10.1073/pnas.0611722104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang L, Grossberg S. From stereogram to surface: How the brain sees the world in depth. Spatial Vision. 2009;22:45–82. doi: 10.1163/156856809786618484. [DOI] [PubMed] [Google Scholar]
- Fazl A, Grossberg S, Mingolla E. View-invariant object category learning, recognition, and search: How spatial and object attention are coordinated using surface-based attentional shrouds. Cognitive Psychology. 2009;58(1):1–48. doi: 10.1016/j.cogpsych.2008.05.001. doi: S0010-0285(08)00036-4 [pii] 10.1016/j.cogpsych.2008.05.001. [DOI] [PubMed] [Google Scholar]
- Fischer B. Overlap of receptive field centers and representation of the visual field in the cat's optic tract. Vision Research. 1973;13(11):2113–2120. doi: 10.1016/0042-6989(73)90188-0. [DOI] [PubMed] [Google Scholar]
- Franconeri SL, Alvarez GA, Enns JT. How many locations can be selected at once? Journal of Experimental Psychology: Human Perception and Performance. 2007;33(5):1003–1012. doi: 10.1037/0096-1523.33.5.1003. doi: 2007-14662-001 [pii] 10.1037/0096-1523.33.5.1003. [DOI] [PubMed] [Google Scholar]
- Fukuda K, Awh E, Vogel EK. Discrete capacity limits in visual working memory. Current Opinion in Neurobiology. 2010;20(2):177–182. doi: 10.1016/j.conb.2010.03.005. doi: S0959-4388(10)00043-7 [pii] 10.1016/j.conb.2010.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gee AL, Ipata AE, Gottlieb J, Bisley JW, Goldberg ME. Neural enhancement and pre-emptive perception: The genesis of attention and the attentional maintenance of the cortical salience map. Perception. 2008;37(3):389–400. doi: 10.1068/p5874. [DOI] [PubMed] [Google Scholar]
- Ghose GM. Attentional modulation of visual responses by flexible input gain. Journal of Neurophysiology. 2009;101(4):2089–2106. doi: 10.1152/jn.90654.2008. doi: 90654.2008 [pii] 10.1152/jn.90654.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberg ME, Bruce CJ. Primate frontal eye fields. III. Maintenance of a spatially accurate saccade signal. Journal of Neurophysiology. 1990;64(2):489–508. doi: 10.1152/jn.1990.64.2.489. [DOI] [PubMed] [Google Scholar]
- Goldman PS, Rakic PT. Impact of the outside world upon the developing primate brain: Perspective from neurobiology. Bulletin of the Menninger Clinic. 1979;43(1):20–28. [PubMed] [Google Scholar]
- Goldsmith M, Yeari M. Modulation of object-based attention by spatial focus under endogenous and exogenous orienting. Journal of Experimental Psychology: Human Perception and Performance. 2003;29:897–918. doi: 10.1037/0096-1523.29.5.897. doi: 10.1037/0096-1523.29.5.897. [DOI] [PubMed] [Google Scholar]
- Golomb JD, Chun MM, Mazer JA. The native coordinate system of spatial attention is retinotopic. Journal of Neuroscience. 2008;28(42):10654–10662. doi: 10.1523/JNEUROSCI.2525-08.2008. doi: 28/42/10654 [pii] 10.1523/JNEUROSCI.2525-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golomb JD, Nguyen-Phuc AY, Mazer JA, McCarthy G, Chun MM. Attentional facilitation throughout human visual cortex lingers in retinotopic coordinates after eye movements. Journal of Neuroscience. 2010a;30(31):10493–10506. doi: 10.1523/JNEUROSCI.1546-10.2010. doi: 30/31/10493 [pii] 10.1523/JNEUROSCI.1546-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golomb JD, Pulido VZ, Albrecht AR, Chun MM, Mazer JA. Robustness of the retinotopic attentional trace after eye movements. Journal of Vision. 2010b;10(3):11–12. doi: 10.1167/10.3.19. doi: 19 10.1167/10.3.19/10/3/19/ [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottlieb J, Kusunoki M, Goldberg ME. Simultaneous representation of saccade targets and visual onsets in monkey lateral intraparietal area. Cerebral Cortex. 2005;15(8):1198–1206. doi: 10.1093/cercor/bhi002. doi: bhi002 [pii] 10.1093/cercor/bhi002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottlieb JP, Kusunoki M, Goldberg ME. The representation of visual salience in monkey parietal cortex. Nature. 1998;391(6666):481–484. doi: 10.1038/35135. doi: 10.1038/35135. [DOI] [PubMed] [Google Scholar]
- Gove A, Grossberg S, Mingolla E. Brightness perception, illusory contours, and corticogeniculate feedback. Visual Neuroscience. 1995;12(6):1027–1052. doi: 10.1017/s0952523800006702. [DOI] [PubMed] [Google Scholar]
- Green CS, Bavelier D. Action video game modifies visual selective attention. Nature. 2003;423(6939):534–537. doi: 10.1038/nature01647. doi: 10.1038/nature01647nature01647 [pii] [DOI] [PubMed] [Google Scholar]
- Green CS, Bavelier D. Effect of action video games on the spatial distribution of visuospatial attention. Journal of Experimental Psychology: Human Perception and Performance. 2006a;32(6):1465–1478. doi: 10.1037/0096-1523.32.6.1465. doi: 2006-22004-012 [pii]10.1037/0096-1523.32.6.1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green CS, Bavelier D. Enumeration versus multiple object tracking: The case of action video game players. Cognition. 2006b;101(1):217–245. doi: 10.1016/j.cognition.2005.10.004. doi: S0010-0277(05)00187-3 [pii] 10.1016/j.cognition.2005.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green CS, Bavelier D. Action-video-game experience alters the spatial resolution of vision. Psychological Science. 2007;18(1):88–94. doi: 10.1111/j.1467-9280.2007.01853.x. doi: PSCI1853 [pii] 10.1111/j.1467-9280.2007.01853.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gronau N, Neta M, Bar M. Integrated contextual representation for objects' identities and their locations. Journal of Cognitive Neuroscience. 2008;20(3):371–388. doi: 10.1162/jocn.2008.20027. doi: 10.1162/jocn.2008.20027. [DOI] [PubMed] [Google Scholar]
- Grossberg S. A neural theory of punishment and avoidance, II: Quantitative theory. Mathematical Biosciences. 1972;15:253–285. [Google Scholar]
- Grossberg S. Contour enhancement, short-term memory, and constancies in reverberating neural networks. Studies in Applied Mathematics. 1973;52:213–257. [Google Scholar]
- Grossberg S. Adaptive pattern classification and universal recoding, II: Feedback, expectation, olfaction, and illusions. Biological Cybernetics. 1976;23:187–202. doi: 10.1007/BF00340335. [DOI] [PubMed] [Google Scholar]
- Grossberg S. Decisions, patterns, and oscillations in nonlinear competitive systems with applications to Volterra-Lotka systems. Journal of Theoretical Biology. 1978a;73(1):101–130. doi: 10.1016/0022-5193(78)90182-0. [DOI] [PubMed] [Google Scholar]
- Grossberg S. Do all neural models really look alike? A comment on Anderson, Silverstein, Ritz, and Jones. Psychological Review. 1978b;85(6):592–596. [PubMed] [Google Scholar]
- Grossberg S. Biological competition: Decision rules, pattern formation, and oscillations. Proceedings of the National Academy of Sciences of the United States of America. 1980a;77(4):2338–2342. doi: 10.1073/pnas.77.4.2338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grossberg S. How does a brain build a cognitive code? Psychological Review. 1980b;87(1):1–51. doi: 10.1007/978-94-009-7758-7_1. [DOI] [PubMed] [Google Scholar]
- Grossberg S. 3-D vision and figure-ground separation by visual cortex. Perception and Psychophysics. 1994;55(1):48–121. doi: 10.3758/bf03206880. [DOI] [PubMed] [Google Scholar]
- Grossberg S. Cortical dynamics of three-dimensional figure-ground perception of two-dimensional pictures. Psychological Review. 1997;104(3):618–658. doi: 10.1037/0033-295x.104.3.618. [DOI] [PubMed] [Google Scholar]
- Grossberg S. The complementary brain: Unifying brain dynamics and modularity. Trends in Cognitive Sciences. 2000a;4(6):233–246. doi: 10.1016/s1364-6613(00)01464-9. doi: S1364-6613(00)01464-9 [pii] [DOI] [PubMed] [Google Scholar]
- Grossberg S. How hallucinations may arise from brain mechanisms of learning, attention, and volition. Journal of the International Neuropsychological Society. 2000b;6(5):583–592. doi: 10.1017/s135561770065508x. [DOI] [PubMed] [Google Scholar]
- Grossberg S. Towards a unified theory of neocortex: Laminar cortical circuits for vision and cognition. Progress in Brain Research. 2007;165:79–104. doi: 10.1016/S0079-6123(06)65006-1. doi: S0079-6123(06)65006-1 [pii] 10.1016/S0079-6123(06)65006-1. [DOI] [PubMed] [Google Scholar]
- Grossberg S. Cortical and subcortical predictive dynamics and learning during perception, cognition, emotion and action. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences. 2009;364(1521):1223–1234. doi: 10.1098/rstb.2008.0307. doi: 364/1521/1223 [pii] 10.1098/rstb.2008.0307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grossberg S, Hong S. A neural model of surface perception: Lightness, anchoring, and filling-in. Spatial Vision. 2006;19(2–4):263–321. doi: 10.1163/156856806776923399. [DOI] [PubMed] [Google Scholar]
- Grossberg S, Huang TR. ARTSCENE: A neural system for natural scene classification. Journal of Vision. 2009;9(4):1–19. doi: 10.1167/9.4.6. doi: 6 10.1167/9.4.6/9/4/6/ [pii] [DOI] [PubMed] [Google Scholar]
- Grossberg S, Kuhlmann L, Mingolla E. A neural model of 3D shape-from-texture: Multiple-scale filtering, boundary grouping, and surface filling-in. Vision Research. 2007;47:634–672. doi: 10.1016/j.visres.2006.10.024. [DOI] [PubMed] [Google Scholar]
- Grossberg S, Markowitz J, Cao Y. On the road to invariant recognition: Explaining tradeoff and morph properties of cells in inferotemporal cortex using multiple-scale task-sensitive attentive learning. Neural Networks. 2011;24:1036–1049. doi: 10.1016/j.neunet.2011.04.001. [DOI] [PubMed] [Google Scholar]
- Grossberg S, Mingolla E, Ross WD. A neural theory of attentive visual search: Interactions of boundary, surface, spatial, and object representations. Psychological Review. 1994;101(3):470–489. doi: 10.1037/0033-295x.101.3.470. [DOI] [PubMed] [Google Scholar]
- Grossberg S, Mingolla E, Viswanathan L. Neural dynamics of motion integration and segmentation within and across apertures. Vision Research. 2001;41(19):2521–2553. doi: 10.1016/s0042-6989(01)00131-6. [DOI] [PubMed] [Google Scholar]
- Grossberg S, Pearson LR. Laminar cortical dynamics of cognitive and motor working memory, sequence learning and performance: Toward a unified theory of how the cerebral cortex works. Psychological Review. 2008;115(3):677–732. doi: 10.1037/a0012618. doi: 2008-09896-006 [pii] 10.1037/a0012618. [DOI] [PubMed] [Google Scholar]
- Grossberg S, Raizada RD. Contrast-sensitive perceptual grouping and object-based attention in the laminar circuits of primary visual cortex. Vision Research. 2000;40(10–12):1413–1432. doi: 10.1016/s0042-6989(99)00229-1. doi: S0042-6989(99)00229-1 [pii] [DOI] [PubMed] [Google Scholar]
- Grossberg S, Swaminathan G. A laminar cortical model for 3D perception of slanted and curved surfaces and of 2D images: Development, attention, and bistability. Vision Research. 2004;44(11):1147–1187. doi: 10.1016/j.visres.2003.12.009. doi: 10.1016/j.visres.2003.12.009S0042698903007995 [pii] [DOI] [PubMed] [Google Scholar]
- Grossberg S, Todorović D. Neural dynamics of 1-D and 2-D brightness perception: A unified model of classical and recent phenomena. Perception and Psychophysics. 1988;43(3):241–277. doi: 10.3758/bf03207869. [DOI] [PubMed] [Google Scholar]
- Grossberg S, Yazdanbakhsh A. Laminar cortical dynamics of 3D surface perception: Stratification, transparency, and neon color spreading. Vision Research. 2005;45(13):1725–1743. doi: 10.1016/j.visres.2005.01.006. doi: S0042-6989(05)00035-0 [pii] 10.1016/j.visres.2005.01.006. [DOI] [PubMed] [Google Scholar]
- Haxby JV, Grady CL, Horwitz B, Ungerleider LG, Mishkin M, Carson RE, et al. Dissociation of object and spatial visual processing pathways in human extrastriate cortex. Proceedings of the National Academy of Sciences of the United States of America. 1991;88(5):1621–1625. doi: 10.1073/pnas.88.5.1621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayden BY, Gallant JL. Time course of attention reveals different mechanisms for spatial and feature-based attention in area V4. Neuron. 2005;47(5):637–643. doi: 10.1016/j.neuron.2005.07.020. doi: S0896-6273(05)00614-8 [pii] 10.1016/j.neuron.2005.07.020. [DOI] [PubMed] [Google Scholar]
- Hayden BY, Gallant JL. Combined effects of spatial and feature-based attention on responses of V4 neurons. Vision Research. 2009;49(10):1182–1187. doi: 10.1016/j.visres.2008.06.011. doi: S0042-6989(08)00320-9 [pii] 10.1016/j.visres.2008.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He S, Cavanagh P, Intriligator J. Attentional resolution and the locus of visual awareness. Nature. 1996;383(6598):334–337. doi: 10.1038/383334a0. doi: 10.1038/383334a0. [DOI] [PubMed] [Google Scholar]
- He ZJ, Nakayama K. Visual attention to surfaces in three-dimensional space. Proceedings of the National Academy of Sciences of the United States of America. 1995;92(24):11155–11159. doi: 10.1073/pnas.92.24.11155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillyard SA, Vogel EK, Luck SJ. Sensory gain control (amplification) as a mechanism of selective attention: Electrophysiological and neuroimaging evidence. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences. 1998;353(1373):1257–1270. doi: 10.1098/rstb.1998.0281. doi: 10.1098/rstb.1998.0281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong S, Grossberg S. A neuromorphic model for achromatic and chromatic surface representation of natural images. Neural Networks. 2004;17(5–6):787–808. doi: 10.1016/j.neunet.2004.02.007. doi: 10.1016/j.neunet.2004.02.007S0893-6080(04)00053-X [pii] [DOI] [PubMed] [Google Scholar]
- Horowitz TS, Klieger SB, Fencsik DE, Yang KK, Alvarez GA, Wolfe JM. Tracking unique objects. Perception and Psychophysics. 2007;69(2):172–184. doi: 10.3758/bf03193740. [DOI] [PubMed] [Google Scholar]
- Huang TR, Grossberg S. Cortical dynamics of contextually cued attentive visual learning and search: Spatial and object evidence accumulation. Psychological Review. 2010;117(4):1080–1112. doi: 10.1037/a0020664. doi: 2010-22285-001 [pii] 10.1037/a0020664. [DOI] [PubMed] [Google Scholar]
- Intriligator J, Cavanagh P. The spatial resolution of visual attention. Cognitive Psychology. 2001;43(3):171–216. doi: 10.1006/cogp.2001.0755. doi: 10.1006/cogp.2001.0755S0010-0285(01)90755-8 [pii] [DOI] [PubMed] [Google Scholar]
- Itti L, Koch C. Computational modelling of visual attention. Nature Reviews Neuroscience. 2001;2(3):194–203. doi: 10.1038/35058500. [DOI] [PubMed] [Google Scholar]
- James W. The principles of psychology. H. Holt and Company; New York: 1890. [Google Scholar]
- Jans B, Peters JC, De Weerd P. Visual spatial attention to multiple locations at once: The jury is still out. Psychological Review. 2010;117(2):637–684. doi: 10.1037/a0019082. doi: 2010-06891-013 [pii] 10.1037/a0019082. [DOI] [PubMed] [Google Scholar]
- Jiang Y, Chun MM. Selective attention modulates implicit learning. Quarterly Journal of Experimental Psychology. 2001;54A:1105–1124. doi: 10.1080/713756001. [DOI] [PubMed] [Google Scholar]
- Kahneman D, Treisman A, Gibbs BJ. The reviewing of object files: Object-specific integration of information. Cognitive Psychology. 1992;24(2):175–219. doi: 10.1016/0010-0285(92)90007-o. doi: 0010-0285(92)90007-O [pii] [DOI] [PubMed] [Google Scholar]
- Kastner S, Ungerleider LG. Mechanisms of visual attention in the human cortex. Annual Review of Neuroscience. 2000;23:315–341. doi: 10.1146/annurev.neuro.23.1.315. doi: 10.1146/annurev.neuro.23.1.315. [DOI] [PubMed] [Google Scholar]
- Kelly F, Grossberg S. Neural dynamics of 3-D surface perception: Figure-ground separation and lightness perception. Perception and Psychophysics. 2000;62(8):1596–1618. doi: 10.3758/bf03212158. [DOI] [PubMed] [Google Scholar]
- Koch C, Ullman S. Shifts in selective visual attention: Towards the underlying neural circuitry. Human Neurobiology. 1985;4(4):219–227. [PubMed] [Google Scholar]
- Kveraga K, Boshyan J, Bar M. Magnocellular projections as the trigger of top-down facilitation in recognition. Journal of Neuroscience. 2007;27(48):13232–13240. doi: 10.1523/JNEUROSCI.3481-07.2007. doi: 27/48/13232 [pii] 10.1523/JNEUROSCI.3481-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamy D, Egeth H. Object-based selection: The role of attentional shifts. Perception and Psychophysics. 2002;64(1):52–66. doi: 10.3758/bf03194557. [DOI] [PubMed] [Google Scholar]
- Lee J, Maunsell JH. A normalization model of attentional modulation of single unit responses. PLoS ONE. 2009;4(2):e4651. doi: 10.1371/journal.pone.0004651. doi: 10.1371/journal.pone.0004651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levi DM. Crowding – An essential bottleneck for object recognition: A mini-review. Vision Research. 2008;48(5):635–654. doi: 10.1016/j.visres.2007.12.009. doi: S0042-6989(07)00556-1 [pii] 10.1016/j.visres.2007.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li N, DiCarlo JJ. Unsupervised natural experience rapidly alters invariant object representation in visual cortex. Science. 2008;321:1502–1507. doi: 10.1126/science.1160028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li N, DiCarlo JJ. Unsupervised natural visual experience rapidly reshapes size invariant object represent in inferior temporal cortex. Neuron. 2010;67:1062–1075. doi: 10.1016/j.neuron.2010.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logan GD. The CODE theory of visual attention: An integration of space-based and object-based attention. Psychological Review. 1996;103(4):603–649. doi: 10.1037/0033-295x.103.4.603. [DOI] [PubMed] [Google Scholar]
- Logothetis NK, Pauls J, Poggio T. Shape representation in the inferior temporal cortex of monkeys. Current Biology. 1995;5:552–563. doi: 10.1016/s0960-9822(95)00108-4. doi: 10.1016/S0960-9822(95)00108-4. [DOI] [PubMed] [Google Scholar]
- Luck SJ, Hillyard SA, Mangun GR, Gazzaniga MS. Independent hemispheric attentional systems mediate visual search in split-brain patients. Nature. 1989;342(6249):543–545. doi: 10.1038/342543a0. doi: 10.1038/342543a0. [DOI] [PubMed] [Google Scholar]
- Martinez A, Teder-Salejarvi W, Vazquez M, Molholm S, Foxe JJ, Javitt DC, et al. Objects are highlighted by spatial attention. Journal of Cognitive Neuroscience. 2006;18(2):298–310. doi: 10.1162/089892906775783642. doi: 10.1162/089892906775783642. [DOI] [PubMed] [Google Scholar]
- Mathot S, Hickey C, Theeuwes J. From reorienting of attention to biased competition: Evidence from hemifield effects. Attention, Perception, and Psychophysics. 2010;72(3):651–657. doi: 10.3758/APP.72.3.651. doi: 72/3/651 [pii] 10.3758/APP.72.3.651. [DOI] [PubMed] [Google Scholar]
- Mathot S, Theeuwes J. Evidence for the predictive remapping of visual attention. Experimental Brain Research. 2010a;200(1):117–122. doi: 10.1007/s00221-009-2055-3. doi: 10.1007/s00221-009-2055-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathot S, Theeuwes J. Gradual remapping results in early retinotopic and late spatiotopic inhibition of return. Psychological Science. 2010b;21(12):1793–1798. doi: 10.1177/0956797610388813. doi: 0956797610388813 [pii] 10.1177/0956797610388813. [DOI] [PubMed] [Google Scholar]
- Matsuzaki R, Kyuhou S, Matsuura-Nakao K, Gemba H. Thalamo-cortical projections to the posterior parietal cortex in the monkey. Neuroscience Letters. 2004;355(1–2):113–116. doi: 10.1016/j.neulet.2003.10.066. doi: S0304394003012746 [pii] [DOI] [PubMed] [Google Scholar]
- McMains SA, Somers DC. Multiple spotlights of attentional selection in human visual cortex. Neuron. 2004;42(4):677–686. doi: 10.1016/s0896-6273(04)00263-6. doi: S0896627304002636 [pii] [DOI] [PubMed] [Google Scholar]
- McMains SA, Somers DC. Processing efficiency of divided spatial attention mechanisms in human visual cortex. Journal of Neuroscience. 2005;25(41):9444–9448. doi: 10.1523/JNEUROSCI.2647-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melcher D. Predictive remapping of visual features precedes saccadic eye movements. Nature Neuroscience. 2007;10(7):903–907. doi: 10.1038/nn1917. doi: nn1917 [pii] 10.1038/nn1917. [DOI] [PubMed] [Google Scholar]
- Melcher D. Dynamic, object-based remapping of visual features in trans-saccadic perception. Journal of Vision. 2008;8(14):1–17. doi: 10.1167/8.14.2. doi: 2 10.1167/8.14.2/8/14/2/ [pii] [DOI] [PubMed] [Google Scholar]
- Melcher D. Selective attention and the active remapping of object features in trans-saccadic perception. Vision Research. 2009;49(10):1249–1255. doi: 10.1016/j.visres.2008.03.014. doi: S0042-6989(08)00145-4 [pii] 10.1016/j.visres.2008.03.014. [DOI] [PubMed] [Google Scholar]
- Miller GA. The magical number seven plus or minus two: Some limits on our capacity for processing information. Psychological Review. 1956;63(2):81–97. [PubMed] [Google Scholar]
- Mitchell JF, Stoner GR, Reynolds JH. Object-based attention determines dominance in binocular rivalry. Nature. 2004;429(6990):410–413. doi: 10.1038/nature02584. doi: 10.1038/nature02584nature02584 [pii] [DOI] [PubMed] [Google Scholar]
- Moore CM, Elsinger CL, Lleras A. Visual attention and the apprehension of spatial relations: The case of depth. Perception and Psychophysics. 2001;63(4):595–606. doi: 10.3758/bf03194424. [DOI] [PubMed] [Google Scholar]
- Moore CM, Fulton C. The spread of attention to hidden portions of occluded surfaces. Psychonomic Bulletin and Review. 2005;12(2):301–306. doi: 10.3758/bf03196376. [DOI] [PubMed] [Google Scholar]
- Moore CM, Yantis S, Vaughan B. Object-based visual selection: Evidence from perceptual completion. Psychological Science. 1998 [Google Scholar]
- Muller MM, Malinowski P, Gruber T, Hillyard SA. Sustained division of the attentional spotlight. Nature. 2003;424(6946):309–312. doi: 10.1038/nature01812. doi: 10.1038/nature01812nature01812 [pii] [DOI] [PubMed] [Google Scholar]
- Nakamura K, Colby CL. Visual, saccade-related, and cognitive activation of single neurons in monkey extrastriate area V3A. Journal of Neurophysiology. 2000;84(2):677–692. doi: 10.1152/jn.2000.84.2.677. [DOI] [PubMed] [Google Scholar]
- O'Craven KM, Downing PE, Kanwisher N. FMRI evidence for objects as the units of attentional selection. Nature. 1999;401(6753):584–587. doi: 10.1038/44134. doi: 10.1038/44134. [DOI] [PubMed] [Google Scholar]
- Olson IR, Chun MM. Temporal contextual cuing of visual attention. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2001;27(5):1299–1313. doi: 10.1037//0278-7393.27.5.1299. [DOI] [PubMed] [Google Scholar]
- Olson IR, Chun MM. Perceptual constraints on implicit learning of spatial context. Visual Cognition. 2002;9:273–302. [Google Scholar]
- Ploran EJ, Nelson SM, Velanova K, Donaldson DI, Petersen SE, Wheeler ME. Evidence accumulation and the moment of recognition: Dissociating perceptual recognition processes using fMRI. Journal of Neuroscience. 2007;27(44):11912–11924. doi: 10.1523/JNEUROSCI.3522-07.2007. doi: 27/44/11912 [pii] 10.1523/JNEUROSCI.3522-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polimeni JR, Balasubramanian M, Schwartz EL. Multi-area visuotopic map complexes in macaque striate and extra-striate cortex. Vision Research. 2006;46(20):3336–3359. doi: 10.1016/j.visres.2006.03.006. doi: S0042-6989(06)00142-8 [pii] 10.1016/j.visres.2006.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Posner MI. Orienting of attention. Quarterly Journal of Experimental Psychology. 1980;32(1):3–25. doi: 10.1080/00335558008248231. [DOI] [PubMed] [Google Scholar]
- Posner MI, Cohen Y, Rafal RD. Neural systems control of spatial orienting. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences. 1982;298(1089):187–198. doi: 10.1098/rstb.1982.0081. [DOI] [PubMed] [Google Scholar]
- Posner MI, Petersen SE. The attention system of the human brain. Annual Review of Neuroscience. 1990;13:25–42. doi: 10.1146/annurev.ne.13.030190.000325. doi: 10.1146/annurev.ne.13.030190.000325. [DOI] [PubMed] [Google Scholar]
- Press WH. Numerical recipes in FORTRAN: The art of scientific computing. 2nd ed. Cambridge University Press; Cambridge, England; New York, NY, USA: 1992. [Google Scholar]
- Pylyshyn Z. The role of location indexes in spatial perception: A sketch of the FINST spatial-index model. Cognition. 1989;32(1):65–97. doi: 10.1016/0010-0277(89)90014-0. doi: 0010-0277(89)90014-0 [pii] [DOI] [PubMed] [Google Scholar]
- Pylyshyn Z, Burkell J, Fisher B, Sears C, Schmidt W, Trick L. Multiple parallel access in visual attention. Canadian Journal of Experimental Psychology. 1994;48(2):260–283. doi: 10.1037/1196-1961.48.2.260. [DOI] [PubMed] [Google Scholar]
- Pylyshyn ZW. Visual indexes, preconceptual objects, and situated vision. Cognition. 2001;80(1–2):127–158. doi: 10.1016/s0010-0277(00)00156-6. doi: S0010-0277(00)00156-6 [pii] [DOI] [PubMed] [Google Scholar]
- Pylyshyn ZW, Storm RW. Tracking multiple independent targets: Evidence for a parallel tracking mechanism. Spatial Vision. 1988;3(3):179–197. doi: 10.1163/156856888x00122. [DOI] [PubMed] [Google Scholar]
- Raizada R, Grossberg S. Context-sensitive bindings by the laminar circuits of V1 and V2: A unified model of perceptual grouping, attention, and orientation contrast. Visual Cognition. 2001;8:431–466. [Google Scholar]
- Raudies F, Neumann H. A neural model of the temporal dynamics of figure-ground segregation in motion perception. Neural Networks. 2010;23:160–176. doi: 10.1016/j.neunet.2009.10.005. [DOI] [PubMed] [Google Scholar]
- Reynolds JH, Alborzian S, Stoner GR. Exogenously cued attention triggers competitive selection of surfaces. Vision Research. 2003;43(1):59–66. doi: 10.1016/s0042-6989(02)00403-0. doi: S0042698902004030 [pii] [DOI] [PubMed] [Google Scholar]
- Reynolds JH, Chelazzi L, Desimone R. Competitive mechanisms subserve attention in macaque areas V2 and V4. Journal of Neuroscience. 1999;19(5):1736–1753. doi: 10.1523/JNEUROSCI.19-05-01736.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reynolds JH, Desimone R. Interacting roles of attention and visual salience in V4. Neuron. 2003;37(5):853–863. doi: 10.1016/s0896-6273(03)00097-7. doi: S0896627303000977 [pii] [DOI] [PubMed] [Google Scholar]
- Reynolds JH, Heeger DJ. The normalization model of attention. Neuron. 2009;61(2):168–185. doi: 10.1016/j.neuron.2009.01.002. doi: S0896-6273(09)00003-8 [pii] 10.1016/j.neuron.2009.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reynolds JH, Pasternak T, Desimone R. Attention increases sensitivity of V4 neurons. Neuron. 2000;26(3):703–714. doi: 10.1016/s0896-6273(00)81206-4. doi: S0896-6273(00)81206-4 [pii] [DOI] [PubMed] [Google Scholar]
- Richards E, Bennett PJ, Sekuler AB. Age related differences in learning with the useful field of view. Vision Research. 2006;46(25):4217–4231. doi: 10.1016/j.visres.2006.08.011. doi: S0042-6989(06)00382-8 [pii] 10.1016/j.visres.2006.08.011. [DOI] [PubMed] [Google Scholar]
- Roelfsema PR, Lamme VA, Spekreijse H. Object-based attention in the primary visual cortex of the macaque monkey. Nature. 1998;395(6700):376–381. doi: 10.1038/26475. doi: 10.1038/26475. [DOI] [PubMed] [Google Scholar]
- Roggeveen A, Pilz K, Bennett P, Sekuler A. Individual differences in object based attention. Journal of Vision. 2009;9(8):143. [Google Scholar]
- Saygin AP, Sereno MI. Retinotopy and attention in human occipital, temporal, parietal, and frontal cortex. Cerebral Cortex. 2008;18(9):2158–2168. doi: 10.1093/cercor/bhm242. doi: bhm242 [pii] 10.1093/cercor/bhm242. [DOI] [PubMed] [Google Scholar]
- Scalf PE, Beck DM. Competition in visual cortex impedes attention to multiple items. Journal of Neuroscience. 2010;30(1):161–169. doi: 10.1523/JNEUROSCI.4207-09.2010. doi: 30/1/161 [pii] 10.1523/JNEUROSCI.4207-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scalf PE, Colcombe SJ, McCarley JS, Erickson KI, Alvarado M, Kim JS, et al. The neural correlates of an expanded functional field of view. Journals of Gerontology Series B - Psychological Sciences and Social Sciences. 2007;62(Spec No. 1):32–44. doi: 10.1093/geronb/62.special_issue_1.32. doi: 62/suppl_Special_Issue_1/32 [pii] [DOI] [PubMed] [Google Scholar]
- Scholl BJ. Objects and attention: The state of the art. Cognition. 2001;80(1–2):1–46. doi: 10.1016/s0010-0277(00)00152-9. doi: S0010-0277(00)00152-9 [pii] [DOI] [PubMed] [Google Scholar]
- Scholl BJ, Pylyshyn ZW, Feldman J. What is a visual object? Evidence from target merging in multiple object tracking. Cognition. 2001;80(1–2):159–177. doi: 10.1016/s0010-0277(00)00157-8. doi: S0010-0277(00)00157-8 [pii] [DOI] [PubMed] [Google Scholar]
- Scholte HS, Spekreijse H, Roelfsema PR. The spatial profile of visual attention in mental curve tracing. Vision Research. 2001;41:2569–2580. doi: 10.1016/s0042-6989(01)00148-1. [DOI] [PubMed] [Google Scholar]
- Schwartz EL. The development of specific visual connections in the monkey and the goldfish: Outline of a geometric theory of receptotopic structure. Journal of Theoretical Biology. 1977;69(4):655–683. doi: 10.1016/0022-5193(77)90374-5. [DOI] [PubMed] [Google Scholar]
- Sekuler R, Ball K. Visual localization: Age and practice. Journal of the Optical Society of America A. Optics and Image Science. 1986;3(6):864–867. doi: 10.1364/josaa.3.000864. [DOI] [PubMed] [Google Scholar]
- Serences JT, Schwarzbach J, Courtney SM, Golay X, Yantis S. Control of object-based attention in human cortex. Cerebral Cortex. 2004;14(12):1346–1357. doi: 10.1093/cercor/bhh095. doi: 10.1093/cercor/bhh095bhh095 [pii] [DOI] [PubMed] [Google Scholar]
- Sereno MI, Huang RS. A human parietal face area contains aligned head-centered visual and tactile maps. Nature Neuroscience. 2006;9(10):1337–1343. doi: 10.1038/nn1777. doi: nn1777 [pii] 10.1038/nn1777. [DOI] [PubMed] [Google Scholar]
- Shomstein S, Yantis S. Configural and contextual prioritization in object-based attention. Psychonomic Bulletin and Review. 2004;11(2):247–253. doi: 10.3758/bf03196566. [DOI] [PubMed] [Google Scholar]
- Silver MA, Ress D, Heeger DJ. Topographic maps of visual spatial attention in human parietal cortex. Journal of Neurophysiology. 2005;94(2):1358–1371. doi: 10.1152/jn.01316.2004. doi: 01316.2004 [pii] 10.1152/jn.01316.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srihasam K, Bullock D, Grossberg S. Target selection by the frontal cortex during coordinated saccadic and smooth pursuit eye movements. Journal of Cognitive Neuroscience. 2009;21(8):1611–1627. doi: 10.1162/jocn.2009.21139. doi: 10.1162/jocn.2009.21139. [DOI] [PubMed] [Google Scholar]
- Swisher JD, Halko MA, Merabet LB, McMains SA, Somers DC. Visual topography of human intraparietal sulcus. Journal of Neuroscience. 2007;27(20):5326–5337. doi: 10.1523/JNEUROSCI.0991-07.2007. doi: 27/20/5326 [pii] 10.1523/JNEUROSCI.0991-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theeuwes J, Mathot S, Kingstone A. Object-based eye movements: The eyes prefer to stay within the same object. Attention, Perception, and Psychophysics. 2010;72(3):597–601. doi: 10.3758/APP.72.3.597. doi: 72/3/597 [pii] 10.3758/APP.72.3.597. [DOI] [PubMed] [Google Scholar]
- Toet A, Levi DM. The two-dimensional shape of spatial interaction zones in the parafovea. Vision Research. 1992;32(7):1349–1357. doi: 10.1016/0042-6989(92)90227-a. [DOI] [PubMed] [Google Scholar]
- Tolias AS, Moore T, Smirnakis SM, Tehovnik EJ, Siapas AG, Schiller PH. Eye movements modulate visual receptive fields of V4 neurons. Neuron. 2001;29(3):757–767. doi: 10.1016/s0896-6273(01)00250-1. doi: S0896-6273(01)00250-1 [pii] [DOI] [PubMed] [Google Scholar]
- Tomasi D, Ernst T, Caparelli EC, Chang L. Practice-induced changes of brain function during visual attention: A parametric fMRI study at 4 Tesla. Neuroimage. 2004;23(4):1414–1421. doi: 10.1016/j.neuroimage.2004.07.065. doi: S1053-8119(04)00425-2 [pii] 10.1016/j.neuroimage.2004.07.065. [DOI] [PubMed] [Google Scholar]
- Tootell RB, Silverman MS, Switkes E, De Valois RL. Deoxyglucose analysis of retinotopic organization in primate striate cortex. Science. 1982;218(4575):902–904. doi: 10.1126/science.7134981. [DOI] [PubMed] [Google Scholar]
- Treisman AM, Gelade G. A feature-integration theory of attention. Cognitive Psychology. 1980;12(1):97–136. doi: 10.1016/0010-0285(80)90005-5. doi: 0010-0285(80)90005-5 [pii] [DOI] [PubMed] [Google Scholar]
- Tyler CW, Kontsevich LL. Mechanisms of stereoscopic processing: Stereoattention and surface perception in depth reconstruction. Perception. 1995;24(2):127–153. doi: 10.1068/p240127. [DOI] [PubMed] [Google Scholar]
- Ungerleider LG, Haxby JV. `What' and `where' in the human brain. Current Opinion in Neurobiology. 1994;4(2):157–165. doi: 10.1016/0959-4388(94)90066-3. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Newsome WT, Maunsell JH. The visual field representation in striate cortex of the macaque monkey: Asymmetries, anisotropies, and individual variability. Vision Research. 1984;24(5):429–448. doi: 10.1016/0042-6989(84)90041-5. [DOI] [PubMed] [Google Scholar]
- Verghese P, Pelli DG. The information capacity of visual attention. Vision Research. 1992;32(5):983–995. doi: 10.1016/0042-6989(92)90040-p. doi: 0042-6989(92)90040-P [pii] [DOI] [PubMed] [Google Scholar]
- Vogel EK, Machizawa MG. Neural activity predicts individual differences in visual working memory capacity. Nature. 2004;428(6984):748–751. doi: 10.1038/nature02447. doi: 10.1038/nature02447nature02447 [pii] [DOI] [PubMed] [Google Scholar]
- Wannig A, Stanisor L, Roelfsema PR. Automatic spread of attentional response modulation along Gestalt criteria in primary visual cortex. Nature Neuroscience. 2011;14:1243–1244. doi: 10.1038/nn.2910. doi: 10.1038/nn.2910. [DOI] [PubMed] [Google Scholar]
- Wolfe JM, editor. Guided search 4.0: Current progress with a model of visual search. Oxford; New York: 2007. [Google Scholar]
- Wolfe JM, Cave KR, Franzel SL. Guided search: An alternative to the feature integration model for visual search. Journal of Experimental Psychology: Human Perception and Performance. 1989;15(3):419–433. doi: 10.1037//0096-1523.15.3.419. [DOI] [PubMed] [Google Scholar]
- Xiao D, Zikopoulos B, Barbas H. Laminar and modular organization of prefrontal projections to multiple thalamic nuclei. Neuroscience. 2009;161(4):1067–1081. doi: 10.1016/j.neuroscience.2009.04.034. doi: S0306-4522(09)00641-1 [pii] 10.1016/j.neuroscience.2009.04.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yantis S, Jonides J. Abrupt visual onsets and selective attention: Voluntary versus automatic allocation. Journal of Experimental Psychology: Human Perception and Performance. 1990;16(1):121–134. doi: 10.1037//0096-1523.16.1.121. [DOI] [PubMed] [Google Scholar]
- Yantis S, Schwarzbach J, Serences JT, Carlson RL, Steinmetz MA, Pekar JJ, et al. Transient neural activity in human parietal cortex during spatial attention shifts. Nature Neuroscience. 2002;5(10):995–1002. doi: 10.1038/nn921. doi: 10.1038/nn921nn921 [pii] [DOI] [PubMed] [Google Scholar]
- Yantis S, Serences JT. Cortical mechanisms of space-based and object-based attentional control. Current Opinion in Neurobiology. 2003;13(2):187–193. doi: 10.1016/s0959-4388(03)00033-3. doi: S0959438803000333 [pii] [DOI] [PubMed] [Google Scholar]
- Youakim M, Bender DB, Baizer JS. Vertical meridian representation on the prelunate gyrus in area V4 of macaque. Brain Research Bulletin. 2001;56(2):93–100. doi: 10.1016/s0361-9230(01)00608-6. doi: S0361-9230(01)00608-6 [pii] [DOI] [PubMed] [Google Scholar]
- Zikopoulos B, Barbas H. Prefrontal projections to the thalamic reticular nucleus form a unique circuit for attentional mechanisms. Journal of Neuroscience. 2006;26(28):7348–7361. doi: 10.1523/JNEUROSCI.5511-05.2006. doi: 26/28/7348 [pii] 10.1523/JNEUROSCI.5511-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]