Fallacies of Last Observation Carried Forward

Abstract

Background

Last Observation Carried Forward (LOCF) is a common statistical approach to the analysis of longitudinal repeated measures data where some follow-up observations may be missing. In a LOCF analysis, a missing follow-up visit value is replaced by (imputed as) that subject’s previously observed value, i.e. the last observation is carried forward. The combination of the observed and imputed data are then analyzed as though there were no missing data.

Purpose

There have been numerous statistical demonstrations of faults of this approach. In 2012 the National Research Council’s Panel on Handling Missing Data in Clinical Trials issued a report that raised concerns with the use of LOCF, and described alternate methods that offer greater statistical validity. Nevertheless, the method persists and its use is rampant. A search of the key word “LOCF” using Google Scholar yielded “about 1360” published citations during 2014 alone, the overwhelming majority presenting the results of scientific studies. However, there has not been a simple explanation of the statistical deficiencies of LOCF. Such a description is presented herein.

Results

A simple repeated measures model is described for quantitative observations at two times (e.g. 1 and 2-years), with complete values at 1-year that are used to impute by LOCF the missing values at 2-years under the missing completely at random (MCAR) assumption. This results in a mixture distribution of observed and imputed values at 2-years with mean and variance that are a function of the mixture of the 1 and 2-year distributions. The expressions show that LOCF is only unbiased when the distribution of the observed values at 1-year is exactly equal to the distribution of the missing values at 2-years, the latter of course being unknown.

Limitations

When the values at 2-years are not randomly missing, no simple expressions for the mean and variance of the mixture distribution are possible without additional unverifiable assumptions.

Conclusion

All analyses using LOCF are of questionable veracity, if not being outright specious (def: appearing to be true but actually false). It is hoped that future studies will make a more vigorous attempt to minimize the amount of missing data, and that more valid statistical analyses will be employed in cases where missing data occurs. LOCF should not be employed in any analyses.

Introduction

Every statistical analysis attempts to provide an unbiased (i.e. reliable) assessment of study results. However, various factors may yield results that are biased (distorted) in some way, perhaps the most common being missing data, i.e. measurements that were potentially measurable or expected under the study design, but were not measured for some reason. The resulting bias arises not just because some data are missing, but more importantly, the reason that the values are missing, or the missing data mechanism.

Little and Rubin¹ review the types of missing data and the underlying mechanism. Data that are missing completely at random do not confer any bias, meaning that the data are missing purely by chance. The simplest case is data that are missing by design or administratively, e.g. when a subject who entered a 5 year study in the second year is administratively missing a year 5 measurement. Missing at random refers to data where the probability of being missing may may depend on other observed data, and adjusting for that data can provide an unbiased result. However, data that are missing not at random will introduce a bias in the analysis results regardless of statistical adjustment for other measured covariates.

A National Research Council panel reviewed the numerous statistical methods that have been proposed to address the problem of non-randomly missing data.^2–5 The report concludes that every method of analysis makes various assumptions that are technically unverifiable, and that the best approach is to minimize the extent of missing data.

Last Observation Carried Forward (LOCF) is among the simplest methods to account for missing data in a longitudinal analysis of repeated measures over time. Historically, its origins are obscure. There was no single statistical article that originally proposed the approach. In fact, there is not a single peer-reviewed statistical publication that describes general conditions under which LOCF provides a statistically unbiased result. Rather, many authors have been critical of LOCF.^6–8 Nevertheless, LOCF remains pervasive. A search for “LOCF” using Google Scholar yielded “about 1360” published citations during 2014 alone, the overwhelming majority presenting the results of scientific studies, all of which are of questionable veracity, if not being outright specious.

Herein I employ the well-established properties of a mixture of observations drawn from two separate distributions to compute the bias that can (will) be introduced by LOCF under a range of conditions.

One-sample Biases

While LOCF is most frequently applied to the analysis of two or more treatment groups, it is instructive to first consider the biases that can be introduced within a single group for data that are missing completely at random, and then for non-randomly missing data.

Missing completely at random data

Assume that the outcome is measured at 1 and 2-years in a single sample of subjects, such as an analysis of the change from baseline after 1 and 2-years of follow-up. The primary analysis consists of an estimate of the mean change at 2-years, with a 95% confidence interval and a one-sample test of significance of the null hypothesis that the mean change is zero using perhaps a paired t-test, or as herein, a simple large sample Z-test.

Assume that the measures at 1-year (X₁) and 2-years (X₂) are randomly drawn from distributions with respective means μ₁ and μ₂ and variances ${\sigma }_1^2$ and ${\sigma }_2^2$. Also assume that all of the X₁ measures are observed but some of the X₂ measures are missing completely at random; meaning that having a missing X₂ is not influenced by the value of X₁ or the true value of X₂. Technically X₁ and X₂ are drawn from a bivariate distribution, such as a bivariate normal, with correlation ρ₁₂. Let τ denote the fraction of X₂ values that are missing and imputed by the X₁ values, where τ is fixed. The Appendix shows that identical results apply when the fraction missing is random.

The set of observed and imputed 2-year values, denoted as X̃₂, then consists of a mixture of samples from two distributions with expected mean⁹

$$E({\stackrel{\sim }{X}}_2)={\stackrel{\sim }{\mu }}_2=\tau {\mu }_1+(1-\tau ){\mu }_2.$$ (1)

The expression for the variance of the observed/imputed values, ${\stackrel{\sim }{\sigma }}_2^2=V({\stackrel{\sim }{X}}_2)$, is presented in the Appendix. Note that since the missing observations are completely random, the mean and variance of X̃₂ do not depend on the correlation of X₁ and X₂.

For a sample of n observed/imputed values with mean ${\stackrel{\sim }{\overline{X}}}_2$ and sample variance V̂ (X̃₂), the one-sample Z-test of the null hypothesis μ₂ = 0 is computed as $\stackrel{\sim }{z}={\stackrel{\sim }{\overline{X}}}_2/{\left[\widehat{V}({\stackrel{\sim }{X}}_2/n)\right]}^{-1/2}$ , with significance (one-sided) at level α if z̃ ≥ Z_1−α. For specified values of the mean μ̃₂ and variance ${\stackrel{\sim }{\sigma }}_2^2$ of the distribution of observed/imputed values, the probability of a statistically significant test result can be obtained as

$$P(\stackrel{\sim }{z}\ge Z_{1-\alpha })=1-\mathrm{\Phi }\left[Z_{1-\alpha }-\frac{{\stackrel{\sim }{\mu }}_2\sqrt{n}}{{\stackrel{\sim }{\sigma }}_2}\right].$$ (2)

A like expression provides the probability of significance for a Z-test with complete data for a given mean and variance μ₂ and ${\sigma }_2^2$.

While the distribution of the observed/imputed values X̃₂ depends on the variances of X₁ and X₂, the possible bias due to the LOCF imputation is principally a function of the mean value μ̃₂. If μ̃₂ ⋚ μ₂ then then analysis of the observed/imputed values is biased, leading to a probability of a significant test ⋛ the true probability.

The following computations assume τ = 0.30 and n = 100.

The null hypothesis

First consider cases where the true mean change from baseline at 2-years is zero, or E(X₂) = μ₂ = 0, for which the probability of significance is the desired level α, 0.05 one-sided herein.

Table 1 then shows the mean of the observed/imputed values (μ̃₂, 30% imputed) and the corresponding variance ${\stackrel{\sim }{\sigma }}_2^2$. The first three cases assume that ${\sigma }_1^2={\sigma }_2^2=20$, i.e. the variance of the imputed values equals that of the true (but missing) values.

Table 1.

Mean μ̃₂ and variance ${\stackrel{\sim }{\sigma }}_2^2$ of the observed/imputed values at year 2, and the probability that a one-sample one-sided test of H₀: μ₂ = 0 would be nominally statistically significant at the 0.05 level, for given mean and variance of the 1 and 2-year values (μ₁, ${\sigma }_1^2$, μ₂, ${\sigma }_2^2$), with a sample size of n = 100, 30% of which are missing completely at random at 2-years and are replaced by the values at 1-year. Cases 1 and 5 also provide the type I error probability and power with no missing data.

Case	μ2	${\sigma }_2^2$	μ1	${\sigma }_1^2$	μ̃2	${\stackrel{\sim }{\sigma }}_2^2$	Pr(significant)
1	0	20	0	20	0	20	0.05
2	0	20	−1	20	−0.3	20.21	0.010
3	0	20	1	20	0.3	20.21	0.164
4	0	20	1	30	0.3	23.21	0.153
5	1	20	1	20	1	20	0.723
6	1	20	−1	20	0.4	20.84	0.221
7	1	20	0	20	0.7	20.21	0.465
8	1	20	2	20	1.3	20.21	0.894
9	1	20	2	30	1.3	23.21	0.854

In case 1, E(X₁) = μ₁ = 0 and V (X₁) = 20, the same as for X₂, and μ̃₂ = 0 and ${\stackrel{\sim }{\sigma }}_2^2=20$ so that no bias is introduced and the probability of a significant result is not affected. In other words, the value 0.05 is the theoretical type I error probability with no missing data, and no LOCF.

In case 2, there is a decrease from baseline at 1-year (μ₁ = −1) that yields a decrease in the observed/imputed values at 2-years, μ̃₂ = −0.3 resulting from the 70% observed values having mean zero and the 30% imputed values having mean −1. While the 1 and 2-year values have the same variance ( ${\sigma }_1^2={\sigma }_2^2=20$), the variance of the observed/imputed values is increased slightly to ${\stackrel{\sim }{\sigma }}_2^2=20.21$ because the distribution is now bimodal. Accordingly, the probability of a significant increasing value (one-sided) is decreased to only 0.010.

In case 3, there is an increase at 1-year (μ₁ = 1) that yields an increase in the observed/imputed values (μ̃₂ = 0.3) resulting from the 30% imputed values having mean 1. Again the variance is increased slightly owing to the bimodal distribution. Accordingly, the probability of a significant increase from baseline (one-sided) is inflated to 0.164. That is, an observed LOCF p-value of exactly 0.05 corresponds to a true false positive probability of 0.164, over 3 times the nominal p-value.

Case 4 is the same as case 3 except that the X₁ variance is also higher ( ${\sigma }_1^2=30$) than the X₂ variance, so that the variance of the observed/imputed values is increased further to ${\stackrel{\sim }{\sigma }}_2^2=32.21$. The resulting inflation in the false positive probability is slightly less at 0.153, but still severely biased. If the variance at 1-year was lower than at 2-years ( ${\sigma }_1^2=10$) the variance of the observed/imputed values is less than the true variance, ${\stackrel{\sim }{\sigma }}_2^2=17.21$, and the false positive probability is increased to 0.178.

By construction, the test will have type I error probability α = 0.05 whenever μ̃₂ = 0, regardless of the value of the variance ${\stackrel{\sim }{\sigma }}_2^2$. Thus, under the null hypothesis of no change from baseline at 2-years, LOCF imputation will only be unbiased when the mean value at 1-year (μ₁) is also zero.

The alternative hypothesis

Now assume that the true change from baseline at 2-years is μ₂ = 1 with variance ${\sigma }_2^2=20$ and n = 100, as above, in which case the probability of a statistically significant one-sided test at p ≤ 0.05 is 0.723, or the power of the study with no missing data.

In case 5, the mean and variance at 1-year are the same as at 2-years, E(X₁) = μ₁ = 1 and V (X₁) = 20, so that the mean and variance of the observed/imputed values is unaffected, μ̃₂ = 1 and ${\stackrel{\sim }{\sigma }}_2^2=20$, and no bias is introduced. Accordingly, the probability of a significant result is not affected, which in this case is the power of the original study (0.723) with no missing data, and no LOCF.

In case 6, there is a decrease from baseline at 1-year (μ₁ = −1). When the 30% imputed values from this distribution are mixed with the 70% observed values with mean μ₂ = 1, the mean change in the observed/imputed values is diluted so that μ e₂ = 0.4, resulting in a markedly reduced probability of a significant result of 0.221. Owing to the bimodal distribution, the variance of the observed/imputed values is increased slightly to ${\stackrel{\sim }{\sigma }}_2^2=20.84$ that has a trivial effect on the probability of a significant result.

In case 7, there is no change from baseline at 1-year (μ₁ = 0) so that again the mean of the observed/imputed values is diluted, μ̃₂ = 0.7 and the variance increased slightly, so that the probability of a significant result is reduced to 0.465.

In case 8, there is a greater change from baseline at 1-year (μ₁ = 2) than at 2-years so that the mean of the mixture of observed/imputed values is now greater than that of the true 2-year values, μ̃₂ = 1.3, and the variance increased slightly, so that the probability of a significant result is substantially increased to 0.893. In case 9 the variance of the 1-year values ( ${\sigma }_1^2=30$) is also greater than that of the true 2-year values that dampens slightly the increased probability of a significant result to 0.854.

Note that these latter probabilities have not been labeled “power”, since they will not correspond to the theoretical probability of rejecting the null hypothesis under the parametric settings of the original study design before the missing data occurs. For the assumptions herein, μ₂ = 1, ${\sigma }_2^2=20$ and n = 100, the power is 0.723 as shown above. Thus, under case 8, the proper interpretation is that the bias in the observed/imputed data introduced by LOCF increases the probability of a significant result to 0.893. Clearly some of the inflation/deflation in the probability of significance under the alternative is a result of the inflation/deflation in the type 1 error probability under the null, but not all.

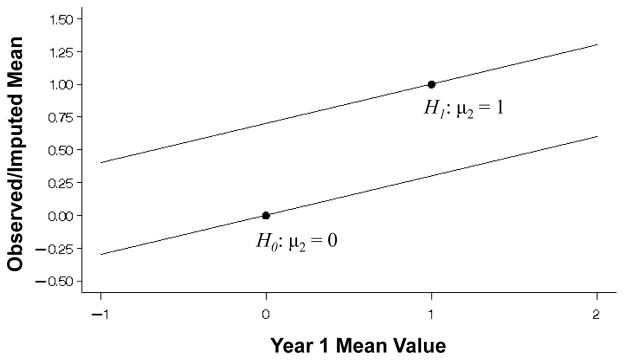
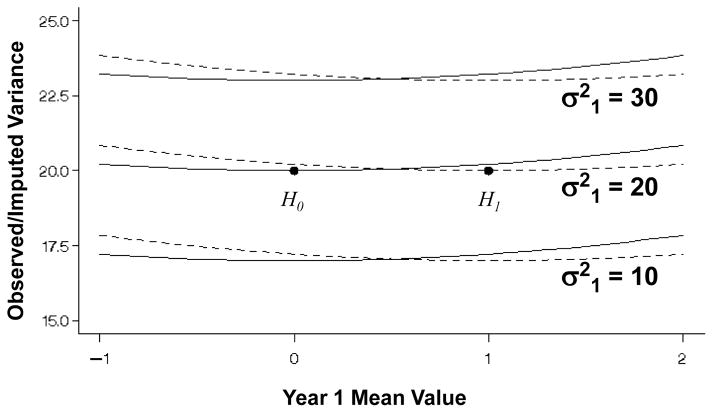
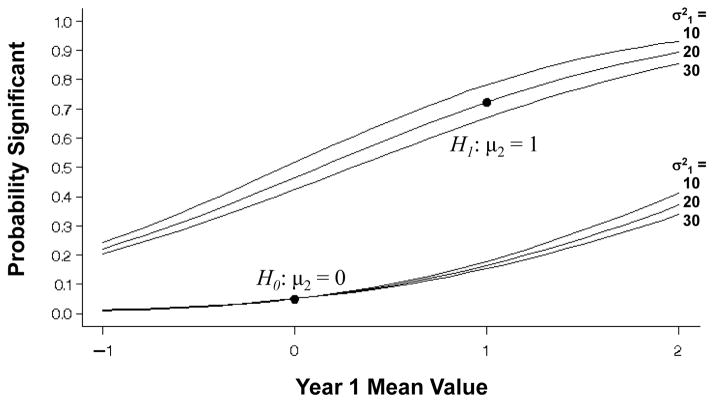
Figure 1 shows the expected mean value of the observed/imputed values (μ̃₂) under the null and alternative hypotheses (μ₂ = 0, μ₂ = 1, respectively) over a range of mean values at 1-year (μ₁) and variances ${\sigma }_1^2=(10,20,30)$. From (1), the expectation at 2-years (μ̃₂) is a simple linear function of the mean value at 1-year (μ₁). Figure 2 displays the variance of the observed/imputed values ( ${\stackrel{\sim }{\sigma }}_2^2$) under the null and alternative hypotheses for 1-year variances ${\sigma }_1^2=(10,20,30)$ and 2-year variance ${\sigma }_2^2=20$ over the range of 1-year mean values. While the variance expression (A.1) is also a function of the mean values, the Figure shows that the variance of X̃₂ is principally a function of the variance of the 1-year values used for the imputation. Figure 3 then shows the probability that a one-sample test of the observed/imputed values at 2-years would be statistically significant (nominally) under the null and alternative hypotheses (lower and upper curves, respectively) as a function of the mean and variance of the 1-year values. Under the null and alternative hypotheses, differences in the variances have little effect on the bias introduced by LOCF.

Figure 1.

Expected mean change from baseline (μ̃₂) in a one-sample analysis at 2-years from equation (1) under the null and the alternative hypotheses (μ₂ = 0 or 1, respectively), for a single sample of n = 100 with 30% missing that are replaced by values at 1-year with mean μ₁ ranging from −1 to 2. The correct values with no missing data are designated by the dots.

Figure 2.

Expected variance of the change from baseline ( ${\stackrel{\sim }{\sigma }}_2^2$) in a one-sample analysis at 2-years from equation (A.1) under the null and the alternative hypotheses (μ₂ = 0 or 1 designated by solid and dashed lines, respectively), for a single sample of n = 100 with 30% missing that are replaced by values at 1-year with mean μ₁ ranging from −1 to 2. Computations assume that the true variance at 2-years is ${\sigma }_2^2=20$ and the variance of the values at 1-year is ${\sigma }_1^2=10$, 20, or 30. The correct variances with no missing data are designated by the dots.

Figure 3.

One-sided probabilities of significance for a one-sample test of the change from baseline at 2-years under the null and the alternative hypotheses (μ₂ = 0 or 1, respectively), with variance ${\sigma }_2^2=20$, for a single sample of n = 100 with 30% missing that are replaced by values at 1-year with mean μ₁ ranging from −1 to 2 and variance ${\sigma }_1^2=10$, 20, 30. The correct probabilities with no missing data are designated by the dots.

Under the null hypothesis μ₂ = 0, LOCF imputation only yields an unbiased result when the mean value at 1-year (μ₁) is also zero (and the variances equal), in which case the probability of a falsely significant result (α) is the desired 0.05 (one-sided). If μ₁ < 0 then α decreases, and if μ₁ > 0 then α increases, possibly substantially.

Under the alternative hypothesis that there truly is a positive change from baseline at 2-years (μ₂ = 1, the upper set of curves), LOCF yields an unbiased result only when the mean value at 1-year (μ₁) is also 1 (and the variances equal), in which case the probability of a significant result equals the power of the initial study design (0.723, indicated by the dot). LOCF introduces a negative bias when there is a lesser effect at 1-year than at 2-years (μ₁ < 1), and a positive bias when if there is a greater effect (μ₁ > 1), so that the expected mean difference at 2-years is an under- or overestimate, respectively, of the true change, and the probability of a significant result is less or greater than that provided by the original design.

Non-randomly missing data

Non-randomly missing data occur when the likelihood that a given datum may be missing, and the true but unobserved value depends on other information (data) that may not have been observed, including the missing X₂ value itself. In this case, the properties of an analysis of the simple change from baseline are more complicated to assess and describe. In terms of the above example, under the alternative hypothesis the true mean value of μ₂ = 1.0 would apply to the 70% observed values, but yet some other mean would apply to those non-randomly missing, say ${\mu }_2^{\ast }$, because the τn missing observations are not a random subset of the true X₂ values. Likewise, owing to the correlation of the 1 and 2-year values, the subset of 1-year values used for imputation are a non-random subset of the X₁ values with some unknown mean ${\mu }_1^{\ast }$. Then from the above equation, the mean of the observed/imputed values becomes

$$E({\stackrel{\sim }{X}}_2)={\stackrel{\sim }{\mu }}_2=\tau {\mu }_1^{\ast }+(1-\tau ){\mu }_2^{\ast }.$$ (3)

Even when the true 1-year values have the same mean as the true 2-year values (μ₁ = μ₂ = 1) then μ̃₂ ≠ 1 and the study results are biased.

Two Sample Biases

The most common application of LOCF is to the comparison of two or more groups at a given point in time, such as at 2-years herein. Again consider the simplest case where the 2-year missing values are missing completely at random within the two groups labeled as A and B. We also assume that the fraction missing (τ) is the same in the two groups. The values in the ith group at the jth time are then distributed with mean values μ_ij and variances ${\sigma }_{ij}^2$, with mean difference at the jth time Δ_j = μ_aj − μ_bj, i = a, b, j = 1, 2.

Then after LOCF imputation, the observed/imputed values within each group have means

$$\begin{array}{lll}E({\stackrel{\sim }{X}}_{a2})\hfill & =\hfill & {\stackrel{\sim }{\mu }}_{a2}=\tau {\mu }_{a1}+(1-\tau ){\mu }_{a2}\hfill \\ E({\stackrel{\sim }{X}}_{b2})\hfill & =\hfill & {\stackrel{\sim }{\mu }}_{b2}=\tau {\mu }_{b1}+(1-\tau ){\mu }_{b2}.\hfill \end{array}$$ (4)

Denote the sample mean difference between the two groups in the observed/imputed values as D̃₂ with expectation

$${\stackrel{\sim }{\mathrm{\Delta }}}_2=E({\stackrel{\sim }{D}}_2)={\stackrel{\sim }{\mu }}_{a2}-{\stackrel{\sim }{\mu }}_{b2}=\tau {\mathrm{\Delta }}_1+(1-\tau ){\mathrm{\Delta }}_2$$ (5)

s a function of the mean differences (Δ₁, Δ₂) between the groups at 1 and 2-years, respectively. The Appendix also presents the expression for the variance of the mean difference, say V (D̃₂). A test of the null hypothesis of no difference between groups H₀: Δ₂ = 0 is then provided by the Z-test with value z̃ equal to the sample mean difference D̃₂ relative to it SE. The probability of a significant result is then provided by

$$P(\stackrel{\sim }{z}\ge Z_{1-\alpha /2})=1-\mathrm{\Phi }\left[Z_{1-\alpha /2}-\frac{{\stackrel{\sim }{\mathrm{\Delta }}}_2}{V{({\stackrel{\sim }{D}}_2)}^{1/2}}\right]$$ (6)

For illustration, assume a common variance ( ${\sigma }_{ij}^2={\sigma }^2$) among the values at 1 and 2-years within the two groups, so that the expected difference between groups at 2-years, and the probability of a significant result, depend principally on the expected differences among the observed values at years 1 and 2, the Δ₁ and Δ₂. Sample computations are presented in Table 2 with similar results to those shown in Table 1.

Table 2.

The expected mean difference (Δ̃₂) between two independent groups A and B of the observed/imputed values at 2-years, the expected variance of the group difference (V(D̃₂)), and the probability that a two-group test of H₀: Δ₂ = 0 would be nominally statistically significant at the 0.05 level one-sided, for given means of the 1 and 2-year values, assuming σ² = 20 at each time in both groups, with a sample size of n = 200 per group, 30% of which are missing completely at random at 2-years and are replaced by the values at 1-year. Cases 2 and 7 also provide the type I error probability and power with no missing data.

Case	μa2	mub2	Δ2	μa1	μb1	Δ1	Δ̃2	V(D̃2)	Pr(significant)
1	1	1	0	1	2	−1	−0.3	0.20105	0.01034
2	1	1	0	1	1	0	0.0	0.20000	0.050
3	1	1	0	1	0	1	0.3	0.20105	0.165
4	1	1	0	1	−1	2	0.6	0.20420	0.376
5	1	0	1	1	2	−1	0.4	0.20420	0.224
6	1	0	1	1	1	0	0.7	0.20105	0.467
7	1	0	1	1	0	1	1.0	0.20000	0.723
8	1	0	1	1	−1	2	1.3	0.20105	0.896

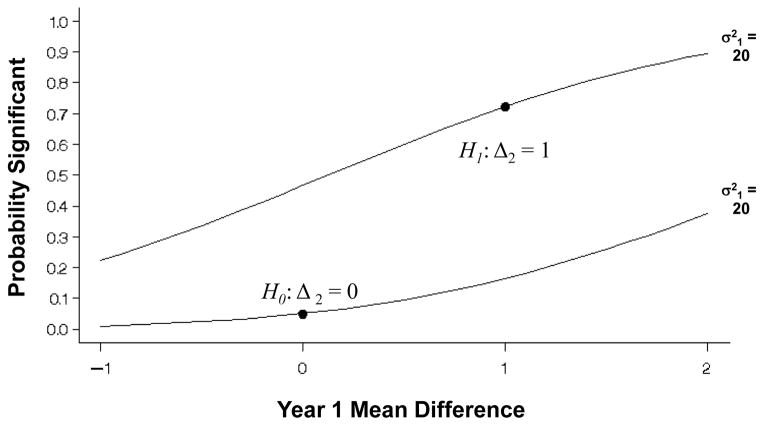
Figure 4 presents the probability of a statistically significant test (z̃) based on the values for Δ₁ and Δ₂ assuming that n = 200 in each group and σ² = 20. As was the case for a single sample, under the null hypothesis Δ₂ = 0, then the analysis of the observed/imputed values is unbiased if Δ₁ = 0 as well. Under the alternative hypothesis of a non-zero mean difference at 2-years (Δ₂ = δ ≠ 0), then the analysis of the observed/imputed values is unbiased when the mean difference at 1-year equals that at 2-years (Δ₁ = δ ≠ 0). Otherwise, the analysis based on the observed/imputed values at 2-years is positively biased E(D̃₂) > Δ₂ when Δ₁ > δ and negatively biased when Δ₁ < δ. Again, since the true mean differences Δ₁ and Δ₂ are unknown, all analyses using LOCF are suspect.

Figure 4.

One-sided probabilities of significance for a test of the difference between two groups A and B at 2-years with mean Δ₂ = μ_a2 − μ_b2 under the null and the alternative hypotheses (Δ₂ = 0 or 1, respectively), for n = 200 per group with 30% missing that are replaced by values at 1-year with mean difference Δ₁ = μ_a1 − μ_b1 ranging from −1 to 2 and variance σ² = 20 within each group at both times. The correct probabilities with no missing data are designated by the dots.

Note that when the difference between the two groups equals the change within a single group (μ₂ = Δ₂), and the variance is the same, then the probability of significance with 2n per group is the same as that for a single group of size n. Thus, the power to detect a difference of 1 in this case also equals 0.723.

Longitudinal Analyses

Now consider that a more general longitudinal mixed model is used to compare the overall group difference in the 1 and 2-year values combined (e.g. LSMEANS), possibly adjusted for a time effect (1 versus 2-years) and the baseline value, taking into account the intercorrelation among the repeated measures. The covariance structure then has three components, the variance of the values at 1 and 2-years ( ${\sigma }_1^2,{\sigma }_2^2$) and the covariance σ₁₂. If some of the X₂ measures are missing and are imputed using 1-year values, then the covariance will be inflated.

The reason is simple. For τ = 0.3, the 70% of subjects with observed 2-year values have correlation ρ₁₂ between the 1 and 2-year values, but the 30% with imputed values have correlation 1.0 since each imputed value at 2-years has exactly the same value as that subject’s 1-year value. Thus, the correlation between the observed/imputed 2-year values and the observed 1-year values is inflated. See the Appendix.

In a repeated measures analysis, the higher the intercorrelaton among the longitudinal measures, the less the total information provided. Thus the inflation in the observed/imputed correlation reduces the information in the data and reduces power.

It should also be noted that LOCF is a form of “single-point imputation” in which the “estimate” of the expected value of the missing value is imputed, but without consideration of the conditional variance. Even if the conditional estimate is unbiased, such methods generally underestimate the overall variance and lead to inflation in the type I error probability.

Discussion

The origins of last observation carried forward are obscure. It was perhaps first used in analyses submitted to the FDA, and the method quickly became pervasive. However, there has not been, to this author’s knowledge, a single refereed statistical publication demonstrating that the method is in general valid (unbiased). Rather, numerous papers have shown, mostly by statistical simulation, that the method can be biased.

Herein, I use a simple mixture model to show that the analysis of the means of a mixture of observed and imputed missing data using LOCF is biased. The only condition where LOCF is unbiased is when the missing data occurs completely by chance and the data used as the basis for the LOCF imputation has exactly the same distribution as does the unknown missing data. Since it can never be proven that these distributions are exactly the same, all LOCF analyses are suspect and should be dismissed.

In some applications LOCF is described as conservative or a “worst case” analysis, such as when patients tend to improve over time so that the 1-year values, and the imputed 2-year values, tend to be worse than the true (but missing) 2-year values. However, the bias introduced by LOCF is a function of the difference between two groups at 1-year, not just the individual group mean values at 1-year. Even though the values at 1-year tend to be worse, the mean difference at 1-year will likely be different from the true difference at 2-years, leading to a biased estimate of the treatment effect at 2-years.

LOCF is commonly applied in studies of new drugs to treat type 2 diabetes. Per FDA guidance,¹⁰ the sponsor must show that the new drug can lower blood glucose levels, as measured by HbA1c %, over a period of 6 to 12 months versus placebo. Typically, the placebo group HbA1c rises slowly whereas the treated group HbA1c decreases substantially (improves) at 3 months but then worsens (increases) over time.^11,12 Many studies also include a provision to terminate therapy if the HbA1c rises. While this may lead to missing data in both groups, the potential bias is clearly greater in the active group since LOCF replaces the missing data with earlier values that tend to be lower (better) than the true missing values, thus overstating the benefits of the treatment.

Unfortunately, many FDA guidances explicitly recommend that submissions use LOCF to address missing data. Further, numerous articles are published every year that claim an effect based on LOCF analyses, all of which are likely biased to some degree. Regulatory agencies and journal editors (and reviewers) should be critical of any study with a substantial fraction of missing data, and should be highly skeptical of the veracity of any results and pursuant claims based on LOCF analyses.

The NRC report,² commissioned by the FDA, describes other approaches to deal with missing data that can provide a less biased assessment of outcomes. However, all such methods require assumptions about the properties of the missing data that are inherently untestable. Accordingly, the NRC report stresses the importance of avoiding missing data to the extent possible. To this end, Lachin¹³ describes the “intention to treat design” in which the complete follow-up of all subjects is encouraged.

In summary, the well-known statistical properties of the mixture of two distributions are employed to demonstrate that LOCF analyses can introduce a positive or negative bias that can grossly inflate or deflate, respectively, the probability of a statistically significant test result under either the null or alternative hypothesis. Accordingly, without exception, all analyses using LOCF are suspect and should be dismissed. Statistically, last observation carried forward is specious (def: appearing to be true but actually false).

Appendix

A. Variance of Observed/Imputed Values Under LOCF

For a single sample, the variance of the combination of observed plus imputed (LOCF) values at time 2 is provided by

$$V({\stackrel{\sim }{X}}_2)={\stackrel{\sim }{\sigma }}_2^2=\tau [{({\mu }_1-{\stackrel{\sim }{\mu }}_2)}^2+{\sigma }_1^2]+(1-\tau )[{({\mu }_2-{\stackrel{\sim }{\mu }}_2)}^2+{\sigma }_2^2]$$ (A.1)

and the variance of the mean of the observed/imputed values is provided by $V\left({\stackrel{\sim }{\overline{X}}}_2\right)={\stackrel{\sim }{\sigma }}_2^2/n$. Note that this variance does not depend on the correlation of the X₁ and missing X₂ values because under the missing completely at random assumption, the LOCF-imputed values are obtained by sampling from the marginal distribution of X₁. Thus the resulting X̃₂ values are a mixture of values from two distributions, rather than a linear combination.

For the case of two independent groups of observed/imputed values, the variances of the observed/imputed values within each group are

$$\begin{array}{l}V({\stackrel{\sim }{X}}_{a2})={\stackrel{\sim }{\sigma }}_{a2}^2=\tau [{({\mu }_{a1}-{\stackrel{\sim }{\mu }}_{a2})}^2+{\sigma }_{a1}^2]+(1-\tau )[{({\mu }_{a2}-{\stackrel{\sim }{\mu }}_{a2})}^2+{\sigma }_{a2}^2]\\ V({\stackrel{\sim }{X}}_{b2})={\stackrel{\sim }{\sigma }}_{b2}^2=\tau [{({\mu }_{b1}-{\stackrel{\sim }{\mu }}_{b2})}^2+{\sigma }_{b1}^2]+(1-\tau )[{({\mu }_{b2}-{\stackrel{\sim }{\mu }}_{b2})}^2+{\sigma }_{b2}^2].\end{array}$$

and the variance of the mean difference with sample size n per group is

$$V({\stackrel{\sim }{D}}_2)=\frac{V({\stackrel{\sim }{X}}_{a2})}{n}+\frac{V({\stackrel{\sim }{X}}_{b2})}{n}.$$ (A.3)

The above model, and the computations presented herein, assume that the fraction missing (τ) is pre-specified or fixed. In practice, however, this fraction could be the expectation of a Bernoulli random variable Y to denote missing versus not, again assuming missing completely at random, so that Y is jointly independent of X₁ and X₂. In this case it follows that E(X̃₂) remains as presented in (2). Decomposing V(X̃₂) = E [V(X̃₂|Y)] + V [E (X̃₂|Y)] yields the same expression as (A.1).

B. Correlation of Measures Under LOCF

Under LOCF the covariance of the observed values at year 1 and the observed/imputed values at year 2 is

$$\begin{array}{l}\mathit{Cov}(X_1,{\stackrel{\sim }{X}}_2)={\stackrel{\sim }{\sigma }}_{12}=(1-\tau )\mathit{Cov}(X_1,X_2)+\tau \mathit{Var}(X_1)\\ =(1-\tau ){\sigma }_{12}+\tau {\sigma }_1^2\end{array}$$ (A.4)

Since ${\sigma }_{12}\le {\sigma }_1{\sigma }_2\cong {\sigma }_1^2$ then

$${\stackrel{\sim }{\sigma }}_{12}\ge (1-\tau ){\sigma }_1{\sigma }_2+\tau {\sigma }_1^2\cong {\sigma }_1^2\ge {\sigma }_{12}.$$ (A.5)

Then the correlation is

$${\stackrel{\sim }{\rho }}_{12}=\frac{{\stackrel{\sim }{\sigma }}_{12}}{{\sigma }_1{\stackrel{\sim }{\sigma }}_2}\ge \frac{{\sigma }_{12}}{{\sigma }_1{\stackrel{\sim }{\sigma }}_2}.$$ (A.6)

Since ${\stackrel{\sim }{\sigma }}_2^2\cong {\sigma }_2^2$ when ${\sigma }_1^2\cong {\sigma }_2^2$, then except for highly irregular situations, ρ̃₁₂ ≥ ρ₁₂.