Semiempirical Quantum-Chemical Orthogonalization-Corrected Methods: Theory, Implementation, and Parameters

Abstract

Semiempirical orthogonalization-corrected methods (OM1, OM2, and OM3) go beyond the standard MNDO model by explicitly including additional interactions into the Fock matrix in an approximate manner (Pauli repulsion, penetration effects, and core–valence interactions), which yields systematic improvements both for ground-state and excited-state properties. In this Article, we describe the underlying theoretical formalism of the OMx methods and their implementation in full detail, and we report all relevant OMx parameters for hydrogen, carbon, nitrogen, oxygen, and fluorine. For a standard set of mostly organic molecules commonly used in semiempirical method development, the OMx results are found to be superior to those from standard MNDO-type methods. Parametrized Grimme-type dispersion corrections can be added to OM2 and OM3 energies to provide a realistic treatment of noncovalent interaction energies, as demonstrated for the complexes in the S22 and S66×8 test sets.

1. Introduction

Over the past decades, semiempirical quantum-chemical (SQC) methods have been widely used in computational chemistry to study molecular structure, stability, spectroscopy, and reactivity.¹ They are computationally much less demanding than ab initio or density functional theory (DFT) methods and can therefore be applied to investigate huge molecules or large sets of molecules and to perform large-scale molecular dynamics simulations, also in the context of quantum mechanics/molecular mechanics (QM/MM) approaches.^1,2

Formally, SQC methods are simplified molecular orbital (MO) treatments. Compared with ab initio MO methods, their computational speed comes from the neglect of many small (mostly two-electron) integrals. To compensate for the associated errors, the remaining integrals are usually represented by functions containing parameters, which are then fitted against experimental or high-level theoretical data to achieve a reasonable compromise between computational speed and accuracy.^1,3,4 Many recent benchmark studies actually show that the accuracy of modern SQC methods may approach or sometimes even exceed that of standard DFT methods, especially for ground-state properties of organic molecules,³⁻¹⁰ despite the fact that for many years method development has been much less intense in the SQC field than in the ab initio and DFT realm.¹¹

Most established modern SQC methods make use of the NDDO (neglect of diatomic differential overlap) integral approximation and are based on the general-purpose MNDO (modified neglect of diatomic overlap) model introduced in 1977.^12,13 Since then, there have been many refinements aimed at enhancing the accuracy and the application range of the original MNDO method,^1,3 for example by increasing the size and quality of the training data during parametrization, by modifying the empirical core repulsion function, and by extending the basis set from sp to spd. The resulting MNDO-type methods include the following SQC treatments (standard acronyms, in parentheses year of publication): AM1¹⁴ (1985), PM3^15,16 (1989), MNDO/d¹⁷⁻¹⁹ (1992), PDDG/MNDO and PDDG/PM3^20,21 (2002), AM1*²² (2003), RM1²³ (2006), PM6⁵ (2007), and PM7⁴ (2013). To enable the treatment of solid-state systems, PM7 uses modified parametric expressions for the electrostatic interactions.⁴ For the latest PMx methods, parameters are available for most elements in the Periodic Table.^4,5

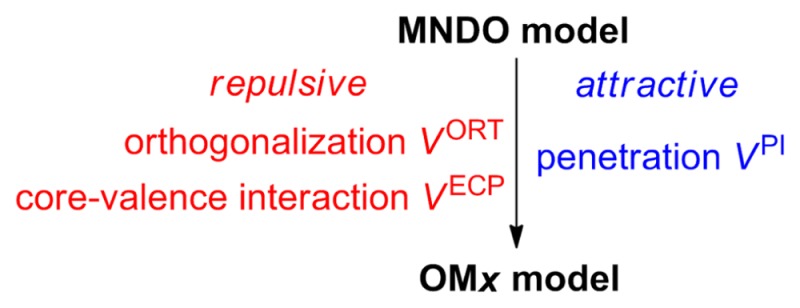
Another line of SQC development at the NDDO level goes beyond the MNDO model by including explicit orthogonalization corrections into the one-electron terms of the Fock matrix.¹ This gives rise to a series of orthogonalization-corrected methods (OMx): OM1^24,25 (1991–1993), OM2^26,27 (1996–2000), and OM3²⁸ (2003). They differ in the extent to which these corrections are applied to the core Hamiltonian part of the Fock matrix (see section 2.2). The orthogonalization terms represent Pauli repulsions, which are formally missing in the Fock matrix of MNDO-type methods where they are mimicked by the empirical repulsive terms in the core repulsion function.^1,29 Their explicit inclusion in the OMx methods overcomes some characteristic shortcomings of MNDO-type methods. For example, it offers significant improvements in the description of conformational properties, hydrogen bonds, and transition states, and it leads to a qualitatively correct asymmetric splitting of bonding and antibonding orbitals (as opposed to the symmetric splitting in MNDO-type methods).¹ Statistical evaluations in benchmark studies show that OMx methods are overall more accurate than MNDO-type methods both for ground-state and excited-state properties.^6,30 However, OMx parameters are currently only available for the elements H, C, N, O, and F, which limits their applicability. The benefits of an explicit SQC treatment of orthogonalization have also been demonstrated in an independent proof-of-principle study at the MNDO level (NO-MNDO method, 2006).³¹

Many recent applications of OMx methods focus on electronically excited states of organic molecules and their dynamics. For the exploration of excited-state potential energy surfaces the OMx methods are clearly superior to standard MNDO-type approaches;³⁰ the semiempirical INDO/S method is adequate only for vertical transitions;³² time-dependent density functional theory (TD-DFT) has well-known limitations for charge-transfer states and for states of multireference character;^33,34 and accurate correlated ab initio approaches are often too costly for larger systems. To account for static correlation effects, OMx studies of excited states employ a multireference configuration interaction (MRCI) treatment,³⁵ with a properly chosen, relatively small active space and with an efficient implementation of (semi)analytic derivatives.^36,37 To quote a few examples, OMx/MRCI excited-state dynamics simulations using surface hopping³⁸ have been reported for azobenzenes^39,40 and other photoswitches,⁴¹⁻⁴³ for a molecular rotary motor,⁴⁴ for a variant of the GFP chromophore,⁴⁵ for DNA bases in different environments,⁴⁶⁻⁵² and for the mechanism of the photoinduced ultrafast Wolff rearrangement.⁵³ Regardless of these successful excited-state studies, we will focus in the remainder of this Article on the OMx performance for ground-state properties, since comprehensive excited-state validations have been presented elsewhere.³⁰

Dispersion interactions play an important role in many parts of chemistry and biochemistry, for example in molecular recognition and noncovalent complex formation.⁵⁴ Dispersion can be treated adequately by correlated ab initio methods but is formally not included in single-determinant MO approaches (at the ab initio, standard DFT, and SQC levels). In recent years, there have been many efforts to remedy this deficiency, especially by the development of simple empirical dispersion corrections, as exemplified by the work of Grimme on DFT methods.⁵⁵⁻⁵⁸

Such corrections have also been applied to various SQC approaches, sometimes combined with further empirical corrections for other types of noncovalent interactions such as hydrogen bonding, which are often described not too well by standard SQC methods.³ General-purpose dispersion-corrected SQC methods include treatments labeled AM1-D and PM3-D;⁵⁹ PM6-DH;⁶⁰ AM1, PM6, and OM3 augmented with DH2 corrections;⁶¹ AM1, PM6, and OM3 augmented with DH+ corrections;⁶² AM1, RM1, PM6, and OM3 with D3H4 corrections;⁶³ PM6-D3H;⁶⁴ PM7;⁴ and PM6-D3H+;⁶⁵ as well as OM2-D3 and OM3-D3¹⁰ (for a recent review see ref (66)). In most of these approaches,⁶⁶ the parameters of the core SQC methods were kept fixed, and only the correction terms were parametrized. A notable exception is the recently proposed PM7 method, for which a full parametrization was performed (with dispersion and all other corrections included simultaneously).⁴

In our own initial work in this area, we augmented the OMx methods with partially reoptimized Grimme dispersion corrections (without changing any of the basic OMx parameters) and showed that this gave much improved results for noncovalent complexes and allowed for realistic QM and QM/MM calculations on the binding between antibody 34E4 and a hapten.⁶⁷ At a later stage, we reoptimized the Grimme DFT-D2 corrections more carefully for OM2 and OM3 using larger training sets;⁶⁸ in the following, the resulting treatments are denoted as OM2-D2 and OM3-D2, respectively. The D3(BJ) dispersion corrections were recently parametrized by the Grimme group for OM2 and OM3.¹⁰ These OM2-D3 and OM3-D3 treatments appear to perform similarly well as many of the computationally more expensive dispersion-corrected DFT approaches.¹⁰

It is obvious from the preceding literature survey that the OMx methods have been available and in use for some time. However, in the case of the more advanced OM2 and OM3 methods, the formalism and the parameters have been fully described only in two Ph.D. theses.^26,28 The main purpose of this Article is to document the underlying methodology, the implementation, and the optimized parameters of the OMx methods in full detail to make them more easily accessible. In addition, we present and discuss the dispersion corrections that can be used in combination with the OMx methods. In terms of validation, we provide numerical results and statistical evaluations for the test sets that have been used during the development of the OMx methods and the associated dispersion corrections. We have performed further extensive benchmarks of the OMx and OMx-Dn methods using many of the recently published validation and test sets. The corresponding results are reported in the following Article on ground-state properties including noncovalent interactions.⁶⁹

2. Methodology

2.1. Overview

The most popular semiempirical methods for studying ground-state molecular properties, e.g., AM1,¹⁴ PM3,¹⁵ PM6,⁵ PM7,⁴ and the PDDG variants,^20,21 are based on the MNDO model.¹² In matrix notation, the basic equations of this model are as follows:

1

2

3

4

5

The MOs ψ are expressed in a minimal valence basis as linear combinations of atomic orbitals ϕ (eq 1). The MO coefficients C are obtained by solving the secular equation in zero-differential-overlap (ZDO) approximation;⁷⁰F is the Fock matrix and E denotes the diagonal matrix of MO energies (eq 2). The Fock matrix is the sum of the one-electron core Hamiltonian matrix H and a two-electron part G that depends on the density matrix P (eq 3). The NDDO integral approximation is invoked in the computation of the Fock matrix, which leads to the neglect of many small integrals (e.g., all three-center and four-center two-electron integrals). The dependence of G on P necessitates an iterative self-consistent-field (SCF) solution of the secular equation, since P is determined by the coefficients C_o of the occupied MOs (eq 4, closed-shell case; superscript “T” denotes the transpose). The total energy E_tot is obtained as the sum of the converged electronic energy E_el and the core–core repulsions E_AB^core between atoms A and B (eq 5). Following semiempirical convention, the total energy of a molecule can be converted into its heat of formation by subtracting the total energies of the constituent atoms (computed at the same level) and adding the experimental heats of formation of the atoms.¹²

All of these basic features of the MNDO model are retained in the OMx methods. In addition, all one-center integrals are treated in exactly the same manner. The one-center one-electron energies are considered to be adjustable parameters that are optimized in the parametrization procedure, while the one-center two-electron integrals are derived from experimental data (atomic spectra) and kept fixed at the values used in MNDO.¹² The OMx methods differ from the MNDO model in the treatment of the two-center terms entering the core Hamiltonian and the Fock matrix.

Conceptually, the MNDO electronic structure model formally neglects the Pauli exchange repulsions, although their effects on energies may be partly retrieved in MNDO-type methods through additional core repulsion potentials and versatile parametrizations.^{4,5,14,15,20,21,71} However, intrinsic deficiencies of the MNDO-type methods are evident in many studies;^{1,24−29,72−75} e.g., the gaps between bonding and antibonding MOs and the corresponding excitation energies are significantly underestimated. The OMx methods include explicit orthogonalization corrections in the core Hamiltonian to model Pauli exchange repulsions in the electronic structure calculations.²⁴⁻²⁸ For the sake of consistency, penetration effects and core–valence interactions are also incorporated into the core Hamiltonian, and the resonance integrals are represented by a nontraditional empirical expression.²⁵

At the implementation stage, there is another major distinction. The two-center Coulomb interactions are represented as parametric functions in MNDO-type methods, while they are computed analytically at the OMx level followed by a uniform Klopman–Ohno scaling.^76,77 The Klopman–Ohno scale factor, f_KO, is chosen such that the resulting two-center two-electron integrals (s^As^A,s^Bs^B) are the same as in the MNDO model^12,78 at all distances R_AB. This ensures that the two-center two-electron integrals converge to the correct one-center limit (i.e., to the MNDO values of the one-center two-electron integrals; see earlier discussion) and that they show the correct asymptotic behavior at large distances; at intermediate distances, the Klopman–Ohno scaling will account for dynamic correlation effects in an average manner. To achieve a balanced treatment of all two-center Coulomb interactions, the Klopman–Ohno scaling is applied not only to the electron–electron repulsions but also to the core–electron attractions and core–core repulsions.

In the next two sections, we present the distinguishing features of the OMx methods and their implementation in more detail.

2.2. OMx Formalism: Core Hamiltonian

The secular equation without overlap (eq 2) is valid in the symmetrically orthogonalized Löwdin basis,^79,80 and hence the Fock matrix should correspond to such an orthogonalized basis in SQC methods. The Löwdin orthogonalization is known to affect the one-electron integrals in the Fock matrix more strongly than the two-electron integrals, and there is numerical evidence that the two-electron integrals surviving under the NDDO approximation are not too different when evaluated in the original nonorthogonal and the orthogonalized basis. In the OMx methods, we therefore decided not to modify the two-electron integrals by orthogonalization corrections.

The one-electron core Hamiltonian of the OMx methods is given by

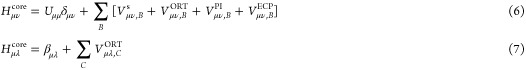where the subscripts μ and ν refer to orbitals centered at the same atom A, λ designates an orbital at a different atom B (B ≠ A), and C is an atom that is neither A nor B; δ_μν denotes the Kronecker delta. The one-electron energies U_μμ are adjustable parameters. The integrals V_μν,B^s represent semiempirical core–electron attractions (superscript “s”) expressed in terms of related two-center two-electron integrals (see later text).¹²

The most important enhancement of the OMx methods over the MNDO model is the inclusion of the valence orthogonalization corrections (V^ORT). Their introduction necessitates the incorporation of two other terms that can be of similar magnitude and exhibit a similar distance dependence: the penetration integrals (V^PI) account for differences between corresponding core–electron attractions and electron–electron repulsions, while the effective core potentials (ECPs) capture the influence of the inner core electrons (V^ECP). The sum of the repulsive orthogonalization corrections (V^ORT), the attractive penetration integrals (V^PI), and the repulsive effective core potentials (V^ECP) normally gives rise to an overall repulsive contribution to the corresponding element of the core Hamiltonian. All these terms are formally neglected in MNDO-type methods, where they are modeled by an empirical effective pair potential in the core repulsion function.

We now present explicit expressions for these terms in the OMx formalism which have been derived previously.²⁴⁻²⁷V_μν,B^ORT and V_μλ,C denote the two-center (atoms A and B) and three-center (atoms A, B, and C) orthogonalization corrections to the core Hamiltonian, respectively. They are given by

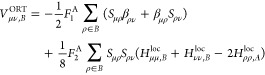8

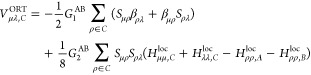9

10

11

12

where S_μρ and β_ρν are elements of the overlap matrix and of the matrix of resonance integrals (defined later), respectively. H_μμ,X^loc is an element of the local core Hamiltonian restricted to atom pair A–X;²⁴⁻²⁶ it is defined as the sum of the one-electron energy U_μμ (atom A) and the semiempirical core–electron attraction V_μν,X to the second atom X in the pair considered. To avoid rotational invariance issues, average local matrix elements are employed for the three p functions at any given atom.²⁶F and G are parameters that are used to adjust the magnitudes of the orthogonalization corrections to the one- and two-center core Hamiltonian, respectively; the subscripts 1 and 2 specify the type of these corrections, while the superscripts A and B denote the associated atoms.

The orthogonalization corrections are incorporated into the different OMx methods to a different extent. The earliest variant (OM1) only contains the corrections to the one-center terms, i.e., V_μν,B^ORT (eq 8). The OM2 method fully includes all correction terms listed previously. However, further analysis showed that the contributions from the second sum in eqs 8 and 9 are often small and of varying sign, and they normally have only a minor influence on the results, while notably increasing the computational effort for large molecules. Therefore, they are neglected in the OM3 method, i.e., F₂ ≡ 0 and G₂ ≡ 0; this is the only formal distinction between OM2 and OM3.

The penetration integrals⁸¹ are treated in the same manner in all OMx methods, as specified in the original OM1 work.²⁵ Briefly, following standard conventions, the semiempirical core–electron attractions V_μν,B^s (superscript “s”) are expressed in terms of related two-center two-electron integrals (μ^Aν^A,s^Bs^B)^s involving the ss charge distribution at atom B. The penetration integrals V_μν,B are the difference between the actual core–electron attractions (V_μν,B^s + V_μν,B) and their semiempirical values V_μν,B^s. In the OMx methods the former are obtained from the analytic core–electron attraction integrals V_μν,B (superscript “a”) by uniform scaling²⁵ with f_KO (see as follows).

13

14

where Z_B is the charge of the core of atom B.

In early semiempirical work, the attractive penetration integrals had been included while neglecting the repulsive orthogonalization corrections, which gave much too short bond lengths and much too large binding energies.^70,82 In most of the later semiempirical methods, both types of interactions were neglected on heuristic grounds,^12,82 assuming that these two terms will cancel and that any remaining effects can be taken into account through small empirical corrections and careful parametrization. The OMx methods treat these terms explicitly, with the motivation to recover electronic effects resulting from an incomplete cancelation of these terms.

In the MNDO model, the core electrons are treated as if they were incorporated into the corresponding nucleus, with a corresponding reduction of the effective nuclear charge experienced by the valence electrons (assuming complete screening); the repulsions between the inner and valence shells arising from orthogonality and exchange effects are also disregarded. By contrast, the OMx methods attempt to incorporate core–valence interactions by means of ECPs for the core electrons, in analogy to ab initio and DFT approaches.⁸³⁻⁸⁶ The ECP contributions are treated differently in the OMx variants. In OM1 the integrals V_μν,B^ECP are evaluated analytically (ab initio) and then subjected to Klopman–Ohno scaling (like all Coulomb interactions).²⁵ The OM2 and OM3 methods employ the following semiempirical ECP formulas derived previously:^26,27

15

where G_μα is an empirical function that is chosen to be of the same form^26,27 as the empirical resonance integral (see eq 17):

16

These expressions contain several adjustable parameters related to the core electrons (index α), namely, α_α, β_α, F_αα, and the core orbital exponent ζ_α needed to evaluate the core–valence overlap integrals S_μα. Extensive numerical tests indicate reasonable qualitative agreement between the ab initio and semiempirical ECPs when using properly adjusted parameters.^26,27

The explicit inclusion of orthogonalization corrections in the OMx methods implies the need for a different treatment of the resonance integrals, which has been introduced and discussed in the original OM1 work.²⁵ In MNDO-type methods, the two-center resonance integrals are taken to be proportional to the overlap integrals.^{4,5,12,14,15,71} This assumption cannot be well justified for an orthogonalized atomic basis. Therefore, on the basis of comparisons with corresponding ab initio matrix elements,^24,25 the following empirical formula is adopted for the resonance integrals in the OMx methods:²⁴⁻²⁸

17

where α^A and β^A are adjustable parameters for the various orbital types of atoms A and B. The preceding expression refers to a local diatomic coordinate system and contains an implicit phase factor.²⁵ The resonance integrals in the molecular coordinate system are obtained by standard rotational transformations.

To summarize, the most important improvement in the OMx methods is the inclusion of valence orthogonalization corrections so that the repulsive Pauli exchange effects can be taken into account in an explicit manner. Penetration integrals for the valence shell and ECPs for the core–valence interactions are also included in the OMx methods for the sake of consistency, in order to ensure a balanced overall treatment. As a further consequence, the two-center resonance integrals are represented by a different kind of empirical formula to better mimic the behavior of the corresponding ab initio matrix elements. Accordingly, the OMx methods go significantly beyond the established MNDO model by incorporating additional interactions in the electronic structure calculation.

2.3. Implementation

The OMx methods employ a minimal valence basis of contracted Gaussian functions (STO-3G for hydrogen and ECP-3G for carbon, nitrogen, oxygen, and fluorine), which has been fully documented previously.^24,25 To allow for fine-tuning, there is one adjustable parameter ζ per element that scales the exponents of all Gaussian primitives in the usual manner (multiplication by ζ²). These scale factors ζ are optimized in the parametrization of the OMx methods but are expected to remain close to 1. All analytic integral evaluations are performed with these scaled basis functions.

The elements of the one-electron core Hamiltonian matrix H are fully specified in the preceding section (see eqs 6–17). Analytic integral evaluations are performed for the valence-shell overlap integrals S_μν (see eqs 8 and 9) and the core–electron attractions V_μν,B^a (see eq 14). In OM1 the core–valence interactions V_μν,B are also evaluated analytically,²⁵ while they are represented in OM2 and OM3 by an empirical expression containing core–valence overlap integrals S_μα (see eq 15). The latter are computed analytically using standard STO-3G basis functions for the core orbitals, with adjustable scale factors ζ_α that are optimized in the parametrization of OM2 and OM3 for each element; their values are expected to be close to the optimum core orbital exponents for Slater-type orbitals.

The two-electron integrals (entering the Fock matrix via G) are treated in the same manner in all OMx methods.²⁵ The semiempirical scheme used in MNDO-type methods for evaluating the two-center two-electron integrals, in terms of a point-charge representation of multipole–multipole interactions,⁷⁸ is replaced by the analytic computation of these integrals over the contracted Gaussian valence orbitals,^24,25 followed by a uniform Klopman–Ohno scaling.^76,77

18

19

f_KO is defined such that the semiempirical two-center two-electron integrals (s^As^A,s^Bs^B)^s are the same as in the MNDO model^12,78 (as required in the one-center limit). The other two-center two-electron integrals (μ^Aν^A,λ^Bσ^B)^s will be of similar magnitude as in MNDO but will generally differ slightly. To achieve a balanced treatment of all two-center Coulomb interactions, the Klopman–Ohno scaling is applied not only to the core–electron attractions (eq 14) and electron–electron repulsions (eq 18) but also to the core–core repulsions E_AB^core between atoms A and B:

20

This completes the description of integral evaluation in the OMx methods. Some further comments seem appropriate concerning the practical implementation of the three-center orthogonalization corrections in OM2 and OM3 (eq 9). Generally speaking, all two-center integrals in the OMx methods are evaluated in a local coordinate system and are then converted to the molecular coordinate system using standard rotational transformations. This is no longer feasible for the three-center orthogonalization corrections which need to be assembled directly in the molecular coordinate system. For this purpose, the overlap matrix S and the matrix of resonance integrals β are precomputed in the molecular coordinate system, as well as the required local core Hamiltonian matrix elements of the type H_μμ,X^loc (eqs 9 and 10); the one-center matrix elements of β are defined to be zero.

For N basis functions, the computation of the three-center orthogonalization corrections (eq 9) formally scales as O(N³), which may raise some concern since all other integral evaluations in SQC methods generally scale as O(N²). However, a careful implementation that exclusively targets the nonzero contributions already allows an efficient evaluation of the three-center orthogonalization corrections (consuming only a fraction of the overall computation time).

Moreover, the contributions for a given combination of atoms (A, B, C) fall off quickly with the interatomic distances R_AC and R_BC because of the steep decline of the corresponding elements of S and β that appear in eq 9. It is thus possible to use prescreening techniques to minimize the computational effort, by utilizing the precalculated matrices S and β. Since the resonance integrals (eq 17) normally fall off faster than the corresponding overlap integrals, a conservative prescreening criterion may be based on the product of the ss overlap integrals for atom pairs A–C and B–C: for example, if this product is smaller than a user-defined cutoff τ₁ the three-center contributions for the combination (A, B, C) can be neglected entirely. This cutoff is available in our code (others can easily be envisioned) but is used only rarely for energy evaluation, in order to avoid sacrificing numerical precision for a rather small computational gain overall.

The three-center orthogonalization corrections for OM3 are formally of first order in overlap. They can be written in matrix form by expressing the first sum in eq 9 as the sum of the matrix product S̃β and its transpose;⁶⁸ the matrix S̃ is the overlap matrix with the diagonal elements set to zero.²⁵

21

22

Multiplication of X_μλ with the appropriate prefactor yields the three-center correction V_μλ,C^ORT for OM3 (eq 9). The use of optimized library routines for matrix multiplication makes this approach an extremely efficient alternative to applying cutoffs in OM3, especially when using graphics processing units (GPUs).⁶⁸

For a direct comparison of the different implementations, wall clock computing times were measured for the evaluation of the OM3 three-center corrections for seven proteins ranging in size from 1097 to 3558 atoms, using a platform with two Intel Xeon X5690 CPUs and two NVIDIA Tesla M2090 GPUs.⁶⁸ The time for the full explicit calculation on a single CPU core (no GPU) served as reference. The measured speedups ranged from 14.0 to 18.0 for the explicit calculation with the cutoff τ₁ = 10^–6, from 8.9 to 13.1 for the evaluation via matrix multiplication (eq 22) on a single CPU core (no GPU), and from 241 to 351 for the same evaluation using one CPU core and one GPU.⁶⁸

In standard MNDO-type methods, the computational effort for a full SCF energy evaluation is dominated by matrix operations that scale as O(N³) and need to be performed in each SCF iteration (diagonalization or pseudodiagonalization of the Fock matrix to solve eq 2, density matrix computation via eq 4, and possibly also DIIS extrapolation). In SCF calculations at the OMx level, the same matrix operations dominate the computational effort, even though the evaluation of the three-center orthogonalization corrections in OM2 and OM3 also scales formally as O(N³); however, this evaluation is required only once at the beginning to construct the core Hamiltonian (and not again in each SCF iteration), and it can be made very efficient as outlined previously. Actual benchmarks on fullerenes up to C₉₆₀ and on clusters up to 1200 water molecules confirm that the evaluation of the core Hamiltonian matrix takes only a minor fraction of the time for a full SCF calculation at the OMx level—less than 10% even in the worst case (largest water cluster, OM2 with full explicit calculation of the three-center orthogonalization corrections).^68,87 In these and other benchmarks, standard MNDO-type and OMx SCF calculations generally take about the same time for all systems considered,⁶⁸ simply because the dominant matrix operations are the same in both cases. Previous work achieved substantial speedups of MNDO-type calculations through shared-memory and distributed-memory message-passing parallelization of these matrix operations (and of integral evaluation and Fock matrix construction);^73−75,88 these implementations can be applied likewise at the OMx level. Finally, MNDO-type and OMx computations benefit from hybrid CPU-GPU computing in the same manner, with large speedups of comparable size.^68,87 In conclusion, MNDO-type and OMx SCF calculations on large molecules are essentially equally fast and equally facile with our current code (for further detailed timing data on large molecules, see ref (87)).

In semiempirical SCF methods, the energy expression can be differentiated analytically with respect to the nuclear coordinates.^89,90 The resulting analytic gradient expressions contain integral derivatives that can be evaluated analytically or by finite difference. In our implementation, the fully analytic approach is available for MNDO-type methods,^89,90 while the integral derivatives are computed by finite difference for the OMx methods.³⁷ In closed-shell SCF calculations with MNDO-type and OMx methods, one may also use a simple finite-difference procedure that involves computing the change in the energy at displaced geometries (with constant density matrix and recalculated values of the integrals that change upon displacement). All these finite-difference techniques are efficient at the SQC level as long as only two-center integrals need to be treated (MNDO-type methods and OM1): the computational effort then scales as O(N²), and gradient evaluation takes only a minor fraction of the time needed for calculating the energy (typically much less than 10%).

The situation becomes less favorable in the case of OM2 and OM3 because of the presence of the three-center orthogonalization corrections, which cause an O(N³) scaling of the finite-difference computation of the corresponding gradient contributions. Even when care is taken to target only the nonvanishing contributions, the computational effort increases rapidly with system size so that it becomes more costly for large systems to evaluate the gradient than the energy. In this situation, prescreening becomes essential for efficiency. In addition to the test on the ss overlap integrals described previously (cutoff τ₁), our current implementation offers a second test: the contribution of the atom triple (A, B, C) to the overall three-center orthogonalization correction is known at the reference geometry (in terms of energy), and if this is only a small fraction (less than a cutoff τ₂) the corresponding contributions to the gradient can be neglected safely.

To illustrate the effects of prescreening, we measured wall clock computing times for OM2 and OM3 calculations on our seven test proteins (1097–3558 atoms, 2699–8727 basis orbitals) on the same platform as before. Without any cutoffs, gradient evaluation was slower than energy evaluation on a single CPU typically by factors of 3–4 (2–3) for OM2 (OM3). Applying the cutoffs τ₁ = τ₂ = 10^–8 led to negligible changes in the Cartesian gradient norm (typically less than 0.02 kcal/(mol·Å)) while accelerating gradient evaluation on a single CPU by factors of 17–24 (11–16) for OM2 (OM3) so that it always took only a fraction of the time needed for energy evaluation with the same cutoffs (15–27%). On the hybrid platform with six CPU threads and two GPUs, combined energy and gradient calculations on the test proteins with the same cutoffs were faster by factors of 7–10 compared with runs on a single CPU, both for OM2 and OM3; wall clock times for the largest protein (3558 atoms) were 1530 (1280) s for OM2 (OM3).

To summarize, in our current implementation of the three-center orthogonalization corrections in OM2 and OM3, prescreening is not required for computing the energy (particularly in OM3) but strongly recommended for gradient evaluation in large systems (default cutoffs, 10^–8).

2.4. Parameters

The parameters of the OMx methods were optimized by an iterative nonlinear least-squares fitting procedure, which minimizes the sum-of-squares (SSQ) of the weighted errors for the chosen properties of reference molecules. For a given set of trial parameters, the Levenberg–Marquardt algorithm^91,92 was used to define a search vector, and a line search along this direction was performed to minimize the SSQ value and thus to determine an improved set of parameters; these steps were iterated until the SSQ value could not be lowered further. The Levenberg–Marquardt algorithm was chosen because it allows for a gradual transition from a steepest descent procedure at the beginning to a Gauss–Newton method when approaching the minimum. It requires knowledge of the Jacobi matrix containing the partial derivatives of the individual errors of the reference properties with respect to the parameters being optimized. The Jacobi matrix was computed by finite difference in the first few iterations and thereafter in regular intervals to limit the computational effort, with approximate updates in between. Further technical details on the parametrization procedure are available in the original reports.^24,26,28

The chosen parametrization algorithm provides a derivative-based method for local optimization of the parameters with respect to the SSQ value. The parameter surface of SQC methods is known to be quite rugged, and the optimization can thus converge to different local minima when starting from different initial sets of parameters. Therefore, many separate parametrization runs with different initial conditions were carried out for each of the OMx methods.^24,26,28

Following semiempirical tradition,¹² the reference properties mainly included heats of formation, geometries, ionization potentials (computed via Koopmans’ theorem), and dipole moments (computed in ZDO approximation). The weights were chosen such that the heats of formation contributed most to the overall SSQ value (followed by the geometries). For each of the OMx methods, parametrizations were first run for hydrocarbons to obtain reasonable CH parameters, which were then kept fixed in subsequent optimizations of the N and O parameters. This provided good starting sets for final simultaneous refinements of all CHNO parameters. The parameters for F were determined separately (with fixed CHNO parameters).

The scope of the CHNO parametrization of OM1 (early 1990s), OM2 (mid 1990s), and OM3 (early 2000s) can be judged from the number of reference molecules employed: OM1, 10–30 initially, 102 for the last refinement;²⁴ OM2, 35–40 typically;²⁶ and OM3, 227 at the final stage.²⁸ Most of the reference molecules were taken from the CHNO and FLUOR training sets of neutral molecules described in the next section.

For the assessment of the resulting parameter sets, test calculations were done for other types of molecules (e.g., in the case of OM3 for radicals, cations, anions, hydrogen-bonded complexes, and peptides) as well as other properties (e.g., vibrational wavenumbers, higher ionization potentials, vertical excitation energies, transition-state energies, and geometries) to compare with corresponding reference data from experiment or from accurate ab initio calculations. In some cases, this motivated the inclusion of other reference molecules into the training set.^24,26,28

To summarize, the parametrizations of the OMx methods did not follow a strictly defined protocol, but there were some common characteristic features. They employed local derivative-based optimization methods, a rather limited number (by current standards) of reference molecules, and ground-state reference properties with focus on energies (heats of formation). The parametrization runs normally yielded several parameter sets with comparable SSQ values, and hence the selection of the final parameters involved some subjective judgment taking into account also the overall performance for other molecules and properties not included in the training set. The final parameters for the OM1, OM2, and OM3 methods are listed in Tables 1–3, respectively.

Table 1. OM1 Parameters.

	H	C	N	O	F
Orbital Exponent: Scale Factor
ζ (au)	1.20948930	1.13551142	1.16081665	1.10190209	1.16498140
One-Center One-Electron Energies
Uss (eV)	–12.83851861	–50.15945000	–71.33505463	–93.04158571	–121.69518463
Upp (eV)		–38.76257345	–56.58315267	–77.59792792	–106.37310634
Resonance Integrals
βs (eV bohr–1/2)	–4.89312435	–7.58632270	–12.00586167	–6.22223757	–5.73558167
βp (eV bohr–1/2)		–4.49894163	–9.64950408	–9.94028730	–16.36168108
βπ (eV bohr–1/2)		–5.91210138	–10.16405908	–11.29342651	–17.22481680
αs (au)	0.09653898	0.09325105	0.10185884	0.10891616	0.19374572
αp (au)		0.05398748	0.08540515	0.09666556	0.13034754
απ (au)		0.10477244	0.14350678	0.15255321	0.22033729
βs(X–H) (eV bohr–1/2)			–8.08332477	–6.45960578
βp(X–H) (eV bohr–1/2)			–11.48923075	–12.47451386
αs(X–H) (au)			0.07514671	0.07953217
αp(X–H) (au)			0.11556228	0.12908958
Orthogonalization Factors
F1	0.54128873	0.50383851	0.63476395	0.68193417	1.19938976
F2	0.84668969	0.66944409	0.31135759	0.47652748	0.49484369

Table 3. OM3 Parameters.

	H	C	N	O	F
Orbital Exponent: Scale Factor
ζ (au)	1.25906452	1.27811536	1.30965521	1.20838191	1.20564838
One-Center One-Electron Energies
Uss (eV)	–12.45828647	–50.55997310	–75.98413465	–105.79319826	–120.65477058
Upp (eV)		–39.60463506	–57.38630489	–78.90502490	–107.50304443
Resonance Integrals
βs (eV bohr–1/2)	–3.40064659	–7.15007507	–13.42485887	–14.42839639	–6.19918959
βp (eV bohr–1/2)		–4.00965991	–5.69143961	–8.77114206	–13.82075048
βπ (eV bohr–1/2)		–5.63958651	–8.25767437	–12.94995697	–18.96710976
αs (au)	0.06931667	0.09197146	0.09461210	0.12962541	0.31128286
αp (au)		0.05274021	0.06941595	0.09275135	0.12448702
απ (au)		0.09864674	0.10511596	0.16086067	0.21596283
βs(X–H) (eV bohr–1/2)		–6.19914817	–11.40440049	–13.56403003	–8.06286638
βp(X–H) (eV bohr–1/2)		–4.23218526	–7.87479008	–9.42200507	–13.92380910
αs(X–H) (au)		0.10023679	0.11356707	0.14516313	0.32623663
αp(X–H) (au)		0.05492720	0.09244486	0.10981869	0.15497349
Orthogonalization Factors
F1	0.25393975	0.41151269	0.58223498	0.55266327	1.03522357
G1	0.35600772	0.10398816	0.05928617	0.06226814	0.14035077
Effective Core Potentials
ζα (au)		5.70000000	6.73673665	7.74239776	8.70367110
Fαα(eV)		–283.81699000	–380.94261410	–512.51900000	–685.41999336
βα (eV bohr–1/2)		–22.48815939	–22.78185605	–26.13251784	–10.62649349
αα (au)		0.15323932	0.15915338	0.18281098	0.00010713

Generally speaking, the parameters for a given element can be classified into five groups: the scale factor for the Gaussian-type basis functions, the one-center one-electron energies, the parameters for the resonance integrals, the coefficients for the orthogonalization corrections, and the parameters for the semiempirical ECPs in the case of OM2 and OM3.

The exponents of all Gaussian primitives in a given contracted basis were allowed to be scaled by a common factor ζ². The optimized scale factors are generally somewhat larger than 1 indicating some contraction (as also encountered in the ab initio case for the hydrogen STO-3G basis).

The one-center one-electron energies U_ss and U_pp are treated as adjustable parameters in the OMx and MNDO-type methods. Their optimized values for a given element are generally of similar magnitude in all methods.

The two-center resonance integrals are highly parametrized in the OMx methods, generally more so than in standard MNDO-type methods. The relevant parameters are distinguished by the subscripts s, p, and π assigning them to the s, p_σ, and p_π orbitals, respectively, in the local coordinate system used for evaluating the resonance integrals. For X–H bonds between a heavy atom and a hydrogen atom, the OMx formalism allows the use of separate heavy-atom parameters, i.e., β_s(X–H), β_p(X–H), α_s(X–H), and α_p(X–H), to enable some fine-tuning if this is deemed to be desirable for a given element. The various resonance parameters are interdependent to some extent, and it is therefore difficult to interpret their optimized values. Meaningful comparisons are best done by plotting the relevant resonance integrals in the local diatomic coordinate system as functions of the interatomic distance. Such plots are available and show qualitatively reasonable behavior both in the bonding region and asymptotically.^24,25,28

The functional form of the orthogonalization corrections in the OMx methods originates from formal expansions of the ab initio corrections (arising from symmetric Löwdin orthogonalization) in terms of overlap.²⁴⁻²⁸ The OMx corrections are scaled by prefactors (e.g., F₁, F₂, G₁, and G₂ in OM2) that are adjusted in the parametrization. Their optimum values are thus expected to be of the order of 1. While this holds roughly, most of these values tend to be somewhat smaller.

The parameters for the semiempirical ECPs used in OM2 and OM3 are listed in Tables 2 and 3, respectively. As expected, the optimized core orbital exponents ζ_α are in most cases reasonably close to the optimum exponent for the corresponding Slater-type core orbital (i.e., atomic number minus 0.3 to account for partial screening), and the atomic Fock matrix elements F_αα for the core orbitals represented by ECPs^26,27 adopt optimized values that are of similar magnitude as the corresponding experimental core ionization potentials. The core orbital parameters α_α and β_α entering the empirical ECP expressions are more difficult to assess; it is again best to inspect plots of all relevant ECP integrals to confirm that semiempirical and corresponding ab initio ECP integrals match reasonably well.^26,28

Table 2. OM2 Parameters.

	H	C	N	O	F
Orbital Exponent: Scale Factor
ζ (au)	1.47386481	1.42036892	1.33175233	1.55214516	1.45216726
One-Center One-Electron Energies
Uss (eV)	–12.64890000	–51.65550844	–74.37638240	–101.82723464	–120.62785370
Upp (eV)		–39.74369825	–57.60067613	–78.92823923	–107.27105397
Resonance Integrals
βs (eV bohr–1/2)	–3.41998220	–7.21406021	–10.84303446	–10.64436974	–6.25438426
βp (eV bohr–1/2)		–4.14394503	–7.62373736	–8.63610952	–13.93492471
βπ (eV bohr–1/2)		–5.97107657	–9.27936312	–9.21201190	–18.73205761
αs (au)	0.06607903	0.09045297	0.08974553	0.13062089	0.26624434
αp (au)		0.05452192	0.08759680	0.09626876	0.12261412
απ (au)		0.10204903	0.13172314	0.13071747	0.21684388
βs(X–H) (eV bohr–1/2)		–6.30164062	–9.49567107	–6.54238767	–6.25104378
βp(X–H) (eV bohr–1/2)		–4.04444703	–8.51180846	–10.11307271	–13.94492971
αs(X–H) (au)		0.09668329	0.11429048	0.11112738	0.44713918
αp(X–H) (au)		0.05283694	0.10673732	0.11891861	0.15648906
Orthogonalization Factors
F1	0.29566861	0.49949211	0.64073384	1.26450169	2.11499396
F2	1.40190659	0.72261226	0.19580808	1.14847352	1.09156321
G1	0.65271563	0.21284361	0.13946233	0.28309603	0.31704089
G2	0.90843670	0.99250289	0.84373060	0.78414131	0.02140504
Effective Core Potentials
ζα (au)		5.16802668	6.93980600	7.58579774	8.71226515
Fαα (eV)		–305.68646337	–407.39202305	–514.45812327	–685.41988599
βα (eV bohr–1/2)		–9.07185084	–9.97910210	–14.16551053	–9.17960365
αα (au)		0.16985745	0.16173024	0.34390559	0.99971548

Further details about the parametrizations for the OMx methods can be found in the original reports.^24,26,28

2.5. Validation

Here we provide a brief assessment of the accuracy of the OMx methods for the standard sets of reference molecules and reference properties used most regularly for parametrization (see preceding discussion). These sets are fully specified in the Supporting Information (Tables S1–S6). The standard CHNO set consists of 140 molecules containing only hydrogen, carbon, nitrogen, and/or oxygen; it is similar to the set used in the original MNDO development in the 1970s.^12,13 The standard FLUOR set comprises 48 fluorine-containing molecules. Both standard sets include only ground-state reference properties, mainly heats of formation, geometry data (bond lengths, bond angles, and dihedral angles), first ionization potentials, and dipole moments.^7,24−28,93

Detailed numerical results for all reference molecules and reference properties are documented in the Supporting Information (Tables S1–S6) for some of the established MNDO-type methods (MNDO, AM1, PM3, PM6, and PM7) and for the OMx methods (OM1, OM2, and OM3). A statistical evaluation of these results is given in Tables 4 and 5 for the CHNO and FLUOR sets, respectively. These tables provide mean absolute errors for the entire set and for chemically defined element-specific subsets.

Table 4. Mean Absolute Errors in Calculated Heats of Formation, Relative Energies and Barriers (kcal/mol), Bond Lengths (Å), Bond Angles (deg), Ionization Potentials (eV), and Dipole Moments (D) for the CHNO Set and Its Subsets: MNDO, AM1, PMx, and OMx.

		method
subset	N	MNDO	AM1	PM3	PM6	PM7	OM1	OM2	OM3
Heats of Formation
overall	140	6.34	5.51	4.17	4.80	3.80	3.46	3.10	3.05
CH	57	5.90	4.89	3.63	4.74	3.50	2.49	1.72	1.63
CHN	32	6.24	4.65	5.02	4.30	4.11	4.27	3.92	3.80
CHO	39	4.80	5.54	3.69	4.53	3.42	3.41	4.53	4.20
CHNO	4	13.52	8.36	3.00	2.59	1.48	6.18	1.96	3.24
HNO	8	13.73	11.93	7.54	9.63	7.71	5.94	3.28	4.53
Bond Lengths
overall	242	0.014	0.017	0.011	0.012	0.011	0.012	0.016	0.019
CH	113	0.011	0.013	0.011	0.009	0.009	0.012	0.010	0.009
CHN	49	0.011	0.015	0.010	0.010	0.009	0.009	0.015	0.027
CHO	57	0.017	0.019	0.011	0.013	0.011	0.013	0.018	0.022
CHNO	5	0.015	0.017	0.016	0.011	0.010	0.013	0.018	0.033
HNO	18	0.036	0.038	0.016	0.036	0.036	0.019	0.049	0.043
Bond Angles
overall	101	2.56	1.90	2.08	2.14	2.31	1.82	2.24	1.85
CH	38	1.81	1.36	1.57	1.64	1.88	1.45	1.46	1.23
CHN	22	2.03	1.86	2.04	1.86	2.04	1.85	2.30	1.82
CHO	31	3.11	2.17	2.43	2.38	2.69	1.95	2.45	2.03
HNO	10	4.83	3.17	3.04	3.91	3.30	2.76	4.42	3.76
Ionization Potentials
overall	52	0.46	0.36	0.42	0.45	0.42	0.32	0.26	0.44
CH	22	0.38	0.27	0.34	0.31	0.37	0.24	0.24	0.37
CHN	13	0.54	0.37	0.52	0.53	0.52	0.33	0.22	0.39
CHO	14	0.57	0.45	0.51	0.48	0.41	0.41	0.34	0.61
HNO	3	0.24	0.52	0.16	0.96	0.52	0.33	0.23	0.45
Dipole Moments
overall	63	0.36	0.24	0.28	0.38	0.38	0.23	0.25	0.26
CH	20	0.30	0.16	0.16	0.24	0.24	0.08	0.11	0.10
CHN	16	0.54	0.48	0.39	0.54	0.54	0.40	0.27	0.33
CHO	19	0.22	0.10	0.25	0.39	0.33	0.23	0.31	0.26
HNO	6	0.40	0.32	0.31	0.38	0.56	0.31	0.49	0.58
Relative Energies
overall	17	9.01	5.70	4.17	2.97	1.97	5.25	1.96	2.83
CH	9	4.34	2.62	1.83	1.19	1.39	3.20	0.52	1.08
CHN	3	9.48	7.37	4.71	2.91	2.17	6.04	4.09	5.65
CHO	3	13.22	7.78	9.30	4.17	3.41	6.63	3.63	3.91
Barriers
overall	60	3.48	2.12	3.01	2.55	2.46	2.31	1.63	1.61
CH	20	4.27	3.31	3.25	3.65	3.32	2.37	1.69	2.01
CHN	10	3.20	1.32	3.17	3.39	3.17	3.03	1.91	1.51
CHO	25	2.42	1.42	2.07	1.46	1.56	1.61	1.50	1.45
CHNO	3	7.98	3.16	7.70	2.35	2.46	5.42	1.43	0.68

Table 5. Mean Absolute Errors in Calculated Heats of Formation (kcal/mol), Bond Lengths (Å), Bond Angles (deg), Ionization Potentials (eV), and Dipole Moments (D) for the FLUOR Set and Its Subsets: MNDO, AM1, PMx, and OMx.

		method
subset	N	MNDO	AM1	PM3	PM6	PM7	OM1	OM2	OM3
Heats of Formation
overall	48	10.81	7.75	5.87	5.21	5.82	4.92	3.41	3.70
CHF	39	9.89	7.37	4.96	4.92	5.57	3.67	3.72	3.88
HNOF	9	14.79	9.42	9.81	6.48	6.90	10.32	2.08	2.93
Bond Lengths
overall	125	0.037	0.028	0.022	0.016	0.017	0.020	0.023	0.024
CHF	104	0.030	0.026	0.020	0.014	0.015	0.018	0.019	0.021
CHNOF	3	0.029	0.052	0.021	0.013	0.017	0.024	0.020	0.014
HNOF	17	0.080	0.037	0.037	0.026	0.026	0.032	0.043	0.044
Bond Angles
overall	69	3.00	3.16	2.75	2.76	2.55	1.97	2.23	1.78
CHF	56	2.59	2.93	2.69	2.64	2.45	1.88	2.06	1.61
CHNOF	3	2.89	3.76	3.41	3.76	2.61	1.30	2.44	1.75
HNOF	9	5.56	4.59	3.05	3.50	3.37	2.43	2.91	2.68
Ionization Potentials
overall	39	0.34	0.53	0.39	0.50	0.46	0.23	0.26	0.32
CHF	29	0.33	0.47	0.32	0.36	0.40	0.20	0.25	0.29
HNOF	9	0.38	0.70	0.57	1.00	0.68	0.30	0.29	0.42
Dipole Moments
overall	39	0.38	0.31	0.29	0.33	0.29	0.27	0.31	0.25
CHF	30	0.41	0.29	0.25	0.31	0.26	0.31	0.33	0.24
HNOF	8	0.29	0.44	0.47	0.42	0.41	0.15	0.26	0.29

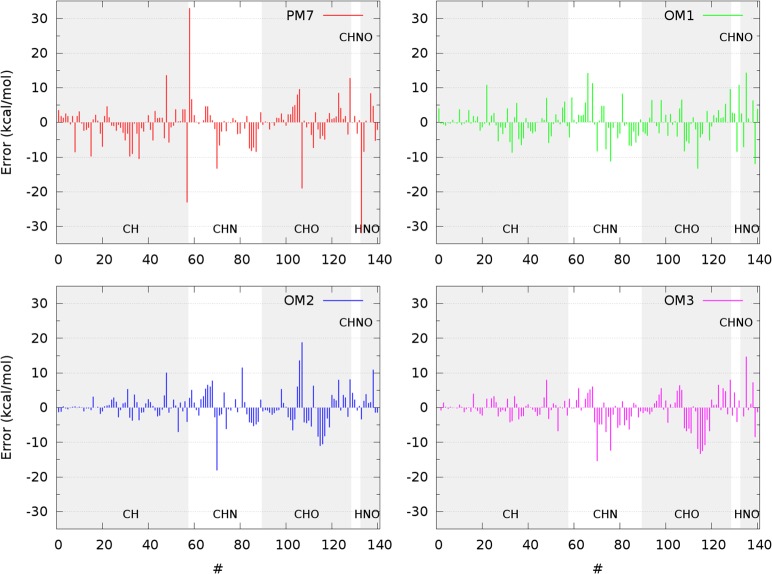
The statistical evaluations suggest the following overall assessment. For the calculated heats of formation, the mean absolute errors (MAEs) are lowest overall for the OMx methods; the most recent MNDO-type method PM7 that has been fitted on a much larger data set is closest in accuracy to the OMx methods, but it has larger outliers (see Figure 1, Supporting Information Tables S1 and S5). Bond lengths and bond angles are reproduced similarly well by most SQC methods investigated presently. Ionization potentials are predicted best by OM2 for the CHNO set and by OM1 and OM2 for the FLUOR set. Dipole moments are again computed similarly well in general (please note that the OMx dipole moments are calculated in ZDO approximation without orthogonalization corrections, the effect of which should be studied in future work). The most accurate results for relative energies and barriers are obtained from OM2 and PM7 and from OM2 and OM3, respectively.

Figure 1.

Error distribution for the heats of formation from OMx and PM7 calculations on the CHNO set. The CH, CHN, CHO, CHNO, and HNO subsets are shown in this order from left to right and are marked with alternating gray and white backgrounds.

Upon the request of a reviewer, we have carried out analogous RM1 calculations. The statistical evaluations of the RM1 results are given in the Supporting Information (Tables S11 and S12) along with a brief assessment. RM1 tends to be generally more accurate than AM1, about as accurate as the PMx methods, and somewhat less accurate than the OMx methods.

We have performed extensive benchmarks on many other validation sets from the literature, to compare the performance of OMx and MNDO-type methods more systematically. These benchmarks are reported in a separate Article.⁶⁹

3. Dispersion Corrections

In this section, we discuss the effects of including dispersion corrections in the OMx methods, without changing any of the basic OMx parameters presented in Tables 1–3. Contrary to other recent semiempirical studies (see Introduction), we do not introduce any hydrogen-bond corrections because the OMx methods normally describe hydrogen bonds already quite well by themselves, even though further improvements can be achieved by specific re-parameterization.⁹⁴ We have previously shown that simple dispersion-corrected OM2 and OM3 approaches are capable of yielding acceptable results for hydrogen-bonded complexes.⁶⁷

The functional form of the dispersion corrections is taken from the work by Grimme, specifically from DFT-D2⁵⁶ and DFT-D3(BJ).^57,58 Our notation is as follows: D2 is used for re-parametrized versions of the DFT-D2 corrections,⁵⁶ while D3 denotes the parametrization of the DFT-D3(BJ) correction^57,58 that has recently been performed by Grimme for OM2 and OM3.¹⁰ The dispersion corrections are added to the SCF energy. For ease of reference, we first outline the relevant formalism before presenting the results.

3.1. D2 Corrections

The D2 dispersion correction E_disp^D2 is given by^56,68

23

Here R_AB is the distance between atoms A and B, C₆^AB is the corresponding dispersion coefficient, s₆ is an element-independent (global) scale factor, and f_damp(R_AB) is a damping function that avoids an unphysical overbinding between atoms A and B that are very close to each other. The cross-terms C₆ are obtained from

24

where C₆^A and C₆ are atomic coefficients derived from the London dispersion formula. The damping function f_damp(R_AB) is defined by^56,68

25

where R₀ is an element-specific parameter that represents the van der Waals radius,⁵⁶ and d is an element-independent (global) parameter that determines the steepness of the damping function.⁵⁵ Tests of an alternative damping function⁹⁵ in the OMx-D2 framework yield results close to those obtained with the aforementioned standard DFT-D2 damping function;⁶⁸ for the sake of brevity, we only present and discuss the latter in the following sections.

3.2. D3 Corrections

Recently, Risthaus and Grimme derived and successfully applied D3(BJ) corrections to OM2 and OM3.¹⁰ The resulting dispersion-corrected methods are labeled as OM2-D3 and OM3-D3 both in the original work¹⁰ and here. The D3(BJ) corrections are defined by⁵⁸

26

where s₆ and s₈ are element-independent (global) parameters, C₆^AB and C₈ are dispersion parameters, and f(R_AB) denotes the Becke–Johnson-type (BJ) damping function⁹⁶⁻⁹⁸ that contains adjustable parameters a₁ and a₂. The dispersion coefficients C₆^AB are derived from TD-DFT calculations of average dipole polarizabilities.⁵⁷ The dispersion coefficients C₈ are obtained recursively from C₆^AB and DFT-derived quantities.⁵⁷

Risthaus and Grimme¹⁰ also applied three-body dispersion corrections (E_disp^ABC)⁵⁷ on top of the preceding two-body corrections. These three-body corrections are important for large dense systems.^99,100 They are defined explicitly in the literature.^10,57 Inclusion of the E_disp corrections has been shown to improve the accuracy of OM2-D3 and OM3-D3 noncovalent interaction energies of large complexes on average by 1.4 kcal/mol¹⁰ but is expected to have little effect on smaller systems.^10,100 We denote OM2-D3 and OM3-D3 calculations that include three-body corrections by OM2-D3T and OM3-D3T, respectively.

3.3. Parameters

The global parameters s₆ and d as well as the element-specific parameters C₆ and R₀ that appear in the D2 dispersion corrections were fitted by optimizing the complexes of the S22 benchmark set^101,102 and using the respective reference interaction energies.⁶⁸ During this fitting, C₆ and R₀ were not allowed to change by more than 10% to ensure that they retain their physical meaning.⁶⁸ The resulting element-specific parameters for H, C, N, and O do not differ significantly from the respective DFT-D2 parameters,^56,68 and therefore we decided to adopt for F the published DFT-D2 parameters (note that there are no fluorine-containing complexes in the S22 set). The final D2 parameters are listed in Table 6.

Table 6. Parameters for the D2 and D3 Dispersion Corrections for OM2 and OM3: s₆, s₈, a₁, a₂, d, C₆ (J·nm⁶·mol^–1), and R₀ (nm) (See Text).

^aTaken from ref (68).

^bTaken from ref (56)., see text.

^cTaken from ref (10).

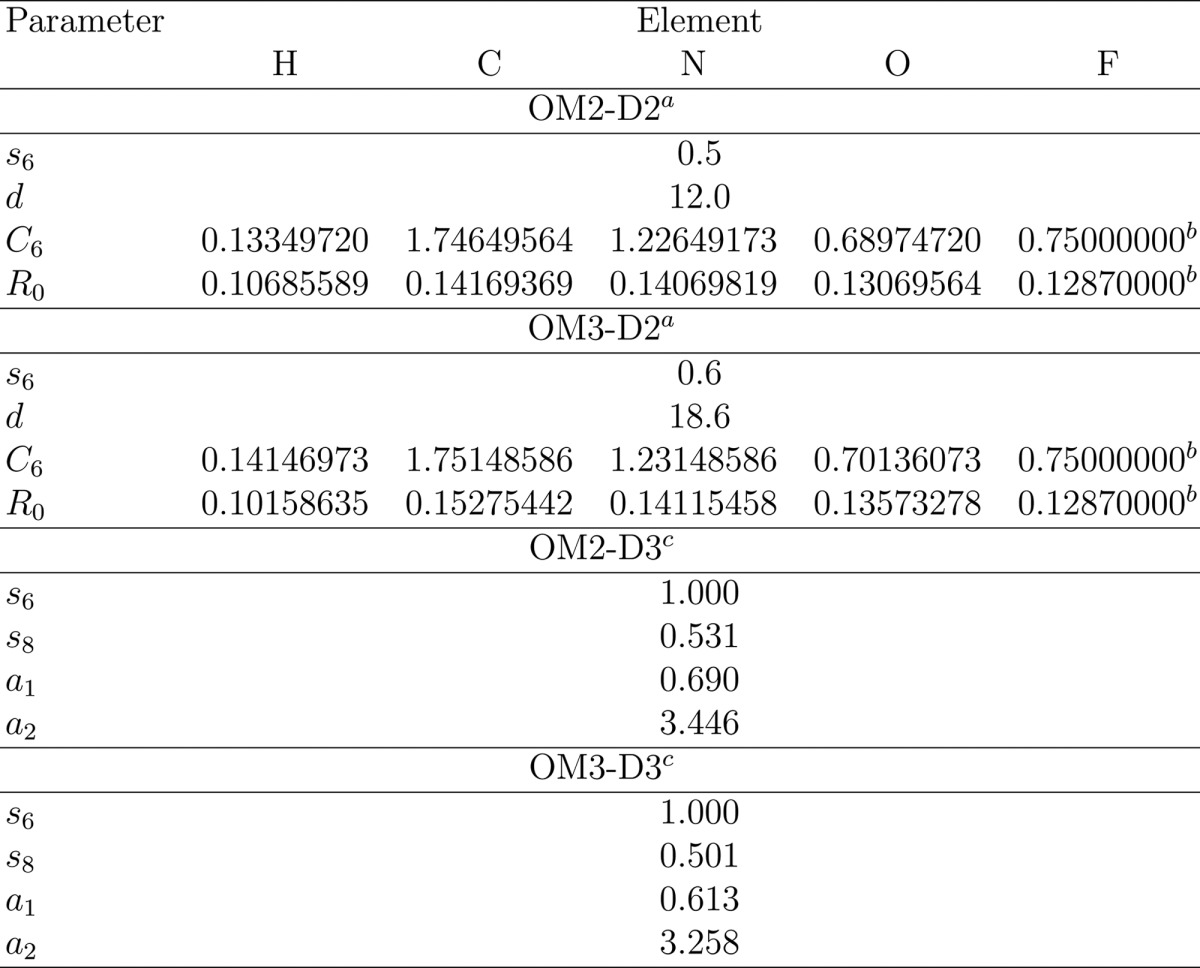
The OM2-D3 and OM3-D3 parameters are taken from the literature.¹⁰ As commonly done, s₆ was fixed to unity,^10,58 while the short-range D3(BJ) parameters (a₁, a₂, and s₈) were fitted against reference data from the S66×8¹⁰³ set.¹⁰ The optimized D3 parameters are included in Table 6.

3.4. Validation

Here we provide an initial assessment of the dispersion-corrected OMx-Dn results for the S22 and S66×8 training sets used during parametrization. Extensive further benchmarks have been performed for several other test sets, which will be reported in a separate Article.⁶⁹

The S22 set is comprised of 22 small noncovalently bound complexes. Most of the reference geometries were obtained at the MP2/cc-pVTZ level with counterpoise corrections, and some also at the CCSD(T) level without counterpoise corrections.^101,102 The standard S22 reference energies have been updated in this study by including more accurate CCSD(T)/CBS values.¹⁰⁴ The S66×8 set samples intermolecular distances in 66 small noncovalently bound complexes, which were optimized at the MP2/cc-pVTZ level with counterpoise corrections;¹⁰³ thereafter the equilibrium distance between the monomers was scaled by factors of 0.9, 0.95, 1.05, 1.1, 1.25, 1.5, and 2.0, and reference energies were calculated at the CCSD(T)/CBS level for the resulting eight geometries.¹⁰³ In both sets, the complexes are divided into three types: electrostatics-dominated (hydrogen bonded), dispersion-dominated, and mixed electrostatics/dispersion.^101,103

We performed single-point calculations at the reference geometries in order to be able to compare the results from different methods. Detailed numerical results are documented in the Supporting Information (Tables S9 and S10) for MNDO-type methods (MNDO, AM1, PM3, PM6, and PM7), for the OMx methods (OM1, OM2, and OM3), and in the case of OM2 and OM3 also for the dispersion-corrected variants (D2, D3, and D3T). Statistical evaluations are given in Table 7 for the PM7 and OMx-Dn methods and in Supporting Information Table S7 for the other SQC methods. These tables provide mean absolute errors of the interaction energies for the S22 and S66×8 sets and for the corresponding subsets.

Table 7. Mean Absolute Errors of the Interaction Energies (kcal/mol) for the S22 and S66×8 Benchmark Sets from Single-Point PM7 and OMx-Dn Calculations at the Reference Geometries.

		method
			OM2			OM3
subset	N	PM7	D2	D3	D3T	D2	D3	D3T
S22
overall	22	0.76	1.16	0.91	0.94	1.25	0.99	0.97
hydrogen bonded	7	0.73	2.32	2.17	2.15	2.65	2.30	2.28
mixed	7	0.70	0.40	0.27	0.28	0.79	0.47	0.50
dispersion	8	0.85	0.81	0.36	0.47	0.44	0.29	0.24
S66×8
overall	528	0.73	0.96	0.78	0.79	0.88	0.69	0.71
electrostatic	184	0.91	1.54	1.43	1.43	1.48	1.30	1.30
mixed	160	0.55	0.52	0.37	0.37	0.53	0.33	0.34
dispersion	184	0.69	0.77	0.49	0.52	0.59	0.41	0.43

In the case of the S22 set, the overall mean absolute error (MAE) is lowest for PM7 (0.76 kcal/mol); the corresponding MAEs for the OMx-Dn methods are slightly higher by 0.15–0.49 kcal/mol. However, the latter are more accurate for the dispersion-dominated and mixed-type complexes, with MAEs of 0.27–0.47 kcal/mol for OM2-D3 and OM3-D3. The largest outlier in the OMx-Dn results is the interaction energy of formic acid dimer which is underestimated by 3.96–5.87 kcal/mol.

Similar trends are found for the interaction energies in the S66×8 set. The overall MAEs for PM7, OM2-D3, and OM3-D3 are close to each other (0.73, 0.78, and 0.69 kcal/mol, respectively), and the OMx-Dn methods again outperform PM7 for dispersion-dominated and mixed-type complexes. The largest outlier in the OMx-Dn results is the interaction energy of acetic acid dimer which is underestimated by up to 7.0 kcal/mol.

Since all complexes in the S22 and S66×8 sets are quite small, it is not surprising that the role of the three-body corrections is negligible (see the D3 and D3T results).

To check the quality of geometry predictions for these noncovalent complexes, we performed full geometry optimizations for the S22 set at the PM7 and OMx-Dn levels and compared the results for 105 selected interatomic distances and for 14 selected bond angles with the ab initio reference values.⁶⁸ Statistical evaluation of the results are given in Table 8 for the PM7 and OMx-Dn methods and in Supporting Information Table S8 for other SQC methods. It is obvious that the MAEs for the selected distances and angles are quite large for all SQC methods investigated presently. Still, the MAEs are significantly lower for the OMx-Dn methods than for PM7 (see Table 8).

Table 8. Mean Absolute Errors in Selected Interatomic Distances (Å) and Angles (deg) from PM7 and OMx-Dn Optimizations for the S22 Set.

		method
			OM2			OM3
subset	N	PM7	D2	D3	D3T	D2	D3	D3T
Selected Interatomic Distances
overall	105	0.565	0.287	0.281	0.424	0.265	0.281	0.285
Selected Angles
overall	14	10.76	2.47	2.63	2.60	1.08	0.86	0.85

For most of the complexes of the S22 set, the PM7 and OMx-Dn methods give qualitatively correct geometry predictions, but there are also cases of failure in which some of the investigated SQC methods yield a qualitatively wrong structure. For example, the reference conformation of the methane dimer is well-reproduced by the OM3-Dn methods but not by OM2-D2 and PM7 (Supporting Information Figure S1). The reference geometry of the T-shaped benzene dimer is predicted correctly by OM2-D2 and OM2-D3, while optimizations with OM3-Dn yield other types of conformers including some that resemble the parallel displaced structure (Supporting Information Figure S2). The optimization of the stacked indole···benzene complex leads to a reasonable structure with PM7, whereas OMx-Dn give a conformer in which benzene is too strongly shifted compared with the reference geometry (Supporting Information Figure S3) For the T-shaped indole···benzene complex, similar problems are encountered as in the case of the T-shaped benzene dimer: for example, optimizations at the OM3-Dn levels lead to a stacked geometry (Supporting Information Figure S4). Finally, in the case of the hydrogen-bonded formic acid dimer, the reference, PM7, and OM2-Dn geometries are similar (with each of the monomers containing an O–H bond), whereas geometry optimizations with OM3 and OM3-Dn converge to a cyclic D_2h structure with a symmetric hydrogen bond characterized by equal O–H distances toward both monomers (Supporting Information Figure S5).

Although the three-body corrections are generally small for the S22 set, their inclusion in the OM2-D3T optimization of the T-shaped benzene dimer produces another conformer of the dimer (Supporting Information Figure S2). This causes the outlier in the MAE value for the OM2-D3T distances, which is much higher than that for OM2-D3 (Table 8).

4. Computational Details

All MNDO, AM1, PM3, and OMx calculations were carried out with our locally modified MNDO2005 program,¹⁰⁵ while the PM6, PM7, and RM1 calculations were done with the MOPAC2012 program.^106,107 Molecules were visualized with Chemcraft 1.7.¹⁰⁸

The SCF energy convergence criterion was set to 10^–9 eV. In addition, the diagonal elements of the density matrix were required to change by less than 10^–9 to achieve SCF convergence in MNDO2005.

By default, geometry optimizations were performed until the gradient norm was smaller than 0.01 kcal/(mol·Å). The optimizations employed the BFGS algorithm in MNDO2005 and the eigenvector following method in MOPAC2012. In the latter case, the full Hessian matrix was constructed using single-sided derivatives and recalculated every 10 steps. In many cases, MOPAC2012 stopped when the heat of formation remained essentially constant. In these cases the gradient norm was usually still smaller than 0.1 kcal/(mol·Å).

Open-shell systems up to triplet spin state were treated with the half-electron approach.¹⁰⁹ Molecular mechanics corrections for PM6 and PM7 were not used. No cutoffs were applied for the three-center orthogonalization corrections in OMx and OMx-Dn calculations.

D3 dispersion corrections were implemented into the MNDO2005 program by adapting code from the DFT-D3 stand-alone program by Grimme (version 3.0 Rev 2).¹¹⁰ The D3 corrections were computed using Becke–Johnson damping and default cutoffs (95 au for two-body terms and 40 au for coordination numbers). The D3T three-body terms were implemented starting from version 3.1 Rev 0 of the same program;¹¹⁰ in this case, we increased the default cutoffs (95 au for two-body terms, coordination numbers, and three-body terms) which had almost no impact on computation times.

5. Conclusions

In previous work we have introduced orthogonalization-corrected SQC methods (OM1, OM2, and OM3) and applied them in various studies, especially in the area of excited-state dynamics. The OMx methods go beyond the MNDO model by including orthogonalization terms, penetration integrals, and ECP integrals in the Fock matrix. In this Article, we describe the underlying theoretical formalism and its implementation in full detail and report all relevant parameters.

The performance of the OMx methods for ground-state properties is demonstrated for a standard set of molecules that has commonly been used in semiempirical method development. In the majority of cases, the OMx results are found to be superior to those from established MNDO-type methods. Further extensive benchmarks have been carried out and are reported separately.⁶⁹

Dispersion interactions are not covered in the OMx formalism but need to be included for a realistic description of noncovalent interactions. This has been done by adding parametrized Grimme-type dispersion corrections to OM2 and OM3 energies (computed without changing the standard OM2 and OM3 parameters). This treatment provides a much improved description of noncovalent interactions in the established S22 and S66×8 test sets. Further advances may be possible by a full reparametrization of the OM2-D3 and OM3-D3 approaches (work in progress).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.5b01046.

• Detailed numerical results for the ground-state properties of all molecules in the CHNO and FLUOR sets for all SQC methods considered, individual interaction energies in the noncovalent complexes of the S22 and S66×8 set for all SQC methods considered, and plots of the optimized geometries of selected noncovalent complexes from the S22 set (PDF)

Author Present Address

^† BASF, Rue Marie de Bourgogne 58, 1000 Brussels, Belgium.

Author Present Address

^‡ Arbentalstrasse 204, 8045 Zürich, Switzerland.

Author Present Address

^§ Leberberg 11, 65193 Wiesbaden, Germany

We thank the European Research Council for financial support through an ERC Advanced Grant (OMSQC).

The authors declare no competing financial interest.