Abstract
A new algorithm for the computation of the overlap between many-electron wave functions is described. This algorithm allows for the extensive use of recurring intermediates and thus provides high computational efficiency. Because of the general formalism employed, overlaps can be computed for varying wave function types, molecular orbitals, basis sets, and molecular geometries. This paves the way for efficiently computing nonadiabatic interaction terms for dynamics simulations. In addition, other application areas can be envisaged, such as the comparison of wave functions constructed at different levels of theory. Aside from explaining the algorithm and evaluating the performance, a detailed analysis of the numerical stability of wave function overlaps is carried out, and strategies for overcoming potential severe pitfalls due to displaced atoms and truncated wave functions are presented.
1. Introduction
The evaluation of matrix elements between many-electron wave functions expanded in different orbital basis sets or over different molecular geometries is a task where the full complexity of these wave functions becomes apparent. Not only the expansion of the wave functions into individual configurations and the construction of the molecular orbitals have to be taken into account, but also the explicit determinantal form, as required by the Pauli principle, comes into play. Furthermore, possible variations of the molecular geometry and the atomic basis functions have to be considered explicitly. The focus of this work is the simplest of these matrix elements, the wave function overlap. A new algorithm for the computation of wave function overlaps is presented, which is distinguished by enhanced computational performance reached through extensive reuse of recurring intermediate quantities. At the same time, a flexible formalism is used allowing for the computation of wave function overlaps for varying wave function expansions, molecular orbitals (MOs), basis sets, and molecular geometries.
Wave function overlaps are widely used in the field of nonadiabatic dynamics, where they allow the evaluation of state-to-state transition probabilities without the need of computing nonadiabatic coupling vectors.1 Aside from the fact that this strategy provides a technical advantage for methods where coupling vectors are not available, it has been shown that, in the case of highly peaked nonadiabatic couplings, wave function overlaps can provide superior numerical stability, in particular when a locally diabatic propagation of the wave functions is carried out.2,3 In the simplest case, the overlap is approximated as a scalar product of the configuration interaction (CI) vectors to provide a qualitative description of changes in wave function character,4−6 possibly after a diabatization of the orbitals.7 Beyond this, exact overlap terms have been derived under a number of assumptions; implementations are available for semiempirical methods,2 plane wave expansions,8 single-reference methods with atom-centered basis sets,9−11 and multireference methods.12,13 These developments were used as a basis for excited state dynamics simulations with a wide range of electronic structure methods, including time-dependent density functional theory,8,9,11,14 complete active space self-consistent field (CASSCF) and multireference CI (MRCI),7,12,15 CAS perturbation theory,16 and correlated single-reference methods.17,18 Despite this wide interest, the practical use of wave function overlaps is hampered by high computational demands, especially when multiconfigurational wave functions are used, which are necessary for the correct description of many nonadiabatic processes. Moreover, the numerical stability of the results with respect to truncation of the wave functions and the consequences of displaced orbitals in the case of varying molecular geometries have received almost no attention so far despite the fact that these can have a crucial impact on the computed results.
The purpose of this work is to present a new general algorithm for the efficient computation of wave function overlaps and to address some related numerical questions. We first discuss the general theory of wave function overlaps in the framework of Slater determinant expansions. Using this foundation, specific algorithmic improvements are explained, which allow for significant enhancement of the efficiency of the code. We then discuss properties of the overlap matrix and outline the application of overlaps for nonadiabatic interactions. As a next step, a path integral over the coupling vector in coordinate space is computed, and the results are compared to standard nonadiabatic theory.19 In addition, the results are verified against two previous implementations.12,13 In order to give practical advice for future applications, the numerical stability of the results with respect to wave function truncation and atom displacements is discussed, and we show how orthogonalization of the overlap matrix can significantly improve the results. Finally, the performance and parallel scaling are evaluated.
2. Theory
2.1. General Formalism
In the following, we use the notation |Ψ⟩ to denote antisymmetric many-electron wave functions constructed as linear combinations of Slater determinants. The coordinates of the electrons are addressed implicitly in the braket formalism. Two sets of electronic wave functions {|ΨI⟩} and {|ΨJ′⟩} are constructed. The only requirement for the relation between these wave functions is that they contain the same number of α and β electrons, but they are otherwise allowed to vary in the wave function expansion, the MOs, the basis set, and the molecular geometry. I and J are arbitrary indices for the individual sets. Typically, I,J = 1 would refer to the ground state and higher indices to the excited states, but there are no formal restrictions with respect to their meaning.
In this section, we will derive a general expression for computing terms of the form
| 1 |
and analogously the whole overlap matrix S between the two sets of states. As a first step, the expansion into Slater determinants
| 2 |
| 3 |
is invoked. Here, {|Φk⟩} and {|Φl′⟩} denote two distinct sets of Slater determinants used in the expansions, dIk and dJl are the CI coefficients forming the CI vectors, and nCI and nCI′ are the number of elements in these CI vectors. It should be noted that the formalism described here is based on Slater determinants rather than on spin-adapted configuration state functions (CSF), which are often used in CI calculations. However, it is always possible to perform the conversion to the Slater determinant basis.
Insertion of eqs 2 and 3 into eq 1 leads to
| 4 |
a double sum over Slater determinant overlaps. We write the Slater determinants, which are constructed from four potentially different sets of spin–orbitals {ϕp}, {ϕq′}, {ϕr}, and {ϕs}, in the form
| 5 |
| 6 |
where the notation k(i) is used to denote the index of the orbital that is at position i in Slater determinant |Φk⟩, n is the number of electrons, nα the number of α spin electrons, and the bar marks the β spin orbitals. In the above equations, it is assumed that the α orbitals are positioned in front of the β orbitals in the Slater determinant. Obtaining this arrangement is always possible but care has to be taken to preserve the correct sign when the columns of the determinants are rearranged.20
The overlap of the two Slater determinants is given by the determinant of the matrix containing all mutual orbital overlaps (see Appendix A and refs (9 and 21)).
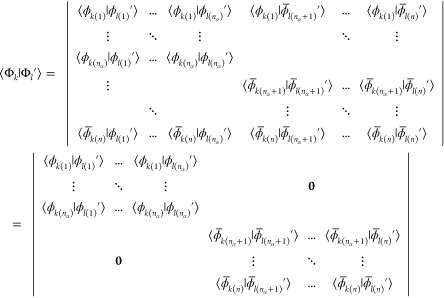 |
7 |
Using the arrangement chosen in eqs 5 and 6, the matrix becomes block diagonal due to the fact that overlaps between orbitals of different spin vanish. The two blocks can, in turn, be evaluated individually
 |
8 |
It is important to realize
at this point that the two factors 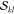 and
and 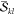 are not unique
to the determinant pair
|Φk⟩ and |Φl′⟩, but that they reappear for other determinants with the
same α or β spin occupation pattern. As will be described
below, precomputing and storing these factors is one of the main points
responsible for efficiency.
are not unique
to the determinant pair
|Φk⟩ and |Φl′⟩, but that they reappear for other determinants with the
same α or β spin occupation pattern. As will be described
below, precomputing and storing these factors is one of the main points
responsible for efficiency.
To evaluate eq 8, it is assumed that the MOs are given in terms of atomic orbitals (AOs)
| 9 |
| 10 |
where the MO coefficients Cpμ and the AOs χμ are both allowed to vary between the bra and the ket. Consequently, the MO overlaps are given as
| 11 |
linear combinations of the mixed AO overlap integrals ⟨χμ|χν′⟩. The overlaps ⟨ϕp|ϕq⟩ of the β orbitals are computed analogously in the case of an unrestricted MO basis.
Two special situations can occur here: the cases of identical AOs and identical MOs in the two wave function expansions. If the AOs on both sides are the same, i.e., χμ = χμ′, then it is not necessary to compute mixed AO overlap integrals, but the ⟨χμ|χν⟩ terms are simply the overlap integrals ⟨χμ|χν⟩ already computed in the standard quantum chemistry job. Furthermore, as discussed in ref (22), it is not necessary to use these integrals at all (e.g., if they are not available for technical reasons). Whenever the MO-coefficient matrix C is square and nonsingular, the AO overlap matrix can be constructed as
| 12 |
In the second case, when the MOs on both sides are the same, i.e., ϕp = ϕp′, the whole formalism is greatly simplified, yielding
| 13 |
and the overlap computation (eq 4) reduces to a simple scalar product of the CI vectors. Assuming eq 13 to be approximately valid allows for computing the overlap as a simple scalar product between CI vectors (expanded either in a Slater determinant or CSF basis), yielding a strategy that has indeed been applied successfully for dynamics simulations (see, e.g., refs (4 and 5)). However, inspection of the above equations shows that the ⟨Φk|Φl′⟩ terms do not only depend on the resolution of quasi-degenerate orbitals, present for example during charge and energy transfer processes,3,23 but are even affected by the phases of the individual orbitals. For this reason, special care has to be taken when such a strategy is applied and a prior diabatization of the orbitals7 may be necessary.
Finally, it is worth noting that an alternative strategy for computing the Slater determinant overlaps lies in a transformation of the orbitals yielding biorthogonal orbitals and consequently biorthogonal Slater determinants, avoiding the necessity for computing the determinants of eq 8. This can be achieved either by a singular value decomposition of the mixed MO overlap matrix shown in eq 11 to obtain the “corresponding orbitals”24,25 or by a somewhat more involved formalism involving nonunitary orbital transformations13,26 as implemented in the Molcas 8.0 suite.27 However, an orbital transformation could significantly enlarge the CI expansion and appears practical only for specific wave function classes. We are not aware of any implementation of such a formalism that allows for the generality aimed at here. Another way of computing matrix elements between nonorthogonal Slater determinants proceeds by a generalized Wick theorem.28
2.2. Implementation
The algorithm presented
above requires the computation of two determinants for every pair
of bra and ket Slater determinants, see eq 8. Without further considerations, this would
lead to a formal scaling on the order of 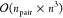 where npair = nCI × nCI′, and n is the number of electrons. This steep scaling
shows that
an efficient implementation is of utmost importance if the code should
be generally applicable. Therefore, an algorithm with more favorable
scaling behavior has been devised.
where npair = nCI × nCI′, and n is the number of electrons. This steep scaling
shows that
an efficient implementation is of utmost importance if the code should
be generally applicable. Therefore, an algorithm with more favorable
scaling behavior has been devised.
The most important realization
is that the factors 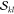 and
and 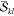 are not unique to a determinant
pair |Φk⟩ and |Φl′⟩.
Assuming, for example, that four determinants are given as
are not unique to a determinant
pair |Φk⟩ and |Φl′⟩.
Assuming, for example, that four determinants are given as
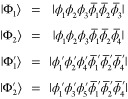 |
it follows that
|Φ1⟩
and |Φ2⟩ share the same α spin part.
This leads to the situation that 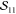 and
and 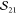 are identical
are identical
 |
and it similarly holds that 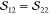 as well as
as well as 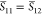 and
and 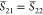 . In summary,
out of the 2 × npair = 8 spin determinants,
there are only nfac = 4 unique factors,
cutting the required
computational effort in half in this toy model. This reduction occurs
independently in the α and β spin spaces and thus also
applies for unrestricted MOs. For larger wave function expansions,
in particular, when a large number of simultaneous α and β
excitations are present, the reduction can be dramatic. Using the
CASSCF(12,12) case as an extreme example, the reduction from 2 × npair = 7.8 × 1011 spin determinants
to nfac = 1.3 × 106 unique
factors exceeds 5 orders of magnitude. In general, it can be worked
out for large CASSCF wave functions that
. In summary,
out of the 2 × npair = 8 spin determinants,
there are only nfac = 4 unique factors,
cutting the required
computational effort in half in this toy model. This reduction occurs
independently in the α and β spin spaces and thus also
applies for unrestricted MOs. For larger wave function expansions,
in particular, when a large number of simultaneous α and β
excitations are present, the reduction can be dramatic. Using the
CASSCF(12,12) case as an extreme example, the reduction from 2 × npair = 7.8 × 1011 spin determinants
to nfac = 1.3 × 106 unique
factors exceeds 5 orders of magnitude. In general, it can be worked
out for large CASSCF wave functions that 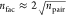 , showing that
CASSCF wave functions profit
optimally from this reduction.
, showing that
CASSCF wave functions profit
optimally from this reduction.
The determinants are first individually
sorted according to their
α and β parts, and the repetitive blocks are identified.
In a next step, all required 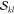 and
and 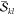 factors are precomputed
and stored in memory.
The final overlap computation amounts to a contraction step of the
form
factors are precomputed
and stored in memory.
The final overlap computation amounts to a contraction step of the
form
| 14 |
where the outer sum over k is implemented as an explicit loop, and the inner sum
over l is realized as a matrix-vector product using
the BLAS
(basic linear algebra subprograms) library. If the number of unique
factors is given as nfac, then the scaling
of the determinant computations is reduced to 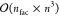 . By contrast, the contraction
step (eq 14) considers
the full
number npair = nCI × nCI′ of CI coefficients and scales as
. By contrast, the contraction
step (eq 14) considers
the full
number npair = nCI × nCI′ of CI coefficients and scales as 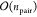 times the number of pairs of states. In
practical calculations, either one of these steps can be the time-critical
one depending on the ratio npair/nfac, the number of electrons n, and the number of states.
times the number of pairs of states. In
practical calculations, either one of these steps can be the time-critical
one depending on the ratio npair/nfac, the number of electrons n, and the number of states.
The downside of precomputing and
storing the factors is the high
memory demand. However, in general we find that whenever the computation
is feasible with respect to CPU time, memory restrictions do not play
a significant role. Furthermore, an additional algorithm was implemented,
which rearranges the CI vectors in a way that the 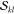 factors can be computed on-the-fly, whereas
only the
factors can be computed on-the-fly, whereas
only the 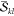 factors have to be precomputed.
This semidirect
algorithm allows for cutting the memory demands in half while showing
similar performance with respect to storing all factors in memory.
A notable loss of performance is only observed when the available
memory is reduced even further.
factors have to be precomputed.
This semidirect
algorithm allows for cutting the memory demands in half while showing
similar performance with respect to storing all factors in memory.
A notable loss of performance is only observed when the available
memory is reduced even further.
Even when the 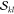 and
and 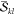 factors are precomputed,
the computation
of determinants is still a time critical step. To make this computation
as fast as possible, we combine two prominent methods of calculating
determinants. As one option, determinants can be computed by Laplace’s
recursive formula29
factors are precomputed,
the computation
of determinants is still a time critical step. To make this computation
as fast as possible, we combine two prominent methods of calculating
determinants. As one option, determinants can be computed by Laplace’s
recursive formula29
| 15 |
where Ãij denotes the matrix A with the ith row and the jth column deleted. A full recursive
implementation of this equation would lead to an undesired factorial
scaling. Therefore, LU factorization is used as the main tool30 because it allows for computing determinants
with 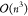 scaling. Taking a close look at eq 15, however, one realizes
that it allows the reuse of intermediates. Especially in the context
of CI expansions, it is observed that many determinants differ only
with respect to the last orbital. In such a case, it is beneficial
to perform a Laplace expansion along the last column and precompute
the cofactors (−1)i+n|Ãin| to be
used for all related determinants. In the present implementation,
an automatic algorithm is used to decide case-by-case which determinants
are computed directly and which ones via their cofactors, as given
in eq 15. The cofactors
are in turn computed by LU decomposition, and no further recursion
is carried out. This procedure is particularly efficient for wave
functions constructed as single excitations out of one or a few references,
and it is therefore complementary to the application of the
scaling. Taking a close look at eq 15, however, one realizes
that it allows the reuse of intermediates. Especially in the context
of CI expansions, it is observed that many determinants differ only
with respect to the last orbital. In such a case, it is beneficial
to perform a Laplace expansion along the last column and precompute
the cofactors (−1)i+n|Ãin| to be
used for all related determinants. In the present implementation,
an automatic algorithm is used to decide case-by-case which determinants
are computed directly and which ones via their cofactors, as given
in eq 15. The cofactors
are in turn computed by LU decomposition, and no further recursion
is carried out. This procedure is particularly efficient for wave
functions constructed as single excitations out of one or a few references,
and it is therefore complementary to the application of the 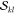 factors, which are applicable for higher
excitation levels. An alternative to this approach would be to use
the matrix determinant lemma as discussed, e.g., in ref (25). However, the advantage
of the present approach is that it does not require any matrix inversions
or other numerically unstable steps.
factors, which are applicable for higher
excitation levels. An alternative to this approach would be to use
the matrix determinant lemma as discussed, e.g., in ref (25). However, the advantage
of the present approach is that it does not require any matrix inversions
or other numerically unstable steps.
In addition to the previous algorithmic changes that do not affect the computed result, we also want to discuss two approximation schemes that do affect the results. First, a threshold t for a truncation of the CI vector is introduced. The elements dIk are sorted by their magnitude, and then all the elements beyond a given index kt are discarded. The index kt in turn is determined as the smallest number giving
| 16 |
The overlaps are computed with respect to the truncated wave function
| 17 |
where, following eq 16, the squared norm of this wave function is greater or equal to t
| 18 |
This approximation allows for significantly reducing the number of terms to be computed while recovering the major part of the wave function.
Truncation of the wave functions will generally lead to an underestimation of the overlaps. To overcome this problem, we suggest a simple correction. If it can be assumed that the angles between the original and truncated wave functions are approximately equal
| 19 |
then the overlap between the normalized functions |ΨI⟩ and |ΨJ′⟩ can be approximated by the renormalization
| 20 |
The assumption of eq 19 should be valid if the same general wave function model is applied for |ΨI⟩ and |ΨJ′⟩. In cases where very accurate values are required, the convergence of the results should be studied by varying the threshold values. Below, an orthogonalization procedure is discussed, which has a similar effect on truncated wave functions but also allows for the correction of terms stemming from orbital displacements.
The second approximation is based on discarding a number ncore of frozen core orbitals. For these orbitals, which are required to be occupied in all the determinants, it is assumed that
| 21 |
and consequently that they are also orthogonal to all noncore orbitals. Under this assumption, these orbitals can simply be eliminated from the calculation leading to smaller determinants in eq 8. Furthermore, as discussed below, discarding core orbitals can improve the numerical stability of the computation if atoms are moved, because displacements of atoms with tight core orbitals can introduce numerical artifacts.
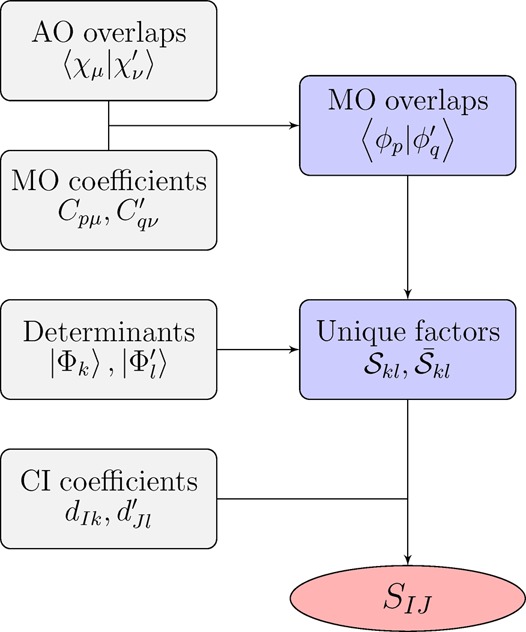
Scheme 1 summarizes
the implemented algorithm. Four types of input quantities are needed:
the mixed AO overlaps, the MO coefficients, the occupation strings
of the determinants, and the CI coefficients. The mixed AO overlaps
have to be computed explicitly in cases where the molecular geometry
or the basis set are varied. Technically, this step is most readily
performed by using a standard integral code and computing the overlap
integrals for a formal double molecule. The MO coefficients are usually
directly available in ASCII format. With respect to the CI vectors,
three preparation steps are necessary: conversion from configuration
state functions to Slater determinants, extraction of the determinant
strings, and rearrangement of the orbitals to comply with eqs 5 and 6. After the input is read, the AO overlaps are combined with the
MO coefficients according to eq 11 to compute the mixed MO overlaps. These are in turn
used in connection with the determinant strings to compute the unique 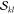 factors (eq 8). In the final step (eq 14), these factors are contracted with the
CI coefficients to give the overlap. The code is written in a modular
fashion, which allows for an easy interface to various quantum chemical
programs and file formats when reading the input quantities shown
on the left in Scheme 1. Currently, interfaces to the Columbus 7.0 and Molcas
8.0 program packages are available for accessing the CI vectors,
MO coefficients, and binary integral files.27,31,32 An extension to the ADF program33 is in progress.
factors (eq 8). In the final step (eq 14), these factors are contracted with the
CI coefficients to give the overlap. The code is written in a modular
fashion, which allows for an easy interface to various quantum chemical
programs and file formats when reading the input quantities shown
on the left in Scheme 1. Currently, interfaces to the Columbus 7.0 and Molcas
8.0 program packages are available for accessing the CI vectors,
MO coefficients, and binary integral files.27,31,32 An extension to the ADF program33 is in progress.
Scheme 1. Schematic Depiction of the Computation of Wave Function Overlaps SIJ with Input Data and Intermediates Shown in Gray and Blue, Respectively.
2.3. Properties of the Overlap Matrix
In this section, we want to inspect the properties of the overlap matrix S under the assumption that the two sets {|ΨI⟩} and {|ΨJ′⟩} are individually orthonormal. Then, a wave function |ΨI⟩ of the first set can be expanded using the resolution of the identity
| 22 |
Here, |ΨI⊥⟩ is used to denote the component of |ΨI⟩ that belongs to the orthogonal complement of the space spanned by the {|ΨJ⟩}. This suggests to think of a decomposition of the wave function |ΨI⟩ in terms of the individual projection components and the “missing part” belonging to the orthogonal complement. Projection of the above equation onto ⟨ΨI|
| 23 |
shows that the combined weight of these components is normalized to unity and consequently that the sum of the squared overlap values along a column (or equivalently a row) of the overlap matrix is less than or equal to one.
If the two sets {|ΨI⟩} and {|ΨJ′⟩} span the same space, then the orthogonal component |ΨI⟩ vanishes, and S becomes the transformation matrix between the two sets. Furthermore, a projection of eq 22 onto a function of the first set ⟨ΨK| immediately shows that S is an orthogonal matrix
| 24 |
In practical applications, the calculated overlap matrix could deviate from orthogonality due to different reasons. For example, when modifying the molecular geometry during a dynamics simulation, such a deviation could be an indication of interactions with external states. In this case, the ∥ΨI⊥∥ value contains important nontrivial information. On the other hand, nonorthogonality of the matrix could simply be present for numerical reasons, e.g., from the wave function truncation or from displaced basis functions. Then, the stability of the results can benefit from an orthogonalization of the raw overlap matrix. For this purpose, a symmetric (Löwdin) orthogonalization is performed following the idea of ref (2). First, a singular value decomposition of the overlap matrix is performed
| 25 |
to determine the transformation matrices U and V along with the singular values λ1,...,λn. Then, the orthogonalized overlap matrix is simply obtained as the matrix product
| 26 |
i.e., all singular values are rescaled to 1. Following numerical tests in ref (3), we suggest applying this procedure for dynamics simulations, preferably in connection with the local diabatization formalism.2 However, special attention has to be paid to interactions with external states.
When a comparison of wave functions constructed with different models is performed, the ∥ΨI⊥∥ term is an integral component of the discussion as it allows for quantifying discrepancies in the description. In such a case, the orthogonalization procedure is not expedient, but a renormalization (eq 20) can be carried out to correct for the wave function truncation.
2.4. Nonadiabatic Interactions
The application of wave function overlaps for nonadiabatic dynamics has been discussed in detail elsewhere.1,8,9,12 Therefore, we shall only present some relations immediately relevant for the following discussion. The symbol |ΨI (R)⟩ is used to denote the parametrical dependency of the electron wave function on the nuclear geometry R, whereas the electronic coordinates are considered only implicitly. In this nomenclature, the nonadiabatic coupling vector between states I and J is defined as
| 27 |
Coupling vectors can be computed by response theory using a similar formalism to the computation of gradients.34−37 Aside from the optimization of conical intersections,35,38 they are indeed widely used in nonadiabatic dynamics simulations.7,39−41 However, there are a number of issues that can come into play for different application areas. First, coupling vectors are only available for a limited number of methods and program packages. Second, the computation of the required one- and two-electron derivative integrals can be the overall time-limiting step if large molecules or extended basis sets are used in connection with restricted wave function expansions. Third, the convergence of the coupled-perturbed MCSCF equation system is not trivial as discussed, e.g., in ref (7). Finally, numerical problems can arise in the case of highly peaked coupling vectors.3,6 For these reasons, it is beneficial to have an efficient and general alternative available, which is provided by wave function overlaps.
To understand the connection between overlaps and coupling vectors, eq 27 is written in the form
| 28 |
where the symbol ∇′ is used to denote the gradient vector with respect to the R′ coordinates. The directional derivative with respect to a displacement vector RD is evaluated as
| 29 |
Replacing the limit with a fixed small value of t and setting ΔR= tRD yields the discrete approximation
| 30 |
Although this expression reduces to the exact directional derivative in the limit of |ΔR| → 0, the linear approximation is not necessarily stable when ΔR is increased. In such cases, the use of a somewhat more extended formalism using a locally diabatic wave function propagation is recommended for dynamics simulations.2,3,41
3. Accuracy and Performance
In this section, we investigate the accuracy and performance of the new implementation of wave function overlaps. First, a general numerical verification of the results will be performed. Then, two crucial numerical questions that have not received much attention so far despite the wide application for wave function overlaps in nonadiabatic dynamics simulations will be addressed. These are concerned with the consequences of wave function truncation as applied to keep the computational effort at an acceptable level and with numerical artifacts stemming from displaced atoms and orbitals. Finally, the performance and the parallel scaling of the individual computation steps are examined.
3.1. Verification
Before proceeding to more specific numerical and performance issues, we want to verify the general numerical accuracy of the present code. For this purpose, we will first show that the results are consistent with general nonadiabatic theory by computing a path integral in molecular coordinate space and then proceed to a comparison of the results with respect to two different implementations. Following previous work by some of us,15 the example molecule used throughout much of this work is selenoacroleine, shown in Figure 1. We will first discuss the torsion θ around its C=C bond, using results computed at the MR-CI level with single excitations (MR-CIS). In Figure 2a, the energies of the lowest two triplet states are plotted with respect to this torsion. Both states have their minimum energy at the planar geometry (θ = 0). At this point, T1 is of nπ* character, whereas T2 is a ππ* state. As the torsion angle is increased, the T1 (nπ*) energy increases strongly, whereas the T2 (ππ*) state shows a flatter profile. At around 55°, the states exhibit an avoided crossing, and at larger torsion angles, they exchange their state character. The path integral over the coupling vector was computed by numerical integration using eq 30.
| 31 |
where R(i) are intermediate geometries. The results are presented in Figure 2b. As expected, the strongest interaction is experienced in the area of the avoided crossing. The value of the line integral over the 0° to 90° rotation amounts to approximately π/2. By symmetry, it is clear that the full rotation over 360° amounts to four times this value. Accordingly, the integral around a closed path gives
| 32 |
a multiple of π, in line with general considerations.19 We have therefore shown that the wave function overlaps computed here give not only a qualitatively but also a quantitatively correct picture of a passage through an avoided crossing, justifying the application of these quantities for nonadiabatic dynamical simulations.
Figure 1.
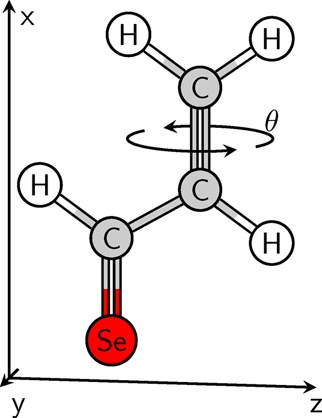
Molecular structure of the selenoacroleine molecule and indication of the torsion angle θ.
Figure 2.
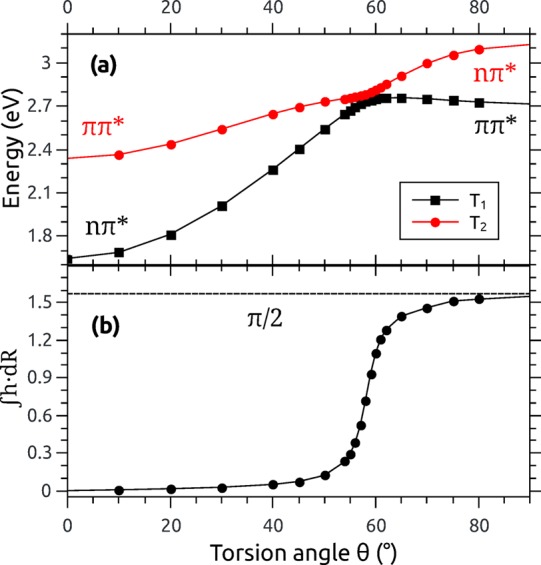
Torsion of selenoacroleine along the CC double bond: (a) Energies of the T1 and T2 states computed at the MR-CIS/ANO-RCC-VDZP level and (b) line integral over the nonadiabatic coupling vector converging against π/2.
As a next step, the numerical
results will be compared to two different
previous implementations, a general overlap code12 that has been extensively used for surface hopping dynamics
within the Newton-X(14,17,40) and Sharc(41−43) packages and an implementation based on the state
interaction formalism13,26 that is part of the Molcas
8.0 program package.27 Furthermore,
results deriving from a simple scalar product of the CI vectors will
be presented. To allow for a quantitative numerical comparison of
results obtained with different program packages, meticulous control
of all wave function parameters is necessary, and therefore, only
a few selected examples are discussed in the following. We again choose
selenoacroleine and compute the overlap between wave functions constructed
at two different geometries around the avoided crossing with θ
= 50° and 55° representing the geometries that could be
present in two subsequent time steps in a dynamics simulation. First,
CASSCF computations are carried out considering 6 electrons in 5 active
orbitals and state-averaging over only the two triplet states, denoted
CASSCF(6,5)[0,2]. As this approach is implemented in Molcas 8.0 as well as in Columbus 7.0, we can compare all of the above
methods for overlap computation, and the results are presented in Table 1. There are nCI = nCI′ = 90 Slater determinants
contained in the CASSCF(6,5) wave function, which in turn means that npair = nCI × nCI = 8100 pair-determinant computations are necessary, each of which
requires the computation of the α and β spin-factors 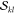 and
and 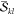 . Thus, in summary, 16200
spin-factors are
involved. Although all of these are computed explicitly in the code
of ref (12), only the nfac = 200 unique ones
of them are evaluated with our new methodology. For this small case,
the computational time expended is negligible in both cases. Almost
perfect numerical agreement is observed with respect to the program
of ref (12), and the
differences are below 1 × 10–9. A comparison
with the state interaction13 computation
shows a semiquantitative agreement, giving a difference of 0.001–0.002
with respect to the previous results. This discrepancy probably derives
from the fact that, as to our understanding, the overlap terms of
displaced AOs ⟨χμ|χν′⟩ are neglected in the state interaction implementation.
The CI vector dot product is also qualitatively correct here, showing
however a somewhat larger discrepancy on the order of 0.005.
. Thus, in summary, 16200
spin-factors are
involved. Although all of these are computed explicitly in the code
of ref (12), only the nfac = 200 unique ones
of them are evaluated with our new methodology. For this small case,
the computational time expended is negligible in both cases. Almost
perfect numerical agreement is observed with respect to the program
of ref (12), and the
differences are below 1 × 10–9. A comparison
with the state interaction13 computation
shows a semiquantitative agreement, giving a difference of 0.001–0.002
with respect to the previous results. This discrepancy probably derives
from the fact that, as to our understanding, the overlap terms of
displaced AOs ⟨χμ|χν′⟩ are neglected in the state interaction implementation.
The CI vector dot product is also qualitatively correct here, showing
however a somewhat larger discrepancy on the order of 0.005.
Table 1. Benchmark of the Numerical Accuracy of the New Wave Function Overlap Code Compared against Previous Implementations and a Simple Scalar Product between CI Vectors: Overlap Terms of the T1 and T2 States of Selenoacroleine between Geometries with 50° and 55° Torsion Computed for Different Wavefunction Expansionsa.
| implem. | method | ⟨T1|T1′⟩ | ⟨T1|T2′⟩ | npair | nfac | t (s) |
|---|---|---|---|---|---|---|
| current | CASSCF(6,5)[0,2] | 0.9236998365 | 0.3525350680 | 8100 | 200 | 0 |
| ref (12) | CASSCF(6,5)[0,2] | 0.9236998368 | 0.3525350673 | 8100 | 16200 | 0 |
| ref (13) | CASSCF(6,5)[0,2] | 0.92560296 | 0.35369919 | |||
| CI vec. | CASSCF(6,5)[0,2] | 0.9330964879 | 0.3555705289 | |||
| current | CASSCF(6,5)[2,2] | 0.6873547950 | 0.7107005295 | 8100 | 200 | 0 |
| ref (12) | CASSCF(6,5)[2,2] | 0.6873547949 | 0.7107005297 | 8100 | 16200 | 0 |
| CI vec. | CASSCF(6,5)[2,2] | 0.7087592682 | 0.7037994229 | |||
| current | MR-CIS(4,3) | 0.9839833569 | 0.1084043350 | 8.32 × 108 | 4.62 × 107 | 33 |
| ref (12) | MR-CIS(4,3) | 0.9839833570 | 0.1084043349 | 8.32 × 108 | 1.66 × 109 | 43769 |
| CI vec. | MR-CIS(4,3) | 0.9830660844 | 0.0903168964 | |||
| current | MR-CIS(6,5) | 0.9752933771 | 0.1676405562 | 5.02 × 1010 | 1.34 × 108 | 673 |
| ref (12) | MR-CIS(6,5) | ∼0.9745715572 | ∼0.1674970271 | <5.02 × 1010 | 1.18 × 1010 | >181021 |
| CI vec. | MR-CIS(6,5) | 0.9560951427 | 0.1457014401 |
npair and nfac denote the
number of Slater determinant pairs in the expansion
and the number of 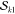 and
and 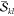 spin factors actually
computed, respectively.
spin factors actually
computed, respectively.
The above calculation including only triplet states was performed for technical reasons, as it allows a comparison to the implementation in Molcas 8.0, which only supports state-averaging within a spin multiplicity. We will now proceed to state-averaging over two singlets and two triplets simultaneously, i.e., the CASSCF(6,5)[2,2] level, which is the level used in the remaining part of this work. As seen in Table 1, the overlap elements are modified significantly by the different orbitals present due to the altered state-averaging, e.g., the ⟨T1|T1′⟩ element is lowered from 0.924 to 0.687. This shows the critical impact that state-averaging can have on the resulting wave functions. Moving from CASSCF to MR-CIS increases the computational time significantly. We start with a smaller active space of 4 electrons in 3 orbitals. For these MR-CIS(4,3) computations, perfect agreement between the new code and the implementation of ref (12) is observed, and at the same time the computational time is reduced by a factor of 1000, i.e., from half a day to half a minute. A factor of approximately 40 of this speedup derives from the reduction in the number of spin factors from 1.7 × 109 to 4.6 × 107, and a similar effect derives from the additional algorithmic improvements, as discussed above. The largest calculation here is MR-CIS(6,5), requiring the computation of 5 × 1010 pair determinants. This computation took approximately 11 min using the new implementation. By contrast, it was not possible for us to compute the exact overlap with the code of ref (12), and a screening formalism12 was used to reduce the number of spin factors to 1.2 × 1010, yielding a computation that could be finished in 2 days. The discrepancy in this case is on the order of 0.001, and the error of a simple CI vector overlap is 1 order of magnitude larger. The results of this comparison are very promising. Although a quantitative agreement with ref (12) is obtained, the results could be accelerated by 3 orders of magnitude, thereby significantly expanding the scope of problems that can be treated.
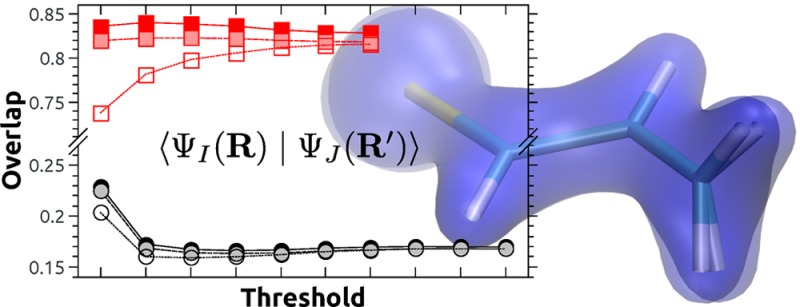
As a second example, selected results on the model iridium complex fac-tris(3-iminoprop-1-en-1-ido)iridum [Ir(C3H4N)3], as shown in Figure 3, will be presented, a system that some of us have studied in detail recently.44 Here, we want to verify our results against the state-interaction implementation in Molcas.13 To construct a job that can be properly compared between the two implementations, the geometry and active space are left unaltered between the bra and ket states. The only parameter varied is the number of singlet states in the state-averaging procedure using values of 1, 4, and 10. The results are presented in Table 2. At first glance, the strong impact that state-averaging exerts on the resulting wave functions is apparent. Switching from one to four states, the overlap between the 11A ground states only amounts to 0.892, and there is also some non-negligible overlap of −0.044 between this state and the excited 21A state. A similar situation is present between nav = 1 and nav′ = 10. By contrast, the ground state wave functions are almost equivalent between four and ten states, showing that the higher excited states require similar orbitals as the lower ones. From a methodological point of view, a quantitative agreement with deviations below 1 × 10–8 between our implementation and ref (13) is observed. In Table 2, the results of a simple scalar product of CI vectors are also shown. These are qualitatively consistent with the actual wave function overlaps but exhibit significantly larger deviations.
Figure 3.
Molecular structure of the model complex Ir(C3H4N)3 studied in this work.
Table 2. Benchmark of the Numerical Accuracy of the New Wavefunction Overlap Code against the Implementation in Molcas 8.0 and a Simple Scalar Product of CI Vectorsa.
| implem. | ⟨nav| | |nav′⟩ | ⟨11A|11A′⟩ | ⟨11A|21A′⟩ |
|---|---|---|---|---|
| current | 1 | 4 | –0.89215658 | 0.04432758 |
| ref (13) | 1 | 4 | –0.89215658 | 0.04432758 |
| CI vec. | 1 | 4 | –0.91830990 | –0.01986185 |
| current | 1 | 10 | 0.88965905 | –0.04019029 |
| ref (13) | 1 | 10 | 0.88965905 | –0.04019029 |
| CI vec. | 1 | 10 | 0.93209422 | 0.01055738 |
| current | 4 | 10 | –0.99748992 | 0.00185985 |
| ref (13) | 4 | 10 | –0.99748993 | 0.00185985 |
| CI vec. | 4 | 10 | –0.95355419 | –0.00559357 |
Overlap terms of the 11A and 21A states of Ir(C3H4N)3 between CASSCF(12,9) wavefunctions considering different numbers of singlet states nav, nav′ in the state-averaging procedure.
In Table 2, the signs of the overlap elements are also given. These signs derive from the overall phases of the wave functions as computed by Molcas. Although the phases possess no physical meaning in isolated calculations, it is crucial to control them in dynamics simulations to obtain smoothly varying matrix elements along a trajectory.41 Here, wave function overlaps offer a clear way to monitor wave function phases, independent of any orbital rotations or orbital phase changes. Indeed, consistent sign information is obtained between the current implementation and the one of ref (13). By contrast, a simple scalar product between CI vectors yields the opposite signs for the off-diagonal elements in this example.
3.2. Wave Function Truncation
Despite the significant algorithmic improvements reported above, it is necessary to allow for a truncation of the wave function to keep the computational cost acceptable for large wave function expansions. For this purpose, the threshold t (eq 16) is used, pertaining to the minimal squared norm of the truncated wave function. Selenoacroleine is considered, and overlaps are computed between the two geometries at θ = 50° and 55° torsion. Computations are performed at the MR-CIS(6,5) and MR-CISD(6,5) levels of theory, and the threshold t is varied systematically. The value for the overlap between the T1 state at 50° and the T2 state at 55° torsion is depicted in Figure 4a. The MR-CISD values (red) differ significantly from the MR-CIS values (black): whereas the former indicate strong nonadiabatic interactions with overlap elements above 0.8, the latter values are below 0.2. This type of discrepancy, which derives from slightly altered potential surfaces due to dynamic electron correlation, is well-known in the literature (see, e.g., ref (45)) and will not be discussed in more detail here. The current focus is an analysis of the numerical stability of the results within a chosen computational protocol. For this purpose, three values are considered: (i) the raw overlap between the truncated wave functions, (ii) the renormalized overlap according to eq 20, and (iii) the orthogonalized overlap value. At the MR-CIS level of theory, all three values are almost equivalent for thresholds above 0.95. A stronger deviation exists for the smallest value of 0.90. However, even in this case, qualitative agreement is found, and all of the wave function phases are reproduced correctly. Furthermore, it is observed that the raw overlaps are always somewhat smaller than the renormalized ones, which are in turn smaller than the orthogonalized ones. The first effect derives from the wave function truncation, and the second derives from the geometric displacement, as will be analyzed in the next section. The convergence of the raw MR-CISD results is significantly worse when compared to MR-CIS. However, the renormalized and the orthogonalized results show satisfactory stability.
Figure 4.
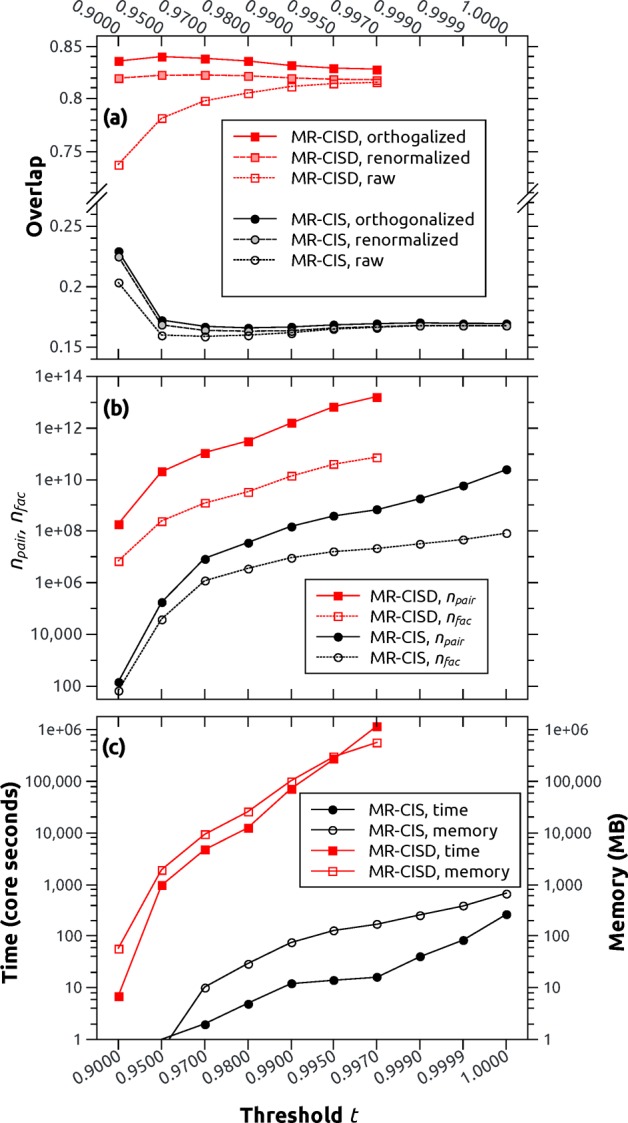
Performance of the wave function overlap
code for the ⟨T1|T2′⟩
element at the MR-CIS(6,5)
and MR-CISD(6,5) levels of theory in the case of selenoacroleine between
geometries with 50° and 55° torsion using varying screening
thresholds t: (a) the overlap considering raw, renormalized,
and orthogonalized results, (b) the total number of determinant pairs
(npair) and the number of unique 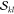 and
and 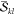 factors (nfac), and (c) the computation time and memory requirements.
factors (nfac), and (c) the computation time and memory requirements.
Figure 4b presents the number of Slater determinant pairs (npair, filled symbols) and the number of actually computed determinant factors as shown in eq 8 (nfac, empty symbols). There is a steep increase in the number of terms to be computed as the threshold goes against 1. In the case of MR-CISD, npair goes up to 1.7 × 1013, whereas in the case of MR-CIS, this value reaches 2.4 × 1010. However, not all of these terms are unique, and the number of factors computed (nfac) is significantly lower than npair, differing by approximately 2 orders of magnitude in most cases. Figure 4c shows the computation time expended and the memory needed. In the MR-CIS case, all of the computations are finished in at most a few minutes, and the memory requirements never exceed one gigabyte (GB). By contrast, for MR-CISD, a steep scaling of time and memory with the threshold becomes apparent. The largest computation shown here requires over a million core-seconds, which amounts to approximately 10 h on 32 cores. Storing all 7.4 × 1010 factors occurring in this case would require 567 GB. To somewhat reduce this workload, a semidirect algorithm is implemented, which reduces the memory requirements by approximately one-half.
The MR-CIS wave function calculation in Columbus 7.0 takes approximately 1 min. The computation of the nonadiabatic coupling vectors adds another 2 min, and the overlaps are computed in only 12 s (t = 0.99). In the case of MR-CISD, two and a half hours are required for the wave function calculation and, again, 2 min are added for the coupling vectors. In this case, the coupling vectors are cheaper than overlaps, which require at least 16 min of computation time (t = 0.95). Still, in both cases, the overlaps can be computed in less time than the wave function calculations. In general, the question of whether nonadiabatic coupling vectors or overlaps are cheaper will depend on the wave function model, the basis set, and the number of electrons, and it is beneficial to have both methods available.
The above results show that qualitative information about wave function character and phase can be obtained in a few seconds when using a threshold value of t = 0.9. Almost converged results are obtained at t = 0.95 or 0.97 while still allowing for favorable computation times when compared to the effort of the actual MR-CI computation. Enhanced numerical stability is obtained if the results are additionally renormalized or orthogonalized. For quantitative applications, we suggest using 0.95 as a minimal threshold value. However, in many cases, larger thresholds are affordable, and for smaller wave function expansions, such as in CASSCF calculations, truncation becomes unnecessary.
3.3. Displacement of Atoms
Whenever atoms are displaced, as is the case most prominently in dynamics simulations, the overlaps are not only affected by the actual nonadiabatic interactions of interest but also by more trivial consequences of the displacement, e.g., the shift of the orbitals in space. As a consequence, the step size in nonadiabatic dynamics simulations will not only affect the general numerical stability of the wave function propagation,3,46 but when overlaps are applied, the specific effect of displaced orbitals should be taken into account, as well. It is worth noting that this problem is not a consequence of the use of atom-centered basis functions, but that it also exists in the complete basis set limit.
To construct a controlled test for this issue, we again consider the selenoacroleine molecule and its two geometries at θ = 50° and 55°. While one geometry (θ = 55°) is kept stationary in space, the other (θ = 50°) is translated in the x-direction (cf. Figure 1) up to a displacement of 0.1 Å. From a physical point of view, the nonadiabatic interactions should not be modified by this translation, and any modulations of the overlap elements are therefore unwanted artifacts. The ⟨T1|T2′⟩ overlap element is computed at the CASSCF(6,5) level of theory using different settings. On the one hand, three numbers of discarded core orbitals are used: 0, 5 (Se-1s, Se-2s, Se-2p), and 12 (also Se-3s, Se-3p, 3 × C-1s). On the other hand, raw and orthogonalized overlaps are plotted. The results are presented in Figure 5. At zero displacement, all values agree, giving a value of 0.71069 for the raw overlaps and 0.71884 for the orthogonalized ones. Once the molecule is displaced, a very steep decline of the raw overlaps (shown as dashed lines) is observed. This effect is particularly pronounced with zero discarded core orbitals, whereas the results are somewhat more stable when this number is increased to 5 or 12. To understand this effect, it is instructive to regard the size of the 1s core orbitals, which can be estimated as a(Z) = a0/Z, where a0 is the Bohr radius and Z is the nuclear charge. The smallest orbital in the system is the Se-1s orbital with a(34) = 0.016 Å. Indeed, this distance corresponds approximately to the displacement where the dashed black curve reaches half its maximum. Once the Se-1s orbital and the other core orbitals are discarded, the decay of the overlap is less steep but still significant. Considering, for example, a displacement of 0.1 Å, which amounts to only a small fraction of an interatomic bond distance, the values for 0, 5, and 12 discarded core orbitals are 9 × 10–7, 0.009, and 0.057, respectively. This decay is problematic for dynamics simulations because even the smallest translation of the molecule, which might occur because of numerical inaccuracies, can affect the computed overlap values. A similar effect, albeit more difficult to quantify, should occur in the case of variations of the molecular geometry. In contrast to the raw overlap values, excellent numerical stability is observed after orthogonalization. Even in the case of 0.1 Å displacement, the orthogonalized overlap matrix elements are all 0.71882 irrespective of the number of discarded core orbitals. The good performance of the orthogonalization process can be understood by the fact that all elements of the overlap matrix are scaled down uniformly by the translation and that the orthogonalization then simply amounts to renormalizing these elements. Two important conclusions can be drawn from Figure 5: First, core orbitals can have an unwanted effect on the overlap values despite not being involved in the nonadiabatic process. Discarding them improves the numerical stability while at the same time saving computational effort. Second, orthogonalization of the overlap matrix is a powerful tool to dispose of unwanted effects deriving from the molecular displacement.
Figure 5.

Computation of the CASSCF(6,5) ⟨T1|T2′⟩ overlap element for a selenoacroleine molecule displaced in the x-direction (θ = 50°) with respect to a stationary one (θ = 55°). Raw overlaps are given as dotted lines, and results after orthonormalization are given as solid lines (all overlapping). The number of discarded core orbitals (ncore) is indicated by the color.
Whereas the focus of this investigation was concerned with the effects of discrete displacements, it would be of interest to evaluate whether a similar procedure can be applied to eliminate the lack of rotational and translational invariance of nonadiabatic coupling vectors.37,47 However, this question is out of the scope of this work.
3.4. Performance and Parallelization
In
a next step, the general performance of the new implementation is
examined. For this purpose, five distinct wave function expansions
are chosen for the selenoacroleine molecule. Aside from the MR-CIS(6,5)
and MR-CISD(6,5) methods discussed before, CASSCF(10,10) and CASSCF(12,12)
computations are also performed to represent the case of larger active
spaces, all using the ANO-RCC-VDZP basis set. Furthermore, the MR-CIS(4,3)-1x
expansion (see Computational Details) is chosen
as a case with only two references in connection with the larger ANO-RCC-VTZP
basis set. Various values of the threshold t were
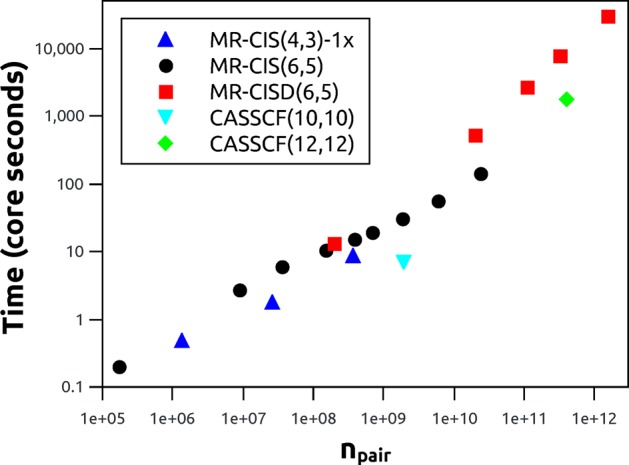
used to produce a set of 20 data points. In Figure 6, the computation times are plotted against
the number of pair determinants npair = nCI × nCI′. All these data points
are roughly on a straight line, highlighting the uniform performance
characteristics of the code with respect to this diverse set of wave
functions. In a simple direct algorithm, formal linear scaling of
the timings with respect to npair is expected
(see section 2.2).
By contrast, the effective scaling behavior seen here, obtained as
the slope in the logarithmic plot, is close to 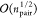 . It is observed that the above algorithm
is particularly efficient for large CASSCF expansions owing to the
fact that these allow for the strongest reduction in the number of
spin factors. In the case of CASSCF(12,12), there are npair = 3.9 × 1011 terms to be computed
that can be represented by only nfac =
1.3 × 106 spin factors. Indeed, in this case, the
computation time is determined by the final contraction (eq 14), whereas the primary
determinant computation (eq 8) requires less than 1% of time. The MR-CIS expansions profit
from the one-step Laplace recursion of eq 15, which again allows for efficient computation
of the determinants. By contrast, the MR-CISD results are somewhat
above the remaining data points, showing that further speedup would
be possible through a more extended use of the Laplace recursion (eq 15) or a similar formalism.
However, also in these cases, 10–20% of the computation time
is used for the contraction step (eq 14), setting a clear limit for the effect of any possible
improvement in the determinant computation.
. It is observed that the above algorithm
is particularly efficient for large CASSCF expansions owing to the
fact that these allow for the strongest reduction in the number of
spin factors. In the case of CASSCF(12,12), there are npair = 3.9 × 1011 terms to be computed
that can be represented by only nfac =
1.3 × 106 spin factors. Indeed, in this case, the
computation time is determined by the final contraction (eq 14), whereas the primary
determinant computation (eq 8) requires less than 1% of time. The MR-CIS expansions profit
from the one-step Laplace recursion of eq 15, which again allows for efficient computation
of the determinants. By contrast, the MR-CISD results are somewhat
above the remaining data points, showing that further speedup would
be possible through a more extended use of the Laplace recursion (eq 15) or a similar formalism.
However, also in these cases, 10–20% of the computation time
is used for the contraction step (eq 14), setting a clear limit for the effect of any possible
improvement in the determinant computation.
Figure 6.
Performance of the wave function overlap code for varying wave function expansions: computation time plotted against the number of determinant pairs (npair).
The parallel performance in shared memory is tested
in the case
of an extended MR-CISD(6,5) calculation on selenoacroleine covering npair = 6.7 × 1012 determinant
pairs (i.e., the t = 0.995 case in Figure 4). The speedup going from 1
to 32 cores is presented in Figure 7a. This figure presents the good scalability of the
code, showing in fact superlinear scaling. In Figure 7b, the total computation time is dissected
into the different relevant steps. The core hours consumed are plotted
against the number of cores, a representation where perfect parallel
scaling amounts to a horizontal line. The two major time-consuming
tasks are the determinant computations (eq 8) and the final contraction of the 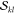 factors with the CI vector (eq 14). Both of these tasks have been
parallelized. As seen in Figure 7b, almost ideal scaling is obtained in the case of
the determinant computations as this is a CPU-time-limited step with
little memory overhead. By contrast, the contraction step shows somewhat
erratic behavior, even providing a superlinear speedup for an intermediate
number of cores. This behavior is probably a consequence of the fact
that this step is limited by memory bandwidth and the precise usage
of various cache levels. Figure 7b also presents timings of the sorting step with a
parallelization up to four cores and the sequential I/O step. The
relative contributions of these steps increase linearly with the number
of cores. However, even at 32 cores, these amount to only 1% of the
total computation time, and further parallelization is not necessary.
factors with the CI vector (eq 14). Both of these tasks have been
parallelized. As seen in Figure 7b, almost ideal scaling is obtained in the case of
the determinant computations as this is a CPU-time-limited step with
little memory overhead. By contrast, the contraction step shows somewhat
erratic behavior, even providing a superlinear speedup for an intermediate
number of cores. This behavior is probably a consequence of the fact
that this step is limited by memory bandwidth and the precise usage
of various cache levels. Figure 7b also presents timings of the sorting step with a
parallelization up to four cores and the sequential I/O step. The
relative contributions of these steps increase linearly with the number
of cores. However, even at 32 cores, these amount to only 1% of the
total computation time, and further parallelization is not necessary.
Figure 7.
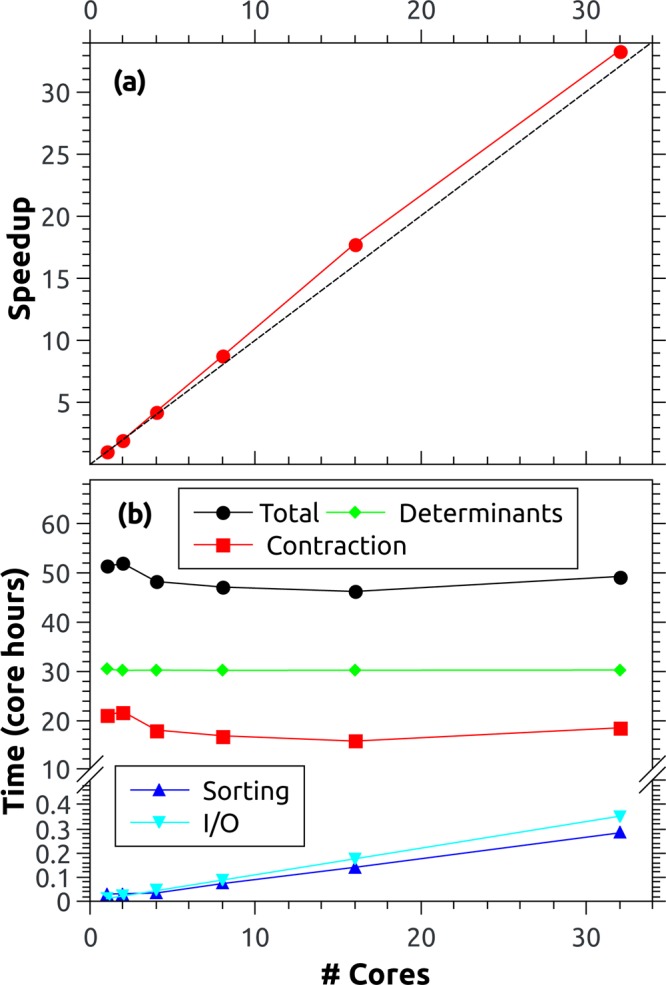
Parallel performance of the overlap code for a selenoacroleine MR-CISD(6,5) computation requiring the evaluation of 6.7 × 1012 Slater determinant overlaps: (a) speedup from 1 to 32 cores and (b) computation times for the different steps as discussed in the text.
4. Conclusions
A new algorithm for the computation of wave function overlaps between many-electron wave functions is presented. By virtue of an optimized algorithm, which makes extended use of recurring intermediates, a highly efficient code was generated, which allows for computations with MR-CISD wave functions, with large active space, and with extended basis sets. Because of the general formalism employed, there are no restrictions with respect to the wave functions except that they have to be given in a Slater determinant expansion based on restricted or unrestricted molecular orbitals. Consequently, it is possible to vary the wave function model, the orbitals, the one-electron basis set, and the molecular geometry. The code is directly applicable to models producing explicit wave functions, i.e., the configuration interaction and multiconfigurational SCF methods. Extensions to time-dependent density functional theory, coupled cluster, and other response theory methods are straightforward using approximations that have been described previously.8,9,17
The code was verified against general nonadiabatic theory19 by computing a circular path integral in coordinate space and against two existing implementations12,13 by using appropriate example computations, showing excellent agreement. Furthermore, the effects of using truncated wave functions were studied, and it was found that values of t = 0.95 or 0.97 for the squared norm of the truncated wave function could already provide satisfactory results. In addition, attention was devoted to understanding unwanted effects deriving from discrete displacements of atoms and orbitals, which naturally occur in dynamics simulations. For both cases, wave function truncation and orbital displacement, it was found that an orthogonalization of the overlap matrix2 can improve the results dramatically.
The wave function overlap code has been interfaced to the Sharc program package41,43 with the focus of performing nonadiabatic dynamics simulations. Because of the general formalism employed, the code is certainly not limited to this application, and other tasks can be envisaged where the new code will be beneficial, for example, the comparison of wave functions constructed at different levels of theory and probing the initial electronic states after β-decay48 or after the photoionization of core-electrons.49 Furthermore, the computation of Dyson norms,50 as required for the simulation of photoelectron spectra, can be achieved by a slight modification of the code. Some of these tasks are currently being investigated by the authors.
5. Computational Details
Most calculations on selenoacroleine were performed using an active space containing 6 electrons in 5 active orbitals (2 × π, nSe, 2 × π*), i.e., CASSCF(6,5) and MR-CI(6,5), in connection with the ANO-RCC-VDZP basis set51 including state-averaging over the lowest two singlet and triplet states. The active space was enhanced for CASSCF(10,10) and CASSCF(12,12) computations, whereas a smaller active space of 3 orbitals (π, nSe, π*) was used for MR-CIS(4,3) and MR-CIS(4,3)-1x computations. In the latter case, the maximum number of reference excitations into the π* orbital was restricted to 1, resulting in only two reference configurations, and the computation was performed using the larger ANO-RCC-VTZP basis set. Scalar relativistic effects were taken into account in these all-electron calculations by using the second-order Douglas–Kroll–Hess Hamiltonian.52 Unless otherwise specified, 12 core orbitals corresponding to the s and p orbitals in the first, second, and third shells on Se and the 1s orbitals on C were frozen in the MR-CI computations and discarded in the wave function overlap computations. For the triplet/triplet overlaps, generally, the ms = −1 wave functions were considered, as these contain fewer determinants than the ms = 0 ones, allowing for speedup of the computations while not affecting the results.
CASSCF computations on Ir(C3H4N)3 were performed by including 12 electrons in 9 orbitals (3 × π, 3 × d, 3 × π*). The iridium atom was described by the LANL2DZ effective core potential (ECP), in its “small-core” version, and the corresponding basis set for the active (5s, 5p, 5d, 6s, 6p) orbital shells,53 whereas for the remaining atoms, the 6-31G* basis set54 was employed.
The MR-CI computations were carried out with the Columbus 7.0 program package31,55,56 using its parallel MR-CI implementation,57,58 whereas Molcas 8.0(27,59) was applied for the integrals and most of the CASSCF calculations. In the cases of comparing different overlap programs, generally no frozen core orbitals were considered to allow for a clear comparison. The benchmark calculations for varying wave function models (Figure 6) were performed on one core of an Intel Xeon E5-2650-V3 CPU at 2.3 GHz, whereas the parallel performance tests (Figure 7) were carried out on an HP DL580G7 server with 512 GB of main memory and 4 Intel E7-4850 (Westmere) CPUs at 2.0 GHz with 10 cores each.
Acknowledgments
The authors thank J. Pittner, H. Lischka, T. Müller, and I. Schapiro for discussions regarding different topics covered in this manuscript. This paper is based upon work supported by the VSC Research Center funded by the Austrian Federal Ministry of Science, Research and Economy (bmwfw). The computational results presented have been achieved in part using the Vienna Scientific Cluster (VSC), Projects 70719 and 70726. The authors also thank the Austrian Science Fund FWF (Project P25827) and the COST actions CM1204 (XLIC) and CM1305 (ECOSTBio).
Appendix A. Slater Determinant Overlaps
In this part, we present a simple derivation for the overlap between two nonorthogonal Slater determinants, a formula that was originally derived by Löwdin.21 Given two Slater determinants
| 33 |
| 34 |
it is shown that their overlap is given by the determinant of the matrix containing all mixed orbital overlaps
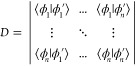 |
35 |
First, the explicit form of the Slater determinants is invoked
| 36 |
| 37 |
where Sn is the symmetric group of order n, i.e., the set of all possible permutations of n elements. This yields the following expression for the overlap
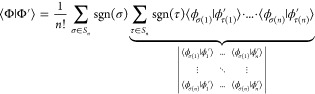 |
38 |
The part underlined is the determinant introduced in eq 35 but with permuted rows. It possesses the value D multiplied by the sign of σ, which in turn means that
| 39 |
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.5b01148.
Molecular coordinates and total CASSCF energies of selenoacroleine and Ir(C3H4N)3 (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Hammes-Schiffer S.; Tully J. C. J. Chem. Phys. 1994, 101, 4657–4667. 10.1063/1.467455. [DOI] [Google Scholar]
- Granucci G.; Persico M.; Toniolo A. J. Chem. Phys. 2001, 114, 10608–10615. 10.1063/1.1376633. [DOI] [Google Scholar]
- Plasser F.; Granucci G.; Pittner J.; Barbatti M.; Persico M.; Lischka H. J. Chem. Phys. 2012, 137, 22A514. 10.1063/1.4738960. [DOI] [PubMed] [Google Scholar]
- Groenhof G.; Bouxin-Cademartory M.; Hess B.; de Visser S. P.; Berendsen H. J. C.; Olivucci M.; Mark A. E.; Robb M. A. J. Am. Chem. Soc. 2004, 126, 4228–4233. 10.1021/ja039557f. [DOI] [PubMed] [Google Scholar]
- Weingart O.; Schapiro I.; Buss V. J. Phys. Chem. B 2007, 111, 3782–3788. 10.1021/jp0683216. [DOI] [PubMed] [Google Scholar]
- Fernandez-Alberti S.; Roitberg A. E.; Nelson T.; Tretiak S. J. Chem. Phys. 2012, 137, 014512. 10.1063/1.4732536. [DOI] [PubMed] [Google Scholar]
- Levine B. G.; Coe J. D.; Virshup A. M.; Martinez T. J. Chem. Phys. 2008, 347, 3–16. 10.1016/j.chemphys.2008.01.014. [DOI] [Google Scholar]
- Tapavicza E.; Tavernelli I.; Rothlisberger U. Phys. Rev. Lett. 2007, 98, 23001. 10.1103/PhysRevLett.98.023001. [DOI] [PubMed] [Google Scholar]
- Mitrić R.; Werner U.; Bonačić-Koutecký V. J. Chem. Phys. 2008, 129, 164118. 10.1063/1.3000012. [DOI] [PubMed] [Google Scholar]
- Novak J.; Mališ M.; Prlj A.; Ljubić I.; Kühn O.; Došlić N. J. Phys. Chem. A 2012, 116, 11467–11475. 10.1021/jp3074865. [DOI] [PubMed] [Google Scholar]
- Du L.; Lan Z. J. Chem. Theory Comput. 2015, 11, 1360–1374. 10.1021/ct501106d. [DOI] [PubMed] [Google Scholar]
- Pittner J.; Lischka H.; Barbatti M. Chem. Phys. 2009, 356, 147–152. 10.1016/j.chemphys.2008.10.013. [DOI] [Google Scholar]
- Malmqvist P.-Å.; Roos B. O. Chem. Phys. Lett. 1989, 155, 189–194. 10.1016/0009-2614(89)85347-3. [DOI] [Google Scholar]
- Barbatti M.; Pittner J.; Pederzoli M.; Werner U.; Mitrić R.; Bonačić-Koutecký V.; Lischka H. Chem. Phys. 2010, 375, 26–34. 10.1016/j.chemphys.2010.07.014. [DOI] [Google Scholar]
- Mai S.; Müller T.; Plasser F.; Marquetand P.; Lischka H.; González L. J. Chem. Phys. 2014, 141, 074105. 10.1063/1.4892060. [DOI] [PubMed] [Google Scholar]
- Tao H.; Levine B. G.; Martínez T. J. J. Phys. Chem. A 2009, 113, 13656–13662. 10.1021/jp9063565. [DOI] [PubMed] [Google Scholar]
- Plasser F.; Crespo-Otero R.; Pederzoli M.; Pittner J.; Lischka H.; Barbatti M. J. Chem. Theory Comput. 2014, 10, 1395–1405. 10.1021/ct4011079. [DOI] [PubMed] [Google Scholar]
- Sapunar M.; Ponzi A.; Chaiwongwattana S.; Mališ M.; Prlj A.; Decleva P.; Došlić N. Phys. Chem. Chem. Phys. 2015, 17, 19012–19020. 10.1039/C5CP02100F. [DOI] [PubMed] [Google Scholar]
- Baer M. Phys. Rep. 2002, 358, 75–142. 10.1016/S0370-1573(01)00052-7. [DOI] [Google Scholar]
- The sign change is given by the sign of the permutation σ that puts the orbitals into the correct order. The sign of the permutation is, in turn, computed as sgnσ = −1invσ where invσ is the number of inversions of the permutation, i.e., the number of pairs of orbitals that are in the wrong order initially.
- Löwdin P.-O. Phys. Rev. 1955, 97, 1474–1489. 10.1103/PhysRev.97.1474. [DOI] [Google Scholar]
- Plasser F.; Lischka H. J. Chem. Theory Comput. 2012, 8, 2777–2789. 10.1021/ct300307c. [DOI] [PubMed] [Google Scholar]
- Plasser F.; Lischka H. J. Chem. Phys. 2011, 134, 34309. 10.1063/1.3526697. [DOI] [PubMed] [Google Scholar]
- Amos A. T.; Hall G. G. Proc. R. Soc. London, Ser. A 1961, 263, 483–493. 10.1098/rspa.1961.0175. [DOI] [Google Scholar]
- Sundstrom E. J.; Head-Gordon M. J. Chem. Phys. 2014, 140, 114103. 10.1063/1.4868120. [DOI] [PubMed] [Google Scholar]
- Malmqvist P.-Å. Int. J. Quantum Chem. 1986, 30, 479–494. 10.1002/qua.560300404. [DOI] [Google Scholar]
- Aquilante F.; Autschbach J.; Carlson R. K.; Chibotaru L. F.; Delcey M. G.; De Vico L.; Galvan I. F.; Ferre N.; Frutos L. M.; Gagliardi L.; Garavelli M.; Giussani A.; Hoyer C. E.; Li Manni G.; Lischka H.; Ma D.; Malmqvist P.-Å.; Müller T.; Nenov A.; Olivucci M.; Pedersen T. B.; Peng D.; Plasser F.; Pritchard B.; Reiher M.; Rivalta I.; Schapiro I.; Segarra-Marti J.; Stenrup M.; Truhlar D. G.; Ungur L.; Valentini A.; Vancoillie S.; Veryazov V.; Vysotskiy V. P.; Weingart O.; Zapata F.; Lindh R. J. Comput. Chem. 2016, 37, 506. 10.1002/jcc.24221. [DOI] [PubMed] [Google Scholar]
- Blaizot J.-P.; Ripka G.. Quantum Theory of Finite Systems; MIT Press, 1986. [Google Scholar]
- Golub G. H.; van Loan C. F.. Matrix Computations, 4th ed.; JHU Press, 2013. [Google Scholar]
- Pan V.; Yu Y.; Stewart C. Computers Math. Applic. 1997, 34, 43–70. 10.1016/S0898-1221(97)00097-7. [DOI] [Google Scholar]
- Lischka H.; Shepard R.; Shavitt I.; Pitzer R. M.; Dallos M.; Muller T.; Szalay P. G.; Brown F. B.; Ahlrichs R.; Boehm H. J.; Chang A.; Comeau D. C.; Gdanitz R.; Dachsel H.; Ehrhardt C.; Ernzerhof M.; Hoechtl P.; Irle S.; Kedziora G.; Kovar T.; Parasuk V.; Pepper M. J. M.; Scharf P.; Schiffer H.; Schindler M.; Schueler M.; Seth M.; Stahlberg E. A.; Zhao J.-G.; Yabushita S.; Zhang Z.; Barbatti M.; Matsika S.; Schuurmann M.; Yarkony D. R.; Brozell S. R.; Beck E. V.; Blaudeau J.-P.; Ruckenbauer M.; Sellner B.; Plasser F.; Szymczak J. J.. COLUMBUS: An Ab Initio Electronic Structure Program, release 7.0; www.univie.ac.at/columbus, 2015.
- Shepard R. Int. J. Quantum Chem. 1991, 40, 865–887. 10.1002/qua.560400613. [DOI] [Google Scholar]
- Te Velde G.; Bickelhaupt F. M.; Baerends E. J.; Fonseca Guerra C.; van Gisbergen S. J. A.; Snijders J. G.; Ziegler T. J. Comput. Chem. 2001, 22, 931–967. 10.1002/jcc.1056. [DOI] [Google Scholar]
- Lengsfield B. H.; Saxe P.; Yarkony D. R. J. Chem. Phys. 1984, 81, 4549. 10.1063/1.447428. [DOI] [Google Scholar]
- Bearpark M. J.; Robb M. A.; Schlegel H. B. Chem. Phys. Lett. 1994, 223, 269–274. 10.1016/0009-2614(94)00433-1. [DOI] [Google Scholar]
- Lischka H.; Dallos M.; Szalay P. G.; Yarkony D. R.; Shepard R. J. Chem. Phys. 2004, 120, 7322–7329. 10.1063/1.1668615. [DOI] [PubMed] [Google Scholar]
- Fatehi S.; Alguire E.; Shao Y.; Subotnik J. E. J. Chem. Phys. 2011, 135, 1–21. 10.1063/1.3665031. [DOI] [PubMed] [Google Scholar]
- Keal T. W.; Koslowski A.; Thiel W. Theor. Chem. Acc. 2007, 118, 837–844. 10.1007/s00214-007-0331-5. [DOI] [Google Scholar]
- Shenvi N.; Subotnik J. E.; Yang W. J. Chem. Phys. 2011, 134, 144102. 10.1063/1.3575588. [DOI] [PubMed] [Google Scholar]
- Barbatti M.; Ruckenbauer M.; Plasser F.; Pittner J.; Granucci G.; Persico M.; Lischka H. WIREs: Comp. Mol. Sci. 2014, 4, 26–33. 10.1002/wcms.1158. [DOI] [Google Scholar]
- Mai S.; Marquetand P.; González L. Int. J. Quantum Chem. 2015, 115, 1215–1231. 10.1002/qua.24891. [DOI] [Google Scholar]
- Mai S.; Marquetand P.; González L. J. Chem. Phys. 2014, 140, 204302. 10.1063/1.4875036. [DOI] [PubMed] [Google Scholar]
- Mai S.; Richter M.; Ruckenbauer M.; Oppel M.; Marquetand P.; González L.. SHARC: Surface Hopping Including Arbitrary Couplings - Program Package for Non-Adiabatic Dynamics; sharc-md.org, 2014.
- Plasser F.; Dreuw A. J. Phys. Chem. A 2015, 119, 1023–1026. 10.1021/jp5122917. [DOI] [PubMed] [Google Scholar]
- Gozem S.; Huntress M.; Schapiro I.; Lindh R.; Granovsky A. A.; Angeli C.; Olivucci M. J. Chem. Theory Comput. 2012, 8, 4069–4080. 10.1021/ct3003139. [DOI] [PubMed] [Google Scholar]
- Nelson T.; Fernandez-Alberti S.; Chernyak V.; Roitberg A. E.; Tretiak S. J. Chem. Phys. 2012, 136, 54108. 10.1063/1.3680565. [DOI] [PubMed] [Google Scholar]
- Yarkony D. R. J. Chem. Phys. 1986, 84, 3206. 10.1063/1.450250. [DOI] [Google Scholar]
- Kaplan I. G.; Smutny V. N. Adv. Quantum Chem. 1988, 19, 289–348. 10.1016/S0065-3276(08)60618-8. [DOI] [Google Scholar]
- Ottosson N.; Børve K. J.; Spångberg D.; Bergersen H.; Sæthre L. J.; Faubel M.; Pokapanich W.; Öhrwall G.; Björneholm O.; Winter B. J. Am. Chem. Soc. 2011, 133, 3120–3130. 10.1021/ja110321q. [DOI] [PubMed] [Google Scholar]
- Spanner M.; Patchkovskii S.; Zhou C.; Matsika S.; Kotur M.; Weinacht T. C. Phys. Rev. A: At., Mol., Opt. Phys. 2012, 86, 053406. 10.1103/PhysRevA.86.053406. [DOI] [PubMed] [Google Scholar]
- Roos B. O.; Lindh R.; Malmqvist P.-Å.; Veryazov V.; Widmark P.-O. J. Phys. Chem. A 2004, 108, 2851–2858. 10.1021/jp031064+. [DOI] [Google Scholar]
- Reiher M. Theor. Chem. Acc. 2006, 116, 241–252. 10.1007/s00214-005-0003-2. [DOI] [Google Scholar]
- Hay P. J.; Wadt W. R. J. Chem. Phys. 1985, 82, 299–310. 10.1063/1.448975. [DOI] [Google Scholar]
- Hariharan P.; Pople J. Theor. Chim. Acta 1973, 28, 213–222. 10.1007/BF00533485. [DOI] [Google Scholar]
- Lischka H.; Shepard R.; Pitzer R. M.; Shavitt I.; Dallos M.; Müller T.; Szalay P. G.; Seth M.; Kedziora G. S.; Yabushita S.; Zhang Z. Y. Phys. Chem. Chem. Phys. 2001, 3, 664–673. 10.1039/b008063m. [DOI] [Google Scholar]
- Lischka H.; Müller T.; Szalay P. G.; Shavitt I.; Pitzer R. M.; Shepard R. WIREs: Comp. Mol. Sci. 2011, 1, 191–199. 10.1002/wcms.25. [DOI] [Google Scholar]
- Dachsel H.; Lischka H.; Shepard R.; Nieplocha J.; Harrison R. J. J. Comput. Chem. 1997, 18, 430–448. . [DOI] [Google Scholar]
- Müller T. J. Phys. Chem. A 2009, 113, 12729–12740. 10.1021/jp905254u. [DOI] [PubMed] [Google Scholar]
- Veryazov V.; Widmark P.-O.; Serrano-Andrés L.; Lindh R.; Roos B. O. Int. J. Quantum Chem. 2004, 100, 626–635. 10.1002/qua.20166. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


