Enhanced (hydrodynamic) transport induced by population growth in reaction–diffusion systems with application to population genetics

Abstract

We consider a system made up of different physical, chemical, or biological species undergoing replication, transformation, and disappearance processes, as well as slow diffusive motion. We show that for systems with net growth the balance between kinetics and the diffusion process may lead to fast, enhanced hydrodynamic transport. Solitary waves in the system, if they exist, stabilize the enhanced transport, leading to constant transport speeds. We apply our theory to the problem of determining the original mutation position from the current geographic distribution of a given mutation. We show that our theory is in good agreement with a simulation study of the mutation problem presented in the literature. It is possible to evaluate migratory trajectories from measured data related to the current distribution of mutations in human populations.

In some cases reaction–diffusion systems can generate enhanced (hydrodynamic) transport due to mechanical or electromagnetic coupling; for example, the occurrence of a reaction produces variations in density or pressure and these variations lead to convection currents (1). This type of phenomenon may occur not only in macroscopic systems but also in single-molecule kinetics (2). In this note we report on a type of enhanced transport in reaction–diffusion systems that does not require mechanical or electromagnetic coupling. We show that under rather general conditions the growth of a species leads to enhanced transport, which may be encountered in the case of diffusing, growing populations and is independent of the detailed kinetics of the process; in particular, it may exist whether the kinetics of the process is linear or nonlinear. The analysis of the enhanced transport induced by population growth is of interest in connection with a broad range of problems in physics, chemistry, and biology, which can be described by reaction–diffusion equations.

The structure of this note is the following. We suggest a deterministic reaction–diffusion model, which describes the transformation, replication, disappearance, and diffusion of a set of interacting species. We derive transport equations for the fractions of the species and show that net population growth can induce enhanced transport for these fractions, even though the motion of individual species is diffusive. We show that the enhanced transport leads to a coherent motion characterized by the same transport (hydrodynamic) velocity for all fractions, provided that the transport and rate coefficients obey a neutrality condition. Further on, we discuss the implications of possible occurrence of solitary waves during the enhanced transport. Finally, we illustrate our approach by studying the geographical spreading of mutations in human populations.

Enhanced Transport for Reaction–Diffusion Systems with Growth

We consider a system made up of different individuals X_u, u = 1, 2,... (molecules, quasiparticles, biological organisms, etc). The species X_u, u = 1, 2,... replicate, transform into each other, die, and at the same time undergo slow, diffusive motion, characterized by the diffusion coefficients D_u, u = 1, 2,..., which are assumed to be constant. The replication and disappearance rates 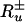of the different species are assumed to be proportional to the species densities x_u, u = 1, 2,...; we have 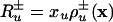, where the rate coefficients 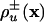are generally dependent on the composition vector x = (x_u); similarly, the rate R_u→v of transformation of species X_u into the species X_v is given by R_u→v = x_uk_uv(x), where k_uv(x) are composition-dependent rate coefficients. Under these circumstances the process can be described by the following reaction–diffusion equations:

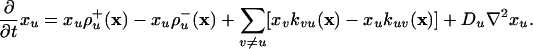[1]

We are interested in the time and space evolution of the fractions of the different species present in the system: γ_u = x_u/x, with 1 = Σ_u γ_u, where x = Σ_u x_u is the total population density. For example, in chemistry γ_u are molar fractions, whereas in population genetics they are gene frequencies. After lengthy algebraic transformations, Eq. 1 leads to the following evolution equations for the total population density x and for the fractions γ_u:

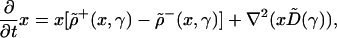[2]

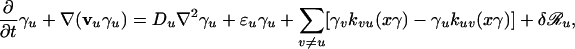[3]

where

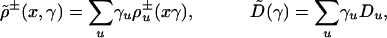[4]

are average rate and transport coefficients,

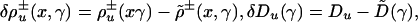[5]

are deviations of the individual rate and transport coefficients from the corresponding average values,

[6]

are transport (hydrodynamic) speeds and expansion coefficients attached to different population fractions,

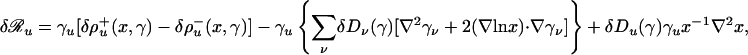[7]

are the components of the rates of change of the population fractions due to the individual variations of the rate and transport coefficients, and γ = (γ₁, γ₂,...) is the vector of population fractions.

We notice that, even though the different species are undergoing slow, diffusive motions, the corresponding population fractions move faster: in the evolution Eq. 3 there are both diffusive terms and convective transport (hydrodynamic) terms depending on the transport speeds v_u given by Eqs. 6. According to Eqs. 6 these transport speeds are generated by the space variations of the total population density and have the opposite sign of the gradient of the total population densities. For a growing population the population cloud usually expands from an original area and tries to occupy all space available. The population density decreases towards the edge of the population cloud; thus the population gradient is negative and the transport velocities are positive, oriented towards the directions of propagation of the population cloud. It follows that the cause of enhanced transport of the species fractions is the net population growth. Because the gradient tends to increase toward the edge of the population wave an initial perturbation of the species fractions generated in the propagation front of the population has good chances of undergoing enhanced transport and spreading all over the system. An initial perturbation produced close to the initial area where the population originates has poor chances of undergoing sustained enhanced transport. It is important to clarify the mathematical and physical significance of the hydrodynamic transport terms ∇(v_uγ_u) in Eq. 3. From the mathematical point of view the terms ∇(v_uγ_u) emerge as a result of a nonlinear transformation of the state variables, from species densities to species fractions. The physical interpretation of the transport terms ∇(v_uγ_u) depends on the direction and orientation of the speed vectors: for expanding populations v_u are generally oriented towards to direction of expansion of the population cloud, resulting in enhanced transport. For shrinking population clouds the terms ∇(v_uγ_u) lead to the opposite effect, that of the transport process slowing down.

In general, different population fractions have different propagation speeds. An interesting particular case is that for which the replication and disappearance rate coefficients and the diffusion coefficients are the same for all species and depend only on the total population density 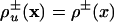, D_u = D. Moreover, we assume that the transformation rates are constant k_uv(x) = k_uv. This type of condition is fulfilled in chemistry by tracer experiments, for which the variation of the rate and transport coefficients due to the kinetic isotope effect can be neglected (refs. 3 and 4 and refs. cited in ref. 4). Similar restrictions are fulfilled in population genetics, in the case of neutral mutations, for which the demographic and transport parameters are the same for neutral mutants and nonmutants, respectively (5, 6). For systems that obey this type of restrictions we use the terms of neutral systems and neutrality conditions, respectively; these terms originated in population genetics. For neutral systems the evolution equations turn into a simpler form,

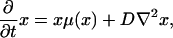[8]

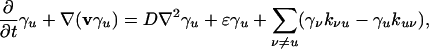[9]

where μ(x) = ρ⁺(x) – ρ^–(x) is the net production rate of the total population. We notice that the total population density obeys a separate equation, which is independent of the species fractions and the evolution equations for the fractions become linear.

It may seem that the existence of the enhanced transport is possibly related to the existence of solitary waves in the system. Our analysis shows that enhanced transport may exist even if a solitary wave does not exist: for example, enhanced transport may exist for linear kinetics, which cannot give rise to solitary waves. Nevertheless, solitary waves, if they exist, are related to enhanced transport. We assume that the total population starts growing from a given initial area and then spreads, occupying all space available. We assume that the net production rate μ(x) in Eq. 8 decreases with the population size x and equals zero for the saturation value x_∞, μ(x_∞) = 0. For isotropic conditions, under these circumstances Eq. 8 may have a solitary wave solution of the Fisher type (7),

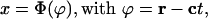[10]

where ϕ and c are the phase and the speed vectors of the solitary wave, respectively, r is the position vector, and Φ(ϕ) is a scalar function of the phase vector. For small absolute values of the phase, |ϕ|, the function Φ(ϕ) reaches the saturation value x_∞, whereas for large |ϕ| it tends toward zero:

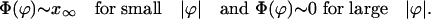[11]

According to Eq. 11 we have two different extreme transport regimes. The first regime, for small phases, corresponds to slow, pure diffusive transport. From Eqs. 6 and 11 we have v ∼ 0, ε ∼ 0 for small |ϕ|. If we neglect the boundary conditions, Eq. 9 can be easily integrated, resulting in

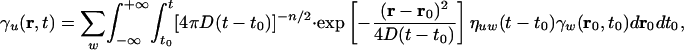[12]

where n is the space dimension and

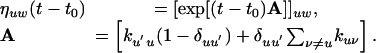[13]

For large phases we have

[14]

For applying Eqs. 14 we need to know the shape of the tail of the function Φ(ϕ) for large |ϕ|. We consider two different cases, that of the exponential tail, which corresponds to Fisher-like solutions, and that of the negative power law tail, which corresponds to self-similar solitary waves. For exponential tails we have

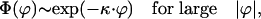[15]

where κ is a damping vector with physical dimension length^–1. It follows that

[16]

and the solution for unlimited space of the evolution Eq. 9 for the species fractions is

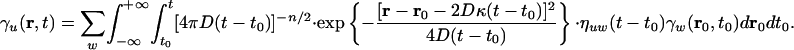[17]

In this case the enhanced transport is stable, characterized by a constant transport speed, and lasts for long times.

For self-similar tails we have

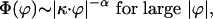[18]

where α is a positive fractal exponent. We obtain

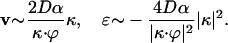[19]

Unfortunately in this case the evolution Eq. 9 for the species fractions cannot be solved exactly. However, we notice that in this case the components of the transport speed decay slowly to zero for large distances; moreover, the expansion coefficient is negative. We draw the conclusion that for solitary waves with long tails, the enhanced transport, if it ever exists, is only a transient effect.

In conclusion, if solitary waves are present, there are two different extreme transport regimes. If the initial perturbation of the fractions of the species occurs in areas where the total population has reached the saturation value x_∞, then the transport of the perturbation is slow and diffusive. For unlimited systems the species fractions can be represented as a superposition of Gaussian distributions with average values zero. The other extreme corresponds to the case where the initial perturbation of the species fractions occurs somewhere in the tail of the population wave. If the tail has an exponential shape, then a stable, enhanced transport may occur, characterized by a constant transport velocity. In this case the time evolutions of the species fractions can be represented as superpositions of Gaussian distributions with moving averages proportional to the diffusion coefficient and to the time interval that has elapsed from the occurrence of the initial perturbation. There is also an intermediate situation where the tail of the population wave is long and obeys a negative power law: in this case enhanced transport might occur, but only for short periods of time.

It is interesting to compare the speed c of propagation of the solitary wave, with the speed v of enhanced transport. The most efficient enhanced transport occurs if these speeds are equal. Otherwise, if |v| < |c| the wave of advance of the perturbation of the species fraction remains behind the wave of advancement of the total population.

Application to Population Genetics

Now we can investigate the problem that suggested the present research, the geographical spreading of neutral mutations in human populations (5, 6). We consider a growing population that diffuses slowly in time and assume that the net rate of growth is a linear function of population density, 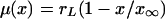, where 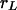is Lotka's intrinsic rate of growth of the population. We assume that, at an initial position and time, a neutral mutation occurs and afterward no further mutations occur. We are interested in the time and space dependence of the local fractions of the individuals, which are the offspring of the individual that carried the initial mutation. The ultimate goal of this analysis is the evaluation of the position and time where the mutation originated from measured data representing the current geographical distribution of the mutation. We limit our analysis to one-dimensional systems, for which a detailed theoretical analysis is possible. Eqs. 8 and 9 become

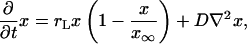[20]

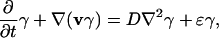[21]

where γ is local fraction of mutants. Eqs. 20 and 21 can be derived from an age-dependent model of population growth and correspond to a large system limit (eikonal approximation) of a stochastic model for population growth.

We notice that Eq. 20 for the total population growth is the well known Fisher equation (7), which has solitary solutions. Two different solitary wave solutions for Eq. 20 have been derived in the literature. There is an asymptotic solution developed by Luther, Fisher, and others (7, 8) and an exact solution derived by Ablowitz and Zeppetella (9). The asymptotic solution gives an excellent representation of the population wave from the top saturation level to the front edge where the total population tends to zero. The usefulness of the exact solution of Ablowitz and Zeppetella has been questioned in the literature (ref. 8, Vol. 1, pp. 451–452) because, although exact, it does not represent all possible solutions and the most relevant solutions may not be represented by it. In our notation the asymptotic solution is

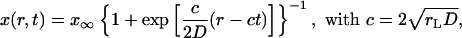[22]

and the exact solution of Ablowitz and Zeppetella is

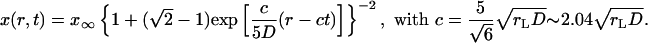[23]

By using Eqs. 22 and 23 we obtain the following expressions for the transport speed ν and for the expansion factor ε:

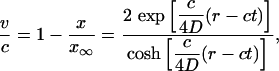[24]

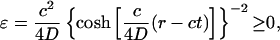[25]

for the Fisher asymptotic solution, and

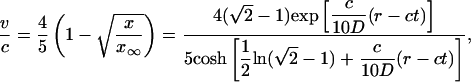[26]

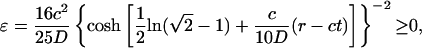[27]

for the exact solution of Ablowitz and Zeppetella. We notice that both solutions lead to constant transport speeds for small population densities, and thus enhanced transport may occur in both cases. The transport speeds are, however, different in the two cases. In the case of the asymptotic solution, for a mutation that occurs at the very edge of the total population wave, x ∼ 0, the transport speed is equal to the speed of propagation front, ν = c; the motion of two waves, for the total population and the mutation, is synchronized. For the solution of Ablowitz and Zeppetella, the maximum surfing speed, ν = 4c/5, is smaller than the speed c and thus the mutant wave remains behind the solitary wave for the total population. We notice that both solutions have exponential tails.

Now we can address the problem of determining the position where a mutation originates. The probability density P(r, t) of the position of the center of gravity of the mutant population can be roughly estimated by normalizing the mutant gene frequency:

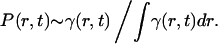[28]

By applying Eq. 28 we get a Gaussian distribution for the position r of the center of gravity of the mutant population both for the diffusive regime and for the enhanced transport:

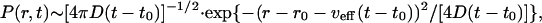[29]

where r₀ and t₀ are the initial position and time where the mutation occurred and ν_eff is an effective transport rate. In Eq. 29 we have ν_eff ∼ 0 for diffusive transport x ∼ x_∞ and ν_eff ∼ c (Fisher solution) or ν_eff ∼ 4c/5 (Ablowitz and Zeppetella solution) for the enhanced transport, x ∼ 0. Although for intermediate cases between these two extremes the probability density P(r, t) is generally not Gaussian, Eq. 29 can be used as a reasonable approximation, where the effective propagation speed ν_eff has an intermediate value between zero (diffusive transport) and the maximum values for enhanced transport corresponding to the two solutions of the Fisher equation. Under these circumstances the average position of the center of gravity of the mutant population increases linearly in time. From Eq. 29 we obtain

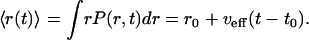[30]

If we examine the current geographical distribution of a mutation it is hard to estimate the value of the population density x at the position and time where the mutation originates. Under these circumstances it makes sense to treat x as a random variable selected from a certain probability density p(x). The only constraints imposed on p(x) are the conservation of the normalization condition 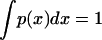, and the range of variation, x_∞ ≥ x ≥ 0. By using the maximum information entropy approach we can show that the most unbiased probability density p(x) is the uniform one:

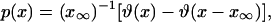[31]

where ϑ(x) is the Heaviside step function. By considering a large sample of different initial conditions, ν_eff can be evaluated as an average value

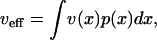[32]

where ν(x) is given by Eqs. 24 and 26. We have

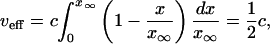[33]

for the Fisher solution and

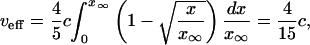[34]

for the Ablowitz and Zeppetella solution.

For the estimation of the initial position of a mutation it is useful to consider the ratio

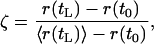[35]

where r(t_L) is the position of the limit of expansion, t_L is the time necessary for reaching the limit of expansion, 〈r(t_L)〉 is the position of the center of gravity of the mutant population for t = t_L, and r(t₀) = r₀ is the position where the mutation originates. In Eq. 35 both r(t_L), the position of the limit of expansion, and 〈r(t_L)〉, the current average position of the center of gravity of the mutant population, are accessible experimentally. It follows that, if the ratio ζ can be evaluated from theory, then r(t₀) = r₀, the point of origin of the mutation, can be evaluated from Eq. 35.By taking into account that the total population wave moves with the speed c and that the average center of gravity moves with the speed ν_eff, we have

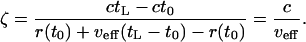[36]

It follows that ζ = 2 for the Fisher solution and ζ = 15/4 = 3.75 for the Ablowitz and Zeppetella solution. We notice that the Fisher solution is in good agreement with the numerical simulations of Edmonds et al. (5), which lead to ζ = 2.2. There are different possible causes for the difference of 0.2 between theory and simulations. Our theoretical computations of the ζ ratio refer to expansion in one dimension, whereas Edmonds et al. computed the ζ ratio for the one-dimensional, longitudinal component of motion in a two-dimensional model. Although the population expansion in their model is predominantly one-dimensional, the population motion on the transversal direction perpendicular to the predominant, longitudinal, direction might lead to the slowing down of the longitudinal motion, resulting in a ζ ratio slightly higher than 2. A simple analysis of a deterministic two-dimensional model with predominant longitudinal motion can be carried out by treating the losses due to transversal motion as perturbations of the longitudinal motion. It turns out that the corrections for the ζ ratio are <0.1 and a difference as big as 0.2 cannot be explained as due to the transversal motion.

Other possible sources of error can be due to the reflecting condition imposed by the boundaries of the system. In the vicinity of the boundaries both the Fisher and Ablowitz and Zeppetella solutions are incorrect. This is, however, a local effect, which leads to corrections of the same order of magnitude as the transversal motion. The only plausible explanation is that the difference between theory and simulations is probably the contribution of random drift, which is taken into account by simulations but ignored in the current theory. According to our theory the highest transport speeds occur for very small population densities, for which the influence of random drift is the strongest. The random drift may lead to population extinction, an effect that is ignored in our approach. It follows that our theory overestimates the contribution of very small population densities to enhanced transport. A crude way of considering the effect of random drift in our theory is to introduce a minimum cutoff value, x_cut, for which the enhanced transport occurs. Below this value, population extinction due to random drift is predominant. By taking the cutoff value x_cut into account, the maximum information approach leads to the following expression for the probability density p(x):

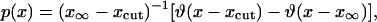[37]

and Eqs. 33 and 34 become

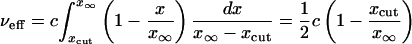[38]

for the Fisher solution and

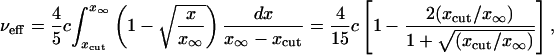[39]

for the Ablowitz and Zeppetella solution. From Eqs. 38 and 39 we get the following corrected value for the ζ ratio:

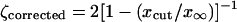[40]

for the Fisher solution and

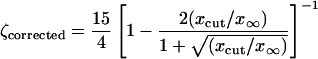[41]

for the Ablowitz and Zeppetella solution. By assuming that ζ_corrected has the value 2.2 obtained in the simulations, from these equations we can evaluate the cutoff value x_cut. We obtain x_cut = x_∞/11 for the Fisher solution. For the Ablowitz and Zeppetella solution, however, from Eq. 41 we get a quadratic equation in 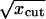with a negative discriminant that has no real solutions. It follows that, according to our corrected theory, in the case of Fisher the solution for population densities <9% from the saturation population densities the random drift makes the enhanced transport impossible. The Ablowitz and Zeppetella solution fails to represent simulation data, because it leads to transport speeds that are too small.

Conclusions

Here we have shown that the growth processes in reaction–diffusion may lead to enhanced transport characterized by hydrodynamic speeds. This phenomenon is the result of the balance between growth and expansion: the growth process increases the driving force of transport, resulting in a transition from slow, diffusive transport to enhanced, hydrodynamic transport, characterized by transport speeds. For the enhanced transport to occur it is not necessary that the system display solitary waves. However, the solitary waves, if they exist, stabilize the enhanced transport, resulting in constant propagation speeds. We have applied our theory to the problem of evaluation of the point of origin of mutations in population genetics from the current geographic distribution of mutations. We have investigated the stabilizing effect of the two types of solitary wave solutions of the Fisher equation, and we have shown that the theoretical predictions made on the basis of the asymptotic Fisher solution are in good agreement with the numerical simulations of Edmonds et al. (5). By comparing the theory with the simulations we have suggested a corrected theory, which takes the contribution of the random drift into account.

The general approach to enhanced transport presented in this note neglects the contribution of random drift. For the application in population genetics we have included the effect of random drift by using a crude mean-field approach. The contribution of random drift can be better described in terms of a space-dependent generalization of the theory of branching chain processes (10). Another interesting problem is the analysis of the connections between the mechanism of enhanced transport discussed in this paper and active Brownian motion (11), with possible implications on the theory of chemotactic motion.