Abstract
We test the backward haplotype transmission association algorithm on genome-scan data previously studied by Rioux et al. [Rioux, J. D., et al. (2000) Am. J. Hum. Genet. 66, 1863–1870]. In their study, multipoint linkage methods were applied to affected sib-pairs with inflammatory bowel disease, and significant linkage evidence points to two susceptibility loci. After we apply our approach to these data with a global search accounting for both joint and marginal effects, very interesting results emerge, many of them intriguing. These results provide compelling support for the application of our approach to other data wherever applicable. Results from this project also make it clear that it is important to reinvestigate available family-based datasets that can be suitably reanalyzed. Given previously collected data in the literature, our approach, with its increased efficiency in using available resources, draws additional crucial information that may lead to novel and surprising results.
Keywords: backward haplotype transmission association, genome scan
During the past two decades, a number of novel statistical methods have been developed to detect association and linkage between markers and disease genes. The success, however, has been largely restricted to simple Mendelian diseases. For more common and complex human disorders, the progress from the efforts of searching susceptibility loci using existing statistical methods has been slow, and the results are often inconsistent. This result is due in part to the fact that most current methods make use of marginal information only and fail to include the useful information of the interaction among the disease loci. It is thus less likely for these methods to have adequate power to find the mutated genes. Additionally, at times a common human disorder may be caused by different sets of mutated genes in different populations, which adds further difficulties in identifying the responsible loci. It is no surprise then that mapping outcomes for complex traits is often unrepeatable from one study population to another.
To address these difficulties and the pressing need for methods capable of dealing with large correlated datasets, we have proposed and developed the backward haplotype transmission association (BHTA) algorithm (1). The proposed approach comprises a set of methods that focus on a backward selection algorithm that deletes unimportant markers one by one until a subset of (important) markers associated with the disease remains. This algorithm selects a small random subset of the markers, applies a measure of information on this subset with respect to the disease, and then reduces the set by the marker whose deletion contributes the most to increasing the information. After successive reductions, the remaining markers are called “returned.” Those markers that are returned most often from many random subsets sampled are considered “important.” In this way, both the joint and marginal effects of all markers are extracted so that the data are analyzed as a whole. As a result, one can expect the detection of more important genetic loci. We have applied our approach to a number of simulated datasets, some of them quite large. Although the results of these simulated studies were extremely encouraging, we felt it important to test our approach and to demonstrate its practical values on a real and large-scale genetic dataset. This report reflects this effort. The current test data were kindly provided to us by the Whitehead Institute for Biomedical Research (Massachusetts Institute of Technology, Cambridge).
In this report, we present our major findings and illustrate the application of our methods to a dataset of patients with inflammatory bowel disease (IBD) collected in Canada. This dataset of IBD pedigrees was first studied by Rioux et al. (2), and the genome-wide search study successfully revealed two susceptibility loci, 5q31-q33 and 19p13, known today as IBD5 and IBD6. There have been several other loci with relevance to IBD etiology identified in the literature since 1996, through various studies. These loci include IBD1 (16q12), IBD2 (12q13), IBD3 (6p21), IBD4 (14q11), and IBD7 (1p36). For a comprehensive review of this search history and relevant information about IBD, see chapter 15 of ref. 3. The wide differences observed among the results of several genome-wide screens and follow-up studies since 1996 suggest that the disease might be related to a number of genes. These genes may have only modest effects on the susceptibility of IBD and may segregate at different frequencies in the different populations studied. For example, the study in ref. 2 presented strong evidence supporting the susceptibility of IBD to the loci IBD5 and IBD6 and suggestive evidence to IBD3, but showed no signs of linkage to the other previously reported loci such as IBD1, -2, -4, and -7.
As a complex disorder, IBD can be further categorized into two distinct diseases, Crohn's disease (CD) and ulcerative colitis (UC). Whereas the data in ref. 2 included CD, UC, and mixed families, we received CD data that accounted for roughly 66% of all data. After we applied our methods to this dataset, we obtained interesting results, some of them intriguing. For example, our selected markers overlapped with all previously reported IBD loci, except IBD6. Four loci that have shown strong association with IBD and that have not been reported previously were also identified.
Materials and Methods
IBD Data. IBD consists principally of UC and CD, two chronic idiopathic inflammatory diseases of the gastrointestinal tract. UC and CD are considered together because of their overlapping clinical, epidemiological, and pathogenetic features and their shared complications and therapies. Cumulative data garnered from epidemiological studies of these IBDs have revealed that relatives of individuals with either CD or UC are at increased risk for developing either form of IBD. These observations suggest that at least some susceptibility genes will be shared by UC and CD. For a comprehensive review of IBD and previous genome-wide screens, see chapter 15 of ref. 3.
Datasets used in this study were retrieved from files (in LINKAGE format) provided by the Whitehead Institute on a study investigated in ref. 2. The dataset contains 112 IBD pedigrees with more than two CD patients (89 with two patients, 20 with three patients, and 3 with four patients), which is ≈66% of the original dataset used in ref. 2. Among the patients, only those with parents on file can be used in the BHTA algorithm; thus, a total of 235 case–parent trios were finally included. Although 467 markers were genotyped on the individuals under study,† 19 of them were monomorphic and 46 had >99% missing. As a result, they were excluded from the screening because they did not contribute transmission information regarding the trait.
BHTA Screening. The BHTA algorithm is an association-based tool that evaluates the strength of a subgroup of markers under study. It deletes unimportant markers that are unassociated with the trait one by one. The algorithm stops when all remaining markers show signs of association with the disease and no further improvements can be achieved by deleting an additional marker. In this section, to illustrate the main ideas clearly and convincingly, we will present our main ideas in terms of complete case–parent trio family data, for which haplotypes are either known or can be inferred. The implementation of BHTA to IBD data, dealing with missingness and other practical issues, is given in the next section.
For simplicity, suppose that k markers are being studied, each with two alleles only. The idea of marker selection is to pick out markers that contribute the least information (regarding the trait) in a dataset, one at a time. The haplotype transmission disequilibrium (HTD) statistic proposed in ref. 1 as an information measure provides a way to achieve this result.
Let SM denote the current set of k markers, SM = {M1, M2,..., Mk}. To evaluate the importance of Mr, 1 ≤ r ≤ k, consider 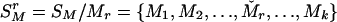 , the rth-deleted marker set. These k – 1 markers totally decide H = 2k–1 possible haplotypes. Let
, the rth-deleted marker set. These k – 1 markers totally decide H = 2k–1 possible haplotypes. Let 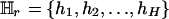 be the set of haplotypes corresponding to
be the set of haplotypes corresponding to 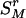 , that is, the haplotypes formed by k – 1 markers, with Mr excluded. Given n diseased children in the dataset, there are 2n parent-to-patient transmission pairs; two haplotypes are observed for each pair—one transmitted the to patient and one untransmitted, denoted by
, that is, the haplotypes formed by k – 1 markers, with Mr excluded. Given n diseased children in the dataset, there are 2n parent-to-patient transmission pairs; two haplotypes are observed for each pair—one transmitted the to patient and one untransmitted, denoted by 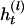 and
and 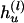 , respectively, for the lth Let the aggregated transmission pair. counts of haplotypes be
, respectively, for the lth Let the aggregated transmission pair. counts of haplotypes be
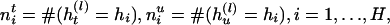 |
[1] |
where “#” stands for “count.” As the measure of disease information contained in the k – 1 markers of 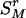 , we use the following HTD score,
, we use the following HTD score,
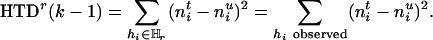 |
[2] |
To evaluate the information contributed by Mr, the information content of the original SM also needs to be estimated. Suppose that the two alleles of the rth marker Mr are ar and br. Denote the numbers of transmissions of the enlarged haplotypes 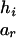 and
and 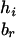 by
by 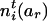 and
and 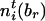 , respectively. Define
, respectively. Define 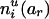 and
and 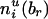 similarly for non-transmissions of the enlarged parental haplotypes to the offspring.
similarly for non-transmissions of the enlarged parental haplotypes to the offspring.
It is easy to see that the transmission counts after and before the deletion of Mr must satisfy
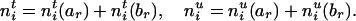 |
[3] |
The information contained in SM (before deletion) can then be measured naturally by
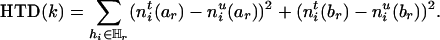 |
[4] |
As the information remained in the rth-deleted marker set 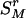 after the deletion, HTDr(k – 1) can be rewritten as
after the deletion, HTDr(k – 1) can be rewritten as
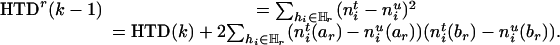 |
[5] |
From this equation, one finds that the amount of information lost by deleting marker Mr can be expressed as the difference between Eqs. 4 and 5, that is,
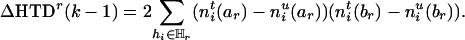 |
[6] |
To track the changes of the HTD score due to the deletion of the marker Mr, we define a slightly modified statistic, the haplotype transmission association (HTA),
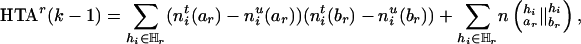 |
[7] |
which is half of ΔHTDr(k – 1) plus an adjusting term 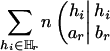 whose magnitude is negligible.‡
whose magnitude is negligible.‡
A positive value of the HTA score indicates that the deleted marker is less important. Guided by such key properties of HTA (for more details, see ref. 1), the BHTA algorithm deletes the least important marker one at a time, where the HTA score is positive, and at its maximum and continues to the next iteration until all of the remaining markers present evidence of importance, that is, HTA scores are negative for all remaining markers.
In practice, the number of markers and their possible interactions included in a large-scale study are often greater than the number of observations. This moderate size of observations will cause a serious problem of sparseness in the haplotype data when dealing with many markers simultaneously. To track the overall importance of all markers under study without running into the above issue of dimensionalities and overwhelming computational complexities, we propose the following two-step marker selection procedure:
Randomly select k (15, for instance) markers of the original set of K markers. Run BHTA on the selected markers and record the markers returned.
Repeat step 1 B times (B typically ≥ 5,000). Markers that are returned more frequently than others will be selected in the resulting set. The criterion used in the present study is based on the distribution of the returning frequencies of all markers (see below for details).
For a detailed discussion of this algorithm (such as the choice of k and B), see ref. 1.
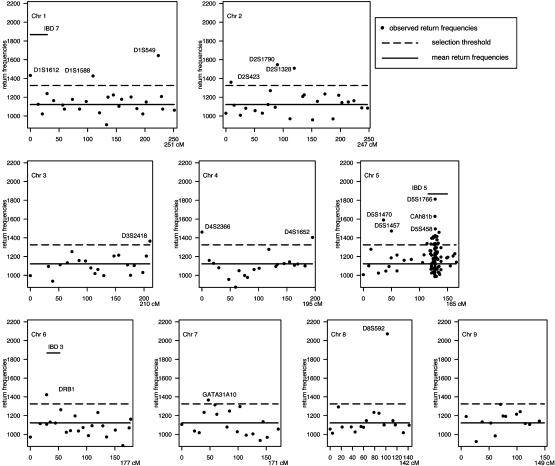
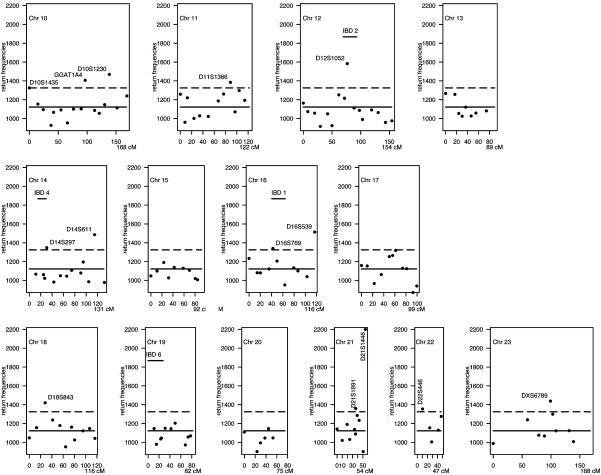
Implementation of BHTA on IBD Data. We applied BHTA two-step marker selection procedure using the 235 affected children that determine 4 × 235 = 940 haplotypes; half of them were transmitted from parents and the other half untransmitted (for data preparation, see the next section). Although BHTA was originally introduced in terms of trio data, its extension to data with more than one affected child per family is straightforward. The validity of this extension is mentioned in the footnote on page 211 of ref. 1. On each set of randomly selected k = 15 markers from all markers, we ran BHTA and recorded the markers returned. Secondly, we repeated this step 100,000 times. Actually, to minimize the noise due to random imputation (see the next section for details) for missingness, we used 10 imputations, and the BHTA was run 10,000 times for each. The combined return frequencies for all markers are plotted in Figs. 3 and 4. The median return is 1,122, which is marked by a horizontal solid line, whereas the selection threshold (1,325) is marked by a broken line. As a result, 48 markers (12%) are above the threshold line. In the same figure, we also included seven horizontal bars to indicate the seven locations of previously reported IBD-susceptibility loci IBD1 to -7. All except IBD6 are included in our final selection of 48 markers.
Fig. 3.
BHTA return frequencies: chromosomes (Chr) 1–9 aggregated return frequencies from BHTA screens are plotted vs. marker locations on the genome. Only markers included in the screening are shown. The median return (1,122) is marked by a horizontal solid line, whereas the selection threshold (1,325) is marked by a broken line. A total of 48 markers with return frequencies above the threshold are selected and labeled with their names for reference (except for the IBD5 region). Discussion on the selection threshold is presented in Implementation of BHTA on IBD Data. Seven horizontal bars indicate the previously reported IBD-susceptibility loci, IBD1–IBD7. All except IBD6 are included in the selection.
Fig. 4.
BHTA return frequencies: chromosomes (Chr) 10–23 aggregated return frequencies from BHTA screens are plotted vs. marker locations on the genome. See legend of Fig. 3.
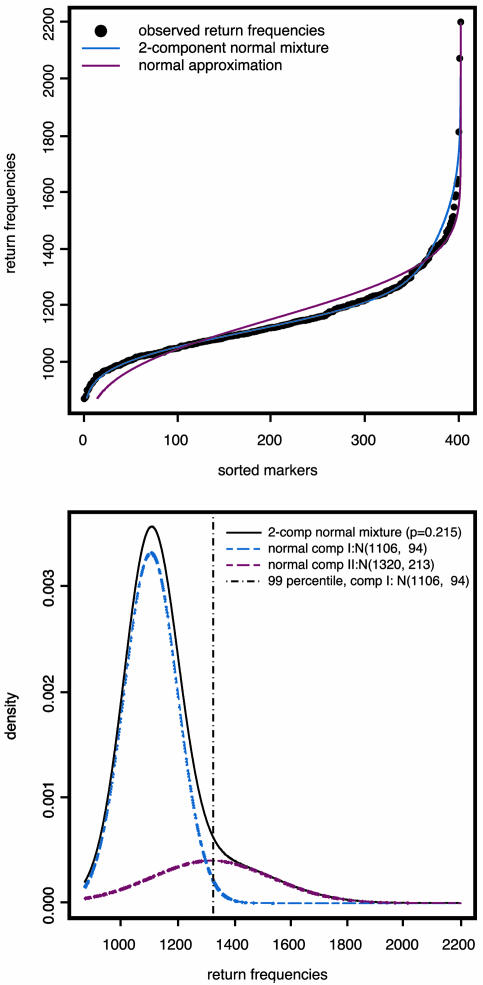
To determine the selection threshold, we first fitted the markers' return frequencies by a simple two-component normal-mixture model, 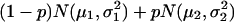 , μ2 > μ1, whereas the first component corresponds to the unimportant markers and the second to the important markers (highly returned). Although the overall suprema of the likelihood do not provide sensible estimates, the local maximum does. Therefore, the local maximum likelihood estimation of the mixture parameter p, with an estimate of 21.5%, suggests that 81 of the 402 markers belong to the high mean distribution. The sorted return frequencies of 402 markers in the IBD dataset are plotted in Fig. 1 Upper. The red line indicates the cumulative distribution function of a single normal distribution for all markers, and the blue line is the fitted normal mixture with
, μ2 > μ1, whereas the first component corresponds to the unimportant markers and the second to the important markers (highly returned). Although the overall suprema of the likelihood do not provide sensible estimates, the local maximum does. Therefore, the local maximum likelihood estimation of the mixture parameter p, with an estimate of 21.5%, suggests that 81 of the 402 markers belong to the high mean distribution. The sorted return frequencies of 402 markers in the IBD dataset are plotted in Fig. 1 Upper. The red line indicates the cumulative distribution function of a single normal distribution for all markers, and the blue line is the fitted normal mixture with 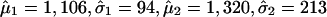 , and p̂ = 0.215 (see density curves in Fig. 1 Lower). To control the false-positive rate conservatively (holding .01 level, see vertical broken line in Fig. 1 Lower), we selected the top 48 markers and claimed their importance.
, and p̂ = 0.215 (see density curves in Fig. 1 Lower). To control the false-positive rate conservatively (holding .01 level, see vertical broken line in Fig. 1 Lower), we selected the top 48 markers and claimed their importance.
Fig. 1.
Normal vs. normal mixture.
Another method used to separate the important group from the unimportant group was based on an idea recently developed by Efron (4). The proposed method suggests the use of an estimated empirical null distribution to perform the inference when a large number of tests, say 300 or more, are simultaneously evaluated. The goal of this application is to divide the data values into two categories: interesting vs. uninteresting. In place of “significant” vs. “nonsignificant,” Efron (4) used the terms “interesting” vs. “uninteresting” in reflecting a difference between a large-scale and a classical individual testing. In our view, the term “interesting group” corresponds to our term “important marker group” used in this report. We also felt that the identification of important markers (or interesting markers) at this stage was more of a screening operation, which intended to reduce the marker size to a much smaller order so that further efforts and investigations can be properly directed. We now apply Efron's method (and similar notations) to our data-return frequencies.
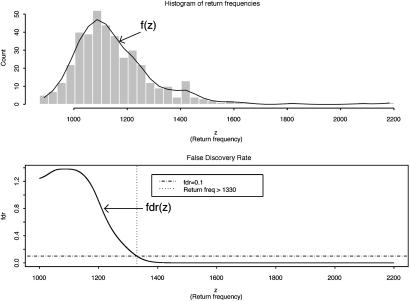
Let z be the return frequency of a marker under evaluation, the distribution density function of z, f(z), is a mixture of two distributions, f0(z) (the unimportant group) and f1(z) (the important group), i.e., it takes the form f(z) = p0f0(z) + p1f1(z), where p0 and p1 are prior probabilities of the important and unimportant groups. As suggested in ref. 4, (i) f(z) was estimated by the natural spline (df = 13) fitted to the histogram counts based on 40 equal intervals (as shown in Fig. 2 Upper); (ii) f0(z) was estimated by 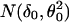 , where δ0 = 1,090 and Θ0 = 82 were the center and the half-width of the central peak of f(z), respectively; (iii) the local false discovery rate fdr(z) was calculated as fdr ≡ f0(z)/f(z) (see Fig. 2 Lower); and (iv) the same selection criterion used in ref. 4, fdr < 0.1, was applied to these return frequencies, which yielded a threshold of 1,330, leading to a final selection of top 47 markers. The final result differed only by one marker from the first method we used. For details on the justification and implementation of this method, see ref. 4.
, where δ0 = 1,090 and Θ0 = 82 were the center and the half-width of the central peak of f(z), respectively; (iii) the local false discovery rate fdr(z) was calculated as fdr ≡ f0(z)/f(z) (see Fig. 2 Lower); and (iv) the same selection criterion used in ref. 4, fdr < 0.1, was applied to these return frequencies, which yielded a threshold of 1,330, leading to a final selection of top 47 markers. The final result differed only by one marker from the first method we used. For details on the justification and implementation of this method, see ref. 4.
Fig. 2.
Histogram of return frequencies with fitted f(z) and local false discovery rate fdr(z). (Upper) The distribution of return frequencies f(z) was estimated by fitting a natural spline to the histogram counts based on 40 equal intervals. (Lower) The horizontal broken line indicates the 0.1 fdr threshold for important marker group, which leads to a return frequency threshold of 1,330 (the vertical dotted line). A total of 47 markers that had return frequencies higher than this threshold were selected for the important group.
Data Preparation for BHTA. Before the BHTA screening algorithm can be implemented on this dataset, several data manipulation steps are required: (i) imputation of missing genotypes, (ii) inference of haplotypes given multilocus unphased genotypes, and (iii) dichotomization of microsatellite markers.
To reduce random noises resulted from imputations and other data manipulation, we ran independent BHTA screenings on 10 independently prepared datasets (imputation, inference, and dichotomization). The major findings in this report were based on aggregated results from these 10 independent trials. The aggregation of independent trails reduced noise caused by random imputation and thus honestly reflected the strength of the individual markers' real signal of importance.
Imputation for missing parental genotypes. Genetic data from a large-scale genome scan inevitably contain a substantial number of missing values due to genotyping errors or unavailable parents. For haplotype-based methods such as BHTA, one must obtain genotype information on all markers for any individual under study. It is essential to circumvent the issue of missing by proper imputation. For current IBD data, >20% of the genotype data were missing for any individual under study whereas the mean amounts were as high as 47%. However, one can infer the missing genotypes using the observed genotypes of other family members (affected or unaffected), perfectly (7% of the time) or probabilistically (93% of the time).
We started with the imputation on missing parental genotypes for two reasons: (i) there were slightly fewer missing values in the children's genotypes and (ii) unaffected child(ren) in the data provided information for the imputation of parental missing genotypes, even though they were not used in the screening. The imputation was carried out by using posterior probabilities of possible full genotypes given observed parental and children's genetic information, marker-by-marker.§ Given a pair of parents of the affected children under study, with missing genotypes at a given marker, denote 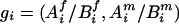 to be a possible full genotype vector. Here
to be a possible full genotype vector. Here 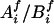 and
and 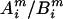 denote the unordered genotypes for the father and mother, respectively. The likelihood of gi being the true genotypes is then
denote the unordered genotypes for the father and mother, respectively. The likelihood of gi being the true genotypes is then
 |
[8] |
After having evaluated all possible gi's, we drew one gi according to the posterior probabilities to finish the imputation. To avoid possible bias, all probability calculations were done under the assumption of no association to the disease trait.
With a complete parental genotype, the imputation of missing genotype for the affected children became trivial and was carried out during the inference of multiloci haplotype phases (see below).
Inference on haplotype phases from multilocus unordered genotypes. After the previous imputation step, parental data were free of missing values. The inference of gametic haplotypes given multilocus unphased genotypes was then carried out by determining the transmitted and untransmitted alleles for each parent-child pair at each marker locus. The inference was implemented under five different scenarios (see Supporting Text, which is published as supporting information on the PNAS web site).
Dichotomization for microsatellite markers. Because the BHTA algorithm primarily works with diallelic markers, we dichotomized the microsatellite markers according to their numbers of repeats (0 if lower than a prespecified value, 1 otherwise), with probability of “allele 0” as close to 0.5 as possible.
Results
Our global search, accounting for both joint and marginal effects, has resulted in a selection of 48 (of a total of 402) important markers that are potentially related to the disease susceptibility (a complete list of these 48 markers is given in Table 3, which is published as supporting information on the PNAS web site). These 48 markers are spread across many of the 23 chromosomes (see Figs. 3 and 4).
Confirmation of Previously Identified IBD Loci. Despite the fact that no linkage evidence was found on other IBD loci (loci 1, 2, 4, and 7) in ref. 2, our selected markers overlap with all previously reported IBD loci, except IBD6 (see Table 1), suggesting that these data contain considerable information that may have not been used in the earlier analysis. The discrepancy of the findings between these two studies provides evidence supporting the use of methods that take into account interactions and extract more of the information available in the data. With conventional approaches, much of the information would not be captured, and many responsible regions are likely to be missed. In addition, our findings independently confirm the evidence of susceptibility in the regions of IBD1 to -4 and -7, which have been reported in other studies based on different datasets.
Table 1. Selected important markers on IBD loci.
| IBD locus | Selected marker |
|---|---|
| IBD 1 (16q12) | D16S769 |
| IBD 2 (12q13) | D12S1052 |
| IBD 3 (6p21) | DRB 1 |
| IBD 4 (14q11) | D14S297 |
| IBD 5 (5q31) | CAh816* |
| IBD 6 (19p13) | |
| IBD 7 (1p36) | D1S1612 |
Twenty-one of 74 markers around the IBD5 locus are selected.
Loci Demonstrating Important Association to IBD. In our approach, the importance of each marker under study is evaluated by its returned frequencies; this number provides a natural way to rank the importance of markers. Treating the distribution of returned frequencies as a mixture of two distributions, one representing the important markers and the other for unimportant markers, we may estimate the parameters of this mixture model and separate out the important markers accordingly. The selection of important markers was achieved through two statistical methods dissecting such a mixture, which returned almost identical results: we selected the top 48 markers (with high return frequencies) and claimed their importance. Furthermore, among the 48 selected markers, the four markers returned most frequently (besides some IBD5 markers) are D1S549 (1q), D5S1470 (5p), D8S592 (8q), and D21S1446 (21q), pointing to four previously uncharacterized loci, none of which have been reported in the present literature. Given that these signals are very strong, further research on these regions could be very fruitful. We identified¶ several genes on these loci that may be of interest to researchers (listed in Table 2). We also believe that medical researchers with expertise in IBD may provide further important insights into these loci.
Table 2. Candidate genes at four loci.
| Marker | Locus | Gene | Notes |
|---|---|---|---|
| D1S549 | 1q32.1 | MDM4 | Plays a role in apoptosis*; shows significant structural similarity to p53-binding protein MDM2. |
| IL24 | Encodes a member of the IL10† family of cytokines; protein encoded is found to induce apoptosis. | ||
| IL20 | The protein encoded by this gene is a cytokine structurally related to IL-10. | ||
| CD55 | Or DAF‡, decay accelerating factor for complement (Cromer blood group system). | ||
| D5S1470 | 5p15.2 | DAP | Acts as a positive mediator of programmed cell death (apoptosis). |
| D8S592 | 8q24.12 | MTBP | Codes MDM2, transformed 3T3 cell double minute 2, p53 binding protein. |
| D21S1446 | 21q22 | DSCR1 | Down syndrome critical region 1. |
IBD have been previously found to evoke the activation of apoptotic genes.
It has been previously found that lack of IL-10 may lead to intestinal inflammation (5).
DAF, or CD55, has been found to have an important role in regulating gut homeostasis and may participate in protecting against IBD (6).
In view of the above findings, it seems important to reinvestigate available family-based datasets that can be suitably reanalyzed by our methods. Because these samples have been collected already, our approach could increase the efficiency of using available resources and obtain additional crucial information.
Discussion
The application of our methods on the IBD data provided significant additional findings that seem above and beyond previously expected and researched results. The major weakness of conventional approaches is that the mapping outcomes are usually unrepeatable from one study to another. This outcome is due in part to the fact that most methods use fractional information from the data. Consequently, the power of detecting those responsible genes with modest effects is seriously reduced. Our approach intends to draw substantially more information from data and subsequently rank all markers according to their overall contributions (reflected by their importance) toward disease. The overall contribution of each marker is measured by its returned frequency (described above) that honestly reflects both the joint (interactive) and marginal effects in the disease etiology. We believe that the proposed approach will also be useful in the future when the information of a large number of dense markers (single nucleotide polymorphisms, for example) becomes available. In the meantime, we strongly recommend that the data already collected be suitably reanalyzed by this approach. We believe that outcomes of these reexaminations could lead to very fruitful and interesting results. The joint returning patterns of subsets of markers carry valuable information about disease clusters, networks, and pathways. This direction deserves further investigation.
Supplementary Material
Acknowledgments
We thank Herman Chernoff for careful reading and insightful comments, which greatly contributed to the presentation of this work. We thank Andrew Gelman for useful comments on an earlier draft of the manuscript. The IBD data were kindly provided to us by Eric Lander and Mark Daly from the Whitehead Institute. Their help toward this study is highly appreciated. We also thank two anonymous reviewers for constructive comments. Our research is partially supported by National Science Foundation Grant DMS-00-71930.
Abbreviations: HTA, haplotype transmission association; BHTA, backward HTA; IBD, inflammatory bowel disease; CD, Crohn's disease; UC, ulcerative colitis; HTD, haplotype transmission disequilibrium.
Footnotes
According to ref. 2, the data included 377 microsatellite markers that were spaced 12 cM apart on average, plus additional microsatellite markers genotyped on the IBD5 region.
The reason for this adjustment is that the modified score HTAr(k – 1) will have an expectation of zero when no marker is in association with the trait. In fact, the adjusting term 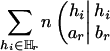 carries no information for association and represents a fixed amount of value loss caused by the deletion of Mr.
carries no information for association and represents a fixed amount of value loss caused by the deletion of Mr.
Certainly, considering the observed genotype on markers nearby will provide more information for the imputation. However, given the disease status of the children, the association among markers has been contaminated by their possible association with the disease trait.
Marker locations were identified through The Genome Database (http://www.gdb.org), and candidate genes were identified through searches in the Entrez Gene Database of the National Center for Biotechnology Information.
References
- 1.Lo, S. H. & Zheng, T. (2002) Hum. Hered. 53, 197–215. [DOI] [PubMed] [Google Scholar]
- 2.Rioux, J. D., Silverberg, M. S., Daly, M. J., Steinhart, A. H., McLeod, R. S., Griffiths, A. M., Green, T., Brettin, T. S., Stone, V., Bull, S. B., et al. (2000) Am. J. Hum. Genet. 66, 1863–1870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.King, R. A., Rotter, J. I. & Motulsky, A. G., eds. (2002) The Genetic Basis of Common Diseases (Oxford Univ. Press, New York), 2nd Ed.
- 4.Efron, B. (2004) J. Am. Stat. Assoc. 99, 96–104. [Google Scholar]
- 5.Leach, M. W., Davidson, N. J., Fort, M. M., Powrie, F. & Rennick, D. M. (1999) Toxicol. Pathol. 27, 123–133. [DOI] [PubMed] [Google Scholar]
- 6.Lin, F., Spencer, D., Hatala, D. A., Levine, A. D. & Medof, M. E. (2004) J. Immunol. 172, 3836–3841. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.