Abstract
Estimates of the effective stiffness of a composite containing multiple types of inclusions are needed for the design and study of functionally graded systems in engineering and physiology. While excellent estimates and tight bounds exist for composite systems containing specific classes and distributions of identical inclusions, these are not easily generalized to complex systems with multiple types of inclusions. For example, three-point parameters are known for only a few inclusion shapes and orientations. The best estimate available for a composite containing multiple classes of inclusions arises from the Kanaun-Jeulin approach. However, this method is analogous to a generalized Benveniste approach, and therefore suffers from the same limitations: while excellent for low volume fractions of inclusions, the Kanaun-Jeullin and Benveniste estimates lie outside of three-point bounds at higher volume fractions. Here, we present an estimate for composites containing multiple classes of aligned ellipsoidal inclusions that lies within known three-point bounds at relatively higher volume fractions of inclusions and that is applicable to many engineering and biological composites.
Keywords: Tendon-to-bone insertion site, enthesis, composite materials, homogenization methods
1. Introduction
Composite structural materials offer the potential for efficient solutions to engineering problems and are central to many mechanical functions in physiology. Extensive effort has been devoted to predicting the overall mechanical responses of composites based on knowledge of the mechanical properties, geometries, and distributions of their constituent phases (e.g.,(Torquato, 2001; Milton, 2002)). However, many challenges remain, especially for composites having inclusions of varying shapes, sizes, and mechanical properties. An additional challenge is that most homogenization techniques provide the best estimates for relatively low volume fractions of inclusions. Here, we present a homogenization scheme that appears to provide reasonable predictions under these conditions.
To highlight the need for this method and the ways that it differs from existing methods, we briefly review literature on both homogenization of multiphase composites as well as the accuracy of micromechanical methods at high volume fraction of inclusions. Predicting effective moduli of composites containing relatively high volume fractions of inclusions is challenging even for materials containing only a single class of inclusions Ferrari (1991); Roumi and Shodja (2007); Ju and Yanase (2010, 2011); Kwon and Dharan (1995). The best of these render good correlation with experimental data for inclusion volume fractions below about 60% or for special distributions of the inclusions. Numerous homogenization techniques use the effective medium method, which builds from the work of Eshelby (1957) by considering an equivalent effective medium embedded with non-interacting inhomogeneities. These include the method of cells Aboudi (1989), the Mori and Tanaka (1973) approach ,the generalized self-consistent method Budiansky (1965); Kerner (1956); Hill (1965), the models of Castañeda and Willis (1995), and the Kuster and Toksöoz (1974) model. These approximations depend only upon the volume fractions and geometries of inclusions and are independent of the spatial or probabilistic distributions of inclusions. Accordingly, they are pertinent to heterogeneous solids containing a low concentration of identical inclusions and cannot be easily generalized to composites with multiple classes of inclusions. Higher-order bounds such as those of Weng (1992); Silnutzer (1972); Torquato and Lado (1986) and Sen et al. (1987) and the three-point bounding technique (e.g., Milton and Phan-Thien (1982)) are far tighter than classic Voigt and Reuss (Hill, 1952) or Hashin and Shtrikman (1963) bounds. However, the parameters needed for three-point bounds and estimates are known only for a few classes of inclusion shapes and orientations (Torquato, 2001). While these can be combined to estimate the mechanics of composites containing multiple class of inclusions (Genin and Birman, 2009), they are limited to cases for which the three-point parameters are known. More recent homogenization procedures (e.g., Tucker III and Liang (1999); Torquato (2001); Kakavas and Kontoni (2006); Sevostianov and Giraud (2013)) are also limited to low inclusion volume fraction.
Although a wealth of literature exists on the estimation of effective elastic properties of composites containing a single class of inclusions, few methods are available for analysis of composites with multiple types of inclusions (Torquato, 2002; Hashin, 1983; Tucker III and Liang, 1999; Hu and Weng, 2000; Christensen, 2012). For example, Lim (2002) presented a generalized mechanics of materials approach to evaluating the moduli of three-phase composites consisting of two types of reinforcement (fibers and/or particles) embedded within the matrix. Kanaun and Jeulin (2001) developed a model allowing for the special statistical distribution of the centers of inclusions of various orientations and shapes. The Maxwell scheme was modified and extended to the case of anisotropic multiphase composites by Sevostianov (2014).
Challenges involved in the homogenization of multiphase composite materials were outlined in a recent paper by Sevostianov and Kachanov (2014). In particular, they pointed that the Mori-Tanaka approach applied to multiphase composites may violate the Hashin-Shtrikman bounds as well as compromise the symmetry of the stiffness tensor. The latter problem was resolved by imposing a symmetrization of the stiffness tensor as demonstrated in their paper. Although the Kanaun and Jeulin (2001) effective field estimate applied to multiphase composites avoids the violation of the symmetry of the stiffness tensor by assuming that different effective fields affect different composite phases, this results in the violation of the principle of superposition. Without the adaptation of different effective fields, the Kanaun-Jeulin estimate is analogous to a generalized formula of Benveniste (1987) that represents a modified Mori-Tanaka approach, and therefore suffers from the same limitations (Genin and Birman, 2009). While excellent for low volume fractions, both the Kanaun-Jeulin and Benveniste estimates lie outside three-point bounds at higher volume fractions. and therefore sufferings from the same limitations (Genin and Birman, 2009). While excellent for low volume fractions, the Kanaun-Jeulin and Benveniste estimates lie outside of three-point bounds at higher volume fractions in cases for which one would desire them to lie within the three-point bounds.
As follows from this discussion, the estimation of effective properties of composites containing high volume fractions of inclusions continues to present a challenge, especially in cases of multiple classes of inclusions. In engineering structures, these issues arise in the study of functionally graded materials (Birman et al., 2013; Suresh et al., 1998; Byrd and Birman, 2007), especially for aerospace applications, that employ high-performance polymers with high volume fractions of inclusions. Hence, it is necessary to predict the effective moduli of composites featuring multiple classes of inclusions over the full range of volume fractions and geometries.
Besides homogenization methods applicable to a broad range of engineering structural materials, our specific interest is the modeling of partially mineralized tissue. Bone, a highly mineralized tissue, is a composite material made up primarily of flexible collagen fibers and a high (50%) volume fraction of stiff mineral inclusions (Alexander et al., 2012). The shapes of these inclusions have been variably described as plate-like (Eppell et al., 2001; Kim et al., 1995), needle-like (Traub et al., 1992), and amorphous (Mahamid et al., 2008; Boonrungsiman et al., 2012). At the attachment of tendon to bone, the volume fraction of the mineral inclusions increases from 0% in tendon to 50% in bone over a distance on the order of tens of micrometers Genin et al. (2009). One important mechanism of toughening in biologic systems such as the tendon-to-bone attachment is stress redistribution associated with the progressive stiffening of collagen fibers by mineral (Liu et al., 2012, 2014; Thomopoulos et al., 2006). Predicting this is particularly important for defining design criteria for tissue engineered constructs needed for improving surgical outcomes (Thomopoulos et al., 2010, 2011). In spite of the progress reflected in the above-mentioned publications, modeling the mineralized collagen tissues remains challenging. Physiologically, debate continues about where mineral lies within collagen, how it accumulates, and the shape it has (Schwartz et al., 2012; Thurner et al., 2007; Pasteris et al., 2008).
The present paper presents an approximation that is applicable to composites with multiple classes of inclusions and that retains high accuracy at higher volume fractions. Expressions for effective moduli were derived under two conditions: (i) we required the total strain energy stored in a homogenized material to equal that in the actual material, with the average inclusion and the average matrix strains evaluated based on Eshelbys approach; and (ii) we modeled the effective matrix and inclusions as acting in parallel. Contrary to the Mori-Tanaka technique, we replaced the evaluation of the strain in the representative volume element using the rule of mixtures with a strain energy equivalence requirement; this leads to a formulation that therefore differs from the Kanaun-Jeulin estimate. Our results suggest that the new formulation is useful at higher volume fractions, although it is less useful at lower volume fractions.
Subsequently, the developed theory was specified for the case of a three-phase composite. For verification of the proposed theory, we compared predictions to experimental data and to other estimates. Our method provided good accuracy for a simultaneously fiber- and particulate-reinforced composite, and lay within three-point bounds at relatively high volume fractions for all cases studied. The method was also applied to study stiffening of tissue at the tendon-to-bone attachment.
2. Estimate of overall elastic properties of a composite
Our model emanates from the Kanaun-Jeulin methodology (Kanaun and Jeulin, 2001) for estimating the stiffness tensor of a three-phase composite. This was shown by Genin and Birman (2009) to arise as an extrapolation of the method of Benveniste (1987) for multiple types of inclusions. These methods under-predict the stiffness of a great number of composites of interest. In this section, we review the Kanaun-Jeulin methodology, then present our adaptation of it.
Like the Kanaun-Jeulin estimate, the adaptation was conducted within the framework of linear elasticity assuming that the perturbed strain in the matrix, due to the presence of inclusions, was not affected by interactions between different types of inclusions. In other words, each type of inclusion affects the strains in the matrix, but the perturbed matrix strain, due to the interaction between these inclusions, was assumed to be of second order. We considered a certain representative volume V0 of an infinite three-dimensional linear elastic medium embedded with N types of linear elastic inclusions that are aligned but randomly distributed. The properties of the matrix and of the different types of inclusions will be identified by the subscripts j = 1 and j > 1, respectively. We assumed perfect adhesion between the matrix and each inclusion. Each type of inclusion had uniform elastic properties and possessed a known geometry.
2.1. Kanaun-Jeulin methodology
The Kanaun-Jeulin methodology expanded upon the Mori-Tanaka approach, in which the tensors of average strain in each type of inclusion can be written in terms of the tensor of the average strain in the matrix by:
| (1) |
where
| (2) |
and . Here, Sj are fourth-order Eshelby tensors corresponding to the jth type of inclusions, and I is a fourth-order identity tensor. Explicit examples of the Eshelby tensor are presented in the appendix for the cases of spheroidal inclusions, penny-shaped inclusions, and long cylindrical inclusions (fibers). Equation (1) can be used jointly with the condition that the stresses on the homogenized and actual representative volume are equal, with matrix and inclusions resisting deformation in parallel:
| (3) |
Noting that σ̄j = Lj∊̄j and combining Eq.(3) and Eq.(1), the resulting system of (j+1) linear algebraic equations can be solved to express the tensor of strains in the matrix and inclusions in terms of the tensor of strains in the homogeneous material:
| (4) |
where j = 1, 2, …N and T1 = I.
This estimate has been shown to provide an underestimate of the strain energy stored by a composite material under a given loading; that is, the estimate is too compliant (Genin and Birman, 2009). This is expected because the approach uses both averaged stresses and averaged strains, which are bound to combine to yield a strain energy lower than that stored by the composite except in special cases.
2.2. Estimate based upon energy-based effective strains
To improve upon this approximation, we replaced the average strains ∊̂i in the phases with effective strains ∊̄j that better represented the energy stored in the composite. That is, we identified effective strains so that the strain energy in the homogenized material equaled that in an actual material, under the above assumptions. We partitioned the energy amongst the phases:
| (5) |
where the sum of the volumes of the matrix and of all phases equals that of the representative volume ( , and σ and ∊ are the tensors of engineering stress and linearized strain, respectively. We defined the effective strain ∊̂j for each phase j within a representative volume so that each term in Eq.(5) can be written as:
| (6) |
Note that ∥ ∊̂j ∥ ≤ ∥ ∊̄j ∥. Then Eq.(5) can be rewritten:
| (7) |
Substituting Eq.(4) into Eq.(7) yields the following explicit expression for the effective stiffness tensor:
| (8) |
Substituting for Q and solving for Le,
| (9) |
where in the last step we employed the fact that L and Ns are symmetric.
2.3. Specific result for effective elastic stiffness of three-phase composites
For the simple case of two types of inclusions within a matrix,
Hence, the effective stiffness tensor is:
| (10) |
3. Results and discussion
We studied Eqs. 9 and 10 in two ways. First, predictions were compared to available experimental data and to several estimates and bounding techniques for the case of glass inclusions in an epoxy matrix, including inclusion volume fractions beyond the range over which the Mori-Tanaka and Benveniste estimates are deemed reliable. Second, we checked predictions against existing models and predictions for three-phase composites. Thereafter, we simulated the spatial variation of the mechanics of partially mineralized collagen fibers.
3.1. Epoxy with glass inclusions
Analytical predictions compared well to two well known experimental datasets for two-phase composites containing randomly distributed elastic spheres: the data of Smith (1976) (E1 = 3:01 GPa, ν1 = 0:394, E2 = 76:0 GPa, ν2 = 0:23), and the data of Richard (1975) (E1 = 1:69 GPa, ν1 = 0:444, E2 = 70:3 GPa, ν2 = 0:21). Predictions were close for effective shear and Young’s moduli for particle volume fractions ranging from 0 to ~ 0:6 (dense) (Figs. 1 and 2). Minor deviations of predictions for effective bulk modulus K and Poisson’s ratio ν were expected due to both datasets relying on uniaxial tests for ν. Predictions lay within three-point bounds at high volume fractions (Figs. 1 and 2). Significantly, this remained the case for the effective Poisson’s ratio and the effective bulk modulus. Like the Benveniste (and hence Kanaun-Jeulin) estimate, the new method lay slightly outside of the three-point bounds at very low volume fractions. The Benveniste estimate follows the Hashin-Shtrikman lower bound and drops increasingly beneath the three-point bounds at larger particle volume fractions (the inverse of this trend occurs for the effective Poisson’s ratio) (cf. (Genin and Birman, 2009)). Like the Mori-Tanaka theory, the Benveniste approach is accurate only for materials containing dilute or low volume fraction distributions of inhomogeneities.
Figure 1.

Estimates and bounds for the effective elastic properties of an isotropic epoxy matrix (E1 = 3:01 GPa, ν1 = 0:394) embedded with spherical glass inclusions (E2 = 76:0 GPa , ν2 = 0:23), compared with the experimental data of. All moduli are normalized by the corresponding moduli of the matrix.
Figure 2.

Estimates and bounds for the effective elastic properties of an isotropic epoxy matrix (E1 = 1:69 GPa, ν1 = 0:444) embedded with spherical glass inclusions (E2 = 70:3 GPa, ν2 = 0:21), compared to the experimental data of Richard, 1975. All moduli are normalized by the corresponding moduli of the matrix
The effect of the aspect ratio of inclusions on effective elastic properties was then evaluated for two-phase composites consisting of an epoxy matrix (E1 = 3:12 GPa, ν1 = 0:38) embedded with 30% aligned glass (E2 = 76 GPa, ν2 = 0:25) ellipsoidal particles of a variable aspect ratio (Fig. 3). As expected, estimates lay within the Hashin-Shtrikman bounds for nearly spherical particles, and within the Voigt-Reuss bounds for both large aspect ratio (continuous fiber-like) and small aspect ratio (disc-like inclusions. Expected trends (e.g., Tucker III and Liang (1999)) were reflected in Fig. 3, including an increase of longitudinal elastic modulus (EL) and a reduction of transverse modulus (ET) for increasing aspect ratios of inclusions that were greater than 1. Asymptotes in all moduli were reached at very small inclusion aspect ratios, when the composite behaves as a matrix embedded with discs oriented perpendicular to the longitudinal axis, and at very high inclusion aspect ratios, when the composite behaves as a matrix embedded with aligned fibers. The Kanaun-Jeulin estimate predicts a more compliant material for all inclusion aspect ratios. The current method appears fully adequate for two-phase composites.
Figure 3.
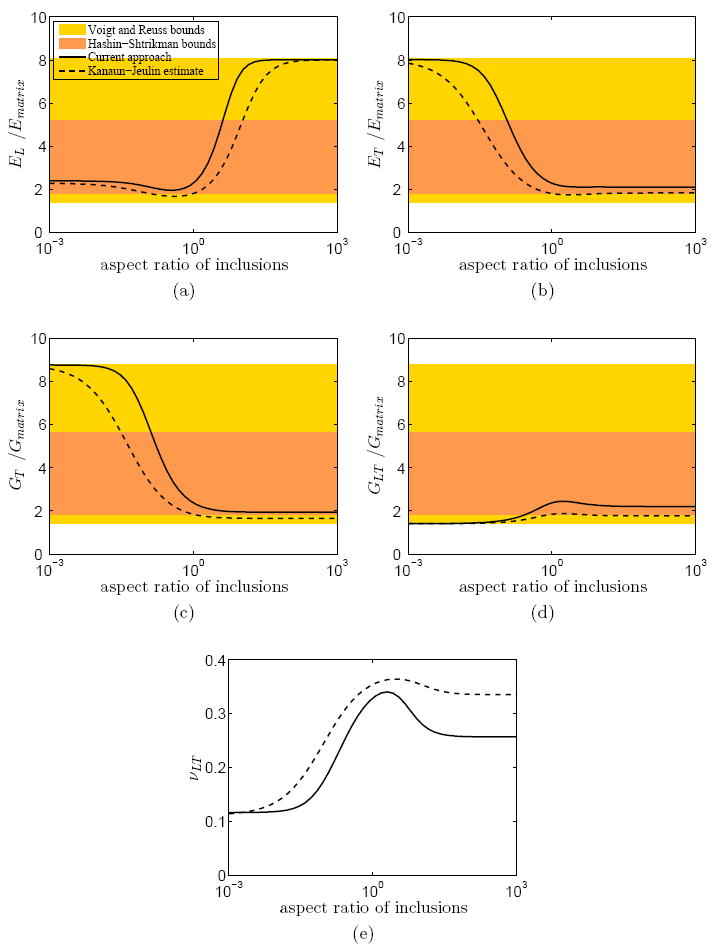
The effect of the aspect ratio of ellipsoidal inclusions (volume fraction f2 = 0:3) on the effective elastic properties of two-phase composites. Note that the volume fraction of the inclusions is considered to be 30%. E1 = 3:12 GPa and ν1 = 0:38 for the epoxy matrix, and E2 = 76 GPa and ν2 = 0:25 for the glass particles. All moduli are normalized by the corresponding moduli of the matrix.
Although much discussion of them can be found, experimental characterizations of three-phase composites are not available in the literature. To assess the validity of the proposed method in predicting effective elastic properties of three-phase composites, we instead compared the current approach to bounds and estimates for a model three-phase system that we studied previously (Genin and Birman, 2009). The model system studied had a matrix of epoxy (E1 = 3:12 GPa, ν1 = 0:38) that was reinforced by both spherical particles (phase 2) and long fibers (phase 3) made of glass (E2 = E3 = 76 GPa, ν2 = ν3 = 0:25). Three types of analyses were compared to the current approach, as presented by Genin and Birman (2009) (Fig. 4). The first were “bounds” that serve not as true bounds but rather as guidelines for appropriate trends. These were obtained by using the three-point bounds (cf. Torquato (2001)) for a matrix that contained a volume fraction f3 of glass fibers; the matrix had properties obtained from the three-point bounds for epoxy reinforced with a volume fraction f2/(f1+f2) of randomly distributed glass spheres. The second were “two-step” estimates obtained using three-point estimates (cf. Torquato (2001)) in the same way (Genin and Birman, 2009). The third was the Kanaun-Jeulin estimate.
Figure 4.

Theoretical predictions and bounds for the effective elastic properties of an epoxy matrix (E1 = 3:12 GPa, ν1 = 0:38) containing inclusions of glass (E2 = 76 GPa, ν2 = 0:25). Two types of inclusions are considered: infinitely long fibers (volume fraction f3) and glass spheres (volume fraction f2, ranging from 0 to the dense packing of 0.63). The upper and lower bounds are calculated using the three-point bounds discussed by Genin and Birman, 2009. Moduli are normalized by those of epoxy.
For the range of particle and fiber volume fractions examined, the Kanaun-Jeulin estimate lay just outside of the “bounds,” with smaller deviations at lower volume fractions of inclusions (Fig. 4). This is expected because the Kanaun-Jeulin approach is acceptable only for relatively low particle volume fractions. In all cases, the properties evaluated by the proposed approach were within the bounds, except for the longitudinal elastic modulus (EL), which was slightly outside the bounds for larger particle volume fractions. Note that, except for estimates obtained for Poisson’s ratio, the “two-step” estimate and the current method were close.
3.2. Partially mineralized collagen fibers
The current approach was then used to estimate the stiffening of collagen fibers by mineral. The accommodation of bioapatite mineral within fibers and fibrils follows a sequence that is debated. A sequence supported by our own work involves mineralization inside of collagen fibrils (“intrafibrillar”) preceding mineralization outside of collagen fibrils (“extrafibrillar”) (Alexander et al., 2012; Schwartz et al., 2012). In this interpretation, bioapatite mineral accumulates inside collagen fibrils at tissue-level volume fractions 0% ≤ ϕm ≤ 21%, displacing water, and then accumulates outside of fibrils, displacing extra-fibrillar matrix proteins (“EFM”). The stochastic finite element estimates of Liu et al. (2014) for the stiffening of fibers associated with this mineralization sequence (symbols in Fig. 5) showed relatively minor stiffening for intrafibrillar mineralization (ϕm ≤ 21%) followed by much higher stiffening beyond a percolation threshold for extrafibrillar mineralization. Due to the long, slender shapes of collagen fibrils, the percolation threshold is higher for the longitudinal modulus of a fiber (ϕm ≈ 30%) than for its transverse modulus (ϕm ≈ 21%). Note that in Fig. 5, the bioapatite volume fraction was plotted for consistency with Liu et al. (2014) as a tissue level volume fraction, ϕm; the fiber-level volume fraction is 25% higher than ϕm. The volume fraction therefore ranged from 0 vol% (typical for tendon) to 41 vol% (typical for bone) (Hellmich et al., 2008; Hellmich and Ulm, 2002; Hamed et al., 2010).
Figure 5.
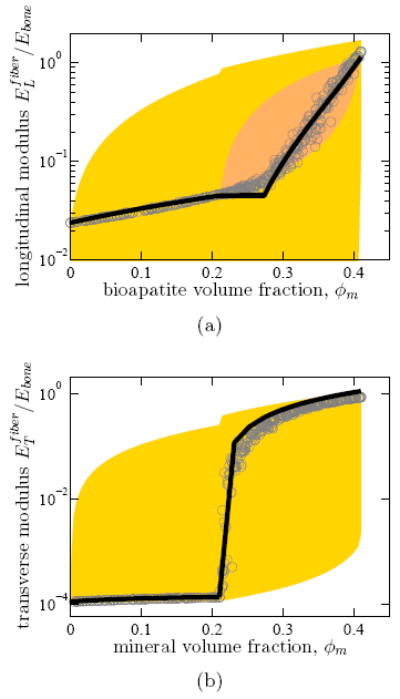
Linear estimation of longitudinal (a) and transverse (b) elastic moduli of partially mineralized collagen fibers (solid lines), plotted against stochastic finite element results of Liu et al. (2014) (gray circles). The darker shaded regions (orange in the online version) correspond to Hashin-Shtrikman type bounds that account for the continuous, fibrous nature of collagen fibrils, and the lighter shaded regions (yellow in the online version) correspond to Hashin-Shtrikman bounds that do not account for this (cf. Liu et al. (2014)).
The modeling of this stiffening was achieved in two stages. In the first stage, mineral accumulated on the inside of collagen fibrils, replacing water. The composite considered in this stage was a three-phase composite consisting of cross-linked collagen fibrils (treated as a transversely isotropic solid), bioapatite mineral, and water. Random spheres of bioapatite mineral replaced random spheres of water within the fibrils in this stage. Each phase was assigned moduli consistent with those used by Liu et al. (2014). The cross-linked collagen fibrils, transversely isotropic and rotationally symmetric about the x3-axis, were assigned Young’s moduli E3 = 814 MPa and E1 = E2 = 8.27 MPa, Poisson’s ratios ν13 = 0.1 and ν12 = 0:3, and shear modulus G13 = 6.53 MPa. Bioapatite mineral was treated as isotropic and much stiffer than the cross-linked collagen fibrils (E=110 GPa, ν=0.27), and water was treated as isotropic, nearly incompressible (ν=0.4999), and of negligible shear resistance. The predictions of the current approach followed the stochastic finite element predictions of Liu et al. (2014) closely in this regime, and was near a Hashin-Shtrikman lower bound accounting for the fibrillar nature of collagen fibrils, as described by Liu et al. (2014) (Fig. 5).
In the second phase, bioapatite mineral accrued on the outside of fibrils, and the nature of the relatively compliant, anisotropic EFM had to be accounted for explicitly. For extrafibrillar mineralization, we note debate in the literature about the shape of mineral inclusions within bone and partially mineralized tissues, and emphasize that uncertainty exists with both the current predictions and with the finite element predictions to which they were compared. We focussed on the following single example as a means of testing the range of validity of the current approach for multi-phase composites. The three-phase composite considered consisted of mineralized fibrils (infinitely long, with moduli calculated as above for ϕm = 0:21), bioapatite mineral (moduli as above), and EFM (isotropic with E = 280 kPa and ν = 0:3). The example chosen was one in which mineral accumulates on the outside of fibrils (within and upon fibers) through plate-like segments that align transverse to the collagen fiber axes (Alexander et al., 2012). Plate-like segments were modeled as randomly distributed mineral platelets oriented perpendicular to the collagen fibril axes. Results were consistent with the finite element simulations of Liu et al. (2014)) at all volume fractions for the transverse moduli, and up to ϕm ≈ 27% for the longitudinal modulus. However, the longitudinal modulus predictions highlight a limitation of the current approach, namely that it does not account for the spatial disposition of the different phases and can miss a percolation threshold. Nevertheless, the current approach was effective at sufficiently high volume fraction to represent the full range of mineralization: higher degrees of mineralization could be modeled by beginning with an extrafibrillar space that was fully dense with bioapatite mineral, then replacing mineral with EFM. This trend, illustrated in the region from 27 vol% to 41 vol% in Fig. 5, matched finite element data very well, and intersected the previous predictions at 27 vol% to provide estimates of mechanical behavior over the full range of mineralization. This is visible as a change in slope in the plots for both longitudinal and transverse moduli.
4. Conclusions
A method was proposed to predict the effective elastic moduli of composites containing multiple types of anisotropic ellipsoidal inclusions. The method employed effective rather than average strains within phases to ensure that the energy stored within phases summed to that stored in the composite. The special cases of two- and three-phase composites were predicted. The method reproduced available experimental data with good accuracy, especially at the higher volume fractions at which the Kanaun-Juelin estimate is expected to perform poorly. The proposed method produced physically consistent results and showed good predictive accuracy. Accordingly, the method is a candidate for the characterization of composites with multiple types of anisotropic inclusions, even if these inclusions have moderate volume fractions and a variety of aspect ratios.
Acknowledgments
This work was funded in part by the National Institutes of Health through grant R01HL109505, and by the National Institutes of Health and National Science Foundation through grant U01EB016422.
Appendix A. Eshelby tensors for various ellipsoidal shapes
For a general ellipsoid, components Sijkl are expressed in terms of (incomplete) elliptic integrals (Eshelby, 1957). For a spheroid, Sijkl are elementary functions of the spheroid’s aspect ratio.
Appendix A.1. General ellipsoid
Components Sijkl are as follows:
| (A.1) |
| (A.2) |
| (A.3) |
| (A.4) |
where a1, a2 and a3 are general ellipsoid semiaxes. Other Sijkl are found from symmetry relations Sijkl = Sjikl = Sijlk and by the cyclic permutation of indices (1,2,3) in quantities Sijkl, ai, Ii and Iij. Those components that cannot be obtained by the cyclic permutation of the above are zeros. Assuming that a1 ≥ a2 ≥ a3, we have:
| (A.5) |
Functions F(θ, k) and E(θ, k) are the incomplete elliptical integrals:
| (A.6) |
and where it is denoted:
| (A.7) |
The following equations (and the equations obtained by their cyclic permutations) express all Iij in terms of I1, I2, I3:
| (A.8) |
| (A.9) |
| (A.10) |
Appendix A.2. Sphere
In this case (a1 = a2 = a3 ≡ a) we have
| (A.11) |
| (A.12) |
| (A.13) |
| (A.14) |
Appendix A.3. Needle
In this case (a1 = a2 = a ≪ a3), the terms a/a3 are negligible, so that, to within higher order terms, Sijkl do not depend on ratio a/a3 and coincide with their limiting values at a/a3→0:
| (A.15) |
| (A.16) |
| (A.17) |
| (A.18) |
| (A.19) |
| (A.20) |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Fatemeh Saadat, Department of Mechanical Engineering & Materials Science, Washington University, St. Louis, MO 63130, USA.
Victor Birman, Engineering Education Center, Missouri University of Science and Technology, St. Louis, MO 63131, USA.
Stavros Thomopoulos, Department of Orthopaedic Surgery, Washington University School of Medicine, St. Louis, MO 63130, USA.
Guy M. Genin, Department of Mechanical Engineering & Materials Science, Washington University, St. Louis, MO 63130, USA
References
- Aboudi J. Micromechanical analysis of composites by the method of cells. Applied Mechanics Reviews. 1989;42:193–221. [Google Scholar]
- Alexander B, Daulton TL, Genin GM, Lipner J, Pasteris JD, Wopenka B, Thomopoulos S. The nanometre-scale physiology of bone: steric modelling and scanning transmission electron microscopy of collagen–mineral structure. Journal of The Royal Society Interface. 2012;9(73):1774–1786. doi: 10.1098/rsif.2011.0880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benveniste Y. A new approach to the application of Mori-Tanaka’s theory in composite materials. Mechanics of Materials. 1987;6(2):147–157. [Google Scholar]
- Birman V, Keil T, Hosder S. Structural Interfaces and Attachments in Biology. Springer; 2013. Functionally graded materials in engineering; pp. 19–41. [Google Scholar]
- Boonrungsiman S, Gentleman E, Carzaniga R, Evans ND, McComb DW, Porter AE, Stevens MM. The role of intracellular calcium phosphate in osteoblast-mediated bone apatite formation. Proceedings of the National Academy of Sciences. 2012;109(35):14170–14175. doi: 10.1073/pnas.1208916109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Budiansky B. On the elastic moduli of some heterogeneous materials. Journal of the Mechanics and Physics of Solids. 1965;13(4):223–227. [Google Scholar]
- Byrd LW, Birman V. Modeling and analysis of functionally graded materials and structures. Applied Mechanics Reviews. 2007;60:195–216. [Google Scholar]
- Castañeda PP, Willis JR. The effect of spatial distribution on the effective behavior of composite materials and cracked media. Journal of the Mechanics and Physics of Solids. 1995;43(12):1919–1951. [Google Scholar]
- Christensen RM. Mechanics of composite materials. Dover-Publications; Mineola, New York: 2012. [Google Scholar]
- Eppell SJ, Tong W, Katz JL, Kuhn L, Glimcher MJ. Shape and size of isolated bone mineralites measured using atomic force microscopy. Journal of orthopaedic research. 2001;19(6):1027–1034. doi: 10.1016/S0736-0266(01)00034-1. [DOI] [PubMed] [Google Scholar]
- Eshelby JD. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proceedings of the Royal Society of London. Series A Mathematical and Physical Sciences. 1957;241(1226):376–396. [Google Scholar]
- Ferrari M. Asymmetry and the high concentration limit of the Mori-Tanaka effective medium theory. Mechanics of Materials. 1991;11(3):251–256. [Google Scholar]
- Genin GM, Birman V. Micromechanics and structural response of functionally graded, particulate-matrix, fiber-reinforced composites. International Journal of Solids and Structures. 2009;46(10):2136–2150. doi: 10.1016/j.ijsolstr.2008.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genin GM, Kent A, Birman V, Wopenka B, Pasteris JD, Marquez PJ, Thomopoulos S. Functional grading of mineral and collagen in the attachment of tendon to bone. Biophys J. 2009;97(4):976–985. doi: 10.1016/j.bpj.2009.05.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamed E, Lee Y, Jasiuk I. Multiscale modeling of elastic properties of cortical bone. Acta Mechanica. 2010;213(1):131–154. [Google Scholar]
- Hashin Z. Analysis of composite materials. Journal of Appllied Mechanics. 1983;50(2):481–505. [Google Scholar]
- Hashin Z, Shtrikman S. A variational approach to the theory of the elastic behaviour of multiphase materials. Journal of the Mechanics and Physics of Solids. 1963;11(2):127–140. [Google Scholar]
- Hellmich C, Kober C, Erdmann B. Micromechanics-based conversion of ct data into anisotropic elasticity tensors, applied to fe simulations of a mandible. Annals of biomedical engineering. 2008;36(1):108–122. doi: 10.1007/s10439-007-9393-8. [DOI] [PubMed] [Google Scholar]
- Hellmich C, Ulm F-J. Micromechanical model for ultrastructural stiffness of mineralized tissues. Journal of engineering mechanics. 2002;128(8):898–908. [Google Scholar]
- Hill R. The elastic behaviour of a crystalline aggregate. Proceedings of the Physical Society. Section A. 1952;65(5):349. [Google Scholar]
- Hill R. A self-consistent mechanics of composite materials. Journal of the Mechanics and Physics of Solids. 1965;13(4):213–222. [Google Scholar]
- Hu G, Weng G. The connections between the double-inclusion model and the Ponte Castañeda–Willis, Mori–Tanaka, and Kuster–Toksöz models. Mechanics of Materials. 2000;32(8):495–503. [Google Scholar]
- Ju J, Yanase K. Micromechanics and effective elastic moduli of particle-reinforced composites with near-field particle interactions. Acta Mechanica. 2010;215(1-4):135–153. [Google Scholar]
- Ju J, Yanase K. Micromechanical effective elastic moduli of continuous fiber-reinforced composites with near-field fiber interactions. Acta Mechanica. 2011;216(1-4):87–103. [Google Scholar]
- Kakavas PA, Kontoni D-PN. Numerical investigation of the stress field of particulate reinforced polymeric composites subjected to tension. International Journal for Numerical Methods in Engineering. 2006;65(7):1145–1164. [Google Scholar]
- Kanaun S, Jeulin D. Elastic properties of hybrid composites by the effective field approach. Journal of the Mechanics and Physics of Solids. 2001;49(10):2339–2367. [Google Scholar]
- Kerner E. The elastic and thermo-elastic properties of composite media. Proceedings of the Physical Society Section B. 1956;69(8):808. [Google Scholar]
- Kim H-M, Rey C, Glimcher MJ. Isolation of calcium-phosphate crystals of bone by non-aqueous methods at low temperature. Journal of bone and mineral research. 1995;10(10):1589–1601. doi: 10.1002/jbmr.5650101021. [DOI] [PubMed] [Google Scholar]
- Kuster GT, Toksöz MN. Velocity and attenuation of seismic waves in two-phase media: Part i. Theoretical formulations. Geophysics. 1974;39(5):587–606. [Google Scholar]
- Kwon P, Dharan C. Effective moduli of high volume fraction particulate composites. Acta Metallurgica et Materialia. 1995;43(3):1141–1147. [Google Scholar]
- Lim TC. Elastic stiffness of three-phase composites by the generalized mechanics-of-materials (GMM) approach. Journal of Thermoplastic Composite Materials. 2002;15(2):155–167. [Google Scholar]
- Liu Y, Thomopoulos S, Birman V, Li J-S, Genin GM. Bi-material attachment through a compliant interfacial system at the tendon-to-bone insertion site. Mechanics of Materials. 2012;44:83–92. doi: 10.1016/j.mechmat.2011.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Thomopoulos S, Chen C, Birman V, Buehler MJ, Genin GM. Modelling the mechanics of partially mineralized collagen fibrils, fibres and tissue. Journal of The Royal Society Interface. 2014;11(92):20130835. doi: 10.1098/rsif.2013.0835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahamid J, Sharir A, Addadi L, Weiner S. Amorphous calcium phosphate is a major component of the forming fin bones of zebrafish: Indications for an amorphous precursor phase. Proceedings of the National Academy of Sciences. 2008;105(35):12748–12753. doi: 10.1073/pnas.0803354105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milton G. The Theory of Composites (Cambridge Monographs on Applied and Computational Mathematics) 1. Cambridge University Press; 2002. [Google Scholar]
- Milton G, Phan-Thien N. New bounds on effective elastic moduli of two-component materials. Proceedings of the Royal Society of London. A Mathematical and Physical Sciences. 1982;380(1779):305–331. [Google Scholar]
- Mori T, Tanaka K. Average stress in matrix and average elastic energy of materials with misffitting inclusions. Acta Metallurgica. 1973;21(5):571–574. [Google Scholar]
- Pasteris JD, Wopenka B, Valsami-Jones E. Bone and tooth mineralization: Why apatite? Elements. 2008;4(2):97. [Google Scholar]
- Richard TG. The mechanical behavior of a solid microsphere filled composite. Journal of Composite Materials. 1975;9(2):108–113. [Google Scholar]
- Roumi F, Shodja H. Elastic solids with high concentration of arbitrarily oriented multiphase particles. Acta Mechanica. 2007;189(3-4):125–139. [Google Scholar]
- Schwartz A, Pasteris J, Genin G, Daulton T, Thomopoulos S. Mineral distributions at the developing tendon enthesis. PloS one. 2012;7(11):e48630. doi: 10.1371/journal.pone.0048630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sen AK, Lado F, Torquato S. Bulk properties of composite media. ii. Evaluation of bounds on the shear modulus of suspensions of impenetrable spheres. Journal of Applied Physics. 1987;62(10):4135–4141. [Google Scholar]
- Sevostianov I. On the shape of effective inclusion in the maxwell homogenization scheme for anisotropic elastic composites. Mechanics of Materials. 2014;75:45–59. [Google Scholar]
- Sevostianov I, Giraud A. Generalization of Maxwell homogenization scheme for elastic material containing inhomogeneities of diverse shape. International Journal of Engineering Science. 2013;64:23–36. [Google Scholar]
- Sevostianov I, Kachanov M. On some controversial issues in effective field approaches to the problem of the overall elastic properties. Mechanics of Materials. 2014;69(1):93–105. [Google Scholar]
- Silnutzer NR. Ph D thesis. Graduate School of Arts and Sciences, University of Pennsylvania; 1972. Effective constants of statistically homogeneous materials. [Google Scholar]
- Smith JC. Experimental values for the elastic constants of a particulate-filled glassy polymer. Journal of Research of the National Bureau of Standards - A Physics and Chemistry. 1976;80:45–49. doi: 10.6028/jres.080A.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suresh S, Mortensen A, Suresh S. Fundamentals of functionally graded materials. Institute of Materials London 1998 [Google Scholar]
- Thomopoulos S, Das R, Birman V, Smith L, Ku K, Elson EL, Pryse KM, Marquez JP, Genin GM. Fibrocartilage tissue engineering: The role of the stress environment on cell morphology and matrix expression. Tissue Engineering Part A. 2011;17(7-8):1039–1053. doi: 10.1089/ten.tea.2009.0499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomopoulos S, Genin GM, Galatz LM. The development and morphogenesis of the tendon-to-bone insertion-what development can teach us about healing. J Musculoskelet Neuronal Interact. 2010;10(1):35–45. [PMC free article] [PubMed] [Google Scholar]
- Thomopoulos S, Marquez JP, Weinberger B, Birman V, Genin GM. Collagen fiber orientation at the tendon to bone insertion and its influence on stress concentrations. Journal of biomechanics. 2006;39(10):1842–1851. doi: 10.1016/j.jbiomech.2005.05.021. [DOI] [PubMed] [Google Scholar]
- Thurner PJ, Erickson B, Jungmann R, Schriock Z, Weaver JC, Fantner GE, Schitter G, Morse DE, Hansma PK. High-speed photography of compressed human trabecular bone correlates whitening to microscopic damage. Engineering fracture mechanics. 2007;74(12):1928–1941. [Google Scholar]
- Torquato S. Random Heterogeneous Materials. Springer; 2001. [Google Scholar]
- Torquato S. Random heterogeneous materials: microstructure and macroscopic properties. Vol. 16. Springer; 2002. [Google Scholar]
- Torquato S, Lado F. Effective properties of two-phase disordered composite media: iif. Evaluation of bounds on the conductivity and bulk modulus of dispersions of impenetrable spheres. Physical Review B. 1986;33(9):6428. doi: 10.1103/physrevb.33.6428. [DOI] [PubMed] [Google Scholar]
- Traub W, Arad T, Weiner S. Growth of mineral crystals in turkey tendon collagen fibers. Connective tissue research. 1992;28(1-2):99–111. doi: 10.3109/03008209209014230. [DOI] [PubMed] [Google Scholar]
- Tucker CL, III, Liang E. Stiffness predictions for unidirectional short-fiber composites: review and evaluation. Composites Science and Technology. 1999;59(5):655–671. [Google Scholar]
- Weng G. Explicit evaluation of Willis’ bounds with ellipsoidal inclusions. International Journal of Engineering Science. 1992;30(1):83–92. [Google Scholar]


