Lipid- and mechanosensitivities of sodium/hydrogen exchangers analyzed by electrical methods

Abstract

Sodium/hydrogen exchangers (NHEs) are ubiquitous ion transporters that serve multiple cell functions. We have studied two mammalian isoforms, NHE1 (ubiquitous) and NHE3 (epithelial-specific), by measuring extracellular proton (H⁺) gradients during whole-cell patch clamp with perfusion of the cell interior. Maximal Na⁺-dependent H⁺ fluxes (J_H+) are equivalent to currents >20 pA for NHE1 in Chinese hamster ovary fibroblasts, >200 pA for NHE1 in guinea pig ventricular myocytes, and 5–10 pA for NHE3 in opossum kidney cells. The fluxes are blocked by an NHE inhibitor, ethylisopropylamiloride, and are absent in NHE-deficient AP-1 cells. NHE1 activity is stable with perfusion of nonhydrolyzable ATP [adenosine 5′-(β,γ-imido)triphosphate], is abolished by ATP depletion (2 deoxy-d-glucose with oligomycin or perfusion of apyrase), can be restored with phosphatidylinositol 4,5-bisphosphate, and is unaffected by actin cytoskeleton disruption (latrunculin or pipette perfusion of gelsolin). NHE3 (but not NHE1) is reversibly activated by phosphatidylinositol 3,4,5-trisphosphate. Both NHE1 and NHE3 activities are disrupted in giant patches during gigaohm seal formation. NHE1 (but not NHE3) is reversibly activated by cell shrinkage, even at neutral cytoplasmic pH without ATP, and inhibited by cell swelling. NHE1 in Chinese hamster ovary fibroblasts (but not NHE3 in opossum kidney cells) is inhibited by agents that thin the membrane (l-α-lysophosphatidylcholine and octyl-β-d-glucopyranoside) and activated by cholesterol enrichment, which thickens membranes. Expressed in AP-1 cells, however, NHE1 is insensitive to these agents but remains sensitive to volume changes. Thus, changes of hydrophobic mismatch can modulate NHE1 but do not underlie its volume sensitivity.

Sodium/hydrogen exchangers (NHEs) are present in simple prokaryotes, lower eukaryotes, and higher eukaryotes including plants, fungi, and animals (1). In prokaryotes, yeast, and plants, the driving force of ΔμH⁺ energizes NHEs to export Na⁺ from the cytosol, whereas in animal cells, ΔμNa⁺ drives NHEs to extrude H⁺. In mammals, eight NHE isoforms (NHE1–NHE8) are cloned (1). NHE1 is a ubiquitous plasma membrane transporter that regulates pH and cell volume. It is implicated in regulating diverse cellular functions including proliferation, adhesion, and migration (2–4). NHE3 is present on endosomal and plasma membranes of epithelial cells, in which it plays a pivotal role in transepithelial Na⁺ transport in multiple organs (5, 6). The functions of other isoforms, present on both cell-surface (NHE2, NHE4, and NHE8) and organellar (NHE6 and NHE7) membranes, remain largely undefined (7, 8).

NHE activities are typically determined by changes in bulk cytoplasmic pH by using fluorescent pH-sensitive dyes, Na²² isotopic flux, or radioactive/fluorescent membrane-permeant buffer trapping. A common protocol is to acidify the cytoplasm and then quantify acid extrusion by NHEs under near V_max conditions during Na⁺-induced pH recovery. Pervasive problems of this approach include low sensitivity, poor time resolution, changes of ion concentrations, and very limited control of the cytoplasmic milieu. Here we describe an approach using pH microelectrodes during whole-cell patch clamp recording. Extracellular H⁺ gradients caused by H⁺ transport are detected by moving cells close to and away from a pH microelectrode in the presence of low buffer concentrations and measuring the H⁺ gradient with cancellation of electrode drift (9–11). Extensive manipulation of the cytoplasmic medium is possible by pipette perfusion, and H⁺ fluxes can be quantified by simulation of buffer diffusion. Using this “self-referencing” pH microelectrode technique, we provide different perspectives on the regulatory properties of NHE1 and NHE3 isoforms, in particular their lipid- and mechanosensitive properties. Specifically, we demonstrate that individual phosphatidylinositides have rapid, specific effects on NHE1 and NHE3 and that NHE1 can be very sensitive to rearrangements of its surrounding lipid domain. However, hydrophobic mismatch does not seem to be the primary molecular signal that mediates NHE1 volume sensing.

Methods

Cell Culture. Chinese hamster ovary (CHO) fibroblasts were maintained in F-12K nutrient mixture, Kaighn's modification (Invitrogen). NHE1-deficient AP-1 cells, derived from CHO cells (12) (a gift from S. Grinstein, Hospital for Sick Children, Toronto), were maintained in α-modified minimal essential medium (Sigma). Opossum kidney (OK) cells were maintained in high-glucose DMEM (Invitrogen). All culture media were supplemented with 10% heat-inactivated FBS (Invitrogen) and 100 units/ml penicillin and 100 units/ml streptomycin, and cells were propagated in a humidified 95%/5% air/CO₂ atmosphere incubator at 37°C. For patch clamp experiments, cells were trypsinized [Ca²⁺- and Mg²⁺-free salt solution containing 0.25% (wt/vol) trypsin and 2 mM EGTA] for 3–5 min and then resuspended in culture medium. Cells were stored at 10°C and used within 2 days. Guinea pig ventricular myocytes were isolated as described (13) and used for experiments within 6 h after isolation. NHE1-deficient AP-1 cells were transfected with Lipofectamine plus (Invitrogen). Cotransfection with the pEGFP plasmid (Clontech) was used for identification. Full-length opossum NHE3 (amino acids Δ1–839) and C-terminal truncations, amino acids Δ1–462 and Δ1–552, were cloned into pcDNA3.1. Full-length rat NHE1 in pCMV was a gift from J. Orlowski (McGill University, Montreal).

Patch Clamp. Membrane potential was held at 0 mV. Signals were recorded on pen recorders (Kipp & Zonen, Delft, The Netherlands). Data points in Figs. 2, 3, 4, 5 give the potential differences recorded by the pH electrode when the cell was moved away from the pH electrode. All results are at 35–37°C.

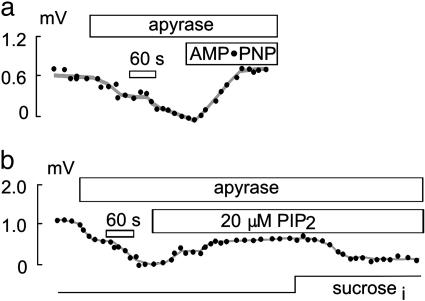
Fig. 2.

Effect of ATP depletion on NHE1 activity in CHO cells. (a and b) Pipette perfusion with apyrase (5 units/ml) leads to a rapid decline in NHE1 activity in CHO cells. Perfusion of 10 mM AMP-PNP in the presence of apyrase (5 units/ml) and 2 mM EDTA leads to a complete recovery of NHE1 activity (a), whereas perfusion with PIP₂ only partially recovers NHE1 activity (b). Even in the absence of ATP, NHE1 activity remains volume-sensitive (b).

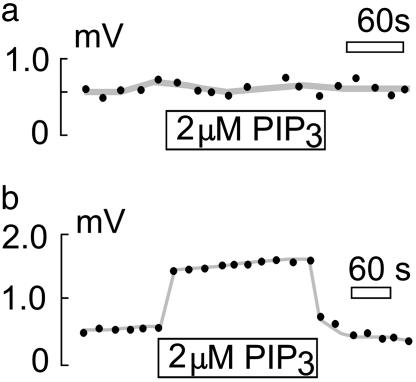
Fig. 3.

Effect of PIP₃ on NHE activity. Shown is pipette perfusion of PIP₃ into CHO (a) and OK (b) cells. NHE3 but not NHE1 activity is stimulated rapidly and reversibly by 2 μM cytoplasmic PIP₃.

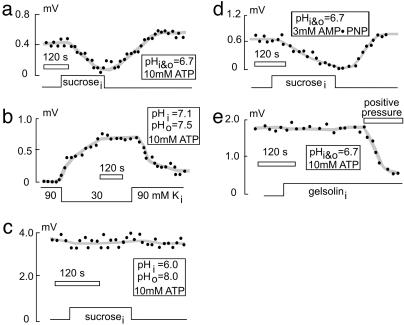
Fig. 4.

Effect of cell-volume changes on NHE1 activity in CHO cells. Pipette perfusion with a hypertonic solution containing sucrose leads to cell swelling and reduction of NHE1 activity. (a) This is reversed by perfusion of hypotonic solution without sucrose, which restores cell volume. (b) Vice versa, perfusion of hypotonic solution leads to cell swelling and increase NHE1 activity, even under conditions of a normal pH_i of 7.1. (c) At maximal activation of NHE1 activity (pH_i 6 and pH_o 8), volume sensitivity of NHE1 is lost. (d) In the absence of MgATP in the pipette solution and replacement by AMP-PNP, volume sensitivity of NHE1 is preserved. (e) Pipette perfusion with gelsolin to depolymerize F-actin does not affect NHE1 activity or NHE1 volume sensitivity.

Fig. 5.

Effect of bilayer modulation by hydrophobic compounds on NHE1 activity. Pipette perfusion (a) or bath application (c) of 1 mM OG strongly inhibits NHE1 activity in CHO cells but does not affect NHE3 activity in OK cells (c). (c) Similar effects occur with pipette perfusion of 10 μM l-α-lysophosphatidylcholine (LPC). Pipette perfusion of 100 μM cholesterol complexed with MCD strongly stimulates NHE1 activity in CHO cells (b) but does not affect NHE3 activity in OK cells (c). (c) Cholesterol depletion with pipette perfusion of 1 mM MCD does not affect either NHE1 or NHE3 activity. (d) NHE1 transfected into AP-1 cells is not affected by pipette perfusion of 1 mM OG or 100 μM cholesterol.

Proton-Selective Microelectrodes. The pH microelectrodes were prepared largely as described (11). Briefly, for measurements in the bath solution, borosilicate glass electrodes (1.2 mm) without filament (World Precision Instruments, Sarasota, FL) were pulled to yield tip diameters of 2–4 μm. The electrodes for intrapipette measurements were manufactured from flexible quartz capillary tubing (PolymicroTechnologies, Phoenix) and pulled on a custom devise using an acetylene flame. When the tip diameters were <2 μm, tips were beveled on the edge of a soft glass bead on the patch-pipette microforge to give diameters of ≈3 μm. Electrode tips were dipped briefly in Sigmacote (Sigma), and excess liquid was blown out by means of a syringe connected to the electrode through a thin polyethylene tube. The electrode was exposed to a stream of hot air for ≈10 s, back-filled with 100 mM KCl (pH 7.0 with 10 mM Hepes), and finally dipped in hydrogen ionophore I mixture B (Fluka) until column lengths were 100–200 μm. The average electrode response was 58 mV per pH unit from pH 6 to 8.

Recording Chamber and the Patch-Pipette Oscillation. Measurements of extrapipette and intrapipette ion gradients, and the physical principles and diffusion models, have been described (11). Briefly, extrapipette pH microelectrodes were mounted with sticky wax in a 1.3-mm-wide slit of a temperature-controlled recording chamber, and a fine, chlorided silver wire was then inserted into the back-filled electrolyte solution and connected to the probe of a high-input resistance (10¹⁵ Ω) electrometer (World Precision Instruments). After obtaining the whole-cell patch clamp configuration, the microscope stage was moved to a position with the cell in front of the ion-selective microelectrode (≈5–10 μm). The patch pipette then was moved manually, either laterally or longitudinally, between two positions (usually 50 μm) far apart enough to detect the entire ion gradient. Pipette perfusion was performed as described (14), with perfusion capillaries placed 50–150 μm from the patch-pipette tip. Individual experiments are representative of at least four experiments.

Solutions. The bath solution for the experiments shown in Fig. 1 contained 140 mM NaCl (30 mM NaCl in the experiment shown in Fig. 1d and 0 mM NaCl but 140 mM KCl for that shown in Fig. 1e), 2 mM CaCl₂, 2 mM MgCl₂, and 0.1 Tris. The pipette solution (Fig. 1, except g) contained 150 mM CsOH, 150 mM l-aspartic acid, 1 mM EGTA, 0.5 mM MgCl₂, 10 mM MgATP, and 10 mM Mes. The pipette solution for the experiment shown in Fig. 1g contained 75 mM CsOH, 75 mM l-aspartic acid, 1 mM EGTA, 0.5 mM MgCl₂, 10 mM MgATP, and 100 mM Mes. Both bath and pipette solutions were pH 6.7 in the experiments shown in Fig. 1 b and d–g. For the experiments shown in Fig. 1 c and h–k, bath pH was 8.0 and pipette pH was 6.0. The bath solution for the experiments shown in Fig. 2 contained 140 mM NaCl, 2 mM CaCl₂, 2 mM MgCl₂, and 0.1 mM Tris, pH 6.7. The pipette solution (Fig. 2) contained 90 mM KCl, 1 mM EGTA, 0.5 mM MgCl₂, 10 mM MgATP, and 50 mM Mes, pH 6.4. The pipette perfusion solution for the experiment shown in Fig. 2a contained 2 mM EDTA and no EGTA or MgCl₂. The bath solution for the experiments shown in Fig. 3 contained 140 mM NaCl, 2 mM CaCl₂, 2 mM MgCl₂, and 0.1 mM, Tris pH 6.7 (8.0 mM for that shown in Fig. 3b). The pipette solution (Fig. 3) contained 150 mM CsOH, 150 mM l-aspartic acid, 1 mM EGTA, 0.5 mM MgCl₂, 10 mM MgATP, and 10 mM Mes, pH 6.7 (6.0 mM for that shown in Fig. 3b).

Fig. 1.

NHE activity assayed by pH microelectrodes: typical extracellular pH gradients detected by pH microelectrodes during whole-cell patch clamp recording. (a) Schematic diagram of the experimental procedure. Relative motion of the cell to the pH microelectrode spans ≈50 μM (arrow). (b–k) Experimental records in which a cell was moved repetitively close to and away from (black bars) the pH microelectrode. Extracellular Na⁺ is 140 mM and pH is 6.7 on both sides unless indicated otherwise. (b) H⁺ gradient next to a CHO cell; upward deflection denotes higher pH. (c) H⁺ gradient next to a CHO cell with pH_o 8.0 and pH_i 6.0. Complete lack of H⁺ gradient next to a CHO cell is shown in d (in the presence of 10 μM ethylisopropylamiloride and 30 mM Na⁺) and e (with extracellular Na⁺ replaced by K⁺). (f) Complete lack of a pH gradient next to an NHE-deficient AP-1 cell. Shown are pH gradients next to a guinea pig ventricular myocyte (g), an OK cell (h), and an AP-1 cell transfected with either wild-type (i) or different C-terminal truncated forms [j (NHE3 Δ1–462) and k (NHE3 Δ1–552)] of opossum NHE3.

The bath solution for the experiments shown in Fig. 4 contained 140 mM NaCl, 2 mM CaCl₂, 2 mM MgCl₂, and 0.1 mM Tris. The pipette solution for the experiments shown in Fig. 4 a, c, and d contained 25 mM CsOH, 25 mM l-aspartic acid (120 mM sucrose), 1 mM EGTA, 0.5 mM MgCl₂, 100 mM Mes, and 10 mM MgATP (Fig. 4 a and c) or 3 mM adenosine 5′-(β,γ-imido)triphosphate (AMP-PNP; Fig. 4d). The pipette solution for the experiment shown in Fig. 4b contained 90 mM (30) KOH, 90 mM (30) l-aspartic acid, 1 mM EGTA, 0.5 mM MgCl₂, 10 mM MgATP, and 50 mM Mes. The pipette solution for that shown in Fig. 4e contained 100 mM CsOH, 100 mM l-aspartic acid, 1 mM EGTA, 0.5 mM MgCl₂, 10 mM MgATP, and 50 mM Mes. The bath solution for the experiments shown in Fig. 5 contained 140 mM NaCl, 2 mM CaCl₂, 2 mM MgCl₂, and 0.1 mM Tris, pH 6.8. The pipette solution (Fig. 5) contained 60 mM KOH, 30 mM l-aspartic acid, 10 mM KCl, 1 mM EGTA, 0.5 mM MgCl₂, 10 mM MgATP, and 50 mM Pipes, pH 6.8. For OK cells, 50 mM sucrose was added to the pipette solution to prevent cell shrinkage.

Recombinant gelsolin (N-terminal, calcium-insensitive part, 45 kDa) was a gift from H. Yin (University of Texas Southwestern Medical Center). Phosphatidyl 3,4,5-trisphosphate (PIP₃) and phosphatidyl 4,5-bisphosphate (PIP₂) were obtained from Echelon Biosciences (Salt Lake City). 3,3′,4′,5-tetrachlorosalicylanilide was obtained from Acros Organics through Fisher Scientific. All other chemicals were obtained from Sigma. Cholesterol-β-methylcylodextrin complexes were prepared as described by Smart and Anderson (15).

Estimation of H⁺ Flux Magnitudes. The calculation of ion fluxes from ion gradients was described (9–11). For whole-cell recording, we approximate the CHO cell shape as a sphere and cardiac myocytes as cylinders. The accuracy of flux estimates is limited mostly by these approximations, and potential errors can be evaluated by comparing calculations with definitively over- and underestimated cell dimensions. Also, inaccuracy may arise, in principle, from the assumption that H⁺ buffer kinetics are very fast in relation to diffusion. However, we have used electrogenic proton ionophores to generate well defined electrogenic H⁺ fluxes in excised patches, and the errors in estimating the proton fluxes from intrapipette proton gradients were <15%.

When H⁺ buffer kinetics are fast in relation to diffusion, and the proton gradients are small in relation to the buffer concentration, the diffusion of free and bound H⁺ can be approximated to take place independently. The flux (J_H+) then can be estimated from the free H⁺ concentration difference between the cell surface and the bulk solution (ΔH⁺), the H⁺ and buffer diffusion coefficients (D_H+ and D_B), the total buffer concentration (B_T), and the pK of the buffer. For a spherical cell,

[1]

Here, r is the cell radius, and ΔB_H+/ΔH⁺ is the steady-state concentration change of bound protons for a small change of free H⁺:

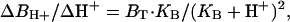[2]

where K_B is log(–pK). The flux carried by free H⁺ is negligible in most experiments.

For cardiac myocytes, we treat the proton flux as if it is occurring from the surface of a cylinder, for which predictions are more complex than from a sphere. Therefore, we carried out finite-difference simulations using dimensions appropriate for cardiac myocytes. For example, the solute concentration difference between a point at the midsurface of a cylinder and a point 0.5 mm away amounts to 18 μM when the total flux from the cylinder is 10^–15 mol/s (i.e., 100 pA), the cylinder is 100 μm long with a radius of 10 μm, and the diffusion coefficient is 10^–5 cm²·s^–1, as estimated for Tris. The predictions are very close to those expected for flux occurring from an infinitely long cylinder with a radius of 10 μm and a flux density of 100 pA per 100 μm, namely 19.5 μM. Based on these simulations, we conclude that the gradient occurring radially from the midpoint of a myocyte can be approximated well by the analytical solution for an extended cylinder:

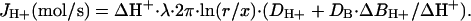[3]

λ is the length of the cylinder, r is the radius, and x is the radial distance from the cylinder midpoint over which the gradient is measured (i.e., 0.5 mm). As in previous studies (9–11), we relate our results on H⁺ fluxes to electrophysiological flux units by calculating the current equivalents of the fluxes (i.e., J_H+/faraday) in pA.

Results

Fig. 1 shows recordings of NHE activity from CHO, OK, and NHE-deficient AP-1 cells and freshly isolated guinea pig ventricular myocytes. CHO cells and ventricular myocytes express the NHE1 isoform (16), whereas OK cells express the NHE3 isoform (17, 18). Whole-cell voltage clamp is established and the cell then is moved to ≈5 μm from the tip of a pH microelectrode mounted in the recording chamber. The spherical cells are moved laterally 50 μm with respect to the pH electrode (Fig. 1a) to identify the presence of an H⁺ gradient (i.e., lower pH close to the cell). Black lines (Fig. 1) denote times when the cell was positioned away from the pH electrode. Drift of the pH electrodes can be significant over long times, but this drift is readily cancelled by the self-referencing procedure. We note that these signals displayed no dependence on the cell membrane potential over the range of –100 to +100 mV (data not shown), indicating that rate-limiting reactions in the NHE transport cycle are not voltage-dependent.

Fig. 1b shows a CHO cell with solutions set to pH 6.7 on both sides of the membrane. The extracellular (bath) Na⁺ concentration is 140 mM, and the cytoplasmic (pipette) solution is nominally Na⁺-free. The electrode response is 0.75 mV on average, which corresponds to a pH difference of 0.013 units, or a free H⁺ difference of 5.8 × 10^–9 M. By using a cell radius of 12 μm, the H⁺ flux calculated from Eq. 1 is 2 × 10^–17 mol·s^–1, equivalent to a current of 2.2 pA. In experiments with a large pH gradient (bath pH 8.0 and pipette pH 6.0) and the same Na⁺ concentrations, the electrode signals are between 1.0 and 4 mV, corresponding to pH gradients of 0.016 and 0.066 unit, respectively. The 1.6-mV signals, presented in Fig. 1c, correspond to an equivalent current of 23.6 pA for a 12-μm-radius cell. The much larger flux, compared with Fig. 1b, reflects the much greater buffer capacity of Tris (pK, 8.1) at pH 8.0. We point out that this flux equivalent is much larger than the maximal Na⁺/K⁺ pump current (≈3 pA) recorded in CHO cells (data not shown). As illustrated in Fig. 1d, the H⁺ flux in CHO cells was completely blocked by ethylisopropylamiloride (10 μM) with 30 mM extracellular Na⁺. We have not analyzed the Na⁺ kinetics in detail, but the H⁺ gradients are nearly as large with 30 mM Na⁺ as with 140 mM Na⁺. No H⁺ flux is recorded when extracellular Na⁺ is replaced by K⁺ (Fig. 1e). As further proof that the signals correspond to NHE activity, Fig. 1f illustrates the complete lack of H⁺ gradients recorded in the NHE-deficient AP-1 cells (same ionic conditions as for those shown in Fig. 1c).

Fig. 1g illustrates similar results using ventricular myocytes without a pH gradient (i.e., the conditions of Fig. 1b). For the 200-μm distance monitored, Eq. 3 indicates that the 1.8-mV signal corresponds to an H⁺ flux equivalent to a 73-pA H⁺ current (10-μm radius, 100-μm length). Values as high as 350 pA are obtained under maximal flux conditions (i.e., with a large pH gradient), which is equal to or greater than maximal Na⁺/K⁺ pump currents recorded in these cells (data not shown). As shown in Fig. 1h, H⁺ gradients recorded under the same conditions in OK cells (i.e., NHE3 activity) are somewhat smaller than in CHO cells. As documented in Fig. 1 i–k, we could readily measure H⁺ gradients in AP-1 cells transfected with wild-type opossum NHE3 or two different C-terminal truncations of opossum NHE3, amino acids Δ1–462 (transmembrane region only) and Δ1–552, respectively (19). In subsequent figures, data points give the potential difference recorded when the cell was moved away from the pH electrode.

One hallmark of NHE1 is inhibition by cellular ATP depletion, suggested to be caused at least in part by loss of the phosphatidylinositide, PIP₂ (20). Consistent with previous studies (21–28), we find that pretreatment of CHO cells for 30 min with 5 mM 2-deoxy-d-glucose and 5 μg/ml oligomycin resulted in complete loss of NHE1 activity in subsequent recordings without addition of ATP to the pipette solution (data not shown). The omission of MgATP from the pipette solution alone, however, does not affect NHE1 activity. Even when large-diameter (6–8 μm) pipettes are used, pipette perfusion with ATP-free solution induces no rundown of NHE activity over >20 min. However, pipette perfusion with the ATP/ADP nucleotidase, apyrase (5 units/ml), rapidly diminishes NHE1 activity (Fig. 2a). In the absence of a pH gradient (i.e., pH 6.7), activity is abolished. In the presence of a large pH gradient [pH outside (pH_o) 8.0 and pH inside (pH_i) 6.0], activity is diminished by only ≈50% (data not shown). Even in the presence of apyrase (5 units/ml) and EDTA (2 mM) to block protein kinase activity, NHE1 activity recovers completely with pipette perfusion of the nonhydrolyzable ATP analogue, AMP-PNP (10 mM). NHE1 activity could also be recovered by pipette perfusion of PIP₂ (20 μM; Fig. 2b). This recovery is almost complete in the absence of an H⁺ gradient (i.e., pH 6.7), but it is only ≈25% complete in the presence of a large pH gradient (pH_o 8.0 and pH_i 6.0, data not shown). In the presence of 10 mM MgATP, perfusion of PIP₂ (10 μM) has no effect on NHE1 activity in CHO or OK cells (data not shown). Effects of PIP₃ were very different. Perfusion of OK cells with 2 μM PIP₃ in the presence of 10 mM MgATP leads to a rapid and reversible increase of NHE3 activity (Fig. 3b). However, perfusion of CHO cells with 2 μM PIP₃ has no effect on NHE1 activity (Fig. 3a).

Next, we examined the volume sensitivity of NHE1 (29–34) in this whole-cell mode with extensive dialysis of the cytoplasm. Cell volume was changed both by application of pressure to the pipette and application of osmotic gradients to the cells. High concentrations of pH buffers (50–100 mM Mes) were used in the pipette to rigorously control cytoplasmic pH, and the distance between the virtual center of the cell and the electrode tip is held constant. Under conditions of nonmaximal NHE1 activation (i.e., without a pH gradient), pipette suction clearly causes cell shrinkage and an increase of the H⁺ efflux, whereas positive pressure and cell swelling lead to a decrease in H⁺ efflux (data not shown). Fig. 4a shows the strong decrease in NHE1 activity typically observed when a CHO cell is swollen by adding 120 mM sucrose. Recovery occurs promptly and completely with perfusion of the initial sucrose-free solution. Minimal NHE activity is recorded with isotonic solutions and with normal cytoplasmic (7.1) and extracellular (7.5) pH (Fig. 4b). However, cytoplasmic perfusion of hypotonic solution greatly activates NHE1 without any prior cytoplasmic acidification, and this activation reverses when cell volume is normalized by perfusion of a more hypertonic solution. Thus, shrinkage alone is a sufficient signal to activate NHE1. With a large pH gradient (pH 6.0 versus pH 8.0), cell shrinkage or swelling is without effect (Fig. 4c). The effect of cell shrinkage clearly involves a change of the activation state of the exchanger, not a change of its maximal activity or presence in the membrane (i.e., its presence in the membrane).

As illustrated in Fig. 4 d and e, volume sensitivity of NHE1 in CHO cells does not require ATP or intact actin cytoskeleton. When MgATP in the pipette is replaced by 3 mM AMP-PNP (Fig. 4d), NHE1 still responds to swelling and shrinkage. Similarly, GTP hydrolysis is not essential, because similar results were obtained with GTPγS (200 μM) in the pipette (data not shown) as well as with PIP₂ in the absence of ATP (Fig. 2b). Pipette perfusion of the actin cytoskeleton disruptor, gelsolin (1 μM; Fig. 4e) has obvious effects on the organization of the cytoplasm (data not shown) but has no effect on the ability of cell swelling to inhibit NHE1 activity. Furthermore, high concentrations of the actin cytoskeleton disruptors latrunculin B (20 μM) and cytochalasin D (20 μM) do not affect NHE1 activity (data not shown). Clearly, disruption of cytoskeleton cannot be the basis of mechanosensitivity or the absence of measurable NHE activities in excised patches (n > 200) despite the fact that we can readily monitor proton fluxes equivalent to 1 pA by using electrogenic protonophores such as 3,3′,4′,5-tetrachlorosalicylanilide (10 μM) (35).

Given that the volume sensitivity of NHE1 does not seem to depend on cell metabolism or on cytoskeleton, we tested whether it might be mediated through the bilayer itself. Hydrophobic mismatch at the channel–bilayer interface is a well established determinant of channel gating for the peptide channel, gramicidin (36), and the bacterial mechanosensitive channel, KcSA (37). The “V”-shaped amphipathic compounds octyl-β-d-glucopyranoside (OG) and l-α-lysophosphatidylcholine are expected to expand the bilayer laterally and to thin it and/or induce local curvatures. Bilayer thinning, in principle, would simulate the effect of cell swelling. Enrichment of membrane with cholesterol, typically achieved with cyclodextrin–cholesterol complexes, can stiffen and thicken the membrane bilayer, which, in principle, would correspond to the effect of cell shrinkage if membrane domains around transporters were stressed at normal volume.

As shown in Fig. 5a, application of OG (1 mM) via pipette perfusion results in complete inhibition of the NHE1 activity in CHO cells within 3 min. Pipette perfusion of cholesterol–β-methylcyclodextrin (MCD) complexes (100 μM) results in rapid and strong activation of NHE1 activity in CHO cells (Fig. 5b). Both OG (1 mM) applied in the bath and pipette perfusion of l-α-lysophosphatidylcholine (10 μM) were equally effective as pipette perfusion of OG (1 mM; Fig. 5c). NHE3 in OK cells is not affected by pipette perfusion of OG (1 mM) or cholesterol–MCD (100 μM) complexes. These findings support in principle the notion that effects of volume changes to NHE1 are mediated by changes of hydrophobic mismatch. However, NHE1 transfected into AP-1 cells is normally volume-sensitive but is not affected by pipette perfusion of OG (1 mM) or cholesterol–MCD complexes (100 μM) for 3 min (Fig. 5d). Also, we mention that NHE1 in CHO cells remains volume-sensitive even after a 20-min application of cholesterol–MCD (100 μM) complexes (data not shown).

Discussion

This study establishes the use of self-referenced pH electrodes to monitor NHE activity with whole-cell voltage clamp and pipette perfusion to manipulate the cytoplasmic side. The utility of this approach is demonstrated by verifying and extending many previous findings about NHE1 and NHE3 regulation. It is demonstrated that NHE1 is directly mechanosensitive and that this mechanosensitivity is probably not mediated through hydrophobic mismatch. Our efforts to maintain NHE activity in membrane patches remain unsuccessful, but the major results obtained in whole-cell recording may provide important clues to solving this enigma.

Our ability to monitor H⁺ fluxes caused by NHE1 in CHO cells is confirmed by three findings: H⁺ fluxes (i.e., H⁺ gradients) depend on extracellular Na⁺, are blocked by ethylisopropylamiloride, and are absent in NHE-deficient AP-1 cells. NHE activity is readily detected over a wide range of pH and Na⁺ gradients in several different cultured cells lines and in freshly isolated guinea pig ventricular myocytes. Thus, detailed characterization of NHE function will readily be possible with these methods. The expression of different C-terminal truncated forms of opossum NHE3 in NHE-deficient AP-1 cells demonstrates that the method will be an attractive means to study NHE mutants with relatively low activity in single cells. The absolute accuracy of our H⁺ flux measurements remains to be proved, but it is certain that the maximal NHE1-mediated H⁺ flux densities are in range of, or greater than, maximal Na⁺ fluxes mediated by Na⁺/K⁺ pumps in cardiac myocytes and CHO cells, respectively. Finally, as expected if NHE1 transport reactions are completely voltage-independent, NHE1 activity is insensitive to changing membrane potential over a 200-mV range.

Grinstein and coworkers (20, 22–24, 29) reported that NHE1 is sensitive to ATP depletion. ATP depletion must be quite extensive to inhibit NHE1, because the simple removal of ATP from the cytoplasmic solutions does not cause NHE1 rundown. In addition, nonhydrolyzable ATP can activate NHE1, and in our hands this activation is stronger than that of PIP₂. Because other polyanions and metal chelators (e.g., EDTA) do not activate NHE, the mechanism of activation is specific and could represent a direct means of regulating NHE1, opposite to the regulation of K_ATP K channels by ATP.

Whereas native NHE1 seems to be located mostly in the plasma membrane (38), NHE3 is also present in submembrane vesicles and internal membranes (39–41), and trafficking of NHE3 is strongly implicated to regulate its activity. PIP₃ has been proposed to promote NHE3 trafficking to the surface membrane and ultimately the fusion of NHE3-containing vesicles to the surface membrane. We have shown here that direct application of PIP₃ to the cytoplasmic side leads to rapid, reversible activation of NHE3 in seconds; whether this is caused by increased numbers of NHE3 exchangers in the surface membrane or direct activation of NHE3 is not defined by the present experiments. Clearly, our method is promising for analyzing the basis of PIP₃-dependent regulation of NHE3 as well as possible roles of PIP₂ in regulating both NHE1 and NHE3.

A central feature of NHE1 regulation is volume sensitivity (29–34), although the underlying molecular mechanisms have remained enigmatic. A recent report mapped NHE1 volume sensitivity to the first extracellular loop (33). In our study, efficient control of cell volume was achieved with pipette perfusion, and we could dissociate volume sensitivity of NHE1 function from the presence of ATP. Because changes in NHE1 activity were observed by applying negative or positive pressure in the patch pipette, osmolarity per se is not a factor. Also, GTPγS and AMP-PNP did not alter NHE1 volume sensitivity in the absence of MgATP. Together, these results constitute strong evidence that nucleotide hydrolysis is not required to regulate NHE1 by volume changes. Furthermore, extensive tests show that intact actin cytoskeleton is not required for NHE1 regulation.

Given these results, the mechanosensitivity of NHE1 might be mediated either by another type of membrane protein network or by membrane lipids themselves. Our results with hydrophobic compounds that modulate some mechanosensitive channels by changing hydrophobic mismatch (36) demonstrate that NHE1 can be affected by modifying physical properties of the membrane bilayer. It is striking that the volume-insensitive isoform, NHE3, is not affected by the same interventions. However, the lack of effects of these interventions on NHE1 expressed in AP-1 cells, in which activity remains volume-sensitive, disfavors hydrophobic mismatch as the primary signal that mediates volume sensitivity. Rather, it seems more likely at this point that protein-interaction partners of NHE1 are the immediate mechanosensors. Some component of the system that is affected by membrane lipids seems to be disrupted in the AP-1 cell line, which was derived by chemical mutagenesis.

In summary, self-referenced pH electrodes (9) are a powerful approach to study NHE activities during whole-cell voltage-clamp recording, being applicable to different cell types, NHE isoforms, and expression systems. We have verified the sensitivity of NHE1 to metabolic state and direct activation by PIP₂ as well as very rapid dependence of NHE3 (but not NHE1) on PIP₃. We have demonstrated strong direct activation of NHE1 by nonhydrolyzable ATP analogues and by cell shrinkage, indicating that direct physical interactions mediate NHE1 mechanosensitivity. Although NHE1 can be strongly modulated by hydrophobic compounds that change hydrophobic mismatch at protein–lipid interfaces, modulation by lipids can be dissociated from modulation by cell volume. Thus, protein-interaction partners of NHE1 probably mediate its volume sensitivity.