Predictive Treatment Management: Incorporating a Predictive Tumor Response Model Into Robust Prospective Treatment Planning for Non-Small Cell Lung Cancer

Abstract

Purpose

We hypothesized that a treatment planning technique that incorporates predicted lung tumor regression into optimization, predictive treatment planning (PTP), could allow dose escalation to the residual tumor while maintaining coverage of the initial target without increasing dose to surrounding organs at risk (OARs).

Methods and Materials

We created a model to estimate the geometric presence of residual tumors after radiation therapy using planning computed tomography (CT) and weekly cone beam CT scans of 5 lung cancer patients. For planning purposes, we modeled the dynamic process of tumor shrinkage by morphing the original planning target volume (PTV_orig) in 3 equispaced steps to the predicted residue (PTV_pred). Patients were treated with a uniform prescription dose to PTV_orig. By contrast, PTP optimization started with the same prescription dose to PTV_orig but linearly increased the dose at each step, until reaching the highest dose achievable to PTV_pred consistent with OAR limits. This method is compared with midcourse adaptive replanning.

Results

Initial parenchymal gross tumor volume (GTV) ranged from 3.6 to 186.5 cm³. On average, the primary GTV and PTV decreased by 39% and 27%, respectively, at the end of treatment. The PTP approach gave PTV_orig at least the prescription dose, and it increased the mean dose of the true residual tumor by an average of 6.0 Gy above the adaptive approach.

Conclusions

PTP, incorporating a tumor regression model from the start, represents a new approach to increase tumor dose without increasing toxicities, and reduce clinical workload compared with the adaptive approach, although model verification using per-patient midcourse imaging would be prudent.

Introduction

Delivering a tumoricidal dose in the radiation treatment of locally advanced non-small cell lung cancer (NSCLC) is challenging because coverage of large target volumes conflicts with normal tissue dose tolerance, especially of the spinal cord and normal lung. Tumor shrinkage is often observed during radiation therapy of NSCLC (1–6). The most commonly proposed planning paradigm to handle tumor shrinkage is adaptive radiation therapy (ART) (7–10). Replanning can be scheduled once or twice based on updated target contours obtained from scheduled resimulations or periodic cone beam computed tomography (CBCT) scans. The resulting adapted plan can either escalate dose to the residual tumor or spare the surrounding healthy lung tissue and adjacent organs at risk (OARs) or both. However, the gain of ART is limited by the increased clinical workload associated with frequent replanning. Furthermore, the turnaround planning time directly affects the performance of ART; the maximal impact is achieved only if there are no additional planning-related delays because a treatment course interruption caused by replanning would allow for repopulation. Any effort to safely reduce or eliminate turnaround time will benefit patients, and removing the need to replan promotes a more efficient workflow. A fresh look at the design of ART is necessary to maximize clinical impact and improve its efficiency.

The current ART process lacks attempts to use prior knowledge of how a tumor is likely to shrink during radiation therapy. Seibert et al (11) reported the use of a nonparametric, memory-based locally weighted regression model to accurately predict the final tumor volume. However, for treatment plan optimization, the location and volume of the residual tumor are equally important. If the geometric location of the residual tumor can be estimated by a predictive model, a robust optimization algorithm can dose-paint to the regression pattern and achieve the best therapeutic ratio with improved efficiency. In this article we investigate the likely clinical properties of such an algorithm and propose a novel predictive treatment planning (PTP) management paradigm to address the challenges faced by ART.

Methods and Materials

Imaging study

A credible prediction model for tumor shrinkage needs support from patient imaging data. For this proof-of-principle study, we used the planning CT and consecutive weekly kilovoltage CBCT scans of 5 patients with locally advanced NSCLC who were enrolled in a prospective imaging protocol approved by our Institutional Review Board (12). Six other patients were in the protocol; for these, either no shrinkage was observed or tumors were not completely visualized on the CBCTs. The gross tumor volume (GTV) was contoured on the CBCTs acquired at the middle and end of the treatment, and then transferred to the planning CT by means of manual rigid registrations to the spine. For each patient, the tumor included mediastinal and primary (lung parenchymal) components. Shrinkage of the primary component was seen for all 5 patients. Figure 1 shows the primary GTV originally seen on the planning CT (GTV_orig, yellow), on the midcourse CBCT (GTV_mid, blue), and on last-treatment CBCT (GTV_resid, red). GTV_mid and GTV_resid are slightly outside GTV_orig because of the uncertainties of bony registration, contour delineation, and lung tissue morphologic changes. The mediastinal GTV_media is shown in cyan, where little change was seen.

Fig. 1.

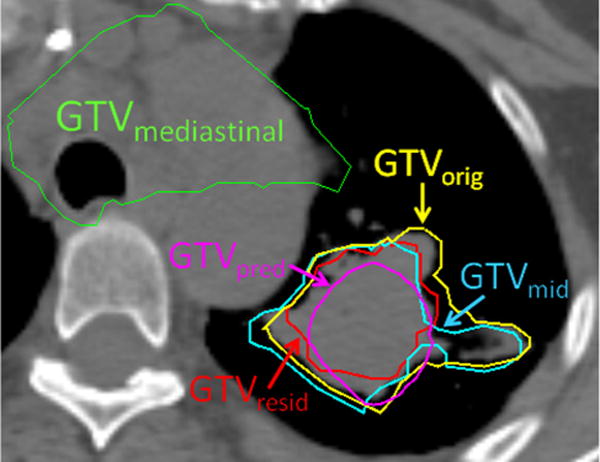
The primary gross tumor volume (GTV) contoured on the midcourse (cyan) and final week (red) cone beam computed tomographic (CT) images are transferred back to the planning CT by manual rigid. The original, predicted, and mediastinal GTVs are shown in yellow, magenta, and green, respectively.

Tumor shrinkage model

We built a tumor shrinkage model based on imaging data to estimate the spatial relationship between GTV_orig and GTV_resid. Each structure is handled by use of a points cloud:

$$GT{V}_{n\times 3}=\left[\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ \cdots & \cdots & \cdots \\ x_n& y_n& z_n\end{array}\right]$$ Eq:1

where n is the number of points, and x,y,z is a point’s position. For each individual patient, the prediction algorithm starts with analyzing the spatial occupancy of both GTV_orig and GTVresid by principal component analysis (13) by using their points clouds as input to the Matlab (MathWorks, Natick, MA) function princomp():

$$\left[\mathit{coef}{f}_{3\times 3},\mathit{scor}{e}_{n\times 3}\right]=\mathit{princomp}(\mathit{GT}{V}_{n\times 3})$$ Eq:2

which performs principal component analysis and returns principal component coefficients (coeff_3×3) and principal component scores (score_n×3). The first principal component represents the largest possible variance of the points cloud, and each successive component has the highest variance possible orthogonal to the preceding components. Together, 3 components represent 3 orthogonal axes where the points cloud has the largest separation. The score of a point is its projection onto the new orthogonal axes. The boundary of the points cloud can be modeled using an ellipsoid:

$$\mathit{EGT}{V}_{6\times 3}=\left[\begin{array}{ccc}{x}_{+1}& y_{+1}& z_{+1}\\ x_{-1}& y_{-1}& z_{-1}\\ x_{+2}& y_{+2}& z_{+2}\\ x_{-2}& y_{-2}& z_{-2}\\ x_{+3}& y_{+3}& z_{+3}\\ x_{-3}& y_{-3}& z_{-3}\end{array}\right]$$ Eq:3

where each row corresponds to a point with the maximal score along 1 principal direction.

If the GTV shape is reasonably consistent between the original tumor and residual tumor, the principal axes of the tumor at the 2 different time points would approximately align with each other. Under this assumption, an affine transformation matrix T maps the ellipsoid modeling the original points cloud to the residual one:

$${\left[\mathit{EGT}{V}_{\mathit{resid}}1\right]}_{6\times 4}={\left[\mathit{EGT}{V}_{\mathit{orig}}1\right]}_{6\times 4}\times T_{4\times 4}$$ Eq:4

T can be solved as:

$$T={\left({\left[\mathit{EGT}{V}_{\mathit{orig}}1\right]}^T\times \left[\mathit{EGT}{V}_{\mathit{orig}}1\right]\right)}^{-1}\times {\left[\mathit{EGT}{V}_{\mathit{orig}}1\right]}^T\times \left[\mathit{EGT}{V}_{\mathit{resid}}1\right]$$ Eq:5

This affine transformation accounts for shrinkage, rotation, shearing, and translation between GTV_orig and GTV_resid. The 5 transformation matrices obtained from 5 clinical cases serve as prior modes of the shrinkage model.

Given the i^th patient’s GTV_orig, its predicted residual position using the shrinkage model of the j^th patient, denoted $\mathit{GT}{V}_{\mathit{pred}}^{\mathit{ij}},$ is estimated by:

$$\left[GT{V}_{\mathit{pred}}^{ij}1\right]=\left[GT{V}_{\mathit{orig}}^{i}1\right]\times T_j$$ Eq:6

Note that for each individual patient, the transformations are performed 4 separate times using the 4 transformation matrices other than its own to ensure an unbiased estimation. The final GTV_pred is determined as the volume that overlaps at least 3 (majority) transformed points clouds. The resultant points cloud for GTV_pred is converted to a set of contours and transferred to the optimization module for visualization and planning. Figure 1 shows an example illustrating the spatial relationship between GTV_orig, GTV_resid, and GTV_pred. To evaluate the accuracy of each prediction, we tabulated the Dice coefficients, the overlap between GTV_resid and GTV_pred, and the interslice mean Hausdorff distances (14) between the surfaces of the 2 volumes.

In addition to uncertainties associated with general tumor shrinkage patterns, the prediction model is also affected by observation uncertainties, such as timing and changes in anatomic pose. A study by Sonke and Belderbos (6) reported an average tumor shrinkage of 1% per day. Therefore, the average change along 1 direction would be less than 1% of the length. Because the maximal tumor length was 10 cm in our study, the average uncertainty in any direction associated with timing was 1 mm/day. To simulate the impact of pose uncertainties, we moved (translation and rotation) the GTV contour on the patient’s final CBCT according to the rigid registration of the spine between it and the CBCTs acquired at earlier weeks. The new contours representing different poses were then used in the prediction model. Five new sets of predictions were obtained by using the poses from the prior 5 weeks of CBCTs. We quantified the impact of anatomic pose by calculating the Hausdorff distances among different predictions.

The dynamic process of tumor shrinkage was then modeled by morphing GTV_orig to GTV_pred in 3 equispaced steps along the 3 spatial dimensions in the imaging coordinate system. Each morphed GTV was expanded to a planning target volume (PTV) with a uniform 1.2-cm margin to account for uncertainties. A series of shell structures was created to account for PTV shrinkage along the treatment course toward its residual value (Fig. 2).

Fig. 2.

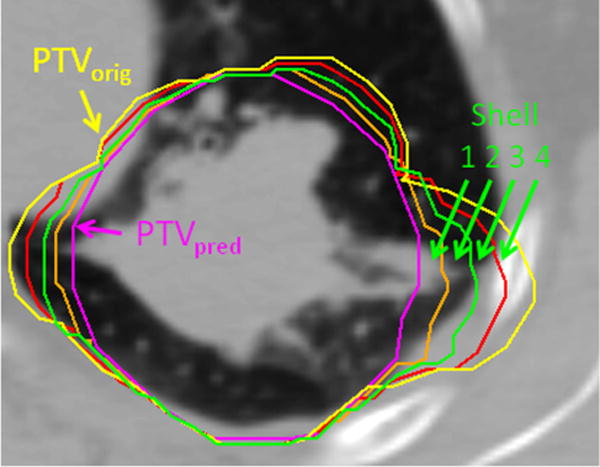
A series of shell structures is created to account for shrinkages from the original to predicted residual planning target volume (PTV).

Dose painting to the shrinking pattern

Instead of prescribing uniform dose to PTV_orig as in the conventional approach, the score-function objective dose in PTP linearly follows the predicted evolving pattern of tumor shrinkage. It starts with the same prescription dose to PTV_orig, but linearly increases dose at each evolving shell, until reaching the highest dose achievable to the innermost PTV_pred consistent with OAR limits. For simplification, all plans used the initial planning CT for OAR localization. Note that although the majority of the outermost part of primary PTV_orig disappeared at the end of treatment, the objective dose to this region was maintained as the clinical prescription dose. The objective dose to the mediastinal PTV was also kept at the clinical prescription dose because little mediastinal shrinkage was observed. This prescription scheme is conservative yet robust to errors introduced by the shrinkage prediction because the optimization is not asked to reduce dose to PTV_orig below prescription. Siker et al (15) suggested that tumor shrinkages are not significant for a good portion of the patient population, but for these patients, PTP does not adversely affect the treatment plan because no OAR limits are violated and the dose to PTV_orig is not reduced relative to what it would receive in a uniform-dose planning paradigm. If there is no shrinkage, the prescribed heterogeneous dose distribution introduces a dose boost to portions of the tumor that may still increase local control. This heterogeneous dose prescription is optimized, and the resulting plans served as the PTP arm in the planning study.

Treatment planning studies

Comparison was made with the clinical treatment plans with which patients were treated. These plans prescribed a uniform dose (D_pre), ranging from 56 Gy to 70 Gy (2-Gy fractions) to PTV_orig, subject to in-house OAR dosimetric constraints. The major constraints include Lyman-Kutcher-Burman Model normal tissue complication probability (NTCP) for lung less than 25% (16), which in practice is satisfied when mean normal lung dose is less than 20 Gy; and a maximal dose to the spinal cord below 50 Gy. Not all plans were pushed to the departmental standard OAR limits because the physician may request lower lung doses because of a patient’s comorbidities.

In addition to comparison with the clinical treated plans, another relevant comparison is between PTP plans and plans prescribed with similar inhomogeneous dose boost (eg, same maximal dose to PTV) (17–21) but without the guidance provided by the shrinkage prediction model. For this control set of plans referred to as GTV-boost, we created 4 equispaced shells that progressed from PTV_orig toward GTV_orig, and increased objective doses accordingly under OAR limits. This GTV-boost approach is equivalent to using GTV_orig as PTV_pred in PTP and superior to applying a random inhomogeneous dose boost because the residual tumor is very likely to lie within the original tumor at the end of treatment.

To simulate midcourse replanning ART, the tumor was delineated on a midcourse CBCT acquired 3 to 4 weeks into the treatment course (after delivery of 30–40 Gy) and registered to the planning scan. An adaptive treatment plan was optimized accounting for the existing dose contributed by the original treated plan such that the updated primary PTV (PTV_mid) received the highest dose achievable, the mediastinal PTV received the original prescription dose, and OAR constraints were respected. The benefit of this implementation of ART comes mainly from the escalated dose to the residual tumor, rather than attempting to lower the dose to the surrounding lung tissue and reduce toxicity. The evenly weighted combination of revised and original plans represents the ART scenario with midcourse replanning.

All treatment plans were designed using sliding window intensity-modulated radiation therapy with 6-MV photons. Five to 7 beams were used with angles selected according to the planners’ judgment. Although treatment plans are optimized based on different targeting schemes, evaluation is based on dosimetric end points of PTV_resid (GTV_resid margined with 1.2 cm). The end points include PTV_resid minimum dose (D_min), mean dose (D_mean), and the dose received by 95% of the volume (D95). Because PTP emphasis is on robustness to prediction model uncertainty, D95 of the volume inside PTV_orig excluding PTV_resid, denoted as PTV_gone, is also evaluated. For OARs, lung (lung-GTV_orig) mean dose, lung NTCP, and spinal cord maximum dose are optimized to match the clinical treated plans.

Results

Tumor shrinkage characteristics

The primary GTV_orig ranged from 3.6 cm³ to 186.5 cm³ (median, 49.4 cm³). The median volumes of the mediastinal GTV and PTV were 170 cm³ and 490 cm³, respectively. For these 5 patients, primary GTV_orig regressed by the middle to late phase of the treatment course: they decreased by an average of 12% of the initial volume (range, 0%–26%) by the middle of the treatment, and eventually decreased an average of 39% (range, 34%–50%) by the end of the treatment (6–7 weeks). The corresponding residual PTV decreased by an average of 27% (range, 23%–51%) at the end. The prediction model estimated more GTV shrinkage: average 47% (range, 28%–62%). The fourth column of Table 1 shows the overlap between GTV_pred and GTV_resid normalized to GTV_resid; the average overlap was 65% (range, 55%–75%). The corresponding overlap between PTV_pred and PTV_resid normalized to PTV_resid was higher, with an average of 79% because the uniform expansion from GTV to PTV smoothed part of the variations. The Dice coefficient that correlated GTV_pred with GTV_resid, and PTV_pred with PTV_resid averaged 0.68 and 0.82, respectively, which agreed with the overlap measure. Meanwhile, for the GTV-boost approach, the Dice coefficient correlating GTV_orig with PTV_resid was lower, average 0.43, given that GTV_orig tended to be smaller than PTV_pred, especially for small tumors. The interslice mean Hausdorff distance between the surfaces of the predicted and observed volumes was 2.5 mm and 3.0 mm, for GTV and PTV, respectively. The 3D relationships between the original (yellow), residual (magenta), and predicted (green) GTV embedded in the lung mesh of the 5 patients are illustrated in the volume rendering Figure 3. The principal axes of the tumor remained anatomically consistent between the residual and original tumors for the 5 cases shown in Figure 3, hence supporting the assumption that is the basis for Eq. 4.

Table 1.

Evaluation of the tumor shrinkage model

Patient	GTVorig(cm3)	GTVresid(cm3)	GTVpred ∩ GTVresid	GTV Dice coefficient	GTV mean surface distance (mm)	PTVpred ∩ PTVresid	PTV Dice coefficient	PTV mean surface distance (mm)
1	49.4	32.1	63.2%	0.69	2.5	77.5%	0.81	2.9
2	59.4	38.6	57.3%	0.66	3.2	76.7%	0.76	4.1
3	9.1	5.5	54.7%	0.69	1.0	76.0%	0.84	1.6
4	3.6	1.8	74.6%	0.64	1.2	88.3%	0.89	1.2
5	186.5	123.5	74.0%	0.71	4.8	76.4%	0.80	5.3

Abbreviations: GTV = gross tumor volume; PTV = planning target volume.

Fig. 3.

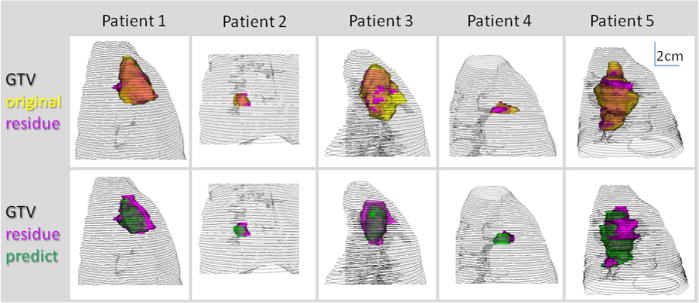
Original (yellow), residual (magenta), predicted (green) gross tumor volume (GTV) and lung mesh of 5 patients are shown in 3-dimensional volume rendering.

The Hausdorff distance variation among GTVs with different simulated anatomic poses was 6.5±2.9 mm, which subsequently caused variations in the prediction results: the Hausdorff distance among different sets of predictions was 1.8±2.6 mm. The overlap function in the prediction model smoothed some of the variations.

Table 2 shows that treatment plans from 4 sets of studies (ie, clinical, GTV-boost, ART, and PTP) had similar OAR-sparing characteristics. The differences in lung NTCP, lung mean dose, and cord maximum dose were not clinically significant. Furthermore, in the PTP arm, D95 of PTV_gone (the disappearing shell that was occupied by PTV_orig but not included in PTV_resid) met the clinical objective and received on average the same prescription dose as the other plans. Although PTP plans unsurprisingly improved dose to PTV_resid compared with conventional clinical plans, they also had better PTV_resid D95 and Dmean, averaging 3.4 Gy (5.4%) and 3.9 Gy (6.2%) higher, respectively, compared with GTV-boost plans, because of the better aid from the prediction model. The improvement of the PTP plan relative to the midcourse adaptive strategy was more moderate: although the averages of D95 for PTV_resid were comparable, D_mean of PTV_resid was on average 5.7 Gy (9.1%) higher for the PTP approach than the midtreatment replanning ART approach. The residual PTV was smaller than the midcourse PTV, making it easier for PTP to create an inhomogeneous distribution where the hotspot coincides with the residual PTV while protecting the surrounding normal tissue. In some patients, another disadvantage for ART in terms of dose escalation is that OAR dose limits were already significantly consumed by the midtreatment stage, leaving little room for replanning maneuvering. The dose distribution and DVH of patient 2 are illustrated in Figures 4a and 4b, respectively. The requested linear dose increase was well maintained.

Table 2.

Dosimetric comparison showing advantage of predictive treatment planning in increasing dose to residual tumor without significantly increasing dose to lung and cord

	Patient	PTVresid D95 (Gy)	PTVresid Dmin (Gy)	PTVresid Dmean (Gy)	PTVgone D95 (Gy)	Lung Dmean (Gy)	Lung NTCP	Cord Dmax (Gy)
1	Clinical	61.5	53.2	62.7	60.6	19.3	0.23	43.0
	GTV boost	63.0	50.1	70.0	61.0	19.5	0.25	44.1
	Replan	63.9	56.3	66.6	61.1	19.7	0.25	42.8
	RPTP	64.1	54.9	72.6	59.3	19.8	0.25	44.0
2	Clinical	61.0	56.4	62.3	60.8	19.5	0.23	45.8
	GTV boost	63.6	59.1	69.6	62.0	19.7	0.25	46.0
	Replan	65.3	59.6	67.3	62.2	19.5	0.24	45.1
	RPTP	66.7	60.3	72.9	59.4	19.7	0.25	45.8
3	Clinical	70.3	69.4	71.4	70.3	18.3	0.15	41.9
	GTV boost	76.0	70.9	83.0	75.5	18.1	0.15	42.6
	Replan	79.7	73.2	81.1	75.1	18.2	0.15	40.6
	RPTP	81.6	74.8	89.7	74.5	18.0	0.15	42.3
4	Clinical	57.0	55.9	57.9	56.0	20.3	0.23	38.3
	GTV boost	59.1	56.5	61.9	56.6	20.3	0.24	37.6
	Replan	60.8	59.6	61.8	56.5	20.3	0.24	37.7
	RPTP	63.3	57.5	65.4	56.1	20.3	0.24	37.7
5	Clinical	61.5	56.6	62.6	60.7	17.7	0.12	46.7
	GTV boost	63.5	58.5	67.3	60.6	18.0	0.14	42.8
	Replan	63.7	54.8	65.7	60.8	17.7	0.13	41.0
	RPTP	66.4	58.2	70.6	59.3	18.0	0.14	42.4
Averaged difference		+6.2	+2.8	+10.8	0	+0.2	+0.01	−0.7
RPTP vs clinical
RPTP vs GTV boost		+3.4	+2.1	+3.9	−1.4	0	0	−0.1
RPTP vs replan		+1.8	+0.4	+5.7	−1.3	+0.1	0	+1.0

Abbreviations: GTV = gross tumor volume; NTCP = normal tissue complication probability; PTV = planning target volume; RPTP = robust predictive treatment planning.

The average differences between planning methods are shown in bold.

Fig. 4.

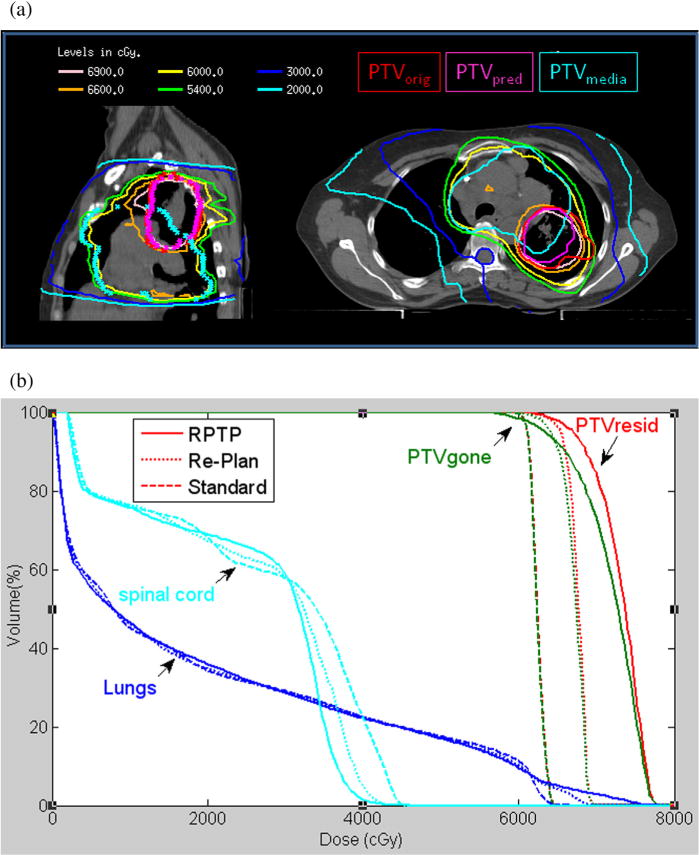
(a) Predictive treatment planning dose distribution. (b) Comparisons of dose-volume histograms demonstrate predictive treatment planning increased dose to the residual tumor while keeping dose to organs at risk comparable.

Discussion

Although we are at an initial stage in developing a quantitative tumor shrinkage model, and the predictions are based on a limited number of patients, the prototype of PTP is demonstrated to be a promising way to take advantage of tumor regression to selectively increase tumor dose. The advantages of PTP over midcourse replanning come not only from the higher mean dose delivered to the residual tumor but also from the more efficient clinical workflow resulting from the elimination of 1 round of labor-intensive planning and subsequent quality assurance. Even if the tumor does not shrink, PTP is preferable to the conventional approach because PTP can escalate dose to portions of the tumor (on average 17% higher in those examples) without underdosing PTV or overdosing OARs.

However, like all new technologies, PTP requires that new processes be developed and validated. It is necessary to optimize the imaging protocol and acquire imaging data from more patients to improve the sensitivity and specificity of the prediction model. Weekly CBCT is currently not optimal to evaluate tumor shrinkage, especially for the mediastinal component, because of its relatively poor imaging quality. Acquiring diagnostic-quality CT, or potentially magnetic resonance imaging (22), for imaging over the course of treatment is preferable. The prediction model also has intrinsic uncertainties caused by observation variations. We would like to further quantify this uncertainty with more patient data and eventually incorporate it into the clinical margin formula to mitigate its effect. The current prediction model used tumor shrinkage data from only 5 patients. As we accumulate more data, we would classify tumor shrinkage (and lack of shrinkage) patterns into subgroups based on metrics such as tumor location, size, relation to chest wall and mediastinum, and medical variables. Given a new case, we would match it to the most suitable subgroup for better prediction. On the basis of the pattern of tumor shrinkage observed in a larger group of patients, imaging timing and frequency could also be optimized. For example, it may be preferable to image more frequently toward the middle to end of radiation therapy, where we observed that the most shrinkage occurred in the 5 patients in this study. With additional improvement of the prediction model, PTP could follow the tumor shrinkage pattern more closely and achieve the best therapeutic ratio possible without the burden of repeated replanning.

Unlike the conventional adaptive therapy framework that uses patient-specific imaging feedback and creates 1 or more new plans to achieve improved outcome, PTP proposes a new concept of feed-forward control in radiation therapy. By integrating the prediction of possible responses to radiation therapy from the initial phase of treatment, PTP is designed to pursue the best therapeutic ratio with an intelligent and aggressive nonuniform dose prescription. Ideally, PTP and feedback ART should be combined. With continuous imaging surveillance such as weekly CT or CBCT during the treatment course, we could verify that dose hotspots coincide with the shrinking residue and do not impinge on a critical serial-response structure such as a major airway. We would also like to readily identify outliers whose tumor progresses during treatment, inasmuch as the shrinking-tumor PTP paradigm is not intended for such patients. Furthermore, the prediction model in PTP can be recalibrated by the new imaging findings, and the treatment plan can be updated accordingly if an ART infrastructure exists in the clinic.

Dose painting has been proposed for treatment of NSCLC by escalating dose to the hypoxic portion of the tumor seen in a pretreatment positron emission tomography (PET) scan (4, 23, 24). Imaging studies suggest that the location of residual metabolically active areas within the primary tumor after therapy may correspond with the high fluorodeoxyglucose uptake volumes observed before radiation therapy (25). Therefore, pretreatment PET scans may allow identification of portions of the tumor that are at risk to harbor residual disease (26). Ideally, the prediction of residual metabolic activity and geometric shrinkage observed on CT could be combined with other factors such as tumor motion (27) to form an integrated probability distribution for dose painting. Incorporating a tumor control probability model in a future PTP version would furthermore facilitate a robust biological optimization to produce the most suitable heterogeneous dose distribution. Heterogeneous dose distribution (ie, prescribing dose to a lower isodose level than that in the interior of the PTV) has long been used in radiosurgery to improve the dose conformality of a treatment plan. Our study also confirms that, for advanced-stage NSCLC, dose to the predicted residual tumor can be escalated without deteriorating OAR sparing.

Conclusion

Predictive treatment planning, incorporating a tumor regression model from the start, is technically feasible. PTP represents a new approach to increase tumor dose without increasing toxicities, and to reduce clinical workload compared with ART, although model verification using per-patient midcourse imaging would be prudent. More imaging data are needed to validate and refine the tumor shrinkage model.

Summary.

We propose a novel treatment planning technique that incorporates predicted lung tumor regression into robust optimization to allow dose escalation to a significant portion of the residual tumor while maintaining coverage of the initial target without increasing dose to surrounding normal tissue. It also has the potential to reduce clinical workload compared with the adaptive approach. Predictive treatment management incorporates a predictive tumor response model into robust prospective treatment planning for non-small cell lung cancer.