Motion Correction of Multi-b-value Diffusion-weighted Imaging in the Liver

Abstract

Rationale and Objectives

Motion artifacts are a significant source of error in the acquisition and quantification of parameters from multi-b-value diffusion-weighted imaging (DWI). The objective of this article is to present a reliable method to reduce motion-related artifacts during free-breathing at higher b-values when signal levels are low.

Materials and Methods

Twelve patients referred for magnetic resonance imaging of the liver underwent a clinical magnetic resonance imaging examination of the abdominal region that included DWI. Conventional single-shot spin-echo echo planar imaging acquisitions of the liver during free breathing were repeated in a “time-resolved” manner during a single acquisition to obtain data for multi-b-value analysis, alternating between low and high b-values. Image registration using a normalized mutual information similarity measure was used to correct for spatial misalignment of diffusion-weighted volumes caused by motion. Registration error was estimated indirectly by comparing the normalized root-mean-square error (NRMSE) values of data fitted to the biexponential intra-voxel incoherent motion model before and after motion correction. Regions of interest (ROIs) were selected in the liver close to the surface of the liver and close to internal structures such as large bile ducts and blood vessels.

Results

For the 12 patient datasets, the mean NRMSE value for the motion-corrected ROIs (0.38 ± 0.16) was significantly lower than the mean NRMSE values for the non–motion-corrected ROIs (0.41 ± 0.13) (P < .05). In cases where there was substantial respiratory motion during the acquisition, visual inspection verified that the algorithm markedly improved alignment of the liver contours between frames.

Conclusions

The proposed method addresses motion-related artifacts to increase robustness in multi-b-value acquisitions.

In biological tissues, microscopic motion detected by diffusion-weighted imaging (DWI) includes both diffusion of water molecules, influenced by the structural components of the tissue, and microcirculation of blood in the capillary network (perfusion). When the diffusion sensitivity parameter, referred to as the b-value, is low, microperfusion causes rapid signal decay. To separate microperfusion effects from tissue diffusion in DWI studies, Le Bihan proposed the intravoxel incoherent motion (IVIM) biexponential model (1–3).

Several studies have applied an IVIM non-monoexponential model to characterize diffusion in tumors of the body (4–10). Application of the IVIM model, however, has been hindered by the presence of bulk motion and physiologic motions such as respiration. DWI is sensitive to both molecular displacement and the mean length of blood perfusion within the capillary network, both of which are of the order of tens of microns (3,11). However, body motion can produce displacements of the order of several millimeters, causing severe artifacts that interfere with calculation of DWI parameters.

Bulk motion and respiration may produce artifacts that can limit the reproducibility of DWI measurements in the abdomen and liver (12–14). Recently, a number of methods have been proposed to address motion artifacts. Studies have suggested that breath-hold DWI could improve the identification of smaller lesions (15). Furthermore, the use of respiratory triggering or breath-holding to obtain DW images with multiple b-values has been investigated (14). Although breath-holding methods substantially improve the robustness of DWI data (16), only a limited number of b-values can be obtained within a breath-hold. Kim et al proposed a scheme that uses short repetition time (TR) to perform breath-hold DWI and diffusion-tensor imaging (DTI) in utero in the presence of motion (17). An additional b = 0 image was acquired to compensate for the incomplete longitudinal magnetization recovery. Rohde et al used a mutual information-based registration technique and a spatial transformation model containing parameters that correct for eddy current-induced image distortion and rigid body motion (18). The purpose of this article is to present a reliable method to estimate motion parameters during free-breathing at higher b-values, when signal levels are low.

This article is organized as follows: First, we formulate the acquisition sequence. Next, we describe the image registration method. We then present the registration results obtained with the proposed acquisition and image processing and evaluate the impact of the method on the robustness of calculated IVIM parameters. Finally, we draw conclusions about the methods presented.

MATERIALS AND METHODS

Biexponential Model for Diffusion

To separate microperfusion effects from pure diffusion in DWI studies, LeBihan presented a model with two compartments model given by (1–3):

$$s\left(b\right)=S\left(0\right)•\left[\right(1-f\left)•\exp \right(-b•D)+f•\exp (-b•D^{\ast }\left)\right]$$ (1)

where D is the slow component of diffusion which describes true diffusion of extravascular water molecules, D★ is the perfusion coefficient, f is the perfusion fraction, and S(b) and S(0) are the signal measured in each individual voxel in the DWI with diffusion sensitivity of b and 0, respectively. To estimate diffusion parameters with this model, diffusion signal is measured for a large number of b-values, ranging from very low (<200 s/mm²) to high (>200 s/mm²).

Magnetic Resonance Imaging Data Acquisition

Our institutional review board waived the requirement for informed consent for this study, which was compliant with the Health Insurance Portability and Accountability Act. Between February 2011 and April 2011, 12 patients (age: 27–76 years, male/female: 5/7) referred for magnetic resonance (MR) imaging of the liver underwent a clinical MR imaging examination of the abdominal region that included DWI. MR imaging was performed with a 3-Tesla whole-body MR imaging unit (Discovery MR750; GE Medical Systems, Waukesha, WI) equipped with a 32-channel phased-array coil.

Motion Correction of Multi-b-value DWI

The proposed technique for motion correction of multi-b-value (MCMB) DWI sequentially collects multiple two-dimensional acquisitions at different b-values using a conventional single-shot spin-echo echo planar imaging (EPI) acquisition with a pair of rectangular gradient pulses along three orthogonal axes (x, y, and z) simultaneously. The acquisition was added to evaluate image quality within the guidelines of our institution. The acquisition scheme is illustrated in Figure 1a. The data are acquired during two phases. First, to reduce T1 enhancement, several frames are acquired at b = 0 at the start of the acquisition to allow for complete longitudinal magnetization recovery. Subsequently, multiple frames are acquired at interleaved high and low b-values to allow improved image registration using only frames with sufficiently high signal.

Figure 1.

Schematic diagram of the motion correction of multi-b-value diffusion-weighted imaging technique. (a) The data are acquired during two phases. Phase 1: Image frames are acquired without diffusion-weighted gradients (b = 0) to minimize T₁-weighting because of incomplete recovery of longitudinal magnetization at shorter TRs. Phase 2: Image frames are acquired with non-zero b-values. High (H₁, H₂, H₃, …) and low (L₁, L₂, L₃, …) b-values are interleaved. This is to allow spatial transformation parameters for low-signal high-b–value images to be approximated using the spatial transformation parameters from adjacent low b-value frames. (b) Three b = 0 frames are acquired (Phase 1) followed by four blocks of b-values (4 × 9, total of 36) (Phase 2). In total, 39 frames are acquired.

Phase 1

Three sets of images are initially acquired without diffusion-weighted gradients (b = 0) to minimize T1-weighting because of incomplete recovery of longitudinal magnetization at shorter TRs. Excitation of data during this period allows longitudinal magnetization to reach equilibrium even with short TR and hence minimize T1-weighting because of incomplete longitudinal magnetization recovery at shorter TRs (17).

Phase 2

During this phase, the distribution of b-values is designed so that higher (H₁, H₂, H₃, …) and lower (L₁, L₂, L₃, …) b-values are interleaved. This method allows spatial transformation parameters for high b-value images with insufficient signal to noise for accurate spatial alignment to be approximated using the spatial transformation parameters from adjacent low b-value frames. Multiple number of excitations (NEX) is not prescribed during the acquisition. Instead, data are obtained using four sets or “blocks” of b-values within a single acquisition (Fig 1b). Hence, the acquisition is time-resolved to permit image registration of data acquired at shorter resolved (1 TR) time intervals.

In our study, we collected images with each of the following nine b-values: 0, 30, 70, 100, 150, 200, 400, 600, and 800 s/mm². Three b = 0 frames were acquired (phase 1) followed by four blocks of b-values (total of 36, 4 × 9) (phase 2). A total of 39 frames were acquired (Fig 1b), 1 NEX, with an acquisition time of 1:28 minutes during free breathing. Axial DWI scans were collected with a 32-channel torso coil (TR/echo time = 2200/88.2 ms, matrix 96 × 96, field of view 400 × 400 mm², 19 slices, slice thickness 7 mm, resolution 4.2 × 4.2 × 7 mm³, with an acceleration factor of 2). Complete liver coverage was often not achieved within a slice prescription and when necessary a second prescription was obtained.

Image Registration: Three-dimensional Affine Transformation

All data were transferred offline to an independent workstation where the processing was performed in MATLAB (version 7.1, Mathworks, Natick, MA). A normalized mutual information (NMI) approach was implemented to measure the similarity cost function of the image registration as:

$$\mathit{NMI}(X,Y)=\frac{H\left(X\right)+H\left(Y\right)}{H(X,Y)}$$ (2)

where X is the reference (or source image) and Y is the target image. The quantities (and H(Y)) are the standard entropy definition entropy functions given by:

$$H\left(X\right)=-\sum _{i}p\left(i\right)•\log p\left(i\right)$$ (3)

where p(i) is the marginal probability distribution and H(X, Y) is the joint distribution function given by:

$$H(X,Y)=\sum _{ij}p(i,j)•\log \frac{p(i,j)}{p\left(i\right)•p\left(j\right)}$$ (4)

where p(i, j) represents the probability estimated using the (i, j) joint histogram bin of the image pixel values of the reference and source image. The joint probability density functions describe the probability that a pair of values, one from each image in the comparison, occurs at the same spatial location. When two image volumes are matched, their mutual information is maximized. Affine transformation in three dimensions was used to register DW images in each acquisition. Three-dimensional (3D) affine transformation describes a global space warping with 12 degrees of freedom. The 3D affine transformation of a point x = (x, y, z)^T can bewritten as (19):

$$\mathcal{A}\left(\mathbf{x}\right)=\mathbf{A}•\mathbf{x}+\mathbf{T}$$ (5)

Where the matrix T represents a 3D translation {T_x, T_y, T_z} and the matrix A represents a 3D linear transformation that includes 3D rotation and the components of the affine transformation, scaling and shear:

$$\mathbf{A}=\mathbf{R}(\theta ,\varphi ,\psi )\left[\begin{array}{ccc}\hfill 1\hfill & \hfill S_{\mathit{xy}}\hfill & \hfill S_{\mathit{xz}}\hfill \\ \hfill S_{\mathit{yx}}\hfill & \hfill 1\hfill & \hfill S_{\mathit{yz}}\hfill \\ \hfill S_{\mathit{zx}}\hfill & \hfill S_{\mathit{yz}}\hfill & \hfill 1\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill S_{\mathit{x}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill S_{\mathit{y}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill S_{\mathit{z}}\hfill \end{array}\right]$$ (6)

where R(θ, ϕ, ψ) is a 3 × 3 rotation matrix, given by:

$$\mathbf{R}(\theta ,\varphi ,\psi )=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cos \theta \hfill & \hfill -\sin \theta \hfill \\ \hfill 0\hfill & \hfill -\sin \theta \hfill & \hfill \cos \theta \hfill \end{array}\right]\times \left[\begin{array}{ccc}\hfill \cos \varphi \hfill & \hfill 0\hfill & \hfill \sin \varphi \hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill -\sin \varphi \hfill & \hfill 0\hfill & \hfill \cos \varphi \hfill \end{array}\right]\left[\begin{array}{ccc}\hfill \cos \psi \hfill & \hfill -\sin \psi \hfill & \hfill 0\hfill \\ \hfill \sin \psi \hfill & \hfill \cos \psi \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$ (7)

and {S_x, S_y, S_z} are scale factors in three orthogonal directions, and {S_xy, S_xz, S_yz, S_yx, S_zx, S_zy are 3D shear parameters in the XY, XZ, YZ, YX, ZX, and ZY directions.

Registration was achieved by finding the transformation that maximized the joint entropy with respect to the marginal entropies. The maximum NMI was found by the quasi-Newton multidimensional optimization method and the resulting transformation map is applied to the floating image. The Newton-Ralphson algorithm was used to optimize the cost function by iterative adjustment of unknown coefficients. To avoid being trapped at local minima, the optimization was initiated with subsampled images at a coarse resolution equal to one-eighth that of the original image. The resolution doubled three times during the optimization process to finally reach that of the final image.

Low signal levels of higher b-value images do not allow reliable calculation of the cost function, even when the NMI approach is used (18). Therefore, for images obtained above a certain b-value threshold, the displacement was quantified by interpolating the affine parameters from adjacent low b-value frames. The b-value threshold was determined empirically based on the ability to accurately contour and easily visualize the organ of interest. The linear interpolation scheme works provided that the motion between adjacent frames is not abrupt. The normalized standard entropy of the source (H(X) corresponding to frame 1) and target images (H(Y) corresponding to all subsequent frames) were compared. Target images that satisfy the criteria: sum(abs(HX-HY))≤0.5 were registered using the NMI-based registration algorithm. In each case, registration was performed using linear interpolation of transformation parameters from adjacent frames target images acquired with b-values with signal below this threshold criterion.

Statistical Analysis

Validation of results from image registration algorithms is limited because of the lack of a gold standard. An indirect measure to establish the reliability of an image registration method such as ours was originally proposed by Andersson and Skare; they used the goodness-of-fit of the apparent diffusion tensor calculation to minimize residual error when fitting data to the diffusion tensor model (20). Here we use the normalized root-mean-square error (NRMSE) to test the results of our registration algorithm. NRMSE is defined as the root-mean-square error between data points and the biexponential model divided by the range of values:

$$\mathit{NRMSE}=\frac{1}{x_{\mathit{data},\mathit{max}}-x_{\mathit{data},\mathit{min}}}\sqrt{\frac{\sum _{i=1}^N{(x_{\mathit{data},i}-x_{\mathit{mod},i})}^2}{N}}$$ (8)

where x_data,i is the (pre- or post-registered) data and x_mod,i is the (pre- or postregistered) biexponential fit, and N is the number of voxels in the ROI. NRMSE is expressed as a percentage, where lower values indicate less residual variance. The NRMSE of each ROI for each patient was calculated and was regarded as an indirect measure of the ability of the registration algorithm to correct for motion. The nonparametric Wilcoxon signed-rank test was used to test statistical significance between pre- and postregistered NRMSEs. A P value of .05 or less was defined as significant.

ROIs were drawn freehand by an experienced radiologist on one image from the first frame of the diffusion image series. ROIs were selected in the liver close to its surface and close to internal structures such as large bile ducts and blood vessels (21). This scheme relies on the assumption that the DWI data is well described by the biexponential model—an assumption that is probably valid for the b-values used.

RESULTS

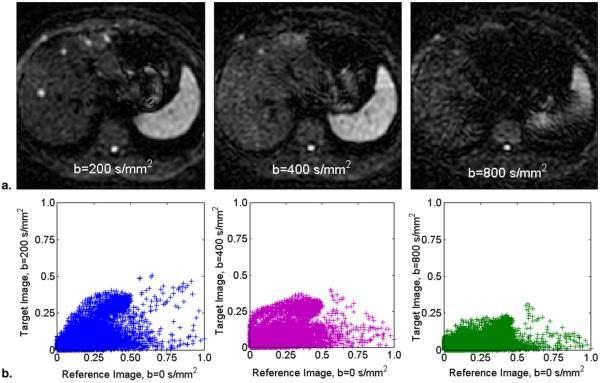
We begin with an examination of signal requirements for robust image registration. Figure 2a shows images obtained at three b-values (200, 400, and 800 s/mm²). Figure 2b shows the corresponding pixel intensity scatter plots. We can see from these figures that diffusion weighting causes a dramatic reduction in the signal-to-noise ratio of the resultant image.

Figure 2.

Images obtained using motion correction of multi-b-value diffusion-weighted imaging. (a) Images obtained with diffusion sensitivity parameters 200, 400, and 800 s/mm². (b) Scatter plots corresponding (from left to right) to the images shown in (a). By comparing the plots, we can detect if the mutual information or pixel distance can be used as a similarity measure. Reduced signal can limit the accuracy of motion correction. We used the criteria sum(abs(HX-HY))<0.5, where HX and HY are the normalized standard entropy of the source and target images. For the plots, the sum(abs(HX-HY))values corresponding to b-values 200, 400 and 800 s/mm² were 0.34, 0.45, and 0.74, respectively, suggesting that b-values >400 s/mm² result in images with low signal and contrast.

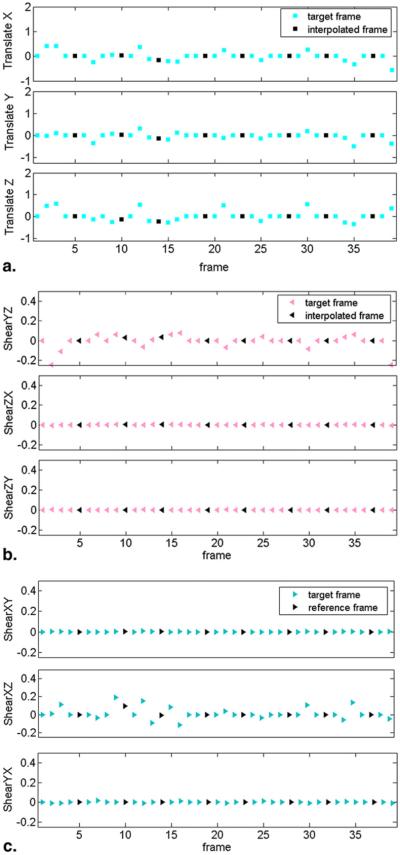
The ability of the algorithm to estimate motion parameters is demonstrated in Figure 3. We only show the translational and shear parameters because they are the primary source of transformation during free-breathing. Motion parameters were estimated during acquisition of high signal low b-value images (colored markers), which can then be interpolated to the adjacent high b-value images that lack sufficient signal for reliable motion estimation (black markers). Overall, the figure demonstrates that the pattern of motion that was observed in the MR data derived from the motion correction procedure can be described as a slowly varying change in orientation.

Figure 3.

Plot of three-dimensional affine transformation parameters for the 39 frames acquired during an abdominal exam. (a) Translational parameters (translate X, translate Y, and translate Z), (b) Shear parameters (shear XY, shear XZ, and shear YX) and (c) (shear YZ, shear ZX, and shear ZY). Motion parameters were estimated during acquisition of high-signal low b-value images (colored markers represent target frames), which can then be interpolated to the adjacent high b-value images that lack sufficient signal for reliable motion estimation (black markers represent interpolated frames).

The plots in Figure 4 demonstrate the variability of the data at each b-value before and after registration throughout the entire data set for 1 patient. For the 12 patient datasets, the mean NRMSE value for the motion-corrected ROIs (0.38 ± 0.16) was significantly lower than the mean NRMSE values for the non-motion-corrected ROIs (0.41 ± 0.13; P < .05; Table 1). In 3/12 cases, the NRMSE before motion correction was greater than 0.5, which can be regarded as substantial motion.

Figure 4.

Regions of interest (ROIs) placed on a diffusion-weighted image (b = 0) of the liver (a). Plots of mean signal intensity and the biexponential fit for the ROIs pre- (b) and postregistration (c). The biexponential parameters D*, D, and f were extracted. The preregistration fitted parameters were D* = 0.04 mm²/s, D = 1.3 × 10⁻³ mm²/s, and f = 0.17 for blue ROI, and D* = 0.014 mm²/s, D = 1.2 × 10⁻³ mm²/s, and f = 0.27 for green ROI. The postregistration fitted parameters were D* = 0.04 mm²/s, D = 1.0 × 10⁻³ mm²/s, and f = 0.25 for blue ROI, and D* = 0.063 mm²/s, D = 0.9 × 10⁻³ mm²/s, and f = 0.44 for green ROI.

TABLE 1.

The Mean NRMSE of Data Fitted to the Biexponential IVIM Model Value before Motion Correction and after Motion Correction for the 12 Patient Datasets

Subject	NRMSE before Motion Correction	NRMSE after Motion Correction
1	0.61	0.59
2	0.65	0.64
3	0.43	0.44
4	0.35	0.36
5	0.61	0.60
6	0.32	0.16
7	0.34	0.27
8	0.27	0.27
9	0.36	0.35
10	0.35	0.33
11	0.40	0.37
12	0.28	0.17
Average ± SD	0.41 ± 0.13	0.38 ± 0.16

IVIM, intra-voxel incoherent motion; NRMSE, normalized root-mean-square error; SD, standard deviation.

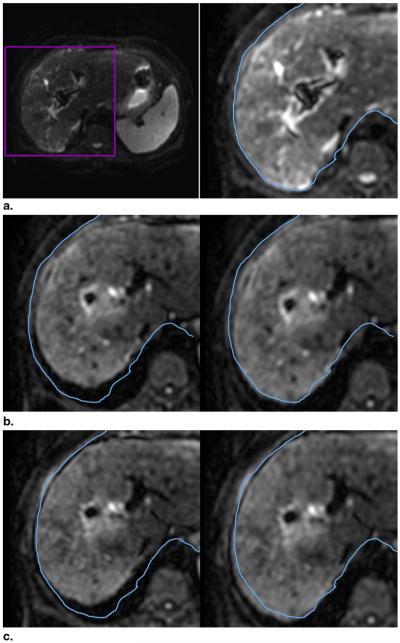
Figure 5 allows comparison of a reference image from frame 1 and pre- and postregistration target images from frames 29 and 36. Postregistration, there is an improvement in the alignment between the liver contour in each target image and the liver contour in the reference image. The figure demonstrates the feasibility of aligning internal organs in DW images during free-breathing.

Figure 5.

Registration of target image to the reference image. (a) Reference image (frame 1, b = 0 s/mm²). For comparison, the contour of the liver (blue) from frame 1 is copied in its original location in each subsequent frame. (b) Pre- (left) and postregistration images of the same slice from frame 29 (b = 70 s/mm²). In the preregistered image, the liver and the contour do not match. Postregistration, there is an improvement in the alignment of the liver edge and the contour copied from frame 1. (c) Similarly, for frame 36 (b = 150 s/mm²), the liver edge in the preregistered image (left) does not match the contour. The alignment is improved in the postregistration image (right).

DISCUSSION

We have presented a method to reduce artifacts caused by motion during acquisition of images at multiple b-values by acquiring datasets in a time-resolved manner and retrospectively correcting for motion. To quantify the amplitude of bulk motion, the displacement parameters at each frame were estimated using 3D affine registration with 12 degrees of freedom.

In this work, we hypothesized that correcting for motion in multi-b-value DWI acquisitions would improve the quantification of perfusion fraction, pseudo-diffusivity, and true diffusion. To test this hypothesis, we compared the mean NRMSE values for the data fit to a biexponential model for ROIs between the pre- and postregistered images. Our results suggest that registration of DW images of the liver acquired with multiple b-values is significantly improved using the proposed method. As shown in Figure 5, after registration, the contour of the liver is somewhat aligned, even if the internal structures are not necessarily aligned. Therefore, although the method can improve the estimation of IVIM parameters located close to the surface of the liver, it is limited in its ability to correct misalignments that are due to the complex nonrigid motion of the organ. To address the substantial residual deformation caused by this nonrigid motion would require intensity-based nonrigid registration of gated MR images, as has been proposed by Rohlfing et al for two-dimensional fast spin-echo liver imaging (22).

In the proposed method four identical sets of diffusion data are acquired; this allows the motion parameters to be sampled more finely than would be possible if multi-NEX imaging were used. However, motion-induced phase errors that occur during diffusion sensitization or during EPI readout are not corrected and can result in severe image degradation. Cardiac pulsation artifacts result in signal loss in DWI and have been shown to artificially increase apparent diffusion coefficient (ADC) measurements in the left lobe of the normal liver compared to the right lobe (23,24). Further work is needed to overcome artifacts related to cardiac motion and motion-induced phase errors that occur during diffusion sensitization using either cardiac gated (25,26) or navigator echo correction methods (27).

DWI at reduced TR can result in adverse T1 and T2 effects. T1 effects occur when images are acquired before the tissue has reached steady-state equilibrium; they result in higher ADC estimates, and are more pronounced for tissues with shortened T1. By acquiring several excitations at the start of the acquisition, the effect of T1 relaxation is minimized, as the tissue will have reached steady-state equilibrium. T2 effects occur when the condition TR < T2 steady-state free precession develops in a train of radiofrequency (RF) pulses, because the transverse magnetization is not destroyed between consecutive RF pulses (28). Although the TRs that were used in this report do not meet this condition (liver T2 is about 40 ms) (29), at lower TRs, by using crusher gradients before each RF pulse, it is possible to dephase the transverse magnetization across a voxel, hence eliminating it before excitation.

It should be noted that we did not account for residual eddy currents induced by diffusion gradient eddy currents and their interactions with the image-encoding gradient pulses, which cause both linear (30) and nonlinear deformation (18) that resembles image misregistration due to subject motion.

Image registration algorithms, including the NMI algorithm, require high-quality images with sufficient signal. At higher b-values, reduced signal and diminished tissue contrast ultimately result in unreliable registration of images. In our approach, for images with higher b-values which were deemed to have insufficient image contrast and signal, a linear interpolation scheme was used whereby transformation parameters from adjacent frames with sufficient signal and contrast parameters were interpolated to obtain an approximation for motion correction. This scheme assumes that motion in the areas of interest is relatively slow and the estimated parameters do not change abruptly. Overall, this assumption is reasonable in cases where the primary source of motion is breathing and the patient has been instructed to breathe shallowly to minimize abrupt changes in the locations of organs.

Published reports comparing respiratory-triggered to breath-hold DWI acquisitions suggest that respiratory-triggered DWI would provide better signal-to-noise ratio, and better CNR of metastases, hepatocellular carcinomas, and abscesses than breath-hold DWI without adversely affecting ADC values (16). However, respiratory-triggered DWI techniques have inherent limitations. First, they prolong the acquisition, which could result in prohibitively long acquisitions when multiple b-values are acquired. Second, irregular breathing patterns of patients or improper placement of a respiratory belt could result in failure to accurately detect respiratory motion. Third, motion unrelated to respiration is not accounted for, and navigator-triggered acquisition techniques or retrospective motion correction methods might still be necessary. The proposed method, with retrospective motion correction during free-breathing, optimizes TR for efficient acquisition of DWI scans at multiple b-values within reasonable scan duration. If motion artifacts persist, lower TRs can be considered, at a potential loss in signal, to reduce artifacts. To establish the clinical utility of the proposed methods, a prospective study should be done, supported with clinical data in larger sample size.

A prior study showed that differences in diffusion parameters such as ADC values between the three diffusion-gradient directions were insignificant (31). In the present study, we assumed the liver parenchyma as well as the liver lesions to be isotropic, justifying the simultaneous acquisition of the three orthogonal directions to minimize the influence of anisotropy.

In conclusion, the proposed method addresses motion-related artifacts to increase robustness in multi-b-value acquisitions.