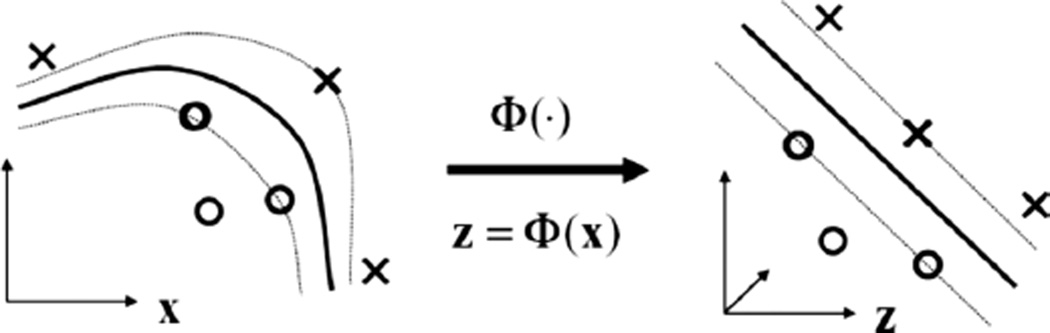Datamining approaches for modeling tumor control probability

Abstract

Background

Tumor control probability (TCP) to radiotherapy is determined by complex interactions between tumor biology, tumor microenvironment, radiation dosimetry, and patient-related variables. The complexity of these heterogeneous variable interactions constitutes a challenge for building predictive models for routine clinical practice. We describe a datamining framework that can unravel the higher order relationships among dosimetric dose-volume prognostic variables, interrogate various radiobiological processes, and generalize to unseen data before when applied prospectively.

Material and methods

Several datamining approaches are discussed that include dose-volume metrics, equivalent uniform dose, mechanistic Poisson model, and model building methods using statistical regression and machine learning techniques. Institutional datasets of non-small cell lung cancer (NSCLC) patients are used to demonstrate these methods. The performance of the different methods was evaluated using bivariate Spearman rank correlations (rs). Over-fitting was controlled via resampling methods.

Results

Using a dataset of 56 patients with primary NCSLC tumors and 23 candidate variables, we estimated GTV volume and V75 to be the best model parameters for predicting TCP using statistical resampling and a logistic model. Using these variables, the support vector machine (SVM) kernel method provided superior performance for TCP prediction with an rs = 0.68 on leave-one-out testing compared to logistic regression (rs = 0.4), Poisson-based TCP (rs = 0.33), and cell kill equivalent uniform dose model (rs = 0.17).

Conclusions

The prediction of treatment response can be improved by utilizing datamining approaches, which are able to unravel important non-linear complex interactions among model variables and have the capacity to predict on unseen data for prospective clinical applications.

Recent advances in 3D treatment planning could potentially pave the way for personalized and patient-specific treatment planning decisions based on estimates of local TCP and/or complication risk to surrounding normal tissues [1]. Accurate prediction of treatment outcomes would provide clinicians with better tools for informed decision making about expected benefits versus anticipated risk. Recently, there has been a burgeoning interest in using radiobiological models to rank patients’ treatment plans in order to identify the ‘optimal’ or at least personalize the patient’s plan [2,3]. For instance, these models could be used as an aid to guide physician-patient treatment choices [4,5]. Alternatively, once a decision has been reached these models could be included in an objective function, and the optimization problem driving the actual patient’s treatment plan can be formulated in terms more relevant to complication risk and tumor eradication [2,6].

Measurement of TCP is a challenging task because it depends on complex physical and biological processes. Classic radiobiology has been defined by the four R’s (repair, redistribution, reoxygenation, and repopulation) [7]. In this context, it is believed that radiation-induced lethality is primarily caused by DNA damage in targeted cells. Two types of cell death have been linked to radiation: apoptosis and mitotic cell death. However, tumor cells radiosensitivity (sometimes referred to as the 5^th R) is controlled via several factors related to tumor DNA repair efficiency (e.g., homologous recombination), cell cycle distribution (cells are least sensitive during S-phase), oxygen concentration (hypoxia), the dose rate, and a host of unknown factors that could affect the tumor microenvironment [8].

There have been extensive efforts over the last two decades to develop mathematical models to provide quantitative estimates of TCP using analytical expressions and statistical considerations of cell kill based on the linear-quadratic (LQ) model [9]. The LQ model provides a simple formalism that embodies repairable and non-repairable radiation damage and ability to distinguish between early and late tissue responses [10]. Mechanistic TCP models using Poisson statistics [11,12] or birth-death models [13] were developed based on this formalism. Several modifications have introduced to these TCP models to account for growth kinetics and inter-patient heterogeneity. The historical development of these mechanistic TCP models has been recently traced by O’Rourke et al. [14].

Despite the fact that TCP models based on the LQ model are useful tools for analyzing the effects of fractionation and dose in conventional radiotherapy, Kirkpatrick and coworkers have recently cautioned against the belief that radiotherapy response simply reflects single- and double-strand DNA breaks [15,16]. For instance, Sachs et al. reviewed the limitations of LQ in cases where high doses are delivered over a short period of time [17]. The problem of overestimation by the LQ of the potency and toxicity of high-dose ablative radiotherapy techniques such as stereotactic body radiotherapy (SBRT) has misled some clinicians to avoid this therapeutic option for years, which is currently being re-considered with promising results [18]. Many technical and biological factors (e.g., cold spots, tumor stem cells, vascular stroma, threshold doses for damage, and epigenetic changes) can complicate cells radio responsiveness that need to be carefully investigated. In addition, acceptance of general model formalism may not always guarantee consistent results on clinical data because model’s parameter selection is typically based on in vitro cell culture experiments. Hence, different parameter choices in heterogeneous populations would frequently lead to different interpretation of outcomes based on these models [19,20].

A different approach based on datamining of patient information libraries (clinical, physical, and biological records) has been proposed to ameliorate these challenges and bridge the gap between mechanistic radiological predictions and observed treatment outcomes. The main idea of data-driven models is to utilize datamining approaches and statistical model building methods to integrate disparate predictive factors that are likely related to tumor control within the same model. Such models may improve predictive power, but they must be simultaneously guarded for over-fitting pitfalls. This approach is motivated by the extraordinary increase in patient-specific biological and clinical information from progress in genetics and imaging technology [21]. In this data-driven approach, dosimetric metrics are mixed with other patient or disease-based prognostic factors [22]. It has been recognized that the TCP may also be affected by multiple clinical and biological factors, such as stage, volume, tumor hypoxia, etc [23,24]. For instance, De Crevoisier et al. reported that rectal distension on the planning computed tomography (CT) scan is associated with an increased risk of biochemical and local failure in patients of prostate cancer when treated without daily image-guided localization of the prostate [25]. Similarly, we found that as tumor distance to the spinal cord decreased, the rate of local tumor failure increased in patients receiving definitive radiotherapy for lung cancer [26]. Moreover, biological markers were found to be predictive of biochemical failure in prostate cancer or radiation-induced lung injury post-radiotherapy treatment [27,28].

We therefore hypothesize that datamining methods can help the tumor control analyst gain a more insightful understanding of complex variable interactions that affect outcome, wider model applicability to clinical data, and better design of prospective clinical trials. In this paper, we describe modeling methods that can effectively probe the interactions of clinical and physical data, and potentially biological data to build predictive models of tumor local control. This will be done initially using our previously developed multi-variable logistic-regression model building techniques [29,30]. However, to further explore the effects of variable interactions on patients’ risk; we will introduce concepts based on non-linear machine-learning methods. For both methods, we show how to validate the model estimates and its prediction ability using information theory and statistical resampling methods. These methods will be demonstrated on a cohort of non-small cell lung cancer (NSCLC) patients with clinical endpoint of local control post-radiotherapy treatment.

Methods and materials

Multi-metric modeling

The approach we adopted for modeling outcomes follows an exploratory datamining based approach. In this context of data-driven outcomes modeling, the observed treatment outcome is considered as the result of functional mapping of multiple dosimetric, clinical, or biological input variables. Mathematically, this could be expressed as: f (x; w*) : X → Y where x_i∈ ℝ^d are the input explanatory variables (dose-volume metrics, patient disease specific prognostic factors, or biological markers) of length d and y_i∈ Y are the corresponding observed treatment outcome (TCP or NTCP), and w* includes the optimal parameters of outcome model f (·) obtained by optimizing a certain objective criteria [22]. There are several choices for characterizing the mapping functional form, which could include linear, logistic, or non-linear kernels. Nevertheless, the typical S-shape of a dose-response curve lends it self to logistic or non-linear kernels forms.

Logistic regression

In this approach, a logit transformation is used [29]:

$$f({\mathbf{x}}_i)=\frac{e^{g({\mathbf{x}}_i)}}{1+e^{g({\mathbf{x}}_i)}},i=1,\dots ,n,$$ (1)

where n is the number of cases (patients), x_i is a vector of the input variable values used to predict f(x_i) for outcome y_i of the i_th patient. The ‘x-axis’ summation g(x_i) is given by:

$$g({\mathbf{x}}_i)={\beta }_{\mathrm{o}}+\sum _{j=1}^d{\beta }_j{x}_{ij},i=1,\dots ,n,j=1,\dots ,d,$$ (2)

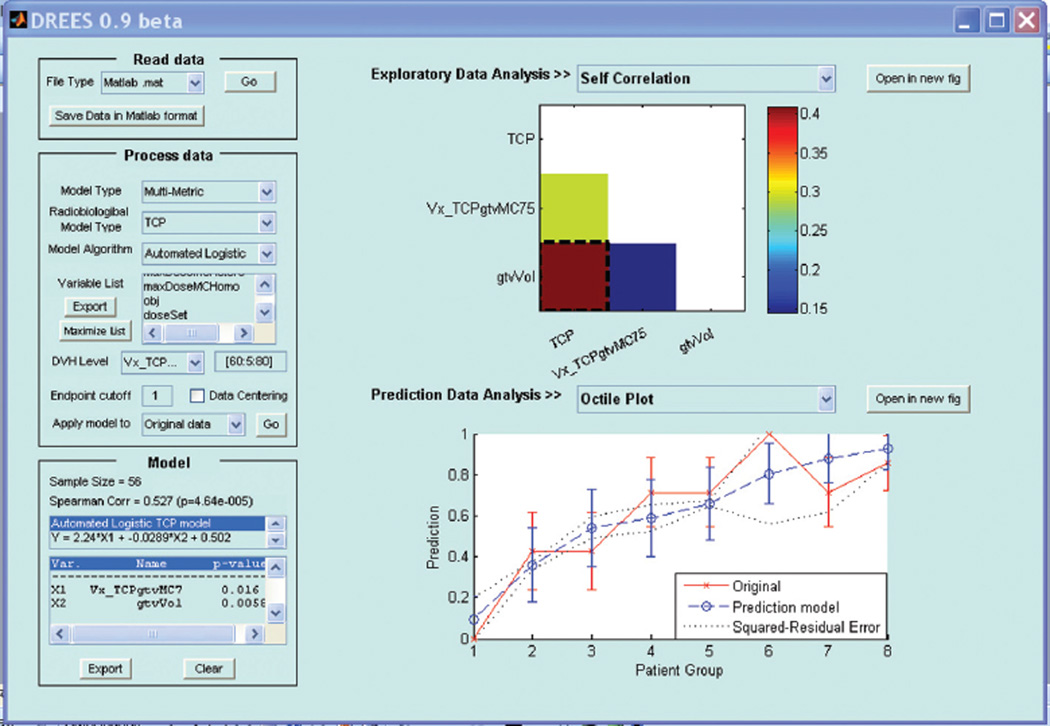
where d is the number of model variables and the β’s are the set of model coefficients determined by maximizing the probability that the data gave rise to the observations. The modeling exercise in this case is decomposed into two steps: (1) model order determination and (2) estimation of the most relevant model parameters. The role of the model order is to create a balance between complexity (increased model order), and the model’s ability to generalize to unseen data. Methods based on information theory (e.g., Akaike information criteria, Bayesian information criteria) or resampling techniques (e.g., cross-validation or bootstrapping could be used). Resampling methods will be adopted here and are discussed below. These methods are implemented in our open source in-house software tool DREES [30] shown in Figure 1 and their detailed description could be found in Deasy and El Naqa [22].

Figure 1.

A snapshot of the dose-response explorer software (DREES) available from: http://radium.wustl.edu/drees.

However, a drawback of the logistic regression formulation is that the model’s capacity to learn is limited. In addition, Equation 2 requires the user’s feedback to determine whether interaction terms or higher order terms should be added. A solution to ameliorate this problem is offered by applying machine-learning methods as discussed in the next section.

Kernel-based methods

Kernel-based methods and its most prominent member, support vector machines (SVMs), are universal constructive learning procedures based on the statistical learning theory [31]. In which, learning is defined as the process of estimating dependencies from data [32]. For discrimination between patients who are at low risk (class ‘−1’) versus patients who are at high risk (class ‘+1’) of radiation therapy, the main idea of the kernel-based technique would be to separate these two classes with ‘hyper-planes’ that maximizes the margin between them in the nonlinear feature space defined by implicit kernel mapping as illustrated in Figure 2. The optimization problem is formulated as:

$$\text{min }L(\mathbf{w},\xi )=\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C\sum _{i=1}^n{\xi }_i$$ (3)

subject to the constraint:

$$y_i({\mathbf{w}}^T\mathrm{\Phi }({\mathrm{x}}_i)+b)\ge 1-{\zeta }_i\hspace{1em}i=1,2,\dots ,n$$

$${\zeta }_i\ge 0\text{ for all }i$$

where w is a weighting vector and Φ(·) is a nonlinear mapping function. The ξ_i represents the tolerance error allowed for each sample being on the wrong side of the margin. Note that minimization of the first term in Equation 3 increases the separation between the two classes (improves generalizabilty), whereas, minimization of the second term improves fitting accuracy. The trade-off between complexity and fitting error is controlled by the regularization parameter C. Higher values of C indicate more complexity and more penalization of fitting error.

Figure 2.

Kernel-based mapping from a lower dimensional space (X) to a higher dimensional space (Z) called the feature space, where non-separable classes become linearly separable. Already established linear theory could be used to estimate the separating hyperplane. Samples on the margin are denoted as support vectors and they define the prediction function, which could be implemented efficiently using the kernel trick.

It stands to reason that such non-linear formulation would suffer from the ‘curse of dimensionality’ (i.e., the dimension of the problem becomes too large to solve) [32]. However, computational efficiency is achieved from solving the dual optimization problem instead of Equation 3, which is convex with a complexity that is dependent only on the number of samples [31]. Moreover, because of its rigorous mathematical foundations, it overcomes the ‘black box’ stigma of other learning methods such as neural networks. The prediction function in this case is characterized only by a subset of the training data known as support vectors s_i:

$$f\left(\mathrm{x}\right)=\sum _{i=1}^{n_s}{a}_i{y}_{i}K({\mathbf{s}}_i,\mathbf{x})+a_0,$$ (4)

where n_s is the number of support vectors, α_i are the dual coefficients determined by quadratic programming, and K(·,·) is a kernel function. An admissible kernel should satisfy Mercer’s positivity conditions since by definition they represent inner product functions [33]:

$$K(\mathbf{x},\mathbf{x}\prime )=\mathrm{\Phi }{(\mathbf{x})}^T\mathrm{\Phi }(\mathbf{x}\prime ),$$ (5)

where the mapping Φ is implicit and need not to be defined. Typically used non-linear kernels include [34,35]:

$$\begin{array}{cc}\text{Polynomials}\hfill & :K(\mathbf{x},\mathbf{x}\prime )={({\mathbf{x}}^T\mathbf{x}\prime +c)}^q\hfill \\ \text{Radial basis function }(\mathrm{R}\mathrm{B}\mathrm{F})\hfill & :K(\mathbf{x},\mathbf{x}\prime )=\text{exp}(-\frac{1}{2{\sigma }^2}{\Vert \mathbf{x}-\mathbf{x}\prime \Vert }^2),\hfill \end{array}$$ (6)

where c is a constant, q is the order of the polynomial, and σ is the width of the radial basis functions. Note that the kernel in these cases acts as a similarity function between sample points in the feature space. Moreover, kernels enjoy closure properties, i.e., one can create admissible composite kernels by weighted addition and multiplication of elementary kernels. This flexibility allows for constructing a neural network by using combination of sigmoidal kernels or one could choose a logistic regression equivalent kernel by replacing the hinge loss in Equation 3 with the binomial deviance [32].

Model variable selection

Any multivariate analysis often involves a large number of variables or features [36]. The main features that characterize the observations are usually unknown. Therefore, dimensionality reduction or subset selection aims to find the ‘significant’ set of features. Although an ideal method should marginalize redundant variables, but such variables usually complicate data exploration without significance. Finding the best subset of features is definitely challenging, especially in the case of linear or non-linear models. The objective is to reduce the model complexity, decrease the computational burden, and improve the model’s performance on unseen data, i.e., its generalizabilty when applied prospectively. In any given pattern recognition problem, there is a large number, K, of features that could be extracted from the patients data to be modeled. Therefore, it is necessary to select a finite set of features d that has the most discriminating power for the problem. An optimal subset could be determined by exhaustive search, which would yield:

$$\sum _{k=1}^K\left(\begin{array}{c}\hfill k\hfill \\ \hfill d\hfill \end{array}\right).$$

However, there are other alternatives [37]. The straightforward method is to make an educated guess based on experience and domain knowledge, then, apply feature transformation (e.g., principle component analysis (PCA)) [37,38], or sensitivity analysis by using organized search such as sequential forward selection (SFS), or sequential backward selection (SBS) or combination of both [37]. In our previous work [29], we used an SFS search for model order determination based on information theory and resampling techniques to select the significant variables.

Visualization of higher dimensional data

Prior to applying a datamining method, it is important to visualize the data distribution, as a screening test. This requires projecting the high-dimensional dataset into a lower dimensional space. Techniques such as principal component analysis (PCA) and multidimensional scaling (MDS) allow visualization of complex data in two-dimensional spaces [33]. In this work, we chose the PCA approach due to its simplicity. In PCA analysis, the principal components (PCs) of a data matrix X (with zero mean) are given by:

$$PC=U^T\mathbf{X}=\sum V^T,$$ (7)

where U∑V^T is the singular value decomposition of X. This is equivalent to transformation into a new coordinate system such that the greatest variance by any projection of the data would lie on the first coordinate (first PC), the second greatest variance on the second coordinate (second PC), and so on.

The term ‘Variance Explained,’ used in PCA plots (cf. Figure 4), refers to the variance of the ‘data model’ about the mean prognostic input factor values. The ‘data model’ is formed as a linear combination of its principal components. Thus, if the PC representation of the data ‘explains’ the spread (variance) of the data about the full data mean, it would be expected that the PC representation captures enough information for modeling.

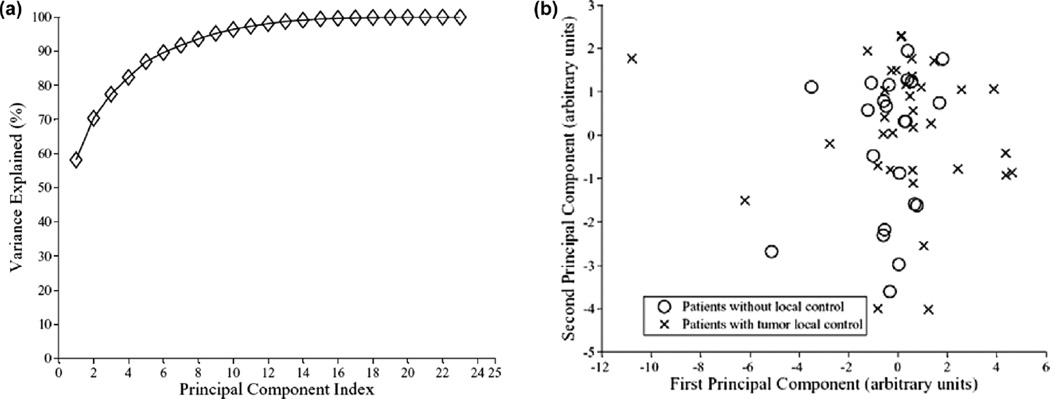
Figure 4.

Visualization of higher dimensional data by principle component analysis (PCA). (a) The variation explanation versus principle component (PC) index. (b) The data projection into the first two principal components space. Note the cases overlap.

Evaluation and validation methods

Evaluation metrics

To evaluate the performance of our models, we used Spearman’s rank correlation (rs), which provides a robust estimator of trend [39]. This is a desirable property, particularly when ranking the quality of treatment plans for different patients. Other metrics could be used as well such as Matthew’s correlation coefficient (MCC) [40], which measures classification rate or the area under the receiver-operating characteristics (ROC) curve (Az) [41].

Statistical validation

We used resampling methods (leave-one-out cross-validation (LOO-CV) and bootstrap) for model selection and performance comparison purposes. These methods provide statistically sound results when the available data set is limited [42]. In LOO-CV, all the data are used for training except for one left out for testing; the sample is permuted in a round-robin fashion, whereas in bootstrap, the data is divided randomly into training and testing samples. A parameter is tuned during LOO-CV, which effectively suppresses contributions from variables that do not clearly contribute to improved model performance. Application of these methods for radiotherapy outcome modeling is reviewed in our previous work [29].

Data set

The set consisted originally of 57 patients with discrete primary lesions, complete dosimetric archives, and follow-up information for the endpoint of local control (22 locally failed cases). One patient with local control was excluded from the analysis using Cook’s distance for detecting outliers as discussed elsewhere [43]. The patients were treated with 3D conformal radiation therapy with a median prescription dose of 70 Gy (60–84 Gy) according to institutional guidelines. The dose distributions were corrected using Monte Carlo simulations [44].

The results presented here are only for demonstrating the use of our techniques and are not intended as formal clinical findings, which are presented elsewhere [26,43]. The clinical data included age, gender, performance status, weight loss, smoking, histology, neoadjuvant and concurrent chemotherapy, stage, number of fractions, tumor elapsed time, tumor volume, and prescription dose. Treatment planning data were de-archived and potential dose-volume prognostic metrics were extracted using CERR [45]. These metrics included Vx (percentage volume receiving at least x Gy), where x was varied from 60 to 80 Gy in steps of 5 Gy, mean dose, minimum and maximum doses, center of mass location in the craniocaudal (COMSI) and lateral (COMLAT) directions. The anterior-posterior center of mass and minimum distance to the spinal cord were excluded from the analysis as being surrogates to tumor volume effects [26,43]. This resulted in a set of 56 patients and 23 candidate variables to model TCP.

Experimental results

The modeling process using non-linear statistical learning starts by applying PCA to visualize the data in two-dimensional space and assess the separability of low-risk from high-risk patients. Non-separable cases are modeled by non-linear kernels. This step is preceded by a variable selection process and the generalizability of the model is evaluated using resampling techniques as explained earlier and analyzed below.

Data exploration

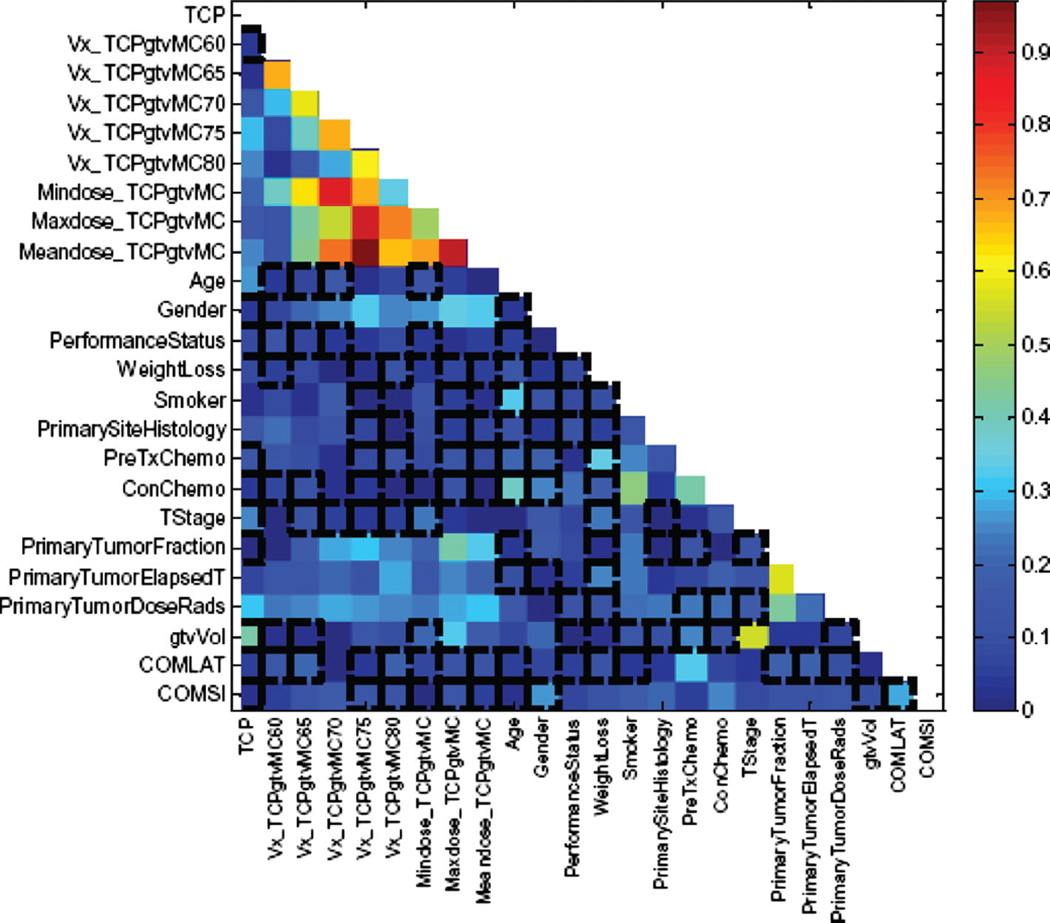
In Figure 3, we show a correlation matrix representation of these variables with clinical TCP and cross-correlations among themselves using bivariate Spearman’s coefficient (rs). Note that many DVH-based dosimetric variables are highly cross-correlated, which complicate the analysis of such data. In Figure 4a and b, we summarize the PCA analysis of this data by projecting it into 2-D space for visualization purposes. Figure 4a shows that two principle components are able to explain 70% of the data. Figure 4b shows a relatively highly overlap between patients with and without local control; indicating potential benefit from using non-linear kernel methods.

Figure 3.

Correlation matrix showing the candidate variables correlations with TCP and among the other candidate variables.

Model building using logistic regression

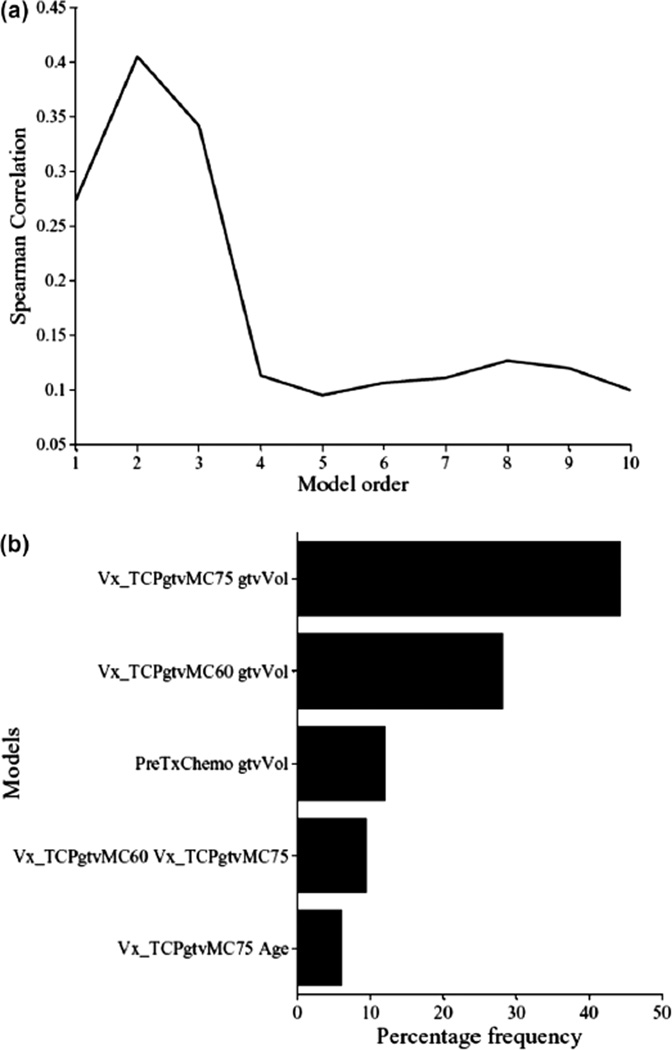
The multi-metric model building using logistic regression is performed using a two-step procedure to estimate model order and parameters. In each step, a sequential forward selection (SFS) strategy is used to build the model by selecting the next candidate variable from the available pool (23 variables in our case) based on increased significance using Wald’s statistics [29]. In Figure 5a, we show the model order selection using the LOO-CV procedure. It is noticed that a model order of two parameters provides the best predictive power with rs = 0.4. In Figure 5b, we show the optimal model parameters’ selection frequency on bootstrap samples (280 samples were generated in this case). A model consisting of GTV volume (β = −0.029, p = 0.006) and GTV V75 (β = +2.24, p = 0.016) had the highest selection frequency (45% of the time). The model suggests that increase in tumor volume would lead to failure, as one would expect due to increase in the number of clonogens in larger tumor volumes and this is well documented in the literature [46–48]. The V75 metric is related to dose coverage of the tumor, where it is noticed that patients who had less than 20% of their tumor covered by 75 Gy were at higher risk of failure [49]. This result is consistent with the observation made by Zhao et al. that high radiation dose can reduce the negative effect of large GTV in NSCLC patients [50]. However, this approach does not account for possible interactions between these metrics nor accounts for higher order non-linearities.

Figure 5.

TCP model building using Logistic regression. (a) Model order selection using LOO-CV. (b) Model parameters estimation by frequency selection on bootstrap samples.

Kernel-based modeling

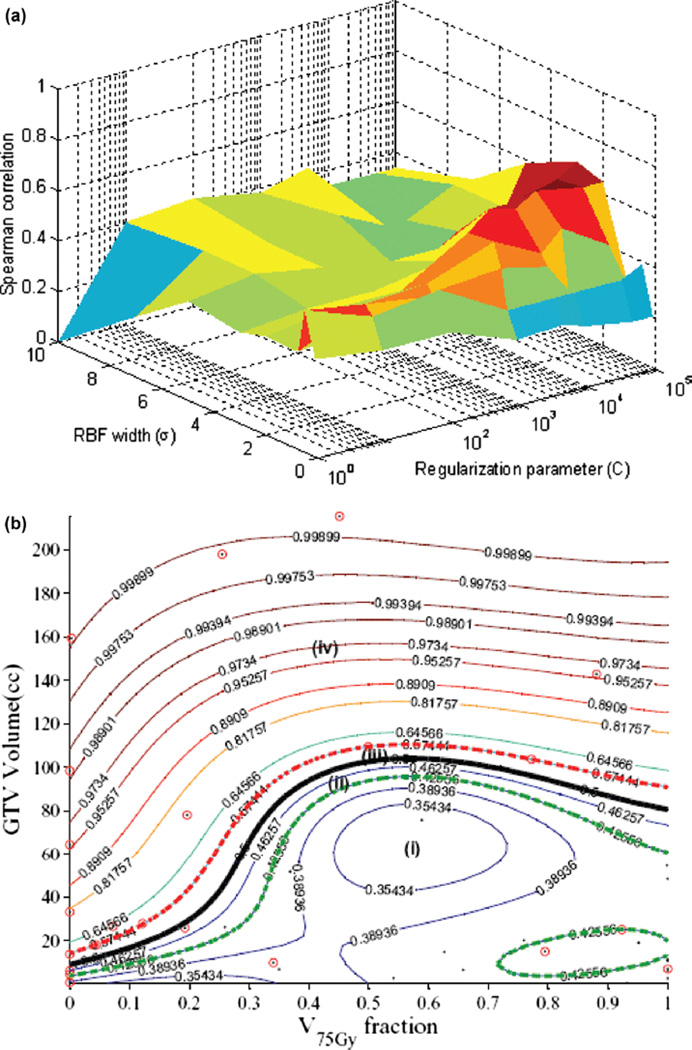
To account for potential non-linear interactions, we will apply kernel-based methods. Moreover, we will use the same variables selected by the logistic regression approach. We have demonstrated recently that such selection is more robust than other competitive techniques such as the recursive feature elimination (RFE) method using in microarray analysis [51]. In this case, a vector of explored variables is generated by concatenation. The variables are normalized using a z-scoring approach to have a zero mean and unity variance [37]. We experimented with different kernel forms, best results are shown for the radial basis function (RBF) in Figure 6a. The figure shows that the optimal kernel parameters are obtained with an RBF width σ = 2 and regularization parameter C = 10000. This resulted in a predictive power on LOO-CV rs = 0.68, which represents 70% improvement over the logistic analysis results. This improvement could be further explained by examining Figure 6b, which shows how the RBF kernel tessellated the variable space non-linearly into different regions of high and low risks of local failure. Four regions are shown in the figure representing high/low risks of local failure with high/low confidence levels, respectively. Note that cases falling within the classification margin have low confidence prediction power and represent intermediate risk patients, i.e., patients with ‘border-like’ characteristics that could belong to either risk group.

Figure 6.

Kernel-based modeling of TCP in lung cancer using the GTV volume and V75 with support vector machine (SVM) and a radial basis function (RBF) kernel. Scatter plot of patient data (black dots) being superimposed with failure cases represented with red circles. (a) Kernel parameter selection on LOO-CV with peak predictive power attained at σ = 2 and C = 10000. (b) Plot of the kernel-based local failure (1-TCP) nonlinear prediction model with four different risk regions: (i) area of low risk patients with high confidence prediction level; (ii) area of low risk patients with lower confidence prediction level; (iii) area of high risk patients with lower confidence prediction level; (iv) area of high risk patients with high confidence prediction level. Note that patients within the “margin” (cases ii and iii) represent intermediate risk patients, which have border characteristics that could belong to either risk group.

Comparison with mechanistic radiobiological models

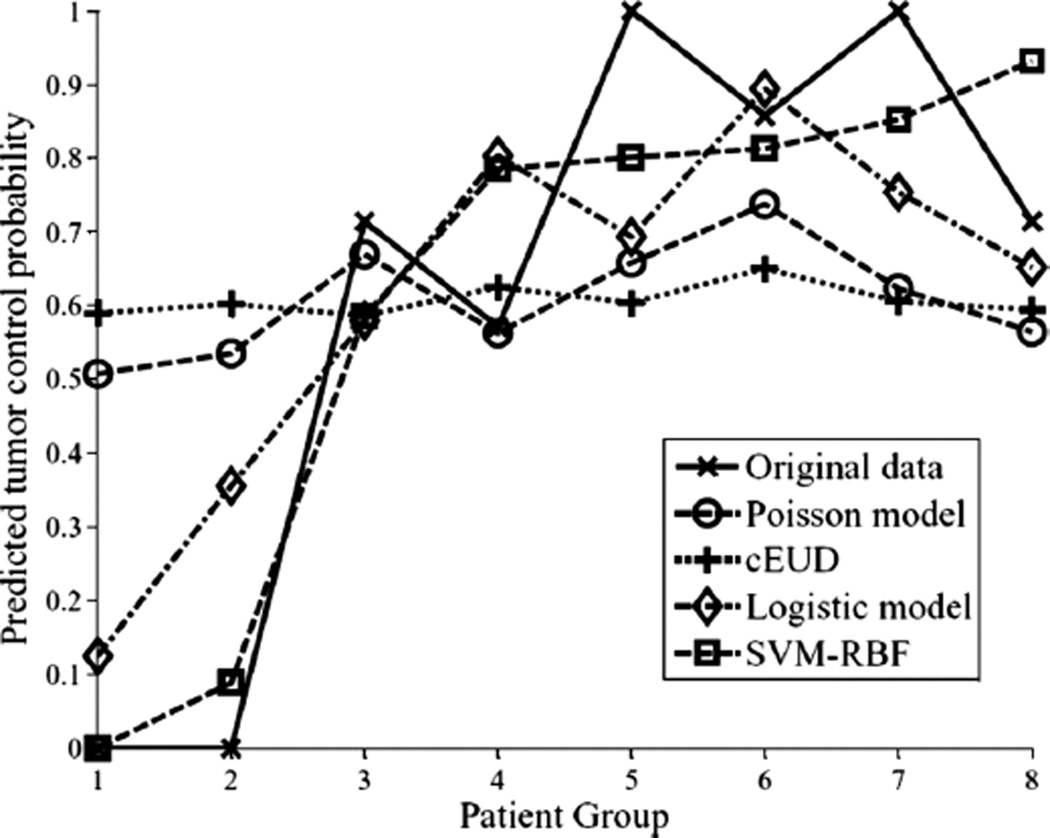
For comparison purposes with mechanistic TCP models with chose the Poisson-based TCP model [11,52] and the cell kill equivalent uniform dose (cEUD) model [53]. The Poisson-based TCP parameters for NSCLC were selected according to Willner et al. [48], in which the sensitivity to dose per fraction (α/β = 10 Gy), dose for 50% control rate (D50 = 74.5 Gy), and the slope of the sigmoid-shaped dose-response at D50 (γ₅₀ = 3.4). The resulting correlation of this model was rs = 0.33. Using D50 = 84.5 and γ₅₀ = 1.5 [54,55] yielded an rs = 0.33 also. This no change could be explained in terms of interval estimates of D50 (41–74.5 Gy) and γ₅₀ (0.8–3.5) reported by Willner et al. [48]. For the cEUD model, we selected the survival fraction at 2 Gy (SF2 = 0.56) according to Brodin et al. [56]. The resulting correlation in this case was rs = 0.17. A summary plot of the different methods predictions as a function of binned patients into equal groups is shown in Figure 7. It is observed that the best performance was achieved by the non-linear (SVM-RBF). This is particularly observed for predicting patients who are at high risk of local failure.

Figure 7.

A TCP comparison plot of different models as a function of patients’ being binned into equal groups using the model with highest predictive power (SVM-RBF). The SVM-RBF is compared to Poisson-based TCP, cEUD, and best 2-parameter logistic model. It is noted that prediction of low-risk (high control) patients is quite similar; however, the SVM-RBF provides a significant superior performance in predicting high-risk (low-control) patients.

Discussion

Tumors’ response to radiotherapy is a complex process due to the involvement of many intertwined microenvironmental, physical, and biological parameters that can change the treatment outcome from one case to another. For instance, we are still building our knowledge about the pathophysiological factors that contribute to the spatial and temporal heterogeneity of tumor hypoxia [57]. Better understanding of the dynamics of this complex process and other biological processes in the tumors microenvironment would provide new opportunities to improve outcomes. Nevertheless, the development of predictive models of tumor response remains an important objective with our best current knowledge in order to provide cancer patients with the best possible treatment. There is plethora in patient’s specific data that needs to be systematically collected and mined in relation to observed outcomes.

In this work, we have presented methods based on datamining to effectively interrogate patient’s clinical, physical, and biological records to extract relevant information and build maximally predictive models of tumor response based on this data. The objective of this methodology is to provide the TCP analyst with further insight into the data and improve our prediction of treatment response. In addition, these methods could improve our current understanding of radiological processes and they could potentially be utilized to develop better mechanistic radiological models based on this new knowledge.

We have presented multi-metric model building based on the classical logistic regression approach and demonstrated that this modeling process could be extended to a non-linear framework that would include higher-order variable interactions and local variable averaging to achieve higher prediction powers. The kernel approach presented here automates the search for higher-than-linear interactions between input variables that may be relevant to tumor local control. This is accomplished through an implicit non-linear mapping to higher dimensional feature space. The SVM kernel approach maximizes the separation between events and non-events in feature space. This approach has been recognized to yield better generalization with small datasets compared to standard maximum likelihood approaches [34,35].

The potential benefit from these methods can be predicted on the basis of principal components analysis as was shown in Figure 4, in which the overlap in the variable space could be resolved via mapping to the higher dimensional feature space according to Cover’s theorem of pattern recognition analysis [58].

The plot in Figure 6b could be used as guideline for better prediction of failure risk based on this model. A good feature of this framework, that it highlights areas where the confidence level of prediction power is weak (inside the margin) versus strong (outside the margin).

One of the main challenges of this datamining framework is the selection of the most relevant variables to include in the model. This is of course important clinically, because it supports increased focus on potentially causative factors. Our selection method based on resampling and information theory seems to produce good generalization results [29], however, this remains an open area for future research. Furthermore, validation on independent datasets such as multi-institutional clinical cooperative groups’ repositories would be required before clinical adoption of these models.

Conclusions

We have demonstrated datamining approaches for model building in radiotherapy based on linear and non-linear statistical learning. The non-linear kernel-based approach provided the best predictive results of TCP. These methods can efficiently and effectively handles high dimensional space of potentially critical features and are known to possess superior statistical power when learning from smaller sample sizes. For cases where non-linear effects are deemed important as tested by PCA, this technique can significantly improve on the best result achieved from the previous methods, by considering variable interactions and ability to generalize to unseen data, which is important for future clinical implementation. Future work will examine other aspects of nonlinear modeling for outcomes, such as incorporating prior information based on mechanistic TCP models, adapting the kernel specifically to the expected response structure, this, as well as addressing the variable selection problem more comprehensively.