On firework blasts and qualitative parameter dependency

Abstract

In this paper, a mathematical model is developed to qualitatively simulate the progressive time-evolution of a blast from a simple firework. Estimates are made for the blast radius that one can expect for a given amount of detonation energy and pyrotechnic display material. The model balances the released energy from the initial blast pulse with the subsequent kinetic energy and then computes the trajectory of the material under the influence of the drag from the surrounding air, gravity and possible buoyancy. Under certain simplifying assumptions, the model can be solved for analytically. The solution serves as a guide to identifying key parameters that control the evolving blast envelope. Three-dimensional examples are given.

1. Introduction

Fireworks are widely used in cultural celebrations, sporting events, political rallies, etc. The full sequence of events for release of a cloud of packed material begins with an initiated detonation that rapidly rips open a thin container (typically a lightweight shell of cardboard), which releases packed pyrotechnic powder particles forming a cloud. Various compounds are mixed together to produce a wide array of colours (e.g. blue (caesium, copper), red (lithium), orange (calcium), yellow (iron), etc.). For a history of fireworks, we refer the interested reader to Plimpton [1], Brock [2], Russell [3], Shimanzu [4], Werrett [5] and Kazuma [6,7].

In this paper, we are primarily interested in qualitatively estimating the time-evolution of the envelope of a cloud emanating from a firework blast (figure 1). The estimation of the time-evolution and the size of the blast is important for both aesthetic and safety reasons. Thus, the main objective of this study is to develop a practical qualitative model which captures the essential physics of detonation and blast envelope growth. A schematic of the model problem is shown in figure 2. In this work, we do not consider detailed models for the interaction between the shock wave and the packed particles (e.g. [8–11]) nor the chemical aspects which are beyond the scope of this work.¹ We make the following simplifying assumptions:

• — The fragments do not interact with one another.

• — The blast fragments are all the same size, assumed spherical with radius R_i=R and receive the same velocity pulse (denoted δv(0)), in the radial direction from the centre of the blast upon detonation. Specifically, the velocity vector pulse is radially outward from the centre of the sphere, co-located at the centre of mass of the pyrotechnic display material

  $$\delta {\mathit{\text{v}}}_i(0)=\parallel \delta \mathit{\text{v}}(0)\parallel \left(\frac{{\mathit{\text{r}}}_i(0)-{\mathit{\text{r}}}_{\mathrm{c}}(0)}{\parallel {\mathit{\text{r}}}_i(0)-{\mathit{\text{r}}}_{\mathrm{c}}(0)\parallel }\right)\stackrel{\mathrm{def}}{=}\parallel \delta \mathit{\text{v}}(0)\parallel {\mathit{\text{n}}}_{ri},$$ 1.1

  where r_i is the position vector of the ith particle, n_ri is the normal/radial direction and

  $${\mathit{\text{r}}}_{\mathrm{c}}(0)=\frac{1}{\left(\sum _{i=1}^N{m}_i\right)}\sum _{i=1}^N{m}_i{\mathit{\text{r}}}_i(0),$$ 1.2

  where N is the number of particles, r_c(0) is the centre of mass of the packed particles and m_i is the mass of each particle. The pulse velocities are added to the velocity vectors immediately before the pulse (v⁻(0))

  $${\mathit{\text{v}}}_i^{+}(0)={\mathit{\text{v}}}_i^{-}(0)+\delta {\mathit{\text{v}}}_i(0).$$ 1.3
• — The magnitude of the initial velocity pulse dictates initial energy released (E), which is assumed to be converted into kinetic energy for the pyrotechnic material at (t=0)

  $$E=\sum _{i=1}^N\frac{1}{2}{m}_i\parallel \delta \mathit{\text{v}}(0){\parallel }^2\Rightarrow \parallel \delta \mathit{\text{v}}(0)\parallel =\sqrt{\frac{2E}{\sum _{i=1}^N{m}_i}}=\sqrt{\frac{2E}{M}},$$ 1.4

  where δv(0) is the velocity of pulse imparted to a fragment in the radial direction, M is the total pyrotechnic material mass, $m_i={\rho }_i\frac{4}{3}\pi R_i^3$ is mass of the individual fragments, where ρ_i is the density of the fragments.
• — The objects in the system are assumed to be small enough to be considered (idealized) as particles, spherical in shape, and that the effects of their rotation with respect to their mass centre are unimportant to their overall motion. The equation of motion for the ith particle in the system is (with m_i=m)

  $$m{\dot{\mathit{\text{v}}}}_i={\mathbf{\Psi }}_i^{\mathrm{tot}}={\mathbf{\Psi }}_i^{\mathrm{drag}}+{\mathbf{\Psi }}_i^{\mathrm{grav}}+{\mathbf{\Psi }}_i^{\mathrm{buoy}},$$ 1.5

  with initial velocity v_i(0) and initial position r_i(0). The gravitational force is ${\mathbf{\Psi }}_i^{\mathrm{grav}}=m\mathit{\text{g}}$, where g=(g_x,g_y,g_z)=(0,0,−9.81) m s⁻². The buoyancy force is ${\mathbf{\Psi }}_i^{\mathrm{buoy}}={\rho }_{\mathrm{a}}\frac{4}{3}\pi R^3\mathit{\text{b}}\stackrel{\mathrm{def}}{=}{m}_{\mathrm{a}}\mathit{\text{b}}$, where b=(b_x,b_y,b_z)=(0,0,9.81) m s⁻² and ρ_a is the density of air. Buoyancy can be important because of the potentially porous nature of the fragments.
• — For the drag, we will employ a general phenomenological model

  $${\mathbf{\Psi }}_i^{\mathrm{drag}}=\frac{1}{2}{\rho }_{\mathrm{a}}{C}_{\mathrm{D}}\parallel {\mathit{\text{v}}}^f-{\mathit{\text{v}}}_i\parallel ({\mathit{\text{v}}}^f-{\mathit{\text{v}}}_i)A,$$ 1.6

  where C_D is the drag coefficient, A is the reference area, which for a sphere is A=πR², ρ_a is the density of the ambient fluid environment and v^f is the velocity of the surrounding medium which, in the case of interest, is air.

Figure 1.

Time-lapse photo of firework material emanating from a blast. Photo available courtesy of the public domain site http://www.photos-public-domain.com/wp-content/uploads/2011/07/. (Online version in colour.)

Figure 2.

Launch and detonation of a firework.

Remark 1.1 —

Later, we will assume that v^f≈0, implicitly assuming that the dynamics of the surrounding medium is unimportant. However, for other applications, such as high-speed flow, the motion of the surrounding fluid can be important, necessitating fully coupled (two-way) particle–fluid interaction models. This is outside the scope of the present work. Generally, this requires the use of solid–fluid staggering-type schemes (e.g. [13–19]). This is discussed further at the end of this paper.

Remark 1.2 —

For the problems under consideration, the non-interaction assumption is quite appropriate since all of the particles are propagating radially outwards with the same initial velocity. Thus, their mutual collisions are negligible. This was also checked against ‘brute-force’ simulations, which are beyond the scope of this paper, using formulations in Zohdi [16,17] which take detailed collisions into account.

2. General fragment trajectories

The differential equation for each fragment in its outward normal direction is (m_i=m), assuming no gravity, buoyancy or fluid velocity (v^f=0). The subscript n indicates the outward normal direction

$$m{\dot{v}}_{\mathrm{in}}=-\frac{1}{2}{\rho }_{\mathrm{a}}{C}_{\mathrm{D}}{v}_{\mathrm{in}}^{2}A,$$ 2.1

where v_in is the outward normal velocity, which can be written as

$${\dot{v}}_{\mathrm{in}}=-K{v}_{\mathrm{in}}^2,$$ 2.2

where for a sphere

$$K=\frac{1}{2m}{C}_{\mathrm{D}}{\rho }_{\mathrm{a}}A=\frac{3C_{\mathrm{D}}{\rho }_{\mathrm{a}}}{8\rho R}.$$ 2.3

Using the chain rule

$$\frac{\mathrm{d}{v}_{\mathrm{in}}}{\mathrm{d}t}=\frac{\mathrm{d}{v}_{\mathrm{in}}}{\mathrm{d}{r}_{\mathrm{in}}}\frac{\mathrm{d}{r}_{\mathrm{in}}}{\mathrm{d}t}=\frac{\mathrm{d}{v}_{\mathrm{in}}}{\mathrm{d}{r}_{\mathrm{in}}}{v}_{\mathrm{in}}=-K{v}_{\mathrm{in}}^2,$$ 2.4

which yields

$$\frac{\mathrm{d}{v}_{\mathrm{in}}}{\mathrm{d}{r}_{\mathrm{in}}}=-K{v}_{\mathrm{in}},$$ 2.5

and subsequently

$$\frac{\mathrm{d}{v}_{\mathrm{in}}}{v_{\mathrm{in}}}=-K\hspace{0.17em}\mathrm{d}{r}_{\mathrm{in}}\Rightarrow {\int }_{v_{\mathrm{oin}}}^{v_{\mathrm{in}}(t)}\frac{\mathrm{d}{v}_{\mathrm{in}}}{v_{\mathrm{in}}}=-{\int }_{r_{\mathrm{oin}}}^{r_{\mathrm{in}}(t)}K\hspace{0.17em}\mathrm{d}{r}_{\mathrm{in}},$$ 2.6

where r_in is the outward normal position, with solution

$$v_{\mathrm{in}}(t)=v_{\mathrm{oin}}\hspace{0.17em}{\mathrm{e}}^{-K(r_{\mathrm{in}}(t)-r_{\mathrm{oin}})},$$ 2.7

with inverse solution, for the blast radius

$$\mathcal{L}(t)=r_{\mathrm{in}}(t)-r_{\mathrm{oin}}=-\frac{1}{K}\hspace{0.17em}\mathrm{Ln}\left(\frac{v_{\mathrm{in}}(t)}{v_{\mathrm{oin}}}\right)=-\frac{8\rho R}{3C_{\mathrm{D}}{\rho }_{\mathrm{a}}}\hspace{0.17em}\mathrm{Ln}\left(\frac{v_{\mathrm{in}}(t)}{v_{\mathrm{oin}}}\right),$$ 2.8

where 1/K has units of metres. This shows the explicit inverse relationship between the size of the blast radius and K, which is a measure of the drag (tending to limit the blast radius growth) and the mass (tending to increase the blast radius growth). One can relate this directly to the energy of detonation and total mass via equation (1.4), using $v_{\mathrm{oin}}=\sqrt{2E/M}$

$$\mathcal{L}(t)=r_{\mathrm{in}}(t)-r_{\mathrm{oin}}=-\frac{8\rho R}{3C_{\mathrm{D}}{\rho }_{\mathrm{a}}}\hspace{0.17em}\mathrm{Ln}\left(\frac{v_{\mathrm{in}}(t)}{\sqrt{2E/M}}\right).$$ 2.9

Remark —

One could directly integrate equation (2.2) in time to yield

$$v_{\mathrm{in}}(t)=\frac{v_{\mathrm{oin}}}{Kt{v}_{\mathrm{oin}}+1}=\frac{\sqrt{2E/M}}{Kt\sqrt{2E/M}+1}$$ 2.10

and

$$r_{\mathrm{in}}(t)=r_{\mathrm{oin}}+\frac{1}{K}\hspace{0.17em}\mathrm{Ln}(Kt{v}_{\mathrm{oin}}+1)=r_{\mathrm{oin}}+\frac{1}{K}\hspace{0.17em}\mathrm{Ln}\left(Kt\sqrt{\frac{2E}{M}}+1\right).$$ 2.11

One can also invert equation (2.11) to yield an expression for the time it takes to achieve a certain blast radius

$$t=\frac{{\mathrm{e}}^{K(r_{\mathrm{in}}(t)-r_{\mathrm{oin}})}-1}{K\sqrt{2E/M}}.$$ 2.12

3. Hybrid drag

Generally speaking, the drag coefficient, which is an empirical parameter which attempts to represent the action of the fluid forces on an object, is not a constant, and would vary with, for example, the Reynolds number. In the zero Reynolds number limit the drag would be that of a Stokesian regime. One possible way to represent the drag coefficient is with a piecewise definition, as a function of the Reynolds number (Chow [20]):

• — for 0<Re≤1, C_D=24/Re,

• — for 1<Re≤400, C_D=24/Re^0.646,

• — for 400<Re≤3×10⁵, C_D=0.5,

• — for 3×10⁵<Re≤2×10⁶, C_D=0.000366 Re^0.4275,

• — for $2\times {10}^6<Re<\mathrm{\infty }$, C_D=0.18,

where the local Reynolds number for a particle is $\mathit{Re}\stackrel{\text{def}}{=}2R{\rho }_{\text{a}}\Vert v^f-v_i\Vert /{\mu }_{\text{f}}$ and μ_f is the fluid viscosity. The viscosity coefficient for air is μ_f=0.000018 Pa s⁻¹. Using the hybrid model reduces the drag at the lower Reynolds number regimes, thus producing a larger blast radius than a constant large drag coefficient. However, to solve the governing equation, when include gravity and buoyancy are included

$$m{\dot{\mathit{\text{v}}}}_i={\mathbf{\Psi }}_i^{\mathrm{drag}}+{\mathbf{\Psi }}_i^{\mathrm{grav}}+{\mathbf{\Psi }}_i^{\mathrm{buoy}}=\frac{1}{2}{\rho }_{\mathrm{a}}{C}_{\mathrm{D}}\parallel {\mathit{\text{v}}}^f-{\mathit{\text{v}}}_i\parallel ({\mathit{\text{v}}}^f-{\mathit{\text{v}}}_i)A+m\mathit{\text{g}}+m\mathit{\text{b}},$$ 3.1

we integrate the governing equations numerically

$$\begin{array}{rl}{\mathit{\text{v}}}_i(t+\mathrm{\Delta }t)& ={\mathit{\text{v}}}_i(t)+\frac{1}{m}{\int }_t^{t+\mathrm{\Delta }t}({\mathbf{\Psi }}_i^{\mathrm{drag}}+{\mathbf{\Psi }}_i^{\mathrm{grav}}+{\mathbf{\Psi }}_i^{\mathrm{buoy}})\hspace{0.17em}\mathrm{d}t\\ & \approx {\mathit{\text{v}}}_i(t)+\frac{\mathrm{\Delta }t}{m}({\mathbf{\Psi }}_i^{\mathrm{drag}}(t)+{\mathbf{\Psi }}_i^{\mathrm{grav}}(t)+{\mathbf{\Psi }}_i^{\mathrm{buoy}}(t)).\end{array}$$ 3.2

Remark —

The piecewise drag law of Chow [20] is a mathematical description for the Reynolds number over a wide range and is a curve-fit of extensive data from Schlichting [21]. As observed in the experimental data, the mathematical function exhibits a discontinuity at Re=3×10⁵, although in an explosion the time a particle spends at this Reynolds number is almost negligible.

4. Numerical example

In order to illustrate the model, the following simulation parameters were chosen (they are not intended to simulate a specific firework event):

• — total simulation duration, 35 s,

• — time to detonation after launch, 3 s,

• — the time-step size, Δt=10⁻⁴ s,

• — launch velocity, v(t=0)=(0,0,100) m s⁻¹ (starting from a launch height of 1 m),

• — detonation energy, E=100 000 J,

• — density of air, ρ_a=1.225 kg m⁻³,

• — core inner packing shell radius (figure 2), R_o=0.01 m (which holds the packed detonation material),

• — core outer packing shell radius (figure 2), R_o=0.025 m (forming a shell of packed pyrotechnic display material),

• — number of fragments, N=1000,

• — density of pyrotechnic display material, ρ=1000 kg m⁻³,

• — total mass, $M=\sum _{i=1}^N{m}_i=0.5\hspace{0.17em}\mathrm{kg}$,

• — the fragment sizes were calculated by R_i=(M/Nρπ(4/3))^1/3 and were packed between the inner and outer shell cited above.

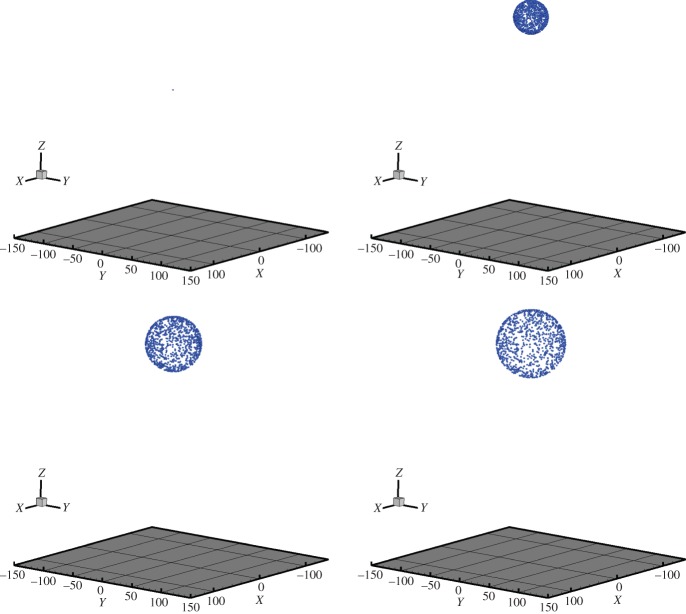
An extremely small (relative to the total simulation time) time-step size of Δt=10⁻⁴ s was used. Further reductions of the time-step size produced no notable changes in the results, thus the solutions generated can be considered to have negligible numerical error. The simulations took under 1 min on a standard laptop. Figures 3 and 4 illustrate the results for the parameters above. With the chosen parameters, the blast radius was approximately 110 m. We note that in the descending phase of the trajectory, the particles nearly achieve a so-called settling steady-state velocity, v_tm (when $\dot{\mathit{\text{v}}}=\mathbf{\text{0}}$), given by assuming a purely vertical trajectory drop

$$\begin{array}{rl}m\dot{v}& =m\mathit{\text{g}}+m_{\mathrm{a}}\mathit{\text{b}}+\frac{1}{2}{\rho }_{\mathrm{a}}A{C}_{\mathrm{D}}\mathit{\text{v}}\parallel \mathit{\text{v}}\parallel \Rightarrow 0\\ & =-mg+m_{\mathrm{a}}g+\frac{1}{2}{\rho }_{\mathrm{a}}A{C}_{\mathrm{D}}{v}_{tm}^2\Rightarrow v_{tm}=\sqrt{\frac{2(m-m_{\mathrm{a}})g}{{\rho }_{\mathrm{a}}{C}_{\mathrm{D}}A}},\end{array}$$ 4.1

where an implicit equation for the settling velocity arises due to the drag coefficient's dependency on C_D(v). We note that the objective of this simulation was not to simulate any specific firework configuration or material, but to illustrate the character of the model. For example, for the pyrotechnic material, the density was selected simply to illustrate the model. When the blast material is ejected, it can be quite porous, not entirely a solid. Thus using a solid density of say, copper or iron, would be inappropriate. Thus, without further information, selecting a density of 1000 kg m⁻³ was a neutral option. This can easily be modified for specific cases.

Figure 3.

From left to right and top to bottom: initial launch of packed particles (small barely visible point), and then the progressive blast with fragments reaching a maximum height. (Online version in colour.)

Figure 4.

From left to right and top to bottom: descent and settling of the fragments. (Online version in colour.)

Remark —

In the low velocity (low Reynolds number) limit, a Stokesian model is most appropriate, which is what the hybrid drag law attempts to incorporate. The drag forces are significantly smaller with a Stokesian model. Comparing a purely Stokesian drag law, which would be valid for small particles and laminar flow (low Reynolds number)

$${\mathbf{\Psi }}_i^{\mathrm{drag},\mathrm{Stokesian}}=c({\mathit{\text{v}}}^f-{\mathit{\text{v}}}_i)={\mu }_{\mathrm{f}}6\pi R_i({\mathit{\text{v}}}^f-{\mathit{\text{v}}}_i),$$ 4.2

where μ_f is the fluid viscosity. We observe the following:

$$\frac{\parallel {\mathbf{\Psi }}^{\mathrm{drag},\mathrm{Stokesian}}\parallel }{\parallel {\mathbf{\Psi }}^{\mathrm{drag}}\parallel }=\frac{12{\mu }_{\mathrm{f}}}{{\rho }_{\mathrm{a}}{C}_{\mathrm{D}}R\parallel {\mathit{\text{v}}}^f-{\mathit{\text{v}}}_i\parallel }.$$ 4.3

For typical parameters for air and spherical particles (using C_D=0.5, which is a mid-range value from the piecewise drag law introduced earlier), we have

$$\frac{\parallel {\mathbf{\Psi }}^{\mathrm{drag},\mathrm{Stokesian}}\parallel }{\parallel {\mathbf{\Psi }}^{\mathrm{drag}}\parallel }=\frac{12{\mu }_{\mathrm{f}}}{{\rho }_{\mathrm{a}}{C}_{\mathrm{D}}R\parallel {\mathit{\text{v}}}^f-{\mathit{\text{v}}}_i\parallel }\approx \frac{0.0004}{R\parallel {\mathit{\text{v}}}^f-{\mathit{\text{v}}}_i\parallel },$$ 4.4

which indicates that for extremely small fragments and low velocities, the Stokesian model dominates, while for larger fragments and large velocities, the phenomenological model dominates. The limiting Stokesian case is discussed further in the appendix.

5. Summary

For general blast conditions, there can be cases where the change in the surrounding fluid's behaviour due to the motion of the particles may be important. With those cases in mind, had the fragment non-interaction approximation not been invoked, a coupled system of equations would arise due to the interaction between the fragments. For example, this entails numerically integrating, in an implicit manner, the governing equations, which leads to (for example using a trapezoidal rule with variable integration metric, 0≤ϕ≤1)

$$\begin{array}{rl}{\mathit{\text{v}}}_i(t+\mathrm{\Delta }t)& ={\mathit{\text{v}}}_i(t)+\frac{1}{m}{\int }_t^{t+\mathrm{\Delta }t}({\mathbf{\Psi }}_i^{\mathrm{grav}}+\sum _{j=1,j\ne i}^K{\mathbf{\Psi }}_{ij}+{\mathbf{\Psi }}_i^{\mathrm{fluid}})\hspace{0.17em}\mathrm{d}t\\ & \approx {\mathit{\text{v}}}_i(t)+\frac{\mathrm{\Delta }t\varphi }{m}\left({\mathbf{\Psi }}_i^{\mathrm{grav}}(t+\mathrm{\Delta }t)+\sum _{j=1,j\ne i}^K{\mathbf{\Psi }}_{ij}(t+\mathrm{\Delta }t)+{\mathbf{\Psi }}_i^{\mathrm{fluid}}(t+\mathrm{\Delta }t)\right)\\ & +\frac{\mathrm{\Delta }t(1-\varphi )}{m}\left({\mathbf{\Psi }}_i^{\mathrm{grav}}(t)+\sum _{j=1,j\ne i}^K{\mathbf{\Psi }}_{ij}(t)+{\mathbf{\Psi }}_i^{\mathrm{fluid}}(t)\right),\end{array}$$ 5.1

where ${\mathbf{\Psi }}_i^{\mathrm{fluid}}$ represents the interaction of fragment i with the fluid and Ψ_ij(t) represents its interaction with the neighbouring j=1,2,…K fragments. The position can be computed via application of the trapezoidal rule again:

$${\mathit{\text{r}}}_i(t+\mathrm{\Delta }t)\approx {\mathit{\text{r}}}_i(t)+\mathrm{\Delta }t(\varphi {\mathit{\text{v}}}_i(t+\mathrm{\Delta }t)+(1-\varphi ){\mathit{\text{v}}}_i(t)),$$ 5.2

which can be consolidated into

$$\begin{array}{rl}{\mathit{\text{r}}}_i(t+\mathrm{\Delta }t)& ={\mathit{\text{r}}}_i(t)+{\mathit{\text{v}}}_i(t)\mathrm{\Delta }t\\ & +\frac{{\varphi }^2{(\mathrm{\Delta }t)}^2}{m}\left({\mathbf{\Psi }}_i^{\mathrm{grav}}(t+\mathrm{\Delta }t)+\sum _{j=1,j\ne i}^K{\mathbf{\Psi }}_{ij}(t+\mathrm{\Delta }t)+{\mathbf{\Psi }}_i^{\mathrm{fluid}}(t+\mathrm{\Delta }t)\right)\\ & +\frac{\varphi (1-\varphi ){(\mathrm{\Delta }t)}^2}{m}\left({\mathbf{\Psi }}_i^{\mathrm{grav}}(t)+\sum _{j=1,j\ne i}^K{\mathbf{\Psi }}_{ij}(t)+{\mathbf{\Psi }}_i^{\mathrm{fluid}}(t)\right).\end{array}$$ 5.3

This yields a coupled system of equations for the interaction between the fragments and the fluid, which would necessitate spatio-temporal discretization for example using finite-element, finite difference, finite volume or discrete element methods, such as those found in Onate et al. [22,23,25], Avci & Wriggers [19], Leonardi et al. [24], Bolintineanu et al. [26] and Zohdi [13–18]. Furthermore, in order to obtain more accurate initial conditions for the system, advanced models would also involve detailed modelling of the initial packing of the material [27,28], and the evolution of heat and the mechanics of the surrounding fluid environment. Such systems are quite complex. Thus, in order to qualitatively understand such systems a priori, the results presented in this paper are useful. Summarizing, in the absence or gravity of buoyancy, one obtains quite simple relations for the velocity of the fragments (under the constant drag coefficient assumption)

$$v_{\mathrm{in}}(t)=v_{\mathrm{oin}}\hspace{0.17em}{\mathrm{e}}^{-K(r_{\mathrm{in}}(t)-r_{\mathrm{oin}})}=\sqrt{\frac{2E}{M}}\hspace{0.17em}{\mathrm{e}}^{-(3C_{\mathrm{D}}{\rho }_{\mathrm{a}}/8\rho R)(r_{\mathrm{in}}(t)-r_{\mathrm{oin}})},$$ 5.4

with inverse solution, for the blast radius

$$\mathcal{L}(t)=r_{\mathrm{in}}(t)-r_{\mathrm{oin}}=-\frac{8\rho R}{3C_{\mathrm{D}}{\rho }_{\mathrm{a}}}\hspace{0.17em}\mathrm{Ln}\left(\frac{v_{\mathrm{in}}}{v_{\mathrm{oin}}}\right)=-\frac{8\rho R}{3C_{\mathrm{D}}{\rho }_{\mathrm{a}}}\hspace{0.17em}\mathrm{Ln}\left(\frac{v_{\mathrm{in}}}{\sqrt{2E/M}}\right).$$ 5.5

Under the non-interaction approximation made earlier, the expressions above can be used for each fragment to compute the trajectory and provide a useful guide for more detailed studies, which are being currently pursued by the author.

Appendix A. Stokesian model

The differential equation for each fragment is (m_i=m)

$$m\frac{\mathrm{d}{\mathit{\text{v}}}_i}{\mathrm{d}t}=c({\mathit{\text{v}}}^f-{\mathit{\text{v}}}_i)+m\mathit{\text{g}}+m_{\mathrm{a}}\mathit{\text{b}}$$ A 1

and can be solved analytically in the normal direction (n_ri) to yield

$$v_{\mathrm{in}}(t)=\left(v_{\mathrm{in}}(0)-v_n^f-\frac{m}{c}\left(g_n+\frac{m_{\mathrm{a}}}{m}{b}_n\right)\right)\hspace{0.17em}{\mathrm{e}}^{-(c/m)t}+v_n^f+\frac{m}{c}\left(g_n+\frac{m_{\mathrm{a}}}{m}{b}_n\right).$$ A 2

The position in the normal direction is

$$r_{\mathrm{in}}(t)=r_{\mathrm{in}}(0)+A_{\mathrm{in}}\frac{m}{c}(1-{\mathrm{e}}^{-(c/m)t})+B_{\mathrm{in}}t,$$ A 3

where $A_{\mathrm{in}}=v_{\mathrm{in}}(0)-v_{\mathrm{in}}^f-(m/c)(g_n+(m_{\mathrm{a}}/m)b_n)$ and $B_{\mathrm{in}}=v_{\mathrm{in}}^f+(m/c)(g_n+(m_{\mathrm{a}}/m)b_n)$. We note that

$$\frac{m}{c}=\frac{2R^2\rho }{9{\mu }_{\mathrm{f}}}.$$ A 4

(a) Gravity and buoyancy-free case

In the normal direction, with no gravity and buoyancy, this collapses to a particularly simple expression for the velocity of each fragment

$$v_{\mathrm{in}}(t)=v_{\mathrm{in}}(0)\hspace{0.17em}{\mathrm{e}}^{-(c/m)t}$$ A 5

and for the position, we have

$$r_{\mathrm{in}}(t)=r_{\mathrm{in}}(0)+v_{\mathrm{in}}(0)\frac{m}{c}(1-e^{-(c/m)t}).$$ A 6

(b) Blast envelope radius

To extract the ‘pure’ blast envelope radius, ignoring the launch velocity, thus v_in(0)=∥δv(0)∥

$$v_{\mathrm{in}}(t)=v_{\mathrm{in}}(0)\hspace{0.17em}{\mathrm{e}}^{-(c/m)t}=\parallel \delta {\mathit{\text{v}}}_{\mathrm{in}}(0)\parallel \hspace{0.17em}{\mathrm{e}}^{-(c/m)t}$$ A 7

and for the position, we have

$$r_{\mathrm{in}}(t)=r_{\mathrm{in}}(0)+v_{\mathrm{in}}(0)\frac{m}{c}(1-{\mathrm{e}}^{-(c/m)t})=r_{\mathrm{in}}(0)+\parallel \delta {\mathit{\text{v}}}_{\mathrm{in}}(0)\parallel \frac{m}{c}(1-{\mathrm{e}}^{-(c/m)t}).$$ A 8

Using equation (1.4) yields

$$v_{\mathrm{in}}(t)=\left(\sqrt{\frac{2E}{M}}\right){\mathrm{e}}^{-(9{\mu }_{\mathrm{f}}/2R^2\rho )t}$$ A 9

and

$$r_{\mathrm{in}}(t)=r_{\mathrm{in}}(0)+\left(\sqrt{\frac{2E}{M}}\frac{2\rho R^2}{9{\mu }_{\mathrm{f}}}\right)(1-e^{-(9{\mu }_{\mathrm{f}}/2R^2\rho )t}).$$ A 10

We define the blast radius

$$\mathcal{L}(t)\stackrel{\mathrm{def}}{=}{r}_{\mathrm{in}}(t)-r_{\mathrm{in}}(0)=\left(\sqrt{\frac{2E}{M}}\frac{2\rho R^2}{9{\mu }_{\mathrm{f}}}\right)(1-e^{-(9{\mu }_{\mathrm{f}}/2R^2\rho )t}).$$ A 11

The maximum radius ($t=\mathrm{\infty }$) is

$$\mathcal{L}(t=\mathrm{\infty })=\left(\sqrt{\frac{2E}{M}}\frac{2\rho R^2}{9{\mu }_{\mathrm{f}}}\right).$$ A 12

The ratio of the radius at any given time to the maximum is

$$\frac{\mathcal{L}(t)}{{\mathcal{L}}_{\mathrm{\infty }}}=1-{\mathrm{e}}^{-(9{\mu }_{\mathrm{f}}/2R^2\rho )t}.$$ A 13

To determine the time for the blast radius to achieve a certain size, $\mathcal{L}(t^{\ast })={\mathcal{L}}^{\ast }$, we may solve for the time from the above

$$t^{\ast }=-\frac{2\rho R^2}{9{\mu }_{\mathrm{f}}}\hspace{0.17em}\mathrm{Ln}\left(\frac{\mathcal{L}(\mathrm{\infty })-{\mathcal{L}}^{\ast }}{\mathcal{L}(\mathrm{\infty })}\right).$$ A 14

The key observations are the exponential (decay-type) growth of the cloud, controlled by the amount of energy in the detonation and the ratio of the surrounding damping and the fragment masses. The growth of the blast sphere is exponential and is controlled by the ratio of the inertial and drag forces, 2R²ρ/9μ_f. The size of the blast sphere is proportional to the square of the size of the particles, the square root of the stored detonation energy, inversely proportional to the square-root of the mass and inversely proportional to the viscosity of the atmosphere. As for the model used in the body of the paper, we note that in the descending phase of the trajectory, for a Stokesian regime, the particles nearly achieve a so-called settling steady-state velocity, v_tm (when $\dot{\mathit{\text{v}}}=\mathbf{\text{0}}$), given by assuming a purely vertical trajectory drop

$$\begin{array}{rl}m\dot{v}& =m\mathit{\text{g}}+m_{\mathrm{a}}\mathit{\text{b}}+{\mu }_{\mathrm{f}}6\pi R^2\mathit{\text{v}}\Rightarrow 0\\ & =-mg+m_{\mathrm{a}}g+{\mu }_{\mathrm{f}}6\pi R^2{v}_{tm}\Rightarrow v_{tm}=\frac{2}{9}\frac{(\rho -{\rho }_{\mathrm{a}})}{{\mu }_{\mathrm{f}}}g{R}^2.\end{array}$$ A 15

Competing interests

There are no competing interests.

Funding

This work was funded in part by the Army Research Laboratory through the Army High Performance Computing Research Center (cooperative agreement number W911NF-07-2-0027).