Model reduction and parameter estimation of non‐linear dynamical biochemical reaction networks

Abstract

Parameter estimation for high dimension complex dynamic system is a hot topic. However, the current statistical model and inference approach is known as a large p small n problem. How to reduce the dimension of the dynamic model and improve the accuracy of estimation is more important. To address this question, the authors take some known parameters and structure of system as priori knowledge and incorporate it into dynamic model. At the same time, they decompose the whole dynamic model into subset network modules, based on different modules, and then they apply different estimation approaches. This technique is called Rao‐Blackwellised particle filters decomposition methods. To evaluate the performance of this method, the authors apply it to synthetic data generated from repressilator model and experimental data of the JAK‐STAT pathway, but this method can be easily extended to large‐scale cases.

1 Introduction

Biochemical reaction process is a complex and high‐dimension dynamics system, which includes a variety of feedback loop [1, 2] and possesses strongly non‐linear kinetic characteristics such as chaos, bifurcation, complex disturbance wave and so on [3–7]. The non‐linear complex and high‐dimension biochemical reaction can be decomposed into several sets of chemical substances, and then combined to consider the whole mechanism. On the basis of biochemical reaction, dynamic modelling is accordingly divided into many subset network modules. Both subset network modules and the whole dynamic characteristics should be analysed [8, 9]. This is defined as model reduction techniques. Model reduction techniques decompose a critical biochemical reactions and variables according to core dynamical characteristics of the system. There are two kinds of techniques mostly used to partition the state variables. One is fast and slow decompositions, another is linear and non‐linear decompositions. The former detailed model reduction approaches have singular perturbation techniques in papers [10, 11], hierarchical approach in paper [12], quasi‐steady‐states approximations in papers [13, 14], partial‐equilibriums in paper [15] and kernel‐based manifold learning techniques in paper [16]. The latter includes quasi‐steady and quasi‐equilibrium in paper [9], hierarchy of coarse grained model in paper [17], distribution state estimation in paper [18] and Rao‐Blackwellised particle filters (RBPFs) in paper [19]. In our work, we focus on linear and non‐linear decompositions by using RBPFs.

In the past, the dynamic model of the non‐linear biochemical reaction is generally based on black‐box framework to estimate the parameters and identify the structures of system. Since there exists large p small n problem (number of unknown parameters p is of much larger than sample size n, p ≫ n) in parameter estimation fields, we take some known parameters and structure of system as priori knowledge and incorporate it into dynamic model. In other words, we estimate the parameters and states in non‐linear biochemical reaction network based on grey‐box framework [20]. As we know, most of biochemical reaction networks are non‐linear and non‐Gaussian, however, in which, linear subsystem are still available. Pseudo‐monomolecular or monomolecular reaction is the simplest reaction described by a set of first‐order reactions. In papers [17, 21, 22], pseudo‐monomolecular or monomolecular reaction subsystems are considered as linear subset network modules, based on which, linear and non‐linear decompositions are easy to be realised. For linear kinetic models, appearing as pseudo‐monomolecular or monomolecular reaction subsystems, we propose to estimate the parameters using conventional Kalman filter algorithm. However, for the remaining non‐linear kinetic models, we develop an algorithm to estimate both states and parameters using the particle filter algorithm. It is known as RBPFs [19, 23–27]. Extended Kalman filter (EKF) [28] and unscented Kalman filter (UKF) [29] are the most widely used joint state and parameter estimation algorithm for the non‐linear state‐space model of biochemical network. In this paper, we will compare the three estimation methods that are RBPF, UKF and EKF in synthetic data generated from repressilator model and experimental data from the JAK‐STAT pathway. The results show that RBPF provides a way to handle high‐dimensional problems and bears very good accuracy with quite reasonable complexity.

2 Non‐linear state‐space models

Consider a general non‐linear dynamic system

$$\begin{array}{rl}{x}_{k+1}^e& =f_k({\mathit{x}}_k^e,{\theta }_k,{\mathit{u}}_k^e)+w_k\\ {\mathit{y}}_k^e& =h_k({\mathit{x}}_k^e,{\theta }_k,{\mathit{u}}_k^e)+v_k,e=1,\dots ,E;k=1,\dots ,T_e\end{array}$$ (1)

where e is the individual and k is the time; ${\mathit{x}}_k^e$ is the state vector of the e individual at a k time; ${\mathit{u}}_k^e$ is the input vector of the e individual at a k time; ${\mathit{y}}_k^e$ is the observation vector of the e individual at a k time; f and h are non‐linear functions, θ is the vector of parameters; The initial state x ₀ is a Gaussian vector with mean $E\left[x_0\right]={\overline{x}}_0$ and covariance matrix $\mathit{E}\left[\left(x_0-{\overline{x}}_0\right){\left(x_0-{\overline{x}}_0\right)}^{\mathrm{T}}\right]=\sum _0$; w and v are vectors of white noises with zero mean and joint covariance matrix

$$\mathit{E}\left[\left(\begin{array}{c}{w}_k\\ v_k\end{array}\right){\left(\begin{array}{cc}{w}_k^{\mathrm{T}}& v_k^{\mathrm{T}}\end{array}\right)}^{\mathrm{T}}\right]=\left[\begin{array}{cc}{Q}_k& 0\\ 0& R_k\end{array}\right]$$

Parameters in a non‐linear dynamic system (1) can be treated as additional states in the system. Thus, the state vector ${\mathit{x}}_k^e$ in (1) is augmented as

$${\xi }_k^e=\left[\begin{array}{c}{\mathit{x}}_k^e\\ \mathit{\theta }\end{array}\right]$$

A state‐space equation treating parameters as states can be written as

$${\xi }_{{}_{k+1}}^e=\left[\begin{array}{c}{x}_{{}_{k+1}}^e\\ {\theta }_k\end{array}\right]=\left[\begin{array}{c}{f}_k({\mathit{x}}_{{}_k}^e,{\theta }_k,{\mathit{u}}_{{}_k}^e)\\ {\theta }_k\end{array}\right]+\left[\begin{array}{c}{w}_k\\ e_k\end{array}\right]=g_k({\xi }_{{}_k}^e,{\mathit{u}}_{{}_k}^e)+{\eta }_k$$

$${\mathit{y}}_{{}_k}^e=h_k({\mathit{x}}_k^e,{\theta }_k,{\mathit{u}}_{{}_k}^e)+v_k==h_k({\xi }_{{}_k}^e,{\mathit{u}}_{{}_k}^e)+v_k$$ (2)

$${\theta }_{k+1}\sim p({\theta }_{k+1}|{\theta }_k)$$

where ${\eta }_k={\left[w_k^{\mathrm{T}},e_k^{\mathrm{T}}\right]}^{\mathrm{T}}$ is a white Gaussian noise with mean zero and covariance matrix

$$\mathit{E}\left[{\eta }_k{\eta }_k^{\mathrm{T}}\right]=\left[\begin{array}{cc}{Q}_k& 0\\ 0& {\mathrm{\Gamma }}_k\end{array}\right]={\phi }_k$$

Supposing a system is divided into two parts: a linear and a non‐linear and the noise is additive, then (2) can be expressed as follows

$$\begin{array}{rl}{x}_{k+1}^{e\mathrm{n}}& =f_k^{\mathrm{n}}(x_k^{e\mathrm{n}},{\theta }_k,{\mathit{u}}_{{}_k}^e)+A_k^{\mathrm{n}}{x}_k^{\mathrm{l}}+B_k^{\mathrm{n}}{\mathit{u}}_{{}_k}^e+w_k^{\mathrm{n}}\\ x_{k+1}^{e\mathrm{l}}& =f_k^{\mathrm{l}}(x_k^{e\mathrm{n}},{\theta }_k,{\mathit{u}}_{{}_k}^e)+A_k^{\mathrm{l}}{x}_k^{e\mathrm{l}}+B_k^{\mathrm{l}}{u}_{{}_k}^e+w_k^{\mathrm{l}}\\ {\mathit{y}}_{{}_k}^e& =h_k(x_k^{e\mathrm{n}},{\theta }_k,{\mathit{u}}_{{}_k}^e)+C{x}_t^{e\mathrm{l}}+D{u}_k^e+e_k\\ {\theta }_{k+1}& \sim p({\theta }_{k+1}|{\theta }_k)\end{array}$$ (3)

where $x_k^{e\mathrm{n}}$ and $x_k^{e\mathrm{l}}$ denote the non‐linear and linear states, respectively, and ${\left[\begin{array}{cc}{x}_k^{e\mathrm{n}}& x_k^{e\mathrm{l}}\end{array}\right]}^{\mathrm{T}}={\mathit{x}}_{{}_k}^e$, ${\omega }_k^{}$ is the process noise given by

$$w_k=\left[\begin{array}{c}{w}_k^{\mathrm{n}}\\ w_k^{\mathrm{l}}\end{array}\right]\sim N\left(0,\left(\begin{array}{cc}{Q}_k^{\mathrm{n}}& {Q^{\ln }}_k\\ {Q^{\ln }}_k^{\mathrm{T}}& Q_k^1\end{array}\right)\right),v_k\sim N(0,R_k)$$

where N(0, σ ²) denotes the normal distribution with 0 as the mean value and σ ² the variance. Moreover, $x_0^{e\mathrm{l}}\sim N({\hat{x}}_{0|-1}^{e\mathrm{l}},P_{0|-1}^{\mathrm{l}})$ and v _k , $x_0^{e\mathrm{n}}$ have arbitrary fixed probability density function (pdf).

Assume

$$p({\theta }_{k+1}|{\theta }_k)=N(a{\theta }_k+(1-a)\ast {\overline{\theta }}_k,h^2{\mathit{V}}_k)$$

where a = ((3δ − 1)/2δ), h ² = 1 − a ², δ is a discount factor (0, 1], typically around $0.95\sim 0.99$.${\overline{\theta }}_k$ is the Monte Carlo mean of the parameters and V _k being the variance matrix of the parameters at time instant k.

We determine the unknown parameter θ by estimating the augmented state ${\xi }_{{}_k}^e$ with $p({\xi }_{{}_k}^e|Y_{{}_k}^e)$; The minimum mean‐squared errors estimation of ${\xi }_{{}_k}^e$ given $Y_{{}_k}^e=\{y_{{}_1}^e,y_{{}_2}^e,\dots ,{\mathit{y}}_{{}_k}^e\}$ is

$$\begin{array}{rl}{\hat{\xi }}_{{}_k}^e& =E[{\xi }_{{}_k}^e|Y_{{}_k}^e]=\int {\xi }_{{}_k}^{e}p({\xi }_{{}_k}^e|Y_{{}_k}^e)\mathrm{d}{\xi }_{{}_k}^e=\int \int ({\mathit{x}}_{{}_k}^e,{\theta }_k)p({\mathit{x}}_{{}_k}^e,{\theta }_k|Y_{{}_k}^e)\mathrm{d}{\mathit{x}}_{{}_k}^e\mathrm{d}{\theta }_k\\ & =\int \int ({\mathit{x}}_{{}_k}^e,{\theta }_k)p({\mathit{x}}_{{}_k}^e|{\theta }_k,Y_{{}_k}^e)p({\theta }_k|Y_{{}_k}^e)\mathrm{d}{\mathit{x}}_{{}_k}^e\mathrm{d}{\theta }_k\\ & =\int \left[\int ({\mathit{x}}_{{}_k}^e,{\theta }_k)p({\mathit{x}}_{{}_k}^e|{\theta }_k,Y_{{}_k}^e)\mathrm{d}{\mathit{x}}_{{}_{\mathit{k}}}^{\mathit{e}}\right]p({\theta }_k|Y_{{}_k}^e)\mathrm{d}{\theta }_k\end{array}$$

$p({\theta }_k|Y_{{}_k}^e)$ is approximated by particle filter, for each given parameter sample, $p({\mathit{x}}_{{}_k}^e|{\theta }_k,Y_{{}_k}^e)$ is given by Kalman filter. This will result in each parameter particle being associated with one Kalman filter recursion.

3 RBPF algorithm for dual estimation

RBPF algorithms for dual estimation is summarised in Fig. 1.

Fig. 1.

RBPF algorithm for dual estimation

The following two applications of the algorithm (see Fig. 1) are from paper [28]; As the length of paper is limited, there is no explanation about the system equation. For detailed explanation, please see paper [28]. As far as signalling pathways, the topological structure of signalling pathways is known. In such case, the most important work is to estimate the parameters of non‐linear models based on Hill or mass action kinetics. The topological structure of network is used as prior knowledge and incorporated into the kinetic models and repressilator model.

4 Kinetic models for JAK2‐STAT5 signalling pathway

System equation [28, 30]

$$\begin{array}{rl}{\dot{x}}_1(t)& =-k_1{x}_1(t)u(t)+2k_4{x}_3(t)I(t\ge \tau )+w_1(t)\\ {\dot{x}}_2(t)& =k_1{x}_1(t)u(t)-k_2{x}_2^2(t)+w_2(t)\\ {\dot{x}}_3(t)& =-k_3{x}_3(t)+0.5k_2{x}_2^2(t)+w_3(t)\\ {\dot{x}}_4(t)& =k_3{x}_3(t)-k_4{x}_3(t)I(t\ge \tau )+w_4(t)\end{array}$$

$$I(t\ge \tau )=⟨\begin{array}{cc}1& t\ge \tau \\ 0& t\prec \tau \end{array}$$

Measurement equation

$$\begin{array}{rl}{y}_1(t)& =x_2(t)+2x_3(t)+e_1(t)\\ y_2(t)& =x_1(t)+x_2(t)+2x_3(t)+e_2(t)\end{array}$$

Model reduction

For decomposing the system and dividing the state variables into linear state variable and non‐linear state variable, let

$$x_t^{\mathrm{n}}=x_2(t)x_t^{\mathrm{l}}=\left[\begin{array}{c}{x}_1(t)\\ x_3(t)\\ x_4(t)\end{array}\right]$$

where $x_t^{\mathrm{l}}$ denotes the state variable with conditional linear dynamics and $x_t^{\mathrm{n}}$ denotes the non‐linear state variable. The system equation can be rewritten as the following

$$\begin{array}{rl}{x}_t^{\mathrm{n}}(t+1)& =(x_t^{\mathrm{n}}(t)-k_2(x_t^{\mathrm{n}}(t)){}^2)+\left[\begin{array}{ccc}{k}_{1}u(t)& 0& 0\end{array}\right]x_t^{\mathrm{l}}+w_t^{\mathrm{n}}\\ x_t^{\mathrm{l}}(t+1)& =\left[\begin{array}{c}0\\ 0.5k_2{(x_t^{\mathrm{n}}(t))}^2\\ 0\end{array}\right]+\left[\begin{array}{ccc}1-k_{1}u(t)& 2k_{4}I(t\ge \tau )& 0\\ 0& 1-k_3& 0\\ 0& k_3-k_{4}I(t\ge \tau )& 1\end{array}\right]+x_t^{\mathrm{l}}(t)+w_t^{\mathrm{l}}\end{array}$$

where

$$f_t^{\mathrm{n}}=(x_t^{\mathrm{n}}(t)-k_2(x_t^{\mathrm{n}}(t)){}^2),A_t^{\mathrm{n}}=\left[\begin{array}{ccc}{k}_{1}u(t)& 0& 0\end{array}\right],w_t^{\mathrm{n}}=w_2(t)$$

$$f_t^{\mathrm{l}}=\left[\begin{array}{c}0\\ 0.5k_2{(x_t^{\mathrm{n}}(t))}^2\\ 0\end{array}\right],A_t^{\mathrm{l}}=\left[\begin{array}{ccc}1-k_{1}u(t)& 2k_{4}I(t\ge \tau )& 0\\ 0& 1-k_3& 0\\ 0& k_3-k_{4}I(t\ge \tau )& 1\end{array}\right],w_t^{\mathrm{l}}=\left[\begin{array}{c}{w}_1(t)\\ w_3(t)\\ w_4(t)\end{array}\right]$$

The measurement equation can be rewritten as the following

$$\left[\begin{array}{c}{y}_1(t)\\ y_2(t)\end{array}\right]=\left[\begin{array}{c}1\\ 1\end{array}\right]x_t^{\mathrm{n}}(t)+\left[\begin{array}{ccc}0& 2& 0\\ 1& 2& 0\end{array}\right]x_t^{\mathrm{l}}(t)+e$$

where

$$ht=\left[\begin{array}{c}1\\ 1\end{array}\right]x_t^{\mathrm{n}}(t),C=\left[\begin{array}{ccc}0& 2& 0\\ 1& 2& 0\end{array}\right],e=\left[\begin{array}{c}{e}_1(t)\\ e_2(t)\end{array}\right]$$

5 Repressilator

System and measurement equation [31]

$$\begin{array}{rl}\frac{\mathrm{d}{R}_1}{\mathrm{d}t}& =\frac{V_{1\max }{K}_{12}^{\mathrm{n}}}{K_{12}^{\mathrm{n}}+P_2^{\mathrm{n}}}-k_{1m}{R}_1+w_1\\ \frac{\mathrm{d}{R}_2}{\mathrm{d}t}& =\frac{V_{2\max }{K}_{23}^{\mathrm{n}}}{K_{23}^{\mathrm{n}}+P_3^{\mathrm{n}}}-k_{2m}{R}_2+w_2\\ \frac{\mathrm{d}{R}_3}{\mathrm{d}t}& =\frac{V_{3\max }{K}_{31}^{\mathrm{n}}}{K_{31}^{\mathrm{n}}+P_1^{\mathrm{n}}}-k_{3m}{R}_3+w_3\\ \frac{\mathrm{d}{P}_1}{\mathrm{d}t}& =k_1{R}_1-k_{1p}{P}_1+w_4\\ \frac{\mathrm{d}{P}_2}{\mathrm{d}t}& =k_2{R}_2-k_{2p}{P}_2+w_5\\ \frac{\mathrm{d}{P}_3}{\mathrm{d}t}& =k_3{R}_3-k_{3p}{P}_3+w_6\end{array}$$

$$\begin{array}{rl}{y}_1(t)& =R_1(t)+e_1\\ y_2(t)& =R_2(t)+e_2\\ y_3(t)& =R_3(t)+e_3\\ y_4(t)& =P_1(t)+e_4\\ y_5(t)& =P_2(t)+e_5\\ y_6(t)& =P_3(t)+e_6\end{array}$$

where R _i is the concentration of mRNA transcript from gene i and P _i is the concentration of proteins translated from R _i . Estimated parameters: V _1max, V _2max, V _3max, k ₁₂, k ₂₃, k ₃₁.

Model reduction

For decomposing the system and dividing the state variables into linear state variable and non‐linear state variable, let

$$x_t^{\mathrm{n}}(t)=\left[\begin{array}{c}{p}_1(t)\\ p_2(t)\\ p_3(t)\end{array}\right],x_t^{\mathrm{l}}(t)=\left[\begin{array}{c}{R}_1(t)\\ R_2(t)\\ R_3(t)\end{array}\right]$$

where $x_t^{\mathrm{l}}$ denotes the state variable with conditional linear dynamics and $x_t^{\mathrm{n}}$ denotes the non‐linear state variable. Then, the system equation can be rewritten as the following

$$x_t^{\mathrm{l}}(t+1)=f_t^{\mathrm{l}}(x_t^{\mathrm{n}})=\left[\begin{array}{c}\frac{V_{1\max }{k}_{12}^3}{k_{12}^3+p_2^3(t)}\\ \frac{V_{2\max }{k}_{23}^3}{k_{23}^3+p_3^3(t)}\\ \frac{V_{3\max }{k}_{31}^3}{k_{31}^3+p_1^3(t)}\end{array}\right]+w_t^{\mathrm{l}},x_t^{\mathrm{n}}(t+1)=A_t^{\mathrm{n}}{x}_t^{\mathrm{l}}=\left[\begin{array}{ccc}1& 0& 0\\ 0& 2& 0\\ 0& 0& 3\end{array}\right]x_t^{\mathrm{l}}+w_t^{\mathrm{n}}$$

where

$$\begin{array}{rl}{f}_t^{\mathrm{l}}(x_t^{\mathrm{n}})& =\left[\begin{array}{c}\frac{V_{1\max }{k}_{12}^3}{k_{12}^3+p_2^3(t)}\\ \frac{V_{2\max }{k}_{23}^3}{k_{23}^3+p_3^3(t)}\\ \frac{V_{3\max }{k}_{31}^3}{k_{31}^3+p_1^3(t)}\end{array}\right],A_t^{\mathrm{l}}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right],A_t^{\mathrm{n}}=\left[\begin{array}{ccc}1& 0& 0\\ 0& 2& 0\\ 0& 0& 3\end{array}\right]\\ f_t^{\mathrm{n}}(x_t^{\mathrm{n}})& =0,w_t^{\mathrm{n}}=\left[\begin{array}{c}{w}_4\\ w_5\\ w_6\end{array}\right],w_t^{\mathrm{l}}=\left[\begin{array}{c}{w}_1\\ w_2\\ w_3\end{array}\right]\end{array}$$

The measurement equation can be rewritten as the following

$$\left[\begin{array}{c}{y}_1(t)\\ y_2(t)\\ y_3(t)\\ y_4(t)\\ y_5(t)\\ y_6(t)\end{array}\right]=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]x_t^{\mathrm{n}}+\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]x_t^{\mathrm{l}}+e$$

where

$$h_t(x_t^{\mathrm{n}})=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right],C=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right],e=\left[\begin{array}{c}{e}_1\\ e_2\\ e_3\\ e_4\\ e_5\\ e_6\end{array}\right]$$

6 Results

6.1 JAK‐STAT pathway

The initial values of the linear state variables of every particle are assumed as: $x_1^0=0.5,x_2^0=0,x_3^0=0$ and $x_4^0=0$. The initial values of the non‐linear state variables of every particle are random number between 0 and 1. The initial values of parameters k ₁, k ₂, k ₃ and k ₄ are random number generated from the following intervals k ₁ ∈ (−0.299, 0.421), k ₂ ∈ (2.16, 2.76), k ₃ ∈ (−0.2534, 0.3466) and k ₄ ∈ (−0.14342, 0.30658). The estimates by the RBPF, the EKF and maximum likelihood (ML) method [32] are close, but significantly different from the estimates by UKF [29] as shown in Table 1. Under the given above initial values, using the concentration of EpoR_A as input, Fig. 2 plot the predicted and observed concentrations of tyrosine phosphorylated STAT5 in the cytoplasm and total STAT5 in the cytoplasm (y ₁ and y ₂) by the RBPF method, the EKF method and the UKF method. The observed data were from experiment data 1. The results of experiment data 2–4 and the estimated parameters were listed in additional files AFigures 1, 2–3 and ATable 1.

Table 1.

Comparison of estimated parameters in the non‐linear state‐space model for the JAK‐STAT pathway using RBPF, EKF, ML approach and UKF

Study	k 1	k 2	k 3	k 4	τ
RBPF (our study)	0.022916	2.343347	0.117178	0.102687	6.1
EKF	0.0211	2.2788	0.1064	0.1057	6 min
ML	0.0210	2.4600	0.1066	0.1066	6.4 min
UKF	0.0515		3.3900	0.3500

Fig. 2.

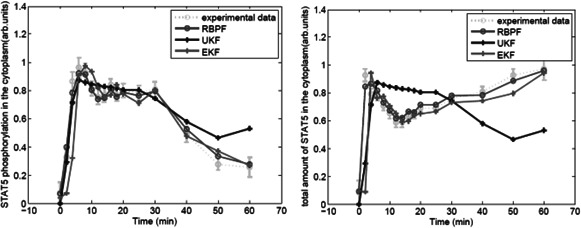
Predicted and observed concentrations of tyrosine phosphorylated STAT5 and total STAT5 in the cytoplasm for experiment 1

Fig. 3.

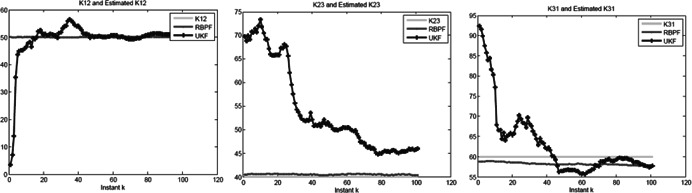
Estimated parameters of K₁₂, K₂₃ and K₃₁ as a function of the time in the non‐linear state‐space model for the synthetic data generated from the repressilator model

6.2 Synthetic data generated from repressilator model

Let k _1m = 1, k _2m = 1, k _3m = 1, k _1p = 1, k _2p = 1, k _3p = 1, K ₁ = 1, K ₂ = 2, K ₃ = 3, n = 3 and V _1max = 150, V _2max = 80, V _3max = 100, K ₁₂ = 50, K ₂₃ = 40, K ₃₁ = 60, the initial values of linear and non‐linear state variables are random numbers between 0 and 1. The initial values of parameters are random number generated from the following intervals: V _1max ∈ (140, 160), V _2max ∈ (70, 90), V _3max ∈ (90, 110), K ₁₂ ∈ (40, 60), K ₂₃ ∈ (20, 40), K ₃₁ ∈ (30, 50). The estimated parameters as a function of time k are shown in Figs. 3 and 4. From Figs. 3 and 4, we can see that at the beginning the estimated parameters quickly converge to the true parameters. This example demonstrates that although the parameters are treated as the states of the systems and hence may change over time, they can reach stable values. The estimated parameters over time k are summarised in ATable 2 in additional files, which demonstrated that the estimates of the parameters were very close to set the value of parameters. In this example, EKF does not converge, high non‐linearity of the repressilator model makes EKF a failure to converge to an optimum. Therefore, we only compare the two methods of RBPF and UKF.

Fig. 4.

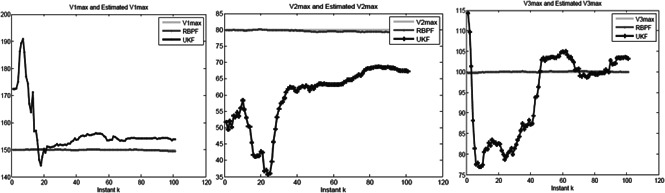
Estimated parameters of V_1max, V_2max and V_3max as a function of the time in the non‐linear state‐space model for the synthetic data generated from the repressilator model

7 Conclusions

To evaluate the performance of our new methods, we have applied it to both synthetic data generated from repressilator model and experimental data of the JAK‐STAT pathway [31, 32]. The structure of both the above examples is known in modelling literature [29, 33]. Therefore, we use structure information and partly known parameters as priori knowledge and then conduct the identification of biochemical reaction networks based on grey box [34–37]. We consider the pseudo‐monomolecular or monomolecular reaction subsystems as linear subset network modules, then the whole dynamic model are decomposed into linear and non‐linear subset modules dynamic model. For linear subset modules dynamic model, we use Kalman filter algorithm to estimate both states and parameters, however, for non‐linear subset modules dynamic model, we adopt the particle filter algorithm to estimate both states and parameters. This model reduction technique is called RBPF. The results show that RBPF method perform well as a new model reduction techniques for high dimension non‐linear dynamic model. As future work, we will apply our algorithms to a high‐dimensional biochemical network in order to improve and validate it.