Whispering gallery mode sensors

Abstract

We present a comprehensive overview of sensor technology exploiting optical whispering gallery mode (WGM) resonances. After a short introduction we begin by detailing the fundamental principles and theory of WGMs in optical microcavities and the transduction mechanisms frequently employed for sensing purposes. Key recent theoretical contributions to the modeling and analysis of WGM systems are highlighted. Subsequently we review the state of the art of WGM sensors by outlining efforts made to date to improve current detection limits. Proposals in this vein are numerous and range, for example, from plasmonic enhancements and active cavities to hybrid optomechanical sensors, which are already working in the shot noise limited regime. In parallel to furthering WGM sensitivity, efforts to improve the time resolution are beginning to emerge. We therefore summarize the techniques being pursued in this vein. Ultimately WGM sensors aim for real-world applications, such as measurements of force and temperature, or alternatively gas and biosensing. Each such application is thus reviewed in turn, and important achievements are discussed. Finally, we adopt a more forward-looking perspective and discuss the outlook of WGM sensors within both a physical and biological context and consider how they may yet push the detection envelope further.

1. Introduction

Sensors are tools for acquiring quantitative information about our surroundings, for example, on the type and concentration of molecules in air or liquid, similar to what is accomplished continuously by our nose and tastebuds. The response of any given sensor device depends on the physical nature of the transducer at hand, with micro- and nano-scale transducers having shown particularly impressive utility and sensitivity in recent years. Such nanotechnology enabled devices often require fabrication tools that have emerged only recently, and therefore these sensors are experiencing a surge in interest and application. One flourishing field of application is that of biomedicine and clinical diagnostics where ideally single molecule sensitivity is sought with a high degree of specificity [1–11]. It also comes as no surprise that physical sensing tasks requiring the quantitative detection of parameters such as pressure, temperature, force, and mass are also increasingly exploiting the opportunities afforded by microand nano-scale sensors [12–19].

Optical micro-sensors, i.e., systems utilizing light, have particularly become a cornerstone technology in modern society, the ubiquity of which can primarily be attributed to their speed, flexibility, and low cost and the wealth of supporting optical technology such as photodiodes, optical fibers, and light sources. The wave nature of light implies that when light is confined in a dielectric microstructure and brought to interfere with itself, only specific optical frequencies can be supported and reside within the cavity without suffering large losses. Resonant microcavities utilizing this principle represent an indispensable route to realizing the next generation of high-performance optical sensors. If the microcavity geometry or material properties change, for example, by deforming or heating the cavity, a change in resonance parameters can be detected, for example, by monitoring changes in light intensity. The microcavity thereby acts as an optical signal transducer. Depending on the material and geometry of the microcavity used to confine the light, optical resonators can be used for a multitude of detection tasks; for instance, microcavities coated with molecular receptors can respond to biomolecules, microcavities modified with magnetorestrictive materials can find use as magnetometers, and microcavities in a rotating frame of reference can be used as gyroscopes.

One specific class of resonant optical sensors, namely those based on microcavities supporting whispering gallery modes (WGMs), has attracted a significant level of interest recently since it affords an extreme level of sensitivity. A longstanding goal for biomedical detectors, environmental monitors, and biosensors in the life sciences has been the ability to detect single molecules and their interactions. Exactly this has now been achieved with optical microcavities that use WGMs [4]. The extreme sensitivity of WGM sensors has not only lead to a breakthrough in biodetection, but has also enabled sensitive probing of physical phenomena, such as the recent readout of the quantum ground state of a micromechanical oscillator via optomechanical coupling [20]. A multitude of other sensor applications are also under active research and development, in which different sensor geometries, materials, surface modifications, and device integration strategies are being explored. In this work we therefore undertake a comprehensive review of the current state of the art of both physical and biological WGM sensors. WGM sensing is now a relatively advanced field, supporting many subdisciplines. As such we depart from the more traditional historical perspective in our review, and instead aim to provide a more scholarly review of the physical aspects of the different WGM sensing modalities, give an overview of the parameters that control and limit the sensor response, and, ultimately, provide our opinion on the future outlook of the many exciting applications for WGM sensors in biology, chemistry, and physics. Given the extensive literature on WGMs, a number of good reviews can already be found, for example, in [21–32]. Throughout this review, we therefore place a greater emphasis on more recent contributions and advances in the field, although we naturally endeavour to reference more seminal works where appropriate. As per the research interests of the authors, greater emphasis is also placed on biosensing applications. Similarly, we have elected to omit some related subdisciplines entirely, for example, those of liquid cavities or far-field scattering based sensing. The structure of this review is thus as follows. We begin with an introductory discussion of WGM resonators in Subsection 2.1 and the fundamental linear properties of WGMs (Subsection 2.2), which can serve as a sensing signal (Subsection 2.3). Following a short analysis of detection limits in WGM sensing systems, we outline a number of important recent works that have aimed to advance these sensitivity constraints in Subsection 3.1. Techniques to improve the time resolution of WGM sensors are detailed in Subsection 3.2. Subsection 3.3 contains an extensive review of specific WGM sensor applications, including temperature, pressure, force, electromagnetic field, gas, and biosensing. Finally, in Subsections 4.1 and 4.2 we consider the outlook of biosensing in which specific detection of a given analyte molecule is frequently sought, in addition to sensing of physical variables, such as force and temperature.

2. Theory of Whispering Gallery Mode Sensing

2.1. Whispering Gallery Mode Resonators

Resonant phenomena in cavities, be they acoustic, optical, mechanical, or otherwise, are frequently dependent on the precise geometric properties, such as size, shape, and composition, of the supporting structure. Accordingly, such resonances are often termed morphology-dependent resonances (MDRs). Arguably, one of the most famous examples of MDRs, in the acoustic domain at least, is that of WGMs. First explained by John William Strutt, better known as Lord Rayleigh [33,34], these modes comprise a traveling pressure wave guided around a closed concave surface, such as the whispering gallery in St. Paul’s Cathedral (see Fig. 1). From a geometric perspective, such bound modes are guided by means of repeated reflections, which, neglecting absorption, scattering, and material dispersion, continue ad infinitum. Within a wave description, however, losses through the surface are present via tunneling or frustration [35], such that the mode, in the absence of an external excitation, experiences a decay in its amplitude, i.e., a finite lifetime. While the terms MDR and WGM are frequently used interchangeably, WGMs, in actuality, represent a subclass of MDRs characterized by their high quality (Q) factors (i.e., low losses) and surface mode nature.

Figure 1.

WGMs supported upon total internal reflection of either an acoustic (left) or an optical (right) wave. Adapted from [36].

Carrying the acoustic nomenclature over to the optical domain, WGMs can also occur in optical cavities possessing a closed concave interface (Fig. 1). Spherical, disc, and ring cavities represent the simplest resonator geometry and have thus seen much attention in the literature over the years. Even as a relatively mature platform technology, these resonators still garner considerable research toward further applications, improved fabrication, and theoretical considerations. Although many such examples will be given throughout this review, the reader is also referred to recent reviews for further details [21,24,26, 30,36,37]. A plethora of alternative geometries, such as toroidal, tubular (including capillary and bottleneck resonators), and microbubble resonators, also exist, each with their own set of relative merits [27,31,32,38–41]. Recently, however, several theoretical and experimental advances have been made regarding less common topographies. Reflow smoothing, which is commonly employed in the fabrication of toroidal resonators to reduce scattering losses from defects and etching artifacts [42], poses a number of challenges with regard to the fabrication of large resonators, as is desirable in WGM-based frequency comb generation and gyroscopes [43,44]. Wedge geometries were therefore proposed as one means to overcome such limitations, since they allow the mode to be pushed away from the scattering surfaces when shallow wedge angles are used [45]. More recently, however, a modified process has been demonstrated allowing resonators of greater size, possessing larger wedge angles and exhibiting Q factors of 10⁹, to be made [46]. Goblet, or conical, polymer resonators are also emerging as a novel WGM resonator geometry, which lends itself to cheap and large-scale fabrication [47,48] and multiplexed functionalization [49]. Flexible coupling between goblet resonators has also been demonstrated [50] allowing potential utility in applications requiring mode tunability [51] (see also below). More exotically, WGM characteristics in hexagonal resonators with varying corner curvature have been studied [52]. Polygonal shapes are of interest, particularly when crystalline resonators are used, since production of small crystalline resonators via laser heated pedestal growth [53] is potentially easier and more robust than the diamond cutting and slurry polishing techniques used to date, due to the underlying crystal structure. In this study larger corner curvatures were found to yield better Q factors and to facilitate mode excitation. Asymmetric and deformed resonators, such as limaçons and deformed toroids, have also been considered by a number of researchers with a view toward manipulating the coupling efficiency to WGMs, or conversely, the associated emission patterns [54–57] for laser applications.

Principally, the existence of WGMs in optical cavities relies on total internal reflection at the external cavity interface (see Fig. 1). Larger refractive index contrasts between the cavity and the host therefore help to minimize radiative losses via stronger confinement of the WGMs, and thus improve the obtainable Q factors. Conversely, a low refractive index contrast facilitates extension of the mode profile beyond the confines of the resonator medium into the sensing domain, thus potentially increasing sensor sensitivity. Material losses, such as absorption and surface scattering, however, also play a key role in determining mode linewidth (see below). The choice of resonator material is hence also a crucial factor in sensor design, motivating the search for novel materials as a means to improve sensor performance and cost. Recent developments in this context for sensing purposes include the use of titanium dioxide (TiO₂) [58], silicon nitride (Si₂N₃) [59], silicon carbide (SiC) [60], hydrogenated amorphous silicon [61], poly(methyl methacrylate) (PMMA) [47], polydimethylsiloxane (PDMS) [62], magnesium fluoride (MgF₂) [63,64], sapphire [65,66], and liquid (paraffin oil) droplets [67,68]. Composite resonators, such as coated spheres, and hybrid metallo-dielectric resonators, have also recently been investigated as a route to improving sensor robustness and signal enhancement, e.g., [69–72]. Full discussion of resonator geometries and material choices is beyond the scope of this review; however, further details can be found in, e.g., [23,27,29].

2.2. Properties and Modeling of Whispering Gallery Modes

A fundamental understanding of WGMs is a prerequisite of good sensor design and development. Significant volumes of literature can be found detailing the fine aspects of WGM theory (see, e.g., [23,37,73] and references therein), such that here we elect to give only a brief overview of the key linear properties of WGMs, which are relevant to WGM sensors. A number of important theoretical and modeling advances made in the last few years will also be discussed. While WGMs possess a number of nonlinear properties, such as thermal and Kerr nonlinearities [69,74–76], these will not be discussed here.

Spectrally, the power stored in a WGM, P(ω), exhibits a Lorentzian lineshape defined by

$$P(\omega )=P_0\frac{{({\gamma }_0/2)}^2}{{(\omega -{\omega }_0)}^2+{({\gamma }_0/2)}^2}.$$ (1)

The principal parameters describing the WGM resonance are therefore its resonance frequency ω₀, full-width at half maximum (FWHM) γ₀, and amplitude P₀. Commonly, the quality factor Q₀ = ω₀/γ₀ is also used to characterize a resonance and physically represents the rate of energy loss relative to the total stored energy. Direct observation of P(ω) is generally not feasible since the energy is trapped within the cavity. Instead, excitation of WGMs must be experimentally inferred through indirect means. One common strategy is that of monitoring the excitation channel. For example, evanescent coupling to WGMs can be achieved by bringing an adiabatically tapered optical fiber close to the resonator surface [77–80]. By monitoring the transmitted power P_t(ω), of the excitation light launched into the fiber as the frequency of incident light is tuned, a characteristic Lorentzian resonance dip can be observed (see Fig. 2). The depth of the observed transmission dip is then dependent on the achievable coupling efficiency, β, such that P_t(ω) = P₀ − βP(ω), where now P₀ represents the input laser power. Similarly, free space [81–84] or prism-coupling strategies [4,77,85,86], in which WGMs are excited either through an incident propagating beam or evanescently through total internal reflection of light from a prism, can be used. In these approaches, the transmitted and reflected powers are monitored. A discussion of the relative advantages of these, and other [87–90], coupling schemes can be found in, for example, [22,23]. Alternatively, excitation of WGMs can be seen in the emission spectra of fluorescent molecules that are either embedded in or coated on the resonator. In this case, due to the increase in the local density of states, the fluorescence is enhanced for frequencies lying spectrally close to WGMs yielding a strong fluorescence enhancement [91–93].

Figure 2.

(Left) Schematic of WGM transmission lineshape before (blue) and after (red) a resonance shift and associated broadening. (Right) Schematic of transmission lineshape before (blue) and after mode splitting induced by a single (green) or multiple (red) perturbing particles.

Multiple loss channels, such as radiation, surface scattering, bulk scattering, and material absorption, can all contribute to the total resonance linewidth [94–97]. Accordingly the FWHM of the WGM resonance can be written in the form γ₀ = γ_rad + γ_sca + γ_mat + …, or equivalently $Q_0^{-1}=Q_{\text{rad}}^{-1}+Q_{\text{sca}}^{-1}+Q_{\text{mat}}^{-1}+\cdots$. The relative dominance of each contribution depends not only on the intrinsic material properties and fabrication quality, but also on the resonator size.

Specifically, for small resonators radiative losses dominate, while as the resonator size increases absorption losses in the host medium play a more prevalent role. As the size increases even further the WGM becomes more confined within the cavity such that the material properties of the cavity govern the final, ultimate, material limited Q, given by Q_abs = 2πn_r/(αλ₀), where n_r is the refractive index of the resonator, with associated absorption coefficient α [95].

Any given WGM resonator, however, can support multiple WGMs of differing order. The precise spectrum of a WGM resonator, as discussed above, is dictated by the geometry and composition of the resonator. Given the multitude of structures supporting WGMs a general analytic solution describing the modal structure, regrettably, does not exist, and must instead be found by numerical or experimental means. Several experimental methods for mode identification have been proposed, including far-field imaging [85,98,99], near-field probing [100,101], and spectroscopy [102,103] based techniques. Nevertheless, for resonators possessing a high degree of symmetry, a number of (approximate) analytic methods exist [39,104–111]. Resonators possessing cylindrical or spherical symmetries are particularly amenable to exact analytic treatment, and shall be used here as a vehicle to introduce a number of concepts. In particular the seminal works of Mie and Debye [112,113] provided a fully rigorous solution for scattering of light from spherical particles, based upon application of Maxwell’s electromagnetic boundary conditions. Resonances of a spherical resonator can then be found by determination of the roots of the denominators of the scattering coefficients, i.e., by solution of the transcendental equation

$$\frac{[n_{h}x{y}_l(n_{h}x)]\prime }{y_l(n_{h}x)}=N\frac{[n_{r}x{j}_l(n_{r}x)]\prime }{j_l(n_{r}x)},$$ (2)

where j_l(x) and y_l(x) are the spherical Bessel functions of the first and second kind, x = n_hω₀R/c is known as the size parameter, n_r (n_h) is the refractive index of the resonator (host medium), c is the speed of light, N is a constant defined below, and R is the resonator radius. Families of modes naturally emerge from the solution of Eq. (2), which are indexed by three mode indices. Azimuthal and radial sets of modes are identified by the mode indices m and s, respectively, while the index l = −|m|, −|m| + 1, …, |m| denotes the polar order of the modes (see Fig. 3). Mode indices are fully analogous to the principal and angular momentum quantum numbers used in atomic optics to parameterize energy eigenstates and can thus also be treated using an effective potential (see Fig. 3) [35]. WGMs correspond to modes of low radial order s = 1, 2, 3, … and large azimuthal and polar order ~nx, where n = n_r/n_h. From the geometric optics point of view, modes of order ~nx correspond to near glancing rays incident upon the interior surface of the resonator, which hence undergo total internal reflection [106]. In addition to the mode indices described above, a further distinction between WGMs can be made on the basis of their polarization. Two distinct polarizations can be supported in an isotropic resonator, namely transverse electric (TE) (N = 1) and transverse magnetic (TM) polarized modes $(N=n_h^2/n_r^2)$, for which the electric- and magnetic-field vectors lie tangential to the resonator surface. The polarization structure for anisotropic resonators, e.g., crystalline resonators possessing birefringence, can, however, become quite complex [114]. Fortunately, optical anisotropies in typical resonator materials are weak, such that to a good approximation WGMs can be regarded as either TE or TM polarized.

Figure 3.

(Top) Iso-intensity surfaces and intensity cross sections (inset) for (left) fundamental TE mode l = m, (middle) second-order radial mode s = 2, and (right) azimuthal mode m = l − 2 in a spherical resonator. (Bottom) Effective potentials and radial wave functions for the same WGMs as in the top row.

Importantly, each WGM occurs at a discrete frequency and, generally, with a different linewidth. Knowledge of these resonant properties is important in, for instance, mode identification, and numerical analysis and is therefore often sought. For example, in sensing applications, knowledge of the spatial overlap of the WGM profile (as follows from the mode index) with a refractive index perturbation, e.g., from an adsorbed particle, can provide useful information in further quantitative analysis [27,115]. An exact analytic solution of Eq. (2) (or its analog in cylindrical or other highly symmetric systems) is generally not possible, such that resonance frequencies must be sought either numerically or by means of analytical approximations. For example, the asymptotic expansions of Lam et al. [106] and their higher-order counterparts [108] utilize an analytic approximation of the Bessel functions [116] to give a closed-form expression describing the (approximate) positions and radiative linewidths of WGMs in spherical resonators. In particular the Lam approximation states that WGMs occur at frequencies ω₀ satisfy

$$nx\approx \nu +\frac{{\alpha }_s{\nu }^{1/3}}{2^{1/3}}-\frac{P}{{(n^2-1)}^{1/2}}+\frac{3}{10}\frac{{\alpha }_s^2}{2^{2/3}{\nu }^{1/3}}-\frac{P(n^2-2P/3)}{{(n^2-1)}^{3/2}}\frac{{\alpha }_s}{2^{1/3}{\nu }^{2/3}}+\cdots ,$$ (3)

where ν = l + 1/2, α_s are the roots of the Airy function Ai(−z) = 0, and P = n or = 1/n for TE and TM modes, respectively. Expressions for the contribution to the resonance linewidth from radiative losses, γ_rad, are also given. Uniform approximations for the eigenfrequencies for a spherical geometry, which provide greater accuracy, have also been reported [117], albeit being more difficult to implement. Equation (3) provides some key insights into WGMs. The physical dependencies of the resonance frequency can, for example, be identified, namely the refractive index of both the resonator and its environment and the resonator size. Indeed, to first order Eq. (3) reads 2πn_rR ≈ lλ₀, where λ₀ is the corresponding wavelength of the WGM, which can be recognized as the condition for constructive interference of the wave upon a round trip around the resonator circumference. In adopting such a coarse approximation, however, the dependency of the WGM resonance frequency on the refractive index of the surrounding environment is lost, such that it is unsuitable for describing many sensing scenarios. Nevertheless, this approximation can prove convenient in predicting a number of optical properties of the resonator. For example, the free spectral range (FSR) of the WGM resonator (that is to say the frequency difference between a mode l and its neighboring mode l + 1) and the resonator finesse follow as FSR = c/(2πnR) and ℱ = Qc/(ω₀nR), respectively.

Going beyond spherical geometries, eikonal, i.e., quasi-geometric, techniques have been proposed as an accurate means of predicting the eigenfrequencies of axially symmetric resonator geometries [96,118]. More recently, however, approximate expressions for the resonance frequencies of spheroidal, so-called quartic, and toroidal resonators, based on Wentzel–Kramers–Brillouin and Einstein–Brillouin–Keller approximations, have been put forward [119]. Moreover, the authors present equations for calculation of the geometric dispersion in these resonator geometries in addition to approximate expressions for the mode distributions. Novel analytic results for large axisymmetric optical resonators have also recently been derived by use of a local curvilinear coordinate system and invoking the strong confinement of fundamental l = |m| WGMs to the equatorial plane of the resonator [111].

Despite the utility of analytic equations, their realm of validity is limited. Recourse must therefore be frequently made to numerical methods, such as the boundary and finite element methods (BEM and FEM, respectively) [120–124], for more irregularly shaped cavities. These techniques are long established, yet improvements are ongoing. Recently, for example, in the case of the BEM, an improved resonance finding algorithm has been proposed, exploiting analytic insight into the behavior of eigenvalues of a generalized problem [125]. The proposed technique, in addition to providing faster convergence, helps avoid spurious, i.e., nonphysical, solutions. FEM-based approaches, however, are also prominent in the literature. Recent innovations in this area have been made by Lu and colleagues. In particular, these authors have developed a fully vectorial mode solver [126] based upon extension of the mode-matching method commonly used in modeling straight discontinuous waveguides or junctions. The simulation volume is discretized into piecewise “slices,” each with its own set of orthonormal modes. By projecting the modes in each slice onto the neighboring segment, the solver is capable of propagating WGMs around large three-dimensional resonators also allowing for possible perturbations from bound particles. The same authors later extended their solver to allow for multimode coupling such that waveguide coupling can also be accommodated [127]. These solvers are also capable of determining the resonance frequency and quality factor by means of arithmetic averages over each simulation slice. Similarly, the work of Yu et al. considers the projection of WGMs onto a superposition of straight waveguide modes [128]; however, in this case quality factors follow by use of a perfectly matched layer (PML), as was recently detailed by Cheema and Kirk [129]. Localized perturbations to WGMs in toroidal [130] and spherical [4] resonators can also be considered (assuming the mode “heals” quickly in space) by means of artificial boundary conditions placed on a small segment of the entire simulation volume that act to mimic the underlying symmetries inherent in WGMs. The increasing flexibility and efficiency of FEM simulations of WGM resonators are in turn allowing for their use for optimization of the resonator geometry, e.g., [129,131,132], or the study of coupled and hybrid systems [52,70,72,133,134].

FEM methods, in general, can suffer from stability problems arising from matrix inversion, an issue that does not arise when using the finite-difference time-domain (FDTD) method. Since the FDTD method is inherently a time domain calculation, simulation of WGMs possessing long lifetimes can be computationally expensive; nevertheless, finite difference modeling of WGMs has attracted some attention. For example, Shirazi et al. have used a two-dimensional finite difference beam propagation method for the study of perturbations of WGMs in a cylindrical system [135], again capable of extracting all key WGM parameters, while Kekatpure has adopted a first principles approach to the solution of Maxwell’s equations to allow resonance frequencies and mode profiles to be accurately determined [136].

2.3. Sensing Mechanisms

Universally, the operational principle in WGM sensors is to monitor changes in the WGM spectral properties prompted by some physical change in the system. From an application point of view, such changes could arise from temperature variations, pressure waves, and the acceleration or introduction of gas or biomolecules, to name but a few possibilities. In light of Eq. (1) sensing principally follows via induced changes in the resonance frequency δω or linewidth, δγ. Further possibilities arise in sensors exploiting multiple WGMs or resonance parameters. We discuss each in turn in what follows.

2.3a. Frequency Shifts

Shifts in resonance frequency occur when the refractive index of the host medium varies. Additionally, shifts are induced by changes in the resonator refractive index and size. Indeed it has been shown that [137]

$$\frac{\mathrm{\Delta }\lambda }{{\lambda }_0}=\frac{\mathrm{\Delta }{n}_h}{n_h}F+\frac{\mathrm{\Delta }{n}_r}{n_r}(1-F)+\frac{\mathrm{\Delta }R}{R},$$ (4)

where F is a sensitivity function related to the phase acquired upon reflection at the resonator surface. Substantially, sensors based on monitoring resonance frequencies over time rely on the first of these possibilities. Refractometers, for example, directly aim to monitor changes in the bulk refractive index of the host environment [see Fig. 4(a)]. It follows from Eq. (3) that the sensitivity of the resonance frequency to bulk refractive index changes is [19]

$$\frac{\partial x}{\partial n_h}=-\frac{n_h}{{(n_r^2-n_h^2)}^{3/2}}[1-\frac{{\alpha }_s}{2^{1/3}}\frac{n_r^2}{n_r^2-n_h^2}{\nu }^{-2/3}]$$ (5)

for TE modes [see Fig. 4(b)]. A similar expression also holds for TM modes but is not given here for brevity. Two design rules immediately follow from Eq. (5), chiefly that greater sensitivity is found in smaller resonators and for lower refractive index contrast. Physically, this behavior is a result of the WGM’s evanescent tail extending further into the host medium, thereby increasing the relative importance of the host medium in determining the effective refractive index seen by the WGM. While it is noted that Eq. (5) does not account for all factors limiting the refractive index sensitivity (see [92,138,139] for an in-depth discussion on this topic), refractometer design nevertheless often strives to improve either, or both, of these factors. For example, much effort is made to increase the mode overlap with the sample. One popular method for this is by use of hollow core resonators [31]. In this vein a microbubble resonator was recently demonstrated, and a refractive index sensitivity of 0.5 nm per refractive index unit (RIU) was reported. Fluorescence-based systems [93,140] are also of interest. Theoretical efforts have also considered the use of graded refractive index profiles, to increase the mode penetration into the hollow core even further [141]. Variation of the refractive index contrast as a means to augment refractive index sensitivity necessitates appropriate choice of the resonator material. Crystalline MgF₂ disc resonators, with refractive index ~1.38, have recently been shown to give a sensitivity of 1.09 nm/RIU in aqueous environments by virtue of the long evanescent decay length of the WGM [64,142]. Comparable sensitivities have also been achieved using an integrated sapphire resonator [143]; however, sensitivities of 30, 570, and 700 nm/RIU have been reported in a microsphere resonator [19], a capillary-based optofluidic ring resonator [144,145], and a nanowire loop resonator [146], respectively. Alternatively, use of hybrid systems exploiting plasmonic properties of metallic structures is a means by which the field intensity can be locally increased in the sensing domain. This strategy was pursued by Hu et al. [71], who coupled a silicon disc resonator to a silver microdisk. While the Q factor of the hybrid resonance was degraded to ~2000 due to losses in the metallic microdisk, a sensitivity of 200 nm/RIU was still achievable. As discussed by Gilardi and coworkers [143], the size of the sensing volume can also play an important role, since high sensitivity may result by virtue of larger sensing domains. Smaller sensing areas are, however, preferable for practical integrated sensors and for facilitating precise analyte delivery. In this vein Gilardi and Beccherelli report a volume normalized sensitivity of 2000 nm/(RIU nl) [143]. The role of hybrid systems exploiting highly localized optical fields, hence reducing the sensing volume, may yet afford opportunities for further gains.

Figure 4.

(a) Resonance shift of a R = 2.91 mm and R = 1.19 mm crystalline WGM resonator upon variation of the bulk refractive index of the surrounding medium (water), as controlled by adding glycerol of differing concentration. (b) Bulk sensitivity of WGM refractometers as a function of resonator refractive index [cf. Eq. (5)], based on a 2 mm resonator in water operating at 795 nm. Reprinted with permission from [142]. Copyright 2014 Optical Society of America.

The ability to detect small changes in refractive index has led researchers to measure low concentrations of analyte materials in solution or as an adsorbed layer, e.g., [66,147,148]. Naturally the question arises as to whether single particle or molecule sensitivity is achievable. Theoretical treatments to the resonance perturbations induced by single particles and/or molecules are plentiful in the literature (see, e.g., [109,149–154]), with recent contributions including [155–162]. Within a weak coupling regime (as opposed to a strong coupling regime), whereby perturbation theory is valid, it can be shown that, for introduction of an inclusion in the host medium of electric permittivity ε_p(r), the resonance shift is given by [151]

$$\frac{\delta \omega }{{\omega }_0}\approx -\frac{{\int }_{V_p}[{\epsilon }_p(\mathbf{r})-{\epsilon }_h]{\mathbf{E}}^{†}(\mathbf{r})·\mathbf{E}\prime (\mathbf{r})\mathrm{d}\mathbf{r}}{2{\int }_V\epsilon (\mathbf{r}){\mathbf{E}}^{†}(\mathbf{r})·\mathbf{E}\prime (\mathbf{r})\mathrm{d}\mathbf{r}}\approx -\frac{\text{Re}[\alpha ]}{2}\frac{f{|\mathbf{E}({\mathbf{r}}_p)|}^2}{{\int }_V\epsilon (\mathbf{r}){|\mathbf{E}(\mathbf{r})|}^2\mathrm{d}\mathbf{r}},$$ (6)

where † denotes the Hermitian adjoint operator, V_p (V) denotes the volume of the inclusion (all space), E (E′) denotes the unperturbed (perturbed) mode distribution, and ε(r) is the original permittivity distribution such that ε(r) = ε_r for r within the WGM resonator and ε_h otherwise. Predominantly, the second expression, known as the reactive sensing principle [150], is used for small perturbations, such as biological particles, where α represents the polarizability of the particle that is centered at r_p and f corresponds to a correction term accounting for the exponential decay length of the WGM [163], typically on the order of 100 nm, over the physical extent of the particle [115]. For very small particles f ≈ 1 and the quasi-static polarizability can be safely used. Spherical particles of radius a, for example, can be treated using the polarizability

$$\alpha =4\pi a^3\frac{({\epsilon }_p-{\epsilon }_h)}{({\epsilon }_p+2{\epsilon }_h)},$$ (7)

where ε_p and ε_h are the electric permitivitties of the particle and the host medium, respectively. For plasmon-enhanced WGM sensors [4,164–166] the overlap of the localized field (or hotspot) with the perturbing biomolecule or nanoparticle [115,167] must also be considered for accurate and quantitative measurements in a similar fashion. Physically, the resonance shift can be associated with the work done in polarizing the perturbing particle. Detection limits derived from the reactive sensing principle have been previously considered [168]; however, more recently these detection limits were placed on a more rigorous footing, for a swept frequency modality, using formal noise limits based on the Cramer Rao lower bound [169], whereby it was shown, for example, that for Gaussian amplitude fluctuations the minimum number of detectable particles, N, is given by

$$N=\frac{(n_r^2-n_h^2)}{\text{Re}[\alpha ]}\frac{R^3}{{|Y_{ll}(\pi /2)|}^2}\frac{F_0}{Q_0}\frac{{(1+Q_c/Q_0)}^3}{4Q_c^2/Q_0^2},$$ (8)

where a fundamental WGM has been assumed; F₀ incorporates the experimental signal-to-noise ratio (SNR), sampling rates, and bandwidth; Q_c describes the contribution of coupling losses to the resonance Q factor; and Y_ll(π/2) are the spherical harmonic functions. Optimal configurations for spherical WGM sensors were identified, including the resonator size, coupling distance, and operational wavelength, from which single particle sensitivity was predicted. Sensitivity limits in other detection schemes, such as the backscattering geometry, and plasmonically enhanced setups [166,170,171] have also been considered (see below).

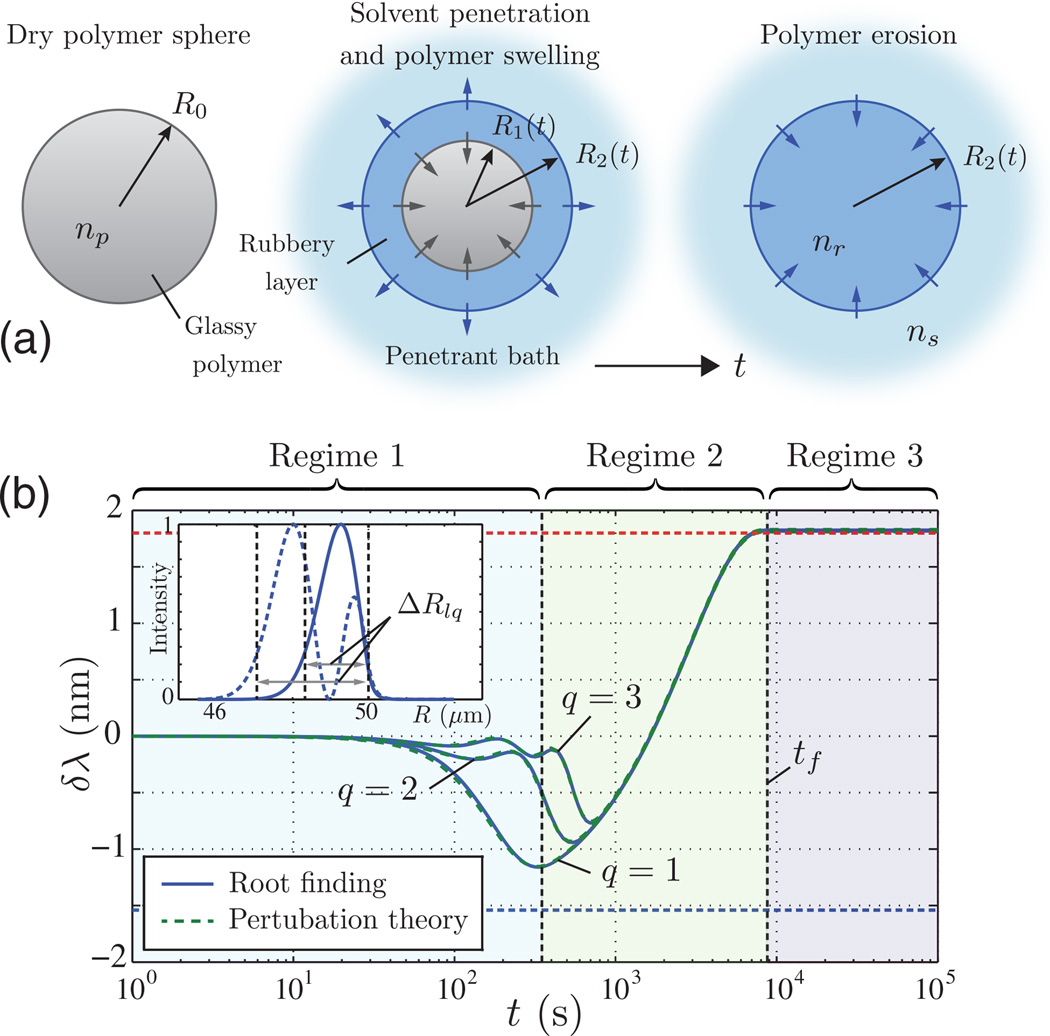
Although less common, sensors based on expansion or morphological changes of the WGM resonator can be found in the literature. One such technique exploits the swelling properties of polymer resonators or coatings to act as the transduction mechanism upon permeation of a gas or other chemical species [172]. This principle was successfully employed, for instance, by Mehrabani et al. [173] to monitor environmental humidity changes. Morphological changes generated from pressure changes and acceleration have also been successfully detected using WGMs [174,175].

2.3b. Line Broadening

A perturbation to a cavity can also produce changes in the linewidth of the resonance. Given that the linewidth is governed by a number of different physical phenomena, so too is the induced change. For example, both additional absorption and scattering losses can be introduced upon the interaction of a WGM with a particle. Similarly to the resonance shifts discussed above, the change in resonance linewidth from additional absorption losses in a bound nanoparticle can be shown to be [4,168]

$$\frac{\delta {\gamma }_{\text{abs}}}{{\omega }_0}\approx \text{Im}[\alpha ]\frac{{|\mathbf{E}({\mathbf{r}}_p)|}^2}{{\int }_V\epsilon (\mathbf{r}){|\mathbf{E}(\mathbf{r})|}^2\mathrm{d}\mathbf{r}}.$$ (9)

The reader is also referred to Ref. [176] for a treatment of broadening due to large planar substrates in a cylindrical geometry. Particle-induced scattering losses are also found. This latter problem has been approached using a rigorous operator method based upon the Weisskopf–Wiener semi-QED treatment [153,177] or a more classical dipole scatterer approach [4], yielding

$$\delta {\gamma }_{\text{sca}}=\frac{n_h^5{\omega }_0^4{\epsilon }_0}{6\pi c^3}\frac{{|\alpha |}^2{|\mathbf{E}({\mathbf{r}}_p)|}^2}{{\int }_V\epsilon (\mathbf{r}){|\mathbf{E}(\mathbf{r})|}^2\mathrm{d}\mathbf{r}}.$$ (10)

It is furthermore well known that WGM resonators possess a degeneracy between counterpropagating WGMs [153,178], which can in specific circumstances act to give rise to an effective broadening [153,179,180]. If a small molecule or nanoparticle enters the evanescent field, coupling between the modes is introduced. Accordingly the system eigenstates now correspond to two orthogonal standing wave type modes in the resonator. For a single perturbing particle the node and antinode of each of these modes are fixed at the particle location [153], such that one resonance is shifted by 2δω, while the other remains spectrally fixed; i.e., a spectral doublet is formed (see Fig. 2). Figure 5 shows the intensity profile of the symmetric and antisymmetric normal modes produced by scattering of a single nanoparticle. The symmetric mode, shown in the left panel, maximally overlaps with the particle, shifting the frequency of the WGM and introducing additional losses. The antisymmetric mode, however, has a node at the position of the particle and thus experiences no interaction. When the shift of the symmetric mode is smaller than the linewidth, i.e., ω₀/Q₀ < 2δω, the relative splitting of the modes is unresolvable and the observed lineshape results from the superposition of the two standing wave modes [179]. The total effective broadening of the aggregate line is thus dependent on the strength of coupling. In particular, for dielectric particles in the low-Q regime the mode broadening has been shown to scale as δω², whereas for the high-Q regime the broadening scales as 2δω since the unresolved mode splitting dominates in this case [179].

Figure 5.

Intensity profiles of the symmetric (left) and antisymmetric (right) normal modes created via nanoparticle backscattering. Reprinted with permission from [185].

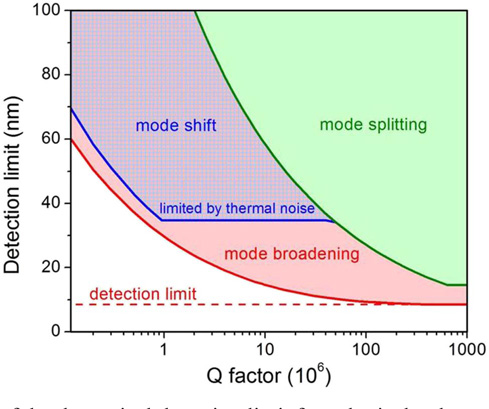
Mode broadening has previously been demonstrated for determining the concentration of an analyte [181], and more recently for sensing individual polystyrene nanoparticles of 70 nm radius and lentiviruses [182] (see Fig. 6). The latter work employed a torodial cavity with Q > 10⁶, which was thermally stabilized by means of a PDMS coating [183]. Scattering losses were assumed to be the principle cause of mode broadening in this case. Moreover, in their work Shao et al. [182] compare the detection limits, as imposed by the noise or probe bandwidth, of a mode broadening based modality to those of other sensing mechanisms such as frequency shifts and mode splittings. The authors’ findings are illustrated in Fig. 7 for the detection of polystyrene nanoparticles whereby it can be seen that for a mode of given Q the mode broadening detection modality outperforms both mode shift and mode splitting (see below) type schemes. Recent theoretical work devoted to rigorous treatment of WGM broadening [179] has also shown that much of the scattering losses from a propagating WGM are coupled into the counterpropagating mode. Indeed, earlier work by Kippenberg et al. has shown that such coupling scales with the Purcell factor of the microcavity [184]. The importance of absorption losses in determining mode broadening has also been noted in a number of recent works [168,169,179], and has been exploited experimentally for the determination of the concentration of gold nanoparticles in liquid droplet resonators [68].

Figure 6.

(a) Mode broadening induced in two resonant WGMs upon binding of 70-nm-radius polystyrene nanoparticles. (b) Experimental transmission spectrum for 0 (top) to 4 (bottom) bound polystyrene nanoparticles with the corresponding enhanced optical images of the torodial microcavity. Reprinted from [182].

Figure 7.

Comparison of the theoretical detection limit for spherical polystyrene nanoparticles in air using different WGM detection modalities: resonance shifts (blue), mode broadening (red), and mode splitting (green). Reprinted from [182].

2.3c. Multimodal Sensing

The sensing mechanisms described hitherto consider the change of one property of a single WGM. Restriction to the use of a single information channel is, however, unnecessary. Indeed, a number of techniques either employing multiple WGMs or combining different sensing signals have been investigated recently. Undoubtedly, the most significant multimodal sensing mechanism used is that based on the measurement of the frequency splitting between two coupled WGMs [185]. Mode splitting arises, as discussed in the previous section, when coupling between degenerate eigenmodes from the presence of a nanoparticle or other perturbation to the cavity is stronger than the associated decay rate of the WGM, i.e., ω₀/Q₀ ≫ 2δω. The advantage in measuring frequency splitting, rather than the absolute WGM frequency, is that both modes exhibit the same susceptibility to thermal noise, thus rendering the frequency splitting insensitive to thermal fluctuations and eliminating slow measurement drifts. Additionally, it was shown in Ref. [186] that the mode splitting detection scheme leads to a robust measurement of particle size given that the refractive index is known. This is due to the fact that both the reactive and dissipative effects from a single particle depend strongly on its angular position as well as the mode profile. This dependence can, however, be eliminated by calculating the ratio between the induced frequency splitting and the additional losses encountered. Although the mode splitting scheme has predominantly been applied for detection of nanoparticles in air, recent studies have expanded this work, demonstrating detection [187] and sizing of nanoparticles [188] in aqueous environments and paving the way for sensitive biological measurements with minimal long-term signal drifts.

Multiple perturbing particles cause the WGM modal structure to become significantly more complicated with modes no longer corresponding to standing waves and also exhibiting nonorthogonality and so-called chirality, or a preferred direction of rotation [155]. Moreover, each eigenmode can individually suffer a shift in frequency [158]. Study of the statistics of the relative shift of multiple binding events has also been shown to allow particle sizing and counting [161]. The relative position of each perturbing particle in the WGM evanescent field also plays a crucial role in dictating the scattering losses due to the relative phase between each scatterer [162], which can again differ between eigenmodes. Periodic arrays of scattering particles whereby the relative phase differences are multiples of π allow constructive interference of each scattered wave, such that the aggregate perturbation for all particles follows by simple linear addition [189].

Not all multimodal methods derive from measuring the frequency difference of split modes. Keng et al., for example, have recently proposed the use of WGMs of slightly differing azimuthal index as a means of determining the position of a binding nanoparticle on the surface of a spherical resonator [115]. The working principle relies on the fact that the mode overlap differs for modes of different m. Combined with analytic knowledge of the mode distributions it is then possible to infer the particle position and hence also extract the particle’s polarizability, e.g., for sizing purposes. Sizing has also recently been demonstrated by combination of the change in mode splitting and broadening [185]. Use of differing polarization modes is also a further possibility, allowing for study of the binding orientation [188,190–192] of nonspherical particles and biomolecules. Alternatively, Jin et al. [193] investigated measurements of low concentrations of nanoparticles; however, their sensing signal was derived from the total broadening of both spectral lines. This facilitated discrimination of splitting effects arising from surface functionalization of the resonator from those of the target analyte, in addition to improving the thermal stability of the sensing signal.

When two high-Q WGM resonators are coupled, resonances from each hybridize to form symmetric and antisymmetric eigenmodes. Two spectral lines can hence be monitored and used as a multimode sensing mechanism. For example, the work of Grudinin and Yu considers the use of two coupled disc resonators [133]. They numerically showed that the gap between the coupled resonators dictated the mode splitting, which could then be monitored to provide a sensitive displacement sensor. Similarly, Boriskina and Dal Negro [51] proposed using the individual shifts of each spectral line as a means to discriminate between perturbations to the system deriving from surface and bulk refractive index changes. The authors show that this method allows measurements of the thickness of thin absorbed layers. If low- and high-Q WGM resonators are coupled, mode interference gives rise to an asymmetric Fano-type resonance, which can also be used for sensing purposes [194]. A similar geometry in which two spectrally distinct, high-Q WGMs in different resonators are excited by means of a single tapered optical fiber has also been used to demonstrate spectrally multiplexed and specific detection of DNA hybridization [195].

3. Sensing

3.1. Sensitivity

WGM sensors have, to date, demonstrated enviable sensitivity levels and have thus found a plethora of applications (see Subsection 3.3). The natural question arises, however, as to what detection limits are ultimately achievable. As has been discussed in numerous papers [168,170,171,196,197], the answer to this question amounts to a comparison between noise sources present in the system as compared to the magnitude of the induced sensing signal. Numerous noise sources can afflict WGM sensors, yet many of these are technical in nature, e.g., laser instabilities, and can thus conceivably be reduced by suitable experimental/technical improvements. Crucially, however, a number of noise sources are fundamental in nature and thus unavoidable. Arguably, the most fundamental limit of detection is that which arises from the quantum nature of light, known as the shot noise limit. While it is possible to go below the shot noise limit via injection of squeezed light, as demonstrated in Ref. [198], we shall not consider this possibility in this article. A WGM sensor based on monitoring WGM resonance shifts and operating with a shot noise limited resolution, for example, has a limit of detection given by [199]

$${\left(\frac{\delta {\omega }_{\text{min}}}{{\omega }_0}\right)}_{\text{shot}}=\frac{1}{Q_0}\sqrt{\frac{ħ{\omega }_0}{P_0\eta \beta \tau }},$$ (11)

where, as above, Q₀ is the optical quality factor, ω₀ is the WGM frequency, P₀ is the coupled optical power, η is the photodetector’s quantum efficiency, β is the transmission efficiency of the cavity, and τ is the averaging time. Considering some typical WGM sensing parameters (e.g., Q = 1 × 10⁷, ω₀/2π = 4 × 10¹⁴ Hz, P₀ = 1 mW, η = 0.9, β = 0.9, and τ = 1 s), we arrive at a minimum detectable shift of only 0.7 Hz, which is much smaller than the shift expected for a single protein such as bovine serum albumin (BSA).

At room temperature, however, noise due to fundamental fluctuations in temperature must also be considered. Temperature variations can induce fluctuations in the cavity refractive index and size and therefore also lead to noise in the resonance frequency known as thermorefractive and thermoelastic noise, respectively [200], the latter of which is negligible relative to the former. Interestingly, temperature fluctuations also translate to variations in the resonance linewidth; however, these variations are commonly assumed to be negligible as based on experimental experience [74,201]. Recent theoretical work has confirmed this point of view by showing that the linewidth variations are on the order of ~1/Q₀ smaller than the associated frequency fluctuations [169].

The dominant noise source in any given sensor is ultimately dictated by the time scales of the physical processes being monitored. Optomechanical position and force sensors, for example, operate at high frequencies and are therefore limited by shot noise. Accordingly superior performance has been reported by a number of groups, as we shall review in the next section. In contrast, biological sensing often entails the measurement of much slower processes, typically over millisecond to second time scales, and inevitably suffers from low frequency noise. At these time scales, thermorefractive noise [200] and frequency jitter [170] can constrain the sensitivities of the WGM frequency shift to several orders of magnitude above the shot noise limit [166,202]. To illustrate this point, in Fig. 8 we show the fundamental limits of detection for a typical microsphere resonator as a function of the measurement time τ. The spectral density of thermorefractive noise for a microsphere was derived in Ref. [200]. For the calculation in Fig. 8, we have used the formulae and WGM parameters given in the supplementary information of Ref. [166]. In addition, we show experimentally measured frequency noise data from Ref. [202]. For short measurement intervals (τ < 1 ms), the frequency noise approaches the theoretical limit predicted for thermorefractive noise. At longer intervals, however, measurements suffer from long-term drift and the frequency noise scales with τ. The optimal length of the averaging window lies in the intermediate region between 1 and 100 ms, where the frequency noise exhibits a τ^1/8 scaling, although the origin of the noise in this region has yet to be identified [202].

Figure 8.

Theoretical detection limits based on shot noise and thermorefractive noise, and experimentally measured Allan deviations for two microtoroidal resonators from Ref. [202].

Currently, methods by which to achieve, and even surpass, current detection limits are thus attracting much research effort. A variety of promising approaches, ranging from enhancing light–matter interactions with plasmonics and the development of new detection schemes that are immune to technical noise sources, to the use of active cavities, have indeed recently been proposed and demonstrated. We thus also review a number of these recent contributions in the following sections. Many of these techniques are mutually compatible, and it is likely that when combined such new detection schemes will afford significant gains in all domains of sensing.

3.1a. Optomechanics

Optical microresonators are in a constant state of motion, exhibiting mechanical resonances in the megahertz range that are driven by Brownian fluctuations [203]. At room temperature, these Brownian fluctuations lead to small displacements in the position of the mechanical oscillator, thereby modulating the optical path length and resonance frequency of the cavity. The mechanical motion of the cavity can then be directly read out by measuring the spectral shift of the WGM near the mechanical resonance frequency. This coupling between the optical and mechanical degrees of freedom is the underlying principle behind the field of cavity optomechanics and plays an important role in a variety of experiments ranging from gravitational wave detection to scanning probe microscopy and to ultraprecise force sensing [18,204–206].

In the frequency range of micro- and nano-scale mechanical oscillators (i.e., megahertz range), modern laser sources and photodetectors offer shot noise limited performance. This has led to some remarkable sensitivities in the optomechanical transduction of position and force. In a recent work, for example, the mechanical motion of a Si₃N₄ nanomechanical beam was resolved via evanescent coupling to the near field of a WGM disk resonator, and a force sensitivity of 74 aN/Hz^1/2 [18] was demonstrated. Force sensitivities can be pushed even further through the use of feedback [18] and post-processing [207].

In addition to force sensing, mechanical resonators may find applications in biosensing due to their sensitivity to changes in the density and viscous damping of the surrounding fluid [208] and oscillator mass [209]. It may seem surprising that optomechanical oscillations can be observed at all in a fluid, due to the increased acoustic damping of the fluid and resulting acoustical radiation losses; however, one method of mitigating this challenge relies on the fact that optomechanical vibrations can be actuated in liquid via radiation pressure [208]. Radiation pressure arises from the transfer of photon momentum to the mechanical system and can lead to a self-sustained excitation of mechanical vibrations in the resonator, which then, in turn, modulate the cavity’s optical resonance frequency. This mechanism served as the basis of detecting changes in the density of the WGM’s surrounding environment in Ref. [208], where the concentration of sucrose in solution was determined by measuring shifts in the mechanical resonance frequency. As the mechanical vibrations were sustained in fluids more viscous than serum, it is possible that in the future optomechanics could be combined with WGM optical sensing under biologically relevant conditions.

3.1b. Plasmonic Enhancement of the Light–Matter Interaction

Metallic nanoparticles are characterized by a strong confinement of electrons that resonate at particular frequencies in response to applied oscillating electromagnetic fields [210]. If a metallic nanoparticle is placed at the surface of a WGM resonator, the oscillation of electrons at the surface of the metal, known as localized surface plasmons, can lead to large enhancements in the local electric-field strength, effectively boosting the interaction between light and matter [4,166,211,212]. Such plasmonic enhancements in the WGM frequency shift have been demonstrated for detection of single nanoparticles [212], viruses [165], proteins [167], and most recently single nucleic acid interactions [4]. In the latest work, the plasmonic enhancement mechanism enabled optical measurement of DNA hybridization kinetics at the single molecule level for the first time, with a sensitivity capable of discriminating single base-pair mismatches [4]. The experimental setup is shown in Fig. 9(a), and includes a prism-based microsphere that can be supplied with gold nanorods (with dimensions 12 nm × 12 nm × 42 nm) and single-stranded DNA (from eight to 22 bases in length) via a PDMS-based microfluidic enclosure. Gold nanorods of this particular size were chosen due to their strong longitudinal plasmon resonances near 780 nm [4,166], with the resulting enhancements in the frequency shift estimated to be around ~1000. Figure 9(b) shows the frequency shifts and linewidth fluctuations of TE- and TM-polarized WGMs during the single nucleic acid interactions. Under these conditions hybridization between DNA strands occurred transiently, resulting in sharp peaks in the frequency shift. On the other hand, hybridization did not significantly affect the WGM linewidth on account of the small size of the DNA strands and negligible absorption and scattering losses.

Figure 9.

(a) Prism-based microcavity biosensing setup. (b) Single nucleic acid interactions with a nanorod-enhanced WGM sensor. Data show different transient events for TE and TM modes, and negligible change in the line width due to a purely reactive effect on the WGMs. Adapted with permission from [4]. Copyright 2014.

Interestingly, the measured enhanced WGM frequency shifts in Ref. [4] were actually larger than those predicted by theoretical analysis, as was also observed in earlier works on the detection of BSA using core-shell type nanoparticles [167]. The origin of this additional enhancement reportedly lies in the intensity hotspots resulting from surface roughness and/or imperfections of the plasmonic nanoparticles. The size dispersion of the plasmonic nanoparticles is also believed to play a role. These works are merely the first attempts in demonstrating the mechanism of plasmonic enhancement, and it is anticipated that future studies will aim to push the scope of WGM sensing further, achieving larger sensitivity enhancements by precisely controlling the size and shape of the nanoparticle.

3.1c. Exceptional Points

The degeneracy of propagating and counterpropagating WGMs has been shown to allow the development of sensitive sensors exploiting mode splitting that is induced by a suitable perturbation, such as binding of a nanoparticle or biomolecule [187,188]. As discussed in Ref. [155] this degeneracy is commonly discussed in the context of a conservative system possessing a Hermitian Hamiltonian. In the case of a Hermitian Hamiltonian, degeneracy occurs when the eigenvalues are equal but the associated mode profiles are orthogonal, and occurs at what is known as a diabolic point in parameter space. WGM resonators, however, constitute open systems; i.e., energy can be lost, e.g., via scattering or radiation losses, which can often be described using a non-Hermitian Hamiltonian. The associated eigenvalues of the Hamiltonian are, as a result, complex, with the real and imaginary parts respectively describing the resonance frequency and linewidth. In addition to the possibility of diabolic points, so-called exceptional points can also exist in such systems [213]. At an exceptional point eigenvalues are once again degenerate; however, in contrast to diabolic points, the optical modes are no longer orthogonal and are in fact identical [155]. Exceptional points, furthermore, exhibit differing sensitivity to perturbations, as compared to diabolic points, by virtue of the differing parameter landscape. Specifically, for a perturbation of strength ε, the resulting resonance shifts and splitting scales with ε, whereas for an exceptional point a scaling proportional to ε^1/2 is found [214]. For suitably small perturbation strengths an enhanced sensitivity can thus be achieved, thus motivating the question as to how WGM sensors can be controlled so as to operate at an exceptional point. One means by which to control the effective Hamiltonian in a WGM sensor is by the introduction of multiple scatterers at specific positions on the resonator [155,196]. Within a two-mode approximation and considering a disc resonator for simplicity it can then be shown that the effective Hamiltonian takes the form [215]

$$H_{\text{eff}}=\left(\begin{array}{cc}\hfill {\omega }_0+\sum _j\delta {\omega }_j\hfill & \hfill \sum _j{s}_j\text{exp}[-i2m{\beta }_j]\hfill \\ \hfill \sum _j{s}_j\text{exp}[i2m{\beta }_j]\hfill & \hfill {\omega }_0+\sum _j\delta {\omega }_j\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill \mathrm{\Omega }\hfill & \hfill A\hfill \\ \hfill B\hfill & \hfill \mathrm{\Omega }\hfill \end{array}\right),$$ (12)

where β_j defines the angular position of each scatterer on the resonator surface, δω_j is the resonance shift induced by the jth particle, and s_j describes the associated scattering strength. Non-Hermitianity of the Hamiltonian is thus seen to arise when (1) the system is open, (2) nonidentical scatterers are present, and (3) a geometric mirror symmetry does not exist. The existence of exceptional points requires B = 0 or, more physically, requires the superposition of the scattered waves from all scatterers to destructively interfere, as controlled by their relative phases and hence scatterer positions. Given this requirement for destructive interference it is evident that the occurrence of exceptional points is closely related to asymmetric backscattering from particles. Indeed, fully asymmetric backscattering implies that all scattered light is coupled into forward propagating modes, i.e., the eigenmodes are identical, as illustrated by the numerical modes shown in Fig. 10. Experimental realization has been demonstrated by the use of two nanotips near a toroidal resonator [196]. By tuning the size of one of the tips the intrinsic splitting of a WGM, arising due to fabrication imperfections, was removed [see Fig. 10(b)], and an exceptional point degeneracy was created in doing so. Exceptional points have also been experimentally seen in chaotic cavities resulting from the asymmetry of the WGM resonator [216]; however, their use in practical sensors, for which a more than threefold enhancement in sensitivity has been theoretically predicted [214], has still yet to be realized.

Figure 10.

(a) Schematic of experimental setup, allowing controlled manipulation of mode splitting via positioning of two nano-probes near a toroidal WGM resonator. (b) Spectral intensity as a function of tip size, which was varied with time, showing mode crossing (top), anticrossing (middle), and shift (bottom) as arising from different tip placements. Reprinted with permission from [196]. Copyright 2010 Optical Society of America. (c) and (d) show simulated eigenmode intensity profiles for two scatterers positioned near a microcavity sensor such that the sensor operates close to an exceptional point. Reprinted with permission from [214]. Copyright 2014 by the American Physical Society.

3.1d. Direct Detection of Backscattered Light

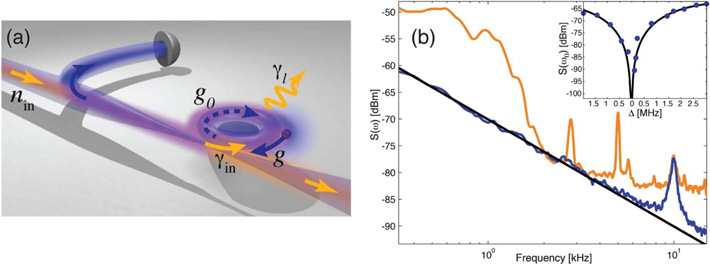
Detection based on mode splitting requires the induced frequency separation between eigenstates to be spectrally resolvable, i.e., the frequency spitting is much larger than the cavity decay rate. Although this is generally true for large nanoparticles, this is not the expected situation for small molecules such as proteins or nucleic acids. In this case the scattering induced by a single particle can be monitored directly by measuring the intensity of the backscattered light as was recently proposed by Knittel et al. [170]. Figure 11(a) illustrates the experimental scheme for backscatter detection. Specifically, in this work a tapered fiber coupler was used to excite a WGM in a microtoroidal resonator, and the backscattered intensity from an evanescently coupled atomic force microscopy (AFM) tip was collected on a photodetector via an in-fiber optical circulator. Both the laser frequency and the tapered fiber position were stabilized using feedback [217,218] to achieve real-time measurement as well as to eliminate drifts. Comparison of the experimental frequency noise power spectra found for a conventional frequency shift (light orange) and the backscattering detection scheme (dark blue) is shown in Fig. 11(b). In both traces the mechanical motion of the AFM tip is apparent around 10 kHz, coinciding with the mechanical resonance frequency of the cantilever. Interestingly, however, detection based on backscattered light is achieved with a 24 dB suppression in technical noise. Importantly, the suppression of noise occurs for zero detuning between the laser frequency and WGM [inset of Fig. 11(b)], in which case there is negligible cross-talk between fluctuations in frequency and the backscatter amplitude. By enforcing the zero-detuning condition, measurements are limited by amplitude noise rather than frequency noise, whereby it is possible to circumvent the laser frequency jitter that so often constrains sensitivity in WGM biosensing [170].

Figure 11.

(a) Illustration of the backscatter-based detection scheme. (b) Frequency noise power spectra for frequency shift (light orange) and backscatter measurements (dark blue). Black line represents a 1/f² fit to the backscatter data. Inset shows the backscattered power spectrum at the modulation frequency as a function of the detuning. Reprinted from [170].

3.1e. Self-Heterodyned Microlasers

An alternative method of measuring mode splitting is based on the detection of a heterodyned beat note between the two split modes. This has been achieved using gain-functionalized microcavities, with both erbium- and ytterbium-doped microlasers [219]. Figure 12 illustrates the detection scheme used for single nanoparticle detection with an erbium-doped microlaser. Continuous pumping of the microlaser within the Er³⁺ absorption band (around 1.45 µm) leads to a transition from spontaneous to stimulated emission in the 1.5 µm wavelength band, with the lasing threshold occurring at relatively low pump powers on the order of microwatts. Due to the broad absorption of Er³⁺ in SiO₂, the erbium ions readily couple to many modes within the cavity, and thus any particle-induced mode splitting in the WGM spectrum will naturally lead to frequency splitting in the lasing spectrum. Mixing the split modes of the microlaser onto a photodetector then gives a heterodyned beat note with frequency that corresponds to the particle-induced mode splitting [219]. Using this scheme the deposition of a number of nanoparticles onto the microlaser surface in air was measured, including 15-nm-radius polystyrene particles, 10-nm-radius gold particles, and influenza A virions. In addition, the authors demonstrated detection of 30 nm radius polystyrene particles in water using a ytterbium-doped microlaser.

Figure 12.

(a) Experimental schematic for nanoparticle detection based on mode splitting of a WGM microlaser. (b) Surface deposition of nanoparticles induces mode splitting in the laser spectrum that can be detected via a heterodyned beat note. Reprinted with permission from [219]. Copyright 2011.

In more recent studies [220,221] particle-induced mode splitting was detected in a similar fashion using a Raman microlaser. In Ref. [220] NaCl particles with radii as small as 10 nm were detected in air [220], while polystyrene particles with radii down to 20 nm were detected in water in Ref. [221]. For a measurement time of 1 s, the noise floor in these measurements was about 14 kHz, which at present sets the record for the lowest noise in a measurement of the WGM frequency shift.

3.1f. Summary

In Table 1, we summarize some of the various strategies that are pushing the limits of detection in WGM sensing. The current state of each detection scheme is given based on the noise floor in the measurement of the WGM spectral shift over a given measurement time. In addition, for each scheme, we have listed the noise equivalent polarizability (α_NEP) of a spherical particle [see Eq. (7)] that could be detected with a SNR of 1. For this calculation, we have assumed a mode volume of V_m = 500 µm³, an operating wavelength of λ = 780 nm, and that the field intensity at the resonator surface is 30% of the intensity maximum.

Table 1.

Summary of Sensitivities for Various WGM Detection Schemes^a

Detection Scheme	Noise Level (kHz)	αNEP (nm3)	τ (s)	Ref.
Standard WGM sensor	800	7 × 103	1	[202]
Erbium-doped microlaser	100	867	-	[219]
Backscatter detection	75	650	0.4	[170]
Raman microlaser	14	121	1.0	[220]

^aFor each scheme, the frequency noise is given for a particular averaging time τ, as well as the noise equivalent polarizability of a spherical particle that could be detected with a signal-to-noise ratio of 1.

3.2. Time Resolution

Apart from sensitivity, another important consideration in many sensing applications is the time resolution of the system. The actual time resolution that one can achieve will depend on the sensing modality (see Subsection 2.3) and details of the experimental setup. In principle, however, the best possible time resolution is set by the response time of the cavity, or roughly the cavity photon lifetime τ = γ⁻¹. Given that a higher Q precludes measurements that occur on time scales faster than the photon lifetime τ, a trade-off exists between sensitivity and time resolution. To get a feel for this limit, a typical WGM resonator with a quality factor of 10⁷ would have a optical decay rate of several megahertz at visible frequencies, and a time resolution of about 100 ns.

For some sensing applications (e.g., temperature sensing or the formation of molecular monolayers), interactions occur over time scales much longer than the cavity decay rate. In this case, the WGM frequency shift can be monitored by implementing a straightforward method based on scanning the laser frequency over the WGM resonance and continuously recording the transmission spectrum with a data acquisition system. The bandwidth of the laser’s piezocontroller, therefore, limits the time resolution of such measurements to a few milliseconds. While this method is simple and capable of resolving slow signals, it is not a direct measurement of the WGM frequency and relies on heavy post-processing for extraction of the frequency shifts or linewidths. To gain access to faster signals (e.g., optomechanical oscillations, conformational changes in molecules, or binding events of single nanoparticles or biomolecules), one should employ a detection scheme based on a continuous frequency or amplitude measurement. In this section, we will review several prevalent methods for real-time WGM measurement.

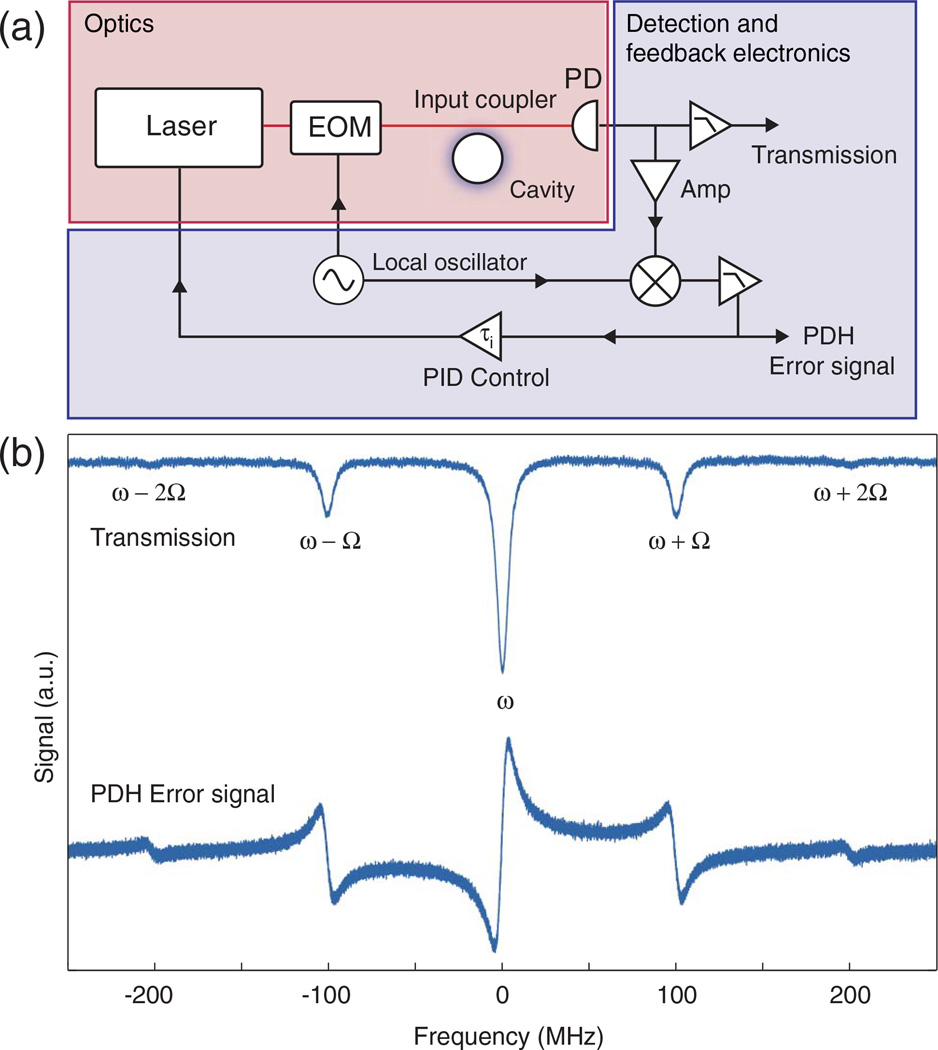
In the Pound–Drever–Hall (PDH) method [199] an electronic feedback loop is implemented to lock the laser frequency to the WGM resonance. Fluctuations in the cavity frequency can then be read out continuously by direct measurement of the feedback error signal. The PDH experimental setup, shown in Fig. 13(a), consists of a WGM resonator that is excited via an input coupler (most commonly a tapered fiber or prism coupler), an electro-optic modulator (EOM), a photodetector, and some locking electronics. In this scheme, the EOM modulates the phase of the cavity’s incident field at frequency Ω, such that the incident field takes the form a_inc = a₀ exp[ω₀t + β sin Ωt], where a₀ exp[iω₀t] is the field prior to the phase modulation and β is the modulation depth. As a result, sidebands are produced at ω ± Ω, ω ± 2Ω, …. In Fig. 13(b), we show the transmission and PDH error signals for a typical microsphere resonator (R = 50 µm, n_r = 1.45, Q = 5 × 10⁷). When the phase is modulated much faster than the cavity decay rate [as in Fig. 13(b)], the sidebands do not acquire any phase information about the cavity. The beating between the carrier and sidebands, however, contains relative phase information between the incident and cavity fields. This is the essence of the PDH technique. The PDH error signal [shown in the bottom of Fig. 13(b)] is obtained by demodulating the photodetector output and can be used to stabilize the frequency of the laser to the WGM. Any fluctuations in the error signal can then be converted to an equivalent WGM frequency shift via a simple calibration.

Figure 13.

Pound–Drever–Hall (PDH) locking scheme. (a) The optical setup consists of a laser source that is phase modulated by an electro-optic modulator (EOM), in addition to an input coupler, a cavity, and a fast photodetector (PD). The PDH error signal is obtained by mixing the amplified output of the PD with the local oscillator. The error signal is then split into two branches: one for detection and one for laser stabilization. (b) Transmission and PDH error signals for a prismcoupled microsphere resonator showing the first-order sidebands at ω ± 100 MHz and the barely visible second-order sidebands.

The PDH technique is used extensively in experiments involving optical cavities. In the field of WGM sensing, it has been used for measurements of near-field optomechanics [222] and for single nanoparticle detection [218]. In Fig. 14 we demonstrate a different application of the PDH method showing that it can be used to probe the conformational changes of biological molecules in real time. In this experiment, we revisit the measurement of conformational changes in bacteriorhodopsin (BR) [192]. Here, a microsphere resonator is coated with a monolayer of BR following the method described in Ref. [192] and excited at λ = 780 nm via a prism coupler. In addition, the microsphere is illuminated with a focused 532 nm laser source. Upon excitation near 532 nm, the retinal molecules in BR undergo a conformational change, such that the surrounding protein environment changes in a manner that can be probed via the evanescent field of the WGM. Figure 14(a) shows the wavelength (and frequency) shift for the conformational changes measured as a result of the 532 nm pulses shown. The initial conformational change occurs quickly [with a measured time constant of 5 ms, shown in Fig. 14(b)], whereas the the relaxation occurs more slowly, over second time scales. Although this measurement involves ensemble averaging over many molecules, the time scale for a single retinal molecule undergoing the same conformational change is about 50 µs, easily detectable for a WGM sensor with Q of 10⁷.

Figure 14.

Measurement of conformational changes in BR. (a) 532 nm pulse scheme used for measurement and corresponding light-induced frequency shifts. (b) The initial conformational change occurs with a time constant of 5 ms.

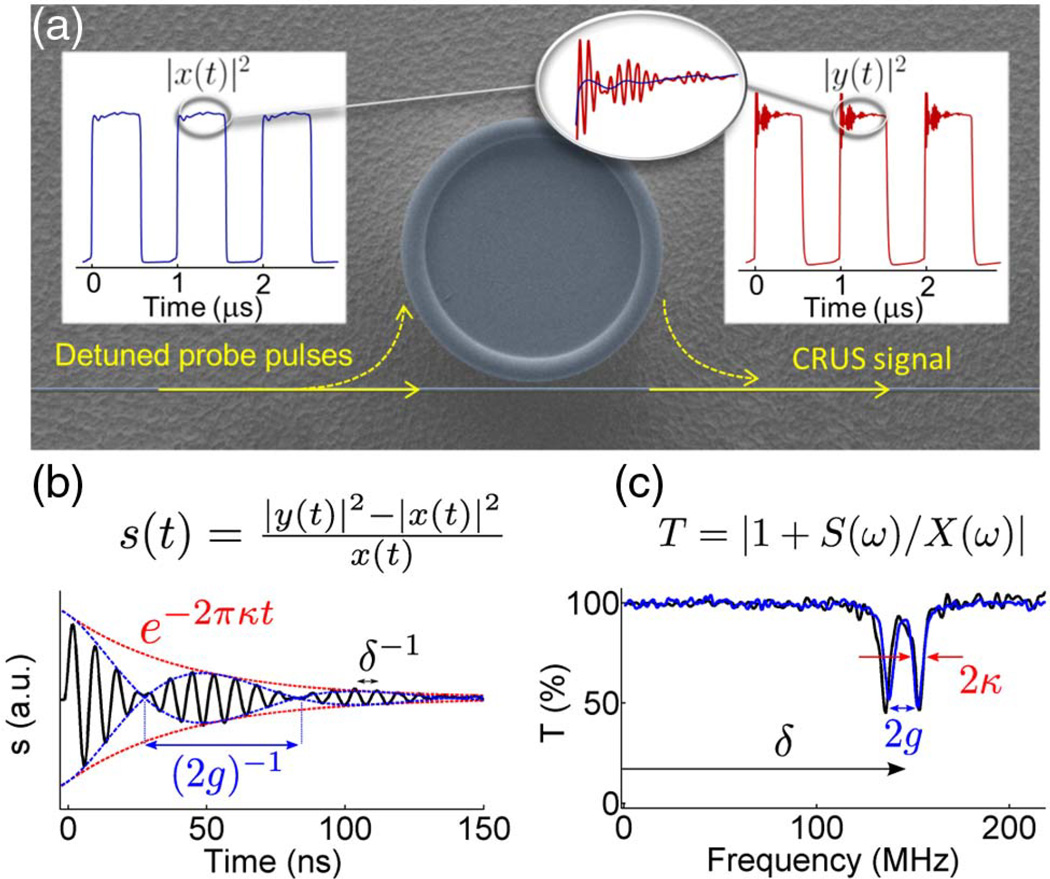
In addition, several other methods achieve fast detection, including the previously discussed microlasers used for single nanoparticle detection [219,220] as well as cavity ring-down optical spectroscopy [223]. In the microlasing experiments, the WGM frequency shift is obtained in real time by measuring changes in the beat note frequency between two counterpropagating modes. In cavity ring-down spectroscopy (CRDS), a spectroscopic approach is taken to enable measurement of the cavity decay rate γ at a very high sampling rate [42,224]. Although CRDS does not monitor the WGM frequency, it is useful for detecting dissipative materials that change the cavity decay rate due to absorption and is thus more closely related to sensing via mode broadening. Since the decay rate is measured, this technique has the advantage of being insensitive to intensity fluctuations of the laser source. Fitting algorithms, however, still play a key role in extraction of the cavity decay time, and hence an associated fitting error results. To avoid this noise use of phase-shift CDRS [225] is now frequently employed [226–229]. By amplitude modulating the input field from a CW laser (such that the rise time is less than the decay time) and monitoring the phase shift of the transmitted field, the ring-down time of the cavity τ can be determined with a time resolution set by the repetition rate of the amplitude modulation. This method has recently been used for measurement of biotin–streptavidin interactions [230], as well as absolute measurements of absorption cross sections for ethylene diamine molecules adsorbing to a silica microresonator [231]. An alternative approach to CRDS is that of cavity ring-up spectroscopy (CRUS) [232]. In CRUS, a sharply rising detuned probe pulse is utilized to produce ring-up signals in the transmitted light intensity recorded upon each pulse (Fig. 15). The time domain signal is recorded with a fast oscilloscope preferably operating in the gigahertz regime. The WGM spectrum is then obtained by Fourier transform of the oscilloscope recordings. Implementing the CRUS technique allows the monitoring of kinetics at unprecedented time resolution, which has been demonstrated by monitoring the optomechanical response of a microtoroid.

Figure 15.

(a) Schematic of cavity ring-up spectroscopy (CRUS) with a WGM resonator. (b) Typical example of the ring-up signal. (c) Fourier transform of the ring-up signal, from which the WGM spectrum is recovered. In this case a split mode is seen. Reprinted from [232].

3.3. Specific WGM Sensor Applications

Hitherto, we have discussed recent efforts in pushing the detection envelope of WGM sensors in terms of both sensitivity and time resolution. Optical microcavities, however, already represent a platform technology finding use in many sensing applications. Our attention now moves to providing a comprehensive review of such applications and the achievements made to date. It is important to note that all such applications employ one of the transduction mechanisms discussed in Subsection 2.3, namely changes in resonator size and shape or a change in the refractive index of the resonator or its surrounding environment. Although changes in refractive index are in themselves interesting from a fundamental point of view and easily detectable (see Subsection 2.3a for a review of refractive index sensing), measurements of such changes are frequently only sought as a means to an end. In particular, both the resonator and the environmental refractive indices are dependent on numerous physical parameters, such as the temperature, pressure, and concentration of constituents in mixtures, which are of greater interest from the perspective of sensing. Ultimately, the underlying principle of many, albeit not all, sensing schemes discussed in the following sections is thus equivalent to those discussed earlier in the context of refractometry.

3.3a. Temperature Sensing

Design of WGM temperature sensors crucially relies on the choice of resonator material since temperature variations are transduced by means of the associated changes in refractive index and expansion/contraction in the resonator. Materials with larger thermo-optic and thermal expansion coefficients (dn/dT and R⁻¹dR/dT) thus result in larger frequency shifts and thus allow precise measurements of temperature to be made. Typically, however, the thermal expansion is an order of magnitude smaller than dn/dT, so that the thermo-optic coefficient primarily motivates the material choice. In this respect, microspherical resonators made of polymers such as polydimethylsiloxane (PDMS) are a good choice, demonstrating sub-millikelvin temperature sensitivity with a tuning coefficient of 0.245 nm/K [233]. A similar approach is applicable on chip by coating silica toroidal microresonators on silicon wafers with PDMS layers [234]. In this case 0.151 nm/K temperature tuning was achieved in air, an order of magnitude larger than with plain silica and approximately a threefold improvement on the use of WGMs in hollow core fibers [235]. WGMs in a fiber-based loop cavity have also shown similar sensitivities of 0.212 nm/K; however, this configuration has been shown to be robust over the wide temperature range of 250–700°C [236]. The thermal response of Nd³⁺-doped barium titano silicate glass microspheres has also recently been explored, and a tuning of 10 pm/K was demonstrated [237].

Although the thermo-optic coefficients of crystalline WGM resonators are typically smaller than those found in polymers, the anisotropy of the crystal allows the differential tracking of two WGM modes of differing polarizations. The different frequency response of TE- and TM-polarized WGM modes can then be used to detect and stabilize temperature, which has been demonstrated down to the nanokelvin regime ~100 nK/Hz^1/2 [238]. In a similar approach [239] a 5 mm CaF₂ disk WGM resonator was used to demonstrate thermometry down to 80 nK/Hz^1/2. In this case, the dual-mode technique does not, however, rely on the anisotropy of the crystal. Instead, two modes with a frequency ratio of approximately 2 are excited in the same resonator, and sensitive measurements of temperature can be realized because of their different temperature dependence. Since anisotropy no longer plays a role this approach can be implemented in a wider range of materials.

For biosensing applications, there are also ongoing efforts to render WGM resonators temperature insensitive and reduce thermal noise. Thermal effects arising from heating of the resonator during excitation of WGMs can cause, for example, a characteristic distortion and broadening of the otherwise Lorentzian lineshape [201]. Cavity perturbations arising from variations in the pump power can be self-correcting [74,201] under certain conditions; however, the use of a thin polymer coating can help to reduce such parasitic effects [182]. Moreover, polymer coatings have also been explored as a means to reduce errors from long-term temperature drifts since these allow tuning of the thermal response of the composite resonators [183,240]. Coatings, such as titanium oxide [241] and silicon, have also been investigated [69].

3.3b. Pressure, Force, and Displacement Sensing

Solid and hollow core WGM resonators have been investigated for pressure sensing. Hydrostatic pressure sensing was found to be feasible in hollow PMMA microspheres [242]. Similarly, tuning of a silica microbubble over wavelength ranges larger than the FSR via variation of the internal aerostatic pressure has also been demonstrated [243]. To render a solid microsphere more sensitive to pressure, a membrane mounted on top of the microsphere can be used as a transducer for the pressure. In this case, the WGM shifts in frequency are due to the mechanical perturbation of the optical mode by the membrane [244]. Acoustic pressure pulses have also been monitored by means of the induced changes in the spectrum of optical WGMs in a quasi-cylindrical microresonator [245]. More recently, perturbations of polar WGMs in solid polystyrene due to the application of uniaxial pressure have been studied [175]. Resonance shifts result due to the change in the optical path length of the WGM and the increase in the local refractive index at the antipodal points of the applied force (which is on the order of millinewtons). Mode splitting was also observed as the applied pressure was increased (see Fig. 16). A similar strategy has also previously been used to monitor deformation of silica and PMMA microspheres [246,247]. Force sensitivity of WGM shifts of 7.664 nm/N, with a resolution of ~10⁻⁵ N, was demonstrated with a 960 µm hollow PMMA sphere. Use of fluorescently doped microspheres has furthermore allowed the direct measurement of the biomechanical stress induced by a live cell during endocytosis [248].

Figure 16.

(a) Experimental scheme for application of a uniaxial pressure to a polystyrene sphere by means of a cantilever. (b) FTIR spectra showing the induced mode shift and splitting upon application of forces of increasing strength. Reprinted with permission from [175]. Copyright 2013, AIP Publishing LLC.

An alternative approach to measuring forces that has attracted recent attention is the use of optomechanical coupling between WGMs and mechanical resonances in, e.g., nearby mechanical resonators or the WGM cavity itself [18,249]. In the former case, a silicon nitride nanomechanical beam was coupled to a disc resonator (see Fig. 17). At room temperature a force sensitivity of 74 aN/Hz^1/2 was reported; however, with the use of dissipative feedback this could be improved to 15 aN/Hz^1/2. For the latter case shot noise limited displacement sensitivities of 10⁻¹⁹ m/Hz^1/2 are achievable [249]. Experimentally, such measurements have been realized with microtoroids held at 1.65 K in a 4He atmosphere. The background noise level of the measurements was around 1.5 × 10⁻¹⁸ m/Hz^1/2, close to the quantum limit [250]. At room temperature, displacement measurements have been demonstrated down to 30 am/Hz^1/2 [251]. These values should be compared to the absolute position displacement sensitivities on the order of 10⁻¹⁹ m/Hz^1/2 achieved with the best present-day optical interferometers, for example, the Laser Interferometer Gravitational Wave Observatory (LIGO) [198]. Rayleigh scattering has also been used to enhance the displacement sensitivity of optomechanical resonators at multi-gigahertz frequencies in the resolved sideband regime [252].

Figure 17.

(a) Scanning electron microscopy image of the hybrid optomechanical force sensor, with (b) zoom in of the coupling region. (c) Optical micrography of the tapered fiber used to couple and read out from the system. (d) FEM simulation of the mode distribution in the resonator near the nanobeam. (e) Mechanical resonance of the nanobeam. Reprinted with permission from [18]. Copyright 2012.

3.3c. Electric- and Magnetic-Field Sensing

Electro- and magneto-striction of a material implies that upon application of an external electric or magnetic field the material undergoes a deformation [253]. Accordingly, use of an electrostrictive or magnetostrictive material as a WGM resonator forms the basis of sensors capable of measuring the strength of applied fields. Accordingly an electric-field sensor has been demonstrated, for example, in PDMS spheres with a 60:1 base silicon elastomer:curing agent ratio [247]. Use of a composite resonator structure, consisting of a silica microsphere with a PDMS coating, was further shown to provide a greater resolution of ~1.85 V/m, as compared to ~200 V/m achieved with a bare PDMS sphere [254]. PDMS microspheres have also been used as the basis for a magnetic-field sensor; however, the addition of magnetically polarizable particles before polymer curing was required to achieve a magnetostrictive response [255].

Hybrid optomechanical resonators are also seeing employ as a means to enhance the sensitivity of field sensors. For instance, by coupling a PDMS cantilever beam to a PDMS microsphere resonator so as to compress the microsphere upon application of an electric field, a sensitivity of dλ/dE = 0.009 pm/Vm⁻¹ was reported representing a 225-fold improvement relative to the bare sphere sensor [256]. Evanescent beam coupling was also explored in the same work. Very recently, a similar hybrid setup was explored by the same group for use as a magnetic sensor [257,258]. Specifically a Metglas slab was mechanically coupled to a resonator via application of a static or harmonically varying magnetic field, such that a sensitivity and resolution of 1.652 pm/µT and 600 nT were realized. A solution more suitable for integration, in which a Terfenol-D disk surrounded by a silica toroidal resonator was used (see Fig. 18), has also recently been demonstrated [16]. This configuration was shown to be particularly sensitive when the magnetic-field modulations excite the mechanical modes of the microcavity. Mechanical oscillations in the Terfenol-D disk then modulate the optical field in the WGM resonator, ultimately yielding a sensitivity of up to 400 nT/Hz^1/2 [16].

Figure 18.

(a) Experimental setup showing a WGM resonator with a Terfenol-D sample attached. (b) Brownian noise spectrum with magnetic excitation at 10.38 MHz. (c) Magnetic-field sensitivity as a function of frequency. (d) System response as a function of applied magnetic-field frequency. Inset: magnified system response centered around 10.385 MHz. Reprinted from [16].

3.3d. Gas Sensing

The use of WGM resonators as gas sensors can derive from a variety of distinct techniques. One such method derives from the use of a coating on the resonator, which is modified upon absorption or adsorption of the desired gas [259]. For example, a humidity sensor based on a hydrophilic coating of SiO₂ nanoparticles has recently been reported [260], as too has ethanol vapor detection using a porous ZnO coating [261]. Polymers and sol-gels represent a more ubiquitous choice of coating, however, with sensing of water vapor [173,262], isopropanol [263], ammonia [264], ethanol [265,266], and hexane vapor [266] having been demonstrated. Due to the variation of chemical susceptibility between differing polymers, and hence the differing magnitudes of associated swelling and/or refractive index changes, chemical discrimination is possible in polymer-based gas sensors by use of multiplexed sensors [266]. Gas chromatography has furthermore also been reported in a capillary resonator that was internally coated with a stationary phase [267]. In this work, detection limits on the order of nanograms were observed, but furthermore different chemical constituents of the gaseous sample could be identified by their differing retention time in the capillary channel. Careful monitoring of resonance shifts due to changes in the surrounding refractive index has also been exploited in self-assembled Rhodamine B doped PMMA hemispherical microlasers for sensing of acetone vapor with a refractive index sensitivity of 130 nm/RIU [268]. On-chip detection of acetylene gas has also been reported [269].

An alternative strategy for gas sensing relies on the responsiveness of WGMs to temperature [74]. In particular, a gas possesses a characteristic thermal conductivity, which can give rise to differing thermal responses. For example, the equilibrium temperature in a thermometry type setup [270] or the thermal relaxation time can be monitored [271], which are both critically dependent on the thermal conductivity of the surrounding gas. Similarly turn-on transients can also be used to discriminate different gases through their thermal conductivity [272].

It is also worthwhile to mention the possibility of using WGM cavities to enhance the absorption spectroscopy of gases [273–275] due to the increased effective absorption path length. In this context, the dip depth of a locked WGM (which is closely related to the resonance linewidth) is monitored, which is modified due to additional absorption losses in the sample gas. This modality has been theoretically shown to give greater sensitivity as compared to frequency-shift and cavity ring-down-based techniques [274], and has been demonstrated for the detection of atmospheric trace gases, such as methane, methyl chloride, and ethene, with a detection limit of ~1000 ppm [273].

Finally, we note that in a similar fashion to gas sensing, it has recently been proposed that absorption of solute molecules by polymer microspheres immersed in a bath can also give rise to shifts in WGM resonance frequencies [172]. Interestingly, by tracking these shifts in real time the anomalous diffusion dynamics of penetrants in glassy polymers can be studied. When glassy polymers, such as polystyrene, are used as the resonator material, a complex process of polymer plasticization, swelling, and erosion can occur (see Fig. 19), such that blueshifts are predicted as the penetrant diffuses across the mode volume, subsequently followed by redshifts associated with resonator swelling (Fig. 19). Ultimately dissolution of the resonator can cause the resonator to shrink with an associated blueshift predicted [172]. The extreme sensitivity of WGMs was shown to imply that absorption of even attolitres of the penetrant could be detected. Moreover, monitoring of dissolution at rates as slow as µm/yr, as are relevant for degradation of environmental plastic pollutants, e.g., PET and polystyrene, is conceivable.

Figure 19.

(a) Schematic of penetrant dynamics upon introduction of a glassy polymer microsphere into a solvent bath. Arrows depict the direction of movement of the polymer interfaces. (b) Temporal evolution of resonance wavelength shift δλ for polystyrene–water polymer-penetrant system. Inset shows radial extent of WGM in an unperturbed 50 µm polystyrene microsphere. Reprinted from [172].

3.3e. Biosensing

WGMs find increasing use as transducers for specific detection of biomolecules [25,27,28]. Particularly attractive for biosensing applications is the capability of a WGM sensor to detect biomolecules in a label-free manner, that is, without requiring any chemical modifications of the analyte molecule. Furthermore, the probing light usually does not alter the biophysical properties of the biomolecule, such as its binding kinetics. Specific biodetection with WGM sensors then relies on recognition of the target analyte by molecular receptors, thereby producing WGM frequency shifts specific to the analyte molecule, which thus necessitates the functionalization of the sensor surface. Biomolecular detection can then be achieved by monitoring the binding of analyte molecules to the receptors, in turn transducing interaction and binding events into detectable optical and electrical signals (see Fig. 20). It is also important to mention that biosensors operate in an aqueous environment, since the mechanisms of molecular recognition require water as the solvent. Examples of receptor molecules that have been used and studied in WGM biosensing applications include oligonucleotides, which bind (hybridize) sequence-specifically to single-stranded nucleic acids [4,277–281]. Other examples include antibodies, which are widely used for detecting proteins [282–286] and aptamers [285,287]. A particular challenge when working with antibodies lies in finding a functionalization protocol that attaches the antibodies to the sensor surface without impeding their specific binding capabilities, maintaining their preferred orientation, etc. [282,288]. Another challenge in all biosensing demonstrations lies in minimizing unspecific interactions at the sensor surface, which can occur, for example, with the various biomolecules present in a complex medium such as blood plasma. The unspecific binding of proteins can generate signals unrelated to the target analyte [281,289,290]. Surface coatings that minimize the unspecific interactions are thus sought [147,281,291,292].

Figure 20.

(a) The principle of WGM biosensing frequently operates by monitoring shifts in the resonance frequency of a WGM upon binding of particles or molecules. (b) Schematic of a typical WGM biosensing setup, wherein WGMs are excited in a microsphere by means of evanescent coupling from a tapered fiber. The sphere is functionalized with receptor molecules, so as to specifically detect the desired analyte molecules. (c) Typical binding trace showing saturation of the wavelength shift as equilibrium is reached. Reprinted from [276].

Biosensing covers a broad spectrum of possible uses, ranging from those requiring lower sensitivity, such as detecting the presence of analyte molecules, to quantitative analysis of single particles requiring much higher sensitivities. We briefly consider each sensing regime across this spectrum in turn.

Quantitative WGM Biodetection with Microspheres

Microsphere WGM resonators are particularly suitable for quantitative readout of the sensor signal since the spherical geometry allows for analytical solutions to the first-order perturbation equation [Eq. (6)], which can be used to determine the resonance frequency or wavelength shift in response to biomolecules binding to the microcavity. For the case of the homogenous and random binding of a biomolecule such as protein or DNA onto the surface of a microsphere resonator, we find that the resonance wavelength shift δλ of a fundamental WGM is related to the surface concentration c_surf of the adsorbed species by [150,293,294]

$$\frac{\delta \lambda }{{\lambda }_0}=\frac{\alpha c_{\text{surf}}}{{\epsilon }_0(n_r^2-n_h^2)R},$$ (13)

where once more α is the excess polarizability of a single biomolecule, ε₀ is the free space permittivity, n_r and n_h are the refractive indices of the microsphere and the surrounding medium, respectively, and R is the radius of the microsphere. The excess polarizability of a biomolecule can hence be obtained from refractive index measurements, more precisely, from measurements of refractive index increments dn_h/dc_sol induced from increasing the concentration c_sol of the biomolecule in solution, according to

$$\alpha =2n_2{\epsilon }_{0}m\frac{d{n}_h}{d{c}_{\text{sol}}},$$ (14)

where m is the mass of the single biomolecule.

Values of dn_h/dc_sol, for the most part, depend on the class of the biomolecule (e.g., DNA, protein, lipid). Examples of some typical dn_h/dc_sol values are given in Table 2 [295]. Combining Eqs. (13) and (14), one can then calculate the surface concentration σ_s of an adsorbed species, and the associated mass loading ρ_s, using the expression [28]

$${\rho }_s={\sigma }_{s}m=\frac{\delta \lambda }{\lambda }\frac{(n_r^2-n_h^2)R}{2n_{h}d{n}_h/d{c}_{\text{sol}}}.$$ (15)

For the case of single nanoparticle binding at the equator of the microsphere where the highest field intensity of a fundamental l = |m| mode resides, we obtain the maximum shift of [149]

$$\frac{\delta {\lambda }_{\text{max}}}{{\lambda }_0}\cong D\frac{a^3}{R^{5/2}{\lambda }_0^{1/2}}\text{exp}[-a/L],$$ (16)

where $D=2n_h^2{(2n_r)}^{1/2}(n_p^2-n_h^2)/(n_r^2-n_h^2)(n_p^2+2n_m^2),L\approx (\lambda /4\pi ){(n_r^2-n_h^2)}^{-1/2}$ is the evanescent field length, n_p is the refractive index of the binding particle, and a is its radius. The scaling factor exp[−a/L] is introduced to take into account the decay of the evanescent field of the WGM across the nanoparticle radius (similar to the factor f in Subsection 2.3)

Table 2.

Typical Values of dn_h/dc_sol for Assorted Biopolymers and Molecules^a

Biomolecule or Biopolymer	dnh/dcsol (cm3/g)at λ0 ≈ 633 nm
Bovine serum albumin	0.183
Deoxyribonucleic acid from calf thymus	0.166
a-chymotrypsinogen	0.171
Dextran	0.147
Gelatin	0.163
Lignin sulfonate—Na	0.188
Mucopolysaccharides	0.110
Polydimethylsiloxane	−0.091
Polyvinyl alcohol 98% hydrolyzed	0.150
RNA	0.160

^aAdapted from [295].

If the nanoparticle does not bind or adsorb to the microresonator, it is possible to use the optical forces provided by the field gradient within the evanescent field to trap the particle near the surface of the microcavity. Additional forces on the nanoparticle, other than the optical trapping force, such as those arising from light absorption and scattering, can then be used to steer the particle around the microsphere in what has been termed a “whispering gallery mode carousel” [296]. As the particle is trapped within the evanescent field of the WGM, resonance wavelength shift signals report on the approximate radial distance h of the nanoparticle from the microresonator surface since

$$\frac{\delta \lambda (h+a)}{\delta \lambda (a)}=\frac{\text{exp}[-(h+a)/L]}{\text{exp}[-a/L]}=\text{exp}[-h/L].$$ (17)

From such measurements of particle position it is possible to extract the confining potential, which is composed of an optical potential attracting the nanoparticle to the microresonator surface, and a repulsive chemical potential preventing the nanoparticle from binding. It is thus possible to use WGM resonators to determine the magnitude of chemical forces that nanoparticles experience at a sensor surface, reminiscent of force measurements with atomic force microscope tips. The trapping of nanoparticles with WGM resonators can also be used to speed up detection by using the optical force to pull the particle to the sensing region [296], or to manipulate the nanoparticles on a WGM biosensor platform for steering and trapping as well as for exposing nanoparticles to molecular analytes [148,296–298].

Detecting the Presence of an Analyte

WGM biosensors probe for the presence of analyte molecules by measuring WGM frequency shifts acquired during exposure of the sensor to the sample. In most WGM biosensor applications a large number of bound analyte molecules are required to generate a detectable signal above the noise floor. Prolonged incubation times are, hence, often needed, such that equilibrium of the binding interaction, producing maximum WGM shifts, can be achieved. The binding of analyte molecules to a receptor-modified sensor surface is, however, a dynamic process in which one discriminates the on-rate constant k_on for binding, defined by dc_surf/dt = k_onc_sol, where c_surf is the surface concentration of the bound analyte and c_sol is the solution concentration of analyte molecules, from the off-rate constant k_off of unbinding, dc_surf/dt = −k_offc_surf. In equilibrium, the sum of both rates is zero, and, in time average, a certain fraction of the binding sites at the sensor surface is saturated with bound analyte molecules, depending on their concentration level in solution (see Fig. 21). To achieve greater surface saturation and hence large WGM biosensor signals (at equilibrium) it is therefore desirable to choose a receptor with a large on-rate constant k_on, combined with a small off-rate constant k_off, i.e., a large affinity. The ratio of the rate constants, known as the dissociation constant K_d = k_off/k_on, should thus be very small. The dissociation constant has units of molarity and signifies the concentration of the analyte solution for which half of the molecular receptors are occupied in equilibrium. With analyte concentrations smaller than K_d the equilibrium sensor signal is smaller. Antibodies, for example, typically exhibit dissociation constants in the nanomolar to femtomolar range. Furthermore, if the incubation time is not long enough the binding reaction does not reach equilibrium. Subsequent measurements therefore also suffer from a small resonance shift.

Figure 21.

WGM biosensor response (sensograms) after exposure to (a) different concentration levels of analyte in solution, affecting the magnitude of the equilibrium shift signal, and (b) initial rate of binding (initial slope), which follows a linear dependence with analyte concentration in solution. (c) shows the measurement of the unbinding reaction from a sensor surface previously saturated with analyte molecules, and (d) shows the dependence of the equilibrium sensor signal on the solution concentration of an analyte. (a)–(c) adapted with permission from [277]. Copyright 2011 American Chemical Society. (d) reprinted from [282]. Copyright 2010, with permission from Elsevier.

Given that the magnitude of induced resonance shifts depends on the number of bound analyte molecules, it is always desirable to achieve a high surface density of receptors during the functionalization process. An upper limit, for a monolayer receptor density on a glass surface, of ~5 × 10¹⁴/cm² has been estimated, approximately corresponding to the density of the glass silanol groups [299]. The time it takes to acquire a large sensor signal in WGM biosensing is further affected by mass transport limitations at the sensor surface. Rapid binding to the sensor can reduce the local number of free analyte molecules, so that a depletion layer forms in the region close to the sensor surface. The effective concentration of analytes in the depletion layer can be much lower as compared to that of the bulk sample solution, therefore slowing down the binding kinetics [147,300].

To amplify a signal in WGM biosensing one can introduce labels. In one recently demonstrated strategy for labeling, the WGM frequency shift signal is amplified by specifically binding a secondary antibody to the already bound analyte molecules, where this antibody is further tethered to a nanoparticle with a large polarizability [301]. In a related approach enzymes are used as labels tethered to secondary antibodies, so that the enzymes produce an insoluble product on the sensor surface after binding of the secondary antibody to the analyte [302]. A different molecular enhancement strategy addresses the problem of oligonucleotide receptors that exhibit effective dissociation constants in the nanomolar range. In the work of Wu et al. [281] the WGM transducer does not track the hybridization of DNA strands, as in a conventional approach. Instead, the oligonucleotides at the sensor surface are already hybridized, and DNA nanotechnology is used to implement a strand displacement reaction (see Fig. 22). The strand displacement reaction is triggered by an analyte oligonucleotide that effectively displaces a single strand from its receptor molecule at the sensor surface, thereby dehybridizing the sensor. Since the analyte molecules are not consumed in this process a single analyte molecule could, in principle, dehybridize a complete WGM sensor, in a catalytic strand displacement reaction lasting for many dehybridization cycles. Using this approach, the detection limit for nucleic acids could be extended by orders of magnitude as compared to direct hybridization, well into the pM range [281]. Interestingly, this approach decouples the sensor signal from the mass of the analyte, affording another means for signal amplification by unloading of large oligonucleotides. The sensor is also reusable for subsequent detections of different nucleic acid strands.

Figure 22.

DNA strand displacement reaction to amplify a WGM biosensor signal. (a) DNA catalytic pathway. C is the nucleic acid detection target that triggers the displacement of DNA strands S and B from the strand P that is attached to the microresonator. The fuel strand F in the surrounding solution drives the catalytic reaction. (b) Catalytic strand displacement causes the unloading (dehybridization) of DNA from the microsphere surface; only DNA strand P remains attached to the microsphere via biotin–streptavidin. Reprinted from [281].

Detecting the Concentration of an Analyte

Going beyond determining the absence or presence of a given analyte is to use WGM biosensors to quantitatively determine the concentration of the analyte molecules in a sample solution. The concentration of analyte can be inferred from the sensor signal generated from surface bound analyte molecules in equilibrium. Specifically, to determine the analyte concentration in solution one needs to know the binding isotherm, that is, the dependence of the amount of specifically bound analyte molecules, and thus the WGM biosensor signal, as a function of analyte concentration (at a fixed operating temperature of the sensor). For independent binding sites, this dependency is described by the Langmuir isotherm [293]. More often, however, the binding mechanism and the dose-response of the sensor are more complicated [147]. In practice, one therefore often calibrates the sensor experimentally to determine the dose-response [282,292]. Alternatively, the concentration of an analyte can also be determined by measuring the on-rate of analyte binding (see Fig. 21), that is, the binding rate, or rate of change of (surface) concentration dc_surf/dt. After first exposure of the sensor surface to the analyte solution, firstorder binding kinetics ars observed, where the binding rate is simply the product of the on-rate and the solution concentration of the analyte, i.e., dc_surf/dt = k_onc_sol [278]. Depending on the sensitivity of the device, which may be able to detect a few, if not single molecules, this method for determining the analyte concentration could be much faster as compared to equilibrium measurements. Another aspect to consider is the total number of receptors, since the rate of change of the sensor signal scales in proportion. Particularly plasmon-enhanced WGM sensors, which boast the highest sensitivity, resolving even single molecule interactions [4], face the challenge of providing enough receptors to determine the concentration of dilute analyte solutions within reasonable time scales [164,167,211].

Single Molecule Biosensing

Very recently, WGM biosensing (as opposed to “biodetection”) has been demonstrated at the single molecule level [4], introducing a new paradigm in WGM sensing. A useful single molecule biosensor should yield information on more than one detection event, allowing for continuous measurements of molecular interactions between the receptor and the analyte molecules in the sample solution. In single molecule biosensing, one thus requires receptors of tailored affinity, since monitoring the binding of a single molecule to a high affinity receptor would simply block the single receptor for subsequent measurements. Such receptors of tailored, modest affinity can be easily designed with nucleic acids, by choosing oligonucleotides with certain sequence lengths [4]. The interactions between a short oligonucleotide and its matching strands are then fleeting, due to the limited number of interacting bases. A WGM sensor functionalized with such tailored, short oligonucleotide receptors can then resolve the transient interactions with complementary strands, recording spike-type events for each specific interaction (see Fig. 23). This approach to single molecule biosensing extends the sensor lifetime so that one can record a large data set, which is then amenable to subsequent statistical analysis.

Figure 23.

(a)–(d) Single molecule biosensing. Different interaction kinetics are observed for single nucleic acids with matching and mismatching sequences. The analyte strand interacts with an oligonucleotide receptor attached via a nanorod to the microresonator surface, thereby leveraging plasmonic WGM signal enhancements. (e) The time intervals between successive single molecule interaction events follow an exponential distribution, indicative of single molecule events. (f) The rate of single molecule interaction events scales linearly with analyte concentration, indicating a single molecule reaction that is governed by a first-order rate equation. Adapted from [4].

Spikes in the WGM resonance shifts signify individual single molecule interaction events, where the time intervals between individual interactions follow an exponential distribution indicating underlying Poisson statistics (see Fig. 23), a further proof for observing single molecules independent of the transducer [4]. The rate of the recorded interactions is directly proportional to concentration of the analyte molecules in solution (see Fig. 23), allowing for continuous concentration measurements with high time resolution and over an extended sensor lifetime. Furthermore, the interaction time for each single molecule event, meaning the dwell time of the analyte molecule at the receptor, which is signified by the duration of the individual spike signals, reports on the specificity of the interaction. For example, a perfectly matching strand resides longer at the oligonucleotide receptor as compared to a DNA strand that carries a single nucleotide mismatch. With this single molecule biosensing scheme that resolves the specificity of molecular recognition in the time domain, it is possible to discriminate matching DNA strands from strands that carry only a single nucleotide mismatch from their markedly different interaction kinetics with a tailored oligonucleotide receptor [4].

Single Molecule WGM Biosensing in Comparison to Other Technology Platforms

There are very few biosensor technologies that exhibit a single molecule detection capability on a sensor structure that can be potentially integrated in a chip-scale device. In Table 3 we compare the WGM single molecule biosensor to other technology platforms capable of single molecule detection. We thereby restrict our comparison to device technologies. As can be seen from Table 3 a WGM single molecule biosensor boasts a number of capabilities and advantages. As compared to nanoplasmonic devices, which rely on microscopy and a spectrometer for acquiring the plasmonic sensor response, a WGM sensor transduces the optical response of a plasmonic nanoparticle upon binding of a biomolecule into a WGM shift signal. The coupled WGM-plasmonic sensor thereby exhibits a much higher sensitivity as compared to that reported for solely photonic or plasmonic platforms. WGM sensors furthermore exhibit a time resolution that is yet unmatched by any of the other approaches. Using pulsed tunable laser excitation of the microcavity at a fixed laser wavelength that is slightly detuned from the WGM resonance, “cavity ring-up spectroscopy” (CRUS) [232] enables a temporal resolution that is limited only by the cavity Q factor, or about 100 ns, in a typical single molecule WGM biosensing experiment. Compared to nanopore sensors that operate in the electrical domain, optical WGM biosensors have the advantage of directly harnessing the specificity provided by a biomolecular receptor. WGM sensors are furthermore not limited to the use of pore molecules or artificial pores. In addition, WGM biosensing is not compromised by the fast transit times of analyte molecules passing through nanopore sensors, which often complicates their specific detection. As compared to the zero-mode waveguide (ZMW) technique, WGM biosensors do not rely on fluorescent labels and exhibit much higher time resolution, making it less likely that any single molecule events will be missed, which is one limitation of ZMW-based DNA sequencing. The fluorescence-based ZMW approach may be more difficult to implement, and labeling restricts its use to certain molecular systems. ZMW sensing is also currently limited to a maximum time resolution of several milliseconds. Field-effect transistors based on carbon nanotubes possess similar label-free detection capabilities to WGM biosensors. The electrical approach, however, can be more difficult to implement and the nanotube more difficult to handle in comparison to a plasmon-enhanced WGM sensor. Field-effect transistors are also more prone to fluctuations of the ionic strength of the buffer solution, and carbon nanotube surface functionalizations may be more difficult to achieve.

Table 3.

Comparison of WGM Single Molecule Biosensing to a Selection of Other Technology Platforms

Sensor [Example Ref.]	WGM, Plasmon Enhanced [4,167]	Nano-Plasmonics [9,11]	Nanopores [303–305]	Zero-Mode Waveguide [306]	Carbon Nanotube Field-Effect Transistor [6]
Sensor domain	optical	optical	electrical	optical	electrical
Sensor structure	glass microsphere+plasmonic nanoparticle	plasmonic nanoparticle (nanorod)	alpha-hemolysine or solid-state nanopore	zero-mode metal-clad waveguide with fluorescence excitation and readout capability	carbon nanotube field-effect transistor
Specificity	directly monitoring specific interaction kinetics of a receptor, i.e., a short oligonucleotide receptor	by monitoring binding events to high affinity receptors such as streptavidin	modified for specific detection; analyte binding results in pore blockage; sequencing from sensor response during DNA translocation; sequencing by digestions	monitoring enzyme kinetics using fluorescent labels, i.e., DNA polymerase using fluorescent nucleotide analogs for sequencing applications	directly monitoring specific interaction kinetics of a receptor, i.e., a short oligonucleotide receptor
Current sensitivity	<2.4 kDa short oligonucleotide, <1 kDa intercalating molecules	~50 kDa protein (streptavidin)	single nucleotide in sequencing by digestion approach	single fluorescently labeled nucleotide	short oligonucleotide
Current time resolution	limited by Q-factor, ~100 ns	~ms	~sub-ms	~ms	~ms
Multiplexing	yes	yes	yes	yes	yes
Receptor molecule properties	transient interactions are monitored; use of nonconventional receptors, e.g., short oligonucleotides, enzymes, low affinity receptors, possible	demonstrations thus far use high affinity receptors	nanopore only, where specific detection relies, i.e., on sequencing by digestion or on modification of the nanopore with specific analyte binding sites	fluorescence labeling required; DNA sequencing has been demonstrated	transient interactions can be monitored, demonstrated for short oligonucleotide receptors monitored at different temperatures
Sensor lifetime	extended sensor lifetime, limited by receptor kinetics and lifetime; no saturation of receptor required	detection requires saturation of receptor	extended sensor lifetime, limited by blockage of pore	limited by lifetime of polymerase	no saturation of receptor molecules is required

Nanoparticle Sizing

WGM sensors can be used to extract further information about analyte molecules and particles. One important capability of WGM sensors is to determine the size of nanoparticles, and potentially the size of biomolecules. This has been demonstrated in the past with influenza virus particles, where statistical analysis of the sensor signal was required to estimate the virus size, ~100 nm, from WGM frequency shift signals [149,307] (see Fig. 24). Sizing of polystyrene beads as small as 12.5 nm was also demonstrated in the same work. A statistical analysis was necessary since the magnitude of the WGM shift signal depends on the binding locations of the individual virus particles, which are randomly distributed on the sensor surface. Statistical analysis of resonance shifts has also been used in, for example, Refs. [149,165], while a correlation-based analysis of resonance fluctuations was employed in Ref. [308]. A theoretical investigation of a statistical analysis of mode splitting for particle sizing has also recently been undertaken [161].

Figure 24.

(a) Schematic of WGM biosensor with transmission spectrum. (b) Steps in resonance frequency observed upon binding of individual Influenza A virions (inset). Adapted from [149] [Copyright (2008) National Academy of Sciences, U.S.A.].

More recently, a mode splitting sensing mechanism in combination with linewidth measurements was introduced to demonstrate single shot sizing of particles. This was possible since the derived sensing signal is insensitive to the nanoparticle binding position, and has even been demonstrated in aqueous solution [185,186]. This technique, however, requires a large Q factor so that the frequency splitting of the modes (= 2δω) is larger as compared to their intrinsic WGM linewidth: 2δω > Γ. This sets a lower bound for nanoparticle sizing, where the achievable precision depends on the Q factor and the noise floor (see Fig. 25), with relatively accurate sizing demonstrated down to ~40 nm radius polystyrene nanoparticles [188].

Figure 25.

WGM resonator will experience either a reactive shift or mode splitting depending on the size of a binding polystyrene particle, the quality factor of the resonance, and the noise level in the system. There are four possible regions: (1) mode splitting with highly accurate size measurement, (2) mode splitting but with erroneous size measurement, (3) reactive shift (mode splitting cannot be resolved or does not take place) with accurate size measurement, and (4) reactive shift with erroneous size measurement. The areas of these regions depend on the diameter (D) of the resonator, (a) D = 80 µm and (b) D = 53 µm. Reprinted with permission from [188]. Copyright 2012 Optical Society of America.

In another novel sizing method, the frequency perturbation of WGMs of different azimuthal mode orders, in slightly elliptical spheroidal resonators, was used as a sensing signal [115]. Due to the differing overlap of the WGM with the binding particle, differing frequency shifts are observed, from which, with analytic knowledge of the mode profiles, the latitude of the binding particle can be determined. With knowledge of the the particle location, a statistical analysis of frequency shifts is again no longer necessary, such that single shot sizing can again be realized [115].

WGMs Combined with Fluorescence and Other Spectroscopies

Fluorescence readouts are useful for working with WGM in the low-Q regime, where the WGMs are identified in the fluorescence spectra of polymer beads soaked or doped with a fluorescent molecule. This approach has been used extensively to develop a fluorescence-based WGM biosensor platform [309–313] (see Fig. 26). In another more recent demonstration ~10 µm WGM fluorescent beads are incorporated in microstructured fibers [314]. Fiber tips have also shown high efficiency for exciting WGMs in fluorescent microbeads [315]. Fluorescent droplets in a microfluidic structure were used to read out WGMs [316], while fluorophores in the solution surrounding spherical beads have been shown to aid the fluorescence readout of WGMs [317]. Fluorescent beads as WGM sensors have also shown interesting in vivo applications, for transducing forces that deform a polymer WGM sensor during phagocytosis of such beads by cells [248]. There is interest in combining WGM biosensing with other spectroscopies, for identifying substances and for aiding specific detection tasks. First demonstrations of combining Raman spectroscopy with microcavities show that Raman spectra can be acquired with such biosensing platforms, where optical trapping of silver particles can aid in generating surface enhanced Raman signals [318]. In another demonstration of combining fluorescence with WGMs, fluorescence spectroscopy has also been used to quantitatively sense green fluorescent proteins by detecting the size distribution of clusters of antibody-coated particles bound by the proteins [148].

Figure 26.

Fluorescence emission of dye-doped polystyrene beads of (a) ~8 µm and (b) 10 µm in diameter, respectively, immersed in water, exhibiting WGM excitations (line I). Line II shows the fluorescence emission of odd-shaped particles that do not support WGMs. Line III shows the difference spectra of (I) and (II). Reprinted from [309]. Copyright 2014 The EPJ Publishing Consortium. With kind permission of The European Physical Journal (EPJ).

Biosensing of Specific Molecular Systems and Sensor Functionalization

Various molecular systems have been studied with WGM biosensors in combination with different surface functionalization protocols. In the context of biosensing, ligand-receptor type interactions based on antibodies conjugated to the sensor surface have recently been explored by heterobifunctional crosslinking of 4-formylbenzamid modified antibodies to 3-N-((6-(N-isopropylidenehydrazino)) nicotinamide)propyltriethoxysilane (HyNic Silane) modified silicon ring resonators, where the thermal oxide layer on silicon is utilized for functionalization with the silane reagent. Using this conjugation protocol, single domain antibodies for detection of the toxin Ricin have been tested [288], as well as the specific detection of intact plant viruses in both purified samples and extracts of ground plant leaves [319].

For nucleic acid detection by receptor-ligand type interactions between single-stranded DNA strands, epoxy groups have been conjugated to glass microtoroids via silane chemistry so that covalent bonds can be formed to amine-modified oligonucleotides. With this protocol, detection of complementary DNA strands has been achieved down to the nanomolar concentration range [279]. In another nucleic acid biosensing approach, biotinylated oligonucleotides are attached via streptavidin to a glass microsphere coated with a biotin–dextran layer, resulting in ~10¹³ oligonucleotide receptors/cm² for direct detection of hybridization, or detection of strand displacement reactions via a catalytic DNA network [281]. This nucleic acid detection protocol uses DNA nanotechnology to extend the thermodynamically controlled detection limits of equilibrium nucleic acid assays well into the picomolar concentration range (<80 pM), and allows the same sensor to be regenerated and reused for subsequent detections of different nucleic acids targets, in purified as well as complex sample solutions. In another approach to nucleic acid detection, RNA (tmRNA) was detected using HyNic Silane modified silicon ring resonators, where in this case amine-modified oligonucleotides were further modified with succinimidyl-4-formylbenzoate, introducing the aryl aldehyde group for conjugation to the HyNic Silane [320]. This and other HyNic Silane demonstrations exemplify the seemingly broad applicability of the HyNic Silane based protocols for functionalizing WGM biosensors with different receptor molecules.

Nucleic acid detection was also studied with plasmonic–photonic WGM biosensors where a particularly simple thiol chemistry protocol has been identified [321], for covalently attaching thiol-modified oligonucleotides to gold nanorods or other gold nanoparticles, requiring only minutes of reaction time [4]. Interestingly, the thiol modification procedure itself can be followed in situ and in real time on the single molecule level using the plasmon-enhanced WGM biosensor platform.

A particularly attractive functionalization strategy uses the light itself to drive a photochemical reaction for conjugating specific receptors to WGM sensors, ideally conjugating the receptors only to the part of the sensor surface that is probed by the WGM mode (see, e.g., Fig. 27). In one demonstration of this strategy, external UV light is used to attach benzophenone-dPEG3-biotin to polymer microgoblet resonators, for subsequent detection of streptavidin [322]. A similar strategy for selective WGM biosensor functionalization relies on a PDMS stamp instead of light. This allows the functionalization procedure to be scaled up, so that many resonators can be modified in parallel. It was shown that different polymer (PMMA) microgoblet WGM laser biosensors can be modified with different chemicals using such a micro contact stamping technique [49]. The PDMS stamp was patterned with different chemicals (“inks”) by polymer pen lithography (see Fig. 27). The technique was then used to modify sensors with 2,4-Dinitrophenol (DNP), so as to demonstrate the biosensing potential by subsequently detecting anti-DNP. Molecules, such as receptors, and other molecular systems are often embedded in lipid-bilayer membranes, and to study these biosystems with WGM biosensors surface functionalization protocols are needed that introduce a membrane or membrane patches onto the sensor surface. Membranes often form on a surface by self-assembly from solutions, and this strategy has been used to coat dimethyldiallylammonium chloride (PDAC) modified glass WGM microsphere resonators with bactriorhodopsin membranes in a layer-by-layer self-assembly protocol. The bacteriorhodopsin-coated WGM sensor was then used to demonstrate the detection of photoinduced conformational changes, monitoring TE and TM WGM shifts in parallel (see Fig. 28), as well as to demonstrate all-optical switching [192,323,324]. More recently, membrane nanodiscs as a model system for natural membranes were attached to silicon ring resonators. Specifically, nanodiscs containing the glycolipid receptor GM1 were immobilized to the sensor surface by direct physisorption to test its interaction with the B subunit of cholera toxin (CTB) [325]. Also more recently it was shown that a WGM glass microsphere can be coated by vesicle fusions from a solution of small unilamellar vesicles formed from 1,2-dipalmitoyl-sn-glycero-3-phoshphocholine and 1,2-dioleoyl-sn-glycero-3-phoshphocholine, and cholesterol [326]. WGM sensor surface coatings can reduce the Q factor, yet maintaining a high Q factor is particularly important in mode-split WGM biosensing. A recent study has thus analyzed the effects of surface coatings on the accuracy of mode-split biosensing measurements [327].

Figure 27.

Schematic of stamp pad technique for parallel functionalization of goblet resonators. (a) Large-scale uniform surface functionalization. (b) Multiplexed surface functionalization using an array of phospholipids with different functional head groups [49]. Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with permission.

Figure 28.

(Top) Schematic of TM (left) and TE (right) WGMs in a dielectric microsphere. (Middle) Three-dimensional ribbon model of seven transmembrane α helixes representing the structure of bacteriorhodopsin embedded in a lipid bilayer with a covalently bound chromophore. (Bottom) Transmission spectra for TM and TE WGMs, showing a resonance shift upon photoexcitation of the adsorbed bacteriorhodopsin (left) and dynamics of a photoinduced transformation observed by tracking TM and TE WGMs (right). Adapted from [192].

The study of protein adsorption is also particularly important since protein adsorption is often the main cause for unspecific signals in WGM biosensing. Understanding the cause of these false positive signals and how to avoid the associated background by blocking of unspecific binding sites is an ongoing effort in WGM biosensing. For example, covalently bound poly(ethylene glycol) (PEG) coatings of varying thickness were investigated as an effective treatment for the prevention of nonspecific protein adsorption onto the biosensor surface [289]. Another study has examined the effect of different silane coatings on a glass microsphere on the kinetics of fibronectin adsorption by testing hydrophilic, neutral hydrophobic, and charged hydrophobic silanized glass surfaces [147]. Also very recently, the mechanisms of adsorption of glucose oxidase enzymes on differently silanized glass microspheres were studied in combination with enzyme activity assays [328]. Unspecific protein adsorption, such as that of BSA, is also often used as a first test of a WGM transducer. For example, first demonstrations of plasmon-enhanced microcavity biosensing relied on this scheme [164,211]. Recent demonstrations with BSA of multimodal sensing in bottle resonators demonstrate detection of BSA adsorptions at the sub-fM concentration level [329].

The parallel detection of many biomarkers (multiplexed detection) is an important goal for demonstrating a biosensor applicable for clinical diagnostics [195]. Recent demonstrations involve the multiplexed detection of cancer biomarkers [290,292,330] and secreted proteins [283]. Multiplexed detection is also important for WGM sensing modalities that rely on WGM imaging [317].

4. Outlook

4.1. Physical Sensors

Photonic devices based on the excitation of WGMs are among a multitude of state-of-the-art physical sensors available today. Two important obstacles currently facing the next generation of WGM sensors are specificity and on-chip integration. One proposal for addressing the problem of specificity relies on inelastic scattering, whereby Raman spectroscopy is combined with WGM sensing to obtain a molecule-specific “fingerprint” of the molecule that is being detected [331]. This could dramatically improve the reliability of current sensors. Another avenue for improving device reliability is complete integration of the WGM sensing system onto a single chip. As microfabrication technology continues to develop, the “resonator in a lab” setups, which have thus far enabled precision measurements of atoms and molecules, could be transformed into a portable “lab on a chip” technology. Chip-based designs benefit from improved mechanical stability, reproducibility, and ease of use. For some applications, such as magnetometry and molecular diagnostics, these improvements will be essential, as many measurements to date have relied on specific and strictly controlled laboratory conditions for operation and would be impractical for many realistic situations due to long-term drifts. Since on-chip photonic devices can be readily modified, they will also enable the engineering of plasmonic hotspots for improved device sensitivity, and simplify integration with microfluidics, cryogenics, as well as other existing technologies such as atom chips. By enabling operation in new environments and allowing for more quantitative measurements these improvements could broaden the physical scope of WGM sensors into both fundamental physics and new branches of applied science.

WGM resonators may potentially allow for the discovery of new physics due to the high optical field strength encountered on plasmon-enhanced WGM biosensors, with opportunities for highly sensitive experiments in nonlinear optics, and measurements of excited-state polarizabilities associated with different excitations in single (fluorescent) molecules. Real-time detection of the photophysics of single molecules is another exciting possibility, as well as the parallel detection and optical manipulation at the single molecule level. Optical nonlinearities, accessible through high field strengths and long photon lifetimes, are also important for WGM-based frequency combs, which are extremely useful in metrology, precision measurement, and sensing applications [332].

Further opportunities are afforded by coupling of multiple WGM resonators, in a similar manner to the use of multiple WGMs within a single resonator. Clearly, coupling multiple WGM resonators together is highly contingent upon microfabrication capabilities, since coupling relies on modes with nearly degenerate resonance frequencies. Nonetheless, a variety of experiments have been carried out for the two-resonator case [333], where the resonance frequency of one resonator can be tuned on resonance with the second thermo-optically. It is well known that interference effects in coupled optical resonators can produce classical all-optical analogues to quantum effects such as electromagnetically induced transparency. Because the transparency window is characterized by a sharp high-Q feature superimposed over a resonance with lower Q, these effects could in theory improve the performance of WGM sensors. In addition, coupled resonator systems can been used for counteracting loss in optical devices, which has important consequences for lasing applications [334].

In addition to the applied sciences, the strong interaction between light and matter in WGMs makes WGMs valuable tools for probing fundamental physics. At cryogenic temperatures, for example, WGMs can allow readout of the quantum ground state of a micromechanical oscillator [20]. This is generally considered to be the starting point for experiments in quantum optomechanics, a field still in its early stages, which is aiming to measure and manipulate quantum behavior in macroscopic objects [335]. Some more exotic mechanical systems, such as a cloud of ultracold atoms [336] or a film of superfluid helium [337], which are well known for certain quantum properties, can also be optomechanically coupled to WGMs. The quantum behavior of the smallest of replicating biological entities, such as viruses, could also be investigated with quantum optomechanics [338]. In general, it is anticipated that these types of experiments will be able to address questions related to the transition from quantum to classical physics, and hopefully elucidate the role that is played by quantum mechanics in everyday phenomena.

4.2. Biosensing

WGM biosensors have proven unprecedented sensitivity levels for the optical detection of label-free biomolecules such as DNA and small intercalating molecules. Advances to date were made possible by the use of plasmonic enhancements, active cavities, and other techniques described in this work. This progress now positions WGM devices among the most sensitive devices in the biosensing field, particularly in comparison with other label-free technologies that can potentially be integrated on chip-scale devices, such as nanoplasmonic systems, FET nanowires, nanomechanical cantilevers, and nanopores. With recent improvements in the engineering and integration of more robust WGM platforms that, for example, use prism couplers or integrated waveguides for evanescent coupling, these biosensors can find a multitude of applications for studies in bioengineering and the life sciences. Particularly attractive is the simplicity of this technology for single molecule detection, enabling important studies into the mechanisms of nanomachines. Biotechnologists and biochemists have always been fascinated by the mechanisms of single enzymes and single motor proteins as well as the self-assembly of larger systems such as ribosomes or virus nanoparticles—not only to understand the fundamental biological and physical mechanisms governing these natural processes, but also because of their potential applications in future devices. WGM biosensors have now entered the arena of single molecule studies providing a new and important tool to study nanomachines in a label-free fashion, in particular not requiring fluorescent labels or tagging of a protein by a microparticle as is required, for example, when working with optical tweezers. Furthermore, the capability of monitoring single molecules with WGM biosensors is not limited to a particular class of biomolecule. Instead, WGM biosensors can monitor any kind of biomolecule, such as DNA, RNA, protein, or lipid-based molecules and assemblies in contrast to label-based techniques such as fluorescence-based techniques or nanopores that are often restricted to analyzing certain membrane channels, such as hemolysine pores. With the extreme sensitivity in hand and, furthermore, the important ability to monitor single nanomachines and interactions between biomolecules with a time resolution potentially much higher than achievable with current fluorescent-based techniques, WGM biosensors are poised to play an important role in revealing the physical and biological mechanisms that govern biological processes at the nanoscale. This, in return, can lead to many important applications that harness the functionality of the biological nanoworld. A single molecule biosensor can monitor biomolecular properties that are otherwise obscured in ensemble measurements. For example, a single molecule biosensor could resolve the fleeting interactions between a molecule and its receptor, with immediate applications in clinical diagnostics, enabling the use of receptor molecules other than high affinity antibodies. Enzymes would be particularly well suited for detection by molecular recognition since they provide the highest specificity by the “lock-and-key” and “induced fit” mechanisms upon transient ligand binding, enabling the detection of even small molecules that would otherwise go undetected by antibodies. Furthermore, monitoring the transient interactions of enyzmes and other nanomachines prolongs the WGM sensor lifetime and enables real-time detection of variations in analyte concentration. Specific molecular interactions in single molecule WGM biosensing furthermore translate into the detection of the specific dwell time of a ligand at the binding site, which is a measurable quantity for assessing the specificity of individual molecular interaction events. The ability to monitor molecular interactions transiently also opens up the possibility for new drug screening approaches, and may enable new biomarker discovery, ligand fishing, and identification of hitherto unknown ligands for commonly known drug targets. After integration in a microfluidic system it will be possible to implement high-throughput approaches that are used to screen for transient molecular interactions. Single molecule biosensors will aid detailed studies into the physics and engineering principles of biological molecules, nanosystems, and biological nanomachines, and will enable new diagnostic and other portable devices that leverage the functionalities found in these systems.

To translate the WGM technology into robust devices such as biosensor microchips, multiplexed and portable environmental monitors, bedside blood- and urine-diagnostic systems, and other lab-on-chip devices, studies in clinical settings are already underway that leverage the improvements in device integration, not only of photonic and plasmonic components but also of microfluidics and electrical components. Establishing the engineering principles and steps to assemble and produce a robust biosensing platform, ultimately on a microchip, will enable the broad use of WGM devices for health and environmental monitoring, and will also open up different routes to commercialization. We foresee a future in which technology, and nanotechnology in particular, will continue to evolve, a future in which we will use not only electronic microchips for computation, but also photonic microchips equipped with microcavities to interface with the surrounding biological world, and biosensors that can sniff out single molecules, that can detect disease proteins at the earliest possible stage, and that can harness the extreme speed and selectivity of enzymes. Such devices can not only spawn new industries but also allow diseases to be diagnosed more rapidly and accurately, enable immediate and personalized access to biological information, and enable the rapid acquisition and subsequent storage of such information. Perhaps biosensors will ultimately evolve into interfaces that allow two-way communication between biological systems and microdevices, morphing the current one-way biosensors into two-way interfaces, with applications as implants, organ-on-chip devices, or neuronal links.

Biographies

Matthew R. Foreman received his Ph.D. in Physics from Imperial College London, UK, in 2010. Thereafter he was awarded an Engineering and Physical Sciences Research Council (EPSRC) Ph.D. Plus fellowship for the continuation of his work on single molecule polarization microscopy. In 2010 he also held a visiting lecturer position at the National Yang Ming University in Taiwan working within the Modern Optics Laboratory. Subsequently, he was based at the UK National Physical Laboratory within the Engineering Measurement Department, where his work focused on the calibration and correction of optical instruments in surface metrology. In 2012 he took up a Max Planck Postdoctoral Research position at the Max Planck Institute for the Science of Light in Erlangen, Germany, before being awarded an Alexander von Humboldt Research Fellowship in 2013 for his work on hybrid plasmonic–photonic whispering gallery mode sensors.

Jon D. Swaim received his Ph.D. in Physics from the University of Queensland for his work on whispering gallery mode sensing. Subsequently, he moved to the Max Planck Institute for the Science of Light in Erlangen, Germany, where he continued his research on high time resolution biosensing. His current research interests include optical sensing, optomechanics, and quantum information science.

Frank Vollmer obtained his Ph.D. in “Physics and Biology” from the Rockefeller University, New York City, New York, in 2004. He then became the leader of an independent research group at the Rowland Institute at Harvard University where he was appointed Rowland Fellow from 2004 to 2009. From 2010 to 2011 he joined the Wyss Institute for Bio-Inspired Engineering at Harvard University as a Scholar-in-Residence. In 2011 he was appointed group leader (untenured associate professor) at the newly established Max Planck Institute for the Science of Light in Erlangen, Germany. Since 2011 he has also been appointed as an Instructor in Medicine and an Associate Bioengineer at Brigham and Women’s Hospital/Harvard Medical School in Boston, Massachusetts, where he directs a satellite laboratory.