Numerical geometry of map and model assessment

Abstract

We are describing best practices and assessment strategies for the atomic interpretation of cryo-electron microscopy (cryo-EM) maps. Multiscale numerical geometry strategies in the Situs package and in secondary structure detection software are currently evolving due to the recent increases in cryo-EM resolution. Criteria that aim to predict the accuracy of fitted atomic models at low (worse than 8 Å) and medium (4–8 Å) resolutions remain challenging. However, a high level of confidence in atomic models can be achieved by combining such criteria. The observed errors are due to map–model discrepancies and due to the effect of imperfect global docking strategies. Extending the earlier motion capture approach developed for flexible fitting, we use simulated fiducials (pseudoatoms) at varying levels of coarse-graining to track the local drift of structural features. We compare three tracking approaches: naïve vector quantization, a smoothly deformable model, and a tessellation of the structure into rigid Voronoi cells, which are fitted using a multi-fragment refinement approach. The lowest error is an upper bound for the (small) discrepancy between the crystal structure and the EM map due to different conditions in their structure determination. When internal features such as secondary structures are visible in medium-resolution EM maps, it is possible to extend the idea of point-based fiducials to more complex geometric representations such as helical axes, strands, and skeletons. We propose quantitative strategies to assess map–model pairs when such secondary structure patterns are prominent.

1. Introduction

In the past decade, significant progress has been made in the 3D imaging of macromolecular assemblies via cryo-electron microscopy (cryo-EM) and in the development of computational algorithms that interpret the resulting volumetric maps at atomic resolution. Modern CMOS detectors combined with movie frame stacking have eliminated much of the specimen drift that has limited cryo-EM imaging using earlier detectors. The new direct detection camera technology is a major breakthrough toward higher-resolution cryo-EM reconstruction (Jin et al., 2008). The new imaging techniques enable the production of many 3D density maps that, at the highest resolution end of the scale (better than 3.4 Å), allow atomic structures to be solved directly. De novo models from high resolution maps (4 Å or better) can also be improved with crystallographic refinement techniques.

Major secondary structure features can be reliably detected in medium (4–8 Å) resolution maps, and structural components can be fitted and docked at even lower resolutions. Although medium to low resolution maps are not currently making headlines, there is an increasing number of such fitted models deposited to public databases and models are being met with significant scrutiny (Henderson et al., 2012). We are concerned with validation strategies and best practices that would help maintain high standards for the structure deposition of such fitted models.

For medium to low resolution maps, electron microscopists have a choice among dozens of rigid body and flexible fitting packages (López-Blanco and Chacón, 2015). In the following study, we describe features of the Situs package, which was first released in 1998 (Wriggers, 2012). The Protein Data Bank (PDB) uses the “Situs colores program to identify transformation matrices that allow spatial overlap of maps deposited to the EM Data Bank (EMDB) and models deposited to the PDB so that they can be viewed together,” and finds “that the unique algorithm in colores is able to identify optimal fit positions even in tricky cases, e.g., where only part of a structure is modelled” (Lawson, 2014). Among 1,014 EMDB entries with an associated atomic model in the PDB (Lawson, 2014), modelers identified the software used in 204 unique cases. The top six programs are as follows: (1) UCSF Chimera (Pettersen et al., 2004; 61 models), (2) MDFF (Trabuco et al., 2008; 28 models), (3) Situs (26 models), (4) EMFit (Rossmann et al., 2001; 24 models), (5) Coot (Emsley et al., 2010; 12 models), and (6) Rosetta (DiMaio et al., 2009; 11 models). We note that the top three programs are complementary (Chimera is widely used for visualization, MDFF is used for molecular dynamics simulations of high-resolution maps, and Situs is traditionally used for rigid-body docking at medium to low resolution).

In this whitepaper, our aim is to focus on opportunities, challenges, and aspirations as they relate to software developed in our laboratories. Numerical geometry methods are described in more detail in figure captions. We proceed in order of increasing cryo-EM resolution as follows. In Section 2, we summarize best practices of model evaluation, which are inspired by applications of our Situs rigid-body docking tools. We next consider cases where the drift of local features can be evaluated due to the existence of a known atomic structure. We conclude with an outlook on the detection of secondary structure features in medium- to high-resolution EM maps, which hold much promise for future validation strategies.

2. Low resolution: Existing best practices for rigid-body fitting

Even in the age of atomic-resolution cryo-EM, the fitting of small fragments to low-resolution maps can be valuable, as has been exemplified by the recent fitting of the so-called SPRY2 domain of ryanodine receptor (RyR1) to four low (worse than 10 Å) resolution maps (Lau and Van Petegem, 2014). The small (~50 kDa) fragment was docked using colores with Laplacian filtering, and the more recent 3.8 Å cryo-EM map of full RyR1 (Yan et al., 2015) confirmed the location with an accuracy of 2.1 Å RMSD (Wang, 2015). Importantly, not all the low-resolution maps gave the same results (only three out of four were correct), but it was clear from the ranking of the correlation coefficients that the odd one was incorrect, i.e. there was little contrast between the correlation coefficients of the top hit and the next ones down in the ranking (Van Petegem, 2015). To assist Situs users in managing similar ambiguities, we feel it is therefore important to describe best practices for fitting and validation.

As an inspiration for currently supported validation options, we recommend the “Supplementary Information” paper by Tung et al. (2010). In this earlier work, Van Petegem’s lab presented a new model of the ABC domains of RyR1. Since their model was in conflict with earlier models, the Situs fitting strategy was extensively scrutinized in that paper. To simplify the listing of best practices, we assume that the fitted subunits are based on reliable crystallographic or NMR structures.

• (1) The use of two or more independent cryo-EM maps. Since cryo-EM progresses incrementally toward higher resolution maps, it is often possible to compare fitting results to older, lower resolution maps derived from different sets of images. In Tung et al. (2010), a 14 Å and a 10 Å map of RyR1 was used to confirm that the model was robust. This idea could be useful to test the robustness of a fitting method or to validate maps. However, the approach does not directly validate models: any discrepancies arising in such comparisons may be due to weaknesses in one of the maps (typically the older one), which is unrelated to the accuracy of the model derived from the new map.

• (2) Statistical confidence analysis. It is possible to estimate the precision of the fitting method in a statistical evaluation of the variability of fits. This can be done using Fisher’s Z-transform of the scoring function (Volkmann, 2009). For example, a precision of 4.4 Å was reported for fits within the 99% confidence level for the maximum peak in the cross-correlation (Tung et al., 2010). Unfortunately, although the two terms are often confused, precision is not a reliable indicator of accuracy (Henderson et al., 2012). The precision of detected features correlates with the accuracy obtained in single molecule fits where all density is accounted for (Wriggers and Birmanns, 2001). However, in cases where a smaller fragment is fitted to a larger map, spurious peaks can arise in the cross-correlation that are far from the true solution (Chacon and Wriggers, 2002).

• (3) Docking contrast. The docking contrast used by Lau and Van Petegem (2014) and Tung et al. (2010) is a feature of the “scoring function landscape” in the Situs colores tool. It measures how the score of the top solution stands out from non-redundant solutions immediately below in the ranking. The success of this criterion depends on how well the atomic fragments match the EM density. The ranking is less reliable if fitted atomic fragments are imperfect to begin with (for example, when homology models are used or in induced fit situations). Also, the use of a Laplacian filter (Chacon and Wriggers, 2002) or multi-fragment docking (see below) yield a different contrast profile compared to a one-at-a time approach.

• (4) The use of two or more independent modeling strategies. We encourage our users to validate their fits with alternative software such as EMFit in which detailed atomic contacts are scored in addition to the density match (Rossmann, 2000). Ideally, different software should yield identical results (Tung et al., 2010). Also, it is useful for maps near 10 Å resolution (or below) to experiment with the Laplacian filter that matches the surface contours (Chacon and Wriggers, 2002). Finally, an important approach to fitting smaller fragments is to test whether their matching recapitulates the full assembly: “The results indicate the RyR1ABC structure is at the size limit for standard cross-correlation-based docking into the current 9.6 Å cryo-EM map, and that Laplacian filtering is absolutely required for docking any smaller units” (Tung et al., 2010).

• (5) Comparisons with other biophysical and biochemical knowledge. This is the most reliable validation strategy because it is independent of the data and modeling work flow. For example, Tung et al. (2010) studied the distribution of disease mutants in their model. They also evaluated surface features and the position of labels as well as results from complementary biophysical and biochemical studies. Fortunately, the modeler is usually experienced in experimental interpretation and validation, since functional conclusions are drawn from the atomic model as part of the publication and deposition process.

The above recommended validation strategies are best practices that will minimize (but not eliminate) the risk of modeling error. Anecdotal evidence suggests that criteria that are solely based on the “scoring landscape”, such as confidence analysis (precision) and docking contrast, are imperfect predictors of accuracy. For example, it is notoriously difficult to predict the global shape of larger homology models, so their fit might produce unambiguous solutions that have high contrast and high precision, yet the fit may be incorrect (Tung et al., 2010). Also, the use of crystallographic validation methods that evaluate the stereochemistry of protein models are limited in terms of predicting the global pose. For example, the influenza B virus receptor-binding site complex of antibody CR8033 exhibits steric clashes with hemagglutinin (Dreyfus et al., 2012), but the model is most likely correct since both subunits were solved in isolation, and induced fit changes in the EM map of the complex can explain the clashes (Dreyfus et al., 2012). We argue, therefore, that at the present time a meta-analysis of multiple criteria that takes into account all experimental knowledge is the most promising strategy in validation.

3. Medium resolution: Tracking by fiducials

From a numerical geometry perspective, the above one-at-a-time rigid body docking requires very little information, namely the centroid and pose (orientation) of the docked molecular structure. In other words, the fitting accuracy is estimated globally for the entire model. A major limitation of this approach is its inability to differentiate between misalignment and internal conforma- tional change. It would be desirable to add flexibility to the model by introducing sampling points that correspond to specific shape features. The displacement of the sampling points would then account for systematic differences between a map and a model, even when both are in (nearly) equivalent conformations. The magnitude of any conformational change can be quantified by the RMSD of the sampling points, and the drift vectors of individual points could provide a sparsely sampled deformation field. One can indeed devise such a model for flexible fitting of models to low-resolution EM maps (Birmanns and Wriggers, 2007). Fig. 1 illustrates the flexible modeling of the myosin motor domain (Wriggers, 2010). In flexible fitting, the deviating atomic structure is brought into register with the EM density by forcing the fiducials to coincide.

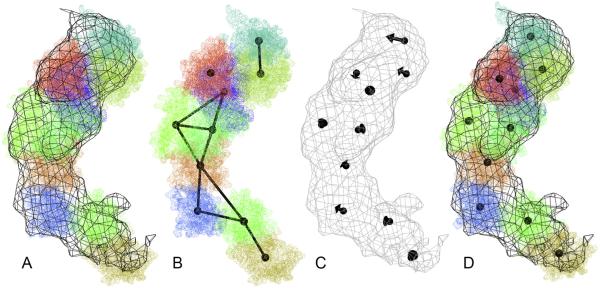
Fig. 1.

Illustration of the motion capture network (Rusu et al., 2008; Wriggers, 2010), which was originally developed for low-resolution flexing and which serves here as an inspiration for feature tracking. (A) Crystal structure of the myosin 2 (subfragment 1) motor domain rigid body fitted to the 14 Å resolution EM density (Wriggers, 2010). Atoms are shown as dotted spheres and the EM density is shown as a black wire mesh. The atom colors correspond to Voronoi cells in (B). The crystal structure does not match the EM density perfectly as indicated by the imperfect overlap. (B) Simulated fiducials (black spheres) used for guiding the flexible fitting of the atomic structure. The colors represent the Voronoi cells (Wriggers et al., 2004) surrounding the fiducials. The fiducials are computed using a so-called vector quantization method based on unsupervised learning (Wriggers et al., 2004). The motion capture network (black distance constraints between fiducials) reflects the topology and rigidity of the atomic structure (Wriggers, 2010) and provides a more robust model. (C) Discretely sampled displacements as a course representation of the conformational difference. Arrows point from the fiducial position in (B) to the position in the EM map. (D) Flexibly fitted atomic structure superimposed with the EM map. The centroids of the Voronoi cells are shifted to their new position. This can be achieved in a molecular dynamics refinement step or by spatial interpolation (Rusu et al., 2008; Wriggers, 2010). Figs. 1 and 2 were created with VMD (Humphrey et al., 1996).

In this work, we are extending the earlier approach to track features in map–model pairs that are deemed to be equivalent in order to search for systematic differences between low- to medium-resolution EM maps and a known atomic structure. We compare three motion-tracking models. The first model, naïve vector quantization (VQ), involves motion capture, but with the stabilizing skeletons (see Fig. 1B) turned off. This is a worst-case scenario, where errors from both model and EM coarse-graining can combine. We expect a more robust fit to be provided by direct cross-correlation maximization between the EM map and a smoothly deformable model using inverse distance weighting (IDW) interpolation, which we developed earlier for flexible fitting (Rusu et al., 2008). Finally, we perform a tessellation of the structure into N rigid Voronoi cells (see Fig. 1), which are fitted simultaneously by maximizing the cross-correlation in a 6N-dimensional search (see Fig. 2).

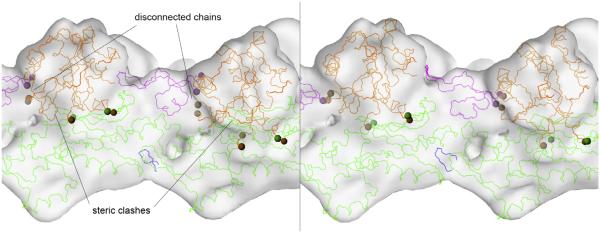
Fig. 2.

Illustration of the effect of simultaneous multi-fragment fitting. Docking of rigid G-actin subunits (green, purple, orange chains) and phalloidin (blue chain) to an F-actin cryo-EM map at 10.5 Å resolution (data provided by Vitold Galkin and Edward H. Egelman). Shown are two adjacent G-actin symmetry mates within a single strand of the two-start actin helix (26.2 degrees rotation, 53.2 Å translation). Spheres denote ends of the fragmented polypeptide chains within each G-actin. Left: traditional one-at-a- time fitting of the rigid subunits suffers from steric clashes and significant separation in the chain ends. Right: simultaneous multi-fragment fitting provides a cleaner model (with reduced chain separation and no steric clashes) that can be “healed” with local molecular dynamics simulation that fuses the separated chains. The cross-correlation coefficient optimized here is a widely used fitting score. Its maximization is equivalent to minimizing the squared differences, which is maximum-likelihood if the errors are normal (as is generally assumed in EM fitting applications, although this may not necessarily be the case). This scoring function has been adopted by a large number of groups, and a number of computer programs based on it are readily available (López-Blanco and Chacón, 2015). Over the years, we have developed Fourier-based techniques to accelerate translational or rotational matching (López-Blanco and Chacón, 2015), and the colores program has become the workhorse for Situs docking (Wriggers, 2012). Lasker et al. (2009) originally discovered that the accuracy of traditional interactive component placement, one at a time, can be increased by simultaneous refinement. In the Situs collage tool, the approach softly enforces shape complementarities between components via normalization of the cross-correlation (Birmanns et al., 2011). The approach also led to an implementation of symmetry constraints during the refinement (Wriggers, 2012), and it opened the door to a new high-dimensional conformational search (López-Blanco and Chacón, 2013) of multiple fragments, which were optimized in parallel using genetic algorithms in combination with tabu search techniques (Rusu and Birmanns, 2010). We have recently adopted this approach, termed voltrac, to trace a-helices in high-resolution EM maps (Rusu and Wriggers, 2012) and to segment filaments in tomograms (Rusu et al., 2012).

We compare in Fig. 3 the geometric features of an atomic structure of GroEL (PDB ID 1XCK) with those of an 11.5 Å resolution map (EMDB ID 1080) and a 6 Å resolution map (EMDB ID 1081). All three structures represent the wild-type specimen and are expected to be equivalent in their conformations. Consequently, our stability tests should yield very small deviations for the EM features from those corresponding to the known crystal structure. We carried out calculations for the more efficient VQ approach up to N = 500, which is just below the maximum meaningful number of features, N_max, contained in EMDB ID 1080 (this number can be estimated from the density-occupied map volume divided by the volume of a cubic resolution element, and yields N_max ~660 for the 11.5 Å map and N_max ~2300 for the 6 Å map). Calculations for the computationally more demanding global deformation and Voronoi tessellation models were carried out up to N = 100.

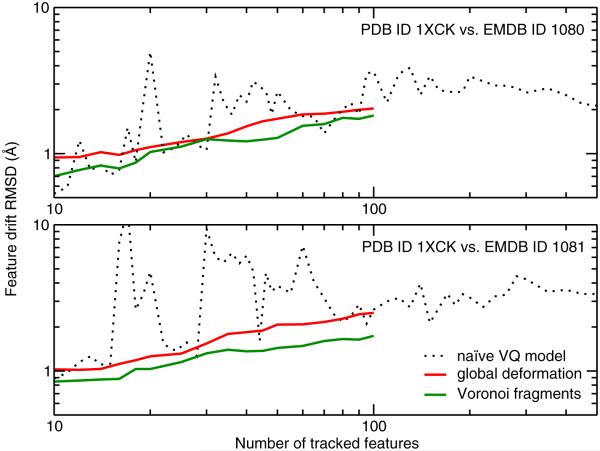
Fig. 3.

Tracking of geometric features. PDB ID 1XCK vs. EMDB ID 1080 (top; GroEL at 11.5 Å resolution) and EMDB ID 1081 (bottom; GroEL at 6 Å resolution). Shown are RMSD values of feature discrepancies observed by (1) naïve vector quantization (Wriggers et al., 2000, black dots), (2) a global deformable model based on IDW interpolation (Rusu et al., 2008, red), and (3) rigid-body multi-fragment model based on Voronoi tessellation (green).

The observed RMSD values give insight into discrepancies between the structures and into limitations of the tracking strategies. All three approaches initially increase their RMSD as the models become more flexible due to increasing numbers of features. The VQ approach requires sufficient point density (N > 100) to track features consistently. VQ is somewhat complementary to the other two approaches (due to its ability to easily reach high N on standard workstations). However, it suffers from intermittent bursts of instability at lower N and at high N values, the curves are not as smooth as those computed by the other approaches. A more consistently accurate fit at lower N values is provided by the deformable model using IDW interpola- tion (Rusu et al., 2008). The observed RMSD varies smoothly between 1 and 2 Å. Finally, the lowest RMSD is consistently provided by the tessellation of the structure into rigid Voronoi cells utilizing multi-fragment refinement (see Fig. 2). This lowest error is an upper bound for the (small) discrepancy between the crystal structure and the EM map due to different experimental conditions. Given that the best performing Voronoi tessellation approach produces a low RMSD below 2 Å, and the VQ approach for high N values is saturating in both cases, we believe that the maximum Voronoi RMSD of ~2 Å is close to the (unknown) structure discrepancy. Interestingly, there is little difference between the Voronoi plots of the 11.5 Å and the 6 Å maps, which suggests a systematic difference between the crystal structure and both EM reconstructions. Assuming that the crystal structure is more reliable than either of the EM maps, the results suggest that at medium to low resolution there might be a risk of over- fitting the atomic structure (e.g. by using an aggressive molecular dynamics approach that would erase all feature discrepancies between the map and the model).

4. Medium to high resolution: Validation using secondary structure elements?

Given the increasing number of available cryo-EM density maps in the medium to high resolution range, the secondary structure features of cryo-EM maps have been well characterized and their features are now well understood. In fact, secondary structure elements are often the most obvious features in density maps at medium to high resolutions. Consequently, we argue in this section that it is useful to generalize the above point-wise tracking (see Fig. 3) to more abstract representations of geometric shapes that are tuned to the specific properties of secondary structure elements. In general, long helices can be detected reliably and b-sheets also begin to become visible at resolutions of 8 Å or better (Baker et al., 2012). It is also possible to predict the location of b-strands at medium resolutions (Si and He, 2014a).

Secondary structures have unique density signatures. Helices, particularly long ones, appear as cylinders, and simple sheets appear as thin twisted layers of density (see Fig. 4). Since Jiang et al. discovered that it is possible to identify helices in sub-nanometer resolution maps (Jiang et al., 2001), various computational methods have been developed to detect helices and b-sheets, including SSEhunter, SSETracer and voltrac (Baker et al., 2007; Dal Palu et al., 2006; Kong and Ma, 2003; Kong et al., 2004; Rusu and Wriggers, 2012; Si and He, 2013; Si et al., 2012; Zeyun and Bajaj, 2008). SSELearner combines image process- ing techniques and machine learning (Si et al., 2012). An example of the helices (red sticks) and b-sheets (green volume) detected using SSETracer is shown in Fig. 4B. It is also possible to obtain a skeleton (pink) that represents possible connected components in the density map (see Fig. 4B). Recently, StrandTwister was developed to detect b-strands (see red lines in Fig. 4C) from b-sheet density through the analysis of b-sheet twists (Si and He, 2014a). The results generated from such detection methods reflect the strength of the density features in secondary structure regions.

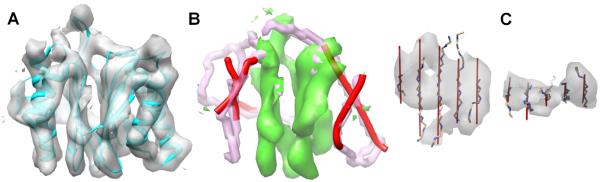
Fig. 4.

Secondary structure detection based on characteristic density patterns. (A) The density map (gray) extracted from EMDB 1733 (6.8 Å resolution) superimposed on its atomic model (cyan; PDB 3C91_H), using the model as a mask. (B) The detected helices (represented as red sticks) and two b-sheets (green density), using SSETracer (Si and He, 2013) and the skeleton (pink) using SkelEM (Al Nasr et al., 2013). (C) The best of the top ten sets of detected b-traces (red lines) using StrandTwister (Si and He, 2014a) are superimposed with the backbone of the b-strands and the density map (gray) of EMDB ID 2165 and PDB ID 4B4T_1 sheet C. Figs. 4 and 5 were created using Chimera (Pettersen et al., 2004).

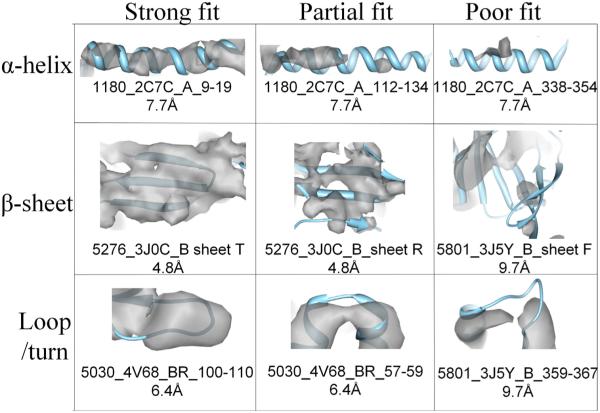
Unfortunately, as more cryo-EM maps become available for examination, it is quite common to see quality variations in the density of secondary structure elements (see Fig. 5). For example, the upper left helix in Fig. 5 exhibits a strong cylinder-like shape, while the upper middle helix shows thinner and discontinuous pieces of a cylinder in the same density map at the same threshold. These quality variations might be due to uneven resolutions across the map, 3D reconstruction artifacts, or heterogeneity of the con- formation. Likewise, it is possible that a matched atomic model does not accurately reflect the EM density due to limitations of the modeling or fitting. Given the increasing number of map–model pairs deposited in the EMDB and PDB, we argue that there is a need to quantify the fitting locally to distinguish those models that agree well with the local density features from those that do not. Fig. 5 is an illustration of such cases, which should be useful to modelers in the community who develop such validation software.

Fig. 5.

Quality variation in density maps at secondary structure regions. Each local region is labeled with EMDB ID, PDB ID, and the resolution of the cryo-EM map. The atomic model (blue ribbon) is aligned with a local density pattern (gray) in the pose taken from the database.

Secondary feature representations can be used to define metrics for evaluating the local fitness of a map–model pair. For example, the helical axes and b-strands in Figs. 4B and 4C could be used to measure lateral helical or strand displacement, or any longitudinal length discrepancy. The density property of secondary structure elements is already widely used for the validation of map–model pairs. Helical density has been characterized using various metrics, such as cross-correlation coefficients with cylindrical templates (Baker et al., 2007; Rusu and Wriggers, 2012), gradient trees (Dal Palu et al., 2006), and local structural tensors (Si and He, 2013; Si et al., 2012; Zeyun and Bajaj, 2008). These methods characterize the cylindrical property along the axis of the helix. The continuity of high density along the axis and the local thickness of the cylindrical density are often indicators of the strength of the helix density feature. The density feature of a b-sheet is less well explored compared to that of a helix. Nevertheless, thinning and pruning has been shown to derive the surface of a b-sheet (Baker et al., 2007). Recent studies suggest that the twist of a b-sheet can also be exploited, even if the strands themselves cannot be visualized (Si and He, 2014a,b).

In summary, we are witnessing the development of quantitative secondary structure-based methods that are able to characterize local discrepancies in a map–model pair. This area of research is in its infancy now but we expect that it will grow significantly in the near future.

5. Conclusions

The overall aim of this paper was to describe and to propose validation tools for medium- to low-resolution cryo-EM based atomic models. The proposed strategies will aid in the routine determination of large-scale structures of biomolecular assemblies and in the validation of structural models that will be deposited to public databases, such as the Protein Data Bank (PDB) and the EM Data Bank (EMDB).

Our tests suggest that multi-fragment rigid body refinement is a superior “motion” model for tracking deformations, and that Voronoi cells of fiducials can be used as templates for tracking conformational differences. This is another successful adaptation of the new fitting paradigm of simultaneous refinement of multiple subunits.

Our work also suggests that flexible fitting methods, such as all-atom molecular dynamics, may accidentally erase meaning- ful differences between atomic structures and EM maps if all discrepancies between models and maps are eliminated. This is a problem that mostly affects medium- to low-resolution maps where the fitted atomic structure might be more reliable than the map density. The ultimate remedy to this problem is to attain higher resolutions that allow cryo-EM to solve atomic structures directly. Nevertheless, medium- to low-resolution maps still dominate the EMDB. It is therefore important to separate flexibly fitted models from rigid ones in a statistical evaluation of map–model pairs.

In this whitepaper, we have also presented various map–model pairs that are potentially useful for testing valida- tion methods based on secondary structure elements. Our “call to arms” seeks to shift the research emphasis from the qualitative detection of secondary structures to the quantita- tive validation of secondary structure patterns. This approach would open doors for new applications in the validation of atomic structures based on secondary structure patterns. It would also improve the reliability of existing methods and provide a local measure of fitness for maps in case of reliable reference structures.

6. Availability

Tools and tutorials for the numerical experiments in this paper will be made available with version 2.8 of Situs (http://situs.biomachina.org).