Abstract
Different neuromodulators often target the same ion channel. When such modulators act on different neuron types, this convergent action can enable a rhythmic network to produce distinct outputs. Less clear are the functional consequences when two neuromodulators influence the same ion channel in the same neuron. We examine the consequences of this seeming redundancy using a mathematical model of the crab gastric mill (chewing) network. This network is activated in vitro by the projection neuron MCN1, which elicits a half-center bursting oscillation between the reciprocally-inhibitory neurons LG and Int1. We focus on two neuropeptides which modulate this network, including a MCN1 neurotransmitter and the hormone crustacean cardioactive peptide (CCAP). Both activate the same voltage-gated current (IMI) in the LG neuron. However, IMI-MCN1, resulting from MCN1 released neuropeptide, has phasic dynamics in its maximal conductance due to LG presynaptic inhibition of MCN1, while IMI-CCAP retains the same maximal conductance in both phases of the gastric mill rhythm. Separation of time scales allows us to produce a 2D model from which phase plane analysis shows that, as in the biological system, IMI-MCN1 and IMI-CCAP primarily influence the durations of opposing phases of this rhythm. Furthermore, IMI-MCN1 influences the rhythmic output in a manner similar to the Int1-to-LG synapse, whereas IMI-CCAP has an influence similar to the LG-to-Int1 synapse. These results show that distinct neuromodulators which target the same voltage-gated ion channel in the same network neuron can nevertheless produce distinct effects at the network level, providing divergent neuromodulator actions on network activity.
Keywords: Neuromodulation, Central pattern generator, Phase plane analysis, Mathematical modeling, Stomatogastric ganglion
1 Introduction
Neuromodulation is prevalent in the nervous system, commonly influencing multiple neurons and synapses within a target network (Nadim and Bucher, 2014). Consequently, network activity is often conditional upon the presence of neuromodulators, which are typically released from neurons and/or act as circulating hormones (Skiebe, 2001; Christie et al., 2010; Harris-Warrick, 2011; Nusbaum and Blitz, 2012). By modifying the properties of neurons and synapses, neuromodulators can reconfigure circuit components and thereby change neural network activity patterns (Lieske et al., 2000; Dickinson, 2006; Dzirasa et al., 2006; Grillner, 2006; Briggman and Kristan, 2008; Marder, 2012; Nusbaum and Blitz, 2012; Rodriguez et al., 2013; Nadim and Bucher, 2014). Moreover, the actions of different neuromodulators can converge to influence a network by targeting the same cellular and/or synaptic mechanisms, in either the same or different network neurons (Nusbaum et al., 2001; Marder and Thirumalai, 2002; Derjean et al., 2010). Alternatively, the same neuromodulator can have a divergent influence by targeting distinct mechanisms in different network components (Nusbaum and Beenhakker, 2002; LeBeau et al., 2005; Doi and Ramirez, 2008; Rodriguez et al., 2013; Nadim and Bucher, 2014).
In this study we investigate the fundamental issue of why distinct neuromodulators have convergent actions on the same neuron(s). Previous studies have proposed that different neuromodulators which activate the same ionic current or modify similar synaptic properties within a network can produce distinct network outputs by targeting distinct sets of neuron types (Swensen and Marder, 2001; Marder and Thirumalai, 2002; Rauscent et al., 2009; Calabrese et al., 2011). From this perspective, there appears to be little advantage for distinct neuromodulators employing convergent actions on the same voltage-gated current in the same neuron. One candidate explanation for such convergence is to provide greater flexibility at the network level. However, the actual purpose of this seemingly redundant convergence of neuromodulatory actions is not well elucidated. Here, we will establish that convergent actions by distinct neuromodulators in the same neuron can have divergent consequences at the network level, thereby increasing the diversity of neuromodulator actions on network output.
We compare the convergent actions of two modulators that activate the same voltage-gated ionic current in the same target neuron, with the distinction that one modulator is released from a projection neuron while the other is released hormonally. Bath application is commonly used to characterize the actions of neuromodulators on networks and their components, as this method often provides a good approximation of the in vivo influence of hormonally-released modulators or neurotransmitters acting in a paracrine fashion (Morgan et al., 2000; Marder and Thirumalai, 2002; Nusbaum and Blitz, 2012). However, bath-applied neuromodulators cannot provide insight regarding the complex synaptic interactions that at least sometimes occur between a modulatory projection neuron and its target networks (Nusbaum, 2002; Briggman and Kristan, 2008; Nassel, 2009; Nadim and Bucher, 2014). Consequently, this method does not necessarily replicate the influence on the target network that occurs from directly activating the appropriate modulatory projection neuron (Nusbaum et al., 2001; Nusbaum and Blitz, 2012).
Here, we examine the effects of convergent neuromodulators on the neuronal circuit that controls the crab (Cancer borealis) gastric mill (chewing) motor pattern, to explore the relative impact of neuronally- and hormonally-released modulatory input. The gastric mill network is located within the stomatogastric ganglion (STG), one of the four ganglia comprising the stomatogastric nervous system (STNS) (Marder and Bucher, 2007). The STG is embedded within the dorsal ophthalmic artery and is therefore continually influenced by hormones. It also receives modulatory input from descending projection neurons whose somata are located in the anterior STNS ganglia. The gastric mill network produces rhythmic bursting (cycle freq. ~0.1 Hz) in two phases which correspond to the protraction and retraction of the teeth in the gastric mill stomach compartment. This rhythmic activity is produced by a rhythm-generating circuit which includes a half-center oscillator composed of the reciprocally-inhibitory neurons LG (lateral gastric) and Int1 (interneuron 1) (Nusbaum and Beenhakker, 2002; Marder and Bucher, 2007).
The gastric mill rhythm is not spontaneously active, in vitro and in vivo (Bartos et al., 1999; Diehl et al., 2013). However, tonic stimulation of a descending projection neuron, modulatory commissural neuron 1 (MCN1), reliably drives the gastric mill rhythm in vitro (Coleman et al., 1995). In addition, within the STG, modulatory synaptic output from the MCN1 axon terminals and presynaptic inhibition of those terminals by the LG neuron are necessary for MCN1 to activate the gastric mill rhythm (Coleman et al., 1995; Calabrese, 1999). Furthermore, the cycle frequency of the MCN1-elicited gastric mill rhythm is strongly regulated within the STG by a local synaptic input from the co-active pyloric network (cycle freq. ~1 Hz) via an inhibitory synapse from the pyloric pacemaker (anterior burster – AB) neuron onto Int1 (Nadim et al., 1998; Bartos et al., 1999).
MCN1 has modulatory excitatory actions on the LG neuron by releasing a peptide neurotransmitter, Cancer borealis tachykinin-related peptide Ia (CabTRP Ia), one of its three known co-transmitters (Blitz and Nusbaum, 1999; Wood et al., 2000). Bath applying CabTRP Ia to the isolated STG elicits a modulator-activated, inward, voltage-dependent ionic current (IMI) in the LG neuron (DeLong et al., 2009b). Bath application of the peptide hormone, crustacean cardioactive peptide (CCAP), to the isolated STG also activates IMI in the LG neuron (DeLong et al., 2009b). In addition, CabTRP Ia, CCAP, and several other (mainly peptidergic) neuromodulators elicit IMI in pyloric circuit neurons when bath applied to the STG, a clear example of convergent actions of neuromodulators (Swensen and Marder, 2000, 2001).
For the gastric mill network, CabTRP Ia and CCAP individually excite the LG neuron (Wood et al., 2000; Kirby and Nusbaum, 2007; Stein et al., 2007; DeLong et al., 2009b). However, neither modulator, nor any combination of MCN1 co-transmitters, elicits a gastric mill rhythm when bath applied to the isolated STG (Wood et al., 2000; Kirby and Nusbaum, 2007). An ongoing MCN1-elicited gastric mill rhythm, though, is modulated by bath applied CCAP. Specifically, CCAP selectively prolongs the protraction phase (when the LG neuron is bursting) without altering the retraction phase (when Int1 is bursting and the LG neuron is inhibited) duration – thus prolonging the overall cycle period of this rhythm (Kirby and Nusbaum, 2007).
A previous explanation for the convergent actions of CabTRP Ia and CCAP on the LG neuron was that the different dynamics of IMI activation by these two peptides results in distinct influences on the two phases of the MCN1-elicited gastric mill rhythm (Kirby and Nusbaum, 2007; DeLong et al., 2009b). In particular, when IMI is activated by CabTRP Ia via synaptic release from MCN1 (IMI-MCN1), it is constrained by the synaptic interactions between the MCN1 axon terminals and the LG neuron. Specifically, MCN1 has a stronger synaptic influence during the gastric mill retraction phase due to LG presynaptic inhibition of MCN1 terminals during the protraction phase (Coleman et al., 1995). This results in the influence of IMI-MCN1 increasing throughout each retraction phase of the MCN1-elicited rhythm, and then waning during each subsequent protraction phase (DeLong et al., 2009b). Consequently, the MCN1 firing rate/rate at which IMI-MCN1 increases determines retraction duration, whereas protraction duration remains relatively constant (Nadim et al., 1998; Bartos et al., 1999; DeLong et al., 2009b). In contrast, IMI activated by bath applied CCAP (IMI-CCAP) is not constrained by synaptic interactions and, as a result, is present during both phases of this rhythm (Kirby and Nusbaum, 2007; DeLong et al., 2009b). At the network level, IMI-CCAP prolongs protraction and prevents a change in retraction duration (DeLong et al., 2009b).
In this study, we use a reduced mathematical model to explain the consequences for network dynamics that result from the distinct CabTRP Ia and CCAP influence on the two phases of the MCN1-elicited rhythm. This model builds upon previous reduced modeling of the MCN1-elicited gastric mill rhythm (Manor et al., 1999; Ambrosio-Mouser et al., 2006; Kintos et al., 2008; Kintos and Nadim, 2014). We focus on how the activation of IMI-MCN1 and IMI-CCAP in the LG neuron can influence oscillations at the network level. These two currents exhibit fast dynamics in the biological system, which allows us to use a separation of time scales to obtain a reduced 2-D model of the MCN1-elicited gastric mill rhythm – similar to (Kintos et al., 2008). This enables us to analyze the network dynamics of the MCN1-elicited gastric mill rhythm via phase plane analysis. Using the reduced model, we first reproduce the influence of each IMI on the MCN1-elicited rhythm as done previously in the biological system (Kirby and Nusbaum, 2007; DeLong et al., 2009b). We then identify new insights regarding how these currents influence the network dynamics, thereby supporting the hypothesis that convergent neuromodulation at the neuron level can result in divergent output at the network level.
2 Methods
Our mathematical model in this study builds upon our previous reduced modeling of the gastric mill rhythm. We first reduced a previously published 3-dimensional model of the MCN1-elicited gastric mill rhythm (Manor et al., 1999) down to 2 dimensions by using the difference in synaptic time scales that is exhibited in the biological system (Kintos et al., 2008). This reduction allowed us to perform a phase plane analysis of the network dynamics of the MCN1-elicited gastric mill rhythm using the geometric properties of the reduced 2-dimensional model. More recently, we extended this reduced model of the MCN1-elicited rhythm to analyze a distinct version of the gastric mill rhythm that is driven by co-activating MCN1 plus a second projection neuron, commissural projection neuron 2 (Kintos and Nadim, 2014). In these previous modeling studies, we focused only on how the synaptic interactions among the network neurons influenced the network dynamics for each distinct version of the gastric mill rhythm.
Here, we construct a reduced 2-dimensional model of the gastric mill rhythm that is driven only by MCN1. What distinguishes this model is that we investigate how activation of IMI (a Modulator-activated, Inward, voltage-gated ionic current) in the LG neuron, by two distinct neuromodulators, influences the network dynamics of the MCN1-elicited gastric mill rhythm. Thus, unlike our previous reduced models, in this model the reciprocally inhibitory gastric mill rhythm generator neurons (Int1 and LG), which comprise the core half-center oscillator of this network, are not both treated as passive neurons.
In order to simplify the network interactions for our mathematical analysis, we account only for the slow envelope of network oscillations in this model. Physiologically, STG neurons exhibit a strong component of graded synaptic transmission (Raper, 1979; Manor et al., 1997), and we consider only the graded component of synaptic transmission between the network neurons in this study. Thus, we ignore action potentials and action-potential-mediated synaptic transmission in the model neurons (Zhao et al., 2011).
2.1 A 3-dimensional model of the IMI-influenced MCN1-elicited gastric mill rhythm
Similar to that of previous reduced modeling of the MCN1-elicited gastric mill rhythm (Manor et al., 1999; Kintos et al., 2008), our mathematical model in this study begins with a system of 3 nonlinear ordinary differential equations given by
| (1) |
| (2) |
| (3) |
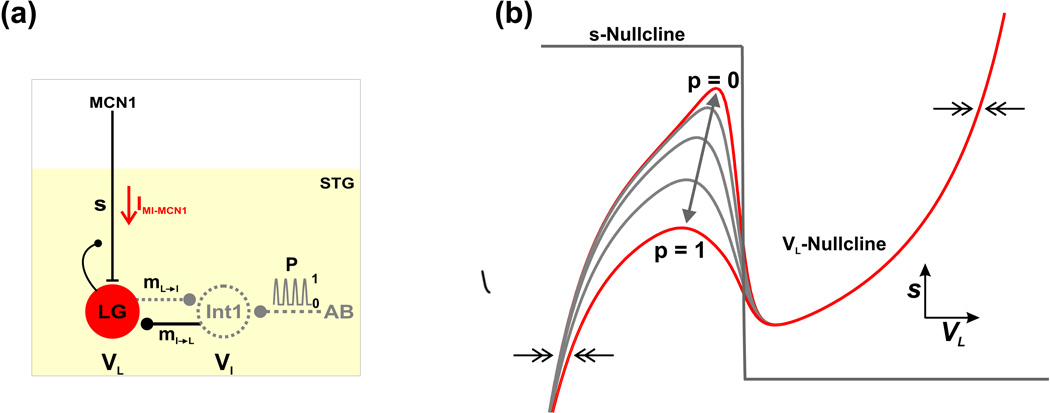
Equations (1)–(3) govern the evolution of the three state variables in this model: the membrane potentials of Int1 (VI) and the LG neuron (VL) and the slow excitatory synaptic input (s) from MCN1 to the LG neuron. Note that in these equations, s denotes the slow activation of a classical excitatory synaptic input (see below) rather than the addition of a voltage-gated ionic current as will be discussed below for other cases. See Fig. 1(a) for a schematic diagram.
Fig. 1.
Circuit diagram and phase plane geometry of the reduced 2-dimensional model. (a) Circuit diagram. The neuron MCN1 projects to the STG to excite the gastric mill network. MCN1 and AB are modeled only through their synaptic influences. The LG neuron and Int1 reciprocally inhibit each other (mL→I and mI→L), and their membrane potentials are denoted by VL and VI, respectively. The LG neuron receives slow excitatory synaptic input from MCN1 (s; gated by the activation of a fast inward current IMI-MCN1) and presynaptically inhibits MCN1. Int1 is inhibited by a periodic, pyloric-timed synaptic input (p) from the pacemaker neuron (AB) of the pyloric circuit. Int1 is modeled implicitly (dashed; see Methods). (b) Phase plane geometry of the 2-dimensional model. The cubic- and step-function-shaped nullclines correspond to the steady-states of VL and s, respectively. The forcing parameter p (Equation (17)) results in a family of cubic VL-nullclines, where the highest/lowest cubic (p = 0/1) corresponds to zero/maximal pyloric input. As p varies between 0 and 1 (double-headed arrow) the VL-nullcline shifts between the two extremes. The pyloric-timed input is gated out when LG is active and, as a result, the right branch of the cubic is not affected by p. The 2-dimensional model resides in a relaxation (fast-slow) regime where the flow in the VL direction (double arrows) is much faster than the flow in the s direction.
In our model, the variable s plays a key role in driving the network oscillations. Previous experiments (Coleman et al., 1995) and modeling (Nadim et al., 1998) have established that the cycle frequency of the MCN1-elicited gastric mill rhythm is strongly determined by the slow buildup and decay of MCN1 synaptic action onto the LG neuron (s in our model). The dynamics of the state variable s in our model are controlled by Equation (3), where the evolution of s is gated by VL due to the local LG presynaptic inhibition of MCN1 axon terminals. In particular, s builds up towards 1 with time constant τLO when VL is below the voltage threshold νthresh for presynaptic inhibition, while s decays towards 0 with time constant τHI when VL is greater than νthresh. Physiologically, the MCN1 to LG synapse works on a much slower time scale than all other synapses in the network (Coleman et al., 1995). We account for this biological fact in our model by assigning large values to the time constants τLO and τHI in Equation (3), see Table 1, so that the network oscillations reside in a relaxation regime.
Table 1.
Parameter values for the reduced 2-dimensional model of the MCN1-elicited gastric mill rhythm corresponding to the MI-MCN1 case
| Int1 | AB (P) | LG | MCN1 input |
|---|---|---|---|
| gLeak,I = 0.75 mS/cm2 | ḡP = 0.85 mS/cm2 | gLeak,L = 1 mS/cm2 | ḡs = 3.75 mS/cm2 |
| ELeak,I = 10 mV | EP = −60 mV | ELeak,L = −60 mV | Es = 50 mV |
| ḡL→I = 2 mS/cm2 | per = 1 sec | ḡI→L = 5 mS/cm2 | νCabTRP = −55 mV |
| EL→I = −80 mV | dur = 0.5 sec | EI→L = −80 mV | kCabTRP = 15 mV |
| νL→I = −30 mV | νq = −35 mV | νI→L = −30 mV | νthresh = −33 mV |
| kL→I = 5 mV | kq = 3 mV | kI→L = 5 mV | τLO = 14 sec |
| CI = 1 µF/cm2 | ḡCCAP = 0 mS/cm2 | τHI = 5 sec | |
| τI = 0.00133̄ sec | ECCAP = 10 mV | ||
| νCCAP = −30 mV | |||
| kCCAP = 15 mV | |||
| CL = 1 µF/cm2 | |||
| τL = 0.001 sec |
Note: For the MI-BOTH case of the model, ḡCCAP = 1.4 mS/cm2 while all other parameters remain unchanged for the intact system.
Now, we describe the remaining terms in Equations (1) – (3) of our model. The parameters CI and CL on the left-hand-side of Equations (1) and (2) represent the membrane capacitance of Int1 and the LG neuron, respectively, and are given a value of 1 µF/cm2 for simplicity. The terms ILeak,I and ILeak,L on the right-hand-side of Equations (1) and (2) represent the leak current of Int1 and the LG neuron, respectively, where the parameters gLeak,_ and ELeak,_ in these terms represent the leak conductance and reversal potential, respectively, of the appropriate neuron. In the absence of projection neuron input in the biological system, Int1 exhibits a high membrane potential and remains active, while the LG neuron exhibits a low membrane potential and remains inactive (Bartos et al., 1999). As in our previous reduced models, we have produced this asymmetry among the reciprocally inhibitory CPG neurons by assigning a high value to ELeak,I and a low value to ELeak,L (see Table 1). Thus, as in our previous reduced modeling (Manor et al., 1999; Kintos et al., 2008; Kintos and Nadim, 2014), the leak current of Int1 appears as a persistent inward current to reproduce the asymmetry in the Int1-LG neuron pair that occurs in the biological system.
The terms IL→I and II→L of Equations (1) and (2) describe the reciprocally inhibitory synapses between Int1 and the LG neuron, where the parameters ḡpre→post and Epre→post represent the maximal conductance and reversal potential, respectively, of the appropriate synapse. Each synapse is gated by the sigmoidal function mpre→post (Vpre), which depends only on the membrane potential of the presynaptic neuron and is modeled by
| (4) |
The parameters νpre→post and kpre→post in Equation (4) specify the half-activation voltage and steepness, respectively, of the appropriate sigmoid.
The term IP of Equation (1) describes the local inhibitory synaptic input from the pyloric pacemaker (AB) neuron onto Int1, where the parameters ḡP and EP represent its maximal conductance and reversal potential, respectively. This synaptic input is gated by the function P(t, VL), which has separate time- and voltage-dependent components and can be written as
| (5) |
Mathematically, this synaptic input acts as a periodic, pyloric-timed forcing input onto the gastric mill network. The time-dependent component of this forcing input is modeled by a half-sine function
| (6) |
where mod() and H() designate the modulo and Heaviside function, respectively, and the parameters per and dur represent the period and duty cycle, respectively, of this periodic function. Physiologically, the cycle frequency of the pyloric rhythm (~1 Hz) is an order of magnitude faster than the cycle frequency of the gastric mill rhythm (~0.1 Hz) (Bartos et al., 1999). As in our previous reduced modeling, we have accounted for this biological fact by assigning appropriate values to the model parameters per and dur (see Table 1). The voltage-dependent component of the forcing input in Equation (5) is modeled by a decreasing sigmoidal function
| (7) |
where the parameters νq and kq specify the half-activation voltage and steepness, respectively. Physiologically, the influence of the pyloric-timed AB to Int1 synapse on the gastric mill rhythm is removed during the active (protraction) phase of the LG neuron (Bartos et al., 1999). The sigmoidal function in Equation (7) accounts for this biological fact in our model by turning off the periodic forcing input of Equation (5) during the active phase of the LG neuron.
The term Is of Equation (2) describes the MCN1 synaptic action onto the LG neuron, where the parameters ḡs and Es represent its maximal conductance and reversal potential, respectively. To describe the dynamics of the MCN1 to LG model synapse, we define IMI-MCN1 to be
| (8) |
which implies that Is = sIMI-MCN1 in Equation (2). The Is term is gated by two components in our model. The first component is the state variable s, whose dynamics are controlled by Equation (3), as described above. The second component that gates the Is term is mMCN1 (VL), which is the activation curve of IMI-MCN1 and is used to model the fact that synaptic release of the neuromodulator CabTRP Ia by MCN1 activates the voltage-gated ionic current IMI in the LG neuron. Physiologically, IMI-MCN1 acts with fast kinetics (DeLong et al., 2009b), and we model its activation by an instantaneous function of the LG membrane potential given by
| (9) |
where the parameters νCabTRP and kCabTRP specify its half-activation voltage and steepness, respectively. Note that the sigmoidal gating of the Is term provided by Equation (9) restricts the excitatory MCN1 action on the LG neuron (s) to low values of VL (during the LG inactive phase), and not for high values of VL (during the LG active phase). Thus, the voltage-gated nature of the MCN1 to LG input, due to the influence of the sigmoid in Equation (9), distinguishes our current model from our previous models of the MCN1-elicited gastric mill rhythm. In cases where we need to compare this model to our previous reduced models, we set mMCN1 (VL) = 1(Kintos et al., 2008; Kintos and Nadim, 2014).
The term IMI-CCAP of Equation (2) describes the IMI current that is activated in the LG neuron by bath application of the peptide hormone modulator CCAP. The parameters ḡCCAP and ECCAP represent its maximal conductance and reversal potential, respectively. Physiologically, IMI-CCAP also acts with fast kinetics (DeLong et al., 2009b), and we model its activation by the instantaneous sigmoidal function of the LG membrane potential given by
| (10) |
where the parameters νCCAP and kCCAP specify its half-activation voltage and steepness, respectively. Consistent with the biological system (DeLong et al., 2009b), IMI-CCAP is not constrained by MCN1 synaptic interactions in our model. Therefore, its influence on the LG neuron is present during both phases of the gastric mill rhythm. In the results section, we will examine the influence of both IMI currents on the network dynamics.
2.2 Reduction to a 2-dimensional model of the IMI-influenced MCN1-elicited gastric mill rhythm
We reduce our model to two dimensions by using the biological fact that, unlike the LG neuron, Int1 is only influenced by synaptic inputs that occur on a fast time scale. Similar to the method of model reduction in our previous work (Kintos and Nadim, 2014), we divide through Equation (1) by the leak conductance of Int1, gLeak,I, to get
| (11) |
where, is the time constant of Int1. Note that, τI ≪ τLO, τHI ; see Table 1. We can then assume that VI adjusts instantaneously to its steady state by setting τI = 0, which makes the left-hand side of Equation (11) equal to zero. This allows for VI to be expressed explicitly in terms of the state variable VL and the periodic forcing function P(t, VL):
| (12) |
Substituting the expression for VI in Equation (12) into the function mI→L (VI), within the II→L term, of Equation (2) gives a 2-dimensional model of the MCN1-elicited gastric mill rhythm:
| (13) |
| (14) |
Thus, in reducing the model to two dimensions, we have absorbed the dynamics that influence VI into the state variable VL. Moreover, the effects of the fast inhibitory synapses that influence Int1 (which are LG inhibition of Int1 and the pyloric-timed AB inhibition of Int1) are absorbed into the lone synapse that emanates from Int1 (which is Int1 inhibition of LG – see circuit diagram of Fig. 1(a)) via the function mI→L (νI (VL;P(t,VL))) within the II→L term of Equation (13).
We can reveal the difference in synaptic time scales within our model by re-writing Equations (13)–(14) as
| (15) |
| (16) |
In Equation (15), p is the periodic forcing function P(t, VL). In Equation (16), and . We note that, as in our previous reduced models (Kintos et al., 2008; Kintos and Nadim, 2014), the evolution of the state variables VL and s in Equations (15)–(16) is practically identical to that of the 3-dimensional model.
2.3 Phase plane geometry of the 2-dimensional model
We use the reduced, 2-dimensional model of Equations (15)–(16) to analyze the network dynamics of the MCN1-elicited gastric mill rhythm. First, we compute the nullclines that correspond to the two state variables, VL and s, in the model. For the VL-nullcline, we note that the presence of the periodic forcing input p (the AB to Int1 synaptic input) in Equation (15) causes the model to become non-autonomous. The input p moves the VL-nullcline within the VL-s phase plane and defines a one-parameter family of cubic VL-nullclines (parameterized by p ∈ [0,1]; Fig. 1(b)) that is given by:
| (17) |
The minimum value (p = 0) corresponds to the unforced system (no pyloric input), whereas, the maximum value (p = 1) corresponds to the peak of the pyloric input. As mentioned above, physiologically, this pyloric-timed input influences the LG neuron only during its inactive phase (Bartos et al., 1999). As such, the periodic forcing input in our model only moves the left branch of the VL-nullcline (which corresponds to the LG inactive phase), while the right branch (which corresponds to the LG active phase) remains unchanged by this input (Kintos et al., 2008; Kintos and Nadim, 2014).
The s-nullcline for the slow variable in our model is given by the step function
| (18) |
The value of the parameter νthresh, which corresponds to the synaptic threshold voltage for LG presynaptic inhibition of MCN1, was chosen so that the s-nullcline intersects the middle branch of the cubic VL-nullcline (Fig. 1(b)), thus giving rise to a stable oscillatory trajectory. Regardless of where the VL- and s-nullclines intersect, the flow in the horizontal direction of the VL − s phase plane is such that dVL/dt > 0 (< 0) above (below) the VL-nullcline (horizontal arrows in Fig. 1(b)). On the other hand, the flow in the vertical direction is such that ds/dt > 0 (< 0) below (above) the s-nullcline.
Because the parameter ε is small in Equations (15)–(16), our 2-dimensional model exists in a relaxation (fast–slow) regime. In particular, the flow in the horizontal (VL) direction of the VL − s phase plane is fast (double-headed horizontal arrows in Fig. 1(b)), while the flow in the vertical (s) direction is much slower. In the limit where ε = 0, the model becomes singularly perturbed, and a general trajectory consists of distinct fast and slow portions (Kintos et al., 2008). It has been previously established that trajectories of fast–slow systems for the case where 0 < ε ≪ 1 (as occurs in Equations (15)–(16) of our model) are closely approximated by the singularly perturbed trajectory that is defined by the ε = 0 system (Mishchenko and Rozov, 1980). We use this fact for our phase plane analysis in the Results section.
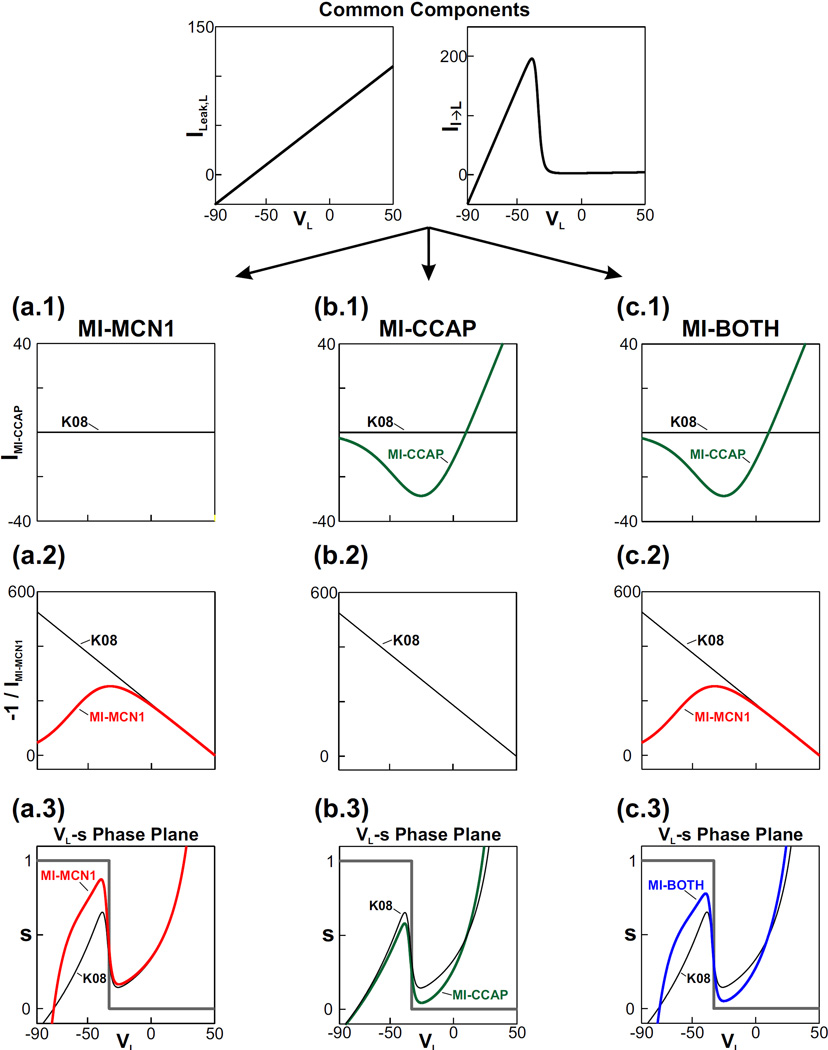
To simplify the presentation of our Results, we will define four sets of models using Equations (15)–(16). Fig. 2 demonstrates how the different factors in Equation (17) give rise to the cubic shape of the VL-nullcline and highlights the distinction among the phase plane diagrams of these four models as described below:
The simplest model arising from these equations is the one previously described by (Kintos et al., 2008) which can be obtained by setting mMCN1 (VL) ≡ 1 and ḡCCAP = 0. We refer to this model as K08 (black VL-nullcline in Fig. 2).
In the second model, we include the influence of the MCN1 modulator-activated current but not the CCAP-activated current. This model is defined by a sigmoidal mMCN1 (VL) from Equation (9) and ḡCCAP = 0. We refer to this model as MI-MCN1. Fig. 2(a.1–a.3) shows how the sigmoidal mMCN1 (VL) alters the VL-nullcline in this model compared to K08.
The third model includes the CCAP modulation but assumes that the MCN1 input is a simple excitatory (non-voltage-gated) synapse as in K08. This model is given by mMCN1 (VL) ≡ 1 and a nonzero ḡCCAP. We refer to this model as MI-CCAP. Fig. 2(b.1–b.3) shows how a nonzero ḡCCAP alters the VL-nullcline in this model compared to K08.
Finally, if both MCN1 and CCAP elicit IMI in the model [i.e. the model has a sigmoidal mMCN1 (VL) and a nonzero ḡCCAP], we refer to it as MI-BOTH. Fig. 2(c.1–c.3) shows how both IMI components alter the VL-nullcline in this model compared to K08.
Fig. 2.
The synaptic and modulatory network interactions in the reduced model (Equation (17)) give rise to the cubic shape of the VL-nullcline. The factors ILeak,L and II→L in the numerator of Equation (17) are common to all cases of the model. Below these common factors, three rows show the current-voltage relationships of the remaining factors in the equation: the first row shows the IMI-CCAP term of the numerator, the second row shows the negative reciprocal of the denominator (IMI-MCN1) and the third row shows the cubic VL-nullcline that results when the factors are combined as in Equation (17). The third row also shows the step-function shaped s-nullcline of Equation (18). The K08 case, which does not include any modulatory inputs, is shown in black for comparison. The three columns below the common factors illustrate three different modulatory cases of the reduced model. (a.1) – (a.3) The MI-MCN1 case (red) includes only IMI-MCN1 in the LG neuron which primarily influences the left branch of the VL-nullcline. (b.1) – (b.3) The MI-CCAP case (green) includes only IMI-CCAP in the LG neuron which influences the VL-nullcline for all values of VL. The MCN1 input to the LG neuron for this case is assumed to be a simple, excitatory, non-voltage-gated synapse, as in the K08 model. (c.1) – (c.3) The MI-BOTH case (blue) includes both IMI-MCN1 and IMI-CCAP in the LG neuron which influences the VL-nullcline for all values of VL.
In the Results section, we primarily focus on the MI-MCN1 and MI-BOTH cases because these are the biologically-relevant cases of IMI activation in the LG neuron (Kirby and Nusbaum, 2007; DeLong et al., 2009b).
All simulations for our 2-dimensional model were performed using the software package XPPAUT (Ermentrout, 2002). The phase plane diagrams comparing the VL-nullclines in Fig. 2 were produced using the software package MATLAB. Parameter values for the 2-dimensional model are listed in Table 1. The values in Table 1 correspond to the MI-MCN1 case (shown in Fig. 2(a.1–a.3)). Changes to these parameter values (to model the other cases shown in Fig. 2) are discussed in the Results section.
3 Results
The focus of our phase plane analysis is to examine how the network oscillations are influenced when IMI is activated in the LG neuron by two distinct neuromodulators: (i) the MCN1 co-transmitter CabTRP Ia (via the MCN1 to LG synapse; the resulting IMI current is called IMI-MCN1) and (ii) the peptide CCAP (via hormonal release to the STG; the resulting IMI current is called IMI-CCAP). As explained in the Methods, we will primarily focus on the two cases where IMI-MCN1 is activated in LG (MI-MCN1) and where both IMI-MCN1 and IMI-CCAP are activated in LG (MI-BOTH) because these are the biologically relevant cases of IMI activation in the LG neuron (Kirby and Nusbaum, 2007; DeLong et al., 2009b).
As described in Fig. 1(b), the presence of the periodic forcing input p in Equation (15), makes the 2-dimensional model non-autonomous. Physiologically, p describes the influence of the local inhibitory synapse from the pacemaker AB neuron of the pyloric network to Int1 (see Methods). Previous experimental and modeling studies have shown that this input has a significant influence on the cycle period of the gastric mill oscillations, but its presence is not necessary for these oscillations to exist (Bartos et al., 1999; Saideman et al., 2007; Kintos et al., 2008). Below, we will start by analyzing the MI-MCN1 model, first in the absence of the pyloric input (p ≡ 0) and then demonstrate the influence of p in this model. The remainder of the Results section will describe the network dynamics in the presence of the pyloric input (p ∈ [0,1]) which better represents the biological network.
3.1 Network dynamics in the MI-MCN1 model in the absence of the pyloric input
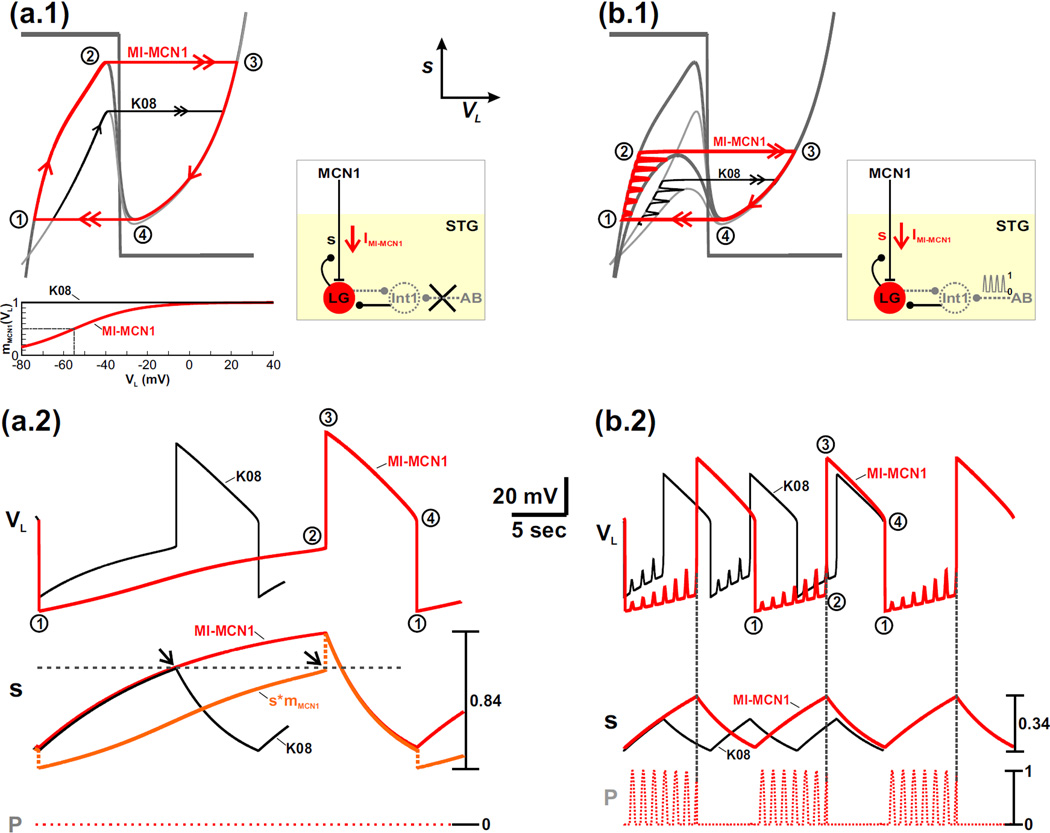
Without the periodic forcing input (p ≡ 0 in Equation (15); schematic circuit diagram in Fig. 3(a.1)), the 2-dimensional model is autonomous so that only a single cubic VL-nullcline exists within the VL − s phase plane. Because the 2-dimensional model resides in a relaxation regime, the trajectory of the unforced system consists of two slow and two fast portions in the phase plane. The slow portions (single red arrows in Fig. 3(a.1)) track the stable outer branches of the VL-nullcline, while the fast portions (double red arrows in Fig. 3(a.1)) occur as horizontal jumps between the outer branches. This fast-slow trajectory captures the network dynamics of the MCN1-elicited gastric mill rhythm in the absence of the local AB-to-Int1 inhibitory synapse (Bartos et al., 1999).
Fig. 3.
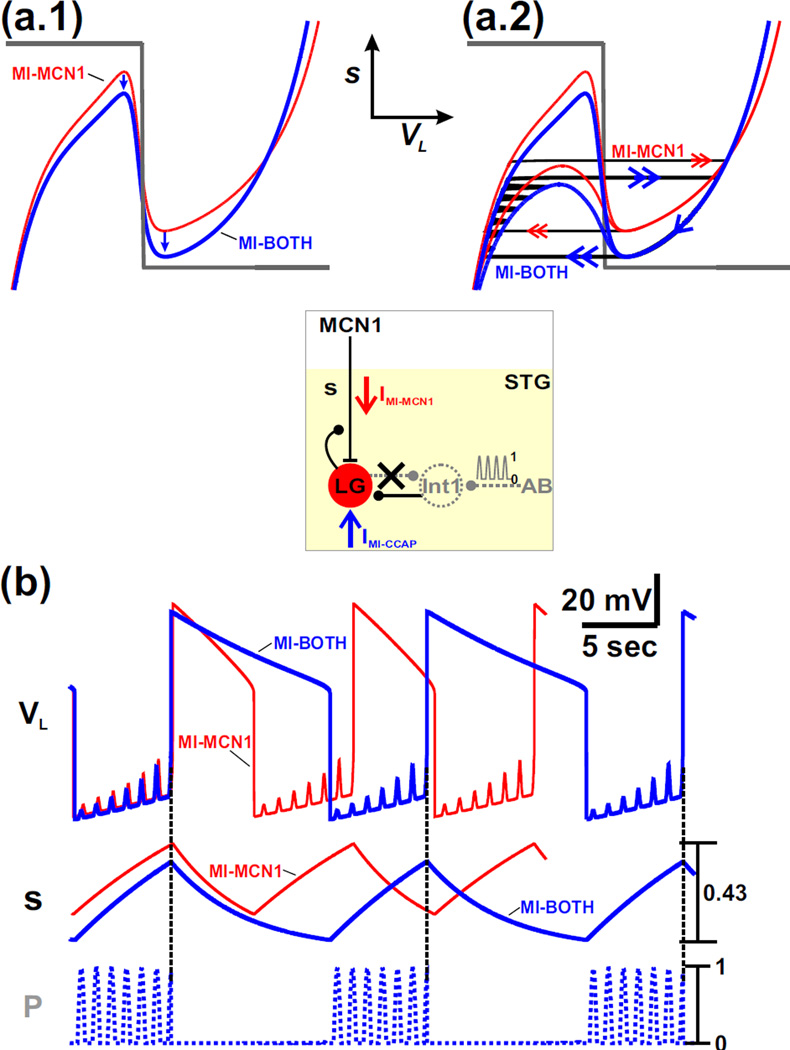
The influence of IMI-MCN1 on the network oscillations is examined by comparing the MI-MCN1 and K08 models. (a.1) Phase plane diagram in the absence of the pyloric-timed input (p = 0). The mMCN1 (VL) activity trace, which gates the MCN1 input to the LG neuron, is shown in the inset for both models. The VL- and s-nullclines (gray) are the same as in Fig. 2(a.3). The red curve illustrates the fast-slow oscillation trajectory of the MI-MCN1 model, where points 1 – 4 are transition points (see text). The distinct oscillation trajectory of the K08 model (black curve) is illustrated for the left branch of the VL-nullcline and for the fast transition to the right branch. The boxed inset shows a schematic diagram of the network circuit for (a.1) and (a.2). (a.2) Corresponding activity traces of VL and s. Points 1 – 4 correspond to the points in (a.1). For the MI-MCN1 model, the value of the MCN1-to-LG input (s*mMCN1) at the fast transition to the LG burst phase matches that of the K08 model (black arrows). The discontinuity in s*mMCN1 is due to the sudden change in the value of mMCN1 as VL shifts to a high value in the transition to the LG burst phase. A similar discontinuity occurs for the other transition to the LG interburst phase. The red curve above the s*mMCN1 trace corresponds to the value of s in the MI-MCN1 model. (b.1) Phase plane diagram in the presence of the pyloric-timed input. The corresponding circuit diagram in shown in the inset. Two cubic VL-nullclines are shown for each model: the upper cubic corresponds to the unforced (p = 0) system from (a.1), while the lower cubic corresponds to the maximally forced (p = 1) system. The red curve again illustrates the oscillation trajectory of the MI-MCN1 model, while the black curve represents the distinct oscillation trajectory of the K08 model. Points 1 – 4 are transition points in the trajectory of the MI-MCN1 model (see text). The boxed inset shows a schematic diagram of the network circuit for (b.1) and (b.2). (b.2) Corresponding time traces of VL and s. Points 1 – 4 correspond to the points in (b.1). The most hyperpolarized value of VL remains the same in (a.2) and (b.2): −74 mV (MI-MCN1 model), −67 mV (K08 model).
The presence of IMI-MCN1 in the LG neuron prolongs the duration of the LG inactive phase (from point 1 to point 2 in Fig. 3(a.1–a.2)) but has much less influence on the duration of the LG active phase (from point 3 to point 4), therefore prolonging the overall cycle period compared to the K08 model (black trajectory in Fig. 3(a.1–a.2)). This implies that the influence of IMI-MCN1 in the biological network is primarily to increase the interburst duration of the LG neuron (i.e. the burst duration of Int1), while maintaining a relatively constant LG burst duration.
The left branch of the cubic VL-nullcline corresponds to the LG inactive phase, where the LG neuron is inhibited by Int1, but the slow excitation s from MCN1 to LG builds up. The voltage-dependent sigmoid mMCN1 (VL) restricts the buildup of this excitatory MCN1 input to low values of VL compared to the K08 case, where mMCN1 (VL) ≡ 1 (see mMCN1 (VL) traces in inset of Fig. 3(a.1–a.2)). As a result, in the MI-MCN1 model, the VL-nullcline exhibits a more hyperpolarized left branch compared to the K08 model (Fig. 3(a.1)). In both cases, the state variable VL slowly increases with s (from point 1 to point 2 in Fig. 3(a.2)) as the trajectory slowly climbs up the left branch of the cubic. The jump point from inactive to active phase of the LG neuron is determined by the fact that the input from MCN1 must reach a critical value and overcome the inhibition by Int1 (Kintos et al., 2008). In the MI-MCN1 model, this input is determined by s*mMCN1 (as compared to only s in the K08 model). As seen in Fig. 3(a.2), at this jump point, the value of s*mMCN1 in the MI-MCN1 model indeed matches the value of s in the K08 model (compare arrows and horizontal dashed line). The fact that in the MI-MCN1 model VL is more hyperpolarized on the left branch, together with the fact that at the jump point the value of s*mMCN1 (where mMCN1 < 1) must match the jump-point value of s for the K08 model, implies that a greater buildup of s is required in the LG neuron in the MI-MCN1 model before the trajectory reaches the left knee of the cubic nullcline (point 2 in the phase plane; Fig. 3(a.1)). This is seen in the higher maximum value of s in the MI-MCN1 model compared to the K08 model (Fig. 3(a.2)).
As the LG neuron transitions into its active phase (point 3), it inhibits Int1 and presynaptically inhibits MCN1. The presynaptic inhibition of MCN1 causes the state variable s to slowly decay. As a result, the trajectory slowly moves down the right branch of the VL-nullcline (from point 3 to point 4 in Fig. 3(a.1)) for both cases, which in turn causes VL to slowly fall with s (Fig. 3(a.2)). Notice that the right branch of the cubic is almost identical for both cases. This is because, in the MI-MCN1 model, mMCN1 (VL) is close to 1 for high values of VL (see the mMCN1 vs. VL graph in the inset of Fig. 3(a.1)). When the trajectory reaches the right knee of the cubic at point 4, it jumps back to the left branch at point 1 for both cases (Fig. 3(a.1)). The jump back to the left branch of the VL-nullcline (from point 4 to point 1 in Fig. 3(a.1)) corresponds to when the fall in VL is sufficient to release Int1. As a result, Int1 inhibition pushes the LG neuron back down into its inactive phase, which in turn removes the LG presynaptic inhibition of MCN1. Then s begins to slowly build up in the LG neuron for both cases and the cycle repeats. At the jump from point 4 to point 1, there is a discontinuity in the value of s*mMCN1, similar to that observed at the other jump point. This discontinuity is due to the sudden change in the value of mMCN1 as VL shifts to a low value (see the mMCN1 vs. VL graph in the inset of Fig. 3(a.1)).
Note that, although the trajectory in the presence of IMI-MCN1 covers a larger portion of the right branch of the VL-nullcline (from point 3 to point 4 in Fig. 3(a.1)), the corresponding duration of the LG active phase is only slightly longer for the MI-MCN1 model compared to the and K08 model (Fig. 3(a.2)).This is because the (exponential) decay of s from a higher starting value in the MI-MCN1 model is more rapid along the right branch of the cubic, compared to the K08 model, which leads to closer values for the LG active phase duration compared to the LG inactive phase duration.
3.2 Network dynamics of the intact system with IMI-MCN1 activation
We now explore how IMI-MCN1 activation in the LG neuron influences the MI-MCN1 model in the presence of p, the AB-to-Int1 inhibitory synapse (see schematic circuit diagram of Fig. 3(b.1)). We consider the same two cases as before for the intact system: the black trajectory corresponds to the K08 model while the red trajectory corresponds to the MI-MCN1 model (Fig. 3(b.1)). Here two cubic VL-nullclines are shown for each case: the higher cubic corresponds to p = 0 (the same as the corresponding VL-nullclines for each case in Fig. 3(a.1)), whereas the lower cubic corresponds to p = 1. See also Fig. 1(b) for comparison.
As before, the trajectory slowly climbs up the left branch of the cubic VL-nullcline (from point 1 to point 2 in Fig. 3(b.1)) as the MCN1 input s slowly builds up in the LG neuron. However, the trajectory shifts back and forth between the p = 0 and p = 1 cubic nullclines due to the influence of the forcing input p (Fig. 3(b.1)). The pyloric-timed transitions between cubics correspond to the fact that AB inhibition of Int1 in turn disrupts the Int1-to-LG inhibitory synapse in the network (see schematic circuit diagram of Fig. 3(b.1)). As a result, in both cases, VL exhibits small-amplitude, pyloric-timed depolarizations during the LG inactive phase (Fig. 3(b.2)).
Notice that the influence of IMI-MCN1 on the left branch of the (family of) VL-nullclines in the MI-MCN1 model is the same as that in the unforced system from Fig. 3(a.1). In particular, activation of IMI-MCN1 in the model LG neuron causes a more hyperpolarized left branch and higher left knee of the VL-nullclines compared to the K08 model (see Fig. 3(b.1)). As a result, the presence of IMI-MCN1 again causes VL to exhibit a more hyperpolarized value from point 1 to point 2 and prolongs the duration of the LG inactive phase (Fig. 3(b.2)).
For both cases, when the trajectory reaches the level of the left knee of the p = 1 VL-nullcline, the next forcing peak from p shifts the VL-nullcline below the phase point and initiates the jump to the right branch from point 2 to point 3 (Fig. 3(b.1)). Thus, in the presence of the forcing input, the jump to the right branch of the VL-nullcline occurs below the left knee of the p = 0 cubic (Fig. 3(b.1)). However, as in the unforced system, a greater buildup of s is required before the jump to the right branch for the MI-MCN1 model (Fig. 3(b.1)). This is also shown by the greater maximum value of s compared to the K08 model in Fig. 3(b.2).
After the trajectory jumps to the right branch of the VL-nullcline, the LG neuron transitions to its active phase, and the network dynamics are similar to that of the unforced system in Fig. 3(a.1) because the pyloric-timed input (p) does not influence the LG active phase (Bartos et al., 1999). Thus, as in the unforced system, activation of IMI-MCN1 in the LG neuron prolongs the cycle period of the MCN1-elicited gastric mill rhythm primarily by prolonging the duration of the LG inactive phase.
The overall influence of the AB-to-Int1 synapse on the MCN1-elicited gastric mill rhythm has been documented in previous experimental (Bartos et al., 1999) and modeling (Nadim et al., 1998) studies. Here, we show that the influence of this synapse on the gastric mill rhythm is not dependent on whether MCN1 activates a voltage-gated current (IMI-MCN1) or a classical excitatory synapse in the LG neuron. First, the onset of the LG active phase is initiated by the pyloric-timed input p (vertical dotted lines in Fig. 3(b.2)). Second, the influence of p decreases the cycle period of the MCN1-elicited gastric mill rhythm (compare Figs. 3(a.2) and 3(b.2)).
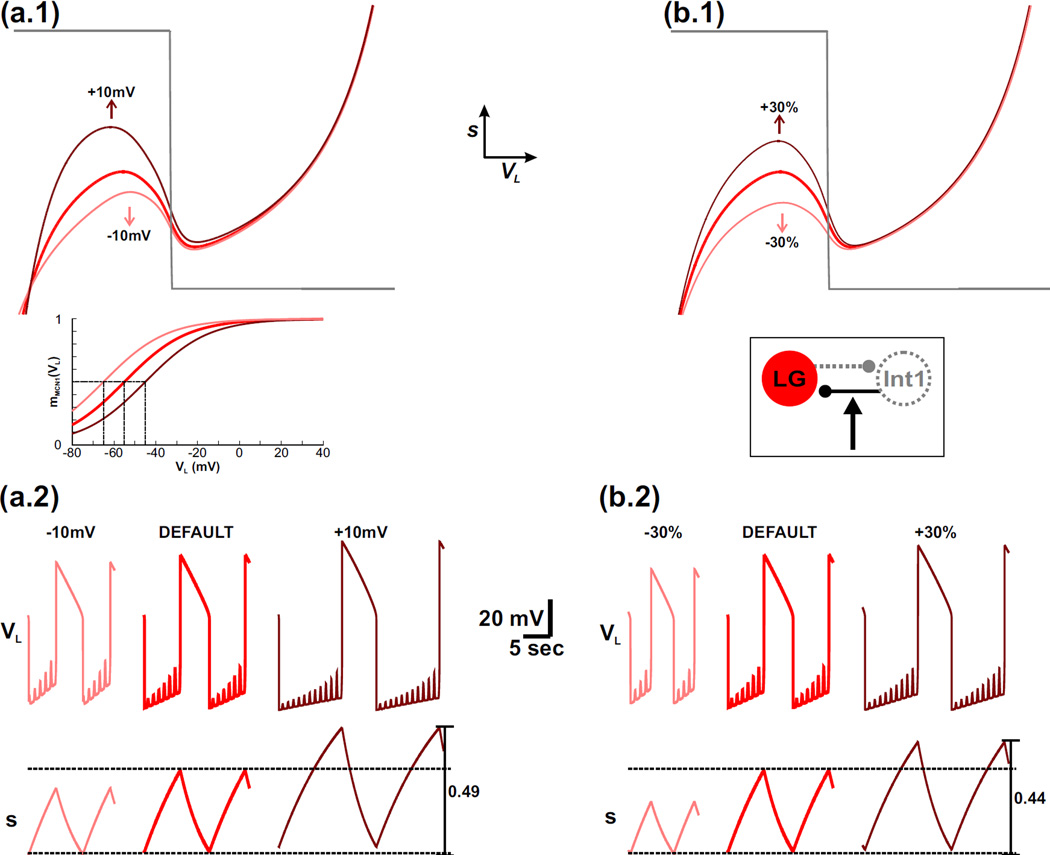
3.3 The effect of the IMI-MCN1 half-activation voltage on the network oscillations
The strength of the MCN1 synaptic input to LG is affected by the position of the half-activation voltage of mMCN1 (VL), modeled by νCabTRP of Equation (9). Our phase plane analysis above shows that the dependence of IMI-MCN1 on VL, described by νCabTRP and kCabTRP, primarily influences the duration of the LG inactive phase of the network oscillations. However, the LG inactive phase is also where the Int1-to-LG inhibition is active and therefore exerts its influence on the duration of this phase (Nadim et al., 1998; Kirby and Nusbaum, 2007). Because both of these factors influence the same phase of the LG oscillations, we examined their relative contributions by comparing the effect of νCabTRP with changing the strength (ḡI→L) of the Int1-to-LG synapse in the model.
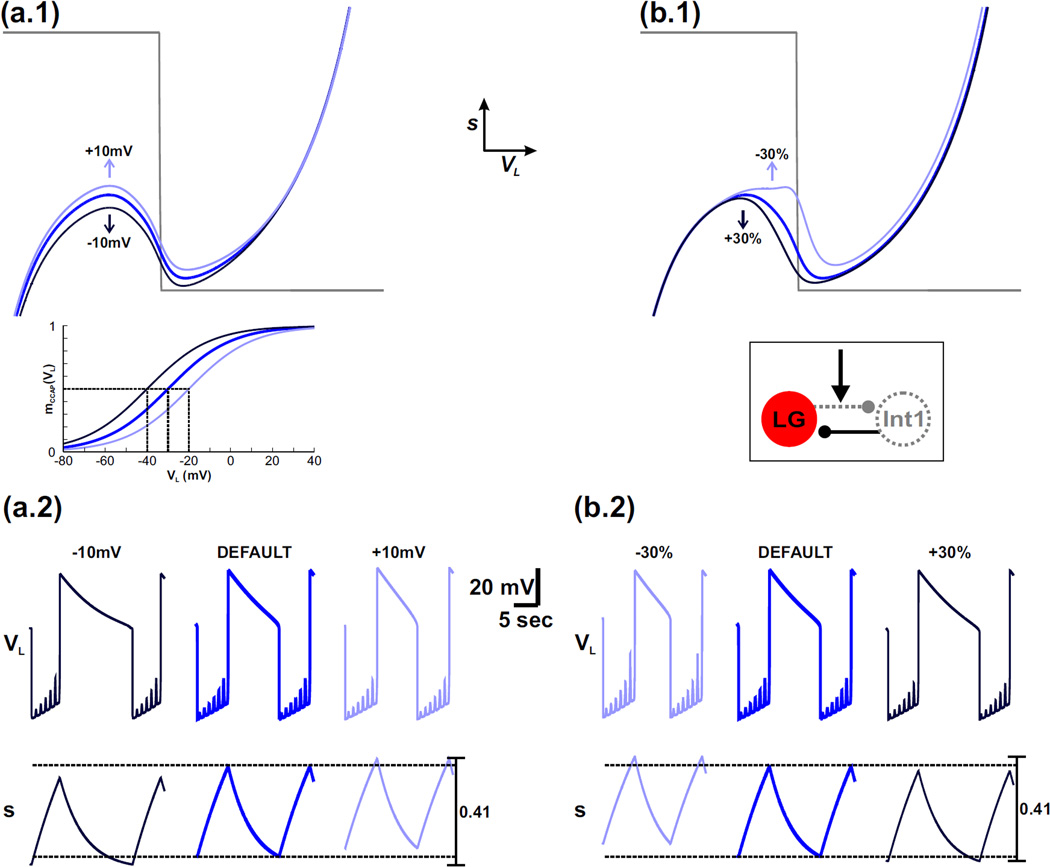
Increasing the default value of νCabTRP by moving it to the right raises the left knee of the VL-nullcline in the phase plane (compare red and dark red nullclines in Fig. 4(a.1); only the p = 1 nullclines are shown for simplicity). This is because the height of the left knee is determined by the value of s at the LG neuron transition from inactive to active phases (point 2 in Fig. 3). As the value of νCabTRP is increased, the sigmoid mMCN1 (VL) shifts to the right (inset of Fig. 4(a.1)) and becomes smaller for a given value of VL. Because the MCN1 to LG excitation is determined by Is = sIMI−MCN1, a smaller value of mMCN1 (VL) on the left branch would require a larger value of s to produce the same influence, thus shifting up the jump point. This change is more clearly seen in the time traces as the higher maximum value of s and corresponding prolonged LG inactive phase when the value of νCabTRP is increased from its default value (Figure 4(a.2) – compare red and dark red).
Fig. 4.
For the MI-MCN1 model, varying the half-activation voltage of IMI-MCN1 produces a similar effect on the network dynamics as varying the strength of the Int1-to-LG inhibitory synapse. For simplicity, only the p = 1 (maximally forced) VL-nullcline is shown in the phase planes. (a.1) – (a.2) The effect of varying the half-activation voltage of IMI-MCN1. The default VL-nullcline is shown in red. The dark red and light red VL-nullclines correspond to when the half-activation voltage of IMI-MCN1 is shifted to the right and left, respectively, by 10 mV. The mMCN1 (VL) activity trace for each case is shown in the inset with the same corresponding colors. The horizontal dashed lines in the s trace of (a.2) correspond to the minimum and maximum values of s. (b.1) – (b.2) The effect of varying the strength of the Int1-to-LG inhibitory synapse. The default VL-nullcline (red in (b.1)) is the same as in (a.1). The dark red and light red VL-nullclines correspond to increasing and decreasing the strength of this synapse, respectively, by 30%. A circuit diagram is shown in the inset. For the default case in (a.2) and (b.2), the most hyperpolarized value of VL is −74 mV.
Conversely, when the value of νCabTRP is decreased from the default, the corresponding sigmoid modeling IMI-MCN1 activation is shifted to the left (inset of Fig. 4(a.1)). As a result, compared to the default case, the left knee of the cubic is lowered in the phase plane so that the LG neuron transitions to its active phase on the right branch of the cubic sooner (red vs light red in Fig. 4(a.1)). This effect is also shown by the lower maximum value of s and corresponding shorter LG inactive phase duration in the time traces (Fig. 4(a.2)).
Varying the value of νCabTRP has little influence on the LG active phase of the network oscillations because mMCN1 (VL) has little effect on the right branch of the VL-nullcline (Fig. 3(a.1) and Fig. 4(a.1)). This is also seen in the similar minimum value of s for all cases in Fig. 4(a.2). Note that varying the steepness of the IMI-MCN1 activation curve (kCabTRP) has little influence on the network oscillations and is not shown due to the similar phase plane structure.
We now examine the effect of the Int1-to-LG synaptic strength on the network oscillations in the model. Increasing the default value of ḡI→L by 30% raises the left knee of the cubic VL-nullcline because a greater buildup of s is required for the LG neuron to escape from Int1 inhibition and transition to its active phase on the right branch of the cubic (compare red and dark red in Fig. 4(b.1)). As before, this effect is also shown by the higher maximum value of s and corresponding prolonged LG inactive phase when ḡI→L is increased from its default value (compare red and dark red in Fig. 4(b.2)). Conversely, decreasing the default value of ḡI→L by 30% lowers the left knee of the cubic VL-nullcline because less buildup of s is required for the LG neuron to escape from Int1 inhibition and transition to its active phase (red vs light red in Fig. 4(b.1)). As before, this effect is also shown by the lower maximum value of s and corresponding shorter LG inactive phase when ḡI→L is decreased in the model (Fig. 4(b.2)).
Similar to the case of the IMI-MCN1 half-activation voltage, the strength of the Int1-to-LG inhibitory synapse has little influence on the right branch of the VL-nullcline in the model (Fig. 4(b.1)). Physiologically, this is because the synapse is inactive when the LG neuron is active and inhibits Int1. This is also shown by the similar minimum value of s for all cases in Fig. 4(b.2).
Thus, we have shown that the IMI-MCN1 half-activation voltage and strength of the Int1-to-LG inhibitory synapse have a similar influence on the MCN1-elicited gastric mill rhythm in our model. In particular, they both increase the cycle period of network oscillations when their corresponding parameters are depolarized/strengthened but decrease the cycle period when those parameters are hyperpolarized/weakened (note the similar trend in Figs. 4(a.2) and 4(b.2)). Moreover, their influence is primarily constrained to the LG inactive phase of the network oscillations, while the trajectory is on the left branch of the VL-nullcline.
3.4 Network dynamics of the intact system with activation of both IMI-MCN1 and IMI-CCAP
So far, we have investigated the influence of IMI-MCN1 on the network dynamics of the MCN1-elicited gastric mill rhythm. Insofar as this current is activated in the LG neuron by MCN1 transmitter release, its influence on the network is constrained by the synaptic interactions between these two neurons. However, the same current is also activated in the LG neuron by the peptide hormone CCAP, and IMI-CCAP modulates the MCN1-elicited gastric mill rhythm in the biological system (Kirby and Nusbaum, 2007). Physiologically, CCAP is released as a circulating hormone, so IMI-CCAP is not constrained by synaptic interactions in the biological system (DeLong et al., 2009b). This leads us to the question of how IMI, when differentially-activated in the LG neuron by MCN1-released CabTRP Ia and circulating CCAP, influences the MCN1-elicited gastric mill rhythm. To address this issue, we examined how activating both currents (IMI-MCN1 and IMI-CCAP) in the model LG neuron affects the behavior of the 2-dimensional model by comparing the MI-MCN1 model with the MI-BOTH model (see Methods). Up to this point, we have separately analyzed the effect of the pyloric input on the gastric mill rhythm in the MI-MCN1 case. For conciseness, from now on we will only describe our analysis for the full system where the pyloric input is present, except where it is indicated otherwise.
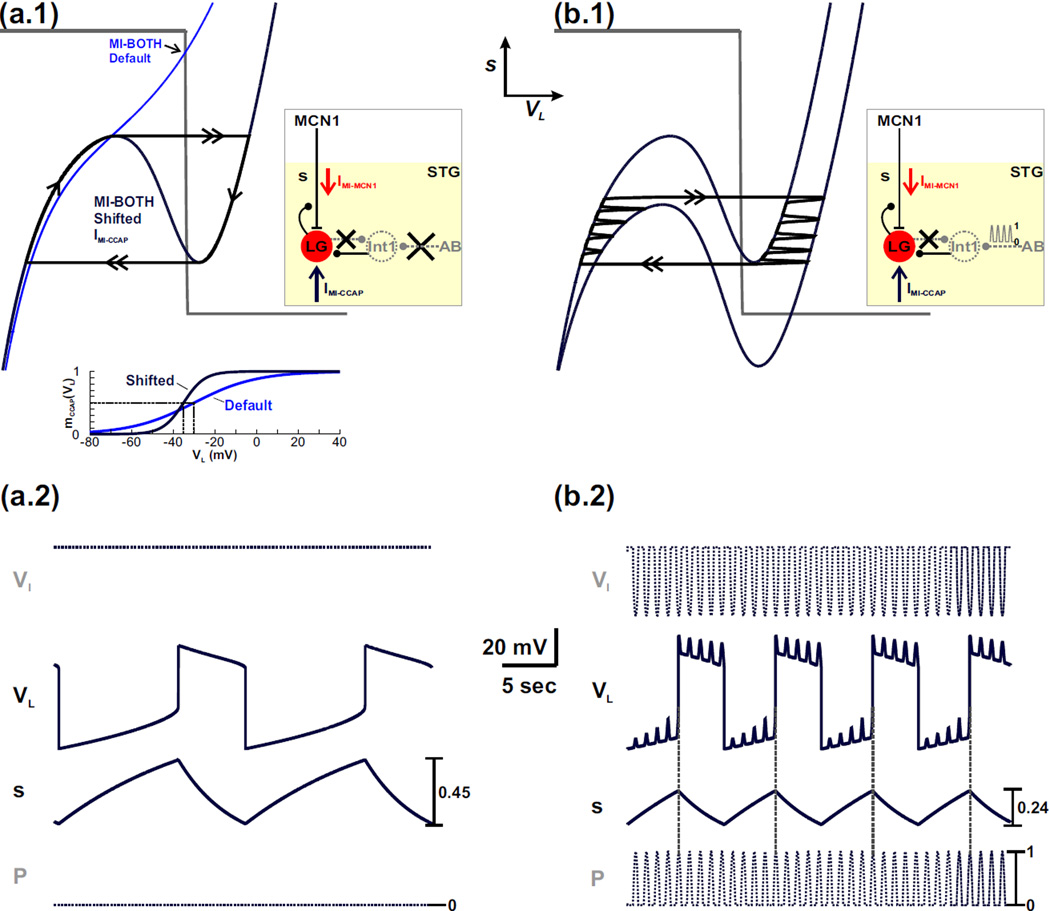
The cubic corresponding to the MI-BOTH case is shifted down compared to the MI-MCN1 case (blue vs red in Fig. 5(a.1)). This is due to the excitatory influence of the inward current IMI-CCAP on the LG neuron. This shift is present at all values of VL, but because of the voltage-dependence of ḡCCAP, it is somewhat larger on the right branch of the cubic nullcline (Fig. 5(a.1)). This shift results in lower knee points on both the left branch and the right branch of the nullcline, corresponding, respectively, to a lower maximum and minimum value of s.
Fig. 5.
The influence of IMI-CCAP on the network oscillations is examined by comparing the MI-BOTH and MI-MCN1 models of the MCN1-elicited gastric mill rhythm. (a.1) Phase plane diagram where only the unforced (p = 0) cubic VL-nullclines are shown for simplicity. The red cubic is the same as that of the MI-MCN1 model in Fig. 3(a.1), while the blue cubic corresponds to the MI-BOTH model. The circuit diagram is shown in the inset. (a.2) The presence of the pyloric-timed input (p) produces the same influence in the phase plane diagram for both models. The unforced (p = 0; upper) and maximally forced (p = 1; lower) cubic VL-nullclines are shown for both models with the same colors as in panel (a.1). The oscillation trajectory of the MI-MCN1 model is the same as in Fig. 3(b.1) and is shown with red arrows, while the trajectory of the MI-BOTH model is shown with blue arrows. (b) The excitatory influence of IMI-CCAP in the MI-BOTH model prolongs the duration of the LG active phase because s must decay to a lower minimum value relative to that of the MI-MCN1 model. Moreover, IMI-CCAP enables s to climb to a lower maximum value before the transition to the LG active phase in the MI-BOTH model so that the LG inactive phase duration remains the same as that of the MI-MCN1 model. Thus, the excitatory influence of IMI-CCAP prolongs the cycle period of the MCN1-elicited gastric mill rhythm by prolonging the duration of the LG active phase and maintaining the LG inactive phase duration. Moreover, as in the MI-MCN1 model, the pyloric-timed input initiates the transition to the LG active phase for the MI-BOTH model (see vertical dashed lines). The most hyperpolarized values of VL are: −74 mV (MI-MCN1 model), −75 mV (MI-BOTH model).
On the left branch of the VL-nullcline, for both cases, the trajectory is shifted back and forth between unforced (p = 0) and maximally-forced (p = 1) nullclines as it climbs up with the slow buildup of s in the LG neuron. The trajectory with the red arrows in Fig. 5(a.2) corresponds to the case where only IMI-MCN1 is activated in the LG neuron (MI-MCN1) and is the same as the corresponding case in Fig. 3(b.1), whereas the trajectory with the blue arrows in Fig. 5(a.2) corresponds to the case where IMI-MCN1 and IMI-CCAP are both activated in the LG neuron (MI-BOTH). Because of the lower left knee point for the MI-BOTH case, the jump to the right branch occurs at a smaller value of s compared to the MI-MCN1 case (Figs. 5(a.2) and 5(b)). Moreover, similar to the MI-MCN1 case, the jump to the right branch of the VL-nullcline is initiated by a pyloric-timed forcing peak for the MI-BOTH case (vertical dashed lines in Fig. 5(b)).
Similarly, on the right branch, because the right knee point is lower in the MI-BOTH case, the trajectory for this case jumps at a lower value of s (Figs. 5(a.2) and 5(b)). The lower right knee point also sits closer to the s-nullcline which results in a slowing of the trajectory and a longer time spent on the right branch in this case. This causes a prolonged LG active phase for the MI-BOTH case compared to the MI-MCN1 case, as reported previously for the biological system (Kirby and Nusbaum, 2007).
Because the jump from the active to inactive phase occurs from a lower knee point in the MI-BOTH case, the trajectory starts at a lower point on the left branch of the VL-nullcline in this case (Fig. 5(a.2)). However, because (as mentioned above) the left knee is also lower for this case, the duration of the LG inactive phase remains similar for both cases (see Fig. 5(b)), again as previously reported for the biological system (Kirby and Nusbaum, 2007).
Thus, for the MI-BOTH case, the hormonal effect of CCAP prolongs the overall cycle period of our model MCN1-elicited gastric mill rhythm by prolonging the LG active phase and maintaining the duration of the LG inactive phase. These observations, captured with a simple phase plane analysis, reproduce the results of previous experiments (Kirby and Nusbaum, 2007) and detailed modeling (DeLong et al., 2009b) of the MCN1-elicited gastric mill rhythm.
The network dynamics of the unforced (p = 0) system for the case of MI-BOTH were not separately considered here because the influence of IMI-CCAP on the unforced system in our model is similar to that shown in Fig. 5. Correspondingly, previous experiments have shown that IMI-CCAP has a similar influence on the MCN1-elicited gastric mill rhythm regardless of the presence of the AB-to-Int1 inhibitory synapse in the network (Kirby and Nusbaum, 2007). In addition, Fig. 2(b.1–b.3) illustrates the case where only IMI-CCAP is activated in the model LG neuron.
3.5 The effect of the IMI-CCAP half-activation voltage on the network oscillations
Our phase plane analysis above shows that IMI-CCAP influences both the left and right branches of the cubic VL-nullcline, but changes only the duration of the active phase of the LG neuron oscillations, similar to the observed influence of CCAP in the biological system (Kirby and Nusbaum, 2007). This is in contrast to IMI-MCN1 which influences primarily the left branch of this nullcline, thereby only affecting the duration of the LG inactive phase (Fig. 3)—an effect that is similar to that of the Int1-to-LG inhibitory synapse (Fig. 4). Given the contrast between the effects of IMI-MCN1 and IMI-CCAP, we examined if the activation curve of IMI-CCAP, which is defined by the parameters νCCAP and kCCAP of Equation (10), could produce a similar influence to that of varying the strength of the LG-to-Int1 inhibitory synapse, the other synapse of the gastric mill half-center.
Figure 6(a.1) shows the effect of varying the parameter νCCAP, which models the half-activation voltage of the sigmoid mCCAP (VL). Only the maximally-forced (p = 1) VL-nullcline is shown in the phase plane, for simplicity, and the default case is shown in blue.
Fig. 6.
For the MI-BOTH model, varying the half-activation voltage of IMI-CCAP produces a similar effect on the network oscillations as varying the strength of the LG-to-Int1 inhibitory synapse. For simplicity, only the p = 1 (maximally forced) VL-nullcline is shown in the phase planes. (a.1) – (a.2) The effect of varying the half-activation voltage of IMI-CCAP. The default VL-nullcline from Fig. 5(a.2) is shown in blue. The darker and lighter blue VL-nullclines correspond to when the half-activation voltage of IMI-CCAP is shifted to the left and right, respectively, by 10 mV. The mCCAP(VL) activity trace is shown in the inset with the same corresponding colors for each case, and the horizontal line in the inset indicates the half-maximum point of mCCAP(VL). Also, in the s-trace of (a.2) the horizontal dashed lines correspond the minimum and maximum values of s. (b.1) – (b.2) The effect of varying the strength of the LG-to-Int1 inhibitory synapse. The default VL-nullcline is the same as in (a.1). The darker and lighter blue VL-nullclines correspond to increasing and decreasing the strength of this synapse, respectively, by 30%. This synapse is activated only during the LG active phase, so it has little effect on the VL-nullcline for low values of VL. A circuit diagram is shown in the inset. The synapse is shown as a gray dotted line in the circuit diagram (arrow in the inset) because its influence was mathematically absorbed into VL in the reduction to a 2-dimensional model (see text). For the default case in (a.2) and (b.2), the most hyperpolarized value of VL is −75 mV.
Shifting the default value of νCCAP to the left moves the sigmoid mCCAP (VL) to the left (blue vs dark blue in the inset of Fig. 6(a.1)), which in turn enhances the excitatory influence of IMI-CCAP by shifting the cubic VL-nullcline downward in the phase plane compared to the default case (blue vs. dark blue in Fig. 6(a.1)). As a result, less buildup of s (the excitatory MCN1 input to the LG neuron) is required before the transition to the LG active phase (blue vs. dark blue in Fig. 6(a.2)). Then, as the trajectory falls down the right branch of the cubic, a greater decay of s is required to overcome the enhanced excitatory influence of IMI-CCAP before the transition back to the left branch of the VL-nullcline (blue vs. dark blue in Fig. 6(a.2)). On the other hand, shifting νCCAP to the right does exactly the opposite (blue vs. light blue in Fig. 6(a.1) and in Fig. 6(a.2)). Consequently, shifting νCCAP to the left or right results in a prolonged or abbreviated LG active phase, respectively (Fig. 6(a.2)). The effect of changing the value of kCCAP had little qualitative influence on the LG oscillations and is not shown.
We now examine how varying the strength of the LG-to-Int1 inhibitory synapse in the model influences the network oscillations. This synapse first appears in Equation (1) as IL→I with maximal conductance ḡL→I. Then, in our reduced model, the influence of this synapse was mathematically absorbed into the II→L (p) term of Equation (15). Changing ḡL→I primarily affects the left knee, rather than the entire left branch, of the VL-nullcline (Fig. 6(b.1)). Physiologically, this is because the LG-to-Int1 synapse is active only when LG is active. Nevertheless, changing ḡL→I has a similar excitatory influence as shifting νCCAP. In particular, increasing ḡL→I shifts the cubic VL-nullcline downward (blue vs. dark blue in Fig. 6(b.1)). Thus, less buildup of s is needed before the transition to the right branch of the cubic (blue vs. dark blue in Figure 6(b.2)). Then, as the trajectory falls down the right branch of the cubic, a greater decay of s is required before the jump back to the left branch of the VL-nullcline (blue vs. dark blue in Fig. 6(b.2)). This effect is similar to shifting νCCAP to the left. Similarly, decreasing ḡL→I does the opposite (blue vs. light blue in Fig. 6(b.1) and 6(b.2)), which is similar to shifting νCCAP to the right. Thus, the IMI-CCAP half-activation voltage and strength of the LG-to-Int1 synapse have a similar effect on the right branch of the cubic VL-nullcline, and thus the duration of the LG active phase of the network oscillations.
3.6 Network oscillations without the intact Int1-LG reciprocal inhibition
Our phase plane analysis showed that each individual synaptic component of the Int1-LG reciprocal inhibition primarily influences the duration of one of the two phases of the MCN1-elicited gastric mill rhythm. In particular, the Int1-to-LG inhibitory synapse primarily influences the duration of the inactive phase of the LG neuron (Fig. 4(b.1)–(b.2)), while the LG-to-Int1 inhibitory synapse primarily influences the duration of the active phase (Fig. 6(b.1)–(b.2)). Experimental evidence suggests that both synaptic components of the Int1-LG half-center are required to sustain the MCN1-elicited gastric mill rhythm (Coleman et al., 1995; Akay et al., 2004).
In parallel, we showed that IMI-MCN1 and IMI-CCAP each has an effect on the network oscillations that is comparable to one of the two Int1-LG reciprocally inhibitory synapses in the model (Fig. 4 for IMI-MCN1 and Fig. 6 for IMI-CCAP). This brings up the question as to what role this seemingly redundant influence (on phase duration(s)) could play at the circuit level. To address this issue, we separately removed each component of the Int1-LG reciprocal inhibition from the network and examined how the influence of the corresponding IMI affected the behavior of the model.
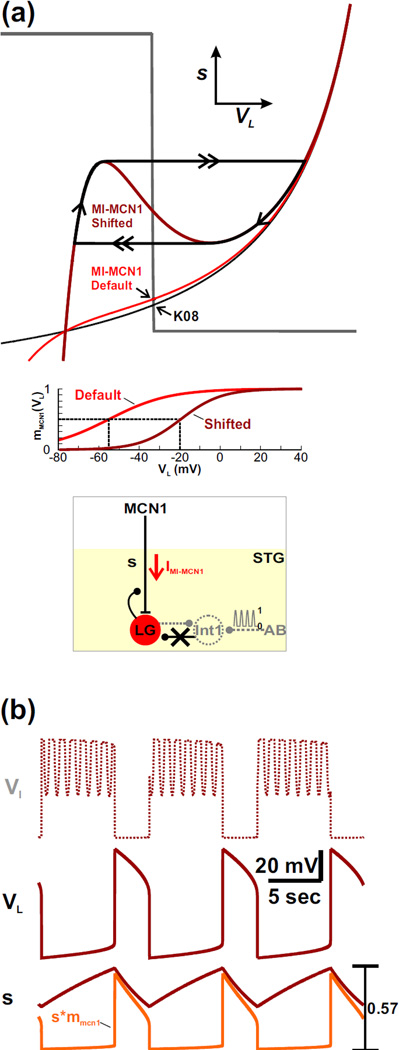
First, we examined how IMI-MCN1 could influence the MCN1-elicited gastric mill rhythm when the Int1-to-LG inhibitory synapse is removed from the model. Removal of this synapse, by setting ḡI→L = 0, changes the VL-nullcline to a monotonic curve regardless of the presence of IMI-MCN1 (black curve for the K08 case; red curve for the MI-MCN1 case in Fig. 7(a)). As a result, the VL- and s-nullclines intersect at a stable fixed point for both cases (black arrows in Fig. 7(a)) and, consistent with the biological system (Akay et al., 2004), the network oscillations are disrupted.
Fig. 7.
IMI-MCN1 enables rhythmic oscillations to persist when the Int1-to-LG synapse is removed from the network. (a) Phase plane diagram. Removal of the Int1-to-LG synapse causes the VL-nullcline to become a monotonic curve. As a result, the VL- and s-nullclines intersect at a stable fixed point (arrows at intersection) so that network oscillations are disrupted. The qualitatively similar black and red monotonic curves correspond to the VL-nullcline of the K08 and MI-MCN1 model, respectively. Shifting the IMI-MCN1 half-activation voltage to the right (see the mMCN1(VL) activity trace in the inset) reproduces the cubic shape of the VL-nullcline in the phase plane (dark red cubic) and restores the network oscillations in the absence of the Int1-to-LG synapse. A circuit diagram is shown in the inset. (b) Activity traces corresponding to the oscillatory trajectory of the dark red cubic VL-nullcline in (a). The activity trace of Int1 (VI) is calculated from VL. The most hyperpolarized values of VI and VL are −56 mV and −58 mV, respectively.
However, the half-activation voltage of IMI-MCN1 influences the network in a manner similar to the strength of the Int1-to-LG synapse (Fig. 4). Consequently, when ḡI→L = 0, shifting νCabTRP to the right (see inset of Fig. 7(a)) has an effect similar to increasing ḡI→L and produces the cubic shape of the VL-nullcline (dark red cubic in Fig. 7(a)). Moreover, the VL- and s-nullclines intersect along the middle branch of the cubic, which allows for a stable limit cycle (Fig. 7(a)) and restores the network oscillations in the absence of the Int1-to-LG synapse (dark red activity traces in Fig. 7(b)).
Although the MCN1-elicited gastric mill rhythm can persist without the Int1-to-LG synapse in our model, the network dynamics of these oscillations are qualitatively different from that of the intact circuit. In particular, the LG neuron is not inhibited by Int1 as the trajectory slowly climbs up the left branch of the cubic VL-nullcline with the slow buildup of s in LG. As a result, the left knee of the VL-nullcline represents the threshold value of the s buildup that enables its excitatory influence to allow the inward current IMI-MCN1 to become regenerative and result in a transition to the LG active phase. In contrast, during the LG active phase, the network dynamics are similar to that of the intact system: the LG neuron inhibits Int1 and presynaptically inhibits MCN1. The latter causes the trajectory to slowly travel down the right branch of the cubic, as in the intact system. Also, similar to the intact network (Fig. 3), the right knee of the cubic represents the level of decay in s that enables IMI-MCN1 to shut off and initiate the transition back to the inactive phase.
Notice that, although direct Int1 inhibition of LG was removed from the circuit, Int1 and the LG neuron still oscillate in anti-phase (Fig. 7(b)). However, the pyloric-timed forcing input p no longer influences VL (dark red trace in Fig. 7(b)) because its influence on the LG neuron was an indirect disinhibition, which is now disrupted because of the absence of the Int1-to-LG synapse. Thus, without direct Int1 inhibition of the LG neuron, the influence of IMI-MCN1 can preserve the Int1-LG anti-phase oscillations but, unlike the intact system, the pyloric input no longer regulates the MCN1-elicited gastric mill rhythm.
As mentioned earlier, IMI-CCAP does not have the same effect as the Int1-to-LG synapse on the network. In fact, in the MI-BOTH case, removing the Int1-to-LG synapse from the model also changes the VL-nullcline to a monotonic curve regardless of the presence of IMI in the network. In this case, shifting the half-activation voltage of IMI-CCAP in either direction retains a stable fixed point and prevents the existence of oscillations (data not shown). However, in the MI-BOTH model, the half-activation voltage of IMI-CCAP has a similar influence on the right branch of the VL-nullcline as the strength of the LG-to-Int1 synapse for the intact network (see Fig. 6). We therefore examined the influence of IMI-CCAP on the MI-BOTH model when this synapse was removed.
First, we examined how removal of the LG-to-Int1 inhibitory synapse influences the network dynamics in the absence of the pyloric-timed input (p = 0). As before, removal of the LG-to-Int1 synapse changes the VL- nullcline to a monotonic curve (Fig. 8(a.1)). Therefore, the VL- and s-nullclines intersect at a stable fixed point (black arrow in Fig. 8(a.1)) and the network oscillations are disrupted. However, shifting the half-activation voltage of IMI-CCAP to the left (see inset of Fig. 8(a.1)) and increasing its maximal conductance can restore the cubic shape of the VL-nullcline (dark blue cubic in Fig. 8(a.1)). Also, in this case, the VL- and s-nullclines intersect along the middle branch of the cubic (Fig. 8(a.1)), which allows for a stable limit cycle and restores the network oscillations (dark blue traces in Fig. 8(a.2)).
Fig. 8.
IMI-CCAP enables rhythmic oscillations to persist in the MI-BOTH model when the LG-to-Int1 inhibitory synapse is removed from the network. (a.1) Phase plane diagram in the absence of the pyloric-timed input (p = 0). A circuit diagram is shown in the inset. Removal of the LG-to-Int1 inhibitory synapse causes the VL-nullcline to become monotonic, which intersects the s-nullcline at a stable fixed point (arrow at intersection) so that network oscillations are disrupted. Shifting the IMI-CCAP half-activation voltage to the left (see the mCCAP (VL) activity trace in the inset) and increasing its maximal conductance in the model reproduces the cubic shape of the VL-nullcline (dark blue cubic) and restores the network oscillations in the absence of the LG-to-Int1 synapse. (a.2) Activity traces corresponding to the oscillatory trajectory of the cubic VL-nullcline in (a.1). The activity trace of Int1 (VI) is calculated from VL. The cubic shape of the VL-nullcline restores oscillatory activity in the LG neuron but not in Int1. (b.1) Phase plane diagram in the presence of the pyloric-timed input. A circuit diagram is shown in the inset. The higher (p = 0) cubic is the same as in (a.1), while the lower cubic corresponds to the maximally forced (p = 1) system. (b.2) Corresponding activity traces for the oscillatory trajectory in (b.1). The activity of VI is again calculated from VL. Int1 exhibits only pyloric-timed activity and, similar to (a.2), does not oscillate in anti-phase with LG. Also, unlike the intact circuit, the pyloric-timed input influences both phases of the LG neuron oscillation when the LG-to-Int1 synapse is removed from the network. The most hyperpolarized values of VI and VL are −27 mV and −74 mV, respectively. The former occurs in (b.2) while the latter is the same in (a.2) and (b.2).
As in the case of Figure 7, despite the cubic shape of the VL-nullcline, the network dynamics in Figure 8(a.1)–(a.2) are qualitatively different from that of the intact system (Fig. 5). In particular, the LG neuron does not inhibit Int1 and the only synaptic influence of the LG neuron is its presynaptic inhibition of MCN1 (schematic circuit diagram of Fig. 8(a.1)). As a result, Int1 remains at its high resting potential in the model (VI trace in Fig. 8(a.2)). Therefore, in the absence of the LG-to-Int1 synapse, the excitatory influence of IMI-CCAP with sufficient strength and the proper activation curve can restore oscillatory activity in the LG neuron but not in Int1. Consequently, the Int1-LG half-center oscillations of the intact MCN1-elicited gastric mill rhythm are disrupted.
In the presence of the pyloric-timed forcing input p, the LG oscillations shown in Figure 8(a.2) (with no LG-to-Int1 synapse) persist (see phase plane in Fig. 8(b.1)), but show pyloric-timed disinhibitions both in the LG inactive phase and the LG active phase. In both phases, Int1 produces only pyloric-timed oscillations but exerts the same influence on the LG neuron independent of its activity phase (Fig. 8(b.2)). This fact is reflected in the shifts of both the left and the right branches of the VL-nullcline (Fig. 8(b.1)). Thus, without direct LG inhibition of Int1, the influence of IMI-CCAP can restore oscillations only in the LG neuron but, unlike the intact system, the pyloric input is not gated out during the LG active phase and therefore influences both phases of the LG neuron oscillations. However, similar to the intact system, the presence of the pyloric-timed input decreases the cycle period of the LG neuron oscillations (compare VL traces in Fig. 8(a.2) and 8(b.2)) and initiates the onset of the LG active phase (dashed horizontal lines in Fig. 8(b.2)).
4 Discussion
Convergent actions of distinct neuromodulators, such as by activating similar ionic currents or modifying similar synaptic properties, can produce distinct outputs in the same neural network when those actions target distinct network components (Di Prisco et al., 2000; Nusbaum et al., 2001; Swensen and Marder, 2001; Marder and Thirumalai, 2002; Bacci et al., 2005; Dickinson, 2006; Lieske and Ramirez, 2006). This well-established property provides a given neural network the flexibility to produce multiple distinct modes of output (Marder, 2012; Nusbaum and Blitz, 2012; Nadim and Bucher, 2014). Here we examined what advantage, if any, is provided by distinct neuromodulators activating the same cellular-level intrinsic property in the same neuron (DeLong et al., 2009b). The goal of our analysis was to determine if such seeming redundancy simply provides the network with more opportunity for producing a given mode of output or if additional network-level advantages exist.
We used a simplified mathematical model of the MCN1-elicited gastric mill rhythm to investigate how rhythm generation is influenced by the convergent actions of two distinct neuropeptide modulators, CabTRP Ia and CCAP. Both modulators activate the same voltage-dependent inward ionic current (IMI) in the rhythm generator neuron LG. However, whereas CabTRP Ia is released into the STG neuropil by the MCN1 axon terminals (Wood et al., 2000), CCAP gains access to the STG as a circulating hormone (Kirby and Nusbaum, 2007). Due to LG presynaptic inhibition of the MCN1 axon terminals during the protraction phase, IMI-MCN1 builds up in the LG neuron during each retraction (LG inactive) phase and decays during each protraction (LG active) phase (Coleman et al., 1995; DeLong et al., 2009b). In contrast, the presence of IMI-CCAP is not constrained by any synaptic interactions (DeLong et al., 2009b). This distinction results in IMI-MCN1 primarily regulating the retraction phase duration while IMI-CCAP primarily regulates protraction phase duration, providing some initial insight that, despite their convergent activation of IMI in the LG neuron, CabTRP Ia and CCAP are not functionally redundant at the network-level.
4.1 The influence of IMI-MCN1 activation on the network oscillations of the intact circuit
We compared the MI-MCN1 model (where IMI-MCN1 is synaptically activated by MCN1 in the LG neuron) to the K08 model (where the MCN1-to-LG synapse was modeled as an ionotropic excitatory synaptic input) to examine whether there was any distinction for rhythm generation bestowed by the voltage-dependent properties of IMI-MCN1 relative to a classical ionotropic excitatory synapse. These two types of excitation were comparable with respect to the ability of the pyloric-timed input to decrease the gastric mill rhythm cycle period and determine the onset of the LG active phase. However, there was also a distinction in that, relative to the ionotropic excitatory synapse in the K08 model, IMI-MCN1 prolonged the MCN1-elicited gastric mill rhythm cycle period, primarily by prolonging the LG inactive phase (i.e. retraction) duration. Both model outcomes, including the impact of the pyloric-timed input and the ability of IMI-MCN1 to prolong retraction, mimicked those occurring in the biological system (DeLong et al., 2009b).
A novel insight resulting from our phase plane analysis was that shifting the half-activation voltage of a voltage-gated ionic current (IMI-MCN1) can influence the gastric mill rhythm cycle period in a manner similar to manipulating the Int1-to-LG classical, voltage-independent inhibitory synapse. Specifically, shifting the half-activation voltage of IMI-MCN1 produced a similar effect on the cubic VL-nullcline to changing the strength of the Int1-to-LG synapse in the model. Both manipulations similarly altered the cycle period primarily by changing the duration of the LG inactive phase, consistent with previous biophysically-detailed modeling of the MCN1-elicited rhythm (Nadim et al., 1998; DeLong et al., 2009b). It would be interesting to determine if the same effect is also observed in the biological system, insofar as previous studies of other voltage-dependent currents have established that the half-activation voltage can be a target of neuromodulation in rhythmic motor systems (Peck et al., 2006; Hawkins et al., 2015).
4.2 The influence of IMI-CCAP activation on the network oscillations of the intact circuit
We compared the MI-BOTH model (where both IMI-MCN1 and IMI-CCAP are activated in the LG neuron) to the MI-MCN1 model (where only IMI-MCN1 is activated in the LG neuron) to examine the influence of IMI-CCAP on the network dynamics. We did not consider the MI-CCAP condition (where only IMI-CCAP is activated in the LG neuron) because in the biological system there is no MCN1-elicited gastric mill rhythm without IMI-MCN1 activation in LG (Wood et al., 2000). It is worth noting, however, that due to the similar phase plane structure, IMI-CCAP has a similar influence on the network oscillations regardless of whether MCN1 acts on LG through ionotropic excitation (the K08 model) or through IMI-MCN1 (the MI-MCN1 model; data not shown).
Phase plane analysis of the MI-BOTH model showed that the influence of IMI-CCAP prolongs the MCN1-elicited gastric mill rhythm cycle period (compared to the MI-MCN1 model) by prolonging the LG active phase and maintaining the duration of the LG inactive phase. These outcomes reflect those of CCAP in the biological system (Kirby and Nusbaum, 2007) and in a biophysically-detailed model of the MCN1-elicited gastric mill rhythm (DeLong et al., 2009b). Also reflecting these previous studies, the influence of IMI-CCAP in the MI-BOTH model shifts down both branches of the cubic VL-nullcline in the phase plane compared to the MI-MCN1 model VL-nullcline. Consequently, there is a greater decay of s (the excitatory MCN1 input to LG) during the LG active phase of the MI-BOTH model before the LG neuron can transition to its inactive phase, thereby prolonging the duration of the subsequent LG active phase. In contrast, during the LG inactive phase, less buildup of s is required before the LG neuron can transition to its active phase due to the excitatory influence of IMI-CCAP, thereby maintaining a similar LG inactive phase duration for the MI-BOTH model compared to the MI-MCN1 model (see also (DeLong et al., 2009b)).
Also, consistent with previous biophysically-detailed modeling (Nadim et al., 1998), varying the strength of the LG-to-Int1 synapse in the MI-BOTH model had less impact on the gastric mill cycle period, compared to that of the Int1-to-LG synapse. Because our phase plane analysis shows that shifting the half-activation voltage of IMI-CCAP (in the MI-BOTH model) can influence the gastric mill rhythm cycle period in a manner similar to that of manipulating the strength of the LG-to-Int1 inhibitory synapse, it would be interesting to determine if IMI-CCAP and the LG-to-Int1 synapse produce a comparable influence in the biological system.
Although IMI-MCN1 and IMI-CCAP are the same current, their measurements under experimental conditions can result in distinct half-activation voltages (DeLong et al., 2009b). Similarly, in our simplified model, the default half-activation voltages of these two currents differed. Although we have not shown the associated modeling data, we note that our overall results can be obtained with similar half-activation voltages of IMI-MCN1 and IMI-CCAP by including in our reduced model the previously identified CCAP excitation of Int1 (Kirby and Nusbaum, 2007). Doing so would make the model quantitatively closer to the biological system, and it would not change our qualitative results. It is noteworthy, however, with respect to the distinct half-activation voltages for IMI-MCN1 and IMI-CCAP in our model that even closely related neuropeptides (i.e. different peptide family members) can distinctly modulate an ionic current by activating different intracellular signaling systems despite binding to the same receptor, or by having different binding affinities for separate receptors on the same target cell (Nusbaum and Blitz, 2012).
4.3 Implications for gastric mill rhythm generation without reciprocal inhibition
Our phase plane analysis demonstrated that convergent action of distinct neuromodulators onto the same rhythm generating neuron of a defined network can provide a more robust mechanism for producing oscillatory activity. The fact that our findings resonate so well with the comparable events in the biological system lends support to our novel modeling result that the core rhythm-generating mechanism(s) underlying neuronal network output need not be preserved during all versions of network operation. For example, for the MI-MCN1 model, removing the Int1-to-LG inhibitory synapse disrupts the MCN1-elicited gastric mill rhythm, as also occurs in the biological system (Akay et al., 2004). However, a shift in the properties of IMI-MCN1 can balance the asymmetry of the missing (Int1-to-LG) inhibitory synapse to restore the network oscillations in the model. In the biological system, such a shift in IMI-MCN1 properties might occur via the influence of a parallel modulatory neuronal or hormonal input.
One distinction from the intact circuit with respect to IMI-MCN1 replacing the Int1-to-LG inhibitory synapse is that the rhythmic pattern produced is different, at least partly because the pyloric-timed input that normally regulates LG, via Int1, is lost. Thus, in this condition there would be a partial loss of the two-way inter-circuit coordination between the gastric mill and pyloric rhythms, with the gastric mill rhythm becoming independent of the pyloric rhythm. In a recent modeling study there was a similar loss of pyloric regulation of the gastric mill rhythm when a distinct version of the gastric mill rhythm was produced without the Int1-to-LG synapse (Kintos and Nadim, 2014). In the biological system, however, the gastric mill regulation of the pyloric rhythm would persist, via LG neuron feedback inhibition of the MCN1 axon terminals removing MCN1 excitation of the pyloric rhythm (Bartos and Nusbaum, 1997).
Similarly, in the MI-BOTH model, removing the LG-to-Int1 inhibitory synapse also disrupts the MCN1-elicited rhythm, but the rhythmic LG activity could be restored by altering the properties of IMI-CCAP. As above, however, the oscillations were different from those of the intact circuit. Here, the LG neuron oscillated, but no longer in anti-phase with Int1. The resulting LG oscillation pattern (pyloric rhythm-timed during both gastric mill rhythm phases) is reminiscent of that during the POC-triggered gastric mill rhythm (White and Nusbaum, 2011). However, in the present case the LG protraction phase pattern results from continued Int1 inhibition of LG, whereas during the POC-rhythm the protraction phase LG pattern results from pyloric rhythm-timed inhibition of MCN1 (Blitz and Nusbaum, 2008).
4.4 Conclusions
From the well-established perspective that neuromodulatory input enables a network to produce multiple outputs, it seems inefficient for distinct neuromodulators to activate the same ionic current in the same neuron. Our simplified mathematical model of the gastric mill CPG suggests that this convergent action is not, in fact, functionally redundant. Instead, the convergent action of CabTRP Ia and CCAP produces a surprisingly divergent influence at the network level, thereby increasing the diversity of mechanisms by which neuromodulators can influence network activity. These differences include preferentially regulating the duration of separate phases of the motor pattern, and having the ability to substitute for the (ionotropic inhibitory) rhythm-generator synapse within the phase whose duration it regulates. Such a substitution would provide more flexibility at the network level, as it would lead to a distinct network output and therefore a distinct behavior due to changes in the network architecture, e.g. through loss of inter-circuit coordination.
Distinct neuromodulators similarly activate convergent cellular-level properties in the same neuron type in the mammalian brain. For example, noradrenaline and serotonin both activate the hyperpolarization activated cation current (Ih) in thalamocortical relay neurons (McCormick and Pape, 1990). Although the network-level consequences of such convergent modulator actions remain unresolved in the larger, less well-defined networks, our modeling results demonstrate that such actions may produce similar network output via an altered network configuration. Such an outcome could enable the network to produce different responses to the same perturbation, such as input from another region of the nervous system. This next level of understanding is also feasible using the MCN1-elicited gastric mill system, insofar as its response to an identified sensory pathway is already well-characterized in both the biological system and a biophysically-detailed model (Beenhakker et al., 2005; DeLong et al., 2009a).
Acknowledgments
Supported by NIH MH060605 (FN), Kenny Fund Fellowship (NK), and NIH NS029436 (MPN).
Appendix
Below is the program code for the xpp file associated with the model. The changes in parameter values needed for some of the figures are listed as comments in the code.
######################## KNN-2015.ode ######################
# 2D model of MCN1-elicited Gastric Mill Rhythm
#
# There are two ways the IMI current is activated in LG
# Synaptically via the MCN1-to-LG synapse (mics)
# Bath application of CCAP (ICCAP)
#
# Param Units C (microF/cm2), g (mS/cm2), v,E,k (mV), t (msec)
################################################################
# initial conditions
init vL=−60 s=1
# Parameters
par gleakL=1 EleakL=−60 IextI=0 gIL=5 EIL=−80
par vIL=−30 kIL=5 gleakI=0.75 EleakI=10 gLI=2 ELI=−80
par vLI=−30 kLI=5 gP=0.85 EP=−60
par gPf=0 per=1000 dur=500 pt=0 ptx=1 vq=−35 kq=3
# gp=0 when the pyloric input is removed
# figs 3a1–a2, 5a1, 8a1–a2
#
# set gPf=1 to get the maximally forced (p=1)
# VL nullcline, also use 0<gPf<1 in fig 1b
#
# For fig 8b1–b2 set pt=1 and ptx=0
par gs=3.75 Es=50 micsoff=1 vmics=−55 kmics=15
# For IMI-MCN1 use micsoff=0
#
# Fig 7 dark red cubic, use vmics=−20 kmics=10
par gccap=0 Eccap=10 vccap=−30 kccap=15
# For IMI-CCAP use gccap=1.4
#
# Fig 8 dark blue cubic, use
# gccap=8 vccap=−35 kccap=5
par tauHI=5000 tauLO=14000 vthresh=−33
par maxamp=0 ton=20000 toff=20100 IextL=0
# Functions
IleakL(x)=gleakL*(x-EleakL)
IIL(x)=gIL*mIL(u(x))*(x-EIL)
mIL(x)=1/(1+exp((vIL-x)/kIL))
u(x)=unum(x,t)/uden(x,t)
unum(x,t)=IextI+(gleakI*EleakI)+(gLI*mLI(x)*ELI)+(gP*P(x,t)*EP)
uden(x,t)=gleakI+(gLI*mLI(x))+(gP*P(x,t))
mLI(x)=1/(1+exp((vLI-x)/kLI))
P(x,t)=(gPf+(sin((Pi*mod(t,per))/dur)*heav(dur-mod(t,per))))*(pt+(ptx*q(x)))
q(x)=1/(1+exp((x-vq)/kq))
Is(x)=gs*s*mics(x)*(x-Es)
mics(x)=micsoff+((1-micsoff)*(1/(1+exp((vmics-x)/kmics))))
Iccap(x)=gccap*micba(x)*(x-Eccap)
micba(x)=1/(1+exp((vccap-x)/kccap))
taus(x)=tauHI+((tauLO-tauHI)*heav(vthresh-x))
# If Iext is needed in LG
IinjL(t)=(maxamp*heav(t-ton)*heav(toff-t))+IextL
Psyn(x,t)=gP*P(x,t)
smics(x)=s*mics(x)
gsmics(x)=gs*s*mics(x)
# ODEs
vL'=IinjL(t)-IleakL(vL)-IIL(vL)-Is(vL)-Iccap(vL)
s'=(heav(vthresh-vL)-s)/taus(vL)
# Aux Var
aux vI=u(vL)
aux P=P(vL,t)
aux Psyn=Psyn(vL,t)
aux mIL=mIL(u(vL))
aux mLI=mLI(vL)
aux mics=mics(vL)
aux smics=smics(vL)
aux gsmics=gsmics(vL)
aux micba=micba(vL)
aux IinjL=IinjL(t)
# settings
@ total=1e5,dt=5,xlo=−80,xhi=50,ylo=−0.1,yhi=1.1
@ xplot=vL,yplot=s,method=stiff
@ maxstor=100000,nmesh=200
done
References
- Akay T, Wood D, Nusbaum MP. Reciprocal Inhibition is not necessary for generation of all gastric mill rhythms; SfN 34th Annual Meeting; San Diego, CA. 2004. [Google Scholar]
- Ambrosio-Mouser C, Nadim F, Bose A. The effects of varying the timing of inputs on a neuronal oscillator. SIAM J Applied Dynamical Systems. 2006;5:108–139. doi: 10.1137/050625795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bacci A, Huguenard JR, Prince DA. Modulation of neocortical interneurons: extrinsic influences and exercises in self-control. Trends Neurosci. 2005;28:602–610. doi: 10.1016/j.tins.2005.08.007. [DOI] [PubMed] [Google Scholar]
- Bartos M, Nusbaum MP. Intercircuit control of motor pattern modulation by presynaptic inhibition. J Neurosci. 1997;17:2247–2256. doi: 10.1523/JNEUROSCI.17-07-02247.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartos M, Manor Y, Nadim F, Marder E, Nusbaum MP. Coordination of fast and slow rhythmic neuronal circuits. J Neurosci. 1999;19:6650–6660. doi: 10.1523/JNEUROSCI.19-15-06650.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beenhakker MP, DeLong ND, Saideman SR, Nadim F, Nusbaum MP. Proprioceptor regulation of motor circuit activity by presynaptic inhibition of a modulatory projection neuron. J Neurosci. 2005;25:8794–8806. doi: 10.1523/JNEUROSCI.2663-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blitz DM, Nusbaum MP. Distinct functions for cotransmitters mediating motor pattern selection. J Neurosci. 1999;19:6774–6783. doi: 10.1523/JNEUROSCI.19-16-06774.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blitz DM, Nusbaum MP. State-dependent presynaptic inhibition regulates central pattern generator feedback to descending inputs. J Neurosci. 2008;28:9564–9574. doi: 10.1523/JNEUROSCI.3011-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briggman KL, Kristan WB. Multifunctional pattern-generating circuits. Annu Rev Neurosci. 2008;31:271–294. doi: 10.1146/annurev.neuro.31.060407.125552. [DOI] [PubMed] [Google Scholar]
- Calabrese RL. Taking the lead from a model. Curr Biol. 1999;9:R680–R683. doi: 10.1016/s0960-9822(99)80438-2. [DOI] [PubMed] [Google Scholar]
- Calabrese RL, Norris BJ, Wenning A, Wright TM. Coping with variability in small neuronal networks. Integr Comp Biol. 2011;51:845–855. doi: 10.1093/icb/icr074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christie AE, Stemmler EA, Dickinson PS. Crustacean neuropeptides. Cell Mol Life Sci. 2010;67:4135–4169. doi: 10.1007/s00018-010-0482-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coleman MJ, Meyrand P, Nusbaum MP. A switch between two modes of synaptic transmission mediated by presynaptic inhibition. Nature. 1995;378:502–505. doi: 10.1038/378502a0. [DOI] [PubMed] [Google Scholar]
- DeLong ND, Beenhakker MP, Nusbaum MP. Presynaptic inhibition selectively weakens peptidergic cotransmission in a small motor system. J Neurophysiol. 2009a;102:3492–3504. doi: 10.1152/jn.00833.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeLong ND, Kirby MS, Blitz DM, Nusbaum MP. Parallel regulation of a modulator-activated current via distinct dynamics underlies comodulation of motor circuit output. J Neurosci. 2009b;29:12355–12367. doi: 10.1523/JNEUROSCI.3079-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derjean D, Moussaddy A, Atallah E, St-Pierre M, Auclair F, Chang S, Ren X, Zielinski B, Dubuc R. A novel neural substrate for the transformation of olfactory inputs into motor output. PLoS Biol. 2010;8:e1000567. doi: 10.1371/journal.pbio.1000567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Prisco GV, Pearlstein E, Le Ray D, Robitaille R, Dubuc R. A cellular mechanism for the transformation of a sensory input into a motor command. J Neurosci. 2000;20:8169–8176. doi: 10.1523/JNEUROSCI.20-21-08169.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickinson PS. Neuromodulation of central pattern generators in invertebrates and vertebrates. Curr Opin Neurobiol. 2006;16:604–614. doi: 10.1016/j.conb.2006.10.007. [DOI] [PubMed] [Google Scholar]
- Diehl F, White RS, Stein W, Nusbaum MP. Motor circuit-specific burst patterns drive different muscle and behavior patterns. J Neurosci. 2013;33:12013–12029. doi: 10.1523/JNEUROSCI.1060-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doi A, Ramirez JM. Neuromodulation and the orchestration of the respiratory rhythm. Respir Physiol Neurobiol. 2008;164:96–104. doi: 10.1016/j.resp.2008.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dzirasa K, Ribeiro S, Costa R, Santos LM, Lin SC, Grosmark A, Sotnikova TD, Gainetdinov RR, Caron MG, Nicolelis MA. Dopaminergic control of sleep-wake states. J Neurosci. 2006;26:10577–10589. doi: 10.1523/JNEUROSCI.1767-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermentrout GB. Simulating, Analyzing, and Animating Dynamical Systems: A Guide to Xppaut for Researchers and Students (Software, Environments, Tools) Philadelphia: SIAM; 2002. [Google Scholar]
- Grillner S. Biological pattern generation: the cellular and computational logic of networks in motion. Neuron. 2006;52:751–766. doi: 10.1016/j.neuron.2006.11.008. [DOI] [PubMed] [Google Scholar]
- Harris-Warrick RM. Neuromodulation and flexibility in Central Pattern Generator networks. Curr Opin Neurobiol. 2011;21:685–692. doi: 10.1016/j.conb.2011.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawkins VE, Hawryluk JM, Takakura AC, Tzingounis AV, Moreira TS, Mulkey DK. HCN channels contribute to serotonergic modulation of ventral surface chemosensitive neurons and respiratory activity. J Neurophysiol. 2015;113:1195–1205. doi: 10.1152/jn.00487.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kintos N, Nadim F. A modeling exploration of how synaptic feedback to descending projection neurons shapes the activity of an oscillatory network. SIAM J Applied Dynamical Systems. 2014;13:1239–1269. doi: 10.1137/130943881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kintos N, Nusbaum MP, Nadim F. A modeling comparison of projection neuron- and neuromodulator-elicited oscillations in a central pattern generating network. J Comput Neurosci. 2008;24:374–397. doi: 10.1007/s10827-007-0061-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirby MS, Nusbaum MP. Peptide hormone modulation of a neuronally modulated motor circuit. J Neurophysiol. 2007;98:3206–3220. doi: 10.1152/jn.00795.2006. [DOI] [PubMed] [Google Scholar]
- LeBeau FE, El Manira A, Griller S. Tuning the network: modulation of neuronal microcircuits in the spinal cord and hippocampus. Trends Neurosci. 2005;28:552–561. doi: 10.1016/j.tins.2005.08.005. [DOI] [PubMed] [Google Scholar]
- Lieske SP, Ramirez JM. Pattern-specific synaptic mechanisms in a multifunctional network. II. Intrinsic modulation by metabotropic glutamate receptors. J Neurophysiol. 2006;95:1334–1344. doi: 10.1152/jn.00506.2004. [DOI] [PubMed] [Google Scholar]
- Lieske SP, Thoby-Brisson M, Telgkamp P, Ramirez JM. Reconfiguration of the neural network controlling multiple breathing patterns: eupnea, sighs and gasps. Nat Neurosci. 2000;3:600–607. doi: 10.1038/75776. [see comment]. [DOI] [PubMed] [Google Scholar]
- Manor Y, Nadim F, Abbott LF, Marder E. Temporal dynamics of graded synaptic transmission in the lobster stomatogastric ganglion. J Neurosci. 1997;17:5610–5621. doi: 10.1523/JNEUROSCI.17-14-05610.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manor Y, Nadim F, Epstein S, Ritt J, Marder E, Kopell N. Network oscillations generated by balancing graded asymmetric reciprocal inhibition in passive neurons. J Neurosci. 1999;19:2765–2779. doi: 10.1523/JNEUROSCI.19-07-02765.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E. Neuromodulation of neuronal circuits: back to the future. Neuron. 2012;76:1–11. doi: 10.1016/j.neuron.2012.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E, Thirumalai V. Cellular, synaptic and network effects of neuromodulation. Neural Netw. 2002;15:479–493. doi: 10.1016/s0893-6080(02)00043-6. [DOI] [PubMed] [Google Scholar]
- Marder E, Bucher D. Understanding circuit dynamics using the stomatogastric nervous system of lobsters and crabs. Annu Rev Physiol. 2007;69:291–316. doi: 10.1146/annurev.physiol.69.031905.161516. [DOI] [PubMed] [Google Scholar]
- McCormick DA, Pape HC. Noradrenergic and serotonergic modulation of a hyperpolarization-activated cation current in thalamic relay neurones. J Physiol. 1990;431:319– 342. doi: 10.1113/jphysiol.1990.sp018332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishchenko EF, Rozov NK. Differential Equations with Small Parameters and Relaxation Oscillators. New York: Plenum Press; 1980. [Google Scholar]
- Morgan PT, Perrins R, Lloyd PE, Weiss KR. Intrinsic and extrinsic modulation of a single central pattern generating circuit. J Neurophysiol. 2000;84:1186–1193. doi: 10.1152/jn.2000.84.3.1186. [DOI] [PubMed] [Google Scholar]
- Nadim F, Bucher D. Neuromodulation of neurons and synapses. Curr Opin Neurobiol. 2014;29C:48–56. doi: 10.1016/j.conb.2014.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadim F, Manor Y, Nusbaum MP, Marder E. Frequency regulation of a slow rhythm by a fast periodic input. J Neurosci. 1998;18:5053–5067. doi: 10.1523/JNEUROSCI.18-13-05053.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nassel DR. Neuropeptide signaling near and far: how localized and timed is the action of neuropeptides in brain circuits? Invert Neurosci. 2009;9:57–75. doi: 10.1007/s10158-009-0090-1. [DOI] [PubMed] [Google Scholar]
- Nusbaum MP. Regulating peptidergic modulation of rhythmically active neural circuits. Brain Behav Evol. 2002;60:378–387. doi: 10.1159/000067791. [DOI] [PubMed] [Google Scholar]
- Nusbaum MP, Beenhakker MP. A small-systems approach to motor pattern generation. Nature. 2002;417:343–350. doi: 10.1038/417343a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nusbaum MP, Blitz DM. Neuropeptide modulation of microcircuits. Curr Opin Neurobiol. 2012;22:592–601. doi: 10.1016/j.conb.2012.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nusbaum MP, Blitz DM, Swensen AM, Wood D, Marder E. The roles of co-transmission in neural network modulation. Trends Neurosci. 2001;24:146–154. doi: 10.1016/s0166-2236(00)01723-9. [DOI] [PubMed] [Google Scholar]
- Peck JH, Gaier E, Stevens E, Repicky S, Harris-Warrick RM. Amine modulation of Ih in a small neural network. J Neurophysiol. 2006;96:2931–2940. doi: 10.1152/jn.00423.2005. [DOI] [PubMed] [Google Scholar]
- Raper JA. Nonimpulse-mediated synaptic transmission during the generation of a cyclic motor program. Science. 1979;205:304–306. doi: 10.1126/science.221982. [DOI] [PubMed] [Google Scholar]
- Rauscent A, Einum J, Le Ray D, Simmers J, Combes D. Opposing aminergic modulation of distinct spinal locomotor circuits and their functional coupling during amphibian metamorphosis. J Neurosci. 2009;29:1163–1174. doi: 10.1523/JNEUROSCI.5255-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez JC, Blitz DM, Nusbaum MP. Convergent rhythm generation from divergent cellular mechanisms. J Neurosci. 2013;33:18047–18064. doi: 10.1523/JNEUROSCI.3217-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saideman SR, Blitz DM, Nusbaum MP. Convergent motor patterns from divergent circuits. J Neurosci. 2007;27:6664–6674. doi: 10.1523/JNEUROSCI.0315-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skiebe P. Neuropeptides are ubiquitous chemical mediators: Using the stomatogastric nervous system as a model system. J Exp Biol. 2001;204:2035–2048. doi: 10.1242/jeb.204.12.2035. [DOI] [PubMed] [Google Scholar]
- Stein W, DeLong ND, Wood DE, Nusbaum MP. Divergent co-transmitter actions underlie motor pattern activation by a modulatory projection neuron. Eur J Neurosci. 2007;26:1148–1165. doi: 10.1111/j.1460-9568.2007.05744.x. [DOI] [PubMed] [Google Scholar]
- Swensen AM, Marder E. Multiple peptides converge to activate the same voltage-dependent current in a central pattern-generating circuit. J Neurosci. 2000;20:6752–6759. doi: 10.1523/JNEUROSCI.20-18-06752.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swensen AM, Marder E. Modulators with convergent cellular actions elicit distinct circuit outputs. J Neurosci. 2001;21:4050–4058. doi: 10.1523/JNEUROSCI.21-11-04050.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White RS, Nusbaum MP. The same core rhythm generator underlies different rhythmic motor patterns. J Neurosci. 2011;31:11484–11494. doi: 10.1523/JNEUROSCI.1885-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood DE, Stein W, Nusbaum MP. Projection neurons with shared cotransmitters elicit different motor patterns from the same neural circuit. J Neurosci. 2000;20:8943–8953. doi: 10.1523/JNEUROSCI.20-23-08943.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao S, Sheibanie AF, Oh M, Rabbah P, Nadim F. Peptide neuromodulation of synaptic dynamics in an oscillatory network. J Neurosci. 2011;31:13991–14004. doi: 10.1523/JNEUROSCI.3624-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]