Abstract
Purpose
In the original SF-6D valuation study, the analytical design inherited conventions that detrimentally affected its ability to predict values on a quality-adjusted life year (QALY) scale. Our objective is to estimate UK values for SF-6D states using the original data and multi-attribute utility (MAU) regression after addressing its limitations and to compare the revised SF-6D and EQ-5D value predictions.
Methods
Using the unaltered data (611 respondents, 3503 SG responses), the parameters of the original MAU model were re-estimated under 3 alternative error specifications, known as the instant, episodic, and angular random utility models. Value predictions on a QALY scale were compared to EQ-5D3L predictions using the 1996 Health Survey for England.
Results
Contrary to the original results, the revised SF-6D value predictions range below 0 QALYs (i.e., worse than death) and agree largely with EQ-5D predictions after adjusting for scale. Although a QALY is defined as a year in optimal health, the SF-6D sets a higher standard for optimal health than the EQ-5D-3L; therefore, it has larger units on a QALY scale by construction (20.9% more).
Conclusions
Much of the debate in health valuation has focused on differences between preference elicitation tasks, sampling, and instruments. After correcting errant econometric practices and adjusting for differences in QALY scale between the EQ-5D and SF-6D values, the revised predictions demonstrate convergent validity, making them more suitable for UK economic evaluations compared to original estimates.
Keywords: UK, SF-6D, Quality of Life, EQ-5D, Time Trade-off
Introduction
Commonplace in economic evaluations and burden of disease analyses, a quality-adjusted life year (QALY) is a preference-based unit of measurement that combines quality of life and quantity of life (e.g., risk of death, survival, and persons). For example, 1 QALY equals the value of optimal health for 1 person for 1 year with 100% certainty. Health valuation on a QALY scale relies on measurements of quality of life, which is typically assessed using a health-related quality of life (HRQoL) instrument, such as the EQ-5D or SF-36 [1,2]. Value on a QALY scale represents the aggregated preferences of a group of individuals, not personal choices or responses, which reflect their own individual utility. To predict value, health valuation studies elicit individual preferences using a variety of discrete-choice and trade-off tasks, such as ranking, time trade-off (TTO) and standard gamble (SG) [3–5].
This paper examines SG responses collected by Brazier and colleagues during the original UK valuation study of the SF-36 [6]. To estimate UK values on a QALY scale for the SF-36 version 1 responses, Brazier and colleagues reduced this instrument to a 6-question SF-6D, making it more similar to the EQ-5D instrument (e.g., monotonic in utility for each item). Their interview-based survey collected 3,518 SG responses from 611 respondents on 249 scenarios. Unlike traditional SG, which involves trades between reduced HRQoL and risk of “immediate death,” the SF-6D SG task traded between reduced HRQoL and the risk of the worst possible health state, also known as “pits.” By collecting SG responses based on the risk of “pits,” the study avoided trade-offs in risk of “immediate death” for all SF-6D states. However, trade-offs including risk of “immediate death” are necessary to estimate value on a QALY scale, therefore, the final task was an SG of “pits” that included risk of “immediate death.” In summary, there was no mention of mortality (risk of “immediate death”) in any of the SG tasks, except the last one (“pits” SG response). With the “pits” and other SG responses, Brazier and colleagues estimated the value of SF-6D health states on a QALY scale. This seminal study serves as a foundation to benefit from 4 key lessons for econometric analyses in health valuation, each of which are addressed in this paper:
Do not arbitrarily transform preference responses.
Model selection greatly influences value prediction.
Do not chain preference responses prior to estimation.
Changing the definition of optimal health changes the unit of measurement on a QALY scale.
Respondents commonly express a willingness to die to avoid any time or risk of an unfavorable health state, resulting in extreme responses at the lower end of the scale [7,8]. In economics, this is known as price inelastic demand (i.e., willingness-to-pay is infinitely negative or positive). For example, in the seminal UK Measurement and Valuation of Health (MVH) study [9,10], many respondents chose “immediate death” over a scenario of 9.75 years in optimal health and 3 months in “pits,” suggesting that 1 year in “pits” equals −39 QALYs (−9.75/0.25). In the original analysis of these TTO responses (and most subsequent analyses), all worse-than-death responses were arbitrarily transformed, changing a third of the data. Following convention, Brazier and colleagues arbitrarily transformed all worse-than-death “pits” SG responses (26.5% of the sample). Why did it become convention in health valuation to arbitrarily change preference responses? There is no theoretical justification for this ratio-based manipulation (e.g., −9.75/0.25 became −0.975). However, it is clear that if only 1 in 40 respondents considers 1 year in “pits” equal to −39 QALYs (i.e., price inelastic), 1 year in “pits” is worse than “immediate death,” regardless of what the other 39 respondents report. Perhaps, knowing this may have been the practical justification for the conventions.
Instead of data manipulation, Craig and colleagues put forth 3 alternative random utility models (RUMs) for preference responses, known as the instant, episodic, and angular random utility models (IRUM, ERUM, and ARUM) [11–13]. These models incorporate worse-than-death responses without altering the data and facilitate semi-parametric estimation of values on a QALY scale. In fact, IRUM is basically the same as the ratio-based approach without data manipulation. ERUM is the conventional approach to most discrete choice experiments that minimizes an additive error in the utility difference by ordinary least squares estimation. Nevertheless, ARUM is attractive for its innovative geometric interpretation of how health attributes sway decisions (i.e., up and down) as well as its functional form, which is nearly identical to an incremental cost-effectiveness ratio. This paper adapts the 3 RUMs to estimate values for the SF-6D using the original SG valuation data and demonstrates the influence of model selection on value predictions.
Imputation is a form of chaining responses (i.e., changing the interpretation of a response based on a previous response). Chaining is different from adaptation, which involves changing a subsequent question based on a previous response (e.g., computer-adaptive testing). Aside from data manipulations, Brazier and colleagues imputed the “pits” SG responses, SGpits, into a formula with the other SF-6D SG responses, SGh, to create “adjusted” SG responses as a way to linearly transform the SGh responses “onto a scale where the best SF-6D response is 1 and death is 0” [6]. Due to this chaining of preference responses prior to estimation, the adjusted responses (SGADJ) have more error than SGh or SGpits alone, diminishing the estimator’s ability to discriminate between SF-6D health states. Many articles have noted the unexpected compression of the original SF-6D value predictions relative to the EQ-5D predictions [14–16]. This paper demonstrates that the range of SF-6D values widens after unchaining the responses, improving their agreement with EQ-5D predictions.
Lastly, this paper assesses predictive validity of the SF-6D predictions compared to the EQ-5D predictions using the 1996 Health Survey for England (HSE). The definition of optimal health varies by instrument; therefore, the QALY scale is specific to each instrument. In comparison, the SF-6D definition of optimal health has 6 domains without problems (i.e., 111111) and is more restrictive (i.e., fewer individuals qualify as Level 1; the SF-6D has 4 to 6 levels for each domain and the EQ-5D have only 3 levels) than the EQ-5D description of optimal health (11111), causing differences in the unit of measurement. After adjusting for differences in QALY scaling, this paper investigates whether the EQ-5D and SF-6D produce similar values, which would be highly advantageous for resource allocation decisions where evidence from both instruments is available.
Methods
The SF-36 is a widely used generic measure of health that generates scores across 8 domains: physical functioning, role limitation due to physical problems, social functioning, bodily pain, general health perceptions, role limitations due to emotional problems, mental health, and vitality [17]. Built from 11 items along 6 domains, the SF-6D was derived for the purposes of health valuation (see Table 1). After the removal of 148 incomplete responses, the original SF-6D valuation study examined 3,518 SG responses from 611 respondents. Three SG responses could not be located at the time of this analysis. Twelve SG responses describing best possible SF-6D state were also excluded, because they contradict the SG task, which is anchored on optimal health. Otherwise, the analytical sample is similar to the original sample. A more detailed description of SF-6D development and the original SF-6D valuation study is available elsewhere [6].
Table 1.
SF-6D Instrument
| SF-6D Item and Level Descriptions | |
|---|---|
| Physical Functioning (PF) | |
| PF1 | Your health does not limit you in vigorous activities |
| PF2 | Your health limits you a little in vigorous activities |
| PF3 | Your health limits you a little in moderate activities |
| PF4 | Your health limits you a lot in moderate activities |
| PF5 | Your health limits you a little in bathing and dressing |
| PF6 | Your health limits you a lot in bathing and dressing |
| Role Limitations (RL) | |
| RL1 | You have no problems with your work or other regular daily activities as a result of your physical health or any emotional problems |
| RL2 | You are limited in the kind of work or other activities as a result of your physical health |
| RL3 | You accomplish less than you would like as a result of emotional problems |
| RL4 | You are limited in the kind of work or other activities as a result of your physical health and accomplish less than you would like as a result of emotional problems |
| Social Functioning (SF) | |
| SF1 | Your health limits your social activities none of the time |
| SF2 | Your health limits your social activities a little of the time |
| SF3 | Your health limits your social activities some of the time |
| SF4 | Your health limits your social activities most of the time |
| SF5 | Your health limits your social activities all of the time |
| Pain (PAIN) a | |
| PAIN1 | You have no pain |
| PAIN2 | You have pain but it does not interfere with your normal work |
| PAIN3 | You have pain that interferes with your normal work a little bit |
| PAIN4 | You have pain that interferes with your normal work moderately |
| PAIN5 | You have pain that interferes with your normal work quite a bit |
| PAIN6 | You have pain that interferes with your normal work extremely |
| Mental Health (MH) | |
| MH1 | You feel tense or downhearted and low none of the time |
| MH2 | You feel tense or downhearted and low a little of the time |
| MH3 | You feel tense or downhearted and low some of the time |
| MH4 | You feel tense or downhearted and low most of the time |
| MH5 | You feel tense or downhearted and low all of the time |
| Vitality (VIT) | |
| VIT1 | You have a lot of energy all of the time |
| VIT2 | You have a lot of energy most of the time |
| VIT3 | You have a lot of energy some of the time |
| VIT4 | You have a lot of energy a little of the time |
| VIT5 | You have a lot of energy none of the time |
Normal work includes work both outside the home and housework.
Each interview began with a short self-completion questionnaire about the respondent’s own health and the ranking of 8 health state cards: 5 SF-6D states, “immediate death,” and the best and worst SF-6D states (i.e., optimal health and “pits”). With each of the 5 SF-6D states, the respondent completed an SG task (SGh) using optimal health and “pits” as comparators. As a final task, the respondents completed an SG task for “pits” (SGpits) using optimal health and “immediate death” as comparators.
Four Econometric Approaches: Original, IRUM, ERUM, and ARUM
Under a random utility model (RUM), an equivalence statement (e.g., A=B) is specified with an error term (e.g., A=B+ε) to capture randomness in utility or response. For example, each SG response equates gambles along a scale using 2 comparators (U1 and U2) to describe the utility of a health state, U(h), for 10 years. These 2 comparators allow the triangulation of the U(h) using a gamble, SG. For example, U(h) may be equal to a gamble of U1 and U2 (e.g., U1*SG + U2*(1−SG) = U(h)), or a comparator, U2, may be equal to a gamble of U1 and U(h) (e.g., U1*SG + U(h)*(1−SG) = U2). In either case, the utility of a health state, U(h), for 10 years is defined by the 2 comparators (U1 and U2) and the gamble, SG.
The primary difference between the RUMs is the placing of the error term, ε (Table 2) [11–13]. The first column in Table 2 represents trade-offs where the health state utility, U(h), is between the comparator utilities, U1 and U2, such as the first 5 SG responses and better-than-dead (BTD) “pits” SG responses. The second column represents trade-offs where U(h) is worse than U1 and U2, such as worse-than-dead (WTD) “pits” SG response. The “instant” RUM has an additive error on the health state utility and the angular RUM has an angular error on the health state utility. The episodic RUM has an additive error in the equivalence statement and does not differentiate between the columns. The intuition behind the 3 RUMs is that error may enter at any or all locations within the equivalence statements, and it is not feasible to test between these non-nested specifications without additional assumptions (e.g., fully parametric likelihood), particularly because SG responses do not conform to any known distribution.
Table 2.
Random Utility Models for Standard Gamble Responses
| RUM | U1>U(h)>U2 | U1>U2> U(h) |
|---|---|---|
| Originala | U1*SG + U2*(1−SG) = U(h) + ε where U2 is either SGBTD or −SGWTD for pits | |
| Instant | U1*SG + U2*(1−SG) = U(h) + ε | U1*SG + (U(h) + ε)*(1−SG) = U2 |
| Episodic | U1*SG + U2*(1−SG) = U(h) + ε | U1*SG + U(h) *(1−SG) + ε = U2 |
| Angular | U1*SG + U2*(1−SG) = tan(atan(U(h)) + ε) | U1*SG + tan(atan(U(h)) + ε)*(1−SG) = U2 |
The original model is the same as IRUM, except that U2 is replaced the pits SG response, chaining together the 2 responses together as one dependent variable.
The original approach is identical to the IRUM specification except for added practices of data manipulation and chaining. After substituting the QALY values for full health and dead into the IRUM specification, the BTD “pits” responses simplify to SGBTD= Upits + εpits and WTD “pits” responses simplify to −SGWTD/(1−SGWTD)= Upits + εpits. For example, SGWTD=97.5% implies that the utility of “pits” for 1 year is −39 QALYs. Instead of −SGWTD/(1−SGWTD), the original study replaced all WTD fractions with −SGWTD, thereby making Upits + ε = SGBTD or −SGWTD. As a result of this arbitrary transformation, the distribution of Upits was arbitrarily bounded above −1 QALY and all “pits” utilities were raised at the individual level, introducing further measurement error.
Under the IRUM specification, the SF-6D responses simplify to SGh + Upits*(1−SGh) = U(h) + εh, where both Upits and U(h) are unknown. Because IRUM specifies Upits as a function of SGpits and its error, the Upits in this formula can be imputed using the SGpits responses, creating an adjusted SGadj = SGh + P*(1−SGh) = U(h) + εh + εpits(1−SGh), where P is either SGBTD or −SGWTD/(1−SGWTD). The second error term in the formula demonstrates the potential error amplification caused by chaining, which increases as SGh decreases (i.e., more similar to “pits” produces more error). Differential error amplification inherently inflates predicted values near “pits” due to decreased capacity to discriminate between health states. The original specification ignored the second error term as well as manipulated the pits responses, resulting in the formula, SGh + P*(1−SGh) = U(h) + ε, where P is either SGBTD or −SGWTD. While data manipulation and chaining independently detracted from an estimator’s capacity to discriminate between health states, chaining also allowed the transformed “pits” responses to contaminate the other SGh responses. Alternatively, the RUM specifications (shown in Table 2) can be estimated without data manipulation or chaining.
Multi-attribute Utility (MAU) Model of SF-6D
For each RUM, we estimate an identical MAU model of the SF-6D decrements, D(h)=1−U(h), as does the original study. Each SF-6D state, h, may be described using a vector from optimal health to “pits” (i.e., 111111 to 645655). The 6 scalars that compose the vector describe the levels on the 6 SF-6D domains. The original MAU model described SF-6D states using 25 of the indicator variables, 1 for each domain level excluding the first level of each domain. Therefore, the coefficients represent decrements in value from the first level. To simplify calculations, our MAU model, D(h), includes 25 domain-level indicator variables representing whether a level or better is present; therefore, each coefficient represents the decrement associated with a level increase. By definition, each decrement is non-negative and the coefficients were constrained to be non-negative using an exponential transformation. All models were estimated assuming finite, independent, symmetrically distributed errors [18] and individual-level clustering without weights. Confidence intervals were estimated by percentile bootstrap with cluster resampling [19].
In addition to estimating the MAU model, 5 SF-6D states along with the pits state were selected to demonstrate state-specific estimation of the IRUM, ERUM, and ARUM models. These states (144341, 241545, 312255, 321144, 424554) were selected because their sample sizes ranged from 28 to 36, much larger than the other 242 states (3 to 18). The pits state has 620 responses. In complement to this demonstration, STATA code (available via the journal website) is provided to simulate the state-specific estimation to facilitate hands-on understanding of these models.
The 1996 HSE is the only nationally representative survey of the UK population with SF-6D and EQ-5D responses (N=20,328). After removing persons under age 18 (4,404; 21%) and adults with missing responses (1,392; 9%), the remaining 14,580 SF-6D and EQ-5D responses were valued using Table 3 and the previously published predictions. The predictions are compared visually and formally to assess convergent validity (i.e., Lin’s coefficient of agreement and mean absolute difference) [20].
Table 3.
Instant, Episodic, and Angular Random Utility Model Estimates in QALY Decrements
| 611 Subjects & 3,503 SGa | Instant | Episodic | Angular | Original | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| D(h) | 95% CI | D(h) | 95% CI | D(h) | 95% CI | D(h) | ||||
| Physical Functioning (PF) | ||||||||||
| PF1 | - | - | - | - | - | - | - | - | - | - |
| PF2 | 0.219 | 0.126 | 0.338 | 0.071 | 0.045 | 0.108 | 0.071 | 0.034 | 0.106 | 0.058 |
| PF3 | 0.000 | 0.000 | 0.002 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.016 | −0.007 |
| PF4 | 0.050 | 0.006 | 0.130 | 0.016 | 0.004 | 0.043 | 0.009 | 0.000 | 0.037 | 0.037 |
| PF5 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | −0.027 |
| PF6 | 0.468 | 0.351 | 0.629 | 0.151 | 0.122 | 0.184 | 0.138 | 0.109 | 0.167 | 0.099 |
| Role Limitations (RL) | ||||||||||
| RL1 | - | - | - | - | - | - | - | - | - | - |
| RL2 | 0.220 | 0.149 | 0.313 | 0.071 | 0.050 | 0.098 | 0.071 | 0.044 | 0.096 | 0.056 |
| RL3 | 0.000 | 0.000 | 0.021 | 0.000 | 0.000 | 0.002 | 0.000 | 0.000 | 0.017 | 0.020 |
| RL4 | 0.043 | 0.004 | 0.114 | 0.014 | 0.002 | 0.040 | 0.010 | 0.000 | 0.035 | 0.002 |
| Social Functioning (SF) | ||||||||||
| SF1 | - | - | - | - | - | - | - | - | - | - |
| SF2 | 0.273 | 0.184 | 0.376 | 0.088 | 0.063 | 0.113 | 0.086 | 0.054 | 0.112 | 0.066 |
| SF3 | 0.017 | 0.000 | 0.087 | 0.006 | 0.000 | 0.026 | 0.005 | 0.000 | 0.029 | −0.018 |
| SF4 | 0.013 | 0.001 | 0.089 | 0.004 | 0.000 | 0.028 | 0.002 | 0.000 | 0.029 | 0.018 |
| SF5 | 0.173 | 0.083 | 0.262 | 0.056 | 0.029 | 0.089 | 0.045 | 0.012 | 0.070 | 0.043 |
| Pain (PAIN) | ||||||||||
| PAIN1 | - | - | - | - | - | - | - | - | - | - |
| PAIN2 | 0.197 | 0.108 | 0.300 | 0.063 | 0.039 | 0.097 | 0.065 | 0.033 | 0.095 | 0.042 |
| PAIN3 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.019 | 0.004 |
| PAIN4 | 0.076 | 0.016 | 0.177 | 0.024 | 0.007 | 0.055 | 0.017 | 0.000 | 0.053 | 0.009 |
| PAIN5 | 0.190 | 0.095 | 0.291 | 0.061 | 0.034 | 0.095 | 0.055 | 0.018 | 0.088 | 0.048 |
| PAIN6 | 0.311 | 0.193 | 0.440 | 0.100 | 0.071 | 0.131 | 0.089 | 0.055 | 0.117 | 0.075 |
| Mental Health (MH) | ||||||||||
| MH1 | - | - | - | - | - | - | - | - | - | - |
| MH2 | 0.237 | 0.139 | 0.351 | 0.076 | 0.048 | 0.110 | 0.086 | 0.047 | 0.117 | 0.043 |
| MH3 | 0.023 | 0.002 | 0.100 | 0.007 | 0.000 | 0.032 | 0.006 | 0.000 | 0.037 | 0.012 |
| MH4 | 0.169 | 0.083 | 0.259 | 0.055 | 0.031 | 0.086 | 0.051 | 0.018 | 0.076 | 0.060 |
| MH5 | 0.146 | 0.072 | 0.247 | 0.047 | 0.024 | 0.080 | 0.038 | 0.011 | 0.070 | 0.010 |
| Vitality (VIT) | ||||||||||
| VIT1 | - | |||||||||
| VIT2 | 0.221 | 0.143 | 0.321 | 0.071 | 0.048 | 0.106 | 0.067 | 0.039 | 0.097 | 0.040 |
| VIT3 | 0.000 | 0.000 | 0.015 | 0.000 | 0.000 | 0.001 | 0.001 | 0.000 | 0.016 | −0.010 |
| VIT4 | 0.000 | 0.000 | 0.036 | 0.000 | 0.000 | 0.008 | 0.000 | 0.000 | 0.015 | 0.010 |
| VIT5 | 0.148 | 0.078 | 0.241 | 0.048 | 0.026 | 0.082 | 0.047 | 0.019 | 0.073 | 0.047 |
Zeros represent non-negative decrement estimated to be less than 0.0005 QALYs. All 95% confidence intervals (CI) were computed using percentile bootstrap techniques. Original decrement estimates were taken from Table 5, column 5 [6].
Results
Table 3 shows the decrement estimates on the QALY scale, D(.), as well as the original estimates published in Table 5, column 5 [6]. Each estimate represents a decrement in value associated with an increase in level. By definition, a decrement is non-negative; however, 6 of the 25 estimates (PF3, PF5, RL3, PAIN3, VIT3, and VIT4) are less than 0.001 QALYs in all models, suggesting that the inclusion of these levels into the SF-6D descriptive system is non-informative. Four of these 6 decrements coincide with negative decrement estimates in the original analysis. Due to the varying sign of the original decrement estimates, IRUM, ERUM, and ARUM decrement estimates cannot be directly compared to the original estimates. For the 19 remaining decrement estimates, the IRUM and ERUM specifications produce larger decrements than the ARUM specification; however, the difference between the ERUM and ARUM estimates is small, ranging from 0.006 to 0.045 QALYs.
A domain decrement is the sum of its level decrements and can be compared by specification. Across all domains, the difference between the ERUM and ARUM domains is positive and insignificant. Each model produces significantly greater domain decrements than the original model, which suggests that the procedures of data manipulation and chaining compressed the domain decrement estimates.
Value prediction is 1 minus the sum of SF-6D state decrements. For example, the estimated value of the worst possible SF-6D state, “pits,” is the 1 minus the sum of all decrements, which is −2.192 under IRUM (95% CI −2.798, −1.694), −0.029 under ERUM (95% CI −0.074, −0.006), and 0.040 under ARUM (95% CI, 0.002, 0.070). This estimate is significantly less than 0 (i.e., “immediate death”) under IRUM and ERUM specifications and greater than 0 for ARUM and original specifications. Although the difference between the ERUM and ARUM estimates is small (0.069 QALYs), it is statistically significant (95% CI 0.037, 0.115). The IRUM predictions lack face validity, because its estimates rank seemingly mild states as significantly worse than “immediate death” (e.g., U222222 = −0.37 QALYs). We considered not reporting the IRUM results to the same degree as the others, but decided the lack of face validity is an important result; and the original protocol dictates that they are presented alongside ERUM and ARUM results.
In Table 4, the IRUM, ERUM, and ARUM are re-estimated including only indicator variables for 5 health states and pits in the MAU regression. Again, the IRUM predicts that all states are worse than dead (i.e., decrement greater than 1), and these predictions have the widest confidence intervals among the 3 models. The ERUM predictions are better than dead (i.e., decrement less than 1) and 23% to 29% lower than the ARUM predictions. Also the ERUM confidence intervals are 19% to 47% narrower than the ARUM confidence intervals. The online appendix is a STATA program that facilitates hands-on learning through simulation of these state-specific estimations. Due to a lack of face validity in the IRUM predictions, SF-6D IRUM predictions are not compared the EQ-5D IRUM predictions.
Table 4.
State-Specific Instant, Episodic, and Angular Random Utility Model Estimates in QALY Decrements
| SF-6D | N | Instant | Episodic | Angular | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| D(h) | 95% CI | D(h) | 95% CI | D(h) | 95% CI | |||||
| 144341 | 30 | 1.617 | 1.236 | 2.085 | 0.380 | 0.312 | 0.454 | 0.509 | 0.422 | 0.606 |
| 241545 | 30 | 1.947 | 1.377 | 2.607 | 0.458 | 0.326 | 0.604 | 0.643 | 0.477 | 0.820 |
| 312255 | 36 | 1.980 | 1.414 | 2.677 | 0.466 | 0.348 | 0.580 | 0.638 | 0.480 | 0.781 |
| 321144 | 36 | 1.883 | 1.327 | 2.476 | 0.443 | 0.330 | 0.561 | 0.619 | 0.472 | 0.764 |
| 424554 | 28 | 2.794 | 2.207 | 3.482 | 0.657 | 0.545 | 0.763 | 0.865 | 0.728 | 1.000 |
| 645655 | 620 | 4.376 | 3.644 | 5.169 | 1.029 | 1.002 | 1.059 | 1.331 | 1.283 | 1.389 |
All 95% confidence intervals (CI) were computed using percentile bootstrap techniques. Simulation code is available on journal website for hands-on learning.
Comparison of SF-6D and EQ-5D Value Predictions
Not all SF-6D and EQ-5D health states are prevalent in the UK. The 1996 HSE contains SF-6D and EQ-5D data on 14,580 persons, including 2,684 of the 18,000 possible SF-6D states and 121 of the possible 243 EQ-5D 3L states. By definition, optimal health equals 1 QALY, which describes 347 persons based on the SF-6D descriptive system (2.4%) and 7,666 persons based on EQ-5D 3L descriptive system (52.6%). Using the ARUM, ERUM, and original estimates for SF-6D states based on Table 3 and for EQ-5D states taken from the published literature [12,13], health utilities were predicted on a QALY scale for all non-optimal SF-6D and EQ-5D states in the 1996 HSE.
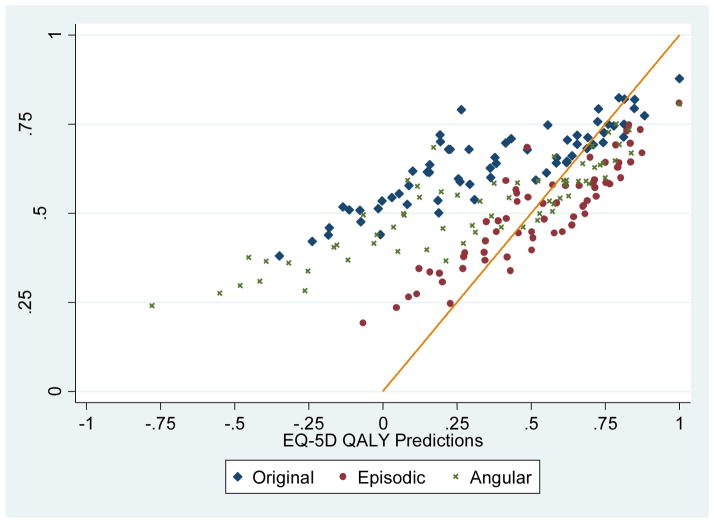
After removing 55 of the 120 EQ-5D states with less than 5 subjects, we constructed 66 EQ-5D subsamples and estimated the mean SF-6D ERUM, ARUM, and original value predictions within each subsample (Figure 1). The concordance between the original SF-6D and EQ-5D predictions is weak (Lin’s coefficient 0.332, respectively), but concordance between the ERUM EQ-5D and SF-6D predictions is moderate (Lin’s coefficient 0.765). However, this evidence of convergent validity under the ERUM does not address discordance at the top end of the scale concerning differences in the definition of optimal health (i.e., 11111 versus 111111).
Figure 1.
Comparing EQ-5D and SF-6D QALY Predictions by Random Utility Model Specification using 1996 Health Survey for England
According to the ERUM predictions, the average health utility within the full sample is 0.874 EQ-5D QALYs or 0.723 SF-6D QALYs, which suggests that 1 SF-6D QALY is worth about 1.209 EQ-5D QALYs (0.874/0.723). Figure 2 further illustrates this finding by examining mean SF-6D and EQ-5D ERUM value predictions by age groups (in 5-year spans). Respondent age 85 and above were included in the final category (>80) due to small sample sizes. Due to differences in their definitions of optimal health, EQ-5D QALY predictions are substantially higher than the SF-6D QALY predictions. Once the SF-6D predictions are multiplied by 1.209, they become nearly identical (mean absolute difference 0.005, Lin’s coefficient 0.995). In summary, multiplying SF-6D QALYs by 1.209 will translate them into EQ-5D QALYs, overcoming differences in descriptive system, trade-off task (TTO vs. SG), and valuation survey sampling.
Figure 2.
EQ-5D and SF-6D ERUM QALY Predictions by Age using 1996 Health Survey for England
Conclusions
Using the unaltered SF-6D SG responses, value predictions under IRUM, ERUM, and ARUM specifications were estimated and compared with the original SF-6D value estimates. Like the original study, this analysis finds that SF-6D levels (PF3, PF5, RL3, PAIN3, VIT3, and VIT4) may be dropped from the SF-6D descriptive system without loss of information. The findings also demonstrate that data manipulation and chaining compressed the original value predictions for SF-6D states. An SF-6D QALY is worth about 21% more than an EQ-5D QALY, and after adjusting for this difference in scale, SF-6D QALY predictions largely agree with EQ-5D QALY predictions.
Aside from data manipulation and chaining, the ERUM has more convergent validity than ARUM (Figure 1) and shows potential to merge evidence from multiple descriptive systems, samples, and valuation tasks. However, this does not address the theoretical justification for selecting angular over episodic errors. Having introduced both models, ARUM is attractive for its innovative geometric interpretation of how health attributes sways decisions; however, ERUM is the conventional approach to most discrete choice experiments, which assume that the additive difference between objects is random. Future research may create a mixed model where both sources of randomness co-exist. Future methodological work may also account for sampling weights, interactions between health indicators in the MAU model, and a relaxation of the constant proportionality assumption inherent to all value estimators.
Since the original SF-6D value analysis, the field of health valuation has undergone a paradigm shift toward discrete choice experiment (DCE) designs [21–23]. DCE designs also address concerns about response monotonicity [24], as shown by Bansback and colleagues, who have adapted ERUM for paired comparisons [25]. The ARUM specification has also been adapted for pair comparisons and may someday be compared to ERUM in the analysis of DCE responses, keeping it a “two horse-race” [26]. From this paper, the more important lesson is that future valuation studies of any design must not repeat the errant econometric practices by the original EQ-5D and SF-6D value analyses (i.e., data manipulation and chaining).
The 21% conversion rate between SF-6D and EQ-5D QALYs is based on the UK sample and 3-level EQ-5D responses. This rate may differ with other samples, EQ-5D/SF-6D translations, and versions due to differences in the definition of optimal health. Recently, the EuroQoL group introduced a 5-level version of their EQ-5D instrument (EQ-5D 5L), expanding the top end of their instrument and changing their definition of optimal health [2]. No study has yet examined the prevalence of 5L optimal health in the UK; however, it may be more similar to the prevalence of SF-6D optimal health. By allowing respondents to report slight problems, the EQ-5D 5L has a more conservative definition of optimal health, thus, its QALYs will likely be higher than the 3L QALYs. An expanding body of literature has focused on the appropriate threshold for cost-utility analyses (e.g., $50,000 per EQ-5D 3L QALY = $60,450 per SF-6D QALY)[27–29]. To set such a threshold, policy makers need to be able to differentiate values on a QALY scale by their referent definitions of optimal health and adjust them to a common metric.
These results breathe new life into the SF-6D descriptive system which has often been challenged based on its limited range, negative coefficients, and discordance with EQ-5D predictions.[30] The design of the original SF-6D valuation study was highly innovative at the time with its introduction of the SF-6D, but these results facilitate the merger of SF-6D values with EQ-5D values after adjusted for differences in the QALY scale. This paper was initially motivated after Craig and Busschbach realized that Dolan changed 34% of the TTO responses prior to EQ-5D valuation analysis using the seminal MVH study data and that Brazier and colleagues inherited this practice, changing 26.5% of their SGpits responses [6,11,31]. After the SF-6D SG responses were unadjusted, unchained, and rescaled, the revised UK estimates are more in “harmony” with the EQ-5D predictions.
Acknowledgments
Funding support for this research was provided by the National Institutes of Health (NIH) Infrastructure grant, “Developing Information Infrastructure Focused on Cancer Comparative Effectiveness Research” (RC2-CA148332; PI: Fenstermacher); and Dr. Craig’s National Cancer Institute (NCI) Career Development Award (K25-CA122176).
Footnotes
The author has no potential conflicts of interest.
References
- 1.Brazier J, Usherwood T, Harper R, KT Deriving a prference-based single index from the UK SF-36 health survey. Journal of Clinical Epidemiology. 1998;51:1115–1128. doi: 10.1016/s0895-4356(98)00103-6. [DOI] [PubMed] [Google Scholar]
- 2.EuroQol Group. [Accessed Oct 07 2014];EQ-5D products: EQ-5D-5L. http://www.euroqol.org/eq-5d/eq-5d-products.html.
- 3.Torrance GW. Social Preferences for Health States: An Empirical Evaluation of Three Measurement Techniques. Socio-Economic Planning Sciences. 1976;10:129–136. [Google Scholar]
- 4.Torrance GW, Thomas WH, Sackett DL. A utility maximization model for evaluation of health care programs. Health Serv Res. 1972;7(2):118–133. [PMC free article] [PubMed] [Google Scholar]
- 5.Tsuchiya A, Ikeda S, Ikegami N, Nishimura S, Sakai I, Fukuda T, Hamashima C, Hisashige A, Tamura M. Estimating an EQ-5D population value set: the case of Japan. Health Econ. 2002;11(4):341–353. doi: 10.1002/hec.673. [DOI] [PubMed] [Google Scholar]
- 6.Brazier J, Roberts J, Deverill M. The estimation of a preference-based measure of health from the SF-36. J Health Econ. 2002;21(2):271–292. doi: 10.1016/s0167-6296(01)00130-8. [DOI] [PubMed] [Google Scholar]
- 7.Lamers LM. The transformation of utilities for health states worse than death: consequences for the estimation of EQ-5D value sets. Med Care. 2007;45(3):238–244. doi: 10.1097/01.mlr.0000252166.76255.68. [DOI] [PubMed] [Google Scholar]
- 8.Patrick DL, Starks HE, Cain KC, Uhlmann RF, Pearlman RA. Measuring preferences for health states worse than death. Med Decis Making. 1994;14(1):9–18. doi: 10.1177/0272989X9401400102. [DOI] [PubMed] [Google Scholar]
- 9.Gudex C. Report of the Centre for Health Economics. University of York; York, United Kingdom: 1994. Time Trade-Off User Manual: Props and Self-Completion Methods. [Google Scholar]
- 10.Williams A. Discussion Paper. Vol. 136. Centre for Health Economics, York Health Economics Consortium, NHS Centre for Reviews & Dissemination, University of York; York: 1995. A measurement and valuation of health: a chronicle; pp. 1–53. [Google Scholar]
- 11.Craig BM, Busschbach JJ. The episodic random utility model unifies time trade-off and discrete choice approaches in health state valuation. Popul Health Metr. 2009;7(1):3. doi: 10.1186/1478-7954-7-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Craig BM, Busschbach JJ. Toward a more universal approach in health valuation. Health Econ. 2010 doi: 10.1002/hec.1650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Craig BM, Oppe M. From a different angle: A novel approach to health valuation. Soc Sci Med. 2009 doi: 10.1016/j.socscimed.2009.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Brazier J, Roberts J, Tsuchiya A, Busschbach J. A comparison of the EQ-5D and SF-6D across seven patient groups. Health Econ. 2004;13(9):873–884. doi: 10.1002/hec.866. [DOI] [PubMed] [Google Scholar]
- 15.Hatoum HT, Brazier JE, Akhras KS. Comparison of the HUI3 with the SF-36 preference based SF-6D in a clinical trial setting. Value Health. 2004;7(5):602–609. doi: 10.1111/j.1524-4733.2004.75011.x. [DOI] [PubMed] [Google Scholar]
- 16.Kharroubi SA, Brazier JE, Roberts J, O’Hagan A. Modelling SF-6D health state preference data using a nonparametric Bayesian method. J Health Econ. 2007;26(3):597–612. doi: 10.1016/j.jhealeco.2006.09.002. [DOI] [PubMed] [Google Scholar]
- 17.Ware JE, Jr, Gandek B, Kosinski M, Aaronson NK, Apolone G, Brazier J, Bullinger M, Kaasa S, Leplege A, Prieto L, Sullivan M, Thunedborg K. The equivalence of SF-36 summary health scores estimated using standard and country-specific algorithms in 10 countries: results from the IQOLA Project. International Quality of Life Assessment. J Clin Epidemiol. 1998;51(11):1167–1170. doi: 10.1016/s0895-4356(98)00108-5. [DOI] [PubMed] [Google Scholar]
- 18.StataCorp: Stata Statistical Software: Release 10. StataCorp LP; College Station, Texas, USA: 2008. [Google Scholar]
- 19.Efron B, Tibshirani R. An Introduction to the bootstrap. Chapman & Hall; New York: 1993. [Google Scholar]
- 20.Lin LI. A concordance correlation coefficient to evaluate reproducibility. Biometrics. 1989;45(1):255–268. [PubMed] [Google Scholar]
- 21.Craig BM, Brown DS, Reeve BB. The Value Adults Place on Child Health and Functional Status. Value in health : the journal of the International Society for Pharmacoeconomics and Outcomes Research. 2015;18(4):449–456. doi: 10.1016/j.jval.2015.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Craig BM, Pickard AS, Stolk E, Brazier JE. US valuation of the SF-6D. Med Decis Making. 2013;33(6):793–803. doi: 10.1177/0272989X13482524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Craig BM, Reeve BB, Brown PM, Cella D, Hays RD, Lipscomb J, Simon Pickard A, Revicki DA. US Valuation of Health Outcomes Measured Using the PROMIS-29. Value in health : the journal of the International Society for Pharmacoeconomics and Outcomes Research. 2014;17(8):846–853. doi: 10.1016/j.jval.2014.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Menzies NA, Salomon JA. Non-Monotonicity in the Episodic Random Utility Model. Health Econ. 2011;20(12):1523–1531. doi: 10.1002/hec.1683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bansback N, Brazier J, Tsuchiya A. A comparison of using discrete choice experiments and the time tradeoff to value health states for quality adjusted life years. Paper presented at the EuroQol Group Meeting; Paris, France. October 2009. [Google Scholar]
- 26.Craig BM. Arctangent Model for Conjoint Analysis. Paper presented at the The 2nd Annual Health Econometrics Workshop; October 1–2, 2010.Ann Arbor, MI: University of Michigan; [Google Scholar]
- 27.Donaldson C, Baker R, Mason H, Jones-Lee M, Lancsar E, Wildman J, Bateman I, Loomes G, Robinson A, Sugden R, Prades J, Ryan M, Shackley P, Smith R. The social value of a QALY: raising the bar or barring the raise? BMC Health Services Research. 2011;11(1):8. doi: 10.1186/1472-6963-11-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lancsar E, Wildman J, Donaldson C, Ryan M, Baker R. Deriving distributional weights for QALYs through discrete choice experiments. Journal of Health Economics. 2011;30(2):466–478. doi: 10.1016/j.jhealeco.2011.01.003. [DOI] [PubMed] [Google Scholar]
- 29.Baker R, Bateman I, Donaldson C, Jones-Lee M, Lancsar E, Loomes G, Mason H, Odejar M, Pinto Prades J, Robinson A, Ryan M, Shackley P, Smith R, Sugden R, Wildma J t.S.R Team. Weighting and valuing quality-adjusted life-years using stated preference methods: preliminary results from the Social Value of a QALY Project. Health Technology Assessment. 2010;14(27):162. doi: 10.3310/hta14270. [DOI] [PubMed] [Google Scholar]
- 30.Whitehurst DG, Norman R, Brazier JE, Viney R. Comparison of contemporaneous EQ-5D and SF-6D responses using scoring algorithms derived from similar valuation exercises. Value Health. 2014;17(5):570–577. doi: 10.1016/j.jval.2014.03.1720. [DOI] [PubMed] [Google Scholar]
- 31.Dolan P. Modeling valuations for EuroQol health states. Medical Care. 1997;35(11):1095–1108. doi: 10.1097/00005650-199711000-00002. [DOI] [PubMed] [Google Scholar]