Abstract
With the motivation of discovering high-temperature superconductors, evolutionary algorithm USPEX is employed to search for all stable compounds in the Sn-H system. In addition to the traditional SnH4, new hydrides SnH8, SnH12 and SnH14 are found to be thermodynamically stable at high pressure. Dynamical stability and superconductivity of tin hydrides are systematically investigated. I m2-SnH8, C2/m-SnH12 and C2/m-SnH14 exhibit higher superconducting transition temperatures of 81, 93 and 97 K compared to the traditional compound SnH4 with Tc of 52 K at 200 GPa. An interesting bent H3–group in I
m2-SnH8, C2/m-SnH12 and C2/m-SnH14 exhibit higher superconducting transition temperatures of 81, 93 and 97 K compared to the traditional compound SnH4 with Tc of 52 K at 200 GPa. An interesting bent H3–group in I m2-SnH8 and novel linear H
m2-SnH8 and novel linear H in C2/m-SnH12 are observed. All the new tin hydrides remain metallic over their predicted range of stability. The intermediate-frequency wagging and bending vibrations have more contribution to electron-phonon coupling parameter than high-frequency stretching vibrations of H2 and H3.
in C2/m-SnH12 are observed. All the new tin hydrides remain metallic over their predicted range of stability. The intermediate-frequency wagging and bending vibrations have more contribution to electron-phonon coupling parameter than high-frequency stretching vibrations of H2 and H3.
Molecular hydrogen’s phase transition to a metallic state has been subject of many experimental and theoretical studies1,2. Although reaching the metallic state in pure solid hydrogen proved elusive, it is in the main focus of many groups and recently, the progress of bringing pure hydrogen to nearly 400 GPa has been reported3,4,5. Following the pioneering work of Ashcroft6, nearly room-temperature superconductivity was predicted in metallic molecular hydrogen7,8.
An alternative approach to metalize hydrogen is to use chemical alloying as a means to exert additional pressure on hydrogen atoms9. Hydrogen-rich compounds such as SiH4 can be metalized at a much lower pressure10. For metallic hydrogen, high Debye temperature and strong electron-phonon coupling are anticipated. The same is expected for hydrogen-rich compounds and it has been suggested that hydrogen-rich compounds are good candidates for high-temperature superconductivity9 Theoretical studies confirm this idea with predicting superconductivity in high-pressure hydrides such as H-Se11, Ca-H12, Sn-H13, Pt-H14 and B-H15. A series of hydrogen-rich compounds have been predicted to have remarkably high Tc values (e.g. 235 K for CaH6 at 150 GPa12, 191 K for H3S at 200 GPa16, 64 K for GeH4 at 220 GPa17) while the highest Tc that had been achieved experimentally was in the complex mercury cuprate (138 K at ambient pressure18 and 166 K at high pressures19). The new record of high Tc was established for H3S, a compound whose existence and superconductivity at 200 K were first predicted theoretically16 in 2014 using USPEX and then observed experimentally20 in 2015, and started a new wave of interest in hydrogen-rich superconductors.
In a previous theoretical study, Tse et al. reported a high-pressure metallic phase of SnH4 with hexagonal P6/mmm symmetry group, which is a layered structure intercalated with H2 units, and is a superconductor with Tc close to 80 K at 120 GPa21. Later, by using evolutionary algorithm USPEX, Gao et al.13 reported two novel metallic phases of SnH4 with space groups P63/mmc and Ama2, which both have hexagonal layers of Sn atoms with semi-molecular H2 units. The reported stability ranges are 96–180 GPa for Ama2, and above 180 GPa for P63/mmc; with Tc values of 15–22 K at 120 GPa and 52–62 K at 200 GPa for Ama2 and P63/mmc, respectively13.
While SnH4 was shown to be a relatively high-Tc superconductor, the possibility of existence of other tin hydrides were not explored so far. At the same time, by now it is proven22 that totally unexpected compounds become stable under pressure, and this gives hope of finding even better superconductors. Hence, in this study, we systematically search for the stable compounds using the highly efficient variable-composition evolutionary searches (VCES). Apart from the previously reported phases of SnH4, there is one metastable tetragonal phase of stannane with higher superconducting critical temperature. Other stable superconducting compounds, SnH8, SnH12 and SnH14, are found to become stable at high pressure. Moreover, we found a semi-molecular group H3– in the I m2 structure of SnH8. Novel H4–is also present in C2/m-SnH12. We calculate a high Tc of 81 K at 220 GPa in the newly predicted compound SnH8, 93 K for SnH12 at 250 GPa, 97 K for SnH14 at 300 GPa and 91 K for the metastable phase of SnH4 at 220 GPa.
m2 structure of SnH8. Novel H4–is also present in C2/m-SnH12. We calculate a high Tc of 81 K at 220 GPa in the newly predicted compound SnH8, 93 K for SnH12 at 250 GPa, 97 K for SnH14 at 300 GPa and 91 K for the metastable phase of SnH4 at 220 GPa.
Results
Evolutionary variable-composition searches for stable compounds and their structures with up to 20 atoms in the primitive unit cell were performed at 150, 200, 250 and 300 GPa. To further investigate the newly found compounds, fixed-composition structure predictions for the most promising compounds were performed, with one to three formula units per cell. Candidate low-enthalpy structures are metastable I4/mmm-SnH4, stable I m2-SnH8, C2/m-SnH12 and C2/m-SnH14. In the I
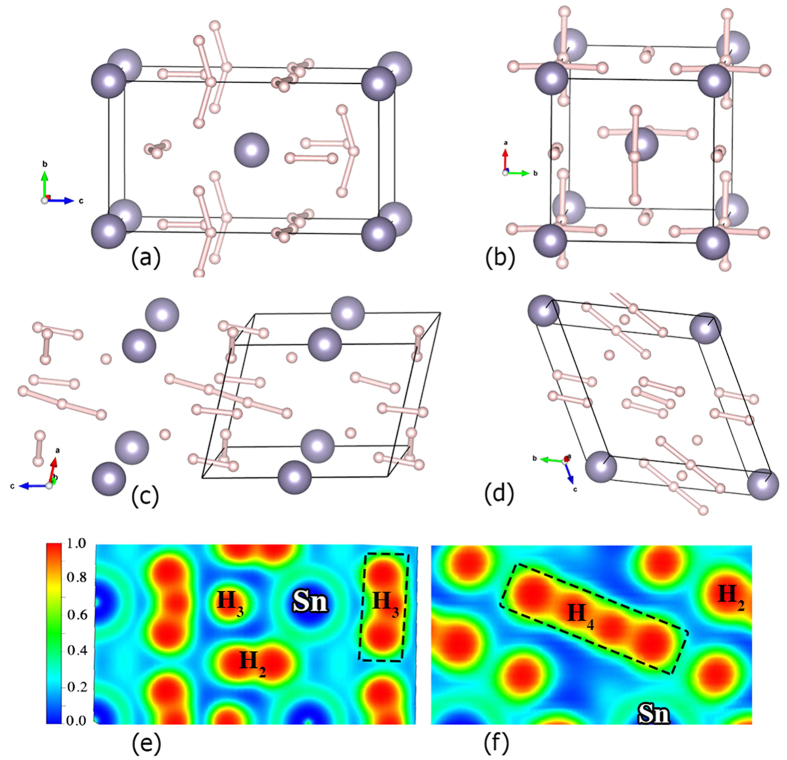
m2-SnH8, C2/m-SnH12 and C2/m-SnH14. In the I m2-SnH8 structure predicted to be stable at pressures above 220 GPa, Sn atoms are packed between H2 and H3 molecular groups, in which the bent H3 units are perpendicular to one another and sepated by 1.35 Å. In C2/m-SnH12, Sn atoms form well-separated close-packed layers intercalated with blocks of H2 and H4 semi-molecules.
m2-SnH8 structure predicted to be stable at pressures above 220 GPa, Sn atoms are packed between H2 and H3 molecular groups, in which the bent H3 units are perpendicular to one another and sepated by 1.35 Å. In C2/m-SnH12, Sn atoms form well-separated close-packed layers intercalated with blocks of H2 and H4 semi-molecules.
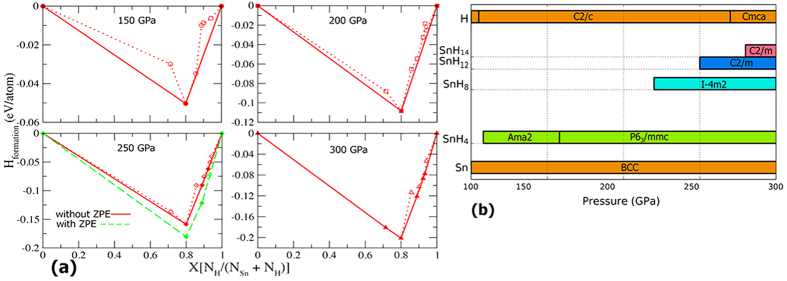
Figure 1(a). shows the enthalpy of formation (ΔH) of Sn-H compounds at selected pressures. Significantly, in addition to reproducing various structures of solid SnH413,21, Sn23 and H224, novel compounds SnH8, SnH12 and SnH14 are found to be stable in a wide pressure range in our systematic evolutionary structure search. It can be seen from Fig. 1(a). that at around 200 GPa the tetragonal SnH8 with the space group of I m2 lies above the convex hull, therefore, is metastable with respect to decomposition to P63/mmc-SnH4 and C2/c-H2. Between 150 to 300 GPa, we predict stable phases of H2, SnH4, SnH8, SnH12, SnH14 and Sn23. Some metastable forms of SnH6, SnH9 and SnH16 are also shown in Fig. 1(a) by open symbols.
m2 lies above the convex hull, therefore, is metastable with respect to decomposition to P63/mmc-SnH4 and C2/c-H2. Between 150 to 300 GPa, we predict stable phases of H2, SnH4, SnH8, SnH12, SnH14 and Sn23. Some metastable forms of SnH6, SnH9 and SnH16 are also shown in Fig. 1(a) by open symbols.
Figure 1. Thermodynamics of the Sn-H system.
(a) Predicted formation enthalpy of SnnHm compounds. Solid red lines denote the convex hull and green dashed line shows the effect of ZPE inclusion at 250 GPa. (b) Predicted pressure-composition phase diagram of the Sn-H system.
SnH4 is thermodynamically stable at pressures above 108 GPa as was predicted in previous report13. It goes through a phase transition at 160 GPa. Upon increasing pressure, at 220 GPa we predict stabilization of SnH8. SnH12 and SnH14 reach stability at the pressures of 250 GPa and 280 GPa, respectively, and remain stable at least up to 300 GPa. The structures of SnHn compounds are found to be dynamically stable within pressure ranges of their stability. In the I m2-SnH8 structure, Sn atoms occupy the 2a Wyckoff site and the H atoms are on the 4e, 8i and 4f sites (detailed structural information is provided in Table 1).
m2-SnH8 structure, Sn atoms occupy the 2a Wyckoff site and the H atoms are on the 4e, 8i and 4f sites (detailed structural information is provided in Table 1).
Table 1. Predicted crystal structures of SnH8, SnH12 and SnH14 at 220, 250 and 300 GPa, respectively.
| Phase | Lattice parameters | Atom | x | y | z |
|---|---|---|---|---|---|
I m2 m2 |
a = 3.076 Å | Sn(2a) | 0.0000 | 0.0000 | 0.0000 |
| SnH8 | c = 5.523 Å | H1(8i) | 0.2729 | 0.0000 | 0.3331 |
| at 220 GPa | H2(4e) | 0.0000 | 0.0000 | 0.6208 | |
| H3(4f) | 0.0000 | 0.5000 | 0.1701 | ||
| C2/m | a = 5.191 Å | Sn(2d) | 0.0000 | 0.5000 | 0.5000 |
| SnH12 | b = 3.065 Å | H1(4i) | 0.0495 | 0.0000 | 0.6553 |
| c = 7.388 Å | H2(4i) | 0.4564 | 0.0000 | 0.7226 | |
| β = 148.95° | H3(4i) | 0.3428 | 0.0000 | 0.8832 | |
| at 250 GPa | H4(8i) | 0.3810 | 0.2399 | 0.1123 | |
| H5(4g) | 0.0000 | 0.1233 | 0.0000 | ||
| C2/m | a = 7.129 Å | Sn(2b) | 0.0000 | 0.5000 | 0.0000 |
| SnH14 | b = 2.730 Å | H1(4i) | 0.3651 | 0.0000 | 0.7031 |
| c = 3.673 Å | H2(4i) | 0.1857 | 0.0000 | 0.9852 | |
| β = 60.71° | H3(4i) | 0.0732 | 0.0000 | 0.6252 | |
| H4(4i) | 0.8063 | 0.0000 | 0.8090 | ||
| at 300 GPa | H5(8i) | 0.2365 | 0.2808 | 0.4035 | |
| H6(2d) | 0.0000 | 0.5000 | 0.5000 | ||
| H7(2c) | 0.0000 | 0.0000 | 0.5000 |
We checked the effects of zero-point energy using phonon calculations25 at 250 GPa. The inclusion of zero-point noticeably lowered the formation enthalpy of SnH8 with respect to SnH4 and H2 (Fig. 1(a)), implying that this compound can be formed at lower pressure. At the same time, SnH12 moves above the convex hull at 250 GPa, suggesting that higher pressure is needed to stabilize C2/m-SnH12. In accord with what we expect, zero-point energy does not change the topology of the phase diagram, but shifts transition pressures.
In I m2-SnH8 structure, the H atoms are split into two categories. Some H atoms form H3 groups, which were previously observed in solid phases of BaH627, in an unstable structure of H5Br ([H3]Br[H2])28, and in an intriguing linear form with the bond length of 0.92 Å in H5Te229. In contrast to H5Br, which has approximately an equilateral triangle form of H3, here we report the formation of H3 in a bent geometry with the angle of 146.2° and bond length of 0.86 Å at 220 GPa in the I
m2-SnH8 structure, the H atoms are split into two categories. Some H atoms form H3 groups, which were previously observed in solid phases of BaH627, in an unstable structure of H5Br ([H3]Br[H2])28, and in an intriguing linear form with the bond length of 0.92 Å in H5Te229. In contrast to H5Br, which has approximately an equilateral triangle form of H3, here we report the formation of H3 in a bent geometry with the angle of 146.2° and bond length of 0.86 Å at 220 GPa in the I m2 structure. The other type of H atoms form H2 groups which are aligned parallel to each other.
m2 structure. The other type of H atoms form H2 groups which are aligned parallel to each other.
I m2 structure can be presented as Sn[H2][H3]2 as shown in Fig. 2(a,b). The bond length in H3 unit is 0.86 Å, whereas H2 has a longer bond length of 0.87 Å. Contrary to isolated H2 molecule, which only has a filled σ bonding orbital, in the H2 and H3 semi-molecules, population of anti-bonding orbitals causes lengthening and weakening of the covalent bond. The slightly longer H-H bond length compared to isolated H2 molecule (0.74 Å) is caused by charge transfer of 0.42 e− and 0.48 e−, as computed using Bader theory26, from Sn to each H2 and H3 unit, respectively. Charge transfer is an important factor in the formation of H2 and H3 units in the H4Te, GeH4, SnH4, CaH4, H5Te2, H5Br, BaH612,17,27,28,29
m2 structure can be presented as Sn[H2][H3]2 as shown in Fig. 2(a,b). The bond length in H3 unit is 0.86 Å, whereas H2 has a longer bond length of 0.87 Å. Contrary to isolated H2 molecule, which only has a filled σ bonding orbital, in the H2 and H3 semi-molecules, population of anti-bonding orbitals causes lengthening and weakening of the covalent bond. The slightly longer H-H bond length compared to isolated H2 molecule (0.74 Å) is caused by charge transfer of 0.42 e− and 0.48 e−, as computed using Bader theory26, from Sn to each H2 and H3 unit, respectively. Charge transfer is an important factor in the formation of H2 and H3 units in the H4Te, GeH4, SnH4, CaH4, H5Te2, H5Br, BaH612,17,27,28,29
Figure 2.
Predicted structures of (a,b) SnH8 [I m2], (c) SnH12 [C2/m] and (d) SnH14 [C2/m]. Large and small spheres represent Sn and H atoms, respectively. Electron localization functions (ELF) for (e) SnH8 [I
m2], (c) SnH12 [C2/m] and (d) SnH14 [C2/m]. Large and small spheres represent Sn and H atoms, respectively. Electron localization functions (ELF) for (e) SnH8 [I m2] at 220 GPa and (f) SnH12 [C2/m] at 250 GPa.
m2] at 220 GPa and (f) SnH12 [C2/m] at 250 GPa.
Analysis of electron localization function (ELF) shows a high ELF value of 0.88 between H atoms within the unit, indicating strong covalent bonding features (Fig. 2(e)). At the same time, the ELF value on the Sn-H bond is very low, reaching just 0.37.
In C2/m-SnH12, intriguing formation of novel H4 semi-molecules are observed; at 250 GPa, they can be represented as two H2-groups separated by just 0.99 Å. Higher pressure of 300 GPa decreases the distance to 0.88 Å, leading to a strong covalent bond in the  units. Fig. 2(f). demonstrates covalent bonds in the linear H4 units with the ELF magnitude of 0.85.
units. Fig. 2(f). demonstrates covalent bonds in the linear H4 units with the ELF magnitude of 0.85.
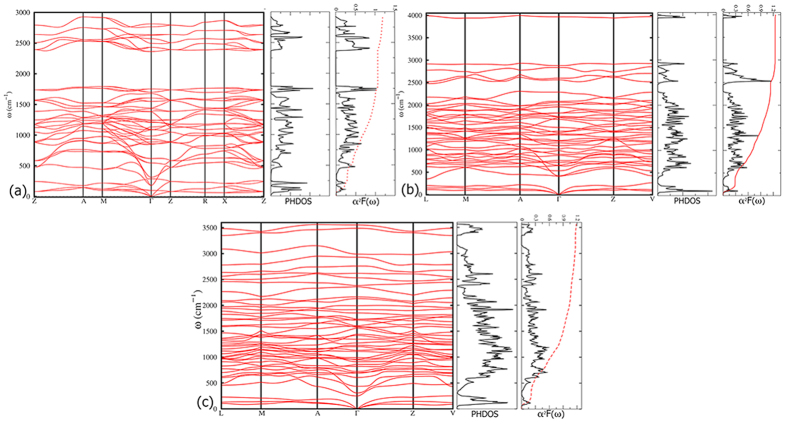
The calculated phonon dispersion curves and phonon density of states for I m2 structure of SnH8 at 220 GPa are shown in Fig. 3(a). Dynamical stability is clearly evidenced by the absence of any imaginary frequencies in the whole Brillouin zone. The low-frequency bands below 250 cm−1 are mainly from the vibrations of Sn atoms. Modes between 300 and 1700 cm−1 are mainly from the H-H wagging vibrations, and higher frequency vibrations above 2300 cm−1 are due to H-H stretching vibrations in H2 and H3 units.
m2 structure of SnH8 at 220 GPa are shown in Fig. 3(a). Dynamical stability is clearly evidenced by the absence of any imaginary frequencies in the whole Brillouin zone. The low-frequency bands below 250 cm−1 are mainly from the vibrations of Sn atoms. Modes between 300 and 1700 cm−1 are mainly from the H-H wagging vibrations, and higher frequency vibrations above 2300 cm−1 are due to H-H stretching vibrations in H2 and H3 units.
Figure 3.
Phonon band structure, phonon DOS, Eliashberg phonon spectral function α2F(ω) and electron-phonon integral λ(ω) of: (a) SnH8 [I m2] at 220 GPa, (b) SnH12 [C2/m] at 250 GPa and (c) SnH14 [C2/m] at 300 GPa.
m2] at 220 GPa, (b) SnH12 [C2/m] at 250 GPa and (c) SnH14 [C2/m] at 300 GPa.
Low-frequency translational modes, mostly from Sn atom, contribute 23.7% (9.2%) to the total λ. Intermediate H-H wagging vibrations make a significant contribution of 65.7% (67.9%), and the rest is from stretching H vibrations, which contribute 10.6% (22.9%) for SnH8 (SnH12). This is different from superconductivity in Cmcm-H2Br28, where Br translational modes make the largest contribution to the total λ and similar to the R m-H4Te29 and P4/mmm-BaH627, where medium-frequency H-wagging and bending modes contribute the most to the EPC. In accord with our expectation, λ increases almost linearly with hydrogen content, where we found 60.2%, 72.2% and 77.1% contribution of H vibrations to the total λ of SnH4, SnH8 and SnH12, respectively. This highlights the dominant role of H in the superconductivity of H-rich compounds.
m-H4Te29 and P4/mmm-BaH627, where medium-frequency H-wagging and bending modes contribute the most to the EPC. In accord with our expectation, λ increases almost linearly with hydrogen content, where we found 60.2%, 72.2% and 77.1% contribution of H vibrations to the total λ of SnH4, SnH8 and SnH12, respectively. This highlights the dominant role of H in the superconductivity of H-rich compounds.
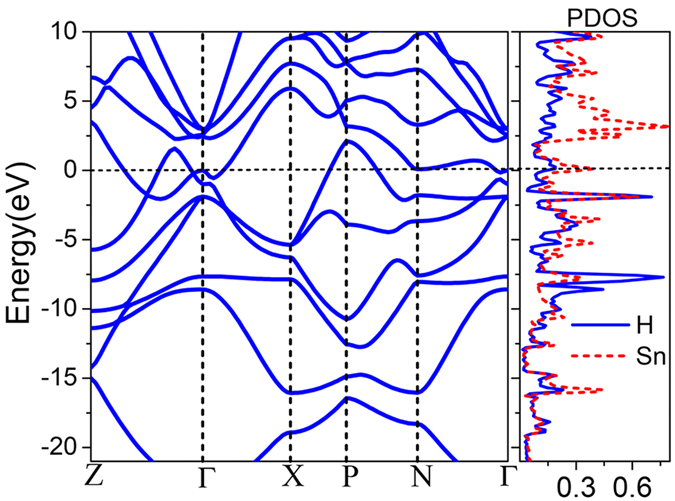
Electronic band structure of I m2-SnH8 is depicted in Fig. 4. Occurrence of flat and steep bands near the Fermi level has been suggested as a condition for enhancing electron-phonon coupling (EPC) and the formation of Cooper pairs.
m2-SnH8 is depicted in Fig. 4. Occurrence of flat and steep bands near the Fermi level has been suggested as a condition for enhancing electron-phonon coupling (EPC) and the formation of Cooper pairs.
Figure 4. Electronic band structure and projected DOS on Sn and H atoms for SnH8 [I m2] at 220 GPa.
m2] at 220 GPa.
We can calculate Tc based on the spectral function α2F(ω) and taking advantage of Allen-Dynes modified McMillan equation (Eq. 1.) by using Coulomb pseudo-potential μ∗ of 0.10 and 0.13 as widely accepted values (see Table 2). At 220 GPa, the predicted Tc values for I m2-SnH8 are 81 K and 72 K using μ∗ values of 0.10 and 0.13, respectively. The calculated Tc slightly decreases with pressure (82 K at 200 GPa and 79 K at 300 GPa using μ∗ = 0.10) with a pressure coefficient of −0.023 K/GPa
m2-SnH8 are 81 K and 72 K using μ∗ values of 0.10 and 0.13, respectively. The calculated Tc slightly decreases with pressure (82 K at 200 GPa and 79 K at 300 GPa using μ∗ = 0.10) with a pressure coefficient of −0.023 K/GPa 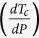 . Reported λ is comparable to H3Se (λ = 1.09) at 200 GPa11, but in I
. Reported λ is comparable to H3Se (λ = 1.09) at 200 GPa11, but in I m2-SnH8 structure, we have a lower
m2-SnH8 structure, we have a lower 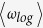 of 919 K (1477 K for H3Se), resulting in a lower Tc value.
of 919 K (1477 K for H3Se), resulting in a lower Tc value.
Table 2. The calculated EPC parameter (λ), logarithmic average phonon frequency (ω log ) and critical temperature (T c ) (with μ* = 0.10 and 0.13) for metastable SnH4, stable SnH8, SnH12 and SnH14 at 220, 220, 250 and 300 GPa, respectively.
| Structure | Pressure (GPa) | λ | ωlog (K) | Tc (K) |
|---|---|---|---|---|
| I4/mmmSnH4 | 220 | 1.180 | 1025 | 91 (μ* = 0.10) |
| 80 (μ* = 0.13) | ||||
I m2-SnH8 m2-SnH8
|
220 | 1.188 | 919 | 81 (μ* = 0.10) |
| 72 (μ* = 0.13) | ||||
| C2/m-SnH12 | 250 | 1.250 | 991 | 93 (μ* = 0.10) |
| 83 (μ* = 0.13) | ||||
| C2/m-SnH14 | 300 | 1.187 | 1099 | 97 (μ* = 0.10) |
| 86 (μ* = 0.13) |
In conclusion, we explored the energetically stable/metastable high-pressure phases of the Sn-H system in detail by means of ab initio evolutionary structure prediction. The results demonstrate that SnH8, SnH12 and SnH14, reported for the first time in this work, are thermodynamically stable compounds that coexist stably with solid Sn, H2 and SnH4 in a wide pressure range starting from 220 to at least 300 GPa.
EPC calculations indicate that high-pressure SnH8, SnH12 and SnH14 are phonon-mediated superconductors with Tc values of 81, 93 and 97 K at pressures of 220, 250, and 300 GPa, respectively. λ is high for SnHn compounds, comparable with H3M-Im m, where M = S and Se11. Structures of SnHn compounds contain
m, where M = S and Se11. Structures of SnHn compounds contain  , bent
, bent 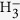 , and linear
, and linear 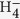 groups. Further experimental studies on the formation of SnHn, n = 8, 12 and 14 at high pressure are needed, and present results will serve as a guide for future experiments.
groups. Further experimental studies on the formation of SnHn, n = 8, 12 and 14 at high pressure are needed, and present results will serve as a guide for future experiments.
Methods
To find stable and low-enthalpy metastable structures, we took advantage of evolutionary algorithm implemented in USPEX code30,31,32, which has been extensively used to predict stable crystal structures with just a knowledge of the chemical composition and without any experimental information15,33,34,35.
In this method, the initial generation of structures and compositions is produced with the random symmetric algorithm34, and subsequent generations are produced by carefully designed variation operators. In order to find all stable stoichiometric compounds and the corresponding stable and metastable structures in the Sn-H binary system, we used VCES method implemented in USPEX30,31.
Structure relaxations were carried out using VASP package36 in the framework of density functional theory (DFT) and using PBE-GGA (Perdew-Burke-Ernzerhof generalized gradient approximation)37. The projector-augmented wave approach (PAW)38 was used to describe the core electrons and their effects on valence orbitals. The plane-wave kinetic energy cutoff was chosen as 1000 eV for hard PAW potentials, and we used Γ-centered uniform k-points meshes to sample the Brillouin zone.
Phonons and thermodynamic properties of Sn-H compounds are calculated using the PHONOPY package25,39. The supercell approach is used with supercell dimensions greater than 10 Å (typically 3 × 3 × 3 replication of the primitive cell). We used valence electron configurations of 4d10 5s2 5p2 and 1s1 for tin and hydrogen, respectively. Phonon frequencies and electron-phonon coupling (EPC) coefficients are calculated using DFPT as implemented in the Quantum ESPRESSO (QE) code40. In the QE calculations, we employed ultrasoft pseudopotentials and PBE-GGA exchange-correlation functional37. A plane-wave basis set with a cutoff of 70 Ry gave a convergence in energy with a precision of 1 meV/atom. The EPC parameter was calculated using 4 × 4 × 3, 5 × 5 × 4 and 5 × 5 × 4 q-point meshes for I m2-SnH8, C2/m-SnH12 and C2/m-SnH14, respectively. Denser k-point meshes, 8 × 8 × 6, 10 × 10 × 8 and 10 × 10 × 8 were used for convergence checks for the EPC parameter λ. The superconducting Tc, was estimated using the Allen-Dynes modified McMillan equation41:
m2-SnH8, C2/m-SnH12 and C2/m-SnH14, respectively. Denser k-point meshes, 8 × 8 × 6, 10 × 10 × 8 and 10 × 10 × 8 were used for convergence checks for the EPC parameter λ. The superconducting Tc, was estimated using the Allen-Dynes modified McMillan equation41:
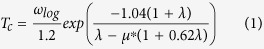 |
where ωlog is the logarithmic average frequency and μ∗ is the Coulomb pseudopotential, for which we used 0.10 and 0.13 values, which often give realistic results. The EPC constant and ωlog were calculated as:
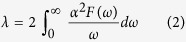 |
and
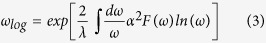 |
Additional Information
How to cite this article: Mahdi Davari Esfahani, M. et al. Superconductivity of novel tin hydrides (SnnHm)under pressure. Sci. Rep. 6, 22873; doi: 10.1038/srep22873 (2016).
Acknowledgments
We thank DARPA (grant W31P4Q1210008), the Government of Russian Federation (14.A12.31.0003) and the Foreign Talents Introduction and Academic Exchange Program (B08040). X.F.Z thanks the National Science Foundation of China (grant no. 11174152), the National 973 Program of China (grant no. 2012CB921900) and the Program for New Century Excellent Talents in University (grant no. NCET-12-0278). Calculations were mainly performed on the cluster (QSH) in our laboratory at Stony Brook University.
Footnotes
Author Contributions M.M.D.E. performed all the calculations presented in this article with help from Z.W., Q.Z. and H.D. Research was designed by A.R.O. S.W, M. R. and X-F. Z. analyzed data. M.M.D.E., A.R.O. and Z.W. wrote the first draft of the paper and all authors contributed to revisions.
References
- Nellis W. J. Dynamic compression of materials: metallization of fluid hydrogen at high pressures. Rep. Prog. Phys. 69, 1479 (2006). [Google Scholar]
- Loubeyre P., Occelli F. & LeToullec R. Optical studies of solid hydrogen to 320 GPa and evidence for black hydrogen. Nature 416, 613–617 (2002). [DOI] [PubMed] [Google Scholar]
- Zha C.-S., Liu Z., Ahart M., Boehler R. & Hemley R. J. High-Pressure Measurements of Hydrogen Phase IV Using Synchrotron Infrared Spectroscopy. Phys. Rev. Lett. 110, 217402 (2013). [DOI] [PubMed] [Google Scholar]
- Howie R. T., Scheler T., Guillaume C. L. & Gregoryanz E. Proton tunneling in phase IV of hydrogen and deuterium. Phys. Rev. B 86, 214104 (2012). [Google Scholar]
- Zha C.-S., Cohen R. E., Mao H.-k. & Hemley R. J. Raman measurements of phase transitions in dense solid hydrogen and deuterium to 325 GPa. Proc. Natl. Acad. Sci. 111, 4792–4797 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashcroft N. W. Metallic hydrogen: A high-temperature superconductor? Phys. Rev. Lett. 21, 1748–1749 (1968). [Google Scholar]
- Cudazzo P. et al. Electron-phonon interaction and superconductivity in metallic molecular hydrogen. II. Superconductivity under pressure. Phys. Rev. B 81, 134506 (2010). [Google Scholar]
- Cudazzo P. et al. Electron-phonon interaction and superconductivity in metallic molecular hydrogen. I. Electronic and dynamical properties under pressure. Phys. Rev. B 81, 134505 (2010). [Google Scholar]
- Ashcroft N. W. Hydrogen dominant metallic alloys: High temperature superconductors? Phys. Rev. Lett. 92, 187002 (2004). [DOI] [PubMed] [Google Scholar]
- Eremets M. I., Trojan I. A., Medvedev S. A., Tse J. S. & Yao Y. Superconductivity in hydrogen dominant materials: Silane. Science 319, 1506–1509 (2008). [DOI] [PubMed] [Google Scholar]
- Zhang S. et al. Phase Diagram and High-Temperature Superconductivity of Compressed Selenium Hydrides. ArXiv e-prints (2015). [DOI] [PMC free article] [PubMed]
- Wang H., Tse J. S., Tanaka K., Iitaka T. & Ma Y. Superconductive sodalite-like clathrate calcium hydride at high pressures. Proc. Natl. Acad. Sci. 109, 6463–6466 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao G. et al. High-pressure crystal structures and superconductivity of Stannane (SnH4). Proc. Natl. Acad. Sci. 107, 1317–1320 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou X.-F. et al. Superconducting high-pressure phase of platinum hydride from first principles. Phys. Rev. B 84, 054543 (2011). [Google Scholar]
- Hu C.-H. et al. Pressure-Induced Stabilization and Insulator-Superconductor Transition of BH. Phys. Rev. Lett. 110, 165504 (2013). [DOI] [PubMed] [Google Scholar]
- Duan D. et al. Pressure-induced metallization of dense (H2S)2H2 with high-Tc superconductivity. Sci. Rep. 4, 6968 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao G. et al. Superconducting high pressure phase of germane. Phys. Rev. Lett. 101, 107002 (2008). [DOI] [PubMed] [Google Scholar]
- Lokshin K. A. et al. Enhancement of Tc in HgBa2Ca2Cu3O8+δ by fluorination. Phys. Rev. B 63, 064511 (2001). [Google Scholar]
- Monteverde M. et al. High-pressure effects in fluorinated HgBa2Ca2Cu3O8+δ. Europhys. Lett. 72, 458 (2005). [Google Scholar]
- Drozdov A. P., Eremets M. I., Troyan I. A., Ksenofontov V. & Shylin S. I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 525, 73–76 (2015). [DOI] [PubMed] [Google Scholar]
- Tse J. S., Yao Y. & Tanaka K. Novel Superconductivity in Metallic SnH4 under High Pressure. Phys. Rev. Lett. 98, 117004 (2007). [DOI] [PubMed] [Google Scholar]
- Zhang W. et al. Unexpected stable stoichiometries of sodium chlorides. Science 342, 1502–1505 (2013). [DOI] [PubMed] [Google Scholar]
- Giefers H. et al. Phonon Density of States of Metallic Sn at High Pressure. Phys. Rev. Lett. 98, 245502 (2007). [DOI] [PubMed] [Google Scholar]
- Pickard C. J. & Needs R. J. Structure of phase III of solid hydrogen. Nature Phys. 3, 473–476 (2007). [Google Scholar]
- Togo A., Oba F. & Tanaka I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 78, 134106 (2008). [Google Scholar]
- Bader R. F. W. Atoms in Molecules: A Quantum Theory. Oxford Univ. Press (1990). [Google Scholar]
- Hooper J., Altintas B., Shamp A. & Zurek E. Polyhydrides of the alkaline earth metals: A look at the extremes under pressure. J. Phys. Chem. C 117, 2982–2992 (2013). [Google Scholar]
- Duan D. et al. Decomposition of solid hydrogen bromide at high pressure. ArXiv e-prints (2015).
- Zhong X. et al. Tellurium Hydrides at High Pressures: High-temperature Superconductors. ArXiv e-prints (2015). [DOI] [PubMed]
- Oganov A. R. & Glass C. W. Crystal structure prediction using ab initio evolutionary techniques: principles and applications. J. Chem. Phys 124, 244704 (2006). [DOI] [PubMed] [Google Scholar]
- Glass C.W., Oganov A.R. & Hansen N. USPEX-Evolutionary crystal structure prediction. Comp. Phys. Comm. 175, 713–720 (2006). [Google Scholar]
- Oganov A.R., Lyakhov A.O. & Valle M. How Evolutionary Crystal Structure Prediction Works-and Why. Acc. Chem. Res. 44, 227–237 (2011). [DOI] [PubMed] [Google Scholar]
- Martinez-Canales M. et al. Novel Structures and Superconductivity of Silane under Pressure. Phys. Rev. Lett. 102 (2009). [DOI] [PubMed] [Google Scholar]
- Lyakhov A.O., Oganov A. R., Stokes H.T. & Zhu Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 184, 1172–1182 (2013). [Google Scholar]
- Oganov A. R. et al. Ionic high-pressure form of elemental boron. Nature 457, 863–867 (2009). [DOI] [PubMed] [Google Scholar]
- Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 ((1996). [DOI] [PubMed] [Google Scholar]
- Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
- Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994). [DOI] [PubMed] [Google Scholar]
- Togo A. & Tanaka I. First principles phonon calculations in materials science. Scr. Mater. 108, 1–5 (2015). [Google Scholar]
- Giannozzi P. et al. Quantum espresso: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009). [DOI] [PubMed] [Google Scholar]
- Allen P. B. & Dynes R.C. Transition temperature of strong-coupled superconductors reanalyzed. Phys. Rev. B 12, 905–922 (1975). [Google Scholar]