Abstract
Efforts to control medical care costs depend critically on how individuals respond to prices. I estimate the price elasticity of expenditure on medical care using a censored quantile instrumental variable (CQIV) estimator. CQIV allows estimates to vary across the conditional expenditure distribution, relaxes traditional censored model assumptions, and addresses endogeneity with an instrumental variable. My instrumental variable strategy uses a family member’s injury to induce variation in an individual’s own price. Across the conditional deciles of the expenditure distribution, I find elasticities that vary from −0.76 to −1.49, which are an order of magnitude larger than previous estimates.
Keywords: censoring, control function, endogeneity, medical care
1 Introduction
Following the recent passage of national health reform legislation in 2010, which focuses on expanding health insurance coverage, controlling costs incurred by the insured is an increasingly important public policy issue. Existing efforts to control costs depend critically on how insured individuals respond to the prices that they face for medical care. The Medicare Modernization Act of 2003 included provisions to encourage price responsiveness by establishing tax-advantaged health savings accounts as an incentive for individuals who enroll in high deductible health insurance plans. The national reform also encourages price responsiveness by establishing plans with substantial patient cost sharing to be offered in health insurance exchanges. Relative to traditional plans, plans with high deductibles and other forms of cost sharing require consumers to face a higher marginal price for each dollar of care that they receive. However, the effects of consumer prices on medical care utilization are not well understood in the current environment.
Econometricians began studying the price elasticity of expenditure on medical care decades ago, but three limitations persist: a lack of estimates that allow the price elasticity to vary across the conditional distribution of expenditure, a difficulty in handling censoring of expenditures at zero, and a need for identification strategies to overcome the insurance-induced endogenous relationship between expenditure and price. Estimates based on the Rand Health Insurance Experiment of the 1970’s, still widely considered to be the standard in the literature, address the identification issue by randomizing consumers into health insurance plans with varying generosities. Although the Rand estimates address censoring using traditional methods, there is a large and enduring controversy over the appropriateness of the parametric assumptions that these methods require. (See Buntin and Zaslavsky (2004), Duan et al. (1983), Mullahy (1998), and Newhouse et al. (1980).) Perhaps even more important than censoring are the issues that arise because medical spending is so skewed. I extend the literature by allowing for heterogeneity in the price elasticity of expenditure across the distribution of expenditure conditional on covariates. In my estimation sample, drawn from a large recent data set of employer-sponsored health insurance claims, just 25% of individuals account for 93% of expenditures, and much variation remains after controlling for observable individual characteristics. It seems reasonable, then, that individuals with drastically different levels of expenditure conditional on observable characteristics could respond differently to price changes.
In this paper, I produce new estimates of the price elasticity of expenditure on medical care that address heterogeneity across the conditional expenditure distribution, censoring, and endogeneity. I use a censored quantile instrumental variable (CQIV) estimator, developed specifically for this application by Chernozhukov et al. (2014). The CQIV estimator is particularly well-suited to address the limitations of the literature.
First, the CQIV estimator allows me to obtain estimates of the price elasticity of expenditure on medical care that vary across the conditional expenditure distribution. Unlike estimators of the conditional mean, which can be very sensitive to values in the tail of the distribution, conditional quantile estimators are inherently more robust to extreme values, which is particularly advantageous given the skewness in the distribution of medical expenditures.
Second, the CQIV estimator allows me to handle censoring at zero without any distributional assumptions. My data are superior to traditional claims data used in previous studies because they allow me to observe enrolled individuals even if they consume zero care. In my estimation sample, approximately 40% of individuals consume zero medical care each year, making censoring an important econometric issue. In the literature, there is controversy over whether to model zero medical expenditures as censored at zero or as “true zeros” that arise through a separate decision process. Although these models generate different mean estimators, the CQIV estimator is the same regardless of the model because it assumes that the zeros arise from the same decision process as the uncensored observations, so I refer to expenditures at zero as “censored” without loss of generality. In contrast, traditional censored mean estimators such as the two-part model, which models the decision to consume any care in one part and the decision of how much care to consume conditional on consuming any care in another part, imply a parametric relationship between the two parts that is not straightforward. In contrast, the CQIV estimator handles censoring nonparametrically in the tradition of Powell (1986).
Third, the CQIV estimator allows me to address endogeneity with a control function approach to an instrumental variable identification strategy. In traditional health insurance policies, the price of an additional dollar of care is a function of expenditure. Thus, the estimated relationship between price and expenditure will be biased away from zero unless this endogeneity is taken into account. The intuition behind my instrumental variable identification strategy is that because of the cost-sharing provisions that govern family health insurance policies, some individuals face lower prices for their own medical care when a family member gets injured. As formalized below, the maintained assumption is that one family member’s injury can only affect another family member’s expenditure through its effect on his marginal price. Although this assumption cannot be tested directly, I take several steps to increase its plausibility. In particular, I model a nuanced interaction of cost sharing provisions among family members, extending the identification strategy used by Eichner (1997, 1998). Moving beyond Eichner (1997, 1998), I focus on injury categories that appear to be exogenous because employees that have them in their families do not spend more on their own medical care before the injuries occur. I also use new data that allows me to observe individuals who have zero medical expenditures, and I develop and implement several tests of robustness.
My main results show that the price elasticity of expenditure on medical care varies from −0.76 to −1.49 across the conditional deciles of the expenditure distribution. Although the CQIV estimator allows the elasticity estimates to vary, the estimates are relatively stable across the conditional deciles.
My estimates are an order of magnitude larger than the Rand estimate of the conditional mean elasticity of −0.22 (Newhouse and the Insurance Experiment Group (1996)). Conditional quantile estimates are not directly comparable to conditional mean estimates without several assumptions, but I consider three types of evidence that suggest that the price elasticity of expenditure on medical care is larger than previous estimates would suggest. First, I examine robustness to the choice of estimator. The underlying variation that I use for identification is so pronounced that I can illustrate it in simple figures. Furthermore, estimates based on traditional estimators in my data are also much larger than those in the literature. Next, I perform tests of my identification strategy, and they support its validity. They suggest that much of the price elasticity that I estimate occurs on the outpatient visit margin. Within-year responses to family injuries drive my results. I also test the robustness of my empirical specification, and in each setting, the variation in the estimates is small relative to the magnitude of the main estimates. Third, I compare the assumptions required here to the assumptions required by the Rand study, and I find differences that could be empirically large.
I discuss the CQIV model and estimation in the next section. In Section 3, I describe my data, I motivate the instrumental variable identification strategy that arises from my empirical context, and I present graphical evidence of the variation that drives my results. In Section 4, I present results based on CQIV and other estimators. In Section 5, I describe the results from several robustness tests, I discuss potential mechanism behind my results, and I provide intuition for why my results differ from those obtained from the Rand Health Insurance Experiment. I conclude and discuss directions for future research in Section 6.
2 CQIV Model and Estimation
Here, I describe the CQIV model and estimation, and I provide intuition to the applied researcher. For further detail, consult Chernozhukov et al. (forthcoming).
2.1 CQIV Model
The CQIV model is based on the following triangular system of equations:
| (1a) |
| (1b) |
| (1c) |
where Y is the observed dependent variable and T(x) ≡ max(x, C) is the transformation function that censors the unobserved uncensored dependent variable Y* from below at censoring point C. In my empirical application, I examine robustness to specifying Y in two ways: Y can represent observed medical spending censored at C = 0, or the logarithm of observed medical spending censored at C = −0.7. (The logarithm of zero is negative infinity, so I censor it at C = −0.7, a value that is smaller than the logarithm of the smallest observed expenditure in the data: 50 cents. Results are robust to the choice of censoring point for values that do not eliminate information.) P is the year-end marginal price of medical care, which is potentially endogenous; W is a vector of covariates; the function u ↦ QY*(u | P, W, V) is the conditional quantile function of Y* given (P, W, V); v ↦ QP (v | W, Z) is the conditional quantile function of P given (W, Z); Z is an indicator for family injury, an instrumental variable that is excluded from Equation (1b); U is a Skorohod disturbance that satisfies the full independence assumption
and V is a Skorohod disturbance that satisfies
The full independence assumption states that the disturbance is distributed uniformly on the interval (0,1), conditional on P, W, Z, V, and C. This assumption requires that the entire distribution of the disturbance in the equation determining Y* is independent of P, W, Z, V and C. This assumption is stronger than the assumption required by related models of the conditional mean, which only require that the mean of the disturbance is independent of the regressors. In my application, the full independence assumption is a formalization of the exclusion restriction that one family member’s injury cannot affect another family member’s expenditure outside of its effect on marginal price, and it should be plausible given the discussion in Section 3.2. The main other assumption required for identification is the relevance condition of Z in Equation (1c). Given these assumptions, we can recover the conditional quantile function of Y* using V as a “control variable.”
The CQIV model allows for nonparametric functional forms for Equations (1b) and (1c). These functional forms could include terms for nonparametric estimation such as power series and splines, and the quantile functions need not be additive in U and V. For simplicity of computation, I specify the following main functional forms:
| (2a) |
| (2b) |
where δ(U) = (α(U), β(U), γ(U)) is the coefficient function of interest. In particular, α(U) yields the marginal effect of price on latent expenditure.
Since the censoring in my application arises from a corner solution decision, I can perform a “corner calculation” to obtain the marginal effect of price on observed expenditure at each U as follows:
where 1{Y* > C} is an indicator for latent expenditure greater than the censoring point at the given U. This calculation is consistent with the recommendation of Wooldridge (2010) and the updated version of Machado and Silva (2008). Applying the corner calculation is not equivalent to estimating an uncensored quantile model.
The CQIV estimator is a conditional quantile estimator, so covariates play an important role. Bitler et al. (2006), who analyze welfare reform experiments, can compute simple quantile treatment effects by subtracting the quantiles of the control group outcomes from the corresponding quantile of the treatment group because assignment to the treatment group is random. In my application, I only claim that my instrument is as good as random conditional on covariates, so I need to include them in all specifications. (See Gilleskie and Mroz (2004) for an approach to estimating the effects of covariates on health expenditures.) Also, covariates are important in the CQIV estimation as discussed below - they are used to predict the observations for which the conditional quantile function is above the censoring point.
The functional form of (2a) allows the coefficients to vary with the quantiles of U (the quantiles of expenditure distribution, conditional on the covariates and the control function). The linearity of (2a) in the parameters is an important feature of this functional form, which is common in quantile models. Given this linearity, we expect results that specify the dependent variable as the level of medical expenditure could be very different from results that specify the dependent variable as the logarithm of medical expenditure. The choice of a logarithmic versus a level specification is not well informed by theory, so I investigate robustness to both specifications.
The choice of how to specify price as an independent variable is also not well informed by theory. As I discuss below, I observe two price changes in my application, first from 1 to 0.2 and then from 0.2 to 0. It is unclear if the response to both price changes should be proportional to those price changes, as required by the previous specification. Therefore, I also investigate robustness to the following functional form, which allows me to test the appropriateness of the previous specification, which it nests:
| (3a) |
| (3b) |
| (3c) |
where 1{P = 1}, is an indicator for a price of one, 1{P = 0} is an indicator for a price of zero, and P = 0.2 is the omitted value. In this specification, I follow the control function approach of Newey et al. (1999). Because the price P only takes on three values, (3a) is nonparametric in P. However, I continue to use the parametric specification of (3c) to estimate the control term. In traditional instrumental variable models of the conditional mean, a rank condition generally implies that a model with two endogenous variables requires two instruments. As in Newey et al. (1999), two instruments are not necessary here because there is only a single endogenous variable, specified nonparametrically in the structural equation.
As in traditional models, we can interact the marginal price variable with a covariate to examine heterogeneity in price responsiveness along an observed dimension. The CQIV model also allows us to examine heterogeneity in price responsiveness along the unobserved dimension U. In what follows, I maintain the agnostic interpretation that the coefficients are a function of the quantiles of unobserved heterogeneity. For stronger interpretations, we can make assumptions about the heterogeneity represented by U. For example, in this application, income is not observed, and if we assume that income is the only dimension of unobserved heterogeneity, then the estimated coefficients will allow us to examine price responsiveness at varying quantiles of the income distribution. If unobserved heterogeneity is one-dimensional and if the quantiles of unobserved heterogeneity are the same as the quantiles of the expenditure distribution conditional on covariates, then the estimated coefficients at the highest quantiles will yield price responsiveness for individuals who spend the most. Alternatively, U could represent the quantiles of unobserved health or hypochondria.
2.2 Estimation
I estimate the model using the CQIV estimator. Here, I provide more intuition for the advantages of the CQIV estimator relative to other models in my empirical context, and I provide practical implementation details. I have already shown that the CQIV model allows the coefficients to vary with the quantiles of interest. In addition, CQIV handles censoring nonparametrically, and it allows for endogeneity.
Censoring induces attenuation bias in quantile regression much in the same way it induces bias in mean regression: when C is observed in the place of a value that should be much smaller, a line that fits the observed values will be biased toward zero. Since quantile regression uses information from the entire sample to generate the estimate at each conditional quantile, if some observations on Y* are censored, the conditional quantile regression lines can be biased toward zero at all conditional quantiles. The Powell (1986) estimator overcomes this difficulty by incorporating censoring directly into the estimator as follows:
where i indexes individuals, and ρu(x) = {(1 − u)1(x < 0) + u1(x > 0)}|x| for a realization u of U. From this objective function, it is clear that regardless of whether values of Y equal to zero arise from a censoring process or through a separate decision process, without the transformation function, T(x) ≡ max(x, C), the conditional quantiles of could be infeasible (beyond the censoring point C) at some quantiles. The transformation function is a nonparametric way to assure that infeasible predictions do not introduce bias into the objective function. Despite its theoretical appeal, direct estimation of this model is rare because the function T(x) induces nonconvexities in the objective function that present computational difficulties.
Chernozhukov and Hong (2002) devised a tractable computational censored quantile regression (CQR) algorithm for Powell’s estimator based on the idea that Powell’s censored regression model estimates the coefficients using observations that are not likely to be censored. The algorithm is a three-step procedure that selects the observations for which the conditional quantile function is above the censoring point. The first step involves a parametric prediction of the probability of censoring based on a probit or logit model. A set fraction of observations that are unlikely to be censored are retained for estimation via quantile regression in the second step. After the second step, a larger set of observations is retained based on the estimated conditional quantiles values of the dependent variable. This sample gets asymptotically close to the ideal sample of “quantile-uncensored,” and consistent estimates are obtained through a third step of quantile regression on this sample. The CQIV computational algorithm uses an analog of the Chernozhukov and Hong (2002) algorithm to handle censoring, with an additional pre-step to handle endogeneity.
The CQIV estimator uses a control function approach to handle endogeneity in the tradition of Hausman (1978). One advantage of the control function approach to endogeneity, in contrast to the moment condition approach to endogeneity used by Chernozhukov and Hansen (2008) in their quantile instrumental variable estimator, is that the control function approach does not require a rank invariance condition on the structural equation. However, a disadvantage is that the assumptions necessary for the control function approach are not technically satisfied when the endogenous variable is discrete. The handling of discrete endogenous variables in control function models is an area that requires more study. Recent work by Frandsen (2014) examines a censored outcome and a binary endogenous regressor in a quantile model. To address the discreteness of my endogenous variable, I estimate a version of the CQIV estimator that uses a Chernozhukov and Hansen (2008) moment condition approach to endogeneity in lieu of the control term approach. This approach does not require continuity in the endogenous variable. The results, reported in Kowalski (2009), are almost identical to those presented here.
As discussed in Chernozhukov et al. (forthcoming), the CQIV estimator does not require an additive error in the first or second stages, which sets it apart from the alternative censored quantile instrumental variable estimator proposed by Blundell and Powell (2007). The Blundell and Powell (2007) estimator requires additive errors in the first and second stages, while allowing for a local nonparametric endogenity correction in the second stage. In the reported estimates, I obtain an estimate of the control term by predicting the OLS residuals from the first stage equation. The results that follow are robust to the inclusion of higher order functions of the control term in the structural equation. Results that use an alternative quantile specification of the first stage as implemented in Chernozhukov et al. (forthcoming) are similar.
I obtain 95% confidence intervals on the coefficients via a nonparametric bootstrap. Online Appendix 1 provides more information on the bootstrap procedure and shows that the results are robust to a weighted bootstrap procedure shown to be consistent by Chernozhukov et al. (forthcoming). In practice, I report the mean of the confidence interval as the point estimate because the discreteness of the covariates can hinder convergence of the quantile estimator at specific combinations of covariates. To facilitate comparison across estimators, I follow the same practice for all estimators in the paper unless otherwise noted.
3 Data
3.1 Data Description
To estimate my model, my data must include medical expenditure and marginal price, and they must allow me to observe family structure so that I can construct my instrument. Data compiled by MEDSTAT Group Inc. (2004) meet these criteria. Medstat data are particularly well-suited to my analysis because the medical claims data identify the beneficiary and insurer contributions on each claim. Because providers often submit claims automatically on behalf of beneficiaries, and because the firms that pay the claims collect the data, incentives are aligned to ensure the accuracy and completeness of the data.
Within the Medstat data, I focus on a US firm in the retail trade industry with over 500,000 insured employees. I use 2004 data in my main analysis, and I also examine 2003 and 2005 in other analyses. I provide details on sample selection in Online Appendix 2. In my main sample, mean-year end medical expenditure by the beneficiary and the insurer is $1,414, but almost 40% of people consume zero care. 57.2% of beneficiaries face a marginal price of one, 39.0% of employees face the coinsurance rate of 0.2, and 3.8% of employees have met the stoploss and face a marginal price of zero. 10.9% of employees have at least one family member who is injured. I provide more extensive summary statistics in Online Appendix 3.
A major advantage of the Medstat data over stand alone claims data is that if beneficiaries do not file any claims or discontinue enrollment, I can still verify their coverage and observe their demographic characteristics in the enrollment database. These data represent an advantage over (Eichner, 1997, 1998). Although I predominantly use cross-sectional variation in the data, I can track individuals and their covered family members over time as long as the subscriber remains at the same firm. One limitation of the Medstat data is that I do not observe employees or family members who are not covered, and I do not observe health insurance options available outside the firm. However, according to the 2006 Annual Survey of Employer Health Benefits conducted by Kaiser Family Foundation and Health Research & Educational Trust (henceforth, “2006 Kaiser Annual Survey of Employer Health Benefits”), 82% of eligible workers enroll in plans offered by their employers, so I should observe a large majority of workers at the firm that I study.
I focus on data from one firm to isolate marginal price variation from other factors that could vary by firm and plan. Traditional employer-sponsored health insurance plans have three major cost sharing parameters: a deductible, a coinsurance rate, and a stoploss. The “deductible” is the amount that the consumer must pay before the insurer makes any payments. Before reaching the deductible, the consumer pays one dollar for one dollar of care, so the marginal price is one. After meeting the deductible, the insurer pays a fractional amount for each dollar of care, and the consumer pays the rest. The marginal price that the consumer pays is known as the “coinsurance rate.” After the consumer has paid the deductible and a fixed amount in coinsurance, the consumer reaches the “stoploss,” and the insurer pays all expenses. For consumers that have met the stoploss, the marginal price is zero.
The main advantage of the firm that I study is that the four plans that it offered in 2003 and 2004 varied only in the deductible and stoploss. Furthermore, one of the offered plans has a $1,000 deductible, which is coincidentally the initial qualifying amount for a plan to be considered “high deductible” by 2003 legislation. Out of concern that plan selection could be correlated with price sensitivity, I rely on within-plan price variation for identification by including plan fixed effects. Plan-related local average treatment effects are possible, and I investigate them by estimating separate specifications by plan.
Table 1 presents a comparison of the cost sharing parameters across plans. The individual deductibles vary from $350 to $1,000, and the family deductible is always three times the individual deductible. Note that each family member must meet the individual deductible before the family deductible can be met. Online Appendix 4 depicts the insurance-induced budget sets for individuals and families, and Online Appendix 5 provides a simple model of how agents maximize utility subject to those budget sets, resulting in a demand curve.
Table 1.
Cost Sharing Comparison
| Cost-sharing Comparison | Plan A | Plan B | Plan C | Plan D | |
|---|---|---|---|---|---|
| Deductible | Individual | $350 | $500 | $750 | $1,000 |
| Family* | $1,050 | $1,500 | $2,250 | $3,000 | |
| Stoploss (Includes Deductible) | Individual | $2,100 | $3,000 | $4,500 | $6,000 |
| Family* | $4,550 | $6,500 | $9,750 | $10,000 $13,000 in 2004 |
|
| Coinsurance (Beneficiary) | In-Network | 20% | 20% | 20% | 20% |
| Out-of-Network | 40% | 40% | 40% | 40% | |
Each family member must meet the individual deductible unless total family spending toward individual deductibles is equal to the family deductible. For example, since the family deductible is three times the individual deductible, if a family has fewer than four members, all family members must meet the individual deductible, and the family deductible does not apply. A similar relationship holds for the stoploss.
The cost sharing parameters provide a very accurate description of the marginal prices that consumers face at this firm. Almost all covered medical spending counts toward the deductible and stoploss, except for spending on prescription drugs, which I do not include in my analysis. In contrast, Duarte (2012) considers Chilean plans that have much more compilicated cost sharing structures.
The only complication in the cost sharing structure at the firm that I study is that the plans offer incentives for beneficiaries to go to providers that are part of a network. All four plans are preferred provider organization (PPO) plans. According to the 2006 Kaiser Annual Survey of Employer Health Benefits, 60% of workers with employer-sponsored health insurance are covered by PPO plans. PPO plans do not require a primary care physician or a referral for services, and there are no capitated physician reimbursements. However, there is an incentive to visit providers in the network because there is a higher coinsurance rate for expenses outside of the network. In the firm that I study, the general coinsurance rate is 20%, and the out-of-network coinsurance rate is 40%. The network itself does not vary across plans. In the data, there are no identifiers for out-of-network expenses, but, as demonstrated in Online Appendix 6, out-of-network expenses are very rare. Accordingly, in my analysis, I assume that everyone who has met the deductible faces the in-network marginal price for care. My main results do not change when I exclude the small number of beneficiaries whose out-of-pocket payments deviate from the in-network schedule.
3.2 Identification
The fundamental question that I attempt to answer in this paper is: How does an individual’s year-end medical expenditure respond to his year-end marginal price for care? A simple identification strategy would compare expenditures of individuals whose families have and have not met the family deductible. The flaw with this simple identification strategy is that individuals in families that have met the family deductible may be more likely to consume medical care for reasons unrelated to its price, such as contagious illnesses or hereditary diseases. For this reason, instead of comparing individuals according to whether their family members have met the family deductible, I compare individuals according to an instrumental variable – whether a family member has an injury.
The first stage effect of a family member’s injury on the individual’s marginal price is possible in families of four or more because of the family deductible and family stoploss structure described above. When one family member receives expenditure-inducing treatment for an injury, the family is more likely to meet the family deductible than it otherwise would have been, and any individual in the family is more likely to face a lower marginal price than his own spending would dictate. Empirically, I find that one family member’s injury does indeed affect another family member’s marginal price.
Given the first stage, the key to the identification strategy is an exclusion restriction: one family member’s injury cannot affect another family member’s medical spending outside of its effect on his marginal price. I aim to rule out mechanical violations of the exclusion restriction in the way that I specify my outcome and estimation sample. I specify the outcome that I study as the medical spending of an individual in a family, and not the medical spending of the entire family so that expenditure for the treatment of one family member’s injury is not included in the outcome variable. Family medical spending would also be an interesting outcome variable, but it would entail a mechanical violation of the exclusion restriction. Since one family member’s injury does have a direct effect on his own medical expenditure, and the injury itself likely influences his decision to consume follow-up medical care and care for secondary illnesses, I use injured family members only to construct the instrument, and I do not include them in the estimation sample. If two or more family members are injured, all injured family members are excluded from the estimation sample. Family injuries have limited persistence across years, so sample selection issues due to the exclusion of injured parties should not be a cause for concern.
Beyond mechanical violations, other potential violations of the exclusion restriction involve indirect effects of one family member’s injury on another family member’s medical spending that occur through a mechanism other than the marginal price. It is possible to think of several mechanisms through which the exclusion restriction could be violated, but as in all instrumental variable applications, the exclusion restriction is a maintained assumption that is fundamentally untestable. However, to increase the plausibility of the exclusion restriction, beyond choosing diagnoses that seem exogenous to a doctor, I use a data-driven method to select categories of injuries for which the exclusion restriction appears to be supported. My approach is motivated by that of Card et al. (2009), who select a subset of diagnoses that appear to have similar rates of appearance in emergency rooms on weekdays and weekends. Using only this subset of diagnosis categories, they measure whether the start of Medicare eligibility at age 65 results in lower mortality.
In my approach, within the class of all diagnosis categories identified as “injuries” through the International Classification of Diseases (ICD-9), I select a set of injury categories for which employees in families with injuries do not appear to spend more than employees in similar families without injuries in the part of the year before the injury occurred. I estimate my main specification using only those categories of injuries in the specification of the instrument. The complete set of injury categories that I include are: fractures; injuries of the thorax, abdomen, and pelvis; injuries to blood vessels; late effect of injuries, poisonings, toxic effects, and other external injuries; foreign body injuries; burns; injuries to the nerves and spinal cord; poisoning by drugs, medicinal and biological substances; and complications of surgical and medical care, not elsewhere classified. As I discuss in Online Appendix 3, 10.9% of employees in my sample have a family member with an injury of one of these types in a given year. Ideally, these injury categories should be severe and unexpected enough that treatment for an injury in these categories should not be related to an underlying family-level propensity to seek treatment, which could lead to a violation of the exclusion restriction.
To further avoid violations of the exclusion restriction, and also to avoid measurement error, in my primary specification I determine the instrument only on the basis of whether an individual was treated for an injury, and not on the basis of the spending associated with the treatment. If the instrument included a measure of injury spending, the instrument could be related to another family member’s medical spending through a family-level propensity to go to expensive doctors, thus violating the exclusion restriction. The disadvantage of specifying the instrument as a dummy variable is that it reduces the variation in the instrument. In alternative specifications detailed in the Online Appendix 12, I incorporate additional variation into the specification of the instrument: variation in the type of injury, variation in the timing of the injury, and variation in the cost of the injury. Results based on all instrument specifications are similar.
3.3 Graphical Evidence
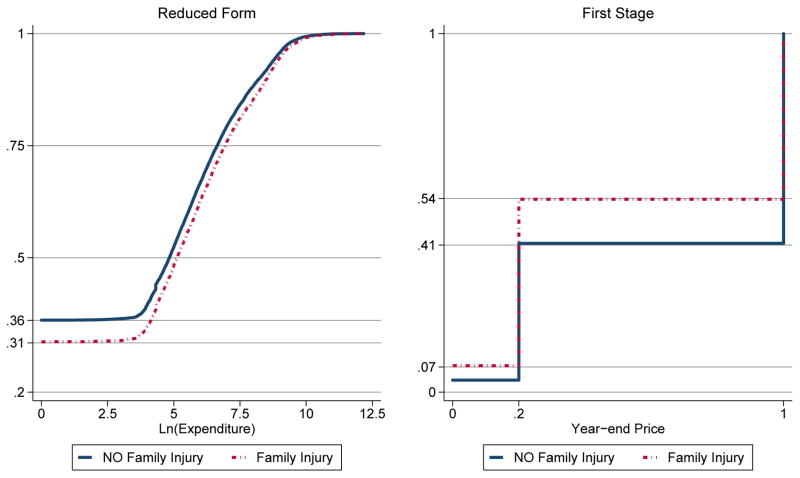
The raw variation in the data that drives my instrumental variable approach is so pronounced that it can be seen graphically, before implementing any estimators. In instrumental variable parlance, the effect of family injury on expenditure is the “reduced form,” and the effect of family injury on the year-end price is the “first stage.” The simple instrumental variable estimate is the ratio of the reduced form to the first stage. To show the variation that drives the instrumental variable strategy, I present graphical depictions of the reduced form and the first stage.
To demonstrate the reduced form, in the left panel of Figure 1, I present the cumulative distribution (cdf) of the logarithm of expenditure conditional on family injury. The cdf for employees with no family injury is represented by a solid line, and the cdf for employees with a family injury is represented by a dashed line. In this depiction, each quantile on the y-axis is associated with a value of the logarithm of expenditure on the x-axis. Median expenditure is $125 among employees with no family injuries and $170 among employees with family injuries. Since the lines never cross, it is clear from the figure that employees with family injuries have higher expenditures at all quantiles. Similarity in the curvature of the two cdfs provides reassurance that not all individuals with family injuries have extremely high expenditures, thus driving the results. The y-intercepts of each line indicate that family injuries affect the extensive margin decision of whether to consume any care; only 31% of people with family injuries consume zero care, as opposed to 36% of people with no family injuries. To examine whether the difference between the lines at all quantiles is driven by effects on the extensive margin, I create a similar figure, not shown here, that depicts cumulative distributions conditional on positive expenditure. The lines of the new figure do not cross, indicating that even among employees with positive expenditure, employees with family injuries have higher expenditure at each quantile.
Figure 1.
Reduced Form and First Stage
To demonstrate the first stage effect of family injury on the year-end price, in the right panel of Figure 1, I present the cumulative distribution of year-end price conditional on family injury. Since the year-end price takes on only three values, the cdf is a step function. The figure shows that employees with family injuries are more likely to face lower prices than their counterparts without family injuries. Labels on the y-axis show that 54% of employees with family injuries spend more than the deductible, while only 41% of employees without family injuries spend more than the deductible. Similarly, 7.4% of employees with family injuries spend more than the stoploss, while only 3.5% of employees without family injuries spend more than the stoploss.
The depiction in the right panel also allows us to assess which price change, the change from 1 to 0.2 or the change from 0.2 to 0, yields the most identification. Following Angrist and Imbens (1995), the vertical difference between the cdfs at the new price is proportional to the weight in an instrumental variable estimate formed from a weighted combination of separate Wald estimates for each price change. Since the difference in the cdfs is largest between 1 and 0.2, the figure indicates that most identification comes from the price change between 1 and 0.2, and some identification comes from the price change between 0.2 and 0.
As a more formal alternative to the right panel of Figure 1, a simple ordinary least squares (OLS) regression of year-end price on family injury and the set of covariates discussed below indicates that having an injury in the family decreases the year-end price by 10 percentage points, with a standard error of 0.7 percentage points. The R-squared of this first stage regression with the covariates partialled out is 0.0060, implying a concentration parameter (defined as NR2/(1 − R2)) of 176. Based on this evidence, “weak instruments bias” is unlikely to be a problem in this application.
The inclusion of covariates should make the estimate more precise. One way to assess the importance of covariates to the instrumental variable strategy is to examine the distribution of each variable conditional on the values of the instrument. Ideally, in this setting, individuals who have an injured family member would be similar in all observable ways to those who do not have an injured family member.
In Online Appendix 3, I report the distribution of covariates conditional on family injury. The distribution of family size shows that individuals with family injuries are slightly more likely to be from larger families, as is to be expected if the incidence of injures is distributed evenly across individuals. Unreported regression results confirm that measures of family size, as well as some of the other covariates, predict the probability of family injury. Given this discrepancy, I include flexible controls for family structure in my formal estimates. It is more likely that the exclusion restriction is satisfied conditional on the covariates. In all of my regressions, I include a dummy for the presence of a spouse on the policy, the year of birth of the oldest and youngest dependent, and the count of family members born in each of the year ranges in the table, with the 1999–2004 range saturated by year. The distribution of the other control variables appears much less sensitive to the instrument. I control for them in my formal estimates because complex interactions between these variables might not be visible in the table.
4 Results
Table 2 reports the main CQIV elasticities, derived from estimating equations that vary the specification of expenditure and price In specifications A and B, price is a single variable that can take on three values: 0, 0.2, and 1. Specifications C and D specify the three values of price nonparametrically as two dummy variables. Specifications A and C model the logarithm of expenditure, and specifications B and D model the level of expenditure.
Table 2.
Main CQIV Elasticities with Alternative Specifications of Expenditure and Price
| 2004 Employee Sample | Censored Quantile IV | Tobit IV | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | |||
| A. Dependent variable: Ln(Expenditure). | |||||||||||
| N= 29,010 | Elasticity | −1.40 | −0.76 | −1.16 | −1.46 | −1.49 | −1.41 | −1.38 | −1.41 | −1.40 | −1.42 |
| lower bound | −1.49 | −1.49 | −1.46 | −1.49 | −1.50 | −1.49 | −1.45 | −1.46 | −1.44 | −1.49 | |
| upper bound | −1.32 | −0.02 | −0.86 | −1.43 | −1.48 | −1.33 | −1.30 | −1.35 | −1.35 | −1.36 | |
|
|
|||||||||||
| Stoploss Elasticity | −0.47 | −0.33 | −0.56 | −0.74 | −0.68 | −0.48 | −0.40 | −0.43 | −0.41 | −0.47 | |
| lower bound | −0.59 | −0.65 | −0.78 | −0.80 | −0.77 | −0.63 | −0.48 | −0.50 | −0.46 | −0.59 | |
| upper bound | −0.34 | 0.00 | −0.33 | −0.68 | −0.58 | −0.34 | −0.32 | −0.35 | −0.35 | −0.36 | |
| B. Dependent variable: Expenditure. | |||||||||||
| Elasticity | −0.26 | 0.14 | −0.64 | −0.67 | −0.50 | −1.21 | −1.35 | −1.33 | −1.39 | −1.50 | |
| lower bound | −1.50 | −0.66 | −0.68 | −0.73 | −1.47 | −1.46 | −1.44 | −1.42 | −1.44 | −1.50 | |
| upper bound | 0.98 | 0.94 | −0.60 | −0.62 | 0.47 | −0.97 | −1.27 | −1.25 | −1.34 | −1.49 | |
|
|
|||||||||||
| Stoploss Elasticity | 0.17 | 0.03 | −0.35 | −0.38 | −0.13 | −0.10 | −0.11 | −0.11 | −0.11 | −0.23 | |
| lower bound | −0.12 | −0.35 | −0.38 | −0.41 | −0.40 | −0.12 | −0.12 | −0.12 | −0.11 | −0.26 | |
| upper bound | 0.47 | 0.41 | −0.32 | −0.35 | 0.14 | −0.09 | −0.10 | −0.10 | −0.11 | −0.21 | |
| C. Dependent variable: Ln(Expenditure). Price specified as two dummy variables. | |||||||||||
| Elasticity | −0.43 | −1.49 | −1.50 | −1.50 | −1.50 | −1.31 | −1.31 | −1.33 | −1.35 | ||
| lower bound | −1.49 | −1.49 | −1.50 | −1.50 | −1.50 | −1.46 | −1.42 | −1.42 | −1.42 | ||
| upper bound | 0.62 | −1.49 | −1.50 | −1.50 | −1.49 | −1.15 | −1.19 | −1.25 | −1.28 | ||
|
|
|||||||||||
| Stoploss Elasticity | 0.22 | −0.73 | −0.89 | −0.88 | −0.82 | −0.77 | −0.74 | −0.71 | −0.69 | ||
| lower bound | −0.43 | −0.84 | −0.91 | −0.88 | −0.85 | −0.82 | −0.78 | −0.74 | −0.74 | ||
| upper bound | 0.88 | −0.62 | −0.87 | −0.87 | −0.80 | −0.72 | −0.69 | −0.67 | −0.64 | ||
| D. Dependent variable: Expenditure. Price specified as two dummy variables | |||||||||||
| Elasticity | −0.16 | −0.17 | −0.26 | −0.29 | −0.36 | −0.84 | −1.27 | −1.28 | −1.27 | ||
| lower bound | −1.50 | −1.50 | −1.50 | −1.50 | −1.50 | −1.47 | −1.42 | −1.38 | −1.34 | ||
| upper bound | 1.19 | 1.17 | 0.99 | 0.92 | 0.78 | −0.20 | −1.13 | −1.19 | −1.20 | ||
|
|
|||||||||||
| Stoploss Elasticity | 0.03 | −0.57 | −0.91 | −0.87 | −0.88 | −0.85 | −0.77 | −0.69 | −0.69 | ||
| lower bound | −0.34 | −0.91 | −0.96 | −0.96 | −0.93 | −0.91 | −0.79 | −0.72 | −0.71 | ||
| upper bound | 0.40 | −0.24 | −0.87 | −0.79 | −0.83 | −0.80 | −0.75 | −0.66 | −0.66 | ||
Unless otherwise noted, price specified as a single variable.
Lower and upper bounds of 95% confidence interval from 200 bootstrap replications.
Controls include: employee dummy (when applicable), spouse dummy (when applicable), male dummy, plan (saturated), census region (saturated), salary dummy (vs. hourly), spouse on policy dummy, YOB of oldest dependent, YOB of youngest dependent, family size (saturated with 8–11 as one group), count family born 1944 to 1953, count family born 1954 to 1963, count family born 1974 to 1983, count family born 1984 to 1993, count family born 1994 to 1998, count family born 1999, count family born 2000, count family born 2001, count family born 2002, count family born 2003, count family born 2004 (when applicable).
I do not specify year-end price in logarithmic form because it can take on a value of zero. Thus, I must transform all of the estimated coefficients into elasticities to obtain the price elasticity of expenditure on medical care. In Online Appendix 7, I discuss several approaches to transform the estimated coefficients into arc elasticities, which are preferable to point elasticities for large price changes. I demonstrate that the choice of arc elasticity transformation can have a large impact on the results, so researchers aiming to compare elasticities across studies should take the elasticity calculation seriously. I show that the midpoint elasticity that I report facilitates comparison to the Rand Health Insurance Experiment, but it has an undesirable property that makes large elasticities approach −1.5. Since most of my identification comes from the larger price change from before to after the deductible - from 1 to 0.2, I report corner arc elasticities from this range.
The elasticity at the 0.6 quantile in specification A is −1.41. To interpret this conditional quantile elasticity, suppose that there are two groups of people. Each group has the same characteristics as controlled for by the regressors, but they differ in the prices that they face. The coefficient at the 0.6 quantile of −1.41 indicates that if we increase price by one percent from the first group to the second group, the 0.6 quantile of expenditure in the second group will be 1.41 percent higher than the 0.6 quantile in the first group. The discussion in Online Appendix 7 related to Table OA7 gives us another way of thinking about this coefficient in the context of the estimated conditional quantiles from which this arc elasticity is derived: if we have two groups of people as controlled for by the regressors, but they face different prices, the group with a price of 1 will have a 0.6 quantile expenditure of $23, but the group with a price of 0.2 will have a 0.6 quantile of expenditure of approximately $1,728. The coefficients at other quantiles can be interpreted analogously.
It is important to note that the quantiles of expenditure are very different from the conditional quantiles of expenditure. Tables OA7 and OA8 in Online Appendix 7 report the quantiles of expenditure, as well as expenditure at each conditional quantile from models that specify the logarithm and the level of expenditure, respectively. The 0.7 quantile of expenditure is $531, which is much smaller than the 0.7 conditional quantile of expenditure of $2,825. This difference arises because the people at the 0.7 quantile of expenditure spend more than 70% of all people, but the people at the 0.7 conditional quantile of expenditure spend more than 70% of people only after controlling for their characteristics. As discussed in Section 2, people with higher expenditures conditional on their covariates might have higher income, higher propensity for hypochondria, or more severe illnesses. Hence, covariates are an important part of the model. As shown in Table 3, coefficients on some covariates have plausible signs but vary dramatically, sometimes to the extent that they are statistically significantly different across conditional quantiles, indicating that there is merit in permitting coefficients to vary with the conditional quantiles in this application.
Table 3.
CQIV Coefficients on Selected Covariates
| Dependent variable: Ln(Expenditure). | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2004 Employee Sample | Censored Quantile IV | Tobit IV | ||||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | ||
| Year-end price | −5.17 | −3.94 | −6.99 | −9.72 | −8.42 | −5.47 | −4.25 | −4.59 | −4.31 | −5.26 |
| lower bound | −6.76 | −7.82 | −10.51 | −11.13 | −10.18 | −7.39 | −5.22 | −5.48 | −4.94 | −6.76 |
| upper bound | −3.58 | −0.07 | −3.48 | −8.32 | −6.66 | −3.55 | −3.28 | −3.70 | −3.68 | −3.76 |
|
| ||||||||||
| Control Term | −1.55 | −4.97 | −5.65 | −3.73 | −1.81 | −0.64 | −0.16 | 0.34 | 0.19 | NA |
| lower bound | −3.09 | −9.93 | −7.66 | −4.99 | −3.52 | −2.23 | −1.11 | −0.55 | −0.46 | NA |
| upper bound | 0.00 | 0.00 | −3.65 | −2.47 | −0.10 | 0.96 | 0.79 | 1.22 | 0.84 | NA |
|
| ||||||||||
| Male | −0.28 | −0.77 | −0.79 | −0.56 | −0.30 | −0.28 | −0.23 | −0.11 | −0.06 | −0.98 |
| lower bound | −0.56 | −1.54 | −1.19 | −0.81 | −0.58 | −0.58 | −0.45 | −0.26 | −0.19 | −1.25 |
| upper bound | 0.00 | 0.00 | −0.38 | −0.30 | −0.02 | 0.02 | −0.02 | 0.04 | 0.07 | −0.72 |
|
| ||||||||||
| $500 Deduct | −0.16 | −0.54 | −0.38 | −0.16 | 0.00 | 0.33 | 0.17 | 0.23 | 0.25 | 0.05 |
| lower bound | −0.32 | −1.07 | −0.64 | −0.32 | −0.17 | 0.09 | 0.05 | 0.12 | 0.15 | −0.16 |
| upper bound | 0.00 | 0.00 | −0.12 | 0.01 | 0.18 | 0.58 | 0.30 | 0.34 | 0.34 | 0.27 |
|
| ||||||||||
| Pacific | −0.07 | −0.41 | −0.39 | −0.21 | −0.02 | 0.26 | 0.25 | 0.25 | 0.13 | 0.15 |
| lower bound | −0.14 | −0.88 | −0.77 | −0.48 | −0.25 | −0.14 | −0.09 | −0.17 | −0.15 | −0.37 |
| upper bound | 0.00 | 0.05 | −0.01 | 0.07 | 0.21 | 0.66 | 0.59 | 0.66 | 0.41 | 0.67 |
|
| ||||||||||
| Salaried Subscriber | 0.03 | 0.11 | 0.06 | 0.01 | 0.05 | 0.22 | 0.14 | 0.11 | 0.11 | 0.35 |
| lower bound | 0.00 | −0.01 | −0.07 | −0.08 | −0.03 | 0.11 | 0.07 | 0.04 | 0.06 | 0.24 |
| upper bound | 0.05 | 0.24 | 0.19 | 0.09 | 0.12 | 0.33 | 0.21 | 0.17 | 0.17 | 0.45 |
|
| ||||||||||
| Spouse on Policy | 0.00 | −0.27 | −0.27 | −0.23 | −0.16 | 0.10 | −0.04 | −0.07 | −0.09 | 0.05 |
| lower bound | −0.05 | −0.68 | −0.57 | −0.47 | −0.35 | −0.26 | −0.26 | −0.28 | −0.26 | −0.29 |
| upper bound | 0.05 | 0.14 | 0.02 | 0.01 | 0.04 | 0.46 | 0.19 | 0.13 | 0.08 | 0.39 |
|
| ||||||||||
| YOB of Oldest Dependent | 0.00 | −0.02 | −0.02 | −0.02 | −0.01 | −0.02 | 0.00 | 0.00 | 0.00 | 0.00 |
| lower bound | −0.01 | −0.05 | −0.04 | −0.04 | −0.02 | −0.04 | −0.02 | −0.01 | −0.01 | −0.03 |
| upper bound | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.01 | 0.01 | 0.01 | 0.00 | 0.02 |
|
| ||||||||||
| YOB of Youngest Dependent | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 |
| lower bound | 0.00 | −0.02 | −0.02 | −0.02 | −0.01 | −0.02 | −0.01 | −0.01 | −0.01 | −0.02 |
| upper bound | 0.00 | 0.03 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 | 0.03 |
|
| ||||||||||
| Family Size of 8 to 11 | −0.78 | 3.99 | 0.20 | 2.55 | 2.09 | 0.87 | 0.95 | 0.97 | 1.66 | 3.00 |
| lower bound | −6.50 | −0.48 | −6.20 | 0.23 | 0.39 | −1.15 | −0.45 | −1.01 | 0.21 | 0.62 |
| upper bound | 4.94 | 8.45 | 6.60 | 4.88 | 3.79 | 2.89 | 2.34 | 2.94 | 3.11 | 5.38 |
|
| ||||||||||
| Count family born 2004 | −0.36 | 0.64 | 0.52 | 0.60 | 0.41 | 0.68 | 0.39 | 0.10 | −0.21 | −0.50 |
| lower bound | −0.88 | −0.65 | −0.21 | 0.02 | −0.14 | 0.17 | 0.05 | −0.24 | −0.51 | −1.16 |
| upper bound | 0.16 | 1.92 | 1.25 | 1.19 | 0.96 | 1.20 | 0.73 | 0.45 | 0.10 | 0.17 |
Omitted categories in estimation: $350 Deduct, Family Size of 4, Northeast, count family born 1934 to 1943.
Omitted catgories from table: $750 Deduct, $1000 Deduct, Family Size of 5, Family Size of 6, Family Size of 7, Middle Atlantic, East North Central, West North Central, South Atlantic, East South Central, West South Central, Mountain, count family born 1944 to 1953, count family born 1954 to 1963, count family born 1974 to 1983, count family born 1984 to 1993, count family born 1994 to 1998, count family born 1999, count family born 2000, count family born 2001, count family born 2002, count family born 2003.
By comparing the four specifications in Table 2, we see that heterogeneity in price responsiveness across the conditional quantiles appears sensitive to whether expenditure is specified in logarithms or levels. Because we have transformed the coefficients into elasticities, we can compare the elasticities across specifications. We see in specifications A and C that when we specify the dependent variable as the logarithm of expenditure, we do not see much heterogeneity in price responsiveness across the conditional quantiles. In specification A, the smallest elasticity is −0.76, and the largest is −1.49. In specification C, the −0.43 elasticity at the 0.10 conditional quantile is much smaller than the others, which vary from −1.31 to −1.50. All of the elasticities are generally statistically different from zero but not from each other. There is no strong pattern across the quantiles, but the elasticity at the conditional median is the largest, and the elasticities generally decreases away from the median in either direction.
In specifications B and D, when we specify the dependent variable as the level of expenditure, we see much more variation in the elasticity across the conditional quantiles. In specification B, aside from one imprecise positive elasticity at the 0.20 quantile, the estimates vary from −0.26 to −1.39, and the elasticities generally get more negative at higher conditional quantiles. The coefficients in specification D follow a similar pattern. As discussed in Online Appendix 7, the elasticities in the levels models are smaller at smaller quantiles because the corner calculation has a larger impact when the conditional quantiles of expenditure is more likely to be zero. This pattern arises because changes in observed expenditure are less likely when observed expenditure is zero, and observed expenditure of zero is more likely in the levels model, not because people at the lowest conditional quantiles have lower latent price responsiveness or because the two models give fundamentally different results. Since theory does not inform the choice of specification, I focus on the logarithmic specification of the dependent variable in Table 3, and I present results from the level specification in Online Appendix tables.
Although price responsiveness appears sensitive to the specification of expenditure, it is not as sensitive to the specification of price. Instead of specifying price as a single variable in the structural equation, specifications C and D specify price as two separate variables following (3a) to allow for heterogeneity in price responsiveness for each of the two price changes. The elasticities, which are calculated for a price change from 1 to 0.2, are similar to their counterparts in which price is specified as a single variable, suggesting that the main specification is appropriate.
In Table 2, I also report “Stoploss Elasticities” that are based on the price change from before to after the stoploss is met - from 0.2 to 0. Online Appendix 8 discusses how the stoploss elasticities might compare to the main elasticities, demonstrating that the comparison could go in either direction. Empirically, the estimates show that the stoploss elasticity is smaller than the main elasticity at almost all quantiles in all four specifications. The magnitudes of the stoploss elasticities are somewhat larger in the specifications that include price nonparametrically - the largest elasticity is −0.91 in specifications C and D, in contrast to −0.74 in specifications A and B.
Given that the elasticities are sensitive to the specification of expenditure, but they are not very sensitive to the specification of price, I investigate the robustness of my results using specifications with expenditure in logarithms and levels but a single price. The specification with a single price allows me to estimate other models such as Tobit IV that cannot allow for two endogenous price variables with a single instrument. I report Tobit IV estimates obtained through the Stata command ivtobit for comparison, and they are generally in the same range as the CQIV estimates.
5 Additional Analysis and Robustness
I perform extensive additional analysis, which I include in the Online Appendix. Although the magnitudes of my estimated elasticities vary across specifications, all of my estimated elasticities are much larger than the elasticity estimate of −0.22 obtained by the Rand Health Insurance Experiment. In Online Appendix 9, I examine results derived from alternative estimators, and I show that, regardless of the estimator, the elasticities that I find are large relative to the literature.
In Online Appendix 10, I examine heterogeneity in treatment effects by observable characteristics. Although one advantage of the CQIV estimator is that allows estimates to vary with unobserved heterogeneity, price responsiveness along observed dimensions is also of interest. I find some evidence that females, salaried employees, and people in the least generous plans are more price responsive, but estimates even among their counterparts are large relative to those in the literature.
In Online Appendix 11 and Online Appendix 12, I show that my results are robust to several alternative estimation samples and specifications of the instrument. I show that within-year injury timing has a limited impact on my results in Online Appendix 13. In Online Appendix 14, I conduct an analysis using data on smaller families on the grounds that because of the structure of plans at the firm that I study, cost sharing interactions cannot occur in families of two. The results do not provide support for the identification assumption, but, as I discuss, the analysis has several limitations.
I also consider variations on the main specification to examine the mechanisms behind my results. In Online Appendix 15, I show key evidence in support of my identification strategy: spending does not respond before an family injury occurs, but it does respond after the injury occurs. In Online Appendix 16, I explore the mechanisms behind my estimated elasticity, and I show that agents mainly respond to price on the outpatient visit margin.
All analyses considered, my main results are an order of magnitude larger than those from the Rand Health Insurance Experiment. In Online Appendix 17, I discuss methodological differences between my approach and the Rand approach. The relative treatment of myopia and foresight is one potential explanation for why the Rand results are so much smaller than mine.
6 Conclusion
This paper makes several contributions. Using detailed data and a rigorous identification strategy, I estimate the price elasticity of expenditure on medical care using a censored quantile instrumental variable estimator. With the CQIV estimator, I go beyond standards in the literature by allowing the elasticity estimate to vary with the conditional quantiles of the expenditure distribution, relaxing the distributional assumptions traditionally used to deal with censoring, and addressing endogeneity.
My main results show that the price elasticity of expenditure on medical care varies from −0.76 to −1.49 across the conditional deciles of the expenditure distribution. Although the CQIV estimator allows the elasticity estimates to vary across the conditional quantiles of expenditure, the estimates are relatively stable across the conditional deciles. My estimated elasticities are an order of magnitude larger than those in the literature. I take several steps to compare my estimates to those in the literature, and I consider several sources of heterogeneity in the estimates. I conclude that the price elasticity of expenditure on medical care is much larger than the literature would suggest.
Supplementary Material
Acknowledgments
I am grateful to Amy Finkelstein, Jonathan Gruber, and Jerry Hausman for their guidance. I would like to thank the following individuals for thoughtful comments: Joseph Altonji, Michael Anderson, Joshua Angrist, David Autor, John Beshears, Soren Blomquist, Tonja Bowen-Bishop, David Card, Amitabh Chandra, Victor Chernozhukov, David Cutler, Ian Dew-Becker, Deepa Dhume, Peter Diamond, Joseph Doyle, Esther Duflo, Jesse Edgerton, Matthew Eichner, Ivan Fernandez-Val, Brigham Frandsen, John Friedman, Michael Greenstone, Raymond Guiteras, Matthew Harding, Naomi Hausman, Panle Jia, Lisa Kahn, Jonathan Kolstad, Fabian Lange, Blaise Melly, Derek Neal, Whitney Newey, Joseph Newhouse, Douglas Norton, Edward Norton, Christopher Nosko, Matthew Notowidigdo, James Poterba, David Powell, Andrew Samwick, Gerardo Sanchez, David Seif, Hui Shan, Mark Showalter, Erin Strumpf, Heidi Williams, and several anonymous referees who gave very constructive suggestions. Seminar participants at Chicago Booth, Brookings, Cornell, Duke, Kellogg, Maryland, Michigan, MIT, NBER Summer Institute, Notre Dame, Rand, Stanford SIEPR, Temple Fox, Texas A&M, Wharton, Wisconsin, Yale, Yale SOM, and the Yale School of Public Health provided helpful feedback. Dr. Kavita Patel provided a helpful clinical perspective. I thank Toby Chaiken for excellent research assistance. Mohan Ramanujan and Jean Roth provided invaluable help with the data. I gratefully acknowledge National Institute on Aging, Grant Number T32-AG00186.
References
- Angrist JD, Imbens GW. Two-stage least squares estimation of average causal effects in models with variable treatment intensity. Journal of the American Statistical Association. 1995;90(430):431–442. [Google Scholar]
- Bitler MP, Gelbach JB, Hoynes HW. What mean impacts miss: Distributional effects of welfare reform experiments. The American Economic Review. 2006;96(4):988–1012. [Google Scholar]
- Blundell R, Powell JL. Censored regression quantiles with endogenous regressors. Journal of Econometrics. 2007;141(1):65–83. Semiparametric methods in econometrics. [Google Scholar]
- Buntin MB, Zaslavsky AM. Too much ado about two-part models and transformation?: Comparing methods of modeling medicare expenditures. Journal of Health Economics. 2004;23(3):525–542. doi: 10.1016/j.jhealeco.2003.10.005. [DOI] [PubMed] [Google Scholar]
- Card D, Dobkin C, Maestas N. Does medicare save lives? The Quarterly Journal of Economics. 2009;124(2):597–636. doi: 10.1162/qjec.2009.124.2.597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chernozhukov V, Fernández-Val I, Kowalski AE. Quantile regression with censoring and endogeneity. The Journal of Econometrics forthcoming 2014. [Google Scholar]
- Chernozhukov V, Hansen C. Instrumental variable quantile regression: A robust inference approach. Journal of Econometrics. 2008;142(1):379–398. [Google Scholar]
- Chernozhukov V, Hong H. Three-step censored quantile regression and extramarital affairs. Journal of the American Statistical Association. 2002;97(459):872–882. [Google Scholar]
- Duan N, Manning J, Willard G, Morris CN, Newhouse JP. A comparison of alternative models for the demand for medical care. Journal of Business & Economic Statistics. 1983;1(2):115–126. [Google Scholar]
- Duarte F. Price elasticity of expenditure across health care services. Journal of Health Economics. 2012;31(6):824–841. doi: 10.1016/j.jhealeco.2012.07.002. [DOI] [PubMed] [Google Scholar]
- Eichner MJ. Ph D thesis. Massachusetts Institute of Technology; 1997. Medical Expenditures and Major Risk Health Insurance. [Google Scholar]
- Eichner MJ. The demand for medical care: What people pay does matter. The American Economic Review. 1998;88(2):117–121. [Google Scholar]
- Frandsen BR. Working paper. Brigham Young University; 2014. May, Treatments effects with censoring and endogeneity. [Google Scholar]
- Gilleskie DB, Mroz TA. A flexible approach for estimating the effects of covariates on health expenditures. Journal of Health Economics. 2004;23(2):391–418. doi: 10.1016/j.jhealeco.2003.09.008. [DOI] [PubMed] [Google Scholar]
- Hausman JA. Specification tests in econometrics. Econometrica. 1978;46(6):1251–1271. [Google Scholar]
- Kaiser Family Foundation and Health Research & Educational Trust. Employer Health Benefits Annual Survey 2006. 2006. [Google Scholar]
- Kowalski AE. Working Paper 15085, National Bureau of Economic Research. 2009. Jun, Censored quantile instrumental variable estimates of the price elasticity of expenditure on medical care. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machado JAF, Silva JMCS. Quantiles for Fractions and Other Mixed Data. Economics Discussion Papers 656. University of Essex, Department of Economics; 2008. Jul, [Google Scholar]
- MEDSTAT Group Inc. Marketscan database. 2004. [Google Scholar]
- Mullahy J. Much ado about two: reconsidering retransformation and the two-part model in health econometrics. Journal of Health Economics. 1998;17(3):247–281. doi: 10.1016/s0167-6296(98)00030-7. [DOI] [PubMed] [Google Scholar]
- Newey WK, Powell JL, Vella F. Nonparametric estimation of triangular simultaneous equations models. Econometrica. 1999;67(3):565–603. [Google Scholar]
- Newhouse JP, Phelps CE, Marquis MS. On having your cake and eating it too: Econometric problems in estimating the demand for health services. Journal of Econometrics. 1980;13(3):365–390. [Google Scholar]
- Newhouse JP the Insurance Experiment Group. Free for All? Lessons from the Rand Health Insurance Experiment. Cambridge: Harvard University Press; 1996. [Google Scholar]
- Powell JL. Censored regression quantiles. Journal of Econometrics. 1986;32(1):143–155. [Google Scholar]
- Wooldridge JM. Econometric Analysis of Cross Section and Panel Data. 2. Cambridge: MIT Press; 2010. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.