Abstract
This paper represents a methodological-substantive synergy. A new model, the Mixed Effects Structural Equations (MESE) model which combines structural equations modeling and item response theory is introduced to attend to measurement error bias when using several latent variables as predictors in generalized linear models. The paper investigates racial and gender disparities in STEM retention in higher education. Using the MESE model with 1997 National Longitudinal Survey of Youth data, I find prior mathematics proficiency and personality have been previously underestimated in the STEM retention literature. Pre-college mathematics proficiency and personality explain large portions of the racial and gender gaps. The findings have implications for those who design interventions aimed at increasing the rates of STEM persistence among women and under-represented minorities.
MSC 2010 subject classifications: Primary Structural equations models, item response theory, STEM retention, higher education
1. Introduction
Researchers across diverse disciplines in the social sciences rely on latent variables (Borsboom, Mellenbergh and van Heerden, 2003) as predictors of an outcome of interest. For example, cognitive proficiencies and non-cognitive personality traits (e.g., motivation and self-esteem), developed when individuals are young, are key to later-life outcomes, including labor market, health, and educational decisions (Heckman, Stixrud and Urzua, 2006).
Of particular interest for this paper is the role that cognitive proficiencies and personality measures play in the racial and gender gaps that exist in college students’ choices to major in one of the science, technology, engineering, or mathematical (STEM) disciplines (Riegle-Crumb et al, 2012; Xie and Shauman 2003). Despite ongoing work by many colleges and universities, women and under-represented minorities (URMs) are still far less likely to major in the STEM disciplines (NCES, 2009). Using generalized linear models (e.g., linear probability models, logistic regressions, or probit analyses), researchers model the racial and gender STEM retention gaps after controlling for a set of covariates, which often include some latent variable(s) such as e.g., academic achievement (Maltese and Tai, 2011), or personality traits (Korpershoek, Kuyper, and van der Werf, 2012).
Because latent variables are hypothetical constructs, they are not observed directly and are difficult to measure accurately. Typically, latent variables are measured by a set of observed test or survey items in which a “test score” (often released by the survey institution) is the estimate of the latent trait. Survey institutions use modern psychometric models such as item response theory (IRT; van der Linden and Hambleton, 1997) to construct and design the test and estimate the test score. Researchers throughout the social sciences often use the test scores as known constants in further statistical analyses. However, the measurement error present in the test score poses an obstacle to accurate estimation of the relationships among the latent construct(s), other covariates in the model, and the outcome of interest. It is well known that analyses which ignore measurement error in covariates are prone to biased results (Fuller, 2006, Stefanski, 2000).
Consider a multiple linear regression,
| (1) |
where Y is the response variable, Z is a 0/1 indicator variable intended to test for a “treatment” effect, and X is a test or survey score intended to measure a latent trait, θ. If X is measured with classical error, (e.g., Xi = θi + νi and νi ~ N(0, τ)), then will be attenuated due to the increased variability in X from the measurement error. will also be biased if Z is correlated with θ. The direction and strength of the bias of will depend on the direction and strength of the correlations among θ, Z and Y (Fuller, 2006). Similar results are seen in logistic and probit regression. When the measurement error is not classical, (as is often the case for latent variables, as I show in Section 3.1), the bias can be in any direction.
When θ is estimated precisely by X the biases in the regression coefficients may not be significant, but when θ is not well-proxied by X, serious misunderstandings that are both statistically and practically significant can occur. The use of noisy measures of latent variables can cause researchers to misestimate the effects of the latent variables on the outcome of interest and the effects of other correlated covariates in the analysis. These kinds of biases are most likely to be significant with short tests or surveys, because shorter tests lead to larger measurement error which in turn leads to larger bias. Given the serious problems with estimates of θ that do not model the measurement error, it is useful to consider more recent methodological advances for modeling the error.
One might argue for the use of instrumental variables (IV, Staiger and Stock, 1997) or nonparametric bounds (e.g., Klepper and Leamer, 1984) to solve the measurement error problem. Each latent variable is obtained from a well-designed cognitive or non-cognitive assessment constructed with an IRT model. The existence of this IRT model as a direct model eliminates the need for refining nonparametric bounds or searching for suitable instruments to adjust for the measurement error in test scores (Junker, Schofield and Taylor, 2012). Schofield (2014) discusses the kinds of problems that arise when trying to implement IV or errors in variables (EIV) models using psychometric data and notes the error structure implied by many IRT models violates several assumptions used in IV.
Richardson and Gilks (1993) provide a unifying Bayesian framework in which to estimate models with covariate measurement error. Their framework involves specifying three sub-models: 1) the structural equation (or an outcome model) relating the outcome of interest Y to the latent variable(s) θ, and any other covariates Z; 2) a measurement model relating the test score(s) and/or item responses X to θ; and 3) a prior or conditioning model for θ. Their approach is based on an assumption of conditional independence relationships between several subsets of variables.
Several researchers have adapted Richard and Gilks’s (1993) framework to study issues in epidemiology. For example Dominici and Zeger (2000) use a time series model to study how measurement error in the estimates of exposure to air pollution affects estimates on mortality. More recently, Haining et al (2010) use a Bayesian structural equations model to study the risk of stroke from air pollution. Skrondal and Rabe-Hesketh (2004) extend the general structural equations model to provide several applications outside of epidemiology but few have considered Richardson and Gilks’s framework for research in educational policy.
Junker, Schofield, and Taylor (2012) develop a structural equations model called the Mixed Effects Structural Equations (MESE) model. The MESE model was rediscovered independently from Richard and Gilks’s (1993) framework and extends the general SEM framework for psychometric data. In the MESE model, the latent variable’s measurement model is defined to be the IRT model used by the survey institution to construct, design and score θ. Unlike other SEM models (such as MIMIC models (Joreskog and Goldberger, 1975 and Krishnakumar and Nagar, 2008) or Fox and Glas’s (2001) MLIRT model), the MESE model includes a conditioning (or prior) model on θ which conditions on the other covariates in the structural model. Junker, Schofield, and Taylor (2012) use the MESE model to study black-white wage gaps after controlling for the effect of literacy skills and find substantial differences in the black-which wage gap when the measurement error of literacy is modeled versus when it is not.
This paper builds on the framework of Richardson and Gilks (1993) and Rabe-Hesketh, Skrondal, and Pickles (2004) to extend Junker, Schofield, and Taylor’s (2012) MESE model. I evaluate the merits of the common practice of treating statistics such as test scores or personality scale scores as if they were simply predetermined data in analyses of STEM retention gaps for females and under-represented minorities (URMs). Using an extended MESE model, I present an alternative model to examining STEM retention that properly accounts for the error in the latent variables. I find significant differences in the gender and racial gaps in STEM retention conditional on math proficiency and personality traits when I model the measurement error in these latent variables versus when I do not. The MESE model extensions are novel in two ways. First, several latent variables are used as predictors and they are allowed to correlate given the other covariates in the structural model. Second, each latent variable is modeled with a different item response theory (IRT) measurement model to estimate the heteroskedastic error structure.
The question of whether STEM retention gaps are predictable by latent traits such as academic achievement or personality traits is not an arcane decomposition. Whether the gap occurs because of deprivation in the latent constructs before entry into college, or whether the gap is due to college teaching practices that unintentionally discriminate against women or URMs results in fundamentally different institutional policies and interventions to address the issue. The hope is that if researchers determine what predicts STEM retention, institutions can develop interventions to empower students with what they need to complete the necessary requirements. Any research that mis-models the effect of the latent traits on STEM retention may lead to inappropriate uses of limited institutional resources.
2. The Mixed Effects Structural Equations Model
Consider the case in which a researcher is interested in estimating the linear regression model,
| (2) |
where Yi represents some outcome of interest for individual i, θ is the (possibly vector-valued) latent trait(s), and Z are some additional covariates of interest measured accurately. Researchers use such models both when they are interested in estimates of β1, the effect of the latent variable(s) θ on the outcome of interest and when they are interested in estimates of β2, the relationship between two (or more) variables after “controlling for” θ. The overall goal is to estimate β = (β0, β1, β2) the vector of the regression coefficients.
If θ is not measured with error, one could either maximize the likelihood, f(Y|β, θ, Z) with respect to β or choose a prior for β and calculate the posterior p(β|Y, θ, Z). However, because θ is a latent variable, it is unobserved and instead X, a proxy test score or a set of item responses is observed. This leaves the likelihood
| (3) |
where Z is known, Y and X are observed, and β is the vector of unknown parameter(s) we wish to estimate. It is clear (3) is a marginal distribution of a more general model in which the unknown θ is integrated out and which can be factored by the Law of Total Probability,
| (4) |
| (5) |
This more general model (5) implies a form of the Mixed Effects Structural Equations Model (MESE; Schofield, 2008; Junker, Schofield, and Taylor, 2012), which suggests three general models corresponding to the structural, measurement, and prior submodels of Richard and Gilks (1993).
2.1. Conditional Independence Assumptions
Following Richardson and Gilks (1993), I will make several conditional independence assumptions to simplify the MESE model. First, I assume Y depends only on θ and Z and that Y ⫫ X|θ such that X provides no additional information about Y once θ is known. Second, I assume θ ⫫ β|Z. Finally, as I show in Section 3.1, good measurement practice and modern psychometric theory allows the assumption that X ⫫ Z, β|θ. I can now write the MESE model in hierarchical form,
| (6) |
| (7) |
| (8) |
where γj are the parameters in the measurement model, α are the parameters in the population model for θ|Z, and β, θ, Y, X, and Z are defined as before. In MESE, the latent variables and the regression coefficients are estimated simultaneously.
The MESE model follows the structural approach advocated in Richardson et al (2002) and can easily be shown to be a general structural equations model (Bollen, 1989). The MESE model is in the spirit of MIMIC models (Joreskog and Goldberger, 1975 and Krishnakumar and Nagar, 2008) which examine the causes of a posited latent variable(s) with multiple observed indicators. The interest in MIMIC models is often in the theoretical explanation of the latent variable or in the relations between the latent variable and some observed variables. The MESE model extends the MIMIC model to cases where the interest is in the effect of the covariates after controlling for the latent variables. Fox and Glas (2001) proposed MLIRT, a similar model to MESE, in which they attempt to control for a latent variable (e.g., IQ) to predict how student performance on a test may be different for schools under different treatments. In MLIRT, the only predictor variables are psychometric latent variables and they do not include a prior model on θ that conditions on the other covariates in the model. MESE extends the MLIRT model to include other fixed effect predictors. Rabe-Hesketh, Skrondal, and Pickles (2004) provide a unifying framework for multilevel structural equations into which the MESE model fits.
2.2. Estimating the MESE model
To estimate the coefficients of interest from (6), the latent variables must be integrated out of the full likelihood, (5). One can either integrate using numerical integration and Newton-Raphson or E-M algorithms (using software such as the gllamm model in Stata (Rabe-Hesketh, S., Skrondal, A. and Pickles, A., 2004 and Rabe-Hesketh, S., Skrondal, A. and Pickles, A., 2005) or Mplus (Muthén and Muthén, 2007)), or through a computational Bayesian approach in which priors are assigned to parameters and a Markov Chain Monte Carlo (MCMC) algorithm is applied to sample directly from the joint posterior distribution and any marginal posterior distributions of interest (using software such as WinBUGS (Spiegelhalter, Thomas and Best, 2000) or JAGS (Plummer, 2003)).
In this paper, I take the Bayesian approach to estimation. The reasons for this are threefold. First, the Bayesian estimation approach becomes comparatively more attractive than likelihood-based methods as the dimension of the latent variables grow, because maximizing the likelihood requires multivariate numerical integration for each observation and the numerical integration becomes computationally prohibitive (Lockwood and McCaffrey, 2014). Second, as Dunson (2001) notes, the Bayesian MCMC approach allows for a more flexible set of submodels, including multilevel correlation structures and different measurement scales for different test items. Under these more complicated models, maximum likelihood approaches to estimation are difficult to implement because of the high dimensional integration required. Third, the Bayesian approach allows for flexibility in assigning hyper priors to the parameters in the measurement models and the conditioning model when these are unknown or unreliably estimated. In the maximum likelihood approach, numerical integration again becomes much more difficult as the number of (nuisance) parameters increases.
3. The Submodels of the MESE Model
Richardson et al. (2002) note once a structural model, such as the MESE model, is built, researchers must choose functional forms for the distributions of the submodels. I turn now to each submodel to describe the appropriate functional forms when the variables measured with error are latent psychometric variables.
3.1. The Measurement Model
The latent variable(s) θ are often obtained from a well-designed cognitive or non-cognitive assessment(s) constructed, developed and scored using item response theory (IRT) models. Thus, it makes sense to use the IRT model as the functional form of (7) in the MESE model. The IRT model is efficient and provides a direct model of θ and its measurement error.1
Latent variables, θ are commonly measured by a set of binary or ordinal items (or sometimes combinations of both) denoted Xij, which is the ith individual’s response to item j. IRT models assume the probability of answering a test or survey item correctly increases as the latent trait underlying the performance on a test or survey increases (van der Linden and Hambleton, 1997).
A novel feature of the MESE model is its flexibility in using different IRT measurement models for different latent constructs. IRT models take on different forms according to the items developed for the test. A common IRT model used for binary items scored right/wrong is the three-parameter logistic (3PL) model,
| (9) |
Samejima’s (1969) graded response model (GRM) is a generalization of (9) used for Likert-scale survey responses and other ordinal items. It is a type of ordered logit model,
| (10) |
In each of these models, xij is the response of individual i to item j, aj is the “discrimination” item parameter, bj is the “difficulty” item parameter and cj is the “guessing” item parameter and is the probability of individual i with proficiency θ scoring k or above on item j.
IRT models provide a direct estimate of the measurement error for θ̂, which is equivalent to the standard error of θ̂. Asymptotically,
| (11) |
where Ij(θi) is the Fisher information.
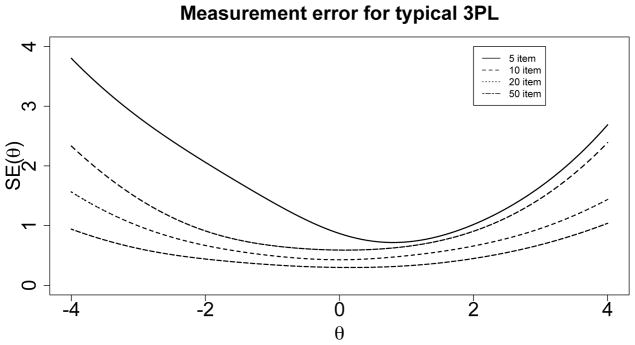
A few points about the measurement error are noteworthy. First, as Figure 1 shows, SE(θ) varies for different values of θ. In general, SE(θ) is largest for those individuals in the tails of the distribution of θ and smallest for those in the middle of the distribution. Second, increases in J, the number of test items, increase precision in the estimation of θi. Thus, the measurement error tends toward 0 as J → →. Large J is often not possible due to time constraints, so θ̂i can be expected to be imprecise, particularly for short tests. Third, because θ is unknown for every individual, so too is the standard error of the estimation. While the information function can be estimated using θ̂, Lockwood and McCaffrey (2014) show using SE(θ̂) to correct for measurement error leads to bias.
Fig 1.
Measurement error for a typical 3-PL model by θ where a ~ Unif(0, 2), b ~ N(0, 1) and c = 0 for all items.
Mis-specification of the IRT model in the MESE model is relatively robust. A simulation study conducted in Schofield (2008) suggests unreliable and/or imprecise item parameters has little effect on the estimates of the regression coefficients in (6). When item parameters are unknown or unreliable, estimation of the MESE model using the Bayesian framework is flexible such that priors can be assigned to the item parameters and these can be estimated simultaneously with θ and the regression coefficients. (See Patz and Junker, 1999 for more on MCMC methods for estimating the item parameters and θ)
3.2. The Conditioning Model
The conditioning model (8) often assumes θ to be multivariate normally distributed and allows for possible differences in the distribution of θ across subgroups of the sample. A novel feature of the MESE model is its flexibility in modeling the latent constructs as associated with one another conditional on the other covariates in the model.
Mis-specification to the shape of the conditioning model is also relatively robust. Schofield (2008) found little bias in the estimates of the regression coefficients of the structural equations in cases where the conditioning model was misspecified, even when the generating distribution of θ was skewed and the conditioning model was assumed normally distributed. Dresher (2006) found poor estimates to the mean and standard deviation of the distribution of θ when she assumed a normal conditional distribution on a θ whose distribution was skewed. Despite these same poor estimates of the θ distribution appearing in Schofield’s (2008) simulation, the estimates of the regression coefficients were not biased.
The choice of which variables to include in the conditioning model (8) is an interesting research question. Many large scale assessments (such as the National Assessment of Educational Progress, NAEP or the Program for International Student Assessment, PISA) follow Mislevy (1991) and condition on a huge set of background covariates to avoid bias in population statistics estimated from the test. Newer research by Schofield et al. (2014) shows that when θ is the independent variable in an analysis, θ must be conditioned on all of the covariates in the structural equation. However, if the response variable Y or any other variable associated with Y conditional on θ that is not already in the structural equation is in the conditioning set, bias will ensue (See Schofield, et al, 2014 for a proof, though the Law of Total Probability as in (5) suggests this result). Thus, the conditioning model in MESE is designed to include only the covariates in the structural equations. Mis-specification of which covariates are in the conditioning model will cause bias (Schofield, et al., 2014), though the size and direction of the bias varies based on the measurement error and the correlation between the covariates and θ.
3.3. The Structural Model
The structural equation, (6) is the equation of primary interest. The estimates of the latent constructs θ are noisy, but they are treated as a random variable in a mixed-effects regression. The functional form of the structural model is dependent on the substantive question of interest and the response variable, Y. The MESE model provides enough flexibility such that the structural model can accommodate several models; among them, any generalized linear model. In the example in Section 4, I use a logistic model.
4. Undergraduate STEM Retention in the United States
Over the past twenty years, there has been a rising concern about the under-representation, and specifically the retention of minorities and women in science, technology, engineering, and mathematics (STEM) disciplines in higher education. The National Center for Education Statistics (NCES, 2009) reports in 2008 only 31.7% and 33.1% of black and Hispanic students persist2 respectively compared to 43.9% of whites. Griffith (2010) studied students who were in their first year of college in 1999 and found only 37% of women versus 43% of men persist to graduate with a STEM major. Several studies (e.g., Riegle-Crumb et al, 2012; Xie and Shauman, 2003; Seymour and Hewitt, 1997) have examined the underlying reasons for the differentials in STEM persistence, by examining persistence after controlling for (latent) variables, such as academic achievement (e.g., Maltese and Tai, 2011), math and science identity (Chang, et al., 2011), interest (Sullins, Hernandez and Fuller, 1995), future time perspective (Husman, et al, 2007), sense of community (Espinosa, 2011), goals (Leslie, McClure and Oaxaca, 1998) or personality traits (Korpershoek, Kuyper and van der Werf, 2012).
Most scholars agree there is a strong positive correlation between math proficiency and STEM retention. While racial differences in STEM retention are often explained by the comparative disadvantage in academic background that under-represented minorities (URMs) have relative to their white peers, several recent studies (Weinberger, 2012; Riegle-Crumb et al, 2012) question the explanation that gender gaps in STEM retention are due to gaps in math achievement. Others (e.g., Korpershoek, Kuyper and van der Werf, 2012) suggest STEM retention gender gaps may be better explained by personality trait differences.
Many of the studies noted above use batteries and surveys with small numbers of items to measure their latent traits (e.g., Chang, et al., (2011) develop a five-item factor to assess students science identity and Leslie, McClure and Oaxaca (1998) use a one item measure of “goal commitments”). Because the number of items is small, I expect the measurement error of these latent traits to be large suggesting the estimates of the latent variables’ effects and the effects of any other covariates correlated with them will be biased when the model does not account for measurement error.
In the remainder of this section, I estimate a typical logistic regression model for “explaining” racial and gender differentials. The central idea is to control for the latent traits in a model that includes 0/1 indicator variables for the racial or gender focal group. If after controlling for these latent traits, the regression coefficients in front of the indicator variables are smaller, then social scientists argue the latent trait may “explain away” some of the racial or gender differential. The model takes the form,
| (12) |
where Yi is a binary measure of STEM persistence, θi = (θ1i, θ2i, . . . , θki) is a vector of k latent variables measuring cognitive and non-cognitive traits, and Zi is a vector of demographic variables including indicator variables for underrepresented minorities (URMs) and female gender. I estimate this model under two different measurement error models for θ. In the first case, θ is replaced by θ̂, the test score published by the survey institution and no measurement error is modeled. In the second model, the regression coefficient estimates are modeled simultaneously with θ, using the MESE approach for which I advocated in Section 2.
4.1. The Data
The data come from the 1997 National Longitudinal Survey of Youth (NLSY97) which is a nationally representative sample of almost 8900 youths who were 12 to 16 years old as of December 31, 1996. The youth have been surveyed yearly since 1997. The survey collects detailed information on many topics including: youth demographics, educational experiences, personality measures, and cognitive assessments.
The NLSY97 data set offers several benefits. First, the NLSY97 is longitudinal and paints a detailed account of the timing, progression, and types of degrees of those surveyed. Second, the NLSY97 is a nationally-representative survey making generalizations possible to the same cohort of students nationwide. Third, the NLSY97 contains item level data to certain academic tests that measure mathematics proficiency and personality measure surveys. Unfortunately, the NLSY97 does not contain certain variables which have been shown to have an effect on STEM retention (such as motivation or future-time perspective). I cannot examine these variables in this study, but I can extrapolate what kinds of bias may exist in other studies.
The variable of interest, Yi is a categorical variable which identifies each individual as: a “stayer,” someone who persisted in a STEM3 major; or a “leaver,” someone who declared a STEM major but did not persist to graduation. Race is operationalized as a 0/1 indicator variable for under-represented minority (URM). URMs include those who self-identify as black, Hispanic, Native American, or of mixed race. Non-URMs self-identify as either white or Asian.4 Gender is similarly operationalized as a 0/1 variable indicating Female gender.
There are a total of six latent variables: one a measure of cognitive proficiency in mathematics and the other five are measures of the Big Five (Costa and McCrae, 1992) personality characteristics of Extraversion, Agreeableness, Conscientiousness, Emotional Stability, and Openness. Measures of mathematics proficiency and personality traits both have been shown to predict STEM retention.
The mathematical proficiency measure is the mathematics Peabody Individual Achievement Test (PIAT; Markwardt, 1998). The observed item responses, Xij for the PIAT are binary (correct/incorrect) responses to the 100 multiple choice items written to test mathematics concepts and facts for individuals between the ages of 6–18 years. The PIAT-R Math Assessment was selected by the NLSY97 to represent a cross-section of various curricula in use across the United States. In addition, previous studies show the PIAT math test’s concurrent validity correlates reasonably with other tests of intelligence and math achievement (Davenport, 1976; Wikoff, 1978).
The non-cognitive trait measures are the Ten Item Personality Inventory (TIPI, Gosling, Rentfrow and Swann, 2003). The TIPI inventory contains two items for each of the five personality traits for a total of a 10-item survey. The observed item responses Xij for the TIPI are an ordinal scale of 7 Likert-type responses. The sub-scale scores are an average of the two items that pertain to each of the Five Factors. Research (e.g., Felder, Felder, and Dietz, 2002; Major, Holland and Oborn, 2012; Korpeshoek et al., 2012; Van Langen, 2005) notes personality traits such as the Big Five may have an effect on gender differences in STEM retention. For the purposes of showing the measurement error bias, the TIPI (in which J = 2 for each of the five latent personality traits) serves as a good example.
Attention is restricted to only those youth who completed either a two or four year college degree by 2010, declared a STEM major at some point in their college career and for whom there are both PIAT and TIPI measures. Table 1 provides some demographic statistics of the NLSY97 sample. Approximately two-fifths of those who initially declare a STEM major leave. Men and nonURMs are more likely to be “stayers” than women and URMs respectively. PIAT math scores are lowest on average for URMs. Similar to findings in Riegle-Crumb et al. (2012), there is little difference in the distribution of PIAT math scores by gender. Little variation exists in any of the TIPI sub-scale scores by URM status. Like Schmitt, et al., (2008), females tend to have higher agreeableness scores and lower emotional stability scores. The high relation between PIAT scores and URM status and between TIPI scores and gender suggest there will be bias in estimates of the racial and gender gaps when using fixed estimates of the PIAT and TIPI scores as predictors.
Table 1.
Sample Characteristics, 1997 National Longitudinal Survey (NLSY97)
| Female | Male | URM | NonURM | Total | |
|---|---|---|---|---|---|
|
| |||||
| N | 163 | 265 | 133 | 295 | 428 |
| Proportion Stayers | 0.49 | 0.67 | 0.50 | 0.65 | 0.60 |
| Mean PIAT Score | 102.6 (16.6) | 104.1 (16.3) | 97.2 (16.7) | 106.4 (15.4) | 103.5 (16.4) |
| Mean TIPI-Extraversion Score | 4.64 (1.49) | 4.46 (1.42) | 4.48 (1.39) | 4.55 (1.47) | 4.53 (1.45) |
| Mean TIPI-Agreeableness Score | 5.23 (1.09) | 4.75 (1.10) | 4.85 (1.08) | 4.96 (1.14) | 4.93 (1.12) |
| Mean TIPI-Conscientiousness Score | 5.94 (0.95) | 5.68 (0.99) | 5.78 (0.96) | 5.78 (0.99) | 5.78 (0.98) |
| Mean TIPI-Emotional Stability Score | 5.04 (1.22) | 5.50 (1.10) | 5.21 (1.17) | 5.38 (1.16) | 5.33 (1.17) |
| Mean TIPI-Openness Score | 5.67 (0.91) | 5.44 (1.07) | 5.62 (1.00) | 5.48 (1.03) | 5.52 (1.02) |
Notes: Author’s calculations, 1997 National Longitudinal Survey of Youth. Sample of only those youth who have completed a two or four-year college degree and declared a STEM major at some point in their college career.
4.2. Methods
To examine the extent of the measurement error in examining STEM retention, I compare three “unadjusted” models that do not adjust for measurement error with three “adjusted” models in which the measurement error is modeled. I control for math proficiency (the PIAT) alone, personality traits (the TIPI) alone, and the two together (in which I allow them to correlate) to understand the effect of each latent trait individually and together. Below, I describe the full model in which I control for both math proficiency and personality traits. The simpler models should be altered accordingly.
I specify the unadjusted model as (12) where Yi = 1 for “stayers” and Yi = 0 for the “leavers.” The covariates include Zi which is a vector that contains two 0/1 indicator variables: one which indicates Female status and one which indicates URM status and θi = (θMi, θEi, θAi, θCi, θESi, θOi) which is a vector of six latent traits where θMi is the latent math proficiency, θEi is the latent extraversion personality trait, θAi is the latent agreeableness personality trait, θCi is the latent conscientiousness personality trait, θESi is the latent emotional stability personality trait, θOi is the latent openness personality trait.
To estimate the “adjusted” models in which I account for measurement error, I specify the MESE model as,
| (13) |
| (14) |
| (15) |
| (16) |
where θ represents the vector of l ∈ {1, . . . , 6} true PIAT and TIPI subscores of individual i, μ is a vector of the means of the six latent traits and Σ is a 6x6 variance-covariance matrix of the six latent traits. The measurement model for the PIAT scores is the 3-PL model, (9).5 The measurement model for the five TIPI scores is the GRM, (10).
It is necessary to estimate item parameters in the IRT models for each of the latent variables, because test publishers have not disclosed them. I estimate the item parameters for the full NLSY97 sample and then fix them at their estimates following standard practice (Ayers and Junker, 2008). In practice, this is how PIAT and TIPI prediction would occur: problems are fixed for the entire sample of test takers, but proficiencies and latent traits may change from year to year.
Both models (adjusted and unadjusted) are estimated using an MCMC algorithm specified in WinBUGS (Spiegelhalter, Thomas and Best, 2000) software.6 Bayesian estimates for the unadjusted models are extremely similar to frequentist ML estimates. For both the unadjusted and adjusted models, N(0, 10) priors were assigned to each β coefficient. In the adjusted models, the prior on the latent variables is assumed to be multivariate normal and conditioned on race and gender (following Schofield, et al, 2014). The hyperprior for Σ is a Wishart (Ik, k) distribution and μk has a flat N(0, 1) prior. The MCMC procedure was run with 3 chains with 10000 iterations each with the first half of the simulations used for burn-in and a thinning interval of 15. Model fit is compared using the DIC fit statistic (Spiegelhalter et al., 2002). Following Gelman and Hill (2007) convergence was assessed using the general rules that R̂ < 1.1 (the potential scale reduction factor) for each parameter and the effective number of simulations neff > 100.
4.3. Results
In Table 2, I report the mean and standard deviation of the MCMC chains for the parameters in the structural model for seven analyses: a baseline model including only indicator variables for the demographic groups (model a); “unadjusted” and “adjusted” models controlling for the PIAT alone (models b–c); the TIPI alone (models d–e); and the PIAT and the TIPI together (models f–g). Estimates in Table 2 demonstrate the bias in assessing the effect of math proficiency and personality traits on STEM retention when not accounting for measurement error. It is notable the bias is much larger in models that adjust for the measurement error of the TIPI scores which contain only two items per scale, versus the PIAT scores.
Table 2.
Logistic Regression of Persistence in STEM (NLSY97)
| (a) | (b) | (c) | (d) | (e) | (f) | (g) | |
|---|---|---|---|---|---|---|---|
|
| |||||||
| Baseline | PIAT | TIPI | TIPI & PIAT | ||||
|
| |||||||
| adjusted for ME? | N | Y | N | Y | N | Y | |
| URM | −0.584* (0.223) |
−0.427* (0.217) |
−0.375 (0.235) |
−0.641* (0.222) |
−0.894* (0.474) |
−0.472 (0.237) |
−0.690 (0.411) |
| Female | −0.704* (0.203) |
−0.717* (0.210) |
−0.728* (0.212) |
−0.594* (0.226) |
−0.128 (0.616) |
−0.612* (0.223) |
−0.270 (0.526) |
| PIAT | 0.330* (0.109) |
0.324* (0.121) |
0.341* (0.113) |
0.400* (0.200) |
|||
| TIPI Extraversion | −0.284* (0.111) |
−0.625 (0.652) |
−0.280* (0.115) |
−0.661 (0.546) |
|||
| TIPI Agreeableness | −0.227 (0.117) |
−0.943 (0.745) |
−0.242* (0.115) |
−0.957* (0.489) |
|||
| TIPI Conscientiousness | 0.082 (0.107) |
0.432 (0.327) |
0.081 (0.106) |
0.444 (0.312) |
|||
| TIPI Emo. Stability | 0.036 (0.114) |
0.397 (0.460) |
0.017 (0.116) |
0.215 (0.388) |
|||
| TIPI Openness | −0.083 (0.113) |
−0.177 (0.948) |
−0.083 (0.116) |
0.354 (0.857) |
|||
|
| |||||||
| N | 428 | 428 | 428 | 428 | 428 | 428 | 428 |
| DIC | 560 | 552 | 554** | 555 | 505** | 547 | 507** |
| Error Rate*** | 36.9% | 35.7% | 36.4% | 32.7% | 23.1% | 32.7% | 22.7% |
Notes: Estimates reported are the mean and standard deviation of the MCMC chains of the parameters in the structural model for a sample of those youth who have completed a two or four-year college degree and who declared a STEM major at some point. All estimates of latent variables have been standardized such that the regression coefficients represent a 1 standard deviation change in the latent trait for comparison purposes.
Statistical significance at the 5% alpha level.
This represents the contribution to DIC (deviance information criteria) that the logistic regression makes. WinBUGS separately reports the contribution to DIC for each separate node or array (Spiegelhalter, et al., 2002). This enables the individual contributions from different parts of the model to be assessed. Because the MESE model is so much more complex than a model that does not model error at all, we want to compare the fit of the structural model in the MESE model with that of the structural model with no error distribution of θ. The total DIC (including the estimation of the latent variables) is 12620, 13734 and 25817.
The error rate is the misclassification rate of the model which equals the sum of the false positive and the false negatives in the model divided by the total number of individuals in the dataset.
As in other work on STEM retention, I find a strong positive correlation between math proficiency and persistence in a STEM discipline, which may be slightly underestimated in the previous literature. A one standard deviation increase in PIAT scores results in a log odds increase of only 0.341 before adjusting for measurement error (model f) and an increase of 0.400 (model g) after adjusting.
The findings also reveal a strong effect of personality. When the measurement error in the TIPI score is not modeled, the effect of personality is highly attenuated. The estimate of the effect of agreeableness in the models that account for measurement error is four times that of the estimates when there is no adjustment for measurement error. The results in model (g) suggest individuals who are less agreeable (i.e., more critical) have a higher probability of persisting in STEM. Korpershoek, Kuyper, and van der Werf (2012) find similar results in examining school subject choices for high school students in the Netherlands.
Note, the standard errors of the estimates of the effect of the personality traits are quite large when the measurement error is modeled. The MESE model will tend to have larger standard errors of the structural model parameters than when the measurement error is not modeled. When the information on θ is small (i.e., the number of items is low as in the TIPI where J = 2), the estimates of θi will be highly variable and less identifiable, resulting in high variation in the estimates of their effect on outcomes. This is easily seen in the substantial increase in the standard errors of the estimates of the parameters in models (e) and (g) in which the measurement error of the TIPI scores is modeled versus models (d) and (f) where the measurement error is not considered.
The estimates of the racial gap are quite different across the seven models. With no control for either math proficiency or personality traits (model a), the log odds of a URM persisting in STEM is 0.584. After controlling for math proficiency without adjusting for measurement error (model b), URMs remain less likely to persist in STEM, but the log odds decreases to 0.427. When adjusting for measurement error in math proficiency (model c), the estimate on the race coefficient becomes insignificant, suggesting comparably-skilled URMs and whites are equally likely to persist in STEM. The racial gap increases when controlling for personality traits and adjusting for the measurement error; however, the standard error of the race coefficient also increases.
The gender gap is more influenced by personality traits than math proficiency. The estimates of the gender gap in STEM retention are similar for the models that do and do not control for math proficiency (similar to results found in Riegle-Crumb et al., 2012). Models (d) and (f), the unadjusted models that include controls for personality traits suggest personality traits may account slightly for differences between men and women. After adjusting for measurement error, models (e) and (g) suggest comparably-skilled and comparably-traited men and women are equally likely to remain in STEM; gender becomes non-significant and the estimate drops dramatically. Supplementary analyses (not shown here) were performed in which each personality sub-score was entered into the model separate from the other personality sub-scores. These analyses suggest the effect of the agreeableness sub-score may have the largest effect on the STEM gender differential.
The results suggest the effect of prior academic achievement has been previously under- estimated in the literature and that it seemingly accounts for close to half the gap in STEM retention among URMs and whites. More striking are the results of the personality measures. Personality measures essentially remove the gender gap in STEM retention and account for over half of the gap (although they do not explain any of the racial STEM gaps.) Moreover, the effect of personality is highly attenuated if the measurement error is not modeled.
5. Conclusion
This paper proposes the Mixed Effects Structural Equations model to appropriately account for measurement error in latent variables when they are used as predictors in regression analyses. The MESE model follows Richard and Gilks’s (1993) Bayesian framework to simultaneously estimates the latent variable and the parameters of interest. The MESE model extends other similar SEM models by modeling several latent traits as correlated conditional on the other covariates and modeling each latent trait with a different IRT measurement model. The IRT model provides a direct model of the heteroskedastic measurement error inherent in psychometric latent variables.
When latent variables are used to examine future outcomes such as college major choice, measurement error will persist. The standard practice in the social sciences of using a point estimate of the latent variable leads to very different results than those models which account for the measurement error. This is particularly true for studies that use batteries and tests which have small numbers of items, such as the TIPI.
The motivating example demonstrates there is both a practically and statistically significant bias when latent variables measured with error are used as predictors in STEM retention analyses and the error is not modeled. I find prior mathematics proficiency and personality have been previously underestimated in the STEM retention literature. In addition and perhaps more importantly, I find the racial and gender gaps change substantially when the measurement error of the latent variables is modeled. When math proficiency is modeled with error, I find an insignificant estimate on the race coefficient, suggesting comparably-skilled URMs and whites are equally likely to persist in STEM. When personality skills are modeled with error, I find comparably-skilled and comparably-traited men and women are equally likely to remain in STEM.
The results presented here suggest interventions aimed at improving persistence of URMs and females in STEM ought to consider the role of prior math proficiency and personality traits – in particular the trait of agreeableness. Individuals who design such interventions must be mindful of the impact person-environment fit can have on individual performance. There is a vast literature on the relationship between personality and vocational interests (e.g., Walsh, 2001, Holland, 1987), which may have significant application to the design of interventions aimed at reducing the gender differentials in STEM retention.
This work does not directly examine the clearly critical role of STEM interest, motivation, or instructional practices, but does suggest when these variables are measured, they are likely measured with error. Future work must examine the extent of the bias in using these variables as predictors of STEM retention. Models such as the MESE model offer opportunities for researchers and practitioners to better understand the complicated influence academic achievement and personality traits have on STEM retention.
Several other areas of educational research use latent variables as predictors. The MESE model is applicable to these areas of educational research as well. The results presented here suggest similar biases will exist in any of these literatures where latent variables are used as predictors but their error is not modeled.
Footnotes
This work was partially supported by Award Number R21HD069778 from the Eunice Kennedy Shriver National Institute of Child Health and Human Development. The content is solely the responsibility of the authors and does not necessarily represent the official views of the Eunice Kennedy Shriver National Institute of Child Health and Human Development or the National Institutes of Health.
Junker, Schofield, and Taylor (2012) note IRT models are flexible enough to use as a direct model for measurement error even in cases in which the test or survey was not constructed using IRT techniques.
Here I define persistence to mean the student declared and then completed a STEM major.
STEM is defined to include biological sciences, computer/information science, engineering, mathematics, and physical sciences.
There is evidence to argue against placing all underrepresented minority students into a single category (Palmer et al., 2011). Analyses were also conducted separating blacks and Hispanics and similar results were found, except with much lower power, so only the results with the URMs grouped together are reported.
Junker, Schofield, and Taylor (2012) note even though the PIAT is not constructed using the 3-PL model, the 3-PL is a suitable IRT model that provides a good direct model for measurement error.
R and WinBUGS code is available from the author.
References
- Ayers E, Junker B. IRT modeling of tutor performance to predict end-of-year exam scores. Educational and Psychological Measurement. 2008;68:972–987. [Google Scholar]
- Bollen KA. Structural equations with latent variables. New York: Wiley; 1989. [Google Scholar]
- Borsboom D, Mellenbergh GJ, Van Heerden J. The theoretical status of latent variables. Psychological Review. 2003;110:203–219. doi: 10.1037/0033-295X.110.2.203. [DOI] [PubMed] [Google Scholar]
- Chang MJ, Eagan MK, Lin MH, Hurtado S. Considering the impact of racial stigmas and science identity: Persistence among biomedical and behavioral science aspirants. Journal of Higher Education. 2011;82(5):564–596. doi: 10.1353/jhe.2011.0030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costa PT, Jr, McCrae RR. Revised NEO personality inventory (NEO-PI-R) and NEO five-factor inventory (NEO-FFI) manual. Odessa, FL: Psychological Assessment Resources; 1992. [Google Scholar]
- Cronbach LJ, Nageswari R, Gleser GC. Theory of generalizability: A liberation of reliability theory. The British Journal of Statistical Psychology. 1963;16:137–163. [Google Scholar]
- Davenport BM. A comparison of the Peabody Individual Achievement Test, the Metropolitan Achievement Test, and the Otis-Lennon Mental Ability Test. Psychology in the Schools. 1976;13:291–297. [Google Scholar]
- Dominici F, Zeger SL. A measurement error model for time-series studies of air pollution and mortality. Biostatistics. 2000;1(2):157–175. doi: 10.1093/biostatistics/1.2.157. [DOI] [PubMed] [Google Scholar]
- Dresher A. Results from NAEP marginal estimation research. Paper presented at the Annual Meeting of the National Council on Measurement in Education; San Francisco, CA. 2006. [Google Scholar]
- Dunson DB. Commentary: Practical Advantages of Bayesian Analysis of Epidemiologic Data. American Journal of Epidemiology. 2001;153(12):1222–1226. doi: 10.1093/aje/153.12.1222. [DOI] [PubMed] [Google Scholar]
- Espinosa LL. Pipelines and pathways: Women of color in undergraduate STEM majors and the college experiences that contribute to persistence. Harvard Educational Review. 2011;81(2):209–240. [Google Scholar]
- Felder RM, Felder GN, Dietz EJ. The Effects of Personality Type on Engineering Student Performance and Attitudes. Journal of Engineering Education. 2002;91(1):3–17. [Google Scholar]
- Fox JP, Glas CAW. Bayesian estimation of a multilevel IRT model using Gibbs sampling. Psychometrika. 2001;66:269–286. [Google Scholar]
- Fuller WA. Measurement error models. New York: Wiley; 2006. [Google Scholar]
- Gelman A, Hill J. Data analysis using regression and multilevel/hierarchical models. New York: Cambridge University Press; 2007. [Google Scholar]
- Griffith A. Persistence of women and minorities in STEM field majors: Is it the school that matters? Economics of Education Review. 2010;29(6):911922. [Google Scholar]
- Gosling SD, Rentfrow PJ, Swann WB., Jr A very brief measure of the big five personality domains. Journal of Research in Personality. 2003;37:504–528. [Google Scholar]
- Haining R, Li G, Maheswaran R, Blangiardo M, Law J, Best N, Richardson S. Inference from ecological models: estimating the relative risk of stroke from air pollution exposure using small area data. Spatial and Spatio-temporal Epidemiology. 2010;1(2–3):123–131. doi: 10.1016/j.sste.2010.03.006. [DOI] [PubMed] [Google Scholar]
- Heckman JJ, Stixrud J, Urzua S. The effects of cognitive and noncognitive abilities on labor market outcomes and social behavior. Journal of Labor Economics. 2006;24:411–482. [Google Scholar]
- Holland JL. Making vocational choices: A theory of vocational personality and work environments. 3. Odessa: Psychological Assessment Resources; 1997. [Google Scholar]
- Husman J, Lynch C, Hilpert J, Duggan MA. Validating measures of future time perspective for engineering students: Steps toward improving engineering education. Proceedings of the American Society for Engineering Education Annual Conference & Exposition; Honolulu, HI. 2007. [Google Scholar]
- Joreskog KG, Goldberger AS. Estimation of a model with multiple indicators and multiple causes of a single latent variable. Journal of the American Statistical Association. 1975;70:631–639. [Google Scholar]
- Junker BW, Schofield LS, Taylor L. The use of cognitive ability measures as explanatory variables in regression analysis. IZA Journal of Labor Economics. 2012;1:4. doi: 10.1186/2193-8997-1-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klepper S, Leamer E. Consistent sets of estimates for regressions with errors in all variables. Econometrika. 1984;52:163–183. [Google Scholar]
- Korpershoek H, Kuyper H, van der Werf MPC. The role of personality in relation to gender differences in school subject choices in pre-university education. Sex Roles. 2012;67:630–645. [Google Scholar]
- Krishnakumar J, Nadar A. On exact statistical properties of multidimensional indices based on principal components, factor analysis, MIMIC and structural equation models. Social Indicators Research. 2008;86(3):481496. [Google Scholar]
- Leslie LL, McClure GT, Oaxaca RL. Women and minorities in science and engineering: A life sequence analysis. The Journal of Higher Education. 1998;69(3):239–276. [Google Scholar]
- Lockwood JR, McCaffrey DF. Correcting for test score measurement error in ANCOVA models for estimating treatment effects. Journal of Educational and Behavioral Statistics. 2014;39(1):22–52. [Google Scholar]
- Major DA, Holland JM, Oborn KL. The influence of proactive personality and coping on commitment to STEM majors. Career Development Quarterly. 2012;60:16–24. [Google Scholar]
- Maltese AV, Tai RH. Pipeline persistence: Examining the association of educational experiences with earned degrees in STEM among U.S. students. Science Education. 2011;95(5):877–907. [Google Scholar]
- Markwardt FC. Peabody Individual Achievement Test–revised manual. Minneapolis, MN: Pearson; 1998. [Google Scholar]
- Mislevy RJ. Randomization-based inference about latent variables from complex samples. Psychometrika. 1991;56:177–196. [Google Scholar]
- Muthén LK, Muthén BO. Mplus User’s Guide. 6. Los Angeles, CA: Muthén & Muthén; 1998–2011. [Google Scholar]
- National Center for Education Statistics (NCES) Students who study science, technology, engineering, and mathematics (STEM) in postsecondary education. NCES Stats in Brief. 2009 (NCES 2009-161) ( http://nces.ed.gov/pubs2009/2009161.pdf)
- Palmer RT, Davis RJ, Maramba D. Racial and Ethnic Minority Student Success in STEM Education: ASHE Higher Education Report. New York: Wiley; 2011. [Google Scholar]
- Patz R, Junker B. A straightforward approach to Markov chain Monte Carlo methods for item response models. Journal of Educational and Behavioral Statistics. 1999;24:146178. [Google Scholar]
- Plummer M. JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. Proceedings of the 3rd International Workshop on Distributed Statistical Computing.2003. [Google Scholar]
- Rabe-Hesketh S, Skrondal A, Pickles A. Maximum likelihood estimation of limited and discrete dependent variable models with nested random effects. Journal of Econometrics. 2005;128(2):301–323. [Google Scholar]
- Rabe-Hesketh S, Skrondal A, Pickels A. Generalized multilevel structural equations modeling. Psychometrika. 2004;69(2):167–190. [Google Scholar]
- Richardson S, Gilks WR. Conditional independence models for epidemiological studies with covariate measurement error. Statistics in Medicine. 1993;12:1703–1722. doi: 10.1002/sim.4780121806. [DOI] [PubMed] [Google Scholar]
- Richardson S, Leblond L, Jaussent I, Green PJ. Mixture models in measurement error problems, with reference to epidemiological studies. Journal of the Royal Statistical Society A. 2002;165(3):549–566. [Google Scholar]
- Riegle-Crumb C, King B, Grodsky E, Muller C. The more things change, the more they stay the same? Prior achievement fails to explain gender inequality in entry in STEM college majors over time. American Educational Research Journal. 2012;49(6):1048–1073. doi: 10.3102/0002831211435229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samejima F. Psychometric Monograph No. 17. Richmond, VA: Psychometric Society; 1969. Estimation of latent ability using a response pattern of graded scores. [Google Scholar]
- Schmitt DP, Realo A, Voracek M, Allik J. Why can’t a man be more like a woman? Sex differences in Big Five personality traits across 55 cultures. Journal of Personality and Social Psychology. 2008;94(1):168–182. doi: 10.1037/0022-3514.94.1.168. [DOI] [PubMed] [Google Scholar]
- Schofield LS. Measurement error in the AFQT in the NLSY79. Economics Letters. 2014;123(3):262–265. doi: 10.1016/j.econlet.2014.02.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schofield LS. Dissertation. Carnegie Mellon University; 2008. Modeling measurement error when using cognitive test scores in social science research. [Google Scholar]
- Schofield LS, Junker BW, Taylor LJ, Black DA. Predictive inference using latent variables with covariates. Psychometrika. 2014 doi: 10.1007/s11336-014-9415-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seymour E, Hewitt NM. Talking about leaving: Why undergraduates leave the sciences. Boulder, CO: Westview Press; 1997. [Google Scholar]
- Skrondal A, Rabe-Hesketh S. Generalized latent variable modeling: Multilevel, longitudinal and structural equation models. Boca Raton, FL: Chapman and Hall/CRC; 2004. [Google Scholar]
- Spiegelhalter DJ, Thomas A, Best NG. WinBUGS version 1.3 user manual. Cambridge, MA: Medical Research Council Biostatistics Unit; 2000. [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian measures of model complexity and fit (with discussion) Journal of the Royal Statistical Society, Series B. 2002;64:583–639. [Google Scholar]
- Staiger D, Stock JH. Instrumental variables regression with weak instruments. Econometrica. 1997;65:557–586. [Google Scholar]
- Stefanski LA. Measurement error models. Journal of the American Statistical Association. 2000;95(452):1353–1358. [Google Scholar]
- Sullins ES, Hernandez D, Fuller C. Predicting who will major in a science discipline: Expectancy-value theory as part of an ecological model for studying academic communities. Journal of Research in Science Teaching. 1995;32(1):99119. [Google Scholar]
- van der Linden WJ, Hambleton RK, editors. Handbook of modern item response theory. Springer-Verlag; New York: 1997. [Google Scholar]
- Van Langen A. Unequal participation in mathematics and science education. Nijmegen: ITS; 2005. [Google Scholar]
- Walsh WB. The changing nature of the science of vocational psychology. Journal of Vocational Behavior. 2001;59:262–274. [Google Scholar]
- Weinberger CJ. Is the science and engineering workforce drawn from the far upper tail of the math ability distribution? 2012 Unpublished manuscript. [Google Scholar]
- Wikoff RL. Correlational and factor analysis of the Peabody Individual Achievement Test and the WISC-R. Journal of Consulting and Clinical Psychology. 1978;46:322–325. doi: 10.1037//0022-006x.46.2.322. [DOI] [PubMed] [Google Scholar]
- Xie Y, Shauman KA. Women in science career processes and outcomes. Cambridge, MA: Harvard University Press; 2003. [Google Scholar]