Count ratio model reveals bias affecting NGS fold changes

Abstract

Various biases affect high-throughput sequencing read counts. Contrary to the general assumption, we show that bias does not always cancel out when fold changes are computed and that bias affects more than 20% of genes that are called differentially regulated in RNA-seq experiments with drastic effects on subsequent biological interpretation. Here, we propose a novel approach to estimate fold changes. Our method is based on a probabilistic model that directly incorporates count ratios instead of read counts. It provides a theoretical foundation for pseudo-counts and can be used to estimate fold change credible intervals as well as normalization factors that outperform currently used normalization methods. We show that fold change estimates are significantly improved by our method by comparing RNA-seq derived fold changes to qPCR data from the MAQC/SEQC project as a reference and analyzing random barcoded sequencing data. Our software implementation is freely available from the project website http://www.bio.ifi.lmu.de/software/lfc.

INTRODUCTION

Quantitative RNA measurement is an essential tool in biological research. The established method is next generation sequencing (NGS), where RNA is converted to cDNA, amplified and sequenced, leaving the researcher with hundreds of millions of 30–100 bases long reads. The most prominent application for quantitative NGS is mRNA-seq (1,2), where the abundance of mRNA is determined. Other examples are ribosomal profiling (3), DNAse-seq (4), RIP-seq (5), CLIP-seq (6–8), ChIP-seq (9,10) and PARS (11).

The basic principle of quantitative NGS is to count sequences belonging to the entities of interest and to take these counts as a measure of abundance of these entities in a biological sample. For example, in mRNA-seq, sequences of random mRNA fragments are determined (in fact, either the prefix in single-end sequencing or the prefix and the suffix in paired-end sequencing of each fragment is sequenced) and the number of all sequences or fragments matching an mRNA is used for quantification. Due to the amplification step during sample preparation, only the relative abundance within the sample can be determined. The often used RPKM or FPKM (1,12) measures for this correspond to the respective fraction of all mRNA in the sample but not the absolute abundance of the mRNA (i.e. the copy numbers per cell).

However, such single-sample or per-experiment measurements are hampered by known biases introduced during sample preparation, e.g. by polymerase chain reaction (PCR) amplification (13,14) or adapter ligation (15,16). As a consequence, some sequences from the same entity are observed orders of magnitude more often than others (1,17). Several computational ad-hoc attempts have been made to correct for such bias (18–20), but cannot remove it completely.

Differential quantification is deemed more reliable, since bias affects all samples equally and should therefore cancel out when samples are compared, e.g. by taking ratios. For several NGS based experiments, differential quantification is inherently necessary. For instance, in ribosomal profiling (3), the observed reads are not only dependent on the translation rate (which is the quantity of interest) but also on the corresponding mRNA expression level, i.e. in order to derive the translation rate, the ribosomal profiling read counts must be compared to corresponding mRNA-seq read counts (21). Analogously, in RIP-seq, the observations are dependent on the rate of bound RNA binding proteins and the total mRNA level (5). For other experiments, differential quantification is not inherently necessary for the experiment itself, but for the biological question. For instance, we have shown that by treating CLIP-seq read counts in a differential manner, context-dependent microRNA binding can be analyzed (22).

Our initial goal was to analyze differential quantification for entities with few reads. This is important for small exons in differentially spliced mRNAs in mRNA-seq or local translation rate changes in ribosomal profiling. It is also of special interest for CLIP-seq, where the sequenced target sites are as short as 30 nucleotides and as few as 5 reads are often deemed enough for a reliable site (6,23). The main problem here is to handle the inherent sampling noise of count data appropriately. For instance, if 4 and 2 reads are observed for a certain entity in two conditions, the actual fold change most certainly was not exactly 2, but rather within some interval around 2. Thus, a credible interval gives more information on the true fold change. Intuitively, we would assume a relatively large interval if only as few reads as 4 and 2 are observed, and a smaller interval for higher counts.

Importantly, the purpose of such credible intervals is different from P-values of available methods such as DEseq (24) or others (25): those methods test for each gene X the null hypothesis H₀ = the treatment does not affect expression of X. An hypothesis test for H₀ is only reasonable when many replicates are available that repeatedly measure expression of X with and without treatment. In contrast, the credible intervals here characterize the measurement uncertainty inherent for sampled count data and can be computed for any pair of experiments, i.e. also when no replicates are available.

We developed a probabilistic model to estimate credible intervals and show that the intuition more sequenced reads means more accurate fold changes is misleading when raw NGS read counts are used. Moreover, using this model we show that known bias does not cancel out when ratios are computed leading to inaccurate fold change estimates. Bias can be handled experimentally by labeling RNA fragments using random barcodes before PCR (14). Thus, additional experimental steps are necessary, that so far have only been applied in a few published studies (7,14). To handle such bias in available data sets, we introduce a novel method to estimate fold changes. We show that fold change estimates are significantly improved by our method using data from the MAQC project (26,27) and that about 20% of genes that are called differentially expressed are affected in a standard RNA-seq setting. Finally, we show that the method can also be applied to the estimation of normalization constants and show that it outperforms the widely used median based normalization.

MATERIALS AND METHODS

Data sets

We downloaded the SAM files of the sequencing data of (14) from GEO (accession numbers GSM849370 and GSM849371). For both replicates, SAM files corresponding to “digital” counts (respecting random barcodes) and “conventional” counts (disrespecting random barcodes) were provided and utilized to generate Figures 2 and 4, respectively. All genome aligned reads from those SAM files were mapped to Escherichia coli genes using Genbank annotations (accession U00096.2). For both digital and conventional counts, normalization constants were computed such that the median log fold change of genes with more than 50 counts in both replicates was 0. For all genes, the Maximum-A-Posteriori (MAP) estimate with no pseudocounts and its 99% symmetric credible interval (see below) were computed. As the true fold change of all genes should correspond to the normalization constant, genes where the normalization constant was outside of the computed credible interval were marked in Figures 2A and 4B. Furthermore, we computed all MAP estimates of local fold changes along all genes, their 99% credible intervals and the median of the posterior distribution. These statistics were plotted on to of the alignment start position to generate Figures 2D and 4D. To test local deviations from the gene fold change (Figures 2E and 4E), the Positive predictive distribution of our Bayesian model was used as follows: we computed the cumulative distribution function for local read counts of the first replicate using the Beta-Binomial distribution parameterized with the sum of the local read counts and the total counts from each replicate.

Figure 2.

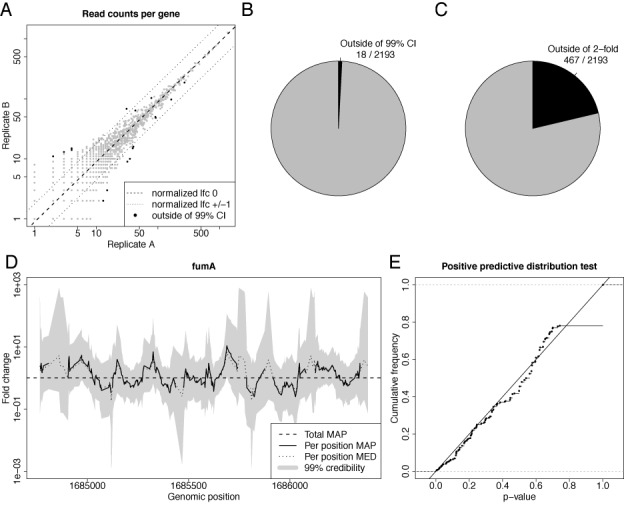
Credible intervals for random barcode RNA-seq data. (A) A scatter plot of the fragment counts from two replicate RNA-seq experiments for each gene is shown. The dashed line corresponds to a log₂ fold change (lfc) of 0, the dotted lines to a lfc of 1 and −1. Black dots correspond to genes where the normalization constant is outside of the 99% fold change credible interval. (B,C) The number of not credible genes and genes deviating more than 2-fold are illustrated; i.e. the number of black dots and dots outside of the dotted lines in Figure 2A, respectively. (D) The MAP fold changes of the local fragment coverage of fumA, their 99% credible intervals as well as the median of the posterior distribution (MED). The horizontal line corresponds to the estimated total fold change of fumA (total MAP). At several positions, the MAP is undefined due to zero coverage in one of the replicates. (E) The distribution of P-values computed by the posterior predictive function is shown for all positions in D. It is essentially a uniform distribution, i.e. the local fold changes indeed are distributed according to the beta binomial distribution, as predicted by our model.

Figure 4.

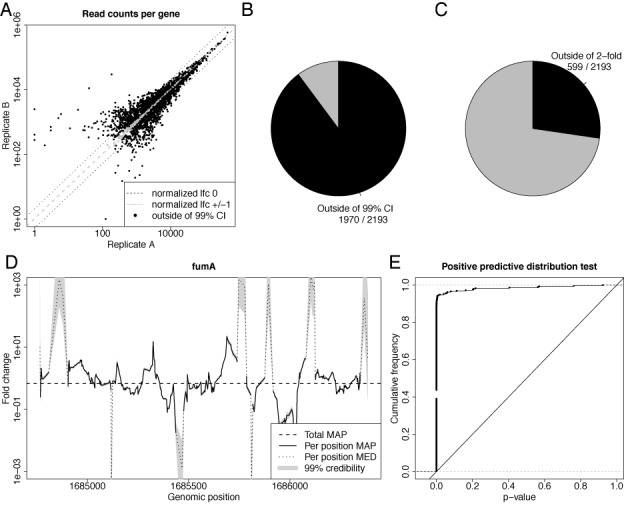
Credible intervals for RNA-seq data. The same plots are shown as in Figure 2, but with reads instead of fragments, i.e. the random barcodes have not been used to infer fragment counts. Thus, this figure and its differences to Figure 2 illustrate the expected results for an RNA-seq without random barcodes. Due to PCR amplification, read counts are artificially inflated, resulting in grossly underestimated sampling noise. See main text for a discussion.

For the validation, we downloaded TaqMan qPCR data from GEO (accession number GPL4097) and computed gene fold changes as described (26). Sequencing data for the same sample were downloaded from SRA (accession number SRA010153), aligned to the human genome (hg19) and transcriptome (Ensembl v70) using bowtie 1.0 (28).

Data from (29) were downloaded from yeastgenome.org and aligned to the yeast genome using STAR (30). Data from the SEQC project (31) have been downloaded from SRA and aligned to the human genome using STAR (30). We only used the data from the official sequencing site Beijing Genomics Institute (BGI), replicates a and b and pooled all lanes from flow cell AC0AYTACXX, as according to the SEQC publication, all data sets were of similar quality.

Hellinger distance and resampling

The squared Hellinger distance between two Beta distributions with parameters (α₁, β₁) and (α₂, β₂) is computed according to

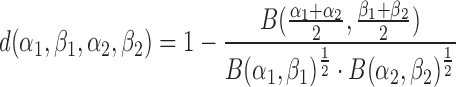(1)

where B is the Beta function. In order to estimate the influence of sampling alone, the following resampling procedure was applied: for gene g with observed count pair o_A, o_B, sample a new count c_A according to a Binomial distribution with parameters n = o_A + o_B and p = p(l) + n where l is the qPCR log fold change p as defined in equation 2 and n a normalization factor computed for this replicate. For the other condition, we set c_B = o_A + o_B − c_A.

Read count ratio model

The following considerations are based on mRNA-seq data, because it is the most widely used quantitative NGS technique and other models have been developed and described specifically for it. However, all results also apply to any quantitative NGS experiment where two conditions are compared.

Probabilistic models for mRNA-seq data draw reads per experiment across all possible genes (1,12,24,25). The basic per-experiment model is as follows: when we have N reads in our experiment and a gene g with relative frequency p_g, the number of reads mapping to g is distributed according to a binomial distribution with parameters N and p_g. Since N is large and p_g is small, the Poisson distribution is a good approximation. The single parameter of the Poisson distribution is its mean and can be estimated using replicate experiments. Then, significantly differentially expressed genes can easily be determined since for the Poisson distribution, mean and variance are equal. However overdispersion (greater variance than mean) is generally observed for per-experiment models (24,25). As a solution, population based estimates of more general distributions, e.g. negative binomial (24) or generalized Poisson (25) are fitted and used for estimating significance. There are a few other variations of this basic model, e.g. to incorporate multi-mapping reads, paired-end reads, to handle positional or sequence bias or to handle sequencing errors (18–20).

We take a fundamentally different approach: instead of drawing reads across entities in a single experiment, we draw the number of reads with the same sequence across two experiments. Then, we estimate a local fold change for the corresponding position within a gene between the experiments. The main advantage of this approach is that any sequence-specific factor that may bias the read count should affect both conditions equally, so it is important to handle such bias as early as possible in the probabilistic model. In contrast, the established method of computing a fold change for a transcript is to first sum all the read counts belonging to it and then to compute the ratio. The major disadvantage of local fold changes is the loss of accuracy: in most cases there are very few reads at a certain position and random sampling strongly affects the estimated fold changes. Thus, the main challenge in our approach is to give a reliable interval estimate for fold changes instead of a point estimate and to find a way to combine multiple local estimates to an overall per-transcript estimate.

Maximum likelihood estimators

Let c₁ and c₂ reads be observed for a certain sequence in two conditions. We call c₁ and c₂ local counts, the sum c₁ + c₂ the total local count and the ratio 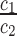local fold change. For fixed log₂ local fold change l and total count n = c₁ + c₂, the probability of getting a local count c₁ follows a binomial distribution with parameters n and p. Here,

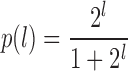(2)

is the probability of drawing a read from the first experiment when the true log₂ local fold change is l. The rationale behind the logistic function p(l) is as follows: if there is abundance a for an RNA fragment in one of the conditions and the true log₂ fold change is l, the abundance in the other sample is a · 2^l. If both samples are pooled and a read is drawn at random, the probability of getting a read from the second condition is 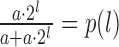. Importantly, the binomial distribution is fundamentally different from the above mentioned per-experiment model. Also, the magnitudes of the parameters involved here do not allow for a Poisson approximation.

The goal is to estimate l from data, which can be done by transforming an estimator for p by

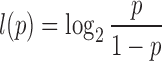(3)

Given the i.i.d. read counts c_{i, j}, with i = 1...N denoting the N positions in a gene and j = 1, 2 denoting the two experiments, the maximum likelihood estimators (ML) for p and l are

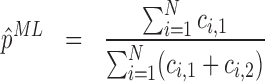(4)

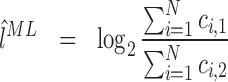(5)

Thus, the ML estimator is equal to the usually used per-transcript count ratio and, thus, disregarding normalization constants, to the RPKM or FPKM ratio (1,12). Furthermore, the ML estimator can be seen as a weighted average of the local counts c_{i, 1} and c_{i, 2}. Large local counts contribute more to the total fold change than small counts.

MAP estimators

However, this point estimator does not tell us anything about our degree of belief in the estimated log fold change. Therefore, we generalize this estimator using Bayesian inference: we assume a Beta distribution as prior for p. Due to its domain and its flexibility the Beta distribution is often used as a prior for probability parameters. Furthermore, it is a conjugate prior to the binomial distribution. Therefore, assuming the prior to be Beta(α,β) and i.i.d. read counts c_{i, j}, the posterior distribution also is a Beta distribution:

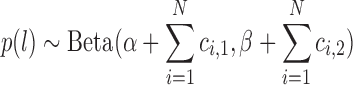(6)

The mode of a Beta(α,β) is at 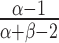and thus, the MAP estimators are

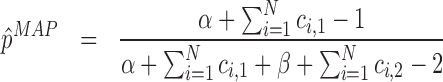(7)

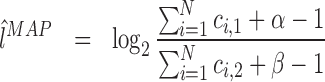(8)

Beta(1,1) is the [0,1]-uniform distribution, therefore for α = β = 1, the MAP estimator is equal to the ML estimator. At first glance, using the Beta distribution seems arbitrary. However, its two parameters α and β have an intuitive meaning: α − 1 and β − 1 are pseudocounts that are often used to avoid division by zero when taking the ratio of counts. Importantly, using no pseudocounts is equivalent to a uniform distribution of the proportion parameter p. However, it does not correspond to a uniform log fold change distribution.

Log fold change distribution

In order to derive the density function of the log fold change corresponding to the binomial proportion parameter, we use the method of substitution.

The density and probability function of the Beta distribution with parameters (α, β) are

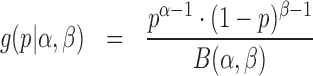(9)

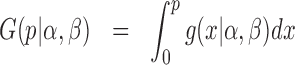(10)

where B is the beta function. By substitution, the probability function of a random variable transformed by equation 2 can be expressed as

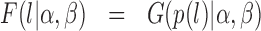(11)

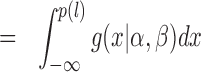(12)

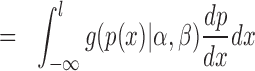(13)

Hence, the density function is

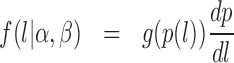(14)

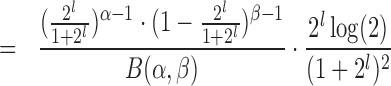(15)

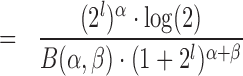(16)

Compute prior parameters

Given the knowledge of an expected log₂ fold change μ with a log₂ tolerance of t with certainty c, the parameters α and β can be computed by numerically via

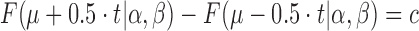(17)

under the constraint that α = 2^μ · β (e.g. by using the bisection method after exponential search for start values). The probability function F of the posterior log fold change distribution can be computed in an efficient and numerically stable way using Beta functions in log space.

RESULTS

Quantitative experiments can be affected by two sources of error, noise and bias. Noise is the random variation observed from repeated measurements and can be controlled using appropriate probabilistic models. In contrast, bias is the systematic deviation of measurements from the true quantity, i.e. in repeated experiments, measurements may not scatter around the true quantity (due to noise), but may deviate reproducibly from it. Removing bias often is much more difficult than handling noise, as the source, type and extent of bias must be known and predictable.

However, under certain conditions, correcting for bias is straight-forward: when the experimenter is interested in ratios of measurements and bias is linear, it cancels out. Linear means that the expected effect of bias can be represented by a fixed multiplicative factor. In many NGS experiments, these conditions appear to hold. First, many NGS experiments are inherently differential, i.e. the quantity of interest is already fold change (see above). And second, linearity can safely be assumed based on the following considerations, exemplary for bias introduced by PCR: during a single PCR cycle a fragment with sequence s is amplified by a certain probability p_s. The expected yield of n copies before this PCR cycle then is (1 + p_s) · n and (1 + p_s)^c · n after c cycles. Here, (1 + p_s)^c is the fixed multiplicative factor that determines a sequence specific linear bias. Thus, PCR may indeed meet the condition of linearity, and a similar argument can be made for the other processes involved in an NGS experiment. If all experimental steps produce linear bias, the total bias is also linear as the product of the biases of the individual steps result in another overall fixed multiplicative factor.

However, it is important to make the distinction what is measured and consequently affected by bias, and what are the entities the experimenter is interested in. In NGS, read counts are measured, i.e. the number of times a certain read sequence is observed. However, the experimenter is not interested in read counts but in the quantity of more coarse-grained objects, e.g. transcripts in RNA-seq or binding sites of transcription factors in ChIP-seq. Thus, distinct measurements (read counts) must be aggregated across these objects.

As a consequence, the fold change of the wanted entity may still be affected by bias. Assume that in one mRNA-seq experiment, only a single fragment i is isolated for a certain mRNA that is amplified poorly (i.e. p_i is small). Furthermore, assume that in another experiment, again a single fragment j is isolated for the same mRNA that is different from fragment i and amplified very efficiently (i.e. p_j is large). The total fold change estimate then is 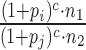. Even if the true mixing ratio is 1 (i.e. n₁ = n₂), the estimated fold change is heavily biased.

In summary, when neglecting bias, there are three building blocks in the differential analysis of NGS data: aggregation, controlling noise and computing ratios. We do not consider replicate experiments or normalization at this stage. Replicate experiments can be incorporated by pooling reads prior to this analysis and normalization can be performed afterward (see analysis and discussion below). Existing methods follow one specific path (see Figure 1). First, reads are aggregated, then the parameters of a probabilistic model are estimated to control noise and finally, fold changes are computed. This is true for the most basic method (1), where read counts are summed up for mRNAs, the mean of a Poisson distribution using measurements of replicate experiments is estimated and the ratio of two means from two conditions is computed. This is also true for more sophisticated methods such as DEseq (24) or others (12,25), where the simple Poisson model is replaced by more general distributions. When bias has to be accounted for, bias correction methods (18–20) have to be incorporated in this workflow prior to read aggregation. Hence, such methods do not exploit the linearity assumption for differential analysis of NGS data.

Figure 1.

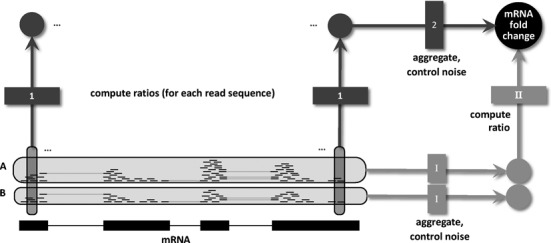
Workflows for differential NGS analysis. Differential analysis of NGS data starts with the aligned reads of two conditions, here exemplified as RNA-seq reads from samples A and B aligned to an mRNA. Existing models take one specific route through the necessary steps defined in the main text: (I) For each sample, reads are aggregated and an appropriate probabilistic model is used to control noise and estimate the sample specific mRNA abundance. (II) These abundance estimates are then divided to give an estimate of the mRNA fold change. Our approach takes a different route by first computing local ratios for all read sequences and then aggregating them using an appropriate noise model for count ratios to estimate the total mRNA fold change. Using a basic noise model for the second step makes both routes equivalent. However, using extensions to it leads to more accurate fold change estimates by exploiting the fact that bias cancels out when taking the ratio of counts of individual sequences. Note that two important aspects of NGS (replicate experiments and normalization) are left out in this figure and are analyzed and discussed below.

To make use of linearity, we assemble these building blocks in a different order in our approach. First we take ratios of read counts to let bias cancel out, and then aggregate ratios and estimate a model built upon aggregated ratios to handle noise (see Figure 1). The major advantage of this workflow is that bias is completely removed under the assumption of linearity. The major problem is that individual read counts and thus individual ratios are heavily affected by noise. Thus, the effectiveness of such an approach depends on the ability of the probabilistic model to handle this random variation.

Here, we develop such a model. First we introduce a basic version and show that its point estimate is equivalent to existing approaches, indicating that the operations aggregate and control noise and compute ratio can be commutative (see again Figure 1). We further show that this basic model introduces two new notions: prior knowledge can be utilized and credible interval estimates can be computed. Then, we test the basic model using a data set where bias can be detected and removed by a clever experimental setup. Finally, we show that the basic model severely underestimates noise in the presence of read count bias and propose and test a more conservative noise model.

Count ratio model

We define local read counts as the number of reads that have been aligned to a certain genomic position. Importantly, genomic position does not only refer to the start position of the alignment, but also includes all potential splice junctions and the alignment end (which is important when reads have different length due to trimming). A local count ratio is the ratio of two local read counts from two conditions or samples or aggregated numbers from sets of replicates or sets of samples/conditions.

Our model is based on the following considerations: given two lists of local read counts we want to determine the true mixing ratio that has led to these counts. If we assume that all n reads belonging to a pair of local read counts were pooled, the local read count from the first condition is binomially distributed with parameters n and p, where p is related to the true log fold change between the two conditions. The lists of local read counts represent repeated and independent measurements of this binomial distribution with the same parameter p. Thus, these lists of local read counts can be used to estimate p, and, by transformation, the true log fold change. In fact, the Maximum Likelihood Estimate (MLE) of this model is mathematically equivalent to the obvious and widely used log fold change, which is the total number of reads in condition 1 divided by the total number of reads in condition 2 (see Methods section for further details).

Furthermore, the Bayesian MAP estimate extends the MLE and introduces the parameters of its prior distribution as pseudocounts that are added to both total numbers of reads. Of note, pseudocounts are widely in use as well to avoid division by zero.

Thus, the basic statistics from the count ratio model are already widely in use. However, it brings three additional benefits for NGS data analysis. First, it introduces a theoretical justification for ad-hoc pseudocounts. Second, we can analytically compute the full posterior distribution or credible intervals for the true log fold change in addition to the above introduced point estimates. And third, our model indicates that the total number of reads can be decomposed into many local read counts, which allows to handle bias in a straight-forward way (see below).

Credible intervals

To test whether our model and its posterior distribution for the log fold change are indeed appropriate, we tested symmetric credible intervals derived by our model using a special RNA-seq data set that recently became available. Usually, it is not possible to distinguish whether high copy numbers of observed sequences are the product of PCR amplification or indeed correspond to multiple copies of the same RNA fragment in the sample before amplification. By using random barcodes in the sequencing adapters, it is possible to make this distinction. In (14) 32+26 million paired-end mRNA-seq reads of two replicates for E. coli were generated that correspond to less than 85.000+58.000 original fragments. Thus, fragment counts should well fit the basic experimental model introduced above. Figure 2A shows a scatterplot of fragment counts for each gene in the two replicates. All genes should lie on a diagonal with slope 1 and an offset corresponding to the difference in sequencing depth of the two libraries and all deviations should be due to sampling noise according to our model. Indeed, only for 18 of 2193 genes, the diagonal is outside of their 99% credible interval. Without our model, we could only check how many genes are deviating more than 2-fold from this line (in this case 467 out of 2193), which could lead to wrong conclusions about the variability of the replicates.

Moreover, we can graphically check the consistency of local fold changes across an mRNA by plotting local credible intervals (i.e. by computing the credible interval not for the whole mRNA but for each individual read count pair; illustrated for fumA in Figure 2D). The estimated mRNA log fold change should be within the bounds of the credible intervals along the whole mRNA (as for fumA; see Figure 2D). If not, deviations cannot be explained by sampling noise introduced by sequencing, but must be due to technical (see below) or biological reasons, e.g. differential splicing.

This can also be tested formally by computing P-values of local fold changes using the Bayesian posterior predictive distribution that computes the probability of observing the measured read count pairs while respecting the uncertainty of the estimated mRNA log fold change (see Figure 2E for the P-value distribution for fumA). Without technical or biological influences, the distributions of these P-values for a single mRNA should resemble a uniform distribution, which can be tested using any hypothesis test for uniformity.

Prior knowledge

Often, prior knowledge is available for differential expression of genes. For instance, the experimenter could be 99% sure that the fold change of a certain gene is 2 with a tolerance of 0.5 fold. Or, when the two conditions under investigation are quite different, we would like to tolerate high fold changes in general, and only small changes, when conditions are highly similar.

Our model allows to incorporate such prior information by transforming it into corresponding pseudocounts α and β (see Methods section for details).

There are a few remarks here. First, even if no pseudocounts are used, i.e. α = β = 1, a specific log₂ fold change distribution is imposed on the fold change estimator (see Figure 3A and B). Specifically, deviations of at most 10 are tolerated with a certainty of about 90%. This does not mean that larger deviations are not allowed: the more data are used for the inference, the less influence has the prior distribution. However, this plays an important role especially for entities with few reads. Second, it is possible to intentionally bias fold changes toward specific values known a-priori by using asymmetric pseudocounts and our framework provides the theoretical background for specifying the intended value as well as its tolerance. For instance, if the log₂ fold change is supposed to lie between 0 and 2 with 50% certainty, α = 3.26 and β = 1.63 must be used. And, finally, α and β may be smaller than 1 (but strictly greater than 0), corresponding to a wider prior log₂ fold change distribution than when no pseudocounts are used (see Figure 3A and B).

Figure 3.

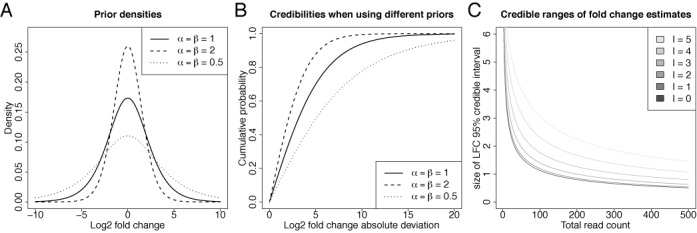
Count ratio priors and posteriors. (A) log₂ densities of beta priors for different parameters are shown. Note that the prior density for the log₂ fold change is different from the prior density of the beta proportion p. The prior without pseudocounts (α = β = 1) has most of its mass between roughly -5 and 5. Smaller or greater tolerances can be achieved by using different choices for α and β. This is especially of importance when sample data are sparse (i.e. NGS read count is small). (B) The same distributions are illustrated by their cumulative probability of absolute log₂ fold changes, i.e. for each symmetric credible interval the probability is shown. More clearly than in (A), this shows that the prior belief of a deviation of at most 5 in both directions is about 75%. If larger deviations need to be tolerated, smaller parameter values have to be chosen. (C) Size of the 95% credible interval for different observed total read counts c₁ + c₂ in two conditions. 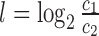is the estimated log₂ fold change, i.e. the black line corresponds to the cases where c₁ = c₂. The measurement uncertainty is high for small and unbalanced c₁, c₂ and slowly approaches 0 for larger read counts.

Sampling accuracy

An important benefit of our model is that it allows to estimate measurement uncertainty due to sampling (see Figure 3C). For instance, given the observed data, a 95% credible interval contains the true log fold change with a probability of 95%. If 50+50 reads have been observed, indicating a likely log fold change of 0, the 95% credible interval is greater than 1, indicating that the range of log fold changes that could have produced those read counts is between −0.5 and 0.5 (see Figure 3C). There are two interesting observations here. First, even for larger number of reads, the size of the credible interval approaches 0 only slowly, e.g. for 250+250 reads, the 95% interval is still greater than 0.5. And second, when the read counts are more unbalanced, the uncertainty is even greater (e.g. for 97+3 reads corresponding to a log fold change l ≈ 5, the interval spans log fold changes 3.5 to 6.5, which is a more than 8-fold difference). This clearly shows that although only considering the point estimate may be convenient, but gives only part of the truth.

Conservative noise estimation

So far we have provided evidence that this basic model is appropriate for data without PCR bias, e.g. when random barcodes are included to distinguish PCR duplicates from duplicate RNA fragments in the sample. First, the fold changes of genes between replicates are highly consistent and deviations can be explained by sampling noise (see above and Figure 2A–C). And second, the same is true for local fold changes within genes (see Figure 2D and E). However, this model should not directly be applied to standard RNA-seq data. If random barcodes are ignored in the E. coli RNA-seq data set, replicate gene fold changes are highly inconsistent, i.e. outside of their credible intervals (see Figure 4B). In addition, the quantiles from the posterior predictive distribution indicate extreme deviations and the estimated local fold change is clearly outside of the credible interval in almost all cases (see Figure 4D and E). This indicates that the basic model severely underestimates noise in the presence of PCR amplified and biased read counts.

Furthermore, when ignoring random barcodes, 599 out of 2193 genes deviate more than 2-fold from the normalization constant (see Figure 4C) as compared to 467 genes, when random barcodes are respected. This clearly shows that PCR bias does not only affect quantification within a single experiment (1,17), but also differential quantification. Importantly, as the fold change estimate of the basic model is equivalent to fold changes derived from existing approaches, this is not only a problem of the proposed basic model but also of the standard method of taking the ratio of total read counts.

The aggregation strategy in the basic model intrinsically assigns high weights to local fold changes derived from large read counts. This is an appropriate way to estimate noise, when large counts are produced by sampling, i.e. the corresponding fold changes are not heavily affected by noise and, thus, relatively stable. However, this is not reasonable, when read counts are artificially increased by PCR. Thus, the idea of the conservative version of this model is to reduce read counts.

We propose and test several ad-hoc procedures for reducing the read count in order to reduce weights of local fold changes. We either compute the logarithm (LOG) or the square root (SQRT) of the original read count, or we divide both read counts c₁ and c₂ by a constant factor, either by max(c₁, c₂) (MAX), log₂(max(c₁, c₂)) (LOGSC) or min(c₁, c₂) (MIN). MAX is the most conservative way of reducing the counts, i.e. it produces the smallest estimates of the fragment counts, and produced the best results, comparable to the estimates exploiting the barcodes(see Table 1). Note that this is different from simply collapsing multi-copy sequences to a single read, which would restrict the dynamic range of fold changes severely.

Table 1. Outlier genes for different methods.

	barcode	reads	MAX	MIN	LOGSC	LOG	SQRT
Deviating >2-fold	467	599	477	504	496	500	525
Outside 99% credible interval	18	1970	16	60	770	767	1233

Downsampling significantly affects the number of genes outside of the 99% credible interval and deviating more than 2-fold.

Evaluation

A crucial point in evaluating the performance of downsampling in estimation of fold changes is the availability of a gold standard to compare to. Quantitative real time PCR (qPCR) is often used as a targeted validation method for sequencing data, albeit issues about its accuracy have been raised recently (31). For the MAQC/SEQC projects (27,31), qPCR measurements have been performed for a large number of genes for standardized samples. Two publications report sequencing data for these two samples. In (26), the samples were sequenced in single-end mode on an Illumina Genome Analyzer II (subsequently called Bullard data set), and in (31), paired-end sequencing was used on an Illumina HiSeq 2000 (subsequently called SEQC data set). Furthermore, Bullard et al. used an older sample preparation protocol than the SEQC study. Comparing fold changes from both NGS data sets to the MAQC qPCR measurements allowed us to investigate whether downsampling is able to improve fold change estimates for NGS data measured using technology a few years old, and whether improvements are still observable for very recent and optimized sequencing techniques.

Consistent with the results from the replicate comparison above, all downsampling methods improve deviations from the qPCR reference significantly (see Figure 5). Importantly, in all cases, there are also many genes where the deviation increases slightly upon downsampling. This can be a consequence of the fact that the qPCR fold changes are in fact not a gold standard and suffer from inaccuracies as well (31). Importantly, the accuracy gain for SEQC data set are less pronounced indicating that sequencing quality may have improved in recent years. However, it is unclear, whether this is a consequence of the sequencing mode (single-end versus paired-end), the sequencing device or differences in sample preparation. Nevertheless, even for the recent data set, downsampling still leads to significantly more accurate fold changes, indicating that there is still room for improvement by computational analysis methods.

Figure 5.

Validation of downsampling. (A/C) qPCR measurements from the MAQC/SEQC project are scattered against corresponding the mRNA-seq derived fold changes (A) for the older data set (26) and (B) for the more recent data set (C). Arrows are drawn for each gene indicating the fold changes before (arrow start) and after (arrow tip) downsampling by LOGSC. Improved fold changes are indicated in blue, worse fold changes in red. Fold changes whose deviation is smaller than two-fold with and without correction are indicated in gray. (B/D) Results are summarized for all procedures. The x-axis corresponds to the absolute difference of log2 fold change upon downsampling, i.e. to the length of an arrow in (A) and (C). Plotted is the log ratio comparing the number of genes that are improved to the number of genes that are made worse by downsampling for a minimal value of absolute difference. Dots correspond to statistically significant odds ratios according to a binomial test (p < 0.01). In (B) especially for LOGSC and MAX, there are significantly more genes where downsampling leads to smaller deviations from the gold-standard than genes with larger deviation. In (D), differences between the downsampling approaches are less pronounced and odds are more modest (but still significantly in favor of improved fold changes).

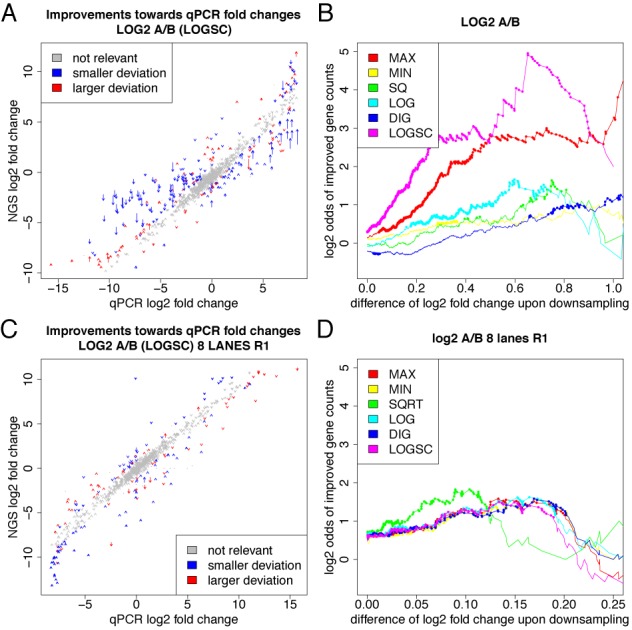
Furthermore, we tested how many genes are affected in a typical mRNA-seq experimental setting (29). Here, due to a missing reference, we cannot check whether corrected fold changes are more accurate than raw fold changes. However, we are interested in the number of genes that are called differentially expressed and affected by correction. In many cases, a set of differentially regulated genes is defined by imposing a cutoff on statistical significance and log fold change, or only on the log fold change if no or too few replicates are available (where the latter is the typical case). For default choices of this cutoff the set of differentially called genes changes by about 20%, i.e. a surprisingly large fraction of genes falls below or exceeds the cutoff due to the correction (see Figure 6). Thus, even if the correction affects fold changes only slightly, the gene sets from typical experiments may change dramatically after correction.

Figure 6.

Affected genes in a typical RNA-seq experiment. (A) In (29), the yeast transcriptome was analyzed using RNA-seq under 18 environmental conditions and here, results are shown for one possible comparison (congo red vs. DNA damage). The x-axis corresponds to absolute log₂ fold change thresholds. The y-axis shows which fraction of all genes that are above the threshold before or after correction are not above the threshold in both cases (black) and, how many genes are called differential before or after correction (gray). (B) The maximal fractions of different calls for log fold change thresholds between 1 and 3 is summarized for all 153 pairwise combinations of these 18 conditions.

Handling replicates

Replicate fold change measurements may be affected by noise (measurement uncertainty due to sampling) and potentially by bias. Here, by replicates we mean technical replicates where repeated sample preparations are sequenced from the same biological sample. Biological replicates may further be affected by natural variation between two equally treated samples.

If the count ratio model is appropriate for NGS data, log fold change credible intervals from technical replicates should overlap (potentially after downsampling has been applied). To test this, we computed the squared Hellinger distance between posterior distributions from technical replicates of the SEQC data set (Replicates a and b for samples A and B measured at BGI; see Figure 7A and B). The Hellinger distance (see Methods above) quantifies the similarity between two probability distributions and is 0 when the distributions are equal and approaches 1 when the distributions differ.

Figure 7.

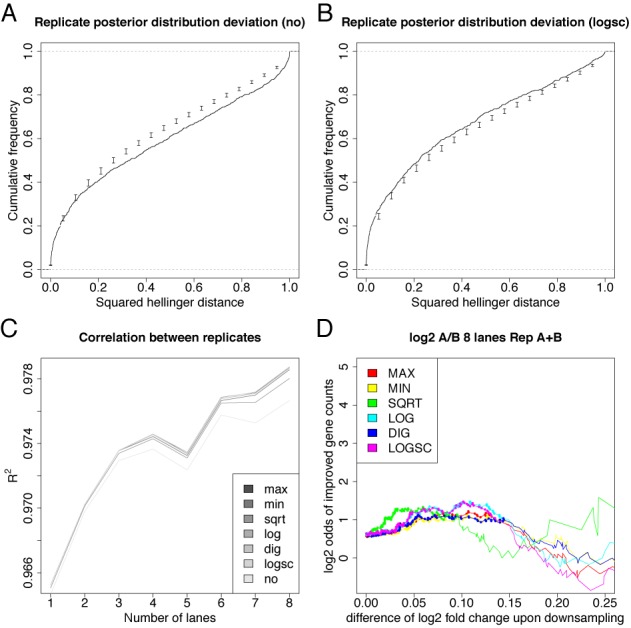
Handling replicates. (A/B) Distribution of the squared Hellinger distance for the posterior distributions of the fold change between replicates for the genes with qPCR measurement without (A) and with LOGSC downsampling (B). Candlesticks show mean ± standard deviation from 100 resampled fold change posterior distributions. Without downsampling, distances are greater than expected, which means that estimates of the credible intervals are too small. This again is evidence that bias is involved for this data set. Indeed, upon controlling bias via downsampling, credible intervals are conservative estimates of the sampling noise. (C) The correlation of replicate log fold changes for genes with qPCR measurement is improved upon downsampling. Here, the coefficient of determination R² is shown when n = 1...8 of the 8 lanes are considered (both replicates from sample A and B were measured on 8 lanes of a flow cell; thus, the number of lanes corresponds to sequencing depth). (D) Fold change estimates are improved for the average fold change computed for replicates (compare to Figure 5D).

When no downsampling is applied, the squared Hellinger distances are slightly larger than expected from a resampling approach (see Methods). Thus, credible intervals overlap less than expected from a model that only incorporates sampling, or, equivalently, credible intervals are slightly to small without downsampling. This is expected, as from the above analyses we know, that bias indeed plays a role in this data set (see Figure 5). However, when downsampling is applied, credible intervals overlap more often than expected, which means that they are a conservative estimate of the range of fold changes with a (in a Bayesian sense) high degree of belief and that the count ratio model with downsampling is appropriate for this data set.

Moreover, as indicated above, when multiple replicates are available, the experimenter may be interested in an average fold change. This can be estimated by pooling all reads before analysis. However, subjecting the pool of all replicates for the same condition to downsampling is not reasonable, as downsampling is supposed to remove PCR duplicates and two reads from distinct replicates may not be the result of the same amplified RNA fragment. Thus, we downsample each replicate separately and sum up downsampled read counts per replicate. Interestingly, this mode of downsampling improves the overall correlation between replicate fold changes (see Figure 7C). Furthermore, the average fold change is improved to a similar extend as for a single replicate upon downsampling (see Figure 7D).

Bayesian modeling suggests a normalization procedure

Due to different sequencing depths, normalization between experiments is necessary. The underlying principle of most normalization procedures is the assumption that either all or some specific genes are not changed on average. Often, a normalization factor is used to transform all fold changes such that they fulfill this assumption. Effectively, in DESeq (24), the median log₂ fold change of all genes is subtracted from all log₂ fold changes, i.e. after normalization, half of all genes appear downregulated, the other half upregulated.

We can extend our computation of gene fold changes to a genome fold change which can be used as a normalization constant. Given the local read counts c_{g, i, j}, with g = 1...G corresponding to all genes, i = 1...N_g denoting the N_g positions in gene g and j = 1, 2 denoting the two experiments, the maximum likelihood estimator of the genome fold change is

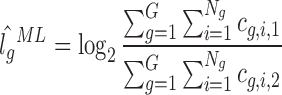(18)

This is equivalent to normalization by RPKM/FPKM. However, as before, this is only reasonable when read counts are not distorted by PCR amplification, i.e. when random barcodes have been used or bias has been reduced by proper downsampling procedures. Indeed, both possibilities, random barcodes and downsampled reads, result in similar normalization constants (see Figure 8A) that perform very well for the whole range of expression in the E. coli experiment (see Figure 8B). Surprisingly, when applied to random barcode data, the robust normalization constant estimate of DESeq appears to be questionable especially for medium to highly expressed genes (e.g. about 70% of all genes with total read count over 50 appear to be upregulated in replicate A; see Figure 8B). Moreover, when the normalization constant is estimated without random barcodes by DESeq (as in a normal RNA-seq experiment), the number of upregulated genes increases even further (see Figure 8B). Overall, for this data set, estimates based on the median of all log₂ fold changes appear to be implausible and would imply questionable conclusions on differentially regulated genes.

Figure 8.

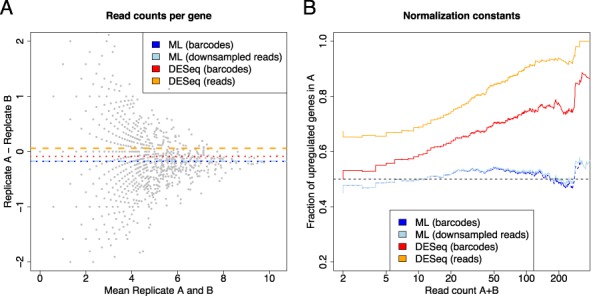
Evaluation of normalization procedures. (A) The four normalization constants correspond to horizontal lines in the MA plot of the observed (random barcode corrected) count data. Constants are either computed using the maximum likelihood estimate from random barcode corrected data (ML barcodes) or from MAX-downsampled read count data (ML downsampled reads), or by using DESeq applied to random barcode corrected (DESeq barcodes) or uncorrected data (DESeq reads). Both ML estimates are almost equal and different from DESeq estimates. Moreover, in contrast to the DESeq estimates, the ML estimates appear to lie in the middle of the points. This trend is more clear in (B), where the fraction of genes that appear upregulated in replicate A is shown for all minimal total expression thresholds. The median-based procedure of DESeq only leads to a 50%-50% ratio for the complete set of genes, but, for instance, about 70% of all genes with total read count of more than 50 appear to be upregulated. In contrast, the ML-based normalization factors behave very well over the whole range of expression thresholds.

DISCUSSION

The standard way of computing fold changes from quantitative NGS data is to compute the ratio of the number of all reads belonging to a certain biological object in condition A and the number of all reads belonging to the same object in condition B. As introduced above, this total fold change is a weighted average of local fold changes, where positions with many reads contribute more to the total fold change than positions with few reads.

Using RNA-seq data where PCR duplicates can be detected using a special experimental setup, we have shown that these weights are only reasonable when no bias is involved in local read counts and that read count bias does not generally cancel out when fold changes are computed. This unexpected result stems from the fact that read counts are aggregated for larger biological objects such as mRNAs, which leads to the fact, that linear bias of read counts is not linear for the larger objects. One way to deal with bias is to develop models that try to predict read count bias based on the observed read sequences. However, such methods suffer from several drawbacks. First, sequencing is a multistep protocol, and each step may introduce some sort of bias into the measurements that might still be unknown. Second, even if the source of bias is known, the biochemical processes behind it are highly complex and existing models gross oversimplifications. Third, even if those models were appropriate, incomplete observations could complicate bias predictions, as only prefixes (for single-end sequencing) or prefixes and suffixes (for paired-end sequencing) of the RNA molecules are usually observed in NGS.

Therefore, we take a different route in the differential analysis of NGS data, which exploits the linearity assumption for bias acting on read counts and avoids the nonlinearity for bias acting on larger biological objects. Instead of first aggregating reads per biological entity for each sample and then computing ratios, we first compute all read count ratios and aggregate them to a total fold change. We have demonstrated that both workflows are equivalent when our proposed basic noise model is used. This means that taking the other route does not cancel out bias for free. If read counts are indeed biased, the basic model will underestimate noise. However, we have also shown that the basic model allows for straight-forward extensions to estimate noise in a more conservative manner, leading to more accurate fold change estimates as established for the MAQC data set.

The proposed extensions are downsampling techniques that effectively reduce read counts proportionally. Instead of giving high-copy number reads high weights for the total fold change, all local fold changes are weighted similarly. Thus, our estimation draws its power from the large number of positions instead of the large number of reads. This is superior whenever amplification and not high-copy number fragments before amplification are the cause for large read counts. And indeed, based on the random barcode data and on the MAQC data, amplification appears to be the main cause for large read counts. However, depending on the extent of amplification bias in a specific data set, preserving at least the order of magnitude of two local read counts (e.g. by using the LOGSC procedure) may lead to more accurate fold change estimates.

Our method does not only provide accurate fold changes, but it computes the full posterior distribution of (log) fold changes. Thus, if either the measurements are unbiased by the experimental design (e.g. by random barcodes), or by applying the proposed downsampling procedures, our model is able to compute reliable credible intervals for fold changes. However, we note that biological relevance of fold changes must be determined by other methods. Biological relevance is often measured by a P-value testing the null hypothesis that some treatment between conditions does not have an effect on a certain mRNA. Checking whether the log fold change 0 is outside of some credible interval does not test biological relevance, as here the null hypothesis only is that the two samples have the exact same copy number of mRNA. To find genes that are indeed affected by a treatment, biological replicates and an appropriate test are necessary, preferably respecting the estimated log fold change intervals (Erhard & Zimmer, manuscript in preparation). Thus, the methods proposed here are especially appropriate for technical replicates, as the noise and bias involved therein is effectively handled. Our methods can nevertheless be applied to biological replicates, e.g. to estimate the effect size of a treatment or the average fold change, but not to estimate biological relevance of treatments.

For all experiments, with or without replicates, proper normalization of samples is an important issue. When the total number of reads is used for normalization, as for RPKM/FPKM, a few high-count and differentially expressed genes may have great influence on the fold change. To avoid this bias, a robust normalization factor as in DESeq is often used. However, we have shown that incorporating many low-count genes may also lead to unrealistic normalization. Thus, we propose to return to the original idea of RPKM/FPKM and either use random barcodes in the experiments or downsampling procedures to overcome the problem of the strong influence of high-count genes. Depending on the experiment, however, it may be necessary to exclude differentially expressed genes from the computation of the normalization constant (32).

mRNA-seq is arguably the most often and widely applied quantitative NGS technique. An important aspect in differential mRNA-seq analysis, which has not been investigated here, is differential splicing, i.e. the differential usage of alternative isoforms of genes between conditions. Visually, such genes can easily be analyzed by plotting local fold changes with credible intervals as in Figure 2D. For example, if the usage of an exon is differential, all local fold changes belonging to it should be distinct from local fold changes from other exons and credible intervals should not overlap. However, to detect differential isoform usage in an automated manner demands further work and evaluation.

CONCLUSION

We demonstrated that bias significantly affects computed fold changes for NGS experiments and proposed a method to remove such bias. We proposed a novel approach to estimate fold changes from NGS data that is based on the aggregation of many local fold changes instead of computing the fold change of aggregated read counts. We used our method to compare RNA-seq derived fold changes to qPCR derived fold changes from the MAQC project (26,27) and to analyze RNA-seq data where random barcodes have been incorporated to control PCR amplification bias. These analyses provided evidence that our method significantly improves estimates of fold changes. Furthermore, by analyzing additional RNA-seq data sets, we show that bias affects about 20% of genes that are called differentially expressed in a typical RNA-seq setting. Finally, our method can also be used to derive credible intervals and to incorporate prior knowledge for fold changes. It can be applied to standard RNA-seq data as an alternative to state-of-the-art methods for fold changes and normalization.

FUNDING

This work was supported by the DFG collaborative research centers SFB 1035 (Conformational switches) and SFB 1123 (Atherosclerosis). Furthermore, the work was supported by the Bavarian Research Network of Molecular Biosystems (BioSysnet).

Conflict of interest statement. None declared.